Evaluation of the Shear Modulus Degradation by a Modified Hyperbolic Function for Unconventional Geomaterials
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of Investigated Geomaterials
2.2. Description of Resonant-Column Apparatus
2.3. Testing Procedures and Experimental Program
3. Analysis of Results and Discussion
3.1. Shear Modulus Degradation
3.2. Proposed Function
4. Conclusions and Outlook
- The CSS and HDS geomaterials are predominantly granular, with a high content of non-plastic fines, while the CL material is classified as low-plasticity clay based on consistency limits and plasticity chart positioning. The presence of heavy minerals resulted in unusually high specific gravities for all three materials, deviating from standard reference values.
- Despite the non-plastic nature of the fines in CSS (32%) and HDS (48%), their content significantly influenced the shear modulus (G) as a function of confining stress (). Under the same conditions of and angular strain (), the G values for HDS were nearly twice those of CSS, despite both being granular materials originating from the same mining process.
- The dynamic stiffness modulus (G) exhibited a substantial reduction with decreasing confining stress (), reinforcing its dependency on stress conditions. The variation of G as a function of angular strain () for different followed a clear trend, which follows a hyperbolic function. Moreover, the maximum shear modulus () varied with following a power–law relationship, with high correlation coefficients ().
- The inverse of G (i.e., ) demonstrated a linear variation with angular strain () for different effective confining stresses (), also exhibiting correlation coefficients () close to unity. However, the inverse of the reference strain parameter () from the Hardin and Drnevich model varied with effective according to a power–law trend, with correlation coefficients () between 0.84 and 0.99.
- A new simplified mathematical model is proposed to evaluate G based solely on angular strain (), effective confining stress (), and four empirical constants. This model allows for the determination of G with a low amount of tests by using three torsional excitations and various , requiring only nine tests.
- To enhance practicality in numerical simulations and simplify the application of complex formulations, this research introduces a generalisation of the hyperbolic model. This novel formulation depends on only two factors and four empirical constants, making it adaptable for a wide range of soil types with minimal testing requirements.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vucetic, M. Cyclic Threshold angular strains in Soils. J. Geotech. Eng. 1994, 120, 2208–2228. [Google Scholar] [CrossRef]
- Oztoprak, S.; Bolton, M.D. Stiffness of sands through a laboratory test database. Géotechnique 2013, 63, 54–70. [Google Scholar] [CrossRef]
- del Pilar Ortiz-Pulido, M.; Gaitán-Serrano, J.F.; Camacho-Tauta, J. Modelo unificado de curvas de degradación del módulo cortante en arenas del río Guayuriba. DYNA 2014, 81, 77–84. [Google Scholar]
- Ishihara, K. Soil Behaviour in Earthquake Geotechnics, 1st ed.; Clarendon Press: Oxford, UK, 1996. [Google Scholar]
- Kramer, S.L. Geotechnical Earthquake Engineering, 1st ed.; Pretince Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Arnold, C.; Macedo, J. A novel experimental database on the cyclic response of mine tailings. Earthq. Spectra 2024, 40, 828–846. [Google Scholar] [CrossRef]
- Santamarina, J.C.; Torres-Cruz, L.A.; Bachus, R.C. Why coal ash and tailings dam disasters occur. Science 2019, 364, 526–528. [Google Scholar] [CrossRef]
- Ubilla, J.; Sáez, E. Numerical Analysis of Radiation Damping in Tailings Dams. J. Earthq. Eng. 2024, 29, 589–609. [Google Scholar] [CrossRef]
- ASTM D4015; Standard Test Methods for Modulus and Damping of Soils by Resonant-Column. ASTM International: West Conshohocken, PA, USA, 2021.
- Davidenkov, N.N. On energy dissipation upon vibrations. Zh. Tekh. Fiz. 1938, 8, 483–499. [Google Scholar]
- Kondner, R.L. Hyperbolic Stress-Strain Response: Cohesive Soils. J. Soil Mech. Found. Div. 1963, 89, 115–143. [Google Scholar] [CrossRef]
- Hardin, B.O.; Black, W.L. Vibration Modulus of Normally Consolidated Clay. Soil Mech. Found. Div. 1968, 94, 353–370. [Google Scholar] [CrossRef]
- Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: Design equations and curves. Soil Mech. Found. Div. 1972, 98, 667–692. [Google Scholar] [CrossRef]
- Iwasaki, T.; Tatsuoka, F.; Takagi, Y. Shear Moduli of Sands under Cyclic Torsional Shear Loading. Soil Found. 1978, 18, 39–56. [Google Scholar] [CrossRef]
- Kokusho, T. Cyclic Triaxial Test of Dynamic Soil Properties for Wide Strain Range. Soil Found. 1980, 20, 45–60. [Google Scholar] [CrossRef]
- Ishibashi, I.; Zhang, X. Unified dynamic shear moduli and damping patios of sand and clay. Soil Found. 1993, 33, 182–191. [Google Scholar] [CrossRef]
- Wichtmann, T.; Triantafyllidis, T. Influence of the Grain-Size Distribution Curve of Quartz Sand on the Small Strain Shear Modulus Gmax. J. Geotech. Geoenviron. Eng. 2009, 135, 14041418. [Google Scholar] [CrossRef]
- Patiño, H.; Martínez, E.; Galindo, R. Dynamic Behavior of a Granular Medium Subjected to Resonant Column Tests: Application to Ottawa Sand. Geotech. Test. J. 2020, 43, 14041418. [Google Scholar] [CrossRef]
- Wichtmann, T.; Triantafyllidis, T. Effect of Uniformity Coefficient on G/Gmax and Damping Ratio of Uniform to Well-Graded Quartz Sands. J. Geotech. Geoenviron. Eng. 2013, 139, 59–72. [Google Scholar] [CrossRef]
- Payan, M.; Khoshghalb, A.; Senetakis, K.; Khalili, N. Effect of particle shape and validity of Gmax models for sand: A critical review and a new expression. Comput. Geotech. 2016, 72, 28–41. [Google Scholar] [CrossRef]
- Molina-Gómez, F.; Viana da Fonseca, A.; Ferreira, C.; Camacho-Tauta, J. Dynamic properties of two historically liquefiable sands in the Lisbon area. Soil Dyn. Earthq. Eng. 2020, 132, 106101. [Google Scholar] [CrossRef]
- Sarkar, D.; Goudarzy, M.; Wichtmann, T. Influence of particle size on the small-strain stiffness in granular soils: Experimental observations and micromechanical interpretation. Géotechnique 2024, 74, 920–934. [Google Scholar] [CrossRef]
- Patiño, H.; Molina-Gómez, F.; Galindo, R.; Viana da Fonseca, A. Stiffness Degradation of Non-Plastic Copper Ore Tailings. Géotechnique Lett. 2025, in press. [Google Scholar] [CrossRef]
- Palomero, F.G. Rio Tinto deposits—Geology and geological models for their exploration and ore-reserve evaluation. In Sulphide Deposits—Their Origin and Processing; Gray, P.M.J., Bowyer, G.J., Castle, J.F., Vaughan, D.J., Warner, N.A., Eds.; Springer: Dordrecht, Germany, 1990. [Google Scholar]
- Patiño, H.; Molina-Gómez, F.; Galindo, R.; Viana da Fonseca, A. Integrated evaluation of stiffness degradation by combining Resonant-Column, Cyclic Triaxial and Cyclic Simple Shear Tests: Application to Riotinto mine tailings. Geomech. Energy Environ. 2025, 41, 100652. [Google Scholar] [CrossRef]
- Ciancimino, A.; Cosentini, R.M.; Foti, S.; Lanzo, G.; Pagliaroli, A.; Pallara, O. The PoliTO–UniRoma1 database of cyclic and dynamic laboratory tests: Assessment of empirical predictive models. Bull. Earthq. Eng. 2023, 21, 2569–2601. [Google Scholar] [CrossRef]
- Li, X.S.; Yang, W.L.; Shen, C.K.; Wang, W.C. Energy-Injecting Virtual Mass Resonant Column System. J. Geotech. Geoenviron. Eng. 1998, 124, 428–438. [Google Scholar] [CrossRef]
- Camacho-Tauta, J.F.; Reyes-Ortiz, O.J.; Jiménez Álvarez, J.D. Comparison between resonant-column and bender element tests on three types of soils. DYNA 2013, 80, 163–172. [Google Scholar]
- Cha, M.; Santamarina, J.C.; Kim, H.-S.; Cho, G.-C. Small-Strain Stiffness, Shear-Wave Velocity, and Soil Compressibility. J. Geotech. Geoenviron. Eng. 2014, 140, 06014011. [Google Scholar] [CrossRef]
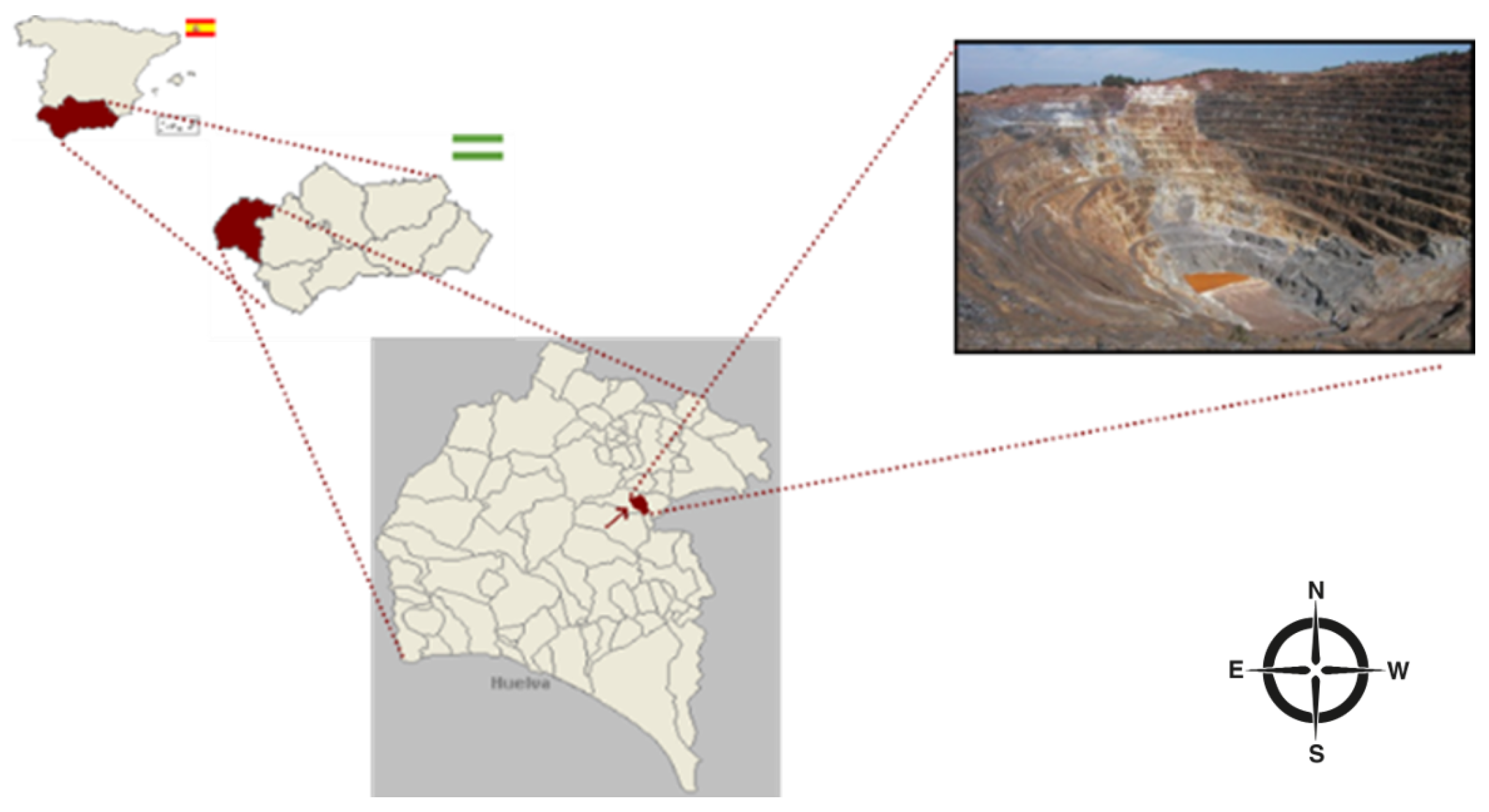

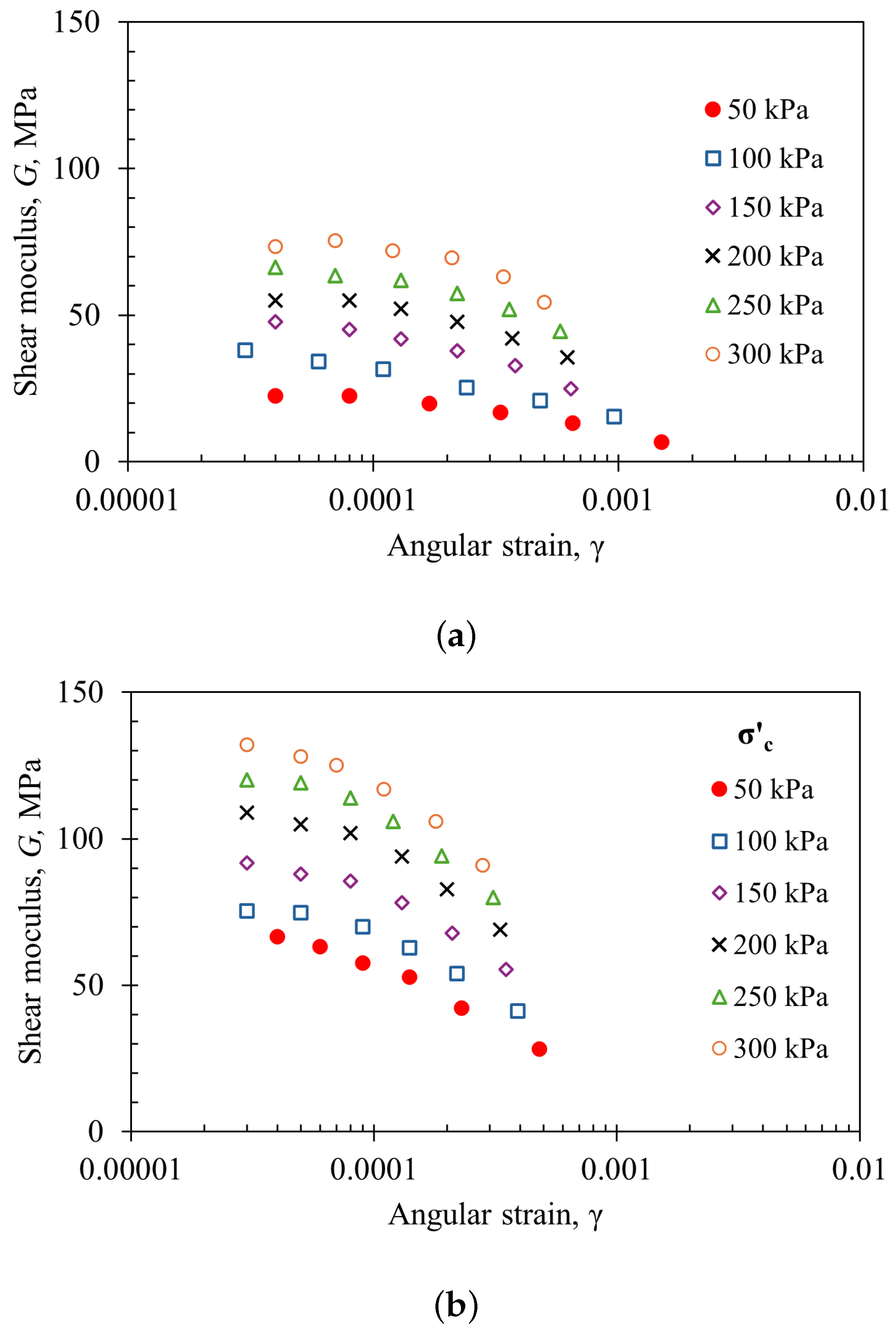
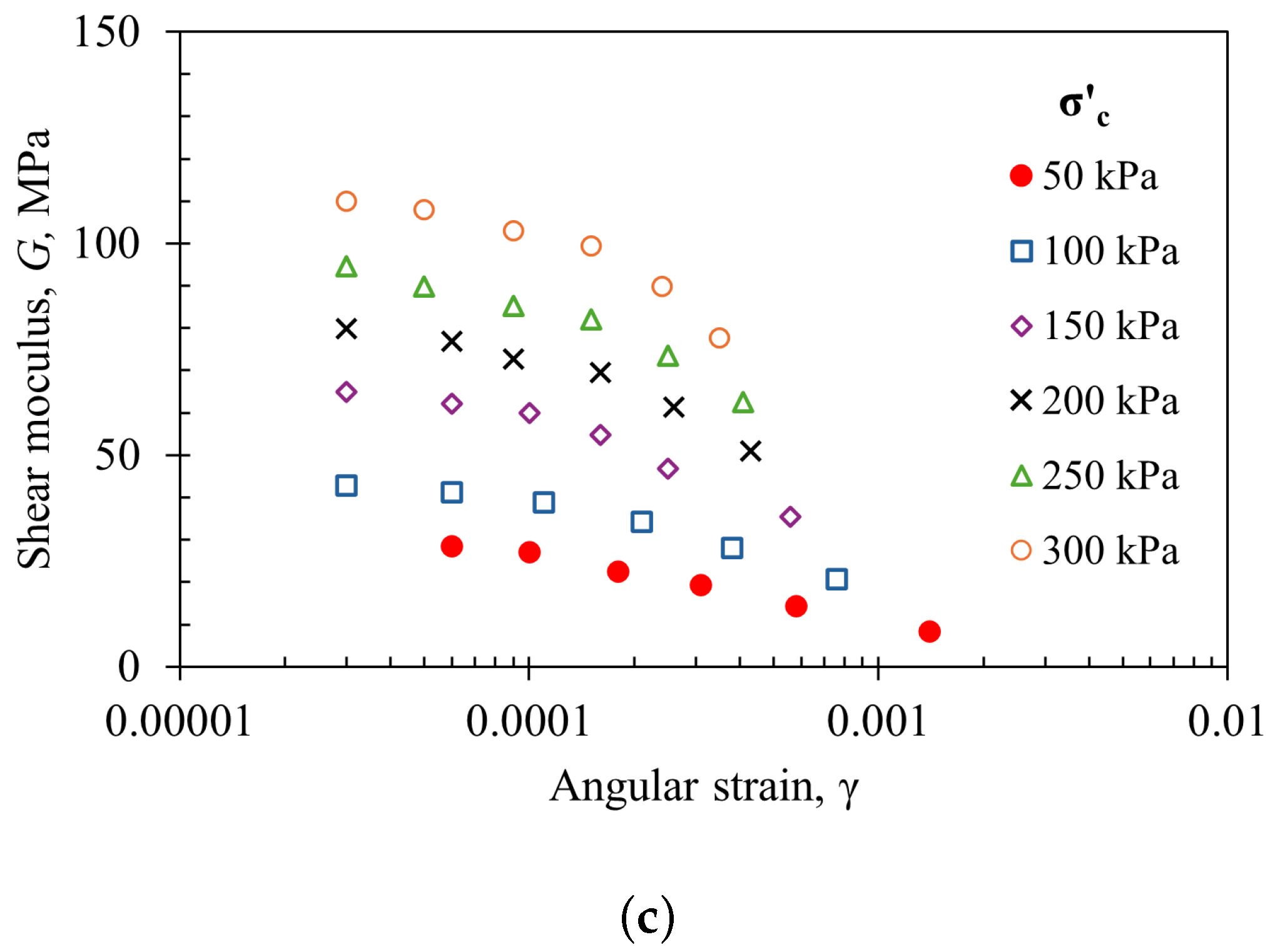
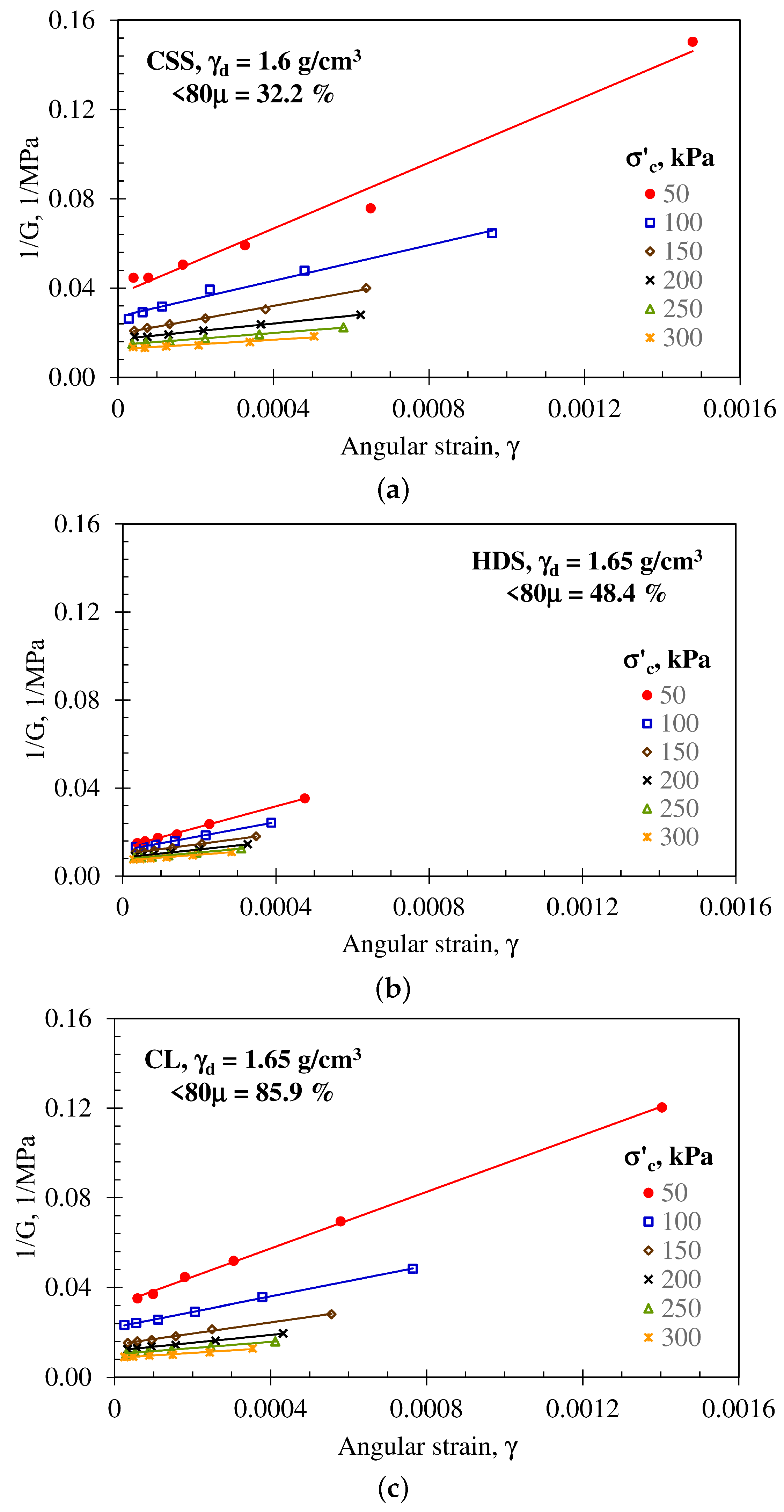
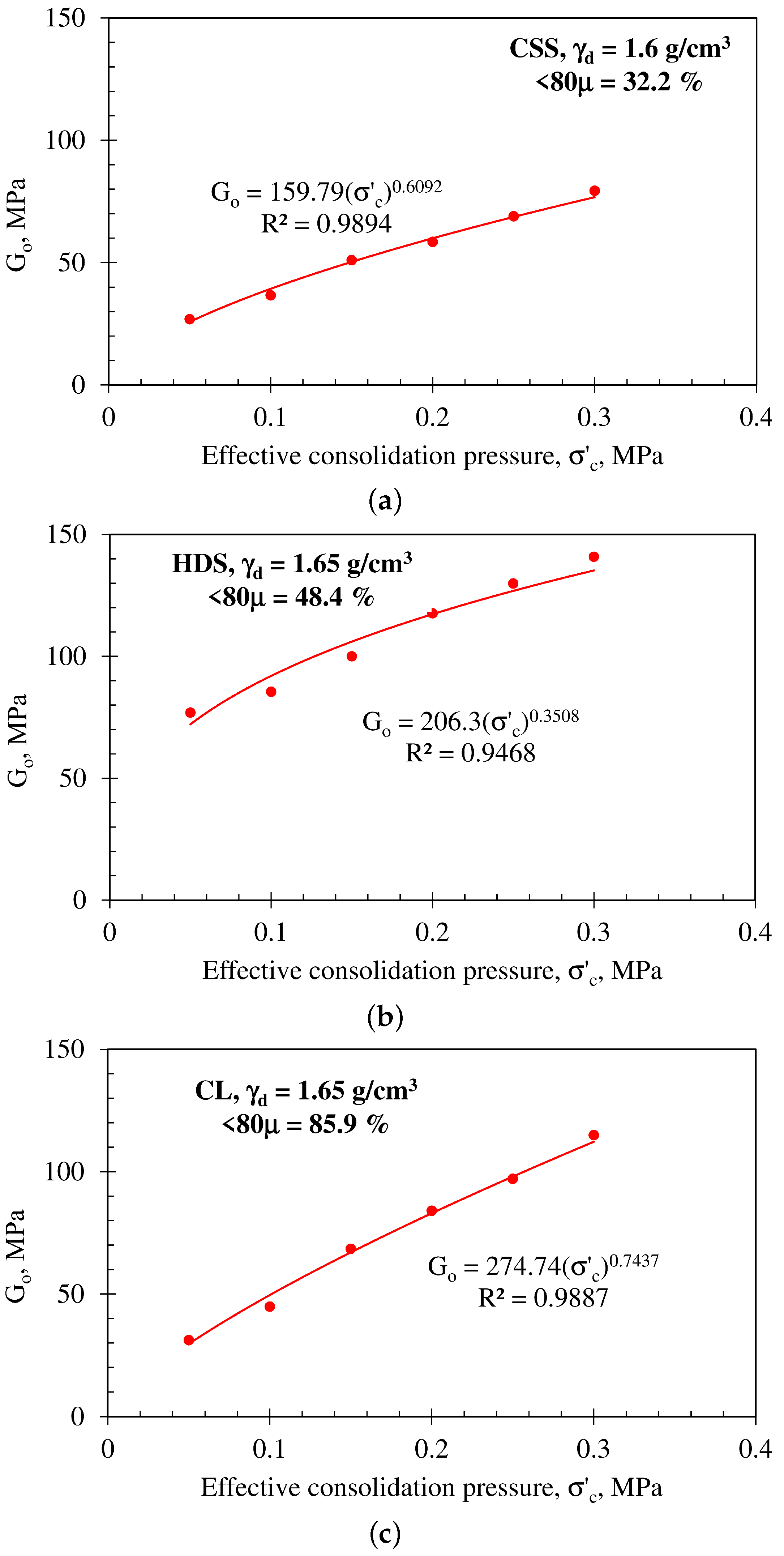

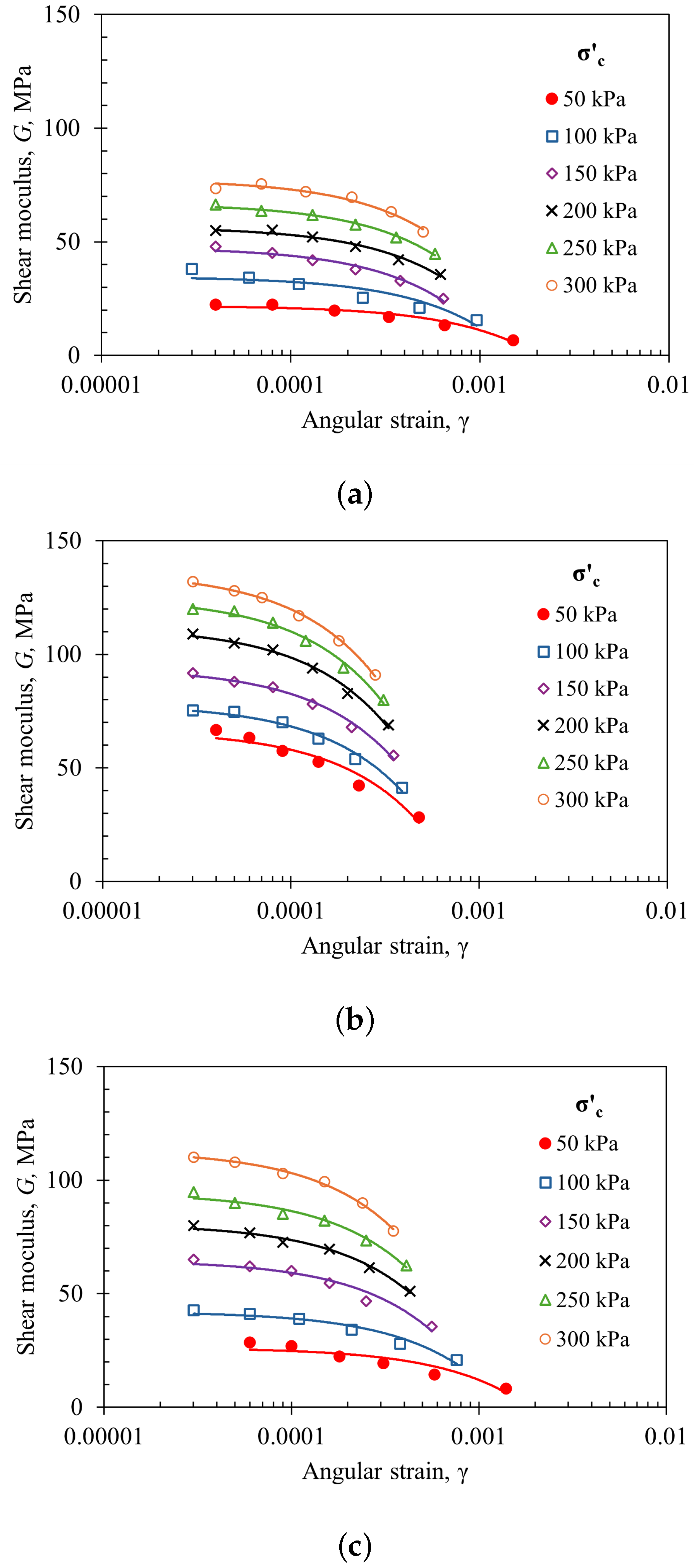
| Material | (%) | FC (%) | LL (%) | PL (%) | PI (%) | () | () |
|---|---|---|---|---|---|---|---|
| CSS | 8.1 | 32.7 | - | - | - | 3.02 | 1.60 |
| HDS | 14.3 | 48.5 | - | - | - | 2.99 | 1.65 |
| CL | 38.5 | 85.9 | 26.9 | 19.9 | 7 | 2.83 | 1.65 |
| Mineral | CSS | HDS | CL |
|---|---|---|---|
| Quartz (%) | 92 | 82 | 23 |
| Phyllosilicates (%) | 8 | 6 | 67 |
| Metallic minerals (%) | 0 | 12 | 0 |
| Constituents | HDS (%) | CSS (%) | CL (%) |
|---|---|---|---|
| 1.03 | 5.94 | 6.49 | |
| CaO | 0.04 | 0.47 | 0.25 |
| 13.06 | 10.41 | 15.78 | |
| O | 0.12 | 1.74 | 0.49 |
| MgO | 0.01 | 0.29 | 2.97 |
| O | 0.03 | 0.15 | 0.11 |
| 0.04 | 0.07 | 0.053 | |
| 19.48 | 4.71 | 0.04 | |
| 53.43 | 66.42 | 13.45 | |
| 0.09 | 0.29 | 51.97 | |
| Loss of ignition | 12.67 | 9.51 | 7.80 |
| Conditions | CSS | HDS | CL | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (kPa) | (V) | (Hz) | (m/s) | (MPa) | (Hz) | (m/s) | (MPa) | (Hz) | (m/s) | (MPa) | |||
| 50 | 0.025 | 50 | 114 | 22.4 | 0.00004 | 87 | 194 | 66.6 | 0.00004 | 55 | 117 | 28.5 | 0.00006 |
| 50 | 0.05 | 50 | 114 | 22.4 | 0.00008 | 85 | 189 | 63.2 | 0.00006 | 53 | 114 | 27 | 0.00010 |
| 50 | 0.1 | 47 | 107 | 19.8 | 0.00017 | 81 | 180 | 57.5 | 0.00009 | 49 | 104 | 22.4 | 0.00018 |
| 50 | 0.2 | 43 | 99 | 16.9 | 0.00033 | 78 | 173 | 52.7 | 0.00014 | 45 | 97 | 19.3 | 0.00031 |
| 50 | 0.4 | 38 | 87 | 13.2 | 0.00065 | 69 | 155 | 42.2 | 0.00023 | 39 | 83 | 14.4 | 0.00058 |
| 50 | 0.8 | 27 | 62 | 6.7 | 0.00150 | 57 | 127 | 28.3 | 0.00048 | 30 | 63 | 8.3 | 0.00140 |
| 100 | 0.025 | 65 | 148 | 38.1 | 0.00003 | 91 | 206 | 75.3 | 0.00003 | 67 | 144 | 42.8 | 0.00003 |
| 100 | 0.05 | 61 | 141 | 34.3 | 0.00006 | 91 | 205 | 74.7 | 0.00005 | 66 | 141 | 41.2 | 0.00006 |
| 100 | 0.1 | 59 | 135 | 31.5 | 0.00011 | 88 | 199 | 70 | 0.00009 | 64 | 137 | 38.9 | 0.00011 |
| 100 | 0.2 | 53 | 121 | 25.4 | 0.00024 | 84 | 188 | 62.8 | 0.00014 | 60 | 128 | 34.2 | 0.00021 |
| 100 | 0.4 | 48 | 110 | 20.9 | 0.00048 | 77 | 174 | 53.9 | 0.00022 | 54 | 116 | 28 | 0.00038 |
| 100 | 0.8 | 41 | 95 | 15.5 | 0.00096 | 68 | 152 | 41.2 | 0.00039 | 47 | 100 | 20.7 | 0.00076 |
| 150 | 0.025 | 72 | 166 | 47.8 | 0.00004 | 100 | 227 | 91.8 | 0.00003 | 83 | 177 | 65 | 0.00003 |
| 150 | 0.05 | 70 | 161 | 45.1 | 0.00008 | 98 | 222 | 87.9 | 0.00005 | 81 | 173 | 62.1 | 0.00006 |
| 150 | 0.1 | 67 | 155 | 41.9 | 0.00013 | 97 | 219 | 85.6 | 0.00008 | 80 | 170 | 60 | 0.00010 |
| 150 | 0.2 | 64 | 148 | 37.8 | 0.00022 | 92 | 210 | 78.2 | 0.00013 | 76 | 163 | 54.7 | 0.00016 |
| 150 | 0.4 | 60 | 138 | 32.8 | 0.00038 | 86 | 195 | 67.8 | 0.00021 | 70 | 150 | 46.7 | 0.00025 |
| 150 | 0.8 | 52 | 120 | 25 | 0.00064 | 78 | 176 | 55.4 | 0.00035 | 61 | 131 | 35.5 | 0.00056 |
| 200 | 0.025 | 77 | 178 | 55 | 0.00004 | 108 | 247 | 109 | 0.00003 | 92 | 197 | 79.9 | 0.00003 |
| 200 | 0.05 | 77 | 178 | 55.1 | 0.00008 | 106 | 243 | 105 | 0.00005 | 90 | 193 | 76.8 | 0.00006 |
| 200 | 0.1 | 75 | 173 | 52.1 | 0.00013 | 105 | 240 | 102 | 0.00008 | 88 | 188 | 72.7 | 0.00009 |
| 200 | 0.2 | 72 | 166 | 47.8 | 0.00022 | 100 | 230 | 94 | 0.00013 | 86 | 184 | 69.6 | 0.00016 |
| 200 | 0.4 | 67 | 156 | 42.1 | 0.00037 | 94 | 215 | 82.7 | 0.00020 | 81 | 173 | 61.4 | 0.00026 |
| 200 | 0.8 | 62 | 143 | 35.7 | 0.00062 | 86 | 197 | 68.9 | 0.00033 | 74 | 157 | 51 | 0.00043 |
| 250 | 0.025 | 84 | 196 | 66.4 | 0.00004 | 113 | 259 | 120 | 0.00003 | 100 | 214 | 94.7 | 0.00003 |
| 250 | 0.05 | 82 | 191 | 63.5 | 0.00007 | 112 | 258 | 119 | 0.00005 | 97 | 209 | 89.9 | 0.00005 |
| 250 | 0.1 | 81 | 189 | 61.8 | 0.00013 | 110 | 253 | 114 | 0.00008 | 95 | 203 | 85.2 | 0.00009 |
| 250 | 0.2 | 78 | 182 | 57.5 | 0.00022 | 106 | 243 | 106 | 0.00012 | 93 | 199 | 82.1 | 0.00015 |
| 250 | 0.4 | 75 | 173 | 52 | 0.00036 | 100 | 230 | 94.1 | 0.00019 | 88 | 189 | 73.5 | 0.00025 |
| 250 | 0.8 | 69 | 160 | 44.6 | 0.00058 | 92 | 212 | 79.9 | 0.00031 | 81 | 174 | 62.5 | 0.00041 |
| 300 | 0.025 | 88 | 206 | 73.5 | 0.00004 | 118 | 272 | 132 | 0.00003 | 108 | 231 | 110 | 0.00003 |
| 300 | 0.05 | 90 | 209 | 75.5 | 0.00007 | 117 | 268 | 128 | 0.00005 | 107 | 229 | 108 | 0.00005 |
| 300 | 0.1 | 88 | 204 | 72 | 0.00012 | 115 | 265 | 125 | 0.00007 | 104 | 223 | 103 | 0.00009 |
| 300 | 0.2 | 86 | 200 | 69.6 | 0.00021 | 112 | 256 | 117 | 0.00011 | 102 | 219 | 99.4 | 0.00015 |
| 300 | 0.4 | 82 | 191 | 63.2 | 0.00034 | 106 | 244 | 106 | 0.00018 | 97 | 209 | 89.9 | 0.00024 |
| 300 | 0.8 | 76 | 177 | 54.4 | 0.00050 | 98 | 226 | 91 | 0.00028 | 90 | 194 | 77.7 | 0.00035 |
| (MPa) | () | ( - ) | (MPa) | |
|---|---|---|---|---|
| CCS | ||||
| 0.05 | 73.702 | 2296 | 31.15 | 0.98 |
| 0.10 | 40.008 | 1465.5 | 36.63 | 0.99 |
| 0.15 | 31.223 | 1593 | 51.02 | 0.99 |
| 0.20 | 17.586 | 1028.4 | 58.48 | 0.99 |
| 0.25 | 13.343 | 920.2 | 68.97 | 0.99 |
| 0.30 | 10.562 | 838.3 | 79.37 | 0.95 |
| HDS | ||||
| 0.05 | 46.833 | 3602.5 | 76.92 | 0.99 |
| 0.10 | 31.945 | 2730.3 | 85.47 | 0.99 |
| 0.15 | 22.949 | 2294.9 | 100 | 0.99 |
| 0.20 | 18.285 | 2151.2 | 117.65 | 0.99 |
| 0.25 | 15.411 | 2001.4 | 129.87 | 0.99 |
| 0.30 | 13.261 | 1867.7 | 140.85 | 0.99 |
| CL | ||||
| 0.05 | 63.235 | 1969.9 | 31.15 | 0.99 |
| 0.10 | 34.177 | 1532.6 | 44.84 | 0.99 |
| 0.15 | 24.765 | 1696.2 | 68.49 | 0.99 |
| 0.20 | 17.471 | 1468.2 | 84.03 | 0.99 |
| 0.25 | 13.699 | 1330 | 97.09 | 0.99 |
| 0.30 | 11.16 | 1282.8 | 114.94 | 0.98 |
| Tailings | A | B | C | D |
|---|---|---|---|---|
| CSS | 159.79 | 0.61 | 496.39 | −0.48 |
| HDS | 206.3 | 0.35 | 1194.50 | −0.36 |
| CL | 274.74 | 0.74 | 1006.60 | −0.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patiño, H.; Molina-Gómez, F.; Galindo-Aires, R.Á. Evaluation of the Shear Modulus Degradation by a Modified Hyperbolic Function for Unconventional Geomaterials. Geosciences 2025, 15, 176. https://doi.org/10.3390/geosciences15050176
Patiño H, Molina-Gómez F, Galindo-Aires RÁ. Evaluation of the Shear Modulus Degradation by a Modified Hyperbolic Function for Unconventional Geomaterials. Geosciences. 2025; 15(5):176. https://doi.org/10.3390/geosciences15050176
Chicago/Turabian StylePatiño, Hernán, Fausto Molina-Gómez, and Rubén Ángel Galindo-Aires. 2025. "Evaluation of the Shear Modulus Degradation by a Modified Hyperbolic Function for Unconventional Geomaterials" Geosciences 15, no. 5: 176. https://doi.org/10.3390/geosciences15050176
APA StylePatiño, H., Molina-Gómez, F., & Galindo-Aires, R. Á. (2025). Evaluation of the Shear Modulus Degradation by a Modified Hyperbolic Function for Unconventional Geomaterials. Geosciences, 15(5), 176. https://doi.org/10.3390/geosciences15050176







