Review of Correlations Between Soil Electrical Resistivity and Geotechnical Properties
Abstract
1. Introduction
1.1. Background and Significance
1.2. Objectives and Scope of the Study
- Develop predictive models linking resistivity with geotechnical parameters such as moisture content, plasticity index, unit weight, dry density, bulk density, and clay content;
- Assess the influence of each parameter on resistivity behavior using both statistical and machine learning techniques;
- Compare model performance across different soil types and stratified conditions to identify patterns in resistivity variation;
- Enhance the interpretability of resistivity data to support non-invasive soil assessment in geotechnical engineering practice.
1.3. Structure of the Paper
2. Fundamentals of Electrical Resistivity in Soils
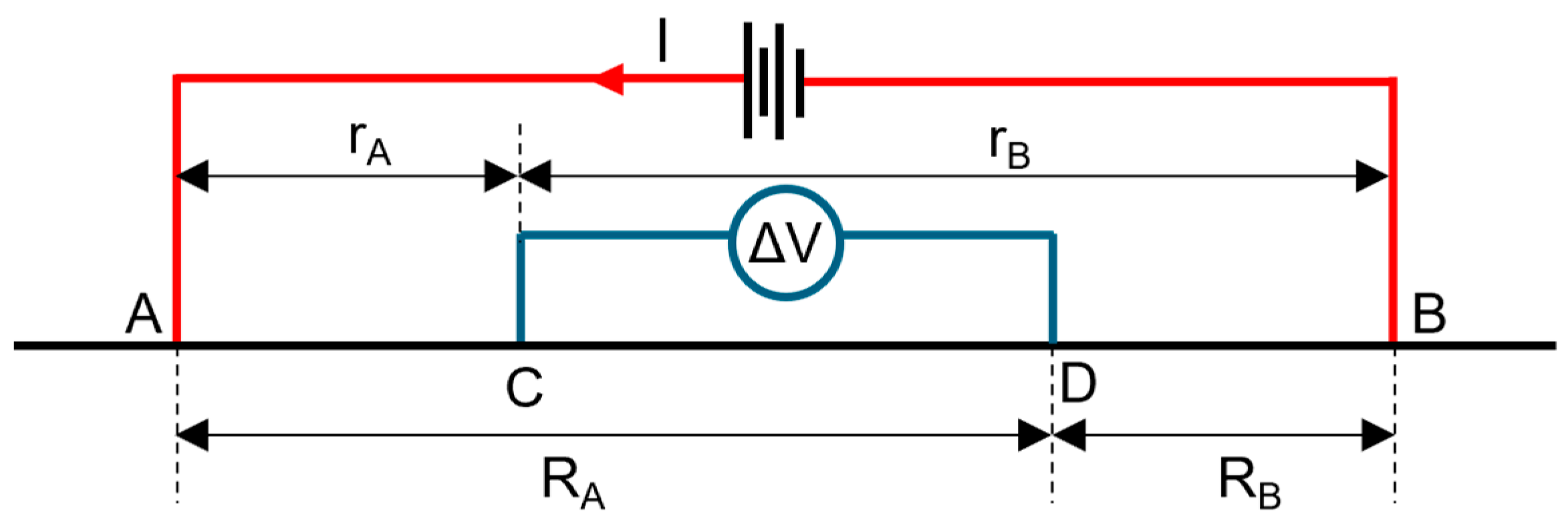
Principles of Electrical Resistivity
3. Correlation Analysis
3.1. Regression Analysis
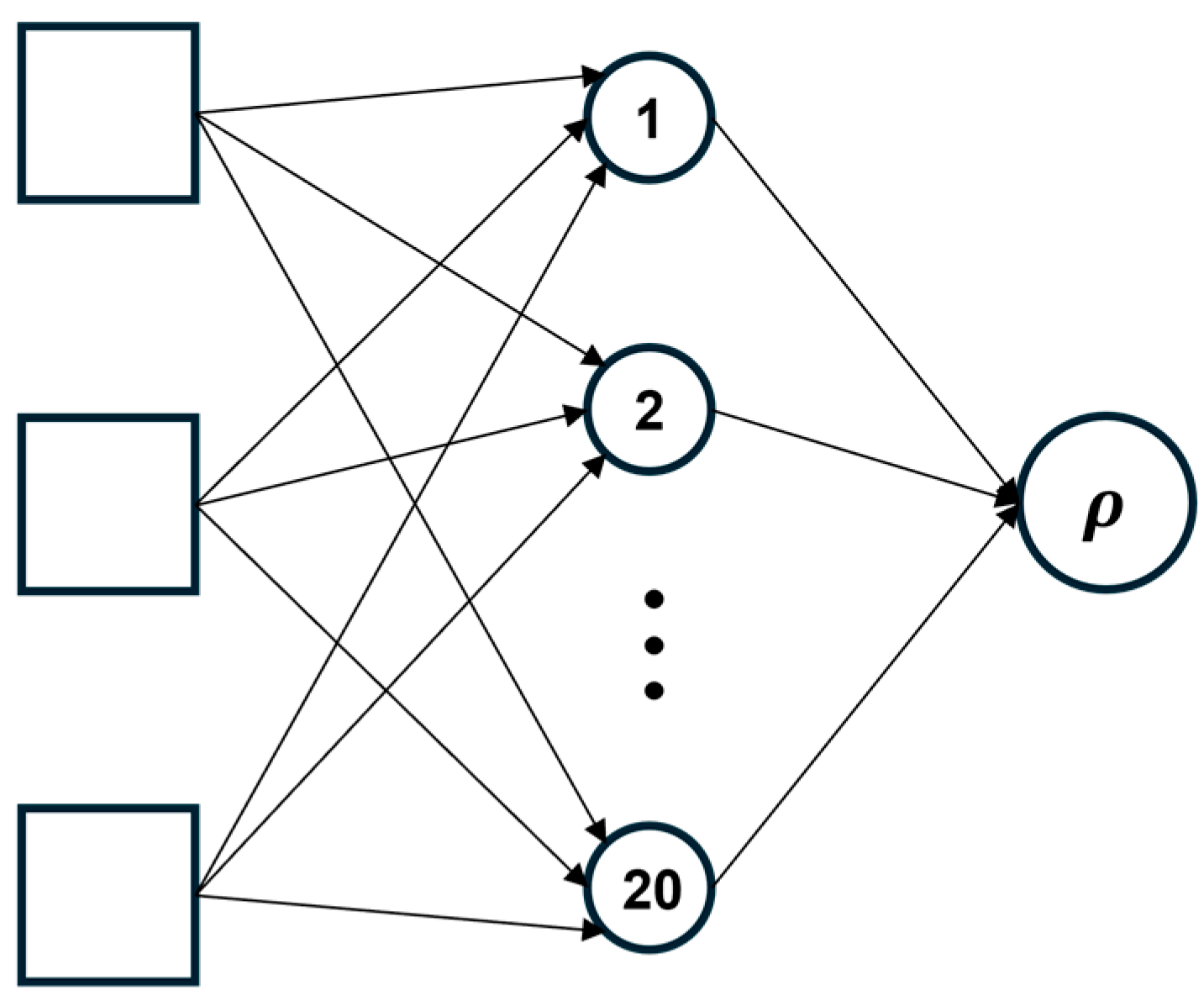
3.2. Artificial Neural Networks
4. Influence of Soil Properties on Electrical Resistivity
4.1. Effect of Moisture Content
4.2. Impact of Plasticity Index
| Author(s) | Soil Type | Findings | Limitation | |
|---|---|---|---|---|
| Long et al., 2012 [47] | Marine clay | The study observed a weak inverse correlation between PI and resistivity, with a tendency to decrease in resistivity as PI increases. This trend is less pronounced at lower PI values due to the low . | - | Salt concentration had a greater effect than PI on resistivity in marine clays. The correlation equations are not reported by the original authors. |
| Osman et al., 2013 [45] | Silty sand | 0.2644 | The study’s plasticity index values were limited to a maximum of 26%, thereby excluding high-plasticity clays. Notable discrepancies with previous research (e.g., Corwin and Scudiero (2019) [43]) were observed, particularly for PI values below 15%, likely due to variations in grain size distribution and soil porosity. | |
| Silty sand | 0.1354 | |||
| Sandy soil | 0.3342 | |||
| Sandy soil | 0.2153 | |||
| Silty sand and sandy soil | 0.5012 | |||
| Silty sand and sandy soil | 0.3613 | |||
| Siddiqui & Osman 2013 [15] | Silty sand | 0.1532 | The PI values in this study ranged only from 0% to 26.27%, excluding high-plasticity clays, which may limit the applicability of results to broader soil types. | |
| Sandy soil | 0.2437 | |||
| Silty sand and sandy soil | 0.4233 | |||
| Siddiqui et al., 2014 [38] | Silty sand and sandy soil | Prediction accuracy is influenced by soil type, with silty sand providing better ANN performance than sand. | - | Regression models failed to capture the nonlinearity in the resistivity–PI relationship, especially for sandy soils where no correlation was found. |
| Lin et al., 2017 [19] | Marine clay | 0.8500 | Spearman’s rank correlation captures only monotonic trends, not precise predictive accuracy, like . The model is based on site-specific Jiangsu marine clay and lacks validation with external data, raising the risk of overfitting to local conditions. | |
| Zhang et al., 2018 [46] | Marine clay | The correlation between plasticity index and resistivity is weak; resistivity decreases with increasing PI below 10% but remains stable (~8 Ω·m) above this threshold. | - | The influences of plasticity index, unit weight, and moisture content are overshadowed by the dominant effects of salt and clay content. Additionally, the limited data for PI > 26% restricts analysis of high-plasticity clays. The correlation equations are not reported by the original authors. |
| Oborie & Akana 2020 [40] | Fined grained soil | 0.5885 | The correlation is limited by the use of simple linear models to represent inherently nonlinear trends. | |
| Sandy soil | 0.4622 | |||
| Fined grained soil and sandy soil | 0.4797 | |||
| Poorly graded sands | Non-plastic | - | ||
| Jusoh et al., 2022 [17] | Clayey sand | 0.0048 | The regression model failed to produce a reliable predictive equation for PI from resistivity due to the extremely low value. | |
| Memon et al., 2024 [48] | Silty sand soil | 0.3090 | The dataset was dominated by silty sand soils, with fewer clay-rich samples, potentially limiting the generalizability of the correlation model. | |
| Clay soil | 0.0750 | |||
| All soil samples | 0.1900 |
4.3. Effect of Clay Content and Mineralogy
4.4. Influence of Unit Weight and Density
4.5. Temperature Dependence of Electrical Resistivity
5. Discussion
5.1. Application of Electrical Resistivity and Geotechnical Properties
5.2. Limitations
- The dataset used in this review primarily comprises fine-grained soils, such as clayey silt, silty clay, and silty sand. As a result, the applicability of the developed models to coarse-grained or heterogeneous soils remains limited. Similar constraints were observed by Jusoh et al. (2022) [17] and Memon et al. (2024) [48], who noted that correlations derived from cohesive soils often fail to generalize across soil classes.
- A significant portion of the data was obtained under laboratory conditions. While this allows precise control of variables, it limits direct transferability to field environments. Validation under natural stratification, variable saturation, and seasonal conditions is needed, as highlighted by Long et al. (2012) [47] and Lin et al. (2017) [19], who reported variability in resistivity behavior due to salinity and pore fluid effects.
- Although this review employed multivariable analysis, several relevant parameters—such as void ratio, mineralogical composition, and electrolyte concentration—were not directly included. Prior studies [46,50] demonstrate that these factors may exert a stronger influence on resistivity than traditional index properties.
- While ANN models performed well in terms of prediction, their black-box nature limits interpretability and generalization across datasets without retraining. This concern, noted by Siddiqui et al. (2014) [38] and Zamanian et al. (2024) [37], highlights the need for combining ANNs with explainable machine learning techniques or hybrid modeling approaches.
- Although the effect of temperature on resistivity is acknowledged, temperature correction factors were not fully incorporated into the predictive models. Given the work of Zhou et al. (2015) [57] and Kizlo and Kanbergs (2009) [44], further investigation into temperature–resistivity dynamics is recommended, especially for applications in seasonally variable climates. Seasonal and diurnal temperature variations can significantly influence resistivity values in field conditions, as resistivity tends to increase with decreasing temperature. Incorporating temperature correction, as recommended by Hen-Jones et al. (2017) [68], is essential for ensuring consistency and accuracy in resistivity measurements across different environmental conditions.
5.3. Implications and Future Research
- Expanding datasets to cover a broader spectrum of soil types and mineralogy;
- Conducting field-scale validation under variable environmental and hydrological conditions;
- Incorporating additional parameters such as salinity, void ratio, and soil mineralogy;
- Exploring hybrid modeling frameworks that integrate ANN performance with the interpretability of regression and physically based models.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IEEE Std 80-2013; IEEE Guide for Safety in AC Substation Grounding. IEEE: Piscataway, NJ, USA, 2015; pp. 1–226. [CrossRef]
- Gouda, O.E.; Amer, G.M.; Elkhodragy, T. Factors affecting the apparent soil resistivity of multi-layer soil. In Proceedings of the 14th International Symposium on High Voltage Engineering, Beijing, China, 25–29 August 2005. [Google Scholar]
- Malanda, S.C.; Davidson, I.E.; Singh, E.; Buraimoh, E. Analysis of soil resistivity and its impact on grounding systems design. In Proceedings of the 2018 IEEE PES/IAS PowerAfrica, Cape Town, South Africa, 26–29 June 2018; pp. 324–329. [Google Scholar] [CrossRef]
- Kearey, P.; Brooks, M.; Hill, I. An Introduction to Geophysical Exploration, 3rd ed.; Blackwell Science Ltd.: Oxford, UK, 2002. [Google Scholar]
- Reynolds, J.M. An Introduction to Applied and Environmental Geophysics, 2nd ed.; Wiley-Blackwell: Chichester, UK, 2011. [Google Scholar]
- Conyers, L.B. Ground-Penetrating Radar for Archaeology, 3rd ed.; Routledge: New York, NY, USA, 2013. [Google Scholar]
- Everett, M.E. Near-Surface Applied Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Zhu, T.; Feng, R.; Hao, J.; Zhou, J.; Wang, H.; Wang, S. The application of electrical resistivity tomography to detecting a buried fault: A case study. J. Environ. Eng. Geophys. 2009, 14, 145–151. [Google Scholar] [CrossRef]
- Giao, P.H.; Chung, S.G.; Kim, D.Y.; Tanaka, H. Electric imaging and laboratory resistivity testing for geotechnical investigation of Pusan clay deposits. J. Appl. Geophys. 2003, 52, 157–175. [Google Scholar] [CrossRef]
- Loke, M.H.; Rucker, D.F.; Chambers, J.E.; Wilkinson, P.B.; Kuras, O. Electrical Resistivity Surveys and Data Interpretation. In Encyclopedia of Solid Earth Geophysics; Gupta, H.K., Ed.; Springer International Publishing: Cham, Switzerland, 2021; pp. 344–350. [Google Scholar] [CrossRef]
- Liu, Y.; Kitanidis, P.K. Chapter 6: Tortuosity and Archie’s Law. In Advances in Hydrogeology; Springer: New York, NY, USA, 2013; pp. 151–172. [Google Scholar] [CrossRef]
- Glover, P.W.J. What is the cementation exponent? A new interpretation. Lead. Edge 2009, 28, 82–85. [Google Scholar] [CrossRef]
- Revil, A.; Cathles, L.M.; Losh, S.; Nunn, J.A. Electrical conductivity in shaly sands with geophysical applications. J. Geophys. Res. Solid Earth 1998, 103, 23925–23936. [Google Scholar] [CrossRef]
- Cosenza, P.; Marmet, E.; Rejiba, F.; Cui, Y.J.; Tabbagh, A. Correlations between geotechnical and electrical data: A case study at Garchy in France. J. Appl. Geophys. 2006, 60, 165–178. [Google Scholar] [CrossRef]
- Siddiqui, F.I.; Osman, S.B.A.B.S. Simple and multiple regression model for relationship between electrical resistivity and various soil properties for soil characterization. Environ. Earth Sci. 2013, 70, 259–267. [Google Scholar] [CrossRef]
- Hazreek, Z.A.M.; Aziman, M.; Azhar, A.T.S.; Chitral, W.D.; Chambers, J.E.; Fauziah, A.; Rosli, S. The behaviour of laboratory soil electrical resistivity value under basic soil properties influences. Earth Environ. Sci. 2015, 23, 012002. [Google Scholar] [CrossRef]
- Jusoh, M.N.H.; Syamsunur, D.; Rahman, N.A.; Olisa, E.; Rahim, A.; Yusoff, N.I.M. Soil parameters model prediction via resistivity value limit to shallow subsurface areas. Shock Vib. 2022, 2022, 3251250. [Google Scholar] [CrossRef]
- Asif, A.R.; Shah, S.S.A.; Noreen, N.; Ahmed, W.; Khan, S.; Khan, M.Y.; Waseem, M. Correlation of electrical resistivity of soil with geotechnical engineering parameters at Wattar area district Nowshera, Khyber Pakhtunkhwa, Pakistan. J. Himal. Earth Sci. 2016, 49, 124–130. [Google Scholar]
- Lin, J.; Cai, G.; Liu, S.; Puppala, A.J.; Zou, H. Correlations between electrical resistivity and geotechnical parameters for Jiangsu marine clay using Spearman’s coefficient test. Int. J. Civ. Eng. 2017, 15, 419–429. [Google Scholar] [CrossRef]
- Sangprasat, K.; Puttiwongrak, A.; Inazumi, S. Comprehensive analysis of correlations between soil electrical resistivity and index geotechnical properties. Results Eng. 2024, 23, 102696. [Google Scholar] [CrossRef]
- Kibria, G.; Hossain, M.S. Investigation of geotechnical parameters affecting electrical resistivity of compacted clays. J. Geotech. Geoenviron. Eng. 2012, 138, 1520–1529. [Google Scholar] [CrossRef]
- Calamita, G.; Brocca, L.; Perrone, A.; Piscitelli, S.; Lapenna, V.; Melone, F.; Moramarco, T. Electrical resistivity and TDR methods for soil moisture estimation in central Italy test-sites. J. Hydrol. 2012, 454–455, 101–112. [Google Scholar] [CrossRef]
- Binley, A.; Slater, L. Resistivity and Induced Polarization Theory and Applications to the Near-Surface Earth; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Pozdnyakova, A.; Pozdnyakova, L. Electrical fields and soil properties. In Proceedings of the 17th World Congress of Soil Science, Bangkok, Thailand, 14–21 August 2002. [Google Scholar]
- Ozcep, F.; Tezel, O.; Asci, M. Correlation between electrical resistivity and soil-water content: Istanbul and Golcuk. Int. J. Phys. Sci. 2009, 4, 362–365. [Google Scholar]
- Pozdnyakov, A.I.; Pozdnyakova, L.A.; Karpachevskii, L.O. Relationship between water tension and electrical resistivity in soils. Eurasian Soil Sci. 2006, 39, S78–S83. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Peck, E.A.; Vining, G.G. Introduction to Linear Regression Analysis, 5th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Lehmann, E.L.; D’Abrera, H.J.M. Nonparametrics Statistical Methods Based on Ranks; Springer: New York, US, 2006. [Google Scholar]
- Abidin, M.H.Z.; Saad, R.; Ahmad, F.; Wijeyesekera, D.C.; Yahya, A.H. Soil moisture content and density prediction using laboratory resistivity experiment. IACSIT Int. J. Eng. Technol. 2013, 5, 731–735. [Google Scholar] [CrossRef]
- Alsharari, B.; Olenko, A.; Abuel-Naga, H. Modeling of electrical resistivity of soil based on geotechnical properties. Expert Syst. Appl. 2020, 14, 112966. [Google Scholar] [CrossRef]
- Ngamkhanong, C.; Keawsawasvong, S.; Jearsiripongkul, T.; Cabangon, L.T.; Payan, M.; Sangjinda, K.; Banyong, R.; Thongchom, C. Data-driven prediction of stability of rock tunnel heading: An application of machine learning models. Infrastructures 2022, 7, 148. [Google Scholar] [CrossRef]
- Zou, K.H.; Tuncali, K.; Silverman, S.G. Correlation and simple linear regression. Radiology 2003, 3, 617–622. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks and Learning Machines; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Shahin, M.; Jaksa, M.B.; Maier, H.R. Artificial neural network applications geotechnical engineering. Aust. Geomech. J. 2001, 36, 49–62. [Google Scholar]
- Shahin, M.; Jaksa, M.B.; Maier, H.R. State of the art of artificial neural networks in geotechnical engineering. Electron. J. Geotech. Eng. 2008, 8, 1–26. [Google Scholar]
- Baghbani, A.; Choudhury, T.; Costa, S.; Reiner, J. Application of artificial intelligence in geotechnical engineering: A state-of-the-art review. Earth-Sci. Rev. 2022, 228, 103991. [Google Scholar] [CrossRef]
- Zamanian, M.; Asfaw, N.; Chavda, P.; Shahandashti, M. Deep learning for exploring the relationship between geotechnical properties and electrical resistivities. Transp. Res. Rec. 2024, 2678, 659–672. [Google Scholar] [CrossRef]
- Siddiqui, F.I.; Pathan, D.M.; Osman, S.B.A.B.S.; Pinjaro, M.A.; Memon, S. Comparison between regression and ANN models for relationship of soil properties and electrical resistivity. Arab. J. Geosci. 2014, 8, 6145–6155. [Google Scholar] [CrossRef]
- Kazmi, D.; Qasim, S.; Siddiqui, F.I.; Azhar, S.B. Exploring the relationship between moisture content and electrical resistivity for sandy and silty soils. Int. J. Eng. Sci. Invent. 2016, 5, 33–35. [Google Scholar]
- Oborie, E.; Akana, T.S. Relationship between soil plasticity index and resistivity of geomaterials. J. Appl. Geol. Geophys. 2020, 8, 1–9. [Google Scholar]
- Cosenza, P.; Ghorbani, A.; Camerlynck, C.; Rejiba, F.; Guérin, R.; Tabbagh, A. Effective medium theories for modelling the relationships between electromagnetic properties and hydrological variables in geomaterials: A review. Near Surf. Geophys. 2009, 7, 563–578. [Google Scholar] [CrossRef]
- Hillel, D. Introduction to Environmental Soil Physics; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Corwin, D.L.; Scudiero, E. Review of Soil Salinity Assessment for Agriculture across Multiple Scales Using Proximal and/or Remote Sensors. Adv. Agron. 2019, 158, 1–130. [Google Scholar] [CrossRef]
- Kižlo, M.; Kanbergs, A. The causes of the parameters changes of soil resistivity. Sci. J. Riga Tech. Univ. Power Electr. Eng. 2009, 25, 43–46. [Google Scholar] [CrossRef]
- Osman, S.B.S.; Siddiqui, F.I.; Behan, M.Y. Relationship of plasticity index of soil with laboratory and field electrical resistivity values. Appl. Mech. Mater. 2013, 353–356, 719–724. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, S.; Cai, G. Correlations between electrical resistivity and basic engineering property parameters for marine clays in Jiangsu, China. J. Appl. Geophys. 2018, 159, 640–648. [Google Scholar] [CrossRef]
- Long, M.; Donohue, S.; L’Heureux, J.; Solberg, I.; Rønning, J.S.; Limacher, R.; O’Connor, P.; Sauvin, G.; Rømoen, M.; Lecomte, I. Relationship between electrical resistivity and basic geotechnical parameters for marine clays. Can. Geotech. J. 2012, 49, 1158–1168. [Google Scholar] [CrossRef]
- Memon, M.B.; Yang, Z.; Qazi, W.H.; Pathan, S.M.; Chalgri, S.R. Assessing Soil Bulk Density, Plasticity Index, Porosity, and Degree of Saturation through Electrical Resistivity using Correlation Analysis. Malays. J. Soil Sci. 2024, 28, 12–25. [Google Scholar]
- Dahlin, T. The development of DC resistivity imaging techniques. Comput. Geosci. 2001, 27, 1019–1029. [Google Scholar] [CrossRef]
- Shevnin, V.; Mousatov, A.; Ryjov, A.; Delgado-Rodriguez, O. Estimation of clay content in soil based on resistivity modelling and laboratory measurements. Geophys. Prospect. 2007, 55, 265–275. [Google Scholar] [CrossRef]
- Rashid, Q.A.A.; Abuel-Naga, H.M.; Leong, E.-C.; Lu, Y.; Al Abadi, H. Experimental-artificial intelligence approach for characterizing electrical resistivity of partially saturated clay liners. Appl. Clay Sci. 2018, 156, 1–10. [Google Scholar] [CrossRef]
- Sarip, M.K.; Madun, A. The influence of clay minerals towards resistivity and chargeability value for groundwater interpretation. Recent Trends Civ. Eng. Built Environ. 2021, 2, 629–637. [Google Scholar]
- Lin, C.-P.; Lin, C.-H.; Wu, P.-L.; Wang, H.; Liu, H.-C. Applications and challenges of engineering geophysics in geotechnical and geo-environmental engineering. Chin. J. Geophys. 2015, 58, 2861–2872. [Google Scholar]
- Uhlemann, S.; Wilkinson, P.B.; Maurer, H.; Wagner, F.M.; Johnson, T.C.; Chambers, J.E. Optimized survey design for electrical resistivity tomography: Combined optimization of measurement configuration and electrode placement. Geophys. J. Int. 2018, 214, 108–121. [Google Scholar] [CrossRef]
- Islam, T.; Chik, Z.; Mustafa, M.M.; Sanusi, H. Modeling of electrical resistivity and maximum dry density in soil compaction measurement. Environ. Earth Sci. 2012, 66, 2393–2401. [Google Scholar] [CrossRef]
- Islam, S.M.T.; Chik, Z.; Mustafa, M.M.; Sanusi, H. Model with artificial neural network to predict the relationship between the soil resistivity and dry density of compacted soil. J. Intell. Fuzzy Syst. 2013, 25, 351–357. [Google Scholar] [CrossRef]
- Zhou, M.; Wang, J.; Cai, L.; Fan, Y.; Zheng, Z. Laboratory investigations on factors affecting soil electrical resistivity and the measurement. IEEE Trans. Ind. Appl. 2015, 51, 5358–5365. [Google Scholar] [CrossRef]
- Abdulwadood, S. Design of Lightning Arresters for Electrical Power Systems Protection. Adv. Electr. Electron. Eng. 2013, 11, 433. [Google Scholar] [CrossRef]
- Hayashi, M. Temperature-electrical conductivity relation of water for environmental monitoring and geophysical data inversion. Environ. Monit. Assess. 2004, 96, 119–128. [Google Scholar] [CrossRef]
- Ma, R.; McBratney, A.; Whelan, B.; Minasny, B.; Short, M. Comparing temperature correction models for soil electrical conductivity measurement. Precision Agric. 2011, 12, 55–66. [Google Scholar] [CrossRef]
- McCleskey, R.B.; Nordstrom, D.K.; Ryan, J.N. Comparison of electrical conductivity calculation methods for natural waters. Limnol. Oceanogr. Methods 2012, 10, 952–967. [Google Scholar] [CrossRef]
- Sheets, K.R.; Hendrickx, J.M.H. Noninvasive soil water content measurement using electromagnetic induction. Water Resour. Res. 1995, 31, 2401–2409. [Google Scholar] [CrossRef]
- Ming, F.; Li, D.Q.; Chen, L. Electrical resistivity of freezing clay: Experimental study and theoretical model. J. Geophys. Res. Earth Surf. 2020, 125. [Google Scholar] [CrossRef]
- Kundu, S.K.; Dey, A.K.; Sapkota, S.C.; Ray, A.; Saha, P.; Mandal, A.; Halder, S. Advanced predictive modelling of electrical resistivity for geotechnical and geo-environmental applications using machine learning techniques. J. Appl. Geophys. 2024, 215, 105557. [Google Scholar] [CrossRef]
- Erzin, Y.; Gumaste, S.D.; Gupta, A.K.; Singh, D.N. Artificial neural network (ANN) models for determining hydraulic conductivity of compacted fine-grained soils. Can. Geotech. J. 2009, 46, 955–968. [Google Scholar] [CrossRef]
- Sorensen, J.A.; Glass, G.E. Ion and temperature dependence of electrical conductance for natural waters. Anal. Chem. 1987, 59, 1594–1597. [Google Scholar] [CrossRef]
- Lin, C.-P.; Lin, C.-H.; Wu, P.-L.; Wang, H.; Liu, H.-C. Applications and challenges of near surface geophysics in geotechnical engineering. Chin. J. Geophys. 2015, 58. [Google Scholar] [CrossRef]
- Hen-Jones, R.M.; Hughes, P.N.; Stirling, R.A.; Glendinning, S.; Chambers, J.E.; Gunn, D.A.; Cui, Y.J. Seasonal effects on geophysical–geotechnical relationships and their implications for electrical resistivity tomography monitoring of slopes. Acta Geotech. 2017, 12, 1159–1173. [Google Scholar] [CrossRef]

| rₛ Value | Strength of Association |
|---|---|
| +1 | Perfect positive |
| −1 | Perfect negative |
| 0 | No association |
| 0.1 to 0.3 or −0.1 to −0.3 | Weak |
| 0.4 to 0.6 or −0.4 to −0.6 | Moderate |
| 0.7 to 0.9 or −0.7 to −0.9 | Strong |
| Author(s) | Soil Type | Findings | Limitation | |
|---|---|---|---|---|
| Cosenza et al., 2006 [14] | Alluvial deposit soil(Coarese dry soil and fine wet soil) | 0.8210 | The correlation was limited by data collection and interpolation errors, as the water content samples were collected from only two boreholes, and the electrical resistivity values were interpolated from 2D inversion data to match the depths of the geotechnical tests. | |
| Ozcep et al., 2009 [24] | Sandy soil | 0.7859 | The study is limited by the use of only certain soil types and by not controlling parameters such as salinity, which significantly influence electrical resistivity. | |
| Ozcep et al., 2010 [25] | Sandy soil | AI, including ANNs and Fuzzy Logic systems, were employed to predict soil water content using electrical resistivity as the input parameter. | - | The models were based solely on sandy soils, lacked multivariate analysis, and were not validated with independent or external data. |
| Kibria & Hossain 2012 [21] | Highly plastic clay | 0.6400 | The study is limited to a specific soil type, which is highly plastic clay. | |
| Abidin et al., 2013 [29] | Loose clayey silt | 0.8927 | The study is limited by its focus on a single soil type and the absence of validation using real field data. | |
| Compacted clayey silt | 0.8853 | |||
| Siddiqui & Osman 2013 [15] | Silty sand | 0.2554 | The study focuses on sandy and silty sand soils, with weak correlation in silty sand. The site-specific models require recalibration for broader application. | |
| Sandy soil | 0.5100 | |||
| All soil sample | 0.5625 | |||
| Siddiqui et al., 2014 [38] | Silty sand and sandy soil | ANNs was employed to predict soil water content using electrical resistivity as the input parameter. | 0.2990 | The study focuses on sandy and silty sand soils with weak correlations, using a small dataset that may reduce statistical reliability and increase overfitting risk. |
| Hazreek et al., 2015 [16] | Clayey silt | 0.8927 | The study lacks field validation, and the broad, overlapping resistivity ranges limit its classification accuracy. | |
| Silty sand | 0.5643 | |||
| Asif et al., 2016 [18] | Clayey sand | 0.964 | The correlation is limited due to data being collected from only one specific site. | |
| Kazmi et al., 2016 [39] | Silty sand and sandy soil | 0.5954 | The correlation is limited by single-site data collection, lack of external validation, and only moderate predictive accuracy. | |
| Silty sand and sandy soil | 0.5442 | |||
| Lin et al., 2017 [19] | Marine clay | 0.9300 | Spearman’s rank correlation captures only monotonic trends, not precise predictive accuracy, like . The model is based on site-specific Jiangsu marine clay and lacks validation with external data, raising the risk of overfitting to local conditions. | |
| Oborie and Akana 2020 [40] | Fined grained soil | 0.2530 | The correlation is limited by the use of simple linear models to represent inherently nonlinear trends, resulting in only moderate to weak correlation strengths. | |
| Sandy soil | 0.0364 | |||
| Poorly graded sands | 0.5810 | |||
| All soil samples | 0.3860 | |||
| Jusoh et al., 2022 [17] | Clayey sand | 0.8784 | The correlation is limited by single-site data collection and lack of external validation. | |
| Sangprasat et al., 2024 [20] | Clayey silt and silty clay | The inverse relationship between resistivity and water content was strong within specific soil types but became weak when all soil samples were analyzed together. | - | The correlation is limited by all tested samples being fine-grained cohesive soils. The correlation equations are not reported by the original authors. |
| Author(s) | Soil Type | Findings | Limitation | |
|---|---|---|---|---|
| Long et al., 2012 [47] | Marine clay | A moderate inverse correlation was observed between clay content and resistivity, with values typically dropping to ~5 Ω·m when clay content exceeds 40–50%. | 0.5900 | The authors note that clay content trends may overlap or be masked by the stronger effects of salt content in pore water, especially in marine environments. The correlation equations are not reported by the original authors. |
| Siddiqui & Osman 2013 [15] | Silty sand and sandy soil | 0.2043 | Although the study did not directly isolate clay content as a parameter, its influence is implied through the D10 of grain-size distribution. | |
| Lin et al., 2017 [19] | Marine clay | 0.5300 | Although Spearman’s coefficient shows a strong monotonic trend, regression results indicate only a moderate predictive relationship. Clay content alone does not control resistivity, as salt content, moisture, and void ratio show stronger correlations. | |
| Rashid et al., 2018 [51] | Kaolinite-dominant mixtures soil | The study examined the electrical resistivity of eight kaolinite dominant mixtures, showing that resistivity decreased with higher bentonite content and increased with higher sand content, under varying moisture and dry density conditions. | - | The study tested limited sand and bentonite contents (10–40%) without considering particle shape or gradation, and results were based solely on laboratory conditions, lacking field validation. The correlation equations are not reported by the original authors. |
| Zhang et al., 2018 [46] | Marine clay | 0.7500 | Clay content correlates with resistivity, but its influence is overshadowed by the stronger effects of salt content and moisture. | |
| Jusoh et al., 2022 [17] | Clayey sand | 0.4093 | of 0.40 indicates that clay content moderately explains resistivity variation, while moisture and porosity have a greater influence. | |
| Zamanian et al., 2024 [37] | Fine-grained soils | A deep learning model revealed that clay content has a weak inverse correlation with electrical resistivity, as confirmed by Spearman’s analysis. While clay affects resistivity through surface area and moisture retention, its predictive influence is less significant than water content or fine fraction in clayey soils. | - | Clay content showed the lowest importance in the deep learning model and only a weak Spearman’s correlation with resistivity, indicating limited predictive value and complex, nonlinear interactions. |
| Author(s) | Soil Type | Findings | Limitation | |
|---|---|---|---|---|
| Islam et al., 2012 [55] | Poorly graded sand with silt, clean sand, clayey sand, and low-plasticity clay | This study confirms a consistent inverse relationship between electrical resistivity and dry density, enabling efficient, non-destructive estimation of soil compaction using resistivity and moisture data. | - | The derived equations are tailored to specific soil types and compositions. Application to other soils would require recalibration or remodeling. The correlation equations are not reported by the original authors. |
| Islam et al., 2013 [56] | Poorly graded sand with silt, clean sand, clayey sand, and low-plasticity clay | The study shows that electrical resistivity decreases with increasing dry density due to denser packing and reduced pore space limiting current flow. | - | The model was developed under controlled laboratory conditions; its robustness in field settings remains to be fully validated. The correlation equations are not reported by the original authors. |
| Rashid et al., 2018 [51] | Kaolinite-dominant mixtures soil | The study found a clear inverse relationship between dry density and electrical resistivity in partially saturated kaolinite-dominant clay liners: resistivity decreases as dry density increases. | 0.5300 | Although Spearman’s coefficient shows a strong monotonic trend, regression results indicate only a moderate predictive relationship. Clay content alone does not control resistivity, as salt content, moisture, and void ratio show stronger correlations. The correlation equations are not reported by the original authors. |
| Abidin et al., 2013 [29] | Clayey silt | 0.7016 | The study is limited by testing only one soil type and lacking field validation. Additionally, the resistivity meter was ineffective in very dry conditions (<8%), restricting its use in arid soils. | |
| Hazreek et al., 2015 [16] | Clayey silt | 0.7318 | The study lacks field validation, and the broad, overlapping resistivity ranges limit its classification accuracy. | |
| Silty sand | 0.8511 | |||
| Jusoh et al., 2022 [17] | Silty sand | 0.3028 | The low adjusted suggests bulk density alone poorly predicts resistivity, with uncontrolled moisture variations likely obscuring stronger correlations. | |
| Long et al., 2012 [47] | Marine clay | The study found a weak and inconsistent correlation between resistivity and unit weight. While a slight decrease in resistivity with increasing unit weight was observed below 50 Ω·m, the trend varied significantly across sites. | - | The authors note that trends may overlap or be masked by the stronger effects of salt content in pore water, especially in marine environments. The correlation equations are not reported by the original authors. |
| Kabria and Hossain 2012 [21] | Highly plastic clay | Results showed a clear inverse relationship: resistivity decreased with increasing unit weight, but changes became minimal beyond 15.72 kN/m3, indicating a compaction threshold with limited further effect. | - | The study is limited to a specific soil type, which is highly plastic clay. The correlation equations are not reported by the original authors. |
| Siddiqui & Osman 2013 [15] | Silty sand | 0.1210 | Moisture content had a significantly stronger influence on resistivity than unit weight, often masking any observable trend. | |
| Sandy soil | 0.1040 | |||
| Silty sand and sandy soil | 0.0990 | |||
| Lin et al., 2017 [19] | Marine clay | 0.7200 | The influence of unit weight on resistivity may be overshadowed by stronger factors like salt content, void ratio, and moisture, all showing very strong correlations (rs > 0.9). | |
| Zhang et al., 2018 [46] | Marine clay | The results showed a weak and inconsistent correlation between resistivity and unit weight; the expected decrease in resistivity with higher compaction was not consistently observed across sites. | - | The effects of salt content and clay fraction were stronger and often masked any observable trend with unit weight. The correlation equations are not reported by the original authors. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sangprasat, K.; Puttiwongrak, A.; Inazumi, S. Review of Correlations Between Soil Electrical Resistivity and Geotechnical Properties. Geosciences 2025, 15, 166. https://doi.org/10.3390/geosciences15050166
Sangprasat K, Puttiwongrak A, Inazumi S. Review of Correlations Between Soil Electrical Resistivity and Geotechnical Properties. Geosciences. 2025; 15(5):166. https://doi.org/10.3390/geosciences15050166
Chicago/Turabian StyleSangprasat, Kornkanok, Avirut Puttiwongrak, and Shinya Inazumi. 2025. "Review of Correlations Between Soil Electrical Resistivity and Geotechnical Properties" Geosciences 15, no. 5: 166. https://doi.org/10.3390/geosciences15050166
APA StyleSangprasat, K., Puttiwongrak, A., & Inazumi, S. (2025). Review of Correlations Between Soil Electrical Resistivity and Geotechnical Properties. Geosciences, 15(5), 166. https://doi.org/10.3390/geosciences15050166







