Abstract
The prediction of structural fractures in concealed coal-bearing strata has always been a complex problem. The purpose of this study was to clarify the tectonic evolution of the study area, i.e., the Tucheng syncline, since the coal-forming period and to predict the development of structural fractures. The tectonic evolution of the study area was divided into three stages using regional tectonic analysis. The paleotectonic stress field of the study area was reconstructed through the field investigation, statistics, and analysis of joints. Based on the tectonic deformation analysis, numerical simulation was used to reveal the stress field characteristics of different tectonic deformation stages, and combined with the Mohr–Coulomb criterion, the degree of structural fracture development in the target layers (No.17# coal seam) of the study area was predicted. This study concludes the following: (1) The study area underwent two tectonic deformations during the Yanshanian period, transitioning from an ellipsoidal columnar shape to a semi-ellipsoidal and stereotyped form, forming a superimposed short-axis syncline, and then tilting southeastward as a whole, and was locally cut by faults during the Himalayan period. (2) The distribution characteristics of the stress field in different tectonic stages vary. The stress concentration zones in the first and second stages have a more obvious symmetry, and the present-day stress concentration zone is located in the center of the syncline basin. (3) The superimposed rock fracture indices are larger in the edge zone parallel to the long axis of the syncline and at the bottom of the syncline, which also indicates a higher degree of structural fracture development at the corresponding locations.
1. Introduction
Natural fractures within coal-bearing strata serve as vital storage spaces and fluid flow pathways for oil and gas, thereby playing a pivotal role in the exploration and exploitation of unconventional gas resources. These fractures can be broadly categorized into endogenous (cleats) and exogenous types, and among exogenous fractures, structural fractures are particularly effective in enhancing the permeability of coalbed methane (CBM) reservoirs, ultimately boosting the productivity of CBM wells [1]. The permeability of coal seams shows a strong exponential relationship with the density of coal seam fractures (joint sets). The stress state of the coal seams influences the opening and closing of these fractures, which is closely linked to the permeability of the coal seams [2,3]. Karimpouli [4] summarized various methods for characterizing and predicting CBM reservoir permeability, including the modeling of reservoir fracture systems. A fracture permeability model for CBM reservoirs, established using fracture porosity and other indicators, can accurately represent the original permeability of the reservoir. This model has been validated through well tests in CBM reservoirs in the south of the Junggar Basin in northwest China [5]. Studies have also demonstrated that joints in shale gas reservoirs are advantageous for enhancing drainage and boosting shale gas production [6]. Over the past decade, the body of literature pertaining to this field has expanded rapidly [7]. Consequently, it is evident that investigating fractures in oil and gas reservoirs holds immense importance for the advancement of unconventional energy sources.
The structural fractures observed in strata are the outcome of the tectonic stress field. The paleotectonic stress field, which accompanies the evolution of tectonic structures, serves as a mirror, reflecting the Earth’s dynamic processes during tectonic movements. Consequently, the examination of the tectonic stress field within a region is invariably intertwined with the study of its tectonic evolution. This integrated approach has gained widespread application since the inception of its theory. For example, in the central–eastern parts of China, researchers studied various field and underground observations. They used the polar stereographic projection method to analyze conjugate shear joint data. From this, they deduced the paleotectonic stress field that certain areas have experienced since the Mesozoic Era. The results of the above studies revealed that in the central–eastern parts of China, the maximum principal stress orientations of the tectonic stress field primarily manifest in the N–S, NW–SE, and NE–SW directions, corresponding to the tectonic evolution during the Indosinian, Yanshanian, and Himalayan periods [8,9,10,11,12]. These research methods have also been successfully used in southwestern China. Studies have indicated that during the Yanshan to Himalayan periods, the region experienced a changing tectonic stress field because of active tectonic movements [13,14,15]. In eastern Sicily and southern Calabria, Italy, researchers analyzed systematic extension joint sets in Pleistocene deposits using quantitative inversion techniques. They inferred that the tectonic stress tensor was responsible for their formation, revealing local disturbances in the regional stress field. This study is crucial for understanding Quaternary tectonic evolution and the current stress state [16]. By conducting a thorough structural analysis of the fracture network, comprising joints, veins, and faults, in the Jurassic strata of Portugal, researchers reconstructed the brittle tectonic history related to the Meso-Cenozoic paleostress trajectory of the Iberian Plate and revealed the tectonic mechanisms of the Lusitanian Basin [17]. The intersecting patterns of joints in the Appalachian Plateau mirror the paleotectonic stress fields of various geological historical periods. Understanding these tectonic cycles aids in elucidating the formation mechanisms of joints with distinct intersecting relationships [18]. The formation and evolution of rock layers involve a multi-stage and diverse geological process. When examining joint development in soft sediments of the Cenozoic Era, it was discovered that joints exhibit varying stress states. These differences are influenced by factors such as regional tectonic style (rifting), stress superposition over time, and the discontinuity of older fractures, which control fracture deformation at various scales [19].
The fracture process is a geomechanical phenomenon that is inevitably affected by pre-existing joints. As the frictional resistance of these joints increases, the rate of fracture growth slows down. On the contrary, an increase in joint dilatancy intensifies the intensity of fracturing [20]. The presence of faults alters the distribution of rock mechanical properties and disrupts the local stress field, making it easier for fractures to develop into faults [21]. As joint spacing decreases, the fracture toughness (FT) and tensile strength (TS) of a rock mass with joints also decrease. Additionally, the geometric characteristics of joints exert a controlling influence on the development of FT, TS, and the fracture process zone (FPZ) [22]. The physical properties of rocks also play a role in the development of joints, with the thickness of the rock bed generally controlling joint density. In addition, other parameters can affect joint density, particularly in carbonate rocks, where an increase in the percentage of grains or bioclasts leads to a decrease in joint density [23]. The tectonic stress field exhibits directionality, and the orientation of joints is governed by the stress field in which they propagate. In bedded rocks, the distribution of joint orientations typically shows non-random variations, with greater variations along the strike than the dip. The presence of nonlinear stress fields complicates these changes in joint orientation, leading to the formation of joint sets during fold development or in rocks with irregular bedding boundaries [24].
The prediction of structural fractures has long been a challenging problem, owing to many factors contributing to their formation. These factors encompass physical attributes such as thickness and composition, mechanical parameters including stress magnitude and stress field characteristics, and temporal considerations like multi-stage processes. The complexity and diversity of these influences underscore the significance of understanding them in tackling the challenge of fracture prediction. Many scholars have studied the prediction of structural fracture development. They have used rock mechanics theory, introduced quantitative indices, and relied on finite element numerical simulations to forecast fracture trends or degrees [8,11,14,25,26,27]. Other researchers have predicted the linear density of fractures by establishing a relationship between coal’s fracture volume density and stress–strain or by deriving an analytical formula for fracture linear density from a strain energy perspective, aided by finite element simulation results [21,28]. However, geological regional factors may affect the quantitative prediction of rock fracture line density, necessitating further exploration.
Numerical simulation plays a crucial role in studying stress fields. A two-dimensional heterogeneous geomechanical model was developed using finite element analysis, with rock mechanics parameters assigned to various rock strata. By applying geomechanical loads to this model, valuable information on the stress distribution within the study area can be obtained [8,11,12,21,29,30]. Three-dimensional geomechanical modeling has been effectively applied in various studies. In these three-dimensional geological models, the target layer is represented as a curved surface, intersected by faults. The simulated stress field results obtained from these models closely resemble real conditions [14,25,26,27,28].
Predicting structural fractures in deep coal seams is challenging, yet past research has made significant progress. The Tucheng area in western Guizhou, China, is rich in coalbed methane but has a complex geological structure and lacks relevant studies. In this paper, the Tucheng syncline serves as a case study. We reconstructed the paleotectonic stress field of the area through joint investigation and statistical analysis, shedding light on the tectonic evolution of the region. Utilizing three-dimensional numerical simulation, we analyzed the stress state during fold formation and, in conjunction with the Mohr–Coulomb criterion, discussed the extent of fracture development in its coal-bearing strata.
2. Geological Setting
2.1. Stratigraphy
The study area, the Tucheng syncline, is located in the northeast of Panzhou City, Guizhou Province, 35 km away from Panzhou City in a straight line. The study area is a short-axis syncline, stretching approximately 30 km in length along its major axis and 8 km along its minor axis. The area, demarcated by the outcrop line of the coal-bearing strata at its base, spans approximately 200 km2. The study area is characterized by plateau middle mountains and a karst–tectonic terrain. Its surface elevation ranges from 1500 to 2000 m. In the study area, the strata, from oldest to newest, include the Upper Carboniferous, Permian, Lower–Middle Triassic, and Quaternary (Figure 1 and Figure 2). Quaternary sediments are very scarce and are only sporadically distributed along the river in the study area. The Quaternary is not depicted in Figure 1 because it cannot be conveniently shown in plan view. The Upper Permian Longtan Formation (P3l) is a coal-bearing formation within the area. This formation typically holds over 50 coal layers, with 32 of them being designated as numbered coal seams. Some very thin and unstable coal seams are not numbered. Out of these, 14 coal seams across the mine field are either mineable or mostly mineable. The total thickness of the coal seams is 20.53 m. The main type of coal is coking coal.
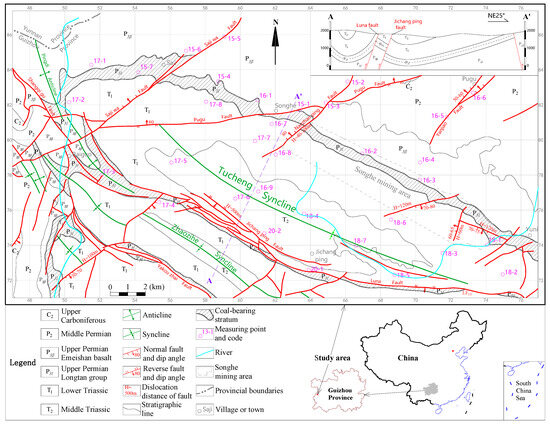
Figure 1.
Structural outline map of the study area.

Figure 2.
Comprehensive stratigraphic column of the study area.
2.2. Tectonics
In the study area, the primary fold is the Tucheng syncline. This syncline is asymmetric, with a gentle dip on its northeast (NE) wing and a steeper dip on its southwest (SW) wing. It is intersected by faults, including the Jichangping fault, and is incomplete in structure. To the southwest of the Tucheng syncline, there are additional folds, namely the Pingdi anticline and the Zhaozihe syncline. These folds are smaller in size, more tightly folded, and incomplete due to fault cutting (Figure 1).
Within the study area, numerous faults have developed, many of which are reverse faults running parallel to the long axis of the syncline. Notably, larger faults like the Jichangping and Luna faults, located on the southwest wing of the syncline, exhibit fault displacements of up to 500 m. The faults that run parallel to the short axis of the syncline are predominantly normal faults, examples being the Nanzhanping and Saji faults. These faults typically have a displacement of no more than 120 m. The Pugu fault, on the contrary, intersects the syncline axis at an oblique angle and is classified as a translational reverse fault. Furthermore, numerous small faults of unknown nature are found around the Tucheng syncline. These faults primarily strike in the NW–SE, NNE–SSW, and ENE–WSW directions (Figure 1).
On a broader spatial scale, the Liupanshui–Qinglong–Panzhou region exhibits a prominent “山”-shaped structural pattern. This structural system, conceptualized by the renowned Chinese geologist Siguang Li [31], derives its name from its resemblance to the Chinese character for “山” (mountain). It comprises five distinct components: a front arc, a reflex arc, a central spine, a horseshoe-shaped shield landmass, and a supporting reflex arc spine (or pillar) (Figure 3). The “山”-shaped structure’s mechanical mechanism is widely attributed to the bending effect of the crossbeam, with two pillars (or reflex arc spines) serving as its two fulcrums. When a compressive force acts perpendicularly on the crossbeam, the pillar sections undergo a reflex arc bending deformation. Between the two pillars, a front arc bending deformation forms. The front arc lies on the outer side of the “neutral layer” where the crossbeam bends, experiencing lateral tension at its top. The spine, on the contrary, is positioned on the inner side of the “neutral layer,” where it undergoes lateral compression as the crossbeam bends. Meanwhile, the horseshoe-shaped land mass is situated in the stress buffer zone adjacent to the “neutral layer,” collectively forming the essential elements of the “山”-shaped structure.
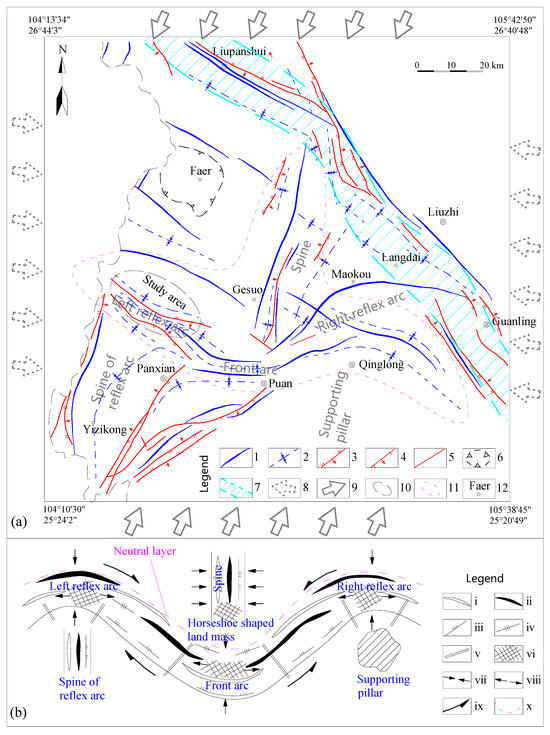
Figure 3.
Outline of the regional tectonic and evolutionary dynamics model. (a) Outline map of the regional structure in the study area (modified according to [32]); (b) the pattern of the “山”-shaped structure, modified from reference [33]. 1, anticline; 2, syncline; 3, reverse fault; 4, normal fault; 5, fault of an unknown nature; 6, structural basin; 7, WZL fault zone; 8, the orientation of the principal stress in the Early Yanshanian period; 9, the orientation of the principal stress in the Late Yanshanian period; 10, study area; 11, “山”-shaped structural belt; 12, village or town. ⅰ, syncline; ⅱ, anticline; ⅲ, thrust fault; ⅳ, squeezing and crushing zone; ⅴ, transverse tensile fault; ⅵ, conjugate shear fracture (or fault); ⅶ, direction of principal compressive stress; ⅷ, direction of principal tensile stress; ⅸ, direction of shear stress; ⅹ, neutral.
A significant fault zone, known as the Weining–Ziyun–Luodian (WZL) fault zone, extends across western Guizhou in the NW–SE direction and traverses the northeast portion of the study area. The WZL fault zone underwent intense deformation during the Yanshanian Movement, spanning from the Late Jurassic–Early Cretaceous to the Late Cretaceous period, characterized by strike slip translation. The dynamic mechanism behind this deformation is linked to the westward compression of the South China Block [15]. The main tectonic pattern of Guizhou was established during the Yanshanian orogeny. The ancient Pacific plate’s subduction created a compressional force in a nearly E–W direction, which significantly influenced the regional deformation of western Guizhou during the Mesozoic and Cenozoic Eras [34].
3. Data and Methods
In this study, the stereographic projection method was first applied to determine the orientation of the principal stress axes at joint observation points, which allowed for the reconstruction of the paleotectonic stress field of the study area. Subsequently, geological models corresponding to the tectonic evolution stages of the study area were established. Material mechanical parameters were assigned to these models, and mechanical simulations were conducted based on the stress field characteristics of each stage. This approach provided the stress distribution of various stages of structural deformation in the coal-bearing strata of the study area.
3.1. Characteristics of Tectonic Joints
A geological field survey was conducted on the Tucheng syncline, covering a field work area of approximately 255 km2. The investigation encompassed its structural features, outcrop lithology, and joint measurements. A total of 33 outcrops were observed, yielding 32 valid data points. At each observation point, a minimum of 50 joints were measured, resulting in a cumulative total of 1893 joints measured across the entire survey area. The predominant orientation of the joint strikes was determined for each observation point. Statistical analysis indicated that the primary joint strikes in the study area were approximately NNE–NE (15–45°) and NW (300–325°) (Figure 4). A total of 807 joints fell within these two intervals, representing 42.6% of the total joint count. Furthermore, the dip angles of the joints in the study area were generally steep, with 76.2% of the joints having a dip angle of 65° or greater.
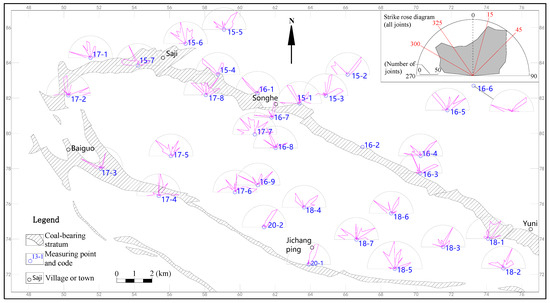
Figure 4.
Strike rose diagrams of joints in the outcrops of the study area.
3.2. Principal Stress Restoration
The fundamental cause of rock (including coal) fracturing is stress-induced failure, with the direct cause of structural fractures being multi-stage tectonic deformation during tectonic evolution. Joints, as typical structural fractures, are closely associated with the paleotectonic stress field. Geologists can analyze and statistically evaluate joints using stereographic projection diagrams to determine the orientations of the maximum (σ1), intermediate (σ2), and minimum (σ3) principal stress axes of conjugate shear joints. The principal stress orientations obtained from multiple observation points enable the reconstruction of the tectonic stress field in the study area [35].
Joints are widely developed in strata that have undergone tectonic deformation. Reconstructing paleotectonic stress fields using conjugate shear joint systems is a traditional and effective method in structural geology. Typically, a sufficient number of joint orientations are measured at outcrops, and a joint density diagram is plotted to identify several high-density points. These high-density points correspond to the normals of joint planes that are particularly well developed in certain orientations and are referred to as predominant joints (Figure 5a). Since initial conjugate joints form in horizontal strata, subsequent tectonic movements often cause strata to tilt or fold, altering the original orientations of conjugate joints. Therefore, in stereographic projection analysis, strata must be restored to their original horizontal state to accurately determine the initial conjugate joint orientations. In the example provided, restoring the strata to a horizontal state reveals that high-density points 1, 2, 3, and 4 (corresponding to the joint plane arcs , , , and , respectively) can be matched. Specifically, high-density points 1 and 4 represent a pair of conjugate joints ( and ), while points 2 and 3 represent another pair ( and ) (Figure 5b). Based on a tectonic evolution analysis of the study area, it was confirmed that the conjugate joints and were formed during the first stage of tectonic deformation, while and were formed during the second stage. This allowed for the determination of the maximum, intermediate, and minimum principal stress orientations for the first and second stages of the tectonic stress field (Figure 5c,d).
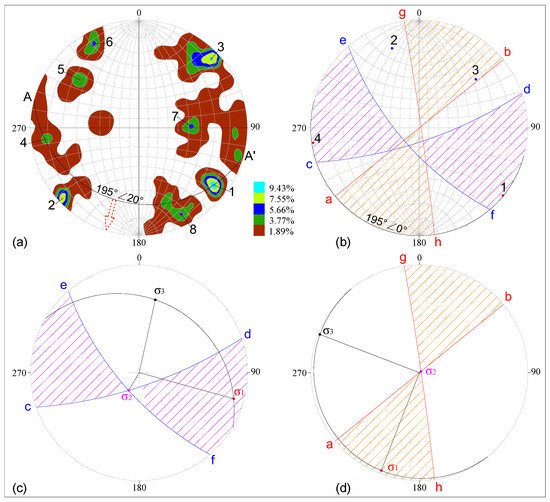
Figure 5.
Determination of the initial principal stress orientations based on the joint statistical results. (a) The joint density map; (b) the matching of preferred joint sets; (c) the conjugate shear joints and the principal stresses formed in the first stage; (d) the conjugate shear joints and the principal stresses formed in the second stage.
3.3. Numerical Simulation of Paleotectonic Stress Fields
3.3.1. Geological Models in Different Stages
Based on the previous analysis, the study area experienced near-horizontal NWW–SEE shortening during the Early Yanshanian period, forming a broad NEN–SWS-oriented syncline. In the Late Yanshanian period, intense near-horizontal NEN–SWS shortening resulted in a semi-ellipsoidal syncline with its long axis oriented NWW–SEE, accompanied by the development of NWW–SEE-oriented reverse faults. Existing research indicates that the maximum burial depth of the Upper Permian in the study region reached 3700 m during the Jurassic period, followed by an uplift to 2300 m in the Cretaceous period (Figure 6). By referring to the tectonic evolution history of the study area, the deformation process of the coal-bearing strata (P3l) can be inferred and simplified to construct geometric models for different tectonic stages.
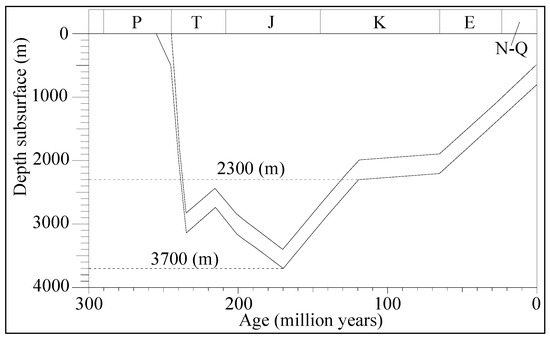
Figure 6.
Burial history of the Upper Permian coal seams in the adjacent area (Panguan syncline), simplified and modified from reference [36].
The Tucheng syncline currently exhibits a short-axis synclinal shape approximating a semi-ellipsoidal structure. The projection of the coal-bearing strata (P3l) forms an ellipse, with a long semi-axis of 12,000–14,000 m and a short semi-axis of 3700–4300 m (Figure 7a). The outer ellipse represents the projection of the P3l’s basal surface, which was estimated and reconstructed based on its dimensions. The current maximum burial depth of the P3l’s basal surface is approximately 2300 m. Considering the deformation characteristics (with Poisson’s ratio set to 0.25), the profile was restored to its maximum burial depth of 3700 m, and the reconstruction process yielded the following results:
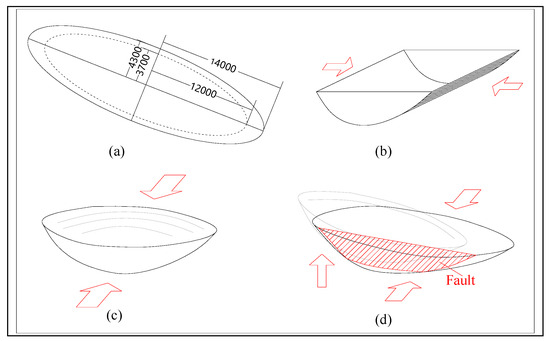
Figure 7.
Geometric models of different tectonic deformation stages in the study area. (a) The present-day projection ellipse of coal-bearing strata; (b) the structural form of the first deformation stage; (c) the structural form of the second deformation stage; (d) the structural form of the third deformation stage.
First Stage: The geometry approximates a semi-cylindrical shape with a chord length of 34,180 m and an arch height of 3700 m (Figure 7b).
Second Stage: The geometry evolves into a semi-ellipsoidal shape. The profile in the long-axis direction has a chord length of 28,000 m, while the short-axis direction has a chord length of 8600 m. The arch height remains 2300 m in both directions (Figure 7c).
Third Stage: Continued compression and uneven uplift introduce additional faults, causing a distortion of the elliptical projection surface (Figure 7d).
3.3.2. Division of Rock Stratum Groups and Rock Mechanical Parameters
The stratigraphic range for numerical simulation extends from the land surface down to the Emeishan Basalt Formation. “Rock stratum groups” are typically divided according to geological formations. The Longtan Formation is a coal-bearing stratum, with the 17# coal seam standing out as the primary mineable seam (average thickness: 2.74 m), easily identifiable in borehole logs. To analyze the mechanical properties of the coal-bearing strata in greater detail, the Longtan Formation was divided into upper and lower sections using the 17# coal seam floor as the boundary. The upper part of the Emeishan Basalt Formation consists predominantly of tuff interbedded with sandstone, mudstone, and several coal seams, which differ significantly in their properties from the lower basalt. Therefore, the upper part was treated as a separate division (Table 1).

Table 1.
Division and thickness statistics of the rock stratum groups.
The elastic modulus and Poisson’s ratio are critical parameters in rock mechanics, typically obtained through laboratory triaxial compression tests. However, the mechanical properties of rock samples do not always represent those of the rock mass. Additionally, due to sampling limitations, laboratory test data are often sparse. Recently, methods for calculating dynamic rock mechanical parameters using acoustic logging data have gained popularity. The dynamic Poisson’s ratio and elastic modulus can be calculated using the following formulas [37]:
In Equations (1) and (2), μd is the dynamic Poisson’s ratio (dimensionless); Ed is the dynamic modulus of elasticity (MPa); ρ is the rock bulk density (g/cm3); Δts is the transverse wave time difference in the stratum (μs/ft); and Δtp is the longitudinal wave time difference in the stratum (μs/ft).
Christensen et al. [37] obtained the relationship between Δts and Δtp based on measured data as follows:
In addition, the bulk modulus (G, MPa) and shear modulus (K, MPa) of rocks can be obtained according to the theory of elasticity as follows:
Based on acoustic logging data from two wells in the study area, the elastic modulus and Poisson’s ratio of the Feixianguan Formation (T1f), the upper Longtan Formation (P3l_a), the lower Longtan Formation (P3l_b), and the upper Emeishan Basalt Formation (P3β_a) were estimated using the above formulas. Further calculations provided the bulk modulus and shear modulus for these rock strata. Due to the absence of acoustic data for other rock stratum groups in the study area, acoustic logging data were collected from analogous rock formations in other regions [38,39]. The rock mechanical parameters of the Yongningzhen Formation (T1yn), Guanling Formation (T2g), and lower Emeishan Basalt Formation (P3β_b) were calculated. Since Equation (3) was derived from empirical data for sandstone, it requires modifications for other lithologies. Thus, while determining the mechanical parameters for each rock stratum group in the study area, values were calculated based on the formulas above and cross-referenced with empirical values for various rock types. Systematic adjustments were made to derive the final values (Table 2).

Table 2.
Classification of rock stratum groups and calculation parameters of the simulation in the study area.
3.3.3. Boundary Conditions of Tectonic Stress
The driving forces of the present-day stress field in eastern China primarily result from the westward subduction of the Pacific Plate beneath the Eurasian continent and the northwestward subduction of the Philippine Plate toward Eurasia. This combined effect causes the dominant orientation of the maximum horizontal principal stress in western Guizhou to align along a distinct NW–SE direction. However, in the vicinity of the study area, the orientation shifts to NWW–SEE (Figure 8).
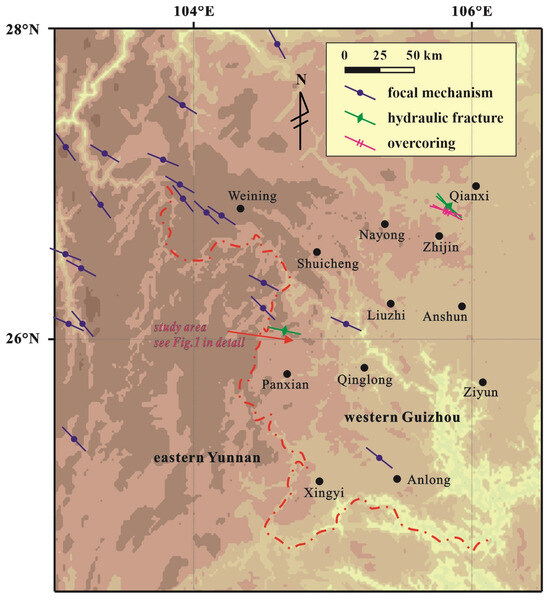
Figure 8.
The maximum horizontal stress orientation in the western Guizhou region. The data are from the World Stress Map (WSM) Database [40,41].
According to the stress data from coal seams in western Guizhou with depths of up to 1250 m, the magnitudes of vertical principal stress (σv), maximum horizontal principal stress (σHmax), and minimum horizontal principal stress (σHmin) exhibit significant variations with depth. Generally, in shallower coal seams, the stress relationship is σv > σHmax > σHmin, whereas in deeper seams, it shifts to σHmax > σv > σHmin [42,43].
Based on the geostress distribution data from the adjacent Panguan syncline’s wells JV-1 and YV-1 on the southern side of the study area [44], linear fitting was conducted to derive the relationship between the maximum and minimum horizontal principal stress values and depth, which is presented as follows:
In Equations (6) and (7), σHmax is the maximum horizontal principal stress (MPa); σHmin is the minimum horizontal principal stress (MPa); and h is the depth (m).
Wan [45,46] estimated paleotectonic stress magnitudes based on the relationship between stress and parameters such as the dynamically recrystallized grain size, subgrain size, and dislocation density in ultramicrostructures. According to his findings, the average differential stress values of paleotectonic stress during the Early Yanshanian period in eastern China ranged from 82.6 to 94.6 MPa, while those during the Late Yanshanian period ranged from 183 to 81 MPa. Similarly, Guo et al. employed the acoustic emission technique to test and estimate paleotectonic stress in northeastern China, reporting an average maximum horizontal stress of 107.6 MPa during the Late Yanshanian period [25]. This value is broadly consistent with Wan’s results. In this study, the paleotectonic stress boundary conditions were set using the estimates provided by Wan.
3.4. Prediction of Structural Fractures
Several strength theories are used to characterize rock fracture and failure, including the maximum tensile strain theory, the Mohr–Coulomb strength theory, the shear strain energy strength theory, the octahedral stress theory, and the Griffith theory. Among these, the Mohr–Coulomb strength theory (also known as the Mohr–Coulomb criterion) provides a comprehensive reflection of rock strength characteristics. This theory is applicable to both brittle and plastic materials, and its mechanical parameters are relatively easy to determine, making it widely used in engineering practice. According to the Mohr–Coulomb criterion, the rock fracture index can be expressed as follows (modified from reference [47]):
In Equation (8), η is the rock fracture index (dimensionless); f is the differential stress (MPa); k is the ultimate strength of the rocks (MPa); σ1 is the maximum horizontal principal stress (MPa); σ3 is the minimum horizontal principal stress (MPa); c is the cohesion (MPa); and φ is the internal friction angle (°).
When η ≥ 1, rock fracturing occurs. A higher η value indicates a greater degree of rock fracture and more developed fractures. Conversely, when η < 1, the rock remains stable, and fractures do not develop. Although real-world conditions may be more complex, this criterion provides a quantitative standard for evaluating the development of structural fractures in rock strata (Figure 9).
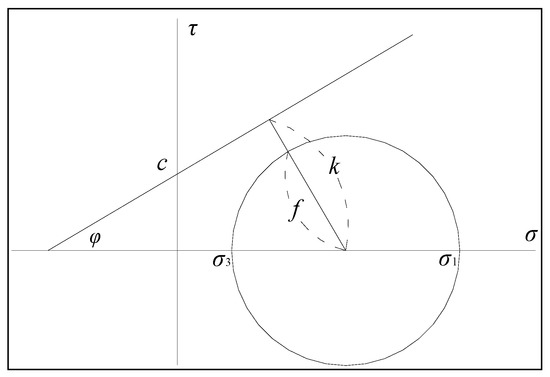
Figure 9.
The Mohr–Coulomb criterion schematic using the rock fracture index, modified from reference [47] (See Equation (8) for the meaning of the letters in the figure).
4. Results
4.1. Tectonic Deformation and Evolution
4.1.1. Mechanical Analysis of Regional Tectonic Deformation
In China, the classification of tectonic movements since the Mesozoic Era differs from the international standard. Specifically, the Alpine tectonic cycle is subdivided into three distinct tectonic cycles: the Indosinian, Yanshanian, and Himalayan cycles [48,49]. In this paper, we adopted the traditional division scheme for the Yanshanian period [48,50]. According to this scheme, the Middle–Late Jurassic period (175–145 Ma) is defined as the “Early Yanshanian period”, while the Late Cretaceous period (96–65 Ma) is termed the “Late Yanshanian period”.
The formation of the “山”-shaped structure in the Liupanshui–Qinglong–Panzhou region is intimately linked to the tectonic evolution during the Yanshanian period in central and western Guizhou. According to Wan Tianfeng’s research (1996, 2004), during the 175–135 Ma period (roughly the “Early Yanshanian” period), the principal tectonic stress in the Chinese mainland was characterized by nearly horizontal compression in the WNW–ESE direction. The maximum principal compressive stress axis was predominantly oriented at 116°∠7° (trend and plunge). Between 96 and 52 Ma (roughly the “Late Yanshanian” period), the tectonic stress in the Chinese mainland showed nearly horizontal compression in the NNE–SSW direction. The maximum principal compressive stress axis was dominantly oriented at 29°∠2° (trend and plunge) [45,46].
Based on the tectonic evolution history and formation mechanism, the “山”-shaped structure in the Liupanshui–Qinglong–Panzhou area can be explained as follows:
(1) During the Middle to Late Jurassic period, which corresponds to the Early Yanshanian period, the study area and its surroundings underwent near-horizontal shortening in a WNW–ESE direction. This tectonic activity resulted in the formation of a series of NNE–SSW-trending structures, primarily comprising fold belts and thrust faults. Notably, these included the folds and thrust faults located north of Gesuo, as well as those along the Panzhou–Yizikong regions. However, some other regions have only experienced relatively weak compression and, as a result, have not developed prominently deformed fold-to-fault belts (Figure 3).
(2) During the Late Cretaceous (Late Yanshanian period), the study area and its surroundings underwent intense NNE–SSW compression, acting nearly horizontally, which led to a significant shortening of the landmass along this direction. At this stage, the study area–Qinglong region can be likened to a crossbeam, with the NNE–SSW-trending structures (i.e., spine) in Gesuo and its northern region exerting compressive forces on this “crossbeam”. The reflective arc spine in the Panzhou–Yizikong area and the pillar to the south of Qinglong constrain the movement at both ends of the crossbeam, resulting in the formation of a reflex arc in the region of stress. As the two reflex arcs are compressed toward the north, a front arc bulges outward to the south between them, also reinforcing the development of the spine in the “山”-shaped structure. Fa’er is encircled by the WZL structural belt and the Gesuo spine, leading to minimal deformation and a simple structure (Figure 3). Thus far, the “山”-shaped structure in the Liupanshui–Qinglong–Panzhou area has essentially come into form.
Upon a broader examination of the surrounding region, it becomes evident that most areas are devoid of Jurassic and Cretaceous strata. Only a few scattered, small synclinal basins persist, containing terrestrial purple-red conglomerates, sandstones, and shales that belong to the Lower–Middle Jurassic and Upper Cretaceous periods. This observation aligns with the tectonic stage divisions in the local area.
4.1.2. Tectonic Evolution of the Study Area
Based on the analysis of tectonic evolution presented above and in conjunction with the present structural features of the study area, the formation and evolution of the Tucheng syncline are relatively well understood. The structural evolution of the study area can be divided into three distinct stages, spanning from the Mesozoic Yanshanian period to the Cenozoic Himalayan period, as outlined below.
(1) During the Early Yanshanian period (spanning the Middle to Late Jurassic), the study area experienced nearly horizontal compressional forces that were oriented WNW–ESE. These forces were not particularly strong, and they led to the formation of a relatively broad and gently dipping syncline with an axis strike of NNE–SSW.
(2) During the Late Yanshanian period (Late Cretaceous), the Tucheng syncline experienced intense horizontal compression in the NNE–SSW direction. This led to a change in the long axis of the original syncline, converting from NNE–SSW to WNW–ESE. Concurrently, reverse faults developed in the WNW–ESE direction. Consequently, the Tucheng syncline is recognized as a superimposed fold, exhibiting the characteristics of a short-axis syncline.
(3) Since the Himalayan period (Paleogene~), uneven uplift has resulted in the entire synclinal basin tilting toward the southeast. Consequently, the outcrop of the coal-bearing strata has transformed from a regular elliptical shape to a skewed one. Simultaneously, continued compression in the NNE–SSW direction has given rise to multiple reverse faults that are parallel to the long axis of the ellipse in the SW wing of the syncline, causing the syncline basin to be incomplete.
4.2. Reconstruction of the Paleotectonic Stress Field
Based on joint statistical data from the study area, the stereographic projection method was employed to determine the orientations and combinations of predominant joints, enabling the classification and matching of conjugate shear joint systems. This process identified the principal stress orientations at each observation point and facilitated the reconstruction of the paleotectonic stress field. The results indicate that the study area underwent two distinct stages of tectonic stress field evolution (Table 3).

Table 3.
Analysis of principal stress at each measuring point.
First Stage (Early Yanshanian period): The tectonic stress field exhibited maximum principal stress traces oriented NWW–SEE. In the western part of the study area, the maximum principal stress axis deviated slightly toward the NW direction.
Second Stage (Late Yanshanian period): The tectonic stress field displayed maximum principal stress traces oriented NEN–SWS, with relatively regular stress trace patterns (Figure 10).
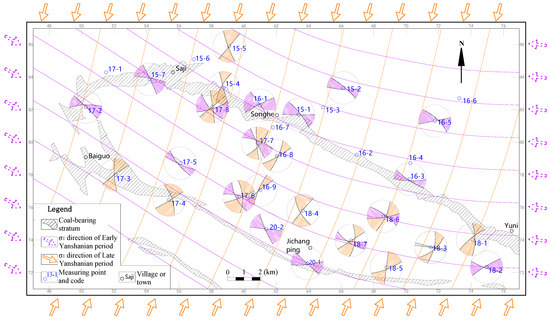
Figure 10.
The maximum principal stress direction of the study area in the Early and Late Yanshanian period.
Stress analysis revealed that most observation points resolved a pair (two groups) of conjugate shear joints, corresponding either to the first or the second stage. A few observation points yielded two pairs (four groups) of conjugate shear joints, representing both stages. Differences in orientation, angle, and other parameters among the conjugate shear joint combinations were observed, likely due to variations in boundary conditions, rock lithology, and stratum thickness across the study area. These local deviations did not affect the overall stress field reconstruction. A small number of observation points were excluded from the analysis due to poor outcrop conditions or the absence of measurable stratigraphic orientations.
4.3. Numerical Simulation of the Paleotectonic Stress Fields in Different Stages
4.3.1. Simulation of the First Stage (Cylindrical Surface Model)
Numerical simulations were conducted using the Flac3D software. After the first stage of horizontal compression, the strata in the study area deformed into a near-semicylindrical fold with an upright axial plane and horizontal hinge. A cylindrical surface equation was derived based on the dimensions of the cylindrical model. The Fish language was used for programming to identify and establish different “rock stratum groups” during modeling (Figure 11a). The model consisted of 90 × 40 × 90 units along the x-, y-, and z-axes, totaling 324,000 units. Using the cylindrical surface equation, the internal rock stratum groups were outlined with regular shapes, meeting the simulation requirements, such as the upper Longtan Formation (P3l_a, Figure 11b).
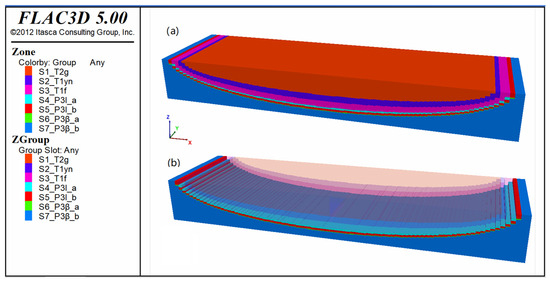
Figure 11.
Cylindrical surface model. (a) Overall framework of 3D model; (b) internal structure of 3D model.
Fish is an embedded programming language in the Flac3D 5.00 software, which has good flexibility and a simple syntax. The types of rock stratum groups and the formula for the elliptic-cylindrical surface were defined through the Fish language. Then, all units of the model were traversed by pointers to identify and create the desired multiple rock stratum groups. In this way, a model with an elliptic-cylindrical shape consisting of multiple rock stratum groups was created (Appendix A.1).
In this model, velocity constraints were applied along the y-axis, with full constraints at the base. Loading was applied along the x-axis, with a basal load of 80 MPa and a stress gradient of 0.015 MPa/m (due to a lack of paleostress gradient data, the present-day stress gradient was used). An elastic mechanics model was employed, with the maximum unbalanced force ratio (computational precision) set to the default value of 1 × 10−5. Upon completing the calculation, the differential stress (σ1 − σ3) was used to visualize the stress state of the target layer (P3l_a). The results showed that the maximum differential stress in the target layer was approximately 54.64 MPa. Stress was concentrated in the central region of the cylindrical surface, with differential stress gradually decreasing symmetrically toward both sides (Figure 12).
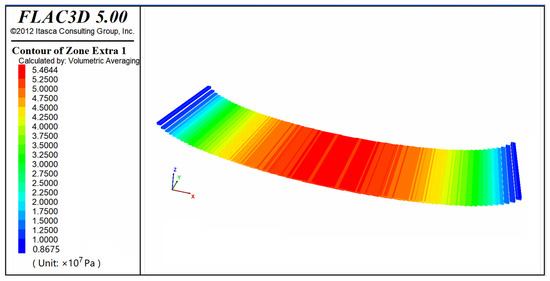
Figure 12.
Differential stress distribution of the upper coal-bearing strata (P3l_a) during the first deformation stage.
4.3.2. Simulation of the Second Stage (Ellipsoid Surface Model)
After experiencing two compressional events from nearly perpendicular directions, the strata in the study area deformed into a near-semi-ellipsoidal synclinal basin. Based on the dimensions of the ellipsoidal model, an ellipsoid surface equation was established. Similarly, the Fish language was used for programming to identify and construct different “rock stratum groups” (Figure 13a). The model consisted of 80 × 50 × 60 units along the x-, y-, and z-axes, totaling 240,000 units. Through the ellipsoid surface equation, the stratigraphic groups, including the upper Longtan Formation (P3l_a, Figure 13b), were outlined effectively.
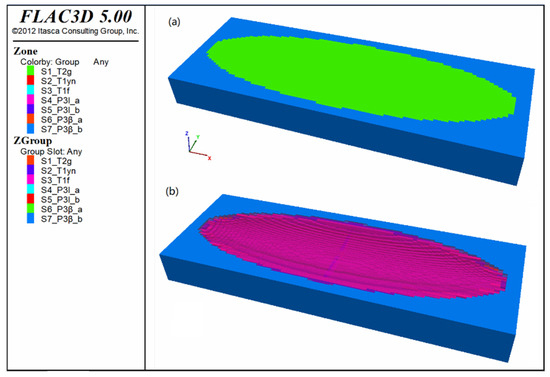
Figure 13.
Ellipsoid surface model. (a) Overall framework of 3D model; (b) internal structure of 3D model.
Velocity constraints were applied along the x-axis, with full constraints at the base. Loading was applied along the y-axis with a basal load of 130 MPa. Given the higher load, the stress gradient was appropriately increased to 0.03 MPa/m. An elastic mechanics model was employed, with computational precision set to the default value of 1 × 10−5. After computation, the differential stress (σ1 − σ3) was used to visualize the stress state of the target layer (P3l_a). The results showed a maximum differential stress of approximately 53.31 MPa. The stress concentration zone primarily appeared along the long axis of the synclinal basin margin, with a secondary location at the basin center. The areas between the basin margin and the basin center, particularly at the ends of the long axis, were low-stress zones, displaying notable symmetry (Figure 14).
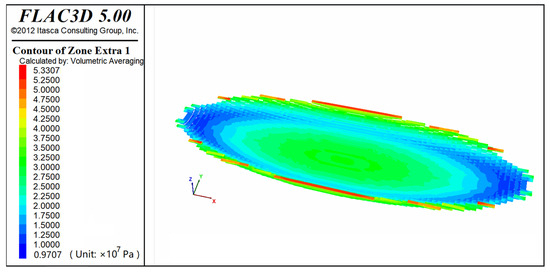
Figure 14.
Differential stress distribution of the upper coal-bearing strata (P3l_a) during the second deformation stage.
4.3.3. Simulation of the Third Stage (Trend Surface Model)
The present-day geological structure of the study area is relatively complex. It is characterized as a short-axis synclinal basin with a long axis oriented NWW–SEE. During the third stage of tectonic activity, the NW side of the synclinal basin experienced uplift, resulting in a near-semi-ellipsoidal synclinal basin with slight distortions. Additionally, faults developed along the SW limb of the syncline, partially cutting the synclinal structure and resulting in it being incomplete (Figure 1). The geological model for the third stage was constructed in two steps: (1) Using the ANSYS 10.0 platform, modules on both sides of the fault were established, and the surface model was created using “skinning” techniques. (2) The modules from the ANSYS platform were imported into Flac3D, where fault planes were added. A trend surface equation for the strata was established, and the Fish language was used to identify and define different “rock stratum groups” (Figure 15).
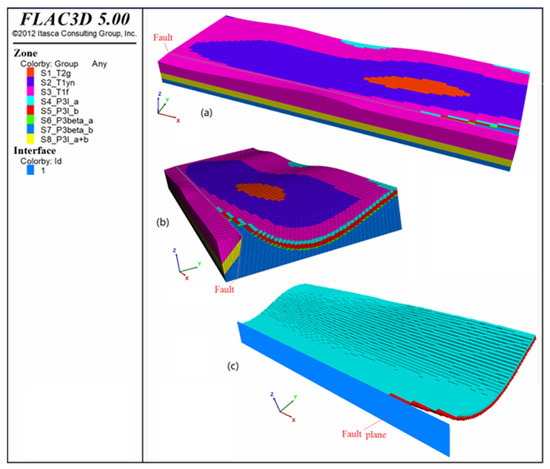
Figure 15.
Trend surface model. (a) Overall framework of 3D model (in long axis direction); (b) overall framework of 3D model (in short axis direction); (c) internal structure of 3D model.
The model contained 134,400 units. Full constraints were applied at the base. Loads were applied along the x- and y-axes, calculated using Equations (6) and (7). The x-axis basal load was 33.68 MPa, and the y-axis basal load was 30.00 MPa, with a stress gradient of 0.015 MPa/m in both directions. An elastic mechanics model was used, with computational precision set to the default value of 1 × 10−5. Upon computation, the differential stress (σ1 − σ3) was used to visualize the stress state of the target layer (P3l_a). The results revealed a maximum differential stress of approximately 23.37 MPa, with the stress concentration zone primarily located at the basin floor (Figure 16).
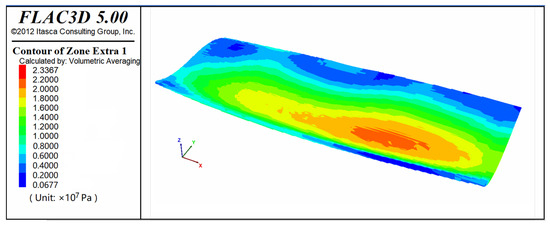
Figure 16.
Differential stress distribution of the upper coal-bearing strata (P3l_a) during the present stage.
4.4. Prediction Results of Structural Fractures
According to Equation (8), combined with the Fish programming language, the rock fracture index (η) was calculated, and its distribution characteristics were visualized in a 3D model in Flac3D. During the first stage of deformation, the fracture index of the coal-bearing strata (P3l_a) showed a maximum at the center, gradually decreasing symmetrically toward both sides. The fracture index in the central region exceeded 1 (Figure 17).
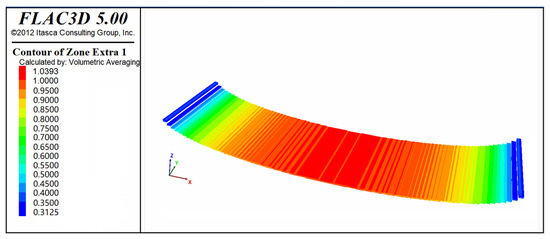
Figure 17.
Distribution of the fracture index (η) for P3l_a during the first deformation stage.
During the second stage of deformation, the coal-bearing strata (P3l_a) were subjected to compressive stress in the NEN–SWS direction, forming a near-ellipsoidal synclinal basin with a long axis oriented NWW–SEE. Both the basin center and the margins, particularly along the long axis, exhibited fracture index values exceeding 1 (Figure 18).
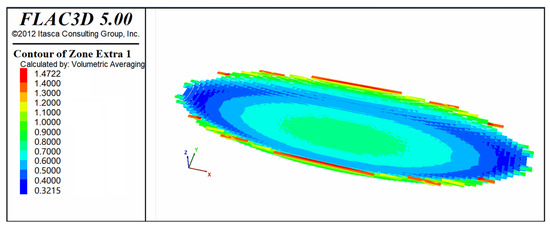
Figure 18.
Distribution of the fracture index (η) for P3l_a during the second deformation stage.
The distribution of the fracture index during the first and second deformation stages correlates well with the differential stress (σ1 − σ3) distribution patterns observed during the same periods (Figure 12 and Figure 14). This consistency supports the theoretical application of the Mohr–Coulomb criterion in rock failure analysis.
An elastic constitutive model was adopted for the stress field simulation in this study. Since the target of the simulation is a static geological body at a specific stage, rather than a dynamic one subjected to long-term deformation, the use of an elastic model is consistent with the assumptions of material continuity and instantaneous deformation. In fact, adopting a plastic constitutive model would yield negligible differences in the simulated stress field. Furthermore, once the stress field is established, failure analysis based on the Mohr–Coulomb criterion—premised on plastic failure—is valid regardless of the method used to derive the stress field.
5. Discussion
5.1. Analysis of the Structural Fracture Development Trend
After the first and second deformation stages, the tectonic framework of the study area became largely established. Furthermore, the structural fractures developed during these stages represent the primary proportion of the present-day structural fractures, reflecting the characteristics of fracture development in the current study area.
The locations and degrees of fracture development differed between the first and second stages. Although the 3D visualization of the coal-bearing strata effectively illustrates the spatial distribution of the fracture index, it is less suitable for observing the superimposed effects of multiple stages. To examine the overall fracture characteristics resulting from the two deformation stages, the fracture index of the basal surface of the upper coal-bearing strata (P3l_a, as defined in Table 1) was extracted. Using the synclinal basin center as the origin, the indices were superimposed and displayed in a planar projection. The results showed that the fracture index was generally greater than 1 after being superimposed, indicating widespread structural fracture development in the coal-bearing strata. However, the fracture development trends varied across different locations. Fracture development was highest at the basin margins along the long axis (NWW–SEE), moderate to high in the synclinal center, and relatively low at both ends of the long axis (Figure 19). Field observations confirmed that although the deep coal seams were not visible, the outcrops of coal-bearing strata at the basin margins exhibited relatively high joint densities.
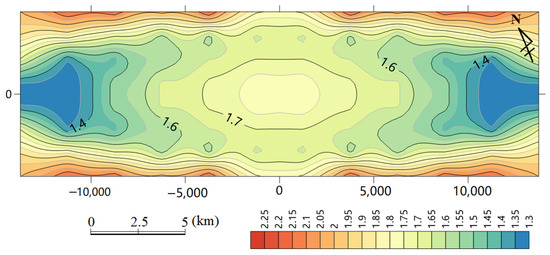
Figure 19.
Dimensionless distribution of the fracture index (η) for the 17# coal seam after deformation superposition.
5.2. The Effect of Structural Position on Structural Fractures
The principle of brittle failure in rocks can be illustrated using a strain ellipse. The short axis of the strain ellipse represents the orientation of the maximum principal stress (σ1), while the long axis corresponds to the minimum principal stress (σ3). The σ1 direction also coincides with the acute bisector of the conjugate shear fracture planes. For a single brittle rock layer in a synclinal structure, the inner side of the hinge zone experiences compressive stress, the outer side experiences tensile stress, and the middle portion is a “neutral layer” with neither compression nor tension. According to this principle, two sets of conjugate shear fractures develop on the inner side of the hinge zone, while a single set of tensile fractures forms on the outer side. Due to interlayer slip during the folding process, a pair of clockwise shear couples act on the synclinal limbs, generating an obliquely oriented strain ellipse and two corresponding sets of conjugate shear fractures. The orientation of these fractures deviates slightly from that of the conjugate shear fractures at the hinge zone (Figure 20a).
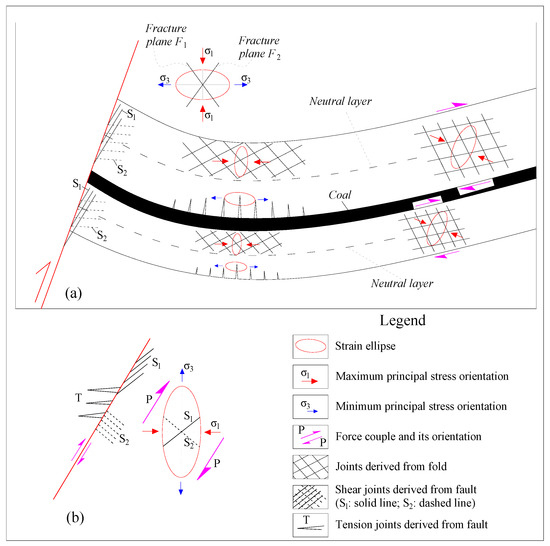
Figure 20.
Schematic diagram of the characteristics and principles of structural fracture development. (a) The development characteristics of structural fractures in a syncline with fault cutting; (b) the principle of structural fracture development at the edge of a reverse fault, modified from reference [33].
In cases where a synclinal limb is truncated by a reverse fault, relative motion between the two fault blocks results in shearing along the fault edges. Based on the same principle, two additional sets of shear fractures can develop on one side of the fault. One fracture set (S1) intersects the fault plane at a small angle, while the other set (S2) intersects the fault plane at nearly a right angle (Figure 20a,b).
Figure 20 illustrates the combination pattern of coal and rock layers in the study area. In the study area, the coal-bearing strata contain multiple coal seams interbedded with brittle rock layers such as sandstone and siltstone. The coal type is primarily coking coal, characterized by a high degree of metamorphism, compactness, and brittleness. Based on the above geomechanical analysis, it is evident that the structural fractures developed in the coal-bearing strata are multi-layered, exhibit various properties, and have complex combinations. The structural fractures in the coal seams are similar to those in the rock layers, but the thinness of the coal seams makes it difficult to depict their fracture development patterns in this Figure.
For the numerical simulations, the stratigraphy was simplified into several layers for modeling purposes. In these simulations, the coal-bearing strata were roughly divided into two layers. Despite this simplification, the distribution characteristics of the rock fracture index shown in the simulation results effectively reflect the trends in structural fracture development. However, it is important to understand that the actual structural fractures are multi-layered and diverse in nature, and occur in complex, coexisting combinations.
5.3. Control of CBM Migration by the Modern Stress Field and Structural Fractures
Previous studies have shown that the orientation of fractures in coal seams is similar to that in rock layers [15]. As described earlier, the predominant joint orientations in the study area are NEN–NE (15–45°) and NW (300–325°), with most dip angles exceeding 65°. Since the coal seams and rock layers in the study area underwent the same tectonic evolution and stress processes, it can be inferred that the development characteristics of coal seam fractures are similar to those of rock layers.
The Tucheng syncline in the study area is an undeveloped CBM gas field. In the Songhe Mine area, test wells have already been drilled, achieving promising gas production results [51]. Based on the characteristics of the structural fractures in the study area, it is recommended that CBM development strategies, including fracturing in coal reservoirs, consider the predominant joint orientations and characteristics of the current in situ stress field. Given that the structural fractures in the study area exhibit clear NEN–NE and NW orientations, alternating these two orientations as the maximum principal stress direction during hydraulic fracturing is likely to facilitate the opening of coal seam fractures, making it a favorable approach.
Coal mining activities are already underway near the study area, particularly in the Songhe mining area, located on the northeast side, known as the NE wing of the syncline, where the mining operations are relatively extensive. As coal is mined, gas is extracted from it, leading to a steady reduction in CBM content in the edge region of the syncline basin. The center of the basin, in the southeastern direction, is the differential stress zone of highest stress, with stress gradually decreasing toward the surrounding areas (Figure 21). CBM tends to diffuse from high to low concentrations and migrate from high-stress to low-stress areas. Based on this, it is speculated that the CBM in the study area follows this trend, diffusing and migrating from the high-stress zone at the basin center to the lower-stress areas around it.
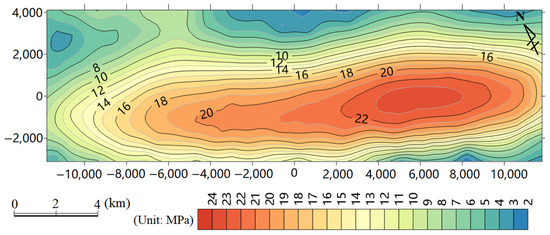
Figure 21.
The distribution of differential stress in the 17 # coal seam at the present stage.
5.4. Problems and Shortcomings
In this paper, during the numerical simulation of the study area, the models of each stage are different, and their corresponding boundary conditions are also different. The boundary conditions of each stage are given with reference to the research results of the related literature, but the following two implied problems need to be pointed out and discussed.
(1) The problem of the paleostress gradient
It is generally assumed that the present-day shear stress at the Earth’s surface is 0, so a geostress gradient can be obtained by geostress testing. However, this should not have been the case during geologic history, especially during the intense extrusion and deformation of the Earth’s crust. Although some scholars have obtained the magnitude of paleostress during a certain period of geologic history through research, no research on paleostress gradients has been seen thus far. Due to the lack of data in this area, the present-day ground stress gradient was used instead of the paleostress gradient in this paper. Taking the elliptic-cylindrical surface model (the first model) as an example, the stress magnitude at the bottom of the model refers to a data point from the literature, which was 80 MPa. The stress magnitude at the ground level was calculated using the present-day ground stress gradient, and the result was 12.5 MPa. It may be that the actual ground stress was greater or lesser than this value, but in the absence of knowledge about the paleostress gradient, such an assumption is always better than having no gradient set (i.e., a gradient of 0).
The size of the paleostress gradient has an effect on the simulation results. However, with the model structure, material parameters, and other boundary conditions unchanged, changes in the paleostress gradient will only affect the numerical values of the simulation results and will have little effect on the stress distribution law in the simulation results. This is acceptable for the purpose of this paper.
(2) Verification of the simulation results
The simulations suggest that structural fractures are strongly developed at the margins of the elliptical basin parallel to the long axis (i.e., high fracture index, Figure 19). Although the relatively high density of joints in the coal-bearing strata in the surface outcrops of the basin margins was also noted in the field observations, which were also described in previous texts, there was a lack of observations and comparisons of the degree of structural fracture development in other locations. This is a practical problem that is difficult to solve. This is because the limited number of boreholes are distributed in the basin margin area, which is also the case for coal mines under mining, and there are only a few coal roads available for observation underground. In addition, there are no conditions for carrying out a large-scale specialized survey of deep underground structural fractures.
In fact, evaluating the degree of structural fracture development in deep coal-bearing strata is itself a current challenge, and the work conducted in this paper is also exploratory for this problem. On the one hand, it is hoped that the study results will have a certain guiding effect on the future development of coalbed methane. On the other hand, it is also expected that the study results of this paper will be verified or corrected in future engineering practice.
6. Conclusions
(1) The study area, the Tucheng syncline, is situated within a regional structure that can be called a “山”-shaped structure. It is specifically located at the left reflex arc of this “山”-shaped structure. The structural evolution of the Tucheng syncline can be clearly divided into three stages. Stage 1: In the Early Yanshanian period (Middle to Late Jurassic), a relatively broad and gentle syncline was formed in the study area as a result of nearly horizontal shortening in the WNW–ESE direction, with an axial orientation of NNE–SSW. Stage 2: During the Late Yanshanian period (Late Cretaceous), a significant shortening occurred in the NNE–SSW direction toward a nearly horizontal orientation. This caused the formation of a short-axis syncline with a long axis trending WNW–ESE and the development of some reverse faults with the same strike as the long axis. Stage 3: Since the Himalayan period (Paleogene~), the entire synclinal basin has tilted to the southeast, and the outcrop of the coal-bearing strata has transformed from a regular elliptical shape to a skewed one. At the same time, faults have further developed and have been locally cut the synclinal basin.
(2) The predominant orientations of the rock joints in the study area are NNE–NE (15–45°) and NW (300–325°), with dip angles typically 65° or steeper. The paleotectonic stress field of the area was reconstructed using joint statistics and the stereographic projection method. It is believed that during the first period (Early Yanshanian period), the maximum principal stress trace was oriented in the WNW–ESE direction, with the maximum principal stress axis deviating northwest in the western part of the study area. During the second period (Late Yanshanian period), the maximum principal stress trace was in the NNE–SSW direction and exhibited a relatively regular pattern.
(3) The results of the numerical simulation showed the following: Stage 1 (Early Yanshanian period): The maximum differential stress of the target layer (No.17# coal seam) is approximately 54.64 MPa. The central region of the cylinder serves as the stress concentration zone, with the differential stress decreasing symmetrically from the center outward to both sides. Stage 2 (Late Yanshanian period): The maximum differential stress of the target layer is approximately 53.31 MPa. The primary stress concentration occurs along the major axis of the syncline’s basin edge, while the secondary stress concentration is located at the center of the basin bottom. The region situated between the basin edge and the basin bottom constitutes a low-stress zone, exhibiting a well-balanced and symmetrical stress distribution. Stage 3 (current stage): The maximum differential stress within the target layer is approximately 23.37 MPa, with the stress concentration localized at the basin’s bottom.
(4) Rock fracture indices for different stages of tectonic deformation were calculated based on the Mohr–Coulomb criterion. The distribution of the rock fracture indices during the first and second stages of deformation aligned with the distribution patterns of differential stress (σ1 − σ3) observed during the corresponding periods. The superimposed rock fracture indices were generally greater than 1, indicating that structural fractures have been extensively developed in the coal-bearing strata. The development trend in structural fractures varied significantly across different regions. Specifically, a higher trend was observed at the basin edge along the long axis direction (WNW-ESE). At the center of the syncline, the trend was moderately high. In contrast, the trends at both ends of the syncline, along the same long axis direction, were relatively lower. The structural fractures that developed in the coal-bearing strata exhibited distinct characteristics: they were multi-layered, possessed diverse properties, and occurred in symbiotic combinations.
Author Contributions
The specific contributions of all authors to the preparation of this manuscript are as follows. J.W.: conceptualization, formal analysis, investigation, methodology, and writing—original draft and editing; L.J.: investigation, writing—original draft preparation, and visualization; T.C.: investigation, data curation, and visualization; X.Z.: project administration, funding acquisition, and writing—review and editing. B.W.: data curation and visualization. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 42030810) and the Guizhou Province Energy Technology Project (No.2023-68). The APC was funded by Grant No. 42030810.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. The Core Program Segments of Fish Language Programming
def set_rock_gro; Define the type of rock stratum groups
array grop_n(7)
grop_n(1)='S1_T2g' ; Guanling Formation
grop_n(2)='S2_T1yn' ; Yongningzhen Formation
grop_n(3)='S3_T1f' ; Feixianguan Formation
grop_n(4)='S4_P3l_a' ; Longtan Formation (Above the floor of coal seam 17#)
grop_n(5)='S5_P3l_b' ; Longtan Formation (Below the floor of coal seam 17#)
grop_n(6)='S6_P3β_a' ; Emeishan basalt (Containing coal seam segments)
grop_n(7)='S7_P3β_b' ; Emeishan basalt (Excluding coal seam sections)
end
def calculat_cyl ; Define the formula for calculating elliptical cylindrical surfaces
flag_1 = x^2/x_1^2+z^2/z_1^2
flag_2 = x^2/x_2^2+z^2/z_2^2
flag_3 = x^2/x_3^2+z^2/z_3^2
flag_4 = x^2/x_4^2+z^2/z_4^2
flag_5 = x^2/x_5^2+z^2/z_5^2
flag_6 = x^2/x_6^2+z^2/z_6^2
end
def Creat_stra ; Create the module of rock stratum groups
p_z = zone_head
loop while p_z # null
x = z_xcen(p_z)
z = z_zcen(p_z)
calculat_cyl
if flag_1 <= 1 then
z_group(p_z)=grop_n(1)
else
if flag_2 <= 1 then
z_group(p_z)=grop_n(2)
else
if flag_3 <= 1 then
z_group(p_z)=grop_n(3)
else
if flag_4 <= 1 then
z_group(p_z)=grop_n(4)
else
if flag_5 <= 1 then
z_group(p_z)=grop_n(5)
else
if flag_6 <= 1 then
z_group(p_z)=grop_n(6)
else ; equivalent to flag_6 > 1
z_group(p_z)=grop_n(7)
end_if
end_if
end_if
end_if
end_if
end_if
p_z=z_next(p_z)
endloop
end
References
- Shi, J.X.; Zeng, L.B.; Zhao, X.Y.; Zhang, Y.Z.; Wang, J.P. Characteristics of natural fractures in the upper Paleozoic coal bearing strata in the southern Qinshui Basin, China: Implications for coalbed methane (CBM) development. Mar. Pet. Geol. 2020, 113, 104152. [Google Scholar]
- Wang, L.L.; Jiang, B.; Wang, J.L.; Wang, J.Y.; Qu, Z.H. Effects of in-situ stress and joint on permeability of the coal bed in Linfen block, southeastern Ordos asin, China. Russ. Geol. Geophys. 2018, 59, 299–312. [Google Scholar] [CrossRef]
- Liu, H.H.; Sang, S.X.; Xue, J.H.; Wang, G.X.; Xu, H.J.; Ren, B.; Liu, C.J.; Liu, S.Q. Characteristics of an in situ stress field and its control on coal fractures and coal permeability in the Gucheng block, southern Qinshui Basin, China. J. Nat. Gas Sci. Eng. 2016, 36, 1130–1139. [Google Scholar]
- Karimpoulia, S.; Tahmasebib, P.; Ramandi, H.L. A review of experimental and numerical modeling of digital coalbed methane: Imaging, segmentation, fracture modeling and permeability prediction. Int. J. Coal Geol. 2020, 228, 103552. [Google Scholar] [CrossRef]
- Yang, S.Y.; Cai, Y.D.; Wei, R.; Zhou, Y.F. A new fracture permeability model of CBM reservoir with high-dip angle in the southern Junggar Basin, NW China. Energy Explor. Exploit. 2019, 37, 125–143. [Google Scholar] [CrossRef]
- Engelder, T.; Lash, G.G.; Uzcátegui, R.S. Joint sets that enhance production from Middle and Upper Devonian gas shales of the Appalachian Basin. AAPG Bull. 2009, 93, 857–889. [Google Scholar]
- Wang, K.; Guo, L.; Xu, C.; Wang, W.J.; Yang, T.; Lin, S.S.; Cai, Y.B. Multiscale characteristics of pore-fracture structures in coal reservoirs and their influence on coalbed methane (CBM) transport: A review. Geoenergy Sci. Eng. 2024, 242, 213181. [Google Scholar] [CrossRef]
- Fang, H.H.; Sang, S.X.; Wang, J.L.; Liu, S.Q.; Ju, W. Simulation of Paleotectonic Stress Fields and Distribution Prediction of Tectonic Fractures at the Hudi Coal Mine, Qinshui Basin. Acta Geol. Sin. 2017, 91, 2007–2023. [Google Scholar] [CrossRef]
- Gong, W.D. Paleo-tectonic Stress Field and Tectonic Evolution since the Mesozoic in the Eastern Mining Area of Pingdingshan. Earth Sci. Res. J. 2019, 23, 347–357. [Google Scholar] [CrossRef]
- Lin, C. Tectonic Stress Reconstruction Based on Structural Features in Tectonic Superposition Areas. Min. Metall. Explor. 2020, 37, 387–397. [Google Scholar] [CrossRef]
- Zhang, H.T.; Xu, G.Q.; Zhan, H.B.; Li, X.; He, J.H. Simulation of multi-period paleotectonic stress fields and distribution prediction of natural Ordovician fractures in the Huainan coalfield, Northern China. J. Hydrol. 2022, 612, 128291. [Google Scholar] [CrossRef]
- Song, L.J.; Wang, Z.Z. Late Triassic tectonic stress field of the southwestern Ordos Basin and its tectonic implications: Insights from finite-element numerical simulations. Geosphere 2023, 19, 770–781. [Google Scholar] [CrossRef]
- Ju, W.; Wang, J.L.; Fang, H.H.; Gong, Y.P.; Zhang, S.J. Paleostress reconstructions and stress regimes in the Nanchuan region of Sichuan Basin, South China: Implications for hydrocarbon exploration. Geosci. J. 2017, 21, 553–564. [Google Scholar] [CrossRef]
- Li, H.; Qin, Q.R.; Zhang, B.J.; Ge, X.Y.; Hu, X.; Fan, C.H.; Tang, H.M. Tectonic Fracture Formation and Distribution in Ultradeep Marine Carbonate Gas Reservoirs: A Case Study of the Maokou Formation in the Jiulongshan Gas Field, Sichuan Basin, Southwest China. Energy Fuels 2020, 34, 14132–14146. [Google Scholar]
- Wang, J.L.; Wang, Y.K.; Zhou, X.Z.; Xiang, W.X.; Chen, C.R. Paleotectonic Stress and Present Geostress Fields and Their Implications for Coalbed Methane Exploitation: A Case Study from Dahebian Block, Liupanshui Coalfield, Guizhou, China. Energies 2024, 17, 101. [Google Scholar] [CrossRef]
- De Guidi, G.; Caputo, R.; Scudero, S. Regional and local stress field orientation inferred from quantitative analyses of extension joints: Case study from southern Italy. Tectonics 2013, 32, 239–251. [Google Scholar] [CrossRef]
- Kumaira, S.; Guadagnin, F.; Magalhães, A.J.; Pimentel, N.L.; Chemale, F., Jr. Post-Jurassic brittle deformation of Lusitanian Basin in the context of W Iberia evolution. Basin Res. 2023, 35, 2165–2192. [Google Scholar] [CrossRef]
- Lash, G.G.; Engelder, T. Tracking the burial and tectonic history of Devonian shale of the Appalachian Basin by analysis of joint intersection style. Geol. Soc. Am. Bull. 2009, 121, 265–277. [Google Scholar] [CrossRef]
- Seminsky, K.Z.; Cheremnykh, A.V. Jointing patterns and stress tensors in Cenozoic sediments of the Baikal rift: Development of the structural-genetic approach. Russ. Geol. Geophys. 2011, 52, 353–367. [Google Scholar] [CrossRef]
- Eshiet, K.I.I.; Sheng, Y.; Yang, D.M. Evaluating the corollary of the interdependency of rock joint properties on subsurface fracturing. Bull. Eng. Geol. Environ. 2021, 80, 567–597. [Google Scholar] [CrossRef]
- Li, H.; Lin, C.Y.; Ren, L.H.; Zhang, G.Y.; Chang, L.J.; Dong, C.M. Quantitative prediction of multi-period tectonic fractures based on integrated geological-geophysical and geomechanics data in deep carbonate reservoirs of Halahatang oilfield in northern Tarim Basin. Mar. Pet. Geol. 2021, 134, 105377. [Google Scholar]
- Roy, D.G.; Singh, T.N.; Kodikara, J. Influence of joint anisotropy on the fracturing behavior of a sedimentary rock. Eng. Geol. 2017, 228, 224–237. [Google Scholar]
- Eyssautier-Chuine, S.; Odonne, F.; Massonnat, G. Control of bioclast abundance on natural joint density in carbonate rocks: Data from Oman, Provence and Languedoc (France). Terra Nova 2002, 14, 198–204. [Google Scholar]
- Whitaker, A.E.; Engelder, T. Characterizing stress fields in the upper crust using joint orientation distributions. J. Struct. Geol. 2005, 27, 1778–1787. [Google Scholar]
- Guo, P.; Yao, L.H.; Ren, D.S. Simulation of three-dimensional tectonic stress fields and quantitative prediction of tectonic fracture within the Damintun Depression, Liaohe Basin, northeast China. J. Struct. Geol. 2016, 86, 211–223. [Google Scholar]
- Liu, H.; Zuo, Y.J.; Rodriguez-Dono, A.; Wu, Z.H.; Sun, W.J.; Zheng, L.L.; Pan, C.; Lin, J.Y.; Du, S.Y. Study on multi-period palaeotectonic stress fields simulation and fractures distribution prediction in Lannigou gold mine, Guizhou. Geomech. Geophys. Geo-Energy Geo-Resour. 2023, 9, 92. [Google Scholar] [CrossRef]
- Xie, Q.; Li, G.; Yang, X.; Peng, H.L. Evaluating the Degree of Tectonic Fracture Development in the Fourth Member of the Leikoupo Formation in Pengzhou, Western Sichuan, China. Energies 2023, 16, 1797. [Google Scholar] [CrossRef]
- Fu, X.L.; Dai, J.S.; Feng, J.W. Prediction of tectonic fractures in coal reservoirs using geomechanical method. Geosci. J. 2018, 22, 589–608. [Google Scholar]
- Ju, W.; Yang, Z.B.; Qin, Y.; Yi, T.S.; Zhang, Z.G. Characteristics of in-situ stress state and prediction of the permeability in the Upper Permian coalbed methane reservoir, western Guizhou region, SW China. J. Pet. Sci. Eng. 2018, 165, 199–211. [Google Scholar]
- Wang, J.L.; Li, M.; Xu, S.C.; Qu, Z.H.; Jiang, B. Simulation of Ground Stress Field and Advanced Prediction of Gas Outburst Risks in the Non-Mining Area of Xinjing Mine, China. Energies 2018, 11, 1285. [Google Scholar] [CrossRef]
- Li, S.G. An Introduction to Geomechanics: The Method and Practice of Geomechanics, Volume I, 2nd ed.; Geological Publishing House: Beijing, China, 1999; pp. 41–49, 80. (In Chinese) [Google Scholar]
- Yue, G.Y. A New Discussion on the Tectonic Framework in Liuzhi–Panxian–Shuicheng Region, Guizhou Province. Geol. Guizhou 1991, 8, 289–300, (In Chinese with English Abstract). [Google Scholar]
- Xie, R.H.; Qu, T.X.; Qian, G.M. Structural Geology; China University of Mining and Technology Press: Xuzhou, China, 1991; p. 230. (In Chinese) [Google Scholar]
- Wang, Y.; Du, W.; Wang, Y.Y.; Lin, R.Q.; Zhang, D.Q.; Zhao, F.P.; Sun, Z.; Chen, Y.; Wang, Y. Meso-cenozoic tectonic evolution of the Ziyun-Luodian fault in SW China. Front. Earth Sci. 2022, 10, 970944. [Google Scholar] [CrossRef]
- Ramsay, J.G.; Huber, M.I. The Techniques of Modern Structural Geology, Volume 2: Folds and Fractures; Academic Press: London, UK, 1997; pp. 641–666. [Google Scholar]
- Dou, X.Z.; Jiang, B.; Qin, Y.; Qu, Z.H.; Li, M. Tectonic Control of Coalbed Methane Reservoirs in Panxian, Western Guizhou. Geol. J. China Univ. 2012, 18, 447–452, (In Chinese with English Abstract). [Google Scholar]
- Yang, X.J.; Zhang, M.; Yan, X.Z. Study on acoustic logging-based rock elasticity parameters. Pet. Geol. Eng. 2008, 22, 39–42, (In Chinese with English Abstract). [Google Scholar]
- Liu, J.; Huang, C.; Zhou, L.; Chen, Q.; Zhang, S.L. Estimation of the rock mechanics and in-situ stress parameters of carbonate reservoirs using array sonic logging: A case study of Shunbei No.4 block. J. Geomech. 2024, 30, 394–407, (In Chinese with English Abstract). [Google Scholar] [CrossRef]
- Wu, Y.Y.; Zhao, Z.A.; Lai, Q.; Zhuang, C.X.; Zhang, Y.H.; Wang, Z.Y. Application of array acoustic logging technology in volcanic reservoir evaluation. Nat. Gas Explor. Dev. 2023, 46, 33–41, (In Chinese with English Abstract). [Google Scholar]
- Heidbach, O.; Rajabi, M.; Reiter, K.; Ziegler, M.; WSM Team. World Stress Map Database Release 2016; GFZ Data Services: Potsdam, Germany, 2016. [Google Scholar] [CrossRef]
- Heidbach, O.; Rajabi, M.; Reiter, K.; Ziegler, M. World Stress Map 2016; GFZ Data Services: Potsdam, Germany, 2016. [Google Scholar] [CrossRef]
- Xu, H.J.; Sang, S.X.; Yang, J.F.; Jin, J.; Hu, Y.B.; Liu, H.H.; Ren, P.; Gao, W. In-situ stress measurements by hydraulic fracturing and its implication on coalbed methane development in Western Guizhou, SW China. J. Unconv. Oil Gas Resour. 2016, 15, 1–10. [Google Scholar]
- Chen, S.D.; Tang, D.Z.; Tao, S.; Xu, H.; Zhao, J.L.; Fu, H.J.; Ren, P.F. In-situ stress, stress-dependent permeability, pore pressure and gas-bearing system in multiple coal seams in the Panguan area, western Guizhou, China. J. Nat. Gas Sci. Eng. 2018, 49, 110–122. [Google Scholar]
- Zhao, X.L.; Ju, W.; Yang, Z.B.; Wang, S.Y. Analysis of Present-day In-situ Stress Difference and Its Influencing Factors Between Two Limbs of Panguan Syncline in Western Guizhou Region. Coal Geol. China 2024, 36, 1–6, (In Chinese with English Abstract). [Google Scholar]
- Wan, T.F. Mesozoic Cenozoic intraplate deformation and tectonic stress field in China. J. Geomech. 1996, 2, 13. (In Chinese) [Google Scholar]
- Wan, T.F. Outline of Chinese Geotectonics; Geological Publishing House: Beijing, China, 2004; pp. 135–165. (In Chinese) [Google Scholar]
- Xie, J.T.; Qin, Q.R.; Fan, C.H. Quantitative Prediction of Fracture Distribution of the Longmaxi Formation in the Dingshan Area, China using FEM Numerical Simulation. Acta Geol. Sin. 2019, 93, 1662–1672. [Google Scholar] [CrossRef]
- Wong, W.H. The Mesozoic orogenic movement in eastern China. Bull. Geol. Soc. China 1929, 8, 33–44. [Google Scholar] [CrossRef]
- Wang, H.Z.; Mo, X.X. An outline of the tectonic evolution of China. Episodes 1995, 18, 6–16. [Google Scholar] [CrossRef] [PubMed]
- Dong, S.W.; Zhang, Y.Q.; Long, C.X.; Yang, Z.Y.; Ji, Q.; Wang, T.; Hu, J.M.; Chen, X.H. Jurassic Tectonic Revolution in China and New Interpretation of the Yanshan Movement. Aata Geol. Sin. 2007, 81, 1449–1461, (In Chinese with English Abstract). [Google Scholar]
- Yang, Z.B.; Zhang, Z.G.; Qin, Y.; Wu, C.C.; Yi, T.S.; Li, Y.Y.; Tang, J.; Chen, J. Optimization methods of production layer combination for coalbed methane development in multi-coal seams. Petrol. Explor. Dev. 2018, 45, 312–320. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).