Abstract
In this study, an ANN-derived innovative model was developed for estimating the failure soil depths of rainfall-induced shallow landslide events, named the SM_EFD_LS model. The proposed SM_EFD_LS model was created using the modified ANN model via the genetic algorithm calibration approach (GA-SA) with multiple transfer functions (MTFs) (ANN_GA-SA_MTF) with a significant number of failure soil depths and corresponding rainfall factors. Ten shallow landslide-susceptible spots in the Jhuokou watershed in southern Taiwan were selected as the study area. The associated 1000 simulations of rainfall-induced shallow landslide events were used in the model’s development and validation. The model validation results indicate that the validated failure soil depths are mainly located within the resulting 60% confidence intervals from the proposed SM_EFD_LS model. Moreover, the estimated failure depths resemble the validated ones, with acceptable averages of the absolute error (RMSE) and relative error (MRE) (11 cm and 0.06) and a high model reliability index of 1.2. In the future, the resulting probabilistic-based failure soil depths obtained using the proposed SM_EFD_LS model could be introduced with the desired reliability needed for early landslide warning and prevention systems.
1. Introduction
Shallow landslides are ordinarily described as potentially damaging geomorphological disasters, mainly triggered by various rainfall intensities over a given duration [1,2,3,4,5]. However, due to a significant increase in extreme weather events as a result of climate change, rainfall-induced landslides frequently and dramatically result in economic, environmental, and human losses, increasing the risk of harm to people’s lives and property [4,5,6,7,8,9,10,11,12]. In the past, various rainfall thresholds were comprehensively introduced in response to shallow landslide occurrence in order to predict them. Thus, numerous investigations have focused mainly on evaluating warning performance based on predicting the likelihood of shallow-landslide occurrence and on boosting efficiency [3,4,9,11,12,13,14].
However, following a rainfall-induced landslide warning, predictions of the corresponding failure characteristics, including landslide locations, timings, and potential soil thickness, should be used to determine landslide size and to create a shallow landslide susceptibility map [5,10,15,16,17]. For example, Bellugi et al. [10] proposed a nonparametric module that employed a spectral clustering search algorithm with 3D slope stability analysis to forecast the potential locations and sizes of shallow landslides and triggering rainfall thresholds without considering observations. In addition to the prediction of potential shallow landslide locations, Baum et al. [5] presented an infiltration-process-based model with analytical pressure–diffusion solutions for unsaturated soil to approximate the occurrence timings of shallow landslides (i.e., failure time step).
However, of the above failure characteristics, initial landslide thickness plays a vital role in simulating landslide susceptibility [17,18,19]. Several physical deterministic approaches have been proposed to predict shallow landslide thickness [19,20,21,22]. For example, Schaller et al. [17] adopted three common AI-derived models (i.e., random forest, the generalized additive model, and the linear regression model) to predict the shallow landslide soil thickness, considering the 21 hydrological and topographical factors within the digital elevation maps of three spatial resolutions. Tufano et al. [19] utilized a 3D slope stability numerical simulation model to emulate the initial soil thickness in shallow landsides under conditions with various hydrological inputs (i.e., rainfall intensities and water pressures) in response to the spatial variability in soil thickness. In addition, AI-created modules have been widely applied in hydrological-related analysis, including slope stability analysis and the identification of landslide displacement [23,24,25,26].
Several physically based and AI-created models have been developed to perform slope stability analyses in order to identify the failure characteristics of shallow landslides, considering a variety of hydrological, topographical, and soil-related features; however, these approaches mainly focus on the estimation of landslide-susceptible locations, timings, and initial soil thickness without estimating the corresponding depths of soil failure due to heavy rainstorms. In addition, the effect of uncertainties attributed to the above rainfall factors is excluded in these estimations of the depths of soil failure. Nevertheless, AI-based models have commonly been applied to model slope stability analyses in order to efficiently evaluate landslide susceptibility considering rainfall and geomorphic features without quantifying the impact of their uncertainty on the resulting failure characteristics (e.g., failure soil depths). Specifically, the ANN-derived model can be effectively capitalized upon by establishing the on-site linear and nonlinear relationships between various input–output combinations with good-quality training datasets [26]. Therefore, this study intends to develop an ANN-derived smart model for efficiently estimating failure soil depths as a result of rainfall-induced shallow landslides and quantifying their corresponding stochastic properties. In this paper, the ANN-derived models and associated methods are introduced in Section 2; the model training and testing datasets are examined in Section 3; the results of the model are discussed in Section 4; and, finally, the findings are summarized in Section 5.
2. Methodology
2.1. Model Concept
To efficiently estimate the probabilistic-based failure soil depths as a result of shallow rainfall-induced landslides, the proposed smart model is developed based on an ANN-derived model, ANN_GA-SA_MTF [26], named the SM_EFD_LS model. The ANN-GA-SA_MTF model is able to produce outputs with the desired stochastic properties considering the uncertainties in model inputs. Ordinarily, an extensive dataset should be prepared to calibrate the ANN parameters (e.g., neuron number and associated weights and activation functions) in modeling the ANN-derived estimations. Therefore, a significant number of rainfall-induced shallow landslide events should be generated in advance. In this study, the slope stability numerical simulation model for unsaturated soil and the gridded rainstorm generation model [4] are used to reproduce the training datasets, consisting of a significant number of rainfall-induced shallow landslide scenarios. Then, the resulting failure characteristics extracted from the training datasets, including the landslide occurrence time, failure soil depths, and triggering rainfall factors, are used as the training dataset of the proposed SM_EFD_LS model. The triggering rainfall factors include the rainfall duration, maximum rainfall intensity, and cumulative rainfall amount of the specific forward durations at the failure time [4]. The variables that correlate highly with the model outputs are commonly selected as the input factors of ANN-derived models [27]. Ahead of training the proposed SM_EFD_LS model, the rainfall factors were identified as the model inputs subject to their temporal and spatial correlation with the estimated failure soil depths. Eventually, the resulting failure soil depths with the desired stochastic properties were quantified via the proposed SM_EFD_LS model under given rainfall factors. The concepts subject to the ANN-derived model and training dataset simulation are briefly addressed below.
2.2. Configuration of Probabilistic-Based ANN-Derived Model
As mentioned above, the ANN-derived ANN_GA-SA_MTF model [26] is configured in the proposed SM_EFD_LS model to provide probabilistic-based failure soil depths under given rainfall factors. The ANN_GA-SA_MTF model evolved through the modification of the conventional ANN model, considering the uncertainties in the training datasets and activation functions; thus, both model outputs and associated stochastic properties can be achieved using the ANN_GA-SA_MTF model with numerous transfer functions (see Table 1). The associated ANN weights are calibrated via the genetic algorithm based on the sensitivities to the model parameters (called the GA-SA algorithm) [27]. Therefore, within the ANN_GA-SA_MTF model, the weighted averages of the resulting model estimates can be obtained as the model outputs using the following equation:
in which denote the number of observations, the activation functions considered, and the appropriate parameter sets; stand for the observed hydrological variables and estimated ones by the ANN_GA-SA_MTF model with the jth set of appropriate parameters for the ith activation function, respectively; and is the weighted factor of the ith activation function with the appropriate parameters calculated with the objective function value .

Table 1.
Transform functions commonly used in the ANN-derived model [28].
In addition, within the ANN_GA-SA_MTF model, the statistical quantiles of various cumulative probabilities corresponding to the estimated hydrological variables are quantified via the weighted likelihood sample quantile estimator method [28]. Here, the maximum likelihood estimator of the unknown distribution function is an empirical one, , which is treated as follows:
where is the indicator variable with a value of 1 if ; otherwise, . Thus, the empirical distribution function is defined as follows:
in which accounts for a set of n order statistics as , with X(1) being the smallest observation and X(n) the largest. Accordingly, the weighted likelihood estimator for the pth quantile is achieved by calculating the weighted average of the order statistics, as follows [28]:
where ω serves as the bandwidth that contains a set order of statistics; in general, ω is less than 2.
This study focuses on the estimation of failure soil depths due to rainfall-induced shallow landslides; accordingly, the relationship between the failure soil depths and the corresponding rainfall factors are established based on the ANN_GA-SA_MTF model, as follows:
where and denote the failure soil depth at location IG and the corresponding rainfall factors.
2.3. Simulation of Rainfall-Induced Shallow Landslide Events
To train the ANN_GA-SA_MTF model for estimating the failure soil depths (see Equation (5)), a training dataset comprising a significant number of failure soil depths and corresponding rainfall factors should be prepared in advance. The shallow landslide is commonly treated as a regional geological disaster. This study uses a rainfall field simulation model to generate the gridded rainstorms. Following this, a physical-based slope-stability simulation model is adopted to carry out rainfall-induced shallow landslide simulation considering the given topographical and soil-related features. Therefore, the training dataset of the proposed SM_EFD_LS model could be obtained by combining the slope stability simulation model with the simulations of the gridded rainstorms. The relevant concepts of the gridded rainstorm and shallow landslide simulations are described in the following subsections.
2.3.1. Simulation of Gridded Rainstorms
Wu et al. [29] proposed a stochastic model for generating gridded short-term rainstorms considering the uncertainty of rainfall in time and space, named the SM_GSTR model. Within the SM_GSTR model, the characteristics of event-based rainstorms should be featured in terms of three rainfall characteristics: the event-based rainfall duration, gridded rainfall depths (i.e., the spatial variates), and gridded storm patterns, i.e., the dimensionless rainfalls at the various dimensionless times (i.e., the spatiotemporal correlated variates). The gridded storm pattern can be grouped into two components: the areal average of the dimensionless rainfall (i.e., the storm pattern).
In generating gridded rainstorms via the SM_GSTR model, the stochastic properties of the above-gridded rainfall characteristics should be computed in advance, including the first four statistical moments, the correlation coefficients, and the appropriate probability functions. Since the above-gridded rainfall characteristics are treated as correlated variables in time and space, the SM_GSTR model adopts a modified Monte Carlo simulation method for the correlated multivariates [30] to reproduce a significant number of gridded rainfall characteristics; these are then combined as simulated hyetographs. The detailed concepts of the SM_GSTR model are described in the investigation by Wu et al. [29].
2.3.2. Simulation of Rainfall-Induced Shallow Landslides
This study employs a modified Iverson equation-based slope stability simulation model under the initial condition of unsaturated soil, developed by Tsai and Chen [31], to simulate rainfall-induced shallow landslide events using simulated gridded rainstorms. Accordingly, the resulting failure soil depths and corresponding triggering rainfall factors were obtained from a significant number of simulated shallow landslide events and used as the model-training datasets. The detailed concepts of Tsai’s numerical simulation model for slope stability are introduced in Tsai’s investigation [31].
2.4. Model Framework
With the above-mentioned model concepts in mind, the development and implementation framework of the proposed SM_EFD_LS model can be summarized as follows:
Step (1) Collect the rainfall data, topographical features, and soil-related parameters within the study area.
Step (2) Extract the gridded rainfall characteristics from the rainfall data used to generate a considerable number of hyetographs of the gridded rainstorms via the SM_GSTR model.
Step (3) Carry out a slope stability simulation via the Tsai model with the generated hyetographs at all grids from Step (2) under the given topographic and soil-related features.
Step (4) Capture the time step of the minimum of the simulated safety factors (FSsim) that are less than the critical value (FScri = 1.0) and use this as the failure occurrence time (i.e., time to FSsim < FScri).
Step (5) Extract a considerable number of failure soil depths and corresponding triggering rainfall factors and use these as the training datasets, including the rainfall durations, maximum rainfall intensities, and the cumulative rainfall amounts of the specific forward durations at the failure occurrence time.
Step (6) Identify the rainfall factors highly correlated with the estimated failure soil depths used in training the proposed SM_EFD_LS model.
Step (7) Train the proposed SM_EFD_LS model by calibrating the parameters of the ANN_GA-SA_MTF model using the training datasets achieved in Steps (5) and (6).
Step (8) Implement the proposed SM_EFD_LS model, considering the rainfall factors, to estimate the failure soil depths and associated stochastic properties (i.e., probabilistic-based failure depths), including the statistical moments and confidence intervals.
Figure 1 shows the schematic process of training and implementing the proposed SM_EFD_LS model.
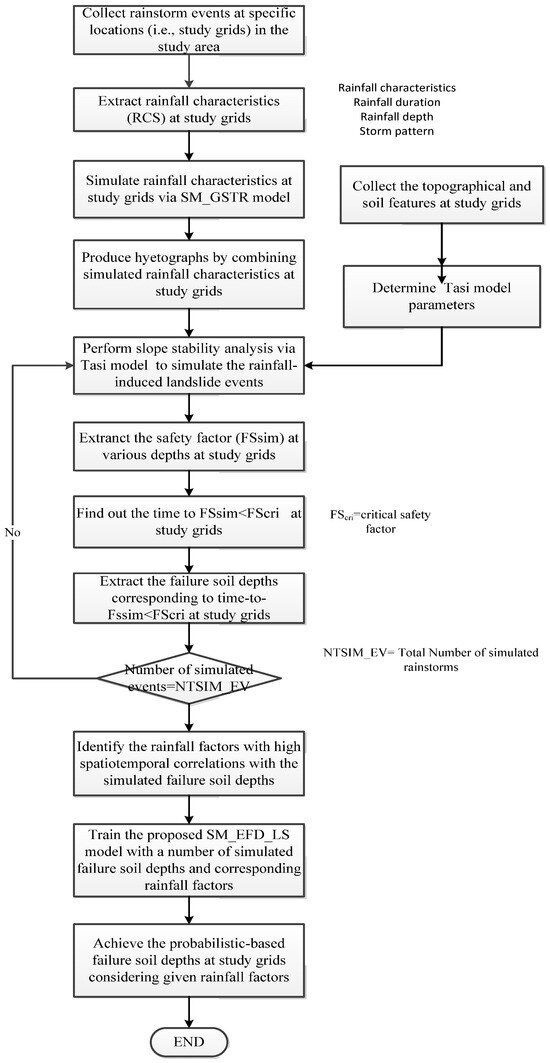
Figure 1.
The schematic framework for developing the proposed SM_EFD_LS model.
3. Study Area and Data
To proceed with the development and validation of the proposed SM_EFD_LS model, a mountainous potential rainfall-induced-landslide-susceptible zone (Jhuokou River watershed) in southern Taiwan is selected as the study area; the associated topographical and soil-related features are used as the study data for the numerical slope stability simulation. Figure 2 displays the study area, Jhuokou River watershed, based on the Taiwan Datum 1997 (TWD) system [32], with the main river length and corresponding catchment extent of roughly 55 km and 529 km2, respectively. As slate soil is inherent in the study area, shallow landslides commonly occur due to heavy rainfall events. In addition to rainfall factors, shallow landslides are likely triggered by the topographical and soil-related features of the region. Thus, in the study area, 10 locations with markedly different slopes () are taken as the study grids. Accordingly, in developing the proposed SM_EFD_LS model, the slope stability numerical model (Tsai model) parameters should be configured individually based on the topographical and soil-related features in the 10 study grids (see Table 2). Before proceeding with the slope stability simulation using the Tsai model, the thickness of the soil layers at the 10 study locations is assigned as 310 cm in advance.
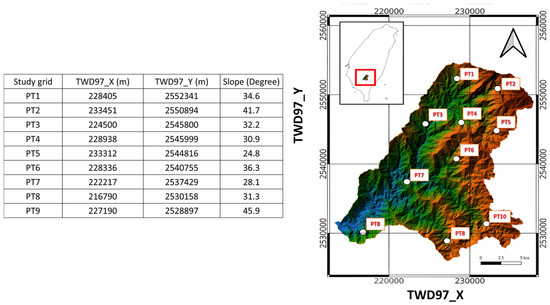
Figure 2.
Locations of the study area and grids based on Taiwan Datum 1997 (TWD97) [4].

Table 2.
Summary of the soil-related properties in the grids of the study area adopted in the Tsai model [4].
In addition to soil-related features, triggering rainstorm data should be given in advance to develop the training datasets for the proposed SM_EFD_LS model. Thus, Wang et al. [4] used the gridded rainstorm simulation model (SM_GSTR model) with 30 historical hourly rainstorms recorded in the study area to reproduce 1000 simulations of hourly rainstorms of various durations (30–120 h). Following this, using the Tsai model with corresponding soil-related parameters (see Table 3) and the above-generated rainstorms for the 10 study grids, the rainfall-induced shallow landslide events could be reproduced, and the failure characteristics could be then extracted as the training datasets. The failure characteristics consist of the occurrent time steps of the estimated safety factors less than 1.0 and corresponding soil depths (called failure soil depths). Wang et al. [4] found that the rainfall duration, maximum rainfall intensity, and rainfall depth, as well as the rainfall amount forward-cumulated from the failure occurrence time to the specific duration, contribute more to shallow landslide occurrence; this is known as the forward-cumulative rainfall amounts of various durations. Figure 3 summarizes the 1000 simulations of the failure occurrence times, failure soil depths, and rainfall factors for the 10 study grids. The detailed process of simulating the rainfall-induced shallow landslide is described in Wang’s investigations [4].

Table 3.
Summary of calibrated regression coefficients of the rainfall factors in the exceedance probability calculation equations.
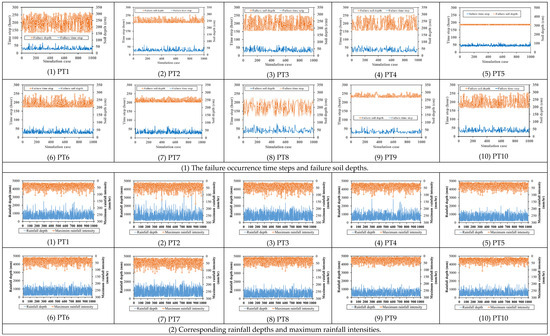
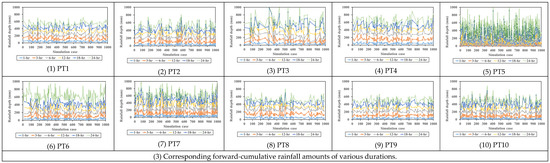
Figure 3.
The 1000 simulations of the failure soil characteristics of 10 study grids within the study area [4].
This study adopts the results of the simulated failure soil depths and corresponding rainfall factors for the study grids from Wang’s investigation [4] for training and validating the proposed SM_EFD_LS model. In detail, within the proposed SM_EFD_LS model, the parameters of the ANN-derived ANN_GA-SA_MTF model are calibrated for the study grids, excluding the fifth study grid, with the above training datasets.
4. Results and Discussion
In this study, to proceed with developing and validating the proposed SM_EFD_LS model, 1000 simulations of the failure soil depths and corresponding rainfall factors (see Figure 3) are used to calibrate the parameters of the ANN_GA-SA_MTF model for the study grids of interest and to demonstrate the accuracy and reliability of the probabilistic-based failure soil depths. In addition, to evaluate the applicability of the proposed SM_EFD_LS model in the early prediction of shallow landslides based on triggering rainfall thresholds, the forward-cumulative rainfall amounts at the study grids could be estimated using landslide-triggering rainfall threshold estimation equations with the given reliabilities [4]:
where accounts for the landslide-triggering rainfall threshold of the warning time (i.e., 3 h forward-cumulative rainfall amount); stands for the rainfall depth; serves as the cumulative rainfall at the time to the maximum rainfall intensity; and are the regression coefficients for the grids in the study area, as listed in Table 3. The above estimated forward-cumulative rainfall amounts and the remaining rainfall factors were treated as the model inputs of the proposed SM_EFD_LS. Accordingly, the resulting failure soil depths at the study grids with consistent reliabilities in the study area could be used for the early warning of rainfall-induced shallow landslides.
4.1. Evaluation of Correlation Between Failure Soil Depths and Rainfall-Related Factors
According to the model development framework (see Section 2.4), the model inputs should be extracted from the rainfall factors mentioned above based on their contribution to shallow landslide occurrence. Therefore, in this study, the above rainfall factors are identified as the input factors of the proposed SM_EFD_LS model by calculating their correlation coefficients with the failure soil depths, as shown in Figure 4 and Figure 5. Figure 4 shows the negative correlation coefficients between the failure soil depths and rainfall-related factors at the study sites with a significant spatial change. For example, for study grid PT1, the failure soil depth has considerable correlation coefficients with the rainfall depth (around −0.2), maximum rainfall intensity (about −0.65), and 1 h, 3 h, and 6 h forward-cumulative rainfall amounts (approximately −0.78). However, at study grid PT10, the correlation coefficients with the above rainfall factors, on average, merely approximate −0.08. This reveals that the failure soil depths are considerably inversely related to the rainfall factors; this implies that heavier rainfall, possibly earlier, triggers landslide occurrence with a high likelihood of achieving a shallower failure soil depth.
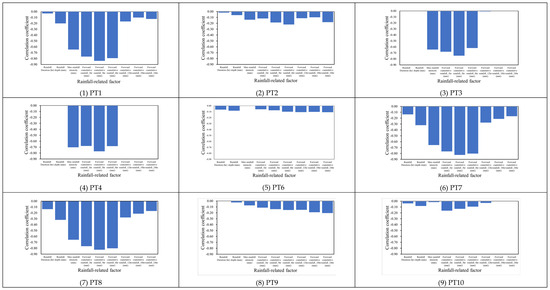
Figure 4.
Correlation coefficients between failure depths and rainfall-related factors for the study grids.
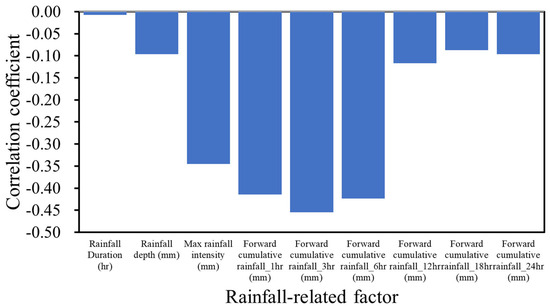
Figure 5.
Average correlation coefficients between failure depths and rainfall-related factors.
As shown in Figure 5, despite the correlation coefficients between failure soil depth and rainfall factors with noticeable spatial change, the averages of the correlation coefficients regarding rainfall depth, maximum rainfall intensities, and forward-cumulative rainfall amounts of 1 h, 3 h, and 6 h (roughly −0.33) considerably exceed the remaining rainfall factors (approximately −0.076). This finding indicates that the above rainfall factors, including rainfall depth, maximum rainfall intensity, and forward-cumulative rainfall amount (1 h, 3 h, and 6 h), more significantly contribute to estimating the failure soil depth. In particular, the 3 h forward-cumulative rainfall amount exhibits a significant relationship with failure soil depth under a correlation coefficient (around −0.5). Therefore, within the proposed SM_EFD_LS model, the 3 h forward-cumulative rainfall depth and maximum rainfall intensity could be selected as the input factors of the ANN-GA-SA_MTF model, with the corresponding failure soil depths as the model output.
4.2. Establishment of the Proposed RA_EFD_LS Model
Based on Section 4.1, within the proposed SM_EFD_LS model, the maximum rainfall intensity and 3 h forward-cumulative rainfall amount are regarded as the ANN_GA-SA_MTF inputs; thus, Equation (5) can be rewritten as follows:
where stands for the failure soil depth, and serve as the rainfall depth, maximum rainfall intensity, and 3 h forward-cumulative rainfall amount. Table 4 illustrates the first set of the ANN_GA-SA_MTF parameters within the proposed SM_EFD_LS model for the study grids (PT1, PT6, PT8, and PT10) [4], revealing that the ANN-GA-SA_MTF parameters vary significantly with the study grid locations. Hence, the resulting failure soil depths can reasonably respond to the variations in the failure soil depths due to the difference in the topographical and soil-related features in space (see Figure 3).

Table 4.
Summary of the first set of ANN_GA-S_MTF parameters for the study grids.
4.3. Validation of the Estimated Probabilistic-Based Failure Soil Depths
In this study, the proposed SM_EFD_LS model could be validated by comparing the failure soil depth estimations and corresponding quantiles to the validations. Thus, ten simulations of the failure soil depths and corresponding rainfall factors (i.e., maximum rainfall intensity and 3 h forward-cumulative rainfall amount) were extracted as the validation events from the training datasets, as shown in Figure 6. Note that the above ten validation events were excluded from the model training.
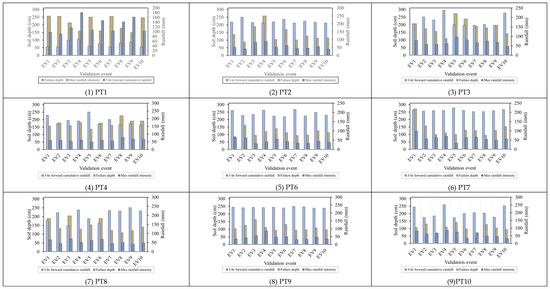
Figure 6.
Validated failure soil depths and corresponding rainfall factors for the study grids.
Figure 6 shows that the validation events exhibit considerable variation in terms of failure soil depths and corresponding rainfall factors; in detail, the maximum rainfall intensity, on average, ranges from 30 mm/h to 100 mm/h with a significant coefficient of variance (around 0.26), and the 3 h forward-cumulative rainfall amounts are mainly located between 100 mm and 300 m with an average of 137 mm. Thus, the resulting failure soil depth changes significantly from 140 cm to 250 cm with an average of 203 cm. The selected validation events result in a noticeable spread in the failure characteristics of shallow landslides within the study area, indicating the appropriateness of the proposed SM_EFD_LS model.
4.3.1. Reliability Evaluation of Estimated Failure Soil Depths
In the reliability evaluation of the estimated failure soil depths, the resulting quantile curves should be established via the proposed SM_EDF_LS model in advance (Figure 7). As shown in Figure 7, the quantiles of the estimated failure soil depths for the various validation events remain consistent at cumulative probabilities of less than 0.1 and more than 0.9. For example, at study grid PT1 with a cumulative probability of 0.5, the failure soil depth quantiles are distributed from 212.2 cm to 226.4 cm with a maximum interval of 14.2 cm; in contrast, for study grid PT1, the difference in the quantiles at a cumulative probability of 0.5 do not significantly exceed 10 cm. The estimated quantile curves of the failure soil depths for the study grids exhibit significant changes between the cumulative probabilities of 0.2 and 0.8, called a 60% confidence interval. As a result, this study focuses on these 60% confidence intervals to evaluate the reliability of the resulting failure soil depths obtained using the proposed SM_EFD_LS model.
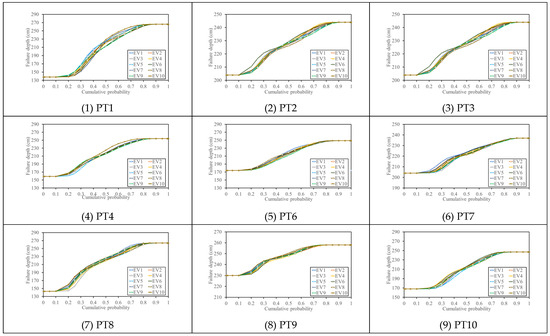
Figure 7.
Failure depth quantiles estimated using the proposed SM_EFD_LS model for various validation events.
The results show that the reliabilities of the estimated failure soil depths using the proposed SM_EFD_LS model are subject to the 60% confidence intervals in comparison to the validations, as shown in Figure 8. The findings show that the validated failure soil depths are significantly distributed in 60% confidence intervals within the study grids. In detail, at study grid PT1, the validated failure soil depths are ordinarily distributed within the 60% confidence interval of around 120 cm. For study grid PT7, with the minimum of 60% confidence intervals, the validated depths mostly approach the lower bounds, but remain in the confidence interval. Consequently, the proposed SM_EFD_LS model based only on the given rainfall factors (i.e., maximum rainfall intensity and 3 h forward-cumulative rainfall amount) can capture the practical failure soil depths with a confidence level of at least 0.6.
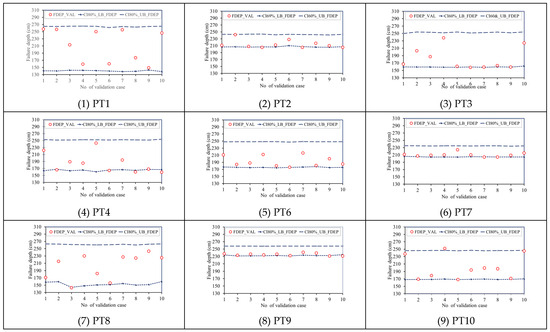
Figure 8.
Comparison of the validated failure soil depths with the resulting 60% confidence intervals obtained using the proposed SM_EFD_LS model.
4.3.2. Accuracy Assessment of Failure Soil Depth Estimates
In addition to the quantiles of the failure soil depths, the proposed SM_EFD_LS model can provide failure soil depth estimates via the ANN_GA-SA_MTF with given rainfall factors. Figure 9 presents a comparison between the estimated failure soil depths for the study grids and the validated depths under given rainfall factors. To quantify the accuracy of the above estimated failure soil depths, the performance indices, including the root mean square error (RMSE), mean relative error (MRE), and model reliability index (KG), are calculated using the following equations.
where stand for the validated and estimated failure soil depths for the ith validation event, respectively, and serves as the number of validation events. Of the above performance indices, the RMSE and RE mainly account for the difference between the estimated and validated failure soil depths; alternatively, the KG index measures the consistency of the estimated failure soil depths with the validations; the KG index approaching 1.0 indicates that the estimated failure soil depths have a more consistent varying trend than the validated soil depths.
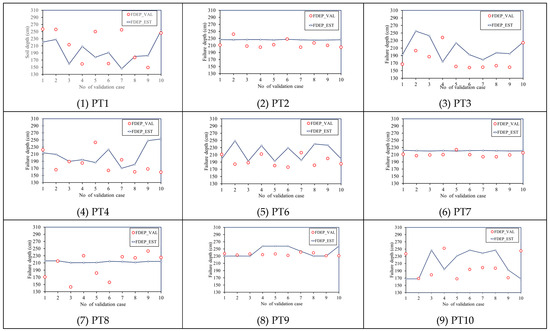
Figure 9.
Comparison between the validated failure depths (FDEP_VAL) and estimated depths (FDEP_EST) using the proposed SM_EFD_LS model for various validation events.
Figure 10 (1) shows that the RMSE values of the estimated failure soil depths exhibit differences from the validated ones with different biases. For example, in study grids PT2, PT7, and PT9, the estimated failure soil depths are significantly close to the validated depths with a low RMSE of around 4.7 cm. Despite the remaining study grids having an RMSE of roughly 13 cm, their MRE values are estimated to be approximately 0.05. For example, for study grid PT1, although the RMSE values of the failure soil depths reach 13 cm, the MRE merely approximates 0.05. In addition, concerning Figure 10, the resulting failure soil depths from the proposed SM_EFD_LS model for the five validation events (EV1, EV2, EV3, EV5, and EV7) are underestimated (around 67 cm); regarding the remaining validation events, the overestimated failure soil depths could be estimated at nearly 25 cm. This indicates that, regardless of whether the failure soil depths have a significant absolute error (RMSE), they are not treated as consistently overestimated and underestimated due to a low relative error (MRE); accordingly, the resulting errors might be regarded as random as a result of the uncertainties in the rainfall factors.
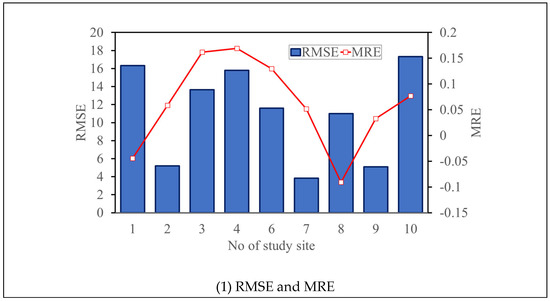
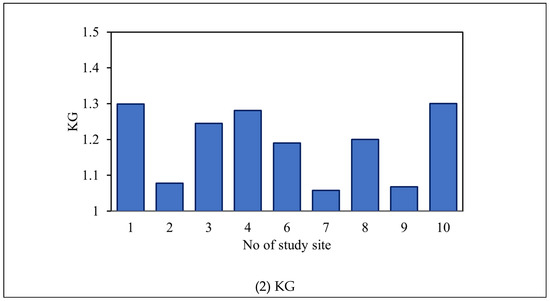
Figure 10.
Performance indices of the estimated failure depths using the proposed SM_EFD_LS model for various validation events.
As well as comparing the difference between the estimated and validated failure soil depths, consistency should also be quantified and evaluated based on the KG index. As shown in Figure 10 (2), the KG index ranges from 1.06 to 1.3 (1.2, on average). Among the study grids of interest, the KG index at grid PT7 is the lowest (about 1.06), indicating that the estimated failure soil depth exhibits a significant relationship with the validated failure soil depths under the considerably low RMSE and MRE (almost 3.83 cm and 0.05, respectively). The largest KG index was obtained for study grid PT7 (approximately 1.3). However, the varying trend of its estimated failure soil depths with the validation events resembles the validated depths with a low MRE of around −0.04.
The proposed SM_EFD_LS model could provide failure soil depths with acceptable bias under the given rainfall factors. Moreover, the resulting failure soil depths obtained using the proposed SM_EFD_LS model resemble the varying trends in the validated depths in space. Therefore, the ability of the proposed SM_EFD_LS model to produce failure soil depths at various locations under the given rainfall with acceptable error and high spatial similarity is verified.
4.4. Application on Regional Probabilistic-Based Failure Soil Depth Estimations
To summarize the above results, the proposed SM_EFD_LS model is able to produce probabilistic-based failure soil depth information using the given maximum rainfall intensity and 3 h forward-cumulative rainfall amount. Thus, to evaluate the change in the failure soil depths due to shallow landslides with different likelihoods, the 3 h rainfall thresholds (i.e., 3 h forward-cumulative rainfall amount) corresponding to the low and high reliabilities (0.2 and 0.8) were calculated using the following triggering-rainfall threshold estimation equation (Equation (6)) with the given rainfall conditions (see Table 5). Accordingly, the resulting failure soil depths and associated 60% confidence intervals were estimated using the proposed SM_EFD_LS model, as shown in Figure 11.

Table 5.
Conditions for estimating gridded failure depths using the proposed SM_EFD_LS model with given rainfall-related factors under various rainfall threshold reliabilities (0.2 and 0.8).
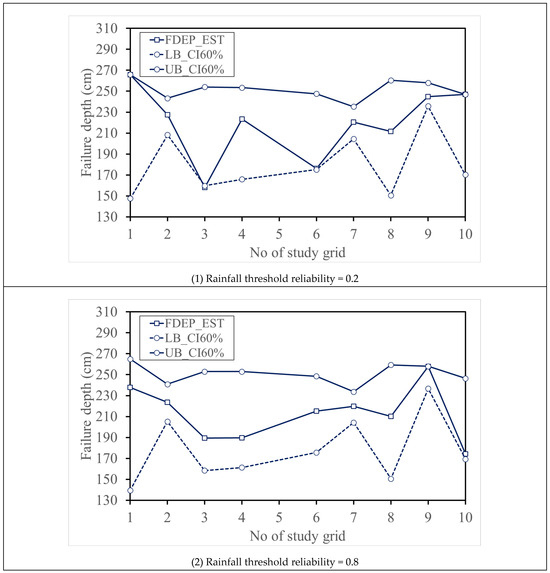
Figure 11.
Quantification of probabilistic-based failure depths (FDEP_EST) at the study sites of interest using the proposed SM_EFD_LS model.
Figure 11 shows that the failure soil depths obtained from the two reliabilities are approximately consistent in terms of the 60% confidence intervals. In detail, study grids PT2, PT7, and PT9 achieve relatively low confidence intervals (approximately 28 cm); however, the broader 60% confidence intervals (roughly 115 cm) are obtained for study grids PT1 and PT8. These results reveal that, regardless of rainfall thresholds, the 60% confidence intervals are poorly impacted by uncertainties in the 3 h forward-cumulative rainfall threshold without considering the uncertainties in the remaining rainfall factors.
Furthermore, the estimated failure soil depths with the 3 h rainfall thresholds of reliability = 0.2 exhibit significant spatial variations (158–266 cm) (about 108 cm). As for the rainfall threshold reliability of 0.8, the resulting failure soil depths range from 175 cm to 258 cm with low spatial variation (around 83 cm). These results indicate that the failure soil depths estimated using the proposed SM_EFD_LS model with the 3 h rainfall thresholds of reliability = 0.2 mostly approach the lower bounds (PT3, PT6, and PT9) and upper bounds (PT1 and PT10) of the 60% confidence intervals (see Figure 11 (1)); however, estimated with the 3 h rainfall thresholds of high reliability (0.8), the resulting failure soil depths (see Figure 11 (2)) markedly depart from the 60% confidence interval bounds and move to the averages. For example, at the study grids PT3 and PT6, the estimated failure soil depths move from the lower bounds (159.7 cm and 175.1 cm) toward the mean lines (189.4 cm and 215.1 cm). In contrast, at study grid PT10, the estimated failure soil depth changes from the upper bound (247 cm) to the lower bound (170 cm). In summary, shallow landslide occurrence can be more accurately identified based on 3 h rainfall thresholds with high reliabilities. Furthermore, due to a significant change in the slope and soil-related features in all of the study grids (see Figure 2), estimated failure soil depths with considerable spatial variations were achieved using the proposed SF_EFD_LS model under identical rainfall conditions, excluding the 3 h forward-cumulative rainfall amount (i.e., 3 h rainfall threshold).
Overall, the proposed SM_EFD_LS model could clearly be combined with the reliability quantification model for landslide-triggering rainfall thresholds to estimate the corresponding probabilistic-based failure soil depths. In addition, the change in the resulting probabilistic-based failure soil depths may be a response to the effect of uncertainties in the rainfall thresholds, altering shallow landslide occurrence. Therefore, the resulting probabilistic-based failure soil depths are advantageous in efficiently providing more failure characteristics, such as landslide location and size, as estimated via the sloping local-based digital elevation models [19].
5. Conclusions
This study mainly proposes an ANN-derived smart model for estimating probabilistic-based failure soil depths due to rainfall-induced shallow landslides, named the SM_EFD_LS model. Within this model, a three-layer ANN-derived model, ANN_GA-SA_MTF [26], was configured to estimate failure soil depths at specific locations and associated stochastic quantiles of various cumulative probabilities considering uncertainties in the rainfall factors. A reliability assessment of the failure soil depths is also carried out based on the resulting quantiles.
To proceed with the model development and validation, 1000 simulations of rainfall-induced shallow landslide events at 10 locations (i.e., study grids) in the Jhuokou River watershed in southern Taiwan [4] are used as the model training datasets. Accordingly, the failure soil depths and corresponding highly correlated rainfall depth, maximum rainfall intensity, and 3 h forward-cumulative rainfall amount are extracted from the training datasets; they are selected as the ANN_GA-SA_MTF model output and inputs, respectively. The ANN_GA-SA_MTF parameters for the study grids could be calibrated, in which ten simulated shallow landslide events are randomly selected for the model validation, excluding the model development. The model validation results indicate that the validated failure soil depths are mostly allocated within the 60% confidence intervals, implying that the proposed SM_EFD_LS model can capture actual shallow landslide failure depths with a likelihood of at least 60%. In addition, the proposed M_EFD_LS model produced failure soil depths subject to given rainfall factors with acceptable biases of 11 cm (RMSE) and 0.06 (MRE); additionally, the estimated failure soil depths exhibited spatial trends that varied significantly more than the validated depths under a high-reliability index of 1.2. Furthermore, as calculated using the proposed SM_EFD_LS model with the 3 h shallow landslide rainfall thresholds of different reliabilities (i.e., 0.2 and 0.8), the change in the corresponding failure soil depths could reasonably reflect the effect of uncertainties in the rainfall thresholds on shallow landslide occurrence and induced failure characteristics. This should be taken into account in the early detection and prevention of shallow landslides.
The proposed SM_EFD_LS model could provide more applicable probabilistic-based failure soil depths under given rainfall factors. Despite the model capturing failure soil depths due to shallow landslides with high likelihood, the model would be validated using practical measurements of shallow landslides to assess its applicability. Accordingly, the effect of climate change on shallow landslides in mountainous areas would be evaluated using the proposed SM_EFD_LS model with rainstorm simulations in the climate change scenario [33,34]. Furthermore, shallow landslide occurrence and the associated failure characteristics can be impacted by variations in topographical variables, hydrological variables (such as surface flow), and soil-related features [7,8,18,18,33,35]. Therefore, regionalizing the proposed SM_EFD_LS model could be achieved by training the ANN_GA-SA_MTF model while considering rainfall, topographical, and soil-related factors as the model inputs; it is expected that, by using this approach, the corresponding ungauged failure soil depths due to rainfall-induced shallow landslides would be obtained to delineate a failure depth contour map.
Author Contributions
Conceptualization, methodology, writing—original draft preparation, writing—review and editing: S.-J.W.; investigation, validation: S.-R.C.; data curation: C.-D.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National United University (Grant No. 113-NUUPRJ-04).
Data Availability Statement
The data are available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Huang, J.; Ju, N.P.; Liao, Y.J.; Liu, D.D. Determination of rainfall thresholds for shallow landslides by a probabilistic and empirical method. Nat. Hazards Earth Syst. Sci. 2015, 15, 2715–2723. [Google Scholar] [CrossRef]
- Piegari, E.; Di Maio, R.; Milano, L. Characteristic scales in landslide modelling. Nonlinear Process. Geophys. 2009, 16, 515–523. [Google Scholar] [CrossRef][Green Version]
- Wu, S.-J.; Hsiao, Y.-H.; Yeh, K.-C.; Yang, S.-H. A probabilistic model for evaluating the reliability of rainfall thresholds for shallow landslides based on uncertainties in rainfall characteristics and soil properties. Nat. Hazards 2017, 87, 469–513. [Google Scholar] [CrossRef]
- Wang, X.-J.; Wu, S.-J.; Tsai, T.-L.; Yen, K.-C. Modeling probabilistic-based reliability assessment of gridded rainfall thresholds for shallow landslide occurrence due to the uncertainty of rainfall in time and space. J. Hydroinform. 2023, 25, 706–737. [Google Scholar] [CrossRef]
- Baum, R.L.; Brien, D.I.; Reid, M.E.; Schulz, W.H.; Tello, M.J. Assessing locations susceptible to shallow landslide initial during prolonged intense rainfall in the Larges, Unuado, and Naranjito municipalities of Puerto Rice. Nat. Hazards Earth Syst. Sci. 2024, 24, 1579–1605. [Google Scholar] [CrossRef]
- Alessio, P. Spatial variability of saturated hydraulic conductivity and measurement-based intensity-duration thresholds for slope stability, Santa Ynez Valley, CA. Geomorphology 2019, 342, 103–116. [Google Scholar] [CrossRef]
- Zheng, S.; Zhang, G.; Yuan, X.; Ye, F.; Fu, W. Failure characteristics of shallow soil slope considering surface runoff and interstitial flow. Geomat. Nat. Hazards Risk 2020, 11, 845–868. [Google Scholar] [CrossRef]
- Fiolleau, S.; Uhlemann, S.; Falco, N.; Dafflon, B. Assessing probability of failure of urban landslides through rapid characterization of soil properties and vegetation distribution. Geomorphology 2022, 423, 108560. [Google Scholar] [CrossRef]
- Vennari, C.; Gariano, S.L.; Antronico, L.; Brunetti, M.T.; Iovine, G.; Peruccacci, S.; Terranova, O.; Guzzetti, F. Rainfall thresholds for shallow landslide occurrence in Calabria, southern Italy. Nat. Hazards Earth Syst. Sci. 2014, 14, 317–330. [Google Scholar] [CrossRef]
- Bellugi, D.; Milledge, D.G.; Dietrich, W.E.; McKean, J.A.; Perron, J.T.; Sudderth, E.B.; Kazian, B. A spectral clustering search algorithm for predicting shallow landslide size and location. J. Geophys. Res. Earth Surf. 2015, 120, 300–324. [Google Scholar] [CrossRef]
- Chien, L.-K.; Hsu, C.-F.; Yin, L.-C. Warning Model for Shallow Landslides Induced by Extreme Rainfall. Water 2015, 7, 4362–4384. [Google Scholar] [CrossRef]
- Naidu, S.; Sajinkumar, K.; Oommen, T.; Anuja, V.; Samuel, R.A.; Muraleedharan, C. Early warning system for shallow landslides using rainfall threshold and slope stability analysis. Geosci. Front. 2018, 9, 1871–1882. [Google Scholar] [CrossRef]
- Zhan, Q.; Wang, S.; Guo, F.; Chen, Y.; Wang, L.; Zhao, D. Early warning model and model test verification of rainfall-induced shallow landslide. Bull. Eng. Geol. Environ. 2022, 81, 318. [Google Scholar] [CrossRef]
- Jiang, H.; Zou, Q.; Zhou, B.; Jiang, Y.; Cui, J.; Yao, H.; Zhou, W. Estimation of Shallow Landslide Susceptibility Incorporating the Impacts of Vegetation on Slope Stability. Int. J. Disaster Risk Sci. 2023, 14, 618–635. [Google Scholar] [CrossRef]
- Milledge, D.G.; Bellugi, D.; McKean, J.A.; Densmore, A.L.; Dietrich, W.E. A multidimensional stability model for predicting shallow landslide size and shape across landscapes. J. Geophys. Res. Earth Surf. 2014, 119, 2481–2504. [Google Scholar] [CrossRef]
- Miazzi, M.M.; Pasqualone, A.; Zammit-Mangion, M.; Savoia, M.A.; Fanelli, V.; Procino, S.; Gadaleta, S.; Aurelio, F.L.; Montemurro, C. A Glimpse into the Genetic Heritage of the Olive Tree in Malta. Agriculture 2024, 14, 495. [Google Scholar] [CrossRef]
- Schaller, C.; Dorren, L.; Schwarz, M.; Moos, C.; Seijmonsbergen, A.C.; van Loon, E.E. Predicting the thickness of shallow landslides in Switzerland using machine learning. Nat. Hazards Earth Syst. Sci. 2025, 25, 467–491. [Google Scholar] [CrossRef]
- Kim, M.S.; Onda, Y.; Uchida, T.; Kim, J.K. Effects of soil depth and subsurface flow along the subsurface topography on shallow landslide predictions at the site of a small granitic hillslope. Geomorphology 2016, 271, 40–54. [Google Scholar] [CrossRef]
- Tufano, R.; Formetta, G.; Calcaterra, D.; De Vita, P. Hydrological control of soil thickness spatial variability on the initiation of rainfall-induced shallow landslides using a three-dimensional model. Landslides 2021, 18, 3367–3380. [Google Scholar] [CrossRef]
- Dietrich, W.E.; Reiss, R.; Hsu, M.; Montgomery, D.R. A process-based model for colluvial soil depth and shallow landsliding using digital elevation data. Hydrol. Process. 1995, 9, 383–400. [Google Scholar] [CrossRef]
- Pelletier, J.D.; Rasmussen, C. Geomorphically based predictive mapping of soil thickness in upland watersheds. Water Resour. Res. 2009, 45, 1–15. [Google Scholar] [CrossRef]
- Ho, J.-Y.; Lee, K.T.; Chang, T.-C.; Wang, Z.-Y.; Liao, Y.-H. Influences of spatial distribution of soil thickness on shallow landslide prediction. Eng. Geol. 2012, 124, 38–46. [Google Scholar] [CrossRef]
- Kainthura, P.; Sharma, N. Machine learning driven landslide susceptibility prediction for the Uttarkashi region of Uttarakhand in India. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2021, 16, 570–583. [Google Scholar] [CrossRef]
- Mondini, A.C.; Guzzetti, F.; Melillo, M. Deep learning forecast of rainfall-induced shallow landslides. Nat. Commun. 2023, 14, 2466. [Google Scholar] [CrossRef]
- Xi, N.; Zang, M.; Lin, R.; Sun, Y.; Mei, G. Spatiotemporal prediction of landslide displacement using deep learning approaches based on monitored time-series displacement data: A case in the Huanglianshu landslide. Georisk: Assess. Manag. Risk Eng. Syst. Geohazards 2023, 17, 98–113. [Google Scholar] [CrossRef]
- Wu, S.-J.; Hsu, C.-T.; Chang, C.-H. Stochastic modeling of artificial neural networks for real-time hydrological forecasts based on uncertainties in transfer functions and ANN weights. Hydrol. Res. 2021, 52, 1490–1525. [Google Scholar] [CrossRef]
- Wu, S.-J.; Lien, H.-C.; Chang, C.-H. Calibration of a conceptual rainfall–runoff model using a genetic algorithm integrated with runoff estimation sensitivity to parameters. J. Hydroinform. 2011, 14, 497–511. [Google Scholar] [CrossRef]
- Yang, J.C.; Tung, Y.K. Establishment of Flow-Duration Curve and the Assessment of Its Certainty; Final Report of Environment Protection Agency: Taiwan, China, 1996.
- Wu, S.-J.; Hsu, C.-T.; Chang, C.-H. Stochastic modeling of gridded short-term rainstorms. Hydrol. Res. 2021, 52, 876–904. [Google Scholar] [CrossRef]
- Chang, C.; Tung, Y.; Yang, J. Monte Carlo Simulation for Correlated Variables with Marginal Distributions. J. Hydraul. Eng. 1994, 120, 313–331. [Google Scholar] [CrossRef]
- Tsai, T.-L.; Chen, H.-F. Effects of degree of saturation on shallow landslides triggered by rainfall. Environ. Earth Sci. 2009, 59, 1285–1295. [Google Scholar] [CrossRef]
- Yang, M.; Tseng, C.-L.; Yu, J.-Y. Establishment and Maintenance of Taiwan Geodetic Datum 1997. J. Surv. Eng. 2001, 127, 119–132. [Google Scholar] [CrossRef]
- Guo, Z.; Ferrer, J.V.; Hürlimann, M.; Medina, V.; Puig-Polo, C.; Yin, K.; Huang, D. Shallow landslide susceptibility assessment under future climate and land cover changes: A case study from southwest China. Geosci. Front. 2023, 14, 101542. [Google Scholar] [CrossRef]
- Tiranti, D.; Ronchi, C. Climate Change Impacts on Shallow Landslide Events and on the Performance of the Regional Shallow Landslide Early Warning System of Piemonte (Northwestern Italy). Geohazards 2023, 4, 475–496. [Google Scholar] [CrossRef]
- Chiu, Y.-Y.; Chen, H.-E.; Yeh, K.-C. Investigation of the Influence of Rainfall Runoff on Shallow Landslides in Unsaturated Soil Using a Mathematical Model. Water 2019, 11, 1178. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).