Previous Article in Journal
Integrating PCA and Fractal Modeling for Identifying Geochemical Anomalies in the Tropics: The Malang–Lumajang Volcanic Arc, Indonesia
Previous Article in Special Issue
Upwellings and Mantle Ponding Zones in the Lower Mantle Transition Zone (660–1000 km)
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 15
Issue 12
10.3390/geosciences15120471
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Hole in the Pacific LLVP and Multipathed SKS

by
Daoyuan Sun
1,2
1
State Key Laboratory of Precision Geodesy, School of Earth and Space Sciences, University of Science and Technology of China, Hefei 230026, China
2
Mengcheng National Geophysical Observatory, University of Science and Technology of China, Bozhou 233500, China
Geosciences 2025, 15(12), 471; https://doi.org/10.3390/geosciences15120471 (registering DOI)
Submission received: 20 September 2025 / Revised: 26 November 2025 / Accepted: 3 December 2025 / Published: 13 December 2025
(This article belongs to the Special Issue Seismology of the Dynamic Deep Earth)
Browse Figures
Review Reports Versions Notes

Abstract

In contrast to a relatively simple whole structure of the African Large Low Velocity Province (LLVP), the Mid-Pacific LLVP appears to be much more complex and likely interacts more with the down-going slab debris from the circum-Pacific subduction zones. Tomographic models show an apparent hole in the Mid-Pacific LLVP, coinciding with observed anomalous SPdKS arrivals. Previous studies have linked these anomalies to a large-scale mega ultra-low velocity zone (ULVZ) exhibiting up to a 45% S-wave velocity reduction. To further investigate this anomaly, we analyzed SKS waveforms from Fiji–Tonga earthquakes recorded by the USArray. Many events display pronounced travel time jumps and waveform distortions near epicentral distances of 100°, consistent with strong multipathing effects. Notably, such complexities are absent in S and SKKS phases, indicating that only the down-going SKS leg is affected. Using waveform modeling, we find that a northeast-dipping high-velocity anomaly approximately 300 km wide, 800 km long, and with a shear velocity increase of ~2% provides a good fit to the observed SKS data. This apparent LLVP hole may represent a localized downwelling within the LLVP or a remnant slab fragment interacting with the deep mantle.

1. Introduction

The two Large Low Velocity Provinces (LLVPs) beneath the Mid-Pacific and South Africa (Figure 1) are the most prominent features at the lowermost mantle, as imaged by global long-period tomography studies as well as free-oscillation observations [1,2,3,4,5,6,7,8,9,10]. While the African LLVP appears relatively simple [11,12], the Mid-Pacific LLVP is notably more complex. The Mid-Pacific LLVP seems to be constructed by several separated blocks [13,14] or broad plumes [7,15], with a possible gap or ‘hole’ between them (Figure 1). Cluster analysis of global lower mantle tomography [16,17] shows a pronounced hole along the southwestern margin of the Pacific LLVP beneath the Fiji–Tonga region, displayed in tomographic models as a region lacking a significant negative velocity anomaly (outlined in the black rectangle in Figure 1). For simplicity, we refer to this region as a ‘hole’ in the Mid-Pacific LLVP. Several explanations have been proposed for this complexity, including past subductions dividing the Mid-Pacific LLVP [14,18,19], an internal downwelling [20,21], two piles merging together [22], or differences in the formation mechanisms compared to the African LLVP [23]. In addition, ultra-low velocity zones (ULVZs) have been observed clustering along the edge of the LLVPs [24,25,26], exhibiting varying geometries and properties [27,28,29,30,31,32,33,34]. These ULVZs further highlight the important role of the subducted slab reaching the core–mantle boundary (CMB), shaping both the ULVZs and LLVPs through thermal and possibly chemical processes. Thus, understanding the detailed features of LLVPs and ULVZs, particularly the hole in the Mid-Pacific LLVP, and their relationship with the slab debris is crucial for lower mantle geodynamic modeling involving the balance between thermal and chemical processes, as well as the history of subduction [25,35,36,37].
Unfortunately, resolving the fine-scale structures of these lower mantle features remains challenging due to limited station coverage and the lack of accurate structures of subducted slabs in existing reference models [39]. This also contributes to the great variety in reported tomographic models depending on datasets and applied methods, as in the example tomographic images in Figure 1. Consequently, the use of waveform observations has proven valuable, particularly in resolving the detailed structure of ULVZs. Early studies of ULVZs involve SKS near critical angle distances, where S converts to Pd traveling along the mantle side of the CMB at the SKS core entry and exit points, constructing SPdKS and SKPdS, respectively [40,41,42,43]. Since it is difficult to distinguish SPdKS and SKPdS [44], we refer to the combined SPdKS and SKPdS energy as SPdKS for simplicity. Essentially, injecting a ULVZ near critical angle produces an earlier observable bifurcation of SKS and SPdKS, with distances smaller than 109° and relatively strong SPdKS out to 120° [41,45,46,47,48]. The rapidly growing dense seismic networks have allowed the global coverage of SPdKS [49,50,51], leading to the development of a ULVZ likelihood map based on a summation of Pdiff segments showing ULVZ-like SPdKS. While some paths seem to be PREM-like, others show strong secondary arrivals as early as 105°, which is argued for the presence of a “mega” ULVZ with a ~45% shear velocity (Vs) reduction [22]. Such a ULVZ with an extreme velocity drop has been observed globally [29,52,53,54,55]. However, strong modeling tradeoffs make precise determinations of the elastic parameters and geometry of the ULVZ challenging. Furthermore, although these models explain the data well, there could be other more complicated possibilities that involve slab–LLVP interactions [18,32,33] and perhaps an enhanced downwelling in the LLVP, as in the African LLVP [20]. If these anomalies exhibit a subvertical structure, they could generate multipathing effects for near vertical incidence phases, such as SKS, distorting their waveforms and potentially complicating the interpretation of ULVZs.
Here, we study the multipathing of SKS sampling of the Mid-Pacific LLVP hole beneath Western Polynesia (Figure 1), which can alternatively be explained by adding a fast anomaly in the lower mantle. We examine SKS data covering a wide distance range and study the different multipathing patterns for various events. Together, these approaches allow us to better resolve the lower mantle structure than previous studies, which typically focused on a more limited data range. The motivation for adding the slab shaped structure in the lower mantle comes from the success of explaining the multipathing of P and S phases following the paths along subduction zones [56,57]. Replacing blurred images from tomography with sharp slab features has proven effective in explaining multipathing features [58,59,60]. We propose that this Mid-Pacific LLVP hole is generated by slab debris or downwelling convection in an LLVP. In this paper, we will address the seismic modeling supporting such an interpretation.

2. Data and Methods

2.1. Waveform Data

There is an abundance of events in the Fiji–Tonga subduction zone recorded by the USArray (Table S1, Figure 2), which allows for enhanced coverage in the lower mantle. Among these, events A–D are further selected for detailed waveform modeling due to their simple source time functions and great focal depths (Table 1). The original horizontal components are rotated to the tangential (SH) and radial (SV) components after deconvolving the instrument responses and bandpass filtered to 1–50 s. The SV waveform data for events A and C are plotted in Figure 3a. Event A samples the region covered by a mega ULVZ-type SPdKS (Figure 2b) with anomalous SKS arrivals at 98~105° (Figure 3a). In contrast, event C presents a typical ULVZ pattern with strong secondary arrivals beyond 109° (Figure 3a).
Geosciences 15 00471 g002
Figure 2. (a) The locations of the events (stars) and the representative great circle paths to the USArray (triangles). The background tomographic image is from the GyPSuM [6] at the CMB. (b) Enlargement of the area marked with the black box in (a). The shaded magenta patches represent the mega ULVZs identified by Thorne et al. (2013) [22]. Black stars mark events A–D (Table 1), which are used for further multipathing analysis and waveform modeling.
Figure 2. (a) The locations of the events (stars) and the representative great circle paths to the USArray (triangles). The background tomographic image is from the GyPSuM [6] at the CMB. (b) Enlargement of the area marked with the black box in (a). The shaded magenta patches represent the mega ULVZs identified by Thorne et al. (2013) [22]. Black stars mark events A–D (Table 1), which are used for further multipathing analysis and waveform modeling.
Geosciences 15 00471 g002
Geosciences 15 00471 g003
Figure 3. Multipathing patterns for SKS. (a) SKS data for events A and B in Figure 2B at the azimuth range of 45–50°. Note the complicated waveforms of SKS at a distance of 98–104° of event A. The data are aligned on the predicted SKS arrivals of the IASP91 model [61]. The vertical dashed lines mark time 0 to aid visualization. (b,c) display the SKS multipathing patterns of the events A, B, and C in Figure 2b. (b) is the travel time anomaly (ΔT) and (c) is multipathing time separation (ΔLR). Event A displays a strong multipathing region (red color in ΔLR map) from Minnesota to Missouri associated with the earlier arrivals (blue color in ΔT map), suggesting multipathing effects from a fast anomaly.
Figure 3. Multipathing patterns for SKS. (a) SKS data for events A and B in Figure 2B at the azimuth range of 45–50°. Note the complicated waveforms of SKS at a distance of 98–104° of event A. The data are aligned on the predicted SKS arrivals of the IASP91 model [61]. The vertical dashed lines mark time 0 to aid visualization. (b,c) display the SKS multipathing patterns of the events A, B, and C in Figure 2b. (b) is the travel time anomaly (ΔT) and (c) is multipathing time separation (ΔLR). Event A displays a strong multipathing region (red color in ΔLR map) from Minnesota to Missouri associated with the earlier arrivals (blue color in ΔT map), suggesting multipathing effects from a fast anomaly.
Geosciences 15 00471 g003
Table 1. Events used for detailed analysis and modeling for SKS *.
Table 1. Events used for detailed analysis and modeling for SKS *.
Event IDDateLongitude (°)Latitude (°)Depth (km)
A29 July 2011179.92−23.78538.95
B21 February 2011178.47−25.95567.48
C19 July 2014−174.18−15.64233.8
D25 April 2021−176.87−21.71247.63
* The event information is from Global CMT (https://www.globalcmt.org/) (accessed on 10 May 2025) [62,63] (Ekström et al., 2012; Dziewonski et al., 1981).

2.2. Multipathing Patterns

The SKS waveforms display considerable complexity at individual stations (Figure 3), which has been noted in Sun and Helmberger [2013] [64] for events recorded by USArray, in general. An efficient method for examining such complexity is processing waveforms with a multipath detector, MPD [65]. In the MPD, an observed waveform is simulated with [S(t) + C × S (t-ΔLR)]/2, where S(t) represents the predicted waveform from a reference model and C is the amplitude ratio. The travel time difference between the data and the reference model (ΔT) is measured with cross correlation between the data and the composed waveform (Figure 3b) [65]. Thus, a large ΔLR indicates a stronger multipathing effect, suggesting that the wavefront encounters a sharp boundary, either in distance or azimuth directions. This can be better captured with a map of the ΔLR across the array, highlighting regions with significant multipathing (Figure 3c). While some observed multipathing features are probably caused by receiver path effects, source complexity etc., they are generally less pronounced than those shown in Figure 3c. Figure 3b,c display a clear picture of SKS behavior over a large range, which is quite simple after sampling the North American tectonic shield (TNA-SNA) boundary [66]. Notably, a distinct circular zone beneath eastern US for event C, centered on the state of Tennessee, shows strong multipathing effects and early arrivals. This anomaly has been well studied in Ko et al. [2017] [60], where there is evidence that the Hess conjugate slab is still partly located in the upper mantle at this location. Additionally, this small cluster of early arrivals, along with complicated waveforms, is also reduced in amplitude. Consequently, to avoid receiver path issues, we concentrate our analysis on azimuths of 45–52° here.
In the azimuth corridor 45–52°, event C behaves PREM-like until reaching the region along the east coast, with a distance of ~109° (Figure 3a). Beyond this distance, the SKS waveforms become multipathed, which is interpreted as a combination of a fully developed SPdKS and SKS (type B in Thorne et al. [2013] [22]). At the southwest end, event B does not exhibit any apparent multipathing features up to 105°. In contrast, event A displays a strong change in both travel time and waveform complexity (Figure 3b,c). Specifically, there is a noticeable jump in early arrivals and elongated waveforms along a corridor starting at ~101°. As events A and B are only separated by a few degrees, the observed jump in travel times for event A is difficult to explain as the structures beneath the stations.
Along the same profile, Bréger and Romanowicz (1998) [67] suggest a strong fast anomaly at the CMB east of the Mid-Pacific LLVP to explain the differential travel times of Sdiff, SKS, and SKKS. Motivated by this, we tested a model that inserts a fast anomaly 65° from event A (Rec_HVZ_model1 in Figure S3a) into GyPSuM. This model reproduces the SKKS-SKS differential travel time reasonably well by advancing SKKS at a distance smaller than 95°. However, because the anomaly locates on the receiver side, it affects all the events in a similar way (Figure S4), inconsistent with the observations. Although such a structure produces multipathed SKS between 92° and 98°, with some partially observed waveform distortion at this distance range for event A, it has difficulties explaining the strong multipathed SKS beyond 100°. We therefore tested a second model by shifting this strong fast anomaly to 91.5° from the event A (Rec_HVZ_model2 in Figure S3a). This configuration produces multipathed SKS beyond 100° and also matches the SKKS-SKS differential travel time variations by advancing the SKS at a large distance. However, this model again predicts similar waveform distortions of SKS for both events B and D (Figure S3), which are not seen in the data (Figure 3). This suggests that the travel time anomalies and the waveform distortion are most likely associated with the down-going SKS leg, which, for event A, samples a sharp structure at the source side [68].
To further illustrate the travel time changes, we plot the SKS travel times along this corridor for multiple events in Figure 4. All record sections are shifted relative to a common station KSCO to correct for possible origin time and source mislocation. The paths to the southwest sample the LLVP hole more than those to the northeast and arrive ~2 s early. A similar ~2 s difference is also noted by Schweitzer and Müller (1986) [68] when examining the differential travel times along the same profile [69,70], which they preferably attribute to a lower mantle anomaly east of Fiji–Tonga.
We also apply MPD analysis to the SKKS of event A (Figure S2), which displays much smaller ΔT and ΔLR, suggesting that SKKS has a relatively simple waveform with no pronounced multipathing, in contrast to the obvious multipathed SKS waveform observed for event A. Taken together, these observations point to the existence of a high-velocity structure in the lower mantle only sampled by the down-going SKS for the southwest events.
Nonetheless, a fast anomaly at the CMB east of the Mid-Pacific LLVP [67] could significantly improve the fit of the differential travel time (Figure S4). However, complicated structures at the northeastern edge of the LLVP, as well as the LLVP itself, will also affect SKS and SKKS [32], and current constraints are insufficient to resolve these details. Furthermore, other lower mantle anomalies, such as the thick Farallon Slab beneath the central U.S. [58], would also affect the SKKS and SKS travel times. Given that a full assessment of these anomalies is not available, we focus here not on matching all travel time variations but on explaining two key observations: the ~2 s early SKS arrivals for the southwest events and the associated multipathing for event A. In the following, we explore whether these features can be reproduced using a simple slab-like high-velocity structure, although the real situation is likely to be much more complicated.

3. Results

Here, to model the waveform, we apply a 2D finite difference code [71], which allows for the relatively broadband generation of global synthetics up to 2 Hz and implementation of a point source. We first generate synthetics for many different tomographic models and select the GyPSuM [6] as an example, as the GyPSuM performs well on travel times for studying the lower mantle structures beneath the Pacific [14,19]. The synthetics for the GyPSuM (Figure 5) do not produce the abrupt change in travel time near 99° nor the multipathing. Even with an enhanced LLVP at the bottom 800 km, the GyPSuM model still does not produce the travel time anomalies and the observed waveform distortions (Figure 5). In contrast, the SKS travel times can be predicted better by incorporating an upper mantle model from Schmandt and Lin (2014) [72]. Since this upper mantle model was generated from data including SKS recorded by USArray assuming a 1D reference model, it maps the lower mantle features needed directly into the receiver’s upper mantle structure. Such an upper mantle model has promise in that sharpening this structure can predict multipathing, as found in the Juan de Fuca slab studies [73]. However, because ray paths of SKKS are approximately the same as those of SKS in the upper mantle, both phases would be affected, which is inconsistent with the observed SKKS travel times and waveforms (Figure 3a), which further suggests that the observed multipathing is caused by a sharp anomaly in the lower mantle. To better evaluate the goodness of the waveform fit, the average cross-correlation coefficients (CCs) between the data and synthetics for distances of 95–115° are computed using a time window from 10 s before to 15 s after the predicted SKS arrival based on the IASP91 model.

3.1. Mega-ULVZ Model

The mega-ULVZ model, with Vs reduction up to 45%, is first proposed for explaining the highly anomalous SPdKS arrivals observed at a distance range of 105–110° along the same corridor here [22]. Through scanning SPdKS arrivals, such mega-ULVZs with extreme Vs reduction have since been routinely detected in both regional studies [52,74] and global compilations [50,51]. As shown in Figure 6, synthetics generated for a 2D profile through the 3D mega-ULVZ models proposed in Thorne et al. (2013) [22] (Figure 2) show extremely large amplitudes of SPdKS and complicated waveforms, even down to 98°, which produce a much lower CC. Moreover, this mega-ULVZ model also produces highly anomalous SPdKS arrivals for event B (Figure 6b). The location and size of the mega-ULVZ strongly affect the behavior of the SPdKS [22,51]. Therefore, I explore mega-ULVZ models with different locations and dimensions. As shown in the right panel of Figure 6, a much smaller mega-ULVZ can reasonably reproduce the multipathing features observed at distances of 96–104° for event A, which is also evidenced by the significantly larger CCs. For event C, however, this model still predicts a large-amplitude secondary SPdKS arrival, which cannot be clearly identified in the data. Unfortunately, I have not been able to find a simplified, box-like mega-ULVZ model that satisfies all the observations across events. In addition, such models also have difficulty explaining the ~2 s early arrival of SKS for the southwesternmost events observed in Figure 4.

3.2. Lower Mantle High-Velocity Block Model

Alternatively, the distorted SKS waveforms observed for event A can be explained by the multipathing effects introduced by a high-velocity structure in the lower mantle. When rays are aligned with the sharp edge of this anomaly, multipathing occurs, producing distorted waveforms [57,58,59,60,73]. The location of the anomaly in the lower mantle is further supported by the relatively simple waveform of the SKKS (Figure 3 and Figure S2). If such an anomaly is located in the upper mantle, it would affect both SKS and SKKS in a similar way over a much broader range of distances. We use a simple idealized model by inserting a thin slab-like structure into the lower mantle of the 2D tomographic model (Figure 7a) to demonstrate its effect on the waveform. Such a model is also motivated by the observation of a high-velocity block at a depth of ~2000 km in GyPSuM (Figure 5a). For the upper mantle, the model from Schmandt and Lin (2014) [72] is used to improve the travel time fit, although our main focus is on the waveforms.
As shown in Figure 7b, this simple model predicts broadening of the waveforms starting at ~90°. A late secondary arrival emerges at ~94°, consistent with the data. Notably, three arrivals, developed by multipathing along both edges, are observed at the distance range of 97–104°, representing well the complicated data with multiple arrivals and showing a high CC. Beyond 106°, the first arrival becomes weaker than the secondary one, which is also predicted by the model. In contrast, the SKKS remains unaffected across the entire distance range, maintaining a simple waveform. It is interesting to note that S/Sdiff for event A shows complicated waveforms, which are caused by the ULVZs located along the northeastern edge of the Pacific LLVP [32,33]. This model also predicts SKKS-SKS differential travel times that are delayed by ~2 s compared with those from the original GyPSuM (Figure S4). Furthermore, due to its thin structure, this anomaly has a limited effect on events B and D (Figure 7c,d), resulting in simple SKS waveforms. In particular, for event D, the bifurcation of SPdKS starts at 108°, which agrees well with the data, suggesting that a strong ULVZ is not required for this case.

4. Discussion

4.1. Sensitivity Tests on Geometry and Velocity of the High-Velocity Anomaly

Due to the complicated dynamic processes in the lower mantle, the detailed morphology of this high-velocity anomaly in the lower mantle is difficult to fully resolve. In addition, as shown in Figure 5, upper mantle structures greatly affect the synthetics, particularly travel times. These complexities, combined with limited ray coverage, make it difficult to constrain the structure of this anomaly in a quantitative manner. Therefore, in this study, we focus on examining the general bulk properties of this anomaly. We use the model shown in Figure 7a as a reference model, characterized by a length L of 750 km, width of 3.5°, δVs of 2%, and dip angle (θ) of 70°. We then explore how different geometry and velocity perturbations affect the waveforms.
The dip angle θ has strong effects on the waveforms (Figure 8). A model with a shallower dip with θ of 65° generates strong second arrivals between 96° and 108°, whereas a more vertical structure with θ of 75° produces weaker waveform distortions. However, when θ is 65°, the CC decreases much more, indicating that a more vertical structure is preferred. The waveforms are also sensitive to the δVs. When δVs is reduced to 1%, the later arrivals become much weaker than those for the reference model. In contrast, a stronger anomaly leads to excessive waveform distortion, which does not match the data and has a much smaller CC. In Figure 9, we further tested a model with a velocity gradient across the anomaly, where δVs is 3% at the center and tapers to 1% toward the edges. This gradient model produces waveforms similar to those of the reference model and with a slightly higher CC, suggesting that both models can reproduce the general bulk properties of the anomaly. Nonetheless, a δVs of 1–2% is preferred if a uniform structure is assumed.
The synthetic tests also reveal that the waveforms are sensitive to the width of the anomaly. As shown in Figure 10, a narrower structure with a width of 2° produces strong secondary arrivals at a distance range of 92–97° but fails to generate clear multipathing at a larger distance. In contrast, a wider anomaly (5°) shows weak multipathing at small distances, with such effects only being observed at distances beyond 106°. Such a wide model also produces a lower CC (Figure 10). However, there are strong tradeoffs between the anomaly’s depth extent, length, and δVs (Figure 10). In general, a shorter anomaly with stronger velocity perturbation and a model located closer to the CMB tends to produce stronger multipathing and greater waveform distortion. Their CCs are generally lower than that of the reference model. It is interesting to note that a model with 1.5 times the length and a δVs of 1.3% (rightmost panel in Figure 10) can yield a larger CC than the reference model, although the overall multipathing patterns remain similar. In summary, our sensitivity tests suggest that the observed waveform complexities of SKS can be explained by a northeast-dipping, high-velocity block situated in the lowermost mantle beneath the Western Polynesia. A model with a width of 2–3.5° and a dip angle of 70–75° provides the best overall fit to the data.

4.2. Three-Dimensional Structure of the Lower Mantle Anomaly

As shown in Figure 2, our sampling region may lie near the edge of the apparent hole. Thus, the influence of 3D multipathing effects from the edge cannot be neglected [59], particularly given the complicated ΔLR patterns observed in Figure 2. However, constructing an accurate 3D model remains difficult due to limited data sampling. Here, to explore the impact of 3D geometry, we create simplified 3D models by extending our preferred 2D lower mantle high-velocity block structure in the azimuthal direction. We then examine how varying its lateral extent affects waveform distortions. Three-dimensional synthetics are generated by SPECFEM3D_GLOBE [75], with simulations accurate down to a period of ~7 s. Waveform examples are displayed in Figure 11. For Model I, with a lateral extent of 600 km, strong multipathed waveforms can be observed at azimuth up to 70°. In contrast, Model III, with a narrow 150 km extent, shows only weak multipathing at large distances. Model II, with an intermediate extent of 300 km, provides a better match to the multipathing patterns observed for event A, suggesting that a moderately extended slab structure is more consistent with the data. A comparison between the data and the synthetics along distance profiles is shown in Figure S5. Because our sampling path lies along the northwestern edge of the 3D structure, it generates much weaker multipathing for azimuths of 45–52° than the 2D synthetics. Therefore, if the edge of this anomaly is indeed located near the azimuth of 45°, a stronger velocity perturbation would be required to reproduce the same multipathing patterns predicted by the 2D simulation. Alternatively, a 3D anomaly with its edge extending further northwest would allow stronger waveform distortions for azimuths of 45–52°. Nonetheless, the proposed 3D lower mantle slab structure here is oversimplified and may also be biased by the event-station geometry used in this study. Future investigation with improved data coverage and more realistic 3D models is needed to robustly constrain the anomaly’s morphology at depth.

4.3. SKS Multipathing on the Identification of the Mega-ULVZ

The discovery of mega-ULVZs is primarily based on observations of highly anomalous SPdKS arrivals [22]. Here, we show that some of these arrivals can also be interpreted as multipathed SKS. This offers an alternative explanation for waveform distortions observed at distances much smaller than the SKS–SPdKS bifurcation distance in a PREM-like model, without invoking extreme ULVZs. Lower mantle slab-like structures with sharp edges are routinely observed in many regions of the lower mantle [58,59,60]. When these sharp structures align with SKS ray paths, they can produce multipathed SKS. Upper mantle slabs [56] or sharp LLVP edges [76] can also affect SKS. Thus, in regions dominated by vertical slab-like structures, careful examination of SKS and SPdKS waveforms over a wide distance range is needed. Comparing multipathing patterns of SKS across different events helps identify these effects. Nonetheless, mega-ULVZs are true and important features, which are consistently detected by SPdKS and other phases [53,54,55]. Studies have shown that the subducted slab in the lower mantle may strongly affect the evolution of the ULVZ [28,32,33,52,54,74,77,78,79,80,81]. Therefore, in some regions, SKS waveforms may be affected by both deep mantle slabs and strong ULVZs, further complicating their characteristics. This highlights the need for more detailed analyses to separate the contributions of slabs and ULVZs.

4.4. Mechanisms for Developing the LLVP Hole

Although our results support the presence of a slab-like high-velocity structure in the lower mantle beneath Western Polynesia, potentially contributing to the formation of the apparent LLVP hole, at the current stage, it is still challenging to understand the exact mechanism forming such a structure (Figure 12). First, because of their limited resolution, current global tomographic models, which generally emphasize long-wavelength structures in the lower mantle, may smooth out separated low-velocity mantle plumes into an apparently uniform structure [82]. Consequently, the LLVP may actually represent a cluster of low-velocity thermo-chemical plumes rather than a single uniform structure [14,23]. In this context, the observed high-velocity features may simply correspond to the gaps between these deep-mantle plumes, a scenario supported by more recent full waveform models [7,15]. These gaps would therefore represent the normal-velocity mantle in contrast to the surrounding low-velocity LLVP.
Nonetheless, if the slab-like high-velocity structure in the lower mantle is indeed a real feature, several explanations are possible. These include the presence of a mega-ULVZ located in the middle of two merged piles [22], a descending slab breaking the LLVP apart [18], or downwelling in a metastable superplume [20,23]. Among these, the slab model is particularly compelling, because the geometries of the LLVPs are thought to be strongly affected by the long-term subduction history [19,35,37,83,84,85]. This also offers a plausible framework for explaining the morphological difference between the African and Mid-Pacific LLVPs [86]. With more continuous and long-lived subduction surrounding the Pacific, descending slabs may have more chances to penetrate or fragment the LLVP, leading to the formation of several separated blocks of the LLVP [13,14,18]. However, detailed dynamic modeling is needed to fully assess the plausibility of this scenario, specifically, how easily a lower mantle slab can break the LLVP and how subduction history alters the LLVP morphology.
Geosciences 15 00471 g012
Figure 12. Possible scenarios of generating the LLVP hole. (a) Mega-ULVZ (brown color) located in the middle of two merged piles (yellow color) [22]. (b) Slab (green color) descending on top of the LLVP (yellow color) and setting the LLVP apart. (c) Downwelling (green color) in a metastable superplume [20,23]. The cold downwelling may also promote possible formation of the D” at the center of the LLVP, as observed in the African LLVP [87].
Figure 12. Possible scenarios of generating the LLVP hole. (a) Mega-ULVZ (brown color) located in the middle of two merged piles (yellow color) [22]. (b) Slab (green color) descending on top of the LLVP (yellow color) and setting the LLVP apart. (c) Downwelling (green color) in a metastable superplume [20,23]. The cold downwelling may also promote possible formation of the D” at the center of the LLVP, as observed in the African LLVP [87].
Geosciences 15 00471 g012

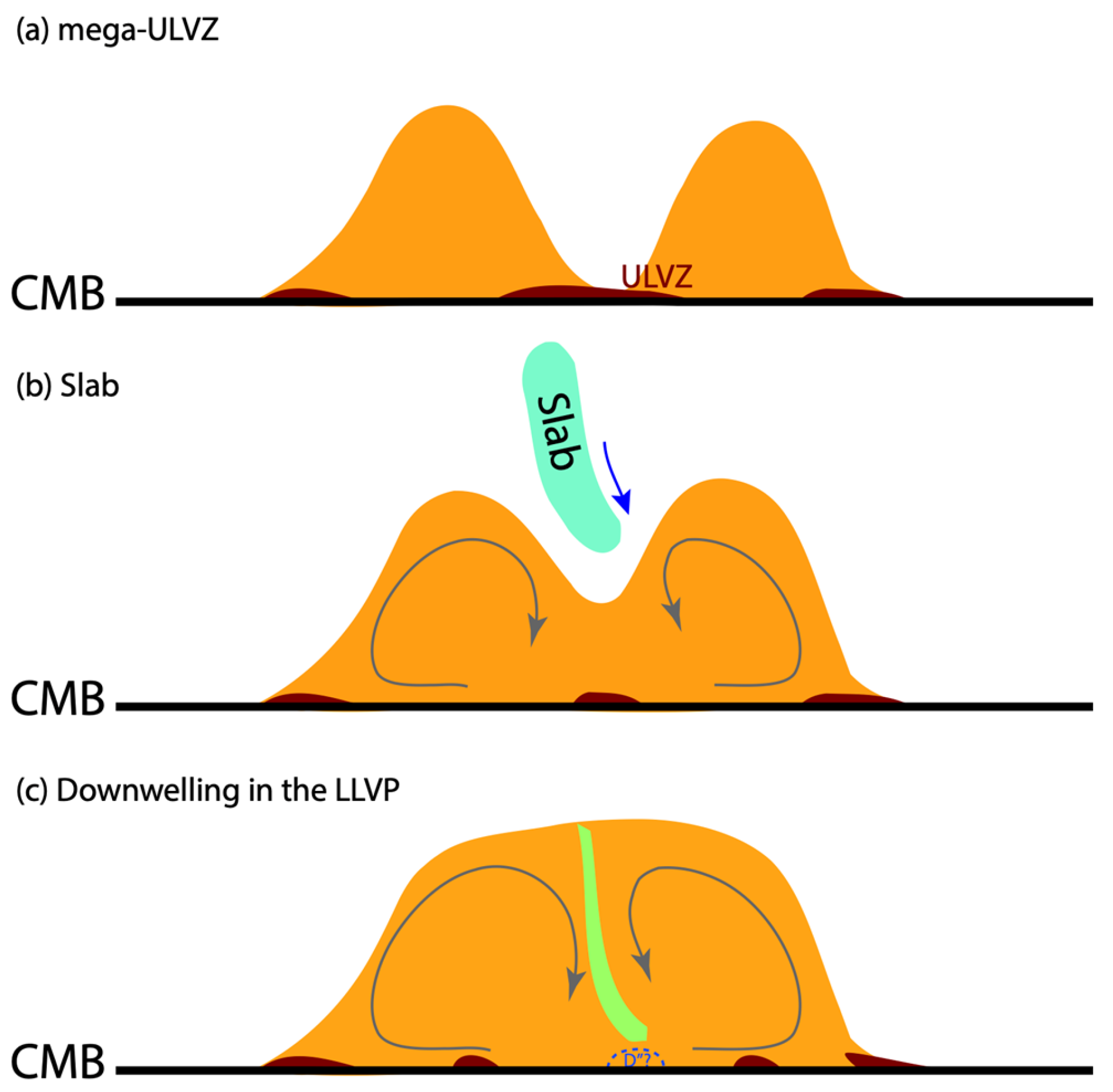
5. Conclusions

Tomographic models reveal an apparent hole within the Mid-Pacific LLVP, located beneath Western Polynesia. Using SKS data from Fiji–Tonga earthquakes recorded by the USArray, we can directly sample this feature and assess its origin. The analysis shows that the anomalous SKS waveforms are best explained by multipathing effects from a localized high-velocity anomaly in the lower mantle rather than a pure ULVZ-related structure. Our 2D waveform modeling shows that a northeast-dipping high-velocity block, approximately 300 km wide, with a shear velocity increase of ~2%, provides a good fit to the observed data. These findings support the view that the Mid-Pacific LLVP is not a monolithic structure but rather a dynamically evolving structure shaped by processes, such as slab penetration and complex thermo-chemical interactions. Accordingly, the Mid-Pacific LLVP hole most likely represents slab–LLVP interactions rather than a pure ULVZ effect. Moreover, extreme caution must be applied to explain seismic observations related to these features. Nonetheless, continued high-resolution seismic imaging and geodynamic modeling are essential for fully resolving the origin and evolution of these deep mantle structures.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/geosciences15120471/s1.

Funding

This research was funded by the National Natural Science Foundation of China (Nos. 42394113 and 42241117), Deep Earth Probe and Mineral Resources Exploration-National Science and Technology Major Project (No. 2025ZD1005200), and National Key R&D Program of China (No. 2023YFF0803204).

Data Availability Statement

The seismograms used in this study are downloaded from the IRIS Data Management Center (http://service.iris.edu) (Last accessed on 10 September 2025).

Acknowledgments

This paper is dedicated to the memory of Don Helmberger, whose guidance and inspiration have profoundly influenced this work. I would like to thank the academic editor and four anonymous reviewers. Their suggestions and comments were greatly appreciated. I also thank Priscilla McLean for her help in preparing the materials for an early version of this paper. The numerical calculations in this study were performed on the supercomputing system at the Supercomputing Center of University of Science and Technology of China.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Ishii, M.; Tromp, J. Normal-mode and free-air gravity constraints on lateral variations in velocity and density of Earth’s mantle. Science 1999, 285, 1231–1236. [Google Scholar] [CrossRef]
  2. Ritsema, J.; Deuss, A.; van Heijst, H.J.; Woodhouse, J.H. S40RTS: A degree-40 shear-velocity model for the mantle from new Rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements. Geophys. J. Int. 2011, 184, 1223–1236. [Google Scholar] [CrossRef]
  3. Cui, C.; Lei, W.; Liu, Q.; Peter, D.; Bozdag, E.; Tromp, J.; Hill, J.; Podhorszki, N.; Pugmire, D. GLAD-M35: A joint P and S global tomographic model with uncertainty quantification. Geophys. J. Int. 2024, 239, 478–502. [Google Scholar] [CrossRef]
  4. Hosseini, K.; Sigloch, K.; Tsekhmistrenko, M.; Zaheri, A.; Nissen-Meyer, T.; Igel, H. Global mantle structure from multifrequency tomography using P, PP and P-diffracted waves. Geophys. J. Int. 2020, 220, 96–141. [Google Scholar] [CrossRef]
  5. Lu, C.; Grand, S.P.; Lai, H.Y.; Garnero, E.J. TX2019slab: A New P and S Tomography Model Incorporating Subducting Slabs. J. Geophys. Res. Solid Earth 2019, 124, 11549–11567. [Google Scholar] [CrossRef]
  6. Simmons, N.A.; Forte, A.M.; Boschi, L.; Grand, S.P. GyPSuM: A joint tomographic model of mantle density and seismic wave speeds. J. Geophys. Res. Solid Earth 2010, 115, B12310. [Google Scholar] [CrossRef]
  7. French, S.W.; Romanowicz, B. Broad plumes rooted at the base of the Earth’s mantle beneath major hotspots. Nature 2015, 525, 95–99. [Google Scholar] [CrossRef]
  8. Masters, G.; Laske, G.; Bolton, H.; Dziewonski, A.M. The relative behavior of shear velocity, bulk sound speed, and compressional velocity in the mantle: Implications for chemical and thermal structure. In Earth’s Deep Interior: Mineral Physics and Tomography from the Atomic to the Global Scale; Geophysical Monograph Series; Karato, S., Forte, A., Liebermann, R., Masters, G., Stixrude, L., Eds.; AGU: Washington, DC, USA, 2000; Volume 117, pp. 63–87. [Google Scholar]
  9. Koelemeijer, P.; Ritsema, J.; Deuss, A.; van Heijst, H.J. SP12RTS: A degree-12 model of shear- and compressional-wave velocity for Earth’s mantle. Geophys. J. Int. 2016, 204, 1024–1039. [Google Scholar] [CrossRef]
  10. Houser, C.; Masters, G.; Shearer, P.; Laske, G. Shear and compressional velocity models of the mantle from cluster analysis of long-period waveforms. Geophys. J. Int. 2008, 174, 195–212. [Google Scholar] [CrossRef]
  11. Wang, Y.; Wen, L.X. Geometry and P and S velocity structure of the “African Anomaly”. J. Geophys. Res. Solid Earth 2007, 112, B05313. [Google Scholar] [CrossRef]
  12. Helmberger, D.V.; Ni, S.D. Seismic modeling constraints on the South African Super Plume. In Earth’s Deep Mantle: Structure, Composition, and Evolution; Geophysical Monograph Series; van der Hilst, R.D., Bass, J.D., Matas, J., Trampert, J., Eds.; AGU: Washington, DC, USA, 2005; Volume 160, pp. 65–84. [Google Scholar]
  13. He, Y.M.; Wen, L.X. Structural features and shear-velocity structure of the “Pacific Anomaly”. J. Geophys. Res. Solid Earth 2009, 114, B02309. [Google Scholar] [CrossRef]
  14. He, Y.M.; Wen, L.X. Geographic boundary of the “Pacific Anomaly” and its geometry and transitional structure in the north. J. Geophys. Res. Solid Earth 2012, 117, B09308. [Google Scholar] [CrossRef]
  15. Munch, F.D.; Romanowicz, B.; Mukhopadhyay, S.; Rudolph, M.L. Deep mantle plumes feeding periodic alignments of asthenospheric fingers beneath the central and southern Atlantic Ocean. Proc. Natl. Acad. Sci. USA 2024, 121, e2407543121. [Google Scholar] [CrossRef]
  16. Lekic, V.; Cottaar, S.; Dziewonski, A.; Romanowicz, B. Cluster analysis of global lower mantle tomography: A new class of structure and implications for chemical heterogeneity. Earth Planet. Sci. Lett. 2012, 357, 68–77. [Google Scholar] [CrossRef]
  17. Cottaar, S.; Lekic, V. Morphology of seismically slow lower-mantle structures. Geophys. J. Int. 2016, 207, 1122–1136. [Google Scholar] [CrossRef]
  18. Wang, J.; Lekic, V.; Schmerr, N.C.; Gu, Y.J.; Guo, Y.; Lin, R. Mesozoic intraoceanic subduction shaped the lower mantle beneath the East Pacific Rise. Sci. Adv. 2024, 10, eado1219. [Google Scholar] [CrossRef]
  19. Li, J.W.; Zhang, B.L.; Sun, D.Y.; Tian, D.D.; Yao, J.Y. Detailed 3D Structures of the Western Edge of the Pacific Large Low Velocity Province. J. Geophys. Res. Solid Earth 2024, 129, e2023JB028032. [Google Scholar] [CrossRef]
  20. Tan, E.; Gurnis, M. Metastable superplumes and mantle compressibility. Geophys. Res. Lett. 2005, 32, L20307. [Google Scholar] [CrossRef]
  21. Sun, D.; Tan, E.; Helmberger, D.; Gurnis, M. Seismological support for the metastable superplume model, sharp features, and phase changes within the lower mantle. Proc. Natl. Acad. Sci. USA 2007, 104, 9151–9155. [Google Scholar] [CrossRef]
  22. Thorne, M.S.; Garnero, E.J.; Jahnke, G.; Igel, H.; McNamara, A.K. Mega ultra low velocity zone and mantle flow. Earth Planet. Sci. Lett. 2013, 364, 59–67. [Google Scholar] [CrossRef]
  23. Tan, E.; Gurnis, M. Compressible thermochemical convection and application to lower mantle structures. J. Geophys. Res. Solid Earth 2007, 112, B06304. [Google Scholar] [CrossRef]
  24. McNamara, A.K. A review of large low shear velocity provinces and ultra low velocity zones. Tectonophysics 2019, 760, 199–220. [Google Scholar] [CrossRef]
  25. McNamara, A.K.; Garnero, E.J.; Rost, S. Tracking deep mantle reservoirs with ultra-low velocity zones. Earth Planet. Sci. Lett. 2010, 299, 1–9. [Google Scholar] [CrossRef]
  26. Yu, S.L.; Garnero, E.J. Ultralow Velocity Zone Locations: A Global Assessment. Geochem. Geophys. Geosyst. 2018, 19, 396–414. [Google Scholar] [CrossRef]
  27. Cottaar, S.; Romanowicz, B. An unsually large ULVZ at the base of the mantle near Hawaii. Earth Planet. Sci. Lett. 2012, 355, 213–222. [Google Scholar] [CrossRef]
  28. Li, J.W.; Sun, D.Y.; Bower, D.J. Slab control on the mega-sized North Pacific ultra-low velocity zone. Nat. Commun. 2022, 13, 1042. [Google Scholar] [CrossRef]
  29. Li, Z.; Leng, K.D.; Jenkins, J.; Cottaar, S. Kilometer-scale structure on the core-mantle boundary near Hawaii. Nat. Commun. 2022, 13, 2787. [Google Scholar] [CrossRef] [PubMed]
  30. To, A.; Fukao, Y.; Tsuboi, S. Evidence for a thick and localized ultra low shear velocity zone at the base of the mantle beneath the central Pacific. Phys. Earth Planet. Inter. 2011, 184, 119–133. [Google Scholar] [CrossRef]
  31. Jenkins, J.; Mousavi, S.; Li, Z.; Cottaar, S. A high-resolution map of Hawaiian ULVZ morphology from ScS phases. Earth Planet. Sci. Lett. 2021, 563, 116885. [Google Scholar] [CrossRef]
  32. Lai, V.H.; Helmberger, D.; Dobrosavljevic, V.V.; Wu, W.B.; Sun, D.Y.; Jackson, J.M.; Gurnis, M. Strong ULVZ and Slab Interaction at the Northeastern Edge of the Pacific LLSVP Favors Plume Generation. Geochem. Geophys. Geosyst. 2022, 23, e2021GC010020. [Google Scholar] [CrossRef]
  33. Sun, D.; Helmberger, D.; Lai, V.H.; Gurnis, M.; Jackson, J.M.; Yang, H.Y. Slab Control on the Northeastern Edge of the Mid-Pacific LLSVP Near Hawaii. Geophys. Res. Lett. 2019, 46, 3142–3152. [Google Scholar] [CrossRef]
  34. Ma, X.L.; Sun, X.L.; Thomas, C. Localized ultra-low velocity zones at the eastern boundary of Pacific LLSVP. Earth Planet. Sci. Lett. 2019, 507, 40–49. [Google Scholar] [CrossRef]
  35. Bower, D.J.; Gurnis, M.; Seton, M. Lower mantle structure from paleogeographically constrained dynamic Earth models. Geochem. Geophys. Geosyst. 2013, 14, 44–63. [Google Scholar] [CrossRef]
  36. Tackley, P.J. Dynamics and evolution of the deep mantle resulting from thermal, chemical, phase and melting effects. Earth-Sci. Rev. 2012, 110, 1–25. [Google Scholar] [CrossRef]
  37. Tan, E.; Leng, W.; Zhong, S.J.; Gurnis, M. On the location of plumes and lateral movement of thermochemical structures with high bulk modulus in the 3-D compressible mantle. Geochem. Geophys. Geosyst. 2011, 12, Q07005. [Google Scholar] [CrossRef]
  38. Simmons, N.A.; Myers, S.C.; Johannesson, G.; Matzel, E. LLNL-G3Dv3: Global P wave tomography model for improved regional and teleseismic travel time prediction. J. Geophys. Res. Solid Earth 2012, 117, B10302. [Google Scholar] [CrossRef]
  39. Lu, C.; Grand, S.P. The effect of subducting slabs in global shear wave tomography. Geophys. J. Int. 2016, 205, 1074–1085. [Google Scholar] [CrossRef]
  40. Rondenay, S.; Cormier, V.F.; Van Ark, E.M. SKS and SPdKS sensitivity to two-dimensional ultralow-velocity zones. J. Geophys. Res. Solid Earth 2010, 115, B04311. [Google Scholar] [CrossRef]
  41. Helmberger, D.V.; Garnero, E.J.; Ding, X. Modeling two-dimensional structure at the core-mantle boundary. J. Geophys. Res. Solid Earth 1996, 101, 13963–13972. [Google Scholar] [CrossRef]
  42. Garnero, E.J.; Helmberger, D.V. A very slow basal layer underlying large-scale low-velocity anomalies in the lower mantle beneath the pacific—Evidence from core phases. Phys. Earth Planet. Inter. 1995, 91, 161–176. [Google Scholar] [CrossRef]
  43. Garnero, E.J.; Helmberger, D.V. Seismic detection of a thin laterally varying boundary layer at the base of the mantle beneath the central-Pacific. Geophys. Res. Lett. 1996, 23, 977–980. [Google Scholar] [CrossRef]
  44. Rondenay, S.; Fischer, K.M. Constraints on localized core-mantle boundary structure from multichannel, broadband SKS coda analysis. J. Geophys. Res. Solid Earth 2003, 108, 2537. [Google Scholar] [CrossRef]
  45. Garnero, E.J.; Helmberger, D.V. Further structural constraints and uncertainties of a thin laterally varying ultralow-velocity layer at the base of the mantle. J. Geophys. Res. Solid Earth 1998, 103, 12495–12509. [Google Scholar] [CrossRef]
  46. Helmberger, D.V.; Wen, L.; Ding, X. Seismic evidence that the source of the Iceland hotspot lies at the core-mantle boundary. Nature 1998, 396, 251–255. [Google Scholar] [CrossRef]
  47. Wen, L.X.; Helmberger, D.V. A two-dimensional P-SV hybrid method and its application to modeling localized structures near the core-mantle boundary. J. Geophys. Res. Solid Earth 1998, 103, 17901–17918. [Google Scholar] [CrossRef]
  48. Vanacore, E.A.; Rost, S.; Thorne, M.S. Ultralow-velocity zone geometries resolved by multidimensional waveform modelling. Geophys. J. Int. 2016, 206, 659–674. [Google Scholar] [CrossRef]
  49. Thorne, M.S.; Garnero, E.J. Inferences on ultralow-velocity zone structure from a global analysis of SPdKS waves—Art. no. B08301. J. Geophys. Res. Solid Earth 2004, 109, 22. [Google Scholar] [CrossRef]
  50. Thorne, M.S.; Leng, K.D.; Pachhai, S.; Rost, S.; Wicks, J.; Nissen-Meyer, T. The Most Parsimonious Ultralow-Velocity Zone Distribution From Highly Anomalous SPdKS Waveforms. Geochem. Geophys. Geosyst. 2021, 22, e2020GC009467. [Google Scholar] [CrossRef]
  51. Thorne, M.S.; Pachhai, S.; Leng, K.D.; Wicks, J.K.; Nissen-Meyer, T. New Candidate Ultralow-Velocity Zone Locations from Highly Anomalous SPdKS Waveforms. Minerals 2020, 10, 211. [Google Scholar] [CrossRef]
  52. Thorne, M.S.; Takeuchi, N.; Shiomi, K. Melting at the Edge of a Slab in the Deepest Mantle. Geophys. Res. Lett. 2019, 46, 8000–8008. [Google Scholar] [CrossRef]
  53. Pachhai, S.; Li, M.M.; Thorne, M.S.; Dettmer, J.; Tkalcic, H. Internal structure of ultralow-velocity zones consistent with origin from a basal magma ocean. Nat. Geosci. 2022, 15, 79–84. [Google Scholar] [CrossRef]
  54. Hansen, S.E.; Garnero, E.J.; Li, M.M.; Shim, S.H.; Rost, S. Globally distributed subducted materials along the Earth’s core-mantle boundary: Implications for ultralow velocity zones. Sci. Adv. 2023, 9, eadd4838. [Google Scholar] [CrossRef]
  55. Jensen, K.J.; Thorne, M.S.; Rost, S. SPdKS analysis of ultralow-velocity zones beneath the western Pacific. Geophys. Res. Lett. 2013, 40, 4574–4578. [Google Scholar] [CrossRef]
  56. Zhan, Z.W.; Helmberger, D.V.; Li, D.Z. Imaging subducted slab structure beneath the Sea of Okhotsk with teleseismic waveforms. Phys. Earth Planet. Inter. 2014, 232, 30–35. [Google Scholar] [CrossRef]
  57. Sun, D.Y.; Helmberger, D. Upper-mantle structures beneath USArray derived from waveform complexity. Geophys. J. Int. 2011, 184, 416–438. [Google Scholar] [CrossRef]
  58. Sun, D.Y.; Gurnis, M.; Saleeby, J.; Helmberger, D. A dipping, thick segment of the Farallon Slab beneath central U.S. J. Geophys. Res. Solid Earth 2017, 122, 2911–2928. [Google Scholar] [CrossRef]
  59. Yu, J.; Sun, D.Y. A Lower Mantle Slab Below the East Asia Margin Constrained by Seismic Waveform Complexity. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024246. [Google Scholar] [CrossRef]
  60. Ko, J.Y.T.; Helmberger, D.V.; Wang, H.L.; Zhan, Z.W. Lower Mantle Substructure Embedded in the Farallon Plate: The Hess Conjugate. Geophys. Res. Lett. 2017, 44, 10216–10225. [Google Scholar] [CrossRef]
  61. Kennett, B.L.N.; Engdahl, E.R. Traveltimes for global earthquake location and phase identification. Geophys. J. Int. 1991, 105, 429–465. [Google Scholar] [CrossRef]
  62. Ekström, G.; Nettles, M.; Dziewonski, A.M. The global CMT project 2004-2010: Centroid-moment tensors for 13,017 earthquakes. Phys. Earth Planet. Inter. 2012, 200, 1–9. [Google Scholar] [CrossRef]
  63. Dziewonski, A.M.; Chou, T.A.; Woodhouse, J.H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. J. Geophys. Res. 1981, 86, 2825–2852. [Google Scholar] [CrossRef]
  64. Sun, D.Y.; Helmberger, D.V.; Jackson, J.M.; Clayton, R.W.; Bower, D.J. Rolling hills on the core-mantle boundary. Earth Planet. Sci. Lett. 2013, 361, 333–342. [Google Scholar] [CrossRef]
  65. Sun, D.Y.; Helmberger, D.; Ni, S.D.; Bower, D. Direct measures of lateral velocity variation in the deep Earth. J. Geophys. Res. Solid Earth 2009, 114, B05303. [Google Scholar] [CrossRef]
  66. Grand, S.P.; Helmberger, D.V. Upper mantle shear structure of north-america. Geophys. J. R. Astron. Soc. 1984, 76, 399–438. [Google Scholar] [CrossRef]
  67. Bréger, L.; Romanowicz, B. Three-dimensional structure at the base of the mantle beneath the central Pacific. Science 1998, 282, 718–720. [Google Scholar] [CrossRef] [PubMed]
  68. Schweitzer, J.; Müller, G. Anomalous difference traveltimes and amplitude ratios of SKS and SKKS from Tonga-Fiji Events. Geophys. Res. Lett. 1986, 13, 1529–1532. [Google Scholar] [CrossRef]
  69. Schweitzer, J. Untersuchungen zur Geschwindigkeitsstruktur im unteren Erdmantel und im Bereich der Kern-Mantel-Grenze unterhalb des Pazifiks mit Scherwellen. Ph.D. Thesis, Frankfurt University, Frankfurt, Germany, 1990; p. 134. [Google Scholar] [CrossRef]
  70. Schweitzer, J. Laufzeiten und Amplituden der Phasen SKS und SKKS und die Struktur des äußeren Erdkerns. Ph.D. Thesis, der Johann Wolfgang Goethe-University, Frankfurt, Germany, 1984; p. 117. [Google Scholar] [CrossRef]
  71. Li, D.Z.; Helmberger, D.; Clayton, R.W.; Sun, D.Y. Global synthetic seismograms using a 2-D finite-difference method. Geophys. J. Int. 2014, 197, 1166–1183. [Google Scholar] [CrossRef]
  72. Schmandt, B.; Lin, F.C. P and S wave tomography of the mantle beneath the United States. Geophys. Res. Lett. 2014, 41, 6342–6349. [Google Scholar] [CrossRef]
  73. Chu, R.S.; Schmandt, B.; Helmberger, D.V. Juan de Fuca subduction zone from a mixture of tomography and waveform modeling. J. Geophys. Res. Solid Earth 2012, 117, B03304. [Google Scholar] [CrossRef]
  74. Festin, M.M.; Thorne, M.S.; Li, M. Evidence for Ultra-Low Velocity Zone Genesis in Downwelling Subducted Slabs at the Core– Mantle Boundary. Seism. Rec. 2024, 4, 111–120. [Google Scholar] [CrossRef]
  75. Komatitsch, D.; Xie, Z.N.; Bozdag, E.; de Andrade, E.S.; Peter, D.; Liu, Q.Y.; Tromp, J. Anelastic sensitivity kernels with parsimonious storage for adjoint tomography and full waveform inversion. Geophys. J. Int. 2016, 206, 1467–1478. [Google Scholar] [CrossRef]
  76. Ni, S.D.; Tan, E.; Gurnis, M.; Helmberger, D. Sharp sides to the African superplume. Science 2002, 296, 1850–1852. [Google Scholar] [CrossRef] [PubMed]
  77. Li, M.M.; McNamara, A.K.; Garnero, E.J.; Yu, S.L. Compositionally-distinct ultra-low velocity zones on Earth’s core-mantle boundary. Nat. Commun. 2017, 8, 177. [Google Scholar] [CrossRef]
  78. Wolf, J.; Long, M.D.; Frost, D.A. Ultralow velocity zone and deep mantle flow beneath the Himalayas linked to subducted slab. Nat. Geosci. 2024, 17, 302–308. [Google Scholar] [CrossRef]
  79. Fan, A.; Sun, X.; Zhang, Z.; Zhang, P.; Zong, J. From Subduction to LLSVP: The Core-Mantle Boundary Heterogeneities Across North Atlantic. Geochem. Geophys. Geosystems 2022, 23, e2021GC009879. [Google Scholar] [CrossRef]
  80. Otsuru, K.; Kawai, K.; Geller, R.J. Subducted Slab Slipping Underneath the Northern Edge of the Pacific Large Low-Shear-Velocity Province in D”. J. Geophys. Res. Solid Earth 2025, 130, e2024JB030654. [Google Scholar] [CrossRef]
  81. Su, Y.; Ni, S.; Zhang, B.; Chen, Y.; Wu, W.; Li, M.; Sun, H.; Hou, M.; Cui, X.; Sun, D. Detections of ultralow velocity zones in high-velocity lowermost mantle linked to subducted slabs. Nat. Geosci. 2024, 17, 332–339. [Google Scholar] [CrossRef]
  82. Davaille, A.; Romanowicz, B. Deflating the LLSVPs: Bundles of Mantle Thermochemical Plumes Rather Than Thick Stagnant “Piles”. Tectonics 2020, 39, e2020TC006265. [Google Scholar] [CrossRef]
  83. Frost, D.A.; Rost, S. The P-wave boundary of the Large-Low Shear Velocity Province beneath the Pacific. Earth Planet. Sci. Lett. 2014, 403, 380–392. [Google Scholar] [CrossRef]
  84. McNamara, A.K.; Zhong, S. Thermochemical structures beneath Africa and the Pacific Ocean. Nature 2005, 437, 1136–1139. [Google Scholar] [CrossRef]
  85. Hu, M.; Gurnis, M.; Jackson, J.M. Influence of subduction history and mineral deformation on seismic anisotropy in the lower mantle. Geophys. J. Int. 2025, ggaf457. [Google Scholar] [CrossRef]
  86. Yuan, Q.; Li, M. Vastly Different Heights of LLVPs Caused by Different Strengths of Historical Slab Push. Geophys. Res. Lett. 2022, 49, e2022GL099564. [Google Scholar] [CrossRef]
  87. Sun, D.; Helmberger, D.; Song, X.D.; Grand, S.P. Predicting a Global Perovskite and Post-Perovskite Phase Boundary. In Post-Perovskite: The Last Mantle Phase Transition; Geophysical Monograph Series; Hirose, K., Lay, T., Yuen, D., Eds.; AGU: Washington, DC, USA, 2007; Volume 174, pp. 155–170. [Google Scholar]
Geosciences 15 00471 g001
Figure 1. Tomographic images of the lower mantle at different depths. From left to right: S-wave tomography model GyPSuM [6], S40RTS [2], SEMUCB-WM1 [7], GLAD-M35 [3], and P-wave tomography model LLNL-G3Dv3 [38]. The focus region is outlined by a black box, highlighting the presence of an apparent hole in the LLVP.
Figure 1. Tomographic images of the lower mantle at different depths. From left to right: S-wave tomography model GyPSuM [6], S40RTS [2], SEMUCB-WM1 [7], GLAD-M35 [3], and P-wave tomography model LLNL-G3Dv3 [38]. The focus region is outlined by a black box, highlighting the presence of an apparent hole in the LLVP.
Geosciences 15 00471 g001
Geosciences 15 00471 g004
Figure 4. Compiled SKS travel time residuals for multiple events. Here, the distance of each event is shifted by fixing the distance from event to the station KSCO to 95.5° (the distance to event A in Figure 1). The color denotes the true distance from the event to the station KSCO. The inset shows the events (stars) used for travel time measurements, colored by their respective distances. Note that the southern group of events (blue color), including event A, display ~2 s faster SKS than the northern group of events (red color).
Figure 4. Compiled SKS travel time residuals for multiple events. Here, the distance of each event is shifted by fixing the distance from event to the station KSCO to 95.5° (the distance to event A in Figure 1). The color denotes the true distance from the event to the station KSCO. The inset shows the events (stars) used for travel time measurements, colored by their respective distances. Note that the southern group of events (blue color), including event A, display ~2 s faster SKS than the northern group of events (red color).
Geosciences 15 00471 g004
Geosciences 15 00471 g005
Figure 5. Comparison between the data and synthetics for different models. (a) displays cross sections along the white line in Figure 2a. From top to bottom: original GyPSuM, a model with the bottom 800 km of the GyPSuM inflated by 1.5 and a model with the upper mantle of the GyPSuM replaced by a North American upper mantle model [72]. Examples of ray paths of SKS (red) and SKKS (black) are displayed in the cross sections. (b) compares the data for event A in Figure 2b at the azimuth range of 47.5–50° (left) with the synthetics generated from the three models shown in (a). The average cross-correlation coefficients (CCs), listed on top of the synthetics, are calculated between data and synthetics over the time window highlighted by gray shading in the left panel. Only data within the distance range of 95–115° are used to calculate the CCs values.
Figure 5. Comparison between the data and synthetics for different models. (a) displays cross sections along the white line in Figure 2a. From top to bottom: original GyPSuM, a model with the bottom 800 km of the GyPSuM inflated by 1.5 and a model with the upper mantle of the GyPSuM replaced by a North American upper mantle model [72]. Examples of ray paths of SKS (red) and SKKS (black) are displayed in the cross sections. (b) compares the data for event A in Figure 2b at the azimuth range of 47.5–50° (left) with the synthetics generated from the three models shown in (a). The average cross-correlation coefficients (CCs), listed on top of the synthetics, are calculated between data and synthetics over the time window highlighted by gray shading in the left panel. Only data within the distance range of 95–115° are used to calculate the CCs values.
Geosciences 15 00471 g005
Geosciences 15 00471 g006
Figure 6. Comparison between the data and synthetics. From left to right: data for events A (a) and B (b) in Figure 2b at the azimuth range of 47.5–50°, synthetics for the mega-ULVZ model shown in Figure 2b, and a modified mega-ULVZ model. The mega-ULVZ models are plotted on top of the synthetics as red boxes. Within the mega-ULVZ, δVs = −45%, δVs = −15%, and δρ = 10%. The three colored heavy dash lines denote the ray paths of SKS in the source side mantle at a distance of 105° for events B, A, and D (from left to right) in Figure 2b.
Figure 6. Comparison between the data and synthetics. From left to right: data for events A (a) and B (b) in Figure 2b at the azimuth range of 47.5–50°, synthetics for the mega-ULVZ model shown in Figure 2b, and a modified mega-ULVZ model. The mega-ULVZ models are plotted on top of the synthetics as red boxes. Within the mega-ULVZ, δVs = −45%, δVs = −15%, and δρ = 10%. The three colored heavy dash lines denote the ray paths of SKS in the source side mantle at a distance of 105° for events B, A, and D (from left to right) in Figure 2b.
Geosciences 15 00471 g006
Geosciences 15 00471 g007
Figure 7. Synthetics for the reference model. The high-velocity block in (a) has a length of 750 km, width of 3.5°, δVs of 2%, and a dip angle of 70°. The three colored dash lines denote the ray paths of SKS in the source side mantle at a distance of 105° for events B, A, and D (from left to right) in Figure 2b. (b–d) Comparison between the data (left) and simulated SV waveforms (right) for events A, B, and D, respectively.
Figure 7. Synthetics for the reference model. The high-velocity block in (a) has a length of 750 km, width of 3.5°, δVs of 2%, and a dip angle of 70°. The three colored dash lines denote the ray paths of SKS in the source side mantle at a distance of 105° for events B, A, and D (from left to right) in Figure 2b. (b–d) Comparison between the data (left) and simulated SV waveforms (right) for events A, B, and D, respectively.
Geosciences 15 00471 g007
Geosciences 15 00471 g008
Figure 8. Sensitivity tests of the dip angle (θ) of the high-velocity block. From left to right: SKS data of event A, synthetics for models with θ of 70° (reference model), 65°, and 70°. All models here have a length of 750 km, width of 3.5°, and δVs of 2%. In each model plot, the reference model is shown as a black outline for comparison. The three colored dash lines on top denote the ray paths of SKS in the source side mantle at a distance of 105° for events B, A, and D (from left to right) in Figure 2b.
Figure 8. Sensitivity tests of the dip angle (θ) of the high-velocity block. From left to right: SKS data of event A, synthetics for models with θ of 70° (reference model), 65°, and 70°. All models here have a length of 750 km, width of 3.5°, and δVs of 2%. In each model plot, the reference model is shown as a black outline for comparison. The three colored dash lines on top denote the ray paths of SKS in the source side mantle at a distance of 105° for events B, A, and D (from left to right) in Figure 2b.
Geosciences 15 00471 g008
Geosciences 15 00471 g009
Figure 9. Sensitivity tests for δVs. From left to right: SKS data for event A, followed by synthetic waveforms for models with δVs of 2%, 1%, and 3%, and a gradient model with δVs decreasing from 3% at the center to 1% at the edges. The three colored dash lines on top denote the ray paths of SKS in the source side mantle at a distance of 105° for events B, A, and D (from left to right) in Figure 2b.
Figure 9. Sensitivity tests for δVs. From left to right: SKS data for event A, followed by synthetic waveforms for models with δVs of 2%, 1%, and 3%, and a gradient model with δVs decreasing from 3% at the center to 1% at the edges. The three colored dash lines on top denote the ray paths of SKS in the source side mantle at a distance of 105° for events B, A, and D (from left to right) in Figure 2b.
Geosciences 15 00471 g009
Geosciences 15 00471 g010
Figure 10. Sensitivity tests for the width, depth extent, and length. From left to right: the reference model, a model with a width of 2°, a model with a width of 5°, a model located right at the core–mantle boundary, a model located 350 km shallower, a model with half the length and a δVs of 4%, and a model with 1.5 times the length and a δVs of 1.3%. The three colored dash lines on top denote the ray paths of SKS in the source side mantle at a distance of 105° for events B, A, and D (from left to right) in Figure 2b.
Figure 10. Sensitivity tests for the width, depth extent, and length. From left to right: the reference model, a model with a width of 2°, a model with a width of 5°, a model located right at the core–mantle boundary, a model located 350 km shallower, a model with half the length and a δVs of 4%, and a model with 1.5 times the length and a δVs of 1.3%. The three colored dash lines on top denote the ray paths of SKS in the source side mantle at a distance of 105° for events B, A, and D (from left to right) in Figure 2b.
Geosciences 15 00471 g010
Geosciences 15 00471 g011
Figure 11. Three-dimensional models of the lower mantle high-velocity anomaly and corresponding synthetics. (a) The 3D model projection at depths of 2500 km (solid rectangle) and 1800 km (dashed rectangle). The purple, blue, and black rectangles denote Models I, II, and III, with lateral extents of approximately 600 km, 300 km, and 150 km, respectively. The background tomographic image is from the GyPSuM at a depth of 2100 km. Black stars mark events A–D as in Figure 2b. Data and synthetics along azimuthal profiles at distances of 99° and 105° are shown in (b,c), respectively. In (b,c), the data are selected with a distance range of 98.5–99.5° and 104–106°, respectively. In the synthetics, black traces represent predictions from the GyPSuM and red traces are synthetics for the 3D models in (a) with different lateral extents.
Figure 11. Three-dimensional models of the lower mantle high-velocity anomaly and corresponding synthetics. (a) The 3D model projection at depths of 2500 km (solid rectangle) and 1800 km (dashed rectangle). The purple, blue, and black rectangles denote Models I, II, and III, with lateral extents of approximately 600 km, 300 km, and 150 km, respectively. The background tomographic image is from the GyPSuM at a depth of 2100 km. Black stars mark events A–D as in Figure 2b. Data and synthetics along azimuthal profiles at distances of 99° and 105° are shown in (b,c), respectively. In (b,c), the data are selected with a distance range of 98.5–99.5° and 104–106°, respectively. In the synthetics, black traces represent predictions from the GyPSuM and red traces are synthetics for the 3D models in (a) with different lateral extents.
Geosciences 15 00471 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Sun, D. The Hole in the Pacific LLVP and Multipathed SKS. Geosciences 2025, 15, 471. https://doi.org/10.3390/geosciences15120471

AMA Style

Sun D. The Hole in the Pacific LLVP and Multipathed SKS. Geosciences. 2025; 15(12):471. https://doi.org/10.3390/geosciences15120471

Chicago/Turabian Style

Sun, Daoyuan. 2025. "The Hole in the Pacific LLVP and Multipathed SKS" Geosciences 15, no. 12: 471. https://doi.org/10.3390/geosciences15120471

APA Style

Sun, D. (2025). The Hole in the Pacific LLVP and Multipathed SKS. Geosciences, 15(12), 471. https://doi.org/10.3390/geosciences15120471

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop