Next Article in Journal
Integrating PCA and Fractal Modeling for Identifying Geochemical Anomalies in the Tropics: The Malang–Lumajang Volcanic Arc, Indonesia
Previous Article in Journal
Mass Movement Risk Assessment in the Loess Hilly Region of Northwest China Using a Weighted Information Theoretic Framework
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Geosciences
Volume 15
Issue 12
10.3390/geosciences15120469
geosciences-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Analyzing the Connectivity of Fracture Networks Using Natural Fracture Characteristics in the Khairi Murat Range, Potwar Region, Northern Pakistan

by
Nasrullah Dasti
* and
Mian Sohail Akram
Institute of Geology, University of the Punjab, New Campus, Lahore 54590, Pakistan
*
Author to whom correspondence should be addressed.
Geosciences 2025, 15(12), 469; https://doi.org/10.3390/geosciences15120469
Submission received: 9 August 2025 / Revised: 7 October 2025 / Accepted: 26 October 2025 / Published: 11 December 2025
(This article belongs to the Topic Advances in Groundwater Science and Engineering)
Browse Figures
Versions Notes

Abstract

Rock fracture connectivity is a developing concept that demonstrates the effectiveness of fracture networks in facilitating the preferential flow of fluid through the medium. This study demonstrates the significance and impact of fracture parameters in determining the connectivity of fracture networks. An attempt is made to define fracture parameters, such as fracture density, length, and the quotient of dispersion in their orientation, in addition to understanding the characteristics of fracture and the connectivity of the fracture network in a specified domain. The results based on field observations and measurements at outcrops of the Khairi Murat Range, including the study of field photographs and images, indicate that the fractional connected area (FCA) significantly determines the connectivity of fracture networks and, conversely, depends upon the fracture parameters. Eight fracture sets identified in the study area represent the intensity of dispersion of the strike angles of the fractures. The angular dispersion, i.e., the Fisher coefficient of strike angle of the fracture sets, ranges from 0.26 to 1, indicating that the fracture sets are systematic and concentrated in one direction. Although fracture density and length establish a linear relationship, fracture network connectivity is surprisingly independent of length. Scale-dependent fracture length plays a significant role in serving as the “backbone” of the network in the connectivity of the fracture system. Instead of the length and size of the cluster, fracture network connectivity is affected by fracture orientation and density. Characterization of the fracture properties-based approach successfully explores the connectivity of fracture networks on an outcrop scale.

1. Introduction

Fractures are ubiquitous in rocks and have long been recognized as an essential property of rock mass due to their numerous applications in various fields [1]. For example, fractures, being essential discontinuities, significantly influence the rock quality in engineering geological applications [2]; the strength of rock masses [3,4,5]; slope stability [6]; and civil structures on the earth’s surface, such as dams and foundations [5,7,8]. The fracture network and its potential connectivity factors are indispensable for the safe construction and development of underground repositories [9], as well as the storage [10] or disposal of hazardous wastes [11,12,13,14,15]. Rock fracture networks are important variables that influence fluid flow through rock masses in the subsurface [16,17]. The interconnectivity of rock fractures and fracture networks is critically important for groundwater transportation and reservoir hydrocarbon potential [18,19,20,21,22]. This research employs a modified version of the methods outlined by [23] to characterize the rock fracture properties in terms of connectivity of fracture networks within rock masses as a medium for fluid transport. The modifications to the method of Ghosh and Mitra [23] are described in Section 4.
Rock fractures are analyzed by the characterization of multiple fracture parameters such as orientation, spacing, aperture, density or frequency, length, roughness, and so on. Several researchers extensively use these parameters for their particular objectives, and they are well documented in the literature. Fracture orientation, density, and length play an important role in determining the connectivity of fracture networks and predicting flow pathways because the connectivity is a measure of the interconnectedness of fractures and fracture networks in a system domain [24,25]. Connectivity of the fracture networks in fractured rock generally depends on three parameters: the degree of connectedness of individual fractures (based on the relative dispersion of the orientation of fracture sets); the number of fractures per unit area, called density in a 2D framework; and fracture trace length [26,27,28]. Several research studies [29,30] have been carried out in an attempt to gain a better understanding of how fracture attributes and their statistical properties contribute to the connectedness of fracture networks [29,31,32,33,34].
Numerous published studies, including the one referenced herein, have proposed various conceptual models, such as the discrete fracture network (DFN) and the equivalent continuum model (ECM), to address the complexities of fluid flow and the diversity of fracture connectivity patterns. These models incorporate different methodologies for simulating fractures, estimating the probabilistic distribution of fracture properties, and generating the resulting fracture networks [29]. Fracture attributes datasets are commonly assumed, synthesized, or integrated using computational techniques to meet model input requirements. The resulting data are then extrapolated across the targeted natural fracture host domain. A wide range of conceptual and numerical models, along with specialized computer codes and software, are being developed rapidly. In recent years, several new modeling and simulation methodologies have been introduced into the literature to analyze systems and their associated geometric parameters [1,35,36,37,38,39,40,41,42,43,44,45,46]. Although exponential advancements in fracture modeling and simulation offer significant advantages and pave the way for innovative research and modern methodologies, the importance of field investigations at the outcrop scale remains indispensable. For novice researchers, the process of collecting geological data directly from the field is often more appealing than the complex and sometimes overwhelming task of selecting optimal models or developing new software and computational tools for simulation and analysis. Field work not only provides tangible insights into geological features but also fosters a deeper, more intuitive understanding that purely computational approaches may lack.
Therefore, to address this problem, we used an analytical and investigative approach based on field data supplemented with numerical values by mathematical equations and statistical methods. Fracture network characterization and fracture connectivity analysis are based on the interpretation of integrated fracture data obtained from field measurements, geo-structural maps, and fracture trace maps developed from field photographs. The objective of this paper is to evaluate and identify the role of fracture properties in the characterization of fracture connectivity using numerical and statistical distribution analyses. The area of Khairi Murat (Figure 1) was selected as a case study for this purpose because it contains excellent outcrop exposures with remarkable imprints of structural features, such as fractures, faults, and folds.

2. Geology and Structure

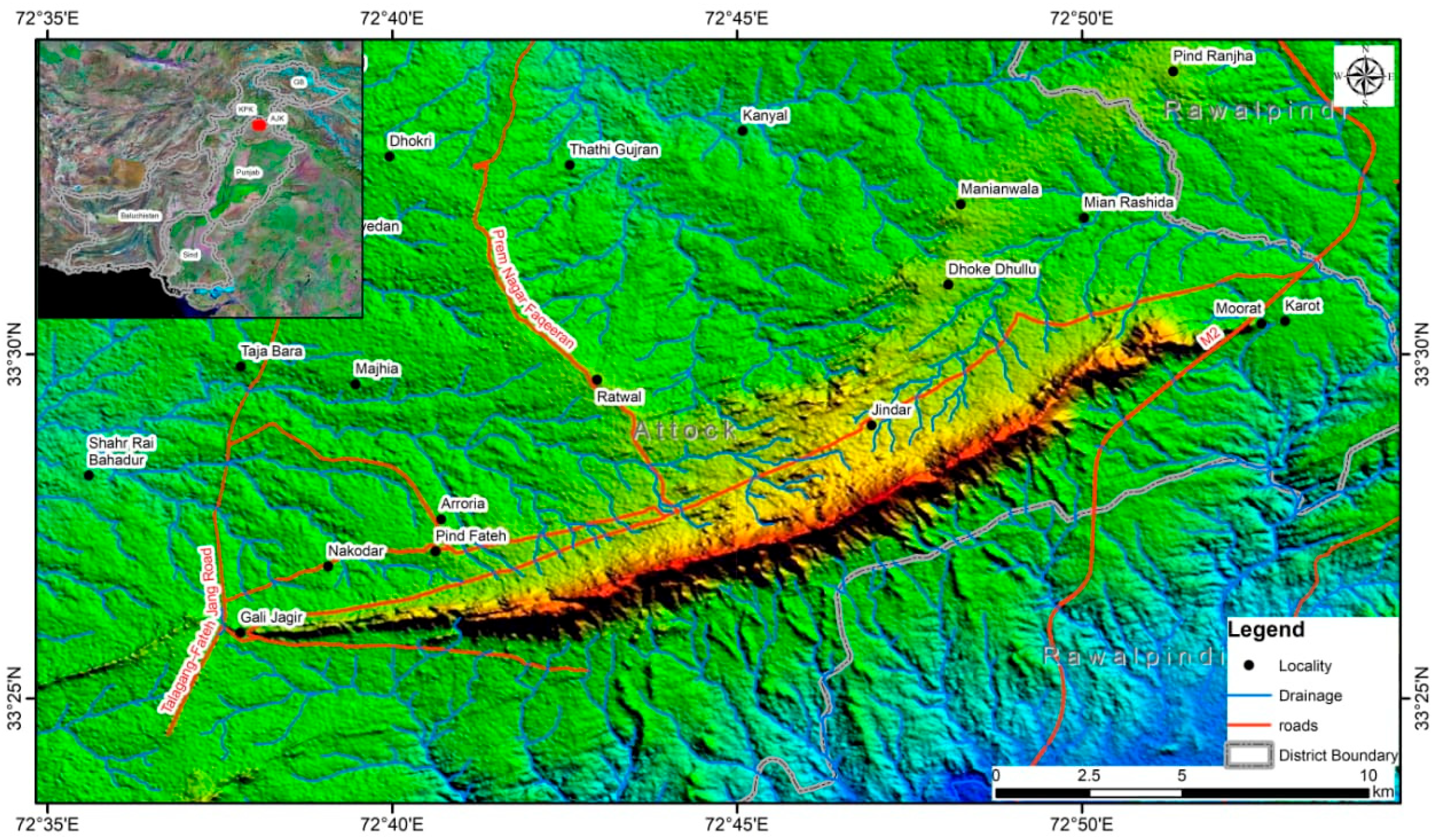
2.1. Geology of the Area

The Khairi Murat Range (KMR) is located about 40 km southwest of Islamabad, the capital city of Pakistan, between the northern limb of the Soan syncline in the south and the Main Boundary Thrust (MBT) in the north. The area is part of the northeastern edge of the Potwar Sub Basin and contains a stratigraphic succession from the Early Eocene to the Middle Pliocene [47,48] (Figure 2). The Early Eocene assemblage of the Charrat Group comprises Margallah Hill Limestone, the Chorgali Formation, and the Kuldana Formation, which collectively preserve a record of shallow marine, marine to continental paleo-environment [49,50,51,52,53,54,55]. Due to a period of non-deposition in the Potwar Fold Belt (PFB), the Early Eocene to Oligocene stratigraphic sequence is missing (Table 1). The Miocene Rawalpindi Group includes the Murree Formation and the Kamlial formations and is extensively exposed in the study area. The lithological units of the Rawalpindi Group consist of thin- to thick-bedded sandstone, cross-bedded siltstone, and mudstone, with remarkable fluvial depositional imprints. The Chinji, Nagri, and Dhok Pathan Formations of the Siwalik Group designate the Mio-Pliocene molasses sequence of sediments that are exposed in the study area [56,57]. Outcrops of these stratigraphic sequences preserve significant records of tectonic events in the form of geological structures [58].

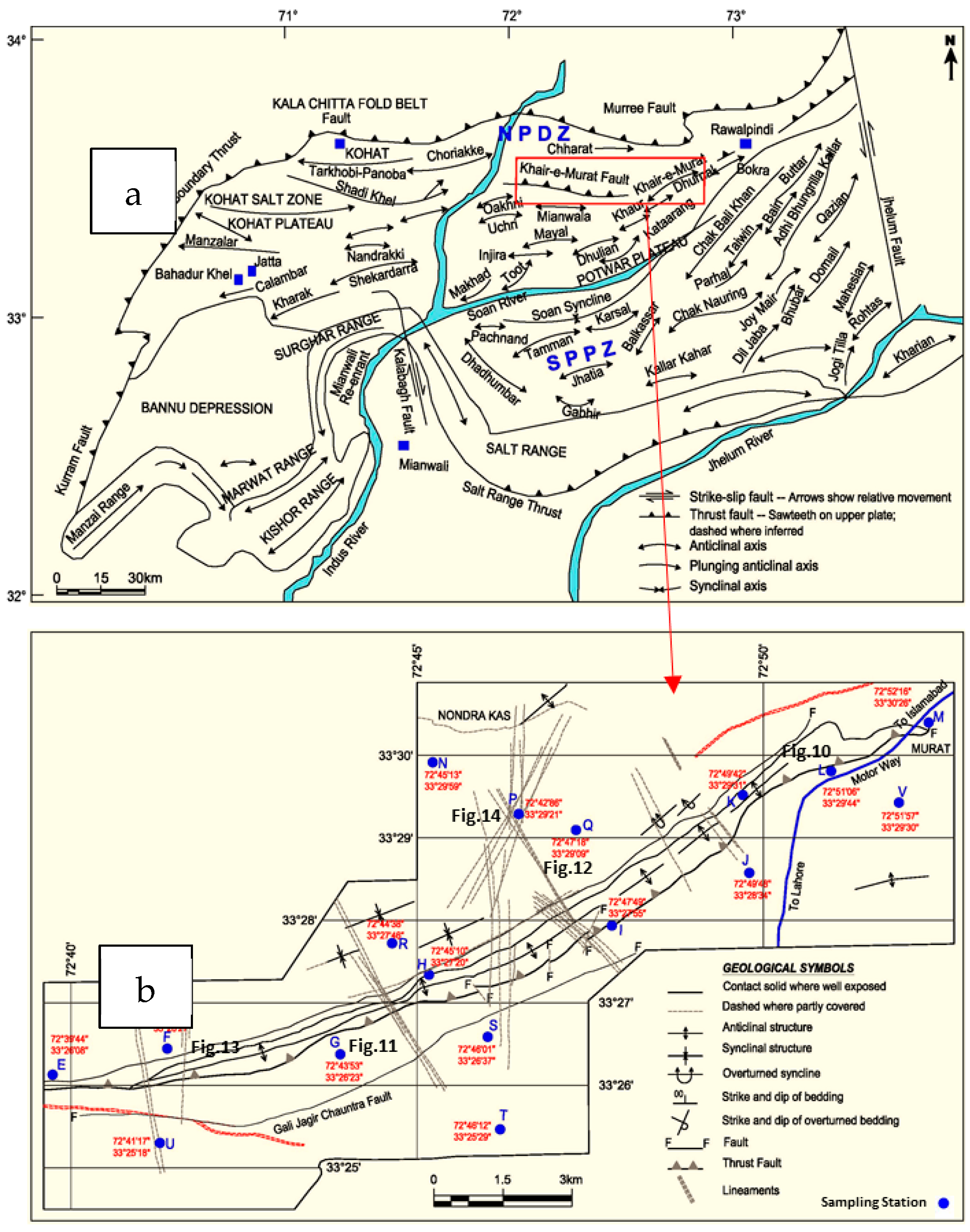
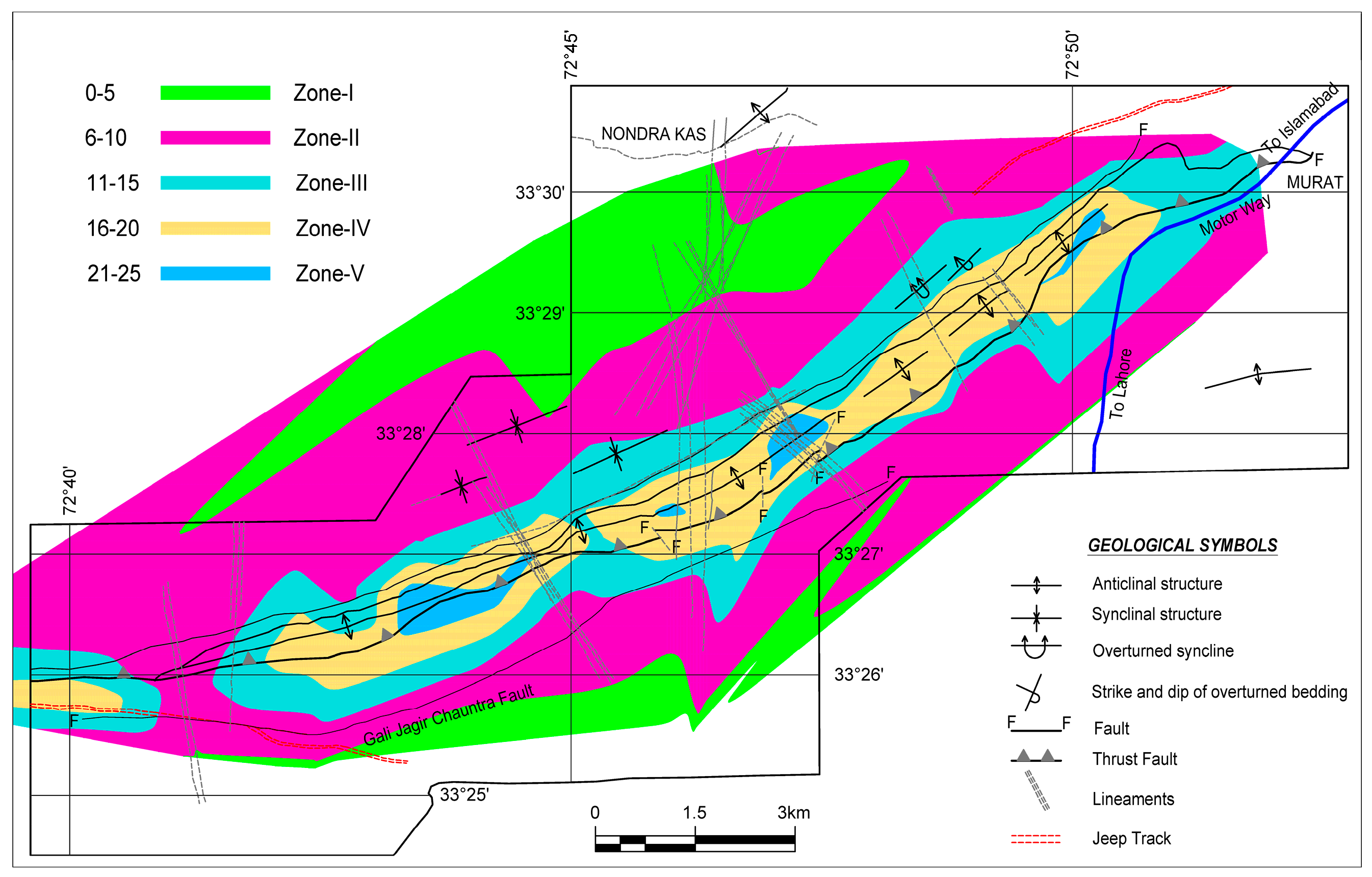
2.2. Structure of the Area

Structurally, the Potwar Plateau is divided into two zones: the North Potwar Deformed Zone (NPDZ) and the South Potwar Platform Zone (SPPZ) (Figure 3a). The study area is located in the North Potwar Deformed Zone (NPDZ). This zone is a product of the Himalayan orogenic deformation system and experiences complex deformation, including imbricate thrusts, ramp-flat duplexes, and triangle zones developed during the Neogene [60,61,62,63,64]. In this zone, the sedimentary sequences are imbricated by southward thrusting and fault-related folding, with a minimum crustal shortening rate of 22 mm per year [65,66]. The southern boundary of the NPDZ is marked by the Khairi Murat Range, which has been tectonically uplifted along the south-verging Khairi Murat Thrust. This high-angle fault, striking NE-SW, runs approximately perpendicular to the tectonic transport direction. The fault is clearly evident where competent Eocene strata overlie the Kuldana and Murree Formations [67]. In the footwall of the Khairi Murat Thrust to the south, the Siwaliks have been thrust over by the Dhurnal fault, a north-facing roof thrust. A triangle zone exists between the Khairi Murat Thrust and the passive back thrust (Dhurnal fault) [58,60,61,62,64,65,68]. The Khairi Murat Anticline is a significant fold in the study area. Its core is composed of Margalla Hill limestone, while its northern limb comprises the Chorgali, Kuldana, and Murree Formations. The southern limb is faulted (Figure 3). The study area also contains several small-scale strike-slip offsets, such as the Gali Jagir-Chauntra fault (Figure 3a,b), and records approximately 55 km of crustal shortening, indicating the complexity of tectonic deformation in this region [69,70].

3. Data Acquisition Techniques and Analysis Methods

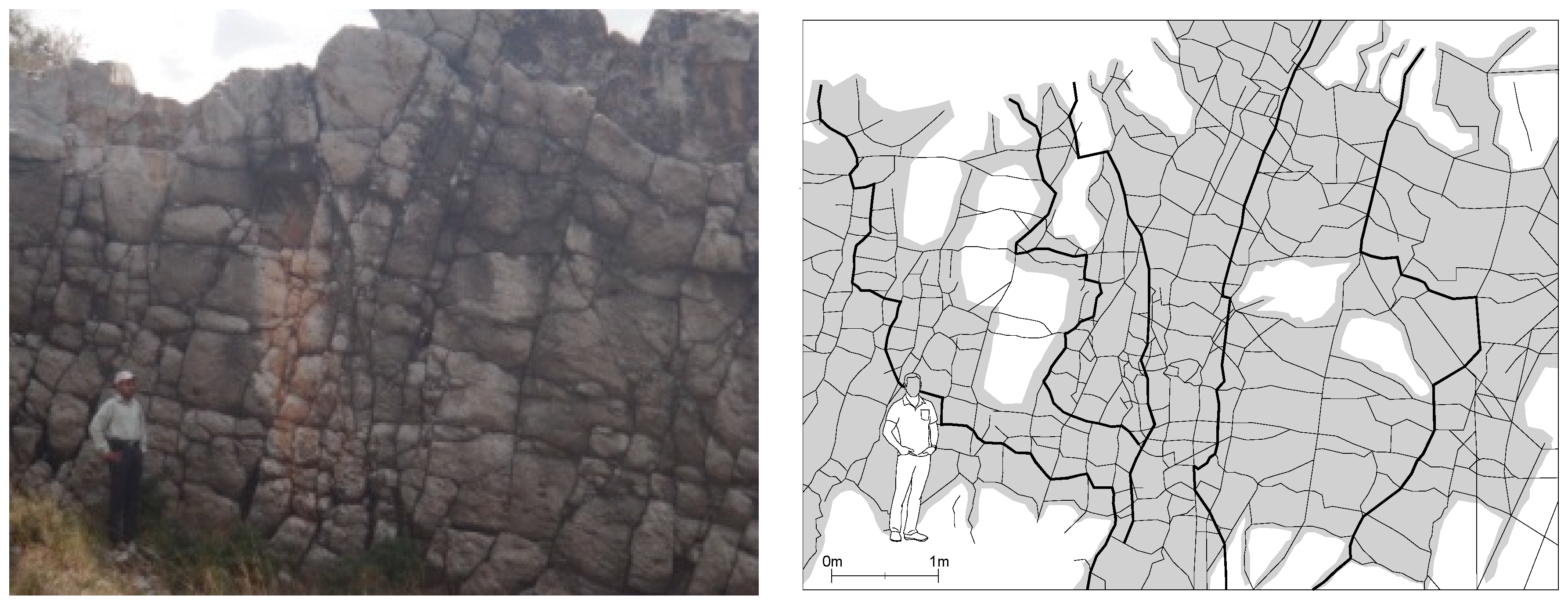
3.1. Data Collection from Outcrops

Rock fracture sampling was conducted at 107 sites within a 35 km × 2.5 km area of the Khairi Murat Range. All possible lithological and structural domains were surveyed. A hand-held GPS device was used to record the positions of the sampling sites so that the fracture maps could be georeferenced. Approximately 3224 individual fractures were mapped across 107 sites in 17 data collection centers (Figure 3b shows the locations of these centers). A series of maps was produced by taking photographs directly from outcrops, focusing on the fractures in the field in sedimentary strata. Two techniques were employed to obtain representative sampling in the study area.

Circular Scanline Technique

The circular scanline method [72,73,74,75], also referred to as the circle inventory window [76], as described by Davis et al. (1996), is a significant and effective tool for fracture data collection. It offers a wide range of applications and provides time-efficient estimates of trace density and mean trace length [77]. A circular scanline is simply a circle drawn on the surface of a rock (Figure 4b). Based on the insights and guidance from [75,78,79], and following the arguments of [80], a fixed-radius circle (sample size) is preferred for measuring fracture properties.
A fracture trace map is created by physically tracing visual fracture signatures directly on outcrop faces. This method minimizes sampling bias by reducing complications associated with the random distribution of fracture lengths and anisotropies in orientations, thereby enhancing practical applicability. The estimator equation developed by [76] is used to determine fracture density from outcrops and photographs (i.e., photographs with known focal length, height, and scale) (Figure 4c,d).

3.2. Data Acquisition in the Lab

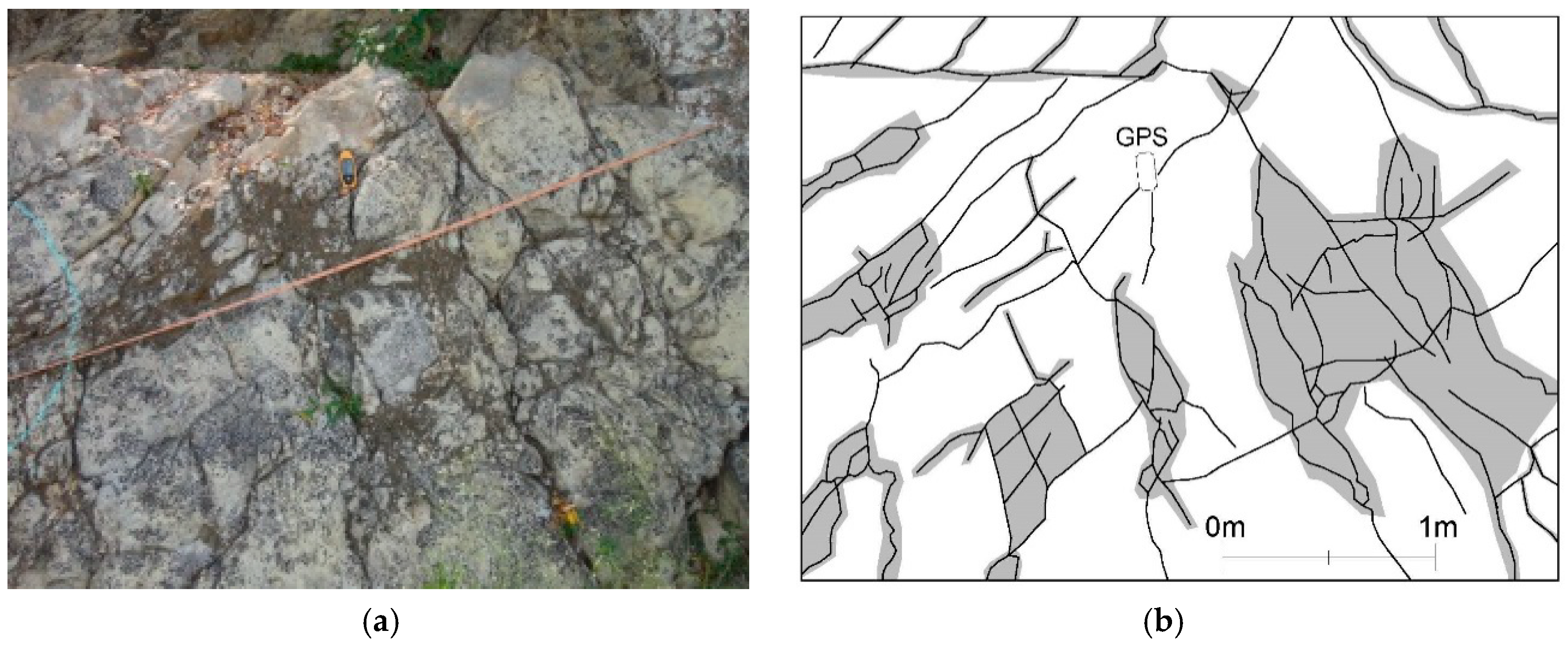
Photograph Trace Maps

AutoCAD (V. 2018) software provides an effective working environment for the characterization and quantification of natural fracture features. All data were digitized and analyzed using this software. Based on shared geometrical and physical properties, such as orientations (with fixed dispersion intervals), dip magnitude, and dip direction, individual fractures were grouped and presented as rose diagrams (Figure 5).

4. Analysis Methods

4.1. Method Adopted from Davis et al. (1996) [76]

The density of fractures at a sampling station is defined as the number of fractures per unit area, as measured using the circle inventory method [81,82]. Fracture density depends on three primary rock mass properties: the mechanical property of the rock unit, bed thickness, and proximity to the structural domain (i.e., intensity of applied stress) [83,84]. In this study, fracture density is quantified as the total number of fractures (regardless of fracture sets) occurring within a unit-radius circle, in accordance with the circle inventory method. The value is mathematically derived using the equation provided as follows [76]:
P f = L π r 2
where
P f = fracture density;
L = cumulative length of all fractures;
r = radius of the inventory circle.
The measure of density is expressed as length per unit area (e.g., ft/ft2, cm/cm2, m/m2, and km/km2) or in reciprocal form. (i.e., ft−1, cm−1, m−1, and km−1). Density values (Table 2) play an important role in establishing the connectivity of fracture networks.

4.2. Method Adopted from Ghosh & Mitra (2009) [23]

The interconnectedness of fractures is determined by fracture characteristics, as described in Section 1. Fracture length, density, and orientation are three major fracture characteristics that influence the connectivity of fracture networks. Interconnected fractures form clusters, which are then linked to nearby clusters by one or more longer fractures. These linking fractures do not allow the fracture networks to remain isolated and are termed “backbone” fractures [14,41,85], previously termed “skeleton” fractures by [86,87]. The interconnection of individual fractures into clusters, along with the linkage of these clusters via backbone fractures, results in fully connected fracture networks. Such networks represent the overall connectivity of the rock fracture system [23,88,89,90].
To estimate the degree of fracture connectedness within the network, a cluster analysis technique adopted from [23] is used.
The mean connectivity and general characteristics of fracture networks in an area can be characterized by the total length of connected fractures (FCL) or the area of connected fracture networks (FCA). Fracture cluster length (FCL) can be expressed as follows:
F C L = T o t a l   l e n g t h   o f   c o n n e c t e d   f r a c t u r e s   T o t a l   s a m p l e   a r e a
Whereas the fractional connected area (FCA) is as follows:
F C A = T o t a l   s u r f a c e   a r e a   o f   r o c k   c o n n e c t e d   b y   f r a c t u r e s   T o t a l   s a m p l e   a r e a
The FCA is generally considered the most suitable way of evaluating the effectiveness of fracture networks in facilitating fluid flow [23,91,92,93]. To estimate the FCA, high-resolution photographs of outcrops exhibiting the best fracture exposure were taken at 67 sites. The analysis was performed using the open-source software Open Plot [94].
The connectivity of the fracture network is often evaluated using percolation theory, which is based on the interconnectivity of fractures and fracture network density, fracture length, and orientation [37]. Complex regional and local stress perturbations generate multiple fractures and fracture sets, including extension and hybrid shear fractures with wide orientation dispersion [95]. Based on the statistical Fisher distribution [96], eight fracture sets were identified. Orientation measurements taken from field outcrops were grouped into fracture sets using the techniques outlined by Michelena et al. (2013) [97] and Zangerl et al. (2022) [98], in conjunction with structural geological criteria derived from field observations [99,100]. Fracture orientations (defined by the strike and dip trends) are used to describe fracture clustering behavior and its effect on network connectivity.

5. Analysis and Results

The region of interest includes complex structural features such as thrusts, faults, folds, deformation bands, and strike-slip components associated with episodic deformation. A significant number of fracture populations related to these deformational features are present in the study area [101]. Based on the explanation of [102] and assuming a constant fracture aperture, it is observed that nearly all fractures measured at sampling stations are open and fluid-conducive fractures. The analytical methods used in this study, when combined with statistical analysis, become twofold helpful tools for investigating fracture network connectivity.

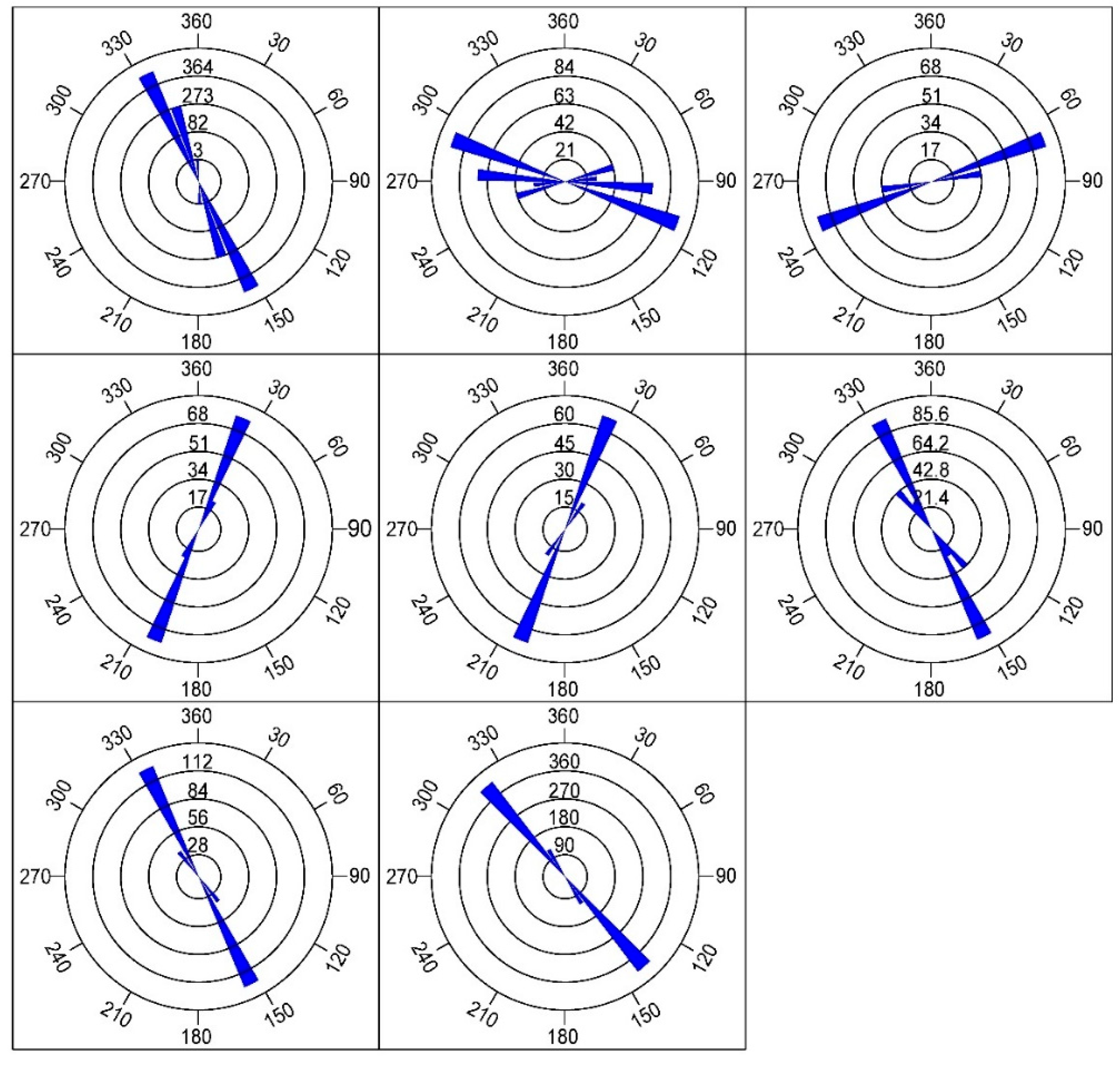
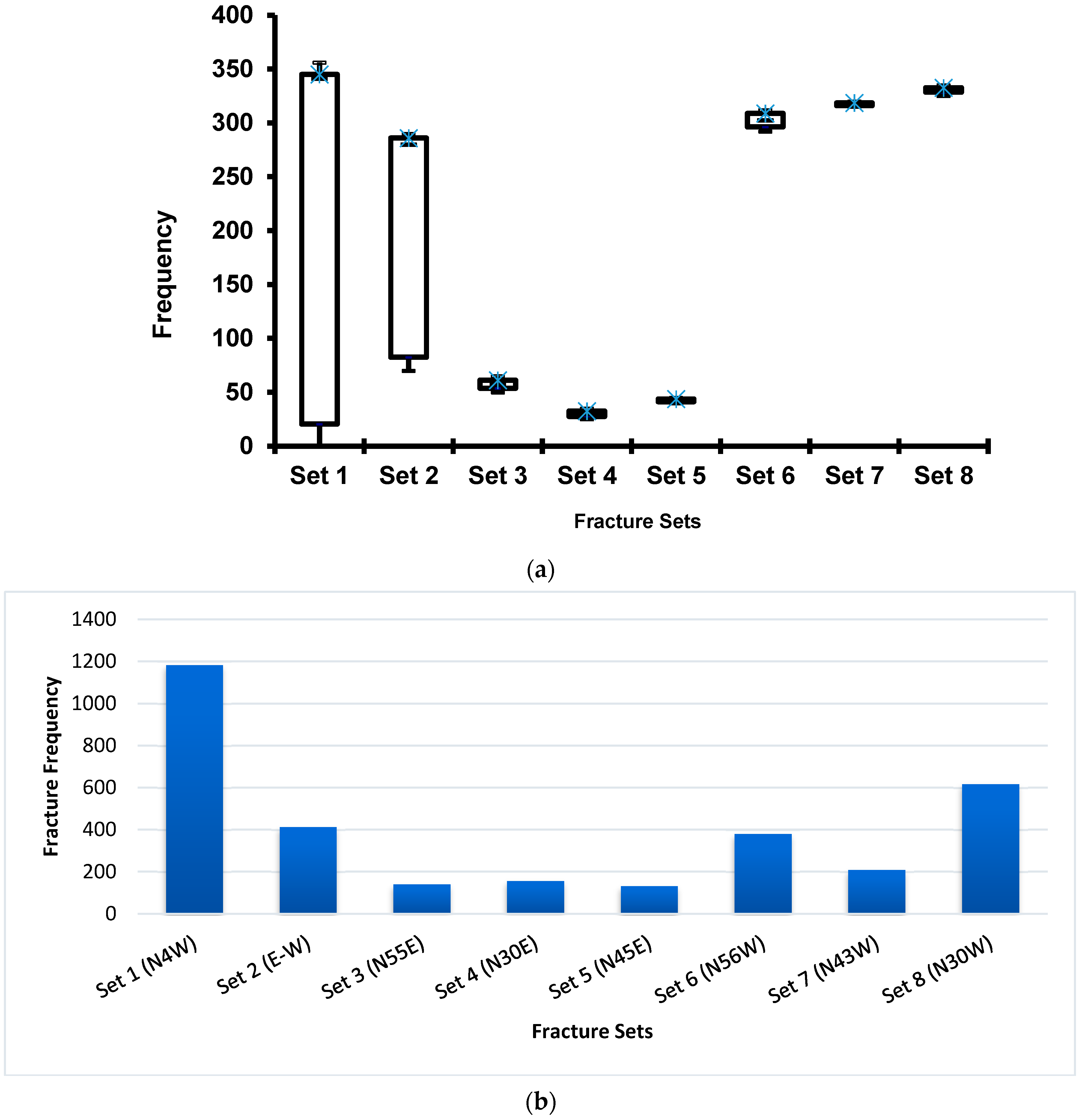
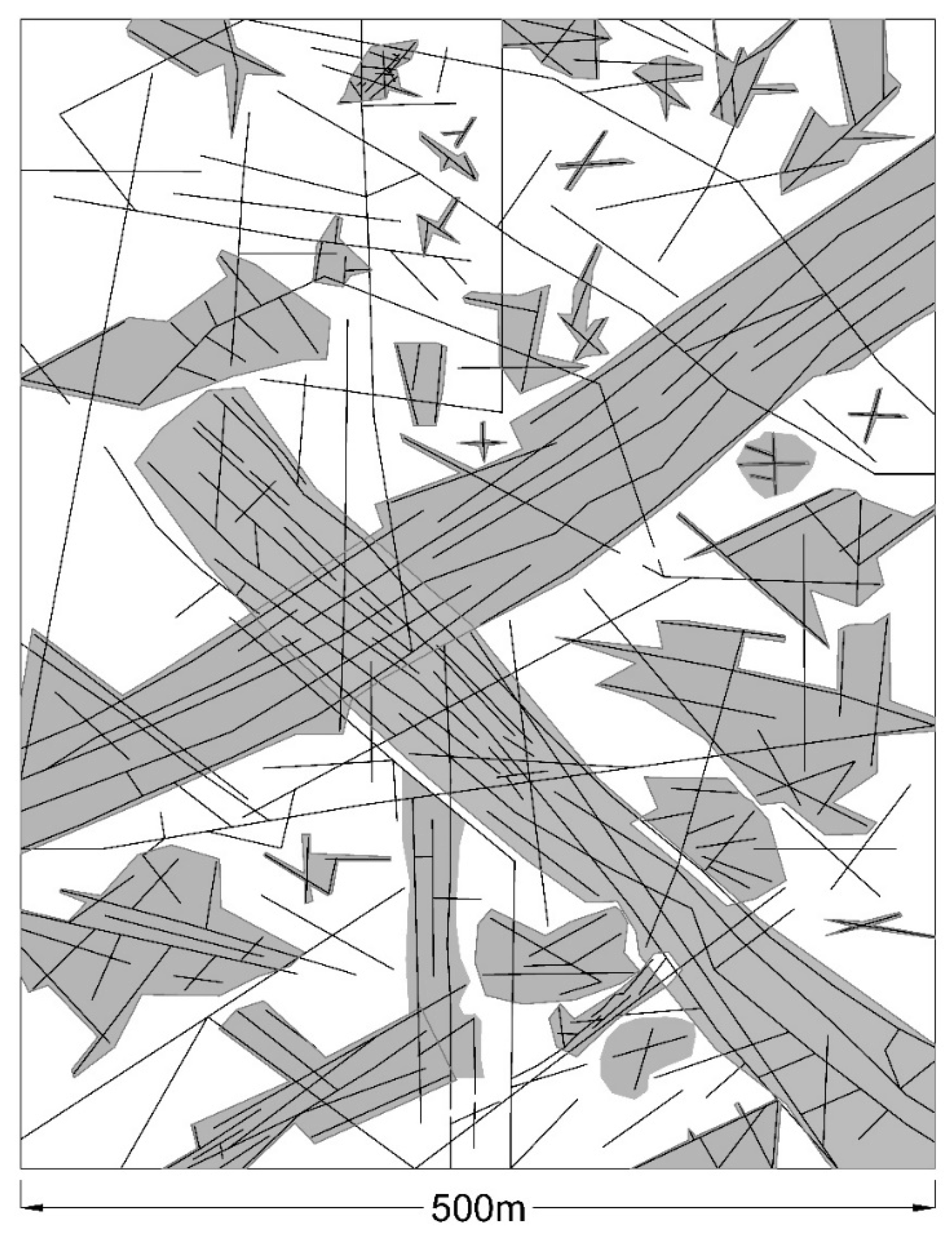
5.1. Fracture Orientation Analysis

Eight fracture sets are identified at 67 surveyed locations in the study area using circular statistics and the methodology described by [99]. Based on their physical characteristics, the entire fracture population was classified into sets considering (a) similarities among strike and dip and (b) the mode of deformation with angular dispersion of 20° for strike and 10° for dip of each set, as shown in the rose diagram (Figure 5). Table 2 shows the mean strike and dip of these eight fracture sets: N4°W/87° (vertical), E-W/49°NW, N55°E/50°SE, N30°E/90 (vertical), N45°E/49°NW, N56°W/45°NE, N43°W/90 (vertical), and N30°W/88° (vertical). These fractures developed in response to their proximity to structural elements and reflect the episodic occurrence of various tectonic events. A broad range of angular scatter in fracture orientation increases the likelihood of individual fractures intersecting to form connected networks. Out of the eight fracture sets, nearly two to three are observed at each measurement station.
Fracture Set-1, which runs from N4°W to N2°E, is the dominant set in the study area, followed by Set-8, the second-largest set with a narrow range of strike angles between N25°W and N35°W. Several fractures in Set-1 strike between N20°W and N20°E, including a north–south (N-S) orientation, with slight distortion in dip and strike angles. Similarly, in Set-2, a number of individual fractures occur along E-W or at orientations of N85°W and N85°E. Set-3 strikes in NE-SW, and Set-4 in ENE-WSW. Set-5 follows the NNW-SSE directions, while Set-6 follows NW-SE. Set-7 trends N40°–45°W. In the study area, there are two groups of orthogonal fracture systems (Set-1 and Set-2, and Set-4 and Set-7) and one group of conjugate fracture systems (Set-3 and Set-5). The fractures in Set-3 and Set-5 are in the same quadrant but dip in opposite directions, i.e., 50°SE and 49°NW, respectively (Table 2). The rose diagram depicts the manual grouping of the total measured population of fractures (Figure 5). A panel of fracture trends (rose diagram) observed in the outcrops of the Khairi Murat Range (study area) is presented in Figure 5. While the rose diagrams in this figure appear to show relatively narrow strike distributions, these represent the dominant orientations of fractures within each mapped area, grouped to highlight the primary fracture directions. The bin size and normalization used in plotting emphasize peak trends, which can visually narrow the apparent spread of orientations. Visual inspection of rose diagrams shows that the fracture population consists of eight fracture sets. Each fracture set has its own independent orientation (dip and strike). Especially, the 6th and 7th (Set-3 and Set-5) positions in the panel show semi-parallel strike and opposite dip direction, representing a conjugate relationship. In contrast, the Box and Whisker plot of the orientation data (Figure 6a) shows the full range of strike orientation of the fracture population observed within each fracture set across the entire study area. Set-1 and Set-2 are more scattered than the other sets of fractures. These include fractures from multiple locations and capture local variations in strike that are not always visible in the rose diagrams. Therefore, the broader strike range in Figure 6a reflects the cumulative variability within each set, while Figure 5 illustrates the local dominant trends. This difference in presentation explains the apparent discrepancy and highlights both the consistency of dominant orientations and the variability present across the network. The frequency distribution of each group is presented in Figure 6b. The statistical characterization of fracture density and clustering in terms of the fractional connected area (FCA) provides a basis for assessing fracture network connectivity.

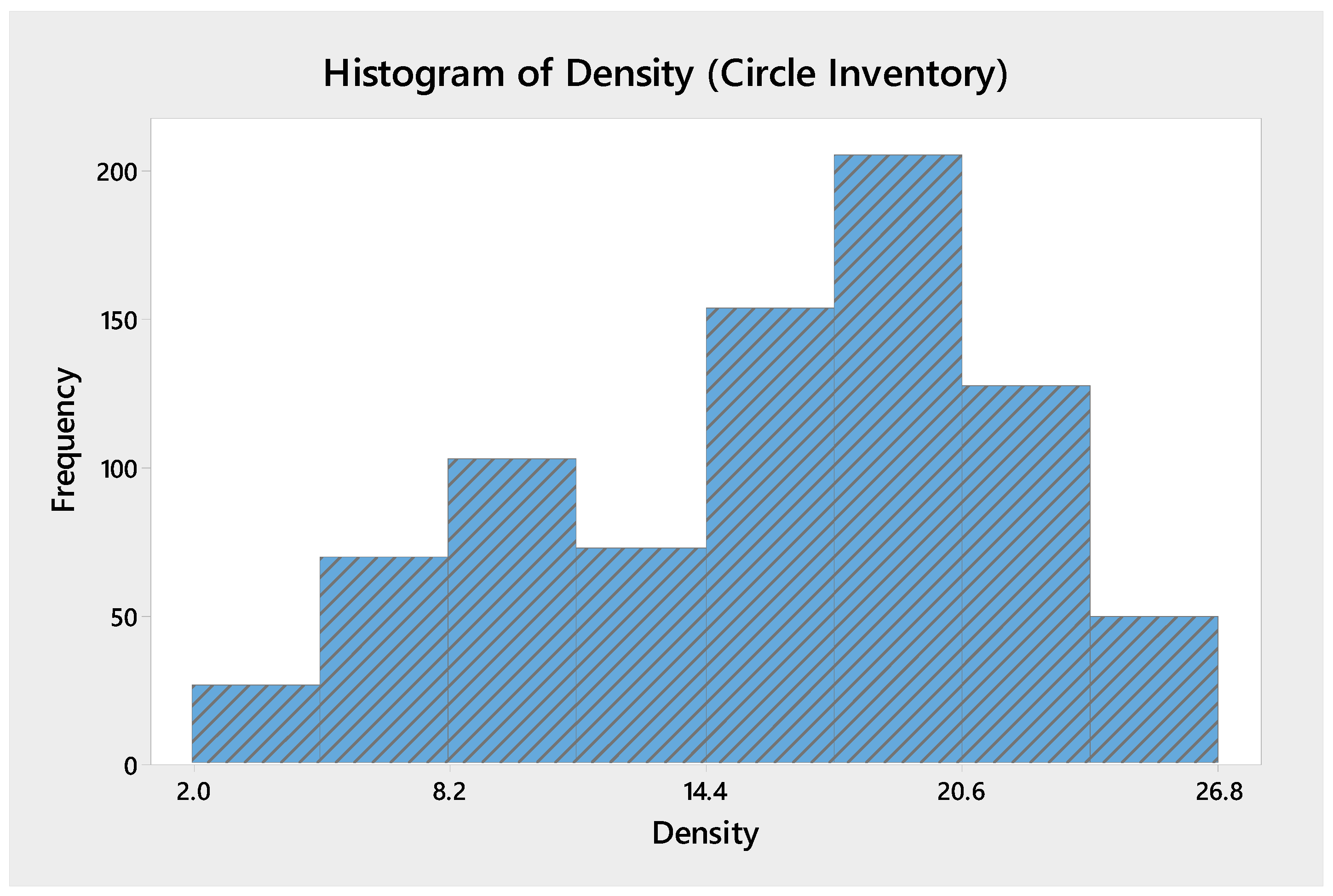
5.2. Fracture Density Analysis

To avoid sampling bias, as described in [75], a uniform circle (with equal radius, i.e., 1 m) was drawn on the bedding surface of exposed outcrops throughout the sampling stations. The entire region was divided into five zones, as shown in the fracture density map (Figure 7). In Zone I, the fracture density varies from 0.5 to 5 fractures per meter, with a mean density of 4.63. Zone II has a density of 6–10 fractures per meter, with a mean density of 8.57. Similarly, Zones III and IV have concentrations ranging from 11 to 16 fractures per meter and 16 to 20 fractures per meter, with mean densities of 13.37 and 18.61, respectively. Zone V has a higher density and varies from 20 to 27 fractures per meter, with a mean density of 22.81, as summarized in Table 3. A visual inspection of the density map (Figure 7) and the superimposition of density values onto the structural map of the study area demonstrate a significant correlation between density and both structural elements and deformation intensity. The histogram (Figure 8) illustrates the frequency distribution of density values measured within the circle inventory dataset. The distribution is unimodal, with a clear concentration of values toward the middle to higher density ranges. This pattern suggests that moderate to moderately high densities are most common within the circle inventory. From this, it can be inferred that the fracture network in the area is relatively well connected, as high density values generally indicate more interconnected fractures. Table 4 shows the statistical properties of cumulative fracture density across the entire region.

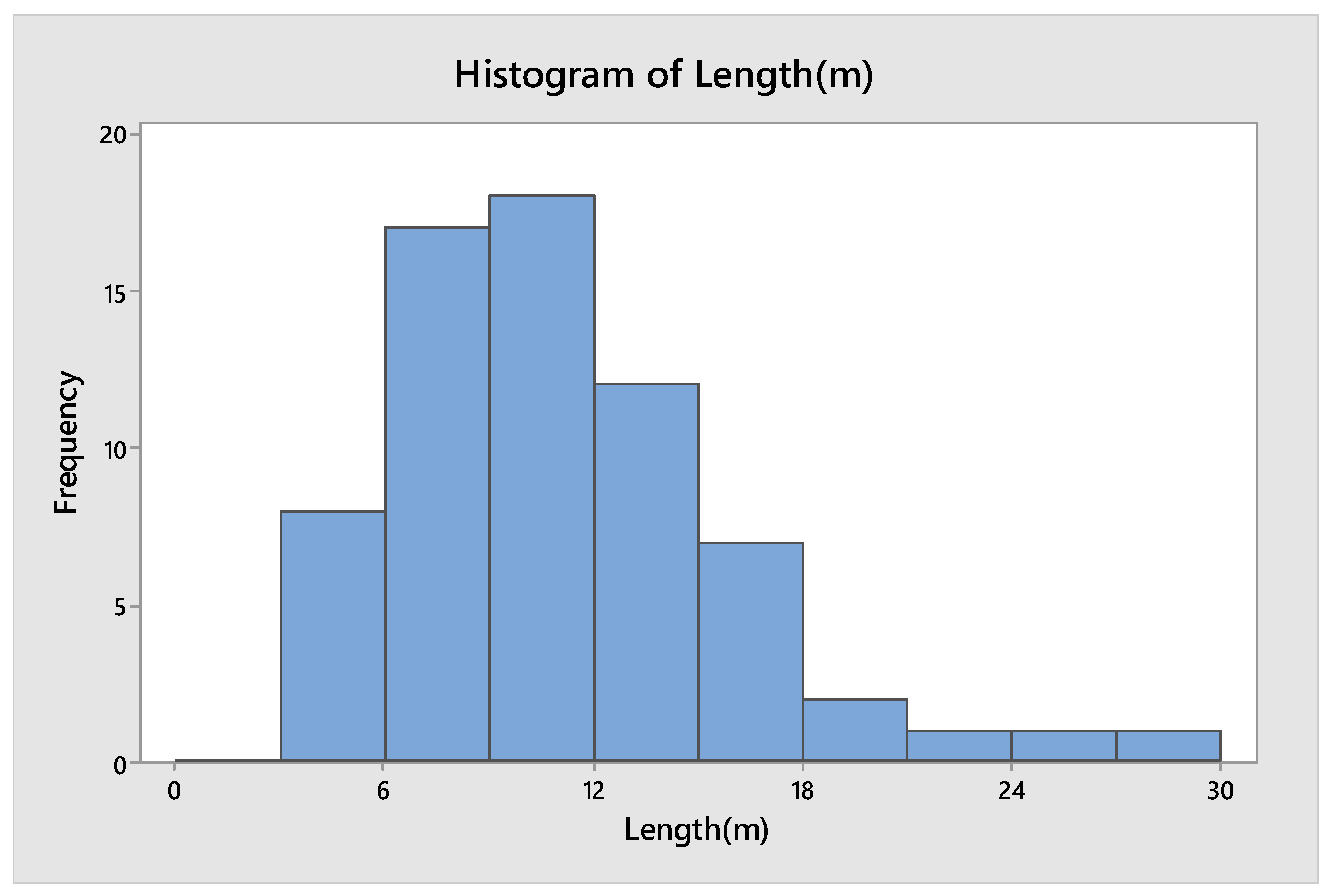
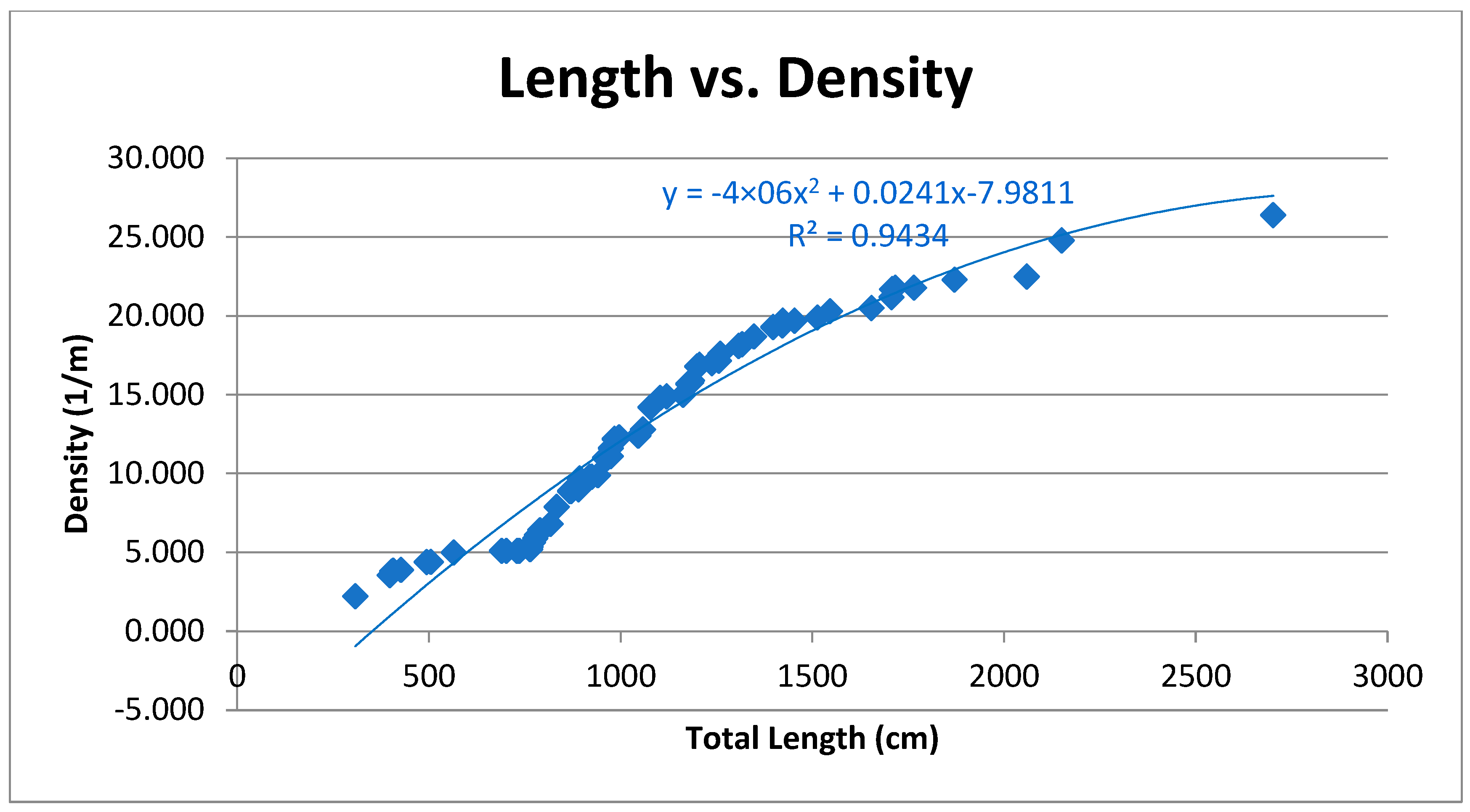
5.3. Fracture Length Analysis

The fracture length distribution for each field-scale fracture group has been examined and quantified using values obtained from both the circle inventory method and fracture trace maps derived from field photographs. Cumulatively, the eight fracture sets have a mean fracture length of 11 m with a minimum of 3 m and a maximum of 27 m. As illustrated in Figure 9 (frequency distribution), the majority of fractures remain in the length bracket of 6 m to 14 m. Shorter fractures are more abundant, while longer fractures are scarce and occur only sparsely in the study area. Similar to fracture density, fracture length is also strongly influenced by structural position and lithological contrasts.

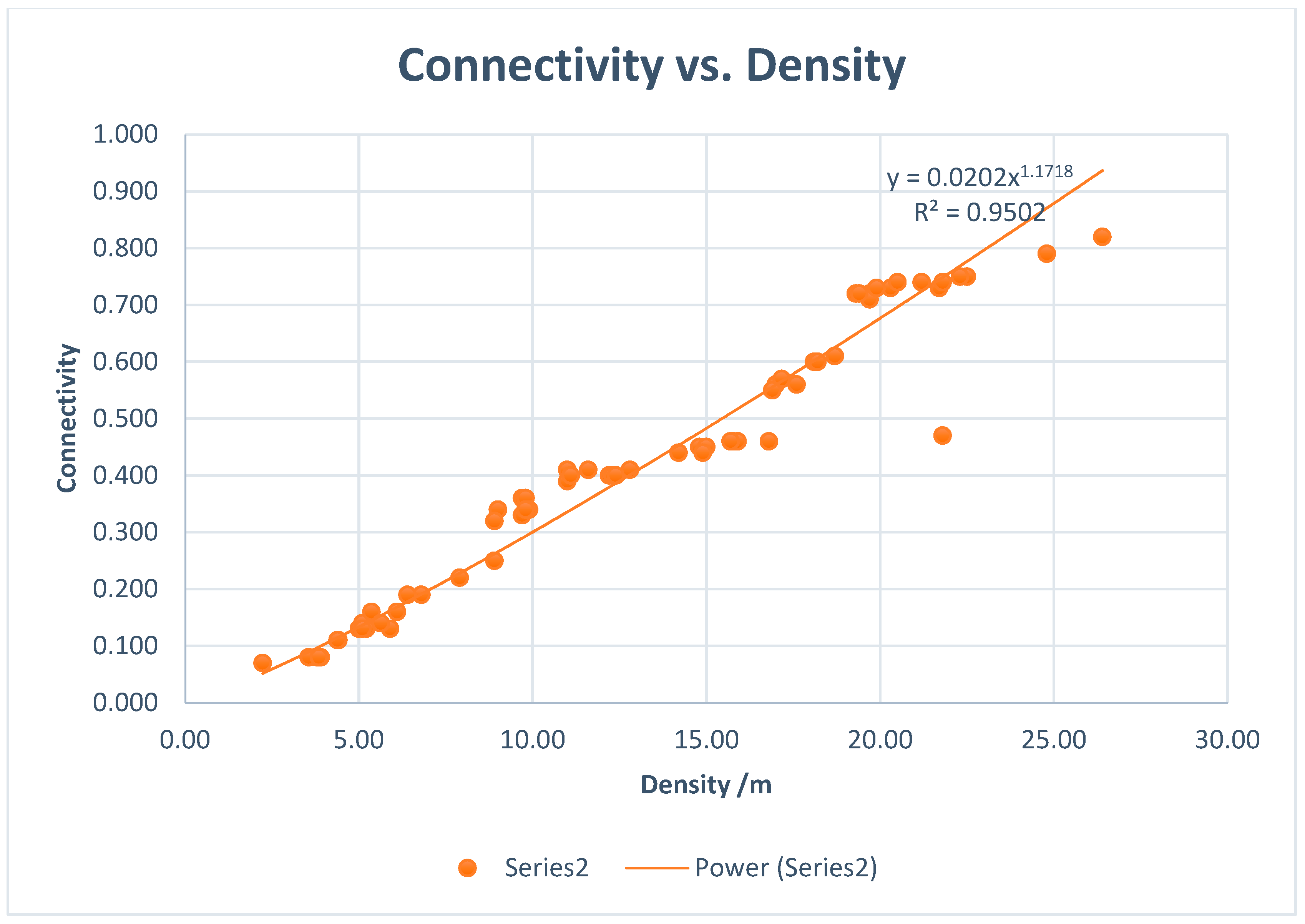
5.4. Connectivity and Cluster Analysis

The 2D fracture trace maps were generated by manually tracing fractures on photographs. The connected fractures were characterized and grouped into clusters and connected areas. Fracture trace maps prepared from satellite imagery were also used to analyze scale-dependent variation in the estimation of the fractional connected area (FCA). Statistics for the FCA, referred to as “connectivity” in this paper, are presented in Table 5. As shown in Table 5, the connectivity of fractures in the study area ranges from a minimum of 0.070 to a maximum of 0.820, with a mean value of 0.404. These estimated connectivity values are considered relative, as absolute values cannot be directly measured from the outcrops.
The number of fracture sets greatly influences the FCA and determines the size of clusters in a given area. The distribution of fracture orientations facilitates the formation of cluster size and affects connectivity. Fracture density is also closely associated with the formation of cluster size and the number of fractures in the system. Furthermore, while the scale and area of observation have minimal effect on properties of individual fractures (e.g., orientation, density, length), they greatly influence properties related to the fracture systems, such as network geometry and connectivity. Figure 10 and Figure 11 represent two sets of fractures. An analysis of these figures clearly shows that clusters in Figure 10 are bigger than those in Figure 11. In Figure 10, the proportional connected area (FCA) of fracture sets is calculated to be 0.30, whereas in Figure 11, it is 0.125, which is smaller than in Figure 10. Similarly, the fracture density in Figure 10 is ten fractures per meter, which is greater than the density in Figure 11, which is four fractures per meter. Figure 12 shows three fracture sets on the same scale as Figure 10 and Figure 11, but the observational region varies. The interconnected area (FCA) goes to 0.71 in this figure (Figure 12), and the estimated density rises to 18 fractures per meter. According to Figure 13, the fracture connected area is 0.74, which is similar to the area shown on a smaller scale (Figure 12), and the density is dependent on the number of fractures (seven fractures per meter) and the dispersion of fracture orientation. Longer fractures dominate as the observational region and scale increase. In Figure 14, it is clear that the longer fractures play a key role in network connectivity (cluster interconnection) and serve as “backbones” in the system’s interconnection process to some extent, but they are limited to indirect control over the FCA, density, and cluster size. The role of longer fractures in connectivity and density variations shown in these examples is scale-dependent. The data collected directly from the outcrops are presented in Figure 15 and demonstrate a non-linear relationship between the density of fractures and the length of individual fractures.
As shown in Figure 16, fracture connectivity is plotted against fracture density (per meter). It is evident that connectivity is directly proportional to density and can be adequately characterized by a linear function, with an R2 close to 0.97. Figure 17 demonstrates that the length data is dominated by short-length fractures and that there is only a weak correlation between connectivity and fracture length. The connectivity vs. length plot (Figure 17) shows that connectivity decreases as the length of individual fractures increases. In the length range of 0–100 cm, connectivity declines, and as the fracture length exceeds 100 cm, the impact on connectivity diminishes.

6. Discussion

As [103] explains, the statistical properties of fracture parameters, on which fracture networks are based, provide valuable insights for evaluating the fracture connectivity of a rock medium through which fluid can find stress-free pathways to flow, and the medium becomes a potential source of economic production. Fracture orientation, length, and density play an indispensable role in the characterization of fracture networks and the estimation of connectivity in fractured media [74].
We investigated the connectivity of fracture networks using fracture geometric properties in this research. Specifically, fracture directions, the coefficient of dispersion, density, and fracture length were analyzed to determine the connectivity of fracture networks. The characterization of these fracture properties was demonstrated to evaluate the connectivity of the fracture system at an outcrop scale in 2D. The variation in fracture strike angle was measured by calculating the coefficient of dispersion (i.e., Fisher coefficient). The coefficient of dispersion depicts the distribution of fracture azimuth in the field area. Fracture sets observed on or near geological structures with a low Fisher coefficient value indicate a non-uniform orientation distribution, whereas a high value indicates a unidirectional fracture orientation pattern. A well-developed cluster is defined by the combinatorial relationship among strike data, FCA (a fraction of the fracture network’s connected area), and FCL (the distribution of trace length in terms of cluster size in the overall sampling area). Fracture length develops a negative exponential relationship with connectivity and has little effect directly on the connectivity of individual fractures but greatly contributes to the interconnection of fracture networks within the fracture system. Fracture density is taken as the number of fractures per unit area. Therefore, longer fractures would not inherently increase that count unless they are associated with areas where short fractures are also more numerous. The strong R2 may be due to the result of co-variation. For example, areas with longer fractures might also contain more fractures in general, leading to higher density. In such a case, fracture length and density are correlated, but not necessarily in a causal way (i.e., long fractures do not directly cause higher fracture density). The determination of the size of clusters can have a substantial and influential effect on fracture connectivity in terms of the fractional connected area of the fractures in the sampled area at a given observational scale. At larger scales, long fractures are more visible and prevalent (see Figure 12, Figure 13 and Figure 14). So, in areas with larger observation windows of higher-resolution mapping, both types of fractures can be expected—i.e., a greater total fracture length (due to longer fractures) and a higher number of fractures (i.e., higher density). This can create a strong correlation between fracture length and density, though this correlation does not necessarily imply causation. The results of twenty-seven fracture trace maps (of which only three maps are presented in this study due to paper length constraints) show that a larger observational scale results in longer fracture trace length, implying a proportional correlation between trace length and observational scale and an inverse relationship with fracture density. The only scale-independent measure is fracture orientation. The fracture properties in a fracture system provide mutually predictable information about the connectivity of fracture networks at various scales.
Our findings in this article are consistent with those of [93] and validate the methodology used by [23]. It is also noted, as shown in the examples of the trace maps described above (Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14), that the number of fractures affects the density of fractures linearly, and that larger clusters are further connected by the backbone (longer) fractures, allowing fracture networks to be interconnected. Increased network interconnection makes the fracture system more productive in terms of easy fluid migration pathways.
This study does not include the characteristics of fracture aperture, the effects of lithological contrast on fracture density, or the controlling factors of length related to the deformation history of the structural domain.

7. Conclusions

Our analysis concludes that connectivity increases directly with the number of short-length fractures, the intensity of fracture orientation dispersion, fracture density, and the scale of observation. However, longer fractures do not directly affect the density of fractures but contribute to the interconnectedness of clusters and fracture networks. This suggests that the presence of longer fractures does not necessarily increase the overall fracture density (i.e., the number of fractures per unit area) but instead serves to enhance network connectivity by linking existing fractures. These longer fractures act as bridges or “backbone” between clusters, improving network connectivity rather than increasing fracture quantity. Although it is concluded that longer fractures do not directly influence fracture density, the data show a strong positive correlation (R2 = 0.94) between fracture length and density. This indicates that in this case, longer fractures are associated with an area of higher fracture density, potentially due to the co-location of short fractures or observational scale effects. Our analysis reveals that fracture connectivity tends to decrease as the length of individual fractures increases, with a notable decline observed when fracture lengths exceed 100 cm. This indicates that, despite their potential role in linking clusters, excessively long fractures may not contribute effectively to overall network connectivity at the studied scale. These findings highlight the importance of short to moderately long fractures in maintaining high connectivity within the fracture network. This observation also suggests a potential threshold length beyond which fractures become structurally isolated or less efficient in enhancing connectivity, which could have implications for fluid modeling and reservoir characterization.
The values of the coefficient of dispersion are estimated to range from 0 to 1. In our analysis, the orientation of all the fracture sets, except Fracture Set-2, is constrained to the value of dispersion coefficient 1, implying that the maximum population of fractures represents fracture sets concentrated in their strike angles and exhibit an orthogonal relationship with one another. The orthogonal geometry of the fractures produces a “T” intersection, whereas a conjugate fracture system increases the number of intersection nodes. This geometrical relationship further indicates that the fracture sets are systematic and can help to increase the likelihood of fracture interconnection. Fracture Set-2 has a uniform distribution with a low coefficient and serves as a “backbone” in fracture network connectivity. Fracture connectivity is essentially determined by the number of fracture sets, orientation dispersion, and fracture set density. Future research needs to incorporate these parameters to investigate how fluid transport and fractures interact in hydrocarbon reservoirs or aquifers. The field data are in good agreement with the trace maps illustrated in the figures described above.
Using the Khairi Murat area as a case study and applying the findings and methodology from this study, it is possible to model the flow issues and transport characteristics of subsurface fractured reservoirs by learning more about the geometrical and hydraulic properties of fractures.

Author Contributions

Data curation, N.D.; Formal analysis, N.D.; Investigation, N.D.; Methodology, N.D.; Project administration, M.S.A.; Resources, N.D.; Software, N.D.; Supervision, M.S.A.; Writing—original draft, N.D. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Acknowledgments

We are highly indebted to the Department of Statistics, Quaid-e-Azam University, Islamabad, for granting us permission to use the computer labs and software for statistical analysis of the data. We are very grateful to the anonymous reviewers for their valuable suggestions and constructive critique that helped improve this manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Alghalandis, Y.F. ADFNE: Open-source software for discrete fracture network engineering, two- and three-dimensional applications. Comput. Geosci. 2017, 102, 1–11. [Google Scholar] [CrossRef]
  2. Andersson, J.; Christiansson, R.; Hudson, J. Site Investigations: Strategy for Rock Mechanics Site Descriptive Model (No. SKB-TR-02-1); Swedish Nuclear Fuel and Waste Management Co.: Solna, Sweden, 2002. [Google Scholar]
  3. Hoek, E.; Martin, C.D. Fracture initiation and propagation in intact rock—A review. J. Rock Mech. Geotech. Eng. 2014, 6, 287–300. [Google Scholar] [CrossRef]
  4. Cao, R.H.; Cao, P.; Lin, H.; Ma, G.W.; Zhang, C.Y.; Jiang, C. Failure characteristics of jointed rock-like material containing multi-joints under a compressive-shear test: Experimental and numerical analyses. Arch. Civ. Mech. Eng. 2018, 18, 784–798. [Google Scholar] [CrossRef]
  5. Lin, H.; Cao, R.H.; Fan, X.; Wang, Y. Damage and fracture behavior of rock. Adv. Civ. Eng. 2019, 2019, 8476537. [Google Scholar] [CrossRef]
  6. Hadjigeorgiou, J.; Grenon, M. Rock slope stability analysis using fracture systems. Int. J. Surf. Min. Reclam. Environ. 2005, 19, 87–99. [Google Scholar] [CrossRef]
  7. Staub, I.; Fredriksson, A.; Outters, N. Strategy for a Rock Mechanics Site Descriptive Model. Development and Testing of the Theoretical Approach (No. SKB-R-02-02); Swedish Nuclear Fuel and Waste Management Co.: Solna, Sweden, 2002. [Google Scholar]
  8. Alfvén, L. Structural and Engineering Geological Investigation of Fracture Zones and Their Effect on Tunnel Construction. Master’s Thesis, Department of Earth Sciences, Uppsala University, Uppsala, Sweden, 2015. [Google Scholar]
  9. Faoro, I.; Elsworth, D.; Candela, T. Evolution of the transport properties of fractures subject to thermally and mechanically activated mineral alteration and redistribution. Geofluids 2016, 16, 396–407. [Google Scholar] [CrossRef]
  10. Ye, Z.; Fan, Q.; Huang, S.; Cheng, A. A one-dimensional line element model for transient free surface flow in porous media. Appl. Math. Comput. 2021, 392, 125747. [Google Scholar] [CrossRef]
  11. Follin, S.; Stigsson, M.; Leven, J. Discrete fracture network characterization and modeling in the Swedish program for nuclear waste disposal in crystalline rocks using information acquired by difference flow logging and borehole wall image logging. In AGU Fall Meeting Abstracts; Moscone Center West, 800 Howard Street: San Francisco, CA, USA, 2006. [Google Scholar]
  12. Karvounis, D.; Jenny, P. Modeling of flow and transport in enhanced geothermal systems. In Proceedings of the 36th Workshop on Geothermal Reservoir Engineering, Stanford University, Stanford, CA, USA, 31 January–2 February 2011. [Google Scholar]
  13. Reeves, D.M.; Rishi, P.; Yong, Z. Hydrogeologic characterization of fractured rock masses intended for disposal of radioactive waste. In Radioactive Waste; IntechOpen Limited: London, UK, 2012. [Google Scholar] [CrossRef][Green Version]
  14. Alghalandis, Y.F.; Xu, C.; Dowd, P.A. Connectivity index and connectivity field towards fluid flow in fracture-based geothermal reservoirs. Worksh. Geotherm. Reserv. Eng. 2013, 38, 417–427. [Google Scholar][Green Version]
  15. Chang, C.; Zhou, Q.; Oostrom, M.; Kneafsey, T.J.; Mehta, H. Pore-scale supercritical CO2 dissolution and mass transfer under drainage conditions. Adv. Water Resour. 2017, 100, 14–25. [Google Scholar] [CrossRef]
  16. Dverstorp, B. Analyzing flow and transport in fractured rock using the discrete fracture network concept. In Hydraulic Engineering; Royal Institute of Technology: Stockholm, Sweden, 1991; pp. 151–164. [Google Scholar]
  17. Pan, J.B.; Lee, C.C.; Lee, C.H.; Yeh, H.F.; Lin, H.I. Application of fracture network model with crack permeability tensor on flow and transport in fractured rock. Eng. Geol. 2010, 116, 166–177. [Google Scholar] [CrossRef]
  18. Dejam, M. Derivation of dispersion coefficient in an electro-osmotic flow of a viscoelastic fluid through a porous-walled microchannel. Chem. Eng. Sci. 2019, 204, 298–309. [Google Scholar] [CrossRef]
  19. Li, Y.; Chen, Y.; Zhang, G.; Liu, Y.; Zhou, C.-B. A numerical procedure for modeling the seepage field of water-sealed underground oil and gas storage caverns. Tunn. Undergr. Space Technol. 2017, 66, 56–63. [Google Scholar] [CrossRef]
  20. Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
  21. Koyama, T.; Li, B.; Jiang, Y.; Jing, L. Numerical modelling of fluid flow tests in a rock fracture with a special algorithm for contact areas. Comput. Geotech. 2009, 36, 291–303. [Google Scholar] [CrossRef]
  22. Acharya, T.; Prasad, R.; Chakrabarti, S. Evaluation of regional fracture properties for groundwater development using hydro-litho-structural domain approach in variably fractured hard rocks of Purulia district, West Bengal, India. J. Earth Syst. Sci. 2014, 123, 517–529. [Google Scholar] [CrossRef]
  23. Ghosh, K.; Mitra, S. Structural controls of fracture orientations, intensity, and connectivity, Teton anticline, Sawtooth Range, Montana. AAPG Bull. 2009, 93, 995–1014. [Google Scholar] [CrossRef]
  24. Pedretti, D.; Bianchi, M. Preliminary results from the use of entrograms to describe transport in fractured media. Acque Sotter.—Ital. J. Groundw. 2019, 8, 7–11. [Google Scholar] [CrossRef]
  25. Ye, Z.; Fan, X.; Zhang, J.; Sheng, J.; Chen, Y.; Fan, Q.; Qin, H. Evaluation of connectivity characteristics on the permeability of two-dimensional fracture networks using geological entropy. Water Resour. Res. 2021, 57, e2020WR029289. [Google Scholar] [CrossRef]
  26. Wu, H.; Pollard, D.D. Imaging 3-D fracture networks around boreholes. AAPG Bull. 2002, 86, 593–604. [Google Scholar] [CrossRef]
  27. Leckenby, R.J.; Sanderson, D.J.; Lonergan, L. Estimating flow heterogeneity in natural fracture systems. J. Volcanol. Geotherm. Res. 2005, 148, 116–129. [Google Scholar] [CrossRef]
  28. Sanderson, D.J.; Nixon, C.W. Topology, connectivity and percolation in fracture networks. J. Struct. Geol. 2018, 115, 167–177. [Google Scholar] [CrossRef]
  29. Hadgu, T.; Karra, S.; Kalinina, E.; Makedonska, N.; Hyman, J.D.; Klise, K.; Wang, Y. A comparative study of discrete fracture network and equivalent continuum models for simulating flow and transport in the far field of a hypothetical nuclear waste repository in crystalline host rock. J. Hydrol. 2017, 553, 59–70. [Google Scholar] [CrossRef]
  30. Somr, M.; Nezerka, V.; Kabele, P.; Svagera, O. Review of Discrete Fracture Network Modeling; Technical Report 74/2016/ENG; Joint Venture of Czech Technical University in Prague and Czech Geological Survey: Dejvice, Czech Republic, 2016; pp. 30–35. Available online: https://inis.iaea.org/collection/NCLCollectionStore/_Public/51/100/51100979.pdf (accessed on 25 October 2025).
  31. Zhang, X.; Sanderson, D.J. (Eds.) Numerical Modelling and Analysis of Fluid Flow and Deformation of Fractured Rock masses; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
  32. Lee, C.C.; Lee, C.H.; Yeh, H.F.; Lin, H.I. Modeling spatial fracture intensity as a control on flow in fractured rock. Environ. Earth Sci. 2011, 63, 1199–1211. [Google Scholar] [CrossRef]
  33. Zhang, F.; Nagel, N.; Lee, B.; Sanchez-Nagel, M. Fracture Network Connectivity—A Key to Hydraulic Fracturing Effectiveness and Microseismicity Generation. In ISRM International Conference for Effective and Sustainable Hydraulic Fracturing, Brisbane, Australia, Paper Number: ISRM-ICHF-2013-053; InTech: London, UK, 2013. [Google Scholar] [CrossRef]
  34. Jiao, C.; Hu, Y.; Xu, X.; Lu, X.; Shen, W.; Hu, X. Study on the effects of fracture on permeability with pore-fracture network model. Energy Explor. Exploit. 2018, 36, 1556–1565. [Google Scholar] [CrossRef]
  35. Xu, C.; Dowd, P.A.; Mardia, K.V.; Fowell, R.J. A connectivity index for discrete fracture networks. Math. Geol. 2006, 38, 611–634. [Google Scholar] [CrossRef]
  36. Sausse, J.; Dezayes, C.; Genter, A.; Bisset, A. Characterization of fracture connectivity and fluid flow pathways derived from geological interpretation and 3D modelling of the deep seated EGS reservoir of Soultz (France). In Proceedings of the Thirty-Third Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 28–30 January 2008. [Google Scholar]
  37. Molebatsi, T.; Torres, S.G.; Li, L.; Bringemeier, D.; Wang, X. Effect of fracture permeability on connectivity of fracture networks. In Proceedings of the International Mine Water Conference, Pretoria, South Africa, 19–23 October 2009. [Google Scholar]
  38. Zhang, S.; Zhang, D.; Feng, G.; Chi, M. Modelling method of heterogeneous rock mass and DEM investigation of seepage characteristics. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 46. [Google Scholar] [CrossRef]
  39. Xu, C.; Dowd, P. A new computer code for discrete fracture network modelling. Comput. Geosci. 2010, 36, 292–301. [Google Scholar] [CrossRef]
  40. Ghaffari, H.O.; Nasseri, M.H.B.; Young, R.P. Fluid flow complexity in fracture networks: Analysis with graph theory and LBM. arXiv 2011, arXiv:1107.4918. [Google Scholar]
  41. Alghalandis, Y.F. Stochastic Modelling of Fractures in Rock Masses. Ph.D. Dissertation, University of Adelaide, Adelaide, Australia, 2014. [Google Scholar]
  42. Le Goc, R.; Darcel, C.; Davy, P.; Pierce, M.; Brossault, M.A. Effective elastic properties of 3D fractured systems. In Proceedings of the 1st International Conference on Discrete Fracture Network Engineering, Vancouver, BC, Canada, 19–22 October 2014; p. 142. [Google Scholar]
  43. Hyman, J.D.; Karra, S.; Makedonska, N.; Gable, C.W.; Painter, S.L.; Viswanathan, H.S. dfn Works: A discrete fracture network framework for modeling subsurface flow and transport. Comput. Geosci. 2015, 84, 10–19. [Google Scholar] [CrossRef]
  44. Maillot, J.; Davy, P.; Le Goc, R.; Darcel, C.; De Dreuzy, J.R. Connectivity, permeability, and channeling in randomly distributed and kinematically defined discrete fracture network models. Water Resour. Res. 2016, 52, 8526–8545. [Google Scholar] [CrossRef]
  45. Lavoine, E.; Davy, P.; Darcel, C.; Munier, R. A Discrete Fracture Network Model with Stress-Driven Nucleation: Impact on Clustering, Connectivity, and Topology. Front. Phys. 2020, 8, 9. [Google Scholar] [CrossRef]
  46. Nyberg, B.; Nixon, C.W.; Sanderson, D.J. NetworkGT: A GIS tool for geometric and topological analyses of two-dimensional fracture networks. Geosphere 2018, 14, 1618–1634. [Google Scholar] [CrossRef]
  47. Kazmi, A.H.; Jan, M.Q. Geology and Tectonics of Pakistan; Graphic Publishers: Earth City, MO, USA, 1997. [Google Scholar]
  48. Kazmi, A.H.; Abbasi, I.A. Stratigraphy & Historical Geology of Pakistan; Department & National Centre of Excellence in Geology: Peshawar, Pakistan, 2008; p. 524. [Google Scholar]
  49. Aziz, H.; Hussain, J.; Tariq, M.; Ehsan, M.; Khurshid, S.; Khan, S.; Anwar, W. Sedimentological and diagenetic analysis of Early Eocene Margalla Hill Limestone, Shahdara area, Islamabad, Pakistan: Implications for reservoir potential. Carbonates Evaporites 2022, 37, 75. [Google Scholar] [CrossRef]
  50. Khan, M.S.; Siddiqui, M.I.; Munir, M.H. Micropalaeontology and Depositional Environment of the Early Eocene Margalla Hill limestone and Chorgali formation of the Khairi Murat Range, Potwar Basin, Pakistan. Pak. J. Hydrocarb. Res. 2006, 16, 51–57. [Google Scholar]
  51. Mujtaba, M. Depositional and Diagenetic Environment of Carbonates of Chorgali Formation, Salt Range-Potwar Plateau, Pakistan. Ph.D. Thesis, University of the Punjab, Lahore, Pakistan, 2001; p. 194. [Google Scholar]
  52. Benchilla, L.; Rudy, S.; Khursheed, A.; François, R. Sedimentology and diagenesis of the Chorgali Formation in the Potwar Plateau and Salt Range, Himalayan foothills (N-Pakistan). Am. Assoc. Pet. Geol. Search Discov. Artic. 2002, 11, 900. [Google Scholar]
  53. Jurgan, H.; Abbas, G. On the Chorgali Formation at the Type Locality. Pak. J. Hydrocarb. Res. 1991, 3, 35–45. [Google Scholar]
  54. Khan, M.Z.; Rahman, Z.U.; Khattak, Z.; Ishfaque, M. Microfacies and diagenetic analysis of Chorgali Carbonates, Chorgali Pass, Khair-E-Murat range: Implications for hydrocarbon reservoir characterization. Pak. J. Geol. 2017, 1, 18–23. [Google Scholar] [CrossRef]
  55. Awais, M.; Hanif, M.; Jan, I.U.; Ishaq, M.; Khan, M.Y. Eocene carbonate microfacies distribution of the Chorgali Formation, Galijagir, Khair-e-Murat Range, Potwar Plateau, Pakistan: Approach of reservoir potential using outcrop analogue. Arab. J. Geosci. 2020, 13, 594. [Google Scholar] [CrossRef]
  56. Shah, I. Stratigraphy of Pakistan; Memoirs Volume 12; Geological Survey of Pakistan: Quetta, Pakistan, 1977.
  57. Ali, A.; Farid, A.; Awan, U.F.; Amin, Y.; Zafar, W.A.; Bangash, A.A.; Ullah, S. Gravity survey to delineate the extension of the Khair-i-Murat Thrust under the sub-Himalayas, Kohat-Potwar region, Pakistan. Himal. Geol. 2023, 44, 117–129. [Google Scholar]
  58. Jadoon, I.A.K.; Frisch, W.; Jaswal, T.M.; Kemal, A. Triangle zone in the Himalayan foreland, north Pakistan. In Himalaya and Tibet: Mountain Roots to Mountain Tops; Macfarlane, A., Sorkhabi, R.B., Quade, J., Eds.; Geological Society of America: Boulder, CO, USA, 1999; Special Paper 328. [Google Scholar]
  59. Geological Survey of Pakistan. Geological Map of Khairi Murat Range, District Attock, Scale 1: 50,000; Map Series No.47; Geological Survey of Pakistan: Quetta, Pakistan, 2001.
  60. Jaswal, T.M.; Lillie, R.J.; Lawrence, R.D. Structure and evolution of the northern Potwar deformed zone, Pakistan. AAPG Bull. 1997, 81, 308–328. [Google Scholar] [CrossRef]
  61. Jadoon, I.A.K.; Frisch, W. Hinterland-divergent tectonic wedge below Riwat thrust, Himalayan foreland, Pakistan: Implications for Hydrocarbon Exploration. AAPG Bull. 1997, 81, 438–448. [Google Scholar]
  62. Jadoon, I.A.K.; Frisch, W.; Kemal, A.; Jaswal, T.M. Thrust geometries and kinematics in the Himalayan foreland (North Potwar deformed zone), North Pakistan. Geol. Rundsch. 1997, 86, 120–131. [Google Scholar]
  63. Jadoon, I.A.K.; Frisch, W.; Jadoon, M.S.K. Structural Traps and Hydrocarbon Exploration in the Salt Range/Potwar Plateau, North Pakistan. In Proceedings of the SPE Annual Technical Conference, Islamabad, Pakistan, 7–8 May 2008; pp. 69–82. [Google Scholar]
  64. Jadoon, I.A.K.; Hinderer, M.; Wazir, B.; Yousaf, R.; Bahadar, S.; Hassan, M.; Jadoon, S. Structural styles, hydrocarbon prospects, and potential in the Salt Range and Potwar Plateau, north Pakistan. Arab. J. Geosci. 2015, 8, 5111–5125. [Google Scholar] [CrossRef]
  65. Moghal, M.A.; Saqi, M.I.; Hameed, A.; Bugti, M.N. Subsurface geometry of Potwar sub-basin in relation to structuration and entrapment. Pak. J. Hydrocarb. Res. 2007, 17, 61–72. [Google Scholar]
  66. Iqbal, M.; Bannert, D. Structural Observation of the Margalla Hills, Pakistan and the Nature of the Main Boundary Thrust. Pak. J. Hydrocarb. Res. 1998, 10, 41–53. [Google Scholar]
  67. Ali, S.K.; Khan, J.; Mughal, M.S.; Lashari, M.R.; Sahito, A.G.; Hameed, F.; Razzaq, S.S. Petrotectonic framework of Siwalik Group in Khairi Murat-Kauliar area, Potwar Sub-Basin, Pakistan. Kuwait J. Sci. 2023, 50. [Google Scholar] [CrossRef]
  68. Kamran, S.M.; Siddiqi, M.I. Structural Geology and Hydrocarbon prospects of Khairi Murat Area, Potwar Sub-basin, Pakistan. Pak. J. Hydrocarb. Res. 2011, 21, 33–40. [Google Scholar]
  69. Baker, D.M.; Robert, J.L.; Robert, S.Y.; Gary, D.J.; Yousuf, M.; Zamin, H.A.S. Development of the Himalayan frontal thrust zone: Salt Range, Pakistan. Geology 1988, 16, 3–7. [Google Scholar] [CrossRef]
  70. Pennock, E.S.; Lillie, R.J.; Zaman, A.S.H.; Yousaf, M. Structural interpretation of seismic reflection data from eastern Salt Range and Potwar Plateau, Pakistan. AAPG Bull. 1989, 73, 841–857. [Google Scholar] [CrossRef][Green Version]
  71. Wandrey, C.J.; Law, B.E.; Shah, H.A. Patala-Nammal Composite Total Petroleum System, Kohat-Potwar Geologic Province, Pakistan; Version 1.0., US Geological Survey Bulletin 2208-B; US Department of the Interior: Washington, DC, USA, 2004. Available online: https://pubs.usgs.gov/bul/b2208-b/ (accessed on 25 October 2025).[Green Version]
  72. Baecher, G.B. Progressively censored sampling of rock joint traces. J. Int. Assoc. Math. Geol. 1980, 12, 33–40. [Google Scholar] [CrossRef]
  73. Mauldon, M. Estimating mean fracture trace length and density from observations in convex windows. Rock Mech. Rock Eng. 1998, 31, 201–216. [Google Scholar] [CrossRef]
  74. Mauldon, M.; Dunne, W.M.; Rohrbaugh, M.B. Circular scanlines and circular windows: New tools for characterising the geometry of fracture traces. J. Struct. Geol. 2001, 23, 247–258. [Google Scholar] [CrossRef]
  75. Rohrbaugh Jr, M.B.; Dunne, W.M.; Mauldon, M. Estimating fracture trace intensity, density, and mean length using circular scan lines and windows. AAPG Bull. 2002, 86, 2089–2104. [Google Scholar] [CrossRef]
  76. Davis, G.H.; Reynolds, S.J.; Cruden, A.R. Structural geology of rocks and regions. Econ. Geol. Bull. Soc. Econ. Geol. 1996, 91, 1163. [Google Scholar]
  77. Mauldon, M.; Rohrbaugh, M.B.; Dunne, W.M.; Lawdermilk, W. Fracture intensity estimates using circular scanlines. In Proceedings of the 37th U.S. Symposium on Rock Mechanics (USRMS), Paper Number: ARMA-99-0777, Vail, CO, USA, 6–9 June 1999. [Google Scholar]
  78. Zeeb, C.; Gomez-Rivas, E.; Bons, P.D.; Blum, P. Evaluation of sampling methods for fracture network characterization using outcrops. AAPG Bull. 2013, 97, 1545–1566. [Google Scholar] [CrossRef]
  79. Kamali, A.; Shahriar, K.; Sharifzadeh, M.; Aalianvari, A.; Esmaeilzadeh, A. Effect of shape and size of sampling window on the deamination of average length, intensity and density of trace discontinuity. In Rock Mechanics and Rock Engineering: From Past to the Future; Taylor & Francis Group: London, UK, 2016; ISBN 978-1-138-03265-1. [Google Scholar]
  80. Peacock, D.C.P.; Harris, S.D.; Mauldon, M. Use of curved scanlines and boreholes to predict fracture frequencies. J. Struct. Geol. 2003, 25, 109–119. [Google Scholar] [CrossRef]
  81. Dershowitz, W.S.; Herda, H.H. Interpretation of fracture spacing and intensity. In Proceedings of the 33rd US Symposium on Rock Mechanics (USRMS), Santa Fe, NM, USA, 3–5 June 1992. [Google Scholar]
  82. Ghosh, A.; Daemen, J.J. Fractal characteristics of rock discontinuities. Eng. Geol. 1993, 34, 1–9. [Google Scholar] [CrossRef]
  83. Goodman, R.E.; Shi, G. Block Theory and its Applications to Rock Engineering; Prentice-Hall International: London, UK, 1985; 338p. [Google Scholar]
  84. Florez-Niño, J.-M.; Aydin, A.; Mavko, G.; Antonellini, M.; Ayaviri, A. Fault and fracture systems in a fold and thrust belt: An example from Bolivia. AAPG Bull. 2005, 89, 471–493. [Google Scholar] [CrossRef]
  85. Zhu, W.; Khirevich, S.; Patzek, T.W. Impact of fracture geometry and topology on the connectivity and flow properties of stochastic fracture networks. Water Resour. Res. 2021, 57, e2020WR028652. [Google Scholar] [CrossRef]
  86. Priest, S.D. Fluid Flow in Discontinuities in Discontinuities Analysis in Rock Engineering; Chapman & Hall: London, UK, 1993; pp. 340–381. [Google Scholar]
  87. Liang, Y. Rock fracture skeleton tracing by image processing and quantitative analysis by geometry features. J. Geophys. Eng. 2016, 13, 273–284. [Google Scholar] [CrossRef]
  88. Stauffer, D. Introduction to Percolation Theory; Taylor & Francis: London, UK, 1985; p. 190. [Google Scholar]
  89. Berkowitz, B.; Balberg, I. Percolation theory and its application to groundwater hydrology. Water Resour. Res. 1993, 29, 775–794. [Google Scholar] [CrossRef]
  90. Berkowitz, B. Analysis of fracture network connectivity using percolation theory. Math. Geol. 1995, 27, 467–483. [Google Scholar] [CrossRef]
  91. Odling, N.E. Network properties of a two-dimensional natural fracture pattern. Pure Appl. Geophys. 1992, 138, 95–114. [Google Scholar] [CrossRef]
  92. Odling, N.E. The development of network properties in natural fracture patterns: An example from the Devonian sandstones of western Norway. In Fractured and Jointed Rock Masses, Proceedings of the Conference on Fractured and Jointed Rock Masses, Lake Tahoe, CA, USA, 3–5 June 1992; Hardcover–Import; Cook, N.G.W., Goodman, R.E., Myer, L.R., Tsang, C.-F., Eds.; A.A. Balkema, Brookfield: Brookfield, VT, USA, 1996; pp. 35–41. [Google Scholar]
  93. Odling, N.E. Scaling and connectivity of joint systems in sandstones from western Norway. J. Struct. Geol. 1997, 19, 1257–1271. [Google Scholar] [CrossRef]
  94. Tavani, S.; Arbues, P.; Snidero, M.; Carrera, N.; Muñoz, J.A. Open Plot Project: An open-source toolkit for 3-D structural data analysis. Solid Earth 2011, 2, 53–63. [Google Scholar] [CrossRef]
  95. Hancock, P.L.; Al-Kahdi, A.; Barka, A.A.; Bevan, T.G. Aspects of analyzing brittle structural structures. Ann. Tecton. 1987, 1, 5–19. [Google Scholar]
  96. Mardla, K. Statistics of Directional Data; Academic Press: New York, NY, USA, 1972. [Google Scholar]
  97. Michelena, R.J.; Godbey, K.S.; Wang, H.; Gilman, J.R.; Zahm, C.K. Estimation of dispersion in orientations of natural fractures from seismic data: Application to DFN modeling and flow simulation. Lead. Edge 2013, 32, 1502–1512. [Google Scholar] [CrossRef]
  98. Zangerl, C.; Koppensteiner, M.; Strauhal, T. Semiautomated Statistical Discontinuity Analyses from Scanline Data of Fractured Rock Masses. Appl. Sci. 2022, 12, 9622. [Google Scholar] [CrossRef]
  99. Ozkaya, S.I. A Simple Formula to Estimate 2D Fracture Connectivity. SPE Reserv. Eval. Eng. 2011, 14, 763–775. [Google Scholar] [CrossRef]
  100. Jiang, L.; Qiu, Z.; Wang, Q.; Guo, Y.; Wu, C.; Wu, Z.; Xue, Z. Joint development and tectonic stress field evolution in the southeastern Mesozoic Ordos Basin, west part of North China. J. Asian Earth Sci. 2016, 127, 47–62. [Google Scholar] [CrossRef]
  101. Dasti, N.; Akram, S.; Ahmad, I.; Usman, M. Rock fractures characterization in Khairi Murat Range, Sub Himalayan fold and thrust belt, North Pakistan. Nucleus 2018, 55, 115–127. [Google Scholar] [CrossRef]
  102. Grodner, M.W.; Clarke, S.M.; Burley, S.D.; Leslie, A.G.; Haslam, R. Combining topology and fractal dimension of fracture networks to characterize structural domains in thrusted limestones. J. Struct. Geol. 2021, 153, 104468. [Google Scholar] [CrossRef]
  103. Renshaw, C.E. Fracture spatial density and the anisotropic connectivity of fracture networks. Geophys. Monogr. Ser. 2000, 122, 203–211. [Google Scholar]
Geosciences 15 00469 g001
Figure 1. Topographic map showing the Khairi Murat Range, the main location of the study area. The study area falls in parts of the Survey of Pakistan Topo-Sheet Nos. 43 C/11 and 43 C/15 at a scale of 1:50,000.
Figure 1. Topographic map showing the Khairi Murat Range, the main location of the study area. The study area falls in parts of the Survey of Pakistan Topo-Sheet Nos. 43 C/11 and 43 C/15 at a scale of 1:50,000.
Geosciences 15 00469 g001
Geosciences 15 00469 g002
Figure 2. Geological maps of the study area. The map contains litho-units and major structural features, including regionally extended lineaments (long black lines) cutting across the main ridge. Lithological details of the geology (of each formation) presented in this map can be viewed in Table 1 (modified and updated after [59]).
Figure 2. Geological maps of the study area. The map contains litho-units and major structural features, including regionally extended lineaments (long black lines) cutting across the main ridge. Lithological details of the geology (of each formation) presented in this map can be viewed in Table 1 (modified and updated after [59]).
Geosciences 15 00469 g002
Geosciences 15 00469 g003
Figure 3. Maps showing (a) regional structures and (b) major structural elements of the study area. Long black free-hand lines cutting across the ridge show (long fractures) lineaments observed from satellite imagery. Blue-filled circles with capital letters show sampling locations. The locations of the subsequent Figures 10–14 are also marked with black text labeled “Fig.” followed by the corresponding figure numbers [59,68,71].
Figure 3. Maps showing (a) regional structures and (b) major structural elements of the study area. Long black free-hand lines cutting across the ridge show (long fractures) lineaments observed from satellite imagery. Blue-filled circles with capital letters show sampling locations. The locations of the subsequent Figures 10–14 are also marked with black text labeled “Fig.” followed by the corresponding figure numbers [59,68,71].
Geosciences 15 00469 g003
Geosciences 15 00469 g004
Figure 4. Presentation of fracture data collection methods. (a) Straight scanline for measuring outcrop fractures. The scanline is placed almost perpendicular to the fracture traces, but this is not performed in this research. (b) A circle of specific diameter is drawn on the outcrop to capture fracture density and cumulative length, applying circular inventory methods. (c) A tract of outcrop from which the fractures are digitally traced for analysis. The man in the picture is for scale. (d) View of fracture intensity and spacing. The ball point is for scale.
Figure 4. Presentation of fracture data collection methods. (a) Straight scanline for measuring outcrop fractures. The scanline is placed almost perpendicular to the fracture traces, but this is not performed in this research. (b) A circle of specific diameter is drawn on the outcrop to capture fracture density and cumulative length, applying circular inventory methods. (c) A tract of outcrop from which the fractures are digitally traced for analysis. The man in the picture is for scale. (d) View of fracture intensity and spacing. The ball point is for scale.
Geosciences 15 00469 g004
Geosciences 15 00469 g005
Figure 5. Rose diagrams showing the dominant fracture orientations within each mapped area. These plots emphasize peak trends using grouped data and a consistent bin size, which may visually narrow the strike distribution compared to the full variability present in each fracture set.
Figure 5. Rose diagrams showing the dominant fracture orientations within each mapped area. These plots emphasize peak trends using grouped data and a consistent bin size, which may visually narrow the strike distribution compared to the full variability present in each fracture set.
Geosciences 15 00469 g005
Geosciences 15 00469 g006
Figure 6. (a) Strike ranges of fracture sets 1 and 2, showing the broader variability in orientation observed across the study area. These ranges include local variations that may not be apparent in rose diagrams (Figure 5), which emphasize dominant local orientations. (b) Histogram showing the cumulative frequency distribution of the mean orientation of eight fracture sets identified in the study area.
Figure 6. (a) Strike ranges of fracture sets 1 and 2, showing the broader variability in orientation observed across the study area. These ranges include local variations that may not be apparent in rose diagrams (Figure 5), which emphasize dominant local orientations. (b) Histogram showing the cumulative frequency distribution of the mean orientation of eight fracture sets identified in the study area.
Geosciences 15 00469 g006
Geosciences 15 00469 g007
Figure 7. A fracture density map based on values obtained by the circle inventory method. The map shows a quick and useful assessment of the concentration of fractures with respect to the position of structural elements in the study area.
Figure 7. A fracture density map based on values obtained by the circle inventory method. The map shows a quick and useful assessment of the concentration of fractures with respect to the position of structural elements in the study area.
Geosciences 15 00469 g007
Geosciences 15 00469 g008
Figure 8. Histogram representing a (cumulative) spatial distribution of fracture density. The density is measured in No. of fractures per meter.
Figure 8. Histogram representing a (cumulative) spatial distribution of fracture density. The density is measured in No. of fractures per meter.
Geosciences 15 00469 g008
Geosciences 15 00469 g009
Figure 9. A histogram of fracture lengths, showing the frequency distribution of fractures binned by their lengths in meters. Unlike a cumulative distribution plot (which shows the number or proportion of fractures longer than a given length), this histogram displays how many fractures fall within each specified length interval. The length is measured by the circle inventory method at all measuring stations and trace maps of field photographs.
Figure 9. A histogram of fracture lengths, showing the frequency distribution of fractures binned by their lengths in meters. Unlike a cumulative distribution plot (which shows the number or proportion of fractures longer than a given length), this histogram displays how many fractures fall within each specified length interval. The length is measured by the circle inventory method at all measuring stations and trace maps of field photographs.
Geosciences 15 00469 g009
Geosciences 15 00469 g010
Figure 10. (a) Outcrop photograph for the fractional connected area (FCA). (b) A fracture trace map represents clusters of connected fractures (shaded area). Total area: 9.465 m2; connected area = 2.795 m2; blank area = 6.669 m2; FCA = 0.30. The location of the figure is presented in Figure 3.
Figure 10. (a) Outcrop photograph for the fractional connected area (FCA). (b) A fracture trace map represents clusters of connected fractures (shaded area). Total area: 9.465 m2; connected area = 2.795 m2; blank area = 6.669 m2; FCA = 0.30. The location of the figure is presented in Figure 3.
Geosciences 15 00469 g010
Geosciences 15 00469 g011
Figure 11. (a) Photograph of the outcrop and a circle with a 1 m radius to measure fracture density and length using the circle inventory method. (b) Trace map of fractures. The shaded area represents the fractional connected area (FCA). Total area: 8 m2; connected area = 1 m2; blank area = 7 m2; FCA = 0.125. The location of the figure is presented in Figure 3.
Figure 11. (a) Photograph of the outcrop and a circle with a 1 m radius to measure fracture density and length using the circle inventory method. (b) Trace map of fractures. The shaded area represents the fractional connected area (FCA). Total area: 8 m2; connected area = 1 m2; blank area = 7 m2; FCA = 0.125. The location of the figure is presented in Figure 3.
Geosciences 15 00469 g011
Geosciences 15 00469 g012
Figure 12. Cluster configuration due to three fracture sets. Two fracture sets make an isolated web-like cluster, but they are well connected through the third fracture set of longer fractures (backbone). Total area: 38 m2; connected area = 27 m2; blank area = 11 m2; FCA = 0.71. The man in the photograph is for scale. The location of the figure is presented in Figure 3.
Figure 12. Cluster configuration due to three fracture sets. Two fracture sets make an isolated web-like cluster, but they are well connected through the third fracture set of longer fractures (backbone). Total area: 38 m2; connected area = 27 m2; blank area = 11 m2; FCA = 0.71. The man in the photograph is for scale. The location of the figure is presented in Figure 3.
Geosciences 15 00469 g012
Geosciences 15 00469 g013
Figure 13. The fracture connectivity pattern and configuration of clusters. The clusters are of larger sizes with longer lengths, but they are isolated in the absence of “backbone” fractures. Total area: 3131 m2; blank area = 1810 m2; connected area = 1353 m2; FCA = 0.74.
Figure 13. The fracture connectivity pattern and configuration of clusters. The clusters are of larger sizes with longer lengths, but they are isolated in the absence of “backbone” fractures. Total area: 3131 m2; blank area = 1810 m2; connected area = 1353 m2; FCA = 0.74.
Geosciences 15 00469 g013
Geosciences 15 00469 g014
Figure 14. A trace map showing four fracture sets represents the size of clusters and connectivity of clusters through longer fractures known as “backbone” fractures. Total area: 314,365 m2; connected area = 139,181 m2; blank area = 175,184 m2; FCA = 0.44. The location of the figure is presented in Figure 3.
Figure 14. A trace map showing four fracture sets represents the size of clusters and connectivity of clusters through longer fractures known as “backbone” fractures. Total area: 314,365 m2; connected area = 139,181 m2; blank area = 175,184 m2; FCA = 0.44. The location of the figure is presented in Figure 3.
Geosciences 15 00469 g014
Geosciences 15 00469 g015
Figure 15. The relationship between the lengths of individual fractures and the density of fractures within a given circle with a known radius.
Figure 15. The relationship between the lengths of individual fractures and the density of fractures within a given circle with a known radius.
Geosciences 15 00469 g015
Geosciences 15 00469 g016
Figure 16. The plot shows a linear relationship between density and connectivity. The plot provides mean values of connectivity and density of 0.40 and 12.6, while the standard deviations of both parameters are 0.231 and 6.504, respectively.
Figure 16. The plot shows a linear relationship between density and connectivity. The plot provides mean values of connectivity and density of 0.40 and 12.6, while the standard deviations of both parameters are 0.231 and 6.504, respectively.
Geosciences 15 00469 g016
Geosciences 15 00469 g017
Figure 17. A graph showing the relationship between fracture trace length and fracture connectivity for a population of measured fractures of various lengths within the study area. Short-length fractures are abundant, while longer fractures are less common but play a key role in enhancing the connectivity of the fracture network and contributing to clustering, acting as the “backbone” of the system.
Figure 17. A graph showing the relationship between fracture trace length and fracture connectivity for a population of measured fractures of various lengths within the study area. Short-length fractures are abundant, while longer fractures are less common but play a key role in enhancing the connectivity of the fracture network and contributing to clustering, acting as the “backbone” of the system.
Geosciences 15 00469 g017
Table 1. Simplified stratigraphic column of Potwar region and the study area (derived from [56]).
Table 1. Simplified stratigraphic column of Potwar region and the study area (derived from [56]).
AgeGroupFormationLithologyLithological DescriptionTectonic Setting
EraPeriodEpoch
CenozoicTertiaryPleisto-
cene		SiwaliksLei
Conglomerate		Geosciences 15 00469 i001ConglomerateMolasses
SoanGeosciences 15 00469 i002Siltstone, Sandstone
& rare conglomerate
PlioceneDhok PathanGeosciences 15 00469 i003Claystone, Siltstone
& minor sandstone
NagriGeosciences 15 00469 i004Claystone
& Sandstone
MioceneChinjiGeosciences 15 00469 i005Claystone &
Sandstone
RawalpindiKamlialGeosciences 15 00469 i006Claystone
& Sandstone
MurreeGeosciences 15 00469 i007Sandstone, Claystone &
Conglomerate
OligoceneUnconformityPlatform
EoceneCheratKohat
(Not Exposed)		Geosciences 15 00469 i008Limestone
KuldanaGeosciences 15 00469 i009Shale
Chor GaliGeosciences 15 00469 i010Limestone,
Dolomite & Shale
Margalla HillSakesarGeosciences 15 00469 i011Limestone
NammalGeosciences 15 00469 i012Shale, Limestone
Table 2. Statistics of fracture sets observed in the study area.
Table 2. Statistics of fracture sets observed in the study area.
Fracture
Set No.		Mean
Orientation		Mean
Strike		Mean
Dip		Dip
Magnitude		Dip
Direction		Fracture
Frequency		Dispersion
Coefficient
1355N4W8790Vertical11820.97
2283E-W8990Vertical4120.26
3058N55E50SE50SE1391.00
4030N30E9090Vertical1561.00
5043N45E49NW50NW1311.00
6302N56W44NE45NE3800.99
7317N43W9090Vertical2081.00
8330N30W8890Vertical6161.00
Table 3. Statistics of fracture density distribution into five zones with respect to structural intimacy.
Table 3. Statistics of fracture density distribution into five zones with respect to structural intimacy.
Zone IZone IIZone IIIZone IVZone V
Mean4.63Mean8.57Mean13.38Mean18.62Mean22.81
Median5.10Median8.95Median12.80Median18.70Median22.05
St. Dev.0.92St. Dev.1.42St. Dev1.86St. Dev.1.31St. Dev1.82
Kurtosis1.40Kurtosis−0.89Kurtosis−1.73Kurtosis−1.56Kurtosis1.15
Skewness−1.12Skewness−0.85Skewness0.06Skewness−0.10Skewness1.47
Minimum2.23Minimum6.10Minimum11.10Minimum16.80Minimum21.20
Maximum5.90Maximum9.90Maximum15.90Maximum20.50Maximum26.40
Table 4. Statistical properties of the cumulative fracture density measured on outcrops and field photographs.
Table 4. Statistical properties of the cumulative fracture density measured on outcrops and field photographs.
VariableTotal
Count		NMeanSE MeanSt. DevMinimumMedianMaximumSkewnessKurtosis
Density (1/m)676712.600.796.502.2312.2026.400.18−1.21
Table 5. The statistics of fracture density, length, and connectivity (FCA) measured at 67 stations.
Table 5. The statistics of fracture density, length, and connectivity (FCA) measured at 67 stations.
VariableNMeanSE MeanSt. DevMinimumQ1MedianQ3Maximum
Density (1/m)6712.600.796.502.235.9012.2018.2026.40
Length (m)6711.100.594.863.087.779.9613.4827.02
Connectivity (FCA)670.400.030.230.070.160.400.600.82
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Dasti, N.; Akram, M.S. Analyzing the Connectivity of Fracture Networks Using Natural Fracture Characteristics in the Khairi Murat Range, Potwar Region, Northern Pakistan. Geosciences 2025, 15, 469. https://doi.org/10.3390/geosciences15120469

AMA Style

Dasti N, Akram MS. Analyzing the Connectivity of Fracture Networks Using Natural Fracture Characteristics in the Khairi Murat Range, Potwar Region, Northern Pakistan. Geosciences. 2025; 15(12):469. https://doi.org/10.3390/geosciences15120469

Chicago/Turabian Style

Dasti, Nasrullah, and Mian Sohail Akram. 2025. "Analyzing the Connectivity of Fracture Networks Using Natural Fracture Characteristics in the Khairi Murat Range, Potwar Region, Northern Pakistan" Geosciences 15, no. 12: 469. https://doi.org/10.3390/geosciences15120469

APA Style

Dasti, N., & Akram, M. S. (2025). Analyzing the Connectivity of Fracture Networks Using Natural Fracture Characteristics in the Khairi Murat Range, Potwar Region, Northern Pakistan. Geosciences, 15(12), 469. https://doi.org/10.3390/geosciences15120469

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop