Overview of Thermo-Hydro-Mechanical Constitutive Models for Saturated Cohesive Soils
Abstract
1. Introduction
2. Methods
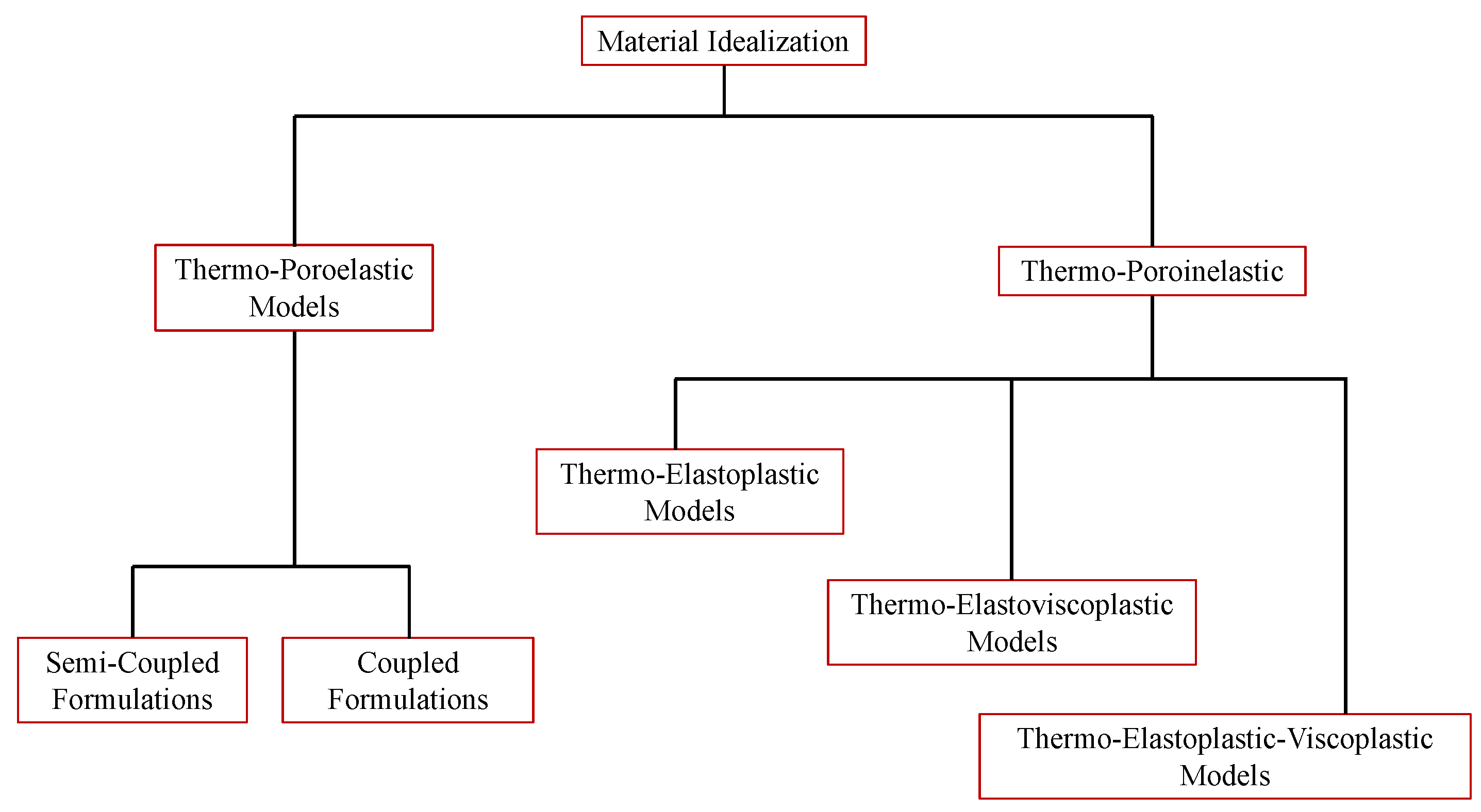
3. General Observations
4. Thermo-Poroelastic Models
4.1. Semi-Coupled Formulations
4.2. Coupled Formulations
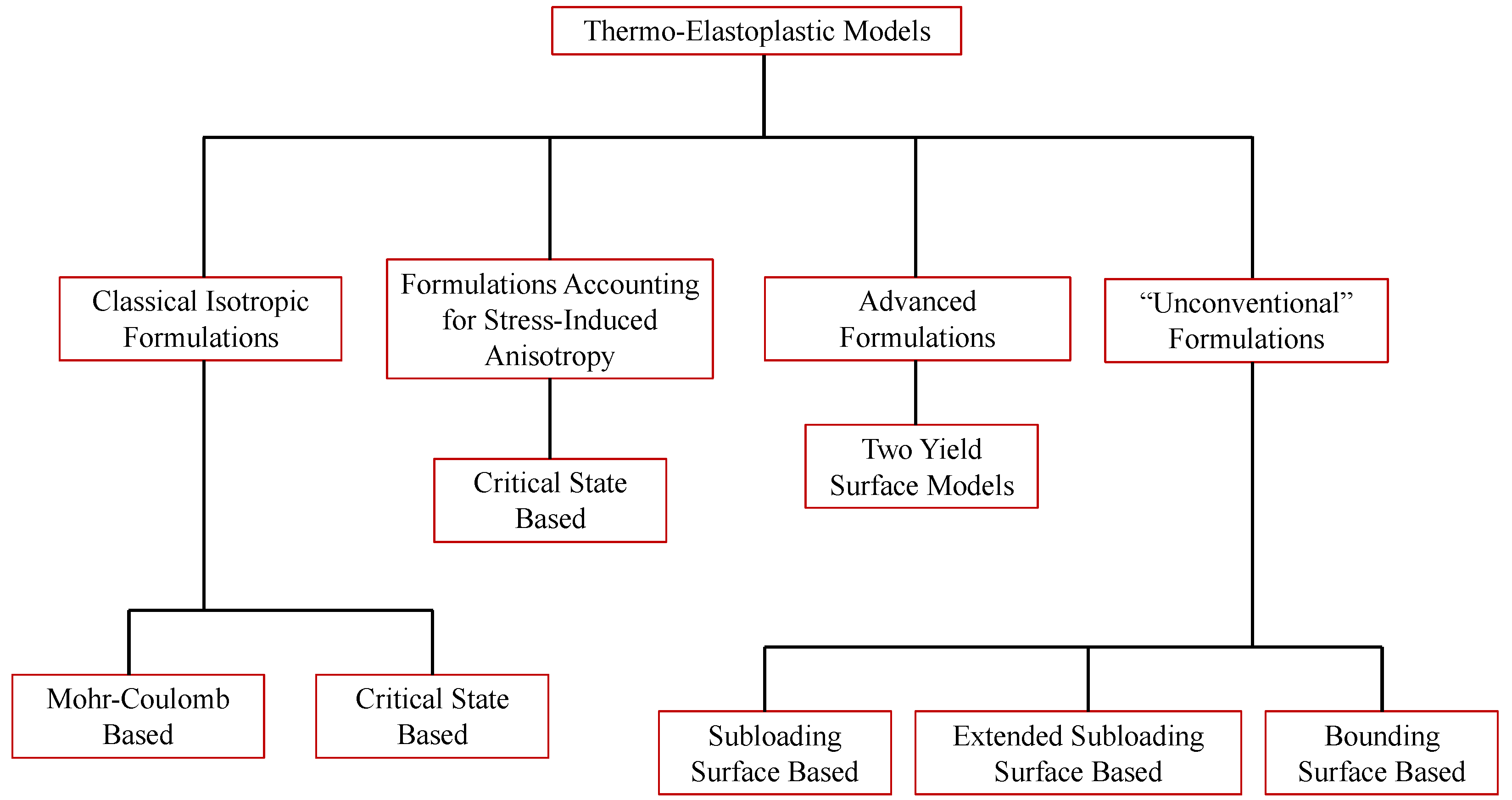
5. Thermo-Elastoplastic Models
5.1. Classical Isotropic Formulations
5.2. Formulations Accounting for Stress-Induced Anisotropy
5.3. Advanced Formulations
5.4. “Unconventional” Formulations
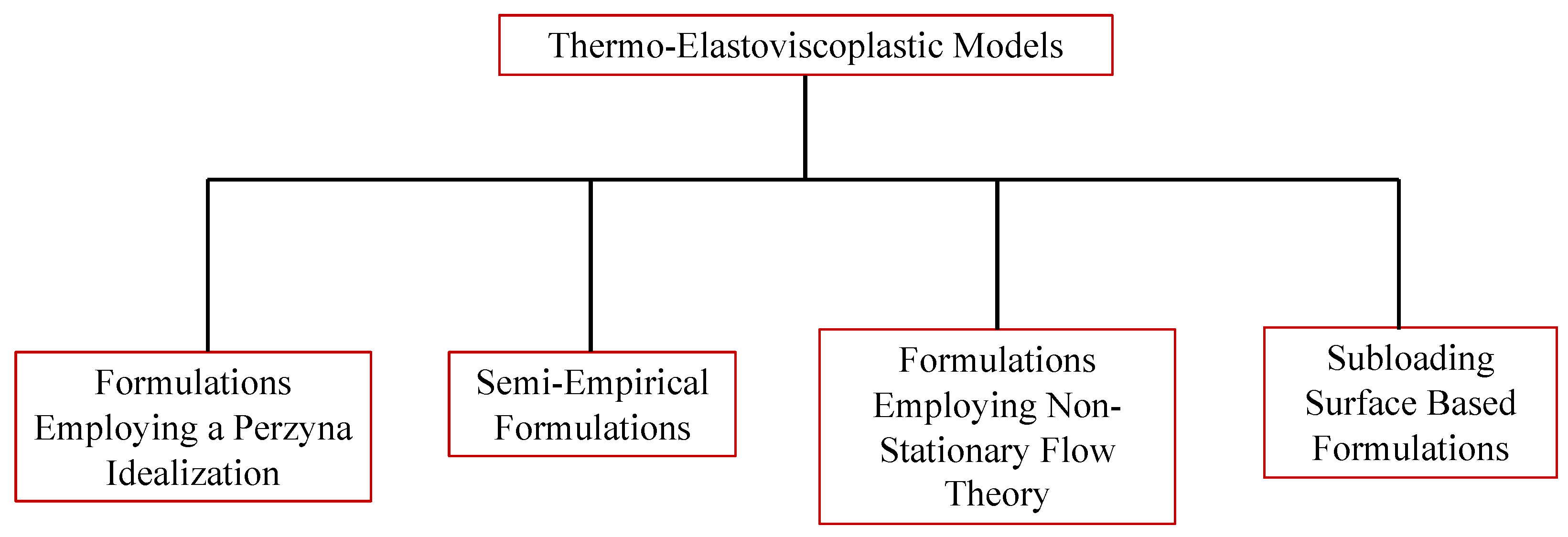
6. Thermo-Elastoviscoplastic Models
6.1. Formulations Employing a Perzyna Idealization
6.2. Semi-Empirical Formulations
6.3. Formulations Employing Non-Stationary Flow Surface Theory
6.4. Formulations Based on the Concept of a Subloading Surface
6.5. Other Formulations
7. Thermo-Elastoplastic-Viscoplastic Formulations
8. Trends in Characterizing the Elastic Response
8.1. Drained Coefficient of Volumetric Thermal Expansion
8.2. Elastic Bulk Modulus
8.3. Elastic Shear Modulus
9. Trends in Characterizing the Thermo-Elastoplastic and Thermo-Viscoplastic Response
10. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GBSM | Generalized Bounding Surface Model |
| MCC | Modified cam clay |
| NC | Normally consolidated |
| OC | Overconsolidated |
| OCR | Overconsolidation ratio |
| THM | Thermo-hydro-mechanical |
References
- Mashayekhi, M. Modeling the Temperature-Dependent Response of Saturated Cohesive Soils in a Generalized Bounding Surface Framework. Ph.D. Thesis, University of Delaware, Newark, DE, USA, 2018. [Google Scholar]
- Kaliakin, V.N.; Mashayekhi, M. Comprehensive overview of the macroscopic thermo-hydro-mechanical behavior of saturated cohesive soils. Technobius 2025, 5, 0071. [Google Scholar] [CrossRef]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of Elasticity and Consolidation for a Porous Anisotropic Solid. J. Appl. Phys. 1955, 26, 182–185. [Google Scholar] [CrossRef]
- Schiffman, R.L. A Thermoelastic Theory of Consolidation. In Environmental and Geophysical Heat Transfer; Cremen, C.J., Ed.; American Society of Mechanical Engineers: New York, NY, USA, 1971; pp. 78–84. [Google Scholar]
- Derski, W.; Kowalski, S.T. Equations of Linear Thermoconsolidation. Arch. Mech. 1979, 31, 303–316. [Google Scholar]
- Bear, J.; Corapcioglu, M.Y. A Mathematical Model for Consolidation in a Thermoelastic Aquifer due to Hot Water Injection or Pumping. Water Resour. Res. 1981, 17, 723–736. [Google Scholar] [CrossRef]
- Aboustit, B.L.; Advani, S.H.; Lee, J.K. Variational principles and finite element simulations for thermo-elastic consolidation. Int. J. Numer. Anal. Methods Geomech. 1985, 9, 49–69. [Google Scholar] [CrossRef]
- Booker, J.R.; Savvidou, C. Consolidation around a point heat source. Int. J. Numer. Anal. Methods Geomech. 1985, 9, 173–184. [Google Scholar] [CrossRef]
- Savvidou, C.; Booker, J.R. Consolidation Around a Heat Source Buried Deep in a Porous Thermoelastic Medium with Anisotropic Flow Properties. Int. J. Numer. Anal. Methods Geomech. 1989, 13, 75–90. [Google Scholar] [CrossRef]
- Britto, A.M.; Savvidou, C.; Gunn, M.J.; Booker, J.R. Finite Element Analysis of the Coupled Heat Flow and Consolidation Around Hot Buried Objects. Soils Found. 1992, 32, 13–25. [Google Scholar] [CrossRef]
- Borsetto, M.; Carradori, G.; Ribacchi, R. Coupled seepage, heat transfer and stress analysis with applications to geothermal problems. In Numerical Heat Transfer; Lewis, R.W., Morgan, K., Zienkiewicz, O.C., Eds.; Wiley–Blackwell: Chichester, UK, 1981; pp. 608–618. [Google Scholar]
- Carter, J.P.; Booker, J.R. Finite Element Analysis of Coupled Thermoelasticity. Comput. Struct. 1989, 31, 73–80. [Google Scholar] [CrossRef]
- Bai, M.; Abousleiman, Y. Thermoporoelastic Coupling with Application to Consolidation. Int. J. Numer. Anal. Methods Geomech. 1997, 21, 121–132. [Google Scholar] [CrossRef]
- Lewis, R.W.; Schrefler, B.A. The Finite Element Method in Static and Dynamic Deformation and Consolidation of Porous Media, 2nd ed.; John Wiley and Sons: Chichester, UK, 1998. [Google Scholar]
- Mitchell, J.K. Fundamentals of Soil Behavior; John Wiley and Sons: New York, NY, USA, 1976. [Google Scholar]
- Barden, L. Consolidation of Clay with Non-linear Viscosity. Géotechnique 1965, 15, 345–362. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Publishing Company: New York, NY, USA, 1972. [Google Scholar]
- Schofield, A.N.; Wroth, C.P. Critical State Soil Mechanics; McGraw-Hill Book Co., Inc.: London, UK, 1968. [Google Scholar]
- Lewis, R.W.; Karahanoglu, N. Simulation of subsidence in geothermal reservoirs. In Proceedings of the Numerical Methods in Thermal Problems, Venice, Italy, 7–10 July 1981; Lewis, R.W., Morgan, K., Schrefler, B.A., Eds.; Pineridge Press: Swansea, UK, 1981; pp. 326–335. [Google Scholar]
- Prager, W. Non-Isothermal Plastic Deformation. In Proceedings of the Konnickl Nederl; Akademie Van Wetenschappen: Amsterdam, The Netherlands, 1958; pp. 176–182. [Google Scholar]
- Borsetto, M.; Cricchi, D.; Hueckel, T.; Peano, A. On Numerical Models for the Analysis of Nuclear Waste Disposal in Geological Clay Formations. In Proceedings of the Numerical Methods for Transient and Coupled Problems, Venice, Italy, 9–13 July 1984; Lewis, R.W., Hinton, E., Bettess, P., Schrefler, B.A., Eds.; Wiley: Swansea, UK, 1984; pp. 603–618. [Google Scholar]
- Hueckel, T.; Borsetto, M.; Peano, A. A Study of Thermo-Plastic-Hydraulic Coupling in Clays Applied to Nuclear Waste Disposal. In Proceedings of the Second International Conference on Constitutive Laws for Engineering Materials: Theory and Application, Tucson, AZ, USA, 5–8 January 1987; Desai, C.S., Ed.; Elsevier: Amsterdam, The Netherlands, 1987; pp. 311–318. [Google Scholar]
- Hueckel, T.; Peano, A. Some Geotechnical Aspects of Radioactive Waste Isolation in Continental Clays. Comput. Geotech. 1987, 3, 157–182. [Google Scholar] [CrossRef]
- Sandhu, R.S.; Liu, H.; Singh, K.J. Numerical Performance of Some Finite Element Schemes for Analysis of Seepage in Porous Elastic Media. Int. J. Numer. Anal. Methods Geomech. 1977, 1, 177–194. [Google Scholar] [CrossRef]
- Hueckel, T.; Borsetto, M. Thermoplasticity of Saturated Soils and Shales: Constitutive Equations. J. Geotech. Eng. ASCE 1990, 116, 1765–1777. [Google Scholar] [CrossRef]
- Roscoe, K.H.; Burland, J.B. On the Generalized Stress-Strain Behaviour of Wet Clay. In Proceedings of the Engineering Plasticity, Cambridge, UK, March 1968; Heyman, J., Leckie, F.A., Eds.; University Press: Cambridge, UK, 1968; pp. 535–609. [Google Scholar]
- Baldi, G.; Hueckel, T.; Peano, A.; Pellegrini, R. Developments in Modelling of Thermo-Hydro-Geomechanical Behaviour of Boom Clay and Clay-Based Buffer Materials; Technical Report Volume 2; Commission of the European Communities, Nuclear Science and Technology: Karlsruhe, Germany, 1991. [Google Scholar]
- Hueckel, T.; Pellegrini, R. Thermoplastic modeling of undrained failure of saturated clay due to heating. Soils Found. 1991, 31, 1–16. [Google Scholar] [CrossRef]
- Del Olmo, C.; Fioravante, V.; Gera, F.; Hueckel, T.; Mayor, J.C.; Pellegrini, R. Thermomechanical properties of deep argillaceous formations. Eng. Geol. 1996, 41, 87–102. [Google Scholar] [CrossRef]
- Hueckel, T.; Pellegrini, R.; Del Olmo, C. A constitutive study of thermo-elasto-plasticity of deep carbonatic clays. Int. J. Numer. Anal. Methods Geomech. 1998, 22, 549–574. [Google Scholar] [CrossRef]
- Baldi, G.; Hueckel, T.; Pellegrini, R. Thermal Volume Changes of the Mineral-Water System in Low-Porosity Clay Soils. Can. Geotech. J. 1988, 25, 807–825. [Google Scholar] [CrossRef]
- Hueckel, T.; François, B.; Laloui, L. Implications of thermal sensitivity of the static internal friction angle. In Proceedings of the 1st International Symposium on Computational Geomechanics (COMGEO I), Juan-Les-Pins, France, 29 April–1 May 2009; Pietruszczak, S., Pande, G.N., Tamagnini, C., Wan, R., Eds.; IC2E International Centre for Computational Engineering: Rhodes, Greece, 2009; Volume I, pp. 104–115. [Google Scholar]
- François, B.; Laloui, L.; Hueckel, T. Explaining thermal failure in saturated clays. Géotechnique 2009, 59, 197–212. [Google Scholar] [CrossRef]
- Hueckel, T. Thermally and chemically induced failure in geomaterials. Rev. Eur. Génie Civ. 2009, 13, 831–867. [Google Scholar] [CrossRef]
- Laloui, L.; Cekerevac, C.; Vulliet, L. Thermo-Mechanical Modelling of the Behaviour of MC Clay. Comput. Methods Adv. Geomech. 2001, 183, 829–835. [Google Scholar]
- Laloui, L.; Cekerevac, C. Thermo-plasticity of clays: An isotropic yield mechanism. Comput. Geotech. 2003, 30, 649–660. [Google Scholar] [CrossRef]
- Laloui, L.; François, B. ACMEG-T: Soil Thermoplasticity Model. J. Eng. Mech. ASCE 2009, 135, 932–944. [Google Scholar] [CrossRef]
- Laloui, L.; Cekerevac, C. Non-isothermal plasticity model for cyclic behaviour of soils. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 437–460. [Google Scholar] [CrossRef]
- Hamidi, A.; Tourchi, S.; Khazaei, C. Thermomechanical Constitutive Model for Saturated Clays Based on Critical State Theory. Int. J. Geomech. 2015, 15, 040140381. [Google Scholar] [CrossRef]
- Hamidi, A.; Khazaei, C. A thermo-mechanical constitutive model for saturated clays. Int. J. Geotech. Eng. 2010, 4, 445–459. [Google Scholar] [CrossRef]
- Wong, P.K.K.; Mitchell, R.J. Yielding and Plastic Flow of Sensitive Cemented Clay. Géotechnique 1975, 25, 763–782. [Google Scholar] [CrossRef]
- Hueckel, T.; Pellegrini, R. A note on thermomechanical anisotropy of clays. Eng. Geol. 1996, 41, 171–180. [Google Scholar] [CrossRef]
- Hueckel, T.; Tutumluer, E. Modeling of elastic anisotropy due to one-dimensional plastic consolidation of clays. Comput. Geotech. 1994, 16, 311–349. [Google Scholar] [CrossRef]
- Rojas, E.; Garnica, P. Thermomechanical anisotropic Model for Soils. Soils Found. 2000, 40, 61–75. [Google Scholar] [CrossRef]
- Wang, L.Z.; Wang, K.J.; Hong, Y. Modeling Temperature-Dependent Behavior of Soft Clay. J. Eng. Mech. 2016, 142, 04016054. [Google Scholar] [CrossRef]
- Shah, I.A.; Dastider, G.A.; Basu, P.; Chatterjee, S. A thermoplastic clay constitutive model with temperature dependent evolution of stress anisotropy. Geomech. Energy Environ. 2024, 38, 100568. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Manzari, M.T.; Papadimitriou, A.G. SANICLAY: Simple anisotropic clay plasticity model. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 1231–1257. [Google Scholar] [CrossRef]
- Robinet, J.C.; Rahbaoui, A.; Plas, F.; Lebon, P. A constitutive thermomechanical model for saturated clays. Eng. Geol. 1996, 41, 145–169. [Google Scholar] [CrossRef]
- Cui, Y.J.; Sultan, N.; Delage, P. A thermomechanical model for saturated clays. Can. Geotech. J. 2000, 37, 607–620. [Google Scholar] [CrossRef]
- Abuel-Naga, H.M.; Bergado, D.T.; Bouazza, A.; Ramana, G.V. Volume change behaviour of saturated clays under drained heating conditions: Experimental results and constitutive modeling. Can. Geotech. J. 2007, 44, 942–956. [Google Scholar] [CrossRef]
- Abuel-Naga, H.M.; Pender, M.; Bergado, D.T.; Bouazza, A. Thermomechanical model for saturated clays. Géotechnique 2009, 59, 273–278. [Google Scholar] [CrossRef]
- Zhu, Q.Y.; Zhuang, P.Z.; Yin, Z.Y.; Yu, H.S. State parameter-based thermomechanical constitutive model for saturated fine-grained soils. Can. Geotech. J. 2021, 58, 1045–1058. [Google Scholar] [CrossRef]
- Golchin, A.; Vardon, P.J.; Hicks, M.A. A thermo-mechanical constitutive model for fine-grained soils based on thermodynamics. Int. J. Eng. Sci. 2022, 174, 103579. [Google Scholar] [CrossRef]
- Zhao, N.; Cheng, X.; Whittle, A.J. Extended TTS Model for Thermal and Mechanical Creep of Clay and Sand. J. Geotech. Geoenvironmental Eng. 2022, 148, 04022044. [Google Scholar] [CrossRef]
- Zhang, Z.; Cheng, X. A fully coupled THM model based on a non-equilibrium thermodynamic approach and its application. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 527–554. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, M. Granular elasticity without the Coulomb condition. Phys. Rev. Lett. 2003, 91, 144301. [Google Scholar] [CrossRef] [PubMed]
- Hashiguchi, K.; Ueno, M. Elasto-plastic Constitutive Laws of Granular Materials. In Proceedings of the Constitutive Equations of Soils, Tokyo, Japan, 13 July 1977; Murayama, S., Schofield, A.N., Eds.; Japanese Society of Soil Mechanics and Foundation Engineering: Tokyo, Japan, 1977; pp. 73–82. [Google Scholar]
- Hashiguchi, K. Subloading surface model in unconventional plasticity. Int. J. Solids Struct. 1989, 25, 917–945. [Google Scholar] [CrossRef]
- Dafalias, Y.F. Bounding Surface Plasticity. I: Mathematical Foundation and the Concept of Hypoplasticity. J. Eng. Mech. ASCE 1986, 112, 966–987. [Google Scholar] [CrossRef]
- Liu, E.L.; Xing, H.L. A double hardening thermo-mechanical constitutive model for overconsolidated clays. Acta Geotech. 2009, 4, 1–6. [Google Scholar] [CrossRef]
- Zhang, S.; Leng, W.; Zhang, F.; Xiong, Y. A simple thermo-elastoplastic model for geomaterials. Int. J. Plast. 2012, 34, 93–113. [Google Scholar] [CrossRef]
- Xiong, Y.L.; Yang, Q.L.; Sang, Q.Y.; Zhu, Y.H.; Zhang, S.; Zheng, R.Y. A unified thermal-hardening and thermal-softening constitutive model of soils. Appl. Math. Model. 2019, 74, 73–84. [Google Scholar] [CrossRef]
- Yao, Y.P.; Zhou, A.N. Non-isothermal unified hardening model: A thermo-elasto-plastic model for clays. Géotechnique 2013, 63, 1328–1345. [Google Scholar] [CrossRef]
- Yao, Y.P.; Hou, W.; Zhou, A.N. UH model: Three-dimensional unified hardening model for overconsolidated clays. Géotechnique 2009, 59, 451–469. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Herrmann, L.R. Bounding Surface Plasticity II: Application to Isotropic Cohesive Soils. J. Eng. Mech. ASCE 1986, 112, 1263–1291. [Google Scholar] [CrossRef]
- Zhou, C.; Ng, C. A thermomechanical model for saturated soil at small and large strains. Can. Geotech. J. 2015, 52, 1–10. [Google Scholar] [CrossRef]
- Hong, P.Y.; Pereira, J.M.; Tang, A.M.; Cui, Y.J. On some advanced thermo-mechanical models for saturated clays. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 2952–2971. [Google Scholar] [CrossRef]
- Hong, P.Y.; Pereira, J.M.; Cui, Y.J.; Tang, A.M. A two-surface thermomechanical model for saturated clays. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 1059–1080. [Google Scholar] [CrossRef]
- Cheng, W.; Chen, R.P.; Hong, P.Y.; Cui, Y.J.; Pereira, J.M. A two-surface thermomechanical plasticity model considering thermal cyclic behavior. Acta Geotech. 2020, 15, 2741–2755. [Google Scholar] [CrossRef]
- Coussy, O. Poromechanics; John Wiley and Sons: Chichester, UK, 2004. [Google Scholar]
- Mašín, D. Coupled Thermohydromechanical Double-Structure Model for Expansive Soils. J. Eng. Mech. 2017, 143, 04017067. [Google Scholar] [CrossRef]
- Alonso, E.E.; Vaunat, J.; Gens, A. Modelling the mechanical behaviour of expansive clays. Eng. Geol. 1999, 54, 173–183. [Google Scholar] [CrossRef]
- Mašín, D. Double structure hydromechanical coupling formalism and a model for unsaturated expansive clays. Eng. Geol. 2013, 165, 73–88. [Google Scholar] [CrossRef]
- Zhou, C.; Fong, K.Y.; Ng, C.W.W. A new bounding surface model for thermal cyclic behaviour. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 1656–1666. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Zhao, X.; Zhang, S.; Zhang, Q. A unified thermo-mechanical bounding surface model for saturated clay and sand. Comput. Geotech. 2024, 173, 106535. [Google Scholar] [CrossRef]
- Adachi, T.; Oka, F.; Mimura, M. State of the Art: Modeling Aspects Associated with Time Dependent Behavior of Soils. In Proceedings of the Measuring and Modeling Time Dependent Soil Behavior; Sheahan, T.C., Kaliakin, V.N., Eds.; ASCE Geotechnical Special Technical Publication: Washington, DC, USA, 1996; pp. 61–95. [Google Scholar]
- Perzyna, P. The Constitutive Equations for Rate Sensitive Plastic Materials. Q. Appl. Math. 1963, 20, 321–332. [Google Scholar] [CrossRef]
- Perzyna, P. Fundamental Problems in Viscoplasticity. Adv. Appl. Mech. 1966, 9, 243–377. [Google Scholar] [CrossRef]
- Hohenemser, K.; Prager, W. Über die Ansätze der Mechanik isotroper Kontinua. Z. Für Angew. Math. Und Mech. 1932, 12, 216–226. [Google Scholar] [CrossRef]
- Prager, W. Linearization in visco-plasticity. OèSterreichisches Ingenieur-Archiv. 1961, 15, 152–157. [Google Scholar]
- Modaressi, H.; Laloui, L. A thermo-viscoplastic constitutive model for clays. Int. J. Numer. Anal. Methods Geomech. 1997, 21, 313–335. [Google Scholar] [CrossRef]
- Kaliakin, V.N.; Dafalias, Y.F. Theoretical Aspects of the Elastoplastic-Viscoplastic Bounding Surface Model for Cohesive Soils. Soils Found. 1990, 30, 11–24. [Google Scholar] [CrossRef]
- Laloui, L.; Leroueil, S.; Chalindar, S. Modelling the combined effect of strain rate and temperature on one-dimensional compression of soils. Can. Geotech. J. 2008, 45, 1765–1777. [Google Scholar] [CrossRef]
- Leroueil, S.; Kabbaj, M.; Tavenas, F.; Bouchard, R. Stress-strain-strain rate relation for the compressibility of sensitive natural clays. Géotechnique 1985, 35, 159–180. [Google Scholar] [CrossRef]
- Laloui, L.; Cekerevac, C. Numerical simulation of the non-isothermal mechanical behaviour of soils. Comput. Geotech. 2008, 35, 729–745. [Google Scholar] [CrossRef]
- Raude, S.; Laigle, F.; Giot, R.; Fernandes, R. A unified thermoplastic/viscoplastic constitutive model for geomaterials. Acta Geotech. 2015, 11, 849–869. [Google Scholar] [CrossRef]
- Kurz, D.; Sharma, J.; Alfaro, M.; Graham, J. Semi-empirical elastic- thermoviscoplastic model for clay. Can. Geotech. J. 2016, 53, 1583–1599. [Google Scholar] [CrossRef]
- Yin, J.H.; Zhu, J.G.; Graham, J. A new elastic viscoplastic model for time-dependent behaviour of normally and overconsolidated clays: Theory and verification. Can. Geotech. J. 2002, 39, 157–173. [Google Scholar] [CrossRef]
- Kelln, C.; Sharma, J.; Hughes, D.; Graham, J. An improved elastic-viscoplastic soil model. Can. Geotech. J. 2008, 45, 1356–1376. [Google Scholar] [CrossRef]
- Fox, P.J.; Edil, T.B. Effects of stress and temperature on secondary compression of peat. Can. Geotech. J. 1996, 33, 405–415. [Google Scholar] [CrossRef]
- Graham, J.; Tanaka, N.; Crilly, T.; Alfaro, M. Modified Cam-Clay modelling of temperature effects in clays. Can. Geotech. J. 2001, 38, 608–621. [Google Scholar] [CrossRef]
- Hamidi, A. A Novel Elasto-Thermo-Viscoplastic Model for the Isotropic Compression of Structured Clays. J. Hazard. Toxic Radioact. Waste 2020, 24, 06020003. [Google Scholar] [CrossRef]
- Liu, M.D.; Carter, J.P. A structured Cam Clay model. Can. Geotech. J. 2002, 39, 1313–1332. [Google Scholar] [CrossRef]
- Fathalikhani, M.; Graham, J.; Kurz, D.; Maghoul, P. Investigation and Modification of a CSSM-Based Elastic-Thermoviscoplastic Model for Clay. Int. J. Geomech. 2022, 22, 04022161. [Google Scholar] [CrossRef]
- Chen, Z.J.; Yin, J.H. A New One-Dimensional Thermal Elastic-Viscoplastic Model for the Thermal Creep of Saturated Clayey Soils. J. Geotech. Geoenvironmental Eng. 2023, 149, 04023010. [Google Scholar] [CrossRef]
- Yin, J.H.; Graham, J. Viscous-Elastic-Plastic Modelling of One-Dimensional Time-Dependent Behaviour of Clays. Can. Geotech. J. 1989, 26, 199–209. [Google Scholar] [CrossRef]
- Yin, J.H.; Graham, J. Equivalent times and one-dimensional elastic viscoplastic modelling of time-dependent stress-strain behavior of clays. Can. Geotech. J. 1994, 31, 42–52. [Google Scholar] [CrossRef]
- Chen, Z.J.; Feng, W.Q.; Chen, W.B.; Yin, J.H. A thermal elastic visco-plastic model for soft clayey soils. Can. Geotech. J. 2024, 61, 208–227. [Google Scholar] [CrossRef]
- Wheeler, S.J.; Näätänen, A.; Karstunen, M.; Lojander, M. An anisotropic elastoplastic model for soft clays. Can. Geotech. J. 2003, 40, 403–418. [Google Scholar] [CrossRef]
- Cheng, W.; Yin, Z.Y. Fractional order viscoplastic modeling of anisotropically overconsolidated clays with modified isotach viscosity. Int. J. Plast. 2024, 172, 103858. [Google Scholar] [CrossRef]
- Qiao, Y.; Ding, W. ACMEG-TVP: A thermoviscoplastic constitutive model for geomaterials. Comput. Geotech. 2017, 81, 98–111. [Google Scholar] [CrossRef]
- Qiao, Y.; Ferrari, A.; Laloui, L.; Ding, W. Nonstationary flow surface theory for modeling the viscoplastic behaviors of soils. Comput. Geotech. 2016, 76, 105–119. [Google Scholar] [CrossRef]
- Yin, Z.Y.; Chang, C.S.; Karstunen, M.; Hicher, P.Y. An anisotropic elastic-viscoplastic model for soft clays. Int. J. Solids Struct. 2010, 47, 665–677. [Google Scholar] [CrossRef]
- Bodas Freitas, T.M.; Potts, D.M.; Zdravkovic, L. Implications of the definition of the Φ function in elastic-viscoplastic models. Géotechnique 2012, 62, 643–648. [Google Scholar] [CrossRef]
- De Gennaro, V.; Pereira, J.M. A viscoplastic constitutive model for unsaturated geomaterials. Comput. Geotech. 2013, 54, 143–151. [Google Scholar] [CrossRef]
- Eyring, H. Viscosity, Plasticity and Diffusion as Examples of Absolute Reaction Rates. J. Chem. Phys. 1936, 4, 283–291. [Google Scholar] [CrossRef]
- Glasstone, S.; Laidler, K.; Eyring, H. The Theory of Rate Process; McGraw-Hill Book Company: New York, NY, USA, 1941. [Google Scholar]
- Maranha, J.R.; Pereira, C.; Vieira, A. Improved subloading thermo-viscoplastic model for soil under strictly isotropic conditions. Geomech. Energy Environ. 2018, 14, 38–47. [Google Scholar] [CrossRef]
- Maranha, J.R.; Pereira, C.; Vieira, A. A viscoplastic subloading soil model for rate-dependent cyclic anisotropic structured behaviour. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 1531–1555. [Google Scholar] [CrossRef]
- Hashiguchi, K.; Okayasu, T. Time-Dependent Elastoplastic Constitutive Equation Based on the Subloading Surface Model and Its Application to Soils. Soils Found. 2000, 40, 19–36. [Google Scholar] [CrossRef] [PubMed]
- Cheng, W.; Yin, Z.Y.; Cui, Y.J.; Peng, M.Z. Nonisothermal fractional order two-surface viscoplastic model for stiff clays. Can. Geotech. J. 2024, 62, 1–17. [Google Scholar] [CrossRef]
- Kong, L.; Yao, Y.; Qi, J. Modeling the combined effect of time and temperature on normally consolidated and overconsolidated clays. Acta Geotech. 2020, 15, 2451–2471. [Google Scholar] [CrossRef]
- Dafalias, Y.F. Bounding Surface Elastoplasticity-Viscoplasticity for Particulate Cohesive Media. In Proceedings of the Deformation and Failure of Granular Materials, IUTAM Symposium on Deformation and Failure of Granular Materials, Delft, The Netherlands, 31 August–3 September 1982; Vermeer, P.A., Luger, H.J., Eds.; A. A. Balkema: Delft, The Netherlands, 1982; pp. 97–107. [Google Scholar]
- Dafalias, Y.F. On Rate Dependence and Anisotropy in Soil Constitutive Modeling. In Proceedings of the Results of the International Workshop on Constitutive Relations for Soils, Grenoble, France, 6–8 September 1982; Gudehus, G., Darve, F., Vardoulakis, I., Eds.; A. A. Balkema: Grenoble, France, 1982; pp. 457–462. [Google Scholar]
- Dafalias, Y.F. On elastoplastic-viscoplastic constitutive modelling of cohesive soils. In Geomechanical Modelling in Engineering Practice; Dungar, R., Studer, J.A., Eds.; A. A. Balkema: Amsterdam, The Netherlands, 1986; Chapter 13; pp. 313–330. [Google Scholar]
- Kaliakin, V.N. Bounding Surface Elastoplasticity-Viscoplasticity for Clays. Ph.D. Thesis, University of California, Davis, CA, USA, 1985. [Google Scholar]
- Kaliakin, V.N.; Dafalias, Y.F. Verification of the Elastoplastic-Viscoplastic Bounding Surface Model for Cohesive Soils. Soils Found. 1990, 30, 25–36. [Google Scholar] [CrossRef]
- Kaliakin, V.N. Numerical Implementation and Solution Strategies for a Thermo-Elastoplastic-Viscoplastic Model For Cohesive Soils. Comput. Syst. Eng. 1994, 5, 203–214. [Google Scholar] [CrossRef]
- Kaliakin, V.N.; Nieto-Leal, A.N.; Mashayekhi, M. Modeling the Time- and Temperature-Dependent Response of Cohesive Soils in a Generalized Bounding Surface Framework. Transp. Infrastruct. Geotechnol. 2018, 5, 250–286. [Google Scholar] [CrossRef]
- Palciauskas, V.V.; Domenico, P.A. Characterization of drained and undrained response of thermally loaded repository rocks. Water Resour. Res. 1982, 18, 281–290. [Google Scholar] [CrossRef]
- Juza, J. An Equation of State for Water and Steam: Steam Tables in the Critical Region and in the Range from 1000 to 100,000 Bars; Academia: Prague, Czechoslovakia, 1966. [Google Scholar]
- Laloui, L. Modélisation du Comportement Thermo-Hydro-Mécanique des Milieux Poreux Anélastique. Ph.D. Thesis, Ecole Centrale, Lille, Paris, 1993. [Google Scholar]
- Bolzon, G.; Schrefler, B.A. Thermal effects in partially saturated soils: A constitutive model. Int. J. Numer. Anal. Methods Geomech. 2005, 29, 861–877. [Google Scholar] [CrossRef]
- Wroth, C.P.; Houlsby, G.T. Soil mechanics—Property characterization and analysis procedures. In Proceedings of the 11th International Conference on Soil Mechanics and Foundations Engineering, San Francisco, CA, USA, 12–16 August 1985; pp. 1–55. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mashayekhi, M.; Kaliakin, V.N. Overview of Thermo-Hydro-Mechanical Constitutive Models for Saturated Cohesive Soils. Geosciences 2025, 15, 401. https://doi.org/10.3390/geosciences15100401
Mashayekhi M, Kaliakin VN. Overview of Thermo-Hydro-Mechanical Constitutive Models for Saturated Cohesive Soils. Geosciences. 2025; 15(10):401. https://doi.org/10.3390/geosciences15100401
Chicago/Turabian StyleMashayekhi, Meysam, and Victor N. Kaliakin. 2025. "Overview of Thermo-Hydro-Mechanical Constitutive Models for Saturated Cohesive Soils" Geosciences 15, no. 10: 401. https://doi.org/10.3390/geosciences15100401
APA StyleMashayekhi, M., & Kaliakin, V. N. (2025). Overview of Thermo-Hydro-Mechanical Constitutive Models for Saturated Cohesive Soils. Geosciences, 15(10), 401. https://doi.org/10.3390/geosciences15100401





