Review of Nano- and Micro- Indentation Tests for Rocks
Abstract
1. Introduction
1.1. Background
1.2. Importance of Indentation Testing
1.3. Application of Indentation Tests in Rock Mechanics
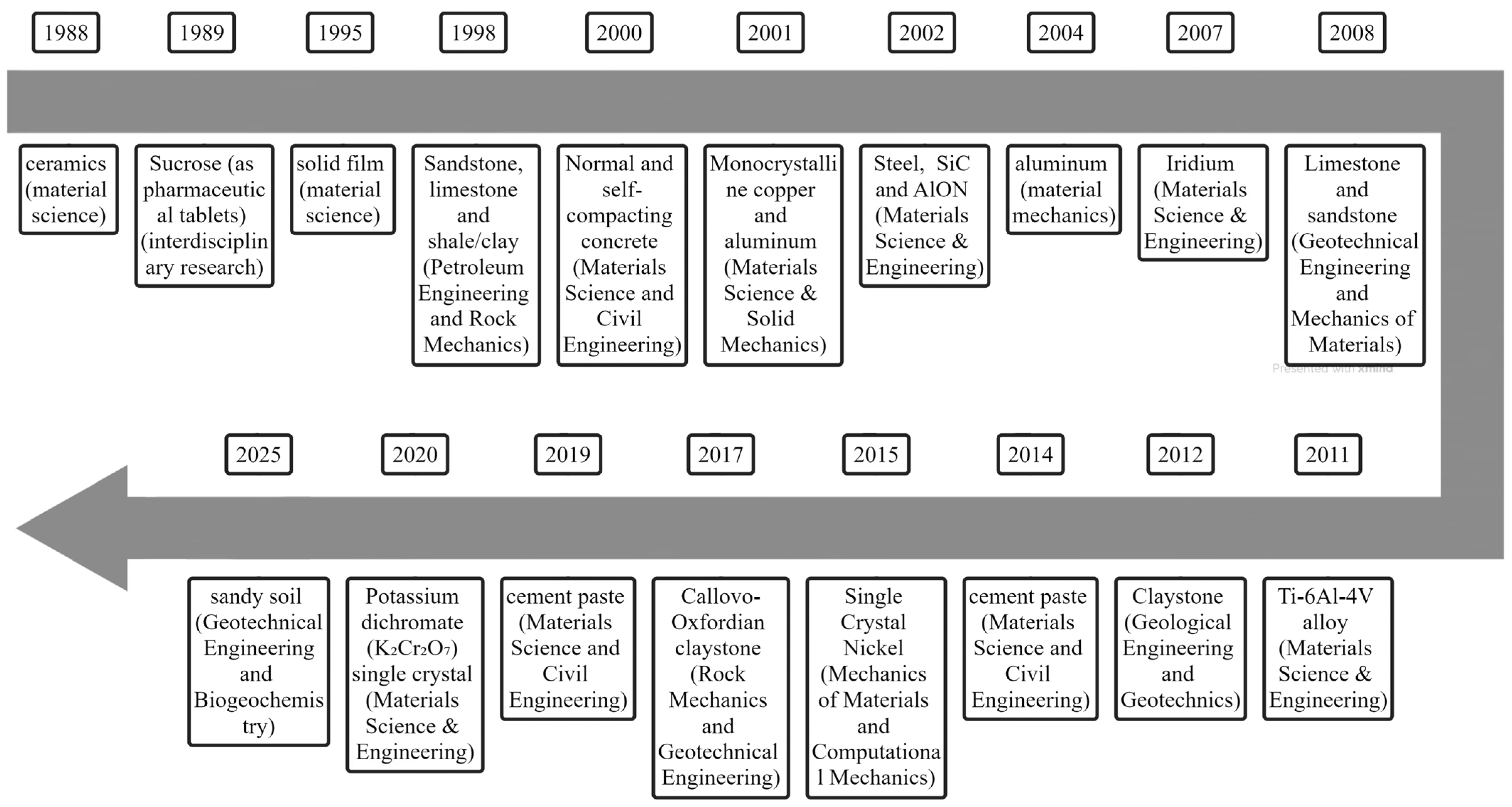
2. Technological Evolution of Indentation Testing
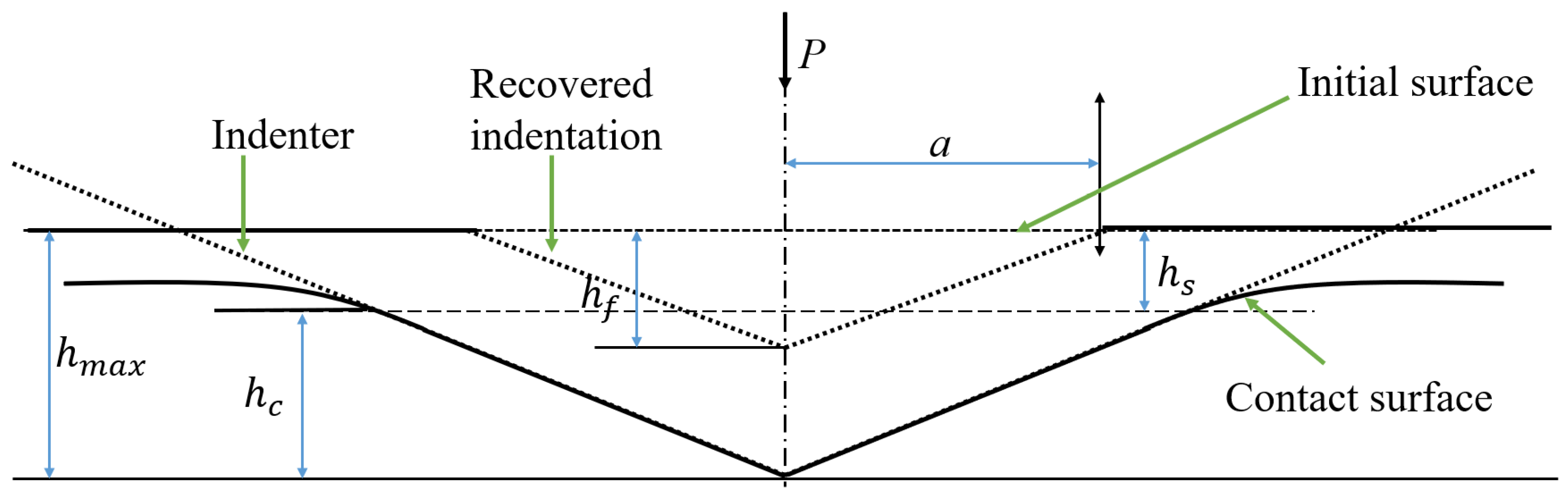
3. Indentation Test Methodology
- Selection of suitable indenter
- 2.
- Sample preparation
- 3.
- Fixation
- 4.
- Appropriate indentation parameters
- Oliver-Pharr method
- 2.
- Doerner–Nix method
- 3.
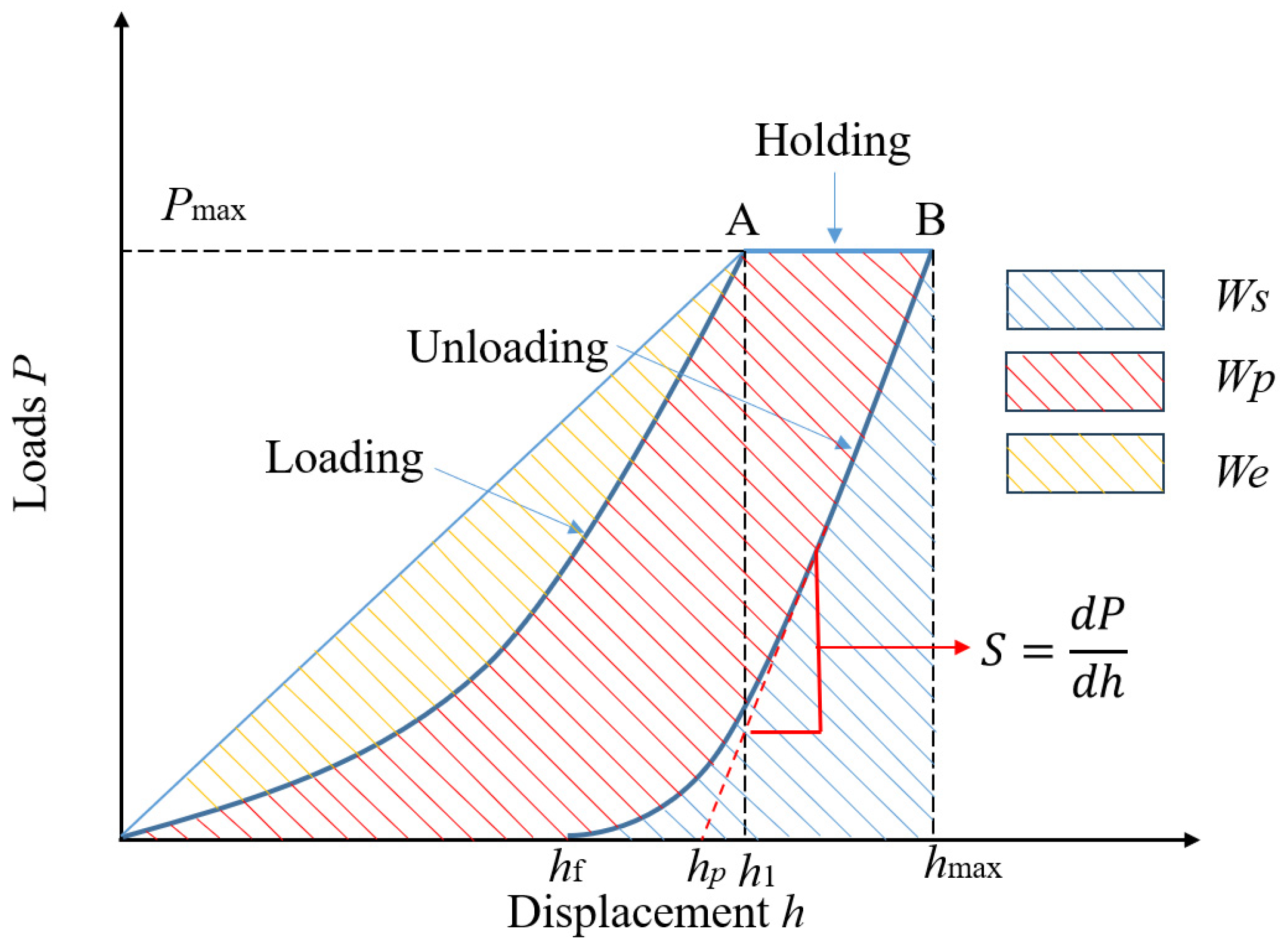
- Energy method
- 4.
- Comparison of methods
4. Interpretation Models
4.1. Classical Models
- Hertz contact theory [118]
- 2.
- Elasto-plastic contact theory (Expanding Cavity Model) [119]
- -
- C and n are dimensionless constants, with and for typical metallic materials.
- -
- E is the modulus of elasticity of the material.
- 3.
- Fracture mechanics model (Lawn crack extension model) [120]
- α: dimensionless constant, depending on indenter geometry and crack type (usually );
- E: modulus of elasticity of the material (GPa);
- H: hardness of the material (GPa), calculated by H = P/Ac (Ac is the projected area of the indentation);
- P: Maximum load of the indentation (N);
- c: Average length from the center of the indentation to the tip of the crack (m).
4.2. Simulation and Verification for Rocks
5. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Walley, S.M. Historical origins of indentation hardness testing. Mater. Sci. Technol. 2012, 28, 1028–1044. [Google Scholar] [CrossRef]
- Wright, J. Jewelry alloys: Hardness and hardenability. In Proceedings of the Santa Fe Symposium on Jewelry Manufacturing, Albuquerque, NM, USA, 4 December 2009; pp. 453–472. [Google Scholar]
- Smith, R.L.; Sandly, G.E. An accurate method of determining the hardness of metals, with particular reference to those of a high degree of hardness. Proc. Inst. Mech. Eng. 1922, 102, 623–641. [Google Scholar] [CrossRef]
- Hays, C.; Kendall, E.G. An analysis of Knoop microhardness. Metallography 1973, 6, 275–282. [Google Scholar] [CrossRef]
- Barbato, G.; Galetto, M.; Germak, A.; Fabrizio, M. Influence of the indenter shape in Rockwell hardness test. In Proceedings of the HARDMEKO 98, Beijing, China, 21–23 September 1998; pp. 21–23. [Google Scholar]
- Chang, Y.-H.; Lin, S.-H.; Chen, H.-L.; Chen, Y.-T.; Huang, X.-C. Annealing effects on grain size, surface roughness, nanoindentation, and magnetic properties of Fe80Ce20 films deposited on PET and PMMA substrates. Materialia 2025, 39, 102310. [Google Scholar] [CrossRef]
- Ban, Y.; Yang, X.; Mi, C. On the nanoindentation of a couple-stress half-plane with Steigmann–Ogden surface effects. Mech. Adv. Mater. Struct. 2025, 1–17. [Google Scholar] [CrossRef]
- Adams, D.S.; Boyce, B.L.; Hooks, D.E.; Garber, K.W.; Klitsner, B.; Price, S.A.; Blob, R. A brief introductory guide to nanoindentation for comparative and evolutionary biologists, with a case study of bone material property diversity across artiodactyl skulls. Integr. Org. Biol. 2025, 7, obaf010. [Google Scholar] [CrossRef]
- Efremenko, B.; Chabak, Y.; Petryshynets, I.; Efremenko, V.; Wu, K.; Arshad, S.; Kromka, F. Microstructure Evolution, Tensile/Nanoindentation Response, and Work-Hardening Behaviour of Prestrained and Subsequently Annealed LPBF 316L Stainless Steel. Materials 2025, 18, 1102. [Google Scholar] [CrossRef]
- Timoshenko, S. History of Strength of Materials; Mcgraw-Hill Book Company Inc.: New York, NY, USA, 1953. [Google Scholar]
- Boulenouar, A.; Mighani, S.; Pourpak, H.; Bernabé, Y.; Evans, B. Mechanical Properties of Vaca Muerta Shales from NanoIndentation Tests. In Proceedings of the 51st U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017. [Google Scholar]
- Veytskin, Y.B.; Tammina, V.K.; Bobko, C.P.; Hartley, P.G.; Clennell, M.B.; Dewhurst, D.N.; Dagastine, R.R. Micromechanical characterization of shales through nanoindentation and energy dispersive x-ray spectrometry. Geomech. Energy Environ. 2017, 9, 21–35. [Google Scholar] [CrossRef]
- Gupta, I.; Sondergeld, C.; Rai, C. Fracture toughness in shales using nano-indentation. J. Pet. Sci. Eng. 2020, 191, 107222. [Google Scholar] [CrossRef]
- Fan, M.; Jin, Y.; Chen, M.; Geng, Z. Mechanical characterization of shale through instrumented indentation test. J. Pet. Sci. Eng. 2019, 174, 607–616. [Google Scholar] [CrossRef]
- Cheng, P.; Zhang, C.; Ma, Z.; Zhou, J.; Zhang, D.; Liu, X.; Chen, H.; Ranjith, P. Experimental study of micromechanical properties alterations of shale matrix treated by ScCO2-Water saturation using nanoindentation tests. Energy 2022, 242, 122965. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, C.; Gamage, R.P.; Zhang, G. Uncovering the creep deformation mechanism of rock-forming minerals using nanoindentation. Int. J. Min. Sci. Technol. 2022, 32, 283–294. [Google Scholar] [CrossRef]
- Sun, C.; Li, G.; Gomah, M.E.; Xu, J.; Sun, Y. Creep characteristics of coal and rock investigated by nanoindentation. Int. J. Min. Sci. Technol. 2020, 30, 769–776. [Google Scholar] [CrossRef]
- Ma, G.; Zhou, W.; Ng, T.-T.; Cheng, Y.-G.; Chang, X.-L. Microscopic modeling of the creep behavior of rockfills with a delayed particle breakage model. Acta Geotech. 2015, 10, 481–496. [Google Scholar] [CrossRef]
- Nastic, A.; Merati, A.; Bielawski, M.; Bolduc, M.; Fakolujo, O.; Nganbe, M. Instrumented and Vickers indentation for the characterization of stiffness, hardness and toughness of zirconia toughened Al2O3 and SiC armor. J. Mater. Sci. Technol. 2015, 31, 773–783. [Google Scholar] [CrossRef]
- Liu, K.; Ostadhassan, M.; Bubach, B. Applications of nano-indentation methods to estimate nanoscale mechanical properties of shale reservoir rocks. J. Nat. Gas Sci. Eng. 2016, 35, 1310–1319. [Google Scholar] [CrossRef]
- Chen, W.; Li, M.; Zhang, T.; Cheng, Y.-T.; Cheng, C.-M. Influence of indenter tip roundness on hardness behavior in nanoindentation. Mater. Sci. Eng. A 2007, 445, 323–327. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Bucaille, J.; Stauss, S.; Felder, E.; Michler, J. Determination of plastic properties of metals by instrumented indentation using different sharp indenters. Acta Mater. 2003, 51, 1663–1678. [Google Scholar] [CrossRef]
- Chollacoop, N.; Dao, M.; Suresh, S. Depth-sensing instrumented indentation with dual sharp indenters. Acta Mater. 2003, 51, 3713–3729. [Google Scholar] [CrossRef]
- Karimzadeh, A.; Ayatollahi, M.R.; Alizadeh, M. Finite element simulation of nanoindentation experiment on aluminum 1100. Comput. Mater. Sci. 2014, 81, 595–600. [Google Scholar] [CrossRef]
- Xie, A.; Ji, X.; Chen, Y.; Zhang, M.; Inoue, S.-I. Nanoindentation measurements of mechanical properties of polyurethane elastomers which crosslinked by β-cyclodextrin. Open J. Org. Polym. Mater. 2016, 6, 112–118. [Google Scholar] [CrossRef]
- Ayatollahi, M.; Alishahi, E.; Doagou-R, S.; Shadlou, S. Tribological and mechanical properties of low content nanodiamond/epoxy nanocomposites. Compos. Part B Eng. 2012, 43, 3425–3430. [Google Scholar] [CrossRef]
- Arnold, M.; Zhao, S.; Ma, S.; Giuliani, F.; Hansen, U.; Cobb, J.P.; Abel, R.L.; Boughton, O. Microindentation—A tool for measuring cortical bone stiffness? A systematic review. Bone Jt. Res. 2017, 6, 542–549. [Google Scholar] [CrossRef] [PubMed]
- Ishimoto, T.; Nakano, T.; Yamamoto, M.; Tabata, Y. Biomechanical evaluation of regenerating long bone by nanoindentation. J. Mater. Sci. Mater. Med. 2011, 22, 969–976. [Google Scholar] [CrossRef]
- Cuy, J.L.; Mann, A.B.; Livi, K.J.; Teaford, M.F.; Weihs, T.P. Nanoindentation mapping of the mechanical properties of human molar tooth enamel. Arch. Oral Biol. 2002, 47, 281–291. [Google Scholar] [CrossRef]
- Karimzadeh, A.; Ayatollahi, M.R. Investigation of mechanical and tribological properties of bone cement by nano-indentation and nano-scratch experiments. Polym. Test. 2012, 31, 828–833. [Google Scholar] [CrossRef]
- Pan, C.; Li, X.; He, L.; Li, J. Study on the effect of micro-geometric heterogeneity on mechanical properties of brittle rock using a grain-based discrete element method coupling with the cohesive zone model. Int. J. Rock Mech. Min. Sci. 2021, 140, 104680. [Google Scholar] [CrossRef]
- Song, R.; Wang, Y.; Sun, S.; Liu, J. Characterization and microfabrication of natural porous rocks: From micro-CT imaging and digital rock modelling to micro-3D-printed rock analogs. J. Pet. Sci. Eng. 2021, 205, 108827. [Google Scholar] [CrossRef]
- Li, X.F.; Li, H.B.; Zhao, J. The role of transgranular capability in grain-based modelling of crystalline rocks. Comput. Geotech. 2019, 110, 161–183. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, X.; Liu, Q.; Yang, Y. A zero-thickness cohesive element-based numerical manifold method for rock mechanical behavior with micro-Voronoi grains. Eng. Anal. Bound. Elem. 2018, 96, 94–108. [Google Scholar] [CrossRef]
- Martin, C.D.; Chandler, N.A. The progressive fracture of Lac du Bonnet granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 643–659. [Google Scholar]
- Jia, L.; Chen, M.; Zhang, W.; Xu, T.; Zhou, Y.; Hou, B.; Jin, Y. Experimental study and numerical modeling of brittle fracture of carbonate rock under uniaxial compression. Mech. Res. Commun. 2013, 50, 58–62. [Google Scholar] [CrossRef]
- Lan, H.; Martin, C.D.; Hu, B. Effect of heterogeneity of brittle rock on micromechanical extensile behavior during compression loading. J. Geophys. Res. Solid Earth 2010, 115, B01202. [Google Scholar] [CrossRef]
- Wang, X.; Cai, M. Modeling of brittle rock failure considering inter-and intra-grain contact failures. Comput. Geotech. 2018, 101, 224–244. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, L.; Zhang, G.; Ho, C. Micromechanical Characterization of Fluid-Shale Interactions via Nanoindentation. In Proceedings of the SPE Asia Pacific Hydraulic Fracturing Conference, Beijing, China, 24–26 August 2016; Volume 24, p. 181833. [Google Scholar]
- Xie, W.; Liu, X.; Zhang, X.; Yang, X.; Zhou, X. A review of rock macro-indentation: Theories, experiments, simulations, and applications. J. Rock Mech. Geotech. Eng. 2024, 16, 2351–2374. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, G.; Qiao, J.; Tang, X. Micromechanical testing and property upscaling of planetary rocks: A critical review. Int. J. Min. Sci. Technol. 2024, 34, 1217–1241. [Google Scholar] [CrossRef]
- Puchi-Cabrera, E.S.; Rossi, E.; Sansonetti, G.; Sebastiani, M.; Bemporad, E. Machine learning aided nanoindentation: A review of the current state and future perspectives. Curr. Opin. Solid State Mater. Sci. 2023, 27, 101091. [Google Scholar] [CrossRef]
- Ma, Z.; Pathegama Gamage, R.; Zhang, C. Application of nanoindentation technology in rocks: A review. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 60. [Google Scholar] [CrossRef]
- Brinell, J. Sätt att bestämma kroppars hårdhet jämte några tillämpningar of detsamma. Tek. Tidskr. 1900, 30, 69–87. [Google Scholar]
- Meyer, E. Untersuchungen über härteprüfung und härte. Z. Vereines Dtsch. Ingenieure 1908, 52, 645–654. [Google Scholar]
- Huang, Y.; Liu, X.; Zhou, Y.; Ma, Z.; Lu, C. Mathematical analysis on the uniqueness of reverse algorithm for measuring elastic-plastic properties by sharp indentation. J. Mater. Sci. Technol. 2011, 27, 577–584. [Google Scholar] [CrossRef]
- Richardson, J.F.; Worner, H.K. A microhardness instrument for studying surface hardness. Aust. J. Dent. 1945, 49, 217. [Google Scholar] [PubMed]
- Lee, M.; Brun, M.K. Fracture toughness measurement by microindentation and three-point bend methods. Mater. Sci. Eng. A 1988, 105, 369–375. [Google Scholar] [CrossRef]
- Duncan-Hewitt, W.C.; Weatherly, G.C. Evaluating the fracture toughness of sucrose crystals using microindentation techniques. Pharm. Res. 1989, 6, 373–378. [Google Scholar] [CrossRef]
- Petzold, M.; Landgraf, J.; Füting, M.; Olaf, J. Application of atomic force microscopy for microindentation testing. Thin Solid Film. 1995, 264, 153–158. [Google Scholar] [CrossRef]
- Ringstad, C.; Lofthus, E.B.; Sonstebo, E.F.; Fjær, E.; Zausa, F.; Fuh, G.F. Prediction of rock parameters from micro-indentation measurements: The effect of sample size. In Proceedings of the SPE/ISRM Rock Mechanics in Petroleum Engineering, Trondheim, Norway, 8–10 July 1998; p. SPE-47313-MS. [Google Scholar]
- Zhu, W.; Bartos, P.J.M. Application of depth-sensing microindentation testing to study of interfacial transition zone in reinforced concrete. Cem. Concr. Res. 2000, 30, 1299–1304. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, X.; Wu, X.; Bai, Y. Theoretical and experimental researches of size effect in micro-indentation test. Sci. China Ser. A Math. 2001, 44, 74–82. [Google Scholar] [CrossRef]
- Quinn, G.D.; Patel, P.J.; Lloyd, I. Effect of loading rate upon conventional ceramic microindentation hardness. J. Res. Natl. Inst. Stand. Technol. 2002, 107, 299. [Google Scholar] [CrossRef]
- Xue, Z.; Huang, Y.; Hwang, K.C.; Li, M. The influence of indenter tip radius on the micro-indentation hardness. J. Eng. Mater. Technol. 2002, 124, 371–379. [Google Scholar] [CrossRef]
- Yang, F.; Peng, L.; Okazaki, K. Microindentation of aluminum. Metall. Mater. Trans. A 2004, 35, 3323–3328. [Google Scholar] [CrossRef]
- Qin, J.; Huang, Y.; Hwang, K.; Song, J.; Pharr, G. The effect of indenter angle on the microindentation hardness. Acta Mater. 2007, 55, 6127–6132. [Google Scholar] [CrossRef]
- Wang, W.; Xu, W.Y.; Corn, S.; Ienny, P. Characterization of mechanical properties of rocks by microindentation test—A new method for testing rock properties. In Boundaries of Rock Mechanics; CRC Press: Boca Raton, FL, USA, 2008; pp. 211–216. [Google Scholar]
- Cai, J.; Li, F.; Liu, T.; Chen, B. Microindentation study of Ti–6Al–4V alloy. Mater. Des. 2011, 32, 2756–2762. [Google Scholar] [CrossRef]
- Wei, P.; Zheng, Y.-Y.; Xiong, Y.; Zhou, S.; Ali Zaoui, K.A. Effect of water content and structural anisotropy on mechanical property of claystone. Appl. Clay Sci. 2012, 69, 79–86. [Google Scholar] [CrossRef]
- Zhang, Q.; Le Roy, R.; Vandamme, M.; Zuber, B. Long-term creep properties of cementitious materials: Comparing microindentation testing with macroscopic uniaxial compressive testing. Cem. Concr. Res. 2014, 58, 89–98. [Google Scholar] [CrossRef]
- Baitsch, M.; Le, K.C.; Tran, T.M. Dislocation structure during microindentation. Int. J. Eng. Sci. 2015, 94, 195–211. [Google Scholar] [CrossRef]
- Auvray, C.; Lafrance, N.; Bartier, D. Elastic modulus of claystone evaluated by nano-/micro-indentation tests and meso-compression tests. J. Rock Mech. Geotech. Eng. 2017, 9, 84–91. [Google Scholar] [CrossRef]
- Mallick, S.; Anoop, M.B.; Rao, K.B. Creep of cement paste containing fly ash-an investigation using microindentation technique. Cem. Concr. Res. 2019, 121, 21–36. [Google Scholar] [CrossRef]
- Borc, J.; Sangwal, K.; Świetlicki, M.; Chocyk, D.; Gładyszewski, G. Vickers microindentation deformation of different cleavage faces of potassium bichromate single crystals: Anisotropy in microhardness and crack formation. Mater. Sci. Eng. A 2020, 790, 139642. [Google Scholar] [CrossRef]
- Xu, K.; Huang, M.; Cui, M.; Jin, G.; Li, S. Micromechanical properties and bonding fracture of EICP-reinforced sand analyzed using microindentation test. Acta Geotech. 2025, 20, 3543–3561. [Google Scholar]
- Pethicai, J.B.; Hutchings, R.; Oliver, W.C. Hardness measurement at penetration depths as small as 20 nm. Philos. Mag. A 1983, 48, 593–606. [Google Scholar] [CrossRef]
- Bobko, C.; Ulm, F.J. The nano-mechanical morphology of shale. Mech. Mater. 2008, 40, 318–337. [Google Scholar] [CrossRef]
- Kong, L.; Hadavimoghaddam, F.; Li, C.; Liu, K.; Liu, B.; Semnani, A.; Ostadhassan, M. AFM vs. Nanoindentation: Nanomechanical properties of organic-rich Shale. Mar. Pet. Geol. 2021, 132, 105229. [Google Scholar] [CrossRef]
- Liu, K.; Ostadhassan, M.; Bubach, B.; Ling, K.; Tokhmechi, B.; Robert, D. Statistical grid nanoindentation analysis to estimate macro-mechanical properties of the Bakken Shale. J. Nat. Gas Sci. Eng. 2018, 53, 181–190. [Google Scholar] [CrossRef]
- Kabir, P.; Akono, A.T. Fluid-rock reactions in Mt. Simon sandstone at microscopic length-scale. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, Seattle, DC, USA, 17–20 June 2018; p. ARMA-2018-219. [Google Scholar]
- Bobko, C.P. Material Invariant Properties and Reconstruction of Microstructure of Sandstones by Nanoindentation and Microporoelastic Analysis. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2005. [Google Scholar]
- Ante, M.A.; Lingareddy, M.G.; Aminzadeh, F.; Jha, B. Nano-and micro-scale deformation behavior of sandstone and shale. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, Seattle, DC, USA, 17–20 June 2018; p. ARMA-2018-055. [Google Scholar]
- Tyurin, A.I.; Victorov, S.D.; Kochanov, A.N.; Shuklinov, A.V.; Pirozhkova, T.S. Methods of micro-and nanoindentation for characterization of local physical and mechanical properties of multiphase materials. AIP Conf. Proc. 2016, 1783, 020227. [Google Scholar] [CrossRef]
- Viktorov, S.D.; Golovin, Y.I.; Kochanov, A.N.; Tyurin, A.I.; Shuklinov, A.V.; Shuvarin, I.A.; Pirozhkova, T.S. Micro-and nano-indentation approach to strength and deformation characteristics of minerals. J. Min. Sci. 2014, 50, 652–659. [Google Scholar] [CrossRef]
- Golovin, Y.I.; Tyurin, A.I.; Victorov, S.D.; Kochanov, A.N.; Samodurov, A.A.; Pirozhkova, T.S. Physico-mechanical properties and micromechanisms of local deformation in thin near-surface layers of complex multiphase materials. Bull. Russ. Acad. Sci. Phys. 2017, 81, 360–364. [Google Scholar] [CrossRef]
- Golovin, Y.I.; Tyurin, A.I.; Victorov, S.D.; Kochanov, A.N.; Pirozhkova, T.S. Size effects and charting the physical and mechanical properties of individual phases and interphases in polycrystalline materials. Bull. Russ. Acad. Sci. Phys. 2018, 82, 856–859. [Google Scholar] [CrossRef]
- Vialle, S.; Lebedev, M. Heterogeneities in the elastic properties of microporous carbonate rocks at the microscale from nanoindentation tests. In Proceedings of the SEG International Exposition and Annual Meeting, New Orleans, LA, USA, 18–23 October 2015; p. SEG-2015-5885016. [Google Scholar]
- Shukla, P.; Taneja, S.; Sondergeld, C.; Rai, C.S. Nanoindentation measurements on rocks. In Proceedings of the 2014 Annual Conference on Experimental and Applied Mechanics, Greenville, SC, USA, 2–5 June 2014; pp. 99–105. [Google Scholar]
- Zhang, Y.; Lebedev, M.; Sarmadivaleh, M.; Barifcani, A. Change in geomechanical properties of limestone due to supercritical CO2 injection. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Perth, Australia, 25–27 October 2016; p. SPE-182285-MS. [Google Scholar]
- Zhang, Y.; Lebedev, M.; Al-Yaseri, A.; Yu, H.; Nwidee, L.N.; Sarmadivaleh, M.; Barifcani, A.; Iglauer, S. Morphological evaluation of heterogeneous oolitic limestone under pressure and fluid flow using X-ray microtomography. J. Appl. Geophys. 2018, 150, 172–181. [Google Scholar] [CrossRef]
- Lebedev, M.; Wilson, M.E.J.; Mikhaltsevitch, V. An experimental study of solid matrix weakening in water-saturated Savonnières limestone. Geophys. Prospect. 2014, 62, 1253–1265. [Google Scholar] [CrossRef]
- Bandini, A.; Berry, P.; Bemporad, E.; Sebastiani, M. Effects of intra-crystalline microcracks on the mechanical behavior of a marble under indentation. Int. J. Rock Mech. Min. Sci. 2012, 54, 47–55. [Google Scholar] [CrossRef]
- Bandini, A.; Berry, P.; Bemporad, E.; Sebastiani, M.; Chicot, D. Role of grain boundaries and micro-defects on the mechanical response of a crystalline rock at multiscale. Int. J. Rock Mech. Min. Sci. 2014, 71, 429–441. [Google Scholar] [CrossRef]
- Konstantinidis, A.A.; Frantziskonis, G.; Askes, H.; Aifantis, E.C. The use of nanoindentation for determining internal lengths and the constitutive response of monument materials: Models and experiments. J. Mech. Behav. Mater. 2016, 25, 57–60. [Google Scholar] [CrossRef]
- Brooks, Z.; Ulm, F.J.; Einstein, H.H.; Abousleiman, Y. A nanomechanical investigation of the crack tip process zone. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, Salt Lake City, UT, USA, 27–30 June 2010; p. ARMA-10-309. [Google Scholar]
- Sly, M.K.; Thind, A.S.; Mishra, R.; Flores, K.M.; Skemer, P. Low-temperature rheology of calcite. Geophys. J. Int. 2020, 221, 129–141. [Google Scholar] [CrossRef]
- Zhang, F.; Guo, H.; Hu, D.; Shao, J.-F. Characterization of the mechanical properties of a claystone by nano-indentation and homogenization. Acta Geotech. 2018, 13, 1395–1404. [Google Scholar] [CrossRef]
- Magnenet, V.; Auvray, C.; Francius, G.; Giraud, A. Determination of the matrix indentation modulus of Meuse/Haute-Marne argillite. Appl. Clay Sci. 2011, 52, 266–269. [Google Scholar] [CrossRef]
- Bartier, D.; Auvray, C. Determination of elastic modulus of claystone: Nano-/micro-indentation and meso-compression tests used to investigate impact of alkaline fluid propagation over 18 years. J. Rock Mech. Geotech. Eng. 2017, 9, 511–518. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Bushan, B. Handbook of Micro/Nano Tribology; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Dao, M.; Chollacoop, N.; Van Vliet, K.J.; Venkatesh, T.A.; Suresh, S. Computational modeling of the forward and reverse problems in instrumented sharp indentation. Acta Mater. 2001, 49, 3899–3918. [Google Scholar] [CrossRef]
- Kucharski, S.; Mroz, Z. Identification of plastic hardening parameters of metals from spherical indentation tests. Mater. Sci. Eng. A 2001, 318, 65–76. [Google Scholar] [CrossRef]
- Ma, D.; Ong, C.W.; Lu, J.; He, J. Methodology for the evaluation of yield strength and hardening behavior of metallic materials by indentation with spherical tip. J. Appl. Phys. 2003, 94, 288–294. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. A simple phenomenological approach to nanoindentation creep. Mater. Sci. Eng. A 2004, 385, 74–82. [Google Scholar] [CrossRef]
- Oyen, M.L.; Cook, R.F. Load–displacement behavior during sharp indentation of viscous–elastic–plastic materials. J. Mater. Res. 2003, 18, 139–150. [Google Scholar] [CrossRef]
- Storåkers, B.; Larsson, P.L. On Brinell and Boussinesq indentation of creeping solids. J. Mech. Phys. Solids 1994, 42, 307–332. [Google Scholar] [CrossRef]
- Lucas, B.N.; Oliver, W.C. Indentation power-law creep of high-purity indium. Metall. Mater. Trans. A 1999, 30, 601–610. [Google Scholar] [CrossRef]
- Takagi, H.; Dao, M.; Fujiwara, M.; Otsuka, M. Experimental and computational creep characterization of Al–Mg solid-solution alloy through instrumented indentation. Philos. Mag. 2003, 83, 3959–3976. [Google Scholar] [CrossRef]
- Suresh, S.; Giannakopoulos, A.E. A new method for estimating residual stresses by instrumented sharp indentation. Acta Mater. 1998, 46, 5755–5767. [Google Scholar] [CrossRef]
- Carlsson, S.; Larsson, P.L. On the determination of residual stress and strain fields by sharp indentation testing.: Part I: Theoretical and numerical analysis. Acta Mater. 2001, 49, 2179–2191. [Google Scholar] [CrossRef]
- Carlsson, S.; Larsson, P.L. On the determination of residual stress and strain fields by sharp indentation testing.: Part II: Experimental investigation. Acta Mater. 2001, 49, 2193–2203. [Google Scholar] [CrossRef]
- Swadener, J.G.; Taljat, B.; Pharr, G.M. Measurement of residual stress by load and depth sensing indentation with spherical indenters. J. Mater. Res. 2001, 16, 2091–2102. [Google Scholar] [CrossRef]
- Abedi, S.; Slim, M.; Hofmann, R.; Bryndzia, T.; Ulm, F.-J. Nanochemo-mechanical signature of organic-rich shales: A coupled indentation–EDX analysis. Acta Geotech. 2016, 11, 559–572. [Google Scholar] [CrossRef]
- Deirieh, A.; Ortega, J.A.; Ulm, F.-J.; Abousleiman, Y. Nanochemomechanical assessment of shale: A coupled WDS-indentation analysis. Acta Geotech. 2012, 7, 271–295. [Google Scholar] [CrossRef]
- Prakash, R.; Nguene, P.C.K.; Benoit, D.; Henkel, K.; Abedi, S. Assessment of local phase to mechanical response link: Application to the chemo-mechanical identification of rock phases subjected to reactive environments. J. Nat. Gas Sci. Eng. 2021, 89, 103857. [Google Scholar] [CrossRef]
- Mashhadian, M.; Verde, A.; Sharma, P.; Abedi, S. Assessing mechanical properties of organic matter in shales: Results from coupled nanoindentation/SEM-EDX and micromechanical modeling. J. Pet. Sci. Eng. 2018, 165, 313–324. [Google Scholar] [CrossRef]
- Du, J.; Luo, S.; Hu, L.; Guo, B.; Guo, D.; Zhang, G. Multiscale mechanical properties of shales: Grid nanoindentation and statistical analytics. Acta Geotech. 2022, 17, 339–354. [Google Scholar] [CrossRef]
- Li, C.; Ostadhassan, M.; Kong, L.; Bubach, B. Multi-scale assessment of mechanical properties of organic-rich shales: A coupled nanoindentation, deconvolution analysis, and homogenization method. J. Pet. Sci. Eng. 2019, 174, 80–91. [Google Scholar] [CrossRef]
- Ulm, F.; Vandamme, M.; Bobko, C.; Ortega, J.A.; Tai, K.; Ortiz, C. Statistical indentation techniques for hydrated nanocomposites: Concrete, bone, and shale. J. Am. Ceram. Soc. 2007, 90, 2677–2692. [Google Scholar] [CrossRef]
- Ahn, J.-H.; Kwon, D. Derivation of plastic stress–strain relationship from ball indentations: Examination of strain definition and pileup effect. J. Mater. Res. 2001, 16, 3170–3178. [Google Scholar] [CrossRef]
- Cao, Y.P.; Lu, J. A new method to extract the plastic properties of metal materials from an instrumented spherical indentation loading curve. Acta Mater. 2004, 52, 4023–4032. [Google Scholar] [CrossRef]
- Zhao, M.; Ogasawara, N.; Chiba, N.; Chen, X. A new approach to measure the elastic–plastic properties of bulk materials using spherical indentation. Acta Mater. 2006, 54, 23–32. [Google Scholar] [CrossRef]
- ISO14577; Metallic Materials—Instrumented Indentation Test for Hardness and Materials Parameters. International Organization for Standardization: Geneva, Switzerland, 2002.
- Su, X.; Chen, P.; Ma, T. Evaluation of shale fracture toughness based on micrometer indentation test. Petroleum 2019, 5, 52–57. [Google Scholar] [CrossRef]
- Fu, G. An extension of Hertz’s theory in contact mechanics. J. Appl. Mech. 2006, 74, 373–374. [Google Scholar] [CrossRef]
- Johnson, K.L. The correlation of indentation experiments. J. Mech. Phys. Solids 1970, 18, 115–126. [Google Scholar] [CrossRef]
- Lawn, B.R.; Evans, A.G.; Marshall, D.B. Elastic/plastic indentation damage in ceramics: The median/radial crack system. J. Am. Ceram. Soc. 1980, 63, 574–581. [Google Scholar] [CrossRef]
- Ma, T.; Liu, K.; Su, X.; Chen, P.; Ranjith, P.G.; Martyushev, D.A. Investigation on the anisotropy of meso-mechanical properties of shale rock using micro-indentation. Bull. Eng. Geol. Environ. 2024, 83, 29. [Google Scholar] [CrossRef]
- Dong, G.; Chen, P. Anisotropy indentation fragmentation mechanism of shale under coupled loads and different deviation angles. Electron. J. Geotech. Eng. 2017, 22, 981–995. [Google Scholar]
- Kumar, V.; Curtis, M.E.; Gupta, N.; Sondergeld, C.H.; Rai, C.S. Estimation of elastic properties of organic matter and Woodford shale through nano-indentation measurements. In Proceedings of the SPE Canada Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012; p. SPE-162778-MS. [Google Scholar]
- Xu, J.; Tang, X.; Wang, Z.; Feng, Y.; Bian, K. Investigating the softening of weak interlayers during landslides using nanoindentation experiments and simulations. Eng. Geol. 2020, 277, 105801. [Google Scholar] [CrossRef]
- Lu, Y.; Li, Y.; Wu, Y.; Luo, S.; Jin, Y.; Zhang, G. Characterization of shale softening by large volume-based nanoindentation. Rock Mech. Rock Eng. 2020, 53, 1393–1409. [Google Scholar] [CrossRef]
- Yang, C.; Xiong, Y.; Wang, J.; Li, Y.; Jiang, W. Mechanical characterization of shale matrix minerals using phase-positioned nanoindentation and nano-dynamic mechanical analysis. Int. J. Coal Geol. 2020, 229, 103571. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, G.; Song, H.; Kang, Y. Experimental investigation of deformation and failure mechanisms in rock under indentation by digital image correlation. Eng. Fract. Mech. 2012, 96, 667–675. [Google Scholar] [CrossRef]
- Song, R.; Wang, Y.; Sun, S.; Cui, M.; Liu, J. Evaluation of elastoplastic properties of brittle sandstone at microscale using micro-indentation test and simulation. Energy Sci. Eng. 2020, 8, 3490–3501. [Google Scholar] [CrossRef]
- Ma, Z.; Gamage, R.P.; Zhang, C. Mechanical properties of α-quartz using nanoindentation tests and molecular dynamics simulations. Int. J. Rock Mech. Min. Sci. 2021, 147, 104878. [Google Scholar] [CrossRef]
| Authors and Year | Significance/Key Results | Method/Parameters | Type of Rocks |
|---|---|---|---|
| Kabir and Akono, 2018 [72] | Used to reveal microseismic activity during geological sequestration of carbon dioxide. | Combining scratch tests, nanoindentation tests, as well as atomic force microscopy. | Sandstone |
| Bobko, 2005 [73] | A new technology has been developed and validated to estimate the volume fraction of composite materials. | A nanoindentation experiment was conducted based on environmental scanning electron microscopy (ESEM) images. | |
| Ante et al., 2018 [74] | Provides important insights into the particle-scale deformation behavior of shale and sandstone. | Young’s modulus, hardness and stiffness of rocks quantified by nanoindentation. | |
| Tyurin et al., 2016 [75] | Size effects on physical and mechanical properties of individual phases and interfaces are investigated. | Hardness in a wide range of rocks has been investigated using micro- and nanoindentation techniques. | |
| Viktorov et al., 2014 [76] | Validation of the operability of the indentation test in the field of rock mechanics. | Young’s modulus, fracture toughness and hardness of rocks and minerals were obtained by micro- and nanoindentation. | |
| Golovin et al., 2017 [77] | Size effects in the local mechanical properties of multiphase materials are studied. | Elasticity modulus, hardness, and crack resistance are determined by means of micro- and nanoindentation. | |
| Golovin et al., 2018 [78] | Size effects in hardness and correlations between the distribution of local physical and mechanical properties and the morphology of the studied samples are found. | Hardness is obtained via micro- and nanoindentation. | |
| Vialle and Lebedev, 2015 [79] | It is possible to correlate the microstructure of mud crystals with their elastic properties. | Young’s moduli were mapped on a microscopic scale using nanoindentation technique combined with scanning electron microscopy (SEM). | Limestone |
| Shukla et al., 2015 [80] | The measurements do not correspond to the Young’s modulus of the rock for coarse-grained rocks, all indentations. | Young’s moduli obtained by nanoindentation and compared with the standard dynamic pulse transmission speed measurement results. | |
| Zhang et al., 2016 [81] | Effect of acidic CO2 fluids on the mechanical properties of porous limestone as host rock for potential CO2 sequestration is explored. | Dynamic Young’s modulus of Savonier limestone cores before and after supercritical carbon dioxide injection were measured using the perimeter nanoindentation technique. | |
| Zhang et al., 2018 [82] | Assessing micro-geomechanical inhomogeneities in rocks. | Range of non-uniform indentation modulus is determined using nanoindentation technique. | |
| Lebedev et al., 2014 [83] | Understanding the mechanism of fluid–rock interaction and its effect on carbonate elastic parameters. | The elastic modulus of limestone was obtained by nanoindentation tests. | |
| Bandini et al., 2012 [84] | Determine the effect of microcracks within the grain on its mechanical behavior. | Young’s modulus, hardness on marble were obtained by nanoindentation tests using three types of indenters (Nu, Vickers, and Berkovich). | Marble |
| Bandini et al., 2014 [85] | Different crack initiation, extension, merging and failure mechanisms as well as stress–strain relationships at the macroscopic scale are more fully explained. | Young’s modulus and hardness on two types of marble (heterogeneous and granular) were obtained by nanoindentation tests. | |
| Konstantinidis et al., 2016 [86] | A gradient elasticity equation is proposed to explain the evolution of the elastic gradient generated by geometry of the indenter-sample system and applied in conjunction with marble nanoindentation data. | Young’s moduli were obtained on Dionysus marble samples by nanoindentation measurements. | |
| Brooks et al., 2010 [87] | The interaction between crack initiation and nano-mechanical properties in the crack tip processing zone of a brittle material (marble) is investigated. | Young’s modulus and hardness were obtained using nanoindentation and nano/micro heterogeneity was assessed. | |
| Sly et al., 2020 [88] | Plastic rheology of calcite at low temperatures using nanoindentation and micro-column compression experiments. | Nanoindentation experiments to obtain indentation hardness. | |
| Zhang et al., 2018 [89] | Verification that nanoindentation technique provides an effective tool to identify elastic properties of the constituent phases of non-homogeneous rocks. | Young’s modulus and hardness of claystone were by nanoindentation technique and homogenization method. | Claystone |
| Magnenet et al., 2011 [90] | Feasibility of biphasic model for predicting indentation modulus using microscopic experimental data is verified. | Quantifying the indentation modulus of clay matrices by nanoindentation tests. | |
| Auvray et al., 2017 [64] | Experiments to demonstrate scale effects on the deformation modulus. | Modulus of deformability were obtained at different sample scales by nano- and microindentations. | |
| Bartier and Auvray, 2017 [91] | Deformation modulus is related to the carbonate content and its distribution. | Determination of deformation modulus of claystone for different depths by nanoindentation. |
| Nanoindentation Test | Microindentation Test | Type of Test |
|---|---|---|
| Tens of microNm to tens of millinewtons (μN-mN) | Tens of millinewtons to a few newtons (mN-N) | Range of loading force |
| Tens of nanometers to a few micrometers (nm-μm) | Several micronmeters to tens of micrometers (μm) | Depth of indentation |
| Micro-regions, thin films, fine-grained materials | Bulk materials, coarse-grained materials | Trial samples |
| High, suitable for analyzing micro-structures | Medium, suitable for analyzing larger structures | Spatial resolution |
| Precise control of loading-holding-unloading is possible | Precise control of loading-holding-unloading is possible | Loading method |
| Hardness, Young’s modulus, creep behavior, fracture toughness, plastic deformation | Hardness, Young’s modulus, plastic deformation, creep behavior, fracture toughness | Measured parameters |
| Fields of Application | Indenter Geometry | Indenter Name |
|---|---|---|
| Microstructural analysis of metals, ceramics, and hardened materials. | Equiaxed diamond pyramid; four faces; 136° facet apex angle. | Vickers |
| Small, long specimens and precision testing where minimal damage is required. | Elongated diamond pyramid; four faces; 172.5° major-edge apex angle; 130° minor-edge apex angle. | Knoop |
| Determination of average hardness of large parts, forgings and castings. | 10 mm diameter ball. | Brinell |
| Commonly used in nanotechnology research to determine the mechanical properties of materials and to analyze in depth the intrinsic properties of materials. | Diamond indenter; three facets; 142° edge-to-opposite facet. | Berkovich |
| Testing special materials with thin surface and high hardness. | Diamond; edge of bases of two base-to-base 66° cones; 2 mm base radius. | Grodzinski |
| Research of optical materials. | Hemisphere of sapphire. | Pfund |
| Research on paint and lacquer. | Pentagonal shape. | Brooks |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Q.; Konietzky, H. Review of Nano- and Micro- Indentation Tests for Rocks. Geosciences 2025, 15, 389. https://doi.org/10.3390/geosciences15100389
He Q, Konietzky H. Review of Nano- and Micro- Indentation Tests for Rocks. Geosciences. 2025; 15(10):389. https://doi.org/10.3390/geosciences15100389
Chicago/Turabian StyleHe, Qingqing, and Heinz Konietzky. 2025. "Review of Nano- and Micro- Indentation Tests for Rocks" Geosciences 15, no. 10: 389. https://doi.org/10.3390/geosciences15100389
APA StyleHe, Q., & Konietzky, H. (2025). Review of Nano- and Micro- Indentation Tests for Rocks. Geosciences, 15(10), 389. https://doi.org/10.3390/geosciences15100389






