On the Ionosphere–Atmosphere–Lithosphere Coupling During the 9 November 2022 Italian Earthquake
Abstract
1. Introduction
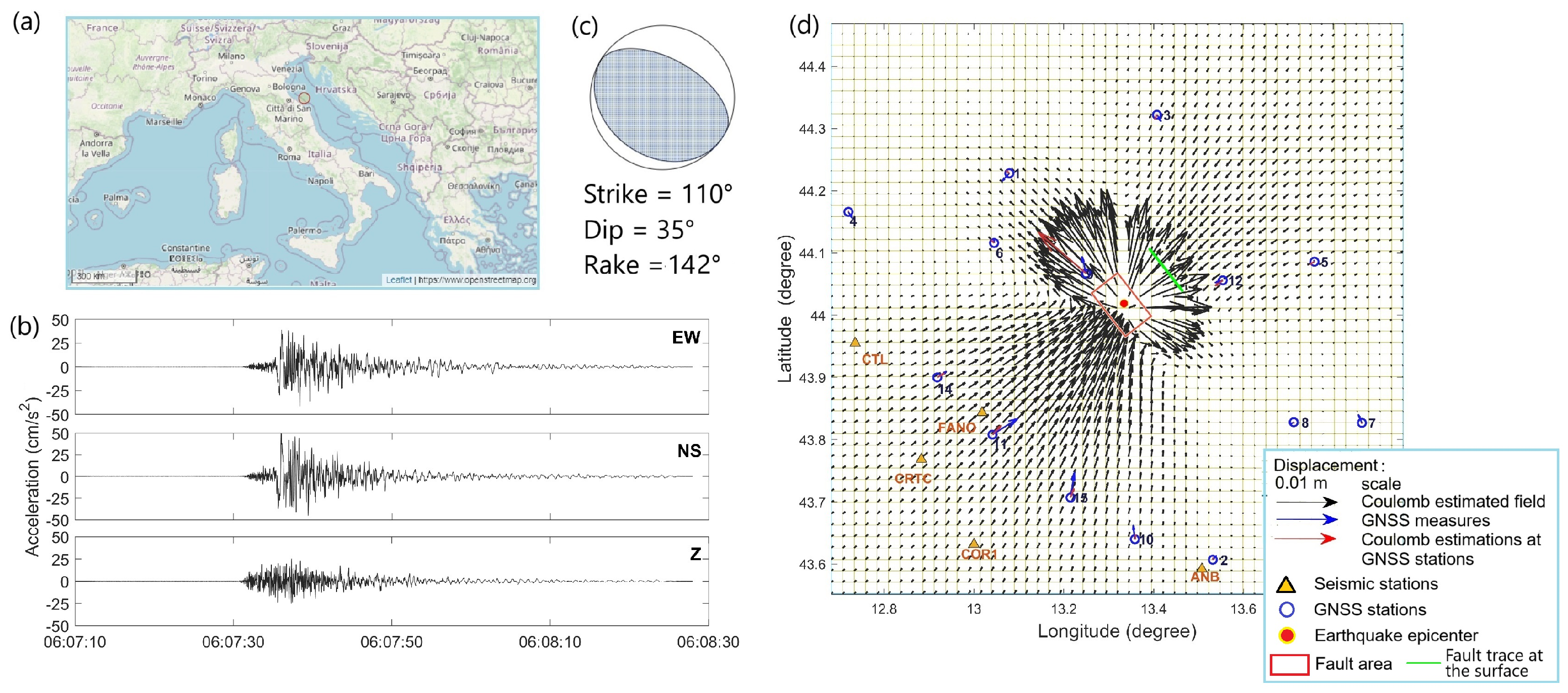
2. The 9 November 2022 Italian Earthquake
Static Displacement Evaluation
3. Co-Seismic Analysis
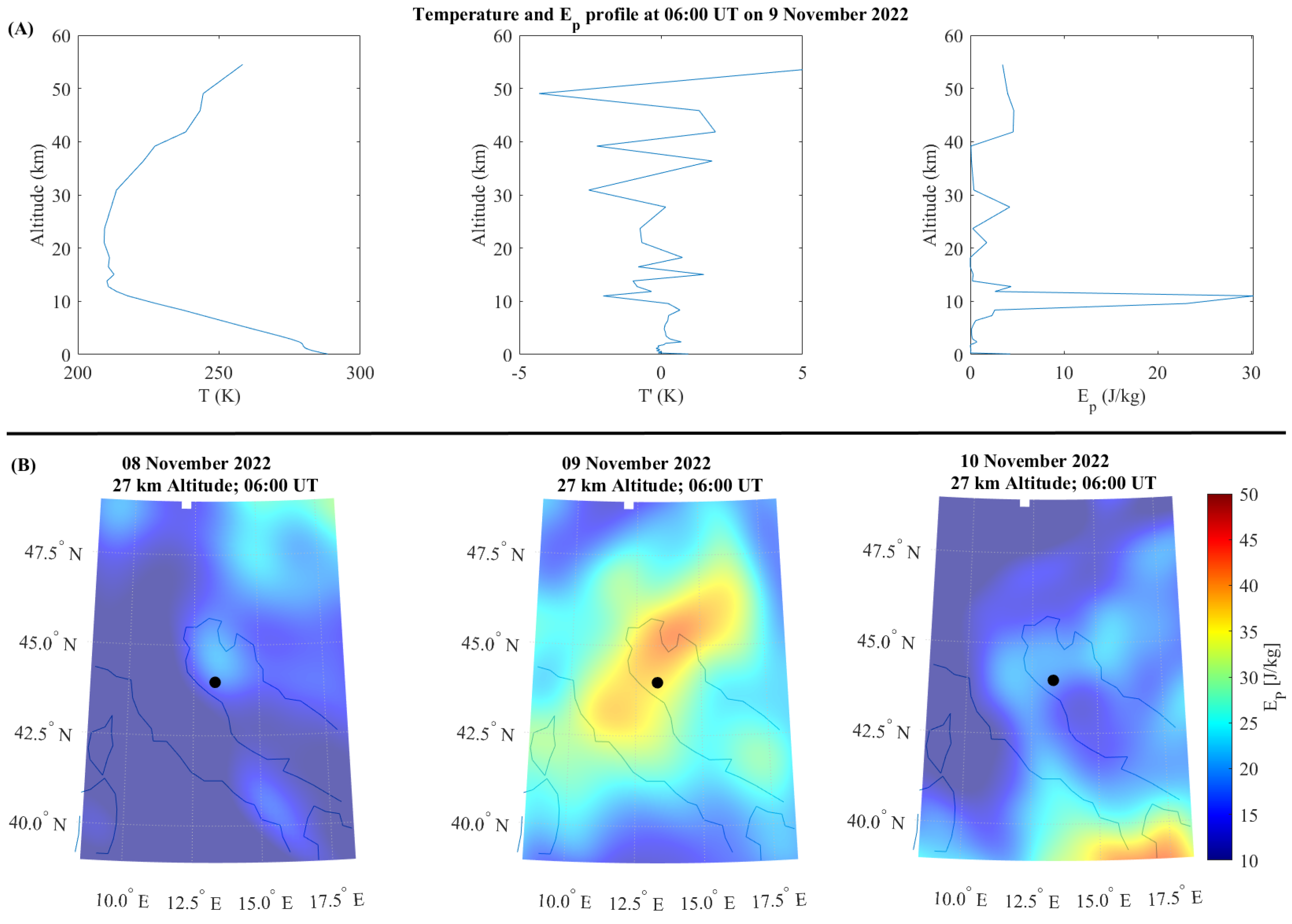
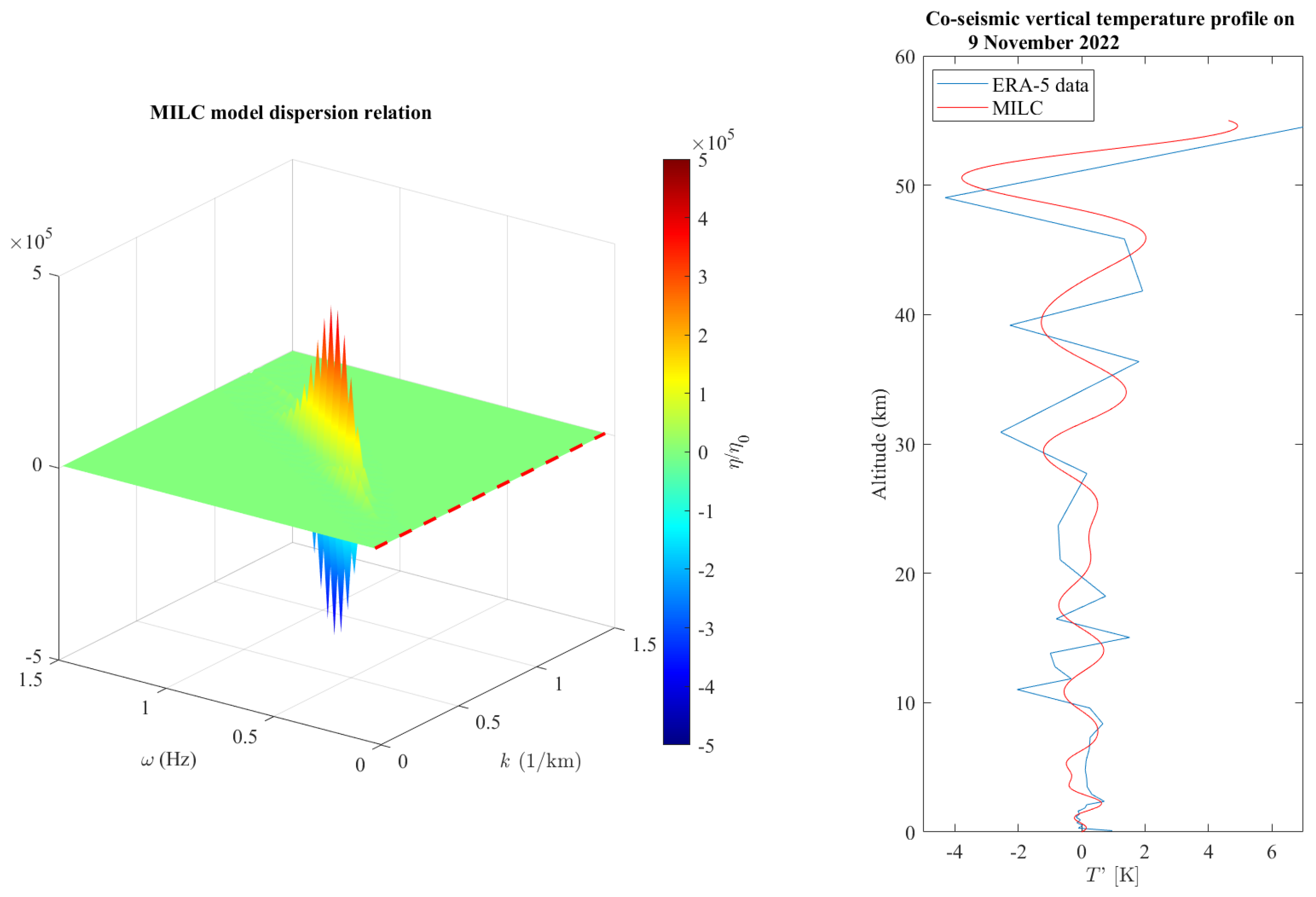
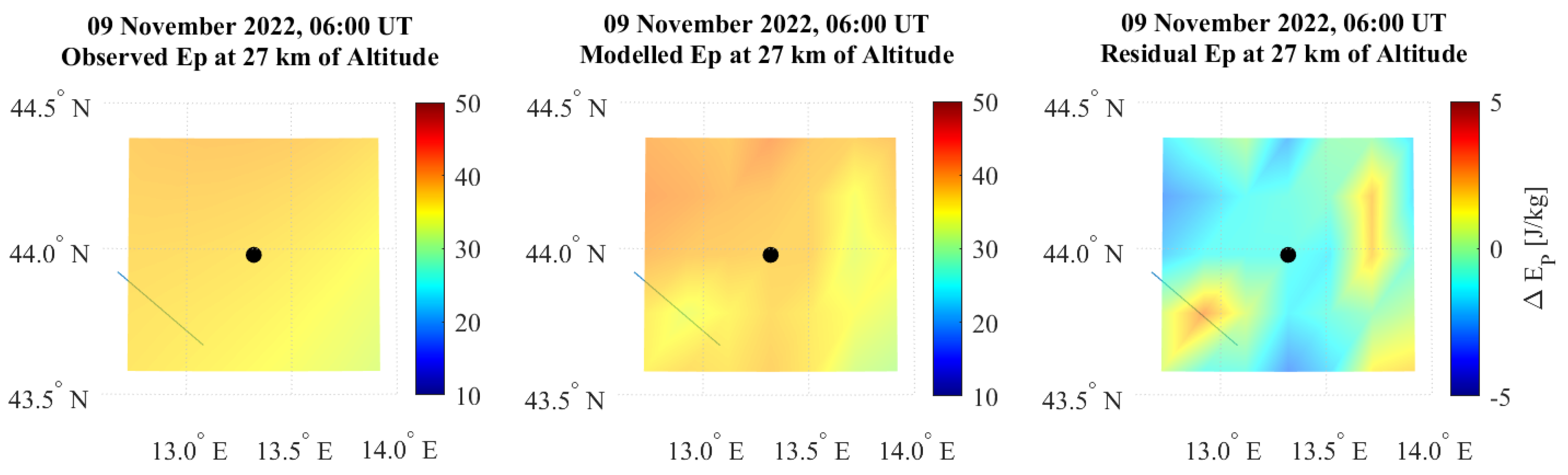
3.1. Atmospheric Temperature and Acoustic Gravity Waves Evaluation
3.2. The Vertical Total Electron Content
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AGW | Acoustic Gravity Wave |
| EE | Earthquake epicenter |
| EQ | Earthquake |
| TID | Traveling Ionospheric Disturbance |
| FIF | Fast iterative Filtering |
| GNSS | Global Navigation Satellite System |
| MILC | Magnetospheric–Ionospheric–Lithospheric Coupling |
| TEC | Total Electron Content |
| vTEC | Vertical TEC |
References
- Hayakawa, M.; Kasahara, Y.; Nakamura, T.; Muto, F.; Horie, T.; Maekawa, S.; Hobara, Y.; Rozhnoi, A.; Solovieva, M.; Molchanov, O. A statistical study on the correlation between lower ionospheric perturbations as seen by subionospheric VLF/LF propagation and earthquakes. J. Geophys. Res. Space Phys. 2010, 115, A09305. [Google Scholar] [CrossRef]
- Liu, J. Earthquake precursors observed in the ionospheric F-region. In Electromagnetic Phenomena Associated with Earthquakes; Transworld Research Network: Trivandrum, India, 2009; pp. 187–204. [Google Scholar]
- Hayakawa, M. Earthquake Prediction with Radio Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Molchanov, O.; Hayakawa, M. Subionospheric VLF signal perturbations possibly related to earthquakes. J. Geophys. Res. Space Phys. 1998, 103, 17489–17504. [Google Scholar] [CrossRef]
- Pulinets, S.; Boyarchuk, K. Ionospheric Precursors of Earthquakes; Springer Science & Business Media: Cham, The Netherlands, 2004. [Google Scholar]
- Piersanti, M.; Materassi, M.; Battiston, R.; Carbone, V.; Cicone, A.; D’Angelo, G.; Diego, P.; Ubertini, P. Magnetospheric–Ionospheric–Lithospheric Coupling Model. 1: Observations During the 5 August 2018 Bayan Earthquake. Remote Sens. 2020, 12, 3299. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) model—An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D.; Karelin, A.; Davidenko, D. Physical bases of the generation of short-term earthquake precursors: A complex model of ionization-induced geophysical processes in the lithosphere-atmosphere-ionosphere-magnetosphere system. Geomagn. Aeron. 2015, 55, 521–538. [Google Scholar] [CrossRef]
- Sorokin, V.; Yaschenko, A.; Hayakawa, M. Formation mechanism of the lower-ionospheric disturbances by the atmosphere electric current over a seismic region. J. Atmos. Sol. Terr. Phys. 2006, 68, 1260–1268. [Google Scholar] [CrossRef]
- Hayakawa, M.; Kasahara, Y.; Nakamura, T.; Hobara, Y.; Rozhnoi, A.; Solovieva, M.; Molchanov, O.; Korepanov, V. Atmospheric gravity waves as a possible candidate for seismo-ionospheric perturbations. J. Atmos. Electr. 2011, 31, 129–140. [Google Scholar] [CrossRef]
- Miyaki, K.; Hayakawa, M.; Molchanov, O. The role of gravity waves in the lithosphere-ionosphere coupling, as revealed from the subionospheric LF propagation data. In Seismo Electromagnetics: Lithosphere-Atmosphere-Ionosphere Coupling; Terrapub: Tokyo, Japan, 2002; pp. 229–232. [Google Scholar]
- Molchanov, O.; Hayakawa, M.; Miyaki, K. VLF/LF sounding of the lower ionosphere to study the role of atmospheric oscillations in the lithosphere-ionosphere coupling. Adv. Polar Up. Atmos. Res. 2001, 15, 146–158. [Google Scholar]
- Muto, F.; Kasahara, Y.; Hobara, Y.; Hayakawa, M.; Rozhnoi, A.; Solovieva, M.; Molchanov, O. Further study on the role of atmospheric gravity waves on the seismo-ionospheric perturbations as detected by subionospheric VLF/LF propagation. Nat. Hazards Earth Syst. Sci. 2009, 9, 1111–1118. [Google Scholar] [CrossRef][Green Version]
- Carbone, V.; Piersanti, M.; Materassi, M.; Battiston, R.; Lepreti, F.; Ubertini, P. A mathematical model of lithosphere–atmosphere coupling for seismic events. Sci. Rep. 2021, 11, 8682. [Google Scholar] [CrossRef]
- Freund, F. Time-resolved study of charge generation and propagation in igneous rocks. J. Geophys. Res. Solid Earth 2000, 105, 11001–11019. [Google Scholar] [CrossRef]
- Freund, F. Pre-earthquake signals: Underlying physical processes. J. Asian Earth Sci. 2011, 41, 383–400. [Google Scholar] [CrossRef]
- Liperovsky, V.; Pokhotelov, O.; Meister, C.V.; Liperovskaya, E. Physical models of coupling in the lithosphere-atmosphere-ionosphere system before earthquakes. Geomagn. Aeron. 2008, 48, 795–806. [Google Scholar] [CrossRef]
- Oyama, K.I.; Devi, M.; Ryu, K.; Chen, C.; Liu, J.; Liu, H.; Bankov, L.; Kodama, T. Modifications of the ionosphere prior to large earthquakes: Report from the Ionosphere Precursor Study Group. Geosci. Lett. 2016, 3, 6. [Google Scholar] [CrossRef]
- Hayakawa, M. The precursory signature effect of the Kobe earthquake on VLF subionospheric signals. J. Commun. Res. Lab. Tokyo 1996, 43, 169–180. [Google Scholar]
- Korepanov, V.; Hayakawa, M.; Yampolski, Y.; Lizunov, G. AGW as a seismo-ionospheric coupling responsible agent. Phys. Chem. Earth 2009, 34, 485–495. [Google Scholar] [CrossRef]
- Nakamura, T.; Korepanov, V.; Kasahara, Y.; Hobara, Y.; Hayakawa, M. An evidence on the lithosphere-ionosphere coupling in terms of atmospheric gravity waves on the basis of a combined analysis of surface pressure, ionospheric perturbations and ground-based ULF variations. J. Atmos. Electr. 2013, 33, 53–68. [Google Scholar] [CrossRef][Green Version]
- Endo, T.; Kasahara, Y.; Hobara, Y.; Sue, T.; Hayakawa, M. A note on the correlation of seismo-ionospheric perturbations with ground motions as deduced from F-net seismic observations. J. Atmos. Electr. 2013, 33, 69–76. [Google Scholar] [CrossRef]
- Hayakawa, M.; Hobara, Y.; Rozhnoi, A.; Solovieva, M.; Ohta, K.; Izutsu, J.; Nakamura, T.; Kasahara, Y. The Ionospheric Precursor to the 2011 March 11 Earthquake Based upon Observations Obtained from the Japan-Pacific Subionospheric VLF/LF Network. Terr. Atmos. Ocean Sci. 2013, 24, 393–408. [Google Scholar] [CrossRef]
- Hayakawa, M.; Hobara, Y.; Yasuda, Y.; Yamaguchi, H.; Ohta, K.; Izutsu, J.; Nakamura, T. Possible precursor to the March 11, 2011, Japan earthquake: Ionospheric perturbations as seen by subionospheric very low frequency/low frequency propagation. Ann. Geophys. 2012, 55, 95–99. [Google Scholar]
- Hayakawa, M.; Rozhnoi, A.; Solovieva, M.; Hobara, Y.; Ohta, K.; Schekotov, A.; Fedorov, E. The lower ionospheric perturbation as a precursor to the 11 March 2011 Japan earthquake. Geomat. Nat. Hazards Risk 2013, 4, 275–287. [Google Scholar] [CrossRef]
- Kamiyama, M.; Sugito, M.; Kuse, M.; Schekotov, A.; Hayakawa, M. On the precursors to the 2011 Tohoku earthquake: Crustal movements and electromagnetic signatures. Geomat. Nat. Hazards Risk 2016, 7, 471–492. [Google Scholar] [CrossRef]
- D’Angelo, G.; Piersanti, M.; Battiston, R.; Bertello, I.; Carbone, V.; Cicone, A.; Diego, P.; Papini, E.; Parmentier, A.; Picozza, P.; et al. Haiti earthquake (mw 7.2): Magnetospheric–ionospheric–lithospheric coupling during and after the main shock on 14 august 2021. Remote Sens. 2022, 14, 5340. [Google Scholar] [CrossRef]
- Carbone, F.; Piersanti, M.; Lepreti, F.; Primavera, L.; Gencarelli, C.N.; Pirrone, N.; Battiston, R. Nonlinear shallow water investigation of atmospheric disturbances generated by strong seismic events. Phys. Rev. E 2023, 108, 035105. [Google Scholar] [CrossRef] [PubMed]
- Latorre, D.; Arcoraci, L.; Battelli, A.; Battelli, P.; Berardi, M.; Cantucci, B.; Castellano, C.; Castello, B.; Cheloni, D.; Ciaccio, M.G.; et al. What we can say (or not) about the seismic sequence of the November 9th 2022, Mw 5.5, earthquake in the Marche offshore: An analysis of the Italian Seismic Bulletin on phase interpretation, velocity models and uncertainties of earthquake locations. In Proceedings of the 41st GNGTS National Conference, Bologna, Italy, 7–9 February 2023. [Google Scholar]
- Maesano, F.E.; Buttinelli, M.; Maffucci, R.; Toscani, G.; Basili, R.; Bonini, L.; Burrato, P.; Fedorik, J.; Fracassi, U.; Panara, Y.; et al. Buried alive: Imaging the 9 November 2022, Mw 5.5 earthquake source on the offshore Adriatic blind thrust front of the Northern Apennines (Italy). Geophys. Res. Lett. 2023, 50, e2022GL102299. [Google Scholar] [CrossRef]
- Luzi, L.; Lanzano, G.; Felicetta, C.; D’Amico, M.; Russo, E.; Sgobba, S.; Pacor, F.; ORFEUS Working Group 5. Engineering Strong Motion Database (ESM) (Version 2.0); Istituto Nazionale di Geofisica e Vulcanologia (INGV): Milano, Italy, 2020; Volume 2. [Google Scholar] [CrossRef]
- Vackář, J.; Burjánek, J.; Gallovič, F.; Zahradník, J.; Clinton, J. Bayesian ISOLA: New tool for automated centroid moment tensor inversion. Geophys. J. Int. 2017, 210, 693–705. [Google Scholar] [CrossRef]
- Pezzo, G.; Billi, A.; Carminati, E.; Conti, A.; De Gori, P.; Devoti, R.; Lucente, F.P.; Palano, M.; Petracchini, L.; Serpelloni, E.; et al. Seismic source identification of the 9 November 2022 Mw 5.5 offshore Adriatic sea (Italy) earthquake from GNSS data and aftershock relocation. Sci. Rep. 2023, 13, 11474. [Google Scholar] [CrossRef]
- Aki, K.; Richards, P. Quantitative Seismology; University Science Books: Sausalito, CA, USA, 2002. [Google Scholar]
- Spassiani, I.; Taroni, M.; Murru, M.; Falcone, G. Real time Gutenberg–Richter b-value estimation for an ongoing seismic sequence: An application to the 2022 marche offshore earthquake sequence (ML 5.7 central Italy). Geophys. J. Int. 2023, 234, 1326–1331. [Google Scholar] [CrossRef]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Sevilgen, V.; Lin, J. Coulomb 3.3 Graphic-rich deformation and stress-change software for earthquake, tectonic, and volcano research and teaching—User guide. Geol. Surv. Open File Rep. 2011, 1060, 63. [Google Scholar]
- Cusano, P.; Ricco, C.; Aquino, I.; Petrosino, S. A First Step towards the Definition of a Link between Ground Tilt and Earthquakes at Mt. Vesuvius (Italy). Appl. Sci. 2022, 12, 12261. [Google Scholar] [CrossRef]
- Falanga, M.; Aquino, I.; Cusano, P.; De Lauro, E.; Petrosino, S.; Ricco, C. Dynamics of the Neapolitan Volcanoes Inferred from Tiltmeter and Seismic Data Analysis: A Review. Pure Appl. Geophys. 2024, 1–24. [Google Scholar] [CrossRef]
- Palano, M.; Pezzo, G.; Serpelloni, E.; Devoti, R.; D’Agostino, N.; Gandolfi, S.; Sparacino, F.; Anderlini, L.; Poluzzi, L.; Tavasci, L.; et al. Geopositioning time series from offshore platforms in the Adriatic Sea. Sci. Data 2020, 7, 373. [Google Scholar] [CrossRef]
- De Lauro, E.; Falanga, M.; De Martino, S. New insights on the Venice high-water phenomenon through a maximum negentropy criterium. Prog. Oceanogr. 2023, 211, 102978. [Google Scholar] [CrossRef]
- Serpelloni, E.; Anderlini, L.; Belardinelli, M. Fault geometry, coseismic-slip distribution and Coulomb stress change associated with the 2009 April 6, M w 6.3, L’Aquila earthquake from inversion of GPS displacements. Geophys. J. Int. 2012, 188, 473–489. [Google Scholar] [CrossRef]
- Hennermann, K.; Berrisford, P. ERA5 Data Documentation. Copernicus Knowledge Base. 2017. Available online: https://confluence.ecmwf.int/display/CKB/ERA5%3A+data+documentation (accessed on 12 December 2024).
- De la Torre, A.; Alexander, P.; Giraldez, A. The kinetic to potential energy ratio and spectral separability from high-resolution balloon soundings near the Andes Mountains. Geophys. Res. Lett. 1999, 26, 1413–1416. [Google Scholar] [CrossRef]
- VanZandt, T. A model for gravity wave spectra observed by Doppler sounding systems. Radio Sci. 1985, 20, 1323–1330. [Google Scholar] [CrossRef]
- Yang, S.S.; Pan, C.; Das, U.; Lai, H. Analysis of synoptic scale controlling factors in the distribution of gravity wave potential energy. J. Atmos. Sol. Terr. Phys. 2015, 135, 126–135. [Google Scholar] [CrossRef]
- Yang, S.S.; Asano, T.; Hayakawa, M. Abnormal gravity wave activity in the stratosphere prior to the 2016 Kumamoto earthquakes. J. Geophys. Res. Space Phys. 2019, 124, 1410–1425. [Google Scholar] [CrossRef]
- Ciraolo, L.; Azpilicueta, F.; Brunini, C.; Meza, A.; Radicella, S.M. Calibration errors on experimental slant total electron content (TEC) determined with GPS. J. Geod. 2007, 81, 111–120. [Google Scholar] [CrossRef]
- Cesaroni, C.; Spogli, L.; Alfonsi, L.; De Franceschi, G.; Ciraolo, L.; Monico, J.F.G.; Scotto, C.; Romano, V.; Aquino, M.; Bougard, B. L-band scintillations and calibrated total electron content gradients over Brazil during the last solar maximum. J. Space Weather Space Clim. 2015, 5, A36. [Google Scholar] [CrossRef]
- Cicone, A.; Zhou, H. Numerical analysis for iterative filtering with new efficient implementations based on FFT. Numer. Math. 2021, 147, 1–28. [Google Scholar] [CrossRef]
- Crowley, G.; Rodrigues, F. Characteristics of traveling ionospheric disturbances observed by the TIDDBIT sounder. Radio Sci. 2012, 47, 1–12. [Google Scholar] [CrossRef]
- Šindelářová, T.; Burešová, D.; Chum, J. Observations of acoustic-gravity waves in the ionosphere generated by severe tropospheric weather. Stud. Geophys. Geod. 2009, 53, 403–418. [Google Scholar] [CrossRef]



| Fault Vertexes | ||
|---|---|---|
| Corners | Latitude (°) | Longitude (°) |
| LL | 44.0356 | 13.2672 |
| UR | 44.0013 | 13.3983 |
| LR | 43.9686 | 13.3428 |
| UL | 44.0683 | 13.3228 |
| SL | 44.1091 | 13.3897 |
| SR | 44.0420 | 13.4653 |
| Coulomb Grid Parameters | ||
| Grid Parameters | Value (km) | |
| Start—x | 43.6 | |
| Start—y | 12.7 | |
| Finish—x | 44.5 | |
| Finish—y | 13.9 | |
| x—increment | 2.0 | |
| y—increment | 2.0 | |
| Size Parameter | Value | |
| Plot size | 2.0 | |
| Shade/Color increment | 1.0 | |
| Exaggeration for disp. and dist. | 5,000,000.00 | |
| Cross-section default | Value (km) | |
| Start—x | 43.6 | |
| Start—y | 12.7 | |
| Finish—x | 44.5 | |
| Finish—y | 13.9 | |
| Distant—increment | 1.0 | |
| Z—depth | 20.0 | |
| Z—increment | 1.0 | |
| Map info (°) | Value | |
| min. lon | 12.6826 | |
| max. lon | 13.9550 | |
| zero. lon | 13.3235 | |
| min. lat | 43.5523 | |
| max. lat | 44.4705 | |
| zero. lat | 44.0130 | |
| EQ Characteristics | Value |
|---|---|
| Length of Fault (km) | 10 |
| (Hz) | 0.0422 |
| (m/s) | 1614.4 |
| (s) | 42.5 |
| PGA | 0.35 g |
| Site Name | Latitude (°) | Longitude (°) |
|---|---|---|
| ANCN | 43.61 | 13.53 |
| ARQT | 42.75 | 13.2 |
| ATBU | 43.48 | 12.55 |
| ATCC | 43.18 | 12.64 |
| ATFO | 43.37 | 12.57 |
| ATLO | 43.32 | 12.41 |
| ATMI | 43.33 | 12.27 |
| ATTE | 43.2 | 12.35 |
| BARO | 42.25 | 12.05 |
| BARS | 42.34 | 13.58 |
| BGDR | 43.89 | 11.89 |
| BLGN | 44.51 | 11.35 |
| BRAS | 44.12 | 11.11 |
| BRIS | 44.22 | 11.77 |
| CAFI | 43.33 | 11.97 |
| CAOC | 42.29 | 13.48 |
| CASP | 42.79 | 10.87 |
| CESI | 43 | 12.9 |
| CONI | 42.41 | 13.39 |
| CRMI | 43.8 | 10.98 |
| CSSB | 43.21 | 12.25 |
| CTEL | 42.86 | 13.19 |
| GNAL | 42.58 | 13.52 |
| GRZM | 44.26 | 11.15 |
| GUMA | 43.06 | 13.34 |
| INGP | 42.38 | 13.32 |
| LNSS | 42.6 | 13.04 |
| LPEL | 42.05 | 14.18 |
| MAON | 42.43 | 11.13 |
| MGAB | 42.91 | 12.11 |
| MLAG | 43.43 | 12.78 |
| MODE | 44.63 | 10.95 |
| MOMA | 42.8 | 12.57 |
| MONA | 42.9 | 13.34 |
| MTER | 42.51 | 13.21 |
| MTRZ | 44.31 | 11.42 |
| MTTO | 42.46 | 12.99 |
| MUR1 | 43.26 | 12.52 |
| MVAL | 43.38 | 12.41 |
| OSSC | 43.52 | 11.25 |
| PARM | 44.76 | 10.31 |
| PIET | 43.45 | 12.4 |
| PIOB | 43.61 | 12.53 |
| PREC | 42.85 | 13.04 |
| RNSP | 43.68 | 12.27 |
| ROPI | 42.33 | 13.34 |
| RSMN | 43.93 | 12.45 |
| RSTO | 42.66 | 14 |
| SACS | 42.85 | 11.91 |
| SGIP | 44.64 | 11.18 |
| SGRE | 42.34 | 13.5 |
| SIGI | 43.34 | 12.78 |
| USSI | 42.97 | 13.13 |
| VALC | 43.28 | 12.28 |
| VALC | 43.28 | 12.28 |
| VCAH | 42.8 | 11.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piersanti, M.; D’Angelo, G.; Recchiuti, D.; Lepreti, F.; Cusano, P.; De Lauro, E.; Carbone, V.; Ubertini, P.; Falanga, M. On the Ionosphere–Atmosphere–Lithosphere Coupling During the 9 November 2022 Italian Earthquake. Geosciences 2025, 15, 22. https://doi.org/10.3390/geosciences15010022
Piersanti M, D’Angelo G, Recchiuti D, Lepreti F, Cusano P, De Lauro E, Carbone V, Ubertini P, Falanga M. On the Ionosphere–Atmosphere–Lithosphere Coupling During the 9 November 2022 Italian Earthquake. Geosciences. 2025; 15(1):22. https://doi.org/10.3390/geosciences15010022
Chicago/Turabian StylePiersanti, Mirko, Giulia D’Angelo, Dario Recchiuti, Fabio Lepreti, Paola Cusano, Enza De Lauro, Vincenzo Carbone, Pietro Ubertini, and Mariarosaria Falanga. 2025. "On the Ionosphere–Atmosphere–Lithosphere Coupling During the 9 November 2022 Italian Earthquake" Geosciences 15, no. 1: 22. https://doi.org/10.3390/geosciences15010022
APA StylePiersanti, M., D’Angelo, G., Recchiuti, D., Lepreti, F., Cusano, P., De Lauro, E., Carbone, V., Ubertini, P., & Falanga, M. (2025). On the Ionosphere–Atmosphere–Lithosphere Coupling During the 9 November 2022 Italian Earthquake. Geosciences, 15(1), 22. https://doi.org/10.3390/geosciences15010022









