Neural Network-Based Climate Prediction for the 21st Century Using the Finnish Multi-Millennial Tree-Ring Chronology
Abstract
1. Introduction
2. Materials and Methods
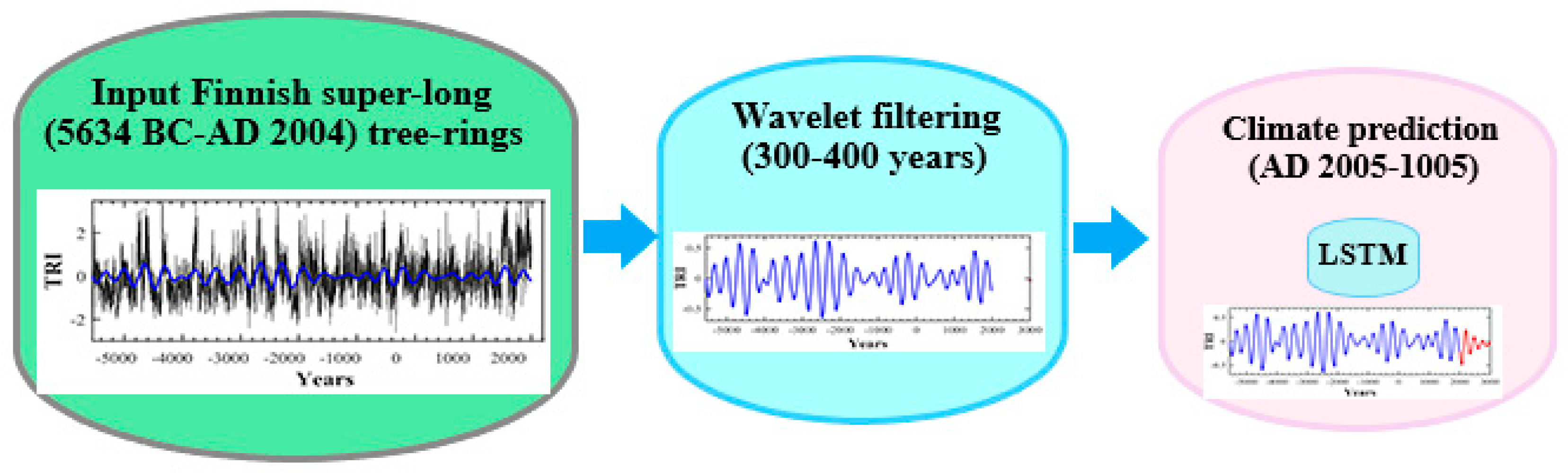
2.1. Data Sets
2.2. Statistical and Wavelet Analysis
2.3. Development and Training of the LSTM Network
2.4. Evaluation of the LSTM Performance
3. Results
3.1. Temperature Trends in Northern Fennoscandia during the Instrumental Period
3.2. LSTM Network Development and Time Series Prediction
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Summary for Policymakers. In Climate Change 2023: Synthesis Report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Lee, H., Romero, J., Eds.; IPCC: Geneva, Switzerland, 2023; pp. 1–34. [Google Scholar] [CrossRef]
- Scafetta, N.; West, B.J. Phenomenological solar contribution to the 1900–2000 global surface warming. Geophys. Res. Lett. 2006, 33, L05708. [Google Scholar] [CrossRef]
- Scafetta, N. Empirical assessment of the role of the Sun in climate change using balanced multi-proxy solar records. Geosci. Front. 2023, 14, 101650. [Google Scholar] [CrossRef]
- Soon, W.; Connoly, R.; Connolly, M. Re-evaluating the role of solar variability on Northern Hemisphere temperature trends since the 19th century. Earth Sci. Rev. 2015, 150, 409–452. [Google Scholar] [CrossRef]
- El-Borie, M.A.; Thabet, A.A.; El-Mallah, E.S.; Abd El-Zaher, M.; Bishara, A.A. The response of the atmosphere to solar variations. Indian J. Phys. 2020, 94, 737–752. [Google Scholar] [CrossRef]
- IPCC. Technical Summary. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007; pp. 56–58. Available online: https://www.ipcc.ch/site/assets/uploads/2018/02/ar4-wg1-ts-1.pdf (accessed on 24 June 2024).
- Helama, S.; Fauria, M.M.; Mielikäinen, K.; Timonen, M.; Eronen, M. Sub-Milankovitch solar forcing of past climates: Mid and late Holocene perspectives. GSA Bull. 2010, 122, 1981–1988. [Google Scholar] [CrossRef]
- Kasatkina, E.A.; Shumilov, O.I.; Timonen, M.; Potorochin, E.O. Millennial-scale solar variability in tree rings of Northern Fennoscandia at the end of the Holocene. Tree-Ring Res. 2023, 79, 1–11. [Google Scholar] [CrossRef]
- Hu, F.S.; Kaufman, D.; Yoneji, S.; Nelson, D.; Shemesh, A.; Huang, Y.; Tian, J.; Bond, G.; Clegg, B.; Brown, T. Cyclic variation and solar forcing of Holocene climate in the Alaskan Subarctic. Science 2003, 301, 1890–1893. [Google Scholar] [CrossRef]
- Kern, A.K.; Harzhauser, M.; Piller, W.E.; Mandic, O.; Soliman, A. Strong evidence for the influence of solar cycles on a Late Miocene lake system revealed by biotic and abiotic proxies. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2012, 329–330, 124–136. [Google Scholar] [CrossRef]
- Steinhilber, F.; Abreu, J.A.; Beer, J.; Brunner, I.; Christl, M.; Fischer, A.; Heikkilla, U.; Kubik, P.W.; Mann, M.; McCracken, K.G.; et al. 9,400 years of cosmic radiation and solar activity from ice cores and tree rings. Proc. Natl. Acad. Sci. USA 2012, 109, 5967–5971. [Google Scholar] [CrossRef]
- Soon, W.; Velasco Herrera, V.M.; Selvaraj, K.; Traversi, R.; Usoskin, I.; Chen, C.-T.A.; Lou, J.-Y.; Kao, S.-J.; Carter, R.M.; Pipin, V. A review of Holocene solar-linked climatic variation on centennial to millennial timescales: Physical processes, interpretative frameworks an a new multiple cross-wavelet transform algorithm. Earth-Sci. Rev. 2014, 134, 1–15. [Google Scholar] [CrossRef]
- Sun, W.; Liu, J.; Wang, B.; Chen, D.; Wan, L.; Wang, J. Holocene multi-centennial variations of the Asian summer monsoon triggered by solar activity. Geophys. Res. Lett. 2022, 49, e2022GL098625. [Google Scholar] [CrossRef]
- Bond, G.; Kromer, B.; Beer, J.; Muscheler, R.; Evans, M.N.; Showers, W.; Hoffmann, S.; Lotti-Bond, R.; Hajdas, I.; Bonani, G. Persistent solar influence on North Atlantic climate during the Holocene. Science 2001, 294, 2130–2136. [Google Scholar] [CrossRef]
- Zharkova, V. Modern Grand Solar Minimum will lead to terrestrial cooling. Temperature 2020, 7, 217–222. [Google Scholar] [CrossRef]
- Lean, J.R.; Beer, J.; Bradley, R. Reconstruction of solar irradiance since 1610, Implications for climate change. Geophys. Res. Lett. 1995, 22, 3195–3198. [Google Scholar] [CrossRef]
- Shindell, D.T.; Schmidt, G.A.; Mann, M.E.; Rind, D.; Waple, A. Solar forcing of regional climate change during the Maunder minimum. Science 2001, 294, 2149–2152. [Google Scholar] [CrossRef] [PubMed]
- Lockwood, M.; Harrison, R.G.; Woolings, T.; Solanki, S.K. Are cold winters in Europe associated with low solar activity? Environ. Res. Lett. 2010, 5, 024001. [Google Scholar] [CrossRef]
- Haigh, J.D. The impact of solar variability on climate. Science 1996, 272, 981–984. [Google Scholar] [CrossRef] [PubMed]
- Marsh, N.D.; Svensmark, H. Low cloud properties influenced by cosmic rays. Phys. Rev. Lett. 2000, 85, 5004–5008. [Google Scholar] [CrossRef]
- Palle, E.; Butler, J. Sunshine records from Ireland, cloud factors and possible links to solar activity and cosmic rays. Int. J. Climatol. 2001, 21, 709–729. [Google Scholar] [CrossRef]
- Tinsley, B.A.; Deen, G.W. Apparent tropospheric response to MeV-GeV particle flux variations: A connection via electrofreezing of supercooled water in high-level clouds? J. Geophys. Res. 1991, 96, 22283–22296. [Google Scholar] [CrossRef]
- Kasatkina, E.A.; Shumilov, O.I.; Lukina, N.V.; Krapiec, M.; Jacoby, G. Stardust component in tree rings. Dendrochronologia 2007, 24, 131–135. [Google Scholar] [CrossRef]
- Ermakov, V.I.; Okhlopkov, V.P.; Stozhkov, Y.I. Influence of cosmic rays and cosmic dust on the atmosphere and Earth’s climate. Bull. Russ. Acad. Sci. Phys. 2009, 73, 416–418. [Google Scholar] [CrossRef]
- Barnett, J. Security and climate change. Glob. Environ. Chang. 2003, 13, 7–17. [Google Scholar] [CrossRef]
- Vaidya, H.N.; Breininger, R.D.; Madrid, M.; Lazarus, S.; Kachouie, N.N. Generalized additive models for predicting sea level rise in coastal Florida. Geosciences 2023, 13, 310. [Google Scholar] [CrossRef]
- Sharapov, D. Northern Sea route and climate change. E3S Web Conf. 2023, 460, 09019. [Google Scholar] [CrossRef]
- Lee, T.; Kim, H.J. Barriers of voyaging on the Northern Sea Route: A perspective from shipping companies. Mar. Policy 2015, 62, 264–270. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, X.; Zha, Y.; Wang, K.; Chen, C. Changing Arctic Northern Sea Route and Transpolar Sea Route: A prediction of route changes and navigation potential before Mid-21st century. J. Mar. Sci. Eng. 2023, 11, 2340. [Google Scholar] [CrossRef]
- NOAA National Centers for Environmental Information, Monthly Global Snow and Ice Report for April 2024. Available online: https://www.ncei.noaa.gov/access/monitoring/monthly-report/global-snow/202404 (accessed on 10 May 2024).
- Moe, A. A new Russian policy for the Northern sea route? State interests, key stakeholders and economic opportunities in changing times. Polar J. 2020, 10, 209–227. [Google Scholar] [CrossRef]
- Helama, S.; Mielikäinen, M.; Timonen, M.; Eronen, M. Finnish supra-long tree-ring chronology extended to 5634 BC. Nor. J. Geogr. 2008, 62, 271–277. [Google Scholar] [CrossRef]
- Guiot, J.; Nicault, A.; Rathgeber, C.; Edouard, J.L.; Guibal, F.; Pichard, G.; Till, C. Last-millennium summer-temperature variations in western Europe based on proxy data. Holocene 2005, 15, 489–500. [Google Scholar] [CrossRef]
- Kalugin, I.; Daryin, A.; Smolyaninova, L.; Andreev, A.; Diekmann, B.; Khlystov, O. 800-yr-long records of annual air temperature and precipitation over southern Siberia inferred from Teletskoye Lake sediments. Quat. Res. 2007, 67, 400–410. [Google Scholar] [CrossRef]
- Ashrafi, K.; Shafiepour, M.; Ghasemi, M.; Najar Araabi, B. Prediction of climate change induced temperature rise in regional scale using neural network. Int. J. Environ. Res. 2012, 6, 677–688. [Google Scholar]
- Chen, L.; Han, B.; Wang, X.; Zhao, J.; Yang, W.; Yang, Z. Machine learning methods in weather and climate applications: A survey. Appl. Sci. 2023, 13, 12019. [Google Scholar] [CrossRef]
- Hamdan, A.; Al-Salaymeh, A.; AlHamad, I.M.; Ikemba, S.; Ewin, D.R.E. Predicting future global temperature and greenhouse gas emissions via LSTM model. Sustain. Energy Res. 2023, 10, 21. [Google Scholar] [CrossRef]
- Khaleghi, M.R. Application of dendroclimatology in evaluation of climatic changes. J. For. Sci. 2018, 64, 139–147. [Google Scholar] [CrossRef]
- Molina, A.A.R.; Bezak, N.; Tootle, G.; Wang, C.; Gong, J. Machine-learning-based reconstructions: A study on Slovenia’s Sava River Basin. Hydrology 2023, 10, 207. [Google Scholar] [CrossRef]
- Helama, S.; Makarenko, N.G.; Karimova, L.M.; Kruglun, O.A.; Timonen, M.; Holopainen, J.; Meriläinen, J.; Eronen, M. Dendroclimatic transfer functions revisited: Little Ice Age and Medieval Warm Period summer temperatures reconstructed using artificial neural networks and linear algorithms. Ann. Geophys. 2009, 27, 1097–1111. [Google Scholar] [CrossRef][Green Version]
- Jevšenak, J.; Levanič, T. Should artificial neural networks replace linear models in tree ring based climate reconstructions? Dendrochronologia 2016, 40, 102–109. [Google Scholar] [CrossRef]
- Jevšenak, J.; Džeroski, S.; Levanič, T. Predicting the vessel lumen area tree-ring parameter of with linear and nonlinear machine learning algorithms. Geochronometria 2018, 45, 211–222. [Google Scholar] [CrossRef]
- Fang, M.; Li, X. An artificial neural networks-based tree ring width proxy system model for paleoclimate data assimilation. J. Adv. Model. Earth Syst. 2019, 11, 892–904. [Google Scholar] [CrossRef]
- Salehnia, N.; Ahn, J. Modelling and reconstructing tree ring growth index with climate variables through artificial intelligence and statistical methods. Ecol. Indic. 2022, 134, 108496. [Google Scholar] [CrossRef]
- Scafetta, N. Impacts and risks of “realistic” global warming projections for the 21st century. Geosci. Front. 2024, 15, 101774. [Google Scholar] [CrossRef]
- Helama, S.; Timonen, M.; Holopainen, J.; Ogurtsov, M.G.; Mielikäinen, K.; Eronen, M.; Lindholm, M.; Meriläinen, J. Summer temperature variations in Lapland during the Medieval Warm Period and the Little Ice Age relative to natural instability of thermohaline circulation on multi-decadal and multi-centennial scales. J. Quatern. Sci. 2009, 24, 450–456. [Google Scholar] [CrossRef]
- Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendrochronology and hydrometeorology. J. Appl. Meteorol. Clim. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- GISTEMP Team. GISS Surface Temperature Analysis (GISTEMP), Version 4; NASA Goddard Institute for Space Studies: New York, NY, USA, 2024. Available online: https://data.giss.nasa.gov/gistemp (accessed on 9 May 2024).
- Lenssen, N.; Schmidt, G.; Hansen, J.; Menne, M.; Persin, A.; Rudy, R.; Zyss, D. Improvements in the GISTEMP uncertainly model. J. Geophys. Res. Atmos. 2019, 124, 6307–6326. [Google Scholar] [CrossRef]
- Granato, C.E. Kendall-Theil Robust Line (KTRLine version 1.0)—A visual basic program for calculating and graphing robust nonparametric estimates of linear regression coefficients between two continuous variables. In Techniques and Methods of the U.S. Geological Survey, Book 4; U.S. Geological Survey: Reston, VA, USA, 2006; Chapter A7; 31p. [Google Scholar] [CrossRef]
- Salas, J.D. Analysis and modelling of hydrologic time series. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993; Chapter 19; pp. 19.1–19.72. [Google Scholar]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Neural Networks and Deep Learning, 2nd ed.; Springer Nature Switzerland AG: Cham, Switzerland, 2023. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Shumilov, O.I.; Kasatkina, E.A.; Mielikäinen, K.; Timonen, M.; Kanatjev, A.G. Palaeovolcanos, solar activity and pine tree-rings from the Kola Peninsula (northwestern Russia) over the last 560 years. Int. J. Environ. Res. 2011, 5, 855–864. [Google Scholar]
- Abdussamatov, H.I. Grand minimum of the solar irradiance leads to the Little ice age. J. Geol. Geosci. 2013, 2, 113. [Google Scholar] [CrossRef]
- Morner, N.-A. The approaching new Grand solar minimum and Little ice age climatic conditions. Nat. Sci. 2015, 7, 510–518. [Google Scholar] [CrossRef]
- Harder, J.W.; Fontenla, J.M.; Pilewskie, P.; Richard, E.C.; Woods, T.N. Trends in solar spectral irradiance variability in the visible and infrared. Geophys. Res. Lett. 2009, 36, L07801. [Google Scholar] [CrossRef]
- Haigh, J.D.; Winning, A.R.; Toumi, R.; Harder, J.W. An influence of solar spectral variations on radiative forcing of climate. Nature 2010, 467, 696–699. [Google Scholar] [CrossRef] [PubMed]
- Kasatkina, E.A.; Shumilov, O.I.; Timonen, M. Solar activity imprints in tree-ring data from northwestern Russia. J. Atmos. Sol. Terr. Phys. 2019, 193, 105075. [Google Scholar] [CrossRef]
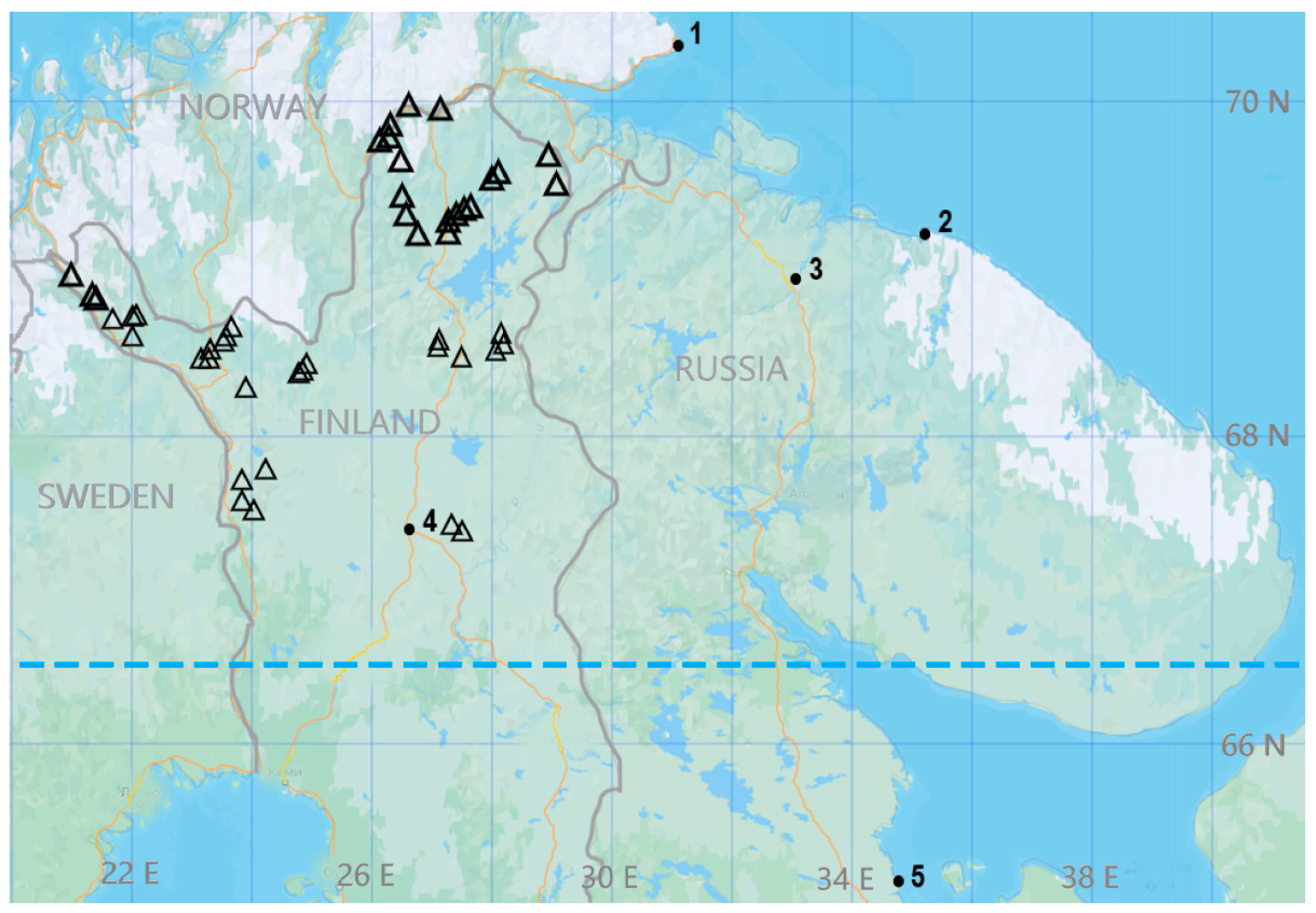



| Station (Coordinates) | Period (Years) | Rate (°C/Decade) 1 |
|---|---|---|
| Vardo (70.4° N, 31.1° E) | 1870–2023 | 0.12 [0.085 0.158] 2 |
| Teriberka (69.2° N, 35.1° E) | 1893–2023 | 0.09 [0.034 0.15] |
| Murmansk (69° N, 33.1° E | 1919–2023 | 0.1 [0.027 0.176] |
| Sodankyla (67.4° N, 26.6° E) | 1908–2023 | 0.15 [0.088 0.202] |
| Kem (65° N, 34.8° E) | 1891–2023 | 0.13 [0.077 0.175] |
| LSTM Parameters | |
|---|---|
| Number of LSTM layers (number of neurons) | 1 (128) |
| Number of fully connected layers | 1 |
| Number of dropout layers (probability) | 1 (0.5) |
| Types of activation function | tanh (state); σ (gate) |
| Optimizer | Adam |
| Learning rate | 0.005 |
| Loss function | mean square error (MSE) |
| Number of epochs | 700 |
| Performance validation | |
| 0.99 | |
| MAE | 0.008 |
| RMSE | 0.0113 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasatkina, E.A.; Shumilov, O.I.; Timonen, M. Neural Network-Based Climate Prediction for the 21st Century Using the Finnish Multi-Millennial Tree-Ring Chronology. Geosciences 2024, 14, 212. https://doi.org/10.3390/geosciences14080212
Kasatkina EA, Shumilov OI, Timonen M. Neural Network-Based Climate Prediction for the 21st Century Using the Finnish Multi-Millennial Tree-Ring Chronology. Geosciences. 2024; 14(8):212. https://doi.org/10.3390/geosciences14080212
Chicago/Turabian StyleKasatkina, Elena A., Oleg I. Shumilov, and Mauri Timonen. 2024. "Neural Network-Based Climate Prediction for the 21st Century Using the Finnish Multi-Millennial Tree-Ring Chronology" Geosciences 14, no. 8: 212. https://doi.org/10.3390/geosciences14080212
APA StyleKasatkina, E. A., Shumilov, O. I., & Timonen, M. (2024). Neural Network-Based Climate Prediction for the 21st Century Using the Finnish Multi-Millennial Tree-Ring Chronology. Geosciences, 14(8), 212. https://doi.org/10.3390/geosciences14080212










