Nonlinear 3D Finite Element Analysis of a Coupled Soil–Structure System by a Deterministic Approach
Abstract
1. Introduction
2. Seismicity of the Area
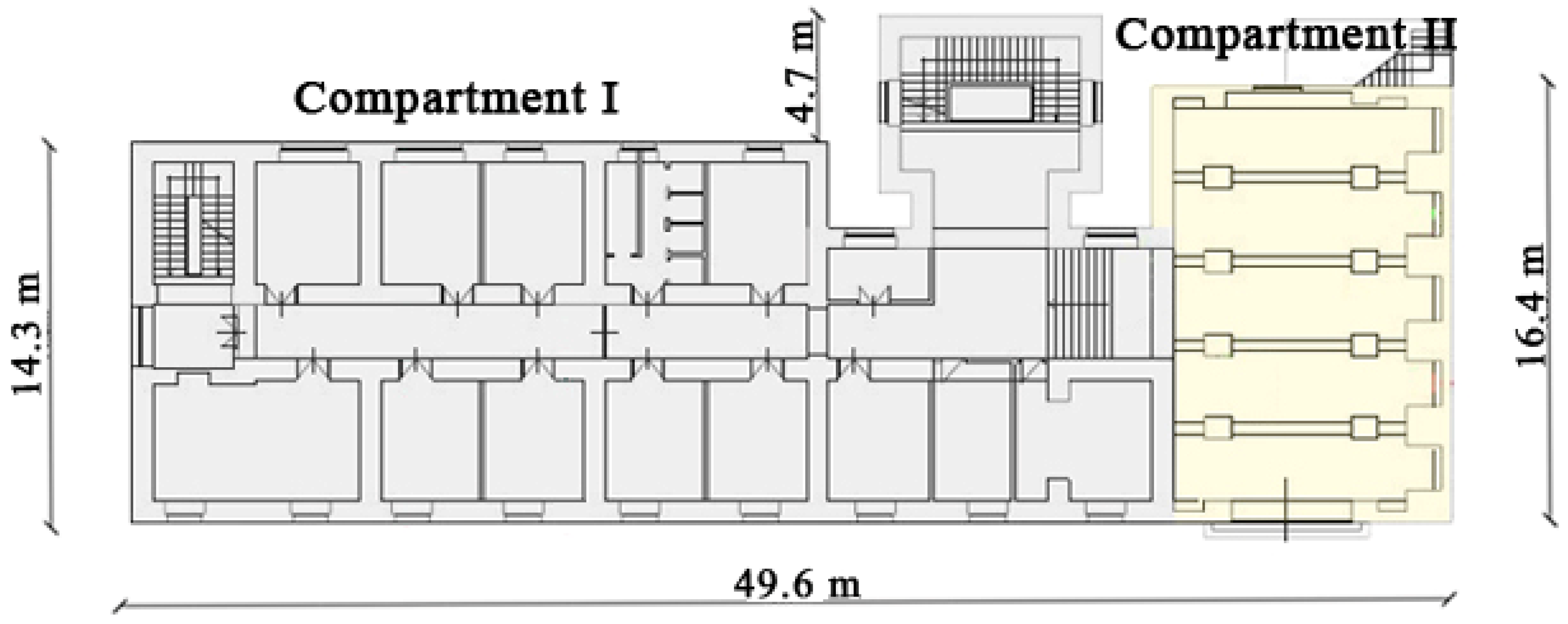
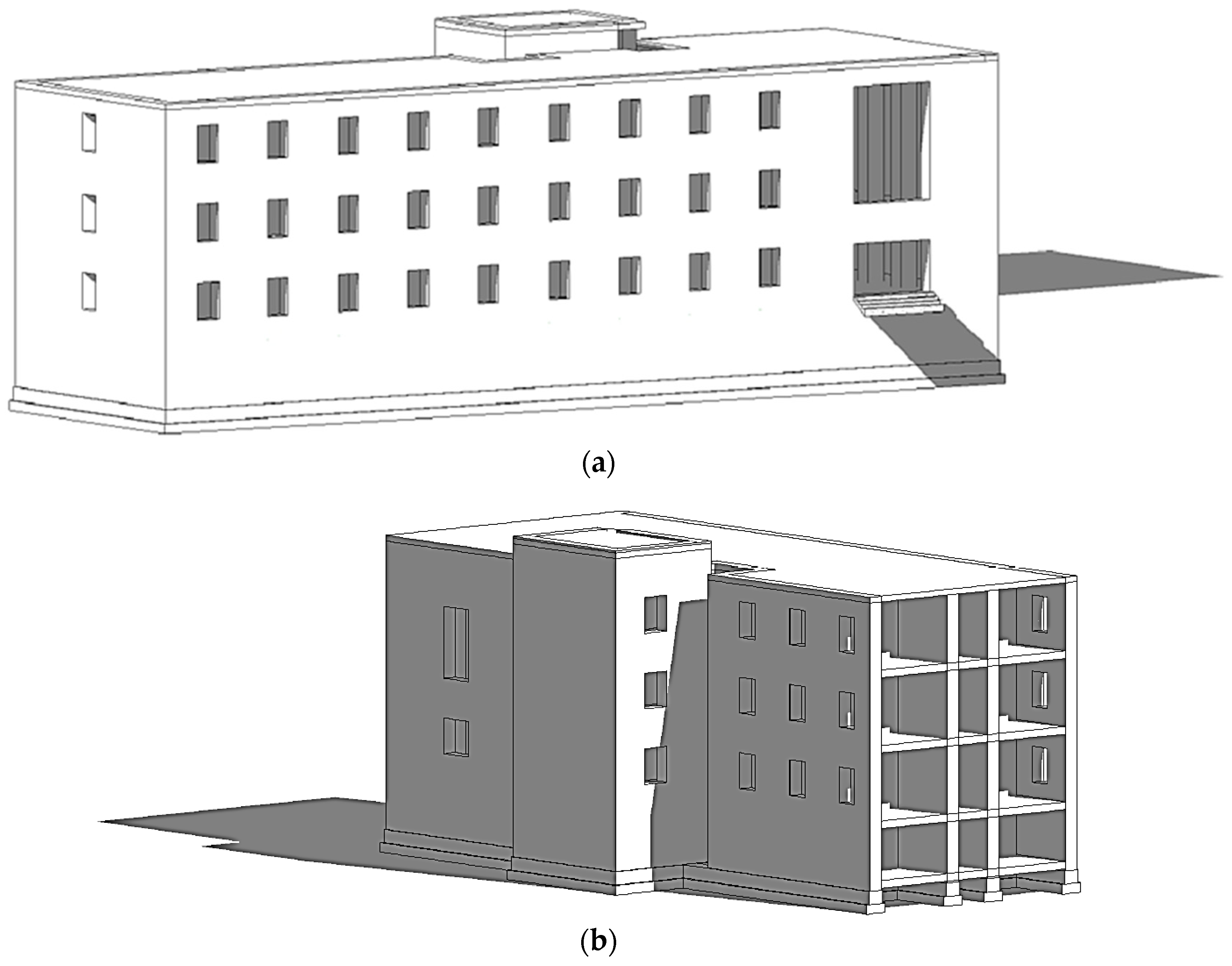
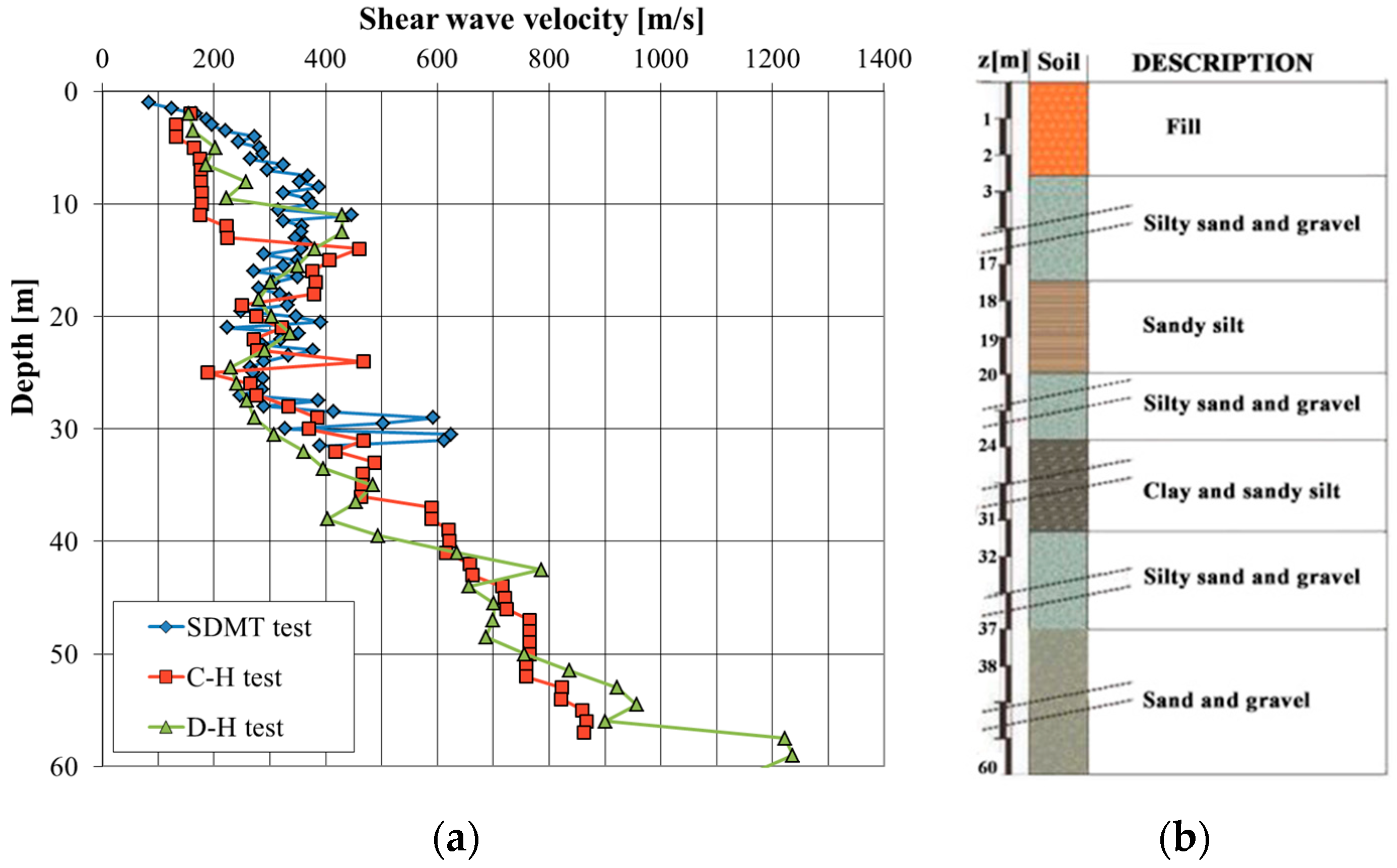
3. Description of the Building and Geotechnical Soil Properties
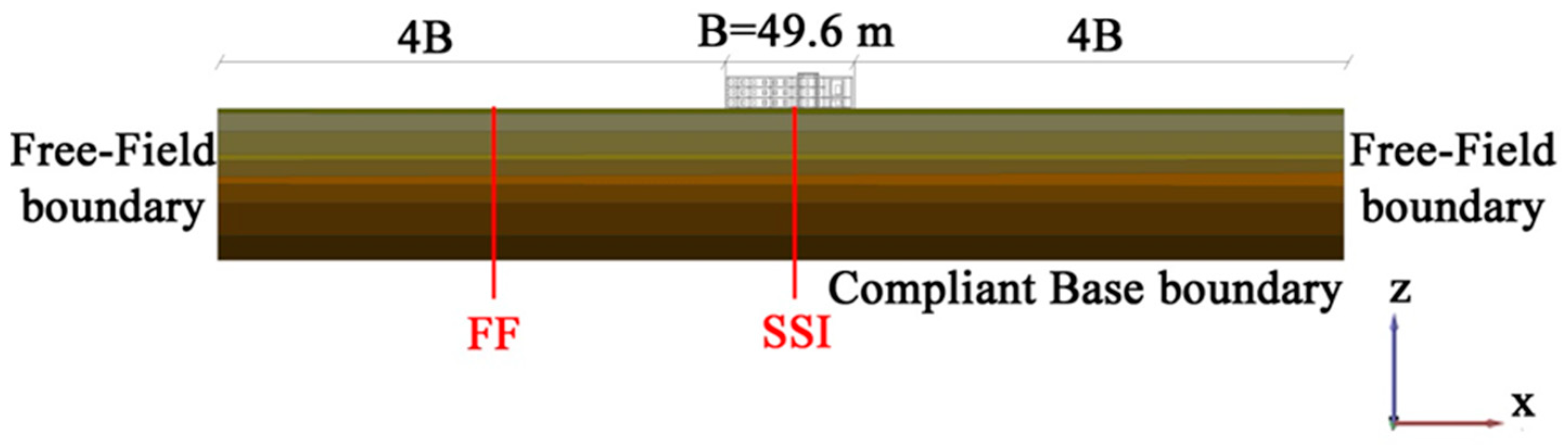
4. Coupled Soil–Structure Model
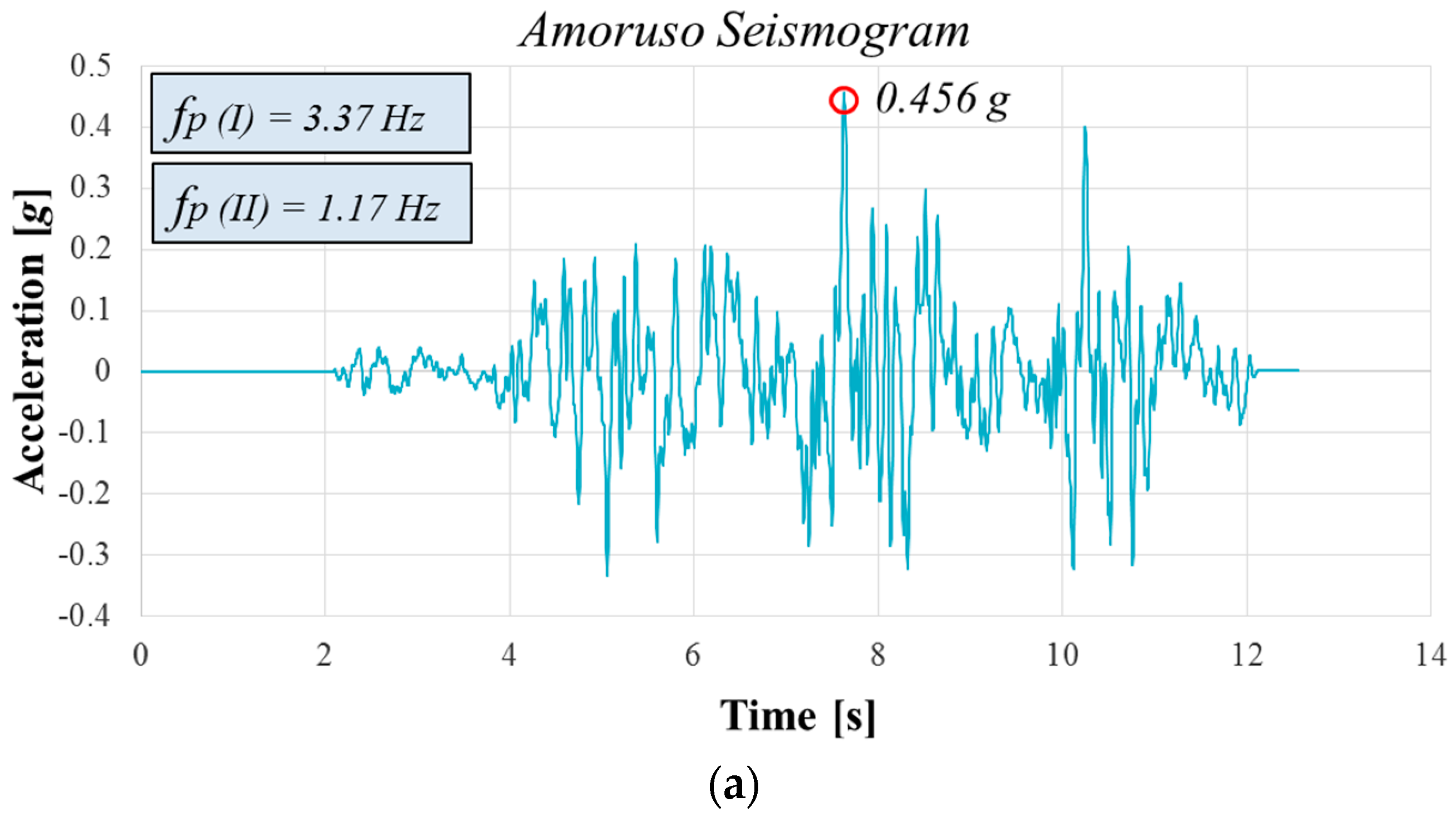
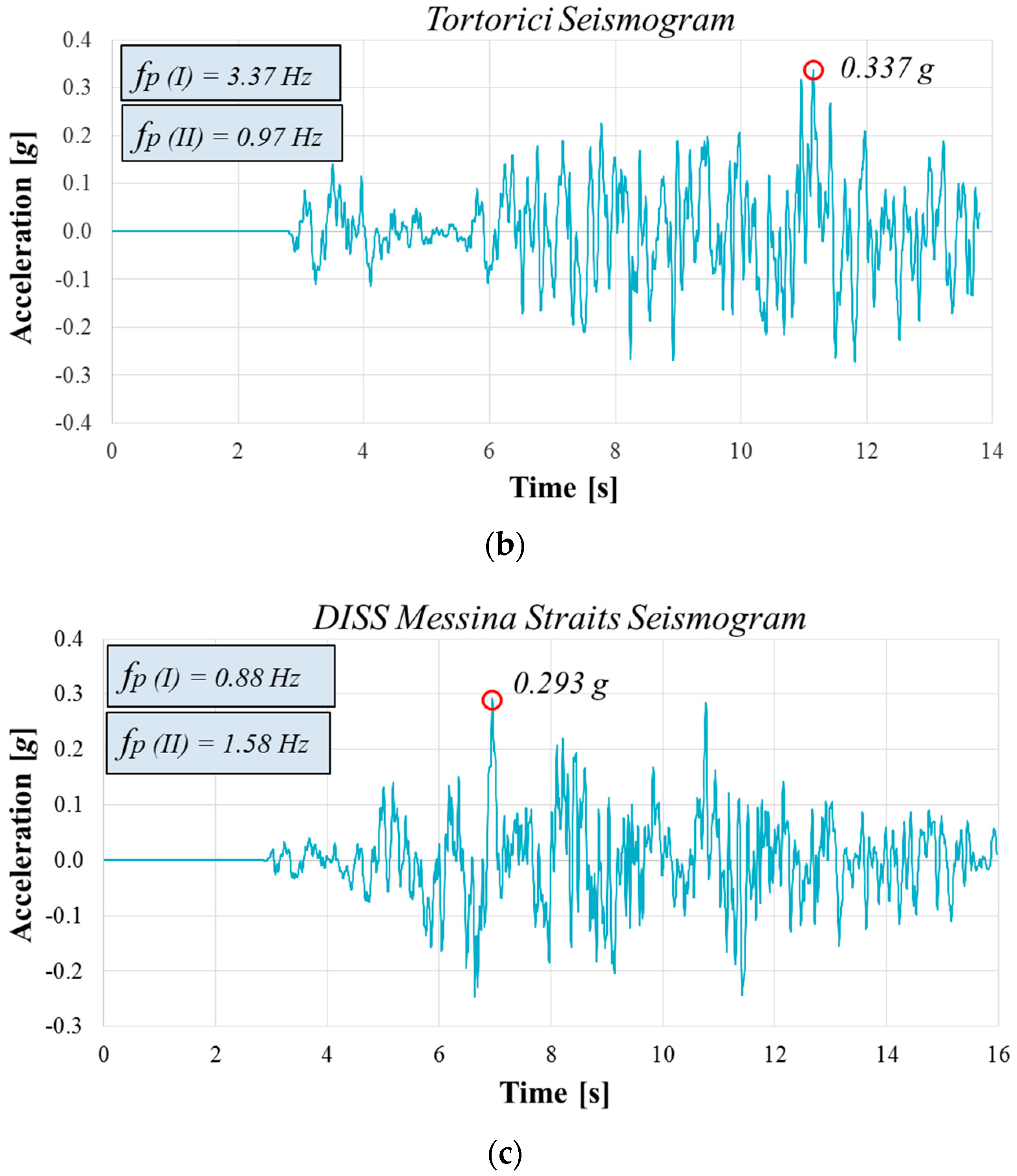
5. Selected Seismic Input
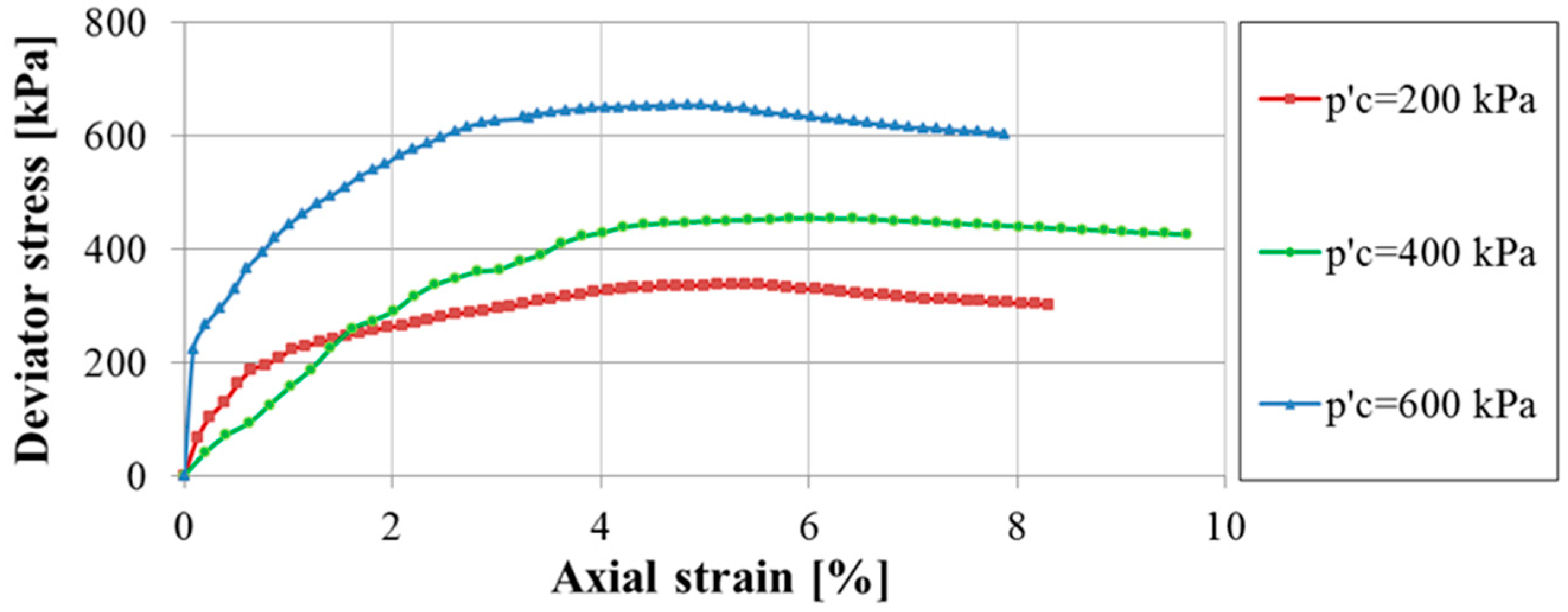
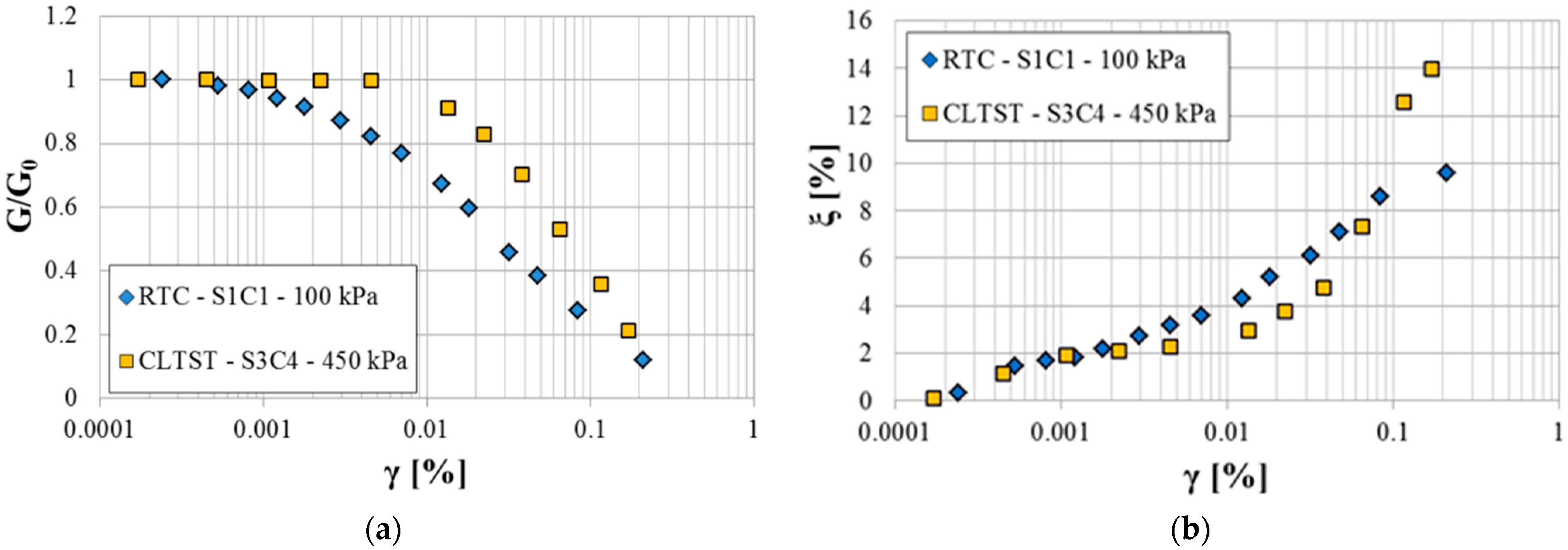
6. Calibration of the HS Small Model
7. Analysis of the Results
8. Discussion
- The presence of the structure causes higher acceleration values at the foundation level. For the period of the studied structure, spectral accelerations obtained for the SSI alignment are greater than those found for the FF condition employing as seismic inputs the Amoruso and Tortorici seismograms. Moreover, in this specific case, the Italian Regulation spectrum [4] appears more conservative in comparison with the spectral acceleration obtained using the Tortorici seismogram and ensures safe operation.
- Results in term of amplification functions, A(f), show that for the Amoruso seismogram, A(f) peaks are close to the first predominant frequency of the input motion. Moreover, the SSI has a positive effect because the second resulting frequency for the FF condition is closer to the frequency of the structure. Considering the Tortorici seismogram, the second predominant frequency of the input motion is near the first resulting frequencies, and A(f) peaks are far from the frequency of the structure. The results obtained using the DISS Messina Straits seismogram show that the first resulting frequency for the SSI condition is close to the second fundamental input frequency, and the A(f) peaks are near the frequency of the structure.
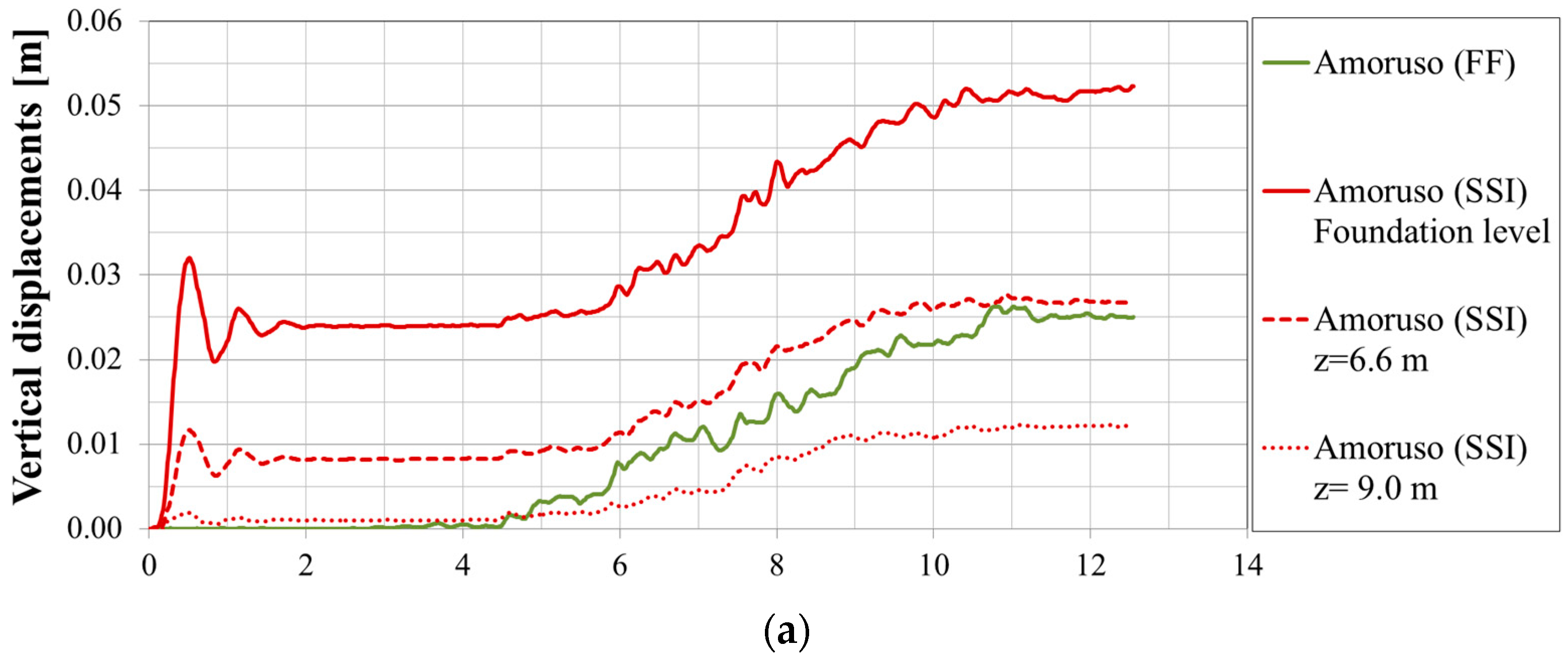
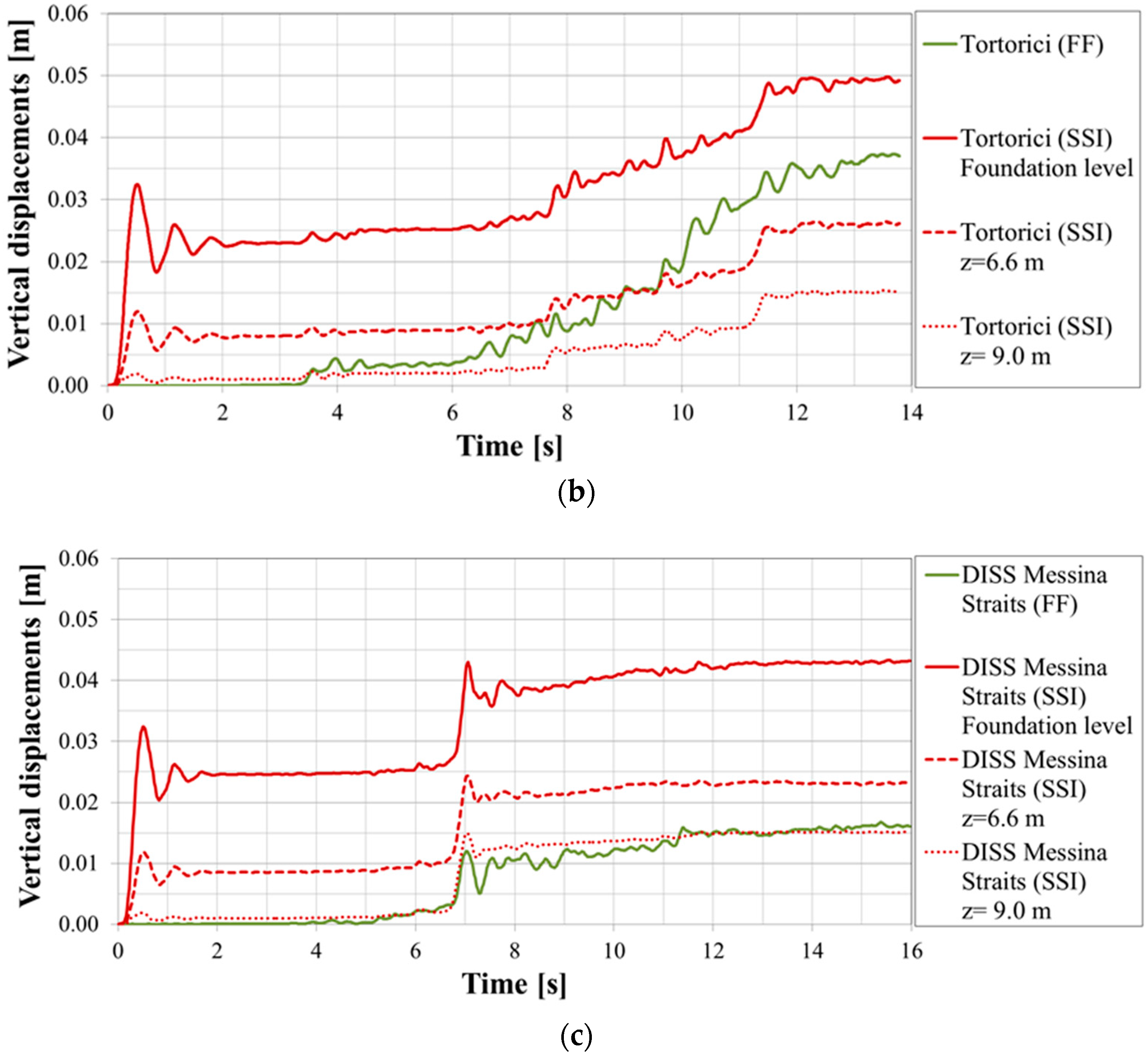
- The time histories of the settlement show that instantaneous settlements occur at the beginning of the dynamic time at the foundation level decreasing with depth along the SSI alignment, while they are zero in the FF condition. Vertical settlements reach the maximum value of about 0.05 m at the end of the dynamic time.
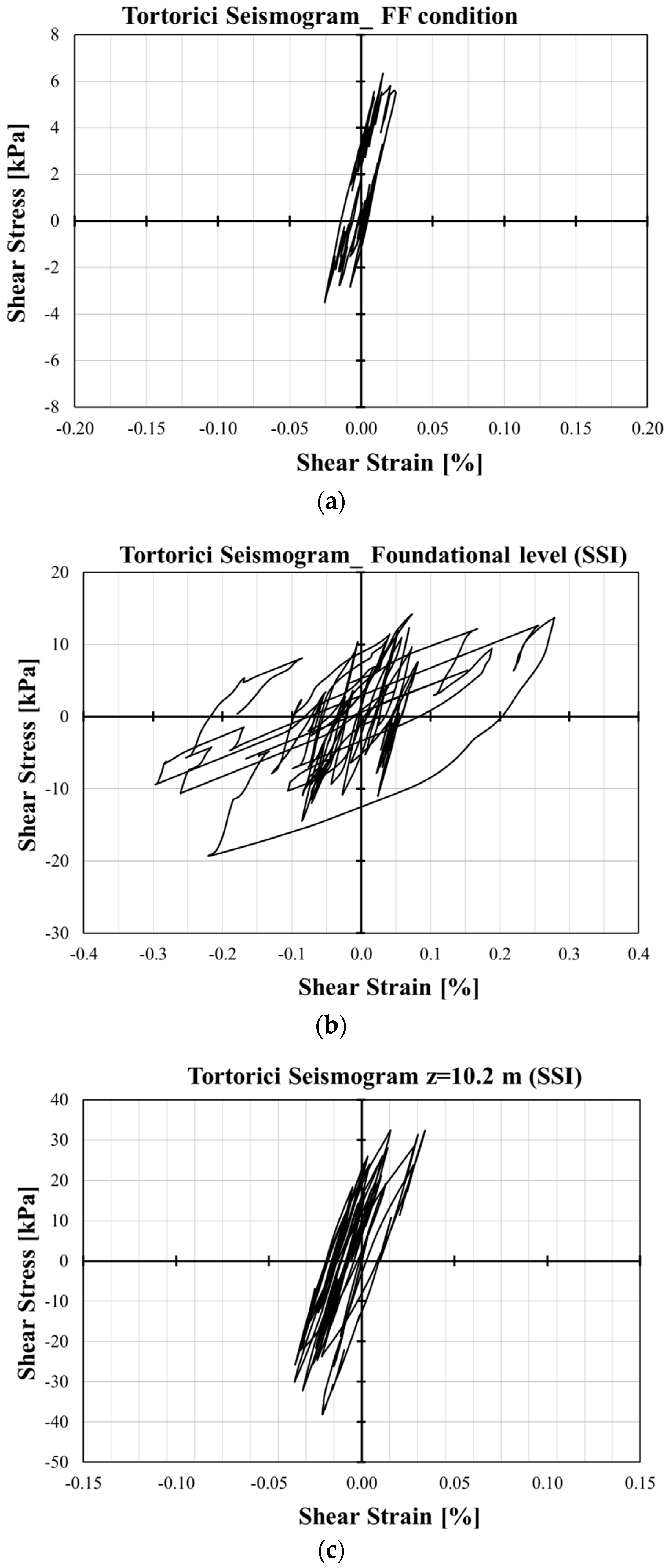
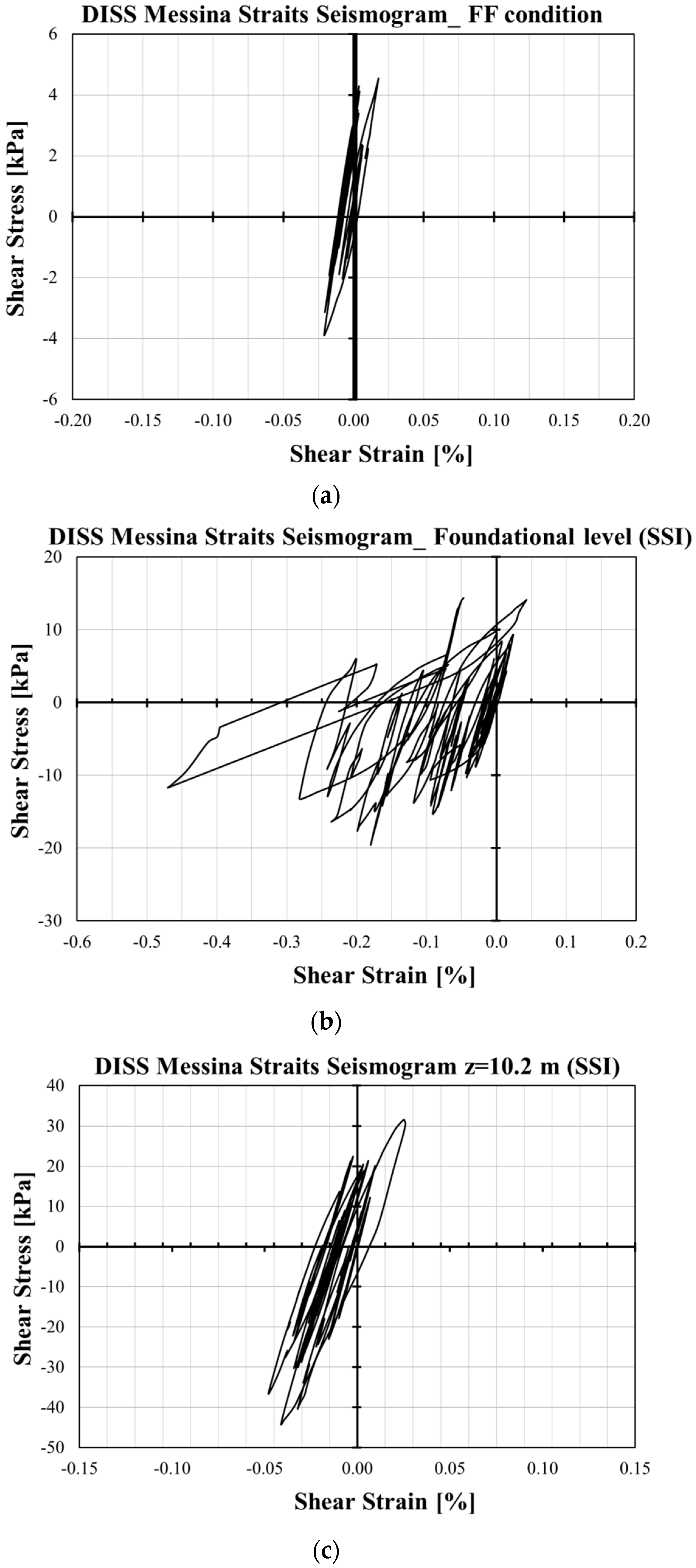
- Shear strain vs. shear stress curves show that shear stresses increase with depth, while the maximum shear strain occurs at the foundation level, exhibiting a highly nonlinear response in comparison with the FF condition. The nonlinear behavior decreases with depth along the SSI alignment.
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pitilakis, D.; Petridis, C. Fragility curves for existing reinforced concrete buildings, including soil–structure interaction and site amplification effects. Eng. Struct. 2022, 269, 114733. [Google Scholar] [CrossRef]
- Vratsikidis, A.; Pitilakis, D.; Anastasiadis, A.; Kapouniaris, A. Evidence of soil-structure interaction from modular full-scale field experimental tests. Bull. Earthq. Eng. 2022, 20, 3167–3194. [Google Scholar] [CrossRef]
- Amendola, C.; Pitilakis, D. Vulnerability assessment of historical cities including SSI and site-effects. In Proceedings of the 3rd International Issmge TC301 Symposium, Naples, Italy, 22–24 June 2022; pp. 836–846. [Google Scholar]
- NTC [2018] D. M. 17/01/2018. New Technical Standards for Buildings. Official Journal of the Italian Republic, 2018. Available online: https://www.gazzettaufficiale.it/eli/gu/2018/02/20/42/so/8/sg/pdf (accessed on 1 December 2023).
- Cavallaro, A.; Fiamingo, A.; Grasso, S.; Massimino, M.R.; Sammito, M.S.V. Local site amplification maps for the volcanic area of Trecastagni, south-eastern Sicily (Italy). Bull. Earthq. Eng. 2024, 22, 1635–1676. [Google Scholar] [CrossRef]
- Cavallaro, A.; Castelli, F.; Ferraro, A.; Grasso, S.; Lentini, V. Site response analysis for the seismic improvement of a historical and monumental building: The case of Augusta Hangar. Bull. Eng. Geol. Environ. 2018, 77, 1217–1248. [Google Scholar] [CrossRef]
- Fiamingo, A.; Bosco, M.; Massimino, M.R. The Role of Soil in Structure Response of a Building Damaged by the 26 December 2018 Earthquake in Italy. J. Rock Mech. Geotech. Eng. 2022, 15, 937–953. [Google Scholar] [CrossRef]
- Massimino, M.R.; Abate, G.; Corsico, S.; Grasso, S.; Motta, E. Dynamic behaviour of coupled soil structure systems by means of FEM analysis for the seismic risk mitigation of INGV building in Catania (Italy). Ann. Geophys. 2018, 61, SE216. [Google Scholar] [CrossRef]
- Oz, I.; Senel, S.M.; Palanci, M.; Kalkan, A. Effect of Soil-Structure Interaction on the Seismic Response of Existing Low and Mid-Rise RC Buildings. Appl. Sci. 2020, 10, 8357. [Google Scholar] [CrossRef]
- Ferraro, A.; Grasso, S.; Massimino, M.R. Site effects evaluation in Catania (Italy) by means of 1-D numerical analysis. Ann. Geophys. 2018, 61, SE224. [Google Scholar] [CrossRef]
- Seylabi, E.E.; Jeong, C.; Dashti, S.; Hushmand, A.; Taciroglu, E. Seismic response of buried reservoir structures: A comparison of numerical simulations with centrifuge experiments. Soil Dyn. Earthq. Eng. 2018, 109, 89–101. [Google Scholar] [CrossRef]
- Schanz, T.; Vermeer, P.; Bonier, P. Formulation and verification of the Hardening Soil model. In Proceedings of the 1st International PLAXIS Symposium on Beyond 2000 in Computational Geotechnics, Rotterdam, The Netherlands, 18–20 March 1999. [Google Scholar]
- Vakili, K.N.; Barciago, T.; Lavason, A.A.; Schanz, J. A practical approach to constitutive models for the analysis of geotechnical problems. In Proceedings of the 3rd International Conference on Computational Geomechanics (ComGeo III), Krakow, Poland, 21–23 August 2013; Volume 1. [Google Scholar]
- Surarak, C.; Likitlersuang, S.; Wanatowski, D.; Balasubramaniam, A.; Oh, E.; Guan, H. Stiffness and strength parameters for hardening soil model of soft and stiff Bangkok clays. Soils Found. 2012, 52, 682–697. [Google Scholar] [CrossRef]
- Benz, T. Small-Strain Stiffness of Soils and Its Numerical Consequences. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2006. [Google Scholar]
- Benz, T.; Vermeer, P.A.; Schwab, R. A small-strain overlay model. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 25–44. [Google Scholar] [CrossRef]
- Grasso, S.; Massimino, M.R.; Sammito, M.S.V. New Stress Reduction Factor for Evaluating Soil Liquefaction in the Coastal Area of Catania (Italy). Geosciences 2021, 11, 12. [Google Scholar] [CrossRef]
- Pino, P.; D’Amico, S.; Orecchio, B.; Presti, D.; Scolaro, S.; Torre, A.; Neri, G. Integration of geological and geophysical data for re-evaluation of local seismic hazard and geological structure: The case study of Rometta, Sicily (Italy). Ann. Geophys. 2018, 61, SE227. [Google Scholar] [CrossRef]
- Tarquini, S.; Isola, I.; Favalli, M.; Battistini, A. TINITALY, a Digital Elevation Model of Italy with a 10 Meters Cell Size (Version 1.0) [Data Set]. Istituto Nazionale di Geofisica e Vulcanologia (INGV), 2007. Available online: https://doi.org/10.13127/TINITALY/1.0 (accessed on 4 December 2023).
- Petruzzelli, F.; Iervolino, I. NODE: A large-scale seismic risk prioritization tool for Italy based on nominal structural performance. Bull. Earthq. Eng. 2021, 19, 2763–2796. [Google Scholar] [CrossRef]
- Lanzo, G.; Silvestri, F. Risposta Sismica Locale, 1st ed.; Helvelius: Napoli, Italy, 1999. [Google Scholar]
- Forcellini, D. Seismic fragility of tall buildings considering soil structure interaction (SSI) effects. Structures 2022, 45, 999–1011. [Google Scholar] [CrossRef]
- Galavi, V.; Petalas, A.; Brinkgreve, R.B.J. Finite element modelling of seismic liquefaction in soils. Geotech. Eng. J. SEAGS AGSSEA 2013, 44, 55–64. [Google Scholar]
- PLAXIS3D, Scientific Manual. 2018. Available online: https://communities.bentley.com/products/geotech-analysis/w/plaxissoilvision-wiki/50826/manuals-archive---plaxis (accessed on 1 December 2023).
- Joyner, W.B.; Chen, A.T.F. Calculation of non linear ground response in earthquake. Bull. Seismol. Soc. Am. 1975, 65, 1315–1336. [Google Scholar]
- Chen, X.; Fang, P.; Chen, Q.; Hu, J.; Yao, K.; Liu, Y. Influence of cutterhead opening ratio on soil arching effect and face stability during tunnelling through non-uniform soils. Undergr. Space 2024, 17, 45–59. [Google Scholar] [CrossRef]
- Chen, X.; Chen, P.; Liu, Y. Large-deformation finite-element analysis of square foundations in spatially variable sediments. Int. J. Geomech. 2023, 23, 8. [Google Scholar] [CrossRef]
- Gaudio, D. Interazione Dinamica Terreno—Struttura di Pozzi di Fondazione di Pile di Ponti e Viadotti. Ph.D. Thesis, Sapienza University of Rome, Rome, Italy, 2017. Available online: https://hdl.handle.net/11573/947638 (accessed on 1 November 2023). (In Italian).
- Bardet, J.P.; Ichii, K.; Lin, C.H. EERA: A Computer Program for Equivalent-Linear Earthquake Site Response Analyses of Layered Soil Deposits; User Manual; University of Southern California: Berkeley, CA, USA, 2000; 40p. [Google Scholar]
- Kottke, A.R.; Rathje, E.M. Technical Manual for Strata. PEER Report. Pacific Earthquake; Engineering Research Center College of Engineering, University of California: Berkeley, CA, USA, 2008. [Google Scholar]
- Mejia, L.H.; Dawson, E.M. Earthquake Deconvolution for FLAC. In Proceedings of the 4th International FLAC Symposium on Numerical Modeling in Geomechanics, Madrid, Spain, 29–31 May 2006; Itasca Consulting Group: Minneapolis, MN, USA, 2006. [Google Scholar]
- Amoruso, A.; Crescentini, L.; Scarpa, R. Source parameters of the 1908 Messina Straits, Italy, earthquake from geodetic and seismic data. J. Geophys. Res. 2002, 107, ESE-4–ESE-11. [Google Scholar] [CrossRef]
- Tortorici, L.; Monaco, C.; Tansi, C.; Cocina, O. Recent and active tectonics in the Calabrian arc (Southern Italy). Tectonophysics 1995, 243, 37–55. [Google Scholar] [CrossRef]
- Basili, R.; Valensise, G.; Vannoli, P.; Burrato, P.; Fracassi, U.; Mariano, S.; Tiberti, M.M.; Boschi, E. The Database of Individual Seismogenic Sources (DISS), version 3: Summarizing 20 years of research on Italy’s earthquake geology. Tectonophysics 2008, 453, 20–43. [Google Scholar] [CrossRef]
- Valensise, G.; Pantosti, D. A 125 Kyr-long geological record of seismic source repeatability: The Messina Straits (southern Italy) and the 1908 earthquake (Ms=7.5). Terra Nova 1992, 4, 472–483. [Google Scholar] [CrossRef]
- Brinkgreve, R.B.J.; Kappert, M.H.; Bonnier, P.G. Hysteretic damping in a small-strain stiffness model. In Proceedings of the Tenth International Symposium on Numerical Models in Geomechanics (NUMOG X), Rhodes, Greece, 25–27 April 2007; pp. 737–742. [Google Scholar]
- Massimino, M.R.; Abate, G.; Corsico, S.; Louarn, R. Comparison Between Two Approaches for Non-linear FEM Modelling of the Seismic Behaviour of a Coupled Soil–Structure System. Geotech. Geol. Eng. 2019, 37, 1957–1975. [Google Scholar] [CrossRef]




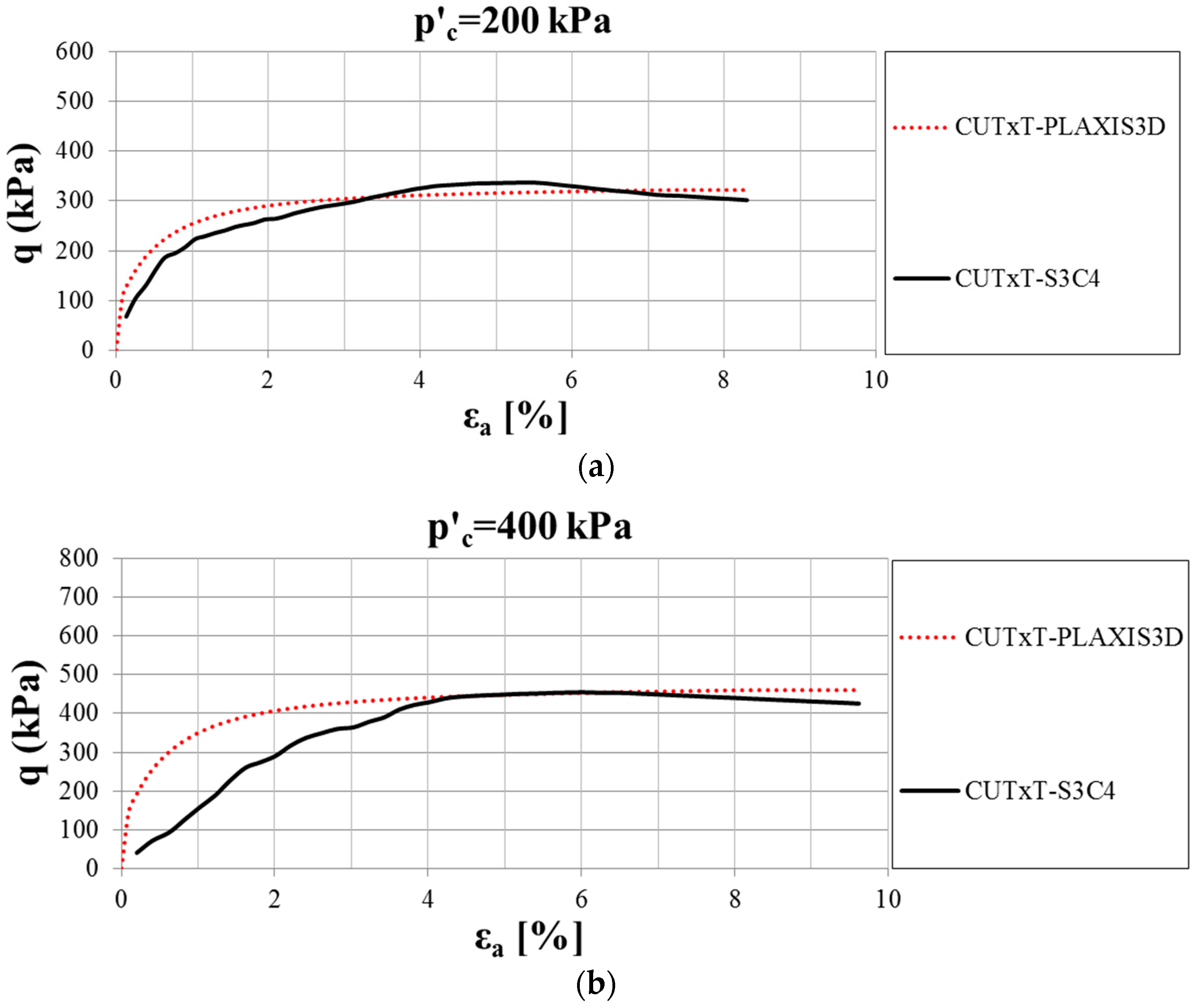

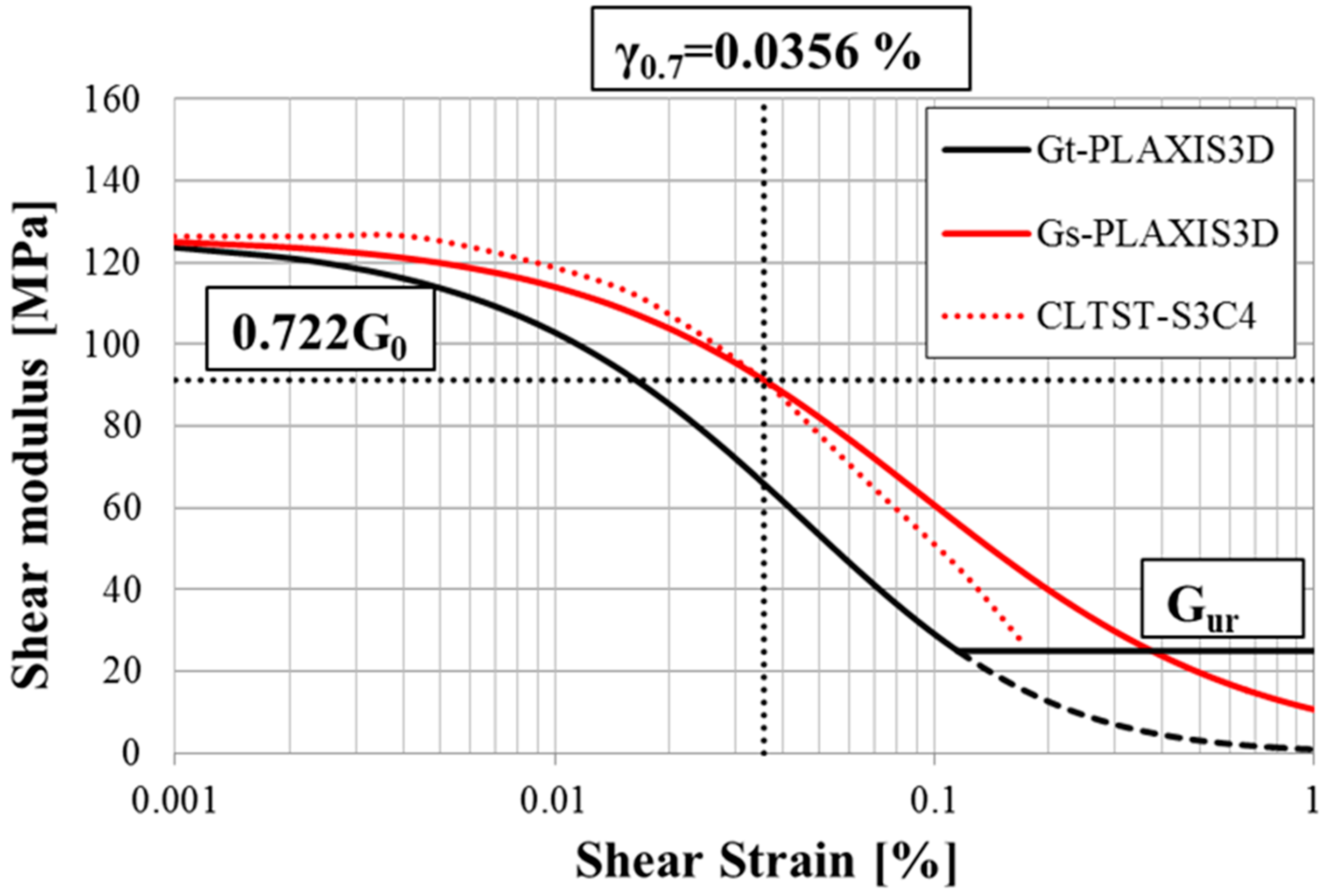
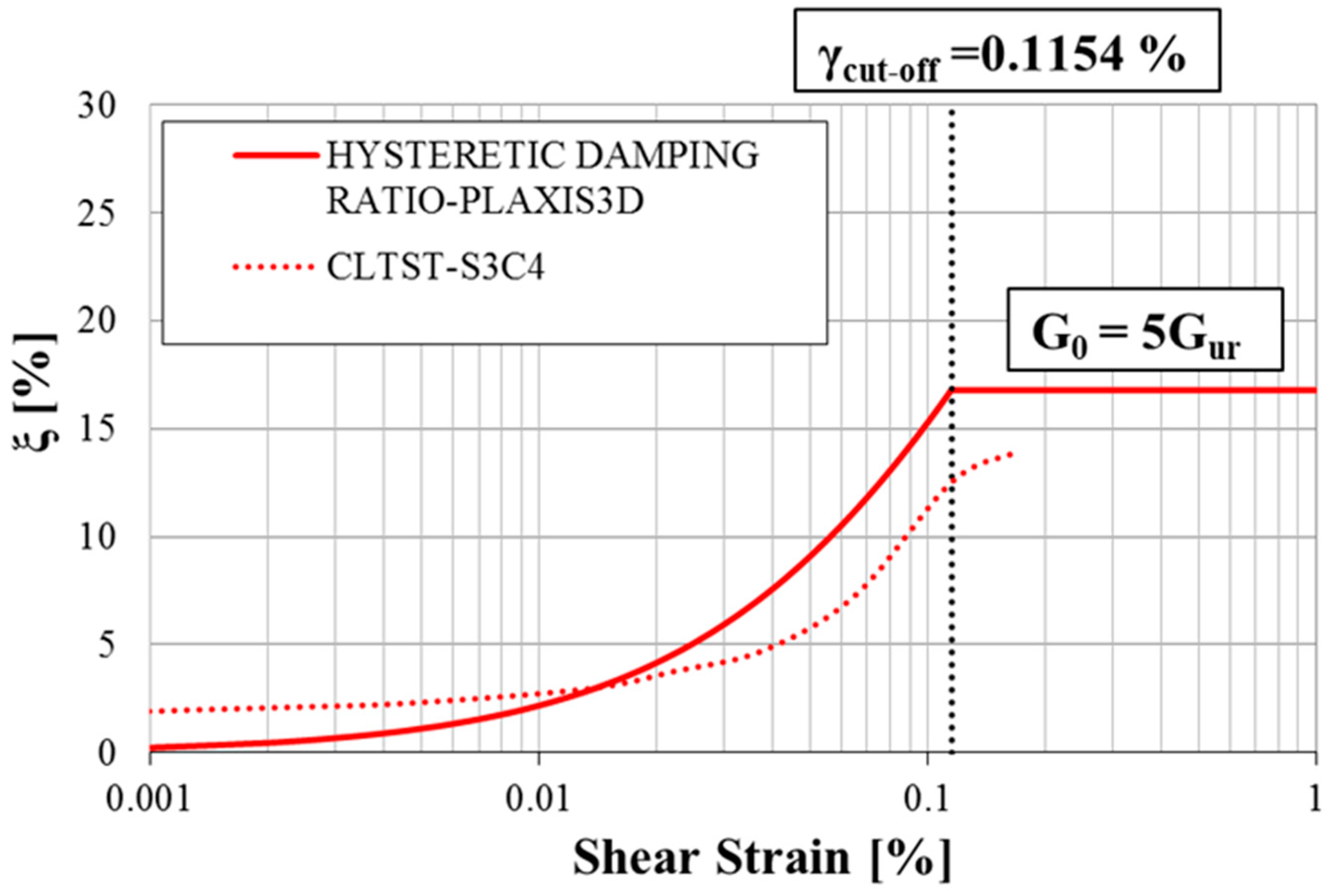





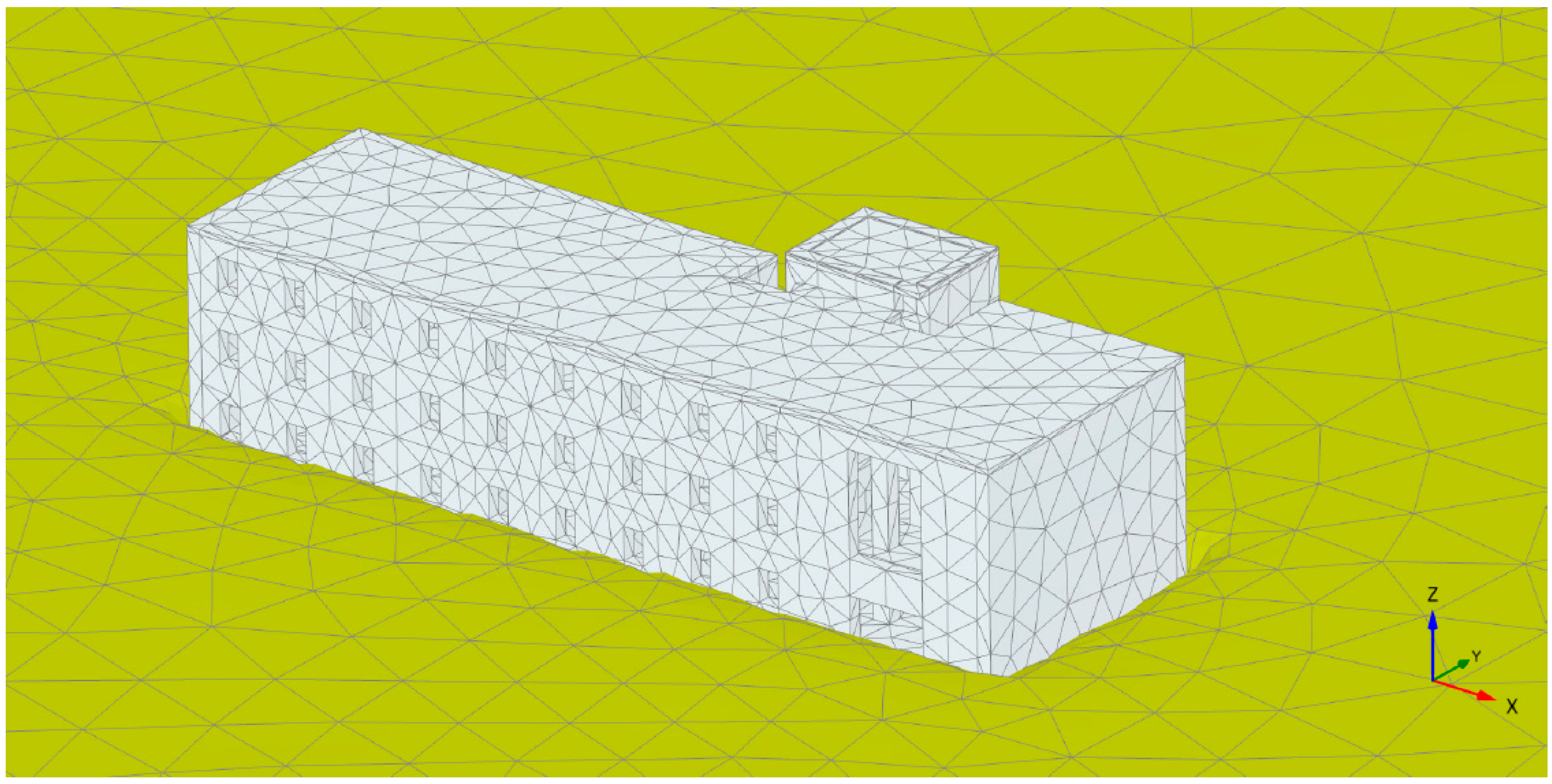

| Parameter | Unit | Value | |
|---|---|---|---|
| Masonry | Compressive strength | MPa | 4.47 |
| Shear strength | MPa | 0.39 | |
| Elastic modulus | MPa | 3120 | |
| Volumetric weight | kN/m3 | 18 | |
| Concrete foundation | Cylindrical resistance | MPa | 7.30 |
| Elastic modulus | MPa | 20,017 |
| Sample | z [m] | γ [kN/m3] | wn [%] | Gs | e | n | Sr [%] |
|---|---|---|---|---|---|---|---|
| S1C1 | 7.00–7.40 | 18.34 | 11.93 | 2.79 | 0.67 | 0.40 | 49.95 |
| S2C1 | 3.00–3.50 | 18.63 | 18.90 | 2.75 | 0.72 | 0.42 | 72.03 |
| S2C2 | 6.00–6.40 | 19.81 | 13.19 | 2.74 | 0.54 | 0.35 | 67.15 |
| S3C1 | 5.50–6.00 | 19.12 | 15.08 | 2.79 | 0.65 | 0.39 | 64.87 |
| S3C2 | 14.60–15.00 | 19.91 | 12.51 | 2.74 | 0.52 | 0.34 | 65.57 |
| S3C3 | 21.00–21.40 | 16.18 | 33.61 | - | - | - | - |
| S3C4 | 27.00–27.50 | 17.95 | 39.78 | 2.76 | 1.11 | 0.53 | 99.11 |
| Parameter | Value | Unit | |
|---|---|---|---|
| Masonry | Unit weight | 18 | kN/m3 |
| Young’s modulus | 3,120,000 | kN/m2 | |
| Poisson’s ratio | 0.20 | - | |
| Damping | 8 | % | |
| Concrete | Unit weight | 24 | kN/m3 |
| Young’s modulus | 20,017,000 | kN/m2 | |
| Poisson’s ratio | 0.25 | - | |
| Damping | 5 | % | |
| Hollow bricks and concrete floors | Unit weight | 18 | kN/m3 |
| Young’s modulus | 20,000,000 | kN/m2 | |
| Poisson’s ratio | 0.20 | - | |
| Damping | 5 | % | |
| Reinforced concrete elements | Unit weight | 25 | kN/m3 |
| Young’s modulus | 28,500,000 | kN/m2 | |
| Poisson’s ratio | 0.25 | - | |
| Damping | 5 | % |
| Layers | CUTxT | VS Values from Geophysical Tests [m/s] | Dynamic Tests |
|---|---|---|---|
| Fill | CUTxT-S3C1 | 146 | RTC-S1C1 |
| Silty sand and gravel 1a | CUTxT-S3C1 | 176 | RTC-S1C1 |
| Silty sand and gravel 1b | CUTxT-S3C1 | 335 | RTC-S1C1 |
| Sandy silt | CUTxT-S3C1 | 318 | RTC-S1C1 |
| Silty sand and gravel 2a | CUTxT-S3C1 | 288 | RTC-S1C1 |
| Sandy silt and clay | CUTxT-S3C4 | 260 | CLTST-S3C4 |
| Silty sand and gravel 2b | CUTxT-S3C4 | 457 | CLTST-S3C4 |
| Silty sand and gravel 3a | CUTxT-S3C4 | 665 | CLTST-S3C4 |
| Silty sand and gravel 3b | CUTxT-S3C4 | 911 | CLTST-S3C4 |
| Parameter | Symbol | Sandy Silt and Clay Layer | Unit |
|---|---|---|---|
| General | |||
| Material model | - | HS small | - |
| Saturated unit weight of soil | γsat | 18 | kN/m3 |
| Stiffness parameters | |||
| Secant stiffness in standard drained triaxial test | E50ref | 20,000 | kN/m2 |
| Tangent stiffness for primary oedometer loading | Eoedref | 20,000 | kN/m2 |
| Unloading/reloading stiffness | Eurref | 60,000 | kN/m2 |
| Reference stress for stiffness | pref | 200 | kN/m2 |
| Power for stress-level dependency of stiffness | m | 0.5 | - |
| Additional stiffness parameters | |||
| Reference shear modulus at very small strains | G0ref | 126,388 | kN/m2 |
| Threshold shear strain at which GS = 0.722 G0 | γ0.7 | 0.000356 | - |
| Strength parameters | |||
| Cohesion | c′ | 38 | kN/m2 |
| Friction Angle | φ′ | 23 | ° |
| Layer | G0ref [kN/m2] | pref [kN/m2] | γ0.7 |
|---|---|---|---|
| Fill | 46,699 | 100 | 0.000121 |
| Silty sand and gravel 1a | 60,638 | 100 | 0.000121 |
| Silty sand and gravel 1b | 242,569 | 100 | 0.000121 |
| Sandy silt | 205,403 | 100 | 0.000121 |
| Silty sand and gravel 2a | 160,979 | 100 | 0.000121 |
| Sandy silt and clay | 126,388 | 200 | 0.000356 |
| Silty sand and gravel 2b | 367,659 | 200 | 0.000356 |
| Silty sand and gravel 3a | 706,657 | 200 | 0.000356 |
| Silty sand and gravel 3b | 1,209,396 | 200 | 0.000356 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castelli, F.; Grasso, S.; Lentini, V.; Sammito, M.S.V. Nonlinear 3D Finite Element Analysis of a Coupled Soil–Structure System by a Deterministic Approach. Geosciences 2024, 14, 100. https://doi.org/10.3390/geosciences14040100
Castelli F, Grasso S, Lentini V, Sammito MSV. Nonlinear 3D Finite Element Analysis of a Coupled Soil–Structure System by a Deterministic Approach. Geosciences. 2024; 14(4):100. https://doi.org/10.3390/geosciences14040100
Chicago/Turabian StyleCastelli, Francesco, Salvatore Grasso, Valentina Lentini, and Maria Stella Vanessa Sammito. 2024. "Nonlinear 3D Finite Element Analysis of a Coupled Soil–Structure System by a Deterministic Approach" Geosciences 14, no. 4: 100. https://doi.org/10.3390/geosciences14040100
APA StyleCastelli, F., Grasso, S., Lentini, V., & Sammito, M. S. V. (2024). Nonlinear 3D Finite Element Analysis of a Coupled Soil–Structure System by a Deterministic Approach. Geosciences, 14(4), 100. https://doi.org/10.3390/geosciences14040100









