Assessment of Unmanned Aerial System Flight Plans for Data Acquisition from Erosional Terrain
Abstract
1. Introduction
2. Materials and Methods
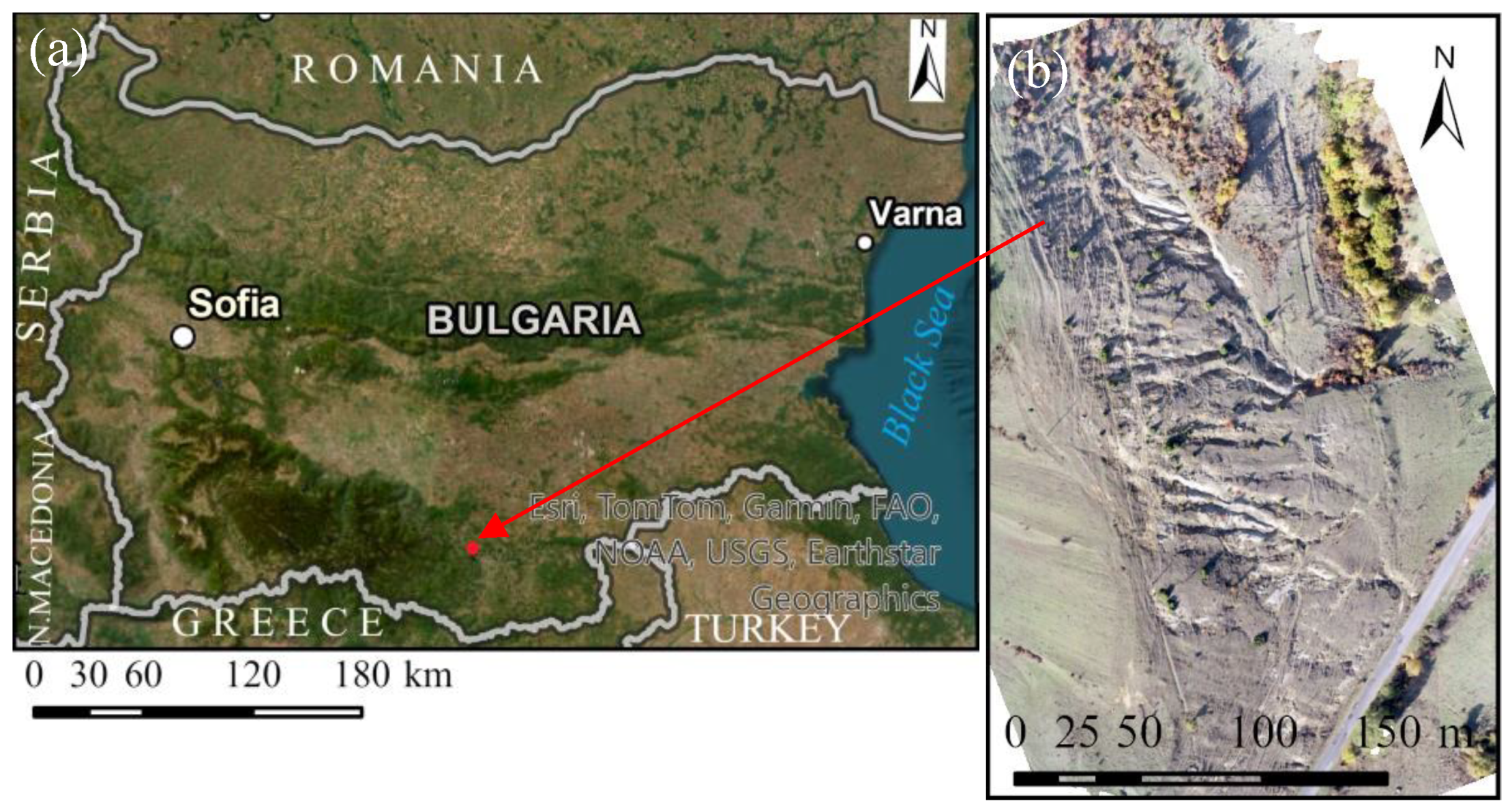
2.1. Study Area
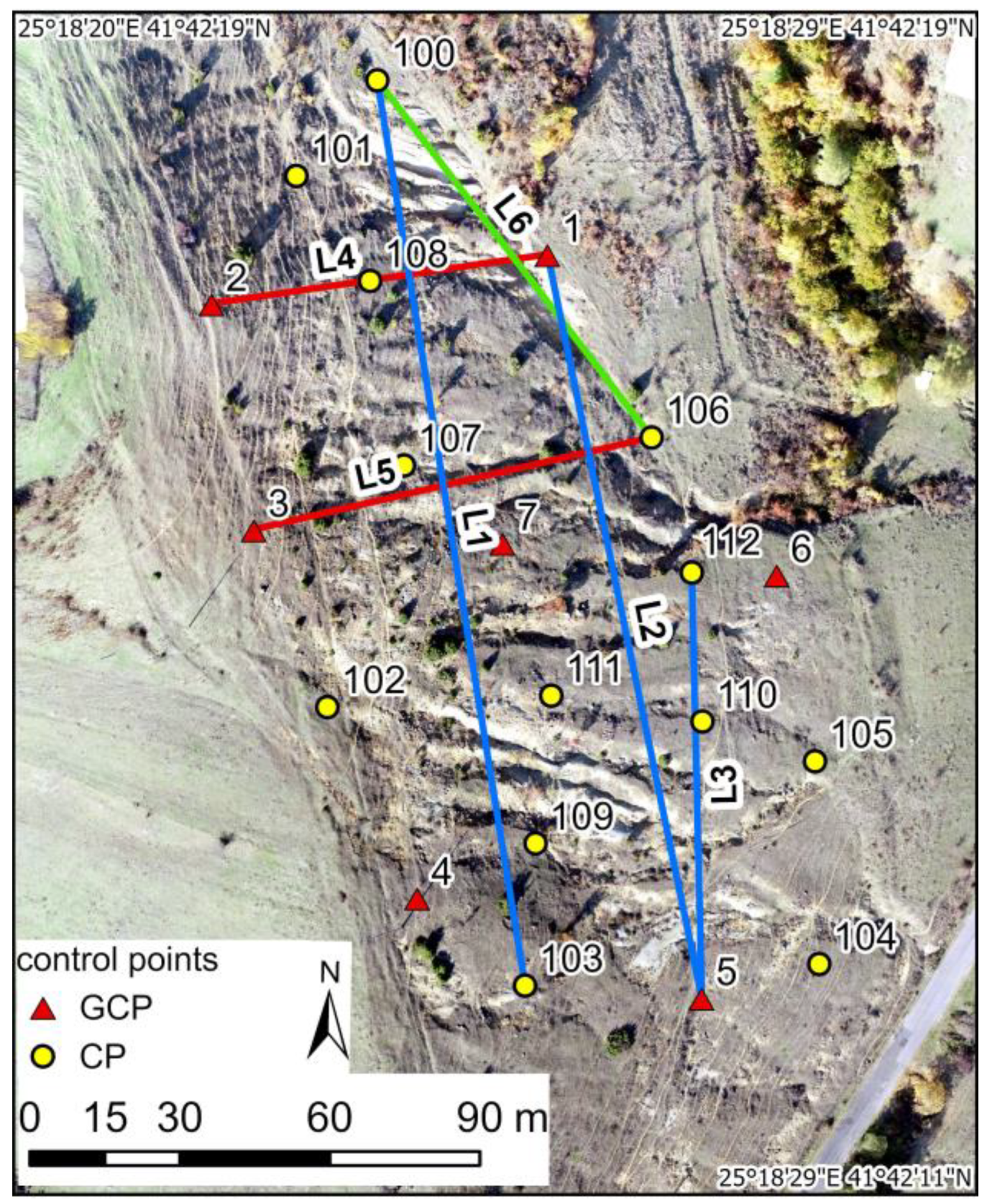
2.2. Equipment and Data Collection
2.3. Photogrammetric Processing and Analysis of the Photogrammetric Products
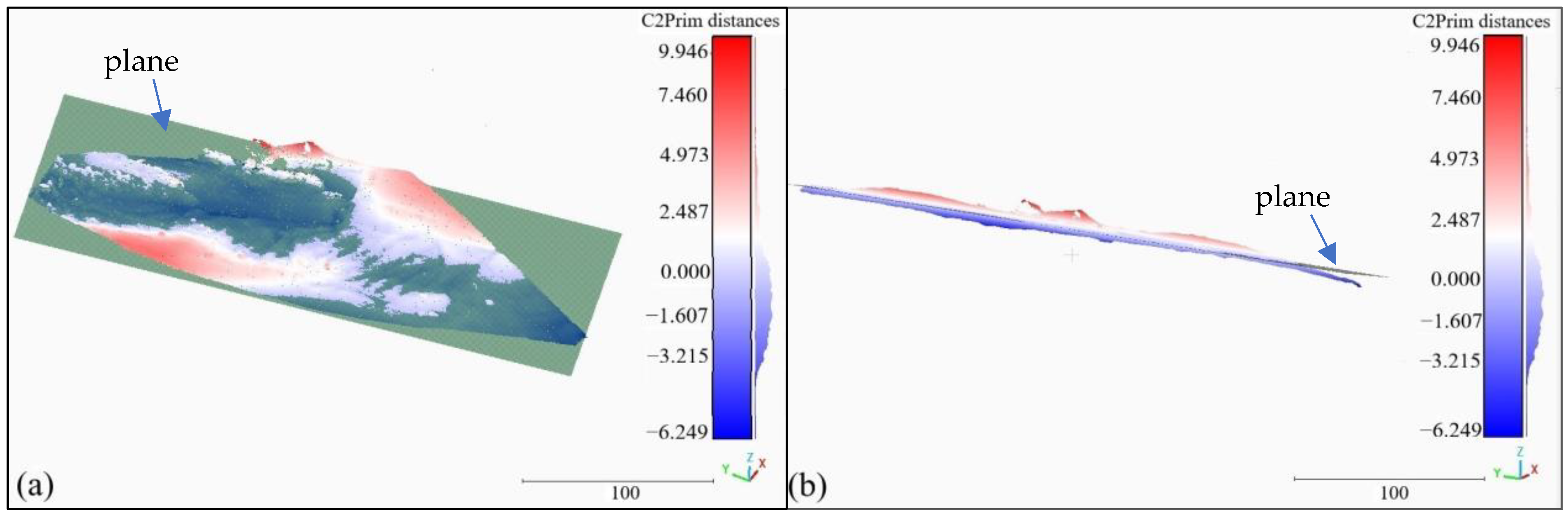
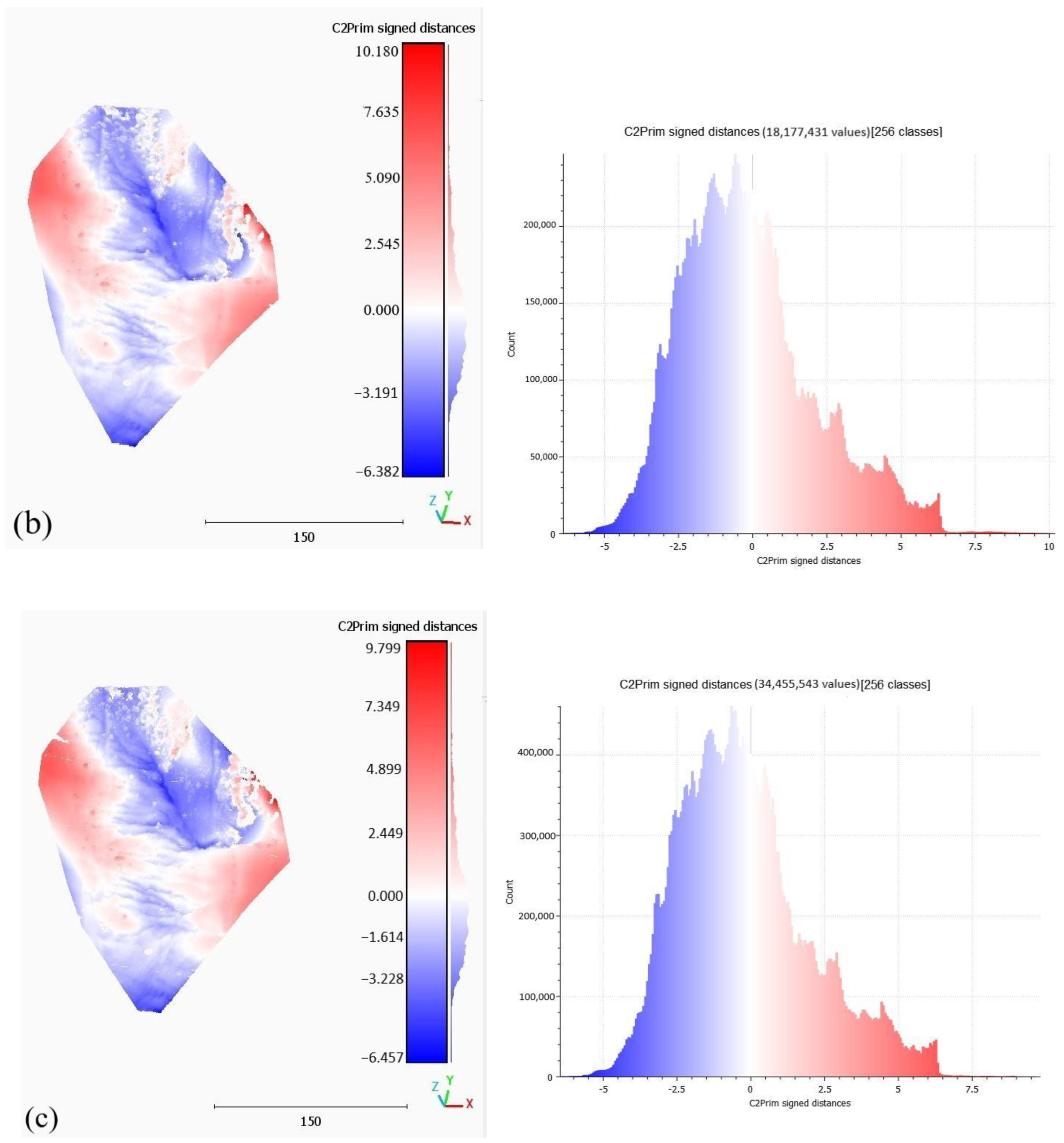
- Point clouds comparison—cloud to plane and cloud to cloud distances
- Evaluation of the DSMs
- Orthophotos
3. Results
3.1. Point Clouds
3.2. Digital Surface Models
3.3. Orthophotos
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, W.-C.; Huanga, W.-C. Close range digital photogrammetry applied to topography and landslide measurements. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 875–880. [Google Scholar] [CrossRef]
- Mokhtar, M.R.M.; Wahab, S.N.A.; Bin, M.N.; Hashim, H.H.; Kasim, A.C. Landslide monitoring using close range photogrammetry. Plan. Malays. J. Malays. Inst. Plan. 2021, 19, 160–168. [Google Scholar] [CrossRef]
- Bazzoffi, P. Measurement of rill erosion through a new UAV-GIS methodology. Ital. J. Agron. 2015, 10 (Suppl. S1), 708. [Google Scholar] [CrossRef]
- Krenz, J.; Greenwood, P.; Kuhn, N.J. Soil degradation mapping in drylands using unmanned aerial vehicle (UAV) data. Soil Syst. 2019, 3, 33. [Google Scholar] [CrossRef]
- Liao, K.; Song, Y.; Xie, S.; Zheng, H. Monitoring of Benggang erosion based on UAV photogrammetry technology. IOP Conf. Ser. Earth Environ. Sci. 2019, 330, 052003. [Google Scholar] [CrossRef]
- Urban, R.; Štroner, M.; Blistan, P.; Kovanič, L.; Patera, M.; Jacko, S.; Ďuriška, I.; Kelemen, M.; Szabo, S. The suitability of UAS for mass movement monitoring caused by torrential rainfall—A study on the talus cones in the Alpine terrain in High Tatras, Slovakia. ISPRS Int. J. Geo.-Inf. 2019, 8, 317. [Google Scholar] [CrossRef]
- Ullman, S. The interpretation of structure from motion. Proc. R. Soc. Lond. 1979, 203, 405–426. [Google Scholar]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-motion’ photogrammetry: A low-cost, effective tool for geoscience applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef]
- Eltner, A.; Sofia, G. Structure from motion photogrammetric technique. Dev. Earth Surf. Process. 2020, 23, 1–24. [Google Scholar] [CrossRef]
- Rosas, M.A.; Clapuyt, F.; Viveen, W.; Vanacker, V. Quantifying geomorphic change in Andean river valleys using UAV-PPK-SfM techniques: An example from the western Peruvian Andes. Geomorphology 2023, 435, 108766. [Google Scholar] [CrossRef]
- Nikolakopoulos, K.G.; Kyriou, A.; Koukouvelas, I.K. Developing a Guideline of Unmanned Aerial Vehicle’s Acquisition Geometry for Landslide Mapping and Monitoring. Appl. Sci. 2022, 12, 4598. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S.; D’Oleire-Oltmanns, S.; Niethammer, U. Optimising UAV Topographic Surveys Processed with Structurefrom-Motion: Ground Control Quality, Quantity and Bundle Adjustment. Geomorphology 2017, 280, 51–66. [Google Scholar] [CrossRef]
- Forlani, G.; Dall’Asta, E.; Diotri, F.; Cella, U.M.d.; Roncella, R.; Santise, M. Quality Assessment of DSMs Produced from UAV Flights Georeferenced with On-Board RTK Positioning. Remote Sens. 2018, 10, 311. [Google Scholar] [CrossRef]
- Nota, E.W.; Nijland, W.; De Haas, T. Improving UAV-SfM time-series accuracy by co-alignment and contributions of ground control or RTK positioning. Int. J. Appl. Earth Obs. Geoinf. 2022, 109, 102772. [Google Scholar] [CrossRef]
- Zimmerman, T.; Jansen, K.; Miller, J. Analysis of UAS Flight Altitude and Ground Control Point Parameters on DEM Accuracy along a Complex, Developed Coastline. Remote Sens. 2020, 12, 2305. [Google Scholar] [CrossRef]
- Lee, S.; Park, J.; Choi, E.; Kim, D. Factors Influencing the Accuracy of Shallow Snow Depth Measured Using UAV-based Photogrammetry. Remote Sens. 2021, 13, 828. [Google Scholar] [CrossRef]
- Seifert, E.; Seifert, S.; Vogt, H.; Drew, D.; Van Aardt, J.; Kunneke, A.; Seifert, T. Influence of Drone Altitude, Image Overlap, and Optical Sensor Resolution on Multi-view Reconstruction of Forest Images. Remote Sens. 2019, 11, 1252. [Google Scholar] [CrossRef]
- Kyriou, A.; Nikolakopoulos, K.; Koukouvelas, I. How image acquisition geometry of UAV campaigns affects the derived products and their accuracy in areas with complex geomorphology. ISPRS Int. J. Geo.-Inf. 2021, 10, 408. [Google Scholar] [CrossRef]
- Jiménez-Jiménez, S.I.; Ojeda-Bustamante, W.; de Jesús Marcial-Pablo, M.; Enciso, J. Digital Terrain Models Generated with Low-Cost UAV Photogrammetry: Methodology and Accuracy. ISPRS Int. J. Geo.-Inf. 2021, 10, 285. [Google Scholar] [CrossRef]
- Amrullah, C.; Suwardhi, D.; Meilano, I. Product accuracy effect of oblique and vertical non-metric digital camera utilization in UAV-photogrammetry to determine fault plane. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-6, 41–48. [Google Scholar] [CrossRef]
- Rossi, P.; Mancini, F.; Dubbini, M.; Mazzone, F.; Capra, A. Combining nadir and oblique UAV imagery to reconstruct quarry topography: Methodology and feasibility analysis. Eur. J. Remote Sens. 2017, 50, 211–221. [Google Scholar] [CrossRef]
- Nesbit, P.R.; Hugenholtz, C.H. Enhancing UAV–SfM 3D model accuracy in high-relief landscapes by incorporating oblique images. Remote Sens. 2019, 11, 239. [Google Scholar] [CrossRef]
- Nesbit, P.R.; Hubbard, S.M.; Hugenholtz, C.H. Direct Georeferencing UAV-SfM in High-Relief Topography: Accuracy Assessment and Alternative Ground Control Strategies along Steep Inaccessible Rock Slopes. Remote Sens. 2022, 14, 490. [Google Scholar] [CrossRef]
- Parmehr, E.G.; Savadkouhi, M.; Nopour, M. The impact of oblique images and flight-planning scenarios on the accuracy of UAV 3D mapping. Photogramm. Rec. 2023, 38, 563–580. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Jordanov, B.; Sarov, S.; Georgiev, S.; Valkov, V.; Balkanska, E.; Grozdev, V.; Marinova, R.; Markov, N. Explanatory Note to Geological Map of Bulgaria, 1:50,000, Map Sheet K-35-75-G (Nikolovo); Ministry of Environment and Water, Bulgarian Geological Survey, Uniscorp Ltd.: Sofia, Bulgaria, 2008; p. 92. (In Bulgarian) [Google Scholar]
- DJI. Phantom 4 RTK User Manual, v.2.4. 2021. Available online: https://dl.djicdn.com/downloads/phantom_4_rtk/20210716/Phantom_4_RTK_User_Manual_v2.4_EN.pdf (accessed on 20 July 2023).
- Liu, Y.; Han, K.; Rasdorf, W. Assessment and Prediction of Impact of Flight Configuration Factors on UAS-Based Photogrammetric Survey Accuracy. Remote Sens. 2022, 14, 4119. [Google Scholar] [CrossRef]
- Haala, N.; Cramer, M.; Rothermel, M. Quality of 3D point clouds from highly overlapping UAV imagery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 40, 183–188. [Google Scholar] [CrossRef]
- Losè, T.L.; Chiabrando, F.; Tonolo, F.G. Boosting the timeliness of UAV large scale mapping. Direct georeferencing approaches: Operational strategies and best practices. ISPRS Int. J. Geo.-Inf. 2020, 9, 578. [Google Scholar] [CrossRef]
- Štroner, M.; Urban, R.; Seidl, J.; Reindl, T.; Brouček, J. Photogrammetry using UAV-mounted GNSS RTK: Georeferencing strategies without GCPs. Remote Sens. 2021, 13, 1336. [Google Scholar] [CrossRef]
- Agisoft LLC. Agisoft Metashape Professional. 2020. Available online: https://www.agisoft.com/pdf/metashape-pro_2_0_en.pdf (accessed on 1 December 2023).
- Özyeşil, O.; Voroninski, V.; Basri, R.; Singer, A. A survey of structure from motion. Acta Numer. 2017, 26, 305–364. [Google Scholar] [CrossRef]
- Lowe, D. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- CloudCompare (Version 2.13 Beta) [GPL Software]. 2023. Available online: https://www.danielgm.net/cc/ (accessed on 28 November 2023).
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- ESRI Inc. ArcGIS Pro Software; version 3.2.1; ESRI Inc.: Redlands, CA, USA, 2023. [Google Scholar]
- Sammartano, G.; Chiabrando, F.; Spanò, A. Oblique images and direct photogrammetry with a fixed wing platform: First test and results in Hierapolis of Phrygia (TK). ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 43, 75–82. [Google Scholar] [CrossRef]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landf. 2014, 39, 1413–1420. [Google Scholar] [CrossRef]
- Jaud, M.; Letortu, P.; Théry, C.; Grandjean, P.; Costa, S.; Maquaire, O.; Davidson, R.; Le Dantec, N. UAV survey of a coastal cliff face—Selection of the best imaging angle. Measurement 2019, 139, 10–20. [Google Scholar] [CrossRef]
- Śledź, S.; Ewertowski, M.W. Evaluation of the Influence of Processing Parameters in Structure-from-Motion Software on the Quality of Digital Elevation Models and Orthomosaics in the Context of Studies on Earth Surface Dynamics. Remote Sens. 2022, 14, 1312. [Google Scholar] [CrossRef]
- Meinen, B.U.; Robinson, D.T. Mapping erosion and deposition in an agricultural landscape: Optimization of UAV image acquisition schemes for SfM-MVS. Remote Sens. Environ. 2020, 239, 111666. [Google Scholar] [CrossRef]




| Indicator | Value |
|---|---|
| UAV altitude (m) | 60 |
| Ground sample distance (cm) | 1.67 ≈ 2 |
| Along the track overlap (%) | 80 |
| Across the track overlap (%) | 80 |
| Point | Northing | Easting | Height (m) | Hz. RMS (m) | Vert. RMS (m) | Satellites Used |
|---|---|---|---|---|---|---|
| 1 | 4618381.220 | 359135.010 | 613.960 | 0.018 | 0.026 | 31 |
| 2 | 4618371.366 | 359067.864 | 642.235 | 0.017 | 0.023 | 35 |
| 3 | 4618326.176 | 359076.314 | 637.090 | 0.018 | 0.024 | 35 |
| 4 | 4618252.511 | 359108.964 | 623.773 | 0.019 | 0.024 | 37 |
| 5 | 4618232.469 | 359165.857 | 605.703 | 0.018 | 0.025 | 34 |
| 6 | 4618317.131 | 359180.885 | 603.648 | 0.020 | 0.026 | 32 |
| 7 | 4618323.493 | 359126.056 | 619.714 | 0.020 | 0.027 | 31 |
| 100 | 4618416.033 | 359101.018 | 625.236 | 0.019 | 0.026 | 32 |
| 101 | 4618396.905 | 359084.878 | 631.483 | 0.019 | 0.026 | 32 |
| 102 | 4618290.638 | 359091.014 | 630.283 | 0.018 | 0.024 | 35 |
| 103 | 4618234.896 | 359130.596 | 616.081 | 0.018 | 0.024 | 36 |
| 104 | 4618239.270 | 359189.416 | 600.595 | 0.019 | 0.025 | 34 |
| 105 | 4618279.774 | 359188.594 | 601.805 | 0.019 | 0.026 | 35 |
| 106 | 4618344.579 | 359155.869 | 607.370 | 0.020 | 0.026 | 30 |
| 107 | 4618338.956 | 359106.313 | 623.936 | 0.021 | 0.027 | 32 |
| 108 | 4618375.844 | 359099.596 | 628.198 | 0.021 | 0.028 | 32 |
| 109 | 4618263.361 | 359132.658 | 615.944 | 0.019 | 0.025 | 35 |
| 110 | 4618287.738 | 359166.025 | 608.150 | 0.020 | 0.025 | 35 |
| 111 | 4618292.918 | 359135.854 | 615.921 | 0.020 | 0.027 | 36 |
| 112 | 4618317.514 | 359163.893 | 607.896 | 0.019 | 0.025 | 30 |
| Capture Type | Average Camera Location Error Total Error (cm) | RMSE (m) GCPs | RMSE (m) CPs |
|---|---|---|---|
| Nadir—single strip | 1.5 | 0.020 | 0.025 |
| Oblique—single strip with gimbal pitch angle at 45° | 1.7 | 0.014 | 0.021 |
| Oblique—cross strip with gimbal pitch angle at 60° | 1.8 | 0.007 | 0.013 |
| Oblique Imagery 60°— Cross Strips | Oblique Imagery 45°— Single Strip | Nadir Imagery 90°— Single Strip | |||
|---|---|---|---|---|---|
| Positive Values | Negative Values | Positive Values | Negative Values | Positive Values | Negative Values |
| 40.99 | 59.01 | 41.91 | 58.09 | 40.96 | 59.04 |
| Capture Type | Mean | Maximum | Minimum |
|---|---|---|---|
| Oblique imagery 45°—single strip | 510 | 1483 | 1 |
| Oblique imagery 60°—cross strips | 1183 | 3460 | 1 |
| Nadir imagery—single strip | 965 | 2858 | 1 |
| Point Cloud for the Creation of the DSM | |||
|---|---|---|---|
| DSM | 60°—Cross Strips | 45°—Single Strip | Nadir—Single Strip |
| DSM—automatically generated in Agisoft in cloud processing | 0.024 (DSM cell size 0.032 m) | 0.040 (DSM cell size 0.049 m) | 0.022 (DSM cell size 0.35 m) |
| DSM—cell size 0.05 m | 0.024 | 0.037 | 0.022 |
| DSM—cell size 0.10 m | 0.023 | 0.037 | 0.022 |
| 60°—Cross Strips Mode Cloud | 45°—Single Strip Mode Cloud | Nadir—Single Strip Mode Cloud | |||
|---|---|---|---|---|---|
| Above the surface | 31,389.58 | 32,255.84 | 31,462.17 | ||
| Below the surface | 35,194.55 | 34,027.38 | 35,083.88 | ||
| Difference: between 60° and 45° clouds | above the surface | below the surface | |||
| −866.26 | 1167.16 | ||||
| Difference: between 60° and 90° clouds | above the surface | below the surface | |||
| −72.59 | 110.67 | ||||
| UAS Data | Distance, m | Difference with the Reference Line, m * | Difference, % |
|---|---|---|---|
| Line 1 (L1) | |||
| Reference lines from X and Y coordinates | 183.536 | ||
| Nadir imagery (90°—single strip) | 183.582 | −0.046 | −0.03 |
| Oblique imagery (45°—single strip) | 183.585 | −0.049 | −0.03 |
| Oblique imagery (60°—cross strips) | 183.580 | −0.044 | −0.02 |
| Line 2 (L2) | |||
| Reference lines from X and Y coordinates | 151.916 | ||
| Nadir imagery (90°—single strip) | 151.951 | −0.035 | −0.02 |
| Oblique imagery (45°—single strip) | 151.937 | −0.021 | −0.01 |
| Oblique imagery (60°—cross strips) | 151.936 | −0.020 | −0.01 |
| Line 3 (L3) | |||
| Reference lines from X and Y coordinates | 85.068 | ||
| Nadir imagery (90°—single strip) | 85.118 | −0.05 | −0.06 |
| Oblique imagery (45°—single strip) | 85.111 | −0.043 | −0.05 |
| Oblique imagery (60°—cross strips) | 85.107 | −0.039 | −0.05 |
| Line 4 (L4) | |||
| Reference lines from X and Y coordinates | 67.865 | ||
| Nadir imagery (90°—single strip) | 67.867 | −0.002 | 0.00 |
| Oblique imagery (45°—single strip) | 67.921 | −0.056 | −0.08 |
| Oblique imagery (60°—cross strips) | 67.881 | −0.016 | −0.02 |
| Line 5 (L5) | |||
| Reference lines from X and Y coordinates | 81.656 | ||
| Nadir imagery (90°—single strip) | 81.660 | −0.004 | −0.01 |
| Oblique imagery (45°—single strip) | 81.658 | −0.002 | 0.00 |
| Oblique imagery (60°—cross strips) | 81.661 | −0.005 | −0.01 |
| Line 6 (L6) | |||
| Reference lines from X and Y coordinates | 90.080 | ||
| Nadir imagery (90°—single strip) | 90.099 | −0.019 | −0.02 |
| Oblique imagery (45°—single strip) | 90.069 | 0.011 | 0.01 |
| Oblique imagery (60°—cross strips) | 90.083 | −0.003 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikolova, V.; Gospodinova, V.; Kamburov, A. Assessment of Unmanned Aerial System Flight Plans for Data Acquisition from Erosional Terrain. Geosciences 2024, 14, 75. https://doi.org/10.3390/geosciences14030075
Nikolova V, Gospodinova V, Kamburov A. Assessment of Unmanned Aerial System Flight Plans for Data Acquisition from Erosional Terrain. Geosciences. 2024; 14(3):75. https://doi.org/10.3390/geosciences14030075
Chicago/Turabian StyleNikolova, Valentina, Veselina Gospodinova, and Asparuh Kamburov. 2024. "Assessment of Unmanned Aerial System Flight Plans for Data Acquisition from Erosional Terrain" Geosciences 14, no. 3: 75. https://doi.org/10.3390/geosciences14030075
APA StyleNikolova, V., Gospodinova, V., & Kamburov, A. (2024). Assessment of Unmanned Aerial System Flight Plans for Data Acquisition from Erosional Terrain. Geosciences, 14(3), 75. https://doi.org/10.3390/geosciences14030075











