Abstract
This work investigates the rainfall infiltration process within homogeneous and stratified colluvial deposits caused by short (1–3 h) and intense (40–90 mm/h) rainfall, using both analytical and numerical infiltration modelling. The findings of the investigation demonstrate that the classic Green–Ampt model can be employed effectively to study homogeneous colluvial covers with permeability equal to or lower than kw = 10−5 m/s and that are subject to a 1 h rainfall with intensity I ≥ 45–50 mm/h. In these circumstances, a top-down saturation front forms within the colluvial deposit, leading to the saturation of a 70–100 cm-thick layer. This critical condition occurs every 5–10 years in the mountain area of the Friuli Venezia Giulia Region (NE Italy), which corresponds to a lower return period of critical hydrologic events when compared with other mountain basins in the Alps due to the higher initial degree of saturation characterising colluvial covers in this area (70–95%). When analysing stratified colluvial covers, the Dagan–Bresler approximate model, as well as the numerical modelling, emphasised the strong influence that abrupt variations in the permeability of the various soil layers have on the infiltration process at depth. In particular, the presence of a top organic soil horizon that is rich in macro-pores and is characterised by a higher permeability (k = 10−4 m/s) actually reduces the possibility of surficial ponding, which is the basic condition of the “piston” models. The highly permeable top soil allows for a rapid downward infiltration up to contact with the underlying colluvial material, which is less permeable (k = 10−5 m/s). Therefore, a perched water table forms starting from the organic soil–colluvium interface, originating pore–water overpressures within the colluvial deposit, with maximum values in the order of 5–10 kPa.
1. Introduction
In the mountain environment, colluvial deposits made up of highly heterogeneous unconsolidated sediments ranging from clayey loam to rock fragments are widespread at the toe of hillslopes [1,2,3,4]. These sediments have been deposited by rainwash, sheet erosion, fluvio–glacial sedimentation, shallow landslides, slow continuous soil creep, or a variable combination of these processes [5,6,7,8,9]. When subjected to rainfall, colluvial covers are involved in an infiltration process that is strongly influenced by the geological and hydraulic characteristics of the soil deposit [10,11]. The rainfall infiltration process results in the progressive saturation of the colluvial deposit, which, in turn, is responsible for the decrease in soil suction and the subsequent potential occurrence of positive pore–water pressures [12,13,14,15]. As a consequence, heavy rainfall events can cause the surficial saturation of thin Alpine colluvial covers, possibly triggering shallow slope failures that can result in substantial damage to farmlands, buildings, and infrastructures, sometimes also provoking injuries and deaths [16,17,18]. Soil slope failures can also be triggered by the snow melting in seasonally cold regions when the infiltration of snowmelt water contributes to a temporary increase in the water content and/or pore–water pressure within the soil deposit [19,20]. These instability processes determine a landslide risk in the Alpine territory, with a recent marked increase due to a significant growth in the occurrence of violent storms that are concentrated over relatively small areas [21].
Under natural conditions, the saturation of a colluvial cover can be achieved by following two distinct basic processes (Figure 1): (i) a top-down progressive saturation due to a downward advancement of the saturation front fed by rainfall which has fallen on the ground surface [22,23,24] (Figure 1a); and (ii) a bottom-up progressive saturation associated with the increasing level of a deeper saturated zone, which is sustained by an underlying permeability threshold [24,25,26] (Figure 1b). In both circumstances, the soil permeability (k), the rainfall intensity (I), and the duration (D), along with the pre-existing degree of saturation (S) of the soil, are decisive in determining the saturation process rate and the amount of water stored within the colluvial deposit [27,28].
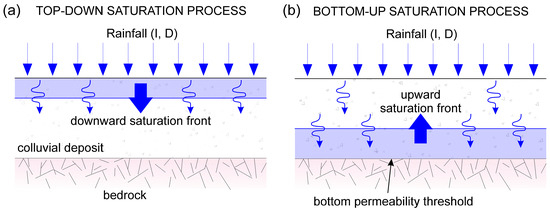
Figure 1.
Saturation processes of a shallow colluvial cover, consisting of a top-down (a) or bottom-up (b) advancement of the saturation front.
Thanks to the widespread diffusion of numerical computation techniques and the extensive availability of numerical codes, the water infiltration process within a colluvial deposit can be effectively modelled, adopting the non-linear differential equation of Richards [29,30,31,32,33,34,35,36,37]. Otherwise, analytical (approximate) infiltration models can be adopted, which are hydrological models that try to reproduce the water seepage into the soil analytically, assuming simplified hypotheses compared to the real phenomenon [38].
In the literature, the rainfall infiltration process through an unsaturated soil has been frequently analysed with the classic Green–Ampt infiltration model (G–A model) [39], sometimes described as a “piston” model, in particular, to study shallow landslides induced by heavy rainfall [40,41,42,43]. Although it is extremely simple, the classic G–A model results in some non-negligible limitations. Among these, it is worth mentioning the following: (i) the impossibility of considering possible variations in the volumetric water content θw in an unsaturated soil; and (ii) the impossibility of considering a stratified cover, i.e., the presence of possible hydrological discontinuities. These limitations do not allow for the analysis of the initial infiltration stage in the unsaturated soil as well as the understanding of the influence of the top organic soil horizon, which is normally characterised by a high permeability [28], and the effect of possible variations of the vertical hydraulic conductivity, as frequently occurs in most real colluvial deposits.
To overcome these restrictions, the G–A model has increasingly been adapted and perfected to consider the actual seepage process in unsaturated soils [44,45,46,47]. Advanced applications of the G–A model have been proposed to simulate infiltration into a layered soil profile or to account for variations of soil hydraulic properties at depth [48,49,50,51].
Under natural conditions, models combining infiltration and soil water redistribution are the best solution when soils are subjected to complex rainfall patterns, that is, periods with a rainfall hiatus or a rainfall rate after time to ponding less than soil-infiltration capacity [38]. Dagan and Bresler [52,53] proposed an approximate infiltration model based on integrated forms of Darcy’s law and the continuity equation, using simplified initial and surface boundary conditions. The Dagan–Bresler infiltration model (D–B model) has the key characteristic of being able to analyse the saturated/unsaturated condition along with a stratified cover made up of multiple soil layers with different permeability.
Despite their limitations, the approximate models are widely adopted owing to their intrinsic simplicity compared with rigorous numerical models [24,25,43,54]. The choice of the water infiltration model to be adopted depends on several factors, including the specifically analysed problem (rainfall-induced landslides, irrigation-related problems, etc.), the scale of the problem (regional or site-specific), the required degree of detail of the analysis and the amount of available constraining data on the geological and hydrological features of the investigated colluvial deposit. It must also be noted that outcomes obtained from the combined adoption of various modelling approaches have been more rarely compared [42,43,55].
In light of the aforementioned aspects, the comparison of the outcomes obtained from an analytical model with those of a rigorous model can be useful to assess the effects of rainfall infiltration on the time and space evolution of water content and/or pore–water pressure within the shallow soil cover. To this end, some simulations of the rainfall infiltration process within homogeneous and stratified colluvial deposits will be presented here in order to explore the progressive saturation of various types of colluvial covers that commonly rest on hillslopes. The simulations assumed the classic G–A model, the less frequently used D–B model, and, for comparison purposes, the rigorous numerical method. The adopted rainfall patterns, which refer to extreme hydrological events of short duration (1–3 h), were deduced from the analysis of the main critical events of intense precipitation recorded in the Friuli Venezia Giulia (FVG) Region (NE Italy) since 1985. Outcomes of the infiltration analyses show both the advantages and drawbacks of using analytical infiltration models in the study of real colluvial deposits. Insights are also drawn on the influence of the hydrogeological characteristics of colluvial covers on the rainfall infiltration process at depth.
2. Colluvial Deposits
Colluvial deposits are widespread within mountain basins, characterised by terrigenous rock mass sequences that include marls, shales, marly limestones, silty sandstones, siltstones, and argillite [1]. The predominantly silty–marly nature of sedimentary sequences, such as those related to flysch rock masses, makes this bedrock an excellent parent material for the generation of loose deposits of colluvial soils, also considering the presence of clayey minerals [56,57,58]. Sliding, mass transportation, material fluidisation, and pedogenetic processes are the main geomorphological processes controlling the stratigraphy of the colluvial deposit, thus determining its total thickness and the possible occurrence of internal stratifications [7,17,59].
Colluvial covers on gentle slopes (dip: 5–15°) are sometimes characterised by a single layer made up of a rather homogeneous soil deriving from the weathering and disruption of the underlying bedrock, accompanied by limited transportation of loose material (Figure 2a). In this circumstance, the thickness of the deposit rarely exceeds 1 m, and the colluvial cover is often overlaid by a very thin (2–10 cm, in most cases) organic soil horizon, which has a negligible effect on the rainfall infiltration process (Figure 2a). In other cases, the top organic soil is thicker (>20 cm) and is characterised by the widespread presence of macro-voids, root development, and possible traces of human reworking (Figure 2b). As a result, the organic soil has a higher permeability compared with the underlying colluvial layer, thus influencing the infiltration process at depth to some extent [28]. The thickness and structure of the top organic soil, which is referred to as the A horizon according to the nomenclature adopted in classic pedology, mainly depends on the soil age and pedogenetic maturity, thus reflecting the age of the underlying colluvial deposit and the stability of the Alpine landform (terrace or slope). Nonetheless, when the thickness of the top soil is not negligible (>20 cm), the colluvial deposit should be considered as a lithostratigraphic complex that is formed by two distinct units with different hydrogeological properties: (i) the top organic soil and (ii) the underlying colluvial layer.

Figure 2.
Typical colluvial deposits characterised by: (a) a single homogeneous soil layer; (b) a two-layered deposit that includes a top organic soil layer; (c) a stratified Alpine terrace made up of three different overlying layers; and (d) a thicker channelised deposit that infilled a buried landslide gully.
In the Alpine environment, deposits of colluvial soils occur along terraced belts that formed as a result of fluvial fill-and-cut sedimentary processes, in particular following the deglaciation of the Alpine valleys [28]. The near-horizontal terrace treads are commonly made up of a 1–3 m thick stratified deposit with a three-layered stratigraphy (Figure 2c and Figure 3a):
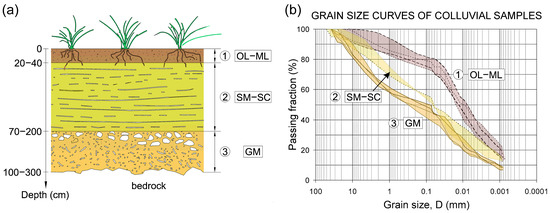
Figure 3.
(a) Stratigraphical section of a layered colluvial deposit on a typical Alpine terrace and (b) grain size distribution curves of the colluvial materials showing three different USCS soil classifications.
- A top 20–40 cm thick organic soil with roots and macro-voids;
- An intermediate 50–150 cm thick colluvial layer;
- A basal 30–150 cm thick colluvial layer mixed with abundant angular rock fragments derived from the local bedrock.
When analysing the three-layered stratigraphy of colluvial deposits occurring on Alpine terraces, three main groups of soils can be differentiated based on their grain size and plasticity properties (Figure 3b). The top soil horizon (layer 1 in Figure 3a) is commonly made up of organic and inorganic silts with medium to low plasticity (OL–ML) (Figure 3b), according to the USCS classification system. The intermediate colluvial layer (layer 2 in Figure 3a) is formed by coarse soils with a low-plastic silty or medium-plastic clayey loamy component (SM–SC). The basal colluvial unit (layer 3 in Figure 3a), being characterised by a greater amount of the coarser fraction that derives from crushing of the underlying bedrock, is generally made up of a gravelly soil with a silty loam of low-to-medium plasticity (GM) (Figure 3b). In some cases, the deepest layer presents an increase in the clay fraction due to the weathering of the bedrock or deriving from pedogenetic processes of the upper layers (illuvial clay).
In some Alpine and fore Alpine areas over the world, surface deposits of colluvial materials can increase, both in frequency and thickness, due to the widespread occurrence of rock masses made up of alternating sequences of sandstone and marl belonging to the Flysch formation of various ages [60,61,62,63,64,65]. Flysch reliefs tend to originate complex geomorphological systems that are characterised by numerous creeks and incised gullies where landslide deposits accumulate due to repeated instabilities of the upper slopes. In these more complex cases, recurring slope failures originate channelised landslide deposits of colluvial materials that have a greater thickness if compared with Alpine-terraced landforms. The overall thickness of the colluvial deposit is highly variable, depending on the number and volume of previous landslide events, and can reach 5–10 m (Figure 2d). These thicker colluvial covers are irregularly stratified and include a number of layers that were deposited as a result of distinct and superimposed landslide masses that infilled buried creeks or landslide gullies.
Overall, colluvial deposits are characterised by a notable grain size heterogeneity as they are typically formed by poorly selected sediments with a silty–clayey-sandy matrix (i.e., a loam); therefore, the particle size ranges from clay to rock fragments (Figure 4). Commonly, the coarser fraction (gravel and sand) is equivalent to the finer fraction (silt and clay). An average particle size composition may be as follows: 30% gravel, 20% sand, 30% silt, and 20% clay (Figure 4a). This means that the gravel fraction is often present in significant quantities (15–50%), including angular and sub-angular elements of variable size, from fine rock fragments to small rock blocks. When considering only the loamy matrix, the content of silt is typically greater than sand and clay, with a relative percentage ratio close to 45:30:25, respectively (Figure 4b).
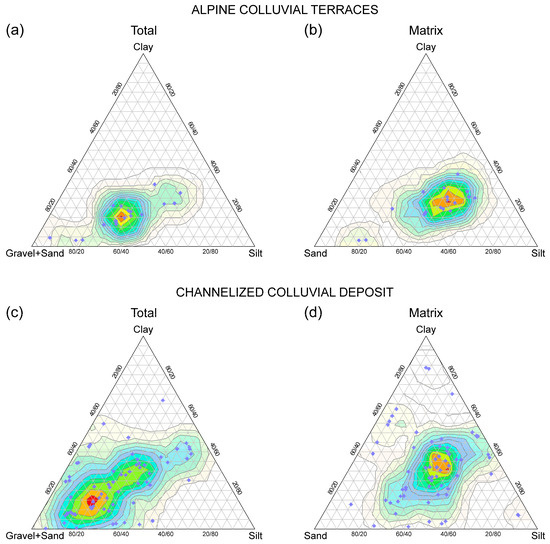
Figure 4.
Geotechnical ternary diagram showing the percentages of coarse and fine soils forming colluvial covers on (a,b) Alpine terraces and (c,d) channelised deposits.
In detail, the grain size composition of colluvial deposits varies depending on some factors, including the lithology of the parent material and the specific geomorphological context. Based on field investigations performed by the authors [28,66], soil samples collected from channelised colluvial deposits (Figure 4c,d) showed a greater grain size variability compared with soils sampled from Alpine colluvial terraces (Figure 4a,b). This was observed for both the total grain size composition (Figure 4a,c) and the loamy matrix (Figure 4b,d). The significant grain size variability of colluvial materials of channelised slopes is due to the specific geomorphological context and sedimentary process, which is closely related to the occurrence of repeated landslide events that originated a very complex stratigraphy and chaotic assemblage of soils that experienced multiple mobilisations. The coarser fraction can prevail over the finer fraction (Figure 4c), owing to the occurrence of a larger content of rock fragments and blocks that were formed by rock mass crushing during the shearing process of the bedrock at the base of the slide. In addition, when the parent rock mass is made up of lithological units that are rich in clay minerals (in particular, marls and weathered clayey interbeds), the clay fraction within the colluvial cover can increase (Figure 4d).
3. Rainfall Characteristics and Soil Saturation
The rainfall input data assumed in the various infiltration models presented in this work were obtained from the study of the main critical hydrological events that have hit the mountain basins of FVG since 1985 (Figure 5). FVG represents the eastern end of the Italian Alps and is located at the northern extremity of the Adriatic Sea (Figure 5a). Owing to the proximity of the sea, the mountain area of FVG is subject to the influx of winds that are rich in humidity and is characterised by a wet and rainy climate. The average yearly rainfall for the Alpine and pre-Alpine areas of FVG, calculated in the period 1961–2013, ranges from about 1500 mm to more than 3200 mm (Figure 5a). These areas are frequently hit by rainstorms characterised by high intensity (40 ≤ I ≤ 100 mm/h) and limited duration (D = 1–6 h, at most) (Figure 5b), which mainly occur during the wet season (September–November) or during the spring (May–June).

Figure 5.
(a) Average yearly rainfall heights of the Friuli Venezia Giulia Region and (b) critical rainfall curves of extreme hydrological events that hit the mountain basins of FVG within the period 1985–2017.
When considering the main critical hydrological events that have occurred in the last 35 years in FVG (particularly in the Carnic Alps), rainstorms characterised by a maximum hourly intensity of I = 40–50 mm/h have a return period (Tr) of 5–10 years (Figure 5b). More severe rainstorms with I = 90–100 mm/h for 1 h or I = 50 mm/h for 3 h occurred with Tr = 50–200 years. The maximum hourly rainfall intensity ever recorded in the analysed period is I = 100 mm/h, registered at the Moggio gauge station and related to the rainstorm that hit the mountain area of FVG on 21–22 June 1996 (Figure 5b). Some critical hydrological events characterised by I ≥ 40–45 mm/h were responsible for the widespread activation of colluvial slope shallow failures that occurred in the mountain basins of FVG [28,67,68].
The characteristically humid climate of FVG with recurrent heavy rainfall events during the year has obvious consequences on the moisture condition of colluvial deposits, depending on their hydrogeological properties. Notably, the initial degree of saturation of soil layers has a strong influence on the rainfall infiltration process within the colluvial deposit when subject to rainfall [28]. Investigations on the soil-moisture condition performed on slopes of the Alpine and pre-Alpine areas of FVG pointed out that colluvial covers are often close to the saturation condition, and average values of the degree of saturation (S) vary from 65–70% to 95–100% [66]. Values of the volumetric water content (θ) that were measured in various periods of the year highlighted an exponential trend of S at depth for both Alpine colluvial terraces (Figure 6a) and channelised slopes (Figure 6b).

Figure 6.
Variations of the degree of saturation at a depth of colluvial covers on (a) Alpine terraces and (b) channelised deposits of FVG.
When considering a stratified colluvial deposit, the top organic soil layer commonly has a lower degree of saturation, which is on average equal to S = 70%, since its higher permeability favours a quick desaturation after the rainfall ends [28]. Although the saturation profiles at depth were observed as being irregular with a number of moisture peaks, the average values of S for the intermediate colluvial layer (layer 2 in Figure 3a) and the basal colluvial soil (layer 3 in Figure 3a) were estimated at about 85% and 95%, respectively, and for most of the year (Figure 6). The high average degrees of saturation correspond with values of θ close to 0.40–0.45. The high water content in the colluvial deposits gives rise to a modest effective porosity, μ = 0.05–0.08, μ being the difference between the total porosity Φ and the volumetric content of water θ of the soil. The effective porosity of the colluvial slopes in the mountain basins of FVG is considerably lower than the value (μ = 0.20) assumed in the surface infiltration models for the slopes of California [69]. This fact indicates that in the soils of the Alpine and pre-Alpine areas of FVG, the useful volume of voids that can be filled by water during heavy rainfall is significantly limited, and consequently, it is easier to reach saturation conditions.
4. Analytical Infiltration Models
The calculation examples that will be described in the following paragraphs represent the application of the G–A and D–B models to simulate the infiltration process induced by short and intense precipitation within a horizontal colluvial cover. Both homogeneous (one layer) and stratified (two and three layers) deposits were analysed in order to investigate the rainfall infiltration process within different types of colluvial covers that commonly characterise Alpine and pre-Alpine gentle slopes.
The number of parameters required using analytical infiltration models depends on their degree of complexity. The simplest G–A model requires four parameters: (1) the initial volumetric water content θi; (2) the porosity φ of the soil; (3) the saturated permeability ksat (m/s); and (4) the average suction value below the saturation front at depth h0 (m). For the D–B model, three additional parameters are required: (5) the suction value of the air at depth hb (m); (6) the pore-connectivity index λ; and (7) the residual volumetric water content θr.
The porosity, degree of saturation, and suction values (h0 and hb) of the various soils were assessed on the basis of large amounts of data collected by the authors and presented in previously published papers [28,66]. Despite the increasing curvilinear trend of the degree of saturation at a depth that was ascertained for real colluvial deposits (Figure 6), both the G–A and D–B infiltration models require a constant volumetric water content θw in the various layers considered. Therefore, the stratified deposit is schematised, assuming different but constant values of the initial water content (θS1, θS2, and θS3) and a corresponding degree of saturation (S1, S2, and S3) for the various soil layers.
When considering the lack of specific in situ infiltration measurements within this study, the permeability of the various soils was assumed on the basis of values reported in the literature [30,70,71], with particular reference to the in situ hydraulic conductivity [23,72,73,74]. In fact, the latter can be even 2–3 orders of magnitude greater than corresponding values obtained from laboratory tests on soil samples [34,72]. Particular attention has been paid to colluvial and/or residual materials, for which saturated permeability values varying in the range of k = 1 × 10−4–1 × 10−6 m/s were suggested [32,40,75,76,77,78].
The analytical expressions of the various infiltration models clearly show that the formation of a perched water table substantially depends on the duration (D) and intensity (I) of the precipitation. In the approximate infiltration modelling, rainfall of low duration (1–3 h) and high intensity (40–90 mm/h) was assumed, according to the rainfall intensities that were actually registered during extreme hydrological events in FVG over the last 35 years (see Section 3).
4.1. Homogeneous Cover
From a phenomenological point of view, the advancement rate of the saturation front in the soil decreases over time as the infiltration process proceeds and tends asymptotically toward the saturated permeability of the material. This fact depends on the gradient of suction, which is higher at the early stages of infiltration and progressively decreases as the infiltration process involves the deeper layers with a higher degree of saturation. To trigger a top-down saturation process, i.e., starting from the ground surface and moving downward, the rainfall intensity (I) has to be equal to or greater than the saturated permeability of the top soil layer, that is, I ≥ ksat. For the classic G–A model, a second condition also has to be respected: the rainfall duration has to be greater than the time required to reach the condition of formation of the saturation front, i.e., the ponding time (Tp), i.e., D ≥ Tp. This means that, in order to apply the G–A model, both conditions I ≥ ksat and D ≥ Tp have to be satisfied.
When using approximate infiltration models, the trend over time of the infiltration process can be reconstructed, even graphically. The diagram in Figure 7 shows the result of a simulation performed with the G–A model for very intense precipitation (I = 90 mm/h for D = 1 h) involving a single homogeneous soil layer (ksat = k1 = 10−5 m/s).
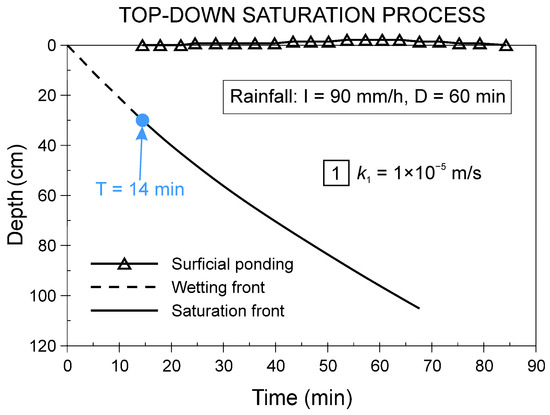
Figure 7.
Characteristic hydrological parameters and evolution of an infiltration process within a homogeneous soil as simulated using the Green–Ampt analytical model.
The saturation front formed at a depth of 30 cm after 14 min from the beginning of heavy rainfall (Figure 7). When considering a single soil layer characterised by a saturated hydraulic conductivity ksat = k1 and an initial water content θi, the critical conditions of I and D related to the saturation of the soil layer can be verified using an approximate model. When only considering the primary condition I ≥ k1, it is possible to calculate the minimum value of the hydraulic conductivity of the material that allows for the formation of the saturated layer. The diagram of Figure 8, which has been reconstructed for a colluvial deposit using the G–A model in the hypothesis of a single homogeneous layer, shows that the saturation of the soil cover is only possible for materials with permeability kw ≤ 10−5 m/s. This means that less permeable materials (for instance, with kw = 10−6 m/s) achieve the saturation condition more easily and even in concomitance with rainfall of lower intensity. In this case, the saturation front forms in the extremely surficial layer (1–5 cm) (Table 1).
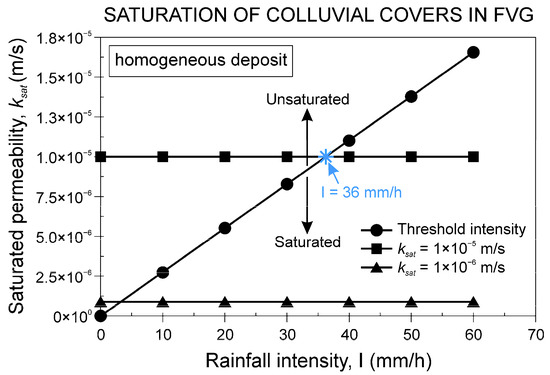
Figure 8.
Rainfall intensity required to allow for the saturation of a colluvial cover in the mountain area of FVG (G–A model: condition I3 ksat).

Table 1.
Comparison between the results of the Green–Ampt model and the Dagan–Bresler model for a homogeneous colluvial deposit and various values of the soil permeability.
If the soil has a permeability kw ≈ 10−5 m/s, as often occurs for colluvial covers, the condition I ≥ kw is satisfied when the rainfall intensity exceeds 36 mm/h (Figure 8). However, when taking into account the ponding time, the saturation condition only occurs for hourly rainfall with an intensity I ≥ 45 mm/h. Although obtained from an approximate model, these data are of key importance since they define a critical intensity threshold over which a surficial saturation process can occur on unsaturated colluvial slopes in the Alpine area of FVG. In addition, it is important to note that the minimum saturation condition, i.e., I = 45 mm/h and D = 1 h, corresponds with extreme hydrologic events that can occur in the mountain area of FVG even once or twice over a decade (Figure 5b) and, as such, they cannot be considered as exceptional.
In more general terms, if we assume specific values of rainfall intensity that are obtained from the hydrological analysis of precipitations related to the mountain area of FVG, we can identify the limit value of hydraulic conductivity (klim) that allows for the saturation of a surficial layer of thickness zsf. For colluvial slopes in California, Pradel and Raad [69] calculated that the formation of a saturated layer of thickness zsf = 1.22 m was possible for a top soil with a permeability equal to klim ≤ 10−6 m/s. This value is lower than klim ≤ 10−5 m/s that we calculated for the mountain slopes of FVG, owing to the higher degree of saturation that actually characterises colluvial deposits in the study area.
The bottom-up saturation process cannot be reproduced with the traditional G–A model since the latter only presupposes the downward movement of a saturation front from the ground surface. For this purpose, the D–B model can be used, which describes the advancement of both the wetting front and the saturation front, thus evaluating the variations in the soil of the volumetric water content θw, starting from the onset of rainfall. When adopting the D–B model, it is possible to evaluate the depth at which the saturation front forms (Figure 9a) as well as the depth reached by the wetting and/or saturation front in the colluvial deposit after a 1 h rainfall with constant intensity (Figure 9b). In the simulations performed, the saturation front formed at a depth that was strongly dependent on both the soil permeability and the rainfall intensity (Figure 9a). In particular, for soils characterised by a high permeability (k1 = 10−4 m/s), the saturation front did not form, whereas colluvial materials with a permeability equal to k1 = 10−5 m/s were particularly sensitive to the intensity of the precipitation. In fact, a maximum depth equal to zsf = 0.65 m was reached as a result of a lower rainfall intensity (I = 47 mm/h) that allowed for saturation (Figure 9a). The marked curvilinear trend indicates that rainfall with an intensity of 45–50 mm/h can give rise to a 50–65 cm thick saturated surficial layer, whereas the thickness is significantly lower for more intense precipitations (Figure 9a). Finally, less permeable materials (k1 = 10−6 m/s) formed a very surficial saturated layer (1–2 cm) at a rather constant depth.

Figure 9.
(a) Depth of formation of the saturation front and (b) depth of the wetting front (zwf) and saturation front (zsf) after a 1 h rainfall, depending on various values of rainfall intensity and for a homogeneous colluvial deposit with different saturated permeability.
When analysing the depth of the saturation/wetting front after a 1 h rainfall, a rather different behaviour was observed, depending on the hydraulic conductivity of the soil that forms the homogeneous deposit (Figure 9b). For soils with higher hydraulic conductivity (kw = 10−4 m/s), the wetting front (dashed line) reached considerable depths (170–270 cm). However, the depth decreases as the rainfall intensity increases. Differently, for colluvial materials with a permeability equal to kw = 10−5 m/s, the saturation front reached a depth that slightly increases as the intensity increases, gradually varying from 60 cm (I = 40 mm/h) to 78 cm (I = 90 mm/h) (Figure 9b). When assuming a lower permeability of the colluvial materials (kw = 10−6 m/s), the saturation front reached a constant depth (18 cm) after a 1 h rainfall regardless of the rainfall intensity. This different behaviour can be explained by taking into account the fact that in more permeable soils, there is a lower degree of initial saturation, and therefore, the increase in the rainfall intensity results in an increase in the degree of saturation of the soil, which is consequently reached at a shallower depth. Differently, for less permeable soils, saturation occurs quickly in the more surficial soil layers, and the increase in rainfall intensity results in a larger amount of water that is transferred to greater depths.
For comparison purposes, the G–A and D–B approximate infiltration models were used to simulate the effects of short and intense precipitations on colluvial covers in the hypotheses of a homogeneous deposit (Table 1). The results obtained highlight the greater applicability of the D–B model compared with the G–A model, particularly when the high permeability of the soil does not allow for the achievement of the saturation condition. In addition, if the duration of precipitation is lower than the ponding time (D < Tp), the saturation front did not form. In this case, only the D–B model provides information about the position of the wetting front (zwf) that moves within the colluvial deposit.
The typical configuration with a permeability of the colluvial layer equal to k2 = 10−5 m/s determines the formation of a saturated layer that reaches a depth of 60–100 cm (Table 1) after one hour of rainfall, depending on the rainfall intensity. When considering intense precipitations of a longer duration (2–3 h), saturation involves greater thicknesses, ranging from 133 cm to 202 cm, for a 2 h and 3 h rainfall, respectively. The thickness values of the saturated layer are fully consistent with depths of shallow landslides triggered by heavy rainfall (z = 0.3–3.0 m) [79,80,81,82], confirming the decisive role played by the perched water table in the achievement of the slope failure condition [83,84,85,86].
Examination of the ponding time Tp indicates that the formation of the saturated layer occurs after a short period of time, ranging from 6 to 100 min; the greater the rainfall intensity, the shorter the period of time (Table 1). The quick process of saturation is also consistent with the numerous testimonies that describe the activation of shallow landslides during or immediately after the phases of maximum intensity of the precipitation [28,40,87].
4.2. Stratified Deposit
In many instances, colluvial terraces have a sub-horizontal stratification related to both geological (for the intermediate and basal units) and pedogenetic (for the top organic soil horizon, i.e., the A horizon) processes. Therefore, when considering a stratified deposit, the stratigraphy and thickness of the different soil layers were schematised according to field evidence acquired from several surveyed case histories (see Section 2), as follows (three-layered stratigraphy):
- A top 30 cm thick organic soil layer;
- A 120 cm thick intermediate colluvial layer;
- A 150 cm thick basal colluvial layer.
The following values were assumed as representative of the saturated permeability at the slope scale of the three soil layers considered in the models, decreasing from top to bottom: (i) k1 = 10−4 m/s for the high-permeable top organic soil; (ii) k2 = 10−5 m/s for the sandy–silty–clayey intermediate colluvium; and (iii) k3 = 10−6 m/s for the silty–clayey basal layer. These values are only indicative and describe the average behaviour of the various materials, thus being useful to verify the influence of hydrological stratifications within the colluvial cover on the rainfall infiltration process.
For a three-layered deposit, the depth reached by the saturation front after an hour of rainfall varies between 90 cm and 100 cm (Table 2), which is greater compared with the homogeneous configuration that neglects the organic soil horizon (Table 1). The main difference between the homogeneous and three-layered models lies in the ability of the three-layered model to describe the hydrological behaviour of the soil that only reaches complete saturation in extreme circumstances. When considering precipitation with I = 50 mm/h and D = 3 h, the wetting front progressively deepens until the saturation front is formed, which occurs 52 min after the start of rainfall (Table 2). The maximum thickness of the saturated layer is about 1.8 m, which was reached after three hours of heavy rainfall.

Table 2.
Results of the Dagan–Bresler approximate model for a three-layer colluvial cover.
Figure 10 shows an infiltration diagram that was obtained by adopting the D–B model for a three-layered colluvial cover affected by a 3 h rainfall with constant intensity (I = 50 mm/h). The diagram shows a progressive increase in the water content over time, and the saturation condition in the upper part of layer 2 reached 53 min after the start of rainfall. The infiltration proceeds downward, and 124 min after the start of rainfall, the top soil layer reaches the saturation condition. In this case, the soil saturation occurs from below, starting from the organic soil–colluvium interface (layer 1–layer 2 interface). Notably, the saturation of the top soil was actually reached at the same time that the deepest colluvial layer (layer 3) started to saturate (123 min) (Figure 10). In the analysed case, the colluvial cover reached the saturation condition for a total thickness of about 135 cm shortly after 2 h of rainfall and close to 180 cm at the end of precipitation (180 min).
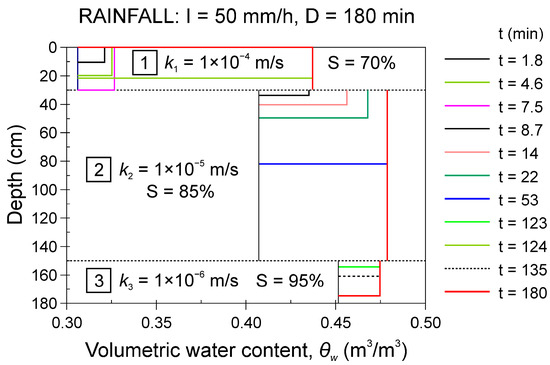
Figure 10.
Results of the Dagan–Bresler analytical model for an infiltration process triggered by a 3 h rainfall (I = 50 mm/h) into a three-layered deposit. Note the highly permeable top soil horizon with high hydraulic conductivity and low saturation degree.
5. Numerical Simulations
To verify the reliability of the analytical models, in particular the D–B model, the rainfall infiltration process was analysed using a rigorous model in which the non-linear differential equation of Richards [29] was solved by adopting the finite element method (FEM) and using the numerical code SEEP/W [88]. The infiltration numerical modelling allowed us to simulate the advancement of the wetting front and the saturation front within a horizontal colluvial cover and to evaluate the influence of the deposit stratification. To this end, both a two-layered and a three-layered stratigraphy were analysed. In detail, the two-layered configuration only considered the top 30 cm thick organic soil layer and the 120 cm thick intermediate colluvial layer, whereas the three-layered model considered the complete stratigraphic sequence previously analysed with the D–B analytical model.
The simple horizontal geometry of the colluvial cover was modelled by employing a mesh with quadrilateral elements (Figure 11), which are much more suitable for modelling ground surface processes because the primary unknown gradients are usually steeper in a direction perpendicular to the surface. The 30 cm thick top soil was modelled with elements of a size of 0.1 m × 0.06 m to guarantee a sufficient number of mesh elements in the vertical direction to properly simulate the infiltration process in this key first layer of the terrace.
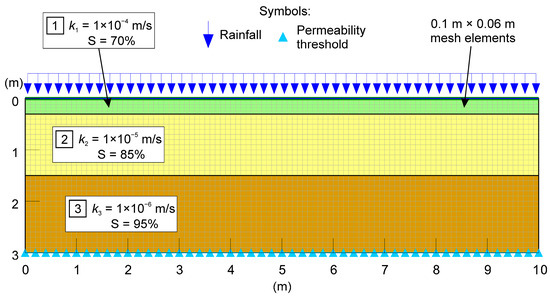
Figure 11.
Calculation section of the simulated colluvial deposit showing the mesh, the saturated permeability, and the degree of saturation of the soil layers, along with the boundary condition applied to the seepage modelling.
The values of the saturated permeability of the various soil layers were assumed to be equal to those employed in the analytical infiltration models (Figure 11). In addition, different volumetric water content and hydraulic conductivity functions were assigned to the hydrogeological units, depending on the matric suction and according to their saturated permeability. The hydraulic permeability functions were evaluated according to the soil–water characteristic curves reconstructed on the basis of some suction experimental measurements that were previously published [28,66].
The initial saturation condition of the colluvial deposit considers, for each of the modelled soil layers, a constant value of the water content over its thickness. To obtain initial degrees of saturation of the soil layers that are consistent with field measurements (Figure 11), a preliminary seepage simulation was carried out, assuming designated boundary conditions. In particular, a design hyetograph made up of alternating rainfall and dry periods was iteratively applied to the topographic surface until the initial water content was reached in the stratified deposit. At this preliminary stage of modelling, a boundary condition consisting of a null pressure head was set along the model bottom to avoid undesired positive pore–water pressures within the soil deposit.
After this stage, the infiltration process within the stratified colluvial cover resulting from an extreme hydrological event was analysed through some transient seepage analyses that considered different values of intensity and duration of precipitation. When analysing a two-layered stratigraphy, a 1 h rainfall with increasing intensity of 40, 50, 70, and 90 mm/h was assumed. For the three-layered stratigraphy, a 3 h rainfall with an intensity of 40 and 50 mm/h and a 2 h rainfall with an intensity of 70 mm/h were considered. In these transient seepage analyses, a no-flux boundary condition was applied at the base of the model to simulate the permeability threshold represented by the basal contact with the underlying bedrock, thus enabling the possible formation of a bottom-up saturation process.
The infiltration diagrams in Figure 12 and Figure 13 compare the outcomes obtained from the D–B approximate model (dashed lines) with the finite element model (solid lines) results for the two-layered deposit and the three-layered deposit, respectively. These diagrams show the trends of θw at depth and the related movement of the wetting/saturation front for the different rainfall intensity and duration values that were considered. The volumetric water content at saturation θS is also shown.
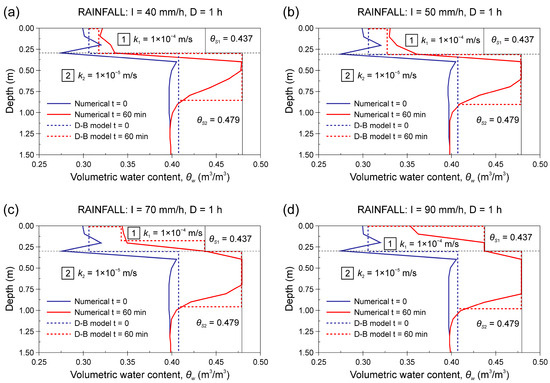
Figure 12.
Variations of the volumetric water content at depth calculated with the Dagan–Bresler model (dashed line) and the numerical model (solid line) for an infiltration process involving a two-layered colluvial deposit and for a 1 h rainfall of variable intensity: (a) 40 mm/h; (b) 50 mm/h; (c) 70 mm/h; and (d) 90 mm/h.
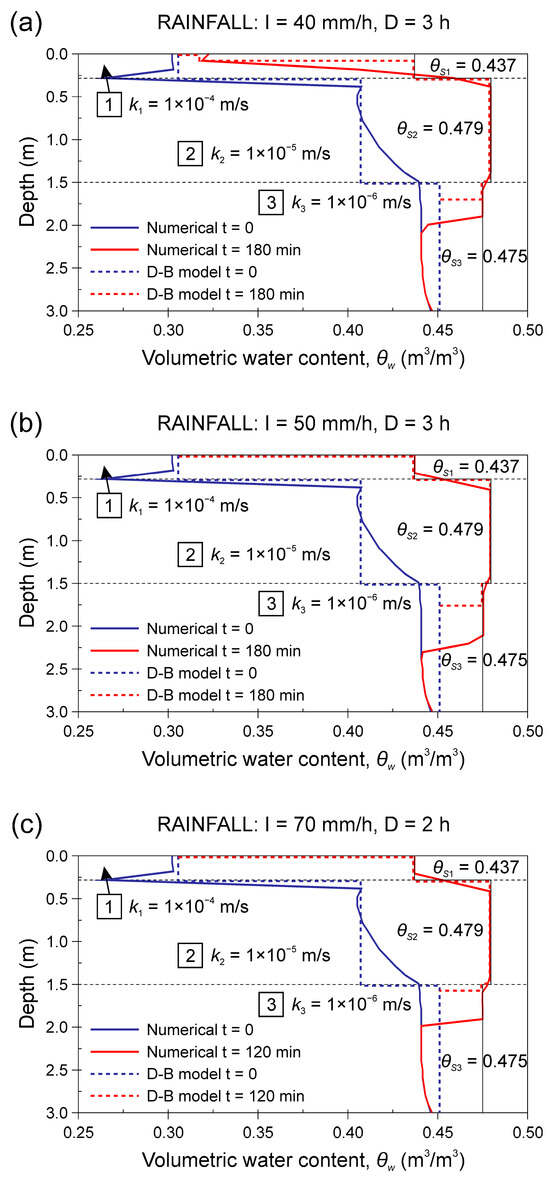
Figure 13.
Results obtained from the Dagan–Bresler model (dashed line) and the numerical model (solid line) for an infiltration process involving a three-layered colluvial deposit and for a hypothesised rainfall of variable intensity and duration: (a) 40 mm/h for 3 h; (b) 50 mm/h for 3 h; and (c) 70 mm/h for 2 h.
Overall, there was a remarkable agreement between the results provided using the D–B analytical model and those obtained from the finite element model. Indeed, both models showed that the thickness of the saturated layer significantly increases as the rainfall intensity increases (Figure 12 and Figure 13). The main difference lay in the water content profile, which was curvilinear in the rigorous numerical model rather than assuming a rectangular block shape in the D–B model. However, when analysing the two-layered stratigraphy (Figure 12), the thickness of the saturated layer that was calculated with the D–B model was generally greater than that provided by the numerical model, but this difference tended to decrease as the rainfall intensity increased. The opposite occurred for the three-layered stratigraphy (Figure 13), in which the depth reached via the saturation front was greater for the numerical model if compared with the analytical D–B model.
For a two-layered colluvial cover, the thickness of the saturated layer varied between about 10 and 50 cm because of a 1 h rainfall of I = 40 mm/h and I = 90 mm/h, respectively (Figure 12). When analysing the three-layered stratigraphy, very intense rainfall with a duration of 2–3 h caused the complete saturation of the intermediate colluvial layer and the partial downward saturation of the basal layer, with a maximum depth reached by the saturation front of about 200–220 cm (Figure 13).
The infiltration numerical modelling highlights the fundamental hydrological role played by the highly permeable organic soil horizon, which is mainly related to the possible occurrence of surficial water ponding. This fact cannot be overlooked, especially if we consider that the ponding condition represents one of the basic assumptions of the approximate infiltration models. Indeed, only in the case of extreme hydrological events (I ≥ 90 mm/h for 1 h, I ≥ 70 mm/h for 2 h or I ≥ 40 mm/h for 3 h) a partial bottom-up saturation occurs within the top soil horizon, while the saturation front simultaneously advances towards the deepest layers of the colluvial cover (Figure 12d and Figure 13).
In the previous examples of rainfall infiltration modelling, the soil water content was only analysed in relation to the duration of the intense precipitation. In fact, the approximate models are not able to analyse the subsequent stage of infiltration at depth and surficial desaturation that occurs after the rainfall ends. This key issue of the infiltration process can be investigated using numerical modelling, also allowing for the analysis of the variations in water content and pore–water pressure within the colluvial cover over time.
When analysing a three-layered colluvial deposit, the main stratigraphic discontinuities had a strong effect on the infiltration process at depth, both during the precipitation and after the rainfall ended (Figure 14). A short and very intense precipitation (I = 90 mm/h, D = 1 h) caused the formation of a top-down saturation front in the upper part of the intermediate colluvial layer (layer 2) and the simultaneous and almost complete bottom-up saturation of the top soil (red line at t = 1 h in Figure 14a). An hour after the end of precipitation (t = 2 h), the top organic soil almost returned to its initial moisture condition, whereas the top-down saturation front advanced up to the top of the basal colluvial layer (layer 3). Afterwards, the downward movement of the saturation front progressively infiltrated the basal colluvial layer, eventually reaching the underlying bedrock about seven hours after the rainfall ended (t = 8 h). Contemporarily, the desaturation process began from the top of layer 2 (Figure 14a).
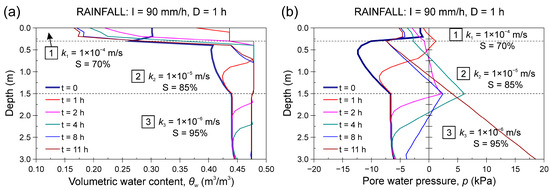
Figure 14.
Results of the infiltration numerical model that assumed a three-layered deposit with different hydrogeological characteristics. Variations in (a) volumetric water content and (b) pore–water pressure over 11 h following a 1 h rainfall with intensity of 90 mm/h.
Variations in the water content were accompanied by variations in the pore pressures within the soil, and the infiltration process determined the progressive decrease in the soil suction (Figure 14b). At the end of the precipitation (t = 1 h), positive pore pressures increased at the organic soil–colluvium interface. Pore–water pressures had a triangular pattern and were null at the saturation front, both at the bottom (within the colluvium) and at the top (within the organic soil). The same pattern also occurred in the following stages, and when the saturation front began to affect the basal colluvial layer (t = 4 h), the positive pressures increased to higher values, ultimately reaching a maximum value of about 7 kPa (Figure 14b). Ten hours after the end of precipitation (t = 11 h), the basal colluvial layer was fully saturated. As a result, pore–water pressures assumed a hydrostatic trend with a value of about 20 kPa at the colluvium–bedrock interface and a suction of about −5 kPa at the ground surface.
6. Conclusions
This work sheds light on the rainfall infiltration process within colluvial deposits caused by short and intense rainfall, using both analytical and numerical infiltration modelling. The analysed examples of colluvial covers consider both homogeneous and stratified configurations (two or three layers) characterised by saturated permeability values varying in the range k = 1 × 10−4–1 × 10−6 m/s, as is widespread in mountain environments all over the world. The intensity (I) and duration (D) of rainfall that were considered in the analyses reflect the characteristics of extreme hydrological events that have affected the Friuli Venezia Giulia Region (NE Italy) over the last 35 years (I ≥ 40 mm/h; D = 1–3 h).
Findings from the investigation demonstrate that the Green–Ampt approximate model can be effectively employed to study homogeneous colluvial covers with permeability equal to or lower than kw = 10−5 m/s that are subject to a 1 h rainfall with an intensity I ≥ 45–50 mm/h. In these circumstances, a top-down saturation front forms within the colluvial deposit, leading to the saturation of a layer with a thickness of 70–100 cm. This means that the critical condition for the saturation of colluvial deposits in the mountain area of FVG is reached every 5–10 years on average, which corresponds to a lower return period of critical hydrologic events compared with other mountain basins in the Alps. This is mainly caused by the higher initial degree of saturation that characterises colluvial covers in the mountain area of FVG during most of the year (S = 70–95%).
However, the present study also stresses two major limitations of the classic Green–Ampt model:
- The inability to simulate the formation of a wetting front, which results in its inapplicability in the case of precipitation with intensity lower than the saturated permeability of the soil (I < ksat);
- The inability to simulate the infiltration process within a stratified deposit is characterised by soil layers with different hydraulic conductivity.
These problems can be solved using the Dagan–Bresler infiltration model since the latter allows for the definition of the wetting front, and it is applicable in all conditions of rainfall intensity, deposit stratification, and soil permeability. Therefore, when studying rainfall infiltration processes in flat or low-tilted stratified colluvial deposits, the Dagan–Bresler model can be effectively employed since it provides results that are consistent with the outcomes of numerical infiltration modelling that assumes the rigorous model of Richards. This is true for both the infiltration time and the depth reached by the wetting/saturation front. The infiltration models performed ascertained that the saturated layer formed after some tens of minutes (in most cases, 10–50 min) in the upper part of the colluvial layer as a result of intense rainfall (I ≥ 50 mm/h) of short duration (D = 1–3 h). The major limitations of the D–B infiltration model are twofold. First, this approximate model considers a ponding condition, which may actually not occur due to the presence of a highly permeable top soil. Secondly, the D–B model is not able to simulate the stage of infiltration at a depth and surficial desaturation that occurs after the rainfall ends.
The D–B approximate model, as well as the numerical modelling, emphasised the strong influence of abrupt variations in the permeability of the various soil layers forming a stratified colluvial cover on the infiltration process at depth. Indeed, the inner hydrogeological discontinuities determine, particularly in the case of highly intense precipitation (I ≥ 70 mm/h), the formation of an ephemeral water table that moves simultaneously upwards and downwards. Localised pore–water overpressures can rise at the main hydrogeological discontinuities within the colluvial deposit, with maximum values in the order of 5–10 kPa. Therefore, an unfavourable condition for slope stability is represented by the occurrence of stratifications within the colluvial deposit or by the presence of an underlying bedrock at low depth, which favour an increase in pore–water pressures as a result of intense rainfall.
This study also demonstrates that the presence of a top organic soil horizon, which is rich in roots and macro-pores (first layer in Figure 3a), actually reduces the possibility of surficial ponding, which is the basic condition for the “piston” infiltration models. As a result, the presence of a top layer characterised by a greater hydraulic conductivity (k1 = 10−4 m/s) and a lower degree of saturation (S = 70%) must be taken into account in the infiltration model to carry out a realistic simulation. The organic soil horizon allows for a rapid downward infiltration up to contact with the underlying colluvial material, which is less permeable (k2 = 10−5 m/s). Therefore, a saturated sub-surficial layer forms starting from the organic soil–colluvium interface. In this circumstance, the advancement of the saturation front occurs both upwards, within the organic soil and downwards, within the colluvial deposit. Outcomes of the numerical infiltration modelling showed that the saturation process mainly involves the low-permeable colluvial materials, whereas the top organic soil horizon is involved in a bottom-up saturation process only in the case of very intense precipitation (I ≥ 90 mm/h for 1 h, I ≥ 70 mm/h for 2 h, or I ≥ 40 mm/h for 3 h). This evidence demonstrates that the ponding condition can only occur for extreme hydrological events that induce complete saturation of the high-permeable top organic soil.
Modelling of the infiltration and saturation processes involving thin shallow colluvial deposits during and after storms is an essential pre-requisite to properly understand the achievement of critical conditions for slope stability of many Alpine landforms. The analysed examples demonstrated that heavy rainfall induces a very rapid infiltration/saturation process with a duration of a few hours (1–6 h, in most cases) involving a 1–3 m-thick colluvial deposit. The rapidity of this process makes this phenomenon difficult to ascertain by means of traditional measuring instruments, especially for stratified situations. As a result, the spatio–temporal evolution of infiltration rate under natural conditions cannot be deduced by direct field measurements. Consequently, infiltration modelling remains an irreplaceable tool to realistically reproduce the rapid changes in the matric suction and/or pore–water pressure within soil deposits that are caused by intense rainfall of short duration. However, both analytical and numerical simulations should be preceded by accurate field surveys aimed at ascertaining the stratigraphy and the degree of saturation of colluvial deposits during the year. After this field characterisation, proper moisture values should be assigned to the various material layers of the schematised model before performing the simulations. In addition, when performing infiltration modelling as well as subsequent slope stability analyses, spatial variability and uncertainty of the geotechnical and hydrological parameters should be considered, even in homogeneous soils [89,90].
Author Contributions
Conceptualization, P.P. and A.B.; methodology, P.P.; software, A.B.; validation, P.P., D.F. and A.B.; investigation, P.P. and A.B.; resources, P.P. and D.F.; data curation, A.B.; writing—original draft preparation, A.B.; writing—review and editing, P.P., D.F. and A.B.; supervision, P.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was carried out in the frame of the project PON 2014–2021 entitled “Hydrogeological instability, infrastructures and resilience: approaches and methodologies to experience a safer territory”, funded by the Ministero dell’Università e della Ricerca of the Italian Government, the European Union, and the University of Udine, in collaboration with the company Alpe Engineering s.r.l. (Prot. n. 782/2022).
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Turner, A.K. Colluvium and talus. In Landslides: Investigation and Mitigation; Transportation Research Board Special Report 247; Turner, A.K., Schuster, R.L., Eds.; National Research Council: Washington, DC, USA, 1996; pp. 525–554. [Google Scholar]
- Goudie, A. Colluvium. In Encyclopedia of Geomorphology; International Association of Geomorphologists; Routledge: New York, NY, USA, 2004; 568p. [Google Scholar]
- Parry, S. The application of geomorphological mapping in the assessment of landslide hazard in Hong Kong. In Developments in Earth Surface Processes—Geomorphological Mapping, Mehods and Applications; Smith, M.J., Paron, P., Griffiths, J.S., Eds.; Elsevier: Amsterdam, The Netherlands, 2011; pp. 413–441. [Google Scholar]
- Borradaile, G. Geological maps and some basic terminology. In Understanding Geology through Maps; Borradaile, G., Ed.; Elsevier: Amsterdam, The Netherlands, 2014; pp. 1–14. [Google Scholar]
- Surian, N.; Pellegrini, G.B. Paraglacial sedimentation in the Piave Valley (Eastern Alps, Italy): An example of fluvial processes conditioned by glaciation. Geogr. Fis. Dinam. Quat. 2000, 23, 87–92. [Google Scholar]
- Colucci, R.R.; Monegato, G.; Žebre, M. Glacial and proglacial deposits of the Resia Valley (NE Italy): New insights on the onset and decay of the Last Alpine Glacial Maximum in the Julian Alps. Alp. Mediterr. Quat. 2014, 27, 85–104. [Google Scholar]
- Millar, S.W.S. Colluvial deposit. In Encyclopedia of Planetary Landforms; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Cremaschi, M.; Trombino, L.; Zerboni, A. Palaeosoils and relict soils: A systematic review. In Interpretation of Micromorphological Features of Soils and Regoliths; Stoops, G., Marcelino, V., Mees, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 863–894. [Google Scholar]
- Mücher, H.; van Steijn, H.; Kwaad, F. Colluvial and mass wasting deposits. In Interpretation of Micromorphological Features of Soils and Regoliths; Stoops, G., Marcelino, V., Mees, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 21–36. [Google Scholar]
- Assouline, S. Infiltration into soils: Conceptual approaches and solutions. Water Resour. Res. 2013, 49, 1755–1772. [Google Scholar] [CrossRef]
- Brutsaert, W. Hydrology: An introduction, 2nd ed.; Cambridge University Press: Cambridge, UK, 2023; 609p. [Google Scholar] [CrossRef]
- Johnson, K.A.; Sitar, N. Hydrologic conditions leading to debris flow initiation. Can. Geotech. J. 1990, 27, 789–801. [Google Scholar] [CrossRef]
- Cai, F.; Ugai, K. Numerical analysis of rainfall effects on slope stability. Int. J. Geomech. 2004, 4, 69–78. [Google Scholar] [CrossRef]
- Rahardjo, H.; Ong, T.H.; Rezaur, R.B.; Leong, E.C.; Fredlund, D.G. Response parameters for characterization of infiltration. Environ. Earth Sci. 2010, 60, 1369–1380. [Google Scholar] [CrossRef]
- Bittelli, M.; Valentino, R.; Salvatorelli, F.; Rossi Pisa, P. Monitoring soil-water and displacement conditions leading to landslide occurrence in partially saturated clays. Geomorphology 2012, 173–174, 161–173. [Google Scholar] [CrossRef]
- Nilsen, T.H.; Wright, R.H.; Vlasic, T.C.; Spangle, W.E. Relative Slope Stability and Land-Use Planning in the San Francisco Bay Region, California; Geological Survey Professional Paper 944; US Government Printing Office: Washington, DC, USA, 1979; 105p.
- Fleming, R.W.; Johnson, A.M. Landslides in Colluvium; US Geological Survey Bulletin 2059-B; US Government Printing Office: Washington, DC, USA, 1994; 28p.
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Siva Subramanian, S.; Ishikawa, T.; Tokoro, T. Stability assessment approach for soil slopes in seasonal cold regions. Eng. Geol. 2017, 221, 154–169. [Google Scholar] [CrossRef]
- Hinds, E.S.; Lu, N.; Mirus, B.B.; Godt, J.W.; Wayllace, A. Evaluation of techniques for mitigating snowmelt infiltration-induced landsliding in a highway embankment. Eng. Geol. 2021, 291, 106240. [Google Scholar] [CrossRef]
- Haque, U.; da Silva, P.F.; Devoli, G.; Pilz, G.; Zhao, B.; Khaloua, A.; Wilipo, W.; Andersen, P.; Lu, P.; Lee, J.; et al. The human cost of global warming: Deadly landslides and their triggers (1995–2014). Sci. Total Environ. 2019, 682, 673–684. [Google Scholar] [CrossRef]
- Li, P.; Li, T.; Vanapalli, S.K. Influence of environmental factors on the wetting front depth: A case study in the Loess Plateau. Eng. Geol. 2016, 214, 1–10. [Google Scholar] [CrossRef]
- Yang, K.-H.; Uzuoka, R.; Thuo, J.N.; Lin, G.-L.; Nakai, Y. Coupled hydro-mechanical analysis of two unstable unsaturated slopes subject to rainfall infiltration. Eng. Geol. 2017, 216, 13–30. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, D.; Zhang, S. Shallow slope instability evolution during rainwater infiltration considering soil cracking state. Comput. Geotech. 2020, 117, 103285. [Google Scholar] [CrossRef]
- Baum, R.L.; Godt, J.W.; Savage, W.Z. Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration. J. Geophys. Res. 2010, 115, F03013. [Google Scholar] [CrossRef]
- Bordoni, M.; Meisina, C.; Valentino, R.; Lu, N.; Bittelli, M.; Chersich, S. Hydrological factors affecting rainfall-induced shallow landslides: From the field monitoring to a simplified slope stability analysis. Eng. Geol. 2015, 193, 19–37. [Google Scholar] [CrossRef]
- Smith, R.E. Infiltration Theory for Hydrologic Applications; Water Resources Monograph, American Geophysical Union: Washington, DC, USA, 2002; 212p. [Google Scholar]
- Paronuzzi, P.; Bolla, A. Rainfall infiltration and slope stability of alpine colluvial terraces subject to storms (NE Italy). Eng. Geol. 2023, 323, 107199. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. Physics 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Tsaparas, I.; Rahardjo, H.; Toll, D.G.; Leong, E.C. Controlling parameters for rainfall-induced landslides. Comput. Geotech. 2002, 29, 1–27. [Google Scholar] [CrossRef]
- Yang, C.; Sheng, D.; Carter, J.P. Effect of hydraulic hysteresis on seepage analysis for unsaturated soils. Comput. Geotech. 2012, 41, 36–56. [Google Scholar] [CrossRef]
- Cuomo, S.; Della Sala, M. Rainfall-induced infiltration, runoff and failure in steep unsaturated shallow soil deposits. Eng. Geol. 2013, 162, 118–127. [Google Scholar] [CrossRef]
- Liang, W.-L.; Uchida, T. Effects of topography and soil depth on saturated-zone dynamics in steep hillslopes explored using the three-dimensional Richards’ equation. J. Hydrol. 2014, 510, 124–136. [Google Scholar] [CrossRef]
- Damiano, E.; Greco, R.; Guida, A.; Olivares, L.; Picarelli, L. Investigation on rainwater infiltration into layered shallow covers in pyroclastic soils and its effect on slope stability. Eng. Geol. 2017, 220, 208–218. [Google Scholar] [CrossRef]
- Peranić, J.; Mihalić Arbanas, S.; Arbanas, Ž. Importance of the unsaturated zone in landslide reactivation on flysch slopes: Observations from Valići Landslide, Croatia. Landslides 2021, 18, 3737–3751. [Google Scholar] [CrossRef]
- Sun, P.; Wang, H.; Wang, G.; Li, R.; Zhang, Z.; Huo, X. Field model experiments and numerical analysis of rainfall-induced shallow loess landslides. Eng. Geol. 2021, 295, 106411. [Google Scholar] [CrossRef]
- Li, X.; Handwerger, A.L.; Buscarnera, G. Viscoplastic modelling of rainfall-driven slow-moving landslides: Application to California Coast Ranges. Landslides 2023, 20, 1101–1113. [Google Scholar] [CrossRef]
- Morbidelli, R.; Corradini, C.; Saltalippi, C.; Flammini, A.; Dari, J.; Govindaraju, R.S. Rainfall infiltration modeling: A review. Water 2018, 10, 1873. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G.A. Studies on soil physics: 1. The flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Dai, F.C.; Lee, C.F.; Wang, S. Analysis of rainstorm-induced slide-debris flows on natural terrain of Lantau Island, Hong Kong. Eng. Geol. 1999, 51, 279–290. [Google Scholar]
- Fourie, A.B.; Rowe, D.; Blight, G.E. The effect of infiltration on the stability of the slopes of a dry ash dump. Géotechnique 1999, 49, 1–13. [Google Scholar] [CrossRef]
- Cho, S.E. Prediction of shallow landslide by surficial stability analysis considering rainfall infiltration. Eng. Geol. 2017, 231, 126–138. [Google Scholar] [CrossRef]
- Tozato, K.; Dolojan, N.L.J.; Touge, Y.; Kure, S.; Moriguchi, S.; Kawagoe, S.; Kazama, S.; Terada, K. Limit equilibrium method-based 3D slope stability analysis for wide area considering influence of rainfall. Eng. Geol. 2022, 308, 106808. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; Or, D.; Kavvas, M.L.; Rolston, D.E.; Biggar, J. Error analyses of simplified unsaturated flow models under large uncertainty in hydraulic properties. Water Resour. Res. 1992, 28, 2913–2924. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; Kavvas, M.L.; Jones, S.E.; Rolston, D.E. Use of Green-Ampt model for analyzing one-dimensional convective transport in unsaturated soils. J. Hydrol. 1996, 178, 337–350. [Google Scholar] [CrossRef]
- Chen, L.; Young, M.H. Green-Ampt infiltration model for sloping surfaces. Water Resour. Res. 2006, 42, W07420. [Google Scholar] [CrossRef]
- Kale, R.V.; Sahoo, B. Green-Ampt infiltration models for varied field conditions: A revisit. Water Resour. Manag. 2011, 25, 3505–3536. [Google Scholar] [CrossRef]
- Beven, K. Infiltration into a class of vertically non-uniform soils. Hydrol. Sci. J. 1984, 29, 425–434. [Google Scholar] [CrossRef]
- Selker, J.S.; Duan, J.; Parlange, J.-Y. Green and Ampt infiltration into soils of variable pore size with depth. Water Resour. Res. 1999, 35, 1685–1688. [Google Scholar] [CrossRef]
- Chu, X.; Mariño, M.A. Determination of ponding condition and infiltration into layered soils under unsteady rainfall. J. Hydrol. 2005, 313, 195–207. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Feng, J. Green–Ampt model for layered soils with nonuniform initial water content under unsteady infiltration. Soil Sci. Soc. Am. J. 2008, 72, 1041–1047. [Google Scholar] [CrossRef]
- Dagan, G.; Bresler, E. Unsaturated flow in spatially variable fields. 1. Derivation of models of infiltration and redistribution. Water Resour. Res. 1983, 19, 413–420. [Google Scholar] [CrossRef]
- Dagan, G.; Bresler, E. Unsaturated flow in spatially variable fields. 2. Application of water flows models to various fields. Water Resour. Res. 1983, 19, 421–428. [Google Scholar] [CrossRef]
- Cho, S.E. Infiltration analysis to evaluate the surficial stability of two-layered slopes considering rainfall characteristics. Eng. Geol. 2009, 105, 32–43. [Google Scholar] [CrossRef]
- Corradini, C.; Melone, F.; Smith, R.E. A unified model for infiltration and redistribution during complex rainfall patterns. J. Hydrol. 1997, 192, 104–124. [Google Scholar] [CrossRef]
- Segalini, A.; Giani, G.P.; Ferrero, A.M. Geomechanical studies on slow slope movements in Parma Apennine. Eng. Geol. 2009, 109, 31–44. [Google Scholar] [CrossRef]
- García-Ruiz, J.M.; Beguería, S.; Alatorre, L.C.; Puigdefábregas, J. Land cover changes and shallow landsliding in the flysch sector of the Spanish Pyrenees. Geomorphology 2010, 124, 250–259. [Google Scholar] [CrossRef]
- Kamiński, M.; Zientara, P.; Krawczyk, M. Electrical resistivity tomography and digital aerial photogrammetry in the research of the “Bachledzki Hill” active landslide—In Podhale (Poland). Eng. Geol. 2021, 285, 106004. [Google Scholar] [CrossRef]
- Zádarová, T.; Penížek, V.; Koubová, M.; Lisá, L.; Pavlů, L.; Tejnecký, V.; Žižala, D.; Drábek, O.; Němeček, K.; Vaněk, A.; et al. Formation of Colluvisols in different soil regions and slope positions (Czechia): Post-sedimentary pedogenesis in colluvial material. Catena 2023, 229, 107233. [Google Scholar] [CrossRef]
- Zanini, E.; Petrella, F.; Ajmone Marsan, F.; Arduino, E. The soils on the flysch area of Western Liguria (Italy). Catena 1988, 15, 381–392. [Google Scholar] [CrossRef]
- Azañón, J.M.; Azor, A.; Yesares, J.; Tsige, M.; Mateos, R.M.; Nieto, F.; Delgado, J.; López-Chicano, M.; Martín, W.; Rodríguez-Fernández, J. Regional-scale high-plasticity clay-bearing formation as controlling factor on landslides in Southeast Spain. Geomorphology 2010, 120, 26–37. [Google Scholar] [CrossRef]
- Anis, Z.; Wissem, G.; Riheb, H.; Biswajeet, P.; Essghaier, G.M. Effects of clay properties in the landslides genesis in flysch massif: Case study of Aïn Draham, North Western Tunisia. J. Afr. Earth Sci. 2019, 151, 146–152. [Google Scholar] [CrossRef]
- Musielok, L.; Buczek, K.; Karcz, T. Relief-induced feedback mechanisms controlling local podsolization occurrence on flysch slopes—Examples from Outer Western Carpathians (southern Poland). Catena 2022, 213, 106124. [Google Scholar] [CrossRef]
- Stumvoll, M.J.; Schmaltz, E.M.; Kanta, R.; Roth, H.; Grall, B.; Luhn, J.; Flores-Orozco, A.; Glade, T. Exploring the dynamics of a complex, slow-moving landslide in the Austrian Flysch Zone with 4D surface and subsurface information. Catena 2022, 214, 106203. [Google Scholar] [CrossRef]
- Önalp, A.; Bol, E.; Özocak, A.; Sert, S.; Ural, N.; Arel, E. Influence of index properties on the cyclic failure of fine-grained soils. Eng. Geol. 2023, 317, 107056. [Google Scholar] [CrossRef]
- Paronuzzi, P.; Del Fabbro, M.; Bolla, A. Soil moisture profiles of unsaturated colluvial slopes susceptible to rainfall-induced landslides. Geosciences 2022, 12, 12010006. [Google Scholar] [CrossRef]
- Paronuzzi, P.; Vanon, R. Eventi pluviometrici critici e dissesti: Studio della franosità del Comune di Paularo (Friuli—Alpi Carniche). Geoing. Ambient. Mineraria 1995, 85, 21–31. [Google Scholar]
- Paronuzzi, P.; Coccolo, A.; Garlatti, G. Eventi meteorici critici e debris flows nei bacini montani del Friuli. L’Acqua, Riv. It. Idrologia Tecnica 1998, 6, 39–50. [Google Scholar]
- Pradel, D.; Raad, G. Effect of permeability on surficial stability of homogenous slopes. J. Geotech. Eng. ASCE 1993, 119, 315–332. [Google Scholar] [CrossRef]
- Li, W.C.; Lee, L.M.; Cai, H.; Li, H.L.; Dai, F.C.; Wang, M.L. Combined roles of saturated permeability and rainfall characteristics on surficial failure of homogeneous soil slope. Eng. Geol. 2013, 153, 105–113. [Google Scholar] [CrossRef]
- Rahardjo, H.; Satyanaga, A.; Leong, E.-C. Effects of flux boundary conditions on pre-water pressure distribution in slope. Eng. Geol. 2013, 165, 133–142. [Google Scholar] [CrossRef]
- Lim, T.T.; Rahardjo, H.; Chang, M.F.; Fredlund, D.G. Effects of rainfall on matric suctions in a residual soil slope. Can. Geotech. J. 1996, 33, 618–628. [Google Scholar] [CrossRef]
- Dapporto, S.; Aleotti, P.; Casagli, N.; Polloni, G. Analysis of shallow failures triggered by the 14–16 November 2022 event in the Albaredo valley, Valtellina (Northern Italy). Adv. Geosci. 2005, 2, 305–308. [Google Scholar] [CrossRef]
- Jeong, S.; Lee, K.; Kim, J.; Kim, Y. Analysis of rainfall-induced landslide on unsaturated soil slopes. Sustainability 2017, 9, 1280. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Shi, Q. A numerical investigation of the stability of unsaturated soil slopes subjected to transient seepage. Comput. Geotech. 1998, 22, 1–28. [Google Scholar] [CrossRef]
- Gasmo, J.M.; Rahardjo, H.; Leong, E.C. Infiltration effects on stability of a residual soil slope. Comput. Geotech. 2000, 26, 145–165. [Google Scholar] [CrossRef]
- Rahimi, A.; Rahardjo, H.; Leong, E.-C. Effect of antecedent rainfall patterns on rainfall-induced slope failure. J. Geotech. Geoenviron. Eng. 2011, 137, 483–491. [Google Scholar] [CrossRef]
- Balzano, B.; Tarantino, A.; Ridley, A. Preliminary analysis on the impacts of the rhizosphere on occurrence of rainfall-induced shallow landslides. Landslides 2019, 16, 1885–1901. [Google Scholar] [CrossRef]
- Rice, R.M.; Corbett, E.S.; Bailey, R.G. Soil slips related to vegetation, topography, and soil in Southern California. Water Resour. Res. 1969, 5, 647–659. [Google Scholar] [CrossRef]
- Shakoor, A.; Smithmyer, A.J. An analysis of storm-induced landsides in colluvial soils overlying mudrock sequences, southestern Ohio, USA. Eng. Geol. 2005, 78, 257–274. [Google Scholar] [CrossRef]
- Li, X.; Lizárraga, J.J.; Buscarnera, G. Regional-scale simulation of flowslide triggering in stratified deposits. Eng. Geol. 2021, 292, 106248. [Google Scholar] [CrossRef]
- Qin, M.; Cui, P.; Jiang, Y.; Guo, J.; Zhang, G.; Ramzan, M. Occurrence of shallow landslides triggered by increased hydraulic conductivity due to tree roots. Landslides 2022, 19, 2593–2604. [Google Scholar] [CrossRef]
- Reid, M.E.; Nielsen, H.P.; Dreiss, S.J. Hydrologic factors triggering a shallow hillslope failure. Bull. Assoc. Eng. Geol. 1988, 25, 349–361. [Google Scholar] [CrossRef]
- Wieczorek, G.F. Landslide triggering mechanisms. In Landslides: Investigation and Mitigation; Transportation Research Board Special Report 247; Turner, A.K., Schuster, R.L., Eds.; National Research Council: Washington, DC, USA, 1996; pp. 76–79. [Google Scholar]
- Khan, M.S.; Hossain, S.; Ahmed, A.; Faysal, M. Investigation of a shallow slope failure on expansive clay in Texas. Eng. Geol. 2017, 219, 118–129. [Google Scholar] [CrossRef]
- Dey, N.; Sengupta, A. Effect of rainfall on the triggering of the devastating slope failure at Malin, India. Nat. Hazards 2018, 94, 1391–1413. [Google Scholar] [CrossRef]
- Brand, E.W.; Premchitt, J.; Phillipson, H.B. Relationship between rainfall and landslides in Honk Hong. In Proceedings of the 4th International Symposium on Landslides, Toronto, ON, Canada, 16–21 September 1984; pp. 377–384. [Google Scholar]
- Geo-Slope International Ltd. Seepage and Stability Modeling with SEEP/W and SLOPE/W; Users Manuals; Geo-Slope International Ltd.: Calgary, AB, Canada, 2016. [Google Scholar]
- Burton, A.; Arkell, T.J.; Bathurst, J.C. Field variability of landslide model parameters. Environ. Geol. 1998, 35, 100–114. [Google Scholar] [CrossRef]
- Tofani, V.; Bicocchi, G.; Rossi, G.; Segoni, S.; D’Ambrosio, M.; Casagli, N.; Catani, F. Soil characterization for shallow landslides modeling: A case study in the Northern Apennines (Central Italy). Landslides 2017, 14, 755–770. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).