A Multiphysics Simulation of the Effects of Wicking Geotextile on Mitigating Frost Heave under Cold Region Pavement
Abstract
1. Introduction
2. Theoretical Background
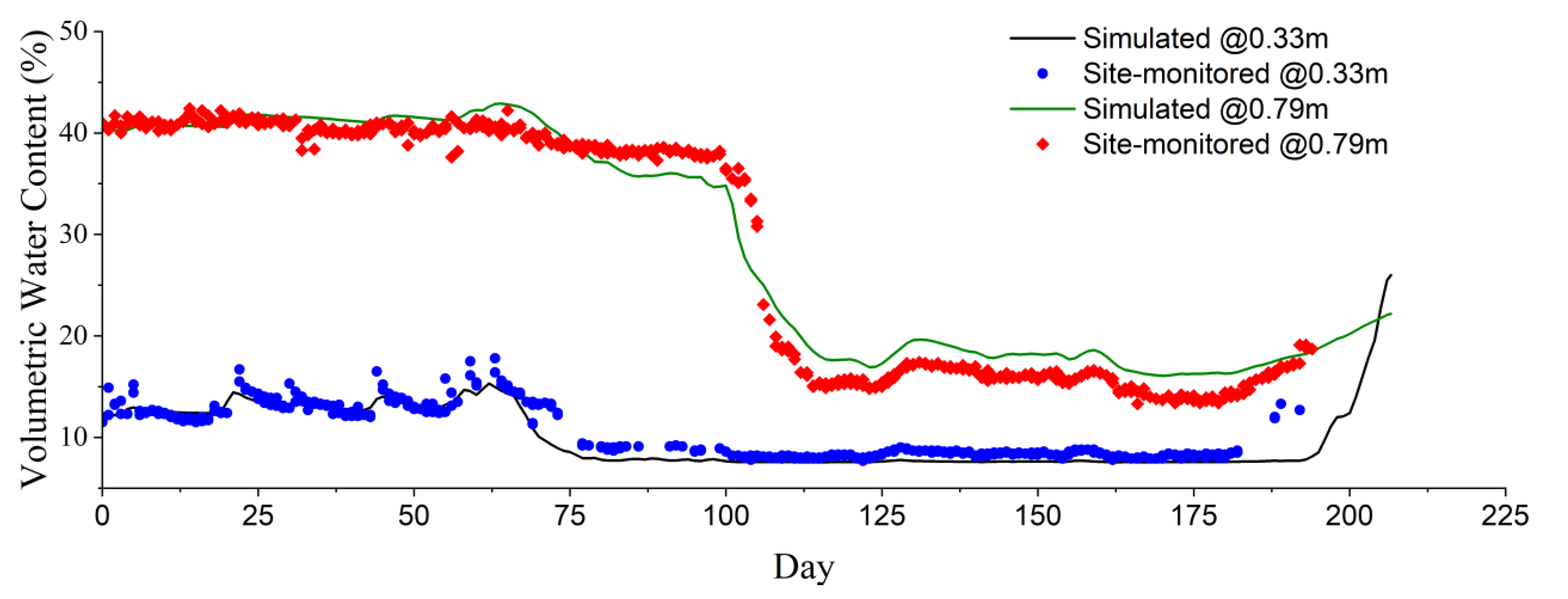
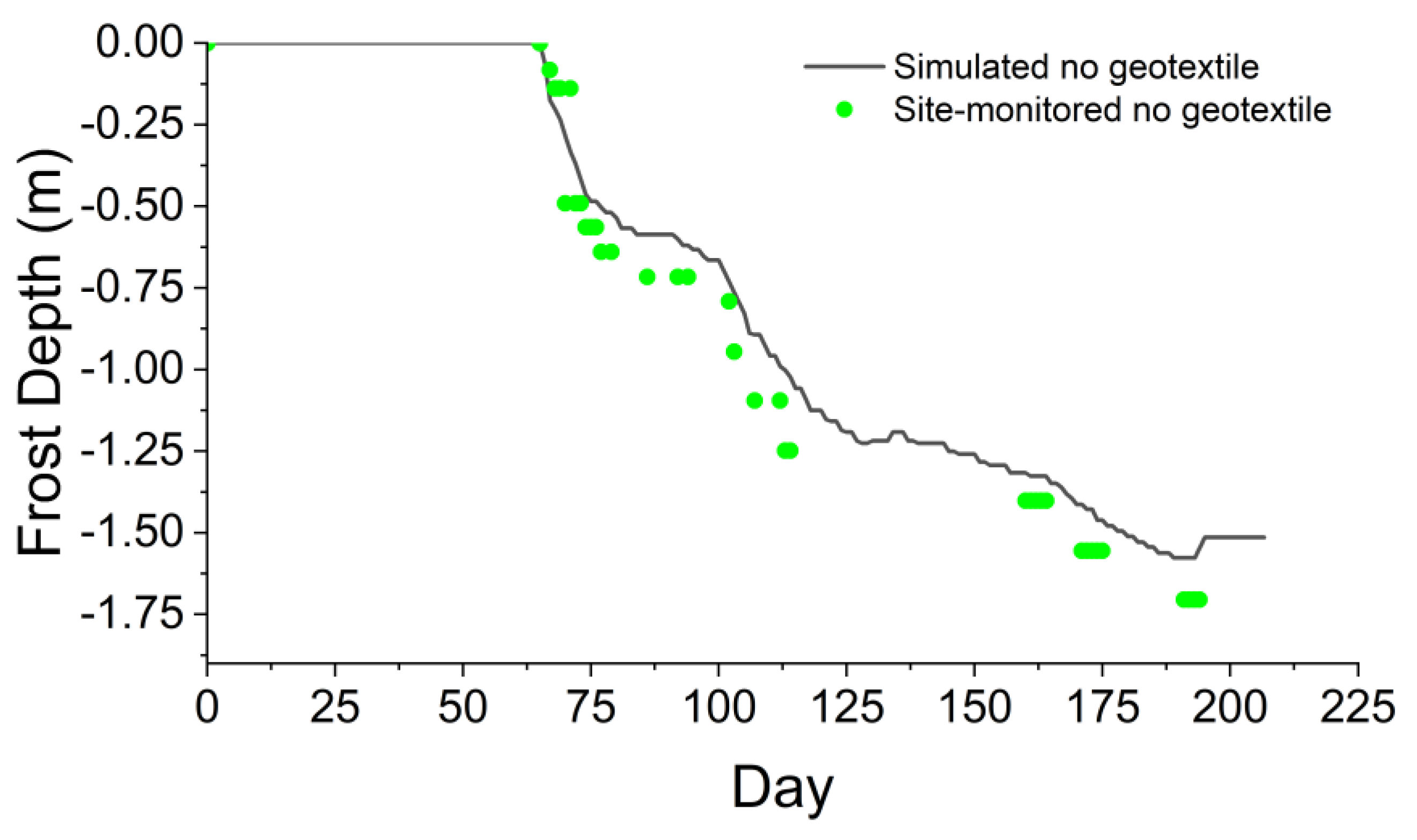
3. Model Validation
4. The Effects of Wicking Geotextile on Frost Heave Mitigation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mukhopadhyay, A.; Ye, D.; Zollinger, D. Moisture-Related Cracking Effects on Hydrating Concrete Pavement; Texas Transportation Institute, Texas A & M University System: College State, TX, USA, 2006; Volume 7. [Google Scholar]
- Puppala, A.J.; Manosuthkij, T.; Nazarian, S.; Hoyos, L.R. Threshold Moisture Content and Matric Suction Potentials in Expansive Clays Prior to Initiation of Cracking in Pavements. Can. Geotech. J. 2011, 48, 519–531. [Google Scholar] [CrossRef]
- Dong, S.; Jiang, Y.; Yu, X. A Novel Random Finite Element Model for Holistically Modeling of the Frost Effects on Soils and Cold Region Pavements. J. Infrastruct. Preserv. Resil. 2022, 3, 16. [Google Scholar] [CrossRef]
- Liu, H.; Han, J.; Al-Naddaf, M.; Parsons, R.L.; Kakrasul, J.I. Field Monitoring of Wicking Geotextile to Reduce Soil Moisture under a Concrete Pavement Subjected to Precipitations and Temperature Variations. Geotext. Geomembr. 2022, 50, 1004–1019. [Google Scholar] [CrossRef]
- Biswas, N.; Puppala, A.J.; Khan, M.A.; Congress, S.S.C.; Banerjee, A.; Chakraborty, S. Evaluating the Performance of Wicking Geotextile in Providing Drainage for Flexible Pavements Built over Expansive Soils. Transp. Res. Rec. 2021, 2675, 208–221. [Google Scholar] [CrossRef]
- Guo, J.; Han, J.; Zhang, X.; Li, Z. Experimental Evaluation of Wicking Geotextile-Stabilized Aggregate Bases over Subgrade under Rainfall Simulation and Cyclic Loading. Geotext. Geomembr. 2021, 49, 1550–1564. [Google Scholar] [CrossRef]
- Lin, C.; Zhang, X.; Galinmoghadam, J.; Guo, Y. Working Mechanism of a New Wicking Geotextile in Roadway Applications: A Numerical Study. Geotext. Geomembr. 2022, 50, 323–336. [Google Scholar] [CrossRef]
- Zornberg, J.G.; Azevedo, M.; Sikkema, M.; Odgers, B. Geosynthetics with Enhanced Lateral Drainage Capabilities in Roadway Systems. Transp. Geotech. 2017, 12, 85–100. [Google Scholar] [CrossRef]
- Lin, C.; Galinmoghadam, J.; Han, J.; Liu, J.; Zhang, X. Quantifying and Incorporating the Benefits of Wicking Geotextile into Pavement Design. J. Transp. Eng. Part B Pavements 2021, 147, 04021044. [Google Scholar] [CrossRef]
- Wu, Y.; Ishikawa, T.; Maruyama, K.; Ueno, C.; Yasuoka, T.; Okuda, S. Modeling Wicking Fabric Inhibition Effect on Frost Heave. Appl. Sci. 2022, 12, 4357. [Google Scholar] [CrossRef]
- Wu, Y. Effect Verification of Wicking Fabric on Inhibition to Frost Heave at Cold Region Pavement. Ph.D. Thesis, Hokkaido University Sapporo, Sapporo, Japan, 2022. [Google Scholar]
- Guo, J.; Wang, F.; Zhang, X.; Han, J. Quantifying Water Removal Rate of a Wicking Geotextile under Controlled Temperature and Relative Humidity. J. Mater. Civ. Eng. 2017, 29, 04016181. [Google Scholar] [CrossRef]
- Wang, F.; Han, J.; Zhang, X.; Guo, J. Laboratory Tests to Evaluate Effectiveness of Wicking Geotextile in Soil Moisture Reduction. Geotext. Geomembr. 2017, 45, 8–13. [Google Scholar] [CrossRef]
- Lin, C.; Zhang, X. Laboratory Drainage Performance of a New Geotextile with Wicking Fabric. J. Mater. Civ. Eng. 2018, 30, 04018293. [Google Scholar] [CrossRef]
- Zaman, M.W.; Han, J.; Zhang, X. Evaluating Wettability of Geotextiles with Contact Angles. Geotext. Geomembr. 2022, 50, 825–833. [Google Scholar] [CrossRef]
- Zhang, X.; Galinmoghadam, J. Performance of Wicking Geotextile on Mitigating Water Pumping Issue on I-44 Highway; Department of Transportation, Construction and Materials Division: Kansas City, MI, USA, 2020. [Google Scholar]
- Ud Din, I.M.; Mir, M.S.; Farooq, M.A. Effect of Freeze-Thaw Cycles on the Properties of Asphalt Pavements in Cold Regions: A Review. Transp. Res. Procedia 2020, 48, 3634–3641. [Google Scholar] [CrossRef]
- Qiao, Y.; Dawson, A.R.; Parry, T.; Flintsch, G.; Wang, W. Flexible Pavements and Climate Change: A Comprehensive Review and Implicatio. Sustainability 2020, 12, 1057. [Google Scholar] [CrossRef]
- Jiang, Y.; Yu, X. Holistic Multiphysics Simulation of the Climatic Responses of Cold Region Pavements. J. Infrastruct. Preserv. Resil. 2023, 4, 24. [Google Scholar] [CrossRef]
- Krantz, W.B. A Generalized Secondary Frost. SIAM J. Appl. Math. 1994, 54, 1650–1675. [Google Scholar]
- Zhan, Y.; Lu, Z.; Yao, H.; Xian, S. A Coupled Thermo-Hydromechanical Model of Soil Slope in Seasonally Frozen Regions under Freeze-Thaw Action. Adv. Civ. Eng. 2018, 2018, 7219826. [Google Scholar] [CrossRef]
- Subramanian, S.S. Numerical Modelling and Geomechanical Analyses of Soil Slope Stability Evaluation in Seasonal Cold Regions. Ph.D. Thesis, Hokkaido University Sapporo, Sapporo, Japan, 2017; pp. 1–117. [Google Scholar]
- Simonsen, E.; Isacsson, U. Thaw Weakening of Pavement Structures in Cold Regions. Cold Reg. Sci. Technol. 1999, 29, 135–151. [Google Scholar] [CrossRef]
- Zhang, X.; Presler, W.; Li, L.; Jones, D.; Odgers, B. Use of Wicking Fabric to Help Prevent Frost Boils in Alaskan Pavements. J. Mater. Civ. Eng. 2014, 26, 728–740. [Google Scholar] [CrossRef]
- Lin, C.; Presler, W.; Zhang, X.; Jones, D.; Odgers, B. Long-Term Performance of Wicking Fabric in Alaskan Pavements. J. Perform. Constr. Facil. 2017, 31, D4016005. [Google Scholar] [CrossRef]
- Noborio, K.; McInnes, K.J.; Heilman, J.L. Two-Dimensional Model for Water, Heat, and Solute Transport in Furrow-Irrigated Soil: II. Field Evaluation. Soil Sci. Soc. Am. J. 1996, 60, 1010–1021. [Google Scholar] [CrossRef]
- Konrad, J.M. Sixteenth Canadian Geotechnical Colloquium: Frost Heave in Soils: Concepts and Engineering. Can. Geotech. J. 1994, 31, 223–245. [Google Scholar] [CrossRef]
- Hansson, K.; Šimůnek, J.; Mizoguchi, M.; Lundin, L.; Genuchten, M.T. Water Flow and Heat Transport in Frozen Soil: Numerical Solution and Freeze–Thaw Applications. Vadose Zo. J. 2004, 3, 693–704. [Google Scholar] [CrossRef]
- Liu, X.; Rees, S.J.; Spitler, J.D. Modeling Snow Melting on Heated Pavement Surfaces. Part I: Model Development. Appl. Therm. Eng. 2007, 27, 1115–1124. [Google Scholar] [CrossRef]
- Wang, C.; Ma, Z. Mathematical Model and Numerical Simulation of Hydrothermal Coupling for Unsaturated Soil Subgrade in the Seasonal Frozen Zone. IOP Conf. Ser. Earth Environ. Sci. 2021, 719, 032042. [Google Scholar] [CrossRef]
- Li, N.; Chen, B.; Chen, F.; Xu, X. The Coupled Heat-Moisture-Mechanic Model of the Frozen Soil. Cold Reg. Sci. Technol. 2000, 31, 199–205. [Google Scholar] [CrossRef]
- Coussy, O.; Monteiro, P. Unsaturated Poroelasticity for Crystallization in Pores. Comput. Geotech. 2007, 34, 279–290. [Google Scholar] [CrossRef]
- Sweidan, A.H.; Niggemann, K.; Heider, Y.; Ziegler, M.; Markert, B. Experimental Study and Numerical Modeling of the Thermo-Hydro-Mechanical Processes in Soil Freezing with Different Frost Penetration Directions. Acta Geotech. 2022, 17, 231–255. [Google Scholar] [CrossRef]
- Dong, S.; Jiang, Y.; Yu, X. Analyses of the Impacts of Climate Change and Forest Fire on Cold Region Slopes Stability by Random Finite Element Method. Landslides 2021, 18, 2531–2545. [Google Scholar] [CrossRef]
- Anderson, D.M.; Tice, A.R.; McKim, H.L. Unfrozen Water and the Apparent Specific Heat Capacity of Frozen Soils. In Second International Conference on Permafrost, Yakutsk, USSR; North American Contribution; Wiley Online Library: Hoboken, NJ, USA, 1973; pp. 289–295. [Google Scholar]
- Cass, A.; Campbell, G.S.; Jones, T.L. Hydraulic and Thermal Properties of Soil Samples from the Buried Waste Test Facility; United States Department of Energy, Pacific Northwest Lab: Washington, DC, USA, 1981; p. 23. [Google Scholar]
- McInnes, K.J. Thermal Conductivities of Soils from Dryland Wheat Regions of Eastern Washington. MS Thesis, Washington State University, Washington, DC, USA, 1981. [Google Scholar]
- van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Koopmans, R.W.R.; Miller, R.D. Soil Freezing and Soil Water Characteristic Curves. Soil Sci. Soc. Am. J. 1966, 30, 680–685. [Google Scholar] [CrossRef]
- Spaans, M. Monte Carlo Models of the Physical and Chemical Properties of Inhomogeneous Interstellar Clouds. Astron. Astrophys. 1996, 307, 271–287. [Google Scholar]
- Deng, Q.; Liu, X.; Zeng, C.; He, X.; Chen, F.; Zhang, S. A Freezing-Thawing Damage Characterization Method for Highway Subgrade in Seasonally Frozen Regions Based on Thermal-Hydraulic-Mechanical Coupling Model. Sensors 2021, 21, 6251. [Google Scholar] [CrossRef]
- Tang, T.; Shen, Y.; Liu, X.; Zhang, Z.; Xu, J.; Zhang, Z. The Effect of Horizontal Freezing on the Characteristics of Water Migration and Matric Suction in Unsaturated Silt. Eng. Geol. 2021, 288, 106166. [Google Scholar] [CrossRef]
- Alavi, M.Z.; Pouranian, M.R.; Hajj, E.Y. Prediction of Asphalt Pavement Temperature Profile with Finite Control Volume Method. Transp. Res. Rec. 2014, 2456, 96–106. [Google Scholar] [CrossRef]
- Huang, K.; Zollinger, D.G.; Shi, X.; Sun, P. A Developed Method of Analyzing Temperature and Moisture Profiles in Rigid Pavement Slabs. Constr. Build. Mater. 2017, 151, 782–788. [Google Scholar] [CrossRef]
- Schlangen, E. Online Help/Manual Module HEAT of FEMMASSE, 1990–2000; Femmasse B.V.: Sittard, The Netherlands, 2000. [Google Scholar]
- Morbidelli, R.; Corradini, C.; Saltalippi, C.; Flammini, A.; Dari, J.; Govindaraju, R.S. Rainfall Infiltration Modeling: A Review. Water 2018, 10, 1873. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, X. Coupled Thermo-Hydro-Mechanical Model for Porous Materials under Frost Action: Theory and Implementation. Acta Geotech. 2011, 6, 51–65. [Google Scholar] [CrossRef]
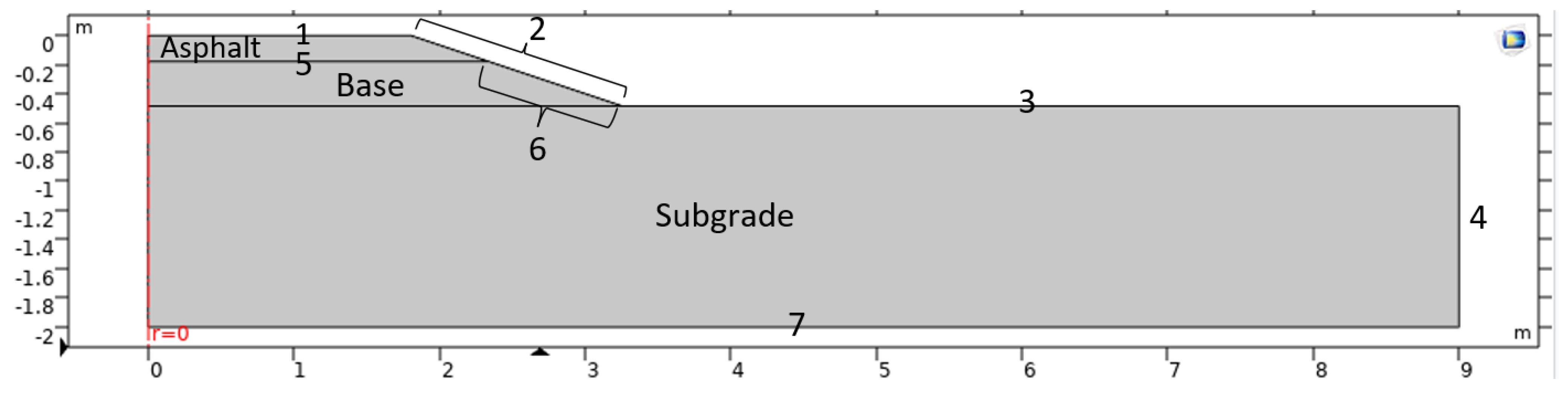
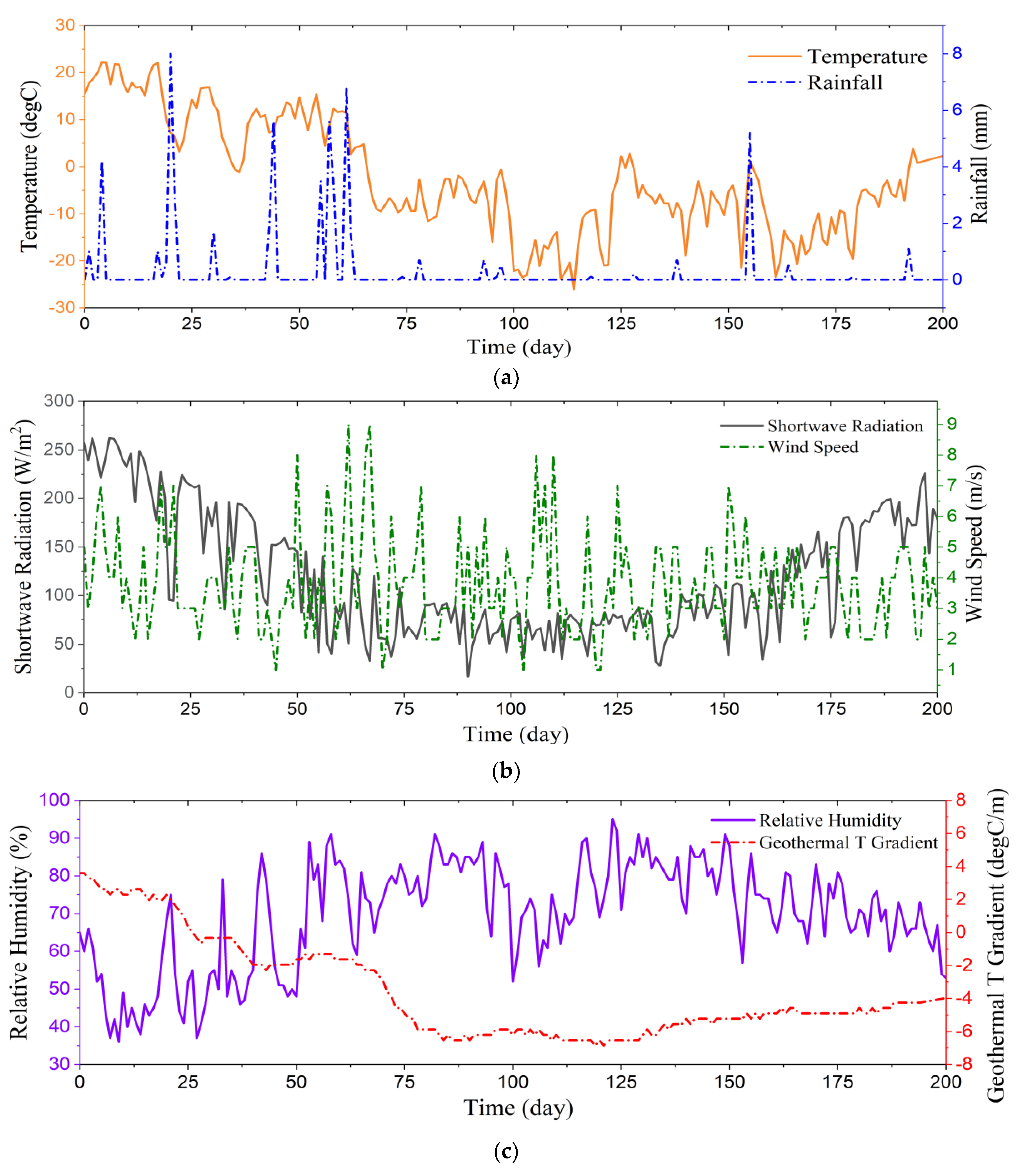


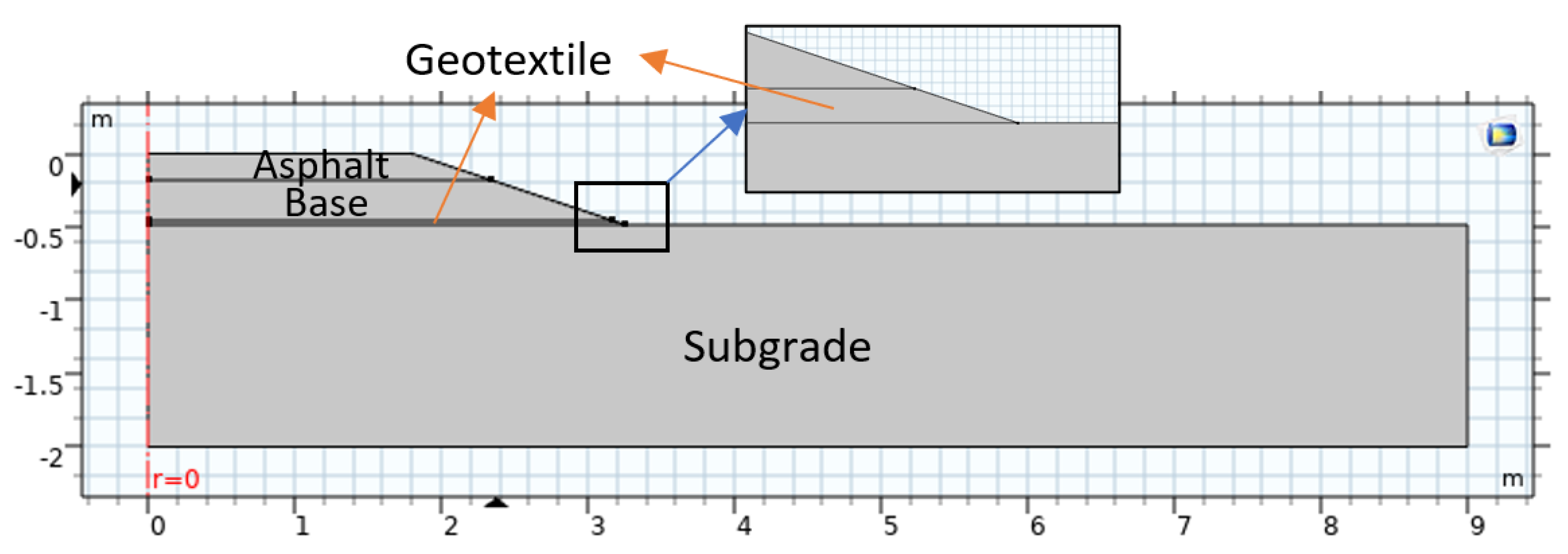
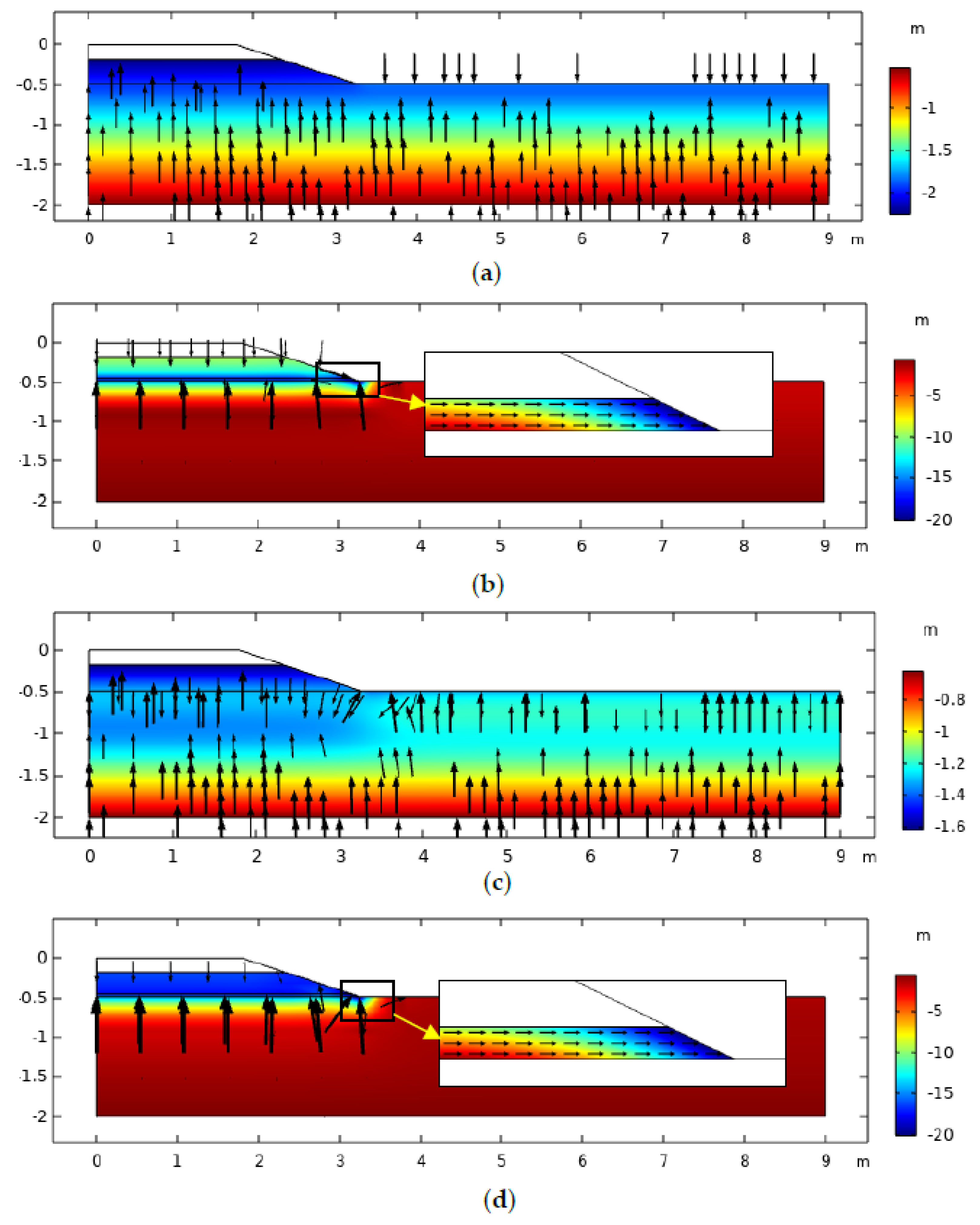


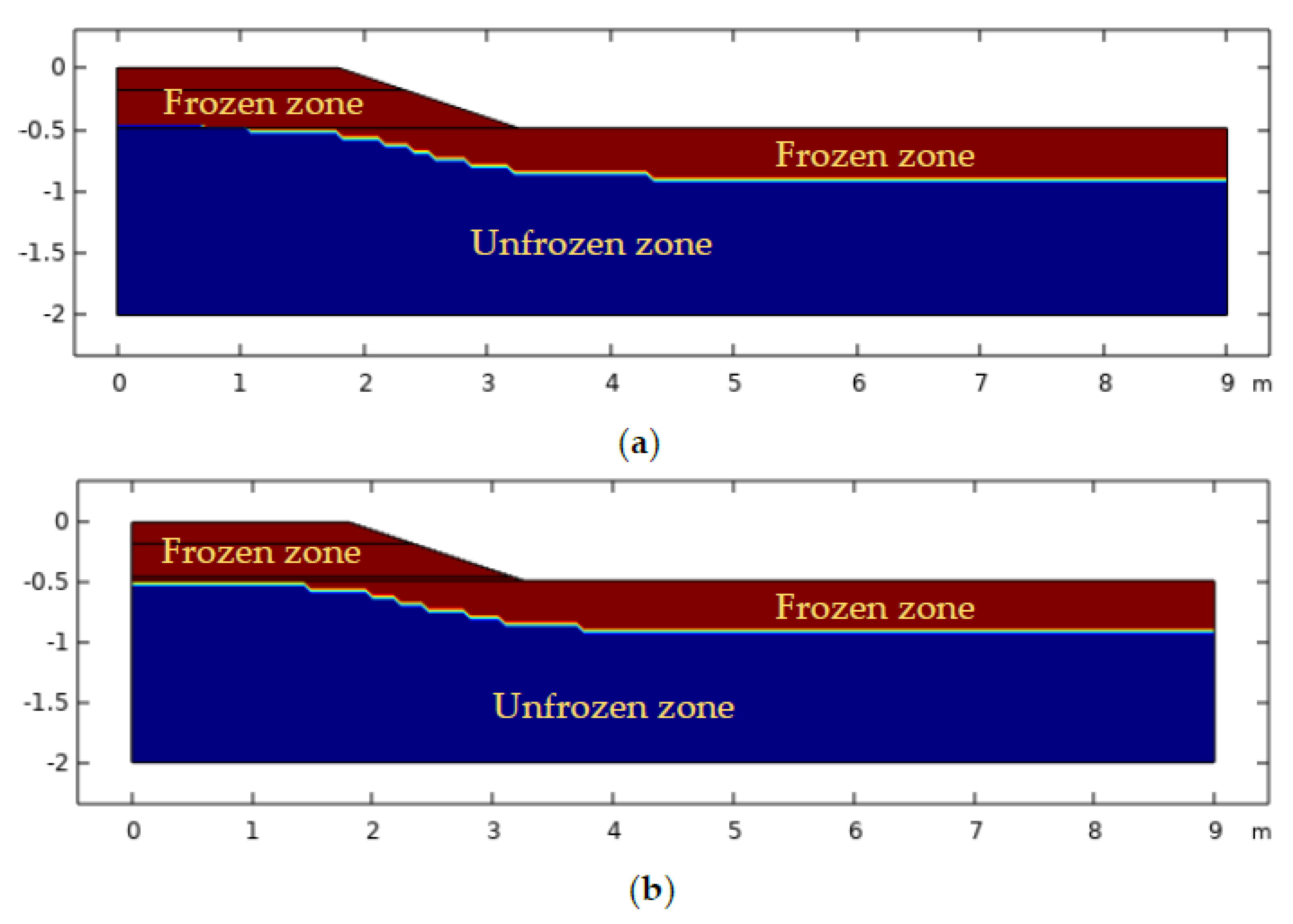

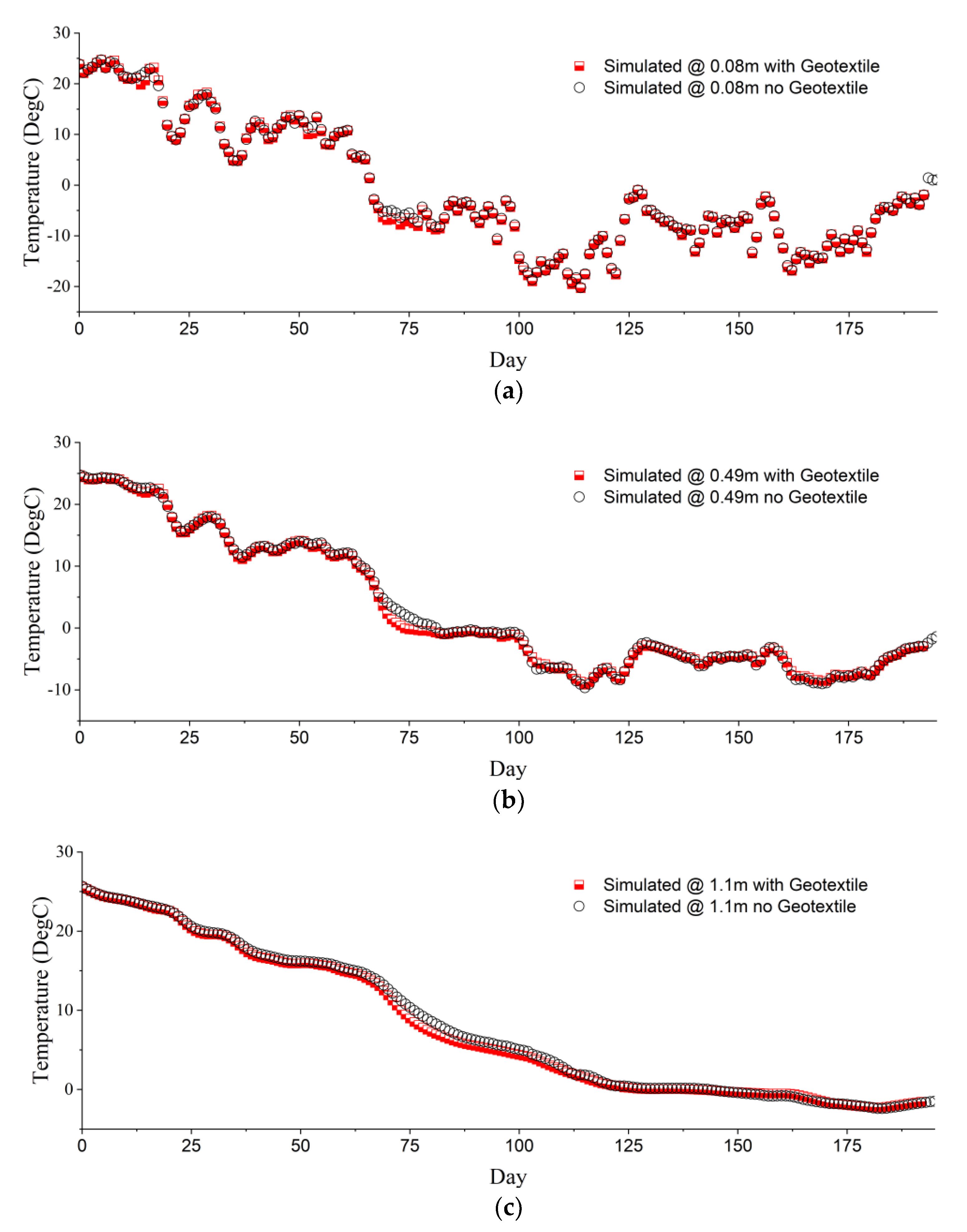
| Layer # | Material | Thickness (m) |
|---|---|---|
| 3 | Asphalt concrete: hot mixed, hot laid AC, dense graded | 0.180 |
| 2 | Unbound (granular) base: crushed stone | 0.305 |
| 1 | Subgrade (untreated): fine-grained soils: silty clay | 1.515 |
| Symbol | Value (Unit) | Description |
|---|---|---|
| 1.9 × 106 [J/(m3*K)] | Volumetric heat capacity of ice | |
| 2.0 × 106 [J/(m3*K)] | Volumetric heat capacity of solid | |
| 1.2 × 103 [J/(m3*K)] | Volumetric heat capacity of air | |
| 4.2 × 106 [J/(m3*K)] | Volumetric heat capacity of liquid | |
| 2.3 × 106 [J/(m3*K)] | Heat capacity of pavement surface layer | |
| 1.1 [W/(m*K)] | Heat conductivity of pavement surface layer | |
| 3.3 × 105 [J/kg] | Freezing latent heat | |
| 3.3 × 108 [J/m3] | Volumetric freezing latent heat | |
| 71.9 [g/s2] | Surface tension of soil water at 25° Celsius | |
| 931 [kg/m3] | Density of ice | |
| 2700 [kg/m3] | Density of soil mass | |
| 1000 [kg/m3] | Density of water | |
| g | 9.8 [m/s2] | Acceleration due to gravity |
| 1.3 × 10−3 [m/s] | Saturated hydraulic conductivity of base | |
| 1.1 × 10−7 [m/s] | Saturated hydraulic conductivity of subgrade | |
| 0.001 [m/s] | Saturated hydraulic conductivity of geotextile | |
| 0.36 | Saturated volumetric moisture content of base | |
| 0.50 | Saturated volumetric moisture content of subgrade | |
| 0.33 | Saturated volumetric moisture content of geotextile | |
| 0.075 | Residual volumetric moisture content of base | |
| 0.01 | Residual volumetric moisture content of subgrade | |
| 0.04 | Residual volumetric moisture content of geotextile | |
| 0.95 | Absorption coefficient on pavement surface | |
| 0.95 | Emission coefficient on pavement surface | |
| albedo | 0.22 | Solar reflectivity |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Alajlan, Z.; Zapata, C.; Yu, X. A Multiphysics Simulation of the Effects of Wicking Geotextile on Mitigating Frost Heave under Cold Region Pavement. Geosciences 2024, 14, 34. https://doi.org/10.3390/geosciences14020034
Jiang Y, Alajlan Z, Zapata C, Yu X. A Multiphysics Simulation of the Effects of Wicking Geotextile on Mitigating Frost Heave under Cold Region Pavement. Geosciences. 2024; 14(2):34. https://doi.org/10.3390/geosciences14020034
Chicago/Turabian StyleJiang, Yusheng, Zaid Alajlan, Claudia Zapata, and Xiong Yu. 2024. "A Multiphysics Simulation of the Effects of Wicking Geotextile on Mitigating Frost Heave under Cold Region Pavement" Geosciences 14, no. 2: 34. https://doi.org/10.3390/geosciences14020034
APA StyleJiang, Y., Alajlan, Z., Zapata, C., & Yu, X. (2024). A Multiphysics Simulation of the Effects of Wicking Geotextile on Mitigating Frost Heave under Cold Region Pavement. Geosciences, 14(2), 34. https://doi.org/10.3390/geosciences14020034







