Optimization of Structural Design in Steel Buildings Based on the Site-Specific Design Spectra of the Mexico Seismic Regulations
Abstract
1. Introduction
2. Seismic Hazard in Mexico
3. Design Spectra in Mexico
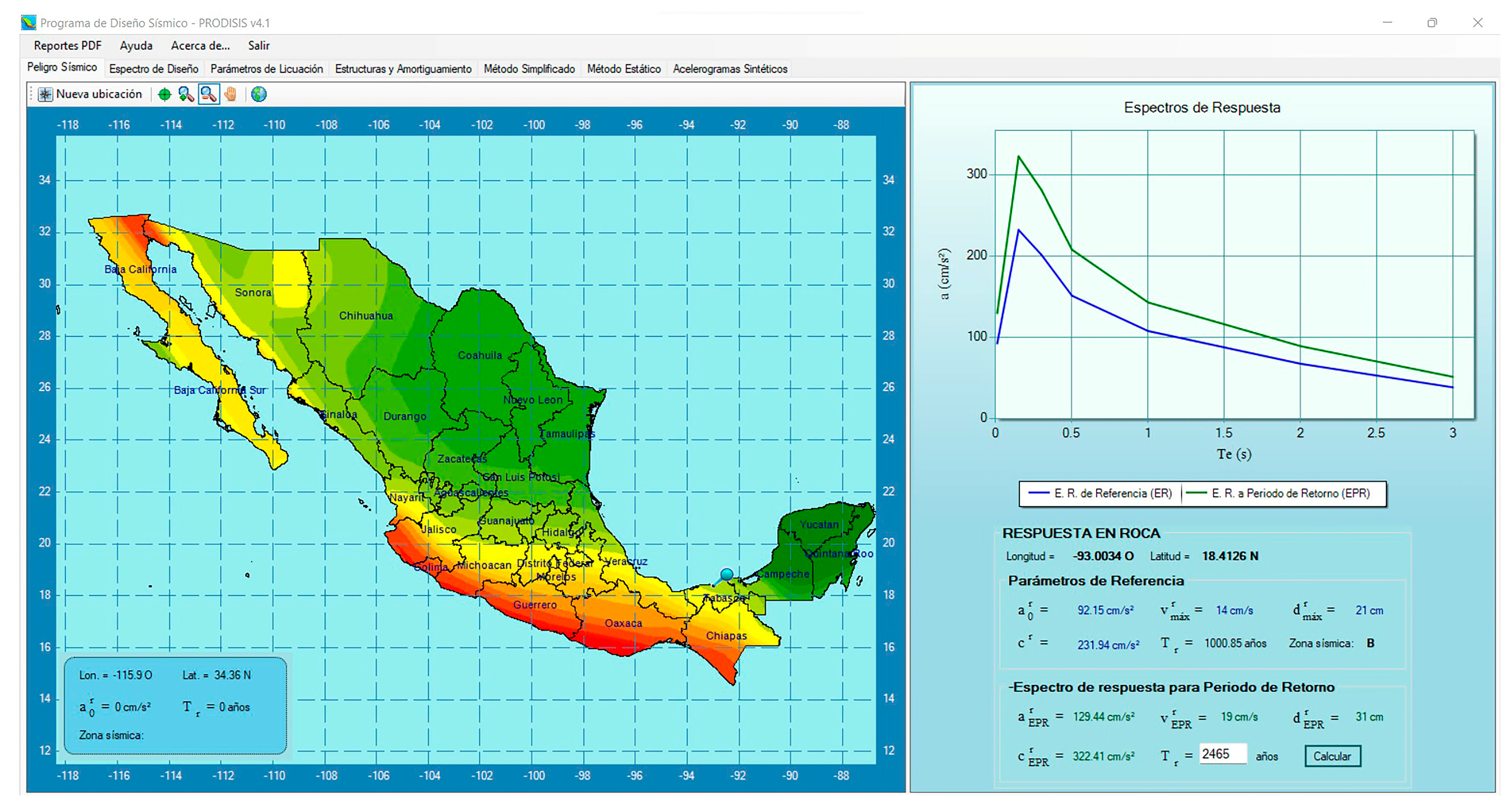
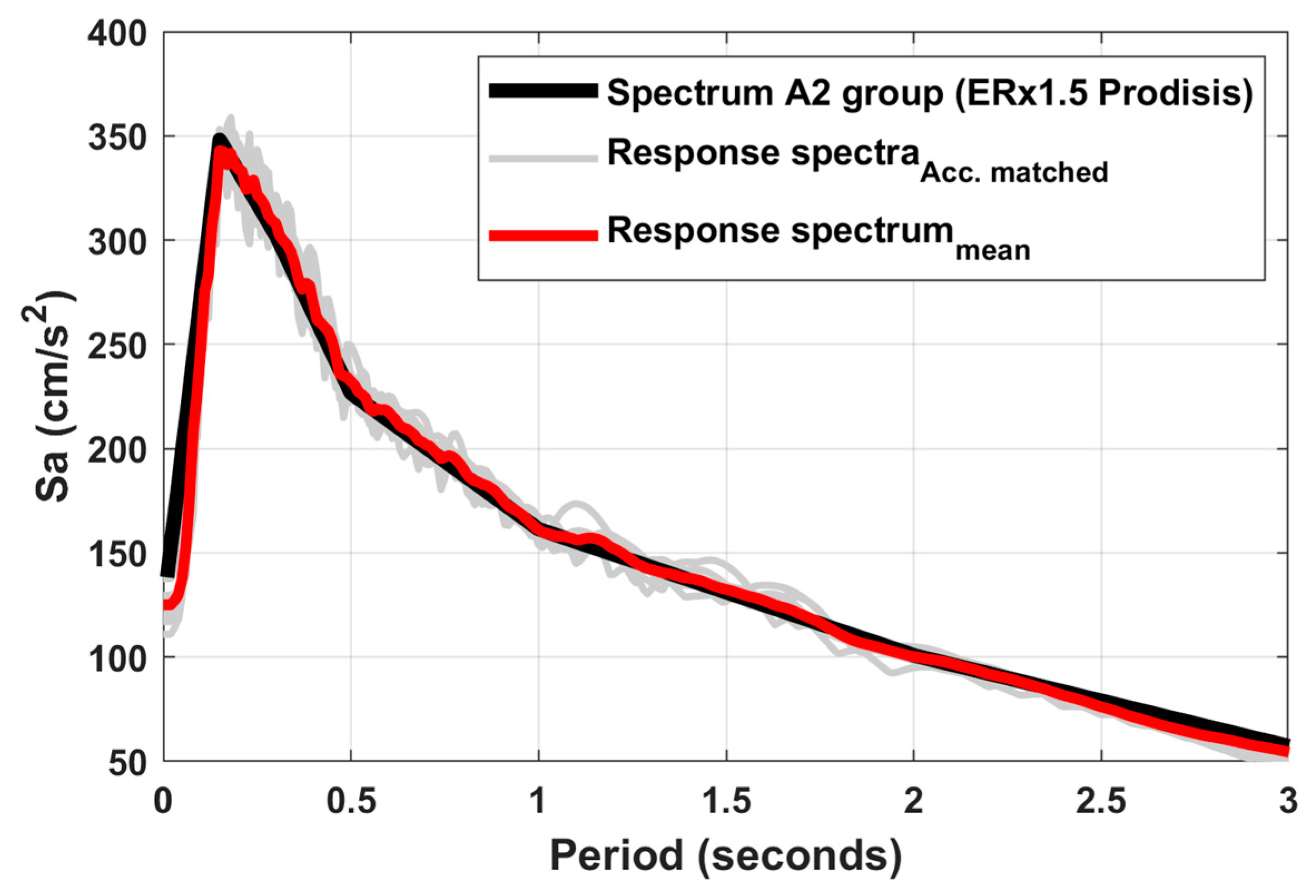
- Select a reference spectrum for rock soil, considering the following options: a) probabilistic spectrum for a specified return period (EPR) of 2475 years for A1 and 10,000 years for A+ from PRODISIS software or a probabilistic seismic hazard study of the site; b) deterministic maximum feasible spectrum by the deterministic seismic hazard analysis for seismicity affecting the site; c) reference seismic hazard spectrum (ER) at the site multiplied by a building importance factor of 1.5; and d) the envelope of the three previous options.
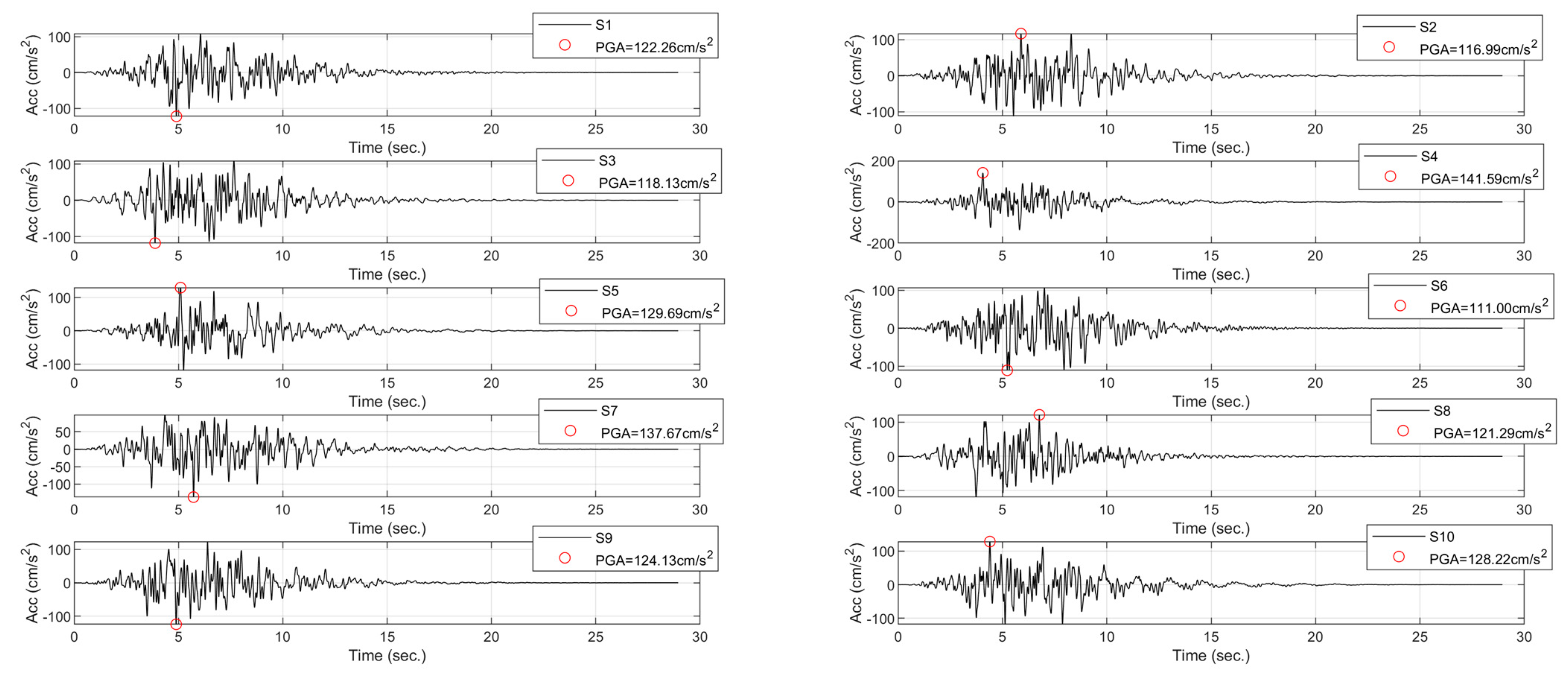
- Generate a set of at least five synthetic accelerograms with equivalent energy content to the reference spectrum in the preceding section. Determine the response spectrum and Fourier spectrum for each synthetic accelerogram.
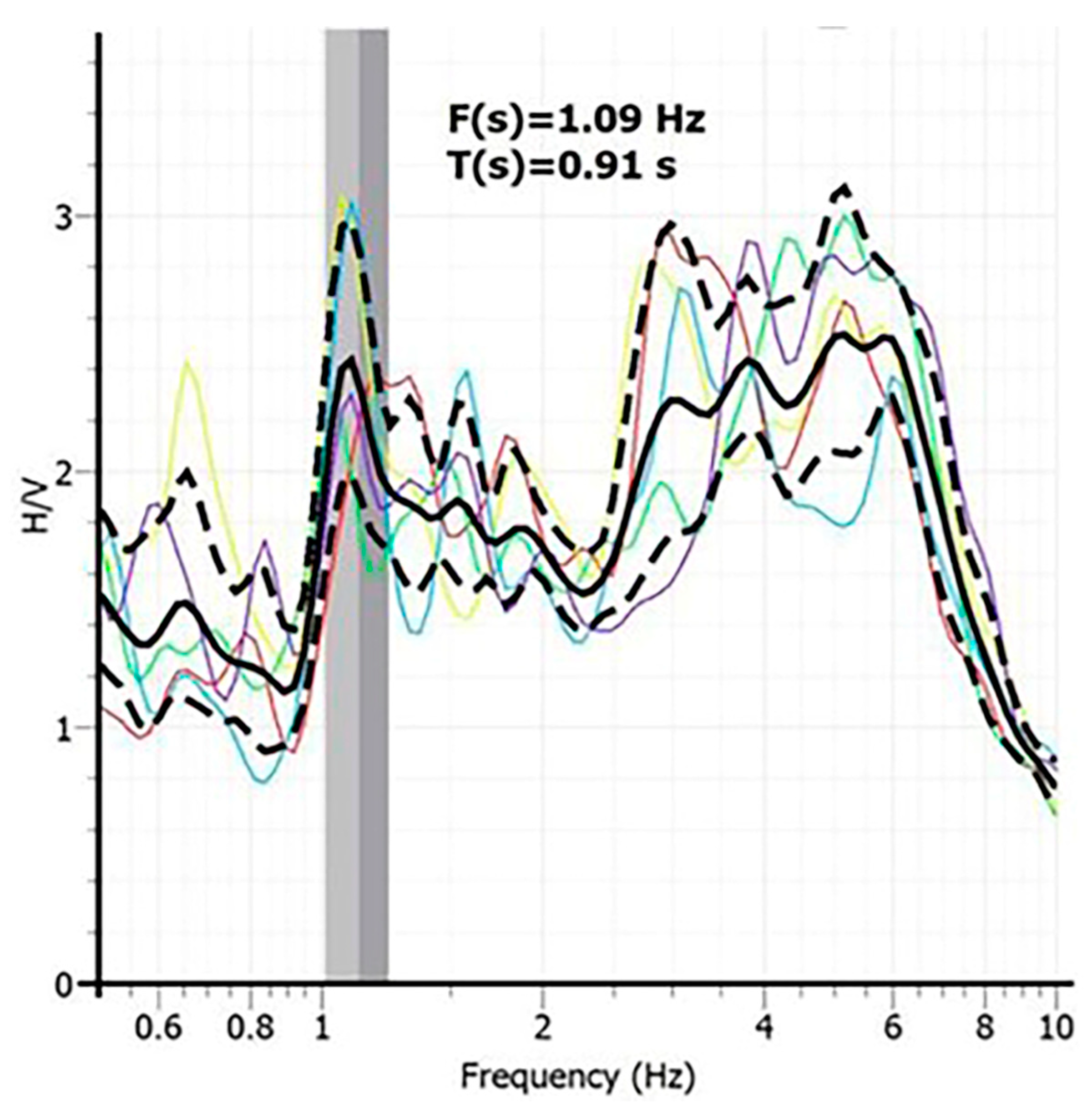
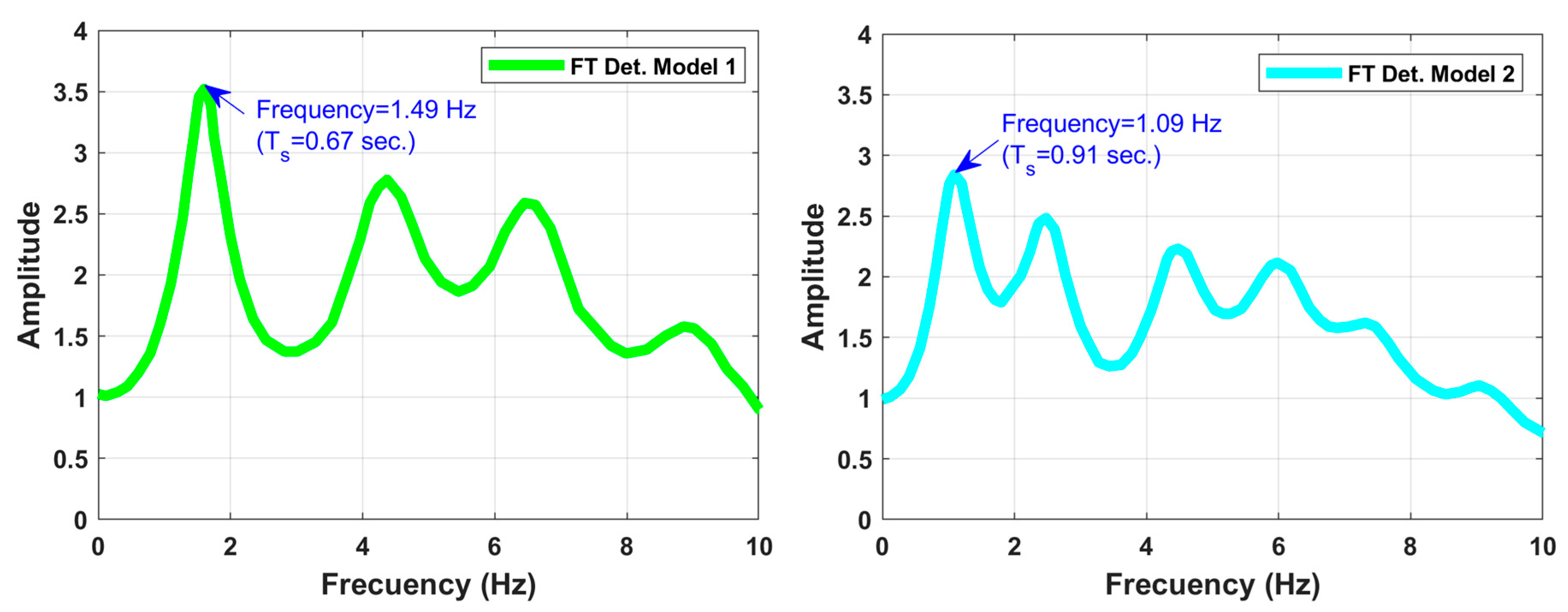
- Conduct detailed explorations in the subsoil of the site with geotechnical and geophysical studies, to determine the so-called “site effect”, that represents the dynamic amplification response on the soil surface of the study area. In this way, it is possible to characterize the stratigraphy of subsoil based on Standard Penetration Tests (SPT), “Down-Hole” surveys, and the H/V ratio analysis of environmental vibration records to obtain the fundamental period or fundamental frequency at the site. With the information properties of each stratum of the subsoil with or without uncertainty and an iterative equivalent linear acceleration method [13,14], it is possible to simulate the propagation of seismic waves from the rock stratum to the surface soil. This results in a Transfer Function (FT) showing the dynamic amplification for each period or frequency of the soil at a specific site.
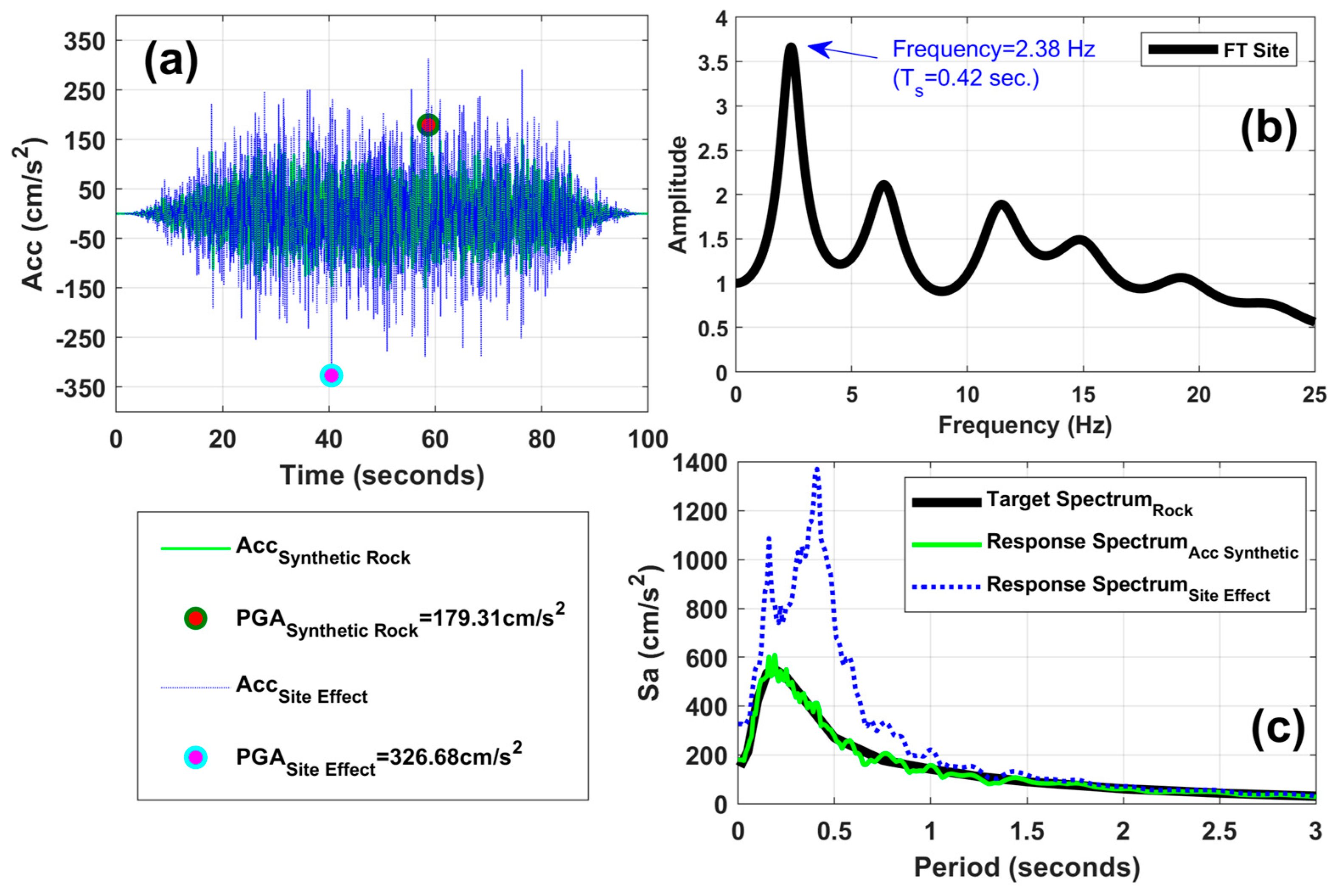
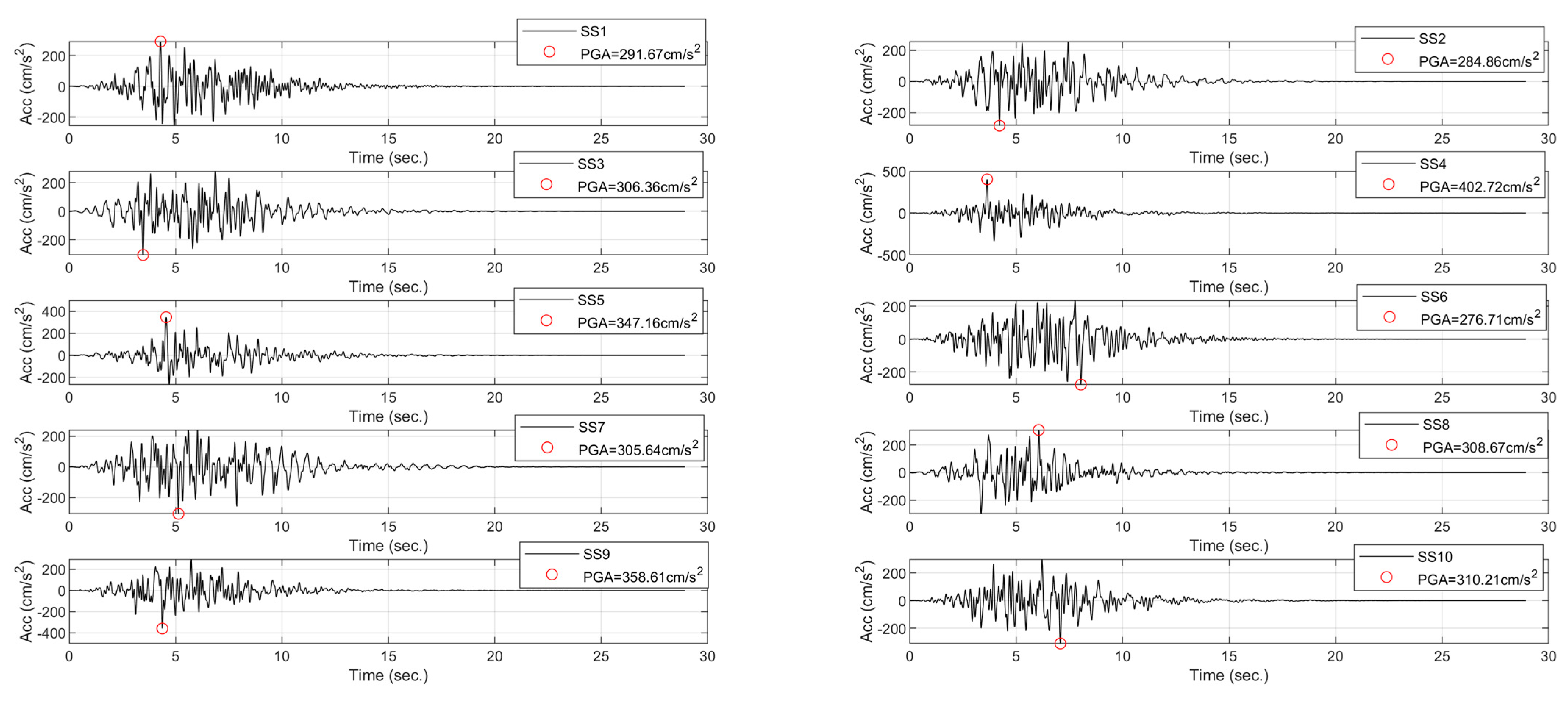
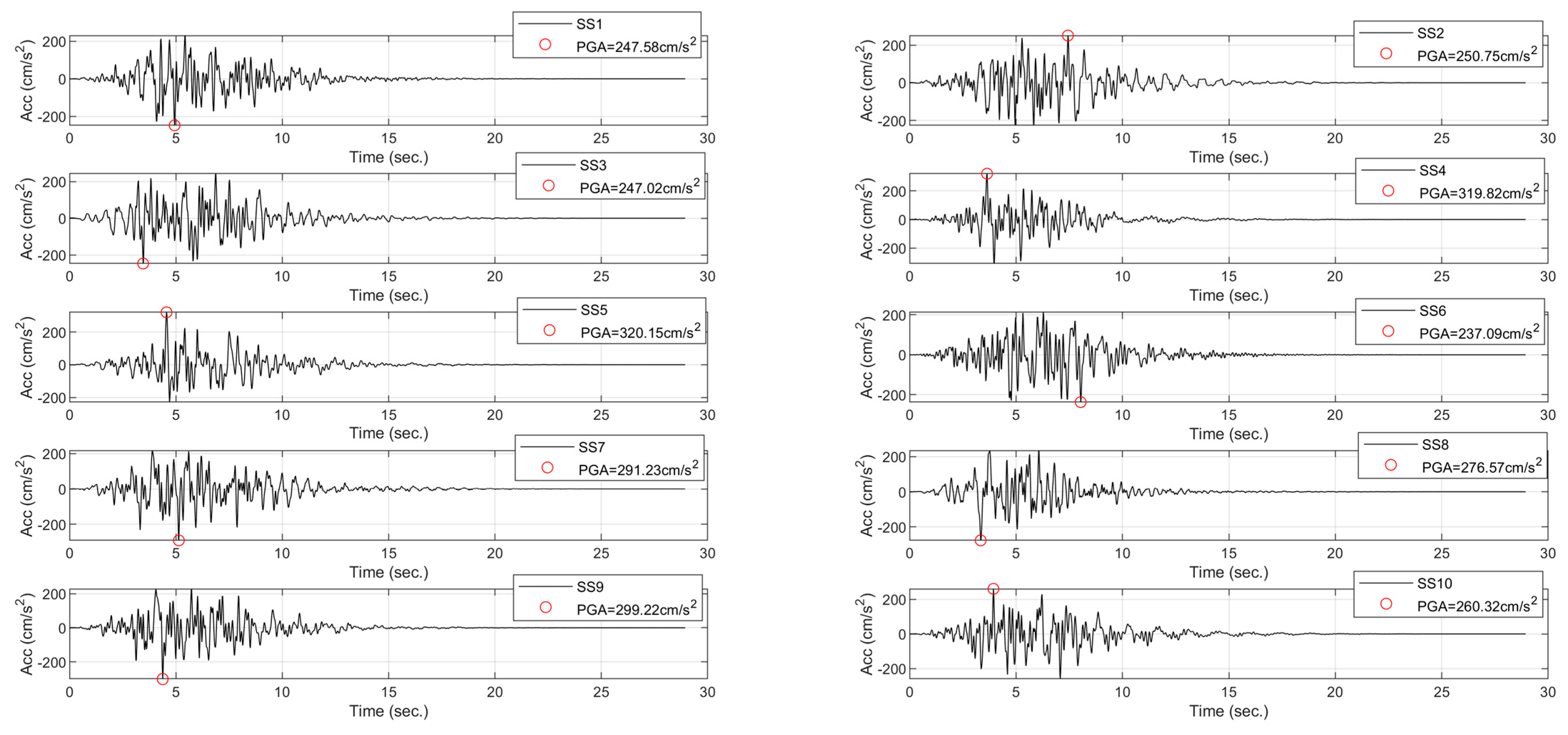
- By means of a convolution process between the Fourier spectrum of the set of synthetic accelerograms in rock and the FT, the respective response spectrum with the site effect on the surface is obtained. Subsequently, through a deconvolution process, the set of synthetic accelerograms on the surface is obtained. Figure 2 illustrates an example of a synthetic accelerogram in rock (Figure 2a) compatible with a target spectrum (Figure 2c) and using the transfer function of Figure 2b and its respective response spectrum (Figure 2c), an accelerogram with the site amplification effect (Figure 2a) is determined. Figure 2 illustrates the amplification in the Peak Ground Acceleration (PGA) and Spectral Accelerations (Sa) in both the accelerogram and response spectrum with the site effect with respect to rock soil.
- The elastic and inelastic response spectra, for each synthetic surface accelerogram from the previous step considering structural damping (generally 5%) and various ductilities (1, 2, 3, and 4), are calculated. Therefore, a response spectrum will be obtained for each synthetic accelerogram amplified by the “site effect”.
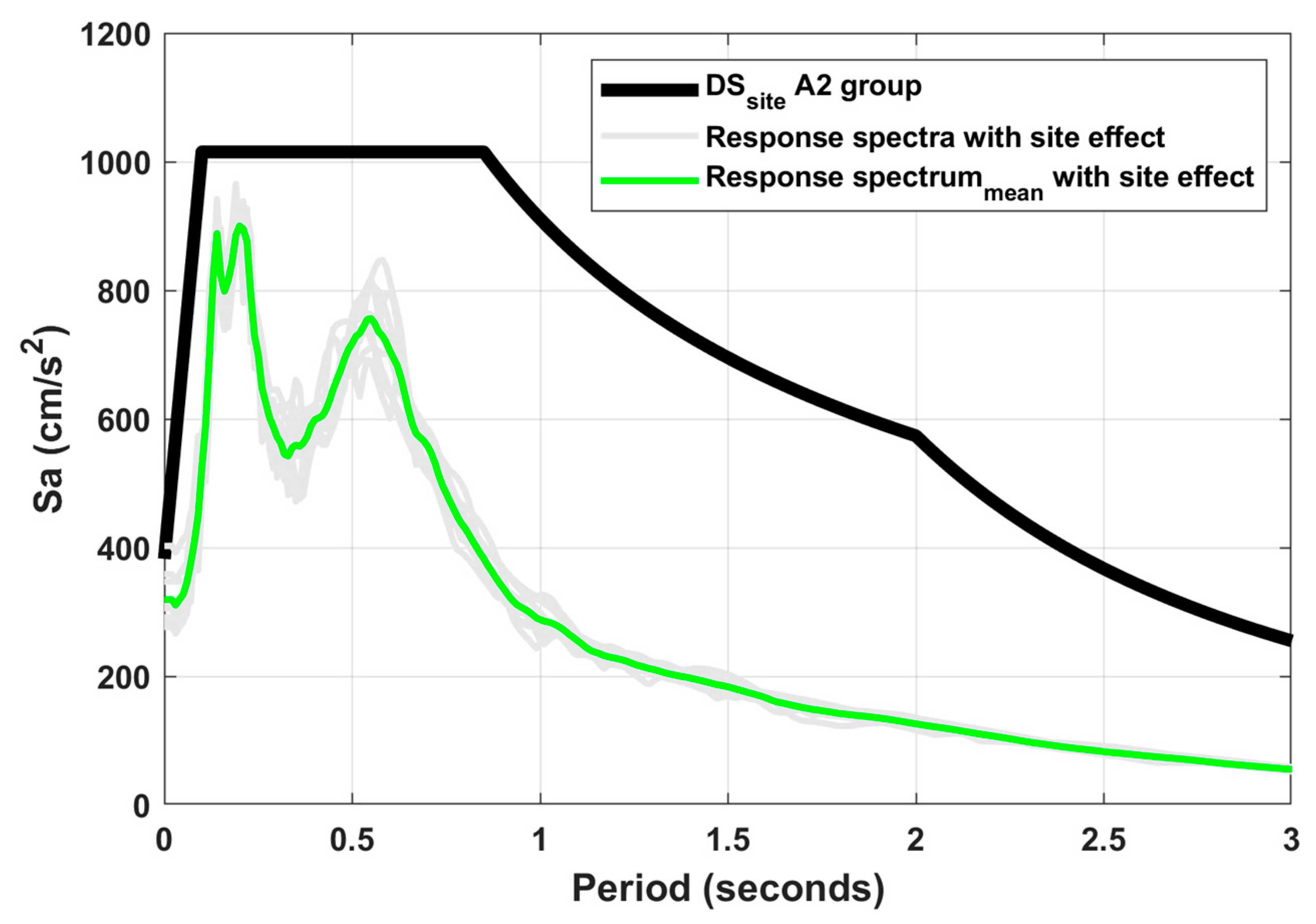
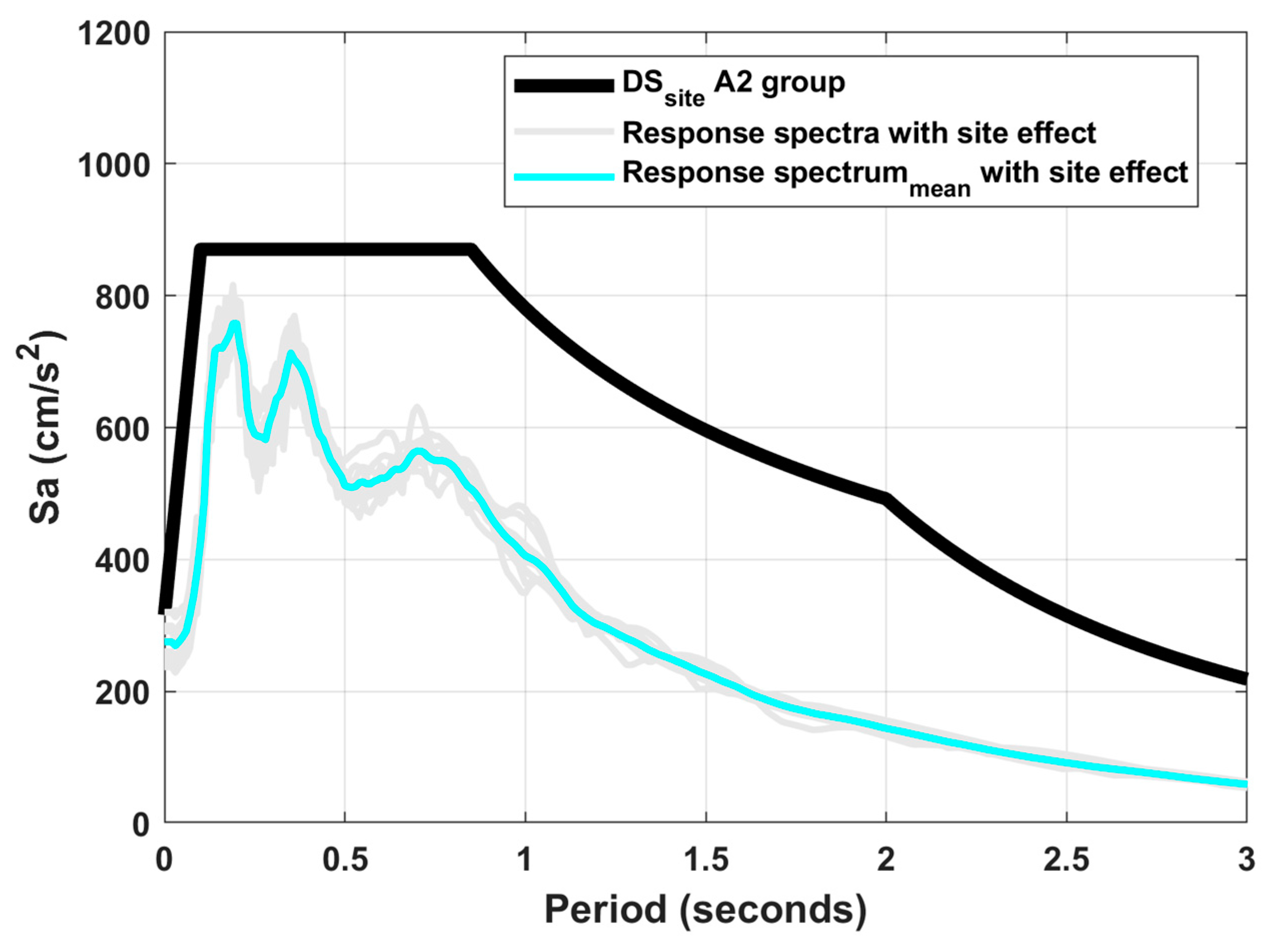
- Finally, the parameters of the Site-Specific Design Spectrum (DSsite) are defined based on the average of the elastic and inelastic surface response spectra. The shape of the DSsite will be constructed according to Equations in Figure A1 of the MDOC-CFE [5]. Ensure that the DSsite covers all structural periods under elastic and inelastic conditions.
4. Soil Type in the Design Spectrum
- The thickness of the soil stratum or depth of firm ground or rock layer (Hs): geotechnical exploration survey, vertical electrical survey, transient electromagnetic survey, wave dispersion tests (MASW and SPAC), among others.
- Shear-wave propagation velocities (Vs): wave dispersion tests (MASW and SPAC), seismic refraction laying, cross-hole, and down-hole, among others.
- Dominant period of ground vibration (Ts): environmental vibration records or site seismic records.
- Damping coefficient of soil (ξs): laboratory tests such as cyclic triaxial, resonant column, etc.
- Soil unit weight (γs): laboratory tests such as triaxial tests, simple compression, etc.
4.1. Scenario 1 with Just Geotechnical Studies
- TYPE I. Firm soil or rock layer in which dynamic amplifications do not occur: soil deposit with Vs ≥ 720 m/s or Hs ≤ 2 m.
- TYPE II. Soils in which intermediate dynamic amplifications occur: soil deposit with 360 m/s ≤ Vs < 720 m/s and Hs > 2 m, or Hs > 30 m and Vs < 720 m/s.
- TYPE III. Soils in which large dynamic amplifications occur: soil deposit with Vs < 360 m/s and 2 m < Hs ≤ 30 m.
4.2. Scenario 2 with Geotechnics and Geophysics Studies
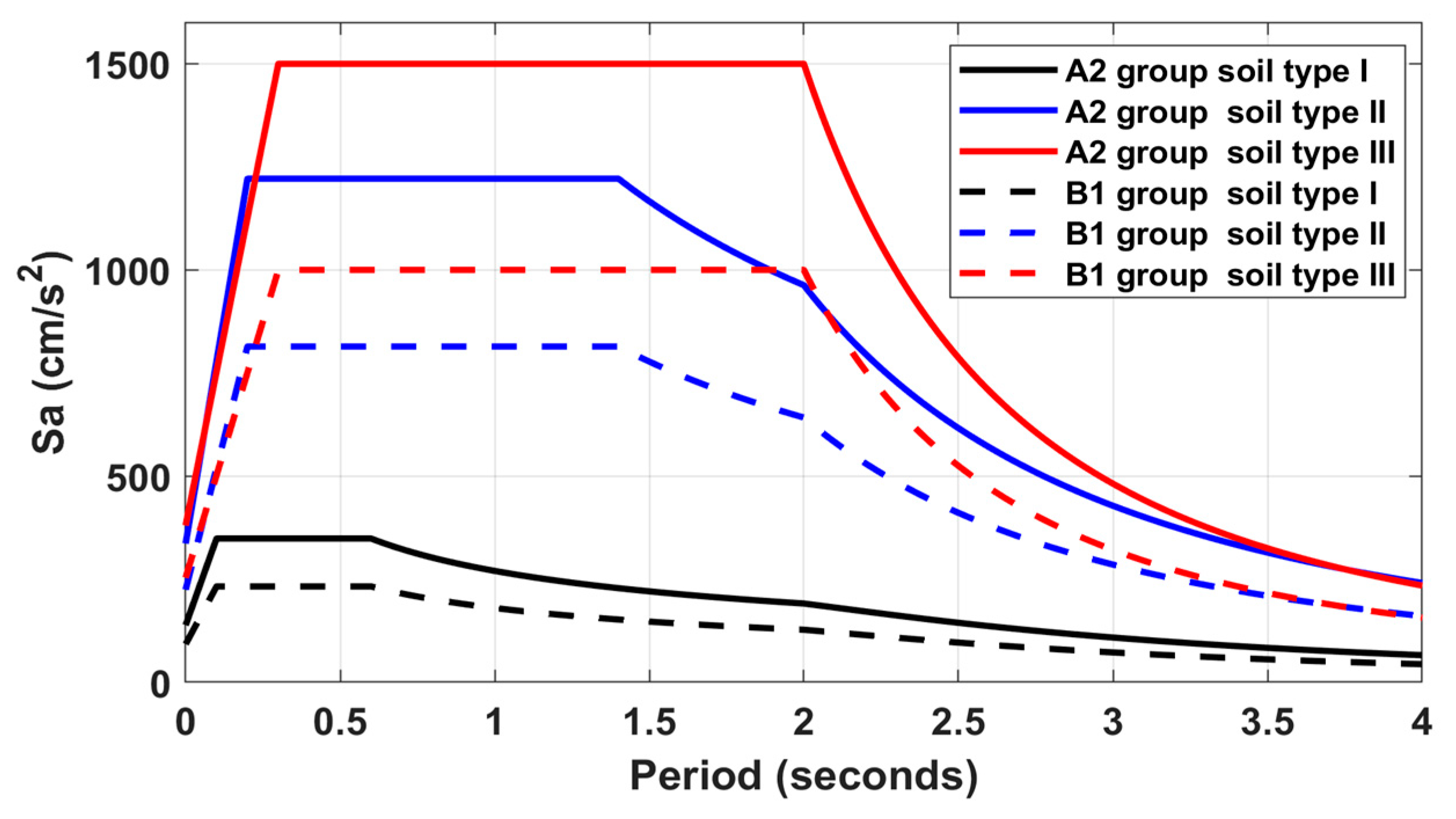
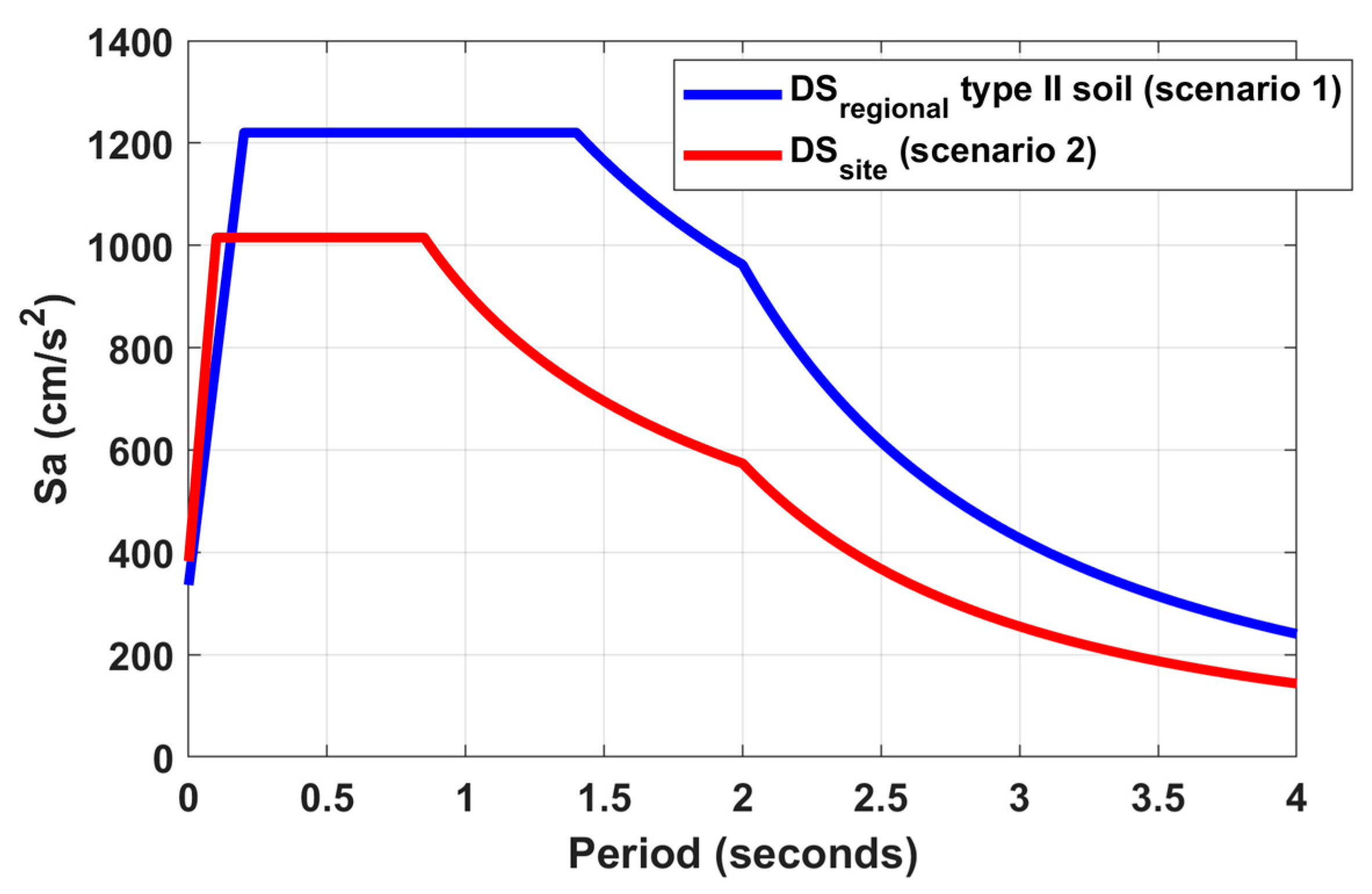
5. Site-Specific Design Spectrum for Buildings in A2 Group
6. Optimization of Structural Design Using the DSsite in Buildings in A2 Group
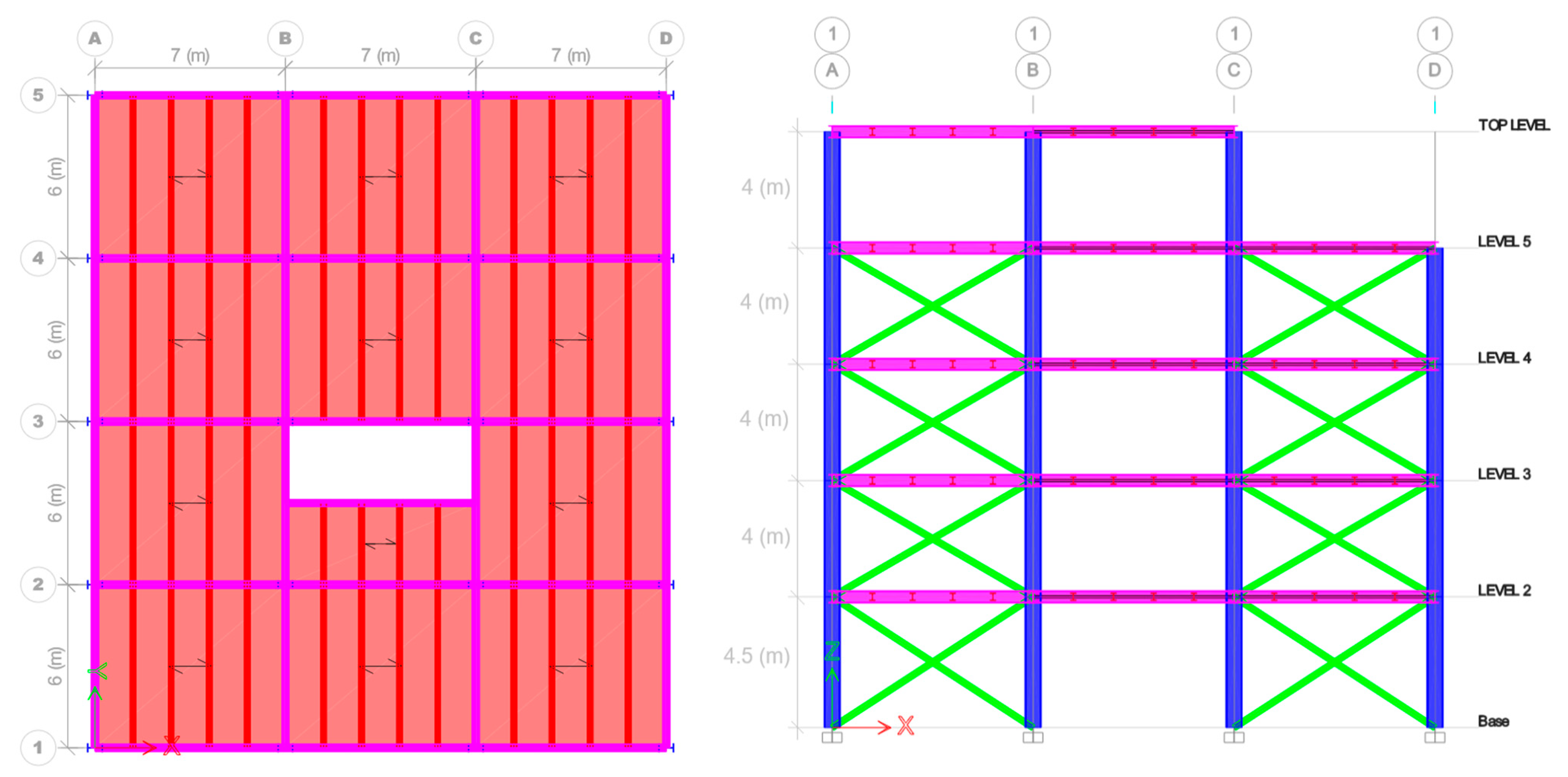
6.1. Characteristics of the Building under Study
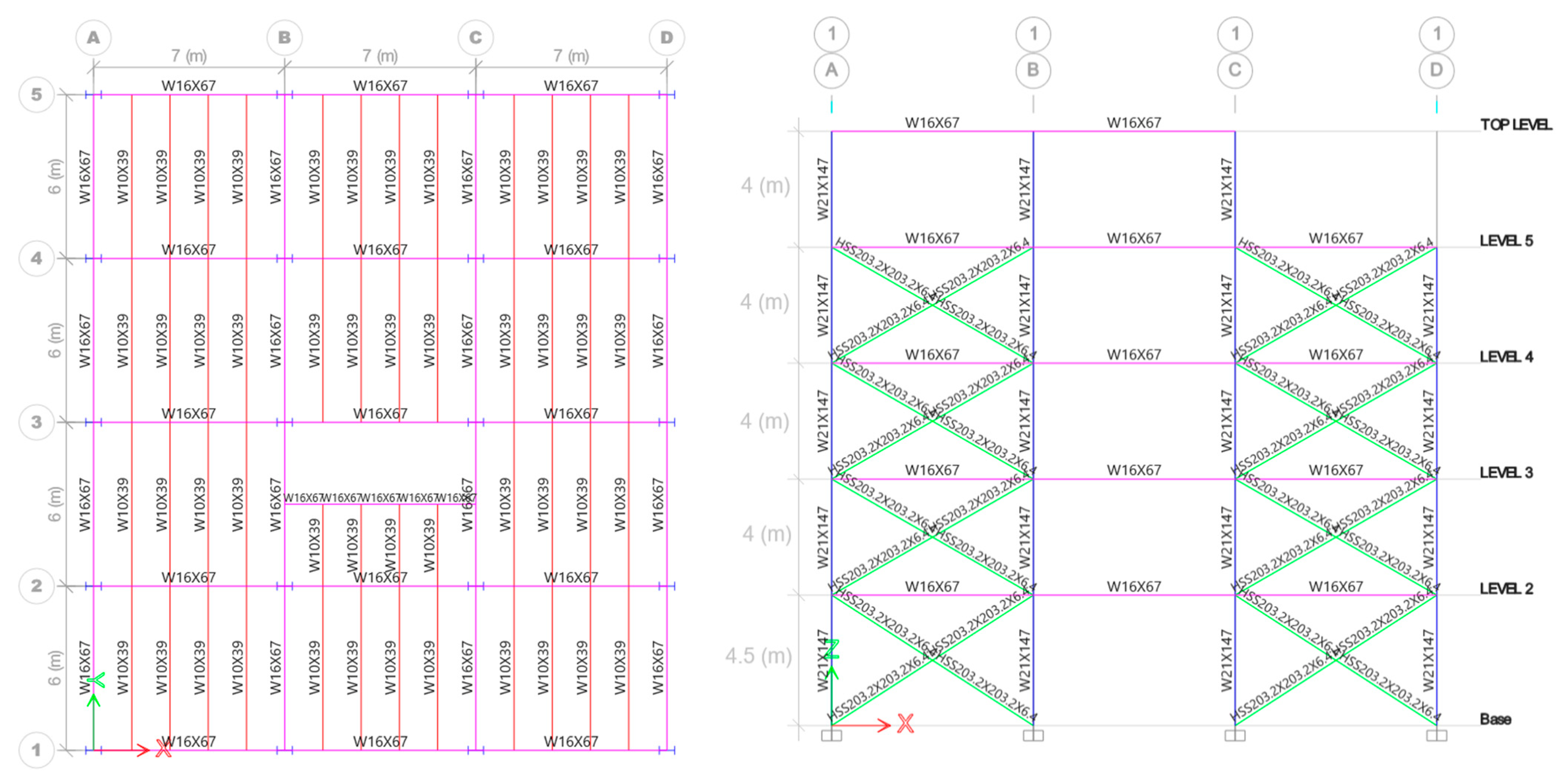
6.2. Structural Design
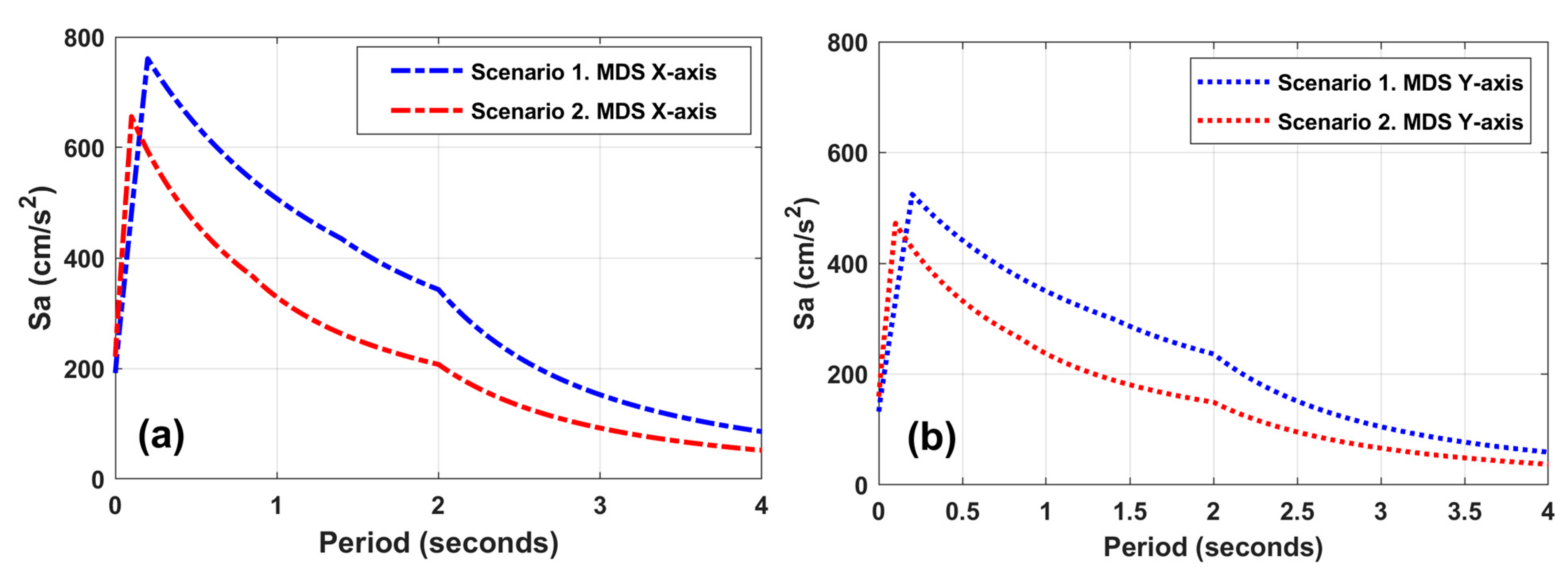
6.3. Modified Design Spectrum
- Sa(T, β(T, ξ)). Design spectrum as a function of structural periods (T) and specific damping β (T, ξ).
- β(T, ξ). Factor that takes into account the damping level (ζ) of the structural system and its material for T.
- Q’(T, Q). Ductility factor, accounting for the inelastic performance of the structure based on the seismic behavior factor (Q) corresponding to each analysis direction and T. Q can assume values of 1.25, 1.5, 2, 3, and 4 [5].
- Ro. Factor incorporating building overstrength. This factor can vary as 2, 2.5, and 3 for different structural systems [5].
- ρ. Redundancy factor determines the redistribution of actions among structural elements for each analysis direction. It can take values of 0.8, 1.0, and 1.25, selected based on the number of frames or lines of defense in the analysis direction [5].
- α. Irregularity factor. This considers the structural regularity through eleven conditions for geometric, load, and rigidity regularity of the system, following MDOC-CFE [5] guidelines. The regularity factor can be 0.7, 0.8, or 0.9 based on the degree of irregularity.
- Acd. Amplification factor for degrading behavior; this considers the rigidity degradation and/or resistance degradation in the structural system in a building founded on soft soils such as type II or III. Acd is a function of the structure fundamental period (Tf) in the analysis direction and the dominant period of the soil (Ts).
6.4. Cost–Benefit Study
7. Conclusions
- In regions lacking seismic instrumentation, utilizing geotechnical, geophysical studies, and environmental vibration records aids in interpreting the soil’s dynamic behavior during seismic events. The results of these tests can be used to incorporate them into seismic hazard studies, and thus obtain the site-specific design spectra according to the MDOC-CFE [5]. This approach allows for a more accurate seismic hazard assessment by incorporating site-specific effects.
- The structural engineer must be very clear about the soil dominant period (Ts) at the site, since, through it, the degrading behavior factor (Acd) applicable for type II and III soils can be considered in the Mexico seismic regulations. The Acd factor can amplify or reduce the modified seismic design spectrum and depends on the ratio between the fundamental structural period of the building (Tf) and Ts. Furthermore, if the Ts is like the Tf, it will be necessary to carry out a soil–structure interaction study to consider the effects of possible resonance in the structure.
- In sites where conventional geotechnical exploration (SPT test) or geophysical studies (Down-Hole test) do not reach the rock basement (type II and III soils), it is essential to carry out environmental vibration records to determine the correct soil dominant period (Ts). Not knowing the Ts of the site can cause bad practice and make certain considerations arbitrary in the design spectrum with PRODISIS [6], potentially causing an overestimation or underestimation of the real seismic demand.
- The cost–benefit analysis for the structural design of the group A2 building in this case study reveals an 18% reduction in the cost of structural elements without compromising the building’s safety. It is crucial to acknowledge the context-specific nature of the study. Generalizing the findings to regions with different geological and seismic conditions may not be feasible. Hence, it is advisable to conduct diverse cost–benefit analyses to assess potential benefits across various scenarios.
- Based on the aspects mentioned throughout this article, it is recommended that, although current regulations in Mexico [5] establish mandatory geotechnical, geophysical studies, environmental vibration records, and seismic hazard study to determine the site-specific design spectrum (DSsite) for constructions in the energy sector (buildings in A1 group or A+ group) and the basic exploration of geotechnics and geophysics for the construction of regional spectra of structures B1 and A2, it is important that, given the current availability and ease of carrying out more complete studies of the dynamic behavior of the soil, it is established as a policy for its implementation for seismic designs in high-security constructions (building A2 group) and medium-security constructions (building B1 group). Especially in areas with soft soils and little or no seismic instrumentation. So that the seismic hazard of the sites is better defined, and this leads to better estimation and management of the seismic risk of cities.
- It is crucial to acknowledge that geotechnical and geophysical data for sites are typically not readily available, it is necessary studies need to be carried out. Nevertheless, these studies are becoming more accessible, and their cost effectiveness renders them feasible for sites of interest. The greater the availability of geotechnical and geophysical studies for a region or city, the more accurately the expected seismic hazard maps can be defined. An illustrative instance of this can be observed in the SASID [31] application, which is part of the seismic design regulations of Mexico City, where site effects have been integrated into the design spectra.
- In future research, it is recommended to explore and compare global alternative methodologies for acquiring site-specific design spectra and assess how their utilization influences other types of buildings [32]. We can also analyze the progressive collapse of the building designed with DSsite, and so determined their seismic performance, fragility, robustness, and damage through incremental nonlinear dynamic analysis for the strong ground motions expected on site [33]. Additionally, it is suggested to conduct comprehensive regional studies where complete information from geotechnical and geophysical studies is available. This approach could involve the utilization of programs such as R-Crisis [34], enabling the creation of seismic hazard maps by considering grids with site effects. These lines of research have the potential to enhance and contribute to the ongoing discourse on seismic risk management.
- Finally, enhancing seismic risk management in countries can be achieved by ensuring the availability and accessibility of data derived from geotechnical and geophysical studies of urban areas. This necessitates a substantial collaborative effort from stakeholders, including architects, engineers, educational and research institutions in both the public and private sectors. The goal is to effectively communicate to society the advantages of adopting policies that reinforce the creation of platforms providing clearer definitions of seismic hazards in a region. This collective effort aims to foster the development of resilient cities, better prepared to withstand seismic events.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
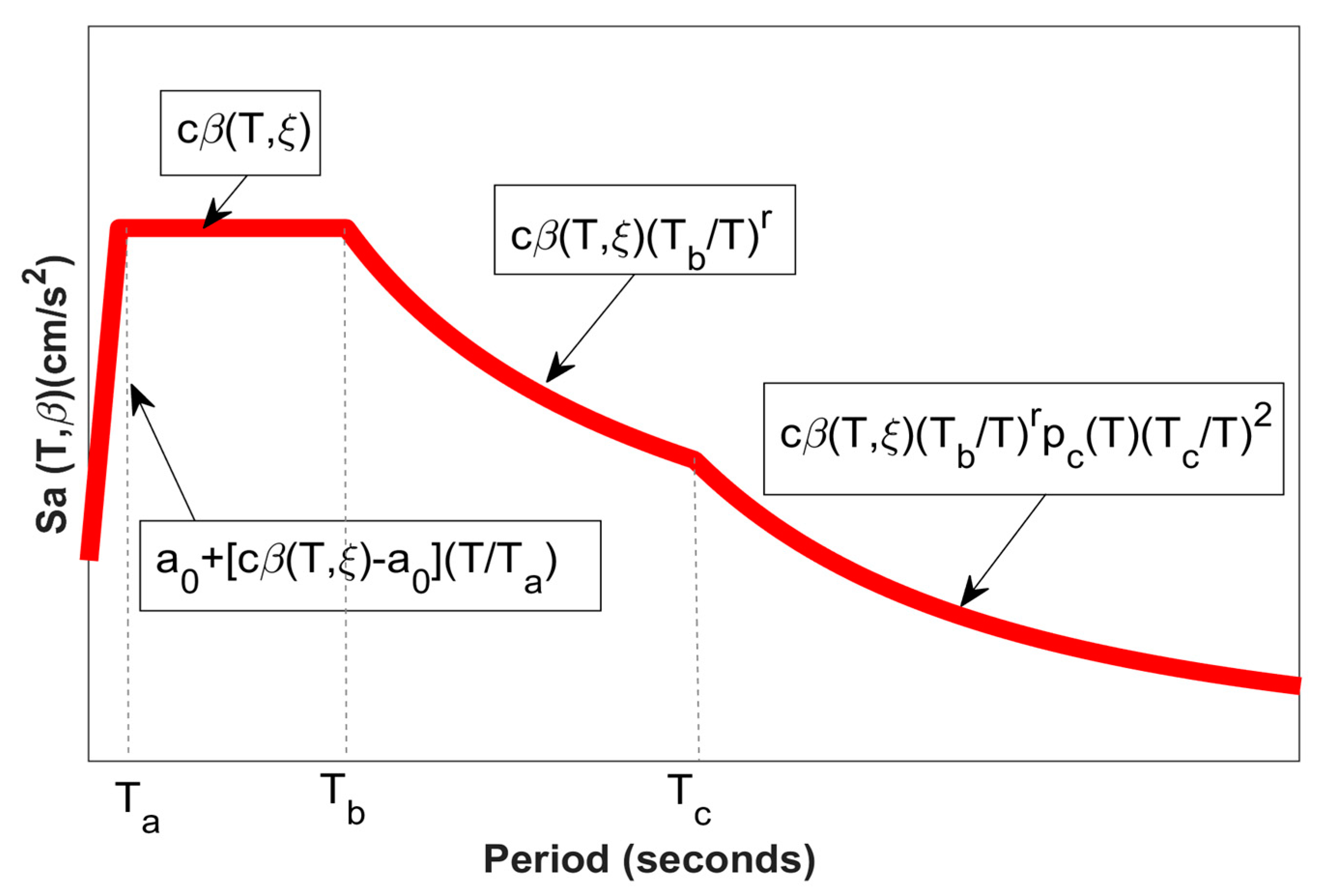
- Sa(T, β(T, ξ)). Design spectrum as a function of structural periods (T) and specific damping β (T, ξ).
- β(T, ξ). Factor that takes into account the damping level (ζ = 5%) of the structural system and its material for T. Where this is estimated as β = (0.05/ζ)λ; with λ= 0.45 if T < Tc or 0.45 (Tc/T) if T≥ Tc.
- a0 = Maximum ground acceleration.
- c = Maximum spectral acceleration.
- Ta = Lower limit of the plateau of the design spectrum.
- Tb = Upper limit of the plateau of the design spectrum.
- Tc = Onset period of the descending branch.
- r = Parameter that controls the drop of the spectral ordinates for Tb ≤ T < Tc.
- k = Parameter that controls the fall of the spectral ordinates for T ≥ Tc.
- pc = Factor used to define the variation of the spectrum in the descending branch, calculated as follows: pc = k + (1 − k)(Tc/T)2
| Type I Soil | Type II Soil | Type III Soil | |
|---|---|---|---|
| Zone A | 1.0 | 2.6 | 3.0 |
| Zone B | 1.0 | 2.6-0.2(ar0-50/50) | 3.0-0.3(ar0-50/50) |
| Zone C | 1.0 | 2.4-0.3(ar0-100/100) | 2.7-0.4(ar0-100/100) |
| Zone D | 1.0 | 2.1-0.5(ar0-200/290) | 2.3-0.6(ar0-200/290) |
| Type I Soil | Type II Soil | Type III Soil | |
|---|---|---|---|
| Zone A | Data of the PRODISIS [6] | 3.8 | 4.2 |
| Zone B | Data of the PRODISIS [6] | 3.8-0.2(ar0-50/50) | 4.2-0.3(ar0-50/50) |
| Zone C | Data of the PRODISIS [6] | 3.6-0.2(ar0-100/100) | 3.9-0.3(ar0-100/100) |
| Zone D | Data of the PRODISIS [6] | 3.4-0.5(ar0-200/290) | 3.6-0.6(ar0-200/290) |
| Type I Soil | Type II Soil | Type III Soil | |
|---|---|---|---|
| ar0 | 32 ≤ ar0 ≤ 490 | 80 ≤ a0 ≤ 690 | 94 ≤ a0 ≤ 752 |
| c | 80 ≤ c ≤ 1225 | 320 ≤ c ≤ 2000 | 390 ≤ c ≤ 2256 |
| Zone | Type Soil | Ta (s.) | Tb (s.) | Tc (s.) | k | r |
|---|---|---|---|---|---|---|
| A | I | 0.1 | 0.6 | 2.0 | 1.5 | 1/2 |
| II | 0.2 | 1.4 | 2.0 | 1.0 | 2/3 | |
| II | 0.3 | 2.0 | 2.0 | 0.5 | 1 | |
| B | I | 0.1 | 0.6 | 2.0 | 1.5 | ½ |
| II | 0.2 | 1.4 | 2.0 | 1.0 | 2/3 | |
| II | 0.3 | 2.0 | 2.0 | 0.5 | 1 | |
| C | I | 0.1 | 0.6 | 2.0 | 1.5 | 1/2 |
| II | 0.2 | 1.4 | 2.0 | 1.0 | 2/3 | |
| II | 0.2 | 2.0 | 2.0 | 0.5 | 1 | |
| D | I | 0.1 | 0.6 | 2.0 | 1.5 | ½ |
| II | 0.1 | 1.4 | 2.0 | 1.0 | 2/3 | |
| II | 0.1 | 2.0 | 2.0 | 0.5 | 1 |
References
- Bertero, V.; Bozorgnia, Y. The early years of earthquake engineering and its modern goal. In Earthquake Engineering from Engineering Seismology to Performance-based Engineering; Chapter 1; CRC Press: Boca Raton, FL, USA, 2004; p. 17. ISBN 9780429204968. [Google Scholar]
- Baker, J.W.; Bradley, B.A.; Stafford, P.J. Seismic Hazard and Risk Analysis; Cambridge University Press: Cambridge, UK, 2021; p. 79. [Google Scholar] [CrossRef]
- McGuire, R.K. Seismic Hazard and Risk Analysis; Institute Earthquake Engineering Research: Oakland, CA, USA, 2004; p. 221. ISBN 0943198011/9780943198019. [Google Scholar]
- Barbat, A.H.; Carreño, M.L.; Pujades, L.G.; Lantada, N.; Cardona, O.D.; Marulanda, M.C. Seismic vulnerability and risk evaluation methods for urban areas. A review with application to a pilot area. Struct. Infrastruct. Eng. 2010, 6, 17–38. [Google Scholar] [CrossRef]
- MDOC-CFE. Manual of Civil Structures Design. Earthquake Design; Federal Electricity Commission (CFE): Mexico City, Mexico, 2015; pp. 1–745. Available online: https://www.gob.mx/ineel/es/articulos/manual-de-diseno-de-obras-civiles-diseno-por-sismo-logro-de-la-ingenieria-de-mexico?tab= (accessed on 10 December 2023). (In Spanish)
- PRODISIS. Seismic Design Program; Electrical Research Institute: Washington, DC, USA, 2015; Available online: https://civil.ineel.mx/prodisis/es/prodisis.php (accessed on 10 December 2023). (In Spanish)
- NTC-RSEE. Complementary Technical Norms for the Review of the Structural Safety of Buildings of the México City; Official Gazette of the Federal Government of Mexico; 2017; pp. 1–712. Available online: https://smie.com.mx/smie-2022/informacion-tecnica/normas-tecnicas-complementarias.php (accessed on 10 December 2023). (In Spanish).
- Arroyo, D.; García, D.; Ordaz, M.; Mora, M.A.; Singh, S.K. Strong ground-motion relations for Mexican interplate earthquakes. J. Seismol. 2010, 14, 769–785. [Google Scholar] [CrossRef]
- Zhao, J.X. Attenuation Relations of Strong Ground Motion in Japan Using Site Classification Based on Predominant Period. Bull. Seismol. Soc. Am. 2006, 96, 898–913. [Google Scholar] [CrossRef]
- Abrahamson, N.A.; Silva, W.J. Empirical Response Spectral Attenuation Relations for Shallow Crustal Earthquakes. Seismol. Res. Lett. 1997, 68, 94–127. [Google Scholar] [CrossRef]
- Esteva, L. Criterios para la construcción de espectros para diseño sísmico. In Proceedings of the 3er Simposio panamericano de estructuras, Caracas, Venezuela, 3–8 July 1967. [Google Scholar]
- Cornell, C.A. Engineering Seismic Risk Analysis. Bull. Seismol. Soc. Am. 1968, 69, 9–48. [Google Scholar] [CrossRef]
- Hashash, Y.; Musgrove, M.; Park, D.; Tsai, C.-C.; Phillips, C.; Groholski, D. DeepSoil v7.0, 1-D Wave Propagation Program for Geotechnical Sire Response. Board of Trustees of University of Illinois at Urbana-Champaign and Youssef Hashash. 2020. Available online: http://deepsoil.cee.illinois.edu/ (accessed on 10 December 2023).
- Pitilakis, D. Waveprop, Function Calculates Displacement Wave Field in A Layered Medium Using Elastic Wave Equation 2023. Available online: https://www.mathworks.com/matlabcentral/fileexchange/60589-waveprop (accessed on 10 December 2023).
- Seed, H.B.; Idriss, I.M. Evaluation of Liquefaction Potential of Sand Deposits Based on Observations and Performance in Previous Earthquakes. En ASCE Annu. Conf. Sess. 1981, 24, 81–544. [Google Scholar]
- Kramer, L.S. Geotechnical Earthquake Engineering, 1st ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1996; pp. 1–653. ISBN 0-13-374943-6. [Google Scholar]
- Nakamura, Y. A method for dynamic characteristics estimation of subsurface using microtremor on the ground surface. Railw. Tech. Res. Inst. Q. Rep. 1989, 30, 25–33. [Google Scholar]
- Zhao, J.X.; Irikura, K.; Zhang, J.; Fukushima, Y.; Somerville, P.G.; Asano, A.; Ohno, Y.; Oouchi, T.; Takahashi, T.; Ogawa, H. An empirical site-classification method for strong-motion stations in Japan using H/V response spectral ratio. Bull. Seismol. Soc. Am. 2006, 96, 914–925. [Google Scholar] [CrossRef]
- Fukushima, Y.; Bonilla, L.F.; Scotti, O.; Douglas, J. Site classification using horizontal-to-vertical response spectral ratios and its impact when deriving empirical ground-motion prediction equations. J. Earthq. Eng. 2007, 11, 712–724. [Google Scholar] [CrossRef]
- Di Alessandro, C.; Bonilla, L.F.; Boore, D.M.; Rovelli, A.; Scotti, O. Predominant-period site classification for response spectra prediction equations in Italy. Bull. Seismol. Soc. Am. 2012, 102, 680–695. [Google Scholar] [CrossRef]
- Pinzón, L.A.; Pujades, L.G.; Macau, A.; Carreño, E.; Alcalde, J.M. Seismic Site Classification from the Horizontal-to-Vertical Response Spectral Ratios: Use of the Spanish Strong-Motion Database. Geosciences 2019, 9, 294. [Google Scholar] [CrossRef]
- Wathelet, M.; Chatelain, J.-L.; Cornou, C.; Di Giulio, G.; Guillier, B.; Ohrnberger, M.; Savvaidis, A. Geopsy: A User-Friendly Open-Source Tool Set for Ambient Vibration Processing. Seismol. Res. Lett. 2020, 91, 1878–1889. [Google Scholar] [CrossRef]
- CSI. ETABS. V21.0.1. Building Analysis and design. Computers and Structures, Inc. Structural and Earthquake Engineering Software. 2023. Available online: https://www.csiamerica.com/products/etabs (accessed on 10 December 2023).
- Gonzalez, A.; Calderon, J. An Overview of the Seismic Elastic Response Spectra and Their Application According to Mexican, U.S., and International Building Codes. Appl. Sci. 2022, 12, 3472. [Google Scholar] [CrossRef]
- Costanzo, S.; D’Aniello, M.; Landolfo, R. Proposal of design rules for ductile X-CBFS in the framework of EUROCODE 8. Earthq. Eng. Struct. Dyn. 2018, 48, 124–151. [Google Scholar] [CrossRef]
- Marino, E.M. A unified approach for the design of high ductility steel frames with concentric braces in the framework of Eurocode 8. Earthq. Eng. Struct. Dyn. 2014, 43, 97–118. [Google Scholar] [CrossRef]
- Longo, A.; Montuori, R.; Piluso, V. Failure Mode Control of X-Braced Frames Under Seismic Actions. J. Earthq. Eng. 2008, 12, 728–759. [Google Scholar] [CrossRef]
- Elghazouli, A.Y. Assessment of European seismic design procedures for steel framed structures. Bull. Earthq. Eng. 2010, 8, 65–89. [Google Scholar] [CrossRef]
- Arcos-Díaz, D.; Díaz, S.A.; Pinzón, L.A.; Jesús, H.; Mora-Ortiz, R.S. Seismic performance assessment based on the interstory drift of steel building. Lat. Am. J. Solids Struct. 2022, 19, e431. [Google Scholar] [CrossRef]
- Díaz, S.A.; Pinzón, L.A.; Vargas-Alzate, Y.F.; Mora-Ortiz, R.S. Seismic Damage “Semaphore” Based on the Fundamental Period Variation: A Probabilistic Seismic Demand Assessment of Steel Moment-Resisting Frames. Buildings 2023, 13, 1009. [Google Scholar] [CrossRef]
- SASID. Seismic Design Action System. Complementary Technical Norms for the Review of the Structural Safety of Buildings of the México City. Gaceta Oficial del Gobierno de México. 2023. Available online: https://sasid.unam.mx/webNormasCDMX/ (accessed on 10 December 2023). (In Spanish).
- Formisano., A.; Nicola Chieffo, N.; Clementi, F.; Mosoarca, M. Influence of Local Site Effects on the Typological Fragility Curves for Class-Oriented Masonry Buildings in Aggregate Condition. Open Civ. Eng. J. 2021, 15, 149–164. [Google Scholar] [CrossRef]
- Formisano, A.; Landolfo, R.; Mazzolani, F.M. Robustness assessment approaches for steel framed structures under catastrophic events. Comput. Struct. 2015, 147, 216–228. [Google Scholar] [CrossRef]
- Ordaz, M.; Martinelli, F.; Aguilar, A.; Arboleda, J.; Meletti, C.; D’Amico, V. R-Crisis V20.3.0. Program for Computing Seismic Hazard. Instituto de Ingeniería de la UNAM and ERN Internacional. Available online: http://www.r-crisis.com/ (accessed on 10 December 2023).
| Group | Classification | Class | Size | Class |
|---|---|---|---|---|
| A+ | Buildings of extreme importance related to energy or industrial sector. For example, hydroelectric and nuclear plants, etc. | A+ | - | - |
| A | Structure import related to energy or industrial sector. For example, power generation, transmission, distribution plants, industrial hydrocarbon processing, storage and distribution facilities, etc. | A1 | - | - |
| Not Related to the energy or industrial sector. For example, schools, hospitals, research centers, stadiums, hotels, emergency systems, etc. | A2 | - | - | |
| B | Common buildings, for example, industrial warehouses, commercial premises, common structures intended for housing or offices, performance halls, warehouses, and urban or industrial structures not included in groups A+ and A. | - | H * > 13 m Ac ** < 400 m2 | B1 |
| - | H * < 13 m Ac ** < 400 m2 | B2 |
| Depth (m) | Thickness, hi (m) | Soil Unit Weight, γsi (kg/m3) | Shear-Wave Propagation Velocities, Vsi (m/s) |
|---|---|---|---|
| 3 | 3 | 1700 | 137 |
| 6 | 3 | 1700 | 131 |
| 9 | 3 | 1700 | 216 |
| 12 | 3 | 1700 | 257 |
| 15 | 3 | 1767 | 215 |
| 18 | 3 | 1817 | 176 |
| 21 | 3 | 1850 | 249 |
| 24 | 3 | 1850 | 194 |
| 27 | 3 | 1867 | 188 |
| 30 | 3 | 1900 | 297 |
| 33 | 3 | 1900 | 259 |
| 36 | 3 | 1900 | 262 |
| 39 | 3 | 1900 | 286 |
| 42 | 3 | 1900 | 304 |
| 45 | 3 | 1900 | 382 |
| Concept | Cost * |
|---|---|
| ** Geotechnical study: Exploration and sampling in the field up to a depth of 30 m on firm ground utilizing the standard penetration test (SPT). This encompasses the execution of field tests, retrieval of altered and unaltered samples, laboratory index and mechanical tests, and preparing a comprehensive technical report. | USD 3300.00 |
| Geophysical study: Conducting a Down-Hole test at a depth of 30 m on site. This involves installing a well casing at a depth of 30 m using a 3” diameter hydraulic PVC, performing field data acquisition, and processing the data to derive seismic soil parameters. | USD 3300.00 |
| Environmental vibration record: Conducting an environmental vibration record to ascertain the dominant period of the soil. Processing and interpreting results through the H/V spectral ratio technique. | USD 1000.00 |
| Seismic hazard study to determine site-specific design spectrum (DSsite): Conduct a seismic hazard study and develop a site-specific design spectrum tailored to structural classifications B2, A1, and A2 following the MDOC-CFE [5]. | USD 8500.00 |
| Total cost USD 16,100.00 |
| Floor | Roof | |
|---|---|---|
| Maximum live loads | 250 kg/m2 | 100 kg/m2 |
| Accidental live Load | 180 kg/m2 | 70 kg/m2 |
| Characteristic/Factor | Scenario 1. DSregional for Type II Soil. | Scenario 2. DSsite | ||
|---|---|---|---|---|
| X-Axis | Y-Axis | X-Axis | Y-Axis | |
| Tf (s.) | 0.482 | 0.534 | 0.482 | 0.534 |
| Ts (s.) | 0.670 | 0.670 | 0.670 | 0.670 |
| β {T, ξ = 0.05} | 1.0 | 1.0 | 1.0 | 1.0 |
| Q’ {T, Q = 2} | 1.21 | 1.38 | 1.21 | 1.38 |
| Ro | 2.0 | 2.0 | 2.0 | 2.0 |
| ρ | 1.0 | 1.25 | 1.0 | 1.25 |
| α | 0.9 | 1.0 | 0.9 | 1.0 |
| Acd | 1.28 | 1.22 | 1.28 | 1.22 |
| Pre-Sized Building | Final Design Scenario 1. DSregional for Type II soil. | Final Design Scenario 2. DSsite | |||
|---|---|---|---|---|---|
| X-axis | Y-axis | X-axis | Y-axis | X-axis | Y-axis |
| 0.482 s. | 0.534 s. | 0.380 s. | 0.422 s. | 0.425 s. | 0.469 s. |
| Scenario | Element | Profile | Length (m) | Weight (Ton.) |
|---|---|---|---|---|
| Scenario 1. DSregional for type II soil. | Column | W 21 plg × 166 lb/ft | 390 | 96.38 |
| Primary beam | W 16 plg × 40 lb/ft | 974 | 58.22 | |
| Secondary beam | W 10 in × 30 lb/ft | 1296 | 58.15 | |
| Braces | HSS 9 in × ½ in | 554.23 | 42.94 | |
| Total weight | 255.68 | |||
| Scenario 2. DSsite | Column | W 14 plg × 109 lb/ft | 390 | 58.15 |
| Primary beam | W 16 plg × 36 lb/ft | 974 | 52.35 | |
| Secondary beam | W 10 plg × 30 lb/ft | 1296 | 58.15 | |
| Braces | HSS 8 in × ½ in | 554.23 | 39.26 | |
| Total weight | 213.08 | |||
| Concept | Unit | Final Design Scenario 1. DSregional for Type II Soil. | Final Design Scenario 2. DSsite | ||||
|---|---|---|---|---|---|---|---|
| Amount | Unit Cost * | Cost | Amount | Unit Cost * | Cost | ||
| Column | ton. | 96.38 | USD 2045.02 | USD 197,099.03 | 58.15 | USD 1941.34 | USD 112,888.92 |
| Primary beam | ton. | 58.22 | USD 1796.11 | USD 104,569.52 | 52.35 | USD 1898.87 | USD 99,405.84 |
| Secondary beam | ton. | 58.15 | USD 1696.42 | USD 98,646.82 | 58.15 | USD 1696.42 | USD 98,646.82 |
| Braces | ton. | 42.94 | USD 1784.57 | USD 76,629.44 | 39.26 | USD 1694.36 | USD 66,520.57 |
| Geotechnical study (SPT test) | test | 1 | USD 3300.00 | USD 3300.00 | 1 | USD 3300.00 | USD 3300.00 |
| Geophysical study: (DownHole test) | test | 0 | USD 3300.00 | USD - | 1 | USD 3300.00 | USD 3300.00 |
| Environmental vibration record: | test | 0 | USD 1000.00 | USD - | 1 | USD 1000.00 | USD 1000.00 |
| Seismic hazard study to determine site-specific design spectrum (DSsite): | study | 0 | USD 8500.00 | USD - | 1 | USD 8500.00 | USD 8500.00 |
| Total cost | USD 480,244.81 | Total cost | USD 393,562.15 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos-Sánchez, J.A.; Díaz, S.A.; Mora-Ortiz, R.S.; Polanco-Sotomayor, G.; Magaña-Hernández, F. Optimization of Structural Design in Steel Buildings Based on the Site-Specific Design Spectra of the Mexico Seismic Regulations. Geosciences 2024, 14, 32. https://doi.org/10.3390/geosciences14020032
Ramos-Sánchez JA, Díaz SA, Mora-Ortiz RS, Polanco-Sotomayor G, Magaña-Hernández F. Optimization of Structural Design in Steel Buildings Based on the Site-Specific Design Spectra of the Mexico Seismic Regulations. Geosciences. 2024; 14(2):32. https://doi.org/10.3390/geosciences14020032
Chicago/Turabian StyleRamos-Sánchez, Juan Antonio, Sergio A. Díaz, René Sebastián Mora-Ortiz, Gabriel Polanco-Sotomayor, and Francisco Magaña-Hernández. 2024. "Optimization of Structural Design in Steel Buildings Based on the Site-Specific Design Spectra of the Mexico Seismic Regulations" Geosciences 14, no. 2: 32. https://doi.org/10.3390/geosciences14020032
APA StyleRamos-Sánchez, J. A., Díaz, S. A., Mora-Ortiz, R. S., Polanco-Sotomayor, G., & Magaña-Hernández, F. (2024). Optimization of Structural Design in Steel Buildings Based on the Site-Specific Design Spectra of the Mexico Seismic Regulations. Geosciences, 14(2), 32. https://doi.org/10.3390/geosciences14020032







