Deterministic Physically Based Distributed Models for Rainfall-Induced Shallow Landslides
Abstract
1. Introduction
2. Shallow Landslide Modeling Methods
2.1. Hydrology
2.2. Slope Stability
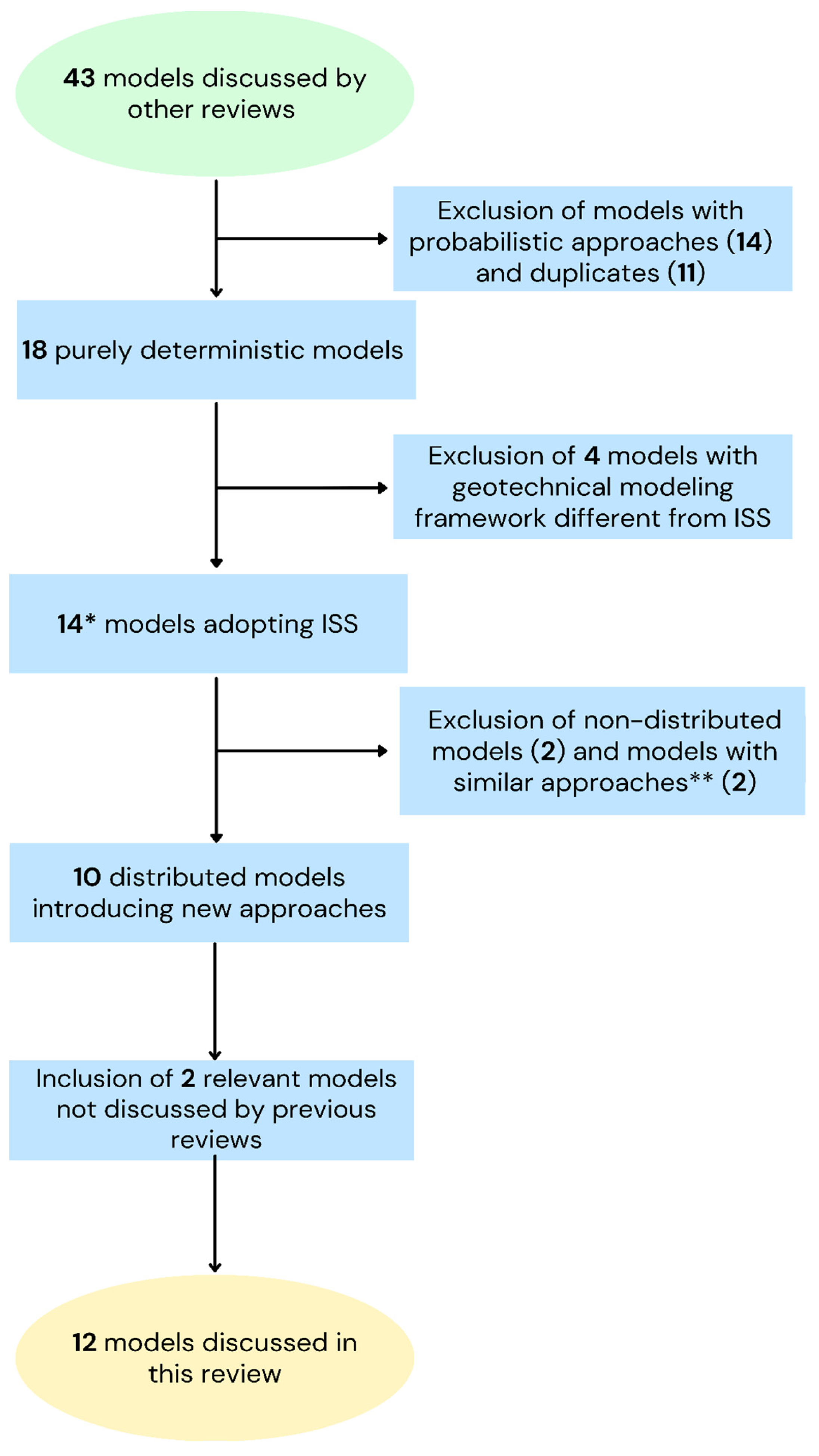
3. Materials and Methods
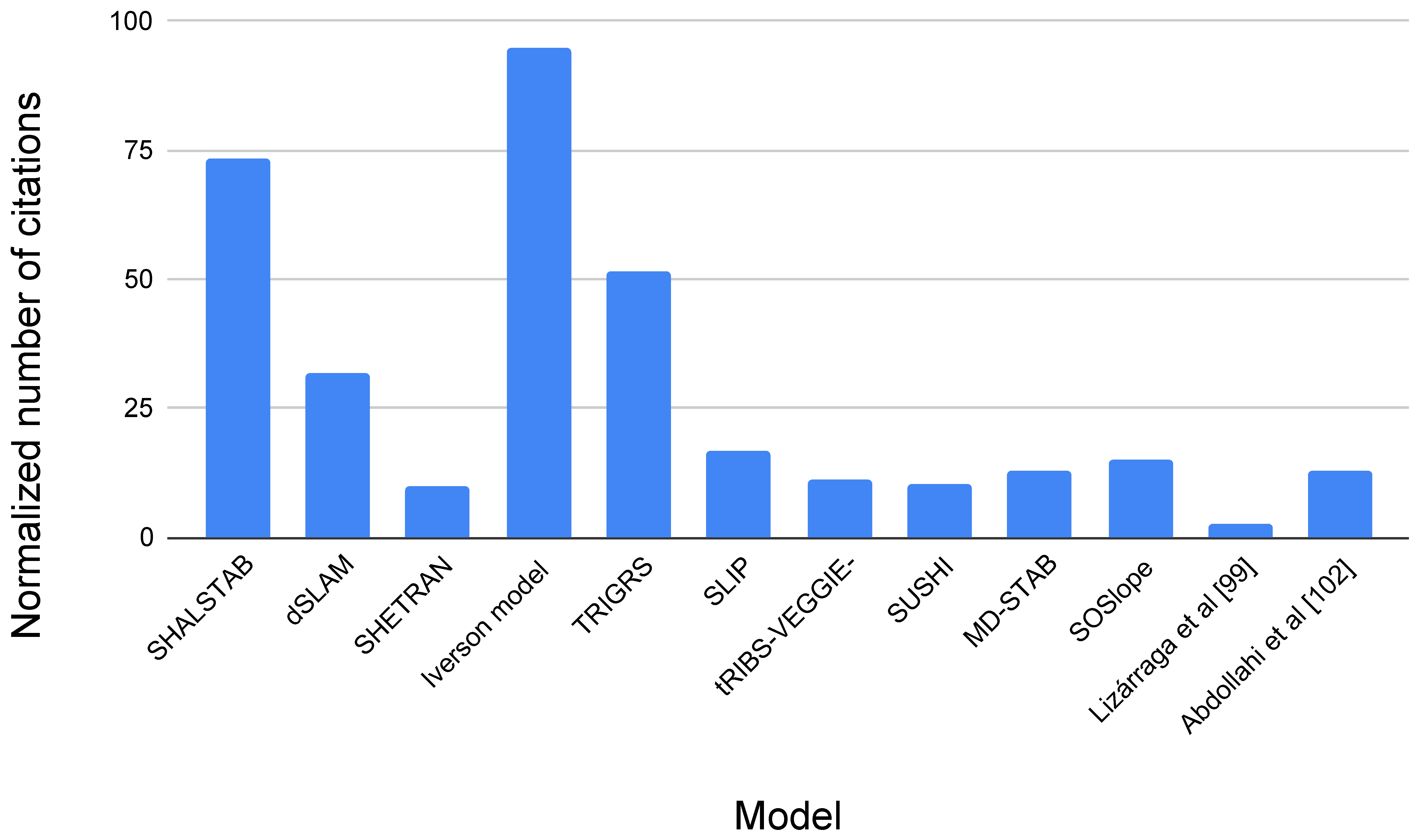
4. Discussion on Models
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Persichillo, M.G.; Bordoni, M.; Meisina, C. The role of land use changes in the distribution of shallow landslides. Sci. Total Environ. 2017, 574, 924–937. [Google Scholar] [CrossRef]
- Cotecchia, F.; Santaloia, F.; Lollino, P.; Vitone, C.; Pedone, G.; Bottiglieri, O. From a phenomenological to a geomechanical approach to landslide hazard analysis. Eur. J. Environ. Civ. Eng. 2016, 20, 1004–1031. [Google Scholar] [CrossRef]
- Crozier, M.J. Deciphering the effect of climate change on landslide activity: A review. Geomorphology 2010, 124, 260–267. [Google Scholar] [CrossRef]
- Gariano, S.L.; Guzzetti, F. Landslides in a changing climate. Earth-Sci. Rev. 2016, 162, 227–252. [Google Scholar] [CrossRef]
- Polemio, M.; Petrucci, O. Rainfall as a Landslide Triggering Factor an Overview of Recent International Research; Thomas Telford Ltd.: London, UK, 1999; pp. 1219–1226. [Google Scholar]
- Guzzetti, F.; Gariano, S.L.; Peruccacci, S.; Brunetti, M.T.; Marchesini, I.; Rossi, M.; Melillo, M. Geographical landslide early warning systems. Earth-Sci. Rev. 2020, 200, 102973. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Guzzetti, F.; Carrara, A.; Cardinali, M.; Reichenbach, P. Landslide hazard evaluation: A review of current techniques and their application in a multi-scale study, Central Italy. Geomorphology 1999, 31, 181–216. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; van Westen, C.; Lombardo, L. Landslide hazard spatiotemporal prediction based on data-driven models: Estimating where, when and how large landslide may be. Int. J. Appl. Earth Obs. Geoinf. 2024, 126, 103631. [Google Scholar] [CrossRef]
- Crosta, G.B.; Frattini, P.J.N.H. Distributed modelling of shallow landslides triggered by intense rainfall. Nat. Hazards Earth Syst. Sci. 2003, 3, 81–93. [Google Scholar] [CrossRef]
- Kyriou, A.; Nikolakopoulos, K.G.; Koukouvelas, I.K. Timely and low-cost remote sensing practices for the assessment of landslide activity in the service of hazard management. Remote Sens. 2022, 14, 4745. [Google Scholar] [CrossRef]
- Nikolakopoulos, K.G.; Kyriou, A.; Koukouvelas, I.K.; Tomaras, N.; Lyros, E. UAV, GNSS, and InSAR Data Analyses for Landslide Monitoring in a Mountainous Village in Western Greece. Remote Sens. 2023, 15, 2870. [Google Scholar] [CrossRef]
- Nikolakopoulos, K.G.; Kyriou, A.; Koukouvelas, I.K. UAV, GNSS, and GIS for the Rapid Assessment of Multi-Occurrence Landslides. Geosciences 2024, 14, 160. [Google Scholar] [CrossRef]
- Tsironi, V.; Ganas, A.; Karamitros, I.; Efstathiou, E.; Koukouvelas, I.; Sokos, E. Kinematics of active landslides in Achaia (Peloponnese, Greece) through InSAR time series analysis and relation to rainfall patterns. Remote Sens. 2022, 14, 844. [Google Scholar] [CrossRef]
- Li, Y.; Duan, W. Decoding vegetation’s role in landslide susceptibility mapping: An integrated review of techniques and future directions. Biogeotechnics 2023, 2, 100056. [Google Scholar] [CrossRef]
- Raia, S.; Alvioli, M.; Rossi, M.; Baum, R.L.; Godt, J.W.; Guzzetti, F. Improving predictive power of physically based rainfall-induced shallow landslide models: A probabilistic approach. Geosci. Model Dev. 2014, 7, 495–514. [Google Scholar] [CrossRef]
- Scaringi, G.; Fan, X.; Xu, Q.; Liu, C.; Ouyang, C.; Domènech, G.; Yang, F.; Dai, L. Some considerations on the use of numerical methods to simulate past landslides and possible new failures: The case of the recent Xinmo landslide (Sichuan, China). Landslides 2018, 15, 1359–1375. [Google Scholar] [CrossRef]
- Milledge, D.G.; Griffiths, D.V.; Lane, S.N.; Warburton, J. Limits on the validity of infinite length assumptions for modelling shallow landslides. Earth Surf. Process. Landf. 2012, 37, 1158–1166. [Google Scholar] [CrossRef]
- Greco, R.; Marino, P.; Bogaard, T.A. Recent advancements of landslide hydrology. Wiley Interdiscip. Rev. Water 2023, 10, e1675. [Google Scholar] [CrossRef]
- Murgia, I.; Giadrossich, F.; Mao, Z.; Cohen, D.; Capra, G.F.; Schwarz, M. Modeling shallow landslides and root reinforcement: A review. Ecol. Eng. 2022, 181, 106671. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Q.; Werner, A.D.; Li, Y.; Jiang, S.; Tan, Z. Root-induced changes of soil hydraulic properties—A review. J. Hydrol. 2020, 589, 125203. [Google Scholar] [CrossRef]
- Ni, J.J.; Leung, A.K.; Ng, C.W.W. Modelling effects of root growth and decay on soil water retention and permeability. Can. Geotech. J. 2019, 56, 1049–1055. [Google Scholar] [CrossRef]
- de Jesús Arce-Mojica, T.; Nehren, U.; Sudmeier-Rieux, K.; Miranda, P.J.; Anhuf, D. Nature-based solutions (NbS) for reducing the risk of shallow landslides: Where do we stand? Int. J. Disaster Risk Reduct. 2019, 41, 101293. [Google Scholar] [CrossRef]
- Vicarelli, M.; Sudmeier-Rieux, K.; Alsadadi, A.; Shrestha, A.; Schütze, S.; Kang, M.M.; Leue, M.; Wasielewski, D.; Mysiak, J. On the cost-effectiveness of Nature-based Solutions for reducing disaster risk. Sci. Total Environ. 2024, 947, 174524. [Google Scholar] [CrossRef] [PubMed]
- DiBiagio, A.; Capobianco, V.; Oen, A.; Tallaksen, L.M. State-of-the-art: Parametrization of hydrological and mechanical reinforcement effects of vegetation in slope stability models for shallow landslides. Landslides 2024, 21, 2417–2446. [Google Scholar] [CrossRef]
- Mao, Z. Root reinforcement models: Classification, criticism and perspectives. Plant Soil 2022, 472, 17–28. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E.; Clifton, A.W. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Godt, J.W.; Baum, R.L.; Savage, W.Z.; Salciarini, D.; Schulz, W.H.; Harp, E.L. Transient deterministic shallow landslide modeling: Requirements for susceptibility and hazard assessments in a GIS framework. Eng. Geol. 2008, 102, 214–226. [Google Scholar] [CrossRef]
- Kuriakose, S.L.; Jetten, V.G.; Van Westen, C.J.; Sankar, G.; Van Beek, L.P.H. Pore water pressure as a trigger of shallow landslides in the Western Ghats of Kerala, India: Some preliminary observations from an experimental catchment. Phys. Geogr. 2008, 29, 374–386. [Google Scholar] [CrossRef]
- Ran, Q.; Hong, Y.; Li, W.; Gao, J. A modelling study of rainfall-induced shallow landslide mechanisms under different rainfall characteristics. J. Hydrol. 2018, 563, 790–801. [Google Scholar] [CrossRef]
- McKenna, J.P.; Santi, P.M.; Amblard, X.; Negri, J. Effects of soil-engineering properties on the failure mode of shallow landslides. Landslides 2012, 9, 215–228. [Google Scholar] [CrossRef]
- Gofar, N.; Rahardjo, H. Saturated and unsaturated stability analysis of slope subjected to rainfall infiltration. MATEC Web Conf. 2017, 101, 05004. [Google Scholar] [CrossRef]
- Gabet, E.J.; Mudd, S.M. The mobilization of debris flows from shallow landslides. Geomorphology 2006, 74, 207–218. [Google Scholar] [CrossRef]
- Iverson, R.M.; Reid, M.E.; LaHusen, R.G. Debris-flow mobilization from landslides. Annu. Rev. Earth Planet. Sci. 1997, 25, 85–138. [Google Scholar] [CrossRef]
- Ridley, A.M. Soil suction—What it is and how to successfully measure it. In Proceedings of the FMGM 2015: Ninth Symposium on Field Measurements in Geomechanics, Sydney, Australia, 9–11 September 2015; Australian Centre for Geomechanics: Crawley, Australia, 2015; pp. 27–46. [Google Scholar]
- Fredlund, D.G. Unsaturated soil mechanics in engineering practice. J. Geotech. Geoenvironmental Eng. 2006, 132, 286–321. [Google Scholar] [CrossRef]
- Bittelli, M.; Valentino, R.; Salvatorelli, F.; Pisa, P.R. Monitoring soil-water and displacement conditions leading to landslide occurrence in partially saturated clays. Geomorphology 2012, 173–174, 161–173. [Google Scholar] [CrossRef]
- Godt, J.W.; Baum, R.L.; Lu, N. Landsliding in partially saturated materials. Geophys. Res. Lett. 2009, 36, L02403. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Bordoni, M.; Meisina, C.; Valentino, R.; Lu, N.; Bittelli, M.; Chersich, S. Hydrological factors affecting rainfall-induced shallow landslides: From the field monitoring to a simplified slope stability analysis. Eng. Geol. 2015, 193, 19–37. [Google Scholar] [CrossRef]
- Leung, A.K.; Garg, A.; Ng, C.W.W. Effects of plant roots on soil-water retention and induced suction in vegetated soil. Eng. Geol. 2015, 193, 183–197. [Google Scholar] [CrossRef]
- Farthing, M.W.; Ogden, F.L. Numerical solution of Richards’ equation: A review of advances and challenges. Soil Sci. Soc. Am. J. 2017, 81, 1257–1269. [Google Scholar] [CrossRef]
- Zha, Y.; Yang, J.; Zeng, J.; Tso, C.H.M.; Zeng, W.; Shi, L. Review of numerical solution of Richardson–Richards equation for variably saturated flow in soils. Wiley Interdiscip. Rev. Water 2019, 6, e1364. [Google Scholar] [CrossRef]
- Cockett, R.; Heagy, L.J.; Haber, E. Efficient 3D inversions using the Richards equation. Comput. Geosci. 2018, 116, 91–102. [Google Scholar] [CrossRef]
- Priono; Rahardjo, H.; Chatterjea, K.; Leong, E.C.; Wang, J.Y. Effect of hydraulic anisotropy on soil–water characteristic curve. Soils Found. 2016, 56, 228–239. [Google Scholar] [CrossRef]
- Jing, Y.S.; Zhang, B.; Thimm, A.; Zepp, H. Anisotropy of soil hydraulic properties along arable slopes. Pedosphere 2008, 18, 353–362. [Google Scholar] [CrossRef]
- Ali, A.; Huang, J.; Lyamin, A.V.; Sloan, S.W.; Cassidy, M.J. Boundary effects of rainfall-induced landslides. Comput. Geotech. 2014, 61, 341–354. [Google Scholar] [CrossRef]
- Liu, H.; Lei, T.W.; Zhao, J.; Yuan, C.P.; Fan, Y.T.; Qu, L.Q. Effects of rainfall intensity and antecedent soil water content on soil infiltrability under rainfall conditions using the run off-on-out method. J. Hydrol. 2011, 396, 24–32. [Google Scholar] [CrossRef]
- Tabacchi, E.; Lambs, L.; Guilloy, H.; Planty-Tabacchi, A.M.; Muller, E.; Decamps, H. Impacts of riparian vegetation on hydrological processes. Hydrol. Process. 2000, 14, 2959–2976. [Google Scholar] [CrossRef]
- Gerke, H.H. Preferential flow descriptions for structured soils. J. Plant Nutr. Soil Sci. 2006, 169, 382–400. [Google Scholar] [CrossRef]
- Montrasio, L.; Valentino, R.; Losi, G.L. Rainfall infiltration in a shallow soil: A numerical simulation of the double-porosity effect. Electron. J. Geotechnol. Eng. 2011, 16, 1387–1403. [Google Scholar]
- Shao, W.; Yang, Z.; Ni, J.; Su, Y.; Nie, W.; Ma, X. Comparison of single-and dual-permeability models in simulating the unsaturated hydro-mechanical behavior in a rainfall-triggered landslide. Landslides 2018, 15, 2449–2464. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L.; Miller, N. Green-Ampt infiltration parameters from soils data. J. Hydraul. Eng. 1983, 109, 62–70. [Google Scholar] [CrossRef]
- Cho, S.E. Prediction of shallow landslide by surficial stability analysis considering rainfall infiltration. Eng. Geol. 2017, 231, 126–138. [Google Scholar] [CrossRef]
- Xiao, S.; Dai, T.; Li, S. Review and Comparative Analysis of Factor of Safety Definitions in Slope Stability. Geotech. Geol. Eng. 2024, 42, 4263–4283. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J. Infinite slope stability under steady unsaturated seepage conditions. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Liu, W.; Yang, Z.; He, S. Modeling the landslide-generated debris flow from formation to propagation and run-out by considering the effect of vegetation. Landslides 2021, 18, 43–58. [Google Scholar] [CrossRef]
- Masi, E.B.; Tofani, V.; Rossi, G.; Cuomo, S.; Wu, W.; Salciarini, D.; Caporali, E.; Catani, F. Effects of roots cohesion on regional distributed slope stability modelling. Catena 2023, 222, 106853. [Google Scholar] [CrossRef]
- Masi, E.B.; Segoni, S.; Tofani, V. Root reinforcement in slope stability models: A review. Geosciences 2021, 11, 212. [Google Scholar] [CrossRef]
- Bischetti, G.B.; Chiaradia, E.A.; Epis, T.; Morlotti, E. Root cohesion of forest species in the Italian Alps. Plant Soil 2009, 324, 71–89. [Google Scholar] [CrossRef]
- Ni, J.J.; Leung, A.K.; Ng, C.W.W.; Shao, W. Modelling hydro-mechanical reinforcements of plants to slope stability. Comput. Geotech. 2018, 95, 99–109. [Google Scholar] [CrossRef]
- Schmaltz, E.M.; Mergili, M. Integration of root systems into a GIS-based slip surface model: Computational experiments in a generic hillslope environment. Landslides 2018, 15, 1561–1575. [Google Scholar] [CrossRef]
- Giadrossich, F.; Cohen, D.; Schwarz, M.; Ganga, A.; Marrosu, R.; Pirastru, M.; Capra, G.F. Large roots dominate the contribution of trees to slope stability. Earth Surf. Process. Landf. 2019, 44, 1602–1609. [Google Scholar] [CrossRef]
- Waldron, L.J. The shear resistance of root-permeated homogeneous and stratified soil. Soil Sci. Soc. Am. J. 1977, 41, 843–849. [Google Scholar] [CrossRef]
- Wu, T.H.; McKinnell, W.P., III; Swanston, D.N. Strength of tree roots and landslides on Prince of Wales Island, Alaska. Can. Geotech. J. 1979, 16, 19–33. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A. Estimating the mechanical effects of riparian vegetation on stream bank stability using a fiber bundle model. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Cohen, D.; Schwarz, M.; Or, D. An analytical fiber bundle model for pullout mechanics of root bundles. J. Geophys. Res. Earth Surf. 2011, 116. [Google Scholar] [CrossRef]
- Schwarz, M.; Cohen, D.; Or, D. Root-soil mechanical interactions during pullout and failure of root bundles. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Schwarz, M.; Giadrossich, F.; Cohen, D. Modeling root reinforcement using a root-failure Weibull survival function. Hydrol. Earth Syst. Sci. 2013, 17, 4367–4377. [Google Scholar] [CrossRef]
- Schwarz, M.; Lehmann, P.; Or, D. Quantifying lateral root reinforcement in steep slopes–from a bundle of roots to tree stands. Earth Surf. Process. Landf. 2010, 35, 354–367. [Google Scholar] [CrossRef]
- Moos, C.; Bebi, P.; Graf, F.; Mattli, J.; Rickli, C.; Schwarz, M. How does forest structure affect root reinforcement and susceptibility to shallow landslides? Earth Surf. Process. Landf. 2016, 41, 951–960. [Google Scholar] [CrossRef]
- Patil, N.G.; Singh, S.K. Pedotransfer functions for estimating soil hydraulic properties: A review. Pedosphere 2016, 26, 417–430. [Google Scholar] [CrossRef]
- Meena, V.; Kumari, S.P.; Shankar, V. Physically based modelling techniques for landslide susceptibility analysis: A comparison. IOP Conf. Ser.: Earth Environ. Sci. 2022, 1032, 012033. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Dietrich, W.E. A physically based model for the topographic control on shallow landsliding. Water Resour. Res. 1994, 30, 1153–1171. [Google Scholar] [CrossRef]
- O’Loughlin, E.M. Prediction of surface saturation zones in natural catchments by topographic analysis. Water Resour. Res. 1986, 22, 794–804. [Google Scholar] [CrossRef]
- Wu, W.; Sidle, R.C. A distributed slope stability model for steep forested basins. Water Resour. Res. 1995, 31, 2097–2110. [Google Scholar] [CrossRef]
- Takasao, T.; Shiiba, M. Incorporation of the effect of concentration of flow into the kinematic wave equations and its applications to runoff system lumping. J. Hydrol. 1988, 102, 301–322. [Google Scholar] [CrossRef]
- Burton, A.; Bathurst, J.C. Physically based modelling of shallow landslide sediment yield at a catchment scale. Environ. Geol. 1998, 35, 89–99. [Google Scholar] [CrossRef]
- Ewen, J.; Parkin, G.; O’Connell, P.E. SHETRAN: Distributed river basin flow and transport modeling system. J. Hydrol. Eng. 2000, 5, 250–258. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European Hydrological System—Systeme Hydrologique Europeen,“SHE”, 1: History and philosophy of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Iverson, R.M. Landslide triggering by rain infiltration. Water Resour. Res. 2000, 36, 1897–1910. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.; Sosio, R. Approaches for defining thresholds and return periods for rainfall-triggered shallow landslides. Hydrol. Process. Int. J. 2009, 23, 1444–1460. [Google Scholar] [CrossRef]
- Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS: A Fortran Program for Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Analysis, Version 2.0, Open File Report 2008-1159; US Geological Survey: Reston, VA, USA, 2008; p. 75.
- Srivastava, R.; Yeh, T.C.J. Analytical solutions for one-dimensional, transient infiltration toward the water table in homogeneous and layered soils. Water Resour. Res. 1991, 27, 753–762. [Google Scholar] [CrossRef]
- Saadatkhah, N.; Tehrani, M.H.; Mansor, S.; Khuzaimah, Z.; Kassim, A.; Saadatkhah, R. Impact assessment of land cover changes on the runoff changes on the extreme flood events in the Kelantan River basin. Arab. J. Geosci. 2016, 9, 687. [Google Scholar] [CrossRef]
- Alvioli, M.; Baum, R.L. Parallelization of the TRIGRS model for rainfall-induced landslides using the message passing interface. Environ. Model. Softw. 2016, 81, 122–135. [Google Scholar] [CrossRef]
- Viet, T.T.; Lee, G.; Thu, T.M.; An, H.U. Effect of digital elevation model resolution on shallow landslide modeling using TRIGRS. Nat. Hazards Rev. 2017, 18, 04016011. [Google Scholar] [CrossRef]
- Montrasio, L.; Valentino, R. A model for triggering mechanisms of shallow landslides. Nat. Hazards Earth Syst. Sci. 2008, 8, 1149–1159. [Google Scholar] [CrossRef]
- Montrasio, L.; Valentino, R.; Corina, A.; Rossi, L.; Rudari, R. A prototype system for space–time assessment of rainfall-induced shallow landslides in Italy. Nat. Hazards 2014, 74, 1263–1290. [Google Scholar] [CrossRef]
- Montrasio, L.; Gatto, M.P.A.; Miodini, C. The role of plants in the prevention of soil-slip: The G-SLIP model and its application on territorial scale through G-XSLIP platform. Landslides 2023, 20, 1149–1165. [Google Scholar] [CrossRef]
- Capparelli, G.; Versace, P. FLaIR and SUSHI: Two mathematical models for early warning of landslides induced by rainfall. Landslides 2011, 8, 67–79. [Google Scholar] [CrossRef]
- Lepore, C.; Arnone, E.; Noto, L.V.; Sivandran, G.; Bras, R.L. Physically based modeling of rainfall-triggered landslides: A case study in the Luquillo forest, Puerto Rico. Hydrol. Earth Syst. Sci. 2013, 17, 3371–3387. [Google Scholar] [CrossRef]
- Arnone, E.; Caracciolo, D.; Noto, L.V.; Preti, F.; Bras, R.L. Modeling the hydrological and mechanical effect of roots on shallow landslides. Water Resour. Res. 2016, 52, 8590–8612. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Bras, R.L.; Vivoni, E.R. Vegetation-hydrology dynamics in complex terrain of semiarid areas: 2. Energy-water controls of vegetation spatiotemporal dynamics and topographic niches of favorability. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Milledge, D.G.; Bellugi, D.; McKean, J.A.; Densmore, A.L.; Dietrich, W.E. A multidimensional stability model for predicting shallow landslide size and shape across landscapes. J. Geophys. Res. Earth Surf. 2014, 119, 2481–2504. [Google Scholar] [CrossRef] [PubMed]
- Cislaghi, A.; Chiaradia, E.A.; Bischetti, G.B. Including root reinforcement variability in a probabilistic 3D stability model. Earth Surf. Process. Landf. 2017, 42, 1789–1806. [Google Scholar] [CrossRef]
- Cohen, D.; Schwarz, M. Tree-root control of shallow landslides. Earth Surf. Dyn. 2017, 5, 451–477. [Google Scholar] [CrossRef]
- Lizárraga, J.J.; Frattini, P.; Crosta, G.B.; Buscarnera, G. Regional-scale modelling of shallow landslides with different initiation mechanisms: Sliding versus liquefaction. Eng. Geol. 2018, 228, 346–356. [Google Scholar] [CrossRef]
- Buscarnera, G.; Di Prisco, C. Soil stability and flow slides in unsaturated shallow slopes: Can saturation events trigger liquefaction processes? Géotechnique 2013, 63, 801–817. [Google Scholar] [CrossRef]
- Lizárraga, J.J.; Buscarnera, G. Safety factors to detect flowslides and slips in unsaturated shallow slopes. Géotechnique 2018, 68, 442–450. [Google Scholar] [CrossRef]
- Abdollahi, M.; Vahedifard, F.; Tracy, F.T. Post-wildfire stability of unsaturated hillslopes against rainfall-triggered landslides. Earth’s Future 2023, 11, e2022EF003213. [Google Scholar] [CrossRef]
- Tracy, F.T.; Vahedifard, F. Analytical solution for coupled hydro-mechanical modeling of infiltration in unsaturated soils. J. Hydrol. 2022, 612, 128198. [Google Scholar] [CrossRef]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Nelson, S.G. Relationship between remotely-sensed vegetation indices, canopy attributes and plant physiological processes: What vegetation indices can and cannot tell us about the landscape. Sensors 2008, 8, 2136–2160. [Google Scholar] [CrossRef]
- Lann, T.; Bao, H.; Lan, H.; Zheng, H.; Yan, C.; Peng, J. Hydro-mechanical effects of vegetation on slope stability: A review. Sci. Total Environ. 2024, 926, 171691. [Google Scholar] [CrossRef] [PubMed]
- Schmaltz, E.M.; Van Beek, L.P.H.; Bogaard, T.A.; Kraushaar, S.; Steger, S.; Glade, T. Strategies to improve the explanatory power of a dynamic slope stability model by enhancing land cover parameterisation and model complexity. Earth Surf. Process. Landf. 2019, 44, 1259–1273. [Google Scholar] [CrossRef]
- Sannino, G.; Tomei, F.; Bittelli, M.; Bordoni, M.; Meisina, C.; Valentino, R. Implementation of a slope stability method in the CRITERIA-1D agro-hydrological modeling scheme. Landslides 2024, 1–20. [Google Scholar] [CrossRef]
- Pack, R.T.; Tarboton, D.G.; Goodwin, C.N. The SINMAP approach to terrain stability mapping. In Proceedings of the 8th Congress of the International Association of Engineering Geology, Vancouver, BC, Canada, 21–25 September 1998. [Google Scholar]
- Simoni, S.; Zanotti, F.; Bertoldi, G.; Rigon, R. Modelling the probability of occurrence of shallow landslides and channelized debris flows using GEOtop-FS. Hydrol. Process. 2008, 22, 532–545. [Google Scholar] [CrossRef]
- Rossi, G.; Catani, F.; Leoni, L.; Segoni, S.; Tofani, V. HIRESSS: A physically based slope stability simulator for HPC applications. Nat. Hazards Earth Syst. Sci. 2013, 13, 151–166. [Google Scholar] [CrossRef]
- van Zadelhoff, F.B.; Albaba, A.; Cohen, D.; Phillips, C.; Schaefli, B.; Dorren, L.K.A.; Schwarz, M. Introducing SlideforMAP; a probabilistic finite slope approach for modelling shallow landslide probability in forested situations. Nat. Hazards Earth Syst. Sci. 2021, 22, 2611–2635. [Google Scholar] [CrossRef]
- Medina, V.; Hürlimann, M.; Guo, Z.; Lloret, A.; Vaunat, J. Fast physically-based model for rainfall-induced landslide susceptibility assessment at regional scale. Catena 2021, 201, 105213. [Google Scholar] [CrossRef]
| Model | Country of Application * | Real Case Study | Hydrology | Vegetation |
|---|---|---|---|---|
| SHALSTAB [75] | United States | Tennessee Valley (colluvial soils), Mettman Ridge (colluvial soils), and Split Creek (silty sands) | Derivation of the critical saturated soil height through TOPOG [76] | - |
| dSLAM [77] | United States | Cedar Creek basin, Oregon Coast Range—real landslides not well documented | Kinematic wave groundwater model [78] | Mechanical basal root reinforcement (WWM) as constant Cr |
| SHETRAN [79] | United Kingdom of Great Britain and Northern Ireland | Kirkton research catchment in Balquhidder, Scotland—real landslides not well documented | Lateral flow: Boussinesq equation; vertical flow: 1D Richards’ equation; snowmelt | ET, interception, spatially variable land use |
| Iverson [82] | - | - | Reduced form of Richards’ equation | - |
| TRIGRS [84] | - | - | Richards’ equation per [85] | Extension by [86] comprises root cohesion and tree surcharge |
| SLIP [90] | Italy | Different areas of Italy | Increase in the saturated portion of the soil with rainfall | Extension by [91] comprises interception and root cohesion |
| SUSHI [92] | Italy | May 1998 Sarno landslides on pyroclastic soils from Campania (Italy) | 1D Richards’ equation (Hydro-SUSHI module) | ET as function of LAI, interception |
| tRIBS-VEGGIE-Landslide [93] | Puerto Rico | Luquillo forest (Puerto Rico)—no real landslides | 1D Richards’ equation | Hydrological effects: transpiration [95], evaporation reduction by canopies; vegetation variable with time, space, and depth (root distribution and root water uptake); root cohesion |
| MD-STAB [96] | United States | November 1996, Coos Bay, Mettnam ridge debris flow (gravelly sand) | Hydrostatic condition | Only mechanical reinforcement: basal and lateral, variable with depth |
| SOSlope [98] | - | - | Macropore water pressure and matrix suction | Mechanical lateral root reinforcement (RBM) |
| Lizárraga et al. [99] | Italy | May 1998 landslides on pyroclastic soils from Campania (Italy) | Authors used TRIGRS to compute hydrology | - |
| Abdollahi et al. [102] | United States | 2019 Las Lomas watershed (California) shallow landslide (sandy loam and loam soils) | 1D Richards’ equation | ET Mechanical basal root reinforcement (AFBM) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sannino, G.; Bordoni, M.; Bittelli, M.; Meisina, C.; Tomei, F.; Valentino, R. Deterministic Physically Based Distributed Models for Rainfall-Induced Shallow Landslides. Geosciences 2024, 14, 255. https://doi.org/10.3390/geosciences14100255
Sannino G, Bordoni M, Bittelli M, Meisina C, Tomei F, Valentino R. Deterministic Physically Based Distributed Models for Rainfall-Induced Shallow Landslides. Geosciences. 2024; 14(10):255. https://doi.org/10.3390/geosciences14100255
Chicago/Turabian StyleSannino, Giada, Massimiliano Bordoni, Marco Bittelli, Claudia Meisina, Fausto Tomei, and Roberto Valentino. 2024. "Deterministic Physically Based Distributed Models for Rainfall-Induced Shallow Landslides" Geosciences 14, no. 10: 255. https://doi.org/10.3390/geosciences14100255
APA StyleSannino, G., Bordoni, M., Bittelli, M., Meisina, C., Tomei, F., & Valentino, R. (2024). Deterministic Physically Based Distributed Models for Rainfall-Induced Shallow Landslides. Geosciences, 14(10), 255. https://doi.org/10.3390/geosciences14100255










