Investigating the Influence of a Pre-Existing Shear Band on the Seismic Response of Ideal Step-like Slopes Subjected to Weak Motions: Preliminary Results
Abstract
1. Introduction
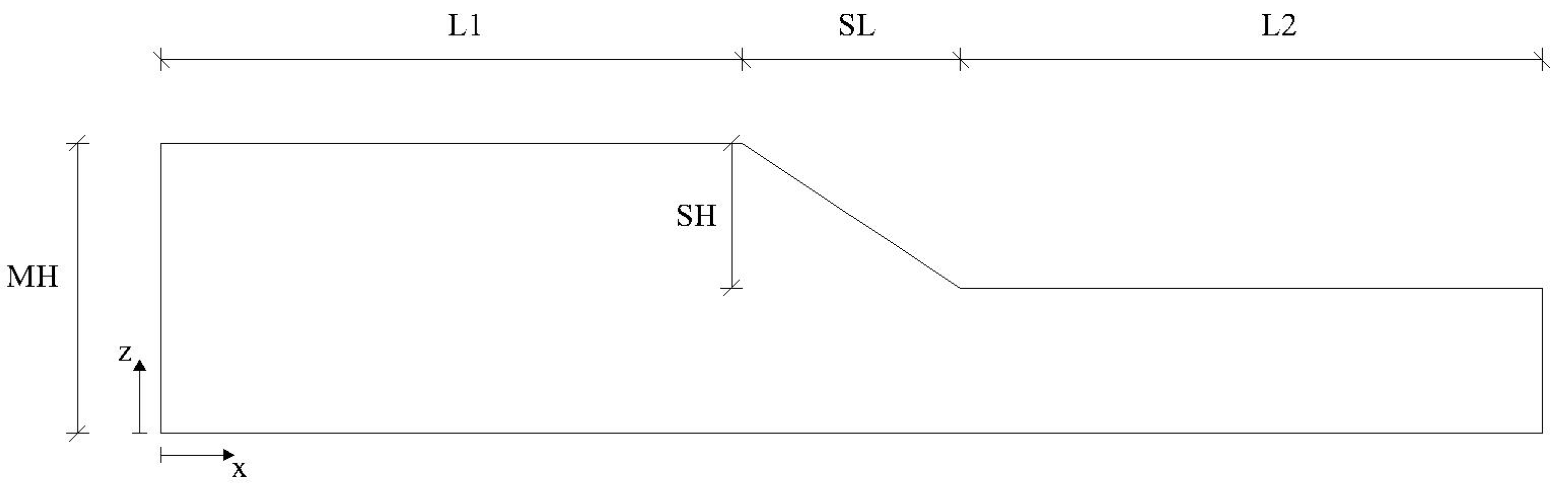
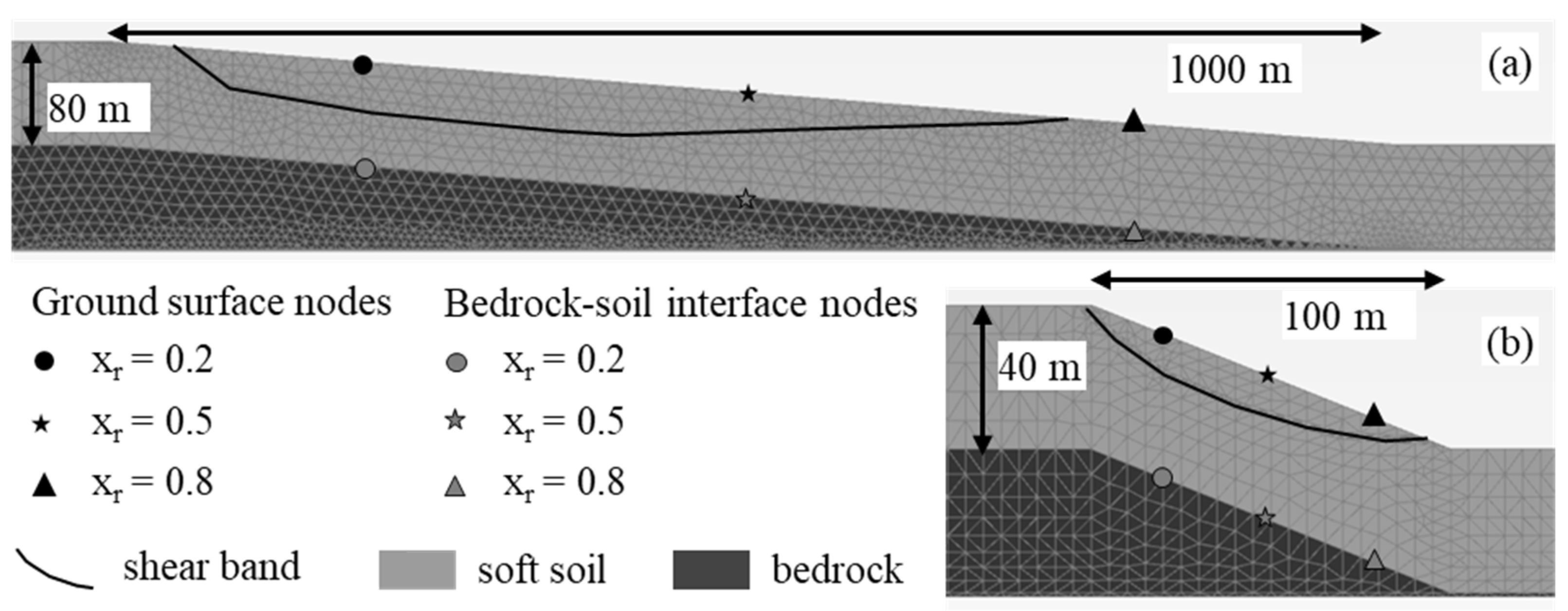
2. Description of the Ideal Case Studies
2.1. Site Conditions
2.2. FE Models
2.3. Constitutive Assumptions
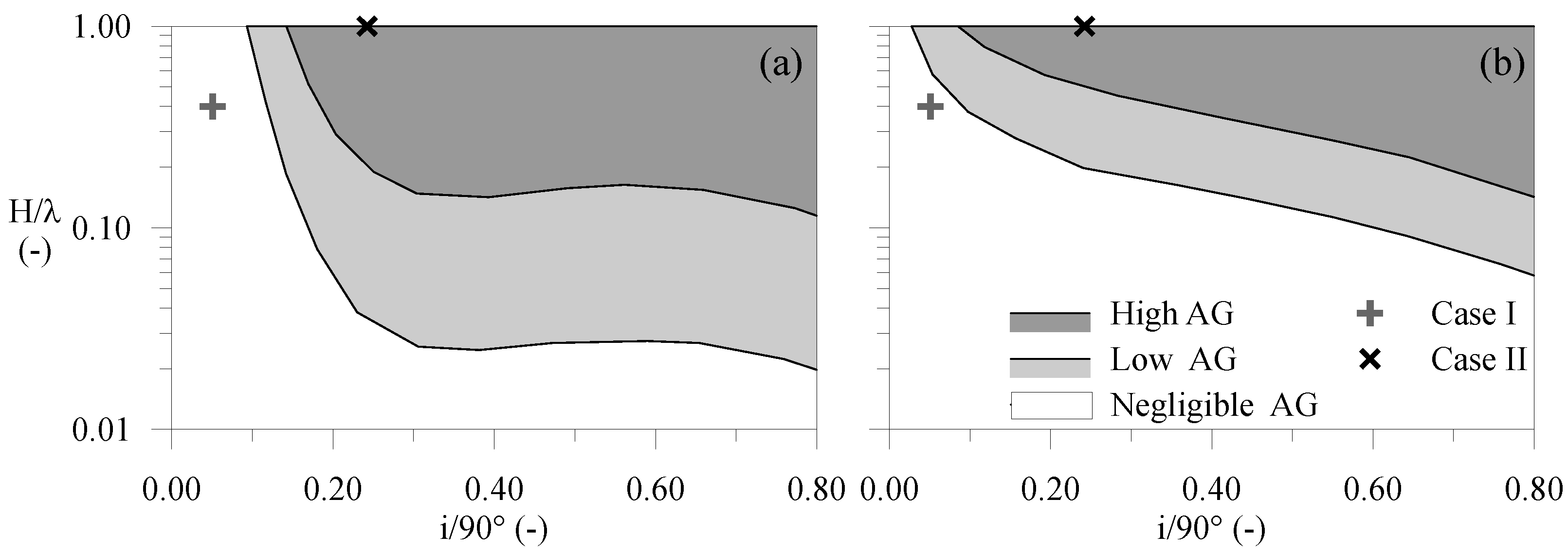
2.4. Input Motions
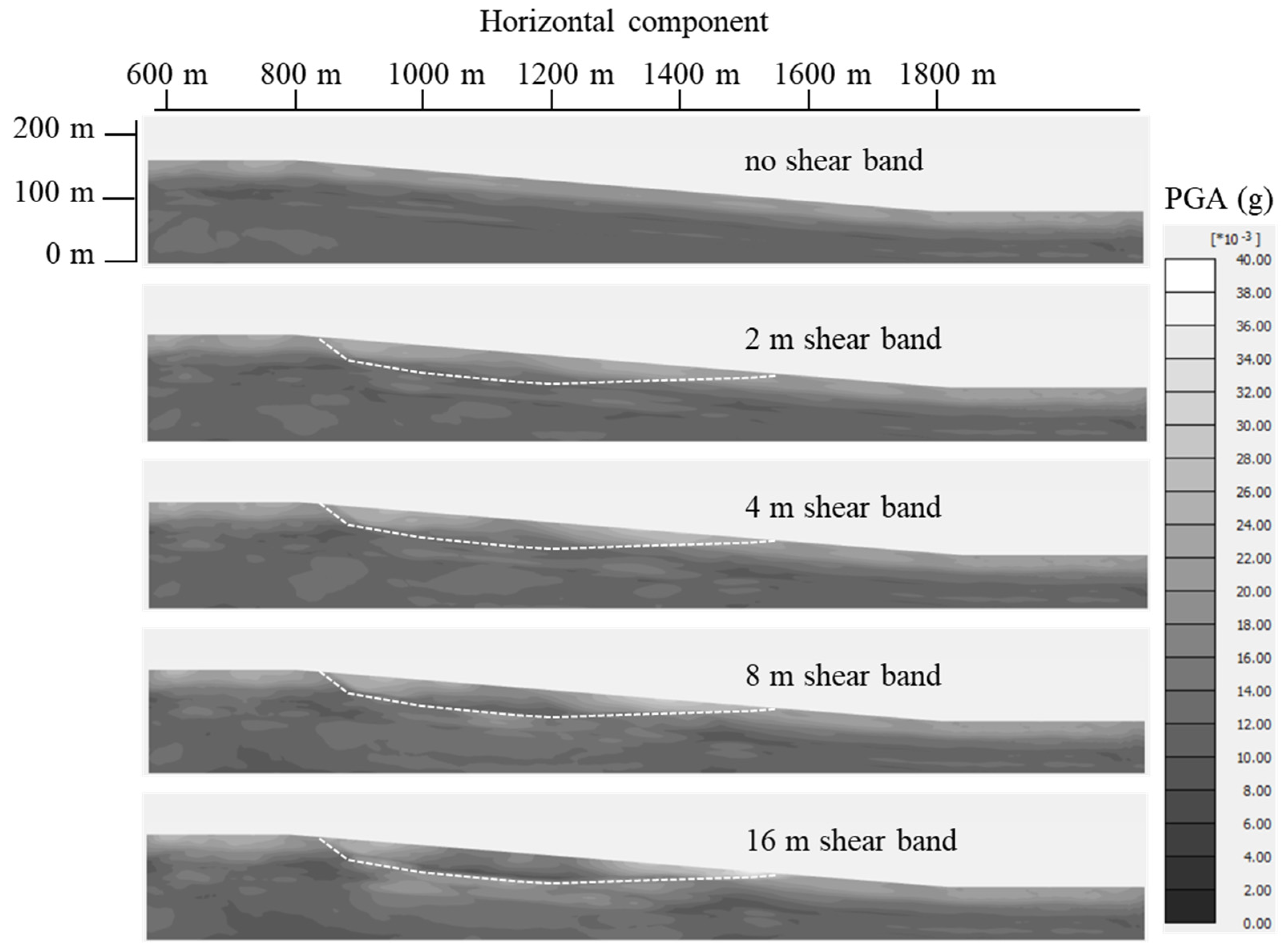
3. Interpretation of the Numerical Results
- (1)
- geomorphological analysis of the area of interest;
- (2)
- collection of soil data (physical and mechanical properties) from available archives;
- (3)
- definition of a preliminary site model including the buried morphology (i.e., shape and thickness of the shear band);
- (4)
- ambient noise measurements aimed at providing Af0 profiles;
- (5)
- performing a parametric analysis by means of numerical simulations based on the preliminary site model and varying the shape and the thickness of the shear band;
- (6)
- comparison between numerical results and site data in terms of Af0 profiles;
- (7)
- selection of the most suitable site model which gives comparable results with site data;
- (8)
- design and execution of site-specific investigations (e.g., continuous coring borehole, inclinometers, etc.) in order to verify the site model selected at the previous point;
- (9)
- release of the definitive subsoil geotechnical model.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kramer, S. Geotechnical Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1996; ISBN 9780133749434. [Google Scholar]
- Gazetas, G. Vibrational characteristics of soil deposits with variable wave velocity. Int. J. Numer. Anal. Methods Geomech. 1982, 6, 1–20. [Google Scholar] [CrossRef]
- Gelagoti, F.; Kourkoulis, R.; Anastasopoulos, I.; Tazoh, T.; Gazetas, G. Seismic Wave Propagation in a Very Soft Alluvial Valley: Sensitivity to Ground-Motion Details and Soil Nonlinearity, and Generation of a Parasitic Vertical Component. Bull. Seismol. Soc. Am. 2010, 100, 3035–3054. [Google Scholar] [CrossRef]
- Ciancimino, A.; Lanzo, G.; Alleanza, G.A.; Amoroso, S.; Bardotti, R.; Biondi, G.; Cascone, E.; Castelli, F.; Giulio, A.D.; d’Onofrio, A.; et al. Dynamic characterization of fine-grained soils in Central Italy by laboratory testing. Bull. Earthq. Eng. 2019, 18, 5503–5531. [Google Scholar] [CrossRef]
- D’Oria, A.F.; Elia, G.; di Lernia, A.; Uva, G. Influence of soil deposit heterogeneity on the dynamic behaviour of masonry towers. In Proceedings of the 3rd International Symposium on Geotechnical Engineering for the Preservation of Momenuments and Historic Sites (TC301–IS Napoli 2022), Naples, Italy, 22–24 June 2022. [Google Scholar]
- Assimaki, D.; Gazetas, G.; Kausel, E. Effects of Local Soil Conditions on the Topographic Aggravation of Seismic Motion: Parametric Investigation and Recorded Field Evidence from the 1999 Athens Earthquake. Bull. Seismol. Soc. Am. 2005, 95, 1059–1089. [Google Scholar] [CrossRef]
- Gazetas, G.; Kallou, P.V.; Psarropoulos, P.N. Topography and Soil Effects in the MS 5.9 Parnitha (Athens) Earthquake: The Case of Adámes. Nat. Hazards 2002, 27, 133–169. [Google Scholar] [CrossRef]
- Elia, G.; di Lernia, A.; Rouainia, M. Ground motion scaling for the assessment of the seismic response of a diaphragm wall. In Proceedings of the 7ICEGE. VII International Conference on Earthquake Geotechnical Engineering, Rome, Italy, 17–20 June 2019; pp. 2249–2257. [Google Scholar]
- Rathje, E.M.; Kottke, A.R.; Trent, W.L. Influence of Input Motion and Site Property Variabilities on Seismic Site Response Analysis. J. Geotech. Geoenviron. Eng. 2010, 136, 607–619. [Google Scholar] [CrossRef]
- Guzel, Y.; Elia, G.; Rouainia, M.; Falcone, G. The Influence of Input Motion Scaling Strategies on Nonlinear Ground Response Analyses of Soft Soil Deposits. Geoscience 2023, 13, 17. [Google Scholar] [CrossRef]
- Pagliaroli, A.; Lanzo, G.; D’Elia, B. Numerical Evaluation of Topographic Effects at the Nicastro Ridge in Southern Italy. J. Earthq. Eng. 2011, 15, 404–432. [Google Scholar] [CrossRef]
- Gobbi, S.; Lenti, L.; Santisi d’Avila, M.P.; Semblat, J.F.; Reiffsteck, P. Influence of the variability of soil profile properties on weak and strong seismic response. Soil Dyn. Earthq. Eng. 2020, 135, 106200. [Google Scholar] [CrossRef]
- Guzel, Y.; Rouainia, M.; Elia, G. Effect of soil variability on nonlinear site response predictions: Application to the Lotung site. Comput. Geotech. 2020, 121, 103444. [Google Scholar] [CrossRef]
- Falcone, G.; Acunzo, G.; Mendicelli, A.; Mori, F.; Naso, G.; Peronace, E.; Porchia, A.; Romagnoli, G.; Tarquini, E.; Moscatelli, M. Seismic amplification maps of Italy based on site-specific microzonation dataset and one-dimensional numerical approach. Eng. Geol. 2021, 289, 106170. [Google Scholar] [CrossRef]
- De Risi, R.; Penna, A.; Simonelli, A.L. Seismic risk at urban scale: The role of site response analysis. Soil Dyn. Earthq. Eng. 2019, 123, 320–336. [Google Scholar] [CrossRef]
- Ciancimino, A.; Foti, S.; Lanzo, G. Stochastic analysis of seismic ground response for site classification methods verification. Soil Dyn. Earthq. Eng. 2018, 111, 169–183. [Google Scholar] [CrossRef]
- Tönük, G.; Ansal, A.; Kurtuluş, A.; Çetiner, B. Site specific response analysis for performance based design earthquake characteristics. Bull. Earthq. Eng. 2014, 12, 1091–1105. [Google Scholar] [CrossRef]
- Geli, L.; Bard, P.Y.; Jullien, B. The effect of topography on earthquake ground motion: A review and new results. Bull. Seismol. Soc. Am. 1988, 78, 42–63. [Google Scholar] [CrossRef]
- Bouckovalas, G.D.; Papadimitriou, A.G. Numerical evaluation of slope topography effects on seismic ground motion. Soil Dyn. Earthq. Eng. 2005, 25, 547–558. [Google Scholar] [CrossRef]
- Rizzitano, S.; Cascone, E.; Biondi, G. Coupling of topographic and stratigraphic effects on seismic response of slopes through 2D linear and equivalent linear analyses. Soil Dyn. Earthq. Eng. 2014, 67, 66–84. [Google Scholar] [CrossRef]
- Falcone, G.; Boldini, D.; Amorosi, A. Site response analysis of an urban area: A multi-dimensional and non-linear approach. Soil Dyn. Earthq. Eng. 2018, 109, 33–45. [Google Scholar] [CrossRef]
- Gatmiri, B.; Arson, C. Seismic site effects by an optimized 2D BE/FE method II. Quantification of site effects in two-dimensional sedimentary valleys. Soil Dyn. Earthq. Eng. 2008, 28, 646–661. [Google Scholar] [CrossRef]
- Falcone, G.; Boldini, D.; Martelli, L.; Amorosi, A. Quantifying local seismic amplification from regional charts and site specific numerical analyses: A case study. Bull. Earthq. Eng. 2020, 18, 77–107. [Google Scholar] [CrossRef]
- Costanzo, A.; D’Onofrio, A.; Silvestri, F. Seismic response of a geological, historical and architectural site: The Gerace cliff (southern Italy). Bull. Eng. Geol. Environ. 2019, 78, 5617–5633. [Google Scholar] [CrossRef]
- di Lernia, A.; Buono, C.; Elia, G. Evaluation of seismic site effects in a real slope through 2D FE numerical analyses. In Proceedings of the 9th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering–COMPDYN2023, Athens, Greece, 12–14 June 2023. [Google Scholar]
- Moczo, P.; Kristek, J.; Bard, P.Y.; Stripajová, S.; Hollender, F.; Chovanová, Z.; Kristeková, M.; Sicilia, D. Key structural parameters affecting earthquake ground motion in 2D and 3D sedimentary structures. Bull. Earthq. Eng. 2018, 16, 2421–2450. [Google Scholar] [CrossRef]
- Zhang, Z.; Fleurisson, J.-A.; Pellet, F. The effects of slope topography on acceleration amplification and interaction between slope topography and seismic input motion. Soil Dyn. Earthq. Eng. 2018, 113, 420–431. [Google Scholar] [CrossRef]
- Zhu, C.; Riga, E.; Pitilakis, K.; Zhang, J.; Thambiratnam, D. Seismic Aggravation in Shallow Basins in Addition to One-dimensional Site Amplification. J. Earthq. Eng. 2020, 24, 1477–1499. [Google Scholar] [CrossRef]
- Zhu, C.; Thambiratnam, D.; Gallage, C. Inherent Characteristics of 2D Alluvial Formations Subjected to In-Plane Motion. J. Earthq. Eng. 2019, 23, 1512–1530. [Google Scholar] [CrossRef]
- Tripe, R.; Kontoe, S.; Wong, T.K.C. Slope topography effects on ground motion in the presence of deep soil layers. Soil Dyn. Earthq. Eng. 2013, 50, 72–84. [Google Scholar] [CrossRef]
- Kwok, A.O.L.; Stewart, J.P.; Hashash, Y.M.A.; Matasovic, N.; Pyke, R.; Wang, Z.; Yang, Z. Use of exact solutions of wave propagation problems to guide implementation of nonlinear seismic ground response analysis procedures. J. Geotech. Geoenviron. Eng. 2007, 133, 1385–1398. [Google Scholar] [CrossRef]
- Schnabel, P.B.; Lysmer, J.; Seed, H.B. SHAKE: A Computer Program for Earthquake Response Analysis of Horizontally Layerd Sites; Report EERC 72-12; Earthquake Engineering Research Center, University of California: Berkley, CA, USA, 1972. [Google Scholar]
- Idriss, I.M.; Lysmer, J.; Hwang, R.; Seed, H.B. QUAD-4: A Computer Program for Evaluating the Seismic Response of Soil Structures by Variable Damping Finite Element Procedures; Report no EERC 73-16; Earthquake Engineering Research Center, University of California: Berkley, CA, USA, 1973. [Google Scholar]
- Amorosi, A.; Boldini, D.; Elia, G. Parametric study on seismic ground response by finite element modelling. Comput. Geotech. 2010, 37, 515–528. [Google Scholar] [CrossRef]
- Régnier, J.; Bonilla, L.; Bard, P.; Bertrand, E.; Hollender, F.; Kawase, H.; Sicilia, D.; Arduino, P.; Amorosi, A.; Asimaki, D.; et al. International Benchmark on Numerical Simulations for 1D, Nonlinear Site Response (PRENOLIN): Verification Phase Based on Canonical Cases. Bull. Seismol. Soc. Am. 2016, 106, 2112–2135. [Google Scholar] [CrossRef]
- Régnier, J.; Bonilla, L.; Bard, P.; Bertrand, E.; Hollender, F.; Kawase, H.; Sicilia, D.; Arduino, P.; Amorosi, A.; Asimaki, D.; et al. PRENOLIN: International Benchmark on 1D Nonlinear Site-Response Analysis—Validation Phase Exercise. Bull. Seismol. Soc. Am. 2018, 108, 876–900. [Google Scholar] [CrossRef]
- Tropeano, G.; Soccodato, F.M.; Silvestri, F. Re-evaluation of code-specified stratigraphic amplification factors based on Italian experimental records and numerical seismic response analyses. Soil Dyn. Earthq. Eng. 2018, 110, 262–275. [Google Scholar] [CrossRef]
- di Lernia, A.; Amorosi, A.; Boldini, D. A multi-directional numerical approach for the seismic ground response and dynamic soil-structure interaction analyses. In Proceedings of the 7ICEGE. VII International Conference on Earthquake Geotechnical Engineering, Roma, Italy, 17–20 June 2019; pp. 2145–2152. [Google Scholar]
- Newmark, N.M. Effects of Earthquakes on Dams and Embankments. Géotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
- Jibson, R.W. Methods for assessing the stability of slopes during earthquakes—A retrospective. Eng. Geol. 2011, 122, 43–50. [Google Scholar] [CrossRef]
- Del Gaudio, V.; Wasowski, J. Advances and problems in understanding the seismic response of potentially unstable slopes. Eng. Geol. 2011, 122, 73–83. [Google Scholar] [CrossRef]
- Lenti, L.; Martino, S. The interaction of seismic waves with step-like slopes and its influence on landslide movements. Eng. Geol. 2012, 126, 19–36. [Google Scholar] [CrossRef]
- Lenti, L.; Martino, S. A parametric numerical study of the interaction between seismic waves and landslides for the evaluation of the susceptibility to seismically induced displacements. Bull. Seismol. Soc. Am. 2013, 103, 33–56. [Google Scholar] [CrossRef]
- Ren, Z.; Chen, C.; Sun, C.; Wang, Y. Dynamic Analysis of the Seismo-Dynamic Response of Anti-Dip Bedding Rock Slopes Using a Three-Dimensional Discrete-Element Method. Appl. Sci. 2022, 12, 4640. [Google Scholar] [CrossRef]
- Rollo, F.; Rampello, S. Probabilistic assessment of seismic-induced slope displacements: An application in Italy. Bull. Earthq. Eng. 2021, 19, 4261–4288. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, C.; Ma, S.; Guo, X.; Yue, M.; Liu, Y. Seismic Response Time-Frequency Analysis of Bedding Rock Slope. Front. Phys. 2020, 8, 558547. [Google Scholar] [CrossRef]
- Leroueil, S. Natural slopes and cuts: Movement and failure mechanisms. Geotechnique 2001, 51, 197–243. [Google Scholar] [CrossRef]
- Chandler, R.J.; Willis, M.R.; Hamilton, P.S.; Andreou, I. Tectonic shear zones in the London Clay Formation. Geotechnique 1998, 48, 257–270. [Google Scholar] [CrossRef]
- Picarelli, L.; Leroueil, S.; Urciuoli, G.; Guerriero, G.; Delisle, M.C. Occurrence and features of shear zones in clay. In Proceedings of the International Workshop on Localization and Bifurcation Theory for Soils and Rocks, Gifu, Japan, 28 September–2 October 1997; pp. 259–270. [Google Scholar]
- Hutchinson, J.N. Methods of locating slip surfaces in landslides. AEG Bull. 1983, 20, 235–252. [Google Scholar] [CrossRef]
- Bordoni, P.; Haines, J.; Di Giulio, G.; Milana, G.; Augliera, P.; Cercato, M.; Martelli, L.; Cara, F.; Horleston, A.; Cattaneo, M.; et al. Cavola experiment site: Geophysical investigations and deployment of a dense seismic array on a landslide. Ann. Geophys. 2007, 50, 627–649. [Google Scholar] [CrossRef]
- Del Gaudio, V.; Wasowski, J. Directivity of slope dynamic response to seismic shaking. Geophys. Res. Lett. 2007, 34, L12301. [Google Scholar] [CrossRef]
- Bozzano, F.; Lenti, L.; Martino, S.; Paciello, A.; Scarascia Mugnozza, G. Self-excitation process due to local seismic amplification responsible for the reactivation of the Salcito landslide (Italy) on 31 October 2002. J. Geophys. Res. 2008, 113, B10312. [Google Scholar] [CrossRef]
- Del Gaudio, V.; Coccia, S.; Wasowski, J.; Gallipoli, M.R.; Mucciarelli, M. Detection of directivity in seismic site response from microtremor spectral analysis. Nat. Hazards Earth Syst. Sci. 2008, 8, 751–762. [Google Scholar] [CrossRef]
- Del Gaudio, V.; Luo, Y.; Wang, Y.; Wasowski, J. Using ambient noise to characterise seismic slope response: The case of Qiaozhuang peri-urban hillslopes (Sichuan, China). Eng. Geol. 2018, 246, 374–390. [Google Scholar] [CrossRef]
- Bouckovalas, G.D.; Papadimitriou, A.G. Aggravation of seismic ground motion due to slope topography. In Proceedings of the 1st European Conference on Earthquake Engineering and Seismology, Geneva, Switzerland, 3–8 September 2006. No. 1171. [Google Scholar]
- Moscatelli, M.; Albarello, D.; Scarascia Mugnozza, G.; Dolce, M. The Italian approach to seismic microzonation. Bull. Earthq. Eng. 2020, 18, 5425–5440. [Google Scholar] [CrossRef]
- Mori, F.; Gaudiosi, I.; Tarquini, E.; Bramerini, F.; Castenetto, S.; Naso, G.; Spina, D. HSM: A synthetic damage-constrained seismic hazard parameter. Bull. Earthq. Eng. 2020, 18, 5631–5654. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Lane, P.A. Slope stability analysis by finite elements. Geotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Henkel, D.J. Discussion. Earth movement affecting L.T.E. railway in deep cutting east of Uxbridge. Proc. Inst. Civ. Eng. Part I 1956, 5, 320–323. [Google Scholar]
- Watson, J.D. Earth movement affecting LTE railway in deep cutting east of Uxbridge. Proc. Inst. Civ. Eng. Part II 1956, 5, 302–316. [Google Scholar]
- Urciuoli, G.; Pirone, M.; Comegna, L.; Picarelli, L. Long-term investigations on the pore pressure regime in saturated and unsaturated sloping soils. Eng. Geol. 2016, 212, 98–119. [Google Scholar] [CrossRef]
- Vassallo, R.; Calcaterra, S.; D’Agostino, N.; De Rosa, J.; Di Maio, C.; Gambino, P. Long-Term Displacement Monitoring of Slow Earthflows by Inclinometers and GPS, and Wide Area Surveillance by COSMO-SkyMed Data. Geosciences 2020, 10, 171. [Google Scholar] [CrossRef]
- Comegna, L.; Picarelli, L.; Urciuoli, G. The mechanics of mudslides as a cyclic undrained-drained process. Landslides 2007, 4, 217–232. [Google Scholar] [CrossRef]
- di Lernia, A.; Cotecchia, F.; Elia, G.; Tagarelli, V.; Santaloia, F.; Palladino, G. Combined use of hydraulic and coupled hydro-mechanical numerical modelling of the response of a clay slope to climatic actions in the long term. Ital. Geotech. J. 2023, accepted. [Google Scholar]
- Cotecchia, F.; Vitone, C.; Petti, R.; Soriano, I.; Santaloia, F.; Lollino, P. Slow landslides in urbanised clayey slopes: An emblematic case from the south of Italy. In Landslides and Engineered Slopes. Experience, Theory and Practice; Taylor and Francis Inc.: Abingdon, UK, 2016; Volume 2, pp. 691–698. ISBN 9781138029880. [Google Scholar]
- Lollino, P.; Giordan, D.; Allasia, P.; Fazio, N.L.; Perrotti, M.; Cafaro, F. Assessment of post-failure evolution of a large earthflow through field monitoring and numerical modelling. Landslides 2020, 17, 2013–2026. [Google Scholar] [CrossRef]
- Lollino, P.; Cotecchia, F.; Elia, G.; Mitaritonna, G.; Santaloia, F. Interpretation of landslide mechanisms based on numerical modelling: Two case-histories. Eur. J. Environ. Civ. Eng. 2016, 20, 1032–1053. [Google Scholar] [CrossRef]
- Bentley PLAXIS 2D CE V20, Reference Manual 2020. Available online: https://www.bentley.com/software/plaxis-2d/ (accessed on 19 April 2022).
- Clough, R.W.; Penzien, J. Dynamics of Structures; Computers & Structures, Inc.: Berkley, CA, USA, 1995. [Google Scholar]
- Mejia, L.H.; Dawson, E.M. Earthquake deconvolution for FLAC. In Proceedings of the 4th International FLAC Symposium on Numerical Modeling in Geomechanics, Madrid, Spain, 29–31 May 2006; Itasca Consulting Group: Minneapolis, MN, USA, 2006. [Google Scholar]
- Bathe, K.J. Finite Element Procedures, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Kuhlemeyer, R.L.; Lysmer, J. Finite Element Method Accuracy for Wave Propagation Problems. J. Soil Mech. Found. Div. 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Mori, F.; Mendicelli, A.; Moscatelli, M.; Romagnoli, G.; Peronace, E.; Naso, G. A new Vs30 map for Italy based on the seismic microzonation dataset. Eng. Geol. 2020, 275, 105745. [Google Scholar] [CrossRef]
- Falcone, G.; Romagnoli, G.; Naso, G.; Mori, F.; Peronace, E.; Moscatelli, M. Effect of bedrock stiffness and thickness on numerical simulation of seismic site response. Italian case studies. Soil Dyn. Earthq. Eng. 2020, 139, 106361. [Google Scholar] [CrossRef]
- Romagnoli, G.; Tarquini, E.; Porchia, A.; Catalano, S.; Albarello, D.; Moscatelli, M. Constraints for the Vs profiles from engineering-geological qualitative characterization of shallow subsoil in seismic microzonation studies. Soil Dyn. Earthq. Eng. 2022, 161, 107347. [Google Scholar] [CrossRef]
- D’Amico, M.; Felicetta, C.; Russo, E.; Sgobba, S.; Lanzano, G.; Pacor, F.; Luzi, L. Italian Accelerometric Archive v 3.1; Istituto Nazionale di Geofisica e Vulcanologia, Dipartimento della Protezione Civile Nazionale: Rome, Italy, 2020. [CrossRef]
- Luzi, L.; Pacor, F.; Puglia, R. Italian Accelerometric Archive v3.0 2019. Available online: https://itaca.mi.ingv.it/ItacaNet_40/#/home (accessed on 19 April 2022).
- Lanzo, G.; Silvestri, F.; Costanzo, A.; D’Onofrio, A.; Martelli, L.; Pagliaroli, A.; Sica, S.; Simonelli, A. Site response studies and seismic microzoning in the Middle Aterno valley (L’aquila, Central Italy). Bull. Earthq. Eng. 2011, 9, 1417–1442. [Google Scholar] [CrossRef]
- Pagliaroli, A.; Moscatelli, M.; Raspa, G.; Naso, G. Seismic microzonation of the central archaeological area of Rome: Results and uncertainties. Bull. Earthq. Eng. 2014, 12, 1405–1428. [Google Scholar] [CrossRef]
- Falcone, G.; Mendicelli, A.; Mori, F.; Fabozzi, S.; Moscatelli, M.; Occhipinti, G.; Peronace, E. A simplified analysis of the total seismic hazard in Italy. Eng. Geol. 2020, 267, 105511. [Google Scholar] [CrossRef]
- Del Gaudio, V.; Muscillo, S.; Wasowski, J. What we can learn about slope response to earthquakes from ambient noise analysis: An overview. Eng. Geol. 2014, 182, 182–200. [Google Scholar] [CrossRef]
- Diaz-Segura, E.G. Numerical estimation and HVSR measurements of characteristic site period of sloping terrains. Geotech. Lett. 2016, 6, 176–181. [Google Scholar] [CrossRef]
- Ashford, S.A.; Sitar, N.; Lysmer, J.; Deng, N. Topographic effects on the seismic response of steep slopes. Bull. Seismol. Soc. Am. 1997, 87, 701–709. [Google Scholar] [CrossRef]
- Castellaro, S.; Mulargia, F. The effect of velocity inversions on H/V. Pure Appl. Geophys. 2009, 166, 567–592. [Google Scholar] [CrossRef]
- Warnana, D.D.; Soemitro, R.A.A.; Utama, W. Application of Microtremor HVSR Method for Assessing Site Effect in Residual Soil Slope. Int. J. Basic Appl. Sci. IJBAS 2011, 11, 73–78. [Google Scholar]
- Wood, C.M.; Cox, B.R. Experimental Data Set of Mining-Induced Seismicity for Studies of Full-Scale Topographic Effects. Earthq. Spectra 2015, 31, 541–564. [Google Scholar] [CrossRef]
- Pischiutta, M.; Fondriest, M.; Demurtas, M.; Magnoni, F.; Di Toro, G.; Rovelli, A. Structural control on the directional amplification of seismic noise (Campo Imperatore, central Italy). Earth Planet. Sci. Lett. 2017, 471, 10–18. [Google Scholar] [CrossRef]
- Pazzi, V.; Tanteri, L.; Bicocchi, G.; D’Ambrosio, M.; Caselli, A.; Fanti, R. H/V measurements as an effective tool for the reliable detection of landslide slip surfaces: Case studies of Castagnola (La Spezia, Italy) and Roccalbegna (Grosseto, Italy). Phys. Chem. Earth 2017, 98, 136–153. [Google Scholar] [CrossRef]
- Setiawan, B.; Jaksa, M.; Griffith, M.; Love, D. Estimating bedrock depth in the case of regolith sites using ambient noise analysis. Eng. Geol. 2018, 243, 145–159. [Google Scholar] [CrossRef]

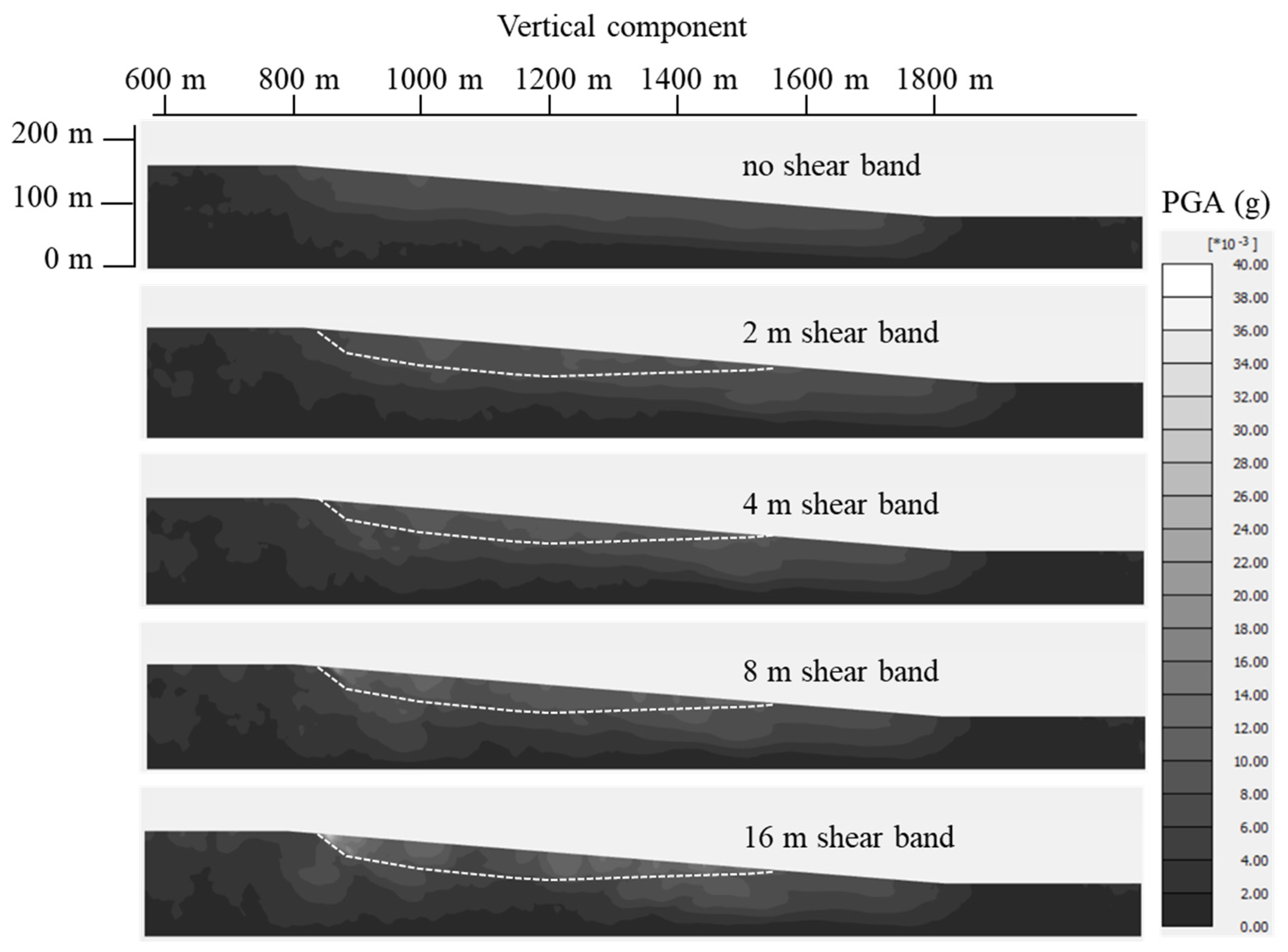
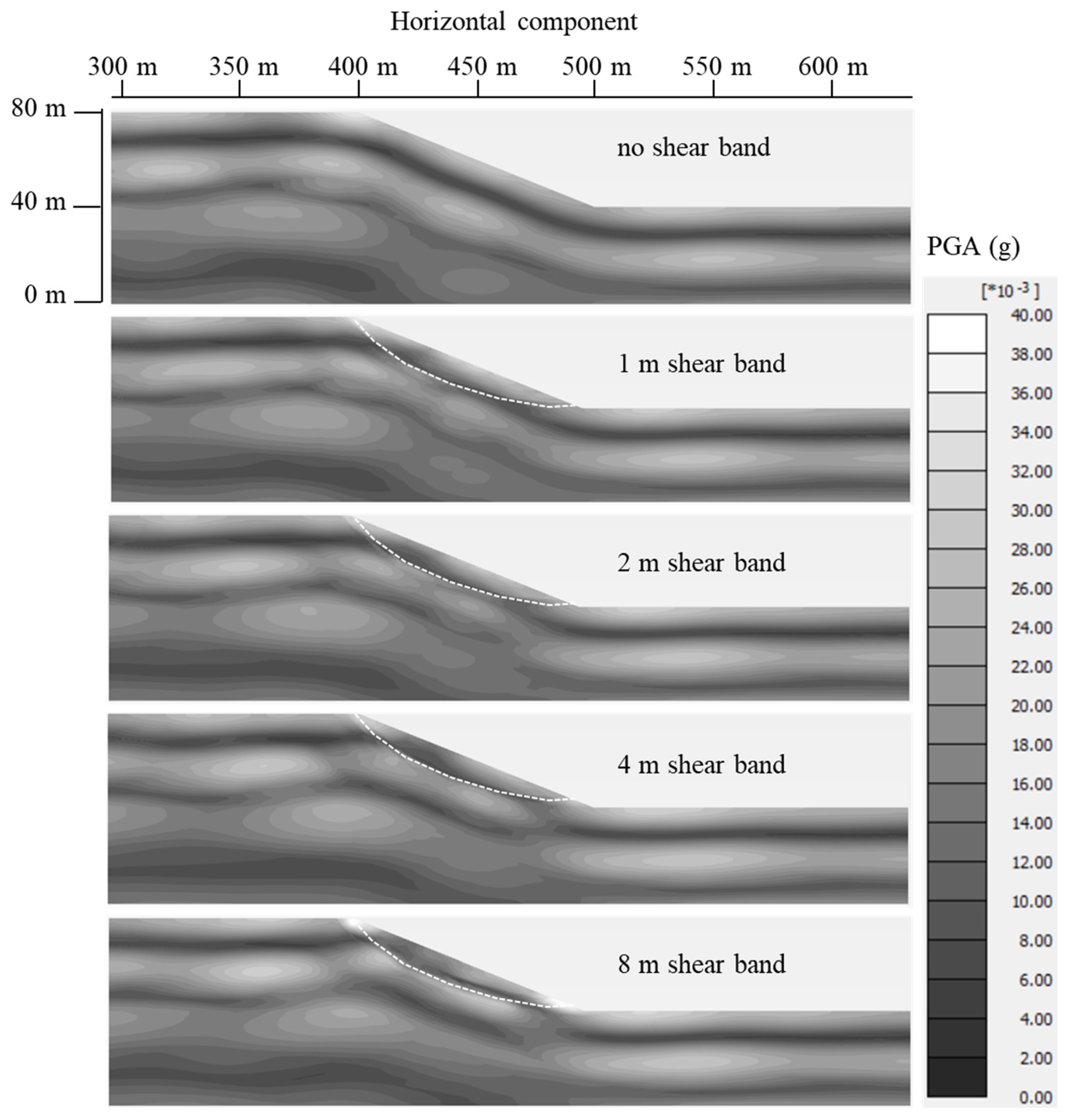

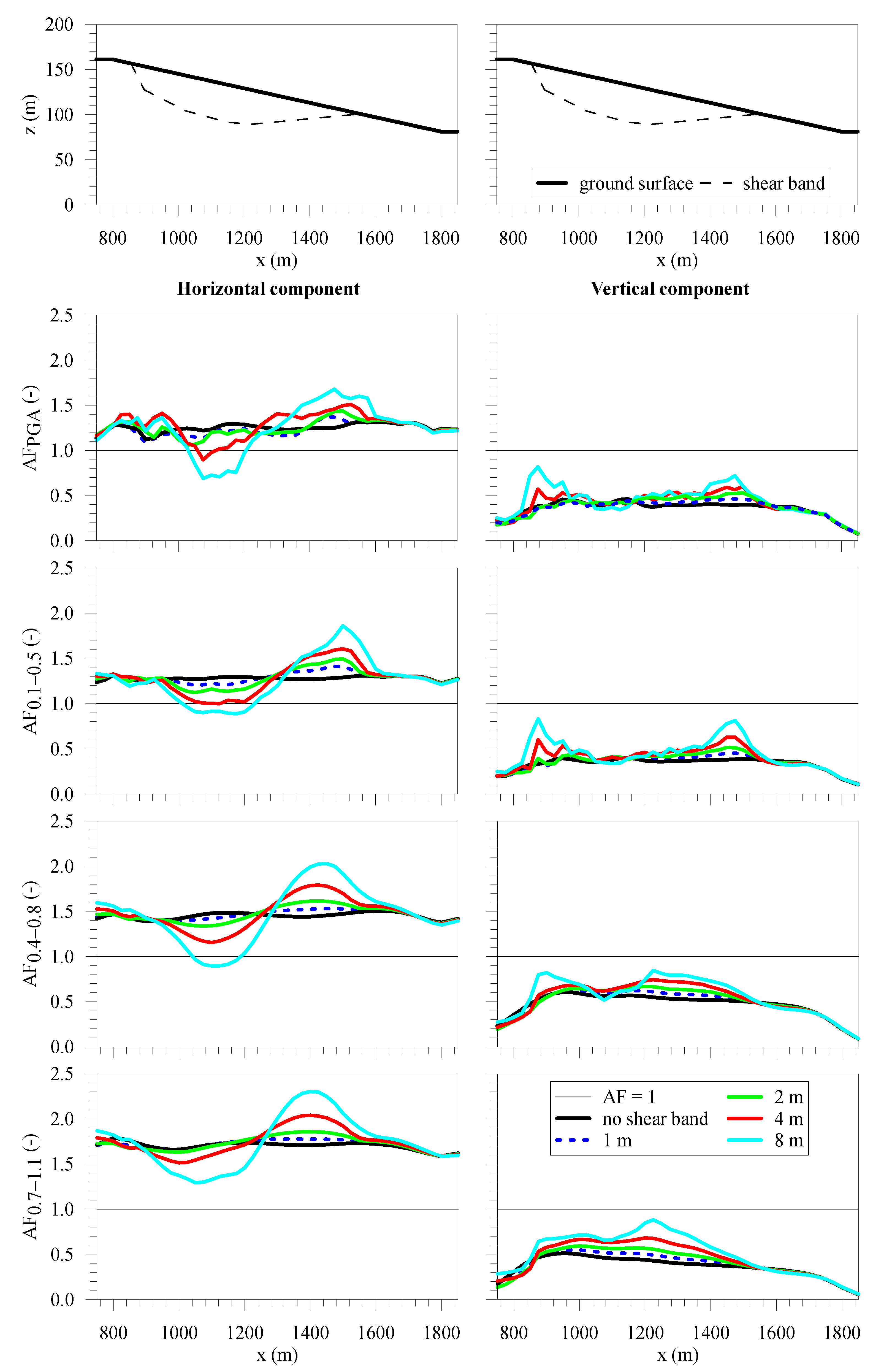
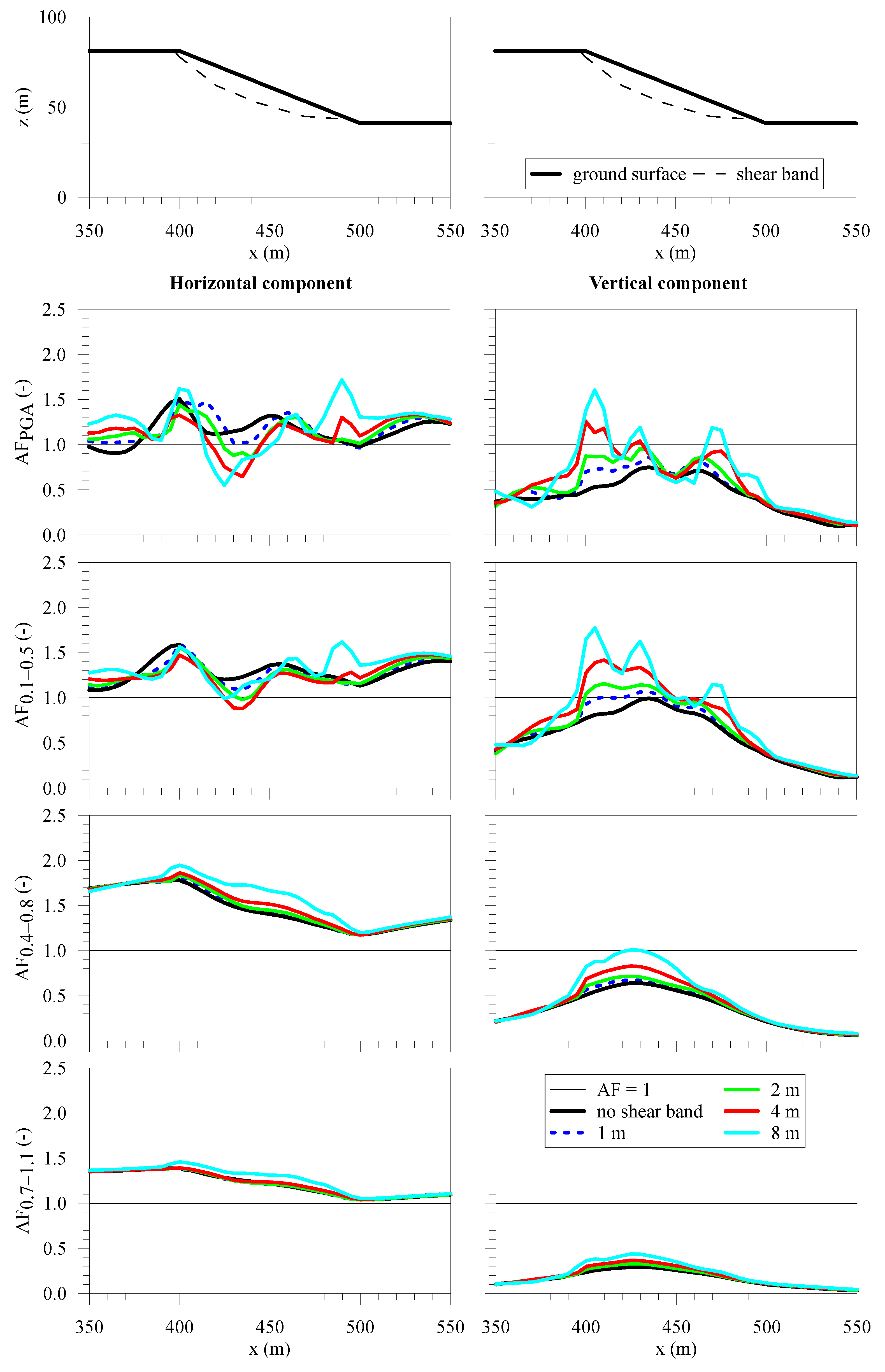
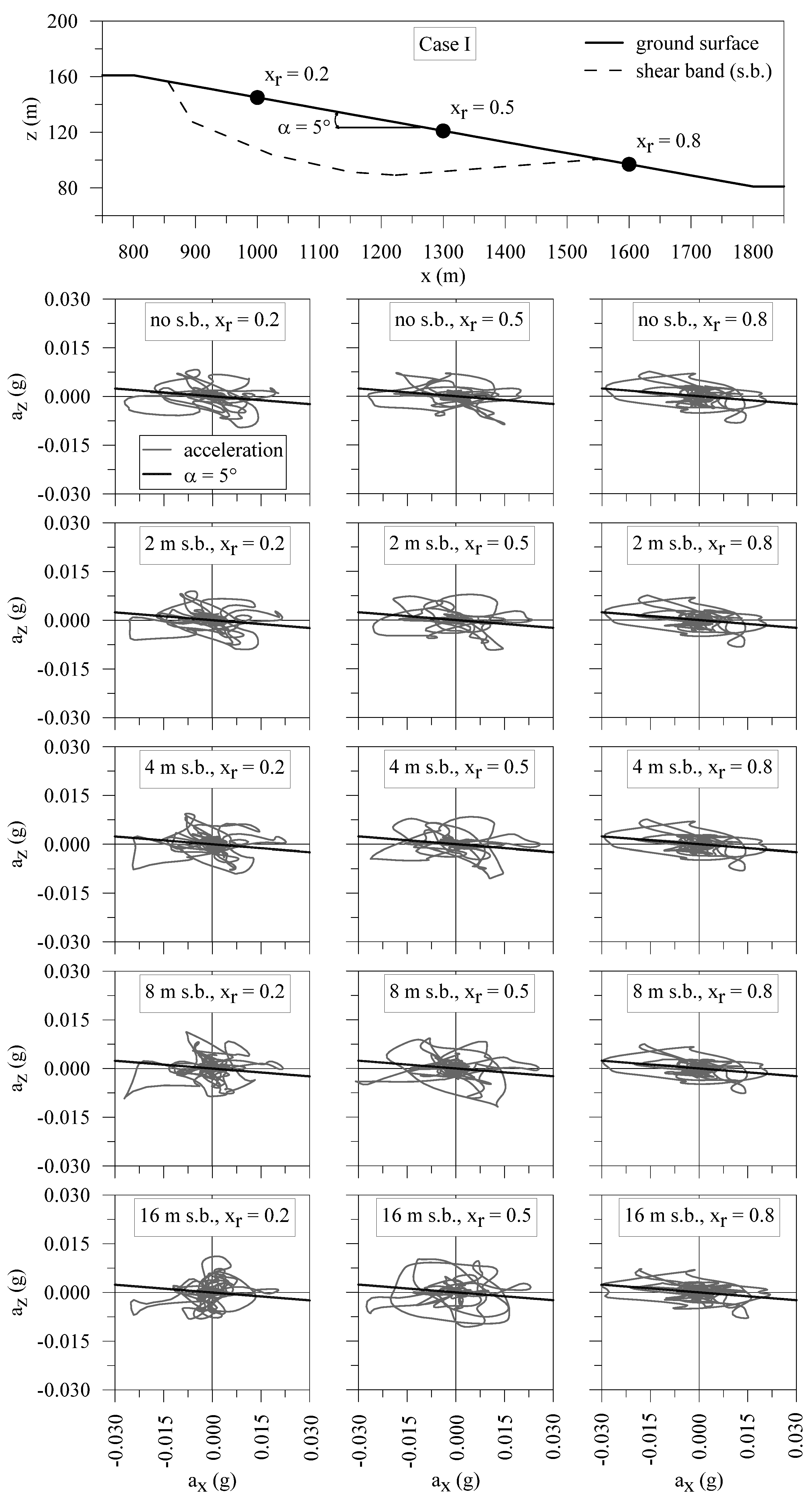
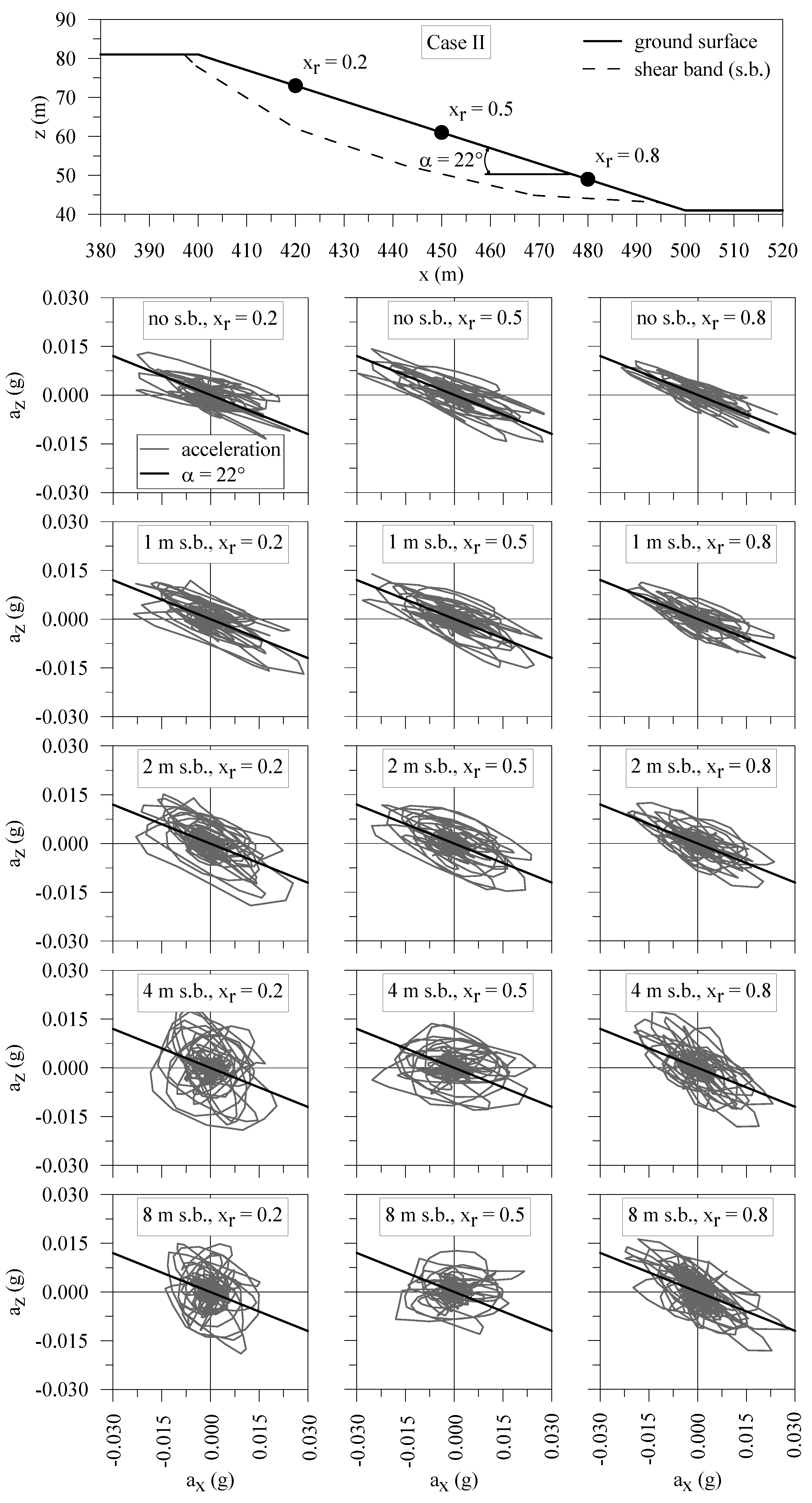
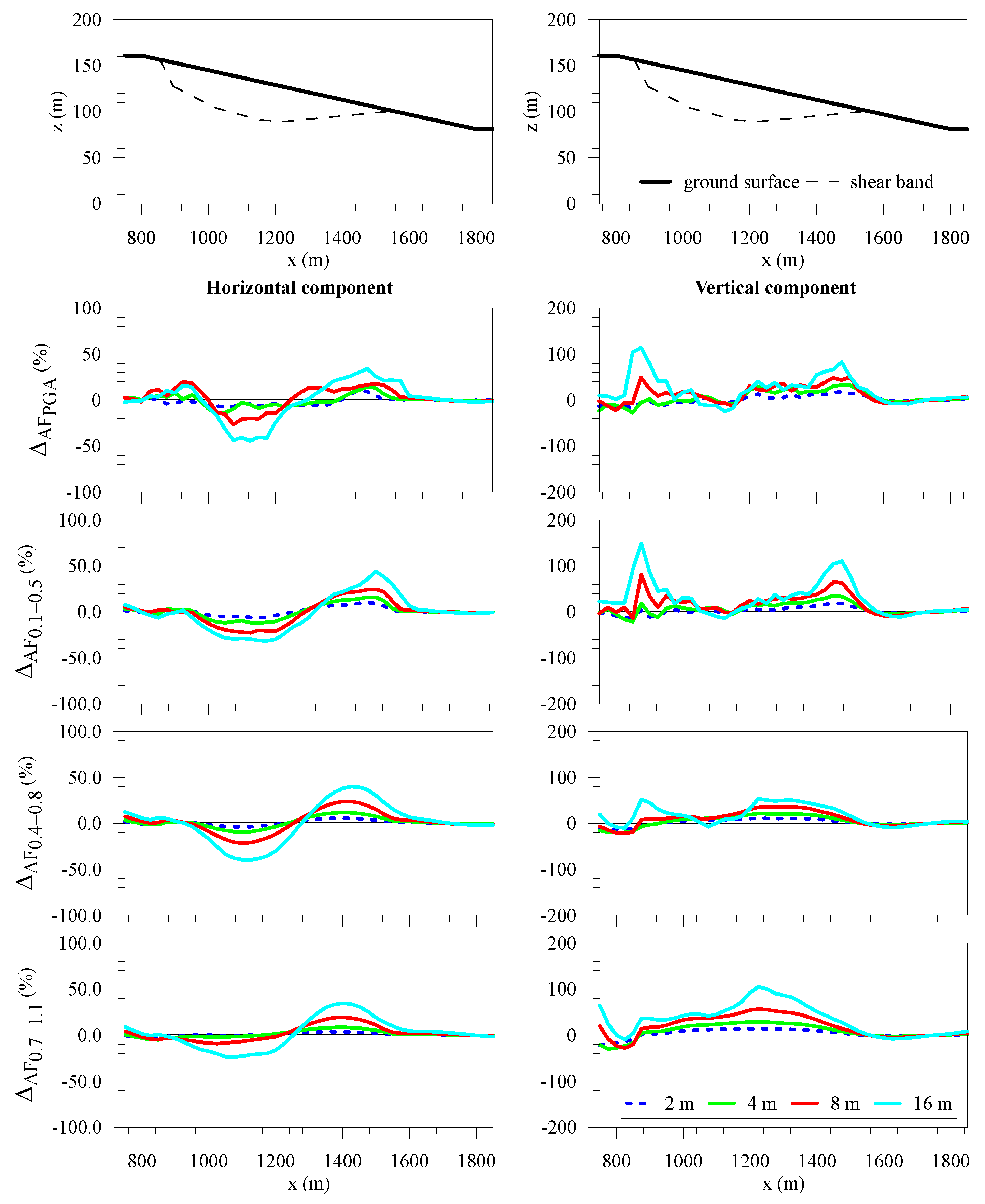
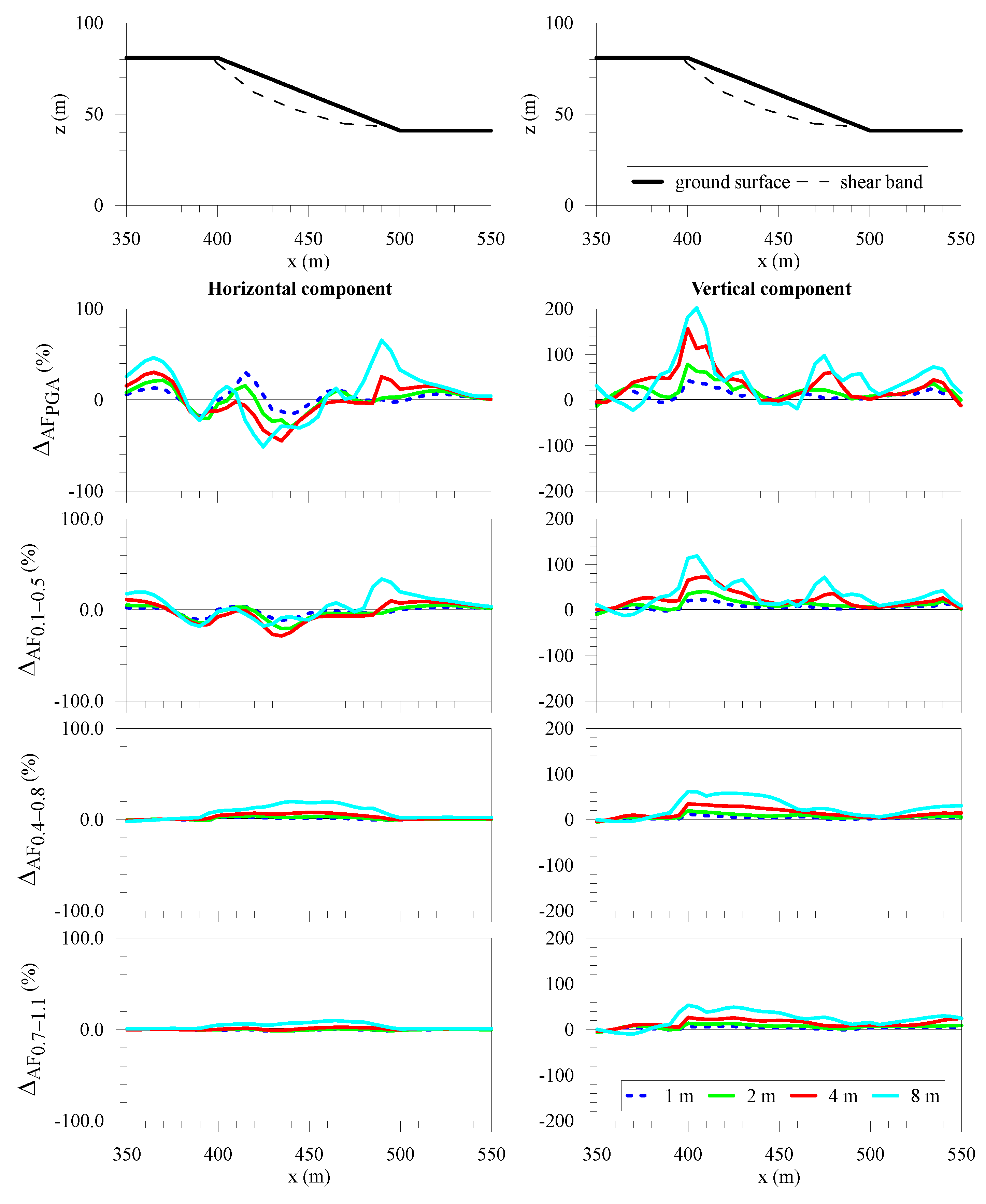
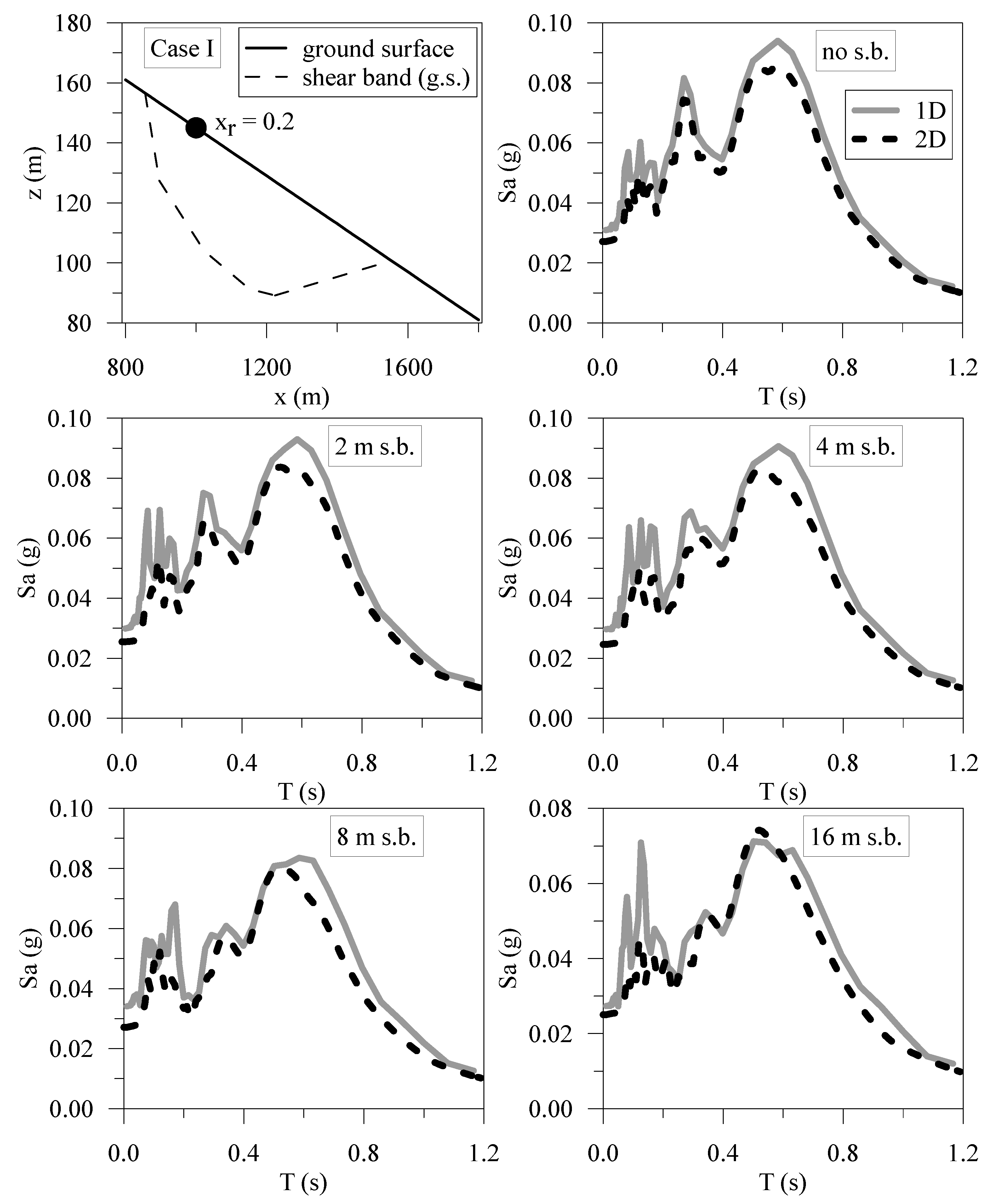
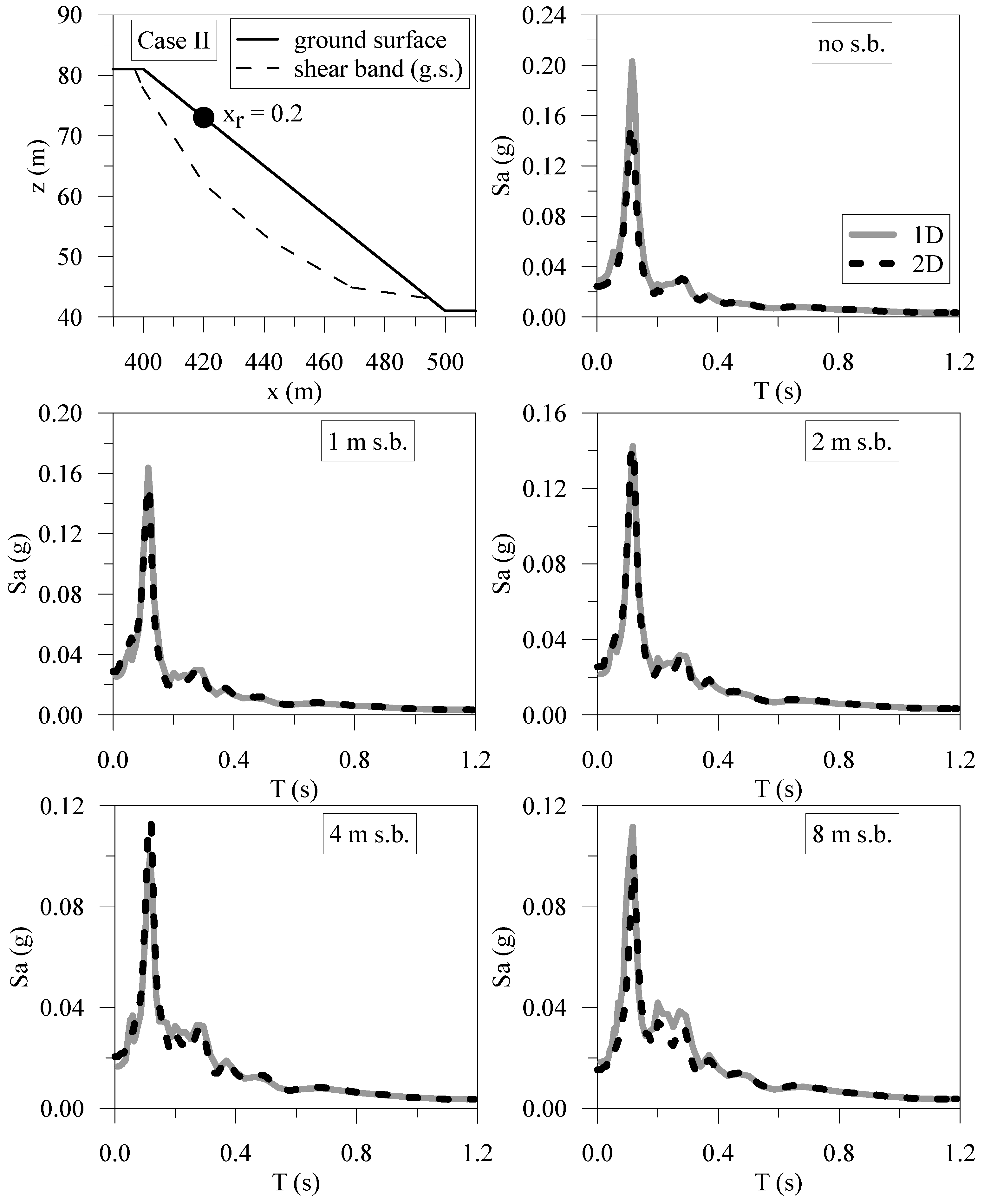
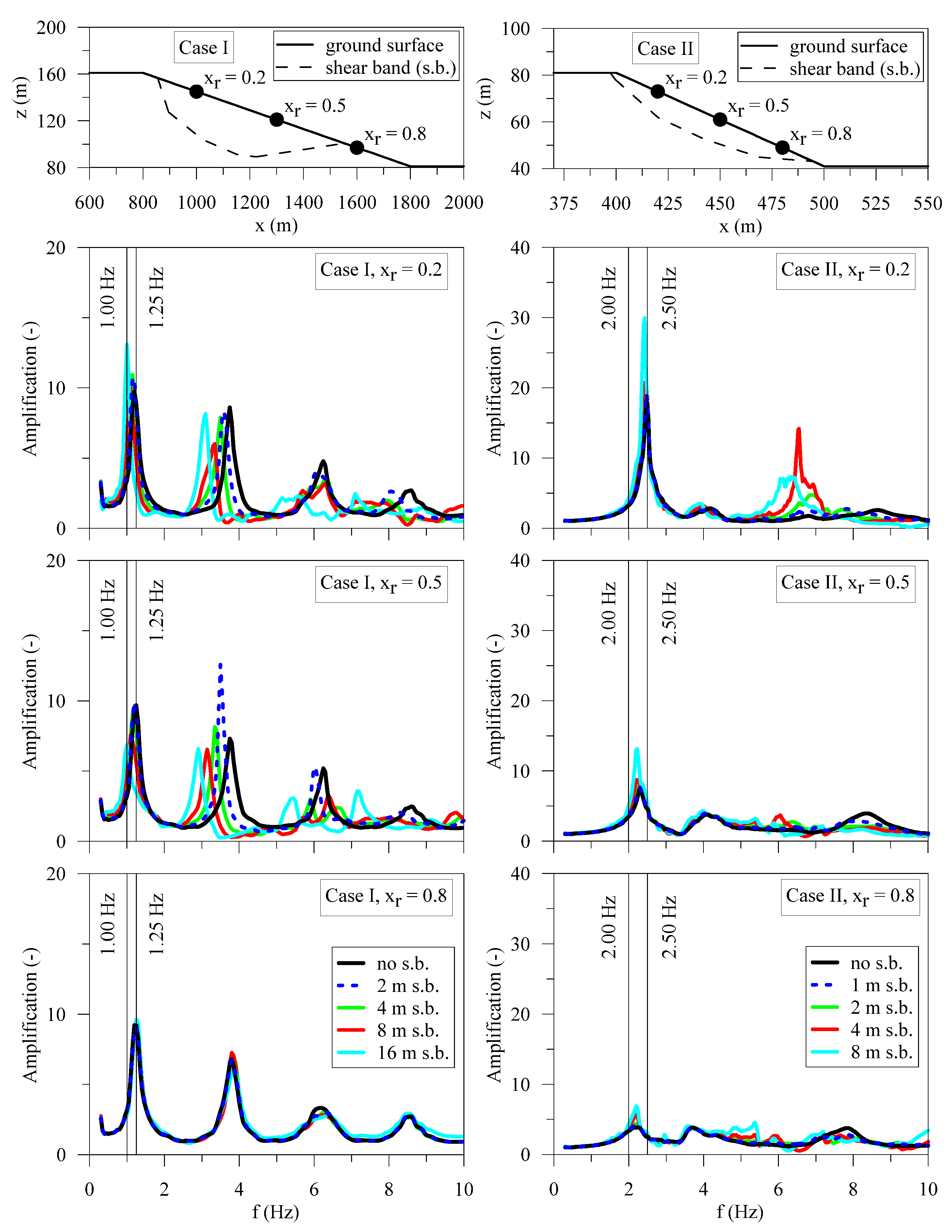
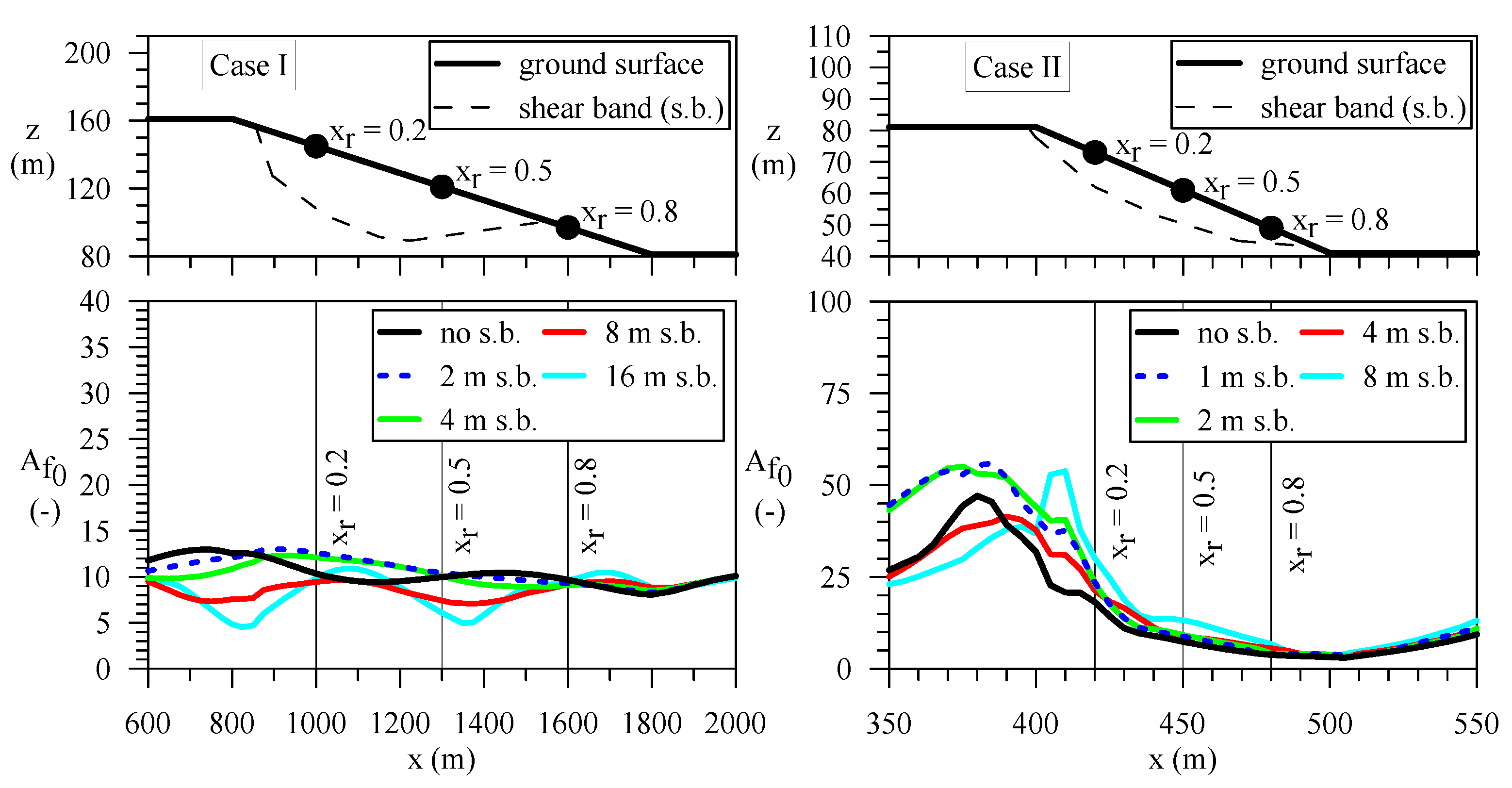
| Material | Soil Unit Weight γsoil (kN/m3) | Poisson’s Ratio ν | Shear Wave Velocity VS (m/s) | Damping Ratio D (%) |
|---|---|---|---|---|
| Soft soil | 20 | 0.25 | 400 | 5 |
| Seismic bedrock | 22 | 0.25 | 800 | 1 |
| Weakened shear band | 18 | 0.25 | 200 | 5 |
| Station ID | Date | Mw | R (km) | PGA (g) | PGV (m/s) | PGD (m) | Name |
|---|---|---|---|---|---|---|---|
| LRS | 9 September 1998 | 5.6 | 18.0 | 0.165 | 0.125 | 0.127 | RM1 |
| RQT | 26 October 2016 | 5.4 | 16.7 | 0.222 | 0.04947 | 0.00495 | RM2 |
| Shear Band Thickness | AFPGA | AF0.1–0.5 | AF0.4–0.8 | AF0.7–1.1 | AFPGA | AF0.1–0.5 | AF0.4–0.8 | AF0.7–1.1 | AFPGA | AF0.1–0.5 | AF0.4–0.8 | AF0.7–1.1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (m) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) | (-) |
| Control point xr | 0.2 | 0.2 | 0.2 | 0.2 | 0.5 | 0.5 | 0.5 | 0.5 | 0.8 | 0.8 | 0.8 | 0.8 |
| Case I | ||||||||||||
| - | 1.24 | 1.28 | 1.42 | 1.66 | 1.24 | 1.28 | 1.45 | 1.72 | 1.32 | 1.30 | 1.50 | 1.72 |
| 2 | 1.16 | 1.24 | 1.40 | 1.66 | 1.16 | 1.32 | 1.51 | 1.78 | 1.33 | 1.30 | 1.52 | 1.74 |
| 4 | 1.12 | 1.17 | 1.37 | 1.63 | 1.19 | 1.32 | 1.55 | 1.83 | 1.34 | 1.31 | 1.54 | 1.75 |
| 6 | 1.24 | 1.12 | 1.30 | 1.51 | 1.40 | 1.31 | 1.60 | 1.93 | 1.36 | 1.32 | 1.56 | 1.76 |
| 8 | 1.14 | 1.03 | 1.18 | 1.37 | 1.25 | 1.20 | 1.58 | 2.01 | 1.38 | 1.38 | 1.61 | 1.81 |
| Case II | ||||||||||||
| - | 1.11 | 1.22 | 1.57 | 1.30 | 1.32 | 1.36 | 1.40 | 1.22 | 1.08 | 1.25 | 1.26 | 1.12 |
| 1 | 1.36 | 1.22 | 1.61 | 1.29 | 1.26 | 1.31 | 1.43 | 1.21 | 1.08 | 1.21 | 1.27 | 1.11 |
| 2 | 1.16 | 1.20 | 1.64 | 1.30 | 1.15 | 1.24 | 1.45 | 1.21 | 1.05 | 1.20 | 1.29 | 1.12 |
| 4 | 0.93 | 1.13 | 1.68 | 1.31 | 1.13 | 1.21 | 1.52 | 1.24 | 1.05 | 1.17 | 1.32 | 1.14 |
| 8 | 0.69 | 1.09 | 1.78 | 1.37 | 0.98 | 1.21 | 1.66 | 1.31 | 1.30 | 1.27 | 1.42 | 1.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Falcone, G.; Elia, G.; di Lernia, A. Investigating the Influence of a Pre-Existing Shear Band on the Seismic Response of Ideal Step-like Slopes Subjected to Weak Motions: Preliminary Results. Geosciences 2023, 13, 148. https://doi.org/10.3390/geosciences13050148
Falcone G, Elia G, di Lernia A. Investigating the Influence of a Pre-Existing Shear Band on the Seismic Response of Ideal Step-like Slopes Subjected to Weak Motions: Preliminary Results. Geosciences. 2023; 13(5):148. https://doi.org/10.3390/geosciences13050148
Chicago/Turabian StyleFalcone, Gaetano, Gaetano Elia, and Annamaria di Lernia. 2023. "Investigating the Influence of a Pre-Existing Shear Band on the Seismic Response of Ideal Step-like Slopes Subjected to Weak Motions: Preliminary Results" Geosciences 13, no. 5: 148. https://doi.org/10.3390/geosciences13050148
APA StyleFalcone, G., Elia, G., & di Lernia, A. (2023). Investigating the Influence of a Pre-Existing Shear Band on the Seismic Response of Ideal Step-like Slopes Subjected to Weak Motions: Preliminary Results. Geosciences, 13(5), 148. https://doi.org/10.3390/geosciences13050148








