Abstract
Thermal pretreatments of rock, such as conventional heating and microwave irradiation, have received considerable attention recently as a viable method of improving the energy efficiency of mining processes that involve rock fracturing. This study presents a numerical analysis of the effects of thermal shock and microwave heating on the mechanical properties of hard, granite-like rock. More specifically, the aim is to numerically assess the reduction of uniaxial compressive strength of thermally pretreated specimens compared to intact ones. We also compare the performance of these two pretreatments (conventional heating and microwave irradiation) in terms of consumed energy and induced damage. Rock fracture is modelled by a damage-viscoplasticity model, with separate damage variables in tension and compression. A global solution strategy is developed for solving the thermo-mechanical problem (conventional heating) and the electromagnetic–thermo-mechanical problem (microwave heating). The electromagnetic part of the microwave heating problem is solved in COMSOL Multiphysics software Version 6.1 first. The electromagnetic solution is used as an input for the thermo-mechanical problem, which is finally solved by means of a staggered explicit solution method. Due to the predominance of the external thermal sources, the thermal and the mechanical parts of the problem in both cases are considered as uncoupled. Three-dimensional finite element simulations are utilized to study the damage-viscoplasticity model. An ore-shaped three-mineral numerical rock specimen is used in uniaxial compression tests.
1. Introduction
In mining operations, crushing and grinding of coarse rock into smaller particles (i.e., comminution) in the material processing stage is notably energy-intensive, accounting for between around 30 and 50 percent of the total consumed energy and between 35 and 50 per cent of the total mining costs [1,2,3,4,5,6]. Moreover, the mining and quarrying sectors in the EU countries cause the emission of thousands of tons of harmful substances into the atmosphere, such as greenhouse and air-polluting fumes, as well as harmful dusts [7]. To alleviate these disadvantages, methods that employ energy-efficient technologies to obtain significant reductions in overall energy usage have been extensively researched. These methods can be, for example, preconditioning or pretreatment processes that weaken rocks before subjecting them to comminution.
In particular, thermal pretreatments have been widely studied in the last twenty years [8]. Previous works have considered rock breakage through convention heating (heat source application via convection or conduction) and microwave irradiation. Conventional heating has been proven to be a beneficial pretreatment of rocks and ores in several industrial applications [9]. Conventional heating uses furnaces, muffles, flame torches etc., in which heat is transferred inwards from the boundary of the objects. Since rock is an aggregate of minerals, heating of rock causes each mineral to expand in different directions depending on their thermal properties [10]. This differential expansion causes thermal stress concentrations at contact points and grain boundaries [11], which may lead to inter-granular or intra-granular breakage of individual mineral grains [12].
In the past two decades, microwave irradiation-based pretreatments for rock fracturing have been extensively studied [13,14]. Microwaves are able to travel through space at the speed of light, leading thus to higher rapidity in heating. This allows one to reduce unwanted or unneeded heating of nearby objects. Microwaves are therefore considered to be more energy efficient than conventional heating methods [15]. Moreover, another advantage of microwave heating is the reduction of secondary waste (gases, dust and noise) production. For polycrystalline rocks (such as granite, for example), a key aspect of microwave heating is its selective nature. Due to the often-times different dielectric properties of the various constituent minerals to microwave irradiation, the heating mechanism is selective [16]. The capacity of each material to absorb microwave irradiation largely varies. For reflective materials, such as good, highly conductive conductors, the penetrative capacity of microwaves is practically null, whereas it is infinite for transparent materials (such as calcite or quartz, which are practically transparent). Materials that absorb microwaves and are heated by them are defined as lossy dielectric materials [17].
Several numerical studies on thermal pretreatments have been conducted in the last twenty years. Tian et al. [18] developed a cluster of particles model to investigate the uniaxial compressive behaviour of granite specimens with different grain sizes. The specimens were heated at 5 °C/min up to target temperatures and then the temperature was kept constant for 4 h. The reduction in the uniaxial compressive strength of the coarse-grained granite specimens was reported to be lower than that for the fine-grained granite specimens. Saksala [19] predicted the temperature effect on the tensile strength of granitic rock. Rock samples were heated uniformly up to target temperatures of 300 °C and 500 °C. Rock breakage was modelled by an embedded discontinuity FEM approach. It was found that it is enough to account for only the temperature dependence of the thermal expansion of quartz. Ma et al. [20] tested numerically three types of microwave antennas with different heights for fracturing blocks of biotite diorite at low power levels (6 kW). They compared the results deriving from different antennas in terms of highest temperature and area, depth and volume of the high temperature zone. Zhu et al. [21] carried out a full 3D study to model thermal response of oil shale under microwave heating. The electromagnetic–thermal–chemical–hydraulic–mechanical parts of the problem were considered fully coupled. Toifl et al. [22] evaluated numerically the stress induced in a 3D specimen heated via microwave irradiation. The irradiation times were 15 s and 25 s with a 25 kW power and a microwave frequency of 2.45 GHz. The study took into account the phase transformation of quartz at high temperatures. Xu et al. [23] proposed a 3D damage-based, electromagnetic–thermo-mechanical coupled model to simulate fracturing of rock under microwave irradiation. They described the damage of rock and its stress–strain behavior via an isotropic elastic damage constitutive law. Some material parameters such as Young’s modulus were assumed to follow a statistical distribution to reflect a real-life case of material heterogeneity.
As for the comparison between the two types of pretreatment, Wei et al. [24] found experimentally that, with regard to concrete liberation and aggregate recycling, microwave irradiation could liberate concrete and recycle aggregate more effectively than conventional heating, with less heating duration and lower energy input required. Shou et al. [25] investigated experimentally the effects of resistance heating (12 kW muffle furnace) and microwave heating (1.5 kW microwave oven with a frequency of 2.45 GHz) and compared these pretreatments in terms of uniaxial compressive strength reduction. They found a similar variation in uniaxial compressive strength in the two groups between 400 °C and 900 °C. Moreover, they observed that microwave irradiation is beneficial to ensure the stability of surrounding rocks by strength reduction due to localized transition plasticity and further promotion of rock structure deterioration in weakening stage.
The present study attempts to evaluate the different outcomes of conventional heating vs microwave irradiation of rock in terms of weakening effect and required energy. To this end, fully 3D simulations reproducing microwave heating and conventional surface heating are performed on granite-like rock specimens. The weakening effect of the pretreatments is measured as the uniaxial compressive reduction percentage of pretreated samples compared to the intact ones. To that end, the simulation method previously developed in [26], which comprises both explicit heterogeneity description and damage evaluation, is used here. The electromagnetic part of the problem (for the microwave heating case) is solved first in a commercial FE software, COMSOL Multiphysics Version 6.1. Then, a staggered explicit approach is developed and then implemented in MATLAB to solve the thermo-mechanical part of the problem (for both microwave and conventional heating cases). For the microwave heating, the thermal loading input source is provided by the microwave induced volumetric power density calculated in COMSOL. For the conventional heating, the heat source is represented by an external heat flux impinging on a portion of the specimen surface. Rock material heterogeneity is represented explicitly by means of 3D Voronoi tessellations of polyhedral cells and rock breakage is modelled via a damage-viscoplasticity model.
2. Rock Constitutive Model
In this section, the theory of the adopted constitutive model for rock is detailed. The model is decomposed in a viscoplastic and a damage part, as in [27]. The viscoplastic part of the model describes the stress states leading to rock failure and controls the inelastic deformation. Viscosity allows one to include rock strain-rate sensitivity. The damage part of the model incorporates stiffness degradation and strength deterioration by means of separate isotropic damage parameters in compression and tension, due to the strong asymmetry of rock behavior. Lastly, a continuum approach, based on viscoplasticity and damage mechanics, is chosen for its computational efficiency and straightforward implementation.
2.1. Bi-Surface Viscoplastic Consistency Model
The viscoplastic part of the model is based upon the viscoplastic consistency approach by [28,29]. A bi-surface criterion combining the Drucker–Prager (DP) criterion for compressive (shear) failure and the modified Rankine (MR) criterion as a tensile cut-off define the stress states that give origin to inelastic strains and damage. The model components for the perfectly viscoplastic case (softening is considered by later inclusion of damage) are
where and are the yield surfaces, is the plastic potential for DP surface (in the case of MR ), is the first invariant of the stress tensor , is the second invariant of the deviatoric part of stress tensor , is the ith principal stress, are the Macaulay brackets, i.e., the positive part operator, and are the DP parameters, and are the viscosity moduli (here ), c and are the dynamic cohesion and tensile strength depending on the viscoplastic increments and , respectively. The Drucker–Prager parameters and are defined in terms of the friction angle . The final parameters to be defined, and , are similar to the ones in Equation (1), but here the dilatancy angle is used instead of the friction angle.
2.2. Damage Formulation and Combining the Damage and Viscoplastic Parts
The response of rock is considerably asymmetrical under tensile and compressive states. This phenomenon is taken into account by separate scalar damage variables for tension and compression. These variables depend on viscoplastic strain and they govern both strength deterioration and stiffness degradation. For both tensile and compressive states, the standard phenomenological isotropic (scalar) damage model is used with an exponential damage function. Therefore, this part of the model is defined by equations
where and are the damage parameters in compression (DP criterion) and tension (MR criterion), respectively. The parameters and control their maximum values. Parameters and are defined according to: the fracture energies and ; uniaxial compressive strength and tensile strength ; the characteristic length of a finite element , which depends on the the element volume . The cumulative equivalent viscoplastic strains under compressive and tensile states, and , respectively, are computed incrementally in the algorithmic implementation. These quantities are driven by the rate of visco-plastic strain tensor . They are defined in Equation (2) according to Koiter’s rule of bi-surface plasticity and surfaces both active and the principal values are . Moreover, the colon symbol in Equation (2) signifies the double contraction operator for tensors, i.e., . Macauley brackets are used in the definition of so that only the positive principal strains contribute to the tensile damage.
The viscoplastic and damage components of the model are combined within the effective principal stress space. Following this strategy, they can be considered independent from one another. Consequently, the calculations related to the viscoplastic component and stress integration are conducted in the effective stress space first, independently of damage. Thus, the robust methods of computational plasticity can be utilized in the stress integration [30]. Lastly, the models proposed by [31,32] are used to specify the nominal effective stress relation:
where and are functions of the stress state introduced to model elastic stiffness recovery effects associated with stress reversals. This corresponds to the experimentally observed closure of previously present defects—microcracks during initial stages of uniaxial compression [33]. The parameters in Equation (3) are material-dependent weighting factors, with , meaning full recovery of elastic stiffness when loading changes from a predominantly tensile state to a predominantly compressive state (for example, when applying uniaxial compression tests after thermal pretreatment). Lastly, the thermal strain tensor is defined as
where the quantities , and are the thermal expansion coefficient, the temperature and the second order identity tensor, respectively.
2.3. Stress Integration of Rock Constitutive Model
The cutting plane return mapping is used to solve the model in Equations (1). In the case of violation of both criteria ( and ), the consistency conditions (Equation (1)) demand the following equations to be verified at the end of each time step: and . The yield surfaces are determined to depend on the increments and the conditions to be satisfied become
By applying the first order expansion of these equations, i.e., the first terms in the vector-valued Taylor series, a linear system is obtained to solve the MR and DP viscoplastic increments:
The components of the gradient tensor are calculated according to the chain rule for the derivative of a composite function. Stress, viscoplastic strain and the internal variables are updated in a standard manner [29], after the solution of the viscoplastic increments by Equation (6). Stress integration is performed in the principal stress space for straightforwardness of calculations. This is convenient, as the return mapping preserves the principal directions for isotropic materials. Lastly, the calculations at level of local integration point are summarized in Algorithm 1. The starting point is the total strain from the global solution and the final step is the calculation of new stress .
| Algorithm 1 Solution process for elemental stresses |
|
3. Simulation Method for Microwave Heating Induced Failure
This section describes the simulation method used here to model microwave heating induced fracture in rock. The electromagnetic–thermo-mechanical problem is outlined in its strong form. The electromagnetic (if present, i.e., in the case of microwave heating) and thermo-mechanical parts of the problem are solved separately with a one-way coupling relationship. Here, the temperature dependence of dielectric properties is not considered, due to lack of solid literature data and experimental results, as done similarly in [22,34]. In the case of microwave heating the internally generated heat due to dielectric dissipation is derived from the electric field and it acts as the input load in the thermo-mechanical part of the problem. In the case of conventional heating, the thermal load is given by a high-intensity heat flux applied to all external surfaces of the sample (except the top and bottom faces). The thermal and mechanical parts of the problem can be considered uncoupled due to the highly prevailing role of the input thermal loads over the heat generated by mechanical dissipation effects. Second, the finite element description of the problem in its strong form is described in brief. Third, a fully explicit solution method based upon a staggered solution procedure is presented for solving the finite element discretized version of the thermal and mechanical parts of the problem.
3.1. Strong Form of the Uncoupled Electromagnetic–Thermo-Mechanical Problem
Modelling of rock breakage induced by thermal loads implies solving the related electromagnetic (if present, i.e., for microwave irradiation)–thermo-mechanical problem. Largely different time scales are involved in the electromagnetic, thermal and mechanical parts of the problem [35]. It is assumed that the electromagnetic cycle periods that relate to the transient formulation of the time-harmonic EM problem are short compared to time scales of the thermal part. Thus the problem is decomposed into two steps. The first one consists in calculating the EM losses. For sinusoidal excitations, the electromagnetic part can be set and solved in the frequency domain to calculate the cycle-averaged losses. In the second step, the previously computed losses act as a constant input thermal load in the time-dependent heat transfer problem.
3.1.1. Formulation of the Electromagnetic Problem
The electromagnetic problem here is conceptualized as an electromagnetic wave [36]. The rock sample is placed inside a 2.45 GHz multimode oven and it is modelled as a lossy dielectric material absorbing part of the wave and reflecting and scattering the remaining part in multiple directions. The Maxwell equation for retrieving the electric field strength is solved in the COMSOL Multiphysics software Version 6.1 as a time harmonic problem (). Its mathematical formulation is [37]
where is the relative permeability, the wave number of free space, is the angular frequency, is the permittivity of free space, is the electrical conductivity, and is the relative permittivity. The real part of the complex relative permittivity is called the dielectric constant . The imaginary part takes into account the dielectric losses. For air, , , . For minerals, and . Here, the dielectric properties are not considered to be temperature-dependent due to the lack of solid and up-to-date data on their temperature dependence.
Perfect electric conductor (PEC) boundary conditions are applied on the oven walls, where is the normal vector on the walls. A waveguide is linked to an RF source (magnetron), and the waveguide dimensions are such that it runs with its dominant TE10 mode [38]. An electromagnetic wave, when penetrating through a lossy dielectric material, loses some of its energy, which is converted into thermal energy within the material. Thus, is the time-averaged volumetric power density absorbed by the dielectric medium in the electro-magnetic field, determined as [39,40]
The volumetric power density acts as the one-way link between the EM and the temperature fields, as will be seen in Section 3.1.2.
3.1.2. Formulation of the Thermo-Mechanical Problem
The global balance equations for the thermo-mechanical problem expressed in strong form are:
where is the material density, is the body force (per unit mass) vector, is (in the case of microwave heating) the power density defined in the previous section and is the specific heat. The conductive heat flow, which associates the heat flux with the temperature, is expressed by Fourier’s law , where k is the thermal conductivity and the temperature. Finally, is the thermo-mechanical coupling term which takes into account the mechanical dissipation and thus includes thermo-elasticity and thermo-plasticity effects in the medium. Due to the magnitude of the external heat source, it can be considered negligible (see [26,41]).
3.2. Finite Element Discretized Form for the Uncoupled Thermo-Mechanical Problem
The finite element formulation for the heat balance equation, following Ottosen and Ristinmaa [35], is
where is the vector of nodal temperatures, , and are the capacity matrix, the conductivity matrix and the external force vector, respectively, defined by the following expressions:
The parameters and k are the specific heat and conductivity, is the temperature interpolation vector, is the internally generated volumetric power density in the solid (due to microwave irradiation). is the gradient of the temperature interpolation vector and 𝖠 is the standard finite element assembly operator.
The mechanical problem is represented by the equation of motion in its finite element discretized form:
The arrays , , and are, respectively, the lumped mass matrix, the external force vector, the kinematic matrix and the stress vector defined in Equation (3).
3.3. Solution Methods for the Global Thermo-Mechanical Problem
A staggered approach is then applied to the uncoupled thermo-mechanical problem so that the thermal and mechanical parts are solved independently. An explicit–explicit scheme is then developed where an isothermal split is applied for the solution of the global thermo-mechanical part of the problem. Staggered schemes are treated more completely in [35,42,43,44]. An explicit time marching scheme is applied to solve the problem of the uniaxial compression tests.
Explicit Scheme for the Uniaxial Compression Tests
The explicit modified Euler time stepping scheme is used for solving the thermo-mechanical problem. The equation of motion (Equation (12)) for the acceleration is solved as
then the response is advanced by [45]
As is the case for explicit time integrators, this scheme is not unconditionally stable with respect to time step . A maximum time step exists and it is determined by the Courant limit. The scheme for solving the global thermo-mechanical problem is represented in Figure 1.
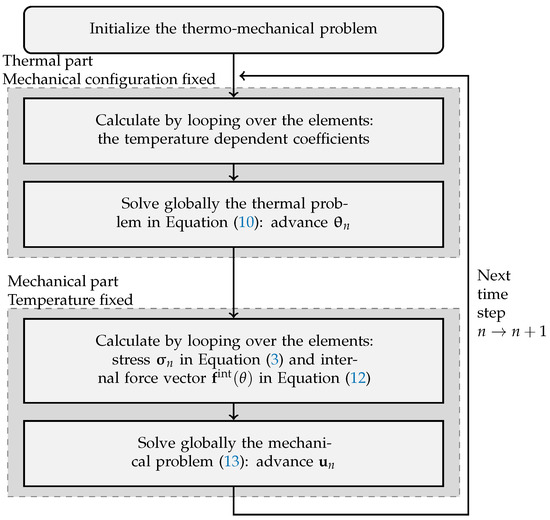
Figure 1.
Explicit–explicit dynamic time integration scheme for the thermo-mechanical problem.
4. Numerical Simulations: Results and Discussion
This section displays the 3D numerical simulation results of microwave heating (electromagnetic–thermo- mechanical problem) and conventional heating (thermo-mechanical problem) tests on numerical, granite-like, ore-shaped specimens and subsequent mechanical tests on pretreated samples.
4.1. Material Heterogeneity and Mesostructure Description
Material heterogeneity is a crucial factor that needs to be considered when studying rock cracking behavior, since it has a large influence on its dielectric, thermal and mechanical response. Granite is a polycrystalline rock consisting of different minerals in the shape of polyhedral grains. Here, the inherent heterogeneity of an idealized granite-like rock is explicitly described by a mesostructure which represents mineral grain aggregation and distribution. This is rendered in practice through a Voronoi tessellation of convex polyhedra (or cells, here the equivalent of mineral grains). In this study, the tessellation is created with the software package Neper [46]. The rock sample generated with this method is a 8000-cell truncated octahedron which can be contained in a box with a length of 59 mm. This specimen is designed to represent in a simplified way the shape of an ore (see Figure 2). There are three constituent minerals (i.e., 30% quartz, 55% feldspar and 15% biotite), in percentages that reproduce a generic granite-like rock [47]. Each grain of the mesostructure and consequently the clusters of linear tetrahedral finite elements inside them, are assigned mineral-specific material properties.
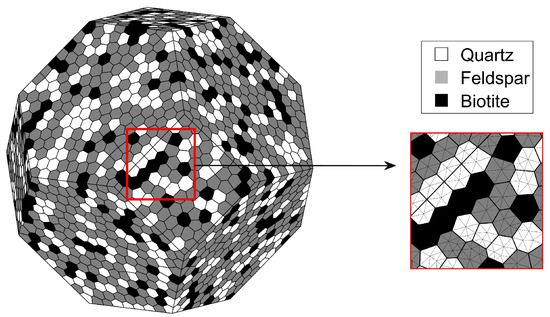
Figure 2.
Numerical rock samples and enlarged detail of the grains (8000 polyhedra) and linear tetrahedra mesh (699,103 elements).
The mineral properties (for intact material at room temperature) are given in Table 1. Dielectric properties are taken from [48] and they are kept constant during the solution of the electromagnetic problem due to the lack of solid data regarding their temperature dependence. The mechanical properties of single minerals are taken mainly (with some modifications) from [49]. The values for density, thermal conductivity and specific heat are taken from [50,51,52], respectively. Lastly, the viscosity is set to · /. This value is chosen in order to stabilize the computations without inducing significant strain rate effects at low-velocity loading.

Table 1.
Material properties and model parameters used in simulations.
In the present study, temperature dependence of certain material parameters is taken into account with a simplified approach (similarly to [54]) which is based on the higher nonlinear behavior of thermal expansion of Quartz up to the transition temperature with respect to the more linear one of feldspar and biotite. For quartz, Young’s modulus, Poisson’s coefficient and thermal expansion coefficient follow temperature dependence as the granite in [55]. Figure 3 shows the nonlinear temperature dependence of normalized thermal expansion coefficient of quartz. For feldspar and biotite, the curve for the thermal expansion coefficient is a linear approximation of the curve for quartz and the other properties are considered time-independent.
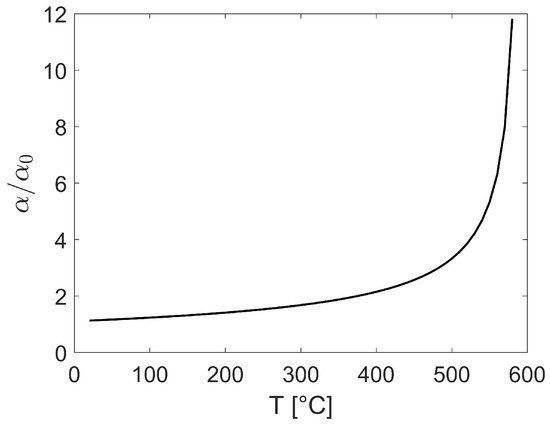
Figure 3.
Normalized thermal expansion coefficient of quartz vs. temperature.
4.2. Thermal Pretreatments on Numerical Rock Sample
In this section, microwave irradiation pretreatment and conventional heating pretreatment are tested on an intact numerical sample and their effect (in terms of temperature rise and resulting damage) is evaluated. The length of the pretreatment and power value in each case are chosen in order to obtain similar values of maximum temperatures.
4.2.1. Microwave Pretreatment on Numerical Rock Sample
The microwave irradiation pretreatment consists in placing the numerical rock sample inside a multimode microwave oven, here represented as a conductive cavity (box) linked to a microwave source set at a side of the cavity. The RF power is fed via a waveguide (WR340); PEC condition is set on all conductive boundaries of the oven. The oven setup is shown in Figure 4. The 2.45 GHz frequency is the standard operating frequency of kitchen ovens and the power level of 1.5 kW is in the typical range of commercial ovens (0.8–1.8 kW) as well. The duration of the pretreatment is 60 s. The multimode resonant cavity size is 276 × 254 × 185 mm. As for the thermal boundary conditions, the outer surface of the specimen is considered insulated with respect to the surrounding air; therefore, all convective effects are neglected. The sample is not restrained from deforming during heating and its initial temperature is 20 °C. The distance between the sample and the waveguide is 120 mm. This distance, found through trial-and-error, offers the best positioning in terms of final temperature level for this particular oven–sample combination. This search for the best placement inside the cavity is due to the fact that in a multimode oven cavity there is a large number of resonance modes, as the microwaves are reflected from the cavity walls. Therefore, the electric field, which derives from the interaction between the microwave radiation, the oven cavity and the lossy material, is highly non-uniform.
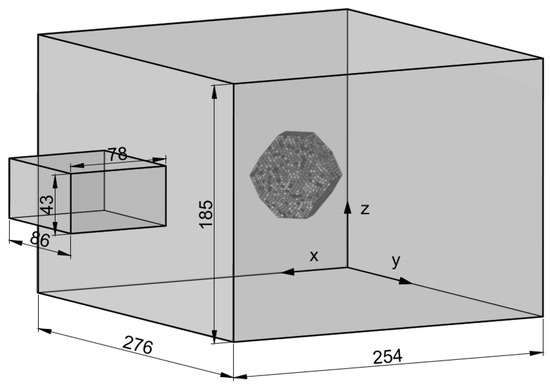
Figure 4.
Oven and waveguide schematic.
In the simulation, mass scaling is applied to increase the critical time step (from s to s), with a large scaling factor justified by the quasi-static nature of the very slow heating of the rock sample [41]. The weighting factors in Equation (3) are both set to zero. In order to solve first the electromagnetic part of the problem, rock mesostructure, after being created with the software package Neper, is imported into COMSOL Multiphysics software in STL format. There, the polygonal Voronoi cells are meshed with the linear tetrahedral finite elements. Finally, after solving the electromagnetic problem in COMSOL, the vector containing the nodal values of the generated volumetric heat is exported from COMSOL to MATLAB, where the external force vector in Equation (11) is assembled and the solution of the thermo-mechanical problem is obtained. Simulation results regarding the electric field, temperature and damage distribution are displayed in Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9.
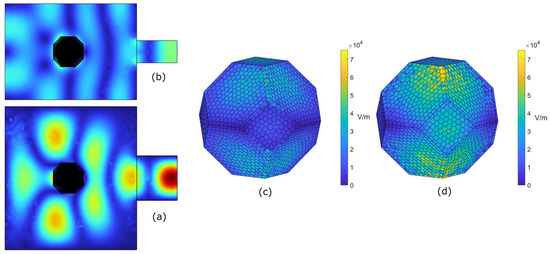
Figure 5.
Microwave pretreatment simulation results at 60 s. Electric field norm in the oven— cross-sectional view (a) and cross-sectional view (b); electric field norm distribution in the sample—front view (c) and back view (d).

Figure 6.
Microwave pretreatment simulation results at 60 s. Mesostructure and volumetric heating in the sample ( plane back view).
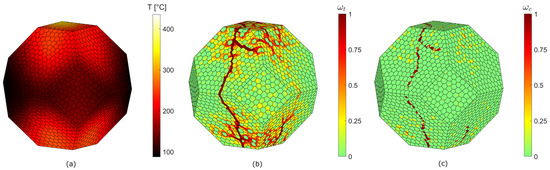
Figure 7.
Microwave pretreatment simulation results at 60 s (front view). Temperature distribution (a) tensile damage distribution as magnitude of damage variable (b), compressive damage distribution as magnitude of damage variable (c).
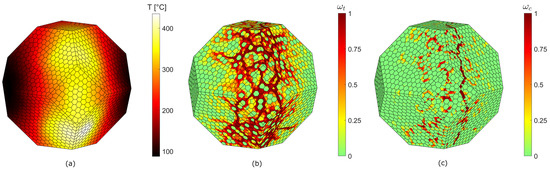
Figure 8.
Microwave pretreatment simulation results at 60 s (back view). Temperature distribution (a) tensile stress distribution as magnitude of damage variable (b), compressive stress distribution as magnitude of damage variable (c).
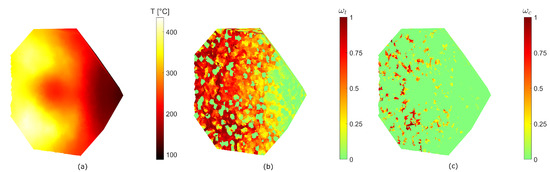
Figure 9.
Microwave pretreatment simulation results at 60 s (cross-sectional view). Temperature distribution (a) tensile stress distribution as magnitude of damage variable (b), compressive stress distribution as magnitude of damage variable (c).
At the end of the pretreatment, the electric field norm distribution is not uniform (Figure 5a,b), in accordance (in terms of qualitative distribution and order of magnitude) with previous studies that used similar multimode microwave setups and material dielectric properties [56,57,58,59]. As a consequence, two main high-temperature hotspots occur in the sample, one at the side that directly faces the waveguide (Figure 5c, here defined as “front view”) and the other at the opposite side (Figure 5d, here defined as “back view”). As can be seen in the figures, hotspots, counter-intuitively with respect to the results of conventional heating methods, may occur on the side that is not facing the microwave source. The maximum temperature attained within the sample is 435 °C (see Figure 7a and Figure 9a). The volumetric heat induced via microwave irradiation (see Equation (8)) can be integrated over the sample volume. The resulting internally generated power is 465 W, which is 31% of the entering 1.5 kW power. Thus, the total energy that enters the oven is 1500 W × 60 s/3600 = 25 Wh, whereas the energy which is effectively utilized to heat the sample is 25 Wh × 31% = 7.75 Wh.
It is remarked that the specimen is free to expand in all directions; therefore, the damage is caused by the existence of a temperature gradient and by the mismatch in thermal properties between each mineral. The predicted tensile damage patterns in Figure 7b and Figure 8b consist of several vertical crack-like damage areas on the specimen’s outer surface. At this temperature level, the value of tensile damage variable is close to 1 therein so that these zones can be interpreted as macrocracks. It can be seen from the results that feldspar grains sustain more damage than the other two minerals. This may be explained by the higher values of the thermal expansion coefficient of quartz and biotite compared to that of feldspar and by the higher tensile strength and elastic modulus of quartz when compared to feldspar and biotite. The differential expansion and contraction of minerals causes higher stresses in the ones with a lower thermal expansion coefficient [60]. Moreover, in this study the thermal expansion coefficient of quartz varies non-linearly with increasing temperatures, whereas for the other two minerals the variation is linear. Finally, the higher values of dielectric properties of biotite lead to a higher heating in this mineral (see Figure 6), which may cause higher thermal stresses and consequently tensile cracks in the surrounding grains [61].
4.2.2. Conventional Heating Pretreatment on Numerical Rock Sample
The conventional heating pretreatment consists of a constant external heat flux that impinges perpendicularly to each external face of the numerical rock sample, with the exception of the top and bottom ones. This corresponds to an idealized laboratory setup where the sample is uniformly heated from multiple directions. The external heat flux is 0.5 MW/m2 (comparable in magnitude to the one produced by an oxy-acetylene torch) and the pretreatment duration is 1 s. The same thermal and mechanical boundary conditions of Section 4.2.1 are used in the analysis. The weighting factors in Equation (3) are both set to zero. The simulation results regarding temperature and damage distribution are displayed in Figure 10 and Figure 11.
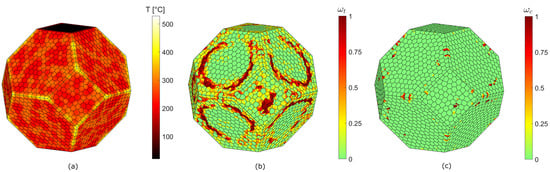
Figure 10.
Conventional heating pretreatment simulation results at 60 s (front view). Temperature distribution (a) tensile damage distribution as magnitude of damage variable (b), compressive damage distribution as magnitude of damage variable (c).
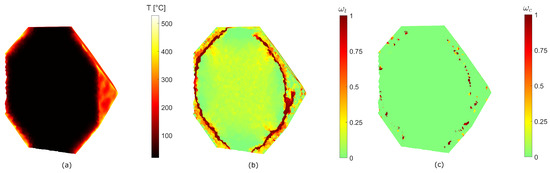
Figure 11.
Conventional heating pretreatment simulation results at 60 s (cross-sectional view). Temperature distribution (a) tensile damage distribution as magnitude of damage variable (b), compressive damage distribution as magnitude of damage variable (c).
At the end of the conventional heating pretreatment, the maximum temperature level is 528 °C. These high temperatures are reached at the edges of the specimen where the contributions of two or more faces are summed. The section view in Figure 11 shows that damage is located close to the outer surface of the sample. The damage distribution is qualitatively similar to the tensile crack distribution in a heat-shocked cylindrical granite specimen [41]. This leads to a circular tensile damage distribution for each face, where damage occurs near these edges. Compared to the microwave heating results of Section 4.2.1, where entire grains seem to be spared by damage, here damage affects grains more uniformly. The power used to heat the sample is given by integration of the surface flux (0.5 MW/m2) over the heated area (0.0106 m2). Therefore, the energy spent during the pretreatment is 1.47 Wh.
4.2.3. Influence of Quartz Content on Temperature and Tensile Damage Distribution during Thermal Pretreatment
The same simulation setups of Section 4.2.1 and Section 4.2.2 are used for testing the effect of different quartz percentages (15% and 45%) in the numerical specimen. In this section all results will be presented in the following order: those derived from the specimen with 15% quartz percentage first, then 30% (reference case) and finally 45%. To obtain the new specimens, the reference case specimen in Section 4.1 is modified in the following way:
- The geometry of tessellation is preserved;
- The original number and location of biotite grains are preserved;
- A certain number of quartz grains (original percentage 30%) replaces or is replaced by feldspar grains.
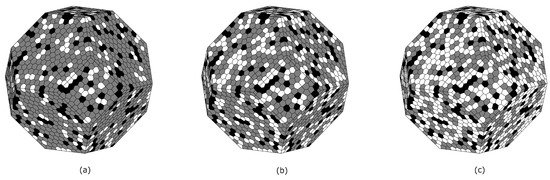
Figure 12.
Rock specimen with different quartz percentages (front view): 15% (a), 30% (reference case) (b), 45% (c).
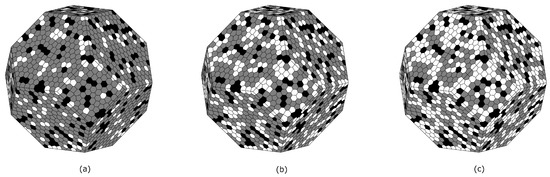
Figure 13.
Rock specimen with different quartz percentages (back view): 15% (a), 30% (reference case) (b), 45% (c).
The tensile damage variable distribution induced via microwave heating on specimens with different quartz percentages is displayed in Figure 14 and Figure 15. Compressive damage distribution is not represented, since compressive damage, as can be seen in Section 4.2.1, is less severe than tensile damage. Temperature distribution is not shown, since it is very similar to Figure 7, Figure 8 and Figure 9.
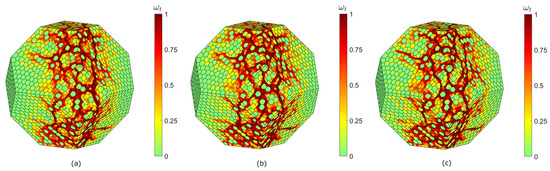
Figure 14.
Microwave heating pretreatment simulation results at 60 s (back view). Tensile damage distribution as magnitude of damage variable for 15% (a), 30% (reference case) (b), 45% (c) quartz percentage.
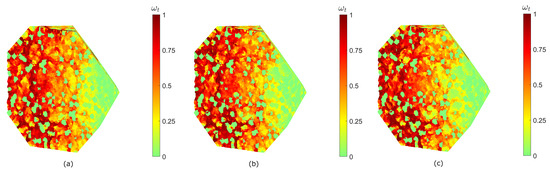
Figure 15.
Microwave heating pretreatment simulation results at 60 s (cross-sectional view). Tensile damage distribution as magnitude of damage variable for 15% (a), 30% (reference case) (b), 45% (c) quartz percentage.
The maximum temperatures in the whole specimen (temperature distribution not shown here) are 405 °C, 435 °C (reference case) and 457 °C. The mean values of all nodal temperatures are 222 °C, 232 °C and 236 °C. The tensile damage distribution shows, similarly to Section 4.2.1, that biotite and quartz grains tend to be spared from damage compared to feldspar (see Figure 13 and Figure 14). The presence of more or less quartz in the specimen slightly modifies the pattern of tensile damage. The mean values of the tensile damage variable in the whole specimen are 0.3266, 0.3339 and 0.3320. These results may suggest increasing overall temperature levels with increasing quartz content. The same cannot be said for tensile damage, since both graphical inspection of its distribution and its quantification do not allow one to establish any immediate correlation between quartz content and tensile damage severity.
The tensile damage variable distribution induced by conventional heating on specimens with different quartz percentages is displayed in Figure 16 and Figure 17. Compressive damage distribution is not represented, since compressive damage, as can be seen in Section 4.2.2, is less severe than tensile damage. The temperature distribution is not shown, since it is not dissimilar to Figure 10 and Figure 11.
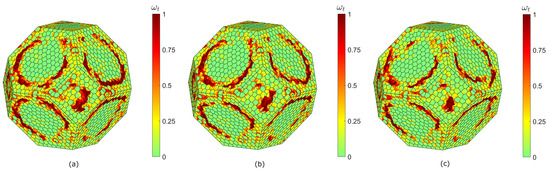
Figure 16.
Conventional heating pretreatment simulation results at 60 s. Tensile damage distribution as magnitude of damage variable for 15% (a), 30% (reference case) (b), 45% (c) quartz percentage.
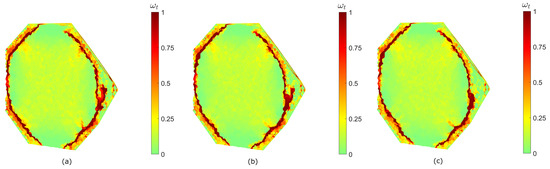
Figure 17.
Conventional heating pretreatment simulation results at 60 s (cross-sectional view). Tensile damage distribution as magnitude of damage variable for 15% (a), 30% (reference case) (b), 45% (c) quartz percentage.
The maximum temperatures in the whole specimen (temperature distribution not shown here) are 528 °C, 528 °C (reference case) and 513 °C. The mean values of all nodal temperatures are 48.33 °C, 47.90 °C and 47.49 °C. The mean values of the tensile damage variable in the whole specimen are 0.2100, 0.2022 and 0.1988. These results may suggest increasing overall temperature and tensile damage levels with decreasing quartz content. This is further confirmed via graphical inspection of tensile damage distribution, which shows the presence of more zones affected by damage in the first specimen compared to the rest of them.
4.3. Uniaxial Compression Test on Numerical Rock Sample
In this section, uniaxial compression tests are performed on an intact numerical sample and pretreated numerical samples. The effect of thermal pretreatment application is evaluated in terms of resulting uniaxial compressive strength reduction of the pretreated numerical samples compared to the intact one.
4.3.1. Uniaxial Compression Test on Intact Numerical Rock Sample
The uniaxial compressive test on the intact specimen is modelled as a constant downward velocity (0.03 m s−1 applied at the top face of the sample). The degrees of freedom at the bottom face are restrained in the z (vertical) direction. The test is conducted first with weighting factors in Equation (3) , then with factors . The results are displayed in Figure 18 and Figure 19.
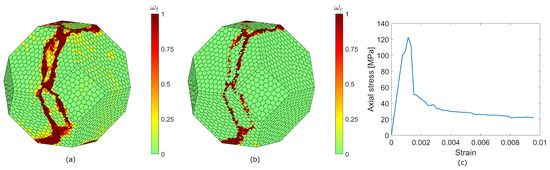
Figure 18.
Uniaxial compression test (weighting parameter ). Tensile damage distribution as magnitude of damage variable (a), compressive damage distribution as magnitude of damage variable (b). Stress–strain curve (c).
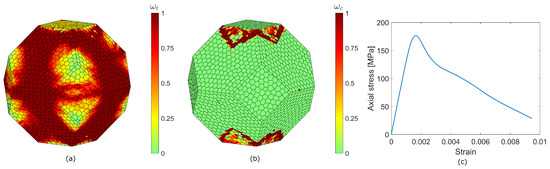
Figure 19.
Uniaxial compression test (weighting parameter ). Tensile damage distribution as magnitude of damage variable (a), compressive damage distribution as magnitude of damage variable (b). Stress–strain curve (c).
The uniaxial compressive strength is 123 MPa in the first case and 177 MPa in the second case. Even if the sample size and shape do not correspond to any recommended standard, it is still possible to detect the typical vertical damage patterns present in uniaxially compressed hard rock [62]. In the case of , the tensile damage is allowed to grow more than the case by the limiting factor in Equation (3) Therefore, the tensile damage variable reaches value 1 in a larger area of the specimen.
4.3.2. Uniaxial Compression Test on Numerical Rock Sample Pretreated with Microwave Irradiation
The uniaxial compressive test on pretreated specimens here is modelled in the same way as in Section 4.3.1, i.e., as a constant downward velocity (0.03 m/s−1 applied at the top face of the sample. The mechanical boundary conditions are the same as well. The thermally pretreated numerical samples are subjected to the mechanical test after being ideally left to cool down naturally at room temperature without forced convection. This corresponds to the in situ or laboratory case where some time passes between the thermal pretreatment application and the mechanical, conventional breaking of rocks. The test is conducted first with weighting factors in Equation (3) , then with factors . The results are displayed in Figure 20 and Figure 21 and they are given only for the back side, since it corresponds to the most damaged area of the sample.
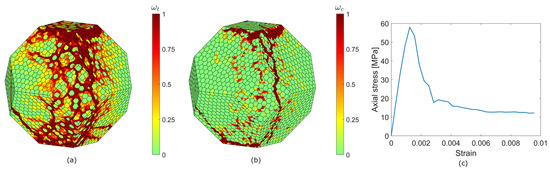
Figure 20.
Uniaxial compression test (weighting parameter )—back view. Tensile damage distribution as magnitude of damage variable (a), compressive damage distribution as magnitude of damage variable (b). Stress–strain curve (c).
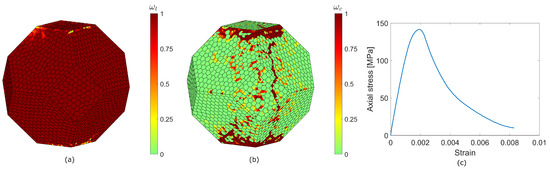
Figure 21.
Uniaxial compression test (weighting parameter )—back view. Tensile damage distribution as magnitude of damage variable (a), compressive damage distribution as magnitude of damage variable (b). Stress–strain curve (c).
The damage distribution at the end of the test seems to follow the vertical damage patterns already established during the microwave treatment. The uniaxial compressive strength is 59 MPa in the first case (52% reduction with respect to the corresponding intact case) and 142 MPa in the second case (20% reduction). The ratio between the uniaxial compressive strength reduction and the energy required in the pretreatment to obtain this reduction is 6.7%/(Wh) and 2.6 MPa/(Wh) for the case.
4.3.3. Uniaxial Compression Test on Numerical Rock Sample Pretreated with Conventional Heating
The uniaxial compressive test on pretreated specimens here is modelled in the same way as in Section 4.3.2, i.e., as a constant downward velocity (0.03 m/s−1) applied at the top face of the sample. The mechanical and thermal boundary conditions are as the same as well. The test is conducted first with weighting factors in Equation (3) , then with factors . The results are displayed in Figure 22 and Figure 23.
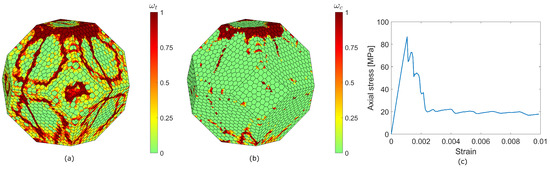
Figure 22.
Uniaxial compression test (weighting parameter )—back view. Tensile damage distribution as magnitude of damage variable (a), compressive damage distribution as magnitude of damage variable (b). Stress–strain curve (c).
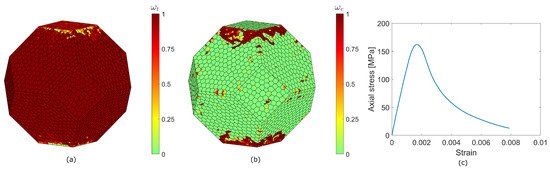
Figure 23.
Uniaxial compression test (weighting parameter )—back view. Tensile damage distribution as magnitude of damage variable (a), compressive damage distribution as magnitude of damage variable (b). Stress–strain curve (c).
In the case of , the damage distribution, at the end of the test, presents new vertical damage patterns and does not follow the already established circular ones. In the case of , the factor in Equation (3) limits , which reaches the value 1 in almost all side facets of the specimen. The uniaxial compressive strength is 86 MPa in the first case (30% reduction with respect to the corresponding intact case) and 162 MPa in the second case (9% reduction). The ratio between the uniaxial compressive strength reduction percentage and the necessary energy 20.5%/(Wh) for the case and 5.8%/(Wh) for the case.
5. Discussion and Conclusions
A 3D numerical method to predict the effects of thermal pretreatments on the compressive strength of granite-like rock was developed in this paper. The study analyzed the effects of two different thermal pretreatments: heating via microwave irradiation in a multimode microwave oven and conventional heating. The study yields the following conclusions:
- A method to simulate rock breakage due to thermal pretreatments (conventional heating and microwave irradiation), based on a continuum approach, is developed and tested in this paper. Rock failure is modelled via a damage-(visco)plasticity model derived from the Rankine and Drucker–Prager yield criteria. Stiffness degradation and strength deterioration are both taken into account by means of separate scalar damage parameters in tension and compression. Moreover, the unilateral conditions of tensile damage of rock are rendered through specific parameters that modelled the extreme cases of complete stiffness recovery or no stiffness recovery during load reversal from tension to compression.
- The adopted explicit staggered scheme proves to be effective in solving the nonlinear coupled problem of thermal cracking due to heating by microwave irradiation and conventional heating. Drastic mass scaling can be applied thanks to the non-inertial nature of the slow heating induced by both pretreatments. Mass scaling allows one to increase the critical time step of the explicit time marching scheme for the mechanical part of the governing global problem.
- Damage patterns are heavily influenced by the nature of the heating pretreatment (volumetric or surface) and by the heterogeneity of the material. Polycrystalline hard rocks such as granite are constituted of minerals with different dielectric, thermal and mechanical properties. Here, heterogeneity was defined explicitly by representing the typical granular texture of polycrystalline hard rock as a Voronoi structure of polyhedral cells. The advantage of this approach is evident especially in the microwave simulation results, where single biotite and quartz grains were entirely spared from damage due to their dielectric, thermal and mechanical properties.
- Conventional heating via heat torch, for these idealized and specific testing conditions, seems to be the best pretreatment in terms of highest ratio of uniaxial compressive strength reduction percentage to required energy seems to be the conventional heating method. However, it must be remarked that this method requires a very high surface heat flux (0.5 MW/m2) to reach the necessary temperature levels and ad hoc thermal equipment to obtain a uniform heating.
- On the other hand, microwave oven appliances are more commonly available, even though they demand longer heating times due to the low dielectric properties of granite. Moreover, the search for the best placement inside the cavity that maximizes the temperature outcomes can be time-consuming. Therefore, different time duration/heating power combinations should be tested in order to find the optimal ratio of strength reduction percentage vs. spent energy.
- The thermal pretreatment simulations are repeated for specimens having different quartz percentages. Two new specimens are created, one with 15% quartz content and the other with 45%. The number and location of biotite grains are preserved. Quartz grains are replaced by feldspar grains to obtain the desired quartz percentages. The results of microwave heating show a slight increase in average temperature with increasing quartz content. However, from the simulation results an immediate correlation between quartz content and tensile damage intensity cannot be established. The results of conventional heating may suggest an influence of quartz content on average temperature and tensile damage severity. In particular, average temperature and tensile damage seem to increase with decreasing quartz content.
- The simulation conditions are not ideal for comparison of these two thermal pretreatments, which are quite different in nature (surface heating vs. volumetric heating). The chosen approach here was to obtain similar temperature values in the samples. A more sound approach to estimate the efficacy of different thermal pretreatments is to compare not temperatures, but entering heat. In that case, the total energy spent during the 60 s microwave heating would be spread across the external heated surface (conventional heating). However, since the duration treatment in this case is quite short (to induce a sudden heat-shock in the sample), the external surface power and the temperatures reached in that case would have been high enough to cause melting in the sample. A solution could be to extend the duration of the conventional heating, but that would probably not produce the desired heat shock effect. Moreover, longer heating times imply lower feasibility and and practical application of the method in real-life mineral processing plant situations.
- Further developments of this study should include modelling of intergranular cracks at grain boundaries to replicate the experimental results of previous studies. Finally, in order to fully evaluate the weakening effect of thermal pretreatments on compressive strength of rock, the present model should be validated via laboratory experiments.
Author Contributions
Conceptualization, M.P., J.K. and T.S.; methodology, M.P., J.K. and T.S.; simulations, M.P.; writing—original draft preparation, M.P.; writing—review and editing, M.P., J.K. and T.S.; supervision, T.S.; funding acquisition, M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Suomen Kulttuurirahasto (Finnish Cultural Foundation), grant number 00220830.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Tromans, D. Mineral comminution: Energy efficiency considerations. Miner. Eng. 2008, 21, 613–620. [Google Scholar] [CrossRef]
- Musa, F.; Morrison, R. A more sustainable approach to assessing comminution efficiency. Miner. Eng. 2009, 22, 593–601. [Google Scholar] [CrossRef]
- Ballantyne, G.; Powell, M. Benchmarking comminution energy consumption for the processing of copper and gold ores. Miner. Eng. 2014, 65, 109–114. [Google Scholar] [CrossRef]
- Curry, J.A.; Ismay, M.J.; Jameson, G.J. Mine operating costs and the potential impacts of energy and grinding. Miner. Eng. 2014, 56, 70–80. [Google Scholar] [CrossRef]
- Napier-Munn, T. Is progress in energy-efficient comminution doomed? Miner. Eng. 2015, 73, 1–6. [Google Scholar] [CrossRef]
- Klein, B.; Wang, C.; Nadolski, S. Energy-Efficient Comminution: Best Practices and Future Research Needs. In Energy Efficiency in the Minerals Industry: Best Practices and Research Directions; Awuah-Offei, K., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 197–211. [Google Scholar]
- Tutak, M.; Brodny, J. Forecasting Methane Emissions from Hard Coal Mines Including the Methane Drainage Process. Energies 2019, 12, 3840. [Google Scholar] [CrossRef]
- Somani, A.; Nandi, T.K.; Pal, S.K.; Majumder, A.K. Pre-treatment of rocks prior to comminution—A critical review of present practices. Int. J. Min. Sci. Technol. 2017, 27, 339–348. [Google Scholar] [CrossRef]
- Fitzgibbon, K.; Veasey, T. Thermally assisted liberation—A review. Miner. Eng. 1990, 3, 181–185. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Shi, L.; Rong, Y.; Hu, J.; Jiang, G.; Wang, Y.; Hu, S. Anisotropic Differences in the Thermal Conductivity of Rocks: A Summary from Core Measurement Data in East China. Minerals 2021, 11, 1135. [Google Scholar] [CrossRef]
- Somerton, W. Thermal Properties and Temperature-Related Behavior of Rock/Fluid Systems; Elsevier Science: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Wu, X.; Huang, Z.; Song, H. Variations of Physical and Mechanical Properties of Heated Granite After Rapid Cooling with Liquid Nitrogen. Rock Mech. Rock Eng. 2019, 52, 2123–2139. [Google Scholar] [CrossRef]
- Forster, J. Dielectric Properties of Minerals and Ores and the Application of Microwaves for Assisted Comminution. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2023. [Google Scholar]
- Teimoori, K.; Hassani, F. Twenty years of experimental and numerical studies on microwave-assisted breakage of rocks and minerals—A review. arXiv 2020, arXiv:2011.14624. [Google Scholar]
- Jones, D.; Lelyveld, T.; Mavrofidis, S.; Kingman, S.; Miles, N. Microwave heating applications in environmental engineering—A review. Resour. Conserv. Recycl. 2002, 34, 75–90. [Google Scholar] [CrossRef]
- Monti, T.; Tselev, A.; Udoudo, O.; Ivanov, I.; Dodds, C.; Kingman, S. High-resolution dielectric characterization of minerals: A step towards understanding the basic interactions between microwaves and rocks. Int. J. Miner. Process. 2016, 151, 8–21. [Google Scholar] [CrossRef]
- Palma, V.; Barba, D.; Cortese, M.; Martino, M.; Renda, S.; Meloni, E. Microwaves and Heterogeneous Catalysis: A Review on Selected Catalytic Processes. Catalysts 2020, 10, 246. [Google Scholar] [CrossRef]
- Tian, W.; Yang, S.; Huang, Y.; Hu, B. Mechanical Behavior of Granite with Different Grain Sizes After High-Temperature Treatment by Particle Flow Simulation. Rock Mech. Rock Eng. 2020, 53, 1791–1807. [Google Scholar] [CrossRef]
- Saksala, T. Numerical Modeling of Temperature Effect on Tensile Strength of Granitic Rock. Appl. Sci. 2021, 11, 4407. [Google Scholar] [CrossRef]
- Ma, Z.; Zheng, Y.; Sun, T.; Li, J. Thermal stresses and temperature distribution of granite under microwave treatment. In Proceedings of the 11th Conference of Asian Rock Mechanics Society, Bristol, UK, 21–25 October 2021; Volume 861. [Google Scholar]
- Zhu, J.; Yi, L.; Yang, Z.; Duan, M. Three-dimensional numerical simulation on the thermal response of oil shale subjected to microwave heating. Chem. Eng. J. 2021, 407, 127197. [Google Scholar] [CrossRef]
- Toifl, M.; Meisels, R.; Hartlieb, P.; Kuchar, F.; Antretter, T. 3D numerical study on microwave induced stresses in inhomogeneous hard rocks. Miner. Eng. 2016, 90, 29–42. [Google Scholar] [CrossRef]
- Xu, T.; Yuan, Y.; Heap, M.J.; Zhou, G.L.; Perera, M.; Ranjith, P. Microwave-assisted damage and fracturing of hard rocks and its implications for effective mineral resources recovery. Miner. Eng. 2021, 160, 106663. [Google Scholar] [CrossRef]
- Wei, W.; Shao, Z.; Zhang, P.; Zhang, H.; Cheng, J.; Yuan, Y. Thermally Assisted Liberation of Concrete and Aggregate Recycling: Comparison between Microwave and Conventional Heating. J. Mater. Civ. Eng. 2021, 33, 04021370. [Google Scholar] [CrossRef]
- Shou, H.Z.; Hu, Q.; Zeng, J.; He, L.; Tang, H.; Li, B.; Chen, S.; Lu, X. Comparative study on the deterioration of granite under microwave irradiation and resistance-heating treatment. Frat. Ed Integrità Strutt. 2019, 13, 638–648. [Google Scholar] [CrossRef]
- Pressacco, M.; Kangas, J.; Saksala, T. Numerical Modelling of Microwave Heating Assisted Rock Fracture. Rock Mech. Rock Eng. 2022, 55, 481–503. [Google Scholar] [CrossRef]
- Saksala, T. Damage–viscoplastic consistency model with a parabolic cap for rocks with brittle and ductile behavior under low-velocity impact loading. Int. J. Numer. Anal. Meth. 2010, 34, 1362–1386. [Google Scholar] [CrossRef]
- Wang, W.M. Stationary and Propagative Instabilities in Metals—A Computational Point of View. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1997. [Google Scholar]
- Wang, W.M.; Sluys, L.J.; de Borst, R. Viscoplasticity for instabilities due to strain softening and strain-rate softening. Int. J. Numer. Meth. Eng. 1997, 40, 3839–3864. [Google Scholar] [CrossRef]
- Grassl, P.; Jirásek, M. Damage-plastic model for concrete failure. Int. J. Solids Struct. 2006, 43, 7166–7196. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oñate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Eberhardt, E.; Stead, D.; Stimpson, B. Quantifying progressive pre-peak brittle fracture damage in rock during uniaxial compression. Int. J. Rock Mech. Min. 1999, 36, 361–380. [Google Scholar] [CrossRef]
- Wang, H.; Rezaee, M.; Saeedi, A.; Josh, M. Numerical modelling of microwave heating treatment for tight gas sand reservoirs. J. Pet. Sci. Eng. 2017, 152, 495–504. [Google Scholar] [CrossRef]
- Ottosen, N.S.; Ristinmaa, M. The Mechanics of Constitutive Modeling; Elsevier Science Ltd.: Oxford, UK, 2005; pp. 637–672. [Google Scholar]
- Poole, C.; Darwazeh, I. Microwave Active Circuit Analysis and Design; Academic Press: Oxford, UK, 2016. [Google Scholar]
- Monk, P. Finite Element Methods for Maxwell’s Equations; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Pozar, D.M. Microwave Engineering; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Haus, H.A.; Melcher, J.R. Electromagnetic Fields and Energy; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Pressacco, M.; Saksala, T. Numerical modelling of heat shock-assisted rock fracture. Int. Numer. Anal. Meth. Geomech. 2020, 44, 40–68. [Google Scholar] [CrossRef]
- Ngo, M.; Brancherie, D.; Ibrahimbegovic, A. Softening behavior of quasi-brittle material under full thermo-mechanical coupling condition: Theoretical formulation and finite element implementation. Comput. Methods Appl. Mech. Eng. 2014, 281, 1–28. [Google Scholar] [CrossRef]
- Felippa, C.A.; Park, C.K. Staggered transient analysis procedures for coupled mechanical systems: Formulation. Comput. Methods Appl. Mech. Eng. 1980, 24, 61–111. [Google Scholar] [CrossRef]
- Martins, J.M.P.; Neto, D.M.; Alves, J.L.; Oliveira, M.C.; Laurent, H.; Andrade-Campos, A.; Menezes, L.F. A new staggered algorithm for thermomechanical coupled problems. Int. J. Solids Struct. 2017, 122–123, 42–58. [Google Scholar] [CrossRef]
- Hahn, G.D. A modified Euler method for dynamic analyses. Int. J. Numer. Meth. Eng. 1991, 32, 943–955. [Google Scholar] [CrossRef]
- Quey, R.; Dawson, P.; Barbe, F. Large-scale 3D random polycrystals for the finite element method: Generation, meshing and remeshing. Comput. Methods Appl. Mech. Eng. 2011, 200, 1729–1745. [Google Scholar] [CrossRef]
- Vázquez, P.; Shushakova, V.; Gómez-Heras, M. Influence of mineralogy on granite decay induced by temperature increase: Experimental observations and stress simulation. Eng. Geol. 2015, 189, 58–67. [Google Scholar] [CrossRef]
- Zheng, Y.L.; Zhao, X.B.; Zhao, Q.H.; Li, J.C.; Zhang, Q.B. Dielectric properties of hard rock minerals and implications for microwave-assisted rock fracturing. Geomech. Geophys. Geo-Energy Geo-Resour. 2020, 6, 97–122. [Google Scholar] [CrossRef]
- Mahabadi, O.K. Investigating the Influence of Micro-scale Heterogeneity and Microstructure on the Failure and Mechanical Behaviour of Geomaterials. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2012. [Google Scholar]
- Schön, J. Physical Properties of Rocks; Elsevier Science and Technology: London, UK, 2011; p. 494. [Google Scholar]
- Clauser, C.; Huenges, E. Thermal Conductivity of Rocks and Minerals. In Rock Physics & Phase Relations; American Geophysical Union (AGU): Washington, DC, USA, 2013; pp. 105–126. [Google Scholar]
- Waples, D.W.; Waples, J.S. A Review and Evaluation of Specific Heat Capacities of Rocks, Minerals and Subsurface Fluids. Part 1: Minerals and Nonporous Rocks. Nat. Resour. Res. 2004, 13, 97–122. [Google Scholar] [CrossRef]
- Park, J.W.; Park, C.; Ryu, D.; Park, E.S. Numerical simulation of thermo-mechanical behavior of rock using a grain-based distinct element model. In ISRM Regional Symposium-EUROCK; Austrian Society for Geomechanics: Salzburg, Austria, 2015. [Google Scholar]
- Saksala, T. 3D Numerical Prediction of Thermal Weakening of Granite under Tension. Geosciences 2022, 12, 10. [Google Scholar] [CrossRef]
- Wang, F.; Konietzky, H. Thermo-Mechanical Properties of Granite at Elevated Temperatures and Numerical Simulation of Thermal Cracking. Rock Mech. Rock Eng. 2019, 52, 3737–3755. [Google Scholar] [CrossRef]
- Santos, T.C.; Costa, L.C.; Valente, M.A.; Monteiro, J.; Sousa, J.; Santos, T. 3D Electromagnetic Field Simulation in Microwave Ovens: A Tool to Control Thermal Runaway. In Proceedings of the COMSOL Conference, Newton, MA, USA, 7–9 October 2010. [Google Scholar]
- Teimoori, K.; Cooper, R. Multiphysics study of microwave irradiation effects on rock breakage system. Int. J. Rock Mech. Min. Sci. 2021, 140, 104586. [Google Scholar] [CrossRef]
- Roshankhah, S.; Teimoori, K.; Mohammadi, K. Thermo-Mechanical Response of Layered Rocks upon Single-Mode Microwave Treatments. In Proceedings of the ARMA/DGS/SEG International Geomechanics Symposium, Virtual, 1–4 November 2021. [Google Scholar]
- Shadi, A.; Ahmadihosseini, A.; Rabiei, M.; Samea, P.; Hassani, F.; Sasmito, A.P.; Ghoreishi-Madiseh, S.A. Numerical and experimental analysis of fully coupled electromagnetic and thermal phenomena in microwave heating of rocks. Miner. Eng. 2022, 178, 107406. [Google Scholar] [CrossRef]
- Molaro, J.L.; Byrne, S.; Langer, S.A. Grain-scale thermoelastic stresses and spatiotemporal temperature gradients on airless bodies, implications for rock breakdown. J. Geophys. Res. Planet 2015, 120, 255–277. [Google Scholar] [CrossRef]
- Ge, Z.; Sun, Q.; Xue, L.; Yang, T. The influence of microwave treatment on the mode I fracture toughness of granite. Eng. Fract. Mech. 2021, 249, 107768. [Google Scholar] [CrossRef]
- Basu, A.; Mishra, D.; Roychowdhury, K. Rock failure modes under uniaxial compression, Brazilian and point load tests. Bull. Eng. Geol. Environ. 2013, 72, 457–475. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).