Fluid Redox Fingerprint of the CaCO3+Antigorite Dehydration Reaction in Subducted Metacarbonate Sediments
Abstract
1. Introduction
- I.
- II.
- III.
- Antigorite breakdown produces either reducing or oxidising fluid (since it spans roughly 8–9 log fO2 [12,16], from a reduced −5 to an oxidised +4 Δlog fO2 units with respect to the Fayalite–Magnetite–Quartz oxygen buffer, FMQ), depending on the P-T path experienced by the subducted rocks [12] or on the pre-subduction redox state of the system [14].
2. Geological and Petrological Setting

| Used (reduced) DM675 El mol | Oxidised DM675 El mol | |
|---|---|---|
| Si | 3.0186 | 3.0186 |
| Fe2+ | 0.1171 | 0.1171 |
| Mg | 4.5242 | 4.5242 |
| Ca | 23.5540 | 23.5540 |
| H2 | 2.7526 | 2.7526 |
| C | 23.5337 | 23.5337 |
| S2 | 0.0604 | 0.0604 |
| O2 | 41.7392 | 42.1649 |
3. Methods
4. Results
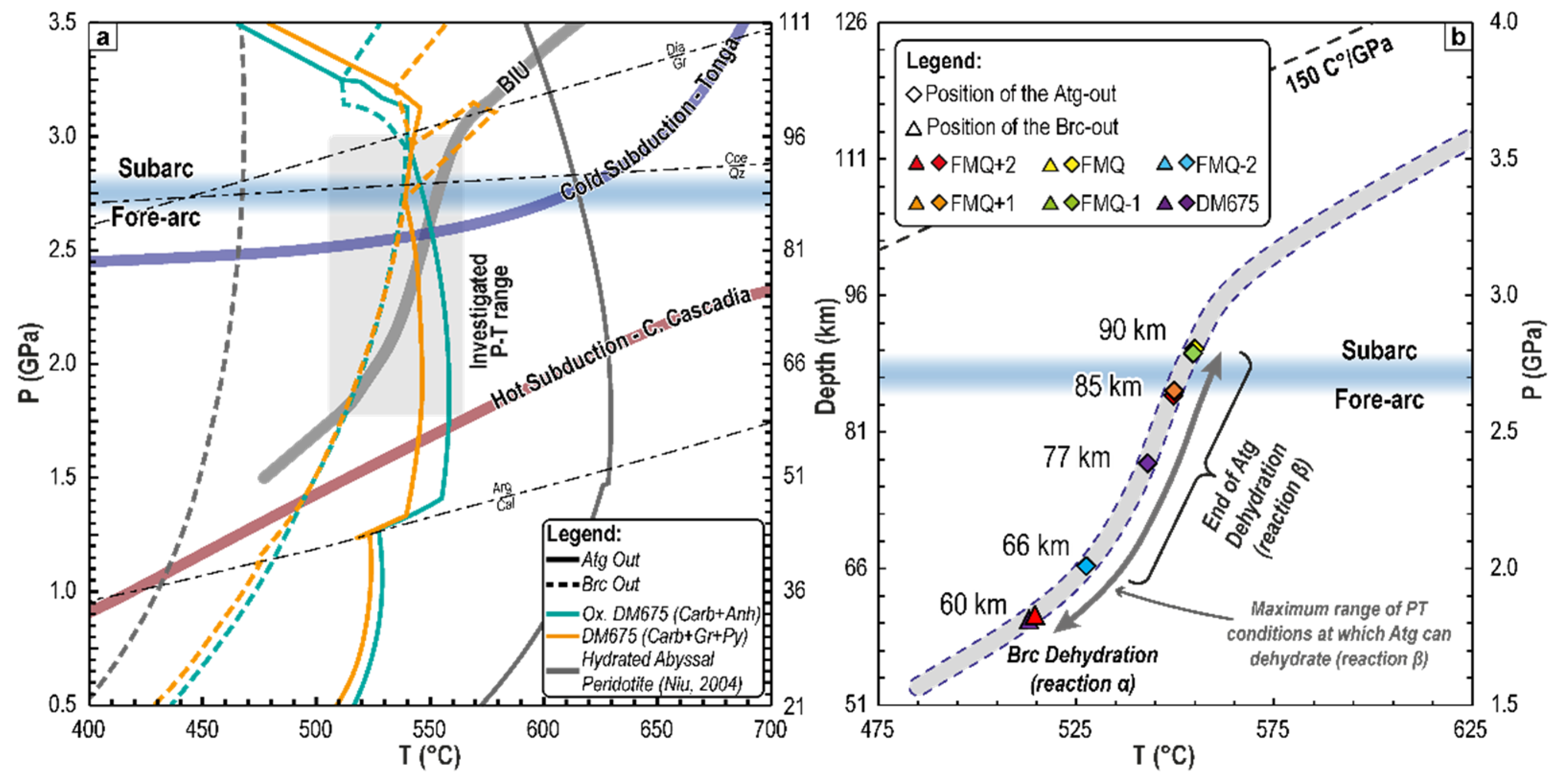
4.1. P-T-fO2 Mineral Phase Relationships during CaCO3+ Antigorite Dehydration Reaction
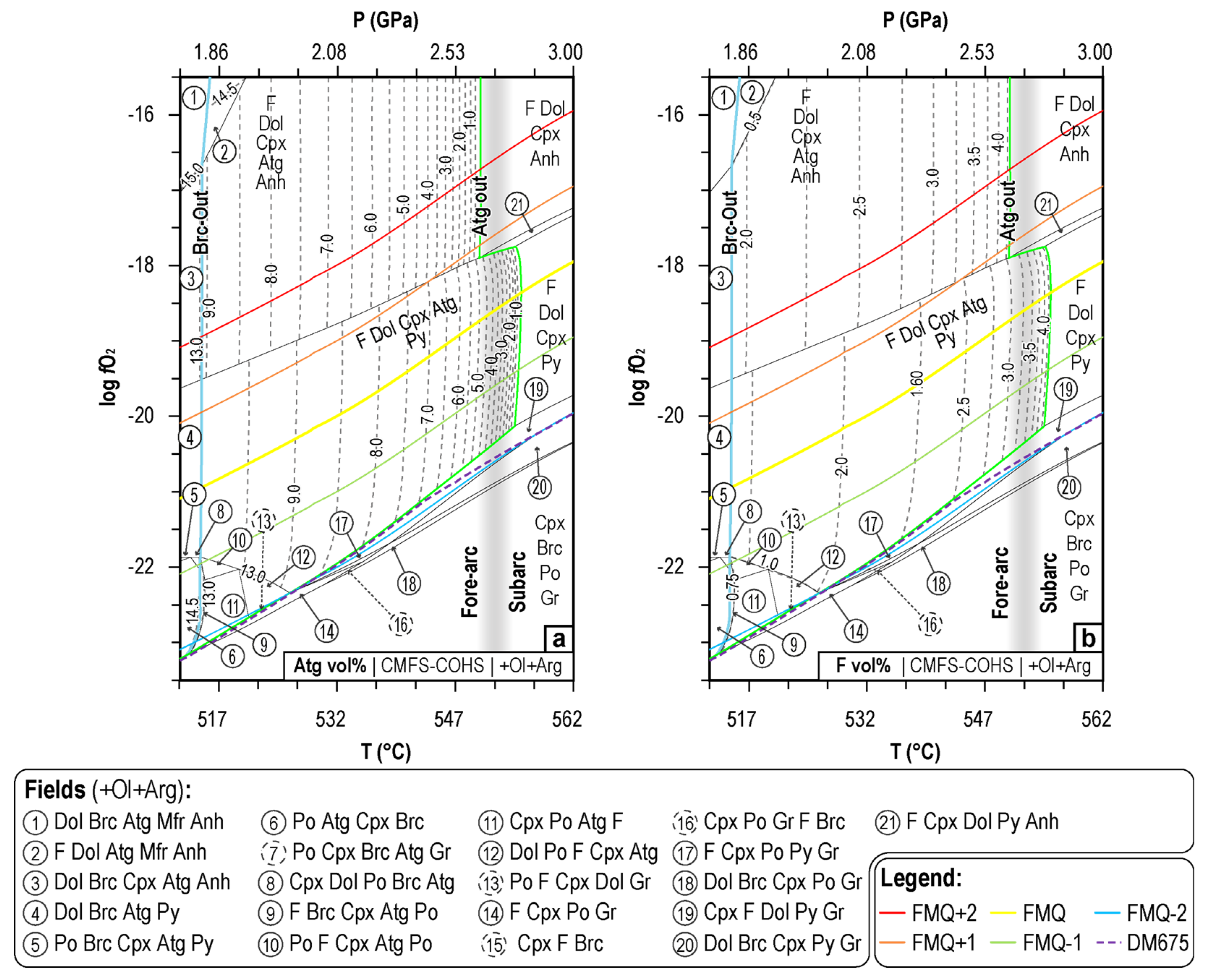
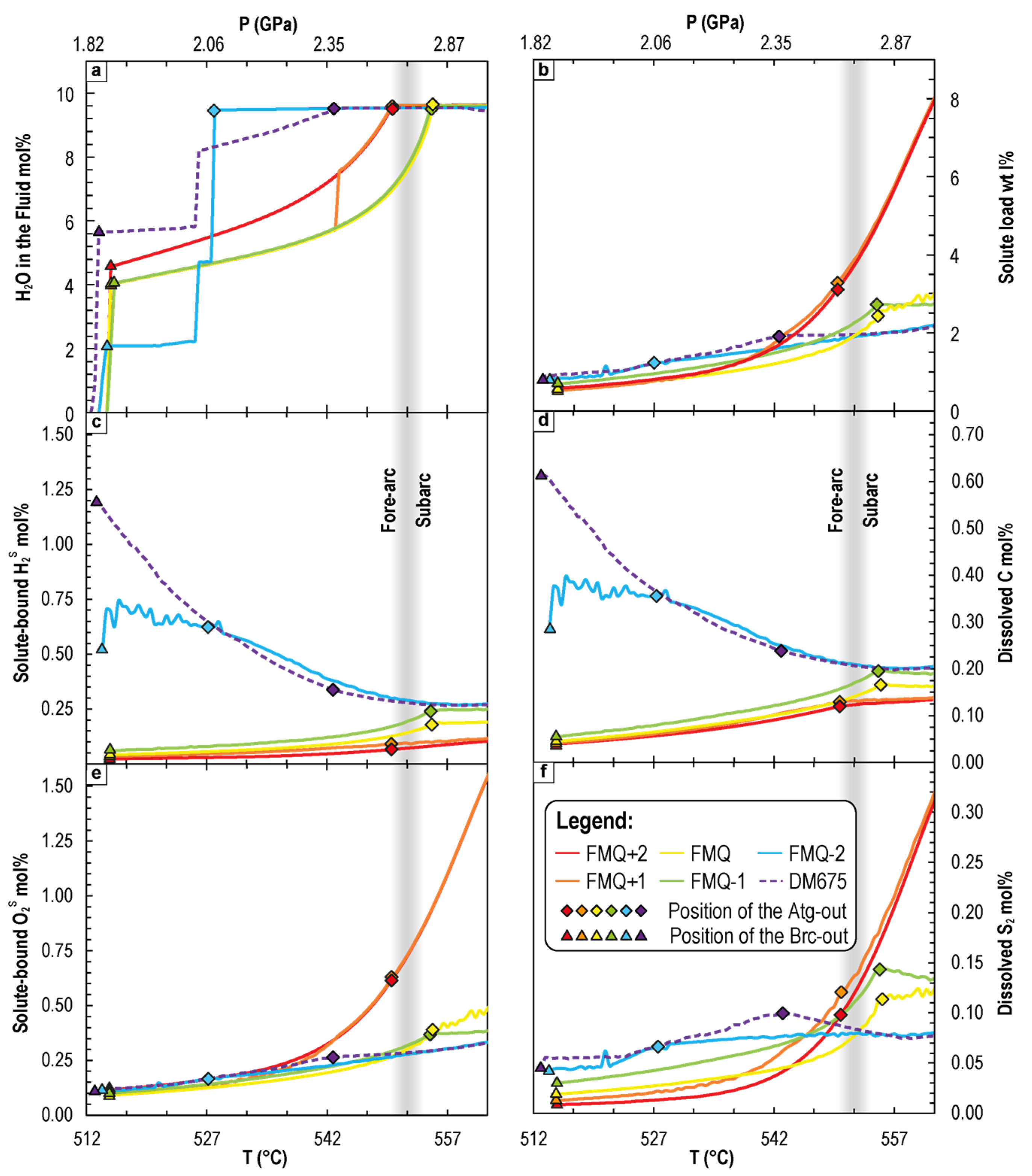
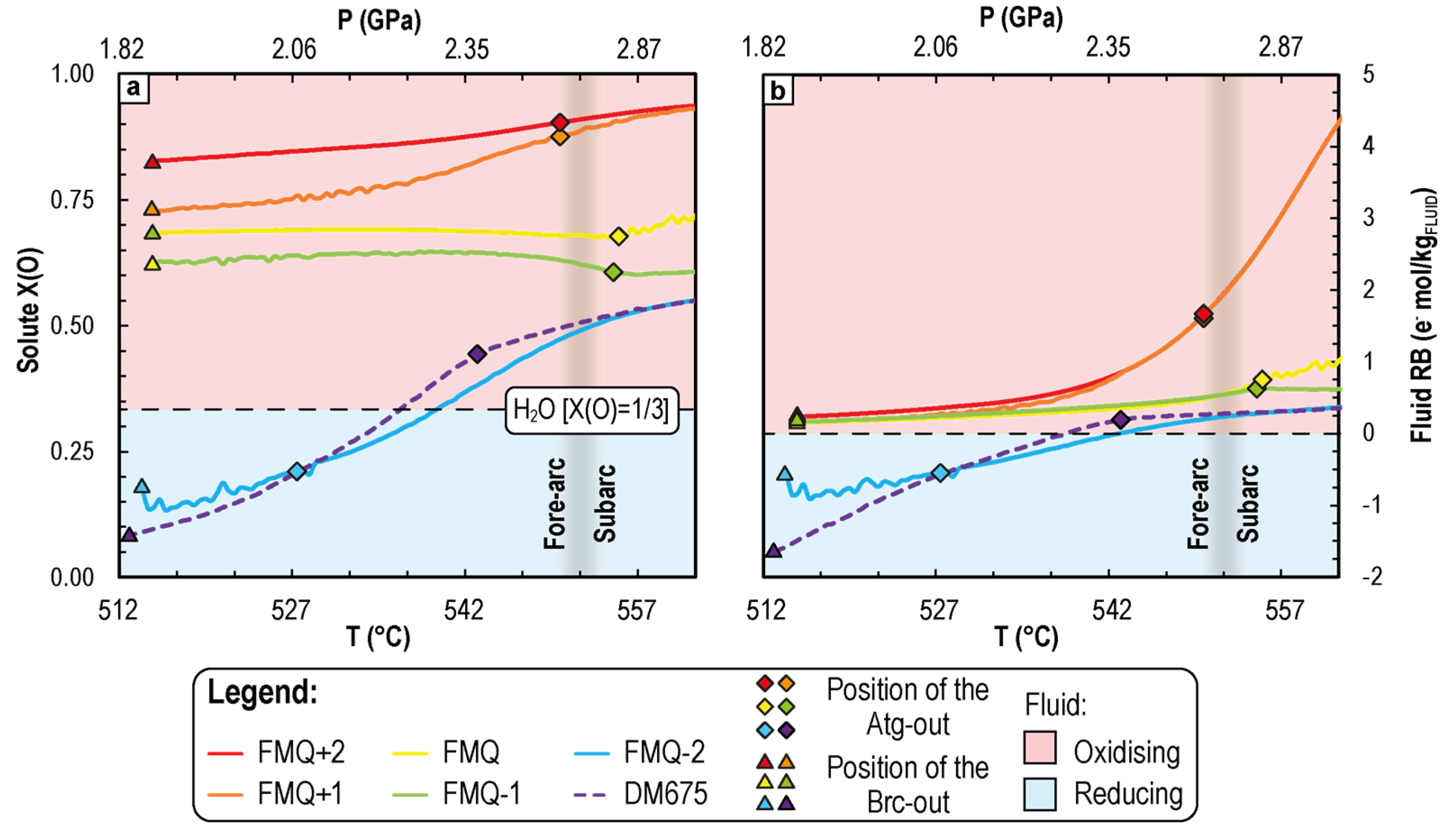
4.2. P-T-fO2 Fluid Phase Relationships during CaCO3+Antigorite Dehydration Reactions
4.2.1. Variation of Dissolved Redox-Sensitive Elements
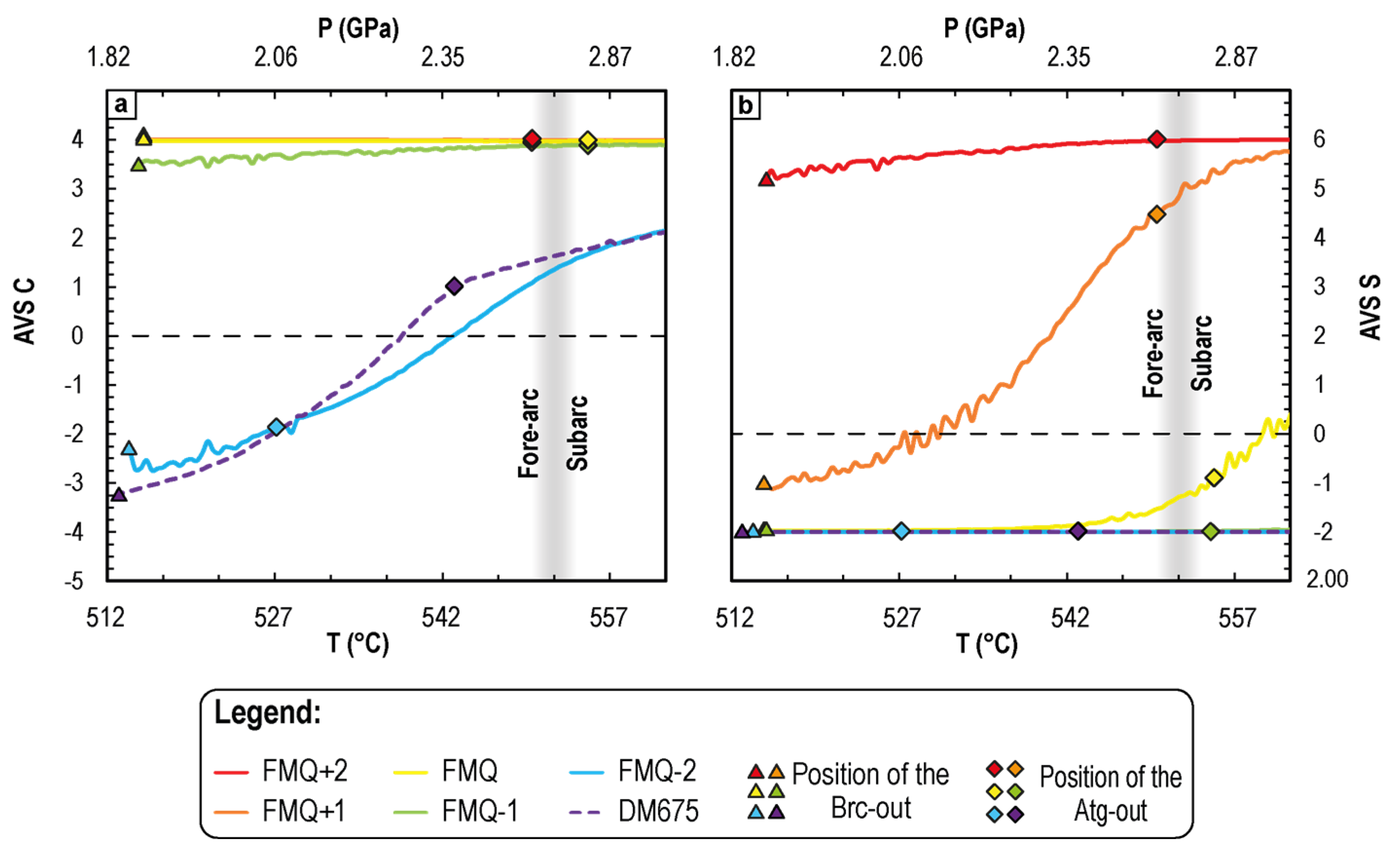
4.2.2. Variation of the Dissolved Average Valence State of C and S
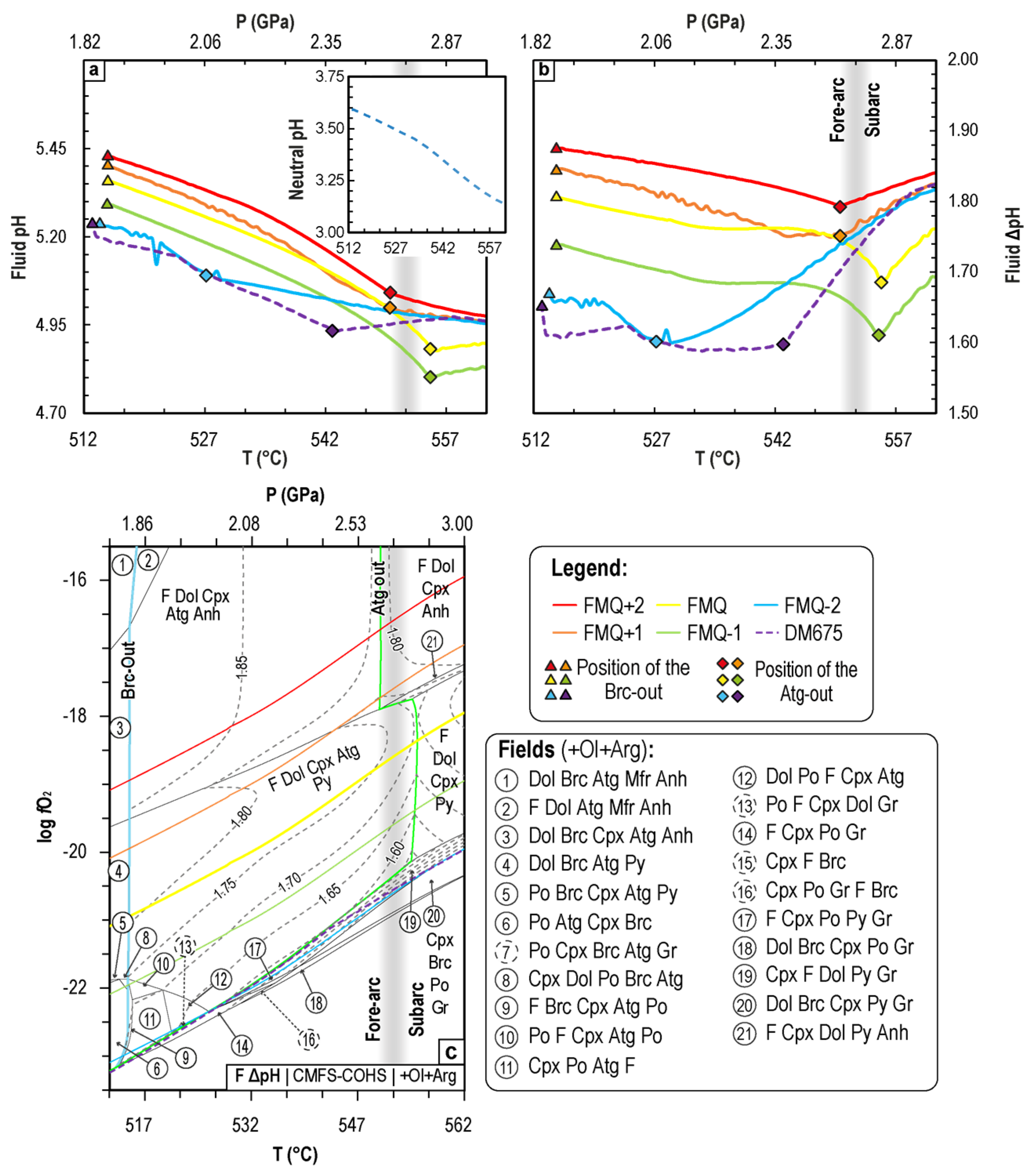
4.2.3. Variation of the Fluid pH
5. Discussion
5.1. Redox-Dependent Fluid Chemistry
5.2. Fluid Redox Budget
5.3. CaCO3+Antigorite Dehydration Reaction: Reducing or Oxidising?
5.4. Linking Fluid Production Processes to Subduction Geodynamics
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wood, B.J.; Bryndzia, L.T.; Johnson, K.E. Mantle oxidation state and its relationship to tectonic environment and fluid speciation. Science 1990, 248, 337–345. [Google Scholar] [CrossRef] [PubMed]
- Frost, D.J.; McCammon, C.A. The redox state of Earth’s mantle. Annu. Rev. Earth Planet. Sci. 2008, 36, 389–420. [Google Scholar] [CrossRef]
- Sun, W.; Huang, R.F.; Li, H.; Hu, Y.B.; Zhang, C.C.; Sun, S.J.; Zhang, L.P.; Ding, X.; Li, C.-Y.; Zartman, R.E.; et al. Porphyry deposits and oxidized magmas. Ore Geol. Rev. 2015, 65, 97–131. [Google Scholar] [CrossRef]
- Chowdhury, P.; Dasgupta, R.; Phelps, P.R.; Costin, G.; Lee, C.T.A. Oxygen fugacity range of subducting crust inferred from fractionation of trace elements during fluid-present slab melting in the presence of anhydrite versus sulfide. Geochim. Cosmochim. Acta 2022, 325, 214–231. [Google Scholar] [CrossRef]
- Bucher, K.; Grapes, R. Petrogenesis of Metamorphic Rocks; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Peretti, A.; Dubessy, J.; Mullis, J.; Frost, B.R.; Trommsdorff, V. Highly reducing conditions during Alpine metamorphism of the Malenco peridotite (Sondrio, northern Italy) indicated by mineral paragenesis and H2 in fluid inclusions. Contrib. Mineral. Petrol. 1992, 112, 329–340. [Google Scholar] [CrossRef]
- Debret, B.; Andreani, M.; Muñoz, M.; Bolfan-Casanova, N.; Carlut, J.; Nicollet, C.; Schwartz, S.; Trcera, N. Evolution of Fe redox state in serpentine during subduction. Earth Planet. Sci. Lett. 2014, 400, 206–218. [Google Scholar] [CrossRef]
- Debret, B.; Sverjensky, D.A. Highly oxidising fluids generated during serpentinite breakdown in subduction zones. Sci. Rep. 2017, 7, 10351. [Google Scholar] [CrossRef]
- Merkulova, M.V.; Muñoz, M.; Brunet, F.; Vidal, O.; Hattori, K.; Vantelon, D.; Trcera, N.; Huthwelker, T. Experimental insight into redox transfer by iron-and sulfur-bearing serpentinite dehydration in subduction zones. Earth Planet. Sci. Lett. 2017, 479, 133–143. [Google Scholar] [CrossRef]
- Piccoli, F.; Hermann, J.; Pettke, T.; Connolly JA, D.; Kempf, E.D.; Vieira Duarte, J.F. Subducting serpentinites release reduced, not oxidized, aqueous fluids. Sci. Rep. 2019, 9, 19573. [Google Scholar] [CrossRef]
- Iacovino, K.; Guild, M.R.; Till, C.B. Aqueous fluids are effective oxidizing agents of the mantle in subduction zones. Contrib. Mineral. Petrol. 2020, 175, 36. [Google Scholar] [CrossRef]
- Lazar, C. Using silica activity to model redox-dependent fluid compositions in serpentinites from 100 to 700 C and from 1 to 20 kbar. J. Petrol. 2020, 61, egaa101. [Google Scholar] [CrossRef]
- Maurice, J.; Bolfan-Casanova, N.; Demouchy, S.; Chauvigne, P.; Schiavi, F.; Debret, B. The intrinsic nature of antigorite breakdown at 3 GPa: Experimental constraints on redox conditions of serpentinite dehydration in subduction zones. Contrib. Mineral. Petrol. 2020, 175, 94. [Google Scholar] [CrossRef]
- Evans, K.A.; Frost, B.R. Deserpentinization in subduction zones as a source of oxidation in arcs: A reality check. J. Petrol. 2021, 62, 1–32. [Google Scholar] [CrossRef]
- Eberhard, L.; Plümper, O.; Frost, D.J. Early release of H2O during subduction of carbonated ultramafic lithologies. Contrib. Mineral. Petrol. 2023, 178, 17. [Google Scholar] [CrossRef]
- Caurant, C.; Debret, B.; Ménez, B.; Nicollet, C.; Bouilhol, P. Redox heterogeneities in a subducting slab: Example from the Monviso meta-ophiolite (Western Alps, Italy). Lithos 2023, 446–447, 107136. [Google Scholar] [CrossRef]
- Padrón-Navarta, J.A.; Sánchez-Vizcaíno, V.L.; Menzel, M.D.; Gómez-Pugnaire, M.T.; Garrido, C.J. Mantle wedge oxidation from deserpentinization modulated by sediment-derived fluids. Nat. Geosci. 2023, 16, 268–275. [Google Scholar] [CrossRef]
- Ding, K.; Seyfried, W.E., Jr. Determination of Fe-Cl complexing in the low pressure supercritical region (NaCl fluid): Iron solubility constraints on pH of subseafloor hydrothermal fluids. Geochim. Et Cosmochim. Acta 1992, 56, 3681–3692. [Google Scholar] [CrossRef]
- Yardley, B.W. 100th Anniversary Special Paper: Metal concentrations in crustal fluids and their relationship to ore formation. Econ. Geol. 2005, 100, 613–632. [Google Scholar] [CrossRef]
- Ferrando, S.; Groppo, C.; Frezzotti, M.L.; Castelli, D.; Proyer, A. Dissolving dolomite in a stable UHP mineral assemblage: Evidence from Cal-Dol marbles of the Dora-Maira Massif (Italian Western Alps). Am. Mineral. 2017, 102, 42–60. [Google Scholar] [CrossRef]
- Groppo, C.; Ferrando, S.; Gilio, M.; Botta, S.; Nosenzo, F.; Balestro, G.; Festa, A.; Rolfo, F. What’s in the sandwich? New P–T constraints for the (U)HP nappe stack of southern Dora-Maira Massif (Western Alps). Eur. J. Mineral. 2019, 31, 665–683. [Google Scholar] [CrossRef]
- Syracuse, E.M.; van Keken, P.E.; Abers, G.A. The global range of subduction zone thermal models. Phys. Earth Planet. Inter. 2010, 183, 73–90. [Google Scholar] [CrossRef]
- Vialon, P. Etude Géologique du Massif Cristallin Dora-Maira: Alpes Cottiennes Internes: Italie. Doctoral Dissertation, Université de Grenoble, Grenoble, France, 1966. [Google Scholar]
- Chopin, C. Coesite and pure pyrope in high-grade blueschists of the Western Alps: A first record and some consequences. Contrib. Mineral. Petrol. 1984, 86, 107–118. [Google Scholar] [CrossRef]
- Compagnoni, R.; Rolfo, F.; Groppo, C.; Hirajima, T.; Turello, R. Geological map of the ultra-high pressure Brossasco-Isasca unit (Western Alps, Italy). J. Maps 2012, 8, 465–472. [Google Scholar] [CrossRef]
- Maffeis, A.; Ferrando, S.; Connolly, J.A.; Groppo, C.; Frezzotti, M.L.; Castelli, D. Thermodynamic analysis of HP-UHP fluid inclusions: The solute load and chemistry of metamorphic fluids. Geochim. Et Cosmochim. Acta 2021, 315, 207–229. [Google Scholar] [CrossRef]
- Compagnoni, R.; Borghi, A.; Cadoppi, P.; Ferrando, S.; Gattiglio, M.; Ruffini, R. The abundance of 47 elements and petrovolumetric models of the crust in the Susa Valley, Western Alps (Site 1). In The Abundance of 55 Elements and Petrovolumetric Models of the Crust in 19 Type Areas from the Crystalline Basements of Italy, with Some Geophysical and Petrophysical Data; Cesare, B., Mazzoli, C., Peruzzo, G., Rizzo, G., Sassi, R., Spiess, R., Eds.; Accademia Nazionale Delle Scienze Detta Dei XL: Roma, Italy, 2003; XXXII; pp. 69–96. [Google Scholar]
- Bebout, G.E.; Agard, P.; Kobayashi, K.; Moriguti, T.; Nakamura, E. Devolatilization history and trace element mobility in deeply subducted sedimentary rocks: Evidence from Western Alps HP/UHP suites. Chem. Geol. 2013, 342, 1–20. [Google Scholar] [CrossRef]
- Epstein, G.S.; Bebout, G.E.; Angiboust, S.; Agard, P. Scales of fluid-rock interaction and carbon mobility in the deeply underplated and HP-Metamorphosed Schistes Lustrés, Western Alps. Lithos 2020, 354, 105229. [Google Scholar] [CrossRef]
- Epstein, G.S.; Bebout, G.E.; Angiboust, S. Fluid and mass transfer along transient subduction interfaces in a deep paleo-accretionary wedge (Western Alps). Chem. Geol. 2021, 559, 119920. [Google Scholar] [CrossRef]
- Groppo, C.; Rapa, G.; Frezzotti, M.L.; Rolfo, F. The fate of calcareous pelites in collisional orogens. J. Metamorph. Geol. 2021, 39, 181–207. [Google Scholar] [CrossRef]
- Plank, T. The Chemical Composition of Subducting Sediments; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Massonne, H.J. Phase relations of siliceous marbles at ultrahigh pressure based on thermodynamic calculations: Examples from the Kokchetav Massif, Kazakhstan and the Sulu terrane, China. Geol. J. 2011, 46, 114–125. [Google Scholar] [CrossRef]
- Wang, S.J.; Teng, F.Z.; Li, S.G. Tracing carbonate–silicate interaction during subduction using magnesium and oxygen isotopes. Nat. Commun. 2014, 5, 5328. [Google Scholar] [CrossRef]
- Tao, R.; Zhang, L.; Li, S.; Zhu, J.; Ke, S. Significant contrast in the Mg-CO isotopes of carbonate between carbonated eclogite and marble from the SW Tianshan UHP subduction zone: Evidence for two sources of recycled carbon. Chem. Geol. 2018, 483, 65–77. [Google Scholar] [CrossRef]
- Zhang, K.J.; Li, Q.H.; Yan, L.L.; Zeng, L.; Lu, L.; Zhang, Y.X.; Hui, J.; Jin, X.; Tang, X.C. Geochemistry of limestones deposited in various plate tectonic settings. Earth-Sci. Rev. 2017, 167, 27–46. [Google Scholar] [CrossRef]
- Farouk, S.; Ahmad, F.; Baioumy, H.; Lehmann, B.; Mohammed, I.Q.; Al-Kahtany, K. Geochemical characteristics of carbonaceous chalk near the Cretaceous/Paleogene transition, central Jordan: Strong metal enrichment of redox-sensitive and biophile elements from remineralized calcitic plankton. Mar. Pet. Geol. 2020, 120, 104535. [Google Scholar] [CrossRef]
- Forshaw, J.B.; Pattison, D.R. Major-element geochemistry of pelites. Geology 2023, 51, 39–43. [Google Scholar] [CrossRef]
- Cannaò, E.; Scambelluri, M.; Bebout, G.E.; Agostini, S.; Pettke, T.; Godard, M.; Crispini, L. Ophicarbonate evolution from seafloor to subduction and implications for deep-Earth C cycling. Chem. Geol. 2020, 546, 119626. [Google Scholar] [CrossRef]
- Stucki, A. High Grade Mesozoic Ophiolites of the Southern Steep Belt, Central Alps. Doctoral Dissertation, ETH Zurich, Zurich, Switzerland, 2001. [Google Scholar]
- Niu, Y. Bulk-rock major and trace element compositions of abyssal peridotites: Implications for mantle melting, melt extraction and post-melting processes beneath mid-ocean ridges. J. Petrol. 2004, 45, 2423–2458. [Google Scholar] [CrossRef]
- Groppo, C.T.; Castelli, D.C.C.; Rolfo, F. HT, Pre-Alpine relics in a spinel-bearing dolomite marble from the UHP Brossasco-Isasca Unit (Dora-Maira Massif, western Alps). Period. Di Mineral. 2007, 76, 155–168. [Google Scholar]
- Gebauer, D.H.P.S.; Schertl, H.P.; Brix, M.; Schreyer, W. 35 Ma old ultrahigh-pressure metamorphism and evidence for very rapid exhumation in the Dora Maira Massif, Western Alps. Lithos 1997, 41, 5–24. [Google Scholar] [CrossRef]
- Ferrando, S.; Frezzotti, M.L.; Petrelli, M.; Compagnoni, R. Metasomatism of continental crust during subduction: The UHP whiteschists from the Southern Dora-Maira Massif (Italian Western Alps). J. Metamorph. Geol. 2009, 27, 739–756. [Google Scholar] [CrossRef]
- Di Vincenzo, G.; Tonarini, S.; Lombardo, B.; Castelli, D.; Ottolini, L. Comparison of 40Ar–39Ar and Rb–Sr data on phengites from the UHP Brossasco–Isasca Unit (Dora Maira Massif, Italy): Implications for dating white mica. J. Petrol. 2006, 47, 1439–1465. [Google Scholar] [CrossRef]
- Gauthiez-Putallaz, L.; Rubatto, D.; Hermann, J. Dating prograde fluid pulses during subduction by in situ U–Pb and oxygen isotope analysis. Contrib. Mineral. Petrol. 2016, 171, 15. [Google Scholar] [CrossRef]
- Bonnet, G.; Chopin, C.; Locatelli, M.; Kylander-Clark, A.R.; Hacker, B.R. Protracted Subduction of the European Hyperextended Margin Revealed by Rutile U-Pb Geochronology Across the Dora-Maira Massif (Western Alps). Tectonics 2022, 41, e2021TC007170. [Google Scholar] [CrossRef]
- Rubatto, D.; Hermann, J. Exhumation as fast as subduction? Geology 2001, 29, 3–6. [Google Scholar] [CrossRef]
- Connolly, J.A. Computation of phase equilibria by linear programming: A tool for geodynamic modeling and its application to subduction zone decarbonation. Earth Planet. Sci. Lett. 2005, 236, 524–541. [Google Scholar] [CrossRef]
- Connolly, J.A.; Galvez, M.E. Electrolytic fluid speciation by Gibbs energy minimization and implications for subduction zone mass transfer. Earth Planet. Sci. Lett. 2018, 501, 90–102. [Google Scholar] [CrossRef]
- Holland TJ, B.; Powell, R. An improved and extended internally consistent thermodynamic dataset for phases of petrological interest, involving a new equation of state for solids. J. Metamorph. Geol. 2011, 29, 333–383. [Google Scholar] [CrossRef]
- Sverjensky, D.A.; Harrison, B.; Azzolini, D. Water in the deep Earth: The dielectric constant and the solubilities of quartz and corundum to 60 kb and 1200 °C. Geochim. Cosmochim. Acta 2014, 129, 125–145. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Sterner, S.M. Equations of state valid continuously from zero to extreme pressures for H2O and CO2. J. Chem. Phys. 1994, 101, 3111–3116. [Google Scholar] [CrossRef]
- de Santis, R.; Breedveld, G.J.F.; Prausnitz, J.M. Thermodynamic properties of aqueous gas mixtures at advanced pressures. Ind. Eng. Chem. Process Des. Dev. 1974, 13, 374–377. [Google Scholar] [CrossRef]
- Holland, T.; Powell, R. Thermodynamics of order-disorder in minerals: II. Symmetric formalism applied to solid solutions. Am. Mineral. 1996, 81, 1425–1437. [Google Scholar] [CrossRef]
- Padrón-Navarta, J.A.; Sánchez-Vizcaíno, V.L.; Hermann, J.; Connolly, J.A.; Garrido, C.J.; Gómez-Pugnaire, M.T.; Marchesi, C. Tschermak’s substitution in antigorite and consequences for phase relations and water liberation in high-grade serpentinites. Lithos 2013, 178, 186–196. [Google Scholar] [CrossRef]
- Evans, K.A.; Powell, R.; Holland, T.J.B. Internally consistent data for sulfur-bearing phases and application to the construction of pseudosections for mafic greenschist facies rocks in Na2O-CaO-K2O-FeO-MgO-Al2O3-SiO2-CO2-O-S-H2O. J. Metamorph. Geol. 2010, 28, 667–687. [Google Scholar] [CrossRef]
- Anovitz, L.M.; Essene, E.J. Phase equilibria in the system CaCO3-MgCO3-FeCO3. J. Petrol. 1987, 28, 389–415. [Google Scholar] [CrossRef]
- O’Neill, H.S. Quartz-fayalite-iron and quartz-fayalite-magnetite equilibria and the free energy of formation of fayalite (Fe2SiO4) and magnetite (Fe3O4). Am. Mineral. 1987, 72, 67–75. [Google Scholar]
- Evans, K.A. Redox decoupling and redox budgets: Conceptual tools for the study of earth systems. Geology 2006, 34, 489–492. [Google Scholar] [CrossRef]
- Tomkins, A.G.; Evans, K.A. Separate zones of sulfate and sulfide release from subducted mafic oceanic crust. Earth Planet. Sci. Lett. 2015, 428, 73–83. [Google Scholar] [CrossRef]
- Whitney, D.L.; Evans, B.W. Abbreviations for names of rock-forming minerals. Am. Mineral. 2010, 95, 185–187. [Google Scholar] [CrossRef]
- Frezzotti, M.L.; Ferrando, S. The chemical behavior of fluids released during deep subduction based on fluid inclusions. Am. Mineral. 2015, 100, 352–377. [Google Scholar] [CrossRef]
- Ferrando, S.; Petrelli, M.; Frezzotti, M.L. Gradual and selective trace-element enrichment in slab-released fluids at sub-arc depths. Sci. Rep. 2019, 9, 16393. [Google Scholar] [CrossRef]
- Connolly, J.A.D. Phase diagram methods for graphitic rocks and application to the system C-O-H-FeO-Eo-2-eO-2. Contrib. Mineral. Petrol. 1995, 119, 94–116. [Google Scholar] [CrossRef]
- Galvez, M.E.; Connolly, J.A.; Manning, C.E. Implications for metal and volatile cycles from the pH of subduction zone fluids. Nature 2016, 539, 420–424. [Google Scholar] [CrossRef] [PubMed]
- Sverjensky, D.A. Thermodynamic modelling of fluids from surficial to mantle conditions. J. Geol. Soc. 2019, 176, 348–374. [Google Scholar] [CrossRef]
- Galvez, M.E.; Manning, C.E.; Connolly, J.A.; Rumble, D. The solubility of rocks in metamorphic fluids: A model for rock-dominated conditions to upper mantle pressure and temperature. Earth Planet. Sci. Lett. 2015, 430, 486–498. [Google Scholar] [CrossRef]
- Galvez, M.E.; Jaccard, S.L. Redox capacity of rocks and sediments by high temperature chalcometric titration. Chem. Geol. 2021, 564, 120016. [Google Scholar] [CrossRef]
- Tumiati, S.; Malaspina, N. Redox processes and the role of carbon-bearing volatiles from the slab–mantle interface to the mantle wedge. J. Geol. Soc. 2019, 176, 388–397. [Google Scholar] [CrossRef]
- Ague, J.J.; Tassara, S.; Holycross, M.E.; Li, J.L.; Cottrell, E.; Schwarzenbach, E.M.; Fassoulas, C.; John, T. Slab-derived devolatilization fluids oxidized by subducted metasedimentary rocks. Nat. Geosci. 2022, 15, 320–326. [Google Scholar] [CrossRef]
- Menzel, M.D.; Garrido, C.J.; López Sánchez-Vizcaíno, V.; Hidas, K.; Marchesi, C. Subduction metamorphism of serpentinite-hosted carbonates beyond antigorite-serpentinite dehydration (Nevado-Filábride Complex, Spain). J. Metamorph. Geol. 2019, 37, 681–715. [Google Scholar] [CrossRef]
- Malusà, M.G.; Guillot, S.; Zhao, L.; Paul, A.; Solarino, S.; Dumont, T.; Schwartz, S.; Aubert, C.; Baccheschi, P.; Eva, E.; et al. The deep structure of the Alps based on the CIFALPS seismic experiment: A synthesis. Geochem. Geophys. Geosystems 2021, 22, e2020GC009466. [Google Scholar] [CrossRef]
- Duan, W.Y.; Li, X.P.; Schertl, H.P.; Willner, A.P. COHS fluids released by oceanic serpentinite in subduction zones: Implications for arc-magma oxidation. Earth Planet. Sci. Lett. 2022, 594, 117709. [Google Scholar] [CrossRef]
- Li, Y.B.; Chen, Y.; Su, B.; Zhang, Q.H.; Shi, K.H. Redox species and oxygen fugacity of slab-derived fluids: Implications for mantle oxidation and deep carbon-sulfur cycling. Front. Earth Sci. 2022, 10, 1–13. [Google Scholar] [CrossRef]
- Fischer, T.P.; Arellano, S.; Carn, S.; Aiuppa, A.; Galle, B.; Allard, P.; Lopez, T.; Shinohara, H.; Kelly, P.; Werner, C.; et al. The emissions of CO2 and other volatiles from the world’s subaerial volcanoes. Sci. Rep. 2019, 9, 18716. [Google Scholar] [CrossRef] [PubMed]
- Carn, S.A.; Fioletov, V.E.; McLinden, C.A.; Li, C.; Krotkov, N.A. A decade of global volcanic SO2 emissions measured from space. Sci. Rep. 2017, 7, 44095. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maffeis, A.; Ferrando, S.; Connolly, J.A.D.; Frezzotti, M.L.; Castelli, D. Fluid Redox Fingerprint of the CaCO3+Antigorite Dehydration Reaction in Subducted Metacarbonate Sediments. Geosciences 2023, 13, 130. https://doi.org/10.3390/geosciences13050130
Maffeis A, Ferrando S, Connolly JAD, Frezzotti ML, Castelli D. Fluid Redox Fingerprint of the CaCO3+Antigorite Dehydration Reaction in Subducted Metacarbonate Sediments. Geosciences. 2023; 13(5):130. https://doi.org/10.3390/geosciences13050130
Chicago/Turabian StyleMaffeis, Andrea, Simona Ferrando, James Alexander Denis Connolly, Maria Luce Frezzotti, and Daniele Castelli. 2023. "Fluid Redox Fingerprint of the CaCO3+Antigorite Dehydration Reaction in Subducted Metacarbonate Sediments" Geosciences 13, no. 5: 130. https://doi.org/10.3390/geosciences13050130
APA StyleMaffeis, A., Ferrando, S., Connolly, J. A. D., Frezzotti, M. L., & Castelli, D. (2023). Fluid Redox Fingerprint of the CaCO3+Antigorite Dehydration Reaction in Subducted Metacarbonate Sediments. Geosciences, 13(5), 130. https://doi.org/10.3390/geosciences13050130








