Long-Term Recurrence Pattern and Stress Transfer along the Kefalonia Transform Fault Zone (KTFZ), Greece: Implications in Seismic Hazard Evaluation
Abstract
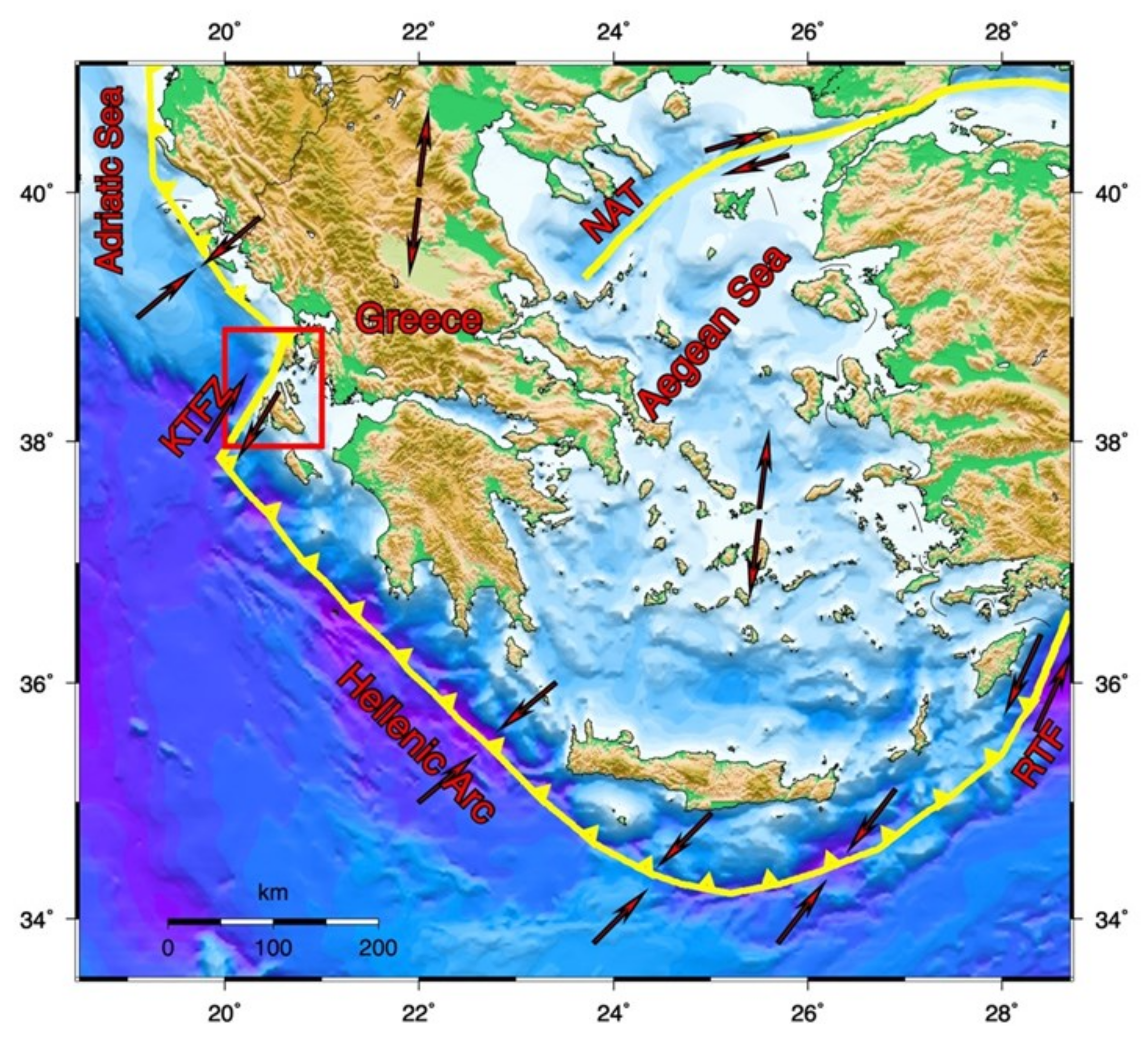
1. Introduction
2. Fault Segmentation Model of Kefalonia Transform Fault Zone and Slip Rate Constraints
| Fault Segment Name | Fault ID | Upper Left Edge of the Fault Segment | Strike (deg) | Dip (deg) | Rake (deg) | L (Km) | W (Km) | Slip Rate (mm/yr) | Stressing Rate (bar/yr) | Ref. | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Lat | Lon | ||||||||||
| Lefkada North | S1 | 38.69 | 20.56 | 18 | 60 | −175 | 16 | 10 | 10 ± 0.5 | 0.8459 | [27,37,46] |
| Lefkada South | S2 | 38.55 | 20.49 | 22 | 64 | 179 | 20 | 12 | 10 ± 0.5 | 0.6907 | [27,40] |
| Paliki North | S3 | 38.26 | 20.0 | 20 | 65 | 177 | 12 | 10 | 19.5 ± 0.5 | 1.9046 | [38,50] |
| Paliki South | S4 | 38.15 | 20.35 | 12 | 45 | 156 | 12 | 10 | 19.5 ± 0.5 | 1.9046 | [38,50] |
| Offshore Kefalonia | S5 | 37.91 | 20.08 | 40 | 45 | 168 | 33 | 20 | 19.5 ± 0.5 | 0.8518 | [31,50] |
| Argostoli | S6 | 38.08 | 20.55 | 299 | 30 | 90 | 15 | 15 | 4.9 ± 1.0 | 0.3495 | [47,53] |
| Ainos | S7 | 38.03 | 20.79 | 300 | 30 | 100 | 35 | 24 | 4.9 ± 1.0 | 0.1809 | [48,53] |
3. Large Earthquake Occurrence (Mw ≥ 6.0) along Kefalonia Transform Fault Zone
| Date | Time | Epicenter | Depth (km) | Mw | Mechanism (deg) | Ref. | |||
|---|---|---|---|---|---|---|---|---|---|
| Lat. (°N) | Lon. (°E) | Strike | Dip | Rake | |||||
| 22 April 1948 | 10:42:45 | 38.620 | 20.570 | 13.9 * | 6.5 | 22 * | 64 * | 179 * | [56] |
| 30 June 1948 | 12:21:13 | 38.800 | 20.600 | 11.0 * | 6.4 | 18 * | 60 * | −175 * | [56] |
| 9 August 1953 | 07:41:07 | 38.430 | 20.500 | 11.0 | 6.4 | 299 | 30 | 90 | [47,56] |
| 12 August 1953 | 19:23:52 | 38.100 | 20.350 | 11.0 | 7.2 | 300 | 30 | 100 | [56,60,63] |
| 17 September 1972 | 14:07:15 | 38.300 | 20.300 | 8.0 | 6.3 | 46 | 66 | −174 | [33,56] |
| 17 January 1983 | 12:41:30 | 38.100 | 20.200 | 9.0 | 7.0 | 39 | 45 | 175 | [56] |
| 23 March 1983 | 23:15:05 | 38.200 | 20.300 | 7.0 | 6.2 | 31 | 69 | 174 | [56] |
| 14 August 2003 | 05:14:55 | 38.815 | 20.606 | 11.0 | 6.2 | 18 | 60 | −175 | [56] |
| 26 January 2014 | 13:55:41 | 38.199 | 20.434 | 13.5 | 6.1 | 20 | 65 | 177 | [57] |
| 3 February 2014 | 03:08:44 | 38.269 | 20.410 | 9.4 | 6.0 | 12 | 45 | 156 | [57] |
| 17 November 2015 | 07:10:07 | 38.677 | 20.577 | 13.9 | 6.5 | 22 | 64 | 179 | [57] |
4. Methods
4.1. Mean Recurrence Time Estimation
4.2. Static Stress Change Calculation
4.3. Large Earthquake (Mw ≥ 6.0) Recurrence Models and Occurrence Probabilities
5. Application and Results
5.1. Mean Recurrence Time of Large Earthquake (Mw ≥ 6.0) Estimation
5.2. Stress Evolution of Kefalonia Transform Fault Zone
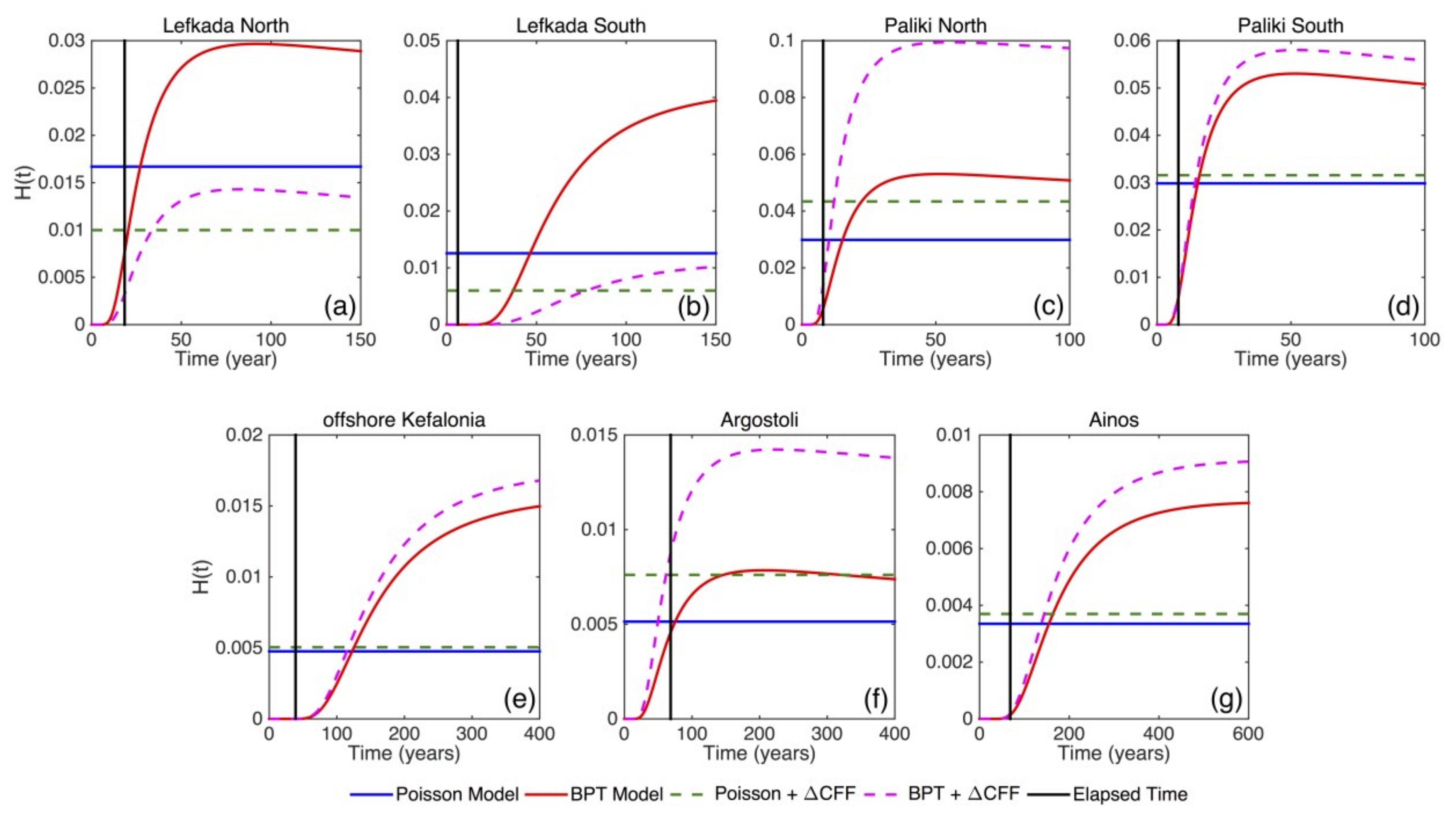
5.3. Recurrence Models and Occurrence Probabilities
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Field, E.H. Computing elastic-rebound-motivated earthquake probabilities in unsegments fault models: A new methodology supported by physics-based simulators. Bull. Seismol. Soc. Am. 2015, 105, 544–559. [Google Scholar] [CrossRef]
- Schwartz, D.P.; Coppersmith, K.J. Fault behavior and characteristic earthquakes: Examples from Wasatch and San Andreas fault zones. J. Geophys. Res. 1984, 89, 5681–5698. [Google Scholar] [CrossRef]
- Reid, H.F. The elastic-rebound theory of earthquakes. Univ. Calif. Pub. Bull. Dept. Geol. Sci. 1911, 6, 413–444. [Google Scholar]
- Kagan, Y.Y.; Jackson, D.D. Long-term earthquake clustering. Geophys. J. Int. 1991, 104, 117–133. [Google Scholar] [CrossRef]
- Dieterich, J.H. A constitutive law for rate of earthquake production and its application to earthquake clustering. J. Geophys. Res. 1994, 99, 2601–2618. [Google Scholar] [CrossRef]
- Scholz, C.H. The Mechanics of Earthquakes and Faulting, 3rd ed.; Cambridge University Press: Oxford, UK, 2019; ISBN 978-1-316-68147-3. [Google Scholar]
- Stein, R.S.; Barka, A.A.; Dieterich, J.H. Progressive failure on the North Anatolian Fault since 1939 by earthquake stress triggering. Geophys. J. Int. 1997, 128, 594–604. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Reasenberg, P.A.; Dieterich, J.H. Stress transfer by the 1995 Mw = 6.9 Kobe, Japan, shock: Effect on aftershocks and future earthquake probabilities. J. Geophys. Res. 1998, 103, 24543–24565. [Google Scholar] [CrossRef]
- Hardebeck, J.L. Stress triggering and earthquake probability estimates. J. Geophys. Res. 2004, 109, B04310. [Google Scholar] [CrossRef]
- Mangira, O.; Kourouklas, C.; Chorozoglou, D.; Iliopoulos, A.; Papadimitriou, E. Modeling the earthquake occurrence with time-dependent processes: A brief review. Acta Geophys. 2019, 67, 739–752. [Google Scholar] [CrossRef]
- Convertito, V.; Faenza, L. Earthquake Recurrence. In Encyclopedia of Earthquake Engineering; Beer, M., Kougioumtzoglou, I.A., Patelli, E., Siu-Kui Au, I., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–22. [Google Scholar]
- Ellsworth, W.L.; Matthews, M.V.; Nadeau, R.M.; Nishenko, S.P.; Reasenberg, P.A.; Simpson, R.W. A physically based earthquake recurrence model for estimation of long-term earthquake probabilities. US Geol. Surv. Open-File Rep. 1999, 99, 22. [Google Scholar]
- Sykes, L.R.; Menke, W. Repeat times of large earthquakes: Implications for earthquake mechanics and long-term prediction. Bull. Seismol. Soc. Am. 2006, 96, 1569–1596. [Google Scholar] [CrossRef]
- Biasi, G.P.; Langridge, R.M.; Berryman, K.R.; Clark, K.J.; Cochran, U.A. Maximum-likelihood recurrence parameters and conditional probability of a ground-rupturing earthquake on the southern Alpine fault, South Island, New Zealand. Bull. Seismol. Soc. Am. 2015, 105, 96–106. [Google Scholar] [CrossRef]
- Ogata, Y. Slip-size-dependent renewal process and Bayesian inferences for uncertainties. J. Geophys. Res. 2002, 107, 2268. [Google Scholar]
- Fitzenz, D.D. Conditional probability of what? Example of Nankai Interface in Japan. Bull. Seismol. Soc. Am. 2018, 108, 3169–3179. [Google Scholar] [CrossRef]
- Field, E.H.; Jackson, D.D.; Dolan, J.F. A mutually consistent seismic hazard source model for Southern California. Bull. Seismol. Soc. Am. 1999, 89, 559–578. [Google Scholar] [CrossRef]
- Console, R.; Falcone, G.; Karakostas, V.; Murru, M.; Papadimitriou, E.; Rhoades, D. Renewal models and coseismic stress transfer in the Corinth Gulf, Greece, fault system. J. Geophys. Res. 2013, 118, 3655–3673. [Google Scholar] [CrossRef]
- Akinci, A.; Vannoli, P.; Falcone, G.; Taroni, M.; Tiberti, M.M.; Murru, M.; Burrato, P.; Mariucci, M.T. When time and faults matter: Towards a time-dependent probabilistic SHA in Calabria, Italy. Bull. Earthquake Eng. 2016, 15, 2497–2524. [Google Scholar] [CrossRef]
- Valentini, A.; Visini, F.; Pace, B. Integrating faults and past earthquakes into a probabilistic seismic hazard model for peninsular Italy. Nat. Hazards Earth Syst. Sci. 2017, 17, 2017–2039. [Google Scholar] [CrossRef]
- Valentini, A.; Pace, B.; Boncio, P.; Visini, F.; Pagliaroli, A.; Pergalani, F. Definition of seismic input from fault-based PSHA: Remarks after the 2016 central Italy earthquake sequence. Tectonics 2019, 38, 595–620. [Google Scholar] [CrossRef]
- Parsons, T. Recalculated probability of M ≥ 7 earthquakes beneath the Sea of Marmara, Turkey. J. Geophys. Res. 2004, 109, B05304. [Google Scholar]
- Murru, M.; Akinci, A.; Falcone, G.; Pucci, S.; Console, R.; Parsons, T. M ≥ 7 earthquake rupture forecast and time dependent probability for the sea of Marmara region, Turkey. J. Geophys. Res. 2016, 121, 2679–2707. [Google Scholar] [CrossRef]
- Papazachos, B.C.; Comninakis, P.E. Geophysical and tectonic features of the Aegean arc. J. Geophys. Res. 1971, 76, 8517–8533. [Google Scholar] [CrossRef]
- McKenzie, D. Active tectonics of the Alpine—Himalayan belt: The Aegean Sea and surrounding regions. Geophys. J. R. Astron. Soc. 1978, 55, 217–254. [Google Scholar] [CrossRef]
- Papazachos, C.B.; Kiratzi, A.A. A detailed study of the active crustal deformation in the Aegean and surrounding area. Tectonophysics 1996, 253, 129–153. [Google Scholar] [CrossRef]
- Kahle, H.G.; Müller, M.V.; Geiger, A.; Danuser, G.; Mueller, S.; Veis, G.; Billiris, H.; Paradissis, D. The strain field in northwestern Greece and the Ionian Islands: Results inferred from GPS measurements. Tectonophysics 1995, 249, 41–52. [Google Scholar] [CrossRef]
- Cocard, M.; Kahle, H.G.; Peter, Y.; Geiger, A.; Veis, G.; Felekis, S.; Paradissis, D.; Billiris, H. New constraints on the rapid crustal motion of the Aegean region: Recent results inferred from GPS measurements (1993–1998) across the West Hellenic Arc, Greece. Earth Planet. Sci. Lett. 1999, 172, 39–47. [Google Scholar] [CrossRef]
- Papazachos, B.C.; Papazachou, C. The Earthquakes of Greece; Ziti Publications: Thessaloniki, Greece, 2003. [Google Scholar]
- Papadimitriou, E.E. Mode of strong earthquake recurrence in the Central Ionian Islands (Greece): Possible triggering due to Coulomb stress changes generated by the occurrence of previous strong shocks. Bull. Seismol. Soc. Am. 2002, 92, 3293–3308. [Google Scholar] [CrossRef]
- Scordilis, E.; Karakaisis, G.F.; Karakostas, V.; Panagiotopoulos, D.G.; Comninakis, P.E.; Papazachos, B.C. Evidence for Transform Faulting in the Ionian Sea: The Cephalonia Island earthquake sequence of 1983. Pure Appl. Geophys. 1985, 123, 388–397. [Google Scholar] [CrossRef]
- Kiratzi, A.; Langston, C. Moment tensor inversion of the 1983 January 17 Kefallinia event of Ionian Island (Greece). Geophys. J. Int. 1991, 105, 529–538. [Google Scholar] [CrossRef]
- Papadimitriou, E. Focal mechanisms along the convex side of the Hellenic Arc. Boll. Geof. Teor. Appl. 1993, 140, 401–426. [Google Scholar]
- Louvari, E.; Kiratzi, A.A.; Papazachos, B.C. The Cephalonia transform fault and its extension to western Lefkada Island (Greece). Tectonophysics 1999, 308, 223–236. [Google Scholar] [CrossRef]
- Papazachos, B.C.; Karakaisis, G.F.; Papadimitriou, E.E.; Papaioannou, C.A. The regional time and magnitude predictable model and its application to the Alpine-Himalayan belt. Tectonophysics 1997, 271, 295–323. [Google Scholar] [CrossRef]
- Hatzfeld, D.; Kassaras, I.; Panagiotopoulos, D.; Amorese, D.; Makropoulos, K.; Karakaisis, G.; Coutant, O. Microseismicity and strain pattern in the northwest Greece. Tectonics 1995, 14, 773–785. [Google Scholar] [CrossRef]
- Karakostas, V.; Papadimitriou, E.; Papazachos, C. Properties of the 2003 Lefkada, Ionian islands, Greece, Earthquake seismic sequence and seismicity triggering. Bull. Seismol. Soc. Am. 2004, 94, 1976–1981. [Google Scholar] [CrossRef]
- Karakostas, V.; Papadimitriou, E.; Mesimeri, M.; Gkarlaouni, C.H.; Paradisopoulou, P. The 2014 Kefalonia doublet (Mw6.1 and Mw6.0) central Ionian Islands, Greece: Seismotectonic implications along the Kefalonia transform fault zone. Acta Geophys. 2015, 63, 1–16. [Google Scholar] [CrossRef]
- Ganas, A.; Elias, P.; Bozionelos, G.; Papathanassiou, G.; Avallone, A.; Papastergios, A.; Valkaniotis, S.; Parcharidis, I.; Briole, P. Coseismic deformation, field observations and seismic fault of the 17 November 2015 M = 6.5, Lefkada Island, Greece earthquake. Tectonophysics 2016, 687, 210–222. [Google Scholar] [CrossRef]
- Papadimitriou, E.; Karakostas, V.; Mesimeri, M.; Chouliaras, G.; Kourouklas, C. The Mw6.5 17 November 2015 Lefkada (Greece) earthquake: Structural interpretation by means of the aftershock analysis. Pure Appl. Geophys. 2017, 174, 3869–3888. [Google Scholar] [CrossRef]
- Svigkas, N.; Atzori, S.; Kiratzi, A.; Tolomei, C.; Antonioli, A.; Papoutsis, I.; Salvi, S.; Kontoes, C. On the Segmentation of the Cephalonia–Lefkada Transform Fault Zone (Greece) from an InSAR Multi-Mode Dataset of the Lefkada 2015 Sequence. Remote Sens. 2019, 11, 1848. [Google Scholar] [CrossRef]
- Karakostas, V.; Papadimitriou, E.; Patias, P.; Georgiadis, C.H. Coastal deformation in Lefkada Island associated with strong earthquake occurrence. Boll. Geofis. Teor. Ed. Appl. 2019, 60, 1–16. [Google Scholar]
- Bonatis, P.; Akinci, A.; Karakostas, V.; Papadimitriou, E.; Kaviris, G. Near-Fault Broadband Ground Motion Simulation Applications at the Central Ionian Islands, Greece. Pure Appl. Geophys. 2021, 178, 3505–3527. [Google Scholar] [CrossRef]
- Schwartz, D.P. Past and future rupture lengths in seismic source characterization—The long and the short of it. Bull. Seismol. Soc. Am. 2018, 108, 2493–2520. [Google Scholar] [CrossRef]
- Visini, F.; Valentini, A.; Chartier, T.; Scotti, O.; Pace, B. Computational tools for relaxing the fault segmentation in probabilistic seismic hazard modeling in complex fault systems. Pure Appl. Geophys. 2020, 177, 1855–1877. [Google Scholar] [CrossRef]
- Karakostas, V.; Papadimitriou, E. Fault complexity associated with the 14 August 2003 Mw6.2 Lefkada, Greece, aftershock sequence. Acta Geophys. 2010, 58, 838–854. [Google Scholar] [CrossRef]
- Underhill, J.R. Late Cenozoic deformation of the Hellenide foreland, western Greece. Geol. Soc. Am. Bull. 1989, 101, 613–634. [Google Scholar] [CrossRef]
- Jenkins, D.A.L. Structural development of western Greece. Am. Assoc. Pet. Geol. Bull. 1972, 56, 128–149. [Google Scholar]
- Cushing, E.M.; Hollender, F.; Moiriat, D.; Guyonnet-Benaize, C.; Theodoulidis, N.; Pons-Branchu, E.; Sepulcre, S.; Bard, P.-Y.; Cornou, C.; Dechamp, A.; et al. Building a three dimensional model of the active Plio-Quaternary basin of Argostoli (Cephalonia Island, Greece): An integrated geophysical and geological approach. Eng. Geol. 2020, 265, 105441. [Google Scholar] [CrossRef]
- Briole, P.; Elias, P.; Parcharidis, I.; Bignami, C.; Benekos, G.; Samsonov, S.; Kyriakopoulos, C.; Stramondo, S.; Chamot-Rooke, N.; Drakatou, M.L.; et al. The seismic sequence of January–February 2014 at Cephalonia Island (Greece): Constrains from SAR interferometry and GPS. Geophys. J. Int. 2015, 203, 1528–1540. [Google Scholar] [CrossRef][Green Version]
- Briole, P.; Ganas, A.; Elias, P.; Dimitrov, D. The GPS velocity field of the Aegean. New observations, contribution of the earthquakes, crustal block models. Geophys. J. Int. 2021, 226, 468–492. [Google Scholar] [CrossRef]
- Jenny, S.; Goes, S.; Giardini, D.; Kahle, H.-G. Eartthquke recurrence parameters from seismic and geodetic strain rates in the Eastern Mediterranean. Geophys. J. Int. 2004, 157, 1331–1347. [Google Scholar] [CrossRef]
- D’Agostino, N.; Metois, M.; Koci, R.; Duni, L.; Kuka, N.; Ganas, A.; Georgiev, I.; Jouanne, F.; Kaludjerovic, N.; Kandic, R. Active crustal deformation and rotations in the southwestern Balkans from continuous GPS measurements. Earth Planet. Sci. Lett. 2020, 539, 116264. [Google Scholar] [CrossRef]
- Console, R.; Murru, M.; Falcone, G.; Catalli, F. Stress interaction effect on the occurrence probability of characteristic earthquakes in Central Appenines. J. Geophys. Res. 2008, 113, B08313. [Google Scholar]
- Goldsworthy, M.; Jackson, J.A. Active normal faulting evolution and interaction in Greece revealed by geomorphology and drainage patterns. J Geol. Soc. Lond. 2000, 157, 967–981. [Google Scholar] [CrossRef]
- Papazachos, B.C.; Comninakis, P.E.; Scordilis, E.M.; Karakaisis, G.F.; Papazachos, B.C. A Catalog of Earthquakes in the Mediterranean and Surrounding Area for the Period 1901–2010; Publ. Geophysics Laboratory, University of Thessaloniki: Thessaloniki, Greece, 2010. [Google Scholar]
- International Federation of Digital Seismograph Networks. Aristotle University of Thessaloniki Seismological Network; Aristotle University of Thessaloniki: Thessaloniki, Greece, 1981. [Google Scholar]
- Papazachos, B.C.; Kiratzi, A.A.; Karacostas, B.G. Towards a homogeneous moment-magnitude determination for earthquakes in Greece and surrounding area. Bull. Seism. Soc. Am. 1997, 87, 474–483. [Google Scholar] [CrossRef]
- Karakostas, V.G.; Papadimitriou, E.E.; Karamanos, C.K.; Kementzetzidou, D.A. Microseismicity and seismotectonic properties of the Lefkada-Kefalonia seismic zone. Bull. Geol. Soc. Greece 2010, 43, 2053–2063. [Google Scholar] [CrossRef]
- Ambraseys, N. Reassessment of earthquakes, 1900-1999, in the Eastern Mediterranean and Middle East. Geophys. J. Int. 2001, 145, 471–485. [Google Scholar] [CrossRef]
- Mavroulis, S.; Lekkas, E. Revisiting the most destructive earthquake sequence in the recent history of Greece: Enviromental effects induced by the 9, 11 and 12 August 1953 Ionian Sea earthquakes. Appl. Sci. 2021, 11, 8429. [Google Scholar] [CrossRef]
- Stiros, S.; Pirazzoli, P.A.; Laborel, J.; Laborel-Doguen, F. The 1953 earthquake in Cephalonia (Western Hellenic Arc): Coastal uplift and halotectonic faulting. Geophys. J. Int. 1994, 117, 834–849. [Google Scholar] [CrossRef]
- McKenzie, D.P. Active tectonics of the Mediterranean region. Geophys. J. R. Astron. Soc. 1972, 30, 109–185. [Google Scholar] [CrossRef]
- Hanks, T.C.; Kanamori, H. A moment magnitude scale. J. Geophys. Res. 1979, 84, 2348–2350. [Google Scholar] [CrossRef]
- Pace, B.; Visini, F.; Peruzza, L. FiSH: MATLAB Tools to Turn Fault Data into Seismic-Hazard Models. Seismol. Res. Lett. 2016, 87, 374–386. [Google Scholar] [CrossRef]
- Peruzza, L.; Pace, B.; Cavallini, F. Error propagation in timedependent probability of occurrence for characteristic earthquakes in Italy. J. Seismol. 2010, 14, 119–141. [Google Scholar] [CrossRef]
- Paradisopoulou, P.M.; Papadimitriou, E.E.; Karakostas, V.G.; Taymaz, T.; Kilias, A.; Yolsal, S. Seismic hazard evaluation in western Turkey as revealed by stress transfer and time-depenndent probability calculations. Pure Appl. Geophys. 2010, 167, 1013–1048. [Google Scholar] [CrossRef]
- Hobbs, T.E.; Cassidy, J.F.; Dosso, S.E.; Brillon, C. Coulomb stress changes following the 2012 Mw 7.8 Haida Gwaii, Canada, earthquake: Implications for seismic hazard. Bull. Seismol. Soc. Am. 2015, 105, 1253–1264. [Google Scholar] [CrossRef]
- Verdecchia, A.; Carena, S. One hundred and fifty years of Coulomb stress history along the California-Nevada border, USA. Tectonics 2015, 34, 213–231. [Google Scholar] [CrossRef]
- Rimando, J.M.; Peace, A.I.; Goda, K.; Sirous, N.; Rosset, P.; Chouinard, L. Coseismic Coulomb stress changes on intraplate faults in the western Quebec seismic zone following three major earthquakes in the past century. Can. J. Earth Sci. 2023. [Google Scholar] [CrossRef]
- Deng, J.; Sykes, L.R. Evolution of the stress field in southern California and triggering of moderate-size earthquakes: A 200-year perspective. J. Geophys. Res. 1997, 102, 39–47. [Google Scholar] [CrossRef]
- Harris, R.A. Introduction to special section: Stress triggers, stress shadows, and implications for seismic hazard. J. Geophys. Res. 1998, 103, 24347–24358. [Google Scholar] [CrossRef]
- Beeler, N.M.; Simpson, R.W.; Hickman, S.H.; Lockner, D.A. Pore fluid pressure, apparent friction, and Coulomb failure. J. Geophys. Res. 2000, 105, 25533–25542. [Google Scholar] [CrossRef]
- Rice, J.R.; Clearly, M.P. Some basic stress diffusion solutions for fluid-saturated elastic porous media with compressible constituents. Rev. Geophys. 1976, 14, 227–241. [Google Scholar] [CrossRef]
- Robinson, R.; McGinty, P.J. The enigma of the Arthur’s Pass, New Zealand earthquake. 2. The aftershock distribution and its relation to regional and induced stress field. J. Seismol. 2000, 105, 16139–16150. [Google Scholar] [CrossRef]
- Matthews, M.V.; Ellsworth, W.L.; Reasenberg, P.A. A Brownian model for recurrent earthquakes. Bull. Seismol. Soc. Am. 2002, 92, 2233–2250. [Google Scholar] [CrossRef]
- King, G.C.P.; Oppenheimer, D.; Amelung, F. Block versus continuum deformation in the western United States. Earth. Planet. Sci. Lett. 1994, 128, 55–64. [Google Scholar] [CrossRef]
- Lin, J.; Stein, R.S. Stress triggering in thrust and subduction earthquakes and stress interaction between the southern San Andreas and nearby thrust and strike-slip faults. J. Geophys. Res. 2004, 109, B02303. [Google Scholar] [CrossRef]
- Ishibe, T.; Satake, K.; Sakai, S.; Shimazaki, K.; Tsuruoka, H.; Yokota, Y.; Nakagawa, S.; Hirata, N. Correlation between Coulomb stress imparted by the 2011 Tohoku-Oki earthquake and seismicity rate change in Kanto, Japan. Geophys. J. Int. 2015, 201, 112–134. [Google Scholar] [CrossRef]
- Erickson, L. User’s Manual for DIS3D: A Three-Dimensional Dislocation Program with Applications to Faulting in the Earth. Master’s Thesis, Stanford University, Stanford, CA, USA, 1986; p. 167. [Google Scholar]
- Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic mapping tools: Improved version released. EOS Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef]
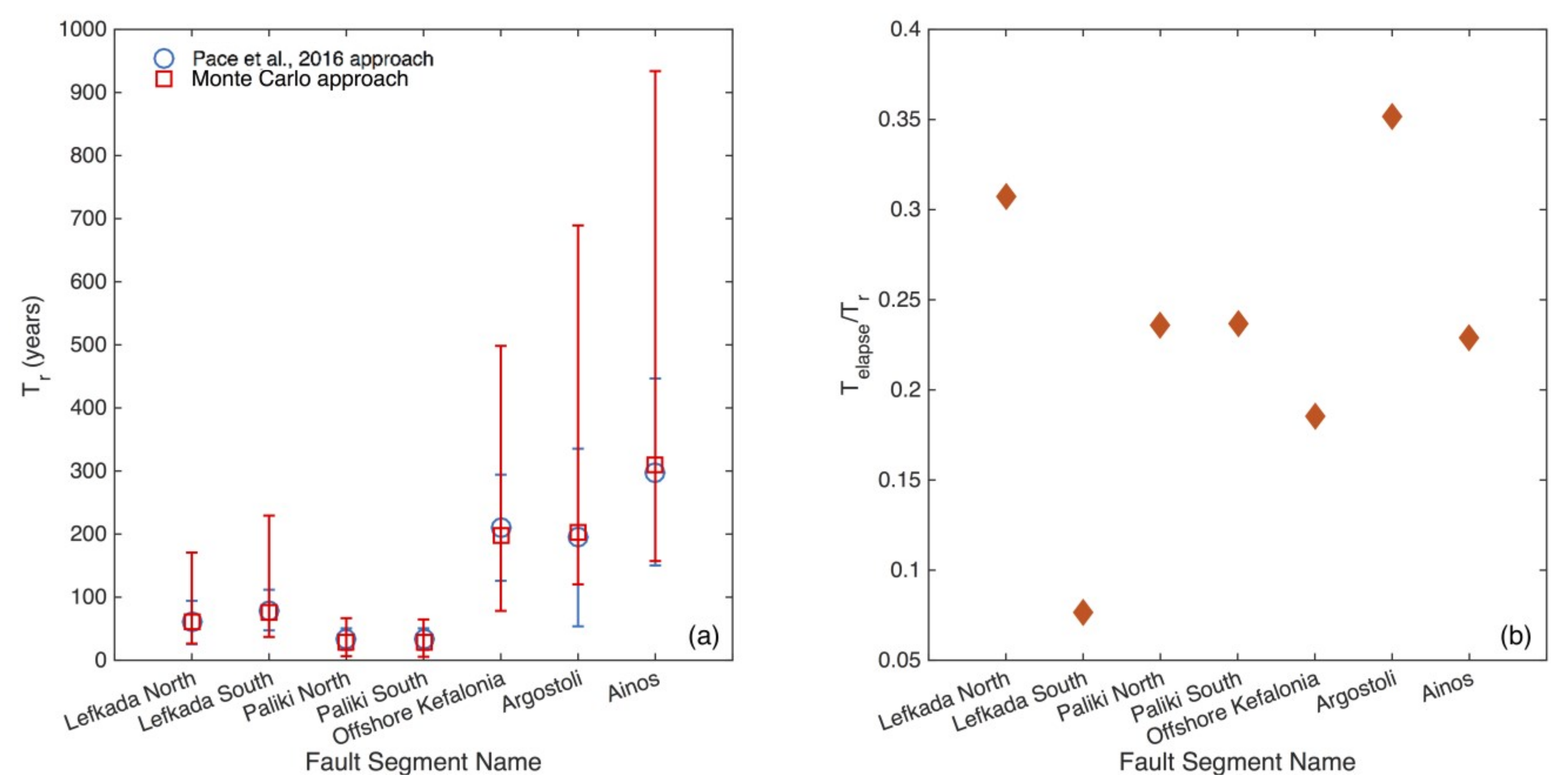
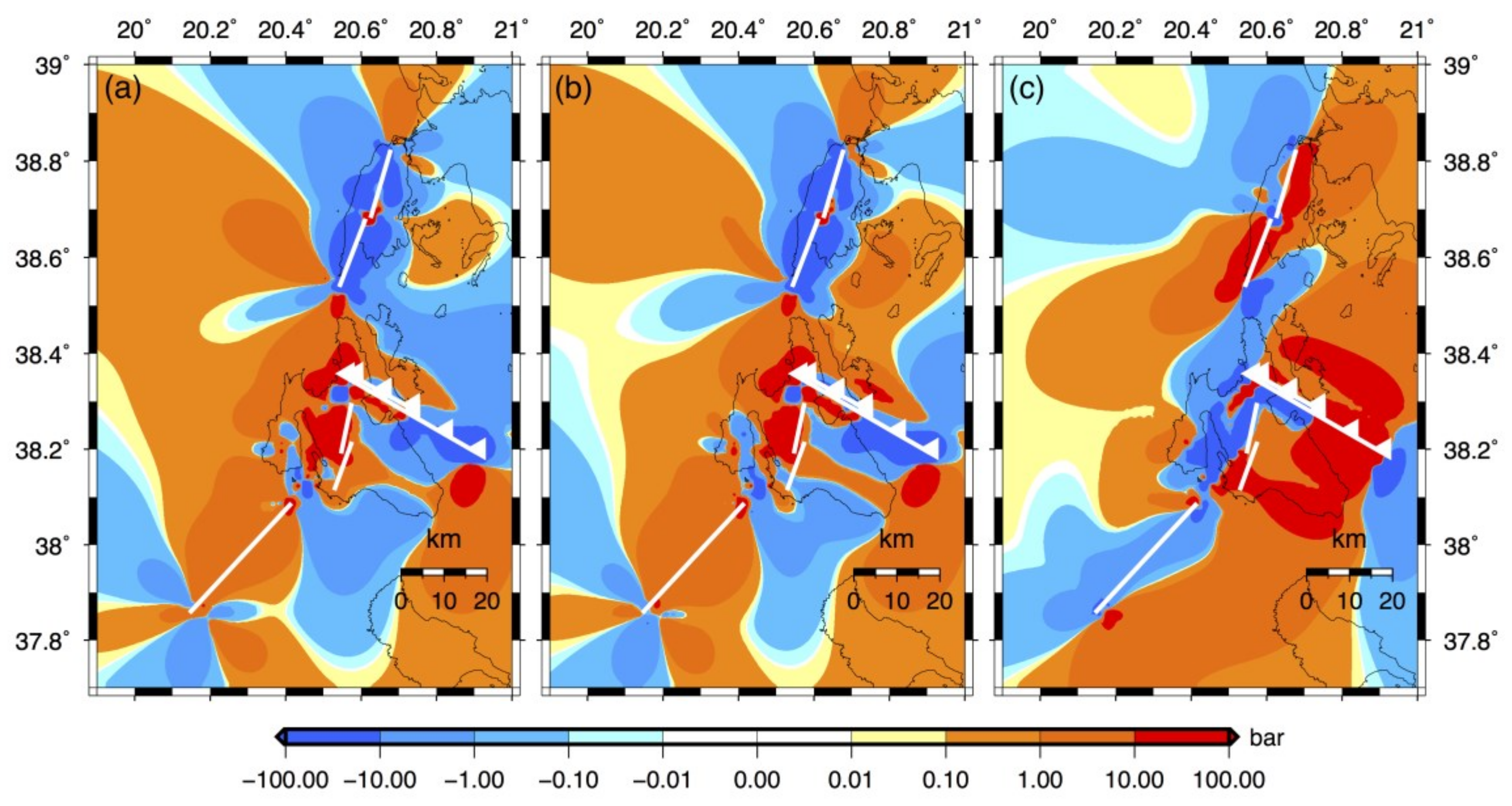
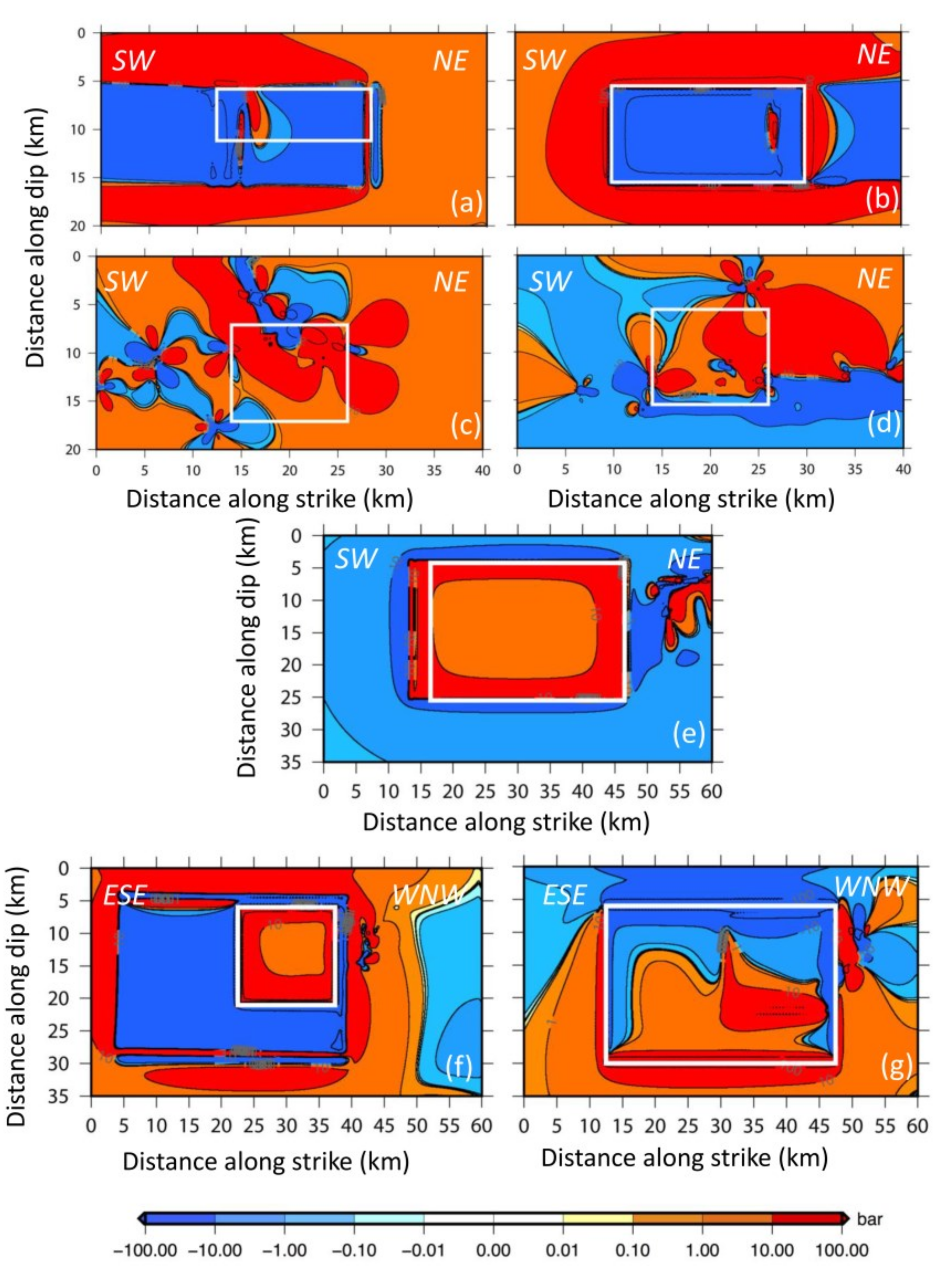
| Fault Segment Name | Mmax_obs | Elapsed Time, Te (Years) | Monte Carlo Method | [65] Method | |||
|---|---|---|---|---|---|---|---|
| Tr (Years) | 67% C. I. (Years) | Tr (Years) | σ (Years) | Cv | |||
| Lefkada North | 6.2 ± 0.2 | 19.4 | 60.8 | [34.4, 109.9] | 59.9 | 34.3 | 0.6 |
| Lefkada South | 6.5 ± 0.2 | 7.1 | 76.1 | [39.1, 153.2] | 79.6 | 32.3 | 0.4 |
| Paliki North | 6.0 ± 0.2 | 8.9 | 29.4 | [23.0, 37.3] | 33.5 | 17.1 | 0.6 |
| Paliki South | 6.1 ± 0.2 | 8.9 | 28.3 | [22.7, 36.4] | 33.5 | 16.9 | 0.6 |
| Offshore Kefalonia | 7.0 ± 0.2 | 39.9 | 197.2 | [118.9, 301.1] | 210.1 | 84.1 | 0.4 |
| Argostoli | 6.4 ± 0.3 | 69.4 | 201.5 | [81.2, 487.8] | 194.6 | 94.2 | 0.7 |
| Ainos | 7.2 ± 0.3 | 69.4 | 309.7 | [152.4, 624.2] | 298.5 | 148.2 | 0.5 |
| Fault Segment Name | ΔCFF (Bar) | Time Shift, Δt (Years) | ||
|---|---|---|---|---|
| Min | Aver | Max | Aver | |
| Lefkada North | −637.02 | −34.03 | 124.88 | −40.23 |
| Lefkada South | −641.06 | −60.18 | 490.64 | −87.14 |
| Paliki North | −355.29 | 19.91 | 669.70 | 10.45 |
| Paliki South | −8.44 | 3.48 | 28.62 | 1.83 |
| Offshore Kefalonia | −44.69 | 10.17 | 53.48 | 11.95 |
| Argostoli | −656.51 | 22.07 | 715.62 | 63.17 |
| Ainos | −615.85 | 5.05 | 535.77 | 27.96 |
| Fault Segment Name | Poisson | Poisson + ΔCFF | BPT | BPT + ΔCFF | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P10 | P20 | P30 | P10 | P20 | P30 | P10 | P20 | P30 | P10 | P20 | P30 | |
| Lefkada North | 0.15 | 0.27 | 0.38 | 0.10 | 0.18 | 0.26 | 0.12 | 0.29 | 0.44 | 0.02 | 0.08 | 0.16 |
| Lefkada South | 0.12 | 0.22 | 0.32 | 0.06 | 0.11 | 0.16 | 10 × 10−6 | 3 × 10−³ | 0.03 | 2 × 10−12 | 2 × 10−7 | 3 × 10−5 |
| Paliki North | 0.26 | 0.45 | 0.59 | 0.40 | 0.62 | 0.70 | 0.19 | 0.47 | 0.57 | 0.50 | 0.78 | 0.89 |
| Paliki South | 0.26 | 0.45 | 0.59 | 0.27 | 0.46 | 0.60 | 0.19 | 0.47 | 0.57 | 0.24 | 0.52 | 0.72 |
| Offshore Kefalonia | 0.05 | 0.09 | 0.13 | 0.05 | 0.09 | 0.14 | 6 × 10−5 | 5 × 10−4 | 3 × 10−3 | 2 × 10−4 | 10 × 10−4 | 6 × 10−3 |
| Argostoli | 0.05 | 0.09 | 0.14 | 0.06 | 0.12 | 0.17 | 0.04 | 0.09 | 0.14 | 0.07 | 0.14 | 0.21 |
| Ainos | 0.03 | 0.06 | 0.09 | 0.04 | 0.07 | 0.10 | 2 × 10−3 | 6 × 10−3 | 0.01 | 3 × 10−3 | 9 × 10−3 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kourouklas, C.; Papadimitriou, E.; Karakostas, V. Long-Term Recurrence Pattern and Stress Transfer along the Kefalonia Transform Fault Zone (KTFZ), Greece: Implications in Seismic Hazard Evaluation. Geosciences 2023, 13, 295. https://doi.org/10.3390/geosciences13100295
Kourouklas C, Papadimitriou E, Karakostas V. Long-Term Recurrence Pattern and Stress Transfer along the Kefalonia Transform Fault Zone (KTFZ), Greece: Implications in Seismic Hazard Evaluation. Geosciences. 2023; 13(10):295. https://doi.org/10.3390/geosciences13100295
Chicago/Turabian StyleKourouklas, Christos, Eleftheria Papadimitriou, and Vasileios Karakostas. 2023. "Long-Term Recurrence Pattern and Stress Transfer along the Kefalonia Transform Fault Zone (KTFZ), Greece: Implications in Seismic Hazard Evaluation" Geosciences 13, no. 10: 295. https://doi.org/10.3390/geosciences13100295
APA StyleKourouklas, C., Papadimitriou, E., & Karakostas, V. (2023). Long-Term Recurrence Pattern and Stress Transfer along the Kefalonia Transform Fault Zone (KTFZ), Greece: Implications in Seismic Hazard Evaluation. Geosciences, 13(10), 295. https://doi.org/10.3390/geosciences13100295










