A 20-Year Journey of Forecasting with the “Every Earthquake a Precursor According to Scale” Model
Abstract
1. Introduction
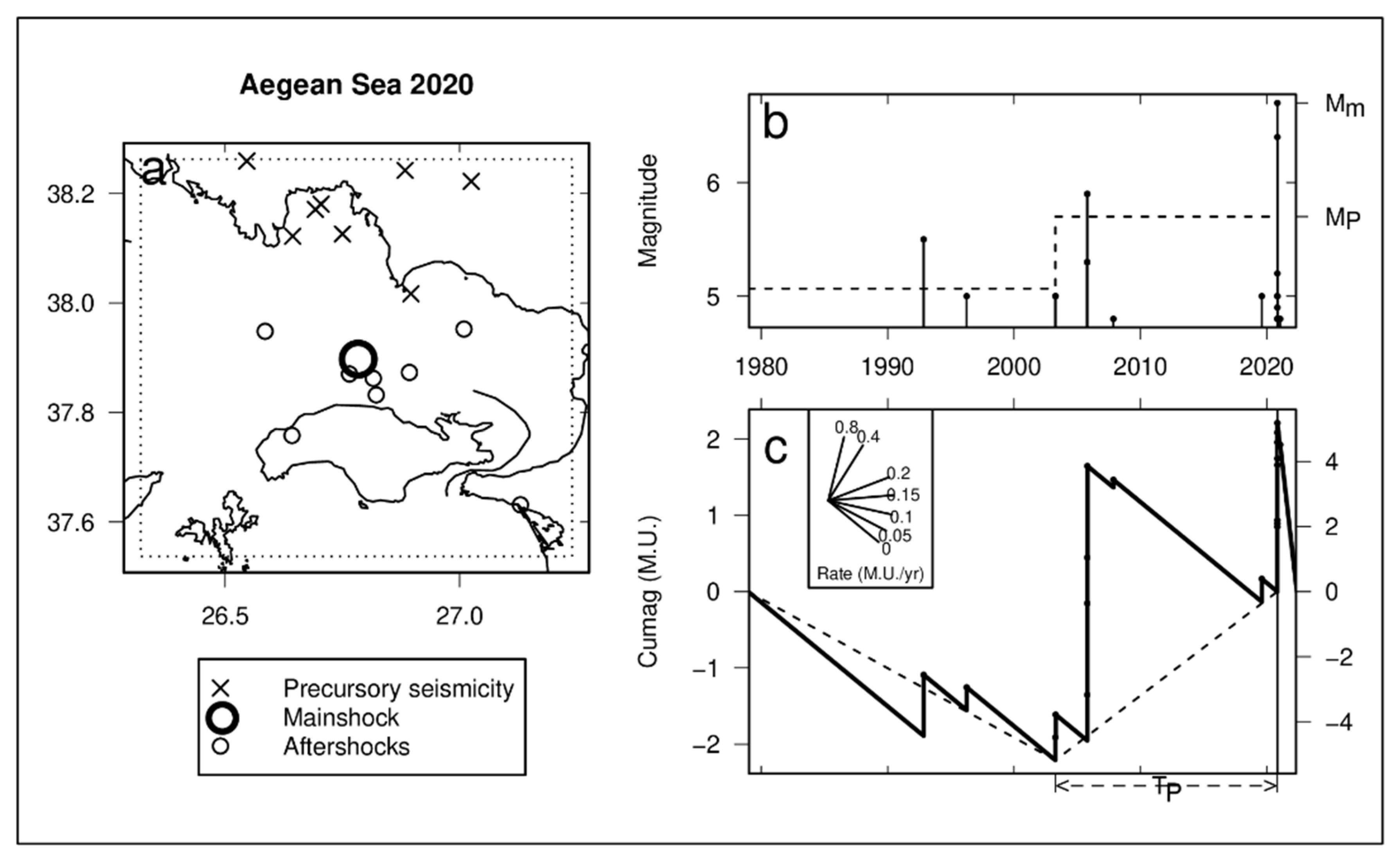
2. Empirical Foundations—The Ψ-Phenomenon
3. Mathematical Description of the EEPAS Model
3.1. Initial Defining Equations
3.2. Fitting and Testing Considerations
4. Combinations and Extensions to Accommodate Aftershocks
4.1. STEP-EEPAS Mixture
4.2. EEPAS with Aftershocks Model
4.3. Janus Model: EEPAS-ETAS Mixture
4.4. Hybrid Forecasting in New Zealand
5. Compensation for Incompleteness of Precursory Earthquakes
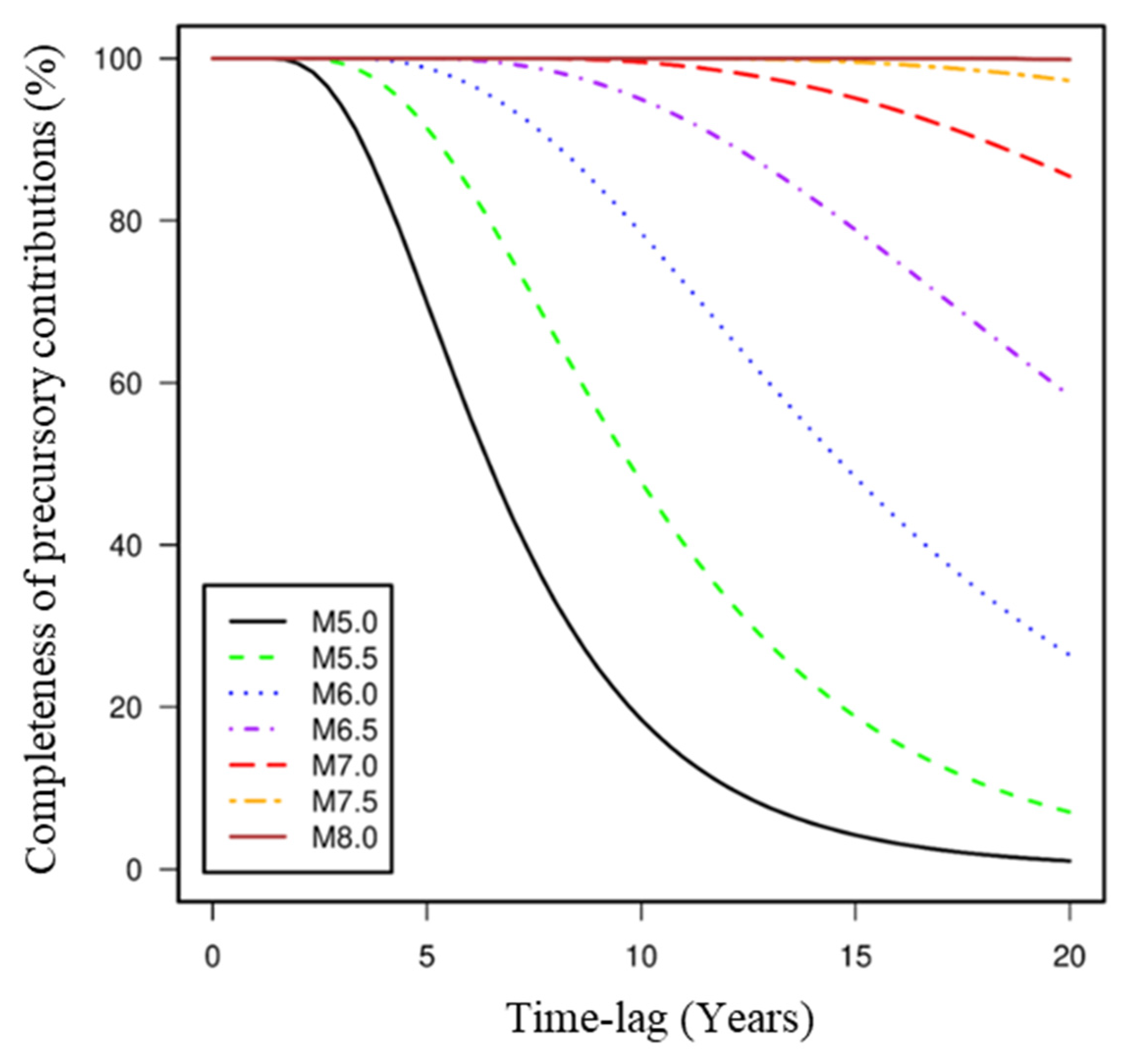
5.1. Magnitude Completeness of Precursory Earthquake Contributions
5.2. Temporal Completeness of Precursory Earthquake Contributions
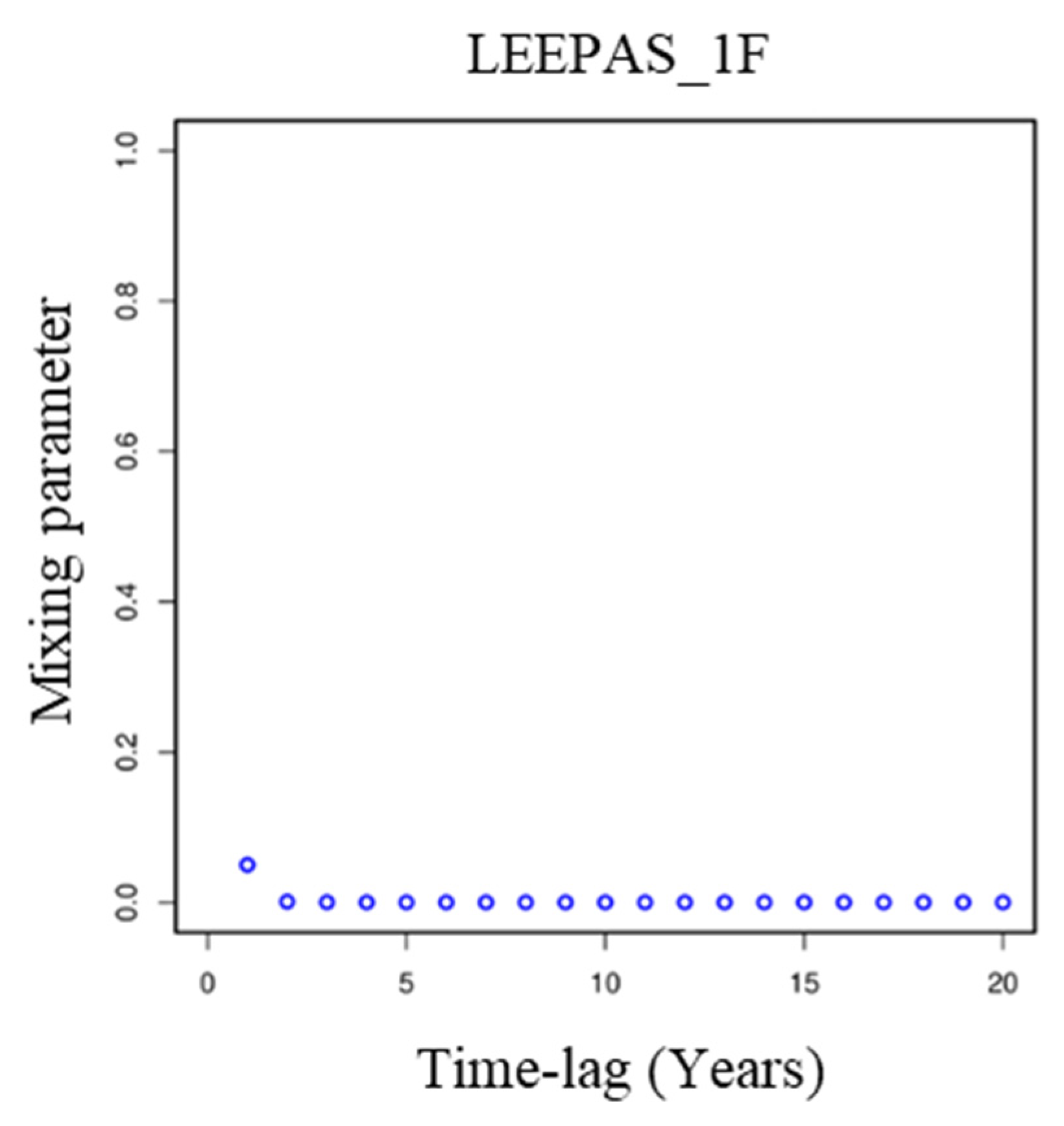
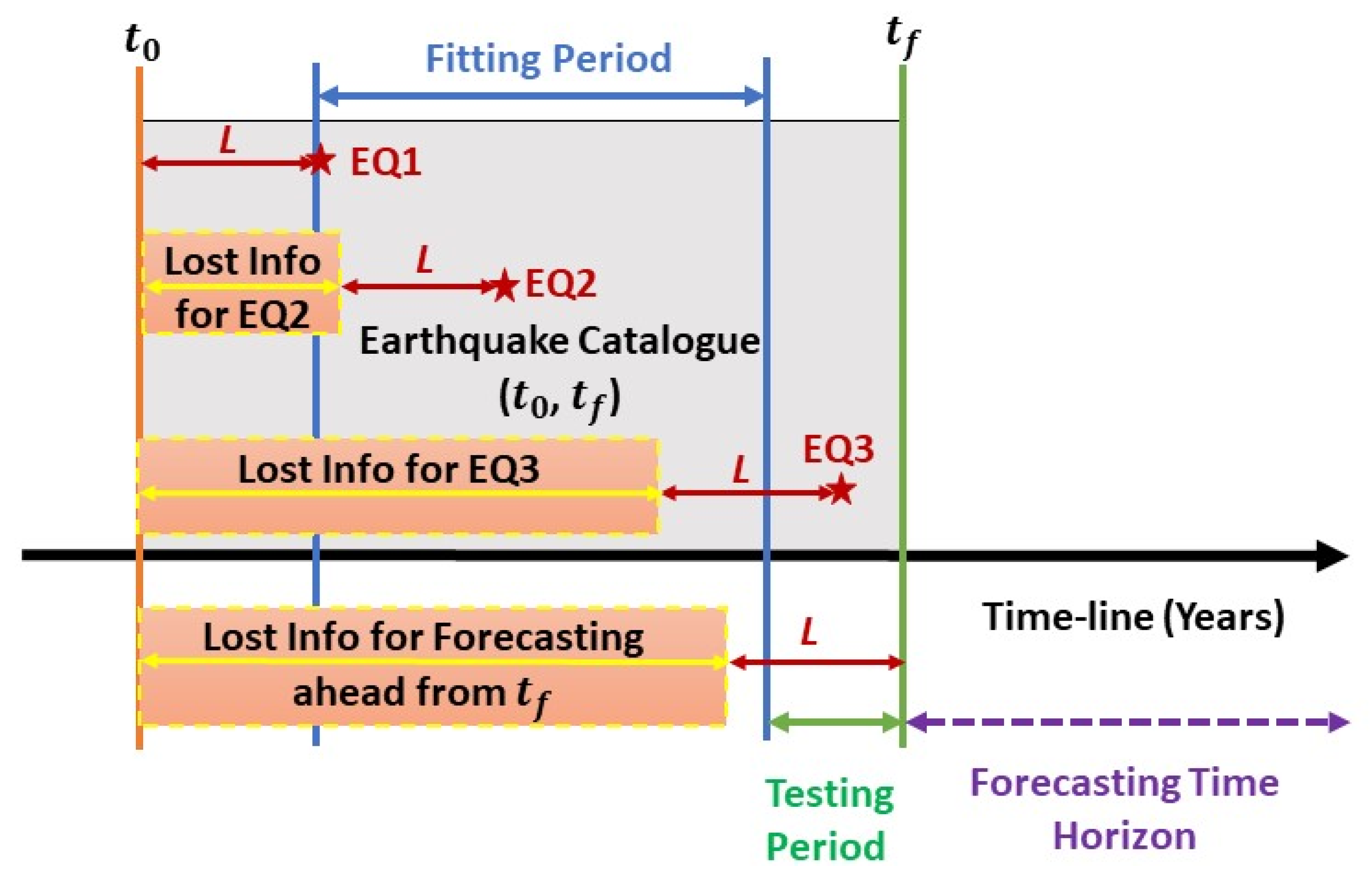
5.3. Compensation for Time-Lag
5.4. Fixing the Lead Time
5.5. Compensating for the Lead Time
6. Earthquake-Rate Dependence and the Space-Time Trade-Off
6.1. An Earthquake-Rate Dependent Version of EEPAS
6.2. Rate Dependence of Time-Distribution in Synthetic Catalogues
6.3. Space-Time Trade-Off
7. Challenges in EEPAS Forecasting: A Journey from What We Know to What We Don’t
7.1. Understanding the Physics behind the Ψ-Phenomenon
7.2. Incorporating Dependence on the Long-Term Earthquake Rate
7.3. A Three-Dimensional Version of EEPAS?
7.4. Target-Earthquake Oriented Compensation for Missing Precursors
7.5. Accommodating Variable Incompleteness of the Earthquake Catalogue
7.6. Optimal Use of the Space-Time Trade-Off
7.7. Development of a Global Forecasting Model
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vere-Jones, D.; Ben-Zion, Y.; Zúñiga, R. Statistical Seismology. Pure Appl. Geophys. 2005, 162, 1023–1026. [Google Scholar] [CrossRef]
- Vere-Jones, D. Foundations of Statistical Seismology. Pure Appl. Geophys. 2010, 167, 645–653. [Google Scholar] [CrossRef]
- Omori, F. On the aftershocks of earthquakes. J. Coll. Sci. Imp. Univ. Tokyo 1885, 7, 111–200. [Google Scholar]
- Utsu, T.; Ogata, Y. The centenary of the Omori formula for a decay law of aftershock activity. J. Phys. Earth 1995, 43, 1–33. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Lindman, M.; Lund, B.; Roberts, R.; Jonsdottir, K. Physics of the Omori law: Inferences from interevent time distributions and pore pressure diffusion modeling. Tectonophysics 2006, 424, 209–222. [Google Scholar] [CrossRef]
- Hainzl, S.; Marsan, D. Dependence of the Omori-Utsu law parameters on main shock magnitude: Observations and modeling. J. Geophys. Res. Solid Earth 2008, 113, B10309. [Google Scholar] [CrossRef]
- Guglielmi, A.V. Interpretation of the Omori law. Izv. Phys. Solid Earth 2016, 52, 785–786. [Google Scholar] [CrossRef][Green Version]
- Faraoni, V. Lagrangian formulation of Omori’s law and analogy with the cosmic Big Rip. Eur. Phys. J. C 2020, 80, 445. [Google Scholar] [CrossRef]
- Mogi, K. Magnitude-Frequency Relation for Elastic Shocks Accompanying Fractures of Various Materials and Some Related problems in Earthquakes (2nd Paper). Bull. Earthq. Res. Inst. Univ. Tokyo 1963, 40, 831–853. [Google Scholar]
- Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in earthquake-size distribution across different stress regimes. Nature 2005, 437, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Amitrano, D. Variability in the power-law distributions of rupture events. Eur. Phys. J. Spec. Top. 2012, 205, 199–215. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Christopoulos, S.-R.G.; Lazaridou-Varotsos, M.S. Identifying the occurrence time of an impending mainshock: A very recent case. Earthq. Sci. 2015, 28, 215–222. [Google Scholar] [CrossRef]
- Evison, F.; Rhoades, D. Precursory scale increase and long-term seismogenesis in California and Northern Mexico. Ann. Geophys. 2002, 45, 479–495. [Google Scholar] [CrossRef]
- Evison, F.F.; Rhoades, D.A. Demarcation and Scaling of Long-term Seismogenesis. Pure Appl. Geophys. 2004, 161, 21–45. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Evison, F.F. Long-range earthquake forecasting with every earthquake a precursor according to scale. Pure Appl. Geophys. 2004, 161, 47–72. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Evison, F.F. Test of the EEPAS Forecasting Model on the Japan earthquake catalogue. Pure Appl. Geophys. 2005, 162, 1271–1290. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Evison, F.F. The EEPAS forecasting model and the probability of moderate-to-large earthquakes in central Japan. Tectonophysics 2006, 417, 119–130. [Google Scholar] [CrossRef]
- Console, R.; Rhoades, D.A.; Murru, M.; Evison, F.F.; Papadimitriou, E.E.; Karakostas, V.G. Comparative performance of time-invariant, long-range and short-range forecasting models on the earthquake catalogue of Greece. J. Geophys. Res. Solid Earth 2006, 111, B09304. [Google Scholar] [CrossRef]
- Rhoades, D.A. Application of the EEPAS model to forecasting earthquakes of moderate magnitude in southern California. Seismol. Res. Lett. 2007, 78, 110–115. [Google Scholar] [CrossRef]
- Rhoades, D.A. Application of a long-range forecasting model to earthquakes in the Japan mainland testing region. Earth Planets Space 2011, 63, 197–206. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Somerville, P.G.; Somerville, F.; de Oliveira, D.; Thio, H.K. Effect of tectonic setting on the fit and performance of a long-range earthquake forecasting model. Res. Geophys. 2012, 2, 13–23. [Google Scholar] [CrossRef]
- Zechar, J.D.; Schorlemmer, D.; Liukis, M.; Yu, J.; Euchner, F.; Maechling, P.J.; Jordan, T.H. The Collaboratory for the Study of Earthquake Predictability perspective on computational earthquake science. Concurr. Comput. Pract. Exp. 2010, 22, 1836–1847. [Google Scholar] [CrossRef]
- Gerstenberger, M.C.; Rhoades, D.A. New Zealand earthquake forecast testing centre. In Seismogenesis and Earthquake Forecasting: The Frank Evison Volume II; Springer: Berlin/Heidelberg, Germany, 2010; pp. 23–38. [Google Scholar]
- Schneider, M.; Clements, R.; Rhoades, D.; Schorlemmer, D. Likelihood- and residual-based evaluation of medium-term earthquake forecast models for California. Geophys. J. Int. 2014, 198, 1307–1318. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Christophersen, A.; Gerstenberger, M.C.; Liukis, M.; Silva, F.; Marzocchi, W.; Werner, M.J.; Jordan, T.H. Highlights from the first ten years of the New Zealand Earthquake Forecast Testing Center. Seismol. Res. Lett. 2018, 89, 1229–1237. [Google Scholar] [CrossRef]
- Gerstenberger, M.; Rhoades, D.; Litchfield, N.; Van Dissen, R.; Abbot, E.; Goded, T.; Christophersen, A.; Bannister, S.; Barrell, D.; Bruce, Z.; et al. The Kaikoura Seismic Hazard Model. N. Z. J. Geol. Geophys. 2022. in revision. [Google Scholar]
- Gerstenberger, M.; McVerry, G.; Rhoades, D.; Stirling, M. Seismic Hazard Modeling for the Recovery of Christchurch. Earthq. Spectra 2014, 30, 17–29. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Liukis, M.; Christophersen, A.; Gerstenberger, M.C. Retrospective tests of hybrid operational earthquake forecasting models for Canterbury. Geophys. J. Int. 2015, 204, 440–456. [Google Scholar] [CrossRef]
- Evison, F.F. The precursory earthquake swarm. Phys. Earth Planet. Inter. 1977, 15, 19–23. [Google Scholar] [CrossRef]
- Evison, F.F. Precursory seismic sequences in New Zealand. N. Z. J. Geol. Geophys. 1977, 20, 129–141. [Google Scholar] [CrossRef]
- Evison, F.F. Fluctuations of seismicity before major earthquakes. Nature 1977, 266, 710–712. [Google Scholar] [CrossRef]
- Evison, F. Multiple earthquake events at moderate-to-large magnitudes in Japan. J. Phys. Earth 1981, 29, 327–339. [Google Scholar] [CrossRef]
- Evison, F. Generalised Precursory Swarm Hypothesis. J. Phys. Earth 1982, 30, 155–170. [Google Scholar] [CrossRef]
- Rikitake, T. Earthquake precursors. Bull. Seismol. Soc. Am. 1975, 65, 1133–1162. [Google Scholar] [CrossRef]
- Rikitake, T. Classification of earthquake precursors. Tectonophysics 1979, 54, 293–309. [Google Scholar] [CrossRef]
- Rikitake, T. Earthquake Forecasting and Warning; Dordrecht Boston: D. Reidel; Hingham, Mass.: Sold and distributed in the U.S.A. and Canada by Kluwer Boston; Center for Academic Publications Japan: Tokyo, Japan, 1982. [Google Scholar]
- Rhoades, D.A.; Evison, F.F. Long-range earthquake forecasting based on a single predictor. Geophys. J. Int. 1979, 59, 43–56. [Google Scholar] [CrossRef]
- Evison, F.F.; Rhoades, D.A. The precursory earthquake swarm in New Zealand: Hypothesis tests. N. Z. J. Geol. Geophys. 1993, 36, 51–60. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Evison, F.F. Long-range earthquake forecasting based on a single predictor with clustering. Geophys. J. Int. 1993, 113, 371–381. [Google Scholar] [CrossRef]
- Evison, F.F.; Rhoades, D.A. The precursory earthquake swarm in New Zealand: Hypothesis tests. N. Z. J. Geol. Geophys. 1997, 40, 537–547. [Google Scholar] [CrossRef]
- Evison, F.F.; Rhoades, D.A. Long-term seismogenic process for major earthquakes in subduction zones. Phys. Earth Planet. Inter. 1998, 108, 185–199. [Google Scholar] [CrossRef]
- Evison, F.F.; Rhoades, D.A. The precursory earthquake swarm and the inferred precursory quarm. N. Z. J. Geol. Geophys. 1999, 42, 229–236. [Google Scholar] [CrossRef][Green Version]
- Evison, F.F.; Rhoades, D.A. The precursory earthquake swarm in Japan: Hypothesis test. Earth Planets Space 1999, 51, 1267–1277. [Google Scholar] [CrossRef]
- Evison, F.; Rhoades, D. The precursory earthquake swarm in Greece. Ann. Geophys. 2000, 43, 991–1009. [Google Scholar] [CrossRef]
- Evison, F.; Rhoades, D. Model of long-term seismogenesis. Ann. Geophys. 2001, 44, 81–93. [Google Scholar] [CrossRef]
- Ogata, Y. Statistical model for standard seismicity and detection of anomalies by residual analysis. Tectonophysics 1989, 169, 159–174. [Google Scholar] [CrossRef]
- Ogata, Y. Space-Time Point-Process Models for Earthquake Occurrences. Ann. Inst. Stat. Math. 1998, 50, 379–402. [Google Scholar] [CrossRef]
- Evison, F.; Rhoades, D. Multiple-mainshock events and long-term seismogenesis in Italy and New Zealand. N. Z. J. Geol. Geophys. 2005, 48, 523–536. [Google Scholar] [CrossRef]
- Papadimitriou, E.E.; Evison, F.F.; Rhoades, D.A.; Karakostas, V.G.; Console, R.; Murru, M. Long-term seismogenesis in Greece: Comparison of the evolving stress field and precursory scale increase approaches. J. Geophys. Res. Solid Earth 2006, 111, B05318. [Google Scholar] [CrossRef]
- Christophersen, A.; Rhoades, D.A.; Colella, H.V. Precursory seismicity in regions of low strain rate: Insights from a physics-based earthquake simulator. Geophys. J. Int. 2017, 209, 1513–1525. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Rastin, S.J.; Christophersen, A. The effect of catalogue lead time on medium-term earthquake forecasting with application to New Zealand data. Entropy 2020, 22, 1264. [Google Scholar] [CrossRef]
- Rastin, S.J.; Rhoades, D.A.; Christophersen, A. Space–time trade-off of precursory seismicity in New Zealand and California revealed by a medium-term earthquake forecasting model. Appl. Sci. 2021, 11, 10215. [Google Scholar] [CrossRef]
- Jackson, D.D.; Kagan, Y.Y. Testable Earthquake Forecasts for 1999. Seismol. Res. Lett. 1999, 70, 393–403. [Google Scholar] [CrossRef]
- Daley, D.J.; Vere-Jones, D. An Introduction to the Theory of Point Processes, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2008; Volume II. [Google Scholar]
- Ogata, Y.; Zhuang, J. Space–time ETAS models and an improved extension. Tectonophysics 2006, 413, 13–23. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Christophersen, A. Time-varying probabilities of earthquake occurrence in central New Zealand based on the EEPAS model compensated for time-lag. Geophys. J. Int. 2019, 219, 417–429. [Google Scholar] [CrossRef]
- Rhoades, D.A. Mixture Models for Improved Earthquake Forecasting with Short-to-Medium Time Horizons. Bull. Seismol. Soc. Am. 2013, 103, 2203–2215. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Schorlemmer, D.; Gerstenberger, M.C.; Christophersen, A.; Zechar, J.D.; Imoto, M. Efficient testing of earthquake forecasting models. Acta Geophys. 2011, 59, 728–747. [Google Scholar] [CrossRef]
- Rastin, S.J.; Rhoades, D.A.; Rollins, C.; Gerstenberger, M.C. How Useful Are Strain Rates for Estimating the Long-Term Spatial Distribution of Earthquakes? Appl. Sci. 2022, 12, 6804. [Google Scholar] [CrossRef]
- Hurvich, C.M.; Tsai, C.-L. Regression and time series model selection in small samples. Biometrika 1989, 76, 297–307. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Gerstenberger, M.C. Mixture models for improved short-term earthquake forecasting. Bull. Seismol. Soc. Am. 2009, 99, 636–646. [Google Scholar] [CrossRef]
- Rhoades, D.A. Long-range earthquake forecasting allowing for aftershocks. Geophys. J. Int. 2009, 178, 244–256. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Gerstenberger, M.C.; Christophersen, A. Development, Installation and Testing of New Models in the New Zealand Earthquake Forecast Testing Centre; CR2010-253; GNS Science: Lower Hutt, New Zealand, 2010; 55p. [Google Scholar]
- Rastin, S.J.; Rhoades, D.; Christophersen, A. Space-time trade-off of precursory seismicity in the EEPAS medium-term forecasting model optimized for New Zealand earthquakes. In Proceedings of the AGU 2020 Fall Meeting, virtual, 1–17 December 2020. [Google Scholar]
- Gerstenberger, M.C.; Wiemer, S.; Jones, L.M.; Reasenberg, P.A. Real-time forecasts of tomorrow’s earthquakes in California. Nature 2005, 435, 328–331. [Google Scholar] [CrossRef] [PubMed]
- Gutenberg, B.; Richter, C.F. Seismicity of the Earth and Associated Phenomena; Princeton, N.J., Ed.; Princeton University Press: Princeton, NJ, USA, 1954. [Google Scholar]
- Utsu, T. A statistical study on the occurrence of aftershocks. Geophys. Mag. 1961, 30, 521–605. [Google Scholar]
- Gledhill, K.; Ristau, J.; Reyners, M.; Fry, B.; Holden, C. The Darfield (Canterbury) earthquake of September 2010: Preliminary seismological report. Bull. N. Z. Soc. Earthq. Eng. 2010, 43, 215–221. [Google Scholar]
- Kaiser, A.; Holden, C.; Beavan, J.; Beetham, D.; Benites, R.; Celentano, A.; Collett, D.; Cousins, J.; Cubrinovski, M.; Dellow, G.; et al. The Mw 6.2 Christchurch earthquake of February 2011: Preliminary report. N. Z. J. Geol. Geophys. 2012, 55, 67–90. [Google Scholar] [CrossRef]
- Yan, W.; Galloway, W. Rethinking Resilience, Adaptation and Transformation in a Time of Change; Springer International Publishing: Berlin, Germany, 2017. [Google Scholar]
- Stirling, M.; McVerry, G.H.; Gerstenberger, M.C.; Litchfield, N.J.; Van Dissen, R.J.; Berryman, K.R.; Barnes, P.; Wallace, L.M.; Villamor, P.; Langridge, R.M.; et al. National Seismic Hazard Model for New Zealand: 2010 Update. Bull. Seismol. Soc. Am. 2012, 102, 1514–1542. [Google Scholar] [CrossRef]
- Gerstenberger, M.C.; Rhoades, D.A.; McVerry, G.H. A hybrid time-dependent probabilistic seismic-hazard model for Canterbury, New Zealand. Seismol. Res. Lett. 2016, 87, 1311–1318. [Google Scholar] [CrossRef]
- Meletti, C.; Galadini, F.; Valensise, G.; Stucchi, M.; Basili, R.; Barba, S.; Vannucci, G.; Boschi, E. A seismic source zone model for the seismic hazard assessment of the Italian territory. Tectonophysics 2008, 450, 85–108. [Google Scholar] [CrossRef]
- Kaiser, A.; Balfour, N.; Fry, B.; Holden, C.; Litchfield, N.; Gerstenberger, M.; D’Anastasio, E.; Horspool, N.; McVerry, G.; Ristau, J.; et al. The 2016 Kaikōura, New Zealand, earthquake: Preliminary seismological report. Seismol. Res. Lett. 2017, 88, 727–739. [Google Scholar] [CrossRef]
- Havskov, J.; Ottemoller, L. Routine Data Processing in Earthquake Seismology: With Sample Data, Exercises and Software; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Rastin, S.J.; Unsworth, C.P.; Gledhill, K.R.; McNamara, D.E. A detailed noise characterization and sensor evaluation of the North Island of New Zealand using the PQLX data quality control system. Bull. Seismol. Soc. Am. 2012, 102, 98–113. [Google Scholar] [CrossRef]
- Bormann, P.; Wielandt, E. Seismic Signals and Noise. In New Manual of Seismological Observatory Practice 2 (NMSOP2); Deutsches GeoForschungsZentrum GFZ: Potsdam, Germany, 2013. [Google Scholar] [CrossRef]
- Rastin, S.J.; Rhoades, D.A.; Rollins, C.; Gerstenberger, M.C.; Christophersen, A.; Thingbaijam, K.K.S. Spatial Distribution of Earthquake Occurrence for the New Zealand National Seismic Hazard Model Revision, GNS Science Report; SR2021-51; GNS Science: Lower Hutt, New Zealand, 2022. [Google Scholar]
- Christophersen, A.; Bourgignon, S.; Rhoades, D.A.; Allen, T.I.; Salichon, J.; Ristau, J.; Gerstenberger, M. Consistent Magnitudes over Time for the Revision of the New Zealand National Seismic Hazard Model, GNS Science Report; SR2021-42; GNS Science: Lower Hutt, New Zealand, 2022. [Google Scholar] [CrossRef]
- Rhoades, D.A. Lessons and Questions from Thirty Years of Testing the Precursory Swarm Hypothesis. Pure Appl. Geophys. 2010, 167, 629–644. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Robinson, R.; Gerstenberger, M.C. Long-range predictability in physics-based synthetic earthquake catalogues. Geophys. J. Int. 2011, 185, 1037–1048. [Google Scholar] [CrossRef]
- Robinson, R.; Van Dissen, R.R.; Litchfield, N. Using synthetic seismicity to evaluate seismic hazard in the Wellington region, New Zealand. Geophys. J. Int. 2011, 187, 510–528. [Google Scholar] [CrossRef]
- Robinson, R.; Benites, R. Synthetic seismicity models for the Wellington Region, New Zealand: Implications for the temporal distribution of large events. J. Geophys. Res. Solid Earth 1996, 101, 27833–27844. [Google Scholar] [CrossRef]
- Richards-Dinger, K.; Dieterich, J.H. RSQSim Earthquake Simulator. Seismol. Res. Lett. 2012, 83, 983–990. [Google Scholar] [CrossRef]
- Imoto, M.; Rhoades, D.A. Seismicity models of moderate earthquakes in Kanto, Japan utilizing multiple predictive parameters. Pure Appl. Geophys. 2010, 167, 831–843. [Google Scholar] [CrossRef]
- Robinson, R.; Benites, R. Upgrading a synthetic seismicity model for more realistic fault ruptures. Geophys. Res. Lett. 2001, 28, 1843–1846. [Google Scholar] [CrossRef]
- Scholz, C.H. The Mechanics of Earthquakes and Faulting, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Eberhart-Phillips, D.; Reyners, M.; Bannister, S.; Chadwick, M.; Ellis, S. Establishing a versatile 3-D seismic velocity model for New Zealand. Seismol. Res. Lett. 2010, 81, 992–1000. [Google Scholar] [CrossRef]
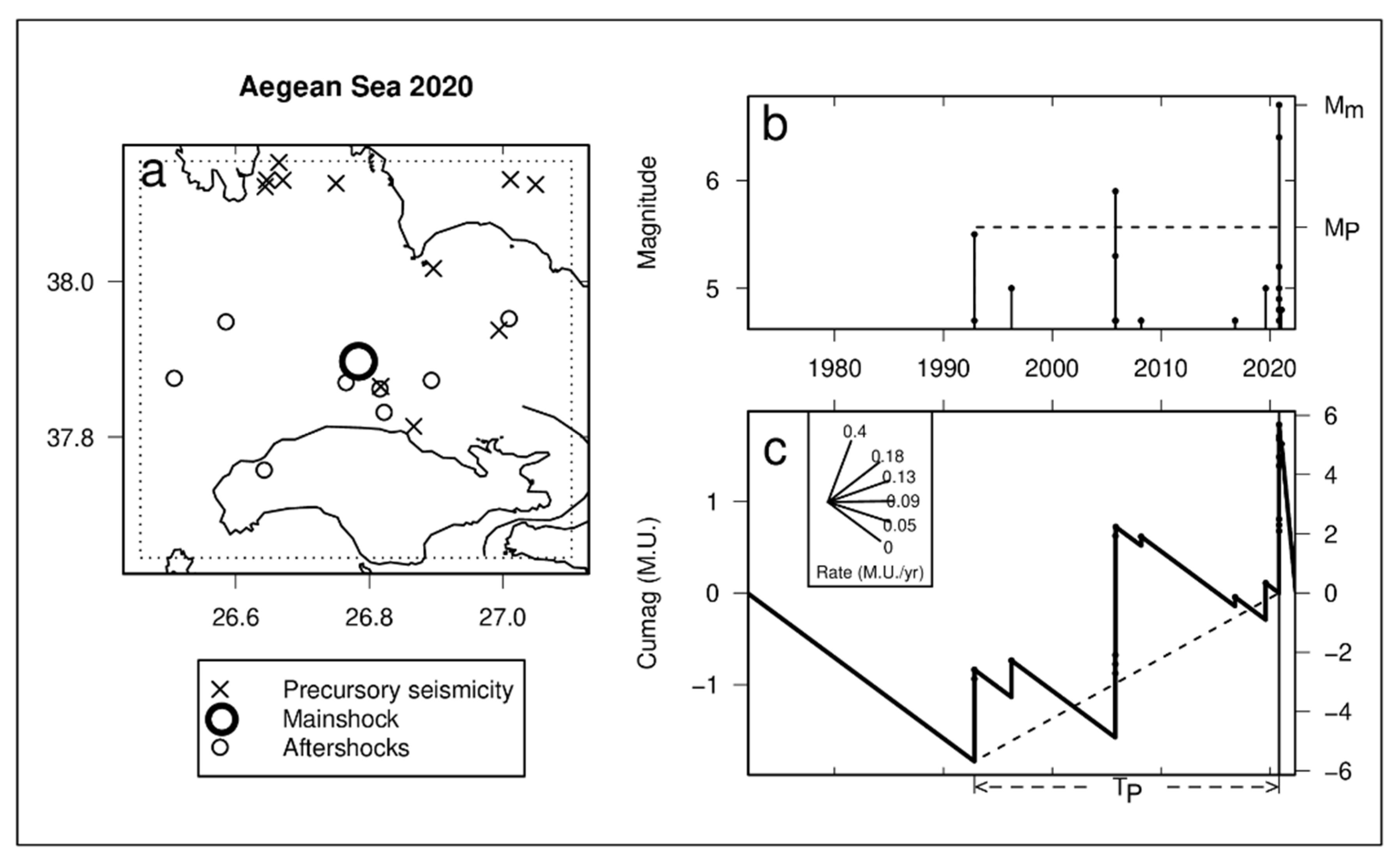
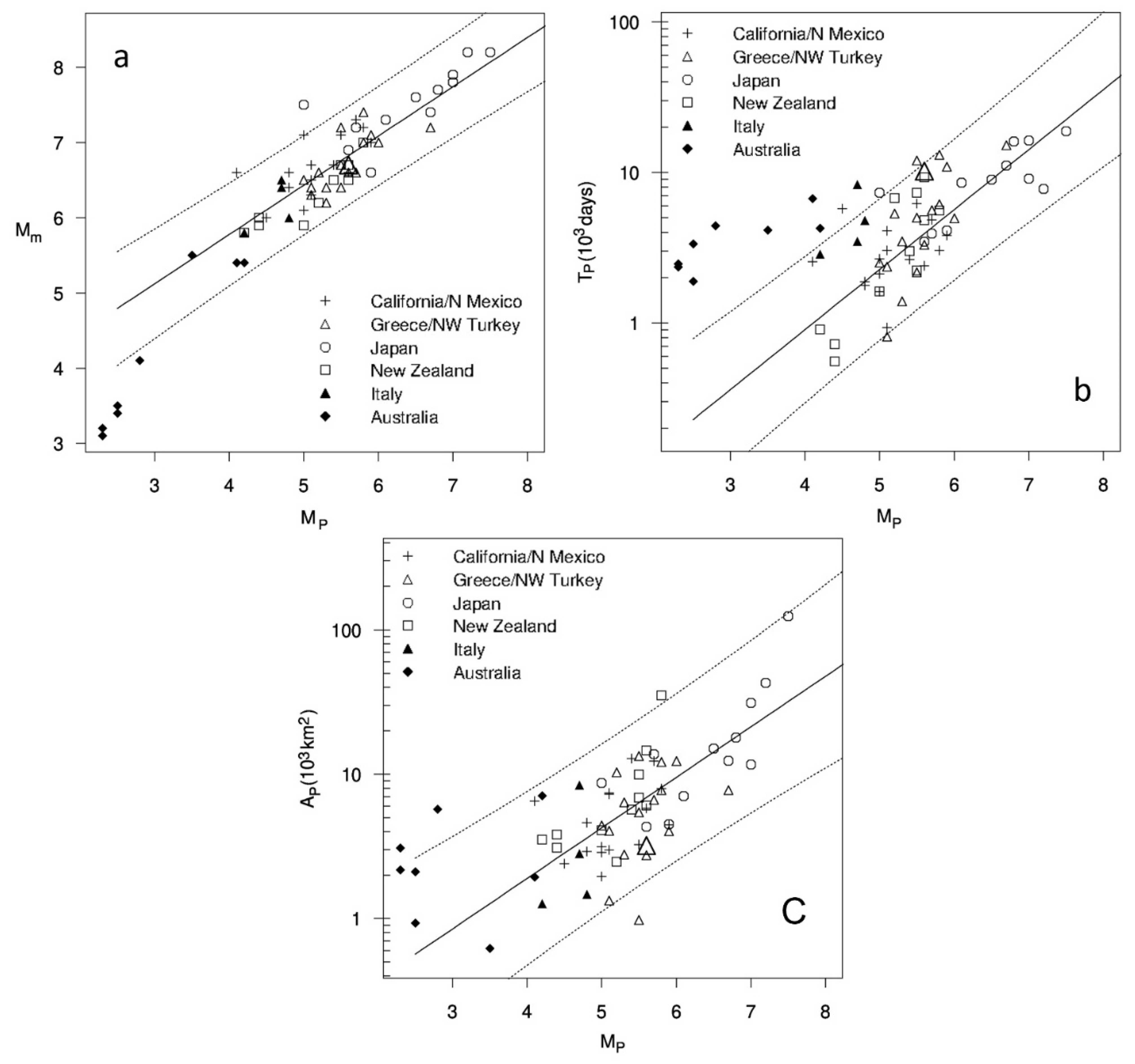
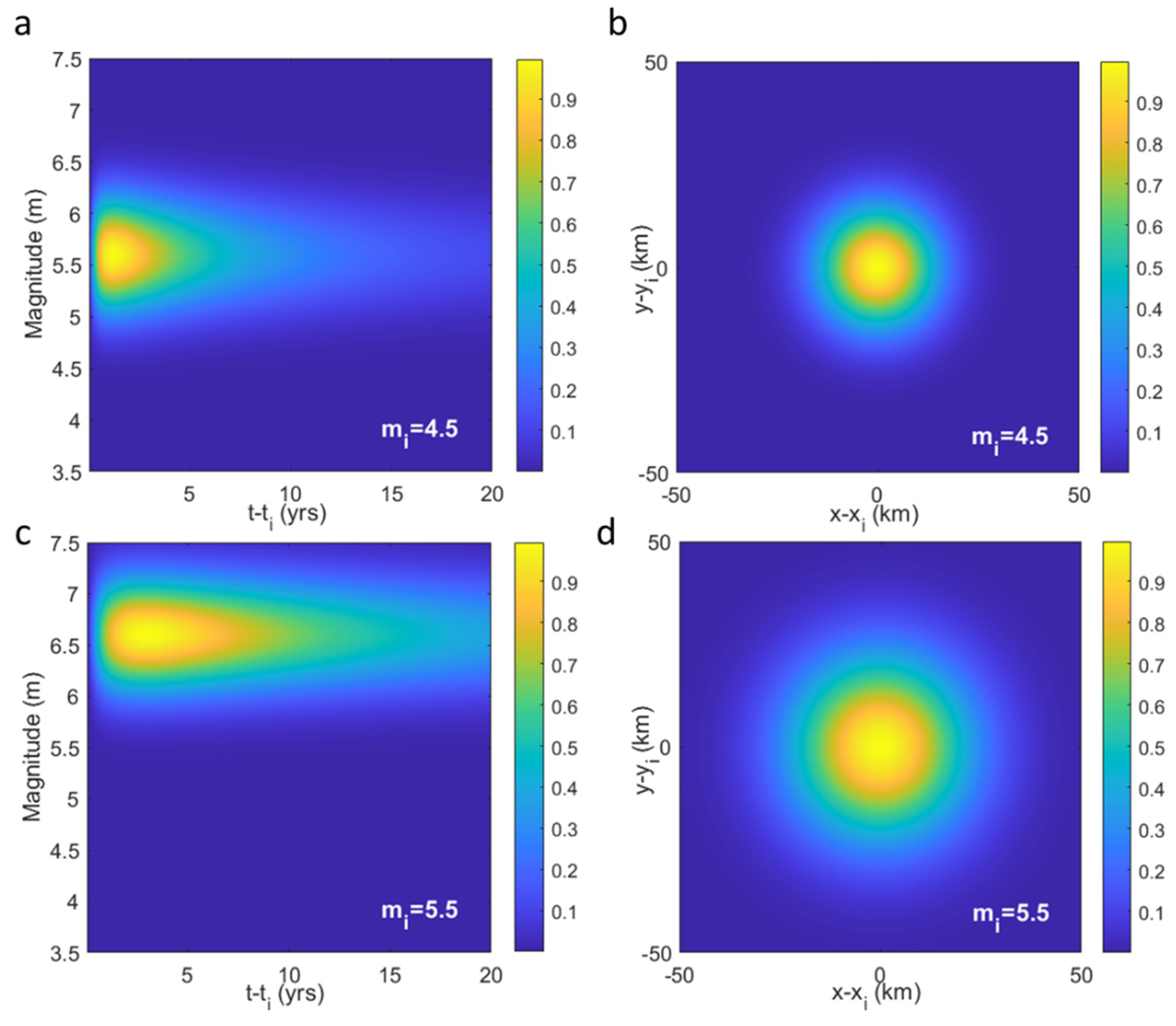


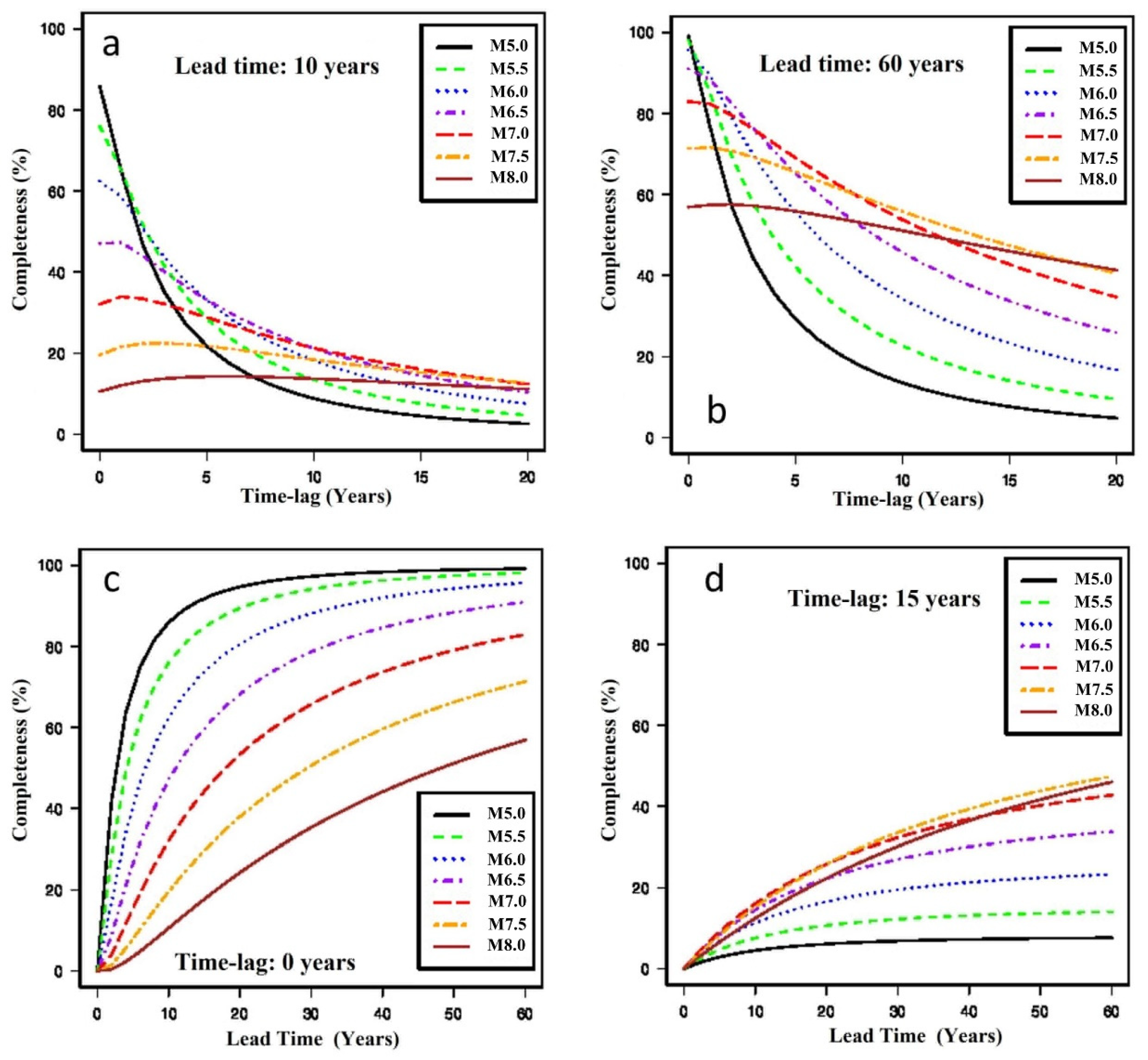



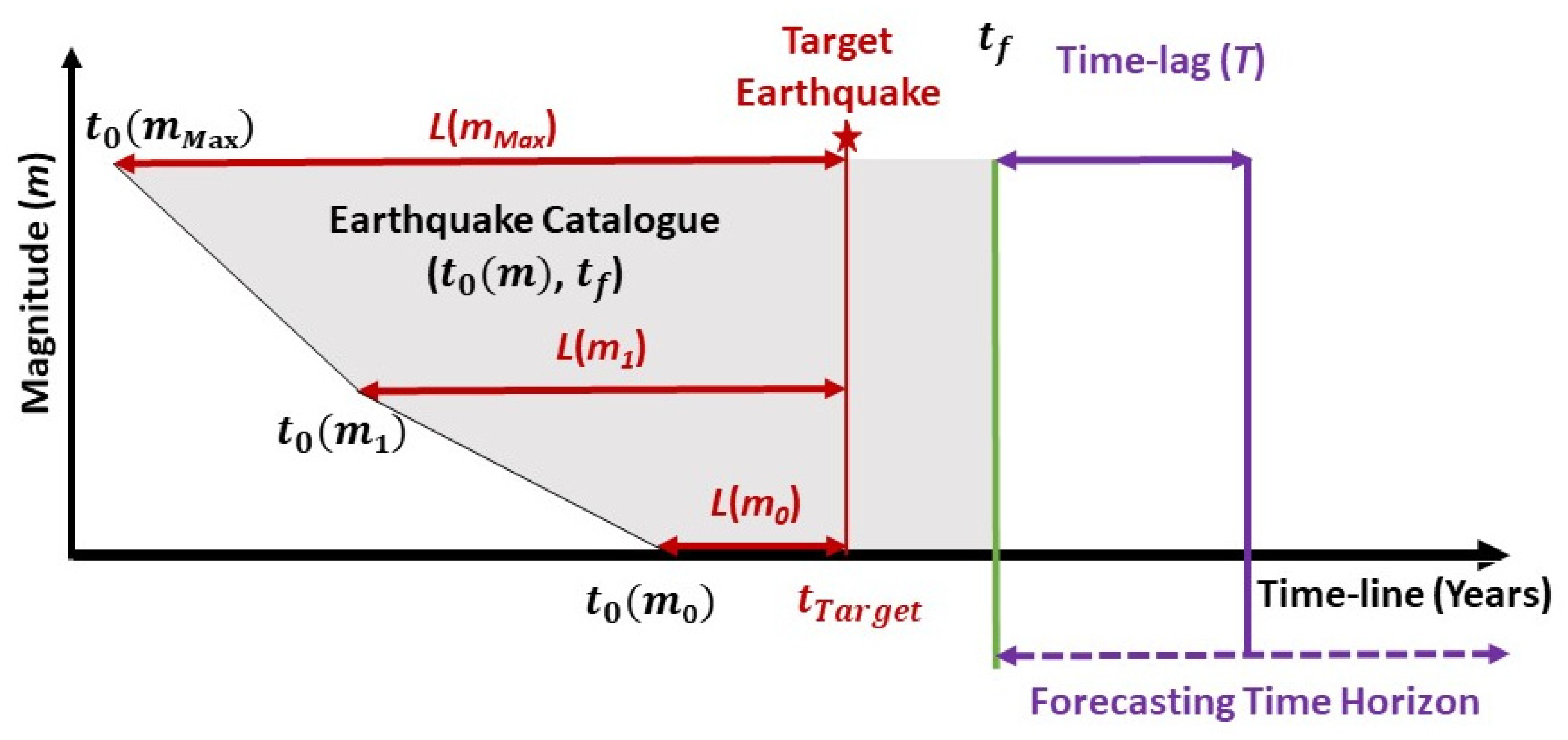
| Term | Description | Reference |
|---|---|---|
| Fitting Period | Subset of a catalogue used for carrying out parameter fitting. | [16] |
| Testing Period | Subset of a catalogue, separate from the fitting period, used for independent testing without further parameter adjustment. | [16] |
| Warm-up eriod | Subset of a catalogue providing information on precursory earthquakes and earthquake rates prior to the fitting period. This provides initial required data for the background component, as well as the time-varying component of EEPAS. | [51] |
| Target Earthquakes | Earthquakes with hypocenters within the region of surveillance and time origins in the fitting or testing periods or the future and magnitudes greater than a chosen threshold, e.g., M > 4.95. | [19] |
| Precursory Earthquakes | Earthquakes with hypocenters within a search region encompassing the region of surveillance with time origins covered by the catalogue and magnitudes greater than the input magnitude threshold, e.g., M > 2.95. | [16] |
| Lead Time | Length of time from start of catalogue to time of occurrence of a target earthquake. | [52] |
| Delay | Time interval between when an earthquake occurs and the earliest time at which it is allowed to contribute to a forecast (e.g., 50 days). | [16] |
| Time-lag | In fitting and testing: sometimes used as a synonym for “Delay”. In forecasting: the time interval between the end of the catalogue and the time for which a forecast is made (e.g., 5 years). | [57] |
| Forecasting Time Horizon | Depending on context, this can mean a future time or the most distant future time for which a forecast is made. It can also refer to the time-lag associated with such a forecast. | [58] |
| Version | Mathematical Description | Reference |
|---|---|---|
| Standard EEPAS | : Background rate density | [16,17,18] |
| STEP-EEPAS mixture | [62] | |
| EEPAS with aftershocks | [63] | |
| Earthquake Rate Dependent EEPAS (ERDEEP) | ; is rate in cell j. | [64] |
| Janus Model: EEPAS-ETAS mixture | 1. | [58] |
| EEPAS Compensated for Time-Lag (LEEPAS) | . | [57] |
| Fixed Lead Time EEPAS (FLEEPAS) | [52,65] | |
| Fixed Lead Time Compensated EEPAS (FLCEEPAS) | φ: 0 ≤ φ ≤ 1. | [52,65] |
| Parameter | EEPAS_0F |
|---|---|
| 2.95 * | |
| 4.95 * | |
| 10.05 *,! | |
| 1.16 † | |
| 1.10 † | |
| 1.0 * | |
| 0.39 † | |
| 1.71 † | |
| 0.39 † | |
| 0.60 † | |
| 0.36 † | |
| 1.63 † | |
| μ | † |
| Parameter | Model | Fitted Value | Fitting Range |
|---|---|---|---|
| a | PPE | 0.55 | unconstrained |
| d | PPE | 5.26 (km) | >1 |
| s | PPE | 2.4 × 10−12 | unconstrained |
| aM | EEPAS | 1.00 | 1.0–2.0 |
| bM | EEPAS | 1.00 * | NA |
| σM | EEPAS | 0.20 | 0.2–0.5 |
| aT | EEPAS | 1.97 | 1.0–2.0 |
| bT | EEPAS | 0.35 | 0.3–0.7 |
| σT | EEPAS | 0.20 | 0.2–0.5 |
| bA | EEPAS | 0.59 | 0.3–0.7 |
| σA | EEPAS | 0.51 | 0.5–10 |
| µ | EEPAS | 0.36 | 0.0–0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rhoades, D.A.; Rastin, S.J.; Christophersen, A. A 20-Year Journey of Forecasting with the “Every Earthquake a Precursor According to Scale” Model. Geosciences 2022, 12, 349. https://doi.org/10.3390/geosciences12090349
Rhoades DA, Rastin SJ, Christophersen A. A 20-Year Journey of Forecasting with the “Every Earthquake a Precursor According to Scale” Model. Geosciences. 2022; 12(9):349. https://doi.org/10.3390/geosciences12090349
Chicago/Turabian StyleRhoades, David A., Sepideh J. Rastin, and Annemarie Christophersen. 2022. "A 20-Year Journey of Forecasting with the “Every Earthquake a Precursor According to Scale” Model" Geosciences 12, no. 9: 349. https://doi.org/10.3390/geosciences12090349
APA StyleRhoades, D. A., Rastin, S. J., & Christophersen, A. (2022). A 20-Year Journey of Forecasting with the “Every Earthquake a Precursor According to Scale” Model. Geosciences, 12(9), 349. https://doi.org/10.3390/geosciences12090349









