Abstract
Strong crustal earthquakes in Greece are typically followed by aftershocks, the properties of which are important factors in seismic hazard assessment. In order to examine the properties of earthquake sequences, we prepared an earthquake catalog comprising aftershock sequences with mainshocks of Mw ≥ 5.5 from 1995 to 2021. Regional aftershock parameters were estimated to highlight variations in aftershock decay and productivity among regions with similar seismotectonic characteristics. A statistically based method of estimating aftershock duration and a metric of relative aftershock productivity to examine the variations among the different cases were employed. From the detailed analysis of the selected seismic sequences, we attempt to unravel the physical mechanisms behind deviations in aftershock duration and productivity and resolve the relative contribution of background seismicity, the Omori–Utsu law parameters and the mainshock faulting properties. From our analysis, the duration of aftershock sequences depends upon the rupture process of the mainshock, independently of its magnitude. The same applies to aftershock productivity, however, other tectonic setting (e.g., seismic coupling) or source-related (e.g., focal depth, stress drop) parameters also contribute. The estimated regional parameters of the aftershock rate models could be utilized as initial ones to forecast the aftershock occurrence rates at the early stage following a mainshock.
1. Introduction
The generation of aftershocks following a strong (e.g., ≥ 5.0) mainshock remains a critical key to understanding the fundamental characteristics of seismogenesis. It is widely accepted that they originate from the relaxation of stress concentrations due to the dynamic rupture caused by the mainshock or to the stress redistribution after its occurrence [1]. The first empirical model describing the nature of aftershocks was introduced by Omori et al. [2], who claimed that the aftershock occurrence rate decays over time following a hyperbolic function, analogous to 1/t. Decades later, the observation that several earthquake sequences presented higher aftershock decay than predicted by the 1/t function led Utsu [3] to formulate a generalized version of the Omori law, most commonly known as the Modified Omori Law (MOL):
where R(t) is the rate of aftershocks at time t, t is the time elapsed from the mainshock occurrence and K, c and p are parameters constrained in each seismic sequence. Among them, the c-value is the most ambiguous, indicating the temporal delay due to the short-term aftershock incompleteness that is observed at the early stage of an aftershock sequence (e.g., [4]). The parameter p expresses the power law decay of the aftershock rate following a mainshock, thus, for sequences with higher estimated p-values, their aftershock rates decay faster with time than those obtaining a lower value. Unlike c and K, the p-value is independent of the cutoff magnitude, and is widely used to draw conclusions about the differences in the behavior of different seismic sequences. Among the MOL parameters, the K-value is considered to be more closely related to aftershock productivity. However, its value appears to depend on the total number of aftershocks and, consequently, on the completeness magnitude () [5,6]. According to Kisslinger [4], the K-value is related to the earliest part of the sequence and originates from the fact that early aftershocks do not follow a constant decay rate, instead their rate is increased in the first hours after the mainshock occurrence and then starts to decrease.
The frequency–magnitude distribution of earthquakes has been described and extensively analyzed through the empirical Gutenberg–Richter (G-R) law [7] which states that earthquake magnitudes are exponentially distributed as:
where N is the total number of earthquakes with magnitudes greater than or equal to M, and , b are constants with the latter being the slope, denoting the ratio of small- to large-magnitude earthquakes. The b-value is considered to vary among different regions reflecting the different stress regimes coming in play (e.g., [8,9]). Consequently, spatiotemporal variations in b-values have been and still remain a subject of discussion in numerous studies attempting to interpret its physical properties (e.g., [10]). Regarding Greece, studies have shown that the spatial variation in b is characterized by a general trend of gradually decreasing values from the outer Hellenic Arc towards NE Greece [11,12,13].
Another widely used empirical relationship in seismology is Båth’s law, which states that within a typical mainshock–aftershock sequence, the difference between the magnitude of the mainshock () and the one of the largest aftershock () is approximately equal to 1.2 [14], independently of the mainshock magnitude. Since then, numerous studies have attempted to validate and extend this empirical law (e.g., [15,16,17]. Drakatos and Latoussakis [18] estimated the relationship between and for earthquakes in Greece (up to 1997), finding an average value close to 1.0 but with high variance.
In the present study, we attempt to systematically review the aftershock properties of strong ( ≥ 5.5) earthquakes in Greece by exploiting the basic models that describe aftershock processes with the ultimate goal being to reveal systematic patterns and properties, enabling us to highlight any anomalies and draw conclusions concerning the interconnection between the examined parameters. The aftershock productivity and the total duration of aftershock sequences are examined taking into account, among others, the magnitude and the faulting style of the mainshock, as well as region-specific characteristics. In Section 2, the dataset of aftershock sequences used and the seismotectonic frame of the study area are described. An overview of the applied methodologies to model aftershock rates and the total duration of seismic sequences follows, along with an objective measure of relative aftershock productivity. Results of the implemented methods are presented in Section 3. In Section 4, the outcomes of the analysis are discussed, focusing on the reasons controlling both regional and intersequence variability in aftershock productivity, as well as the effect of tectonic setting properties on aftershock duration. Finally, the main conclusions of the present study are summarized in Section 5.
2. Data and Methods
2.1. Selection of Aftershock Sequences
In order to examine the aftershock properties of earthquake sequences in Greece, we used an earthquake catalog compiled from the bulletins of the Central Seismological Station of the Geophysics Department of the Aristotle University of Thessaloniki (geophysics.geo.auth.gr/ss/). Aiming to use accurate data with a satisfactory number of aftershocks, a mainshock magnitude threshold of ≥ 5.5 was set, covering the time period from 1995 to 2021. Spatiotemporal constraints were applied to select aftershocks associated with each mainshock. An earthquake with ≥ 5.5 is characterized as mainshock in cases where a higher magnitude one has not occurred within 3 fault lengths (3*L) from its epicenter, estimated using the well-established empirical relation of Wells and Coppersmith [19], 60 days before and 10 days after its occurrence. Then, aftershocks were associated with each mainshock if they occur within 3*L from its epicenter, a value already adopted for global aftershock forecasts [20], also taking into account that aftershock zone scaling is considered independent from the faulting type of the mainshock [21]. From the initial catalog, a list of 73 aftershock sequences was obtained (Figure 1; Table 1) for the period 1995–2021. Isolated mainshocks (as they were identified with the above criteria, but without aftershocks) were excluded from the analysis. Additionally, the rupture type of each mainshock was classified according to their focal mechanism as provided by the Global Centroid Moment Tensor (GCMT) database. The classification was performed using the FMC program developed by Alvarez-Gomez [22] which is based on a hierarchical clustering analysis using the parameters provided by the focal mechanism solutions.
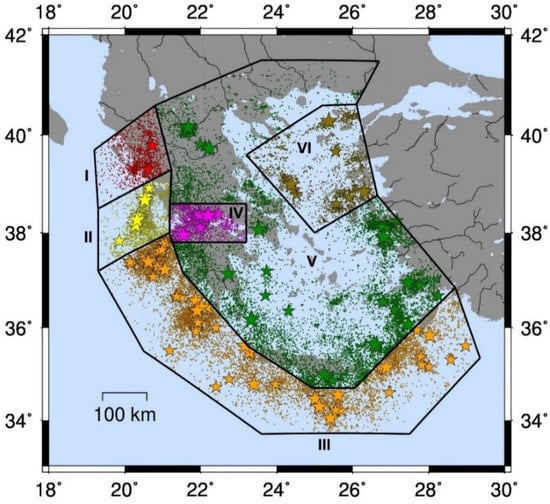
Figure 1.
Map of the study area along with the selected seismic zones (Zone I: Continental Collision; Zone II: Central Ionian Islands; Zone III: Oceanic Subduction; Zone IV: Corinth Gulf; Zone V: Back Arc Area; Zone VI: North Aegean). Stars denote the identified mainshocks (Mw ≥ 5.5) and circles the epicenters of earthquakes that occurred with M ≥ 2.5 from 1995 to 2021. Both are color-coded according to each seismic zone.

Table 1.
List of the mainshocks ( ≥ 5.5) identified, resulting in 73 aftershock sequences (excluding isolated mainshocks). Column 8 denotes the style of faulting through the classification of the focal mechanism solutions provided by GCMT (N: Normal; N-SS: Normal-Strike-Slip; SS: Strike-Slip; SS-N: Strike-Slip-Normal; SS-R: Strike-Slip-Reverse; R: Reverse; R-SS: Reverse-Strike-Slip).
2.2. Modeling of the Aftershock Rates
Aftershock rate models constitute a powerful tool to describe aftershock sequences and most importantly to evaluate the predicted aftershock decay rate which can be of crucial significance in disaster management following a strong earthquake. The statistical framework proposed by Reasenberg and Jones [5] (RJ89), which has been utilized for decades by USGS as a forecast tool to estimate the probability of occurrence of strong aftershocks following M ≥ 5.0 mainshocks in California, was employed to model aftershock rates. The RJ89 model describes aftershock occurrence as a non-stationary Poisson process combining the G-R relationship and MOL. The rate of aftershocks at time t after a mainshock () is estimated as:
where b is the slope of the frequency–magnitude distribution (G-R), a is the parameter representing aftershock productivity and p, c are the parameters of MOL denoting the temporal aftershock decay and the time shift before its beginning, respectively. is the lower magnitude threshold of the sequence. Reasenberg and Jones [5] fitted Equation (3) using a dataset of seismic sequences in California and provided the median parameters of a = −1.67, b = 0.91, p = 1.08 and c = 0.05 which were established as the “generic” California parameters. Since then, Hardebeck et al. [23] updated these parameters by introducing updated data and more detailed regionalization. The RJ89 model has also been successfully used on a global scale. A prime example is the work of Page et al. [20] who used a large global dataset and grouped tectonically uniform areas to determine the RJ89 parameters for each tectonic regime. The RJ89 model has significant advantages in estimating generic parameters but it comes with several assumptions, with the most important being that all aftershocks are triggered by the mainshock, which is not always true. As a result, in cases where large aftershocks trigger their subsequent aftershocks and in seismic swarms, where similar-sized events occur, the model may perform inadequately.
Following the approach of Page et al. [20], we estimated mean regional aftershock parameters to optimally detect spatial variations in productivity and aftershock decay that may signify variations in the predominant stress field and tectonic loading processes. The study area was divided into distinct tectonic regions (Figure 1), based on the general zonation scheme suggested by Vamvakaris et al. [13]. Ultimately, six seismic zones were defined based on common seismotectonic characteristics. Zones I and III are generally related to reverse or thrust faulting, Zones II and VI to strike-slip faulting and IV, V to normal faulting (Figure 2).
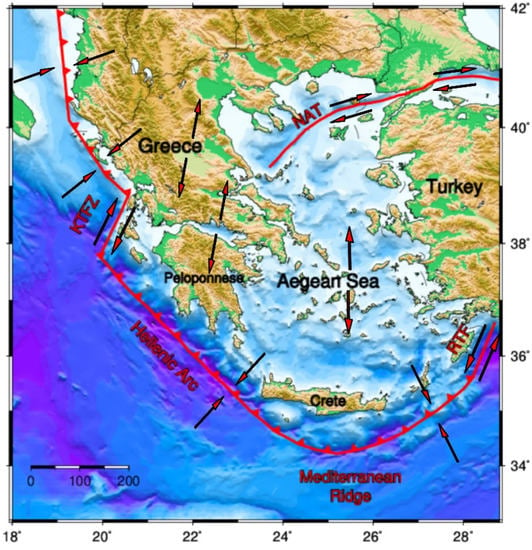
Figure 2.
The main geodynamic features of Greece. Red lines denote the active boundaries and the red arrows the relative motions (NAT: North Aegean Trough; KTFZ: Kefalonia Transform Fault Zone; RTF: Rhodes Transform Fault).
Zone I is characterized by the active compressional stress field due to the continental collision between the Apulian and the Aegean microplate [24,25]. Active deformation is related to reverse faulting, with a general NW–SE strike following the coastline of NW Greece. Moving to the south (Zone II), this stress field is terminated by a major transform fault zone, namely, the Kefalonia Transform Fault Zone (KTFZ) which is characterized by dextral strike-slip sense of motion, often accompanied with thrust components [26,27,28]. Mostly NE–SW to NNE–SSW dextral strike-slip faults dominate the area, being responsible for the highest seismicity among the other regions [29]. The southernmost part of the KTFZ is connected to the NW edge of the Hellenic subduction front, the western part of which forms Zone III. The limits of this zone illustrate the amphitheatrical shape of the Hellenic Subduction zone, starting from a general NW–SE trend to the west, then bending (E–W) and finally obtaining a SW–NE direction reaching the SW coasts of Turkey (Figure 2). Thrust faulting dominates this zone, producing large-magnitude earthquakes, however, significant strike-slip earthquakes have also occurred in its easternmost part (e.g., [30]). Zone IV includes the extension stress field dominating the Corinth Gulf forming faults with a general E–W strike, formed under a N–S extensional deformation stress field. Normal faulting is predominant in this zone, although seismicity is often manifested as seismic swarms (e.g., [31,32]) with distinct triggering and driving processes, different than in the other normal faulting-related areas such as the ones enclosed in Zone V. This broad seismic zone includes (i) the area north of the subduction zone, with the presence of N–S to NNW–SSE striking normal faults, (ii) the relatively low-seismicity area of the central Aegean Sea, (iii) the eastern Aegean area with normal faults, generally striking E–W, which have hosted several strong events in the past [33], (iv) the Central Greece area, excluding the Corinth Gulf, and, finally, (v) the area of northern Greece within which the levels of seismicity vary spatially but contains several strong earthquakes hosted around specific normal fault zones [34], the latter being parts of the back arc area. Lastly, Zone VI encompasses the North Aegean region, where dextral strike-slip motion dominates at the western prolongation of the northern branch of the North Anatolian Fault along the NE–SW trending North Aegean Trough (Figure 2).
2.3. Aftershock Duration
Aftershock duration () is defined as the time interval in which the overall seismicity is dominated by aftershock activity. It signifies, therefore, the time elapsed since the mainshock occurrence up to when the seismicity rate returns to the average background seismicity rate. Dieterich [35] suggested that under the rate-and-state friction law [36], an aftershock sequence decays hyperbolically as described in the Omori law, and returns to the background seismicity rate after an elapsed time Ta, which is independent of the mainshock magnitude and varies inversely with the fault stressing rate (Equation (4)):
where A is a constitutive parameter of the time-dependent friction, σ is the normal stress on the fault and is the stressing rate. Other researchers, however, consider this definition to be the “apparent aftershock duration” and the “true” aftershock duration to be the triggering time T which is the duration of the physical triggering process of a single event and can be significantly longer than the first one [37].
There are several approaches to assess which are mainly differentiated by the selection of spatiotemporal criteria to estimate the seismicity rates. In this study, the aftershock areas were designed to include aftershocks both on the fault plane and in the surrounding area (3*L), which may be triggered by stress transfer. We followed the method proposed by Sebastiani et al. [38], which is based on the mean values difference significance test. Prior to the calculations, aftershock catalogs were compiled for each seismic sequence, starting from each mainshock and their corresponding was estimated by applying the Goodness-of-Fit Method (GFT) proposed by Wiemer and Wyss [39] considering the 95% confidence interval level of residuals. In cases where this threshold was not reached, the 90% level was kept instead.
For each seismic sequence, the following procedure was executed. A temporal sequence of daily rates of events with magnitudes above the threshold was computed for all catalog data (), with the occurrence time of the mainshock considered as the origin time. was then split into two subsets of equal length. The first one contained the last T-values of daily rates, whereas the other was not stable and was formed each time by incorporating successive T-values from the first -T-values of the full catalog. Then, the mean value (μ) and variance () of each pair of subsets (that never intersect) were estimated and formed the sequence :
The lengths of and T were calibrated for each seismic sequence separately, ensuring that the sample size T is adequate and is wide enough to include the end of the aftershock sequence. was then considered as the first time that is less than 3 (99.9% significance level) assuming that can be approximated by a Gaussian random variable [40].
2.4. Aftershock Productivity
It is well documented that the number N of aftershocks following a mainshock increases with the mainshock magnitude . This pattern is expressed via the productivity law (e.g., [18,41,42,43]):
where k depends on the number of aftershocks over the magnitude of completeness threshold and α controls the relative number of aftershocks activated corresponding to mainshock magnitude (). Variations in α have been reported among different regions, for example, Felzer et al. [42] suggested a value of 1.0 for California, whereas Helmstetter [41] indicated a value of 0.8 for southern California. On the other hand, Drakatos and Latoussakis [18] calculated a value of 0.9 for the Greek territory.
In this study, the productivity law was fitted through linear least squares regression after dividing the data into 0.1 bins and using the median number of aftershocks for each bin (Figure 3). The spatial selection of aftershocks of seismic sequences from 1995 to 2021 was the same as described in Section 2.1, but this time was estimated using the full catalog in order to obtain a uniform magnitude threshold ( = 3.5). Three temporal windows (10, 60 and 120 days) were used to count aftershocks and test the sensitivity of the calculations. Variations between each temporal window were negligible, resulting in a value of α = 0.7. Based on this, each aftershock sequence was associated with a Relative Productivity (RP) value following the definition of Dascher-Cousineau et al. [43]:
where N is the detected number of aftershocks of the seismic sequence and Ñ(M) is the expected number of aftershocks predicted from Equation (6) for the mainshock magnitude . The abovementioned approach was utilized to effectively compare the aftershock productivity of seismic sequences of different mainshock magnitudes and investigate the reasons behind their fluctuations. It is, therefore, crucial that the used measure of productivity is independent of mainshock magnitude to avoid linking variations in productivity with deviations in the average size of earthquakes [43]. Then, having assigned a value of relative aftershock productivity to each seismic sequence, we attempt to analyze certain properties such as their faulting style and other source-related parameters to seek answers about the reason behind their increased or decreased aftershock production.
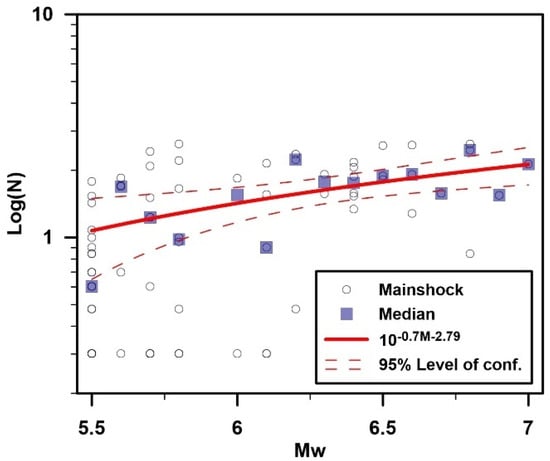
Figure 3.
Logarithm of the number of aftershocks of mainshocks with Mw ≥ 5.5 for 60 days after the mainshock occurrence for seismic sequences that occurred between 1995 and 2021. The productivity law is fitted through linear least squares regression using the median log number of aftershocks for each 0.1 magnitude bin.
3. Results
3.1. Aftershock Rates
Stacked fits of the mean aftershock rates were performed using different time intervals after the mainshock occurrence (10, 60, 120 days) to test the sensitivity of the results. Furthermore, the spatial constraint that was used (3*L) was deemed as the optimum solution to secure the entirety of selected aftershocks and reduce the background events as much as possible. The b-value of the G-R law for the catalog was estimated at 1.06 through the maximum likelihood method [44], with a = 3.5 considering the 95% confidence interval level of residuals. The aftershock rate analysis was then performed through two approaches. First, stacked fits were performed assuming a uniform b-value (b = 1.06) for all zones (Figure 4) and then region-specific ones were estimated (Table S1). Throughout the analysis, the c-value was set to a uniform mean value (c = 0.1) that was obtained from sequence-specific MOL fits.
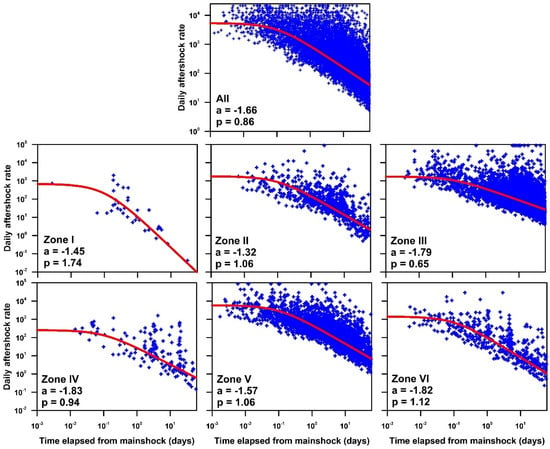
Figure 4.
Stacked fits of the RJ89 model for seismic sequences located within each seismic zone of Figure 1. Red lines denote the maximum likelihood fit of the aftershock rates for M ≥ Mc.
Figure 4 shows the variations in aftershock productivity between the selected seismic zones in the first 60 days after each mainshock occurrence. The 60-day stacked fit of all regions provide the “generic” mean parameters for Greece (a = −1.66, p = 0.86, c = 0.1) and can be used to estimate interval probabilities of strong aftershocks as a forecasting tool. Zones I and II are revealed to be the most productive ones, whereas Zones III, IV and VI are the most deficient in aftershocks. In particular, sequences belonging to Zones I and II appear to be 2–4 times more productive. As far as the estimated p-values are concerned, aftershock sequences located within Zones I and VI decay faster than the rest, whereas Zones III and IV exhibit the slowest decay rates. However, it is worth noting that Zone I encloses the smallest amount of data, making the computations more sensitive compared to other zones. Using mainshocks with ≥ 5.0 for this zone leads to a drop in p-value (below 1.0) whereas the results regarding the other zones remain stable. In the Supplementary Materials, the results of 10- and 120-day stacked fits are provided (Table S2). In general, with a longer considered time window, the aftershock decay rate slightly increases, whereas the a-values show minimal adjustments. In all cases, the relative ranking of values regarding each zone remains the same. On the other hand, when using the region-specific b-values (Table S1), the productivity is scaled depending on their deviation from the generic b-value of the uniform catalog. This makes Zone VI more productive than previously, and the opposite applies to Zone I. The stacked fits corresponding to the “generic” b-value are herein presented as a more robust measure of highlighting their differences.
3.2. Båth’s Law
We further verified that the quantity ΔΜ (-), the difference in magnitude between the mainshock () and the strongest aftershock ), is independent of and the same also applies for ΔΤ, the time difference between the mainshock occurrence and the origin time of the largest aftershock. Average and median ΔΜ for a magnitude range of 5.5 to 7.0 are in the order of 1.2 (Figure 5), in full agreement with Båth’s empirical law. Among the different faulting styles, strike-slip-related sequences tend to produce stronger, larger aftershocks (ΔΜ~0.9), whereas mainshocks associated with reverse faulting tend to have a bigger ΔΜ (~1.4).
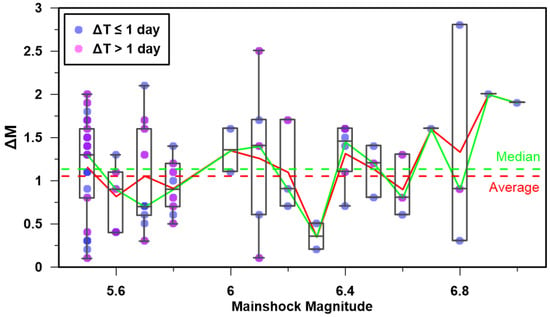
Figure 5.
Magnitude difference (ΔΜ) between the mainshock and its largest aftershock. Dashed green and red lines correspond to the median and average ΔΜ, respectively.
Regarding ΔΤ, the results indicate that in most cases (~56%), the largest aftershock occurred during the first 24 hours following the mainshock, which is in very good agreement with the findings of Drakopoulos [45] who reported that 60% of the examined cases of mainshocks in Greece are followed by their largest aftershock during the first day after their occurrence. Other studies using global data also acknowledge the fact that the largest aftershock is expected to occur rather early during a certain aftershock sequence than later [46].
3.3. Aftershock Duration ()
Aftershock duration () is an indispensable component for the comprehensive understanding of aftershock patterns and crucial to seismic hazard assessment, given that if is not properly constrained, aftershocks may be misinterpreted as background events, leading to the overestimation of seismic hazard [47]. We attempted to estimate for the selected seismic sequences and investigate the factors that influence their fluctuations. The final subset of reliably estimated out of the entire dataset is limited to the cases that have an adequate number of aftershocks with magnitudes above the , which varies from case to case, and to those who pass the significance level test (Table S3). From our analysis, no correlation between and mainshock size (for comparable magnitude bins) was identified, as several researchers have also pointed out (e.g., [47,48,49]). A main goal of this study was to determine whether the different tectonic settings influence . Figure 6a,b reveal that seismic sequences associated with pure Reverse Faulting (RF) present lower -values compared to pure Strike-Slip (SS) and Normal (NF) ones. In particular, the median value of for reverse faulting sequences was found equal to 117 days, whereas the other ones (395 days for strike-slip and 407 days for normal) exhibit larger and relatively similar durations. for mainshocks with an oblique rupture process (SS oblique, RF oblique) are also shown separately in Figure 6b. Among them, two can be distinguished from their counterparts. First, mainshock 7 (Table 1) exhibits a relatively short compared to both NF and SS sequences. The area hosting this sequence belongs to Zone VI (Figure 1) and more specifically to the area west of Chios Island, which is characterized by the transition from strike-slip to normal faulting displaying oblique faulting [50]. Evidence of swarm-like activity is explicit in this area [50,51] and given that the controlling factors in the duration of swarms (e.g., fluid diffusivity) are different from the mainshock–aftershock type sequences, that could be the reason behind its short . On the other hand, mainshock 63 (Table 1), namely, the Zakynthos 2018 sequence (e.g., [45]), exhibits a prolonged , especially compared to pure RF sequences. According to Karakostas et al. [52], the mainshock rupture (R-SS) led to the synchronous activation of multiple nearby fault segments through either static or dynamic stress transfer. As a result, a broad area was activated with an intense and long-lasting aftershock activity.
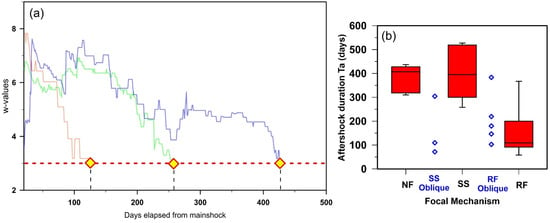
Figure 6.
(a) Examples of the methodology applied to estimate Ta for a strike-slip (green), normal (blue) and reverse (orange) faulting mainshock. The dashed horizontal line denotes the threshold value of wt = 3 corresponding to 99.9% significance level. (b) Results for all seismic sequences are presented classified by faulting style (NF: Normal Faulting; SS: Strike-Slip; RF: Reverse Faulting; SS Oblique, RF Oblique).
We then examined the dependence of on the background seismicity rate and fault slip rate, both being proxies of the stressing rate. Background seismicity rates () were calculated using seismicity up to 4 years prior to the mainshock occurrence and geodetic slip rate data were acquired from the literature (e.g., [53]). Fault slip rates were estimated according to the coupling ratio to account solely for its coseismic portion [54]. Our analysis suggests that both and slip rates exhibit weak to moderate inverse correlation with (Figure 7). Therefore, appears to be more closely related to stressing rate than to the mainshock magnitude, a view that is consistent with the rate-and-state friction law [35].
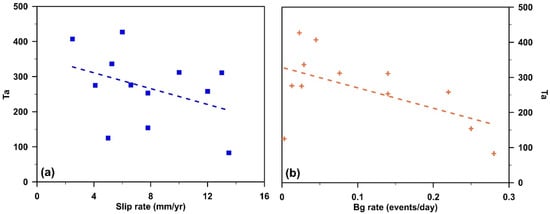
Figure 7.
Aftershock duration (Ta, in days) as a function of (a) fault slip rate (blue squares) and (b) background seismicity rate (orange crosses). Data points are binned by mainshock magnitude.
3.4. Relative Productivity (RP)
Each seismic sequence was assigned with its corresponding relative productivity (RP) value (Table S3). Then, the dataset was subdivided according to the faulting style of the mainshock, as detailed in Table 1. The focal mechanism of the mainshock appears to have an influence on aftershock productivity, as demonstrated in Figure 8. Sequences originated from reverse faulting mainshocks appear to have 2–2.5 times fewer aftershocks than sequences related to normal or strike-slip faulting and the same applies to their (Figure 6b). Normal faulting mainshocks produce the greater number of aftershocks on average with the strike-slip faulting ones following closely. Considering the oblique focal mechanisms, it is observed that strike-slip motion accompanied with either thrust or a normal component enhances aftershock production and the same applies to reverse faulting with pure thrusting being at the bottom of average RP-values. On the contrary, more aftershocks are promoted by pure normal faulting than in instances where combined relative motion comes in play. To assess whether the tectonic setting is the only contributing factor to the relative productivity, we also examined the resulting RP-values according to the zonation scheme described in Section 2.2 to define certain geographic areas and draw conclusions. A synthesis of the parameters tested is shown in ascending order of median RP-values (Figure 8). The results indicate that the low RP-values regarding reverse faulting are mainly driven by mainshocks that occurred along the Hellenic Subduction zone (Zone III), especially its central and eastern part, taking into account that reverse faulting ones outside this zone (e.g., II and V) yield higher values. The primacy of the central Ionian Islands area (Zone II) is also evinced, being the most productive among all areas. If the tectonic setting was the only controlling factor on productivity, then strike-slip mainshocks outside this region should not have fewer aftershocks. However, the results indicate that strike-slip sequences within other regions (e.g., Zones V, VI) produce fewer aftershocks, implying that other parameters, such as the stressing rate, may decisively contribute.
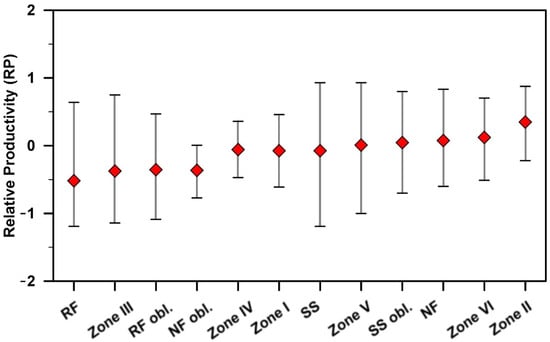
Figure 8.
Relative aftershock productivity (RP) in relation to the style of faulting classification (RF, SS, NF, RF oblique, SS oblique, NF oblique) and according to the zonation scheme of this study (Zones I–VI). Red diamonds represent the median RP-value, and the caps denote the extent of calculated RP-values.
Figure 9 illustrates the RP ranking of the selected seismic sequences (Table 1 and Table S3) along with 11 cases of isolated mainshocks which were not assigned with an RP-value. From the spatial distribution of RP-values, regional variations are once again highlighted as well as presumable anomalies in adjoining regions. First, the western part of the Hellenic Arc is more productive than its central and eastern parts, hosting intense seismic sequences such as the 6.8 Zakynthos 2018 (e.g., [52]), the 6.8 Methoni 2008 (e.g., [55]) or the remarkably prolific 5.7 Zakynthos 2006 seismic swarm (e.g., [56]) (mainshocks 63, 36 and 29, respectively; Table 1). Moving towards the eastern part, the vast majority of seismic sequences exhibit negative RP-values apart from the cases of 6.4 S. Crete 2009 [57] and the 6.1 Kasos 2015 [58] (mainshocks 42 and 55; Table 1).
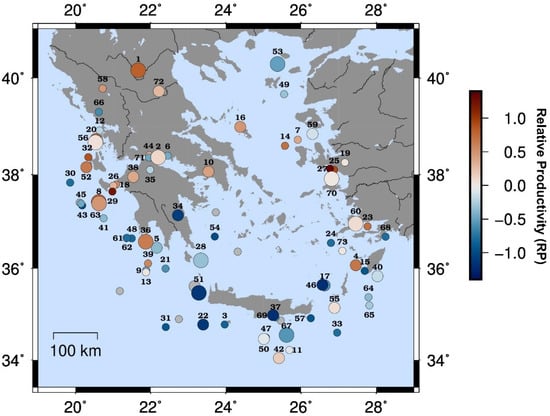
Figure 9.
Map of mainshocks (Mw ≥ 5.5), color-coded according to the relative productivity value of their respective sequences. Gray circles indicate isolated mainshocks (without aftershocks). The serial numbers of each mainshock correspond to those of Table 1.
The highest average RP is obtained in the central Ionian Islands area, irrespectively of mainshock magnitude. Aftershock sequences originating from strike-slip faulting outside this area seem to vary from case to case. As a case in point, the two sequences belonging to the N. Aegean region (zone VI), namely, the 6.1 Skyros 2001 (e.g., [59]) and the 6.9 N. Aegean 2014 (e.g., [60]) (events 26 and 53; Table 1), demonstrate a contrasting behavior. Despite their difference in moment release (by orders of magnitude), the latter is highly unproductive compared to the former, having almost half its (Table S3). Regarding normal faulting sequences, they appear to have a smaller spread in RP-values compared to the other faulting styles. For example, the recent strong events in the Eastern Aegean, namely, the 6.4 Lesvos 2017 (e.g., [61]), the 6.6 Kos 2017 (e.g., [62]) and the 7.0 Samos 2020 (e.g., [63]) sequences (mainshocks 59, 60 and 70, respectively; Table 1), have RP-values assigned close to zero, implying that their aftershock production was typical, given their respective order of magnitude. A rare antithetical example is the 6.5 Kozani 1995 sequence (e.g., [64]) (mainshock 1; Table 1) that occurred in an area not often visited by strong events, causing severe damage, which altered the seismic hazard of the area [65] and was among the events that led to the update of the Greek Building Code. A multi-segment rupture process led to the generation of numerous aftershocks, however, their almost synchronous activation served to limit to customary levels (Table S3).
4. Discussion
The application of the Reasenberg and Jones [5] (RJ89) model on a regional level uncovered several properties of aftershock sequences following strong ( ≥ 5.5) mainshocks in Greece. The central Ionian Islands area (Zone II) appears to be almost four times more productive compared to the Corinth Gulf (Zone IV) which presents lower productivity values, with the Hellenic Subduction (Zone III) and the N. Aegean (Zone VI) areas following closely. These three areas exhibit similar a-values, however, the underlying mechanisms behind their low aftershock production are different. The Corinth Gulf area is characterized by the dominance of swarm-like activity [51,66] associated with the presence of fluid flow [67] which in turn has been linked to low aftershock productivity (e.g., [68]), whereas in the N. Aegean area, swarm-like and mainshock–aftershock activity coexist [51]. The differences between the generation process of these two distinct manifestations of seismicity affect their expansion both in space and time. Swarms are primarily a result of fault weakening processes due to fluid intrusions onto a fault zone, whereas mainshock–aftershock activity is an outcome of stress changes caused by the fault slip (or possible afterslip) of the mainshock. As a result, the productivity and duration of swarms are highly variable, being affected by properties such as diffusivity and crustal permeability (e.g., [69]). The decreased aftershock productivity of the Hellenic Subduction zone area may be attributed to the focal depths of the mainshocks located within this zone, which are the largest among the others. Focal depth has been attested to be inversely related to productivity [43,70]. This could be explained, to a certain extent, with the variation in the stress drop among relatively shallow and deep mainshocks and the stress homogeneity of the rupture area due to elevated pressure and temperature values at these focal depths. Deeper mainshocks tend to have higher stress drop than shallower mainshocks of comparable magnitude [71] which in turn is associated with lower aftershock production. Moreover, higher stress drop mainshocks are generally connected with smaller rupture dimensions, as a larger amount of energy is released per unit fault area. As a result, a more restricted area around the mainshock is exposed to stress transfer and triggering in the adjacent area.
Another property examined in this study is the aftershock duration () of the selected sequences, which, contrary to productivity, does not scale with mainshock magnitude [47,48]. The most important outcome of our analysis is the dependence of on the style of faulting of the mainshock. Sequences whose mainshocks are originated from extensional tectonic settings (normal faulting) tend to have longer than compressional ones (reverse faulting). Transform fault zones (strike-slip) also exhibit long durations on average, however, they are more scattered, revealing region-specific dependencies. Valerio et al. [72] reached a similar conclusion using two different techniques, stating that sequences related to extensional setting are more abundant in aftershocks and last longer than those related to contractional regimes. A possible explanation for this can be ascribed to the different type of energy release dominating in each type of faulting. Thrust fault blocks move against gravity and quickly consume the energy to elevate the fault hanging wall upwards (fewer aftershocks, smaller ), whereas normal fault blocks move in favor of gravity, thus gravitational forces prevail over elastic stress release [72,73]. As a result, when normal faults are activated, inertia is perpetuated by gravity (more aftershocks, higher ) until a gravitational equilibrium is reached [74].
Our data suggest a possible negative correlation between and background seismicity rate as well as the fault slip rate, both being proxies of the stressing rate. However, our dataset is relatively too small to draw definitive conclusions due to the fact that the reliable estimation of was possible only for a subset of the total data. According to the rate-and-state framework [35], as the stress step increases, the subsequent aftershock productivity becomes higher. In other words, an area with a low background seismicity rate (related to a background stressing rate ) will need more time to respond in an abrupt stress step τ than a region with higher , where less time is needed for seismicity rate to return to its background level. However, we often find typical examples of highly productive sequences in areas of increased . This has been addressed by Page and van der Elst [75] who argued that over a limited spatial scale, variations in stressing rate and background seismicity may reflect the local fault population in a given area. It is therefore projected that both background events and aftershocks are more likely to occur in areas with a higher concentration of faults.
Deviations in intersequence productivity among the zones are more intricate to interpret. For this reason, a measure of Relative Productivity (RP) was employed. RP is closely related to the a-value of the RJ89 model but is more efficient to assess variations in productivity on an earthquake-by-earthquake basis [43], provided that it is independent of the mainshock magnitude. The map illustrating RP-values in Greece for the study period (Figure 9) reveals once again the influence of the tectonic regime. The different behavior of these regimes, apart from the faulting style that comes in play, may be accredited to the level of seismic coupling characterizing these regions. The convergence between the African and the Eurasian plate along the Hellenic Arc occurs mostly aseismically, indicating only a fractional coupling across its interface (e.g., [54,76]). On the contrary, the Ionian Islands are considered a fully coupled area, with almost all seismic moment released seismically [77]. Seismic coupling and aftershock productivity could well be interconnected, as the accumulated elastic energy (strain rate) depends on the locking degree of fault systems [78]. It is therefore expected that areas with highly locked fault zones store a larger extent of stored elastic energy which in turn leads to more aftershocks.
Another source-related parameter that may explain variations in productivity and between aftershock sequences is the stress drop of the mainshock. Studies on the stress drop parameter in Greece (e.g., [79,80]) have revealed significant disparity between reverse faulting mainshocks compared to normal and strike-slip faulting ones, with the latter obtaining notably lower values. Our results imply an inverse relationship between productivity and stress drop, providing space for physical interpretation. For instance, two highlighted cases are the 6.5 Kozani 1995 and M6.5 Aigio 1995 sequences (e.g., [81]) (mainshocks 1 and 2, respectively; Table 1) which exhibit low stress drops [79] whilst having elevated RP-values (Figure 9) and a profuse duration compared to the rest. Our interpretation of the connection between stress drop and aftershock productivity lies in the available extent that is prone to failure after the mainshock occurrence. For a given mainshock magnitude, higher stress drop is akin to a smaller rupture area that subsequently leads to diminished aftershock production in contrast with lower stress drop values [71].
5. Conclusions
A comparative analysis of aftershock sequences following strong ( ≥ 5.5) mainshocks in Greece was performed using two methods to assess aftershock productivity on a regional as well as on a case-by-case basis. We tested the efficacy of Båth’s law and implemented a statistical method to estimate the total duration of the sequences. The central Ionian Islands area emerges as the one with the highest aftershock productivity whereas the Hellenic Trench exhibits the most inhibited aftershock activity. We find that aftershock productivity depends on the rupture process of the mainshock, however, other source-related parameters such as the focal depth and stress heterogeneity are contributing factors, leading to regional variability. The herein obtained results indicate that, irrespectively of the mainshock magnitude, the total duration of aftershock sequences is controlled by the rupture process of the mainshock. Extensional stress regimes exhibit longer durations compared to the other ones, presumably due to the different form of energy release coming in play. The examination of more source-related (i.e., by exploiting finite-fault solutions) or other parameters may constitute the scope of future studies in an effort to highlight variations amidst the aftershock sequences following strong ( ≥ 5.5) mainshocks in Greece.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/geosciences12090328/s1. Table S1 lists the b-values calculated for each zone through the maximum likelihood estimate along with the confidence interval level of residuals. In Table S2, the results of the stacked fits of the RJ89 model using variable time windows (10, 60, 120 days) and mean (b = 1.06) or region-specific b-values are presented. Table S3 demonstrates the list of mainshocks used for the analysis, their focal mechanism classification (column 8), their relative placement among the designed zones (column 9) and the aftershock duration (Ta) (column 10) and relative productivity (RP) (column 11) of their aftershock sequence.
Author Contributions
Conceptualization, P.B., V.G.K., E.E.P. and G.K.; methodology, P.B., V.G.K., E.E.P. and G.K.; software, P.B.; validation, P.B.; formal analysis, P.B., V.G.K. and G.K.; data curation, P.B.; writing—original draft preparation, P.B.; writing—review and editing, V.G.K., E.E.P. and G.K.; visualization, P.B. and E.E.P.; supervision, V.G.K.; funding acquisition, G.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The seismic data used in this study are publicly available at https://doi.org/10.7914/SN/HT.
Acknowledgments
The authors would like to thank the two anonymous reviewers for the constructive and detailed comments that contributed to the improvement of the manuscript. Geophysics Department Contribution 964.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Scholz, C.H. The Mechanics of Earthquakes and Faulting, 3rd ed.; Cambridge University Press: Oxford City, UK, 2019; ISBN 978-1-316-68147-3. [Google Scholar]
- Omori, F. On the Aftershocks of Earthquakes. J. Coll. Sci. Imp. Univ. Tokyo 1895, 7, 111–120. [Google Scholar]
- Utsu, T. A Statistical Study on the Occurrence of Aftershocks. Geophys. Mag. 1961, 30, 521–605. [Google Scholar]
- Kisslinger, C. Aftershocks and Fault-Zone Properties. In Advances in Geophysics; Elsevier: Amsterdam, The Netherlands, 1996; Volume 38, pp. 1–36. ISBN 978-0-12-018838-3. [Google Scholar]
- Reasenberg, P.A.; Jones, L.M. Earthquake Hazard after a Mainshock in California. Sci. New Ser. 1989, 243, 1173–1176. [Google Scholar] [CrossRef] [PubMed]
- Ommi, S.; Zafarani, H.; Zare, M. Aftershock Decay Rates in the Iranian Plateau. Pure Appl. Geophys. 2016, 173, 2305–2324. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of Earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in Earthquake-Size Distribution across Different Stress Regimes. Nature 2005, 437, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Scholz, C.H. On the Stress Dependence of the Earthquake b Value. Geophys. Res. Lett. 2015, 42, 1399–1402. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhou, S. The Spatiotemporal Variation of the B-Value and Its Tectonic Implications in North China. Earthq. Sci. 2014, 27, 301–310. [Google Scholar] [CrossRef]
- Hatzidimitriou, P.; Papazachos, B.; Karakaisis, G. Quantitative Seismicity of the Aegean and Surrounding Area. In Proceedings of the XXIV Gen. Assembly of E.S.C., Athens, Greece, 19–24 September 1994; pp. 155–164. [Google Scholar]
- Papazachos, C. An Alternative Method for a Reliable Estimation of Seismicity with an Application in Greece and the Surrounding Area. Bull. Seismol. Soc. Am. 1999, 89, 111–119. [Google Scholar] [CrossRef]
- Vamvakaris, D.A.; Papazachos, C.B.; Papaioannou, C.A.; Scordilis, E.M.; Karakaisis, G.F. A Detailed Seismic Zonation Model for Shallow Earthquakes in the Broader Aegean Area. Nat. Hazards Earth Syst. Sci. 2016, 16, 55–84. [Google Scholar] [CrossRef]
- Båth, M. Lateral Inhomogeneities of the Upper Mantle. Tectonophysics 1965, 2, 483–514. [Google Scholar] [CrossRef]
- Vere-Jones, D. A Note on the Statistical Interpretation of Båth’s Law. Bull. Seismol. Soc. Am. 1969, 59, 1535–1541. [Google Scholar] [CrossRef]
- Lombardi, A.M. Probabilistic Interpretation of «Bath’s Law». Ann. Geophys. 2002, 45, 455–472. [Google Scholar] [CrossRef]
- Console, R.; Lombardi, A.M.; Murru, M.; Rhoades, D. Båth’s Law and the Self-Similarity of Earthquakes: BÅTH’S LAW. J. Geophys. Res. Solid Earth 2003, 108, 2128. [Google Scholar] [CrossRef]
- Drakatos, G.; Latoussakis, J. A Catalog of Aftershock Sequences in Greece (1971–1997): Their Spatial and Temporal Characteristics. J. Seismol. 2001, 5, 137–145. [Google Scholar] [CrossRef]
- Wells, D.L.; Coppersmith, K.J. New Empirical Relationships among Magnitude, Rupture Length, Rupture Width, Rupture Area, and Surface Displacement. Bull. Seismol. Soc. Am. 1994, 84, 974–1002. [Google Scholar]
- Page, M.T.; van der Elst, N.; Hardebeck, J.; Felzer, K.; Michael, A.J. Three Ingredients for Improved Global Aftershock Forecasts: Tectonic Region, Time-Dependent Catalog Incompleteness, and Intersequence Variability. Bull. Seismol. Soc. Am. 2016, 106, 2290–2301. [Google Scholar] [CrossRef]
- Kagan, Y.Y. Aftershock Zone Scaling. Bull. Seismol. Soc. Am. 2002, 92, 641–655. [Google Scholar] [CrossRef]
- Álvarez-Gómez, J.A. FMC—Earthquake Focal Mechanisms Data Management, Cluster and Classification. SoftwareX 2019, 9, 299–307. [Google Scholar] [CrossRef]
- Hardebeck, J.L.; Llenos, A.L.; Michael, A.J.; Page, M.T.; van der Elst, N. Updated California Aftershock Parameters. Seismol. Res. Lett. 2019, 90, 262–270. [Google Scholar] [CrossRef]
- McKenzie, D. Some Remarks on the Development of Sedimentary Basins. Earth Planet. Sci. Lett. 1978, 40, 25–32. [Google Scholar] [CrossRef]
- King, G.; Sturdy, D.; Whitney, J. The Landscape Geometry and Active Tectonics of Northwest Greece. Geol. Soc. Am. Bull. 1993, 105, 137–161. [Google Scholar] [CrossRef]
- Scordilis, E.M.; Karakaisis, G.F.; Karacostas, B.G.; Panagiotopoulos, D.G.; Comninakis, P.E.; Papazachos, B.C. Evidence for Transform Faulting in the Ionian Sea: The Cephalonia Island Earthquake Sequence of 1983. Pure Appl. Geophys. 1985, 123, 388–397. [Google Scholar] [CrossRef]
- Papadimitriou, P. Etude de La Structure Du Manteau Superieur de l’ Europe et Modelisation Des Ondes de Volume Engendrees Par Des Seismes Egeens. Ph.D. Thesis, University of Paris, Paris, France, 1988. [Google Scholar]
- Kiratzi, A.A.; Langston, C.A. Moment Tensor Inversion of the 1983 January 17 Kefallinia Event of Ionian Islands (Greece). Geophys. J. Int. 1991, 105, 529–535. [Google Scholar] [CrossRef]
- Sakkas, V.; Kapetanidis, V.; Kaviris, G.; Spingos, I.; Mavroulis, S.; Diakakis, M.; Alexopoulos, J.D.; Kazantzidou-Firtinidou, D.; Kassaras, I.; Dilalos, S.; et al. Seismological and Ground Deformation Study of the Ionian Islands (W. Greece) during 2014–2018, a Period of Intense Seismic Activity. Appl. Sci. 2022, 12, 2331. [Google Scholar] [CrossRef]
- Kiratzi, A.; Aktar, M.; Svigkas, N. The 10 June 2012 MW 6.0 Earthquake Sequence in the Easternmost End of the Hellenic Arc. Bull. Geol. Soc. Greece 2013, 47, 1138. [Google Scholar] [CrossRef][Green Version]
- Kapetanidis, V.; Deschamps, A.; Papadimitriou, P.; Matrullo, E.; Karakonstantis, A.; Bozionelos, G.; Kaviris, G.; Serpetsidaki, A.; Lyon-Caen, H.; Voulgaris, N.; et al. The 2013 Earthquake Swarm in Helike, Greece: Seismic Activity at the Root of Old Normal Faults. Geophys. J. Int. 2015, 202, 2044–2073. [Google Scholar] [CrossRef]
- Mesimeri, M.; Karakostas, V.; Papadimitriou, E.; Tsaklidis, G.; Jacobs, K. Relocation of Recent Seismicity and Seismotectonic Properties in the Gulf of Corinth (Greece). Geophys. J. Int. 2018, 212, 1123–1142. [Google Scholar] [CrossRef]
- Kourouklas, C.; Mangira, O.; Console, R.; Papadimitriou, E.; Karakostas, V.; Murru, M. Short-Term Clustering Modeling of Seismicity in Eastern Aegean Sea (Greece): A Retrospective Forecast Test of the 2017 Mw = 6.4 Lesvos, 2017 Mw = 6.6 Kos and 2020 Mw = 7.0 Samos Earthquake Sequences. Acta Geophys. 2021, 69, 1085–1099. [Google Scholar] [CrossRef]
- Mountrakis, D.; Tranos, M.; Papazachos, C.; Thomaidou, E.; Karagianni, E.; Vamvakaris, D.A. Neotectonic and Seismological Data Concerning Major Active Faults, and the Stress Regimes of Northern Greece. In Development of the Eastern Mediterranean Region; Geological Society of London: London, UK, 2006; Volume 260, pp. 649–670. ISBN 978-1-86239-198-7. [Google Scholar]
- Dieterich, J. A Constitutive Law for Rate of Earthquake Production and Its Application to Earthquake Clustering. J. Geophys. Res. Solid Earth 1994, 99, 2601–2618. [Google Scholar] [CrossRef]
- Dieterich, J.H. Modeling of Rock Friction: 1. Experimental Results and Constitutive Equations. J. Geophys. Res. 1979, 84, 2161. [Google Scholar] [CrossRef]
- Hainzl, S.; Christophersen, A.; Rhoades, D.; Harte, D. Statistical Estimation of the Duration of Aftershock Sequences. Geophys. J. Int. 2016, 205, 1180–1189. [Google Scholar] [CrossRef]
- Sebastiani, G.; Govoni, A.; Pizzino, L. Aftershock Patterns in Recent Central Apennines Sequences. J. Geophys. Res. Solid Earth 2019, 124, 3881–3897. [Google Scholar] [CrossRef]
- Wiemer, S. Minimum Magnitude of Completeness in Earthquake Catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Lehmann, E.L. Elements of Large-Sample Theory; Springer Texts in Statistics; Springer: New York, NY, USA, 1999; ISBN 978-0-387-98595-4. [Google Scholar]
- Helmstetter, A. Is Earthquake Triggering Driven by Small Earthquakes? Phys. Rev. Lett. 2003, 91, 058501. [Google Scholar] [CrossRef] [PubMed]
- Felzer, K.R. A Common Origin for Aftershocks, Foreshocks, and Multiplets. Bull. Seismol. Soc. Am. 2004, 94, 88–98. [Google Scholar] [CrossRef]
- Dascher-Cousineau, K.; Brodsky, E.E.; Lay, T.; Goebel, T.H.W. What Controls Variations in Aftershock Productivity? J. Geophys. Res. Solid Earth 2020, 125, e2019JB018111. [Google Scholar] [CrossRef]
- Aki, K. Maximum Likelihood Estimate of b in the Formula LogN a—BM and Its Confidence Limits. Earthq. Res. Inst. Univ. Tokyo 1965, 43, 237–239. [Google Scholar]
- Drakopoulos, J. Characteristic Parameters of Fore- and Aftershock Sequences in the Area of Greece. Ph.D. Thesis, University of Athens, Athens, Greece, 1968. [Google Scholar]
- Tahir, M.; Grasso, J.-R.; Amorèse, D. The Largest Aftershock: How Strong, How Far Away, How Delayed?: BÅTH’S LAW. Geophys. Res. Lett. 2012, 39, L04301. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S. Why Aftershock Duration Matters for Probabilistic Seismic Hazard Assessment. Bull. Seismol. Soc. Am. 2018, 108, 1414–1426. [Google Scholar] [CrossRef]
- Ziv, A. Does Aftershock Duration Scale with Mainshock Size? Geophys. Res. Lett. 2006, 33, L17317. [Google Scholar] [CrossRef]
- Godano, C.; Tramelli, A. How Long Is an Aftershock Sequence? Pure Appl. Geophys. 2016, 173, 2295–2304. [Google Scholar] [CrossRef]
- Karakostas, V.G.; Papadimitriou, E.E.; Tranos, M.D.; Papazachos, C.B. Active Seismotectonic Structures in the Area of Chios Island, North Aegean Sea, Revealed from Microseismicity and Fault Plane Solutions. Bull. Geol. Soc. Greece 2010, 43, 2064–2074. [Google Scholar] [CrossRef][Green Version]
- Bountzis, P.; Papadimitriou, E.; Tsaklidis, G. Identification and Temporal Characteristics of Earthquake Clusters in Selected Areas in Greece. Appl. Sci. 2022, 12, 1908. [Google Scholar] [CrossRef]
- Karakostas, V.; Kostoglou, A.; Chorozoglou, D.; Papadimitriou, E. Relocation of the 2018 Zakynthos, Greece, Aftershock Sequence: Spatiotemporal Analysis Deciphering Mechanism Diversity and Aftershock Statistics. Acta Geophys. 2020, 68, 1263–1294. [Google Scholar] [CrossRef]
- Reilinger, R.; McClusky, S.; Vernant, P.; Lawrence, S.; Ergintav, S.; Cakmak, R.; Ozener, H.; Kadirov, F.; Guliev, I.; Stepanyan, R.; et al. GPS Constraints on Continental Deformation in the Africa-Arabia-Eurasia Continental Collision Zone and Implications for the Dynamics of Plate Interactions. J. Geophys. Res. Solid Earth 2006, 111, B05411. [Google Scholar] [CrossRef]
- Jenny, S.; Goes, S.; Giardini, D.; Kahle, H.-G. Earthquake Recurrence Parameters from Seismic and Geodetic Strain Rates in the Eastern Mediterranean. Geophys. J. Int. 2004, 157, 1331–1347. [Google Scholar] [CrossRef]
- Howell, A.; Palamartchouk, K.; Papanikolaou, X.; Paradissis, D.; Raptakis, C.; Copley, A.; England, P.; Jackson, J. The 2008 Methoni Earthquake Sequence: The Relationship between the Earthquake Cycle on the Subduction Interface and Coastal Uplift in SW Greece. Geophys. J. Int. 2017, 208, 1592–1610. [Google Scholar] [CrossRef]
- Papadimitriou, E.; Gospodinov, D.; Karakostas, V.; Astiopoulos, A. Evolution of the Vigorous 2006 Swarm in Zakynthos (Greece) and Probabilities for Strong Aftershocks Occurrence. J. Seismol. 2013, 17, 735–752. [Google Scholar] [CrossRef]
- Bocchini, G.M.; Novikova, T.; Papadopoulos, G.A.; Agalos, A.; Mouzakiotis, E.; Karastathis, V.; Voulgaris, N. Tsunami Potential of Moderate Earthquakes: The July 1, 2009 Earthquake (Mw 6.45) and Its Associated Local Tsunami in the Hellenic Arc. Pure Appl. Geophys. 2020, 177, 1315–1333. [Google Scholar] [CrossRef]
- Kiratzi, A.A. The 16 April 2015 MW6.1 Earthquake Sequence near Kasos Island at the Eastern Hellenic Subduction Zone. Bull. Geol. Soc. Greece 2016, 50, 1163. [Google Scholar] [CrossRef]
- Karakostas, V.G.; Papadimitriou, E.E.; Karakaisis, G.F.; Papazachos, C.B.; Scordilis, E.M.; Vargemezis, G.; Aidona, E. The 2001 Skyros, Northern Aegean, Greece, Earthquake Sequence: Off—Fault Aftershocks, Tectonic Implications, and Seismicity Triggering. Geophys. Res. Lett. 2003, 30, 12-1–12-14. [Google Scholar] [CrossRef]
- Kiratzi, A.; Tsakiroudi, E.; Benetatos, C.; Karakaisis, G. The 24 May 2014 (Mw6.8) Earthquake (North Aegean Trough): Spatiotemporal Evolution, Source and Slip Model from Teleseismic Data. Phys. Chem. Earth Parts ABC 2016, 95, 85–100. [Google Scholar] [CrossRef]
- Papadimitriou, P.; Kassaras, I.; Kaviris, G.; Tselentis, G.-A.; Voulgaris, N.; Lekkas, E.; Chouliaras, G.; Evangelidis, C.; Pavlou, K.; Kapetanidis, V.; et al. The 12th June 2017 Mw = 6.3 Lesvos Earthquake from Detailed Seismological Observations. J. Geodyn. 2018, 115, 23–42. [Google Scholar] [CrossRef]
- Karakostas, V.; Ilieva, M.; Kostoglou, A.; Tondaś, D.; Papadimitriou, E.; Mesimeri, M.; Koca, B. The 2017 Kos Sequence: Aftershocks Relocation and Coseismic Rupture Process Constrained from Joint Inversion of Seismological and Geodetic Observations. Tectonophysics 2022, 833, 229352. [Google Scholar] [CrossRef]
- Karakostas, V.; Tan, O.; Kostoglou, A.; Papadimitriou, E.; Bonatis, P. Seismotectonic Implications of the 2020 Samos, Greece, Mw 7.0 Mainshock Based on High-Resolution Aftershock Relocation and Source Slip Model. Acta Geophys. 2021, 69, 979–996. [Google Scholar] [CrossRef]
- Hatzfeld, D.; Karakostas, V.; Ziazia, M.; Selvaggi, G.; Leborgne, S.; Berge, C.; Guiguet, R.; Paul, A.; Voidomatis, P.; Diagnourtas, D.; et al. The Kozani-Grevena (Greece) Earthquake of 13 May 1995 Revisited from a Detailed Seismological Study. Bull. Seismol. Soc. Am. 1997, 87, 463–473. [Google Scholar] [CrossRef]
- Pavlou, K.; Kaviris, G.; Chousianitis, K.; Drakatos, G.; Kouskouna, V.; Makropoulos, K. Seismic Hazard Assessment in Polyphyto Dam Area (NW Greece) and Its Relation with the Earthquake of 13 May 1995 (Ms = 6.5, NW Greece). Nat. Hazards Earth Syst. Sci. 2013, 13, 141–149. [Google Scholar] [CrossRef]
- Kaviris, G.; Millas, C.; Spingos, I.; Kapetanidis, V.; Fountoulakis, I.; Papadimitriou, P.; Voulgaris, N.; Makropoulos, K. Observations of Shear-Wave Splitting Parameters in the Western Gulf of Corinth Focusing on the 2014 Mw = 5.0 Earthquake. Phys. Earth Planet. Inter. 2018, 282, 60–76. [Google Scholar] [CrossRef]
- Michas, G.; Kapetanidis, V.; Kaviris, G.; Vallianatos, F. Earthquake Diffusion Variations in the Western Gulf of Corinth (Greece). Pure Appl. Geophys. 2021, 178, 2855–2870. [Google Scholar] [CrossRef]
- Hainzl, S.; Zakharova, O.; Marsan, D. Impact of Aseismic Transients on the Estimation of Aftershock Productivity Parameters. Bull. Seismol. Soc. Am. 2013, 103, 1723–1732. [Google Scholar] [CrossRef]
- Amezawa, Y.; Maeda, T.; Kosuga, M. Migration Diffusivity as a Controlling Factor in the Duration of Earthquake Swarms. Earth Planets Space 2021, 73, 148. [Google Scholar] [CrossRef]
- Gomberg, J.; Bodin, P. The Productivity of Cascadia Aftershock Sequences. Bull. Seismol. Soc. Am. 2021, 111, 1494–1507. [Google Scholar] [CrossRef]
- Wetzler, N.; Brodsky, E.E.; Lay, T. Regional and Stress Drop Effects on Aftershock Productivity of Large Megathrust Earthquakes: Megathrust Aftershock Productivity. Geophys. Res. Lett. 2016, 43, 12012–12020. [Google Scholar] [CrossRef]
- Valerio, E.; Tizzani, P.; Carminati, E.; Doglioni, C. Longer Aftershocks Duration in Extensional Tectonic Settings. Sci. Rep. 2017, 7, 16403. [Google Scholar] [CrossRef]
- Doglioni, C.; Carminati, E.; Petricca, P.; Riguzzi, F. Normal Fault Earthquakes or Graviquakes. Sci. Rep. 2015, 5, 12110. [Google Scholar] [CrossRef] [PubMed]
- Bignami, C.; Valerio, E.; Carminati, E.; Doglioni, C.; Petricca, P.; Tizzani, P.; Lanari, R. Are Normal Fault Earthquakes Due to Elastic Rebound or Gravitational Collapse? Ann. Geophys. 2020, 63, 1–15. [Google Scholar] [CrossRef]
- Page, M.T.; van der Elst, N.J. Aftershocks Preferentially Occur in Previously Active Areas. Seism. Rec. 2022, 2, 100–106. [Google Scholar] [CrossRef]
- Laigle, M.; Sachpazi, M.; Hirn, A. Variation of Seismic Coupling with Slab Detachment and Upper Plate Structure along the Western Hellenic Subduction Zone. Tectonophysics 2004, 391, 85–95. [Google Scholar] [CrossRef]
- Briole, P.; Ganas, A.; Elias, P.; Dimitrov, D. The GPS Velocity Field of the Aegean. New Observations, Contribution of the Earthquakes, Crustal Blocks Model. Geophys. J. Int. 2021, 226, 468–492. [Google Scholar] [CrossRef]
- Hainzl, S.; Sippl, C.; Schurr, B. Linear Relationship between Aftershock Productivity and Seismic Coupling in the Northern Chile Subduction Zone. J. Geophys. Res. Solid Earth 2019, 124, 8726–8738. [Google Scholar] [CrossRef]
- Chouliaras, G.; Stavrakakis, G.N. Seismic Source Parameters from a New Dial-up Seismological Network in Greece. Pure Appl. Geophys. 1997, 150, 91–111. [Google Scholar] [CrossRef]
- Margaris, B.N. Source Spectral Scaling and Stress Release Estimates Using Strong-Motion Records in Greece. Bull. Seismol. Soc. Am. 2002, 92, 1040–1059. [Google Scholar] [CrossRef]
- Bernard, P.; Briole, P.; Meyer, B.; Lyon-Caen, H.; Cattin, R.; Hatzfeld, D.; Lachet, C.; Lebrun, B.; Deschamps, A.; Courboulex, F.; et al. The Ms = 6.2, 15 June 1995 Aigion Earthquake (Greece): Evidence for Low Angle Normal Faulting in the Corinth Rift. J. Seismol. 1997, 1, 131–150. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).