Mapping Gully Erosion Variability and Susceptibility Using Remote Sensing, Multivariate Statistical Analysis, and Machine Learning in South Mato Grosso, Brazil
Abstract
:1. Introduction
2. Materials and Methods
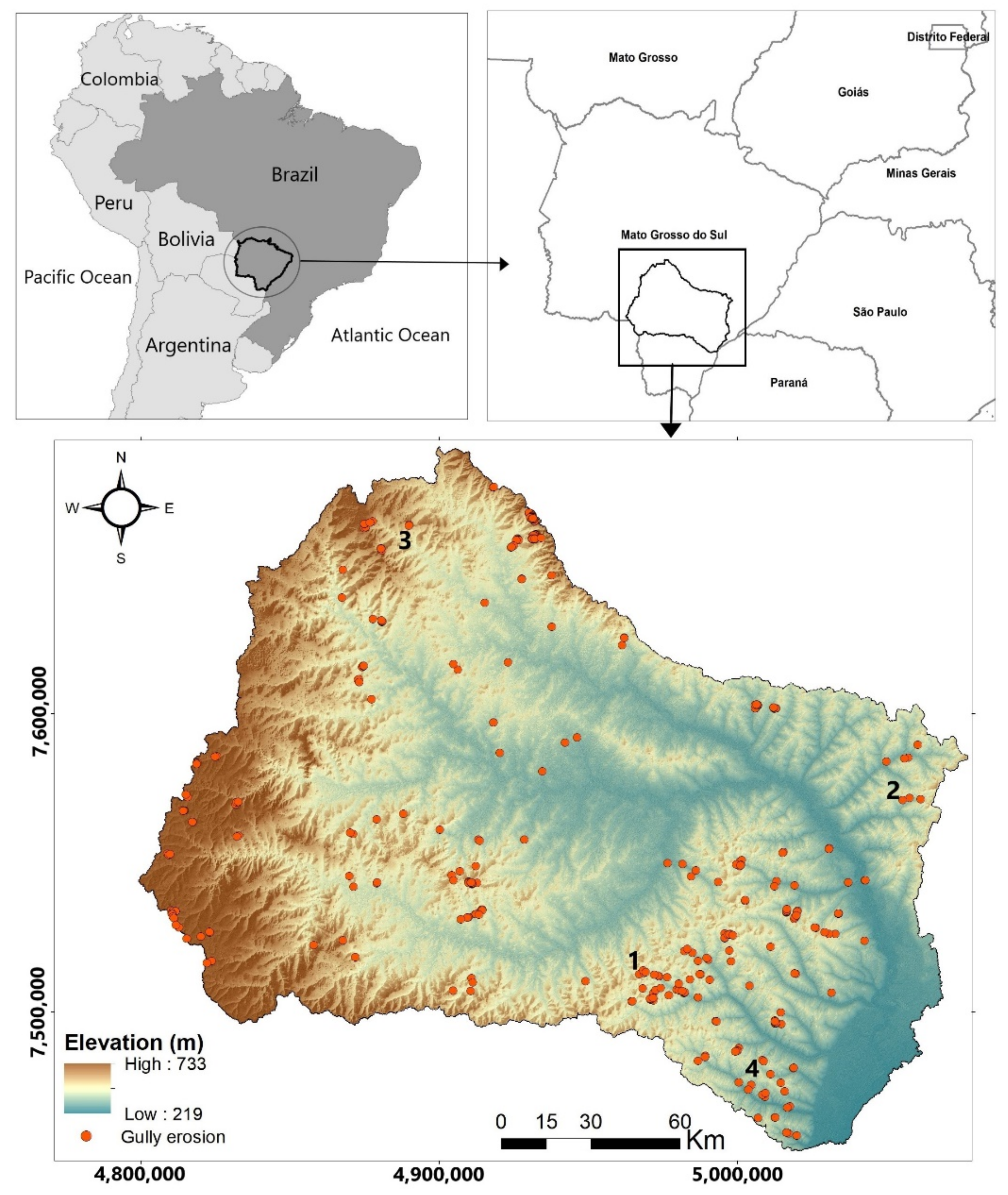
2.1. Study Area
2.2. Input Variables Map
2.2.1. Gully Erosion Inventory
2.2.2. Selection of Environmental Parameters
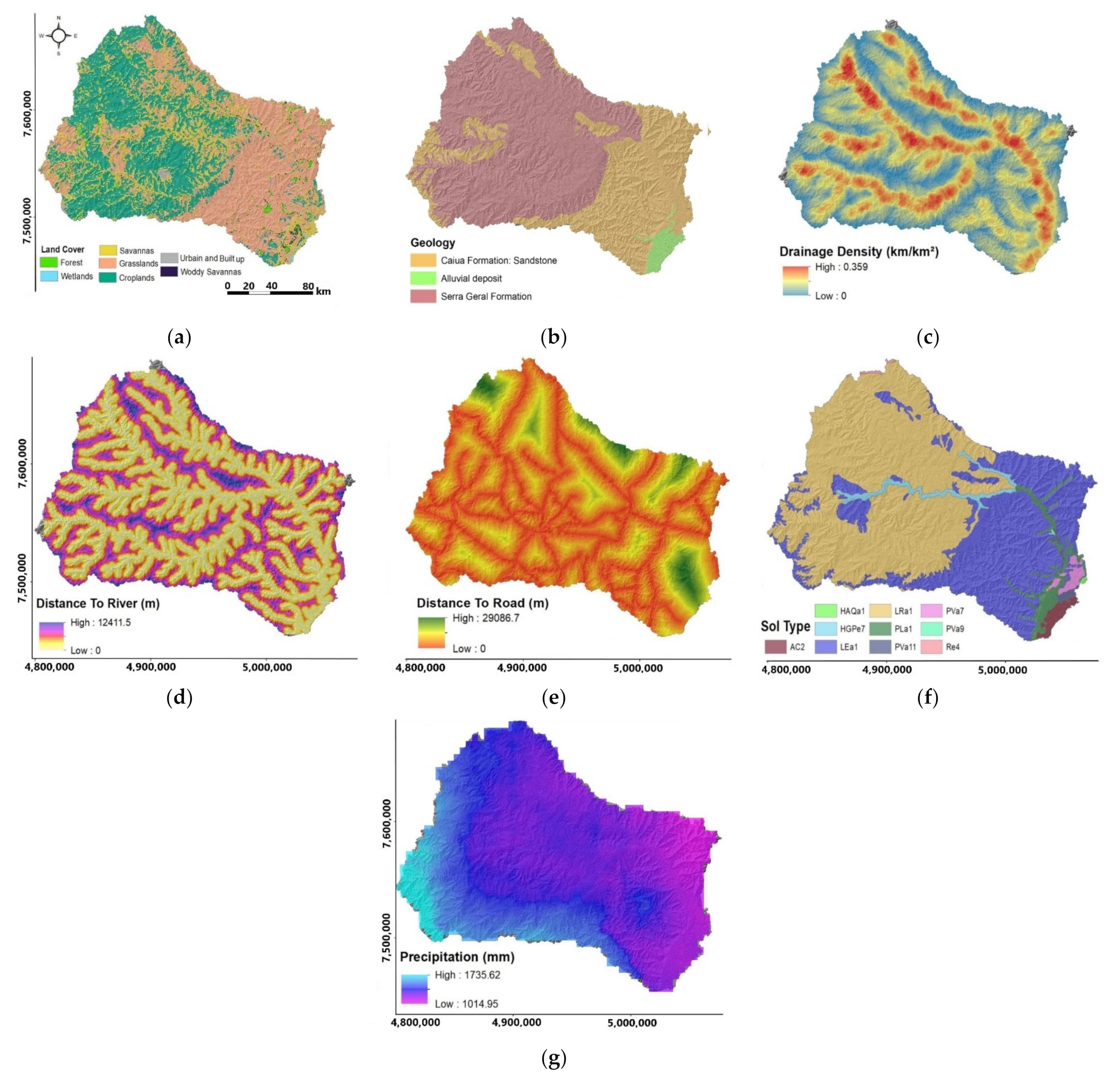
- Elevation is one of the most important factors affecting erosive phenomena with, in general, a positive relationship between elevation and the formation of gully and rill erosion [30]. The elevation map (Figure 3a) is derived from a 30 m resolution SRTM digital elevation model (DEM) obtained from the USGC Earth explorer website.
- Exposure (frequently referred to as Aspect, Figure 3c) is defined as the direction of maximum slope. This parameter indirectly affects gully erosion as it controls microclimate, sun exposure time, moisture retention, evapotranspiration, weathering rates, vegetation cover, and denudation processes [15,32,33]. This parameter has also been calculated from the 30 m resolution SRTM DEM.
- The topographic wetness index (TWI) represents the water accumulated in each pixel of the study surface [15]. It reflects the effect of topography on the distribution and zonation of saturation sources that may generate runoff (Figure 3e) [32,34,35]. TWI is calculated using a DEM (cell size = 30 m) and several GIS software tools to calculate slope, flow direction, flow accumulation, and slope angle [36].
- The topographic position index (TPI) indicates the upper and lower parts of the landscape, represented by the difference in elevation in each DEM cell (30 m) relative to the average elevation of surrounding cells [32]. Ridges and depressions are characterized by positive and negative values, respectively (Figure 3f). The TPI index results from comparing the elevation of each cell in a DEM with the average elevation of a specified neighborhood around that cell. The TPI is positive when the cell is higher than its surroundings (ridges and hilltops), and negative for depressed features such as valleys.
- Land cover and use can directly affect erosion [24]. The development of gullies is sometimes analyzed as an ancient phenomenon that has had its share of contribution to the morphology of Brazilian landscapes [3], but there are many studies that attest to the role of anthropogenic activities in contributing to and accelerating erosive processes [37]. Previous analysis, however, recognized that the effects are not always significant [25]. Therefore, a land cover map was made (Figure 4a) from the Moderate-Resolution Imaging Spectro-radiometer (MODIS) Land Cover Type 1 with a resolution of 500 m that has been resampled to a resolution of 30 m. The coding used for the land cover parameter is as follows: 1 = urban and built up, 2 = croplands, 3 = wetlands, 4 = grasslands, 5 = woody savannah, 6 = savannah, and 7 = forest.
- Geology is a critical parameter influencing erosive processes due to the strength of the rocks and soil formations that develop there, and the presence of lithological discontinuities [19,24]. Geological data of the study area were obtained from CRPM [38]. The three dominant geologic units are Quaternary alluvial deposits, basalts of the Serra Geral formation, and sandstones of the Caiuá formation (Figure 4b). The following code was assigned to each formation: Alluvial deposit = 1, Serra Geral formation = 2, and Caiuá formation = 3.
- Drainage density represents the number of streams per unit area. It reflects the surface permeability and infiltration rate, which control the intensity of surface runoff, and may be a factor in the gully formation process [32]. The calculation was conducted using the drainage network with the “Line density” tool in GIS software from the 30 m resolution SRTM DEM (Figure 4c).
- The distance to rivers determines the role of the dense river network in determining the stability of soil covers. It was calculated from the drainage network using the “Euclidean Distance” tool on the GIS tool with a resolution of 30 m (Figure 4d).
- Distance to roads is one way to approach the influence of anthropogenic activities on erosion development. Erosion initiated at the edge of the road network is considered one of the major sources of soil instability and has received scientific attention in recent decades [39,40,41,42]. Road construction can destabilize slopes and locally increase surface runoff, requiring appropriate stabilization and drainage measures during excavation and construction [19]. Distance to roads was calculated from the road network in the South Mato Grosso State using the “Euclidean Distance” tool on the GIS tool (Figure 4e).
- Soil properties, especially aggregate stability, affect surface erosion and water infiltration, and therefore influence the erosion process [43,44]. The soil type classes were extracted from the soil map (1/1,000,000) of the South Mato Grosso State of the Brazilian Geographic and Statistical Institute IBGE (Figure 4f). Table 1 shows the codes that have been assigned to each soil type.
- Precipitation is one of the main drivers of water-related erosion processes. The influence of precipitation on erosion depends on the duration and extent of rainfall events [32]. Pore filling increases pore pressure and reduces the effective normal force on a slope, potentially leading to destabilization of materials (rock or soil) [19]. We used the Climate Hazards Group InfraRed Precipitation with Station data (CHIRPS) to calculate the average annual precipitation over a 5-year period (2015–2020) for each sector (Figure 5g). CHIRPS is a 35+ year quasi-global rainfall dataset from 1981 to present, with a spanning range from 50° S to 50° N (and all longitudes). CHIRPS incorporates 0.05° climate CHPclim satellite imagery, together with in situ station data to create a gridded rainfall time series for trend analysis and seasonal drought monitoring (Figure 4g).
2.3. Data Analysis and Modeling
2.3.1. Principal Component Analysis
2.3.2. Gully Susceptibility Prediction
- Multivariate discriminant analysis (MDA) is a conventionally and widely used tool to study groups of observations that may have different characteristics [45]. MDA has shown good performance for classification and modeling in several hydrological and hydrochemical studies [14,46,48,49,50,51]. MDA is a generalization of Fisher’s linear discriminant, a method used in statistics, pattern recognition, and machine learning to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination, called discriminant functions, may be used as a linear classifier, or, more commonly, to reduce the dimensionality between before and after the classification. The discriminant function can be defined as follows:where F, V1, and W1 represent the discriminant score, the independent variables, and the discriminant weights, respectively.F = V1W1 + V2W2… + VnWn,
- Logistic regression (LR) is a statistical model that can describe the relationship between the probability of a binary response variable and a set of corresponding explanatory variables. It is a generalized linear model using a logistic function as a link function [52,53]. In this study, the logistic regression algorithm has been used to predict the probability of gully erosion to develop (value = 1) or not (value = 0) based on the optimization of the regression coefficients and using a logit natural logarithms model. This result always varies between 0 and 1. A threshold is selected, above which a gully is likely to develop.
- Classification and regression tree (CART) is an effective decision tree-based algorithm and has proven to be powerful technique for handling classification problems. The CART generates a sequence of sub-trees for classification problems by growing a large tree instead of using stopping rules. Therefore, it is able to construct complex trees for solving complicated problems with large datasets. CART has been widely used in many studies of natural hazards such as landslides, subsidence, urban flooding, etc. [11,19,20,52]. Here, it is be applied to the prediction of gully development following a four-step procedure: (1) building the tree, (2) stopping the building of the tree, (3) pruning the tree, and (4) selecting the optimal tree for classifying gully or non-gully classes [19,54]. For this method, we also deployed the Gini index method to create binary divisions with a maximum tree depth of 4.
- Random forest is a method for learning sets of regressions and classifications based on the construction, at the time of testing, of many uncorrelated decision trees [55], using the Gini index of impurities [20,56]. The RF model uses bootstrap sampling, to be implemented in the evaluation, which allows another unused subset, also called the out-of-bag data (OOB), to be used for validation. Therefore, for the construction of the RF model, several tests were performed to find the best number of trees from 40 to 200 to obtain the best result. For this study, the OOB error is minimal for a number of 60 in the prediction for a given point to belong to the gully class or not. The final result is the class selected by most trees.
2.3.3. Validation, Performance Metrics and Evaluation Criteria
2.3.4. Contribution Analysis of Parameters
3. Results
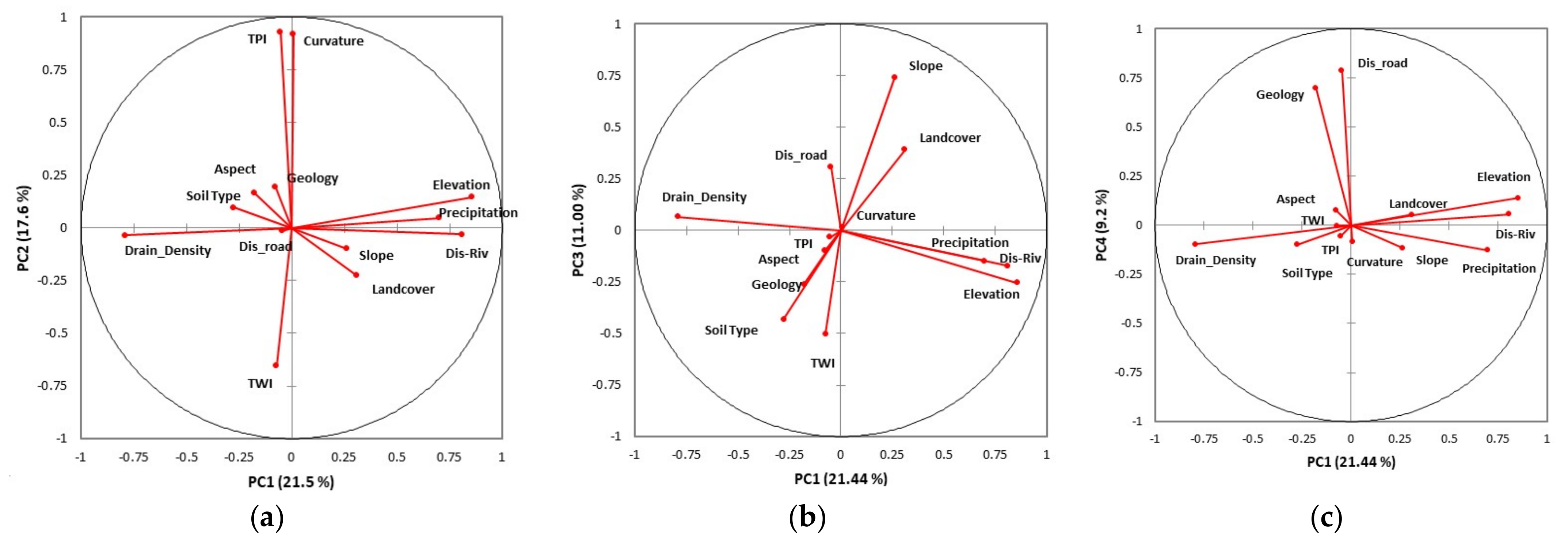
3.1. Principal Component Analysis and Distribution of PCs
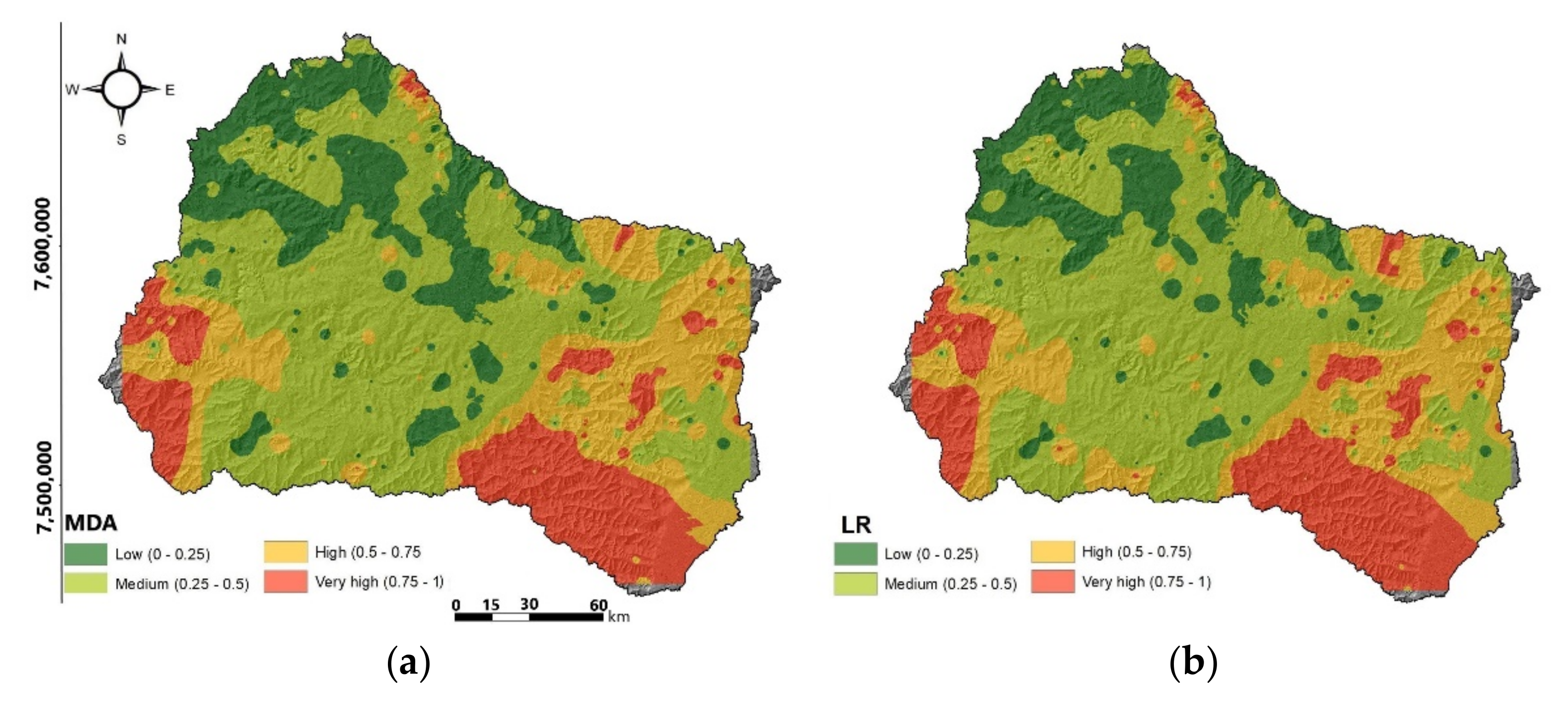
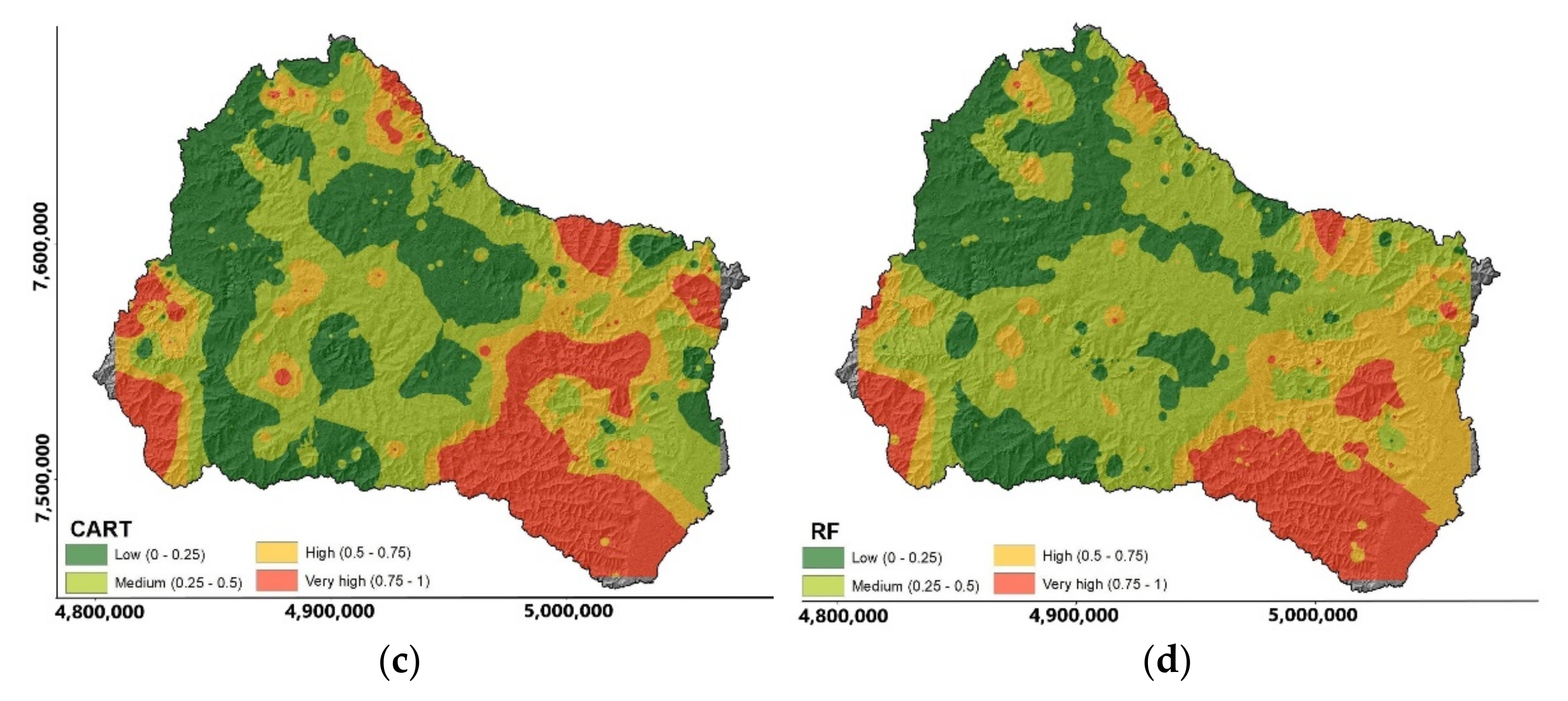
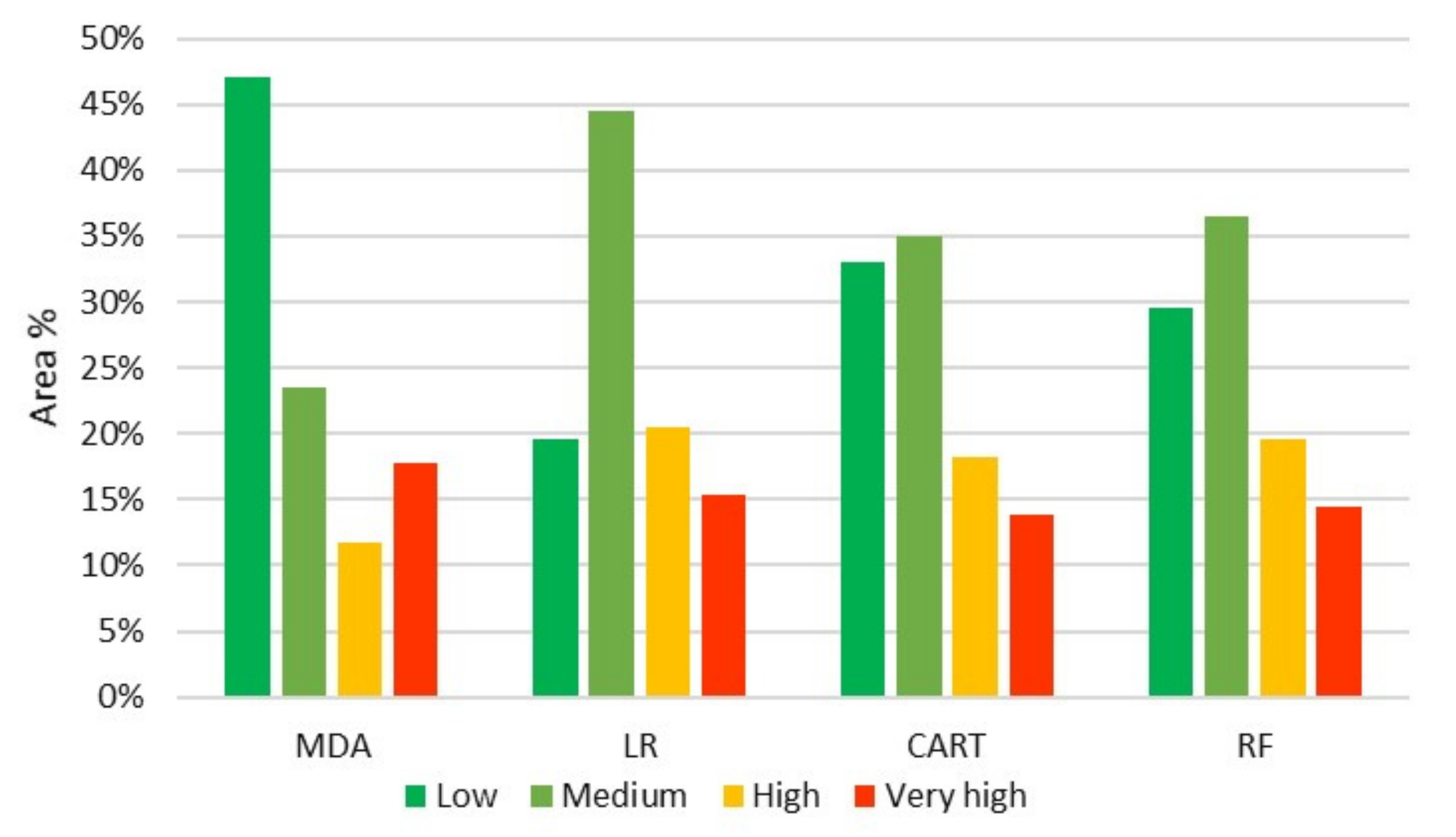
3.2. Machine Learning
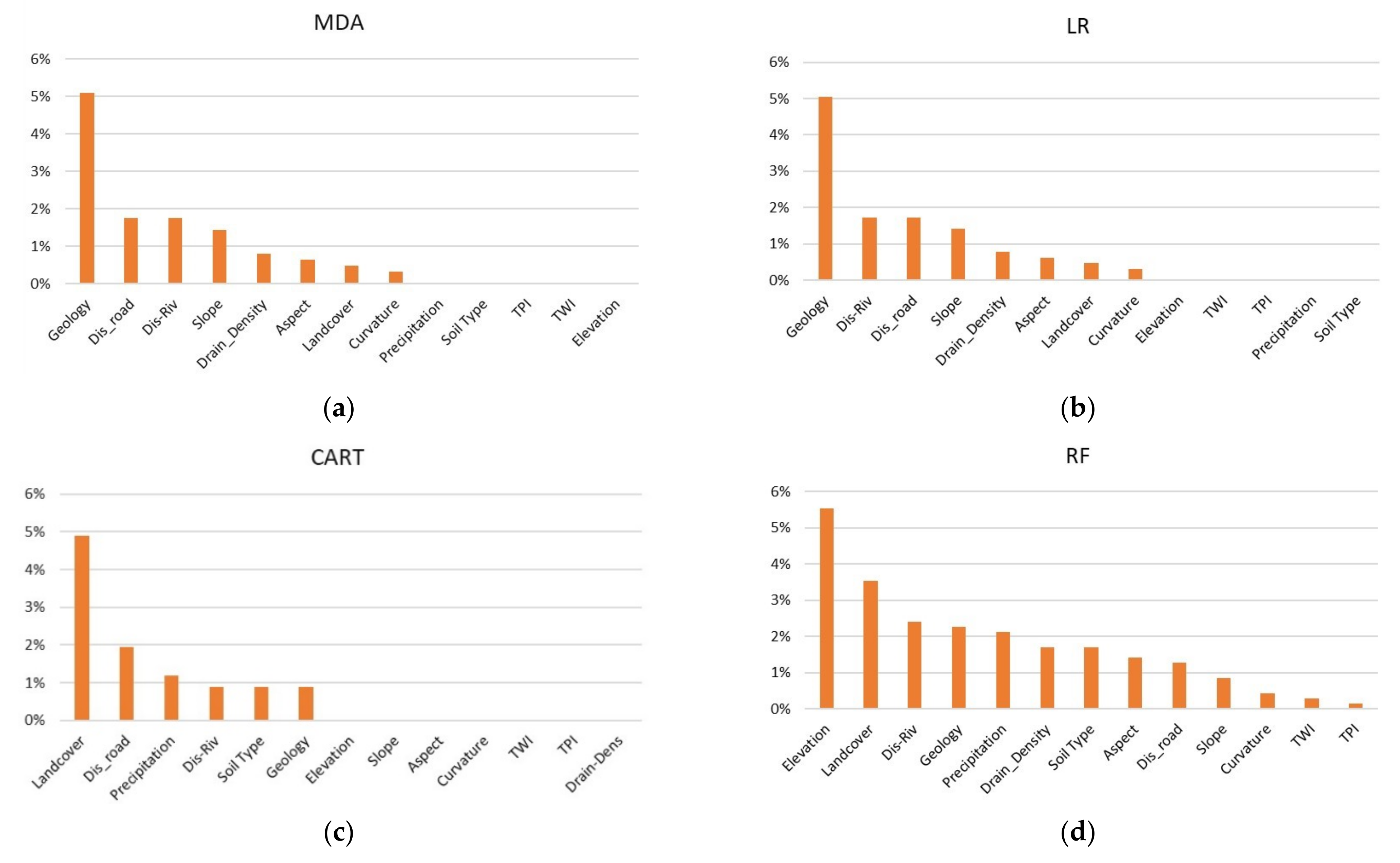
3.3. Contribution of Factors to Susceptibility Mapping
4. Discussion
4.1. Processes Associated with the Diversity of Gully Conditions
4.2. A Multi Parameter Contribution to Gully Formation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Martineli Costa, F.; Bacellar, L.A.T. Analysis of the influence of gully erosion in the flow pattern of catchment streams, Southeastern Brazil. CATENA 2007, 69, 230–238. [Google Scholar] [CrossRef]
- Castillo, C.; Gómez, J.A. A century of gully erosion research: Urgency, complexity and study approaches. Earth-Sci. Rev. 2016, 160, 300–319. [Google Scholar] [CrossRef]
- De Bacellar, L.A.P.; Coelho Netto, A.L.; Lacerda, W.A. Controlling factors of gullying in the Maracujá Catchment, southeastern Brazil. Earth Surf. Process. Landf. 2005, 30, 1369–1385. [Google Scholar] [CrossRef]
- Guerra, A.J.T.; Fullen, M.A.; Bezerra, J.F.; Jorge, M.C.O. Gully Erosion and Land Degradation in Brazil: A Case Study from São Luís Municipality, Maranhão State. In Ravine Lands: Greening for Livelihood and Environmental Security; Dagar, J.C., Singh, A.K., Eds.; Springer: Singapore, 2018; pp. 195–216. ISBN 978-981-10-8043-2. [Google Scholar]
- Tricart, J. Ecodinâmica; Instituto Brasileiro de Geografia e Estatística: Rio de Janeiro, Brazil, 1977. [Google Scholar]
- Christofoletti, A. Análise de Sistemas em Geografia: Introdução; Hucitec/Edusp: São Paulo, Brazil, 1979. [Google Scholar]
- Ross, J. Análise empírica da fragilidade dos ambientes naturais e antrópizados. Rev. Dep. Geogr. São Paulo 1994, 8, 63–74. [Google Scholar] [CrossRef] [Green Version]
- Crepani, E.; de Medeiros, J.S.; Hernandez Filho, P.; Florenzano, T.G.; Duarte, V.; Barbosa, C.C.F. Sensoriamento Remoto e Geoprocessamento Aplicados ao Zoneamento Ecológico-Econômico e ao Ordenamento Territorial; Inpe: São José dos Campos, Brazil, 2001. [Google Scholar]
- Conoscenti, C.; Angileri, S.; Cappadonia, C.; Rotigliano, E.; Agnesi, V.; Märker, M. Gully erosion susceptibility assessment by means of GIS-based logistic regression: A case of Sicily (Italy). Geomorphology 2014, 204, 399–411. [Google Scholar] [CrossRef] [Green Version]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Conoscenti, C. Gully erosion susceptibility mapping using GIS-based multi-criteria decision analysis techniques. CATENA 2019, 180, 282–297. [Google Scholar] [CrossRef]
- Bouramtane, T.; Kacimi, I.; Bouramtane, K.; Aziz, M.; Abraham, S.; Omari, K.; Valles, V.; Leblanc, M.; Kassou, N.; El Beqqali, O.; et al. Multivariate analysis and machine learning approach for mapping the variability and vulnerability of urban flooding: The case of Tangier city, Morocco. Hydrology 2021, 8, 182. [Google Scholar] [CrossRef]
- Tiouiouine, A.; Jabrane, M.; Kacimi, I.; Morarech, M.; Bouramtane, T.; Bahaj, T.; Yameogo, S.; Rezende-Filho, A.T.; Dassonville, F.; Moulin, M.; et al. Determining the relevant scale to analyze the quality of regional groundwater resources while combining groundwater bodies, physicochemical and biological databases in southeastern france. Water 2020, 12, 3476. [Google Scholar] [CrossRef]
- Chang, K.-T.; Merghadi, A.; Yunus, A.P.; Pham, B.T.; Dou, J. Evaluating scale effects of topographic variables in landslide susceptibility models using GIS-based machine learning techniques. Sci. Rep. 2019, 9, 12296. [Google Scholar] [CrossRef] [Green Version]
- Choubin, B.; Borji, M.; Mosavi, A.; Sajedi-Hosseini, F.; Singh, V.P.; Shamshirband, S. Snow avalanche hazard prediction using machine learning methods. J. Hydrol. 2019, 577, 123929. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef] [PubMed]
- Darabi, H.; Choubin, B.; Rahmati, O.; Torabi Haghighi, A.; Pradhan, B.; Kløve, B. Urban flood risk mapping using the GARP and QUEST models: A comparative study of machine learning techniques. J. Hydrol. 2019, 569, 142–154. [Google Scholar] [CrossRef]
- Dodangeh, E.; Panahi, M.; Rezaie, F.; Lee, S.; Tien Bui, D.; Lee, C.-W.; Pradhan, B. Novel hybrid intelligence models for flood-susceptibility prediction: Meta optimization of the GMDH and SVR models with the genetic algorithm and harmony search. J. Hydrol. 2020, 590, 125423. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Tien Bui, D. Spatial prediction of landslides using a hybrid machine learning approach based on Random Subspace and Classification and Regression Trees. Geomorphology 2018, 303, 256–270. [Google Scholar] [CrossRef]
- Rahmati, O.; Falah, F.; Naghibi, S.A.; Biggs, T.; Soltani, M.; Deo, R.C.; Cerdà, A.; Mohammadi, F.; Tien Bui, D. Land subsidence modelling using tree-based machine learning algorithms. Sci. Total Environ. 2019, 672, 239–252. [Google Scholar] [CrossRef] [PubMed]
- Garosi, Y.; Sheklabadi, M.; Conoscenti, C.; Pourghasemi, H.R.; Van Oost, K. Assessing the performance of GIS- based machine learning models with different accuracy measures for determining susceptibility to gully erosion. Sci. Total Environ. 2019, 664, 1117–1132. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Sadhasivam, N.; Kariminejad, N.; Collins, A.L. Gully erosion spatial modelling: Role of machine learning algorithms in selection of the best controlling factors and modelling process. Geosci. Front. 2020, 11, 2207–2219. [Google Scholar] [CrossRef]
- De Freitas Sampaio, L.; Crestana, S.; Rodrigues, V.G.S. Study of Gully Erosion in South Minas Gerais (Brazil) Using Fractal and Multifractal Analysis. In Proceedings of the IAEG/AEG Annual Meeting Proceedings, San Francisco, CA, USA, 26 August 2018; Shakoor, A., Cato, K., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 6, pp. 217–222. [Google Scholar]
- Real, L.S.C.; Crestana, S.; Ferreira, R.R.M.; Rodrigues, V.G.S. Evaluation of gully development over several years using GIS and fractal analysis: A case study of the Palmital watershed, Minas Gerais (Brazil). Environ. Monit. Assess. 2020, 192, 434. [Google Scholar] [CrossRef]
- Lana, J.C.; de Tarso Amorim Castro, P.; Lana, C.E. Assessing gully erosion susceptibility and its conditioning factors in southeastern Brazil using machine learning algorithms and bivariate statistical methods: A regional approach. Geomorphology 2022, 402, 108159. [Google Scholar] [CrossRef]
- Milani, E.; Rangel, H.; Bueno, G.; Stica, J.; Winter, W.; Caixeta, J.; Neto, O. Bacias Sedimentares Brasileiras-Cartas Estratigraficas. Bol. Geociênc. Da Petrobras 2007, 15, 183–205. [Google Scholar]
- Fernandes, L.A.; Coimbra, A.M. O grupo caiuá (Ks): Revisão estratigráfica e contexto deposicional. Rev. Bras. Geociênc. 1994, 24, 164–176. [Google Scholar] [CrossRef]
- Hembram, T.K.; Saha, S.; Pradhan, B.; Maulud, K.N.A.; Alamri, A.M. Robustness analysis of machine learning classifiers in predicting spatial gully erosion susceptibility with altered training samples. Geomat. Nat. Hazards Risk 2021, 12, 794–828. [Google Scholar] [CrossRef]
- Roy, J.; Saha, S. Integration of artificial intelligence with meta classifiers for the gully erosion susceptibility assessment in Hinglo river basin, Eastern India. Adv. Space Res. 2021, 67, 316–333. [Google Scholar] [CrossRef]
- Zhang, P.; Yao, W.; Liu, G.; Xiao, P. Experimental study on soil erosion prediction model of loess slope based on rill morphology. CATENA 2019, 173, 424–432. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Comparison of a logistic regression and Naïve Bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. CATENA 2016, 145, 164–179. [Google Scholar] [CrossRef]
- Hembram, T.K.; Paul, G.C.; Saha, S. Comparative Analysis between Morphometry and Geo-Environmental Factor Based Soil Erosion Risk Assessment Using Weight of Evidence Model: A Study on Jainti River Basin, Eastern India. Environ. Process. 2019, 6, 883–913. [Google Scholar] [CrossRef]
- Jaafari, A.; Najafi, A.; Pourghasemi, H.R.; Rezaeian, J.; Sattarian, A. GIS-based frequency ratio and index of entropy models for landslide susceptibility assessment in the Caspian forest, northern Iran. Int. J. Environ. Sci. Technol. 2014, 11, 909–926. [Google Scholar] [CrossRef] [Green Version]
- Conforti, M.; Aucelli, P.P.C.; Robustelli, G.; Scarciglia, F. Geomorphology and GIS analysis for mapping gully erosion susceptibility in the Turbolo stream catchment (Northern Calabria, Italy). Nat. Hazards 2011, 56, 881–898. [Google Scholar] [CrossRef]
- Shit, P.K.; Nandi, A.S.; Bhunia, G.S. Soil erosion risk mapping using RUSLE model on jhargram sub-division at West Bengal in India. Model. Earth Syst. Environ. 2015, 1, 28. [Google Scholar] [CrossRef] [Green Version]
- Kopecký, M.; Macek, M.; Wild, J. Topographic Wetness Index calculation guidelines based on measured soil moisture and plant species composition. Sci. Total Environ. 2021, 757, 143785. [Google Scholar] [CrossRef]
- De Castro, S.S.; de Queiroz Neto, J.P. Soil Erosion in Brazil from Coffee to the Present-day Soy Bean Production. In Natural Hazards and Human-Exacerbated Disasters in Latin America; Latrubesse, E.M., Ed.; Developments in Earth Surface Processes; Elsevier: Amsterdam, The Netherlands, 2009; Volume 13, pp. 195–221. [Google Scholar]
- CRPM Mapa Geodiversidade do Estado do Mato Grosso do Sul. Available online: https://rigeo.cprm.gov.br/handle/doc/14703 (accessed on 20 January 2022).
- Cao, L.; Wang, Y.; Liu, C. Study of unpaved road surface erosion based on terrestrial laser scanning. CATENA 2021, 199, 105091. [Google Scholar] [CrossRef]
- Katz, H.A.; Daniels, J.M.; Ryan, S. Slope-area thresholds of road-induced gully erosion and consequent hillslope–channel interactions. Earth Surf. Process. Landf. 2014, 39, 285–295. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, L.; Fang, Q.; Hou, R. Contributions of runoff from paved farm roads to soil erosion in karst uplands under simulated rainfall conditions. CATENA 2021, 196, 104887. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Y.; Chen, Y.; Liang, F.; Liu, H. Assessment of future flash flood inundations in coastal regions under climate change scenarios—A case study of Hadahe River basin in northeastern China. Sci. Total Environ. 2019, 693, 133550. [Google Scholar] [CrossRef] [PubMed]
- Defersha, M.B.; Melesse, A.M. Effect of rainfall intensity, slope and antecedent moisture content on sediment concentration and sediment enrichment ratio. CATENA 2012, 90, 47–52. [Google Scholar] [CrossRef]
- Wu, X.; Wei, Y.; Wang, J.; Xia, J.; Cai, C.; Wei, Z. Effects of soil type and rainfall intensity on sheet erosion processes and sediment characteristics along the climatic gradient in central-south China. Sci. Total Environ. 2018, 621, 54–66. [Google Scholar] [CrossRef]
- Bouramtane, T.; Yameogo, S.; Touzani, M.; Tiouiouine, A.; El Janati, M.; Ouardi, J.; Kacimi, I.; Valles, V.; Barbiero, L. Statistical approach of factors controlling drainage network patterns in arid areas. Application to the Eastern Anti Atlas (Morocco). J. Afr. Earth Sci. 2020, 162, 103707. [Google Scholar] [CrossRef]
- Bouramtane, T.; Tiouiouine, A.; Kacimi, I.; Valles, V.; Talih, A.; Kassou, N.; Ouardi, J.; Saidi, A.; Morarech, M.; Yameogo, S.; et al. Drainage Network Patterns Determinism: A Comparison in Arid, Semi-Arid and Semi-Humid Area of Morocco Using Multifactorial Approach. Hydrology 2020, 7, 87. [Google Scholar] [CrossRef]
- Rezende-Filho, A.T.; Valles, V.; Furian, S.; Oliveira, C.M.S.C.; Ouardi, J.; Barbiero, L. Impacts of lithological and anthropogenic factors affecting water chemistry in the upper Paraguay River Basin. J. Environ. Qual. 2015, 44, 1832–1842. [Google Scholar] [CrossRef]
- Tiouiouine, A.; Yameogo, S.; Valles, V.; Barbiero, L.; Dassonville, F.; Moulin, M.; Bouramtane, T.; Bahaj, T.; Morarech, M.; Kacimi, I. Dimension Reduction and Analysis of a 10-Year Physicochemical and Biological Water Database Applied to Water Resources Intended for Human Consumption in the Provence-Alpes-Côte d’Azur Region, France. Water 2020, 12, 525. [Google Scholar] [CrossRef] [Green Version]
- Anderson, R.H.; Farrar, D.B.; Thoms, S.R. Application of discriminant analysis with clustered data to determine anthropogenic metals contamination. Sci. Total Environ. 2009, 408, 50–56. [Google Scholar] [CrossRef] [PubMed]
- Wilson, S.R.; Close, M.E.; Abraham, P. Applying linear discriminant analysis to predict groundwater redox conditions conducive to denitrification. J. Hydrol. 2018, 556, 611–624. [Google Scholar] [CrossRef]
- Yameogo, S.; Nikiema, J.; Compaore, N.F.; Tiouiouine, A.; Rezende-filho, A.T.; Barbiero, L.; Valles, V. Discrimination de deux formations hydrogéologiques à partir de l’analyse mathématique des concentrations hydrochimiques d’eau souterraine en contexte sahélien de socle d’Afrique de l’Ouest: Cas de la commune de Markoye, Burkina Faso. Ann. L’université Joseph KI-ZERBO–Sér. C 2020, 17, 31–52. [Google Scholar]
- Felicísimo, Á.M.; Cuartero, A.; Remondo, J.; Quirós, E. Mapping landslide susceptibility with logistic regression, multiple adaptive regression splines, classification and regression trees, and maximum entropy methods: A comparative study. Landslides 2013, 10, 175–189. [Google Scholar] [CrossRef]
- Zhu, Z.; Lin, C.; Zhang, X.; Wang, K.; Xie, J.; Wei, S. Evaluation of geological risk and hydrocarbon favorability using logistic regression model with case study. Mar. Pet. Geol. 2018, 92, 65–77. [Google Scholar] [CrossRef]
- Loh, W.-Y. Classification and regression trees. WIREs Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- Shmueli, G. To Explain or to Predict? Stat. Sci. 2010, 25, 289–310. [Google Scholar] [CrossRef]
- Monteiro, J.M.; Rao, A.; Shawe-Taylor, J.; Mourão-Miranda, J. A multiple hold-out framework for Sparse Partial Least Squares. J. Neurosci. Methods 2016, 271, 182–194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pal, K.; Patel, B.V. Data Classification with k-fold Cross Validation and Holdout Accuracy Estimation Methods with 5 Different Machine Learning Techniques. In Proceedings of the 2020 Fourth International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 11–13 March 2020; pp. 83–87. [Google Scholar]
- Yadav, S.; Shukla, S. Analysis of k-Fold Cross-Validation over Hold-Out Validation on Colossal Datasets for Quality Classification. In Proceedings of the 2016 IEEE 6th International Conference on Advanced Computing (IACC), Bhimavaram, India, 27–28 February 2016; pp. 78–83. [Google Scholar]
- Tanner, E.M.; Bornehag, C.-G.; Gennings, C. Repeated holdout validation for weighted quantile sum regression. MethodsX 2019, 6, 2855–2860. [Google Scholar] [CrossRef]
- Abraham, S.; Huynh, C.; Vu, H. Classification of Soils into Hydrologic Groups Using Machine Learning. Data 2020, 5, 2. [Google Scholar] [CrossRef] [Green Version]
- Arabameri, A.; Chen, W.; Loche, M.; Zhao, X.; Li, Y.; Lombardo, L.; Cerda, A.; Pradhan, B.; Bui, D.T. Comparison of machine learning models for gully erosion susceptibility mapping. Geosci. Front. 2020, 11, 1609–1620. [Google Scholar] [CrossRef]
- Moradi, E.; Abdolshahnejad, M.; Borji Hassangavyar, M.; Ghoohestani, G.; da Silva, A.M.; Khosravi, H.; Cerdà, A. Machine learning approach to predict susceptible growth regions of Moringa peregrina (Forssk). Ecol. Inform. 2021, 62, 101267. [Google Scholar] [CrossRef]
- Park, N.-W. Using maximum entropy modeling for landslide susceptibility mapping with multiple geoenvironmental data sets. Environ. Earth Sci. 2015, 73, 937–949. [Google Scholar] [CrossRef]
- Chowdhuri, I.; Pal, S.C.; Arabameri, A.; Saha, A.; Chakrabortty, R.; Blaschke, T.; Pradhan, B.; Band, S.S. Implementation of Artificial Intelligence Based Ensemble Models for Gully Erosion Susceptibility Assessment. Remote Sens. 2020, 12, 3620. [Google Scholar] [CrossRef]
- Azareh, A.; Rahmati, O.; Rafiei-Sardooi, E.; Sankey, J.B.; Lee, S.; Shahabi, H.; Ahmad, B. Bin Modelling gully-erosion susceptibility in a semi-arid region, Iran: Investigation of applicability of certainty factor and maximum entropy models. Sci. Total Environ. 2019, 655, 684–696. [Google Scholar] [CrossRef]
- Mattivi, P.; Franci, F.; Lambertini, A.; Bitelli, G. TWI computation: A comparison of different open source GISs. Open Geospat. Data Softw. Stand. 2019, 4, 6. [Google Scholar] [CrossRef]
- Qin, C.; Zheng, F.; Zhang, X.J.; Xu, X.; Liu, G. A simulation of rill bed incision processes in upland concentrated flows. CATENA 2018, 165, 310–319. [Google Scholar] [CrossRef]
- Stolte, J.; Liu, B.; Ritsema, C.J.; van den Elsen, H.G.M.; Hessel, R. Modelling water flow and sediment processes in a small gully system on the Loess Plateau in China. CATENA 2003, 54, 117–130. [Google Scholar] [CrossRef]
- Jiang, Y.; Shi, H.; Wen, Z.; Guo, M.; Zhao, J.; Cao, X.; Fan, Y.; Zheng, C. The dynamic process of slope rill erosion analyzed with a digital close range photogrammetry observation system under laboratory conditions. Geomorphology 2020, 350, 106893. [Google Scholar] [CrossRef]
- Sangireddy, H.; Carothers, R.A.; Stark, C.P.; Passalacqua, P. Controls of climate, topography, vegetation, and lithology on drainage density extracted from high resolution topography data. J. Hydrol. 2016, 537, 271–282. [Google Scholar] [CrossRef] [Green Version]
- Bernatek-Jakiel, A.; Poesen, J. Subsurface erosion by soil piping: Significance and research needs. Earth-Sci. Rev. 2018, 185, 1107–1128. [Google Scholar] [CrossRef]
- Boulet, R.; Curmi, P.; De Queiroz-neto, J.P.; Pellerin, J. A contribution to an understanding of landscape development through three-dimensional morphological analysis of a pedological cover (Paulinia, State of Sao Paulo, Brazil). Géomorphol. Reli. Process. Environ. 1995, 1, 49–59. [Google Scholar] [CrossRef]
- Furian, S.; Barbiéro, L.; Boulet, R. Organisation of the soil mantle in tropical southeastern Brazil (Serra do Mar) in relation to landslides processes. CATENA 1999, 38, 65–83. [Google Scholar] [CrossRef] [Green Version]
- Salomão, F.X.T. Processos Erosivos Lineares em Bauru (SP): Regionalização Cartográfica Aplicada ao Controle Preventivo Urbano e Rural; São Paulo University: São Paulo, Brazil, 1994. [Google Scholar]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Bezerra, M.O.; Baker, M.; Palmer, M.A.; Filoso, S. Gully formation in headwater catchments under sugarcane agriculture in Brazil. J. Environ. Manag. 2020, 270, 110271. [Google Scholar] [CrossRef]
- Merten, G.H.; Minella, J.P.G. The expansion of Brazilian agriculture: Soil erosion scenarios. Int. Soil Water Conserv. Res. 2013, 1, 37–48. [Google Scholar] [CrossRef] [Green Version]
- Guerra, A.J.T.; Fullen, M.A.; Jorge, M.C.O.; Alexandre, S.T. Erosão e Conservação de Solos no Brasil. Anuário Inst. Geociênc.-UFRJ 2014, 37, 81–91. [Google Scholar] [CrossRef]
- Lee, S.; Lee, M.-J.; Jung, H.-S. Data Mining Approaches for Landslide Susceptibility Mapping in Umyeonsan, Seoul, South Korea. Appl. Sci. 2017, 7, 683. [Google Scholar] [CrossRef] [Green Version]
- Naimi, B.; Skidmore, A.K.; Groen, T.A.; Hamm, N.A.S. Spatial autocorrelation in predictors reduces the impact of positional uncertainty in occurrence data on species distribution modelling. J. Biogeogr. 2011, 38, 1497–1509. [Google Scholar] [CrossRef]
- Rahmati, O.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Feizizadeh, B. Evaluation of different machine learning models for predicting and mapping the susceptibility of gully erosion. Geomorphology 2017, 298, 118–137. [Google Scholar] [CrossRef]
- Sun, D.; Wen, H.; Wang, D.; Xu, J. A random forest model of landslide susceptibility mapping based on hyperparameter optimization using Bayes algorithm. Geomorphology 2020, 362, 107201. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- França, S.; Cabral, H.N. Predicting fish species richness in estuaries: Which modelling technique to use? Environ. Model. Softw. 2015, 66, 17–26. [Google Scholar] [CrossRef]
- Mellor, A.; Boukir, S.; Haywood, A.; Jones, S. Exploring issues of training data imbalance and mislabelling on random forest performance for large area land cover classification using the ensemble margin. ISPRS J. Photogramm. Remote Sens. 2015, 105, 155–168. [Google Scholar] [CrossRef]
- King, M.W.; Resick, P.A. Data mining in psychological treatment research: A primer on classification and regression trees. J. Consult. Clin. Psychol. 2014, 82, 895–905. [Google Scholar] [CrossRef]
- Lemon, S.C.; Roy, J.; Clark, M.A.; Friedmann, P.D.; Rakowski, W. Classification and regression tree analysis in public health: Methodological review and comparison with logistic regression. Ann. Behav. Med. 2003, 26, 172–181. [Google Scholar] [CrossRef]
- Marshall, R.J. The use of classification and regression trees in clinical epidemiology. J. Clin. Epidemiol. 2001, 54, 603–609. [Google Scholar] [CrossRef]
- Dunn, J. Optimal Trees for Prediction and Prescription. Massachusetts Institute of Technology: Cambridge, MA, USA, 2018. [Google Scholar]
- Quinlan, J.R. Simplifying decision trees. Int. J. Man. Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef] [Green Version]
- Youssef, A.M.; Pourghasemi, H.R. Landslide susceptibility mapping using machine learning algorithms and comparison of their performance at Abha Basin, Asir Region, Saudi Arabia. Geosci. Front. 2021, 12, 639–655. [Google Scholar] [CrossRef]
- Saha, T.K.; Pal, S.; Talukdar, S.; Debanshi, S.; Khatun, R.; Singha, P.; Mandal, I. How far spatial resolution affects the ensemble machine learning based flood susceptibility prediction in data sparse region. J. Environ. Manag. 2021, 297, 113344. [Google Scholar] [CrossRef] [PubMed]






| Code | Map Code | Description | WRB/FAO (Soil Taxonomy) |
|---|---|---|---|
| 1 | AC2 | Complex association with dominance of hydromorphic quartz sand | |
| 2 | HAQa1 | Hydromorphic quartz sand | Arenosols (entisols) |
| 3 | HGPe7 | Low humic eutrophic gley clay texture and subdominantly eutrophic plintosol | Gleysols (entisols, alfisols, inceptisols) |
| 4 | LEa1 | Dark red latosol clay texture (developed from sandstone) | Ferralsols (oxisols) |
| 5 | LRa1 | Purple latosol very clayey texture (developed from basalt) | Ferralsols (oxisols) |
| 6 | PLa1 | Aqueous planosol with predominantly sandy and moderate texture | Planosols (alfisols) |
| 7 | PVa11 | Damp, dystrophic yellow-red Podzolico with moderate texture | Acrisols (ultisols) |
| 8 | PVa7 | Dystrophic yellow-red Podzolico | Acrisols (ultisols) |
| 9 | PVa9 | Wet yellow-red Podzolico | Acrisols (ultisols) |
| 10 | Re4 | Homogeneous eutrophic litholite soils | Regosols (entisols) |
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| Eigenvalue | 2.8 | 2.3 | 1.4 | 1.2 |
| Variance explained (%) | 21.5 | 17.6 | 11 | 9.2 |
| Cumulative % | 21.5 | 39.1 | 50.1 | 59.3 |
| Statistical Index | MDA | LR | CART | RF |
|---|---|---|---|---|
| Accuracy (%) | 78.47 | 77.62 | 82.81 | 86.09 |
| Specificity (%) | 74.36 | 75.91 | 88.09 | 85.40 |
| Sensitivity (%) | 82.47 | 79.33 | 77.57 | 86.79 |
| Precision (%) | 76.78 | 77.05 | 86.76 | 85.45 |
| Statistical Index | MDA | LR | CART | RF |
|---|---|---|---|---|
| Accuracy (%) | 72.50 | 78.54 | 84.38 | 89.83 |
| Specificity (%) | 71.42 | 81.39 | 80.61 | 90.24 |
| Sensitivity (%) | 73.33 | 75.67 | 88.61 | 88.46 |
| Precision (%) | 67.56 | 77.78 | 81.39 | 86.61 |
| MDA | LR | CART | RF | |
|---|---|---|---|---|
| ROC Curve | 0.850 | 0.861 | 0.920 | 0.931 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouramtane, T.; Hilal, H.; Rezende-Filho, A.T.; Bouramtane, K.; Barbiero, L.; Abraham, S.; Valles, V.; Kacimi, I.; Sanhaji, H.; Torres-Rondon, L.; et al. Mapping Gully Erosion Variability and Susceptibility Using Remote Sensing, Multivariate Statistical Analysis, and Machine Learning in South Mato Grosso, Brazil. Geosciences 2022, 12, 235. https://doi.org/10.3390/geosciences12060235
Bouramtane T, Hilal H, Rezende-Filho AT, Bouramtane K, Barbiero L, Abraham S, Valles V, Kacimi I, Sanhaji H, Torres-Rondon L, et al. Mapping Gully Erosion Variability and Susceptibility Using Remote Sensing, Multivariate Statistical Analysis, and Machine Learning in South Mato Grosso, Brazil. Geosciences. 2022; 12(6):235. https://doi.org/10.3390/geosciences12060235
Chicago/Turabian StyleBouramtane, Tarik, Halima Hilal, Ary Tavares Rezende-Filho, Khalil Bouramtane, Laurent Barbiero, Shiny Abraham, Vincent Valles, Ilias Kacimi, Hajar Sanhaji, Laura Torres-Rondon, and et al. 2022. "Mapping Gully Erosion Variability and Susceptibility Using Remote Sensing, Multivariate Statistical Analysis, and Machine Learning in South Mato Grosso, Brazil" Geosciences 12, no. 6: 235. https://doi.org/10.3390/geosciences12060235
APA StyleBouramtane, T., Hilal, H., Rezende-Filho, A. T., Bouramtane, K., Barbiero, L., Abraham, S., Valles, V., Kacimi, I., Sanhaji, H., Torres-Rondon, L., de Castro, D. D., Vieira Santos, J. d. C., Ouardi, J., Beqqali, O. E., Kassou, N., & Morarech, M. (2022). Mapping Gully Erosion Variability and Susceptibility Using Remote Sensing, Multivariate Statistical Analysis, and Machine Learning in South Mato Grosso, Brazil. Geosciences, 12(6), 235. https://doi.org/10.3390/geosciences12060235









