Abstract
We experimentally determined the hydraulic properties of fractures within various rock types, focusing on a variety of Variscan rocks. Flow-through experiments were performed on slate, graywacke, quartzite, granite, natural fault gouge, and claystone samples containing an artificial fracture with a given roughness. For slate samples, the hydraulic transmissivity of the fractures was measured at confining pressures, pc, at up to 50 MPa, temperatures, T, between 25 and 100 °C, and differential stress, σ, acting perpendicular to the fracture surface of up to 45 MPa. Fracture transmissivity decreases non-linearly and irreversibly by about an order of magnitude with increasing confining pressure and differential stress, with a slightly stronger influence of pc than of σ. Increasing temperature reduces fracture transmissivity only at high confining pressures when the fracture aperture is already low. An increase in the fracture surface roughness by about three times yields an initial fracture transmissivity of almost one order of magnitude higher. Fractures with similar surface roughness display the highest initial transmissivity within slate, graywacke, quartzite and granite samples, whereas the transmissivity in claystone and granitic gouge material is up to several orders of magnitude lower. The reduction in transmissivity with increasing stress at room temperature varies with composition and uniaxial strength, where the deduction is lowest for rocks with a high fraction of strong minerals and associated high brittleness and strength. Microstructural investigations suggest that the reduction is induced by the compaction of the matrix and crushing of strong asperities. Our results suggest that for a given surface roughness, the fracture transmissivity of slate as an example of a target reservoir for unconventional EGS, is comparable to that of other hard rocks, e.g., granite, whereas highly altered and/or clay-bearing rocks display poor potential for extracting geothermal energy from discrete fractures.
1. Introduction
Extracting geothermal energy from underground is of major interest in the transition from energy recovered from conventional resources such as coal or oil towards renewable energies [1]. Geothermal energy is expected to have a great potential to meet future energy demands. However, exploitation is highly dependent on the presence of accessible hot fluids within the reservoir formation to ensure sufficient energy extraction. In contrast to hydrothermal geothermal systems, where steam or hot water is extracted from the subsurface, hot (>150 °C) and deep (>3 km), but low permeable, reservoir rocks represent the largest geothermal energy resources [2,3,4,5]. To facilitate the extraction of geothermal energy from tight reservoirs, a network of highly conductive fractures is required that serves as heat exchanger [6,7,8] in Enhanced Geothermal Systems (EGS). An EGS typically relies on two wells, an injection and a production well, which are connected by a network of open (conductive to fluid flow) fractures. In order to create such a fracture network, artificial fractures are often generated by hydraulic fracturing (HF). These are believed to be connected to pre-existing natural fractures in the reservoir [9]. The efficiency and sustainability of an EGS are critically dependent on sufficient water flow through the fracture network and on the conductive properties of the separate fractures [1]. This prerequisite, in addition to a relatively high geothermal gradient, is necessary to successfully run an EGS over several years [10,11].
Fluid flow within rough natural fractures is a complex process, influenced by many parameters, for example thermodynamic boundary conditions, surface roughness and chemical processes, such as mineral precipitation [12]. In addition, the bedding and cleavage orientation of anisotropic rocks such as shale or slate can have a strong effect on the development and permeability of fractures [13,14,15]. The surface roughness of natural and artificially created fractures has a strong impact on the (hydraulic) aperture [12,16,17,18]. Fracture transmissivity can rapidly decrease with increasing confining pressure (pc) [12,16] and increasing effective stress, σ, oriented perpendicular to the fracture surface (e.g., [19]). Increasing temperature, T, may (completely) seal fractures in sediments by thermal expansion [17]. Fracture sealing may be also induced by mineral precipitation processes, depending on fluid and rock composition [10,12,20]. Injecting fluid into a fluid-bearing fracture with a different composition may lead to dissolution-precipitation reactions due to local changes in the chemical equilibrium, which typically results in a decrease in fracture transmissivity [10,17,21,22]. The transmissivity may be also reduced by the clogging of flow channels due to the migration of fine particles, e.g., clay [1,13,23,24] or by the production of a fine-grained gouge layer resulting from shear displacement [19]. On the other hand, fracture transmissivity may be enhanced with low effective normal stress acting on the fracture due to shear-induced dilatancy, resulting in self-propping of the fracture surfaces [1,12,16,20,25]. The transmissivity of the propped fractures may be influenced by proppant embedment (e.g., [24]).
Many existing EGS are located in granitic rocks, which often exhibit a relatively large amount of natural, highly permeable, open fractures and have a high potential for successfully creating fracture networks with stimulation techniques [26,27]. However, metamorphic rocks may also be considered as potential host rocks for EGS. Within the European initiative ‘Multidisciplinary and multi-context demonstration of Enhanced Geothermal Systems Exploration and Exploitation Techniques and potentials (MEET)’, the suitability of Variscan rocks, such as granites [27], quartzites [28], slates and graywacke [29,30,31] were investigated to assess their potential for extracting geothermal energy. In this study, we focused on the influence of confining pressure, stress, temperature, and surface roughness on the fracture transmissivity of Wissenbach slate which is the expected target rock for a planned EGS in Göttingen, Germany, dedicated to heating the University Campus [31]. Since the productivity of fractured rocks may be influenced by their composition, as well as their metamorphic and alteration grade, we additionally performed flow through experiments at elevated stress on fractured graywacke, quartzite, fresh and altered (gouge) granite, and claystone, where the latter may be regarded as an end-member rock type of highly altered formations. This may help to assess the potential of different geological settings for future EGS.
2. Materials and Methods
2.1. Sample Material
Most of the experiments were performed on slates derived from the Middle Devonian (Eifelian age) Wissenbach Slate (WBS) Formation, one of the intended reservoir target horizons for the planned EGS in Göttingen. Because only a few existing wells in the Göttingen area penetrate the Paleozoic rock units below the Permian and Mesozoic sedimentary cover [29,31], rock samples were taken from an analogue site in the Western Harz Mountains. Samples were prepared from cores collected at a depth of 1134–1210 m from the scientific well ‘Hahnenklee’, which was drilled in the northwestern part of the Harz mountains in the early 1980’s [32,33,34,35,36]. On macroscopic scale, WBS appears as black, homogeneous, argillaceous rock with sporadically distributed pyrite aggregates (<0.25 mm). The very few carbonate layers that occur are aligned parallel to the visible and characteristic cleavage, which is rarely interrupted by carbonate-filled veins (<0.5 mm). An X-Ray diffraction (XRD) analysis revealed that this metamorphic rock is mainly composed of quartz (Qtz), calcite (Ca), dolomite (Dol), muscovite (Ms), illite (Ill), chlorite (Chl), and feldspar (Fsp) with minor amounts of apatite (Ap), pyrite (Py), and organic matter (Om). The bulk composition was categorized into three main groups consisting of mechanically weak (Phyl = phyllosilicates), intermediate strong (Cb = carbonates), and strong (QFSO = Qtz + Fsp + Sulfides + Oxides) minerals (Table 1) and plotted in a ternary diagram (Figure 1).

Table 1.
Petrophysical and mechanical properties.
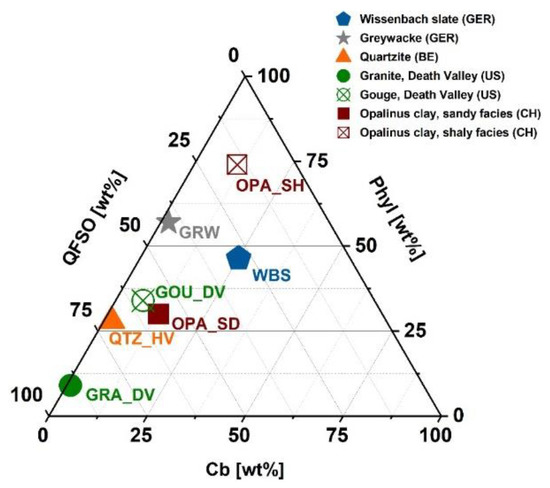
Figure 1.
Ternary plot displaying mineral composition of investigated samples. Composition is separated into mechanically strong (QFSOP = Qtz + Fsp + Sulfides + Oxides), intermediate strong (Cb = Carbonates), and weak (Phyl = Phyllosilicates) fractions. Mineral data given in wt%., WBS = Wissenbach slate, GRW = Graywacke, QTZ_HV = Quartzite Havelange, GRA_DV = Granite Death Valley, GOU_DV = Gouge Death Valley, OPA_SD = Opalinus clay, sandy facies, OPA_SH = Opalinus clay, shaly facies.
Optical and electron microscopy revealed a complex (expressed by a large range of mineral types and grain sizes), fine-grained microstructure of the starting material (Figure 2a,b), with quartz, feldspar, chlorite and carbonates making up the largest mineral grains (<50 µm) that are dispersed in the phyllosilicate-rich matrix. Cleavage planes are characterized by phyllosilicates whose longest axes are oriented subparallel to each other. The bulk density of dried (110 °C for >48 h) WBS is in the range of around 2.8 g/cm3 with a respective porosity measured with He-pycnometry (Micrometrics, AccuPyc 1340) of ϕHe ≈ 2 vol% (including micro pores). Matrix permeability, kmatrix, is less than 10−19 m2, which is the detection limit of the gas permeameter used at TU Darmstadt (K. Bär, personal communication).

Figure 2.
Optical micrographs (left column) and SEM-backscattered (BSE) images (right column) of investigated starting materials showing different composition and grain size (see text for details). (a,b) Wissenbach slate, (c,d) graywacke, (e,f) quartzite, (g,h) granite, (i,j) altered granitic gouge, (k,l) Opalinus clay—sandy facies, and (m,n) Opalinus clay—shaly facies. Note different scales. Dol = Dolomite, Cal = Calcite, Chl = Chlorite, Qtz = Quartz, Om = Organic Matter, Fsp = Feldspar, Py = Pyrite, Bt = Biotite, Zn = Zinc, Kfs = Kalifeldspar, Ap = Apatite, Ill = Illite, Pl = Plagioclase, Hem = Hematite, Sd = Siderite.
Another potential unit that has sufficient thickness for developing an EGS at the Göttingen site are Lower Carboniferous (Kulm facies) graywacke-successions [31]. Graywacke (GRW) samples also originate from an analogue site in the Western Harz Mountains and were taken at a depth of 843 m from the well ‘Wulpke-2′ that was drilled in the 1980′s [32]. This grey to light-green marine psammite shows angular detrital quartz and feldspar grains (<200 µm) embedded in a fine-grained matrix made up of chlorite, feldspar and mica (Figure 2c,d). The samples were taken from a relatively homogeneous part without any obvious grading. Larger, planar aligned biotite grains (<400 µm) indicate the macroscopically visible bedding orientation. The main mineral components determined by the XRD analysis show dominantly quartz, feldspar and micas with minor amounts of carbonates. Porosity and bulk density of dried samples are 0.7 vol% and 2.67 g/cm3, respectively.
A further demonstration site studied in the frame of the MEET-project is the Havelange deep borehole in Belgium (Wallonia). Here, Variscan quartzite formations are being considered for the development of potential EGS. Therefore, we also studied the fracture transmissivity of quartzite samples (QTZ_HV) obtained from a depth of z = 4732 m of the Havelange well, drilled in the Dinant Synclinorium in the early 1980′s [28]. The grey to light-green samples are characterized by a granoblastic fabric of fine-grained (<150 µm) quartz with illite and sparsely appearing dolomite (Figure 2e,f). The Lower Devonian (Pragian) samples contain roughly 77 wt% quartz and 20 wt% clays and micas with minor amounts of dolomite. The porosity of the used samples was lowest off all the tested materials and ranges around ϕHe ≈ 0.2 vol%.
To capture the influence of alteration on fracture transmissivity, tests were performed on fresh (GRA_DV), altered and sheared granite gouge (GOU_DV) samples recovered from an exposure located in the Noble Hills area in the southern part of the Death Valley (US) as an easily accessible analogue material to Variscan granites [37,38]. The light-reddish to pinkish, equigranular Noble Hill granite (Figure 2g,h) is mainly composed of medium to coarse grained (<3 mm) plagioclase (35 wt%), quartz (30 wt%), K-feldspar (30 wt%) and biotite (10 wt%) [38] with an initial porosity of 1.3 vol%. On the other hand, the light-yellowish to orange gouge (Figure 2i,j), which was highly altered due to multiple shearing events and weathering processes, is characterized by granite clasts (<5 mm) and brecciated quartz veins (<1 cm) embedded in a carbonate- and clay-rich matrix [37]. In contrast to the granite, the gouge displays a high porosity of 12.6 vol%.
In addition, we performed measurements on claystone samples to shed light on the influence of consolidation and metamorphic grades on fracture transmissivity in clay-rich formations, which may result from alteration processes in hard rocks. Claystone material was recovered from the Opalinus Clay Formation (OPA), whose mechanical properties have been well-studied in the context of nuclear waste disposal (e.g., [39,40,41]). Compared to WBS, these rocks exhibited a much lower burial depth and temperature [42]. We investigated samples from the sandy (OPA_SD) (Figure 2k,l) and shaly facies (OPA_SH) (Figure 2m,n), both collected from the Underground Research Laboratory (URL) ‘Mont Terri’ (Switzerland, St. Ursanne), gratefully provided by the Swiss Federal Office of Topography–swisstopo. The fine-grained OPA_SD is mainly composed of Qtz (48 wt%), carbonates (20 wt%), and Fsp (9 wt%), but contains a distinctly lower amount of weak sample constituents (30 wt%), such as clay and mica, compared to WBS samples (Figure 1). Note that these values may vary by about 10 wt% because of the compositional heterogeneity of this facies (e.g., [41]). The matrix permeability of OPA_SD is in the same range compared to WBS (kmatrix_OPA_SD = 10−19–10−21 m−2) [43], whereas the porosity of OPA_SD (ϕHe_OPS_SD = 11.8 vol%) is significantly higher. In comparison to the sandy facies of OPA, the shaly facies contain less quartz (9 wt%) and more clay minerals (74 wt%). The main constituents of OPA_SH are clay minerals, quartz, carbonates, feldspar, pyrite, and organic matter. The permeability of OPA_SH is similar to that of OPA_SD (kmatrix_OPA_SH = 10−19–10−21 m−2, [43]), but with a slightly higher porosity of 13.8 vol%.
2.2. Methods
Flow through experiments were performed on cm scale specimens at various pc, T, σ-conditions using a modified MuSPIS (multiple sample production and injection simulator, [10]) apparatus for long-term petrophysical investigations. The sample assembly consists of two separate cylindrical objects with a thickness of t* = 10 mm (Figure 3a,b, Table A1), which were isolated by rubber (neoprene) jackets from the confining medium (hydraulic oil) inside the pressure vessel.
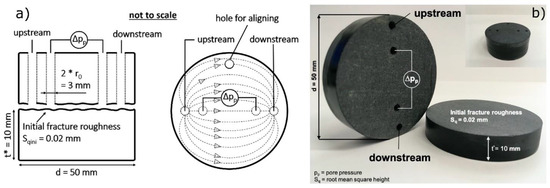
Figure 3.
Schematic experimental setup of performed flow through experiments (a) and an example of a Wissenbach slate sample (b). Flow direction (dashed lines) is upstream borehole to downstream borehole. Differential pore pressure, ∆pp, for the determination of fracture transmissivity is measured using a highly accurate pressure transducer by utilizing two additional boreholes. d = diameter, t* = thickness.
The confining pressure is controlled by a syringe pump (Isco 65D, max pc = 138 MPa). The maximum temperature is T = 200 °C, using a resistance-heating element (Thermocoax) mounted on a cylindrical stainless-steel tube placed inside the pressure vessel. To measure the transmissivity of the surface between the two disks, a continuous fluid flow at a pre-defined constant fluid pressure can be generated using two syringe pumps (Isco 100DM), which are connected to the surface via boreholes (up- and downstream boreholes in Figure 3a). The maximum pore (fluid) pressure is pp = 70 MPa at flowrates of Q = 2.5 × 10−2 − 1 × 10−6 L/min. The fluid pressure is measured separately across two additional boreholes with an additional pressure transducer (Siemens Sitrans P DS III), which is capable of measuring differential pressures of ∆pp = ± 10 mbar (1000 Pa). This was so that we could measure very low-pressure differences at low flow rates within the fracture. As our experiments were performed on low permeable rocks (matrix permeability <10−17 m2), we assumed the contribution of fluid flow through the matrix to be negligible. Deviatoric stresses up to σ = 100 MPa perpendicular to the interface can be applied using an axial piston driven by another syringe pump (Isco 65D). The axial load is measured using an internally mounted load cell (200 kN). The displacement of the axial piston is measured by Linear Variable Differential Transformers (LVDT) with an uncertainty of ±1 µm, allowing to correlate fracture transmissivity with changing fracture aperture and sample deformation induced by variations in axial stress, confining pressure, and temperature.
For anisotropic rocks, the disks were prepared with the cylinder axis oriented perpendicular to bedding. The surface roughness of the artificial fracture, represented by the interface of the two sample disks, was controlled by grinding the flat saw-cut surfaces using SiC-grains of a defined diameter (Kl60 ≈ 260 µm). The resulting initial fracture surface roughness, Sq (root mean square value), prior to testing was Sq_ini = 0.016 ± 0.003 mm, except for the granitic gouge that revealed a considerably higher initial roughness of Sq_ini = 0.247 mm (Table 1), which was measured with a surface scanner (white light profilometer, Keyence VR3200, accuracy ≈ 3µm). Since we also tested the influence of roughness on fracture transmissivity, an additional sample of Wissenbach slate was roughened with K600 SiC-grains (diameter ≈ 9 µm) resulting in lower Sq_ini of 0.006 mm.
Experiments on Wissenbach slate, Havelange quartzite, graywacke and the fresh Noble Hill granite from the Death Valley were performed using distilled water at a constant fluid pressure of pp = 1 MPa (downstream borehole in Figure 3) as fluid flowing through the artificial fracture. Samples prepared from Opalinus Clay, and the gouge material from the Death Valley were tested using Argon gas to avoid sample disintegration during fluid flow. For comparison, one additional test on slate was also performed with Argon. Due to the high compressibility of the Argon gas, these experiments were performed at elevated pp = 10 MPa to reduce the apparent permeability enhancement through the Klinkenberg effect (e.g., [44]). The effective confining pressure peff = pc − pp was kept constant (4 MPa) throughout most experiments so as to compare results gained with either distilled water or Argon gas. In a few cases, peff could not be held constant, for example, during tests with step-wise increasing confining pressure. Here, pp was kept below pc to avoid a ‘blow-up’ of the fracture.
Fracture transmissivity was calculated by assuming the fluid flow pattern within the fracture to be comparable to the flow of electric current through a resistive solid within an insulating medium (dashed lines in Figure 3a). Assuming that the up- and downstream borehole form the dipole of a magnetic field and comparing Ohm’s law with Darcy’s law for steady fluid flow to characterize the transmissivity of thin cracks in various rocks, Ohm’s law may be rewritten as [19,45]:
where the term k∗t is the transmissivity of the fracture, with k and t representing fracture permeability and fracture thickness, respectively. Q is the volumetric flow rate, η is the (temperature-dependent) dynamic viscosity of the fluid, 2a is the distance between up- and downstream borehole with radius r0, ∆pp is the pressure difference within the fracture, and B (=0.75 for our geometry) is a geometry factor accounting for the aspect ratio of the fracture [19]. Here, we assumed single-phase fluid flow within the fracture, which is certainly a simplification compared to multi-phase fluid flow that may occur in natural fractures and the surrounding matrix [12].
A detailed microstructural analysis of the starting and the post-experimental samples was performed on mechanically as well as broad ion-beam polished, carbon-coated thin sections using a scanning electron microscope (SEM FEI Quanta 3D dual beam). SEM sections were prepared perpendicularly to the fracture surface. Broad ion-beam (BIB JEOL IB-19520CCP) polishing was used for the gouge and OPA samples to avoid preparation-induced damage of clay minerals. Due to its fragile character, the gouge was additionally solidified using epoxy resin prior to broad ion beam-milling.
In addition, we performed uniaxial compression (UCS) tests to determine the basic mechanical properties such as the uniaxial compressive strength (σUCS) and tangent Young’s Modulus (E) of each sample material. The tests were performed according to the suggested ISRM method [46] using cylindrical specimens with a length-to-diameter ratio of 2:1. Results from UCS tests (Table 1) indicate that despite the high content of weak mineral phases, the strength and stiffness of WBS are comparable to granite, quartzite and graywacke samples that contain significantly more strong minerals. Furthermore, triaxial compressive strength (σTCS) and static secant Young’s modulus of WBS were determined in constant strain rate tests of = 5 × 10−4 s−1 at simulated reservoir conditions with a confining pressure of pc = 50 MPa and temperature of T = 100 °C using a Paterson-type deformation apparatus [47].
3. Results
In total, we performed five flow through experiments on Wissenbach slate to investigate the evolution of fracture transmissivity with changing confining pressure, differential stress oriented perpendicular to the fracture interface, temperature, and surface roughness. In addition, six tests under room temperature, constant confining pressure and stresses up to 45 MPa were conducted on the other rock types to evaluate the influence of composition on fracture transmissivity. The experimental duration for most of the experiments was between one and two weeks. Fracture transmissivity was determined after reaching steady-state flow conditions at the different thermodynamic boundary conditions.
Previously performed triaxial tests reveal σTCS = 498 ± 20 MPa and E = 69 ± 14 GPa (Table 1) that are comparable to the mechanical data of Westerly granite, Panzhihua gabbro or Novaculite [48] obtained at the same conditions.
3.1. Effect of Thermodynamic Boundary Conditions
Fracture fluid flow experiments at elevated pc, T and σ-conditions were performed on Wissenbach slate samples with an average initial fracture surface roughness of Sq = 0.019 mm.
The influence of temperature on fracture transmissivity was evaluated at a confining pressure of pc = 5 MPa and pore pressure of pp = 1 MPa in the range of T = 20–100 °C (Table 2).

Table 2.
Fracture transmissivity in Wissenbach slate at elevated temperatures (pc = 5 MPa, σ = 0 MPa).
Except for a moderate decrease from T = 20 °C to T = 40 °C, fracture transmissivity does not change significantly at up to 100 °C (Figure 4), showing that the fracture transmissivity of Wissenbach slate is insensitive to changes in temperature at a low confining pressure.
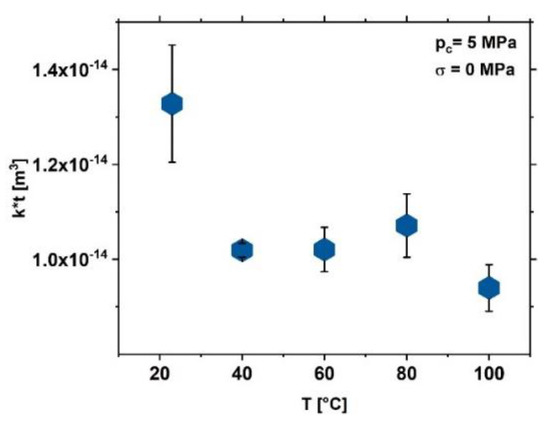
Figure 4.
Effect of temperature, T, on fracture transmissivity, k∗t, in Wissenbach slate. Fracture transmissivity decreases only slightly from T = 20 °C towards T = 40 °C and remains almost constant with increasing temperature up to 100 °C. Experimental conditions are indicated.
Hydrostatic tests with confining pressures ranging from pc = 2–25 MPa and pp = 1 MPa were performed at a constant temperature of T = 25 °C (Table 3).

Table 3.
Fracture transmissivity in Wissenbach slate at elevated confining pressures (σ = 0 MPa, T = 25 °C).
Fracture transmissivity decreased non-linearly by about one order of magnitude from ≈1.5 × 10−14 m3 to 1.7 × 10−15 m3 with increasing confining pressures, approaching almost constant values at high pc (Figure 5a).
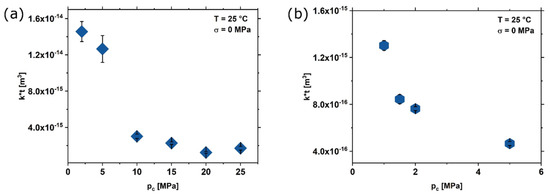
Figure 5.
Effect of confining pressure, pc, on fracture transmissivity, k∗t, in Wissenbach slate with high (Sq = 0.0196 mm) (a) and low (Sq = 0.006 mm) initial roughness (b). Fracture transmissivity is decreasing with increasing confining pressure. At relatively low pc (≤5 MPa), fracture transmissivity is up to one order of magnitude lower for the sample with low initial roughness.
Experiments performed at pc = 5 MPa, pp = 1 MPa and T = 25 °C reveal a similar decrease in fracture transmissivity with increasing axial differential stress of σ = 0–45 MPa, but with a roughly 2-fold higher transmissivity than measured at similar pc values (Table 4, Figure 6a).

Table 4.
Fracture transmissivity in Wissenbach slate at elevated differential stress (pc = 5 MPa, T = 25 °C) using water as flow medium.
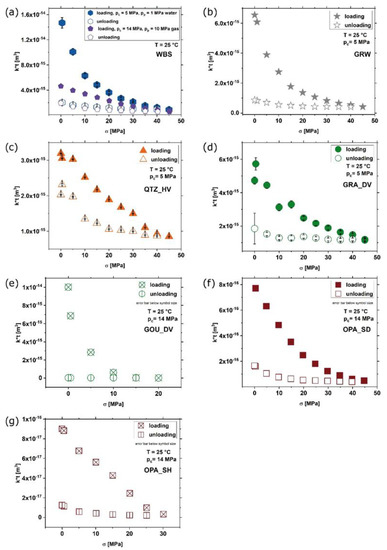
Figure 6.
Effect of differential stress, σ, on fracture transmissivity, k∗t, in Wissenbach slate (a), Graywacke (b), Quartzite-Havelange (c), Granite-Death Valley (d), Gouge-Death Valley (e), Opalinus clay-sandy facies (f), and Opalinus clay-shaly facies (g). Experiments conducted at pc = 14 MPa were performed using Argon gas as flow medium (gouge, OPA), all other with distilled water. The effective pressure (pc − pp) is 4 MPa in all cases. Experimental conditions are indicated. Note different scales.
Interestingly, upon unloading, the fracture transmissivity did not recover and remained considerably lower than the initial transmissivity. For comparison, we performed a second test on the WBS slate using Argon gas as fluid medium at pc = 14 MPa, pp = 10 MPa, i.e., a similar effective pressure of pc_eff = pc − pp = 4 MPa, assuming that Terzaghi’s principle [49] is valid. For this sample, the initial transmissivity was found to be distinctly lower than of the sample with water as the fluid medium (Table 5, small symbols in Figure 6a), but approaching similar values at high σ (≥40 MPa) and showing similar residual transmissivity upon unloading.

Table 5.
Fracture transmissivity in Wissenbach slate at elevated differential stress (pc = 14 MPa, T = 25 °C) using Argon gas as flow medium.
For the sample tested with water, after the axial loading (phase I) and unloading (phase II) steps, we subsequently increased pc from 5 to 50 MPa (phase III), resulting in a fracture transmissivity slightly lower than that measured at σ = 45 MPa (Table 6, Figure 7), confirming the stronger influence of pc on transmissivity reduction than of σ as described above.

Table 6.
Fracture transmissivity in Wissenbach slate at elevated differential stress, confining pressures and temperatures.
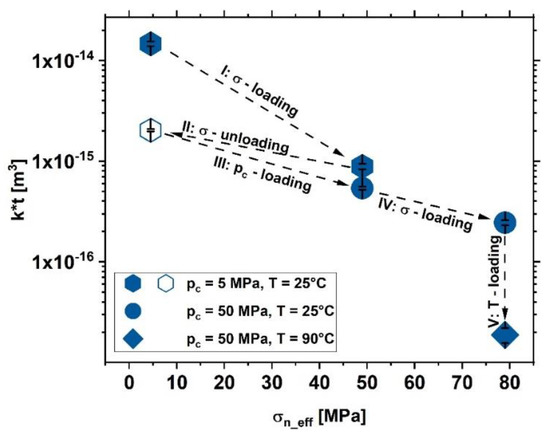
Figure 7.
Combined effect of differential stress, σ, confining pressure, pc, and temperature, T, on fracture transmissivity, k∗t, plotted versus effective normal stress, σ n_eff, acting on the fracture surface in Wissenbach slate. Fracture transmissivity decreases along σ-loading path (I) and recovers only partly during unloading (II). Increasing pc (III), σ (IV) and T (V) further decreases fracture transmissivity.
Note that for comparison we plotted the transmissivity data which are presented in Figure 7 as a function of the effective normal stress σn_eff = σ + pc − pp, acting normal to the fracture surface. In phase IV, axial stress was increased again to σ = 30 MPa at a constant pc of 50 MPa (σn_eff = 79 MPa), which yields a further transmissivity reduction, again with a lower gradient than observed in phase III (Figure 7). Finally, we increased temperature from 25 to 90 °C at constant σ and pc (phase V), which induced a strong transmissivity reduction of almost one order of magnitude.
3.2. Effect of Fracture Surface Roughness
The influence of reduced fracture surface roughness on the change of fracture transmissivity with increasing confining pressure of up to 5 MPa was measured on the Wissenbach slate at T = 25 °C (Table 7).

Table 7.
Low-roughness-fracture transmissivity in Wissenbach slate at elevated confining pressures (σ = 0 MPa, T = 25 °C).
The initial fracture surface roughness of this sample was Sq_ini_low = 0.006 mm, which is roughly three times smaller than the surface roughness of previously examined samples (Sq_ini= 0.019 mm). Comparable to the rough surface, fracture transmissivity decreases non-linearly with increasing confining pressure (Figure 5b), but at a similar pc the transmissivity values are about one order of magnitude lower (Table 3). At higher confining pressures (pc > 5 MPa), we were not able to resolve transmissivity due to technical issues (below measurable range).
3.3. Effect of Sample Composition
To determine the impact of composition on fracture transmissivity, we performed flow through experiments at T = 25 °C, with an effective pressure of pc_eff = 4 MPa, and by increasing differential stress up to 45 MPa. Tests were conducted at pc = 5 MPa, pp= 1 MPa using water as fluid medium for samples WBS, GRW, QTZ_HV and GRA_DV. For the clay-rich samples GOU_DV, OPA_SD and OPA_SH, we used Argon at pc =14 MPa and pp = 10 MPa to avoid disintegration and swelling of the samples. As observed for WBS (Figure 6a), in all other rocks, fracture transmissivity decreased non-linearly with increasing σ and demonstrated limited recovery upon unloading (Figure 6, Table 8).

Table 8.
Fracture transmissivity of and Graywacke (GRW), Quartzite-Havelange (QTZ_HV), Granite Death-Valley (GRA_DV), Gouge-Death Valley (GOU_DV), Opalinus clay-sandy facies (OPA_SD), Opalinus clay-shaly facies (OPA_SH) at elevated differential stress and T = 25 °C.
The initial transmissivity of the graywacke sample (Figure 6b) is comparable to that of Havelange quartzite (Figure 6c) and Noble Hill granite (Figure 6d). However, the fracture transmissivity of the graywacke decreases at a higher rate upon differential loading, whereas the transmissivity of quartzite and granite decreases almost at the same point. The permanent reduction in transmissivity after unloading is lowest for the quartzite followed by the granite. On the other hand, the graywacke shows a reduction in transmissivity almost threefold that of the quartzite. Compared to WBS, the quartzite and granite were less sensitive to increasing stress, while the graywacke demonstrated a comparable sensitivity (Figure 6). The Death Valley gouge shows a very strong transmissivity reduction already at low stress and almost no recovery after unloading (Figure 6e), which is likely related to the relatively high preparation-related initial roughness, almost an order of magnitude higher than of the other rocks. For Opalinus Clay, transmissivity within the sandy facies (Figure 6f) is about one order of magnitude higher than for the shaly facies (Figure 6g). Interestingly, the non-linearity of transmissivity with increasing stress is least pronounced for OPA_SH. Note that the maximum stress on OPA_SH and GOU_DV samples was less than for the other rocks to avoid potential major creep deformation of these weak rocks.
For comparison, all data are shown in Figure 8 in a semi-logarithmic scale, revealing that hard rocks such as granite and quartzite display transmissivity of several orders of magnitude higher at high σ and less irreversible damage than relatively weak OPA and gouge. Moreover, slate and graywacke transmissivity is also relatively high (in the same range as of granite and quartzite transmissivity) at high σ but shows much less reversibility upon unloading. Note, however, that the initial roughness of the gouge sample is higher than of the other tested rocks, which may obscure the systematics to some extent.
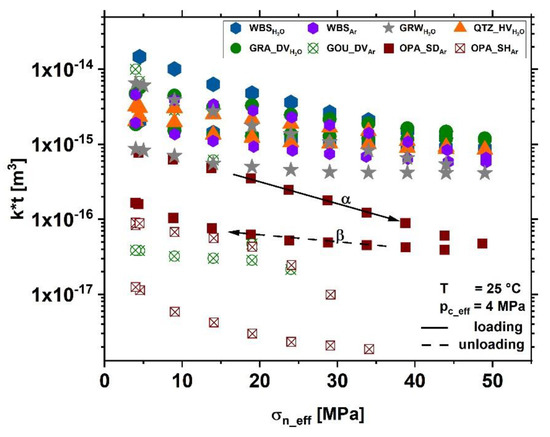
Figure 8.
Comparison of the influence of effective normal stress, σn_eff, acting on the fracture surface on fracture transmissivity, k∗t. Data are the same as shown in Figure 6, but plotted in semi-logarithmic scale. α and β indicate the linear slopes for fitting of the loading and unloading path to an exponential relationship (c.f., Equation (2)). Note that for unloading the slope is deviating from linearity at low stress.
3.4. Microstructures
After each experiment, the topography of the fracture surface of each sample was measured again with a white light profilometer in order to quantify changes due the applied experimental procedures. Thin sections of the tested specimens were then prepared for a subsequent SEM analysis.
In order to compare the surface topographies before and after the experiments, we show surface height distribution of the lower sample half (without injection/production holes, see Figure 3a) of each sample in Figure A1 and Figure A2. In comparison to the initial surface, the height distribution of WBS samples (Figure A1) measured after testing at increasing pc, σ or T became slightly wider but remained more or less unaffected. This is also reflected by the determined surface roughness measurements, which are relatively similar to the initial roughness values (Table 1). The same applies to the other samples, showing slight widening of height distributions after deformation (Figure A2). However, height distributions of the quartzite and granite samples show the least changes (Figure A2b,c), indicating no obvious change in the topography after loading. On the other hand, the distribution and fracture roughness of the gouge (Figure A2d, Table 1) display the highest grade of asperity degradation, although the maximum applied stress did not exceed 20 MPa. Independent of the facies, the surface of fractures within the Opalinus Clay (Figure A2e,f) exhibit a moderate alteration due to axial loading.
SEM micrographs of the Wissenbach slate and of the other rocks prepared perpendicular to the fracture surface are shown in Figure 9 and Figure 10, respectively.

Figure 9.
Scanning electron microscope-back scattered electron (SEM-BSE) photographs of sections prepared from Wissenbach slate (WBS) samples. All thin sections have been prepared perpendicular to the artificially prepared macro fracture located at the top of each image. Panel (a) shows the initial (ini_rough) fracture prior to testing. Subscripts ‘T’, ‘pc’, and ‘pc_σ_T’ refer to tests performed at increasing temperature (b), confining pressures (c), a combination of pressure, stress, and temperature (d,e). Panel (f) shows the post-experimental profile of the sample with initial low roughness. Arrows indicate microfracturing and intracrystalline plasticity (see text for details). Note the different scales.

Figure 10.
Scanning electron microscope-back scattered electron (SEM-BSE) photographs of sections prepared from samples of various formations after applying differential stress normal to the fracture surface. All thin sections have been prepared perpendicular to the artificially prepared macro fracture (located at the top of each figure). (a) Graywacke (GRW), (b) quartzite recovered from the Havelange borehole (QTZ_HV), (c) granite recovered from the Death Valley (GRA_DV), (d) gouge like material recovered from the Death Valley (GOU_DV), (e) Opalinus clay material recovered from the sandy facies (OPA_SD), (f) Opalinus Clay recovered from the shaly facies (OPA_SH). Arrows indicate testing-induced damage (see text for details). Note different scales.
For WBS, in comparison to the intact initial rough artificial fracture surface (Figure 9a), the matrix close to the surface of samples after testing is severely damaged (Figure 9b–e). Samples being step-wisely exposed to increasing temperature locally displayed a slightly flattened fracture surface profile (Figure 9b, white arrow). Sporadically, quartz, carbonate and dolomite grains are fractured, potentially induced by local stress concentration. On the other hand, small intergranular fractures (<5 µm opening; black arrow in Figure 9b) oriented subparallel to the macroscopic artificial fracture can be frequently observed, which may be partially induced by unloading and/or cooling and follows a cleavage orientation. Deformation microstructures of the sample deformed at varying confining pressure of up to 25 MPa are similar compared to the previously described sample. However, the density of intergranular, cleavage-parallel fractures is higher in comparison (Figure 9c). Damage of the sample subjected to combined pressure, axial stress, and temperature variations was highest when a large number of intra- and transgranular cracks in calcite, dolomite and quartz mineral grains (white arrow in Figure 9d) were detected. In addition, this sample shows several bent, kinked and delaminated micas (black arrows in Figure 9d,e), indicative for crystal plasticity. Furthermore, we observed boudinage micas suggesting shear motion at grain boundary surfaces (white arrows in Figure 9e). For all samples, the maximum damage zone is limited to <150 µm below the fracture surface profile line. As expected, the surface of the sample with a low initial roughness was considerably smoother compared to the other samples (Figure 9f). Except for the subparallel fractures with a small aperture, damage of the surface by the applied pressure was hardly visible, likely because of the relatively low applied confinement.
The damage near the fracture surface of the other rocks after stress stepping varies with composition. The graywacke sample shows some spalling microfractures in quartz and feldspar grains close to the fracture interface (white and black arrow in Figure 10a). Rarely, minor intergranular fractures (aperture < 5 µm) propagate into the rock. The damage zone is limited to <150 µm.
In the Havelange quartzite, microfractures in quartz are confined to single grains. The intragranular cracks form near the surface and lead to the spalling of grain fragments, indicative of small grain contact areas during differential loading (white arrow in Figure 10b). Despite the high number of fractures, the grain shape still remains relatively intact, resulting in a recognizable topography of asperities on the fracture surface. The damage zone below the fracture surface does not exceed 150 µm and is limited to the first layer of grains below the fracture boundary. The Noble Hill granite also exhibited spalling in quartz and feldspar grains at the contact to the fracture surface (white arrow in Figure 10c). In addition, we observed several intra- and trans-granular fractures opening subparallel to the loading direction (black arrow in Figure 10c) as well as the refracturing of previously healed, pre-existing fractures. Compared to the quartzite, the damage zone in the granite sample was found to be significantly larger. Single fractures extend up to 700 µm below the surface. Due to the high alteration and tectonic overprint [37], deformation structures that were generated by our experimental procedure were difficult to identify in the gouge from the Death Valley. Besides the cataclastic fabric and alteration of minerals (e.g., siderite, white arrow Figure 10d), we identified deformation features such as strongly bent phyllosilicates, the collapse of pore space and altered mineral grains (area between dashed white lines in Figure 10d). Clastic mineral grains (quartz, carbonates, feldspars) and mineral fragments show rare evidence of experimentally induced fractures. We observed several intergranular fractures that potentially opened during unloading (black arrow in Figure 10d). Note that the milling artefacts at the fracture surface are caused by the partly remaining resin, which was applied after testing to avoid preparation-induced damage. Opalinus Clay of the sandy (Figure 10e) and shaly (Figure 10f) facies typically displayed matrix deformation by the bending of phyllosilicates (open arrow in Figure 10e) and small fractures opening subparallel to the fracture surface (black arrows in Figure 10e,f). Clastic mineral grains in the sandy facies display several transgranular microfractures (white arrow in Figure 10e). On the other hand, the shaly facies show a significantly lower amount of fractured mineral grains compared to the sandy facies. Furthermore, these are limited to calcite grains and fossil shells, whereas quartz grains remained unfractured (white arrows in Figure 10f). In both facies, the “card house” structure of the clay matrix observed in the undeformed material collapsed with clay minerals being reoriented, with their longest axis parallel to the facture surface and perpendicular to the maximum principal stress direction. The damage zone extends up to 150 µm below the surface in the sandy facies and up to 300 µm in the shaly facies.
4. Discussion
Our set of flow through experiments demonstrated that at given fracture surface roughness increasing confining pressure, differential stress, and temperature at elevated pressure reduces the fracture transmissivity of slates (Figure 4, Figure 5, Figure 6 and Figure 7). Furthermore, the initial transmissivity reduced considerably for smooth surfaces compared to rough surfaces (Figure 5). A strong influence of sample composition and associated mechanical properties on transmissivity is also evident (Figure 6 and Figure 8). These effects will be discussed in the following paragraphs.
4.1. Influence of Thermodynamic Boundary Conditions (T, pc, σ) on Fracture Transmissivity of Wissenbach Slate
Temperature has a strong effect on the interaction between the fluid transported through the fracture and the adjacent host rock [50,51,52,53]. The rate of dissolution of asperities is often enhanced at high temperatures and can reduce the mean fracture aperture due to mineral precipitation [52,53,54,55]. For WBS flushed with water, [22] observed a slight (few %), time-dependent fracture permeability decline in long-term flow through tests at pc = 10 MPa, σ = 0 MPa and elevated temperatures up to 90 °C due to pressure solution and free face dissolution. However, using saline fluids, the authors measured an increase in permeability with increasing T, probably related to enhanced dissolution kinetics. In our tests with distilled water, we observed that at pc = 5 MPa and σ = 0 MPa the fracture transmissivity of WBS was hardly affected by temperature between 25 and 100 °C (Figure 4), except a small decrease (≈23%) between 25 and 40 °C. This confirms that temperature sensitive processes, like chemical dissolution-precipitation processes or stress corrosion at areas of high stress concentration were not very effective within the relatively short time span of our experiments. In contrast, transmissivity dropped considerably more (≈93%) at pc = 50 MPa and σ = 30 MPa in response to a temperature increase from 25 to 90 °C (Figure 7). This observation suggests that thermal dilation is more effective at high effective normal stress since the mean fracture aperture is lower than at low pc, σ conditions (e.g., [52,56]). However, performing experiments over a longer time range may be necessary to reliably record chemical processes such as diffusion and mineral precipitation as reported by [22]. These authors performed similar flow-through experiments on samples prepared from the same slate material emphasizing the effect of fluid-rock interactions on the time-dependent transmissivity of fractures.
Concerning the influence of pressure and stress on transmissivity, we observed that the transmissivity is slightly (about two times) higher at enhanced pc compared to a similar enhancement of σ alone, although the effective stress acting normal to the interface is the same (e.g., Figure 7). The difference may be explained by the increasing strength of the matrix adjacent to the fracture and the suppression of tensile fracturing with increasing pressure, whereas with increasing stress but constant (low) confining pressure the strength of the aggregate is lower than at high pc. In both cases, the observed reduction in fracture transmissivity with increasing pc or σ (Figure 5 and Figure 6) is likely induced by indentation and damage of fracture surface asperities (Figure 9 and Figure 10), resulting in a change of contact area and therefore mean aperture. A similar trend of decreasing fracture transmissivity induced by mechanical and/or pressure solution processes is reported for other rocks, e.g., shales, (tight) sandstones, granites, and granodiorite [1,16,19,50,52,53,57,58,59].
Interestingly, the transmissivity of WBS at low applied stress was distinctly lower for the sample tested with Argon at pc = 14 MPa, pp = 10 MPa than for the sample flushed with water at pc = 5 MPa, pp = 1 MPa, i.e., at the same effective pressure (Figure 6a). The difference may be attributed to the experimental protocol, where in the case of Argon the initial 14 MPa confining pressure was applied before applying the fluid pressure. This may induce more initial damage of the surface compared to the test with water at only 5 MPa confining pressure (cf., Figure 5a). In addition, it is not well established that Terzaghi’s principle of effective stresses, i.e., pc_eff = pc − δ pp with δ =1, is valid here because at the microscale asperities are in contact, which reduces the Biot coefficient δ to a value < 1. This effect may result in a higher effective pressure in the experiment conducted with Argon gas compared to that with water, which would reduce the transmissivity difference at low stress. On the long term, chemical effects may also contribute to the transmissivity evolution due to different chemical fluid-rock interaction rates for different types of fluids.
In Figure 11, a comparison of our data with that measured by [19] on Westerly granite, Pennant sandstone and Bowland shale is presented, revealing that the influence of effective pressure on transmissivity disappears at high pc_eff. The transmissivity of WBS appears to be comparable to that of Pennant sandstone, whereas the transmissivity of our granite appears to be considerably lower than that of Westerly granite. Bowland shale exhibits the lowest transmissivity values, which are even lower than our clay-rich samples. The difference may be attributed to the initial roughness of the samples used by [19], which was unfortunately not provided by the authors.
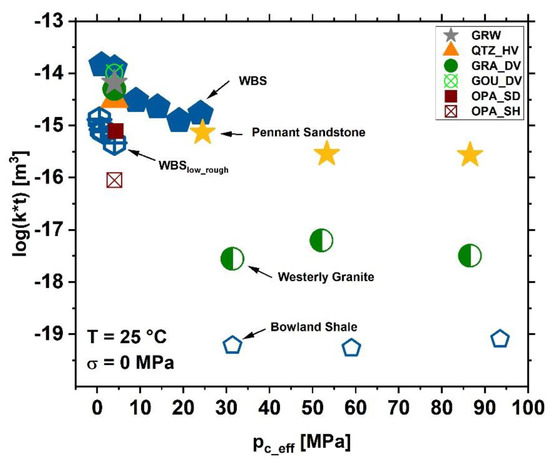
Figure 11.
Effect of effective confining pressure, pc_eff = pc − pp, on fracture transmissivity, k∗t, in Wissenbach slate (WBS) in comparison with other formations as reported by [19]. Data of the other formations investigated here (at σ = 0 MPa, c.f., Figure 6) are shown in addition.
The non-linear transmissivity reduction with increasing pressure and/or stress (Figure 5, Figure 6 and Figure 8) may be explained by the initial elastic deformation of the asperities that is gradually replaced by irreversible damage due to high stress concentrations. Since the effective contact area also increases with load (e.g., [60]), deformation or the breaking of further asperities or grains in the vicinity of the fracture surface become increasingly hampered and additional deformation is increasingly promoted by matrix deformation. As a consequence, the fluid flow pattern likely changes towards a higher tortuosity of the flow path and probably towards more localized flow through channels at high pressures, as also observed for other rocks (e.g., [50]). A number of theoretical attempts were made to relate fracture transmissivity to surface roughness and the applied normal stress (e.g., [61,62,63,64,65,66]). From that and from empirical correlations based on experiments, the change in fracture permeability with stress was described by a hyperbolic relationship [67], power law [68], or an exponential law [17,61]. Here, we used an exponential law of the following form:
where c is a constant and x is the slope in a plot of ln(k∗t) vs. σn_eff, with x = α for the loading path and x = β for the unloading path (c.f., Figure 8). For WBS, β is about 3 times smaller than α (Table 9), showing that irreversible damage changes the stress-sensitivity of transmissivity considerably.

Table 9.
Influence of host rock composition on fracture transmissivity.
4.2. Sample Composition and Mechanical Properties
To better quantify the influence of composition and mechanical properties on fracture transmissivity, we applied the exponential law on the transmissivity–stress data of all other rocks, yielding values in the range of −0.03 and −0.32 for α, and −0.008 and −0.064 for β (Table 9).
Lowest (absolute) α-values were fitted for granite and quartzite samples, whereas absolute α-values of the graywacke and slate are about twice as high and comparable to the sandy facies of OPA. Lowest (absolute) β-values were found in the granite and graywacke. In order to relate these values to composition, we superimposed them in ternary diagrams (Figure 12).
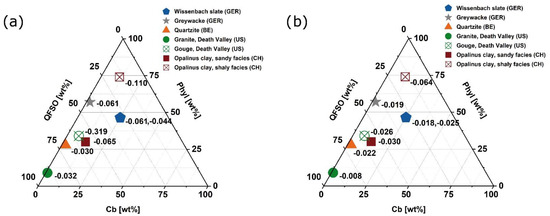
Figure 12.
Influence of sample composition on the (effective) stress-sensitivity of fracture transmissivity indicated by superimposed α-values for the loading path (a) and by β-values for the unloading path (b). The (absolute) sensitivity generally decreases for a high fraction of strong (QFSO) minerals and low amount of weak (Phyl) constituents.
Low (absolute) α-values, indicative of a weak reduction in transmissivity at elevated stress appear to be correlated with a high fraction of strong components (QFSO) and a low amount of weak constituents (Phyl), whereas carbonates appear to have no influence (Figure 12a). For the unloading sensitivity β, which is high for strong fracture transmissivity recovery, we observed a trend of enhanced unloading recovery with an increasing quantity of weak minerals and decreasing amount of QFSO (Figure 12b). Note that other parameters, which likely influence α and β, for example, porosity and cementation, are not captured in the diagrams.
In addition, we compared the σ-sensitivity of transmissivity for the different rock types with their brittleness defined by composition. Here, we used the empirical brittleness definition suggested by [69]:
where fxx is the fraction of minerals xx given in wt% and wQFSO, wCb, and wPhyl are the weighting factors ranging from 0 to 1. We set wQFSO = wPhyl = 1 and wCb = 0.5 as suggested by [69]. Calculated brittleness values are given in Table 9, ranging from 0.16 to 0.90. Based on the simplified assumption that in the absence of strong (QFSO) minerals the mechanical behavior is dominantly ductile, B values can vary between 0 and 1, indicating ductile and brittle deformation behavior, respectively. For rocks with high brittleness, the effect of increasing pressure or axial stress on fracture transmissivity is expected to be lower than for those with low B values. With the exception of the gouge, absolute values of α decrease with increasing Bcompo (Figure 13a) in line with the common assumption that the deformation of brittle rocks is less stress-sensitive than that of ductile rocks. The low α value of the gauge-like material recovered from the Death Valley is most likely due induced by the high initial roughness and a high porosity of about 13 vol% (Table 1). Similarly, the (absolute) unloading sensitivity β seems to slightly decrease with increasing brittleness (Figure 13b), which may be explained by the crushing of strong and brittle minerals at the fracture surface at elevated stresses, where the produced fines prevent the recovery of fracture transmissivity during unloading.
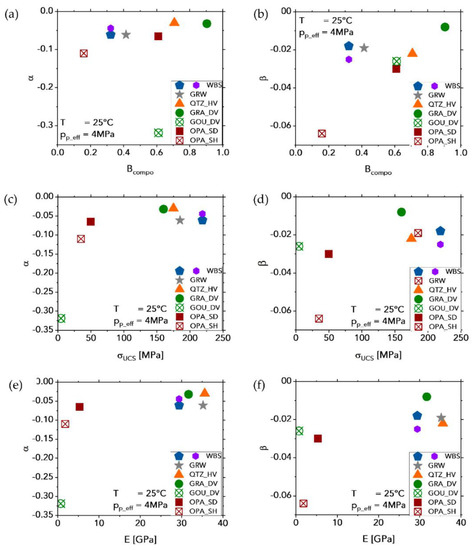
Figure 13.
Influence of brittleness based on composition, Bcompo, uniaxial compressive strength, σUCS, and static Young’s modulus, E, on the (effective) stress-sensitivity of fracture transmissivity, α, for the loading path (a,c,e) and for the unloading path β (b,d,f), respectively. The (absolute) sensitivity decreases with increasing brittleness, strength, and elastic stiffness.
Another parameter that likely explains the stress-sensitivity of the fracture transmissivity of the different investigated rocks are their mechanical properties. The measured unconfined uniaxial strength, σUCS, and the static Young’s moduli, E, vary over wide range and appear to be linearly correlated (Table 1, Figure A3), as has been observed frequently (e.g., [48,70]). Compared to composition-based brittleness, both (absolute) α and β values decrease with increasing σUCS and E (c.f., Figure 13c–f, respectively), revealing that rocks with a high strength and/or elastic stiffness are less sensitivity to stress-induced damage of the fracture surface and associated transmissivity reduction.
4.3. Implications for EGS in Different Host Rocks
An assessment of the performance and sustainability of fractured rock systems for EGS requires knowledge of the response of fractures to the acting effective stress, temperature, and fluid flow. The effective normal stress on fractures changes during and after hydraulic stimulation of reservoirs. As may be expected, our results of flow through experiments on various rock types (i.e., slate, quartzite, graywacke, granite, claystone, and gouge material) demonstrate that the key parameters that determine the stress resistance of fracture transmissivity are fracture surface roughness and the mechanical properties of the respective rock material. Fractures with similar surface roughness display the highest transmissivity in slate, quartzite, graywacke, and fresh granite, all of which contain a high amount of strong minerals and display high brittleness, high strength, and high elastic stiffness. On the other hand, in weak and porous rocks such as claystone and gouge material, transmissivity is reduced by several orders of magnitude by deformation of the soft matrix and limited crushing of contact asperities. Therefore, highly altered, clay-bearing formations are not favorable candidates for EGS. For hard rocks, grain size may also play a role if fracture propagation is predominantly intergranular. For example, the grain size of slate and graywacke is much smaller than that of quartzite and granite (Figure 2), so that at the microscale the real contact area of fine-grained rocks is higher, which reduces the stress acting on contact asperities, thereby maintaining a higher transmissivity.
Our results also imply that beside fracture surface roughness and composition, the degree of consolidation and metamorphic grade affects the potential of reservoir rocks for EGS. For example, the shaly facies of Opalinus Clay, graywacke and slate are relatively rich in phyllosilicates (Figure 1), but the latter two experienced a higher degree of metamorphosis with a strong cementation of grains, resulting in a much higher strength and elastic stiffness (Figure A3). Accordingly, fractures in slates are much more resistant against stress-induced fracture closure than in OPA (Figure 8).
We also noticed that (for slate samples) an increase in the fracture surface roughness (Sq) by about three times yields a fracture transmissivity of almost one order of magnitude higher at a low effective pressure (<5 MPa), which vanishes at high pressure (up to 25 MPa in our experiments), possibly due to the fact that the mechanical strength of slate at the microscale is not sufficient to resist high effective stresses. During hydraulic stimulation in EGS, tensile fractures are created that may connect to a preexisting fracture network. The surface roughness of these fractures is likely higher than the roughness of the artificially prepared surfaces in our study. For example, we measured a significantly larger (up to 20×) and more heterogeneously distributed roughness of tensile fractures created in WBS by Brazilian Disk (BD) experiments in divider, short-transverse, and arrester configuration following the ISRM suggested method [71]. However, even fractures with high initial roughness, e.g., created during hydraulic fracturing, may show a strong transmissivity decline at high stress conditions as long as they are not self-propped by shearing or artificially kept open by the addition of proppants (e.g., [72]). For the latter, high stress may crush the proppants and embed them into the matrix, which leads again to a transmissivity reduction (e.g., [73]).
Other parameters, which were not investigated in this study, may also affect the efficiency and sustainability of an EGS in different formations, for example self-propping due to a shear deformation event or fine production and clogging of flow path by ongoing deformation. Additionally, chemical effects due to long-term fluid–rock interactions or scaling may change the fracture transmissivity, depending on fluid and rock composition and thermodynamic boundary conditions.
5. Conclusions
Fracture transmissivity decreases asymptotically with increasing confining pressure and stress due to the damage caused to surface asperities and the matrix deformation of weak rocks, which is largely irreversible. A lower initial roughness also reduces transmissivity, while a temperature increase only significantly reduces the transmissivity by thermal dilation if the fracture aperture is already low. As may be expected, the fracture transmissivity of hard brittle rocks with a high fraction of strong minerals is less sensitive to stress-induced fracture closure and exhibits less irreversible damage. However, since the transmissivity of slates is much higher than of claystone, as well as the transmissivity of granite compared to a highly altered and sheared granitic gouge, the grade of consolidation, metamorphosis, and alteration of rocks is also important for fluid flow within discrete fractures under in situ conditions. Our results suggest that Variscan metamorphic rocks such as slate, graywacke and quartzite can be considered as host rocks for unconventional Enhanced Geothermal systems, with resistance to fracture transmissivity against thermodynamic boundary conditions that is as good as that of granite or quartzite for similar initial fracture roughness.
Author Contributions
Conceptualization, J.H.; methodology, J.H. and V.S.; software, J.H., V.S. and E.R.; validation, J.H., V.S., C.C., H.M. and E.R.; formal analysis, J.H.; investigation, J.H. and V.S.; resources, J.H., V.S. and C.C.; data curation, J.H. and V.S.; writing—original draft preparation, J.H.; writing—review and editing, J.H., V.S., C.C., H.M. and E.R.; visualization, J.H., V.S., C.C. and E.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the “Multidisciplinary and multi-context demonstration of Enhanced Geothermal Systems Exploration and Exploitation Techniques and potentials (MEET)” research project funded by the European Union’s Horizon 2020 research and innovation programme under Grant Agreement No. 792037.
Data Availability Statement
Not applicable.
Acknowledgments
We thank Michael Naumann for the construction of the modified MuSPIS apparatus and for their assistance with the uniaxial and triaxial deformation as well as fracture transmissivity experiments, Stefan Gehrmann for sample and thin section preparation, Anja Schreiber for carbon coating of SEM samples, Bianca Wagner and Bernd Leiss from the University of Göttingen for XRD results and providing Wissenbach slate and graywacke samples, Yves Vanbrabant from Institut Royal des Sciences Naturelles de Belgique for providing Havelange quartzite samples, Ghislain Trullenque and Johanne Klee from Institut Polytechnique LaSalle Beauvais for providing granite and gouge samples, and Kristian Bär and Aysegül Turan from the Technical University of Darmstadt for providing some mechanical and petrophysical data.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
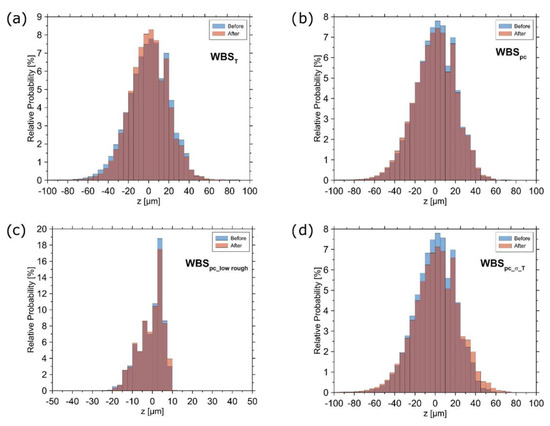
Figure A1.
Fracture surface height distribution before and after experiments for Wissenbach slate tested at different temperatures (a), confining pressures (b,c), and a combination of different pressures, stresses and temperatures (d). Initial sample roughness was Sq = 0.019 mm in (a,b,d) and Sq = 0.006 mm in (c).
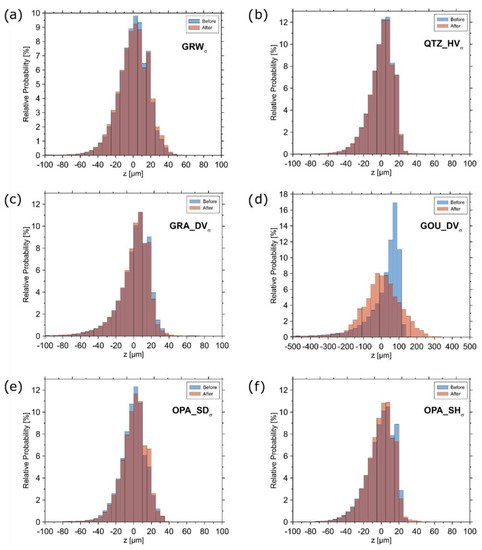
Figure A2.
Fracture surface height distribution before and after testing at elevated stresses for graywacke (a), quartzite (b), fresh granite (c), altered granitic gouge (d), Opalinus clay—sandy facies (e), and Opalinus clay—shaly facies (f). Wissenbach slate tested at different temperatures (a), confining pressures (b,c), and a combination of different pressures, stresses and temperatures (d).
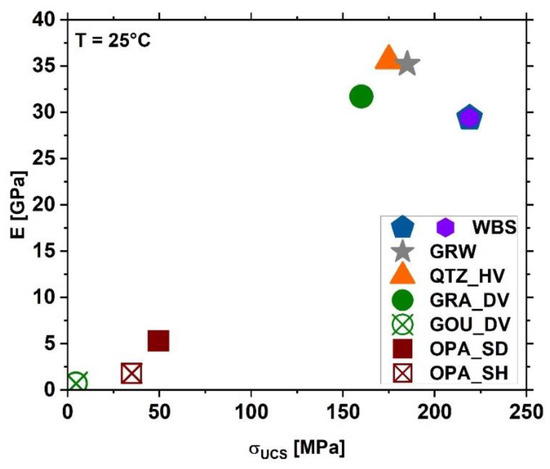
Figure A3.
Static Young’s modulus E vs. uniaxial compressive strength σUCS of all tested rock types.

Table A1.
List of symbols.
Table A1.
List of symbols.
| Symbol | Description | Unit |
|---|---|---|
| ρ | Bulk density | g/cm3 |
| ρg | Grain density | g/cm3 |
| ϕHe | Sample Porosity (using Helium pycnometry) | vol% |
| kmatrix | Matrix permeability | m2 |
| σUCS | Uniaxial compressive strength | MPa |
| σTCS | Triaxial compressive strength | MPa |
| E | Static Young’s modulus | GPa |
| pc | Confining pressure | MPa |
| pp | Fluid pressure | Pa |
| T | Temperature | °C |
| σ | Axial deviatoric stress | MPa |
| Sq | Fracture surface roughness (root mean square) | mm |
| k | Fracture permeability | m2 |
| t | Fracture thickness/hydraulic aperture | mm |
| Q | Volumetric flow rate | ml/min |
| η | Dynamic viscosity | Pa∗s |
| 2a | Distance between up- and downstream borehole | mm |
| r0 | Radius of up- and downstream borehole | mm |
| ∆pp | Differential pore pressure within the fracture | Pa |
| ∆x | Distance within the fracture over which is ∆pp measured | mm |
| B | Geometry factor | / |
| Bcompo | Brittleness based on composition | / |
| wxx | Mineral weighting factor | / |
| fxx | Mineral fraction | wt% |
References
- Vogler, D.; Amann, F.; Bayer, P.; Elsworth, D. Permeability evolution in natural fractures subject to cyclic loading and gouge formation. Rock Mech. Rock Eng. 2016, 49, 3463–3479. [Google Scholar] [CrossRef]
- Lu, S.M. A global review of enhanced geothermal system (EGS). Renew. Sustain. Energy Rev. 2018, 81, 2902–2921. [Google Scholar] [CrossRef]
- Favier, A.; Lardeaux, J.M.; Corsini, M.; Verati, C.; Navelot, V.; Géraud, Y.; Diraison, M.; Ventalon, S.; Voitus, E. Characterization of an exhumed high-temperature hydrothermal system and its application for deep geothermal exploration: An example from Terre-de-Haut Island (Guadeloupe archipelago, Lesser Antilles volcanic arc). J. Volcanol. Geotherm. Res. 2021, 418, 107256. [Google Scholar] [CrossRef]
- Roche, V.; Bouchot, V.; Beccaletto, L.; Jolivet, L.; Guillou-Frottier, L.; Tuduri, J.; Bozkurt, E.; Oguz, K.; Tokay, B. Structural, lithological, and geodynamic controls on geothermal activity in the Menderes geothermal Province (Western Anatolia, Turkey). Int. J. Earth Sci. 2019, 108, 301–328. [Google Scholar] [CrossRef] [Green Version]
- Beauchamps, G.; Ledésert, B.; Hébert, R.; Navelot, V.; Favier, A. The characterisation of an exhumed high-temperature paleo-geothermal system on Terre-de-Haut Island (the Les Saintes archipelago, Guadeloupe) in terms of clay minerals and petrophysics. Geotherm. Energy 2019, 7, 6. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Witherspoon, P.A.; Ohnishi, Y. Theory of heat extraction from fractured hot dry rock. J. Geophys. Res. 1975, 80, 1120–1124. [Google Scholar] [CrossRef]
- Liotta, D.; Brogi, A.; Ruggieri, G.; Zucchi, M. Fossil vs. active geothermal systems: A field and laboratory method to disclose the relationships between geothermal fluid flow and geological structures at depth. Energies 2021, 14, 993. [Google Scholar] [CrossRef]
- Brogi, A.; Alçiçek, M.C.; Liotta, D.; Capezzuoli, E.; Zucchi, M.; Matera, P.F. Step-over fault zones controlling geothermal fluid-flow and travertine formation (Denizli Basin, Turkey). Geothermics 2021, 89, 101941. [Google Scholar] [CrossRef]
- Li, Q.; Xing, H.; Liu, J.; Liu, X. A review on hydraulic fracturing of unconventional reservoir. Petroleum 2015, 1, 8–15. [Google Scholar] [CrossRef] [Green Version]
- Milsch, H.H.; Spangenberg, E.; Kulenkampff, J.; Meyhöfer, S. A new apparatus for long-term petrophysical investigations on geothermal reservoir rocks at simulated in-situ conditions. Transp. Porous Media 2008, 74, 73–85. [Google Scholar] [CrossRef] [Green Version]
- Voltolini, M.; Ajo-Franklin, J. Evolution of propped fractures in shales: The microscale controlling factors as revealed by in situ X-Ray microtomography. J. Pet. Sci. Eng. 2020, 188, 106861. [Google Scholar] [CrossRef]
- Crandall, D.; Moore, J.; Gill, M.; Stadelman, M. CT scanning and flow measurements of shale fractures after multiple shearing events. Int. J. Rock Mech. Min. Sci. 2017, 100, 177–187. [Google Scholar] [CrossRef]
- Carey, J.W.; Lei, Z.; Rougier, E.; Mori, H.; Viswanathan, H. Fracture-permeability behavior of shale. J. Unconv. Oil Gas Resour. 2015, 11, 27–43. [Google Scholar] [CrossRef]
- Leung, C.T.O.; Zimmerman, R.W. Estimating the Hydraulic Conductivity of Two-Dimensional Fracture Networks Using Network Geometric Properties. Transp. Porous Media 2012, 93, 777–797. [Google Scholar] [CrossRef]
- Stober, I.; Bucher, K. Hydraulic conductivity of fractured upper crust: Insights from hydraulic tests in boreholes and fluid-rock interaction in crystalline basement rocks. Geofluids 2015, 15, 161–178. [Google Scholar] [CrossRef]
- Cho, Y.; Apaydin, O.G.; Ozkan, E. Pressure-dependent natural-fracture permeability in shale and its effect on shale-gas well production. SPE Reserv. Eval. Eng. 2013, 16, 216–228. [Google Scholar] [CrossRef]
- Gutierrez, M.; Øino, L.E.; Nygård, R. Stress-dependent permeability of a de-mineralised fracture in shale. Mar. Pet. Geol. 2000, 17, 895–907. [Google Scholar] [CrossRef]
- Liu, E. Effects of fracture aperture and roughness on hydraulic and mechanical properties of rocks: Implication of seismic characterization of fractured reservoirs. J. Geophys. Eng. 2005, 2, 38–47. [Google Scholar] [CrossRef]
- Rutter, E.H.; Mecklenburgh, J. Influence of normal and shear stress on the hydraulic transmissivity of thin cracks in a tight quartz sandstone, a granite, and a shale. J. Geophys. Res. Solid Earth 2018, 123, 1262–1285. [Google Scholar] [CrossRef] [Green Version]
- Blöcher, G.; Kluge, C.; Milsch, H.; Cacace, M.; Jacquey, A.B.; Schmittbuhl, J. Permeability of matrix-fracture systems under mechanical loading—Constraints from laboratory experiments and 3-D numerical modelling. Adv. Geosci. 2019, 49, 95–104. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.; Milsch, H. Permeability variations in illite-bearing sandstone: Effects of temperature and NaCl fluid salinity. J. Geophys. Res. Solid Earth 2020, 125, 9. [Google Scholar] [CrossRef]
- Cheng, C.; Herrmann, J.; Wagner, B.; Leiss, B.; Stammeier, J.A.; Rybacki, E.; Milsch, H. Long-Term Evolution of Fracture Permeability in Slate: An Experimental Study with Implications for Enhanced Geothermal Systems (EGS). Geosciences 2021, 11, 443. [Google Scholar] [CrossRef]
- Walsh, S.D.C.; Smith, M.; Carroll, S.A.; Crandall, D. Non-invasive measurement of proppant pack deformation. Int. J. Rock Mech. Min. Sci. 2016, 87, 39–47. [Google Scholar] [CrossRef]
- Zhang, J.; Ouyang, L.; Zhu, D.; Hill, A.D. Experimental and numerical studies of reduced fracture conductivity due to proppant embedment in the shale reservoir. J. Pet. Sci. Eng. 2015, 130, 37–45. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, N.; Ishibashi, T.; Ohsaki, Y.; Tsuchiya, Y.; Tamagawa, T.; Hirano, N.; Okabe, H.; Tsuchiya, N. X-ray CT based numerical analysis of fracture flow for core samples under various confining pressures. Eng. Geol. 2011, 123, 338–346. [Google Scholar] [CrossRef]
- Schill, E.; Genter, A.; Cuenot, N.; Kohl, T. Hydraulic performance history at the Soultz EGS reservoirs from stimulation and long-term circulation tests. Geothermics 2017, 70, 110–124. [Google Scholar] [CrossRef]
- Vidal, J.; Genter, A. Overview of naturally permeable fractured reservoirs in the central and southern Upper Rhine Graben: Insights from geothermal wells. Geothermics 2018, 74, 57–73. [Google Scholar] [CrossRef]
- Vanbrabant, Y.; Stenmans, V.; Burlet, C.; Petitclerc, E.; Meyvis, B.; Stasi, G.; Abarim, R.; Bar, K.; Goovaerts, T. Havelange deep borehole (Belgium): A study case for the evaluation of metasedimentary formations as potential geothermal reservoir—H2020 MEET project. In Proceedings of the EGU General Assembly Conference 2020, Online, 4–8 May 2020; p. 10943. [Google Scholar]
- Leiss, B.; Tanner, D.; Vollbrecht, A.; Wemmer, K. Neue Untersuchungen zur Geologie der Leinetalgrabenstruktur; Universitätsverlag Göttingen: Göttingen, Germany, 2011. [Google Scholar]
- Leiss, B.; Tanner, D.; Vollbrecht, A.; Wemmer, K. Tiefengeothermisches Potential in der Region Göttingen—Geologische Rahmenbedingungen. In Neue Untersuchungen zur Geologie der Leinetalgrabenstruktur; Leiss, B., Tanner, D., Vollbrecht, A., Arp, G., Eds.; Universitätsverlag Göttingen: Göttingen, Germany, 2011; pp. 163–170. [Google Scholar] [CrossRef]
- Leiss, B.; Wagner, B.; Heinrichs, T.; Romanov, D.; Tanner, D.C.; Vollbrecht, A.; Wemmer, K. Integrating deep, medium and shallow geothermal energy into district heating and cooling system as an energy transition approach for the Göttingen University Campus. In Proceedings of the World Geothermal Congress 2021, Reykjavik, Iceland, 24–27 October 2021; pp. 1–9. [Google Scholar]
- Brinckmann, J.; Brüning, U. (Eds.) Das Bundesbohrprogramm im West-Harz, Paläogeographische Ergebnisse (The Federal Drilling Program in the Western Harz Mountains: Paleogeographic Results and Five Additional Contributions to the Geology of the Western Harz Mountains); Geologisches Jahrbuch Reihe D: Hanover, Germany, 1986; Band D. [Google Scholar]
- Gerling, P.; Kockel, F.; Krull, P. The HC Potential of Pre-Westphalian Sediments in the North German Basin—A Synthesis; DGMK-Research Report 43; 1999. Available online: https://www.osti.gov/etdeweb/biblio/695510 (accessed on 7 April 2022).
- Littke, R.; Krooss, B.; Uffmann, A.K.; Schulz, H.M.; Horsfield, B. Unconventional gas resources in the Paleozoic of Central Europe. Oil Gas Sci. Technol. 2011, 66, 953–977. [Google Scholar] [CrossRef] [Green Version]
- Schubert, M. Die Dysaerobe Biofazies der Wissenbach Schiefer (Rheinisches Schiefergebirge, Harz, Devon); Institute der Georg-August-Universit: Göttingen, Germany, 1996. [Google Scholar]
- Sáez, R.; Moreno, C.; González, F.; Almodóvar, G.R. Black shales and massive sulfide deposits: Causal or casual relationships? Insights from Rammelsberg, Tharsis, and Draa Sfar. Miner. Depos. 2011, 46, 585–614. [Google Scholar] [CrossRef]
- Klee, J.; Potel, S.; Ledésert, B.; Hébert, R.; Chabani, A.; Barrier, P.; Trullenque, G. Fluid-rock interactions in a Paleo-geothermal reservoir (Noble Hills Granite, California, USA). Part 1: Granite pervasive alteration processes away from fracture zones. Geosciences 2021, 11, 325. [Google Scholar] [CrossRef]
- Klee, J.; Chabani, A.; Ledésert, B.A.; Potel, S.; Hébert, R.L.; Trullenque, G. Fluid-rock interactions in a paleo-geothermal reservoir (Noble hills granite, california, usa). part 2: The influence of fracturing on granite alteration processes and fluid circulation at low to moderate regional strain. Geosciences 2021, 11, 433. [Google Scholar] [CrossRef]
- Amann, F.; Wild, K.M.; Loew, S.; Yong, S.; Thoeny, R.; Frank, E. Geomechanical behaviour of Opalinus Clay at multiple scales: Results from Mont Terri rock laboratory (Switzerland). Swiss J. Geosci. 2017, 110, 151–171. [Google Scholar] [CrossRef]
- Bossart, P.; Bernier, F.; Birkholzer, J.; Bruggeman, C.; Connolly, P.; Dewonck, S.; Fukaya, M.; Hexfort, M.; Jensen, M.; Matray, J.-M.; et al. Mont Terri rock laboratory, 20 years of research: Introduction, site characteristics and overview of experiments. Swiss J. Geosci. 2017, 110, 3–22. [Google Scholar] [CrossRef] [Green Version]
- Schuster, V.; Rybacki, E.; Bonnelye, A.; Herrmann, J.; Schleicher, A.; Dresen, G. Experimental deformation of Opalinus Clay at elevated temperature and pressure conditions: Mechanical properties and the influence of rock fabric. Rock Mech. Rock Eng. 2021, 54, 4009–4039. [Google Scholar] [CrossRef]
- Nussbaum, C.; Kloppenburg, A.; Caër, T.; Bossart, P. Tectonic evolution around the Mont Terri rock laboratory, northwestern Swiss Jura: Constraints from kinematic forward modelling. Swiss J. Geosci. 2017, 110, 39–66. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Matray, J.M.; Gonçalvès, J.; Jaeggi, D.; Gräsle, W.; Wieczorek, K.; Vogt, T.; Skyes, E. Comparative study of methods to estimate hydraulic parameters in the hydraulically undisturbed Opalinus Clay (Switzerland). Swiss J. Geosci. 2017, 110, 85–104. [Google Scholar] [CrossRef] [Green Version]
- McKernan, R.; Mecklenburgh, J.; Rutter, E.; Taylor, K. Microstructural controls on the pressure-dependent permeability of Whitby mudstone. Geol. Soc. 2017, 454, 39–66. [Google Scholar] [CrossRef] [Green Version]
- Ji, Y.; Hofmann, H.; Rutter, E.H.; Xiao, F.; Yang, L. Revisiting the Evaluation of Hydraulic Transmissivity of Elliptical Rock Fractures in Triaxial Shear-Flow Experiments. Rock Mech. Rock Eng. 2022, 1–9. [Google Scholar] [CrossRef]
- Bieniawski, Z.T.; Bernede, M.J. Suggested methods for determining the uniaxial compressive strength and deformability of rock materials: Part 1. Suggested method for determining deformability of rock materials in uniaxial compression. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 138–140. [Google Scholar] [CrossRef]
- Paterson, M.S. A high-pressure, high-temperature apparatus for rock deformation. Int. J. Rock Mech. Min. Sci. 1970, 7, 517–526. [Google Scholar] [CrossRef]
- Rybacki, E.; Reinicke, A.; Meier, T.; Makasi, M.; Dresen, G. What controls the mechanical properties of shale rocks?—Part I: Strength and Young’s modulus. J. Pet. Sci. Eng. 2015, 135, 702–722. [Google Scholar] [CrossRef]
- von Terzaghi, K. Die Berechnung der Durchas- sigkeitsziffer des Tones aus dem Veriauf der hydrodynamischen Spannungserscheinungen, Sitzungsber. Akad. Wiss. Wien Math Naturwiss. 1923, 132, 105. [Google Scholar]
- Cheng, C.; Milsch, H. Evolution of fracture aperture in quartz sandstone under hydrothermal conditions: Mechanical and chemical effects. Minerals 2020, 10, 657. [Google Scholar] [CrossRef]
- Li, F.B.; Sheng, J.C.; Zhan, M.L.; Xu, L.M.; Wu, Q.; Jia, C.L. Evolution of limestone fracture permeability under coupled thermal, hydrological, mechanical, and chemical conditions. J. Hydrodyn. 2014, 26, 234–241. [Google Scholar] [CrossRef]
- Lima, M.G.; Vogler, D.; Querci, L.; Madonna, C.; Hattendorf, B.; Saar, M.O.; Kong, X.Z. Thermally driven fracture aperture variation in naturally fractured granites. Geotherm. Energy 2019, 7, 23. [Google Scholar] [CrossRef]
- Yasuhara, H.; Kinoshita, N.; Ohfuji, H.; Lee, D.S.; Nakashima, S.; Kishida, K. Temporal alteration of fracture permeability in granite under hydrothermal conditions and its interpretation by coupled chemo-mechanical model. Appl. Geochem. 2011, 26, 2074–2088. [Google Scholar] [CrossRef]
- Kamali-Asl, A.; Ghazanfari, E.; Perdrial, N.; Bredice, N. Experimental study of fracture response in granite specimens subjected to hydrothermal conditions relevant for enhanced geothermal systems. Geothermics 2018, 72, 205–224. [Google Scholar] [CrossRef]
- Yasuhara, H.; Elsworth, D. Compaction of a rock fracture moderated by competing roles of stress corrosion and pressure solution. Pure Appl. Geophys. 2008, 165, 1289–1306. [Google Scholar] [CrossRef] [Green Version]
- Rutqvist, J. Fractured rock stress-permeability relationships from in situ data and effects of temperature and chemical-mechanical couplings. Geofluids 2015, 15, 48–66. [Google Scholar] [CrossRef] [Green Version]
- Cao, N.; Lei, G.; Dong, P.; Li, H.; Wu, Z.; Li, Y. Stress-dependent permeability of fractures in tight reservoirs. Energies 2019, 12, 117. [Google Scholar] [CrossRef] [Green Version]
- Rutter, E.H.; Mecklenburgh, J. Hydraulic conductivity of bedding-parallel cracks in shale as a function of shear and normal stress. Geol. Soc. 2017, 454, 67. [Google Scholar] [CrossRef]
- Yasuhara, H.; Elsworth, D. Evolution of permeability in a natural fracture: Significant role of pressure solution. J. Geophys. Res. 2004, 109, 03204. [Google Scholar] [CrossRef]
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids; Clarendon Press: Oxford, UK, 1964; Volume 2, No. 2. [Google Scholar]
- Huo, D.; Benson, S.M. An Experimental Investigation of Stress-Dependent Permeability and Permeability Hysteresis Behavior in Rock Fractures. Dynamics of Fluids and Transport in Complex Fractured-Porous Systems. Geophys. Monogr. 2015, 210, 99–114. [Google Scholar]
- Gangi, A.F. Variation of whole and fractured porous rock permeability with confining pressure. Int. J. Rock Mech. Min. Sci. 1978, 15, 249–257. [Google Scholar] [CrossRef]
- Tsang, Y.W.; Witherspoon, P.A. The dependence of fracture mechanical and fluid flow properties on fracture roughness and sample size. J. Geophys. Res. 1983, 88, 2359–2366. [Google Scholar] [CrossRef] [Green Version]
- Walsh, J.B. Effect of pore pressure and confining pressure on fracture permeability. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 429–435. [Google Scholar] [CrossRef]
- Witherspoon, P.A.; Wang, J.S.Y.; Iwai, K.; Gale, J.E. Validity of cubic law for fluid-flow in a deformable rock fracture. Water Resour. Res. 1980, 16, 1016–1024. [Google Scholar] [CrossRef] [Green Version]
- Zimmerman, R.W.; Chen, D.W.; Cook, N.G.W. The effect of contact area on the permeability of fractures. J. Hydrol. 1992, 139, 79–96. [Google Scholar] [CrossRef] [Green Version]
- Barton, N.; Bandis, S.; Bakhtar, K. Strength, Deformation and Conductivity Coupling of Rock Joints. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1985, 22, 121–140. [Google Scholar] [CrossRef]
- Gale, J.E. The effects of fracture type induced versus natural on the stress-fracture closure-fracture permeability relationships. In Proceedings of the 23rd U.S. Symposium on Rock Mechanics, University of California, Berkeley, CA, USA, 25–27 August 1982; pp. 290–298. [Google Scholar]
- Rybacki, E.; Meier, T.; Dresen, G. What controls the mechanical properties of shale rocks?—Part II: Brittleness. J. Pet. Sci. Eng. 2016, 144, 39–58. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, J.; Rybacki, E.; Sone, H.; Dresen, G. Deformation experiments on Bowland and Posidonia shale—Part I: Strength and Young’s modulus at ambient and in situ pc-T conditions. Rock Mech. Rock Eng. 2018, 51, 3645–3666. [Google Scholar] [CrossRef] [Green Version]
- Ulusay, R. The ISRM Suggested Methods for Rock Characterization, Testing and Monitoring 2007–2014; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Durham, W.B.; Bonner, B.P. Self-propping and fluid flow in slightly offset joints at high effective pressures. J. Geophys. Res. 1994, 99, 9391–9399. [Google Scholar] [CrossRef]
- Reinicke, A.; Rybacki, E.; Stanchits, S.; Huenges, E.; Dresen, G. Hydraulic fracturing stimulation techniques and formation damage mechanisms—Implications from laboratory testing of tight sandstone–proppant systems. Geochemistry 2010, 70 (Suppl. S3), 107–117. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).