Seismicity Patterns Prior to the Thessaly (Mw6.3) Strong Earthquake on 3 March 2021 in Terms of Multiresolution Wavelets and Natural Time Analysis
Abstract
:1. Introduction
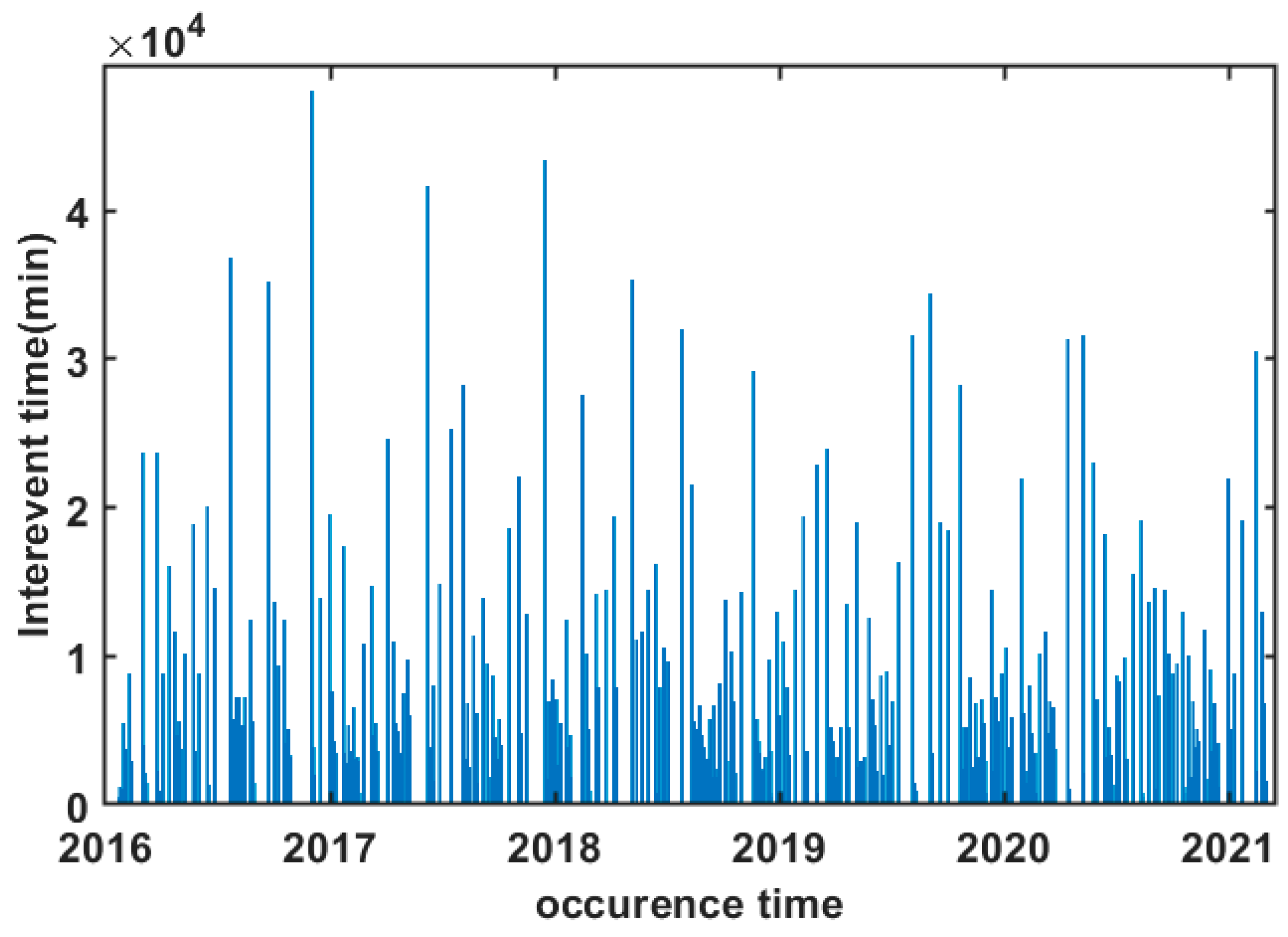
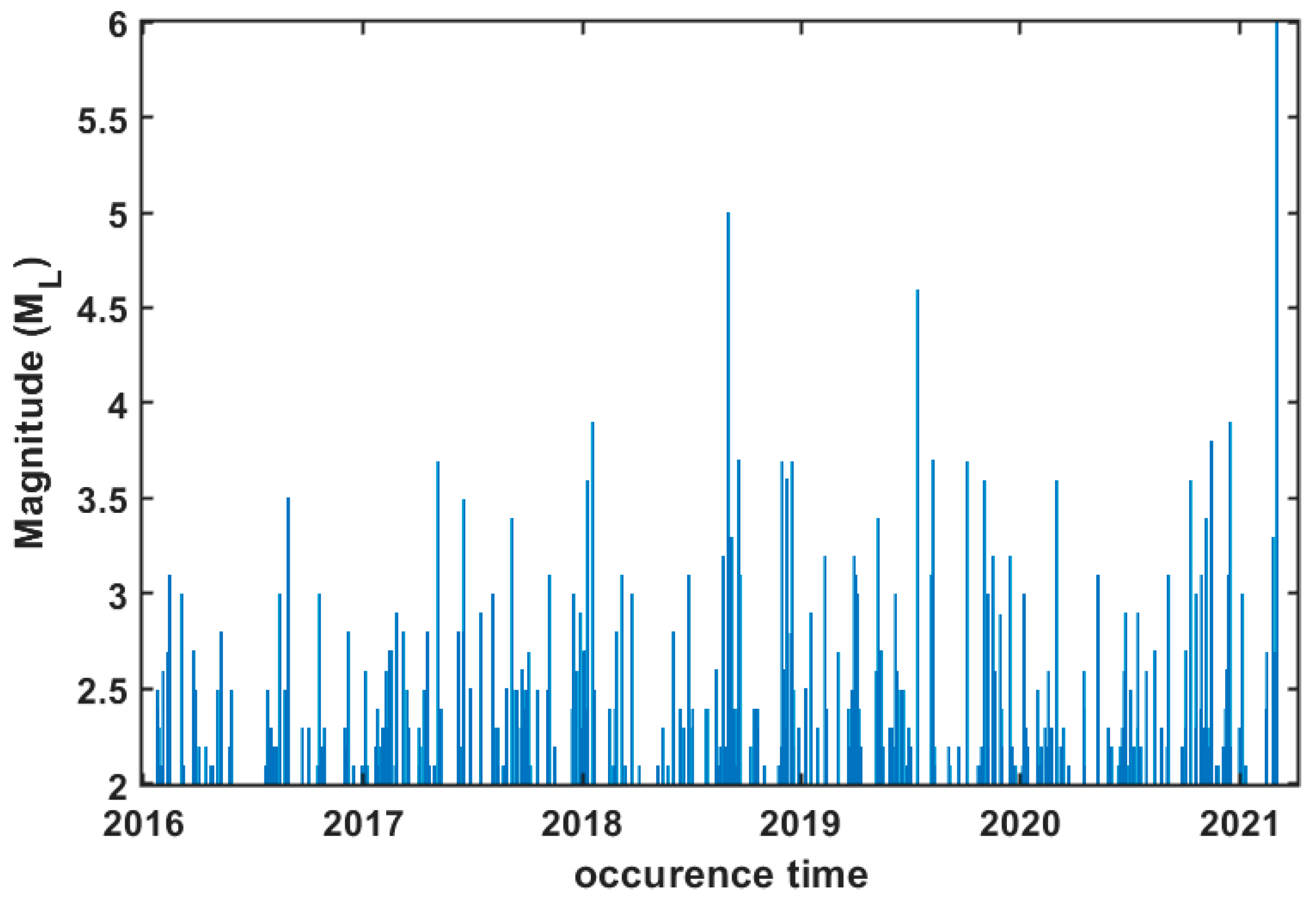
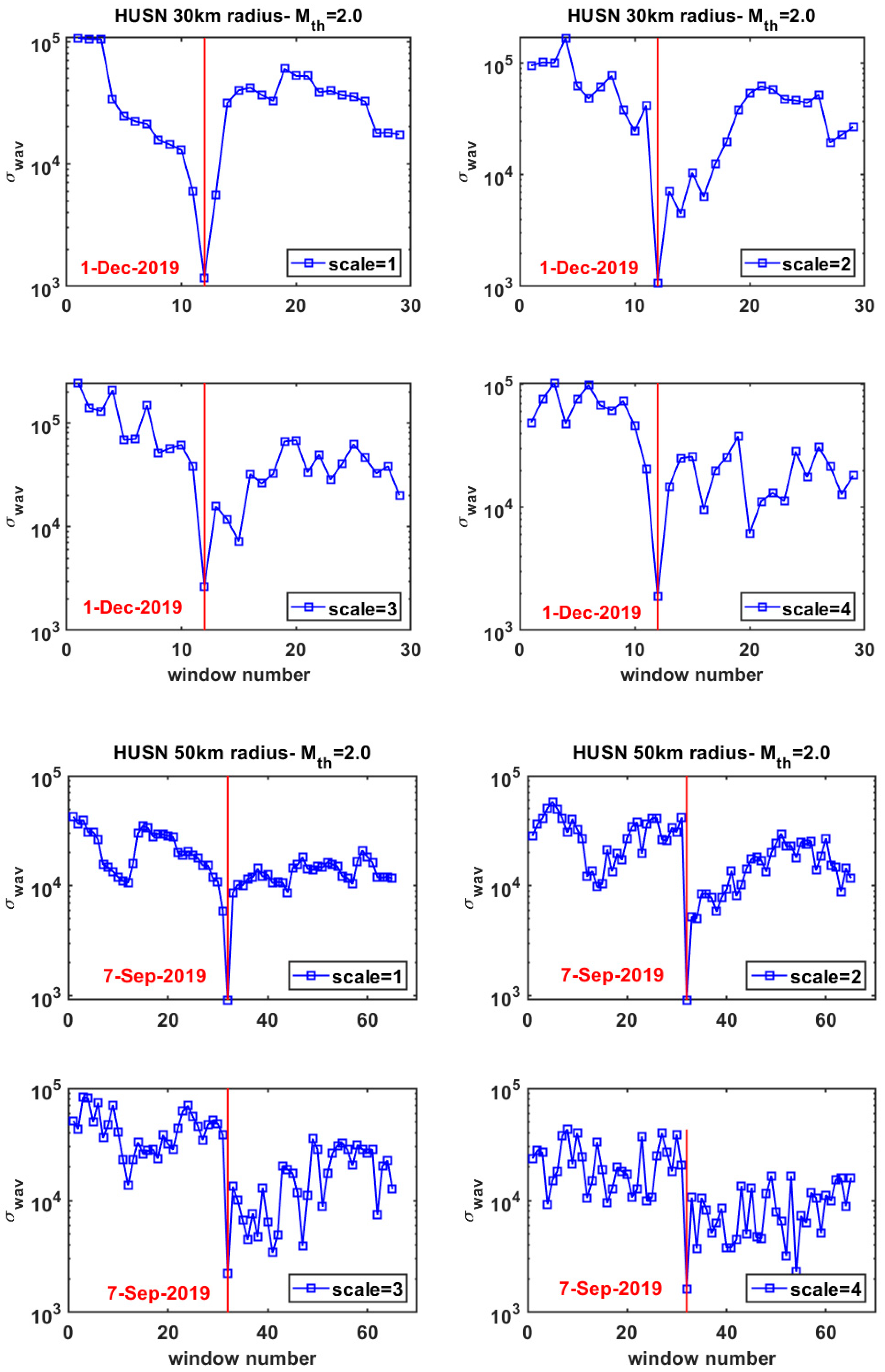
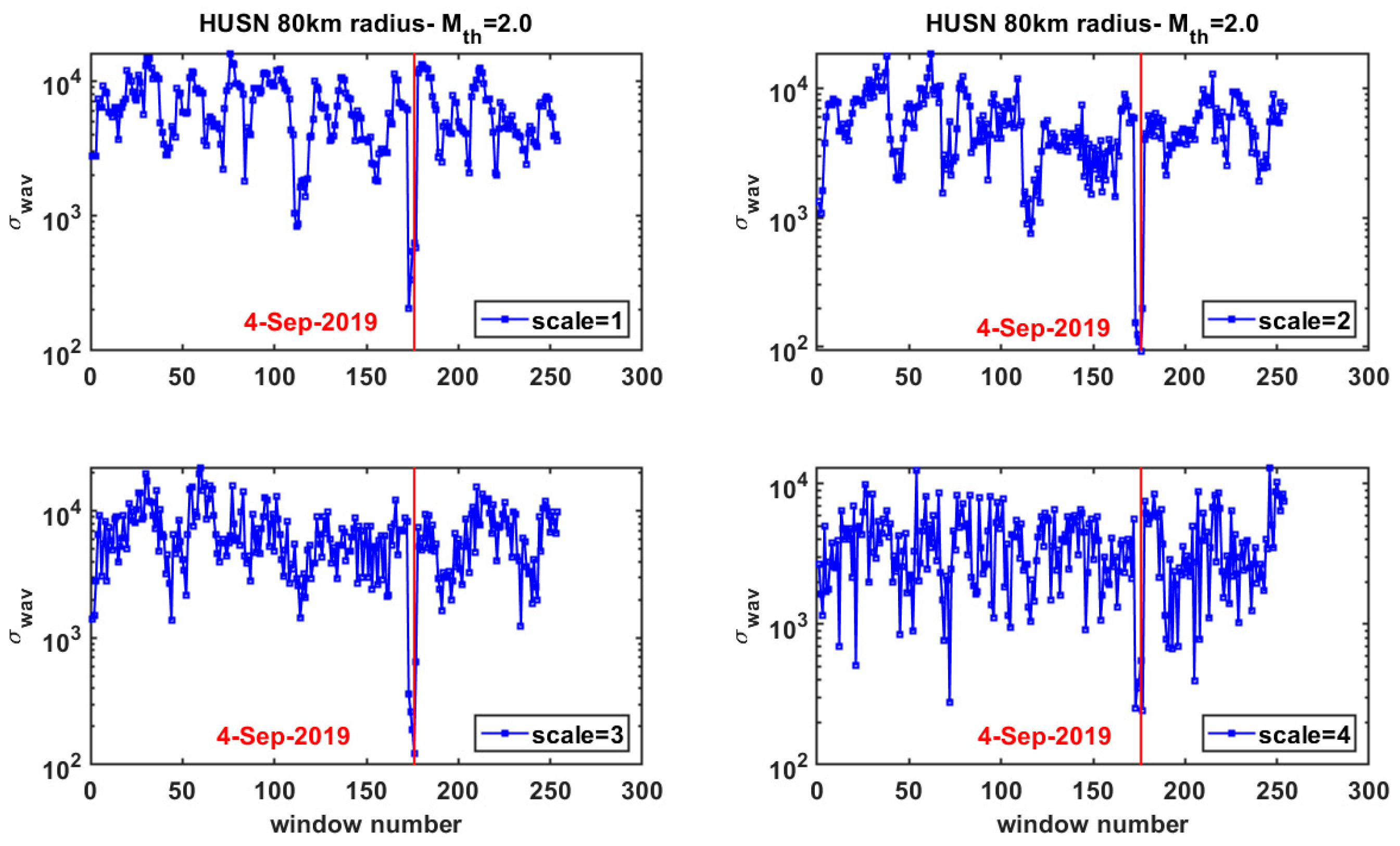
2. Multiresolution Wavelets Analysis in the Seismicity of Thessaly Region
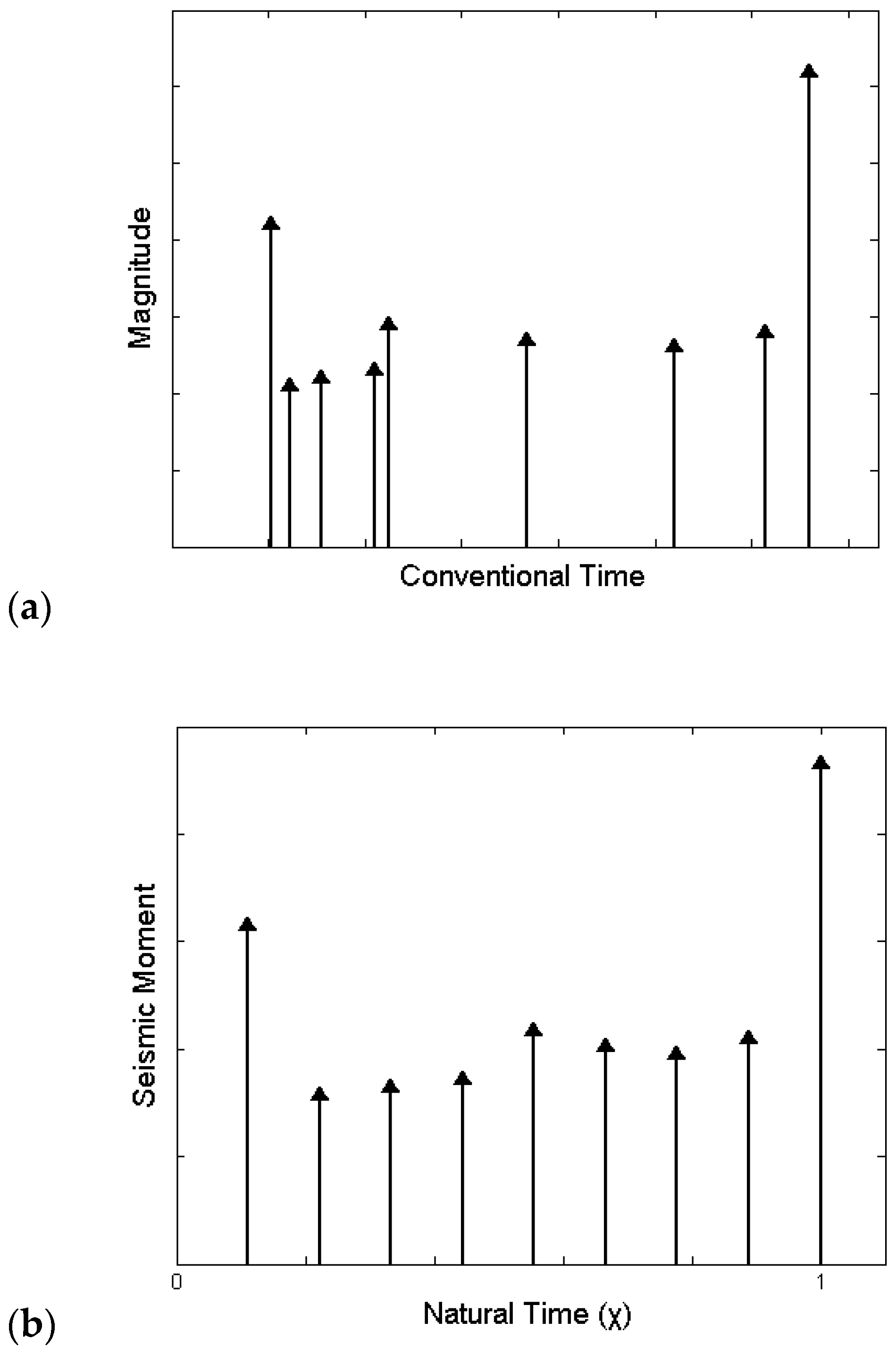
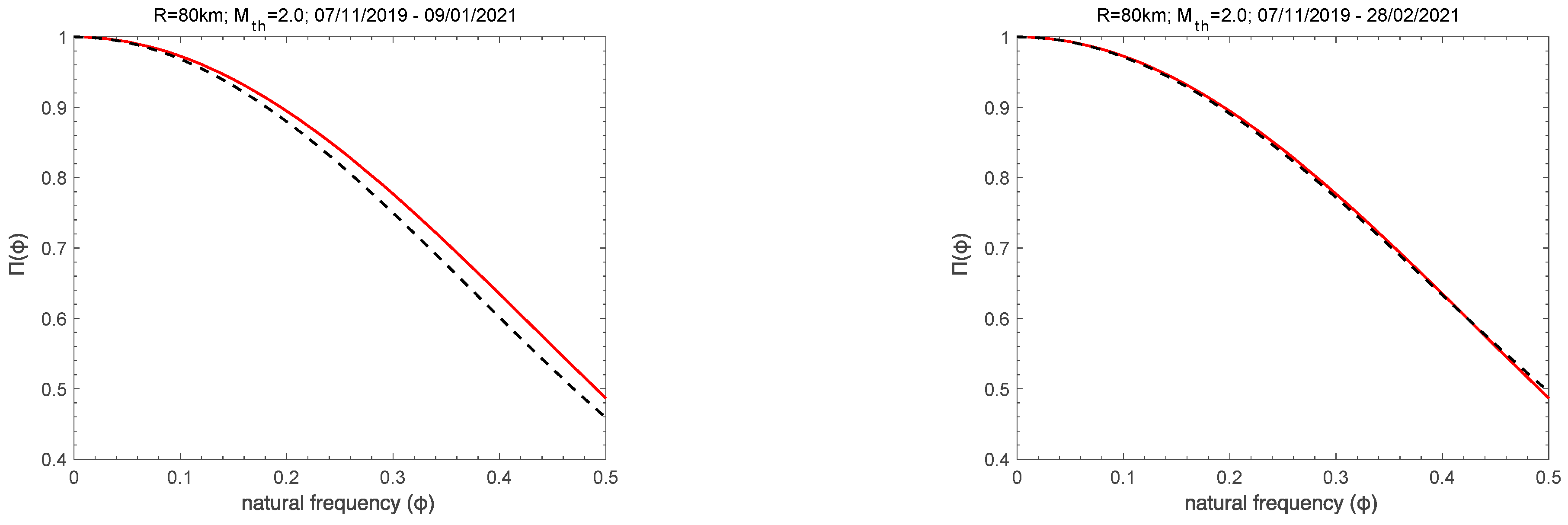
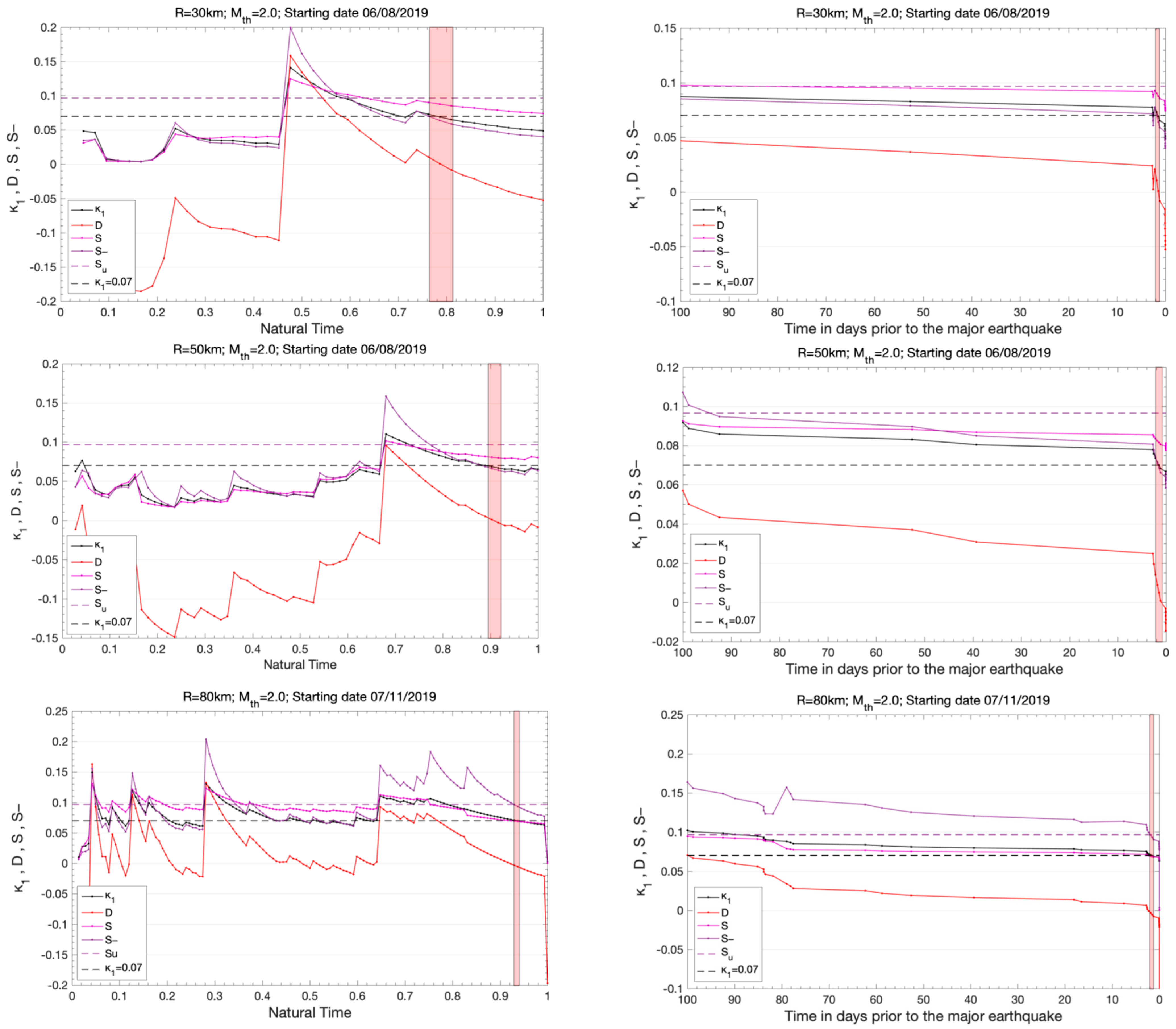
3. Natural Time Analysis of Seismicity before the Thessaly Mw6.3, March 2021 Earthquake
- (i).
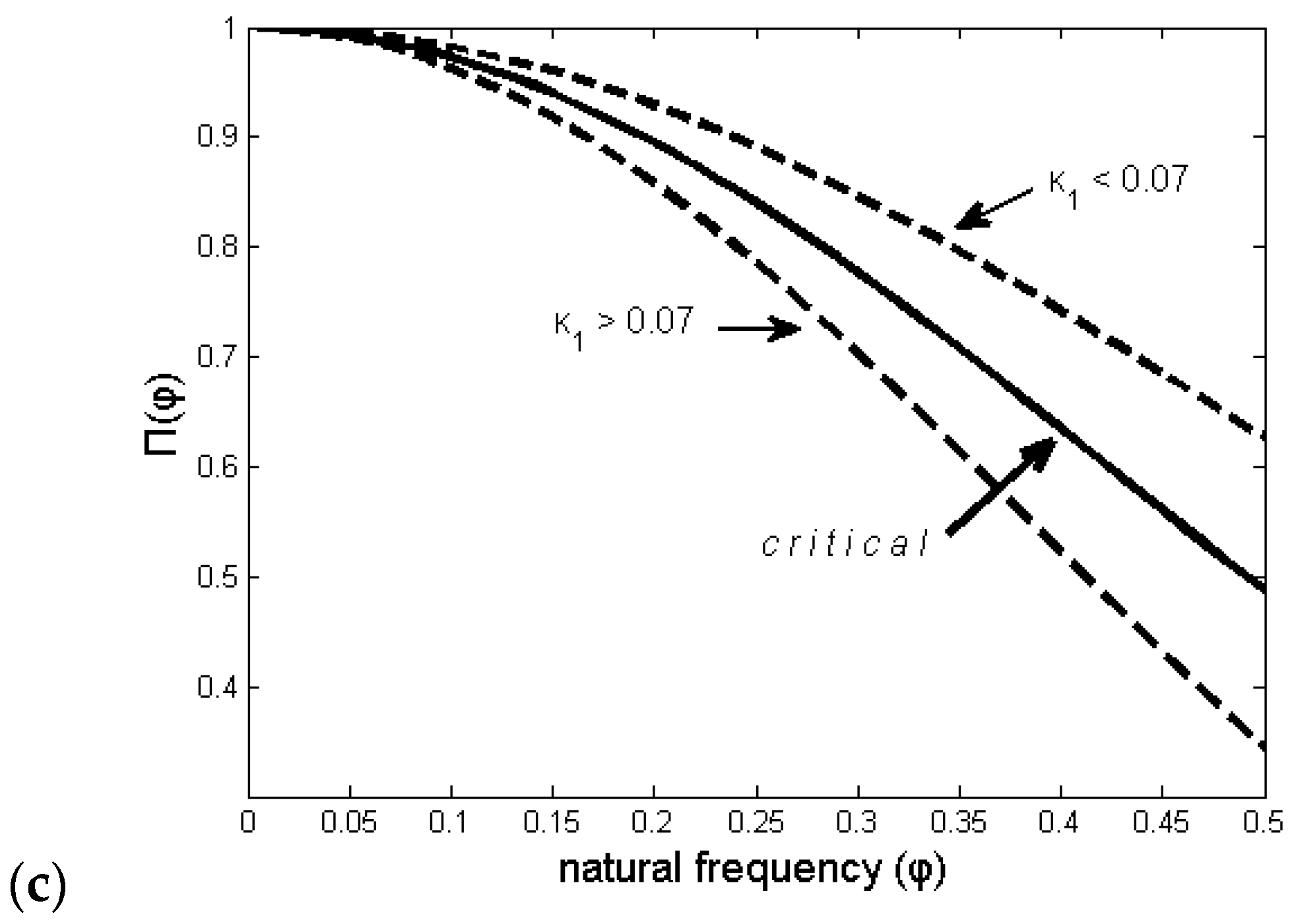
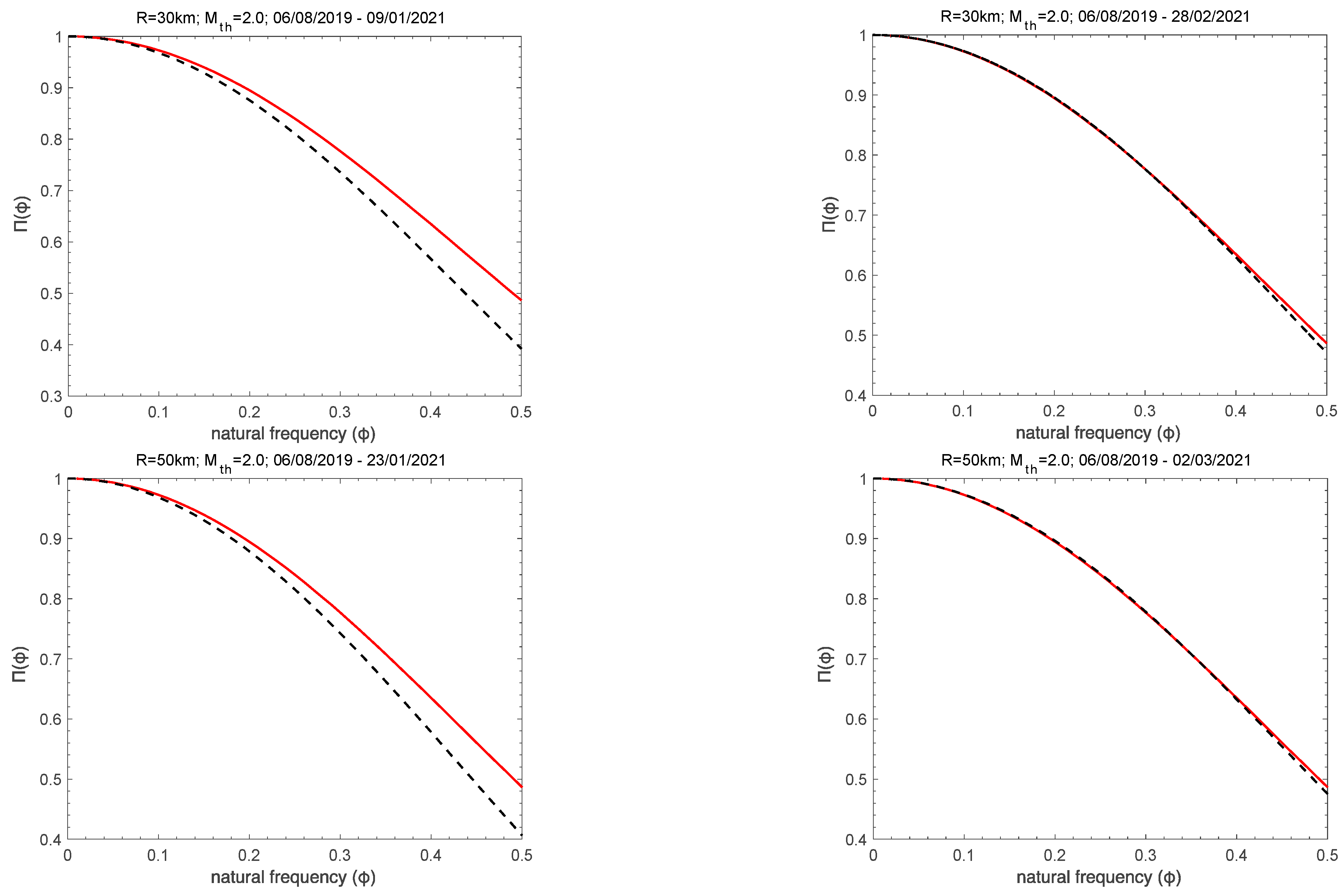
- The “average” distance D, defined by the normalized power spectra Π(ω) of the evolving seismicity and by the theoretical estimation of Π(ω) for κ1 = 0.070, should be less than 10−2.
- (ii).
- The parameter κ1 should approach the critical value of κ1 = 0.070 by “descending from above”.
- (iii).
- Both natural time entropies, Snt and Snt−, should be lower than the entropy of uniform noise Su = (ln2/2) − 1/4 when κ1 approaches 0.070.
- (iv).
- Since the dynamic evolution of the system is expected to be self-similar in the critical state, the time of the true coincidence should not vary upon changing (within reasonable limits) either the magnitude threshold, Mth, or the area used in the calculation.
4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Caputo, R. Inference of a seismic gap from geological data: Thessaly (Central Greece) as a case study. Ann. Geophys. 1995, 38, 1–19. [Google Scholar] [CrossRef]
- Caputo, R.; Chatzipetros, A.; Pavlides, S.; Sboras, S. The Greek Database of Seismogenic Sources (GreDaSS): State-of-the-art for northern Greece. Ann. Geophys. 2013, 55, 859–894. [Google Scholar] [CrossRef]
- Caputo, R.; Helly, B.; Pavlides, S.; Papadopoulos, G. Palaeoseismological investigation of the Tyrnavos Fault (Thessaly, Central Greece). Tectonophysics 2004, 394, 1–20. [Google Scholar] [CrossRef]
- Caputo, R.; Pavlides, S. Greek Database of Seismogenic Sources (GreDaSS); Università Degli Studi di Ferrara: Ferrara, Italy, 2013. [Google Scholar]
- Caputo, R.; Pavlides, S. Late Cainozoic geodynamic evolution of Thessaly and surroundings (central-northern Greece). Tectonophysics 1993, 223, 339–362. [Google Scholar] [CrossRef]
- Chatzipetros, A.; Lazos, I.; Pavlides, S.; Pikridas, C.; Bitharis, S. Determination of the active tectonic regime of Thessaly, Greece: A geodetic data based approach. In Proceedings of the XXI International Congress of the CBGA, Salzburg, Austria, 10–13 September 2018; p. 227. [Google Scholar]
- Tolomei, C.; Caputo, R.; Polcari, M.; Famiglietti, N.A.; Maggini, M.; Stramondo, S. The use of interferometric synthetic aperture radar for isolating the contribution of major shocks: The case of the march 2021 thessaly, greece, seismic sequence. Geosciences 2021, 11, 191. [Google Scholar] [CrossRef]
- Caputo, R.; Helly, B.; Rapti, D.; Valkaniotis, S. Late Quaternary hydrographic evolution in Thessaly (Central Greece): The crucial role of the Piniada Valley. Quat. Int. 2021, in press. [Google Scholar] [CrossRef]
- Caputo, R.; Bravard, J.-P.; Helly, B. The Pliocene-Quaternary tecto-sedimentary evolution of the Larissa Plain (Eastern Thessaly, Greece). Geodin. Acta 1994, 7, 219–231. [Google Scholar] [CrossRef]
- Caputo, R.; Piscitelli, S.; Oliveto, A.; Rizzo, E.; Lapenna, V. The use of electrical resistivity tomography in active tectonics. Examples from the Tyrnavos Basin. Greece. J. Geodyn. 2003, 36, 19–35. [Google Scholar]
- Ganas, A.; Valkaniotis, S.; Briole, P.; Serpetsidaki, A.; Kapetanidis, V.; Karasante, I.; Kassaras, I.; Papathanassiou, G.; Karamitros, I.; Tsironi, V.; et al. Domino-style earthquakes along blind normal faults in Northern Thessaly (Greece): Kinematic evidence from field observations, seismology, SAR interferometry and GNSS. Bull. Geol. Soc. 2021, 58, 37–86. [Google Scholar] [CrossRef]
- Ganas, A.; Oikonomou, I.A.; Tsimi, C. NOAfaults: A digital database for active faults in Greece. Bull. Geol. Soc. 2017, 47, 518–530. [Google Scholar] [CrossRef] [Green Version]
- Kouskouna, V. The (December 28th, 1891) January 9th, 1892 Larisa (Central Greece) earthquake. Bull. Geol. Soc. 2001, 34, 1425–1432. (In Greek) [Google Scholar]
- Papadimitriou, E.; Karakostas, V. Episodic occurrence of strong (Mw ≥ 6.2) earthquakes in Thessalia area (central Greece). Earth Planet. Sci. Lett. 2003, 215, 395–409. [Google Scholar] [CrossRef]
- Papazachos, B.C.; Papazachou, C. The Earthquakes of Greece; Ziti Publ. Co.: Thessaloniki, Greece, 2003; p. 286. (In Greek) [Google Scholar]
- Bak, P.; Tang, C. Earthquakes as a self-organized critical phenomenon. J. Geophys. Res. Space Phys. 1989, 94, 15635–15637. [Google Scholar] [CrossRef] [Green Version]
- Kiyashchenko, D.; Smirnova, N.; Troyan, V.; Vallianatos, F. Dynamics of multifractal and correlation characteristics of the spatio-temporal distribution of regional seismicity before the strong earthquakes. Nat. Hazards Earth Syst. Sci. 2003, 3, 285–298. [Google Scholar] [CrossRef]
- Kiyashchenko, D.; Smirnova, N.; Troyan, V.; Vallianatos, F. Seismic hazard precursory evolution: Fractal and multifractal as-pects. Phys. Chem. Earth 2004, 29, 367–378. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F.; Sammonds, P. Non-extensivity and long-range correlations in the earthquake activity at the West Corinth rift (Greece). Nonlinear Process. Geophys. 2013, 20, 713–724. [Google Scholar] [CrossRef] [Green Version]
- Rundle, J.B.; Turcotte, D.L.; Shcherbakov, R.; Klein, W.; Sammis, C. Statistical physics approach to understanding the multiscale dynamics of earthquake fault systems. Rev. Geophys. 2003, 41, 5-1–5-30. [Google Scholar] [CrossRef] [Green Version]
- Sornette, D. Critical Phenomena in Natural Sciences; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: Berlin, Germany, 2009. [Google Scholar]
- Uritsky, V.; Smirnova, N.; Troyan, V.; Vallianatos, F. Critical dynamics of fractal fault systems and its role in the generation of pre-seismic electromagnetic emissions. Phys. Chem. Earth 2004, 29, 473–480. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Benson, P.; Sammonds, P. Natural time analysis of critical phenomena: The case of acoustic emis-sions in triaxially deformed Etna basalt. Phys. A Stat. Mech. Appl. 2013, 392, 5172–5178. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G. Non-extensive and natural time analysis of seismicity before the Mw6.4, October 12, 2013 earthquake in the South West segment of the Hellenic Arc. Phys. A Stat. Mech. Appl. 2014, 414, 163–173. [Google Scholar] [CrossRef]
- Telesca, L.; Lapenna, V.; Alexis, N. Multiresolution wavelet analysis of earthquakes. Chaos Solitons Fractals 2004, 22, 741–748. [Google Scholar] [CrossRef]
- Telesca, L.; Hloupis, G.; Nikolintaga, I.; Vallianatos, F. Temporal patterns in southern Aegean seismicity revealed by the mul-tiresolution wavelet analysis. Commun. Nonlinear Sci. Numer. Simul. 2007, 12, 1418–1426. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Hloupis, G. Multiresolution wavelets and natural time analysis before the January–February 2014 Cephalonia (Mw6.1 & 6.0) sequence of strong earthquake events. Phys. Chem. Earth 2015, 85, 201–209. [Google Scholar]
- Varotsos, P.A.; Sarlis, N.; Skordas, E. Long-range correlations in the electric signals that precede rupture. Phys. Rev. E 2002, 66, 11902. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, P.A.; Sarlis, N.; Skordas, E.; Lazaridou, M.S. Natural entropy fluctuations discriminate similar-looking electric signals emitted from systems of different dynamics. Phys. Rev. E 2005, 71, 11110. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, P.; Sarlis, N.; Tanaka, H.K.; Skordas, E. Similarity of fluctuations in correlated systems: The case of seismicity. Phys. Rev. E 2005, 72, 41103. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, P.A.; Sarlis, N.; Skordas, E.; Tanaka, H.K.; Lazaridou, M.S. Entropy of seismic electric signals: Analysis in natural time under time reversal. Phys. Rev. E 2006, 73, 31114. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Varotsos, P.A.; Skordas, E.; Sarlis, N.; Lazaridou, M.S. Fluctuations, under time reversal, of the natural time and the entropy distinguish similar looking electric signals of different dynamics. J. Appl. Phys. 2008, 103, 14906. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, P.; Sarlis, N.; Skordas, E. Detrended fluctuation analysis of the magnetic and electric field variations that precede rupture. Chaos Interdiscip. J. Nonlinear Sci. 2009, 19, 23114. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, P.A.; Sarlis, N.; Skordas, E.S. Natural Time Analysis: The New View of Time. In Natural Time Analysis: The New View of Time; Springer: New York, NY, USA, 2011. [Google Scholar]
- Varotsos, P.; Sarlis, N.V.; Skordas, E.S.; Uyeda, S.; Kamogawa, M. Natural time analysis of critical phenomena. Proc. Natl. Acad. Sci. USA 2011, 108, 11361–11364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarlis, N.; Skordas, E.; Lazaridou, M.S.; Varotsos, P. Investigation of seismicity after the initiation of a Seismic Electric Signal activity until the main shock. Proc. Japan Acad. Ser. B 2008, 84, 331–343. [Google Scholar] [CrossRef]
- Sarlis, N.; Skordas, E.; Varotsos, P. Multiplicative cascades and seismicity in natural time. Phys. Rev. E 2009, 80, 22102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarlis, N.; Skordas, E.; Varotsos, P. Nonextensivity and natural time: The case of seismicity. Phys. Rev. E 2010, 82, 21110. [Google Scholar] [CrossRef] [Green Version]
- Abe, S.; Sarlis, N.V.; Skordas, E.S.; Tanaka, H.K.; Varotsos, P.A. Origin of the Usefulness of the Natural-Time Representation of Complex Time Series. Phys. Rev. Lett. 2005, 94, 170601. [Google Scholar] [CrossRef] [Green Version]
- Saltas, V.; Vallianatos, F.; Triantis, D.; Stavrakas, I. Complexity in Laboratory Seismology: From Electrical and Acoustic Emis-sions to fracture. In Complexity of Seismic Time Series; Chelidze, T., Telesca, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Thurner, S.; Lowen, S.B.; Feurstein, M.C.; Heneghan, C.; Feichtinger, H.G.; Teich, M.C. Analysis, Synthesis, and Estimation of Fractal-Rate Stochastic Point Processes. Fractals 1997, 5, 565–595. [Google Scholar] [CrossRef] [Green Version]
- Abry, P.; Flandrin, P.; Taqqu, M.S.; Veitch, D. Wavelets for the analysis, estimation, and synthesis of scaling data. In Self-Similar Network Traffic and Performance Evaluation; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Abry, P.; Flandrin, P.; Taqqu, M.S.; Veitch, D. Self-similarity and long-range dependence through the wavelet lens. In Theory and Applications of Long-Range Dependence; Doukhan, P., Oppenheim, G., Taqqu, M.S., Eds.; Birkhäuser: Basel, Switzerland, 2002; pp. 527–556. [Google Scholar]
- Abry, P.; Veitch, D. Wavelet analysis of long-range-dependent traffic. IEEE Trans. Inf. Theory 1998, 44, 2–15. [Google Scholar] [CrossRef]
- Wornell, G.W.; Gaumond, C.F. Signal Processing with Fractals: A Wavelet Based Approach. J. Acoust. Soc. Am. 1999, 105, 18. [Google Scholar] [CrossRef] [Green Version]
- Teich, M.C.; Heneghan, C.; Lowen, S.B.; Turcott, R.G. Estimating the Fractal Exponent of Point Processes in Biological Systems Using Wavelet- and Fourier-Transform Methods. In WAVELETS in Medicine and Biology; Informa UK Limited: London, UK, 2017; pp. 383–412. [Google Scholar]
- Evangelidis, C.P.; Triantafyllis, N.; Samios, M.; Boukouras, K.; Kontakos, K.; Ktenidou, O.-J.; Fountoulakis, I.; Kalogeras, I.; Melis, N.S.; Galanis, O.; et al. Seismic Waveform Data from Greece and Cyprus: Integration, Archival, and Open Access. Seism. Res. Lett. 2021, 92, 1672–1684. [Google Scholar] [CrossRef]
- National Observatory of Athens, Institute of Geodynamics. National Observatory of Athens Seismic Network; National Observatory of Athens, Institute of Geodynamics: Athens, Greece, 1997. [Google Scholar] [CrossRef]
- Aristotle University of Thessaloniki Seismological Network. Permanent Regional Seismological Network Operated by the Aristotle University of Thessaloniki; Aristotle University of Thessaloniki Seismological Network: Thessaloniki, Greece, 1981. [Google Scholar] [CrossRef]
- Godano, C.; Caruso, V. Multifractal analysis of earthquake catalogues. Geophys. J. Int. 1995, 121, 385–392. [Google Scholar] [CrossRef] [Green Version]
- Öncel, A.O.; Main, I.G.; Alptekin, O.; Cowie, P.A. Spatial variation in the fractal properties of seismicity in the north Anatolian fault zone. Tectonophysics 1996, 257, 189–202. [Google Scholar] [CrossRef]
- Hainzl, S.; Scherbaum, F.; Beauval, C. Estimating Background Activity Based on Interevent-Time Distribution. Bull. Seismol. Soc. Am. 2006, 96, 313–320. [Google Scholar] [CrossRef] [Green Version]
- Corral, Á.; Christensen, K. Comment on “Earthquakes Descaled: On Waiting Time Distributions and Scaling Laws.”. Phys. Rev. Lett. 2006, 96, 109801. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Scale-free statistics of time interval between successive earthquakes. Phys. A Stat. Mech. Appl. 2005, 350, 588–596. [Google Scholar] [CrossRef] [Green Version]
- Uyeda, S.; Kamogawa, M.; Tanaka, H. Analysis of electrical activity and seismicity in the natural time domain for the volcanic-seismic swarm activity in 2000 in the Izu Island region, Japan. J. Geophys. Res. Space Phys. 2009, 114, 2310. [Google Scholar] [CrossRef] [Green Version]
- Chatzopoulos, G. Accelerating deformation seismicity patterns before the 3 March 2021 Thessaly strong earthquake. First results. Bull. Geol. Soc. 2021, 58, 87–104. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallianatos, F.; Michas, G.; Hloupis, G. Seismicity Patterns Prior to the Thessaly (Mw6.3) Strong Earthquake on 3 March 2021 in Terms of Multiresolution Wavelets and Natural Time Analysis. Geosciences 2021, 11, 379. https://doi.org/10.3390/geosciences11090379
Vallianatos F, Michas G, Hloupis G. Seismicity Patterns Prior to the Thessaly (Mw6.3) Strong Earthquake on 3 March 2021 in Terms of Multiresolution Wavelets and Natural Time Analysis. Geosciences. 2021; 11(9):379. https://doi.org/10.3390/geosciences11090379
Chicago/Turabian StyleVallianatos, Filippos, Georgios Michas, and George Hloupis. 2021. "Seismicity Patterns Prior to the Thessaly (Mw6.3) Strong Earthquake on 3 March 2021 in Terms of Multiresolution Wavelets and Natural Time Analysis" Geosciences 11, no. 9: 379. https://doi.org/10.3390/geosciences11090379
APA StyleVallianatos, F., Michas, G., & Hloupis, G. (2021). Seismicity Patterns Prior to the Thessaly (Mw6.3) Strong Earthquake on 3 March 2021 in Terms of Multiresolution Wavelets and Natural Time Analysis. Geosciences, 11(9), 379. https://doi.org/10.3390/geosciences11090379







