Abstract
For an accurate multiscale property modelling of fractured crystalline geothermal reservoirs, an enhanced characterisation of the geometrical features and variability of the fracture network properties is an essential prerequisite. Combining regional digital elevation model analysis and local outcrop investigation, the study comprises the characterisation of the fracture pattern of a crystalline reservoir analogue in the Northern Odenwald, with LiDAR and GIS structural interpretation. This approach provides insights into the 3D architecture of the fault and fracture network, its clustering, and its connectivity. Mapped discontinuities show a homogeneous length distribution, which follows a power law with a −2.03 scaling factor. The connectivity of the fracture network is heterogenous, due to a fault control at the hectometric scale. Clustering is marked by long sub-vertical fractures at the outcrop scale, and strongly enhance heterogeneity around weathered fracture and fault corridors. The multi-variable dataset created within this study can be used as input data for accurate discrete fracture networks and fluid-flow modelling of reservoirs of similar type.
1. Introduction
Natural permeable fracture zones are primary exploration and exploitation targets in granitic deep geothermal systems [1]. In the Northern Upper Rhine Graben, no clear quantitative overview of the structural network of these potential reservoirs is available yet. Such a dataset is crucial to estimate rock property variability and compartmentalisation by faults and fracture networks for deep geothermal and heat storage projects in crystalline units [2,3,4,5,6].
The crystalline basement of the northern Odenwald may be a potential location for the geothermal underground research laboratory GeoLaB to implement high flow rate experiments to understand, design, and increase the acceptability of Enhanced Geothermal Systems (EGS) [7]. Thus, the structural investigation of such units is essential. The hydraulic yields of geothermal reservoirs in crystalline rocks are controlled by the structural architecture of fault and fracture corridors and its associated hydrothermal alteration history controlling the present-day permeability [8,9,10]. Economically, the hydrothermalised and fractured top granitic basement is more promising due to naturally enhanced flow properties [11]. Thus, the structural architecture needs to be investigated, as the permeability of fracture zones is the highest in these features [3,9,12,13]. A quantification of the fault and fracture network, which can be achieved by analogue investigation, is required to predict such rock media behaviour.
This study aims to reach a quantitative knowledge basis of faulted crystalline reservoirs structural architecture in the Upper Rhine Graben (URG) vicinity, especially at the sub-seismic scale (objects that cannot be resolved with conventional seismic techniques). This near-surface dataset is thus of importance, as it provides the basis to estimate the input parameters of 3D fractured reservoir models. The dataset is used to build a conceptual model with sub-domain definitions and quantification of the fracture network geometry. Such a model predicts ranges of fracture density, intensity and connectivity, and improves the understanding of the interconnections between structural features at different scales.
This study identifies the scale dependence of the clustering of the fracture network around fault zones and their control by the primary fault system orientation. In conceptual models of granitic and granodioritic reservoirs, structure-dependent, asymmetrical fracturing and weathering influence the reservoir architecture and the localisation of natural drains [2,14].
2. Geological Context
The Odenwald Crystalline Complex is part of the Mid-German Crystalline High, located south of the Rheic suture between Armorica and Laurussia (Figure 1a).
The western Odenwald, also called Bergsträsser Odenwald, is by definition divided into three units [15]: the Frankenstein Massif in the North-West (Unit I), the Flasergranitoid zone (Unit II), and the South Odenwald (Unit III). The Western Odenwald is separated from the Eastern Odenwald (also called Böllsteiner Odenwald) by the N010° E striking Otzberg Fault Zone (OTZ). Unit (I) and Unit (II) are tectonically independent, as the age [16] of the Frankenstein complex differs from the age of crystalline units in the Bergsträsser granitic units, and as a Carboniferous [16] tectonic fault zone delimits the two units. The crystalline Odenwald is a deeply eroded paleo subduction-related volcanic arc of the active Armorican margin, as suggested by the age and nature of the granitic plutons in the Frankenstein massif [17]. The Variscan orogeny is subdivided into four deformation phases [18]. Compressional phases D1 and D2 during the Variscan orogeny initiated thrust sutures [18,19]. In the late Carboniferous, the area underwent two phases of deformation, namely, D3 with normal to oblique sinistral strike shearing and D4 with normal shearing. D3 has a NE-SW striking direction, and D4 strikes NNE-SSW. Furthermore, D4 expressed localised strain zones and contributed to the formation of brittle deformation structures. During D4, the emplacement of syntectonic plutons in the northern Odenwald was facilitated by a transtensive to extensive stress field [18]. This extensional regime continues during the Permian, with the development of large intra-mountainous basins filled with coal and siliciclastic deposits (Saar-Nahe, Lorraine) [20,21]. These sandstones are locally associated with basaltic and rhyolitic volcanic episodes. During the Mesozoic, the area entered a subsidence regime, with continuous sedimentary deposition from Triassic up to Early Cretaceous [22]. From the Late Cretaceous until the Early Eocene, a regional uplift caused the erosion of a large section of the sedimentary units down to the Lower Triassic [20,23,24].
The Cenozoic tectonic history of the Odenwald is marked by the URG rift opening [25,26,27,28]. The URG development is characterised by passive rifting in the alpine foreland [23,27,29,30,31] and is associated in the Northern URG (NURG) with reactivation of faults systems of Variscan age [24,32,33]. This extensive regime is associated locally with basaltic and trachytic volcanism [25]. Granodioritic and granitic dykes intrude the diorites of the northern Frankenstein Complex [15,25]. In the southern part of the Frankenstein complex, gabbroic intrusions that emplaced at 362 ± 9 Ma [16] are the predominant rock type. Amphibolites and hornfels compose the host rock of these intrusions [16,17]. Several fault systems structure the Frankenstein Massif. The major one is the N000-N020 striking OTZ on the east, delimitating it from Unit IV. A second system of fault zone delimitates the western border of the Frankenstein Massif from the URG.
The Mainzer Berg quarry is located in the northern part of the Frankenstein Massif, between Darmstadt and Dieburg (Figure 1a). The area is structured by different fault systems, striking N000–N020° E and N110–130° E. Quartz monzodiorite, Bt-Hbl granodiorite, and Bt-Hbl granite are identified in the nearby GA1 and GA2 wells [25,34,35]. Intrusive bodies inside the diorite unit are composed of granite and granodiorite. These intrusions, reported 1 km north of the quarry, are orientated N160–N170° E. The quarry is mainly composed of granite and granodiorite, in which mafic unit remnants crop out in the NE part. Locally, a multi-kilometric fault system crosses the Messel pit with an N030–N040° E direction. Several secondary faults, striking mainly N010–N020° E, and secondly N040° E, N090° E, N110–N120° E, and N160° E, are exposed in the Mainzer Berg area. This study describes these fault systems and their damage zone architecture in detail.
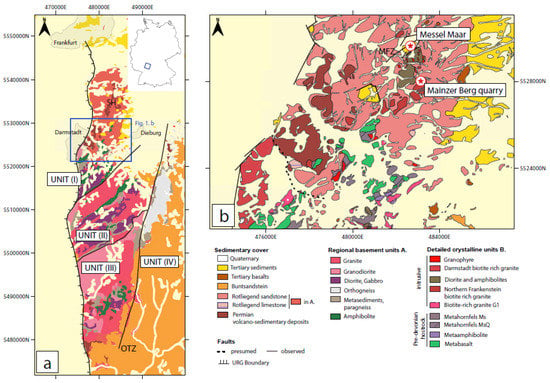
Figure 1.
Geological context. (a) Odenwald 1/300,000 geological map adapted from [36] with the different Odenwald units Unit I corresponds to the Sprendlinger Horst (SH) and the Frankenstein Complex, Unit II to the central Flaser Granitoid Zone, Unit III contains the granitic southern units, with Weschnitz and Tromm Plutons, and Unit IV is the Böllsteiner Odenwald. The Otzberg Fault (OTZ) delimits unit IV from the western Odenwald. (b) Detail of the blue box of (a); 1/25,000 map of the northern Unit I (adapted from [36]). Mainzer Berg quarry and Messel Maar detailed crystalline units lithologies and the main faults are mapped (Messel Fault Zone (MFZ) [25]).
3. Materials and Methods
This outcrop is a suitable analogue of crystalline geothermal reservoirs. It is constituted by granodiorite and biotite-rich granite, representing the magmatic basement of this section of the NURG [37,38]. Before the URG Cenozoic rifting, the NURG area and the Unit (I) of the Odenwald belonged to the same unit, and underwent a similar deformation history. Thus, it is expected that localities of Mainzer berg would show a similar fracture pattern as what can be encountered on URG rift shoulders. A multi-methodological and multi-scalar approach allowed us to access the fracture network geometry and dimension.
Digital Elevation Model (DEM) analysis focuses on the regional-scale fault and discontinuity patterns investigation, with 25 m and 1 m resolution, respectively. The methodology for lineament analysis, followed in this study, is described in previous work [3,6,39,40]. A lineament is traced when a discontinuity is identified on the hill shaded DEM. Lineaments are depicted by X and Y coordinates of start and endpoints. From these coordinates, length and strike are computed. For poly-segmented lineaments, a mean strike value is given, calculated from the straight line separating the start and endpoint of the full lineament. Misinterpretations are avoided by simultaneous observation and digitalisation on four shade orientations: N000° E, N045° E, N090° E, and N135° E. The regional-scale investigations with DEM allow the identification of discontinuities with lengths ranging from several tens of kilometres down to several tens of meters, e.g., seismic scale in the frame of reservoir characterisation.
At the outcrop scale, a quantitative approach with remote sensing technologies such as LiDAR (Light imaging, detection and ranging) has the advantage to allow a structural analysis, thanks to high-resolution point clouds [41,42]. The reliability and usability of LiDAR-derived data for discontinuity analysis was the focus of several previous publications [43,44,45].
The structural data are approached by a classical 2D GIS interpretation combined with LiDAR point cloud acquisition for semi-automatised fracture plane recognition. The LiDAR device used is a RIEGL VG 400, equipped with a Nikon Camera for RGB acquisition. Raw LiDAR datasets have been processed using RiSCAN PRO and further treated with the open-access CloudCompare software.
The point clouds of the chosen quarry walls (Figure 2a) were treated under the following workflow. (1) Cleaning the data using the Noise and Canupo filtering to remove vegetation and non-interpretable areas. (2) Norm calculation, conversion into dip direction. (3) Automatic plane recognition via a RANSAC shape detection plugin [46] with settings that vary depending on the distance to the fitting plane and the distance of investigation in the point cloud. For long-range acquisitions, the distance feature range was selected up to 20 cm. For close-ups (spots A, B and C), a limit to 5 cm was fixed to avoid merging several fracture planes into one, thus reducing the plane recognition errors. Angle variation maximum was set to 20°. (4) Manual quality checks to remove planes that do not represent natural fractures. (5) Export of the detected fracture planes properties to calculate volumetric fracture density and intensity (noted P30 and P32, respectively [47,48]).

Figure 2.
(a) Location of acquired profiles on satellite image (Google) in the Mainzer Berg quarry (location see Figure 1). (b) Field photography of profile A, with position of a weathered fracture corridor, detailed in close-up (g). (c) Field photography of profile B. (d) Field photography of profile C, with position of close ups (h,i), detailing the weathered fault cores. (e) Field photography of profile D. (f) Field photography of profile E. (g) Close up from profile A. (h) Close up from profile C, with a clay-rich weathered fault core surrounded by a fractured damage zone. (i) Close up from profile C, showing a second clay weathered fault core. The clustering and contrast between the fault core and the damage zone are stronger in (h) than in (i). On (g–i), the orange dashed lines mark the outer limits of the clay rich zones of the fault core.
The cluster analysis of the LiDAR extracted planes is performed using Stereonet 11 [49]. Parameters for the clustering are the trend, the plunge, the number of elements included in the cluster, and Fisher distribution statistical parameters a95, a99, and kappa [50].
The (x,y,z) points clouds from the outcrop surface were also rasterised and incorporated in QGIS to extract a hill shade image from the LiDAR data using the same orientation panel as for the DEM investigation. For each profile, two views were projected, e.g., the top view, corresponding to a horizontal plane, and the side view, corresponding to a vertical plane. Fault and fracture network features were digitised and interpreted on these images to extract properties such as fracture position, apparent fracture length, apparent fracture orientation from top-view projection, and apparent dip from the side-view shot. The classification of the different fault zone compartments follows [51,52]. The number of connections per line (noted CL [53]), areal fracture density and intensity (noted P20 and P21, respectively [47,48]) were calculated from the digitised layers. Fracture connectivity and node topology were assessed using the MATLAB Plugin FracPaQ® [54], following the I-X-Y node classification detailed in [53,55,56]. On specific profiles (C, D, and E), spacing and coefficient of variation, noted Cv, were calculated along artificial scanlines to determine if the spatial distribution of the fracture network is clustered (Cv > 1) or randomly distributed (Cv < 1) [48]. The scanline methodology is a classical approach to characterise the fracture variability in 1D [57,58]. Artificial scanline sampling provides an overview of the fracture clustering and spacing, independently from the scanline orientation. Spacing was calculated between each fracture crossing the scanline and expressed as distance-occurrence frequency diagrams [59]. This approach allows more insight into the clustering aspect of the fracture network and quantifies the deviation to a uniformly distributed fracture pattern [59].
Cumulative length distributions of discontinuities were then analysed and fitted to a power law. On a local scale, log-normal and exponential fits may also be valid [60,61,62,63]. However, the multiscale character of the fracture network investigated here requires a power law. For crystalline rocks, this approach is commonly used [2,3,6,40,64]. Power law exponent b gives insights into the structural architecture and connectivity [40,60,65]. When b is equal to 2, the analysed property has a fractal character. When b < 2, the length population is mainly composed of long fractures, whereas when b > 2, the fracture network comprises short size elements [64]. Fracture network characterisation was also amended by field observations, such as the fracture aperture measurements approach [58], and visual characterisation of fracture mineralisation.
This multi-method approach allows an extensive, almost contact-free, and multiscale investigation of structural objects.
4. Results
4.1. Regional Lineaments
Overall, P20 and P21 on 25 m resolution DEM reach 1.09 × 10−6 lineament.m−1 and 1.46 × 10−3 m·m−2, respectively (Figure 3a, Table 1). Density and intensity increase, with P20 of 2.47 × 10−6 lineament.m−1 and P21 of 2.16 × 10−3 m·m−2 when the DEM resolution increases to 1 m (Figure 3b, Table 1). The lineament analysis in the area of interest around the Mainzer Berg granodiorite (Figure 3c, Table 1) shows P20 4.7 × 10−5 lineament.m−1 and P21 of 6.97 × 10−3 m·m−2. In the Messel pit, identified lineaments have P20 of 3.14 × 10−5 lineament·m−1 and P21 of 7.06 × 10−3 m·m−2. On satellite imaging of the Mainzer Berg quarry, lineament density and intensity reach 1.89 × 10−4 lineament·m−1 and 1.26× 10−2 m·m−2, respectively. The lineament density and intensity are higher in crystalline rocks than in sedimentary and volcanic Permian deposits. In all the observed scales, lineaments are mainly orientated N010° E and N080° E. In the vicinity of the Mainzer Berg quarry, the multi kilometre-scale lineaments are orientated N010° E, N050° E, and N100° E–120° E. In the Mainzer Berg quarry walls, identified discontinuities are of smaller size (<100 m). Local lineaments have a preferred orientation of N020° E and N100° E. The length varies between 4 and 356 m, having a mean of 66 m (interpretation of satellite imaging, Table 1). In comparison, the Messel Maar is affected by an N045° E striking strike-slip fault and exhibits sub orthogonal lineaments and secondary faults orientated N000° E–N010° E and N150° E–N170° E as recorded in a previous study [25]. Length of lineaments in the Messel Maar range from 37 to 1918 m, with a mean length of 224 m.
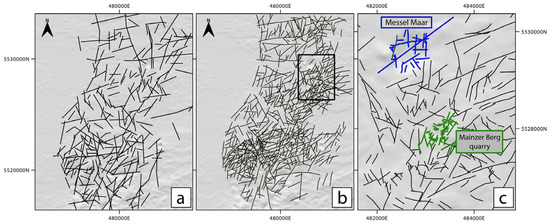
Figure 3.
Lineament analysis maps. (a) Regional analysis 25 m resolution DEM. (b) Regional analysis 1 m resolution DEM. Black rectangle locates the window. (c) Mainzer Berg area local lineament analysis, with local orthophoto analysis. Blue lines represent lineaments observed in the Messel pit [25], green lines the lineaments observed in satellite imaging of the Mainzer Berg quarry.

Table 1.
Lineament analysis statistics, with dimension features, power law parameters a, b, and rsq (r2), and areal fracture density and intensity.
4.2. LiDAR Imaging at the Outcrop Scale of the Structural Network
The five sections analysed in Mainzer Berg quarry exhibit the variability of the fracture pattern in each profile (A to F). A is orientated N010 and exposes several zones of high fracture intensity with 50 cm to 1 m thickness. The fractures apertures vary from 1 to 5 mm. Several of those fracture corridors present fractures filled with clay minerals. Profile B, orientated N110, crosscuts a high-intensity fracture corridor. Clays and hematite infills were identified in these fractures with apparent apertures varying from 0.5 to 8 mm. Several measured planes also exhibit cataclastic infills, especially in large opening structures. Profile C is located in the southern part of the quarry with an orientation of N100° E and crosses a clearly defined fault zone with two fault cores of variable fracture intensity associated to clay-rich alteration. The fault zone here reaches the boundary with the overlaying Rotliegend deposits. Profile D, orientated N170° E, presents large fractures (length above 5 m), but no clearly defined corridors. Profile E is orientated N090° E and presents several fracture corridors with a 50° apparent dip angle. Some of the fracture planes exhibit clay infills. However, the alteration in clays in fracture planes is not as pronounced as for profile C (Figure 2).
LiDAR extracted datasets of the five profiles show a complex fracture pattern (Figure 4 and Table 2). On profile A, fracture density reaches 0.02 m−1, and fracture intensity, 1.17 m·m2. Fracture length varies from 1.85 to 37.37 m, with a mean length of 10.98 m. On profile B, fracture density reaches 0.03 m−1, and fracture intensity, 0.33 m·m−2. Fracture length varies from 0.82 to 15.15 m, with a mean length of 3.99 m. On profile C, fracture density reaches 0.03 m−1, and fracture intensity, 2.51 m·m−2. Fracture length varies from 1.26 to 40.66 m, with a mean length of 12.27 m. On profile D, fracture density reaches 1× 10−3 m−1, and fracture intensity, 0.25 m·m−2. Fracture length varies from 4.61 to 41.79 m, with a mean length of 15.68 m. On profile E, fracture density reaches 4 × 10−3 m−1, and fracture intensity, 1.37 m·m−2. Fracture length varies from 4.26 to 61.63 m, with a mean length of 23.22 m.
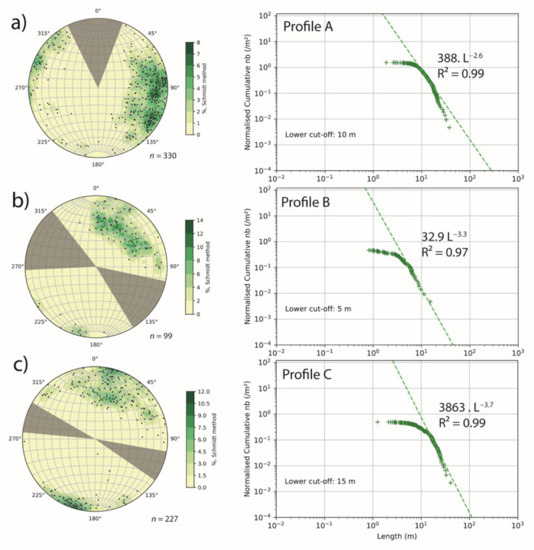
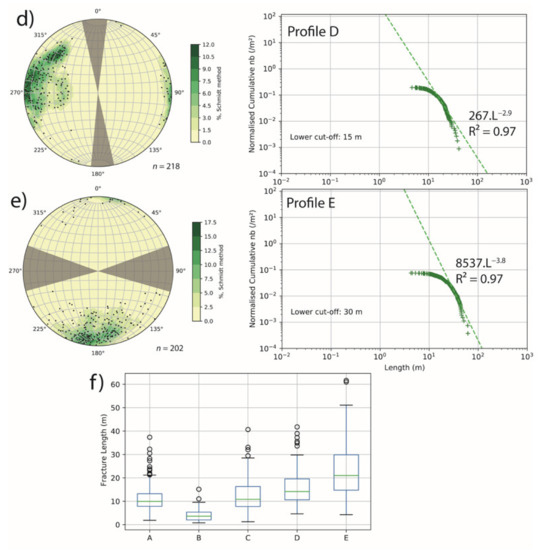
Figure 4.
Fracture network properties extracted from LiDAR profiles (see Figure 2 and Figure 5). For (a–c) Left column: Schmidt canvas with lower hemisphere projection stereograms, in grey undersampled fracture orientation due to the orientation of scanned walls; right column: cumulative length distributions. Fracture network properties extracted from LiDAR profiles (d,e): Left column: Schmidt canvas with lower hemisphere projection stereograms, in grey undersampled fracture orientation due to the orientation of scanned walls; right column: cumulative length distributions. (f) Box plot diagram of fracture length for the five sections.

Table 2.
LiDAR fracture network statistics, with dimension features, power law parameters a, b, and R2, and areal fracture density and intensity.
On the five profiles, power law trends can be extracted (Table 2), with coefficient a varying from 32.9 to 8537.1, with an average of 911.8; and coefficient b varying from −3.8 to −2.69, with an average of −3.29.
Eleven clusters describe 55% of the fracture orientation distribution (Table 3). Kappa here represents the parameter to estimate the distribution of fracture orientation [50] and varies from 42.2 to 190.

Table 3.
Cluster analysis and geometrical features of associated fracture sets from LiDAR datasets.
4.3. GIS Structural Analysis of Profiles
The digitalisation of fractures and faults on the profiles adds complementary information to the fracture pattern characterisation (Figure 5 and Figure 6, Table 4).
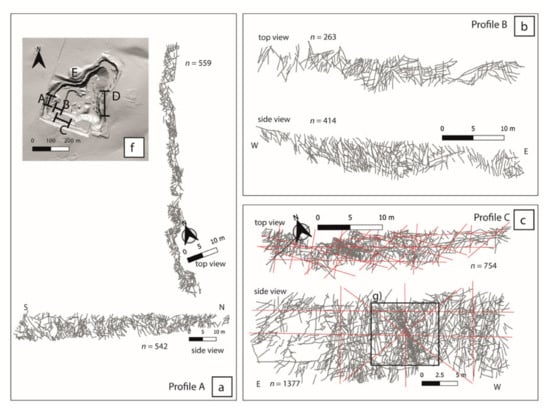
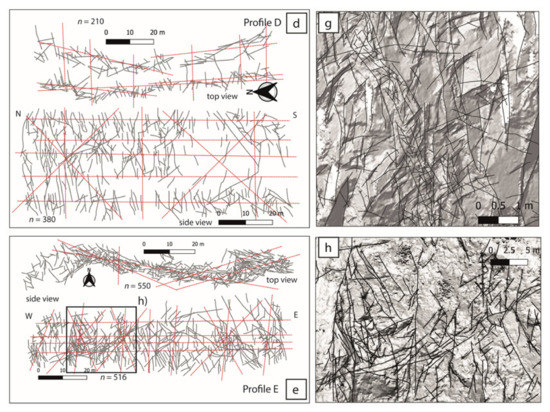
Figure 5.
GIS digitised profiles. (a) Fracture maps, top and side views from profile A. (b) Fracture maps, top and side views from profile B. (c) Fracture maps, top and side views from profile C. The red dashed lines represent the digital scan-lines positions. (d) Fracture maps, top and side views from profile D. (e) Fracture maps, top and side views from profile E. The red dashed lines represent the digital scanlines positions for (c–e). Please note the different orientations of the profiles as indicated by the respective north arrow. (f) Location of the profiles in the quarry. (g) Close up on fault core identified on profile C. (h) Close-up on fracture corridor identified on profile E.
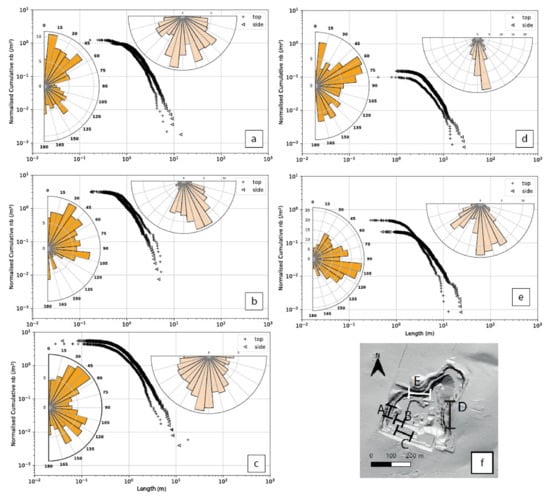
Figure 6.
Orientation and length features from GIS interpreted profiles. (a) Features for profile A. (b) Features for profile B. (c) Features for profile C. (d) Features for profile D. (e) Features for profile E. For (a–e), dark orange vertical rose diagram represent the strike distribution, extracted from the top view, and light orange the dip distribution, interpreted from the side view, all plotted along with the cumulative length distribution for each view (black crosses and triangles). (f) Mini map with the location of profiles in the quarry.

Table 4.
Fracture network properties as derived from GIS profile analysis, with length range, power law parameters a, b, and R2 (fit quality), areal fracture density and intensity, cut-off value for the power law fit, n (number of digitised elements), and extent of area investigated.
Several common orientations are identified along the five profiles.
N005–N015° E orientated fractures are mainly present in profiles A and D. N030° E orientated fractures are present in the southern part of the quarry (profiles B and C). Fractures orientated N045–N055° E are present mainly in profiles A, B, C, and D. Orientation N075° E is present in the fracture network in the north-eastern part of the quarry (profiles D and E). N100–N115° E orientated fractures are mostly present in profiles B, C, and E. Orientations N135–145° E are present in profiles A, C, and E. The last cluster of fractures orientated N150–N170° E is mainly present in the SE part of the quarry (profiles C and D).
Fracture length (Table 4) varies from 0.03 to 18.03 m for top-view interpretation and from 0.04 to 33.47 m for side-view interpretation. Mean lengths range around 2 m (2.096 m for top-view, 2.688 m for side-view).
Fracture density ranges from 0.1 to 4.44 m−1 for top-view interpretation, and from 0.15 to 5.46 m−1 for side-view interpretation. Fracture intensity ranges from 0.46 to 4.13 m·m−2 for top-view, and from 0.8 to 5.54 m·m−2 for side-view interpretation.
Power law fitting curves are parametrised with a coefficient ranging from 0.23 to 6.94, with an average of 2.37 for top-view and 1.45 for side-view interpretation. The coefficient b of the power law ranges from −4.39 to −1.24, with an average of −2.52 and −2.03 for top- and side-view interpretation.
Artificial scanlines were traced on three sections (C, D, and E) to extract P10 and Cv values from the GIS fracture maps (Table 5). Profile C has the highest P10 values, with an average P10 of 2.60 and 3.31 fracture.m−1 for the top and side projection, respectively. Profile D has P10 average values of 0.45 and 0.43 fracture.m−1, and profile E 1.04 and 0.77 fracture.m−1.

Table 5.
Summary of the fracture parameters from artificial scanlines. Ns, number of artificial scanlines per section; P10, fracture density as item/m; Nf, number of fractures per scanline; Cv, spacing.
4.4. Fault Zone Domains
The Mainzer Berg southern quarry wall offers good outcrop conditions to analyse the structural architecture of one of the secondary faults affecting the granodioritic intrusions. Four different subdomains can be defined in this outcrop section (Figure 7a,b). From east to west, a damage zone with increasing fracture density towards the west. The minimal thickness of this damage zone DZ1 reaches more than 15 m. The internal fracture network is characterised by a few long sub-horizontal fractures (length > 10 m). Fracture orientations follow an N100-115° E main strike, with a secondary direction striking N030° E. Horizontal connectivity is mainly represented by I and X nodes (Figure 7c), which characterise a rather stochastic network with few cross-joints [66,67]. The random distribution observed on the horizontal plane is absent on the vertical plane (Figure 7d). In the vertical direction, an increased number of Y nodes is observed. The structural network presents slight compartmentalisation by the large sub-horizontal fractures, on which secondary fractures abduct with a 65° to sub-orthogonal angle. Towards the west, the increasing amount of sub-vertical long fractures marks the transition to the next subdomain FC1.
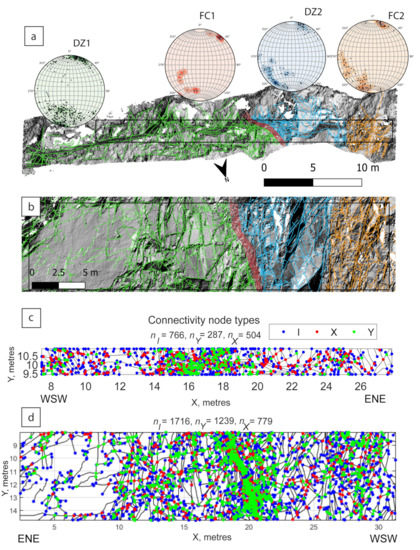
Figure 7.
Subdomains around the secondary fault zone outcropping on profile C. (a) Top view interpreted section with orientations of LiDAR identified planes for each sub-domain of the faulted area. (b) Side view. Black rectangles represented analysed zones on (c,d). Green lines are fractures that belong to the second damage zone (DZ1). Red lines are fractures that belong to the fault core 1 (FC1). Blue lines are fractures that belong to the second damage zone (DZ2). Orange lines are fractures that belong to the second fault core (FC2). (c) Connectivity node map of top view a. (d) Connectivity node map of side view b.
DZ1 is adjacent to the strongly deformed fault core. The thickness of this first fault core FC1 varies between 30 cm and 80 cm, and the whole entity is orientated N305–315° E. Vertically, sub-vertical fractures of more than 5 m in length delimit the borders of FC1. In between these long delimitating structures, most of the fracture network is composed of more minor fractures (length < 1 m) crosscutting the long vertical fractures, with a 40° to sub-orthogonal angle. The fractures composing this fault core are challenging to identify by the LiDAR workflow due to their small size. On the horizontal plane (Figure 7c), I and Y node networks mainly control the connectivity, typical for fault systems [52,55]. Vertical connectivity is primarily present as Y nodes, resulting from the geometrical relationship between compartmentalising long fractures and smaller ones (Figure 7d). At the western limit of FC1, fracture intensity reduces, changing to another subdomain of the fault system.
An 8 m thick second damage zone (DZ2) constitutes the third subdomain (Figure 7a,b). The structure of DZ2 is described by the presence of two sets of long sub-vertical fractures delimiting fracture corridors. The fracture corridors strike N310–320° E, sub-parallel to FC1 main strike. A secondary set, with strike varying from N135° E to N160° E, with lower dip of 55–65° E and associated conjugate fractures with apparent dip toward the west, crosscuts the large fracture corridors. The substantial reduction of Y nodes number, associated with a higher number of I and X nodes on the horizontal map, marks the transition to FC1 (Figure 7c). This reduction characterises a switch to a more stochastic topology of the facture network. Vertical connectivity also shows a high amount of I nodes (Figure 7d), suggesting a lower connection rate between fractures in DZ2 compared to DZ1 and FC1.
DZ2 is bordered on the west by a second fault core FC2, striking N010–N020° E. It comprises secondary fractures, mainly striking N300° E, delimited by long fractures, striking N010 and N020° E. Despite their clear presence on GIS imaging, these major fractures do not have an intense relief and are not detected by the LiDAR. The average fracture length is 1.5 m, and sub-vertical fractures, extending up to above 5 m, structure FC2. Horizontal and vertical node networks in FC2 show fewer Y nodes than in FC1, suggesting lower connectivity between fractures in this fault core.
5. Discussion
5.1. Clustering of the Fracture Network
As mentioned before, the fracture network in the Mainzer Berg quarry southern wall is clustered by clearly defined subdomains (Figure 7). Relative spacing analysis on profiles C, D, and E (Figure 8a,b, Table 5) show that this clustering is also present on profiles that do not exhibit a clearly defined fault system. Clustering of the fracture network exists, even in the background fracture pattern of the granodioritic pluton (profiles D and E, Figure 8b). Clustering here depends on the direction of analysis, as the Cv value is, on average, close to 1 (with variation from 0.54 to 1.89) (Figure 8). P10 values computed from the artificial scanlines on profiles C, D, and E (Figure 5d–f) show two configurations (Figure 8b). On profile C, P10 values are high, and the coefficient of variation is varying between 0.65 and 1.4, typical of a highly fractured media with a relatively uniform distribution of the fracture network. In contrast, profiles D and E have a smaller P10, but the high Cv suggests a stronger fracture network compartmentalisation. Spacing expressed as occurrence along with the relative distance [59] allows us to detect potential clustering of the fracture distribution (Figure 9). The curves that express the most substantial clustering have the highest deviation to the random distribution (black lines in Figure 9). This enhanced clustering is specific to few directions on the three profiles. For profile C, as illustrated by Figure 2 and Figure 7, clustering is the strongest for scanlines orthogonal to the several observed fault cores (lines 5, 6, 9 on vertical view, Figure 9a, and lines 9, 10, 16, 17 on horizontal view, Figure 9b). On the other hand, scanlines sub-parallel to the strike of the fault core have a rather random distribution pattern (lines 7 and 10, Figure 9a). Parallel to the central axis of fault cores, the fracture network is randomly distributed in spacing.
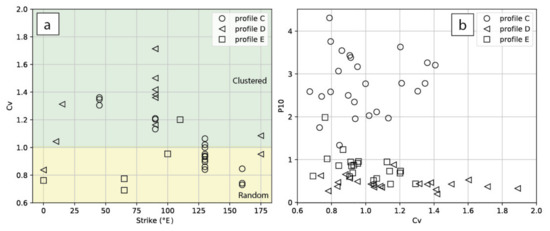
Figure 8.
(a) Cv distributions versus strike from GIS artificial scanlines on profiles C, D, and E. Fracture networks are clustered when Cv is above 1, and with a random distribution for Cv under 1. (b) Cv versus P10 from GIS artificial scanlines on profiles C, D, and E. Profile C has the highest P10 values. Cv distribution is less dispersed than for profiles D and E.
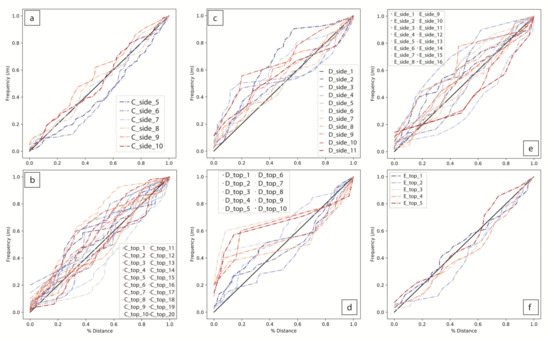
Figure 9.
Distance-occurrence frequency diagrams for 1D artificial scanlines on profiles C, D, and E. (a) From top view interpretation of profile C. (b) From side view interpretation of profile C. (c) From top view interpretation of profile D. (d) From side view interpretation of profile D. (e) From top view interpretation of profile E. (f) From side view interpretation of profile E. Black lines represent a completely random distribution of fracture spacing along a scanline (1:1).
On the two other profiles, D and E, clustering is identified on lines 1, 4, and 9 on the side view (Figure 9c), and lines 6, 9, and 10 on the top view (Figure 9d). However, here, the lower fracture density nuances the real impact of this clustering on flow anisotropy. On the vertical projection of profile E, clustering is the highest in scanlines crosscutting long fracture planes (lines 5, 8, 9, 14, 15, 16; Figure 9e). Clustering also increases towards the eastern side of the profile, as observed on lines 2 and 5, which show the highest horizontal clustering (Figure 9f).
5.2. Topology of the Fracture Network, Influence on Connectivity and Flow Properties
The analysis of the fracture network topology is helpful to characterise relationships between fracture and their mechanical interactions [56].
IXY topology from the fracture network is interpreted from the digitised profiles (Figure 10), and the number of connections per line (noted CL [53]) is calculated from this topological analysis.
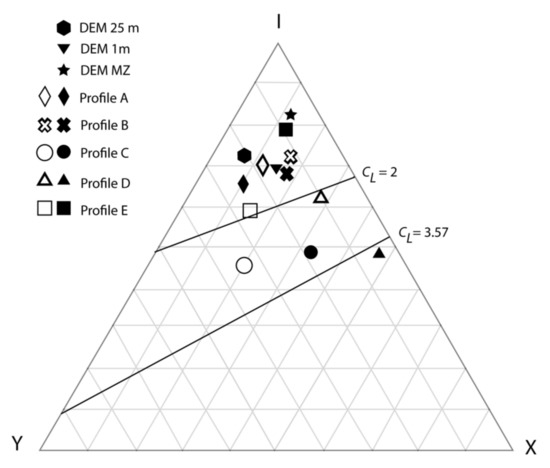
The horizontal connectivity of lineaments is estimated on the three digitised layers. All have a CL under 2, suggesting poor connectivity.
However, the effect of censoring could explain these restrained connectivity patterns, as the shape of the scanned area has a limited (x,y) extension, and the length of several fractures is equal to the extension of the investigation area. For areas where the investigation surface is far more extensive than the size of investigated elements (example of profile D), CL increases to 3.58, reaching a highly connected network level.
By comparing horizontal CL and vertical CL, obtained from top and side views of the profiles, respectively, the difference between connectivity values highlights its anisotropic character.
The anisotropic character of fracture connectivity is low. For profiles A and B, the connectivity is relatively low (CL < 2) and slightly higher in the horizontal plane. For these two small size profiles, which height is below 5 m, the connectivity is lower than for profiles C, D, and E, which have a broader angle of observation and consider larger size objects.
Profile C has a CL between 2 and 3.57, characterising a relatively well-connected fracture network. The horizontal connectivity extracted from the top view is characterised by the prominence of Y nodes, whereas a higher number of X nodes depicts the vertical topology of the network. In the damage zones of the clearly defined fault zone (profile C, Figure 7), the angle between abutting minor fractures and the corridor bounding long fractures is relatively high (above 60°), suggesting clustering of the mechanical deformation. Inside fault cores, however, the angle between the different families of fractures is lower than 45°. This angle difference can be associated with a synthetic shear component, as observed for the Messel Fault zone [25,34] and associated minor shear faults.
Profile D has the highest observed CL, with vertical CL around 2, and horizontal CL above 3.57, suggesting a very well-connected network in the horizontal direction. CL is higher on horizontal than on vertical planes on profile D. Profile D also exhibits a high amount of X nodes, suggesting a different spatial organisation of the fracture topology than the other profiles. A high amount of very long and steeply dipping fractures intersect each other and favour these X nodes.
The opposite trend with higher CL is observed for profile E on the vertical plane (CL around 2) than on the horizontal plane (CL largely below 2). The higher Y nodes number suggests a topology on the vertical planes, where certain fractures abduct others, consistent with the observed corridor geometries. These corridors are sub-parallel to each other and, thus, not allowing high horizontal connectivity. Long, 45–50° dipping fractures, associated with an enhanced clustering, favour vertical planes connectivity and accentuate the connectivity anisotropy.
5.3. Multiscale Laws of Fault and Fracture Network in Granitic and Granodioritic Units
The multiscale character of the discontinuity network is demonstrated here on five orders of magnitude from the DEM, LiDAR, and 2D GIS structural analysis (Figure 11). The cumulative distribution of element lengths shows a good fit with a typical and continuous power law behaviour on 2D datasets, with an exponent of −2.03. The 3D datasets from the LiDAR have a similar slope. However, the LiDAR curve does not fit the 2D trend due to the higher intensity of elements detected. This artificial shift created by the 3D calculation of fracture plane dimensions directly affects the fracture intensity, over-estimated by the LiDAR compared to intensities measured on 2D GIS. Concerning lineament and fracture orientation, there is a global shift of the main directions of deformation depending on the scale of observation.
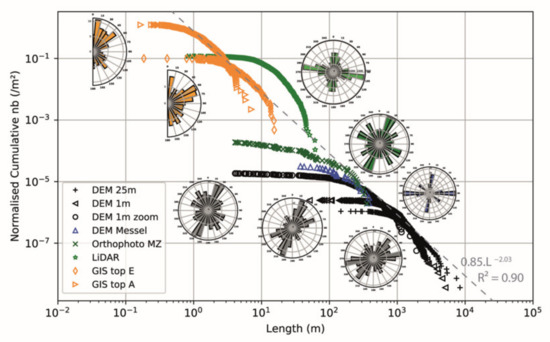
Figure 11.
Multiscale length distribution of lineaments in the northern Odenwald and associated strike changes. As LiDAR is a 3D dataset, they do not fit the general trend of the other 2D datasets.
At the regional scale, primary directions are N045° E, N080–090° E, and N150° E. These directions are associated with the boundaries between the different Northern Odenwald units [15] and lineaments of the Variscan orogeny in general [3,6,68]. N045° E, N010° E, N090° E and N130° E lineaments structure the Messel system [25]. NE striking elements were already reactivated in the transtensive shearing phase D3 [15,18,34]. The EW direction is specific to Messel, as it is minor in 25 m and 1 m resolution regional DEMs and almost unrepresented in local 1 m DEMs. This EW direction is compatible with antithetic conjugated structures. In the Mainzer Berg vicinity, main directions are N015–030° E, N060° E, N130° E, and N150° E. N015–N030° E is the primary deformation direction, indicating two possible origins for these deformation features: (1) N015–030° E structures to the shear direction of the Otzberg fault zone (N010° E), and (2) influence of R (N060° E) and R’ (N015–N030° E) conjugated structures to the Messel strike-slip (N045° E) system. Directions N130° E and N150° E may be associated with the role of conjugated structures of the URG shearing zone [25], which were active since the Permian (faulting and weathering [69]). These directions are also present at the regional scale, linked with the shearing phase D4 [15,18], and thus could play a role in the orientation of favourable for permeable fault zones and fracture corridors. This trend could also extend to structural features of the buried reservoirs in the Upper Rhine Graben as in the SW-NE striking transfer zone [33].
Direction N060° E also constitutes one of the outcrop scale main orientations, as identified on both LiDAR and GIS datasets. However, N060° E is minor at the hectometric and kilometric scales. This orientation variability could suggest that small scale features striking EW can be decomposed into a sub-structure striking N060–N070° E and that the N045° E direction is only somewhat restricted to clearly defined fault systems such as in Messel (reactivated during Cenozoic) [25].
The observed multi-scalar behaviour of length distribution is typical for crystalline lithologies [3,67].
For DEM lineament topological analysis, a shift is observed from a Y-node prominent geometry to an X node geometry, with the resolution increase from 25 m to 1 m (Figure 10). Y-node geometry is typical for fault-related lineaments with a clustering behaviour [48,52,56]. Thus, elements identified at this scale may be considered as tectonic structures. The topology extracted from the network is dependent on the resolution of the input data, regardless of the size of the investigated area. Thus, there is no clear multiscale continuity in the behaviour of discontinuity topology.
5.4. Conceptual Granitic Reservoir Model from the Analogue
The investigation of the Mainzer Berg quarry suggests a structural architecture of the granodioritic reservoir, which is comparable to previous studies on crystalline basement [14,67,70,71].
The structural alignment of crystalline lithological boundaries controlled by granitic plutons and associated faults constitutes the first level of heterogeneity.
In the granitic pluton, the pluton magmatic fabric can control the structural architecture [72,73,74] and by fault systems and their associated clustering. The background fractures show strikes that follow the regional trend and a relatively random spacing. In fault zones, the fracture network is clustered into fracture corridors. The transition between these fracture geometries is marked by the modification of the fracture network topology, which compartmentalises the reservoir with an increased role of metric-size fractures. This compartmentalisation is supported by long sub-vertical fractures delimitating fault corridors in the fault zone vicinity.
These large-sized fracture corridors and secondary fault systems can reach the sedimentary cover, enhancing mineral alteration in high intensity subdomains (FC1, profile C). Such configurations are typical for permeable fracture zones targeted in deep geothermal systems [1,14]. The understanding of the spatial configuration of these features is thus essential for crystalline reservoir exploration. From this analogue study, the fracture network connectivity and topology are closely linked to the architecture of corridors and the intensity of deformation concentration within these corridors.
The transition to the buried geothermal reservoir structural analysis reveals that N-S, NW-SE fault systems are major. In contrast, NE-SW systems have secondary importance on localisation of dilation and are thus more eager to present permeable fracture corridors [5]. With the orientation of the present in situ stress field with the maximum horizontal stress being NNW-SSE orientated, the fracture and fault systems are preferably orientated for shear and tensional reactivation and thus act as permeable corridors. Mapped lineaments intensities are higher in granitic and granodioritic plutons than in sedimentary and paragenetic metamorphic domains. Similar variability is reported in the crystalline basement regionally [3,6]. It can be explained by (1) a more substantial relief in granitic domains than in the Sprendlinger Horst area and (2) shallower dip angles of structures in sedimentary and gneisses than in granitic and granodioritic units. Because of more sub-vertical features present in batholiths, these items are more easily identified in lineament mapping [6].
6. Conclusions
The Mainzer Berg quarry offers a 3D live overview of the structural architecture of a granodioritic reservoir analogue, exposing a heterogenous fracture pattern with clearly compartmentalised faults and fracture corridors, as well as less deformed areas. This study provides a large dataset of quantitative estimation of fracture network dimensions and architecture related to large-scale structural features. The need to quantify the fracture pattern parameters implies the statistical estimation of the orientation, length, and spacing of fractures and faults on five orders of magnitude, which are provided here. A global power law with an exponent of −2.03 fits the length distribution. Thus, it could be considered a homogeneous value for the different potential discrete fracture network modelling scales.
However, orientation variation is scale-dependent. At the regional scale, major elements structuring the lineament network are the Messel (N045° E) and Otzberg (N010° E) faults, and secondly, the URG boundary fault, striking NS. The lithological boundaries and associated fault systems orientated ENE-WSW also describe the structural architecture. These regional directions are not expressed with the same proportion at all scales, suggesting compartmentalisation of the deformation, starting from the hectometric scale down to the metric scale. Secondly, the heterogeneity of the fracture pattern at the outcrop scale and the variable clustering of the fracture network should be integrated into modelling approaches to quantify flow properties in such lithologies and structural contexts. Such scale dependency of specific parameters controlling the connectivity and the clustering of lineaments and fractures and thus also the hydraulic and mechanical reservoir properties are demonstrated herein. It has to be considered for the multiscale characterisation of implementation sites, heat storage and deep geothermal reservoirs, or the GeoLAB tunnelling project.
Supplementary Materials
The data presented in this article are available on the following repository: https://doi.org/10.48328/tudatalib-571.
Author Contributions
This research was made collaboratively by all authors, following this repartition: conceptualisation, C.B. and K.B.; methodology, C.B., M.F. and L.S.; validation, C.B., K.B. and I.S.; investigation, C.B. and M.F.; resources, C.B., M.F. and L.S.; writing—original draft preparation, C.B.; writing—review and editing, M.F., L.S., K.B. and I.S.; supervision, K.B. and I.S.; funding acquisition, K.B. and I.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Interreg NWE Programme through the Roll-out of Deep Geothermal Energy in North-West Europe (DGE-ROLLOUT) Project (www.nweurope.eu/DGE-ROLLOUT). The Interreg NWE Programme is part of the European Cohesion Policy and is financed by the European Regional Development Funds (ERDF). The TU Darmstadt funds the APC under the agreement of Open-Access Publication Fund.
Data Availability Statement
Data used in this study is available in the Supplementary Materials section.
Acknowledgments
The Hessian Service for Soil Management and Geoinformation (HVBG) provided the elevation dataset used here. We also would like to thank the MHI Gruppe for granting access to the quarry.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vidal, J.; Genter, A. Overview of naturally permeable fractured reservoirs in the central and southern Upper Rhine Graben: Insights from geothermal wells. Geothermics 2018, 74, 57–73. [Google Scholar] [CrossRef]
- Place, J.; Géraud, Y.; Diraison, M.; Herquel, G.; Edel, J.B.; Bano, M.; Le Garzic, E.; Walter, B. Structural control of weathering processes within exhumed granitoids: Compartmentalisation of geophysical properties by faults and fractures. J. Struct. Geol. 2016, 84, 102–119. [Google Scholar] [CrossRef]
- Bertrand, L.; Jusseaume, J.; Géraud, Y.; Diraison, M.; Damy, P.C.; Navelot, V.; Haffen, S. Structural heritage, reactivation and distribution of fault and fracture network in a rifting context: Case study of the western shoulder of the Upper Rhine Graben. J. Struct. Geol. 2018, 108, 243–255. [Google Scholar] [CrossRef]
- Aquilina, L.; Boulvais, P.; Mossmann, J.R. Fluid migration at the basement/sediment interface along the margin of the Southeast basin (France): Implications for Pb-Zn ore formation. Miner. Depos. 2011, 46, 959–979. [Google Scholar] [CrossRef]
- Meixner, J.; Schill, E.; Grimmer, J.C.; Gaucher, E.; Kohl, T.; Klingler, P. Structural control of geothermal reservoirs in extensional tectonic settings: An example from the Upper Rhine Graben. J. Struct. Geol. 2016, 82, 1–15. [Google Scholar] [CrossRef]
- Meixner, J.; Grimmer, J.C.; Becker, A.; Schill, E.; Kohl, T. Comparison of different digital elevation models and satellite imagery for lineament analysis: Implications for identification and spatial arrangement of fault zones in crystalline basement rocks of the southern Black Forest (Germany). J. Struct. Geol. 2018, 108, 256–268. [Google Scholar] [CrossRef]
- Meller, C.; Schill, E.; Bremer, J.; Kolditz, O.; Bleicher, A.; Benighaus, C.; Chavot, P.; Gross, M.; Pellizzone, A.; Renn, O.; et al. Acceptability of geothermal installations: A geoethical concept for GeoLaB. Geothermics 2018, 73, 133–145. [Google Scholar] [CrossRef]
- Dezayes, C.; Lerouge, C. Reconstructing Paleofluid Circulation at the Hercynian Basement/Mesozoic Sedimentary Cover Interface in the Upper Rhine Graben. Geofluids 2019, 2019, 4849860. [Google Scholar] [CrossRef]
- Baujard, C.; Genter, A.; Dalmais, E.; Maurer, V.; Hehn, R.; Rosillette, R.; Vidal, J.; Schmittbuhl, J. Hydrothermal characterization of wells GRT-1 and GRT-2 in Rittershoffen, France: Implications on the understanding of natural flow systems in the rhine graben. Geothermics 2017, 65, 255–268. [Google Scholar] [CrossRef] [Green Version]
- Glaas, C.; Vidal, J.; Genter, A. Structural characterisation of naturally fractured geothermal reservoirs in the central Upper Rhine Graben. J. Struct. Geol. 2021, 148, 104370. [Google Scholar] [CrossRef]
- Stober, I.; Bucher, K. Hydraulic and hydrochemical properties of deep sedimentary reservoirs of the Upper Rhine Graben, Europe. Geofluids 2015, 15, 464–482. [Google Scholar] [CrossRef]
- Kushnir, A.R.L.; Heap, M.J.; Baud, P.; Gilg, H.A.; Reuschlé, T.; Lerouge, C.; Dezayes, C.; Duringer, P. Characterising the physical properties of rocks from the Paleozoic to Permo-Triassic transition in the Upper Rhine Graben. Geotherm. Energy 2018, 6, 16. [Google Scholar] [CrossRef]
- Koltzer, N.; Scheck-wenderoth, M.; Bott, J.; Cacace, M.; Frick, M.; Sass, I.; Fritsche, J.; Bär, K. The Effect of Regional Fluid Flow on Deep temperatures (Hesse, Germany). Energies 2019, 12, 2081. [Google Scholar] [CrossRef] [Green Version]
- McCaffrey, K.J.W.; Holdsworth, R.E.; Pless, J.; Franklin, B.S.G.; Hardman, K. Basement reservoir plumbing: Fracture aperture, length and topology analysis of the Lewisian Complex, NW Scotland. J. Geol. Soc. Lond. 2020, 177, 1281–1293. [Google Scholar] [CrossRef]
- Stein, E. The geology of the Odenwald Crystalline Complex. Mineral. Petrol. 2001, 72, 7–28. [Google Scholar] [CrossRef]
- Kirsch, H.; Kober, B.; Lippolt, H.J. Age of intrusion and rapid cooling of the Frankenstein gabbro (Odenwald, SW-Germany) evidenced by40Ar/39Ar and single-zircon207Pb/206Pb measurements. Geol. Rundsch. 1988, 77, 693–711. [Google Scholar] [CrossRef]
- Dörr, W.; Stein, E. Precambrian basement in the Rheic suture zone of the Central European Variscides (Odenwald). Int. J. Earth Sci. 2019, 108, 1937–1957. [Google Scholar] [CrossRef]
- Krohe, A. Structural evolution of intermediate-crustal rocks in a strike-slip and extensional setting (Variscan Odenwald, SW Germany): Differential upward transport of metamorphic complexes and changing deformation mechanisms. Tectonophysics 1992, 205, 357–386. [Google Scholar] [CrossRef]
- Will, T.M.; Schulz, B.; Schmädicke, E. The timing of metamorphism in the Odenwald–Spessart basement, Mid-German Crystalline Zone. Int. J. Earth Sci. 2017, 106, 1631–1649. [Google Scholar] [CrossRef]
- Anderle, H.J. The evolution of the South Hunsrück and Taunus Borderzone. Tectonophysics 1987, 137, 101–114. [Google Scholar] [CrossRef]
- Izart, A.; Barbarand, J.; Michels, R.; Privalov, V.A. Modelling of the thermal history of the Carboniferous Lorraine Coal Basin: Consequences for coal bed methane. Int. J. Coal Geol. 2016, 168, 253–274. [Google Scholar] [CrossRef]
- Böcker, J.; Littke, R.; Forster, A. An Overview on Source Rocks and the Petroleum System of the Central Upper Rhine Graben; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 0053101613303. [Google Scholar]
- Bourgeois, O.; Ford, M.; Diraison, M.; Le Carlier de Veslud, C.; Gerbault, M.; Pik, R.; Ruby, N.; Bonnet, S.; de Veslud, C.L.C.; Gerbault, M.; et al. Separation of rifting and lithospheric folding signatures in the NW-Alpine foreland. Int. J. Earth Sci. 2007, 96, 1003–1031. [Google Scholar] [CrossRef]
- Schumacher, M.E. Upper Rhine Graben: Role of preexisting structures during rift evolution. Tectonics 2002, 21, 6-1–6-17. [Google Scholar] [CrossRef]
- Mezger, J.E.; Felder, M.; Harms, F.J. Crystalline rocks in the maar deposits of Messel: Key to understand the geometries of the Messel Fault Zone and diatreme and the post-eruptional development of the basin fill. Z. Dtsch. Ges. Geowiss. 2013, 164, 639–662. [Google Scholar] [CrossRef]
- Lutz, H.; Lorenz, V.; Engel, T.; Häfner, F.; Haneke, J. Paleogene phreatomagmatic volcanism on the western main fault of the northern Upper Rhine Graben (Kisselwörth diatreme and Nierstein-Astheim Volcanic System, Germany). Bull. Volcanol. 2013, 75, 741. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, P.A.; Dèzes, P. Cenozoic uplift of Variscan Massifs in the Alpine foreland: Timing and controlling mechanisms. Glob. Planet. Chang. 2007, 58, 237–269. [Google Scholar] [CrossRef]
- Cloetingh, S.; Cornu, T.; Ziegler, P.A.; Beekman, F.; Ustaszewski, K.; Schmid, S.M.; Dèzes, P.; Hinsch, R.; Decker, K.; Lopes Gardozo, G.; et al. Neotectonics and intraplate continental topography of the northern Alpine Foreland. Earth-Sci. Rev. 2006, 74, 127–196. [Google Scholar] [CrossRef]
- Sissingh, W. Tertiary paleogeographic and tectonostratigraphic evolution of the Rhenish Triple Junction. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2003, 196, 229–263. [Google Scholar] [CrossRef]
- Ford, M.; Le Carlier de Veslud, C.; Bourgeois, O. Kinematic and geometric analysis of fault-related folds in a rift setting: The Dannemarie basin, Upper Rhine Graben, France. J. Struct. Geol. 2007, 29, 1811–1830. [Google Scholar] [CrossRef]
- Dèzes, P.; Schmid, S.M.M.; Ziegler, P.A. Evolution of the European Cenozoic Rift System: Interaction of the Alpine and Pyrenean orogens with their foreland lithosphere. Tectonophysics 2004, 389, 1–33. [Google Scholar] [CrossRef]
- Derer, C.E. Tectono-Sedimentary Evolution of the Northern Upper Rhine Graben (Germany), with Special Regard to the Early syn-Rift Stage. Dissertation 2003, pp. 1–99. Available online: https://bonndoc.ulb.uni-bonn.de/xmlui/handle/20.500.11811/1930 (accessed on 27 August 2021).
- Derer, C.E.; Schumacher, M.E.; Schäfer, A. The northern Upper Rhine Graben: Basin geometry and early syn-rift tectono-sedimentary evolution. Int. J. Earth Sci. 2005, 94, 640–656. [Google Scholar] [CrossRef]
- Gu, Y.; Rühaak, W.; Bär, K.; Sass, I. Using seismic data to estimate the spatial distribution of rock thermal conductivity at reservoir scale. Geothermics 2017, 66, 61–72. [Google Scholar] [CrossRef]
- Molenaar, N.; Felder, M.; Bär, K.; Götz, A.E. What classic greywacke (litharenite) can reveal about feldspar diagenesis: An example from Permian Rotliegend sandstone in Hessen, Germany. Sediment. Geol. 2015, 326, 79–93. [Google Scholar] [CrossRef]
- Thews, J.-D. Erläuterungen zur Geologischen Übersichtskarte von Hessen 1:300000 (GÜK300 Hessen) Teil I: Kristallin, Ordoviz, Silur, Devon, Karbon.- Geologische Abhandlungen von Hessen, Bd. 96, 1996, Hessisches Landesamt für Umwelt und Geologie; Wiesbaden. Available online: https://www.hlnug.de/themen/geologie/geologische-landesaufnahme/produkte/guek300 (accessed on 3 September 2021).
- Frey, M.; Weinert, S.; Bär, K.; van der Vaart, J.; Dezayes, C.; Calcagno, P.; Sass, I. Integrated 3D geological modelling of the northern Upper Rhine Graben by joint inversion of gravimetry and magnetic data. Tectonophysics 2021, 813, 228927. [Google Scholar] [CrossRef]
- Weinert, S.; Bär, K.; Sass, I. Database of petrophysical properties of the Mid-German Crystalline Rise. Earth Syst. Sci. Data 2021, 13, 1441–1459. [Google Scholar] [CrossRef]
- Luby, S.; Geraud, Y.; Diraison, M.; Wicker, M.; Bertrand, L.; Bossennec, C. Multiscale investigation focusing on the lineament of the Pan-African basement (Eastern Egypt). In Proceedings of the Fourth Naturally Fractured Reservoir Workshop, Ras Al Khaimah, United Arab Emirates, 11–13 February 2020; pp. 1–5. [Google Scholar]
- Chabani, A.; Trullenque, G.; Ledésert, B.A.; Klee, J. Multiscale Characterization of Fracture Patterns: A Case Study of the Noble Hills Range (Death Valley, CA, USA), application to geothermal reservoirs. Geosciences 2021, 11, 280. [Google Scholar] [CrossRef]
- Mikita, T.; Balková, M.; Bajer, A.; Cibulka, M.; Patočka, Z. Comparison of different remote sensing methods for 3d modeling of small rock outcrops. Sensors 2020, 20, 1663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zeng, Q.; Lu, W.; Zhang, R.; Zhao, J.; Ren, P.; Wang, B. LIDAR-Based Fracture Characterisation and Controlling Factors Analysis: An Outcrop Case from Kuqa Depression, NW China; Elsevier B.V.: Amsterdam, The Netherlands, 2018; Volume 161, ISBN 0500300100. [Google Scholar]
- Fisher, J.E.; Shakoor, A.; Watts, C.F. Comparing discontinuity orientation data collected by terrestrial LiDAR and transit compass methods. Eng. Geol. 2014, 181, 78–92. [Google Scholar] [CrossRef]
- Vöge, M.; Lato, M.J.; Diederichs, M.S. Automated rockmass discontinuity mapping from 3-dimensional surface data. Eng. Geol. 2013, 164, 155–162. [Google Scholar] [CrossRef]
- Biber, K.; Khan, S.D.; Seers, T.D.; Sarmiento, S.; Lakshmikantha, M.R. Quantitative characterisation of a naturally fractured reservoir analog using a hybrid lidar-gigapixel imaging approach. Geosphere 2018, 14, 710–730. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. RANSAC based out-of-core point-cloud shape detection for city-modeling. Proc. Terr. Laserscanning 2007, 26, 214–226. [Google Scholar]
- Bisdom, K.; Gauthier, B.D.M.; Bertotti, G.; Hardebol, N.J. Calibrating discrete fracture-network models with a carbonate three- dimensional outcrop fracture network: Implications for naturally fractured reservoir modeling. AAPG Bull. 2014, 7, 1351–1376. [Google Scholar] [CrossRef]
- Ortega, O.J.; Marrett, R.A.; Laubach, S.E. A scale-independent approach to fracture intensity and average spacing measurement. Am. Assoc. Pet. Geol. Bull. 2006, 90, 193–208. [Google Scholar] [CrossRef]
- Allmendiger, R. Stereonet 11 | Rick Allmendinger’s Stuff. Available online: http://www.geo.cornell.edu/geology/faculty/RWA/programs/stereonet.html (accessed on 27 July 2021).
- Fisher, N.; Lewis, T.; Embleton, B. Statistical Analysis of Spherical Data; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Peacock, D.C.P.; Dimmen, V.; Rotevatn, A.; Sanderson, D.J. A broader classification of damage zones. J. Struct. Geol. 2017, 102, 179–192. [Google Scholar] [CrossRef]
- Peacock, D.C.P.; Nixon, C.W.; Rotevatn, A.; Sanderson, D.J.; Zuluaga, L.F. Glossary of fault and other fracture networks. J. Struct. Geol. 2016, 92, 12–29. [Google Scholar] [CrossRef]
- Sanderson, D.J.; Nixon, C.W. Topology, connectivity and percolation in fracture networks. J. Struct. Geol. 2018, 115, 167–177. [Google Scholar] [CrossRef]
- Rizzo, R.E.; Healy, D.; Farrell, N.J.; Heap, M.J. Riding the Right Wavelet: Quantifying Scale Transitions in Fractured Rocks. Geophys. Res. Lett. 2017, 44, 11808–11815. [Google Scholar] [CrossRef] [Green Version]
- Putz-Perrier, M.W.; Sanderson, D.J. The distribution of faults and fractures and their importance in accommodating extensional strain at Kimmeridge Bay, Dorset, UK. Geol. Soc. Lond. Spec. Publ. 2008, 299, 97–111. [Google Scholar] [CrossRef]
- Peacock, D.C.P.; Sanderson, D.J.; Rotevatn, A. Relationships between fractures. J. Struct. Geol. 2018, 106, 41–53. [Google Scholar] [CrossRef]
- Gillespie, P.A.; Walsh, J.J.; Watterson, J.; Bonson, C.G.; Manzocchi, T. Scaling relationships of joint and vein arrays from The Burren, Co. Clare, Ireland. J. Struct. Geol. 2001, 23, 183–201. [Google Scholar] [CrossRef]
- Watkins, H.; Bond, C.E.; Healy, D.; Butler, R.W.H. Appraisal of fracture sampling methods and a new workflow tocharacterise heterogeneous fracture networks at outcrop. J. Struct. Geol. 2015, 72, 67–82. [Google Scholar] [CrossRef]
- Sanderson, D.J.; Peacock, D.C.P. Line sampling of fracture swarms and corridors. J. Struct. Geol. 2019, 122, 27–37. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of fracture systems in geological media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef] [Green Version]
- Primaleon, L.P.; McCaffrey, K.J.W.; Holdsworth, R.E. Fracture attribute and topology characteristics of a geothermal reservoir: Southern negros, philippines. J. Geol. Soc. Lond. 2020, 177, 1092–1106. [Google Scholar] [CrossRef]
- Choi, J.-H.H.; Edwards, P.; Ko, K.; Kim, Y.-S.S. Definition and classification of fault damage zones: A review and a new methodological approach. Earth-Sci. Rev. 2016, 152, 70–87. [Google Scholar] [CrossRef]
- Olson, J.E. Sublinear scaling of fracture aperture versus length: An exception or the rule? J. Geophys. Res. 2003, 108, 2413. [Google Scholar] [CrossRef]
- Odling, N.E.; Gillespie, P.; Bourgine, B.; Castaing, C. Variations in fracture system geometry and their implications for fluid flow in fractured hydrocarbon reservoirs. Pet. Geosci. 1999, 5, 373–384. [Google Scholar] [CrossRef]
- Bertrand, L.; Géraud, Y.; Le Garzic, E.; Place, J.; Diraison, M.; Walter, B.; Haffen, S. A multiscale analysis of a fracture pattern in granite: A case study ofthe Tamariu granite, Catalunya, Spain. J. Struct. Geol. 2015, 78, 52–66. [Google Scholar] [CrossRef]
- Martinelli, M.; Bistacchi, A.; Mittempergher, S.; Bonneau, F.; Balsamo, F.; Caumon, G.; Meda, M. Damage zone characterisation combining scanline and scan-area analysis on a km-scale Digital Outcrop Model: The Qala Fault (Gozo). J. Struct. Geol. 2020, 140, 104144. [Google Scholar] [CrossRef]
- Laubach, S.E.; Lamarche, J.; Gauthier, B.D.M.; Dunne, W.M.; Sanderson, D.J. Spatial arrangement of faults and opening-mode fractures. J. Struct. Geol. 2017, 108, 2–15. [Google Scholar] [CrossRef]
- Bertrand, L.; Géraud, Y.; Diraison, M. Petrophysical properties in faulted basement rocks: Insights from outcropping analogues on the West European Rift shoulders. Geothermics 2021, 95, 102144. [Google Scholar] [CrossRef]
- Liang, F.; Niu, J.; Linsel, A.; Hinderer, M.; Scheuvens, D.; Petschick, R. Rock alteration at the post-Variscan nonconformity: Implications for Carboniferous-Permian surface weathering versus burial diagenesis and paleoclimate evaluation. Solid Earth 2021, 12, 1165–1184. [Google Scholar] [CrossRef]
- Le Garzic, E.; de L’Hamaide, T.; Diraison, M.; Géraud, Y.; Sausse, J.; de Urreiztieta, M.; Hauville, B.; Champanhet, J.M. Scaling and geometric properties of extensional fracture systems in the proterozoic basement of Yemen. Tectonic interpretation and fluid flow implications. J. Struct. Geol. 2011, 33, 519–536. [Google Scholar] [CrossRef]
- McCaffrey, K.J.W.; Sleight, J.M.; Pugliese, S.; Holdsworth, R.E. Fracture formation and evolution in crystalline rocks: Insights from attribute analysis. Geol. Soc. Spec. Publ. 2003, 214, 109–124. [Google Scholar] [CrossRef]
- Žák, J.; Vyhnálek, B.; Kabele, P. Is there a relationship between magmatic fabrics and brittle fractures in plutons?: A view based on structural analysis, anisotropy of magnetic susceptibility and thermo-mechanical modelling of the Tanvald pluton (Bohemian Massif). Phys. Earth Planet. Inter. 2006, 157, 286–310. [Google Scholar] [CrossRef]
- Žák, J.; Verner, K.; Ježek, J.; Trubač, J. Complex mid-crustal flow within a growing granite–migmatite dome: An example from the Variscan belt illustrated by the anisotropy of magnetic susceptibility and fabric modelling. Geol. J. 2019, 54, 3681–3699. [Google Scholar] [CrossRef]
- Zibra, I.; White, J.C.; Menegon, L.; Dering, G.; Gessner, K. The ultimate fate of a synmagmatic shear zone. Interplay between rupturing and ductile flow in a cooling granite pluton. J. Struct. Geol. 2018, 110, 1–23. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).