Calculation of Potential Evapotranspiration and Calibration of the Hargreaves Equation Using Geostatistical Methods over the Last 10 Years in Central Italy
Abstract
:1. Introduction
Aim of the Study and State of the Art
2. Materials and Methods
- Gross error checking;
- Temporal consistency;
- Spatial consistency.
2.1. Study Area
2.2. Quality Control, Homogenization and Reconstruction of Climate Data
- RH (Relative Humidity), from 1% to 100%;
- Ws (Wind speed), from 0.1 to 75 m/s [40];
- Persistence check;
- Maximum variability check.
- = wind speed 2 m above the ground m/s−1;
- = measured wind speed h m above the ground m/s−1;
- = height of the measurement above the ground.
2.3. Methods for ET0 Calculation
- Cn = the numerator constant for the reference crop type and time step;
- Cd = the denominator constant for the reference crop type and time step;
- Rn = net radiation;
- u2 = wind speed 2 m above the ground (m/s−1);
- ∆ = slope of saturation vapor pressure curve at mean temperature (KPa °C−1);
- γ = theoretical psychrometric constant;
- es = mean saturation vapour pressure at the air temperature T(KPa);
- ea = actual vapour pressure derived from RH mean;
- G = soil heat flux (MJ m−2 day−1).
- ρ = atmospheric density (Kg/m3);
- P = atmospheric pressure at elevation z (KPa);
- R = specific gas constant 287 (J Kg−1 K−1);
- Tkv = virtual temperature (K).
- Tk = absolute temperature (K) 273 + Tmean (°C);
- P = atmospheric pressure at elevation z (KPa).
- Rl = average daily (24 h) stomata resistance of a single leaf (s m−1);
- LAI = leaf area index.
- ra = aerodynamic resistance (s m−1);
- zm = height measurement (m);
- zh = height temperature and humidity measurements (m);
- k = Von Karman constant (0.41);
- Uz = wind speed measurements at height zm (m s−1);
- d = zero plane displacement of wind profile (m).
- 0.0023 = empirical Hargreaves coefficient (HC);
- 17.8 = empirical temperature Hargreaves constant (TH);
- 0.5 = empirical Hargreaves exponent.
2.4. Data Analysis and Interpolations
3. Results
3.1. Quality Control
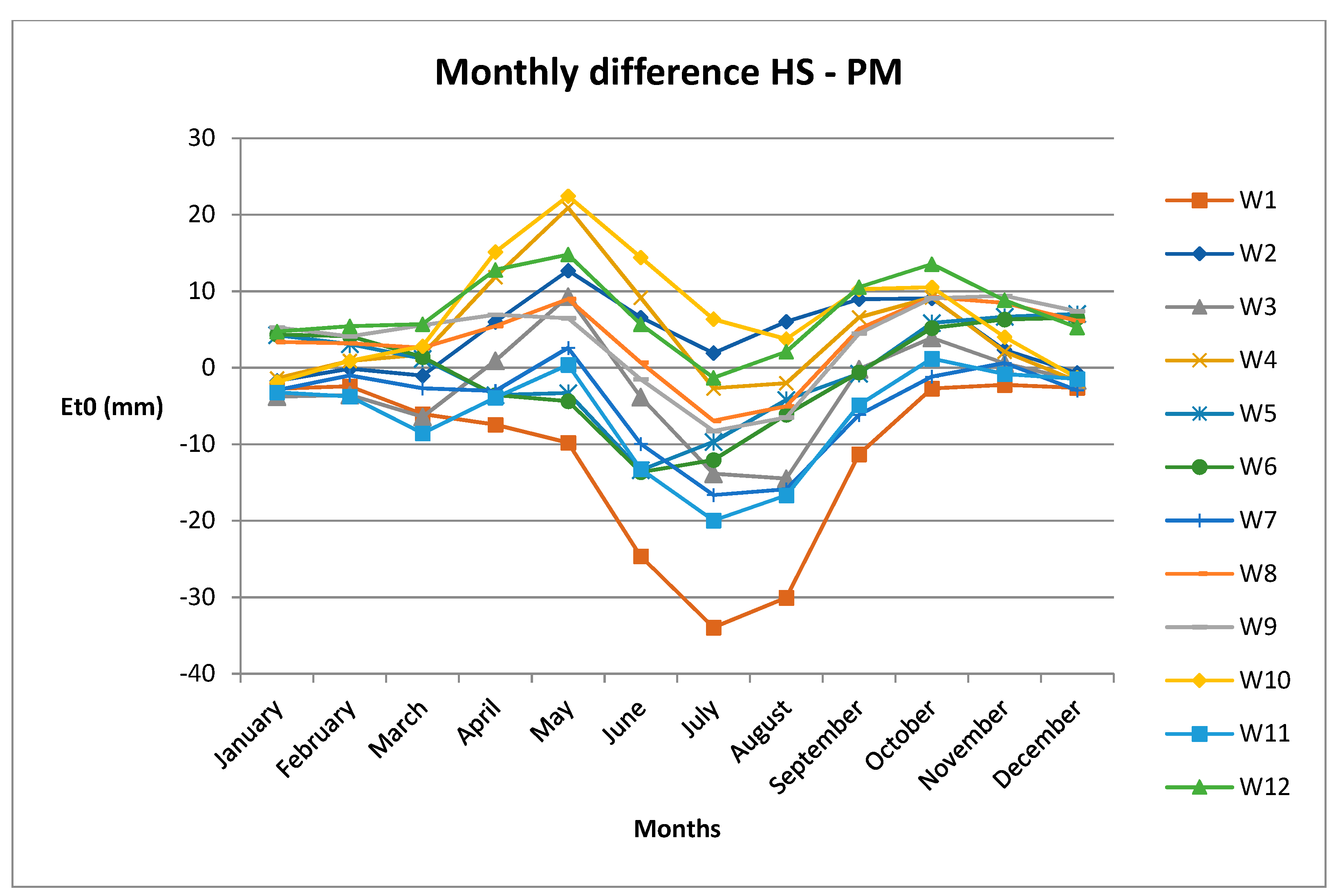
3.2. Comparison between Penmann Monteith’s and Hargreaves ET0 Calculation Methods
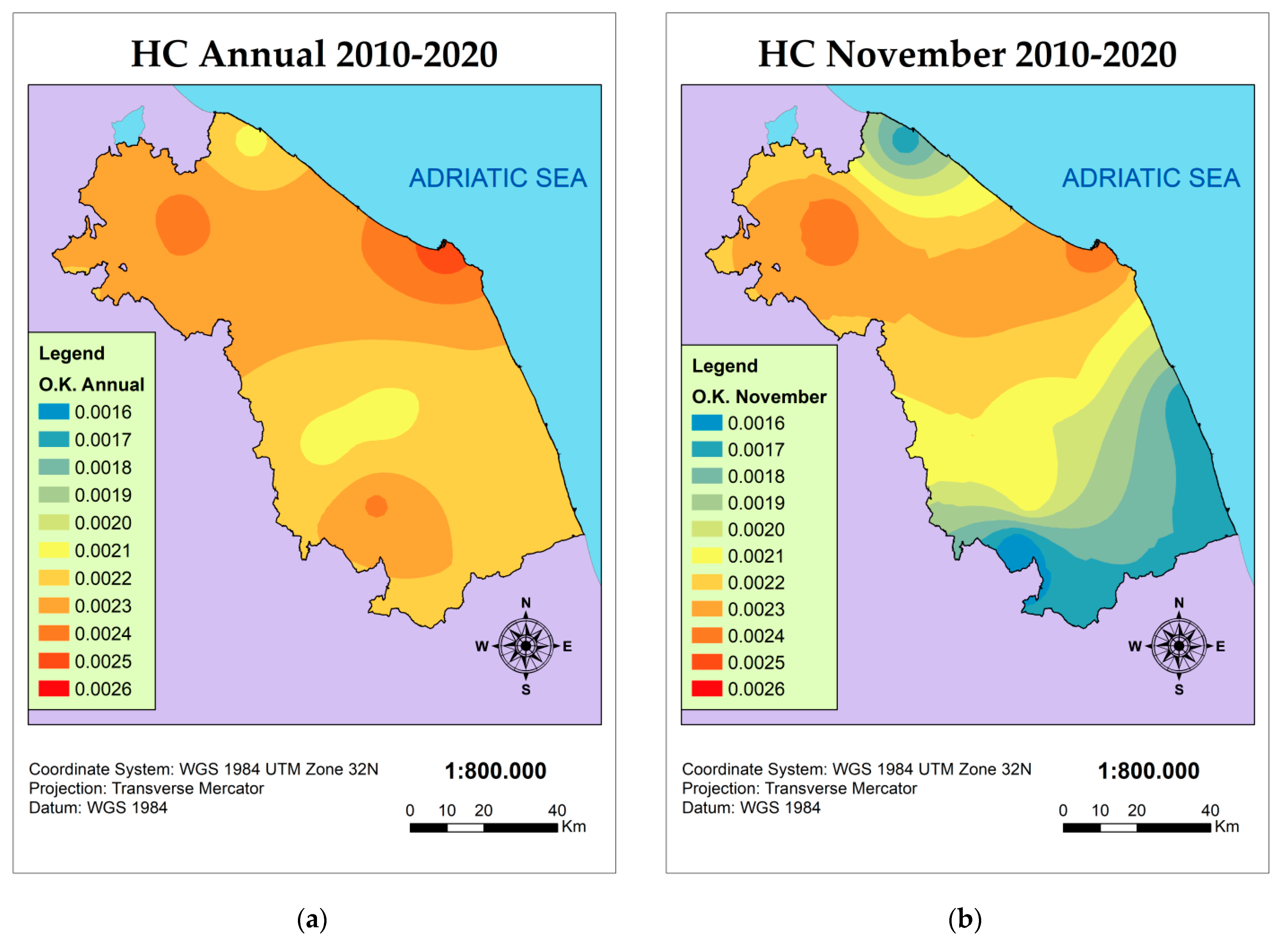
3.3. Interpolation of the Hargreaves Coefficient HC
3.4. Calculation of ET0
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop. Evapotranspiration: FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; p. 20. [Google Scholar]
- López-Urrea, R.; Montoro, A.; Mañas, F.; López-Fuster, P.; Fereres, E. Evapotranspiration and crop coefficients from lysimeter measurements of mature ‘Tempranillo’ wine grapes. Agric. Water Manag. 2021, 112, 13–20. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; Burt, P. Climate and Territorial Suitability for the Vineyards Developed Using GIS Techniques. In Exploring the Nexus of Geoecology, Geography, Geoarcheology and Geotourism: Advances and Applications for Sustainable Development in Environmental Sciences and Agroforestry Research; Springer: Cham, Switzerland, 2019; pp. 11–13. [Google Scholar]
- Moller, M.; Alchanatis, V.; Cohen, Y.; Meron, M.; Tsipris, J.; Naor, A.; Ostrovsky, V.; Sprintsin, M.; Cohen, S. Use of thermal and visible imagery for estimating crop water status of irrigated grapevine. J. Exp. Bot. 2007, 58, 827–838. [Google Scholar] [CrossRef] [Green Version]
- Saadi, S.; Todorovic, M.; Tanasijevic, L.; Pereira, L.S.; Pizzigalli, C.; Lionello, P. Climate change and Mediterranean agriculture: Impacts on winter wheat and tomato crop evapotranspiration, irrigation requirements and yield. Agric. Water Manag. 2015, 147, 103–135. [Google Scholar] [CrossRef]
- Kashyap, P.S.; Panda, R.K. Evaluation of evapotranspiration estimation methods and development of crop-coefficients for potato crop in a sub-humid region. Agric. Water Manag. 2001, 50, 9–25. [Google Scholar] [CrossRef]
- Garcia, M.; Raes, D.; Jacobsen, S.E. Evapotranspiration analysis and irrigation requirements of quinoa (Chenopodium quinoa) in the Bolivian highlands. Agric. Water Manag. 2003, 60, 119–134. [Google Scholar] [CrossRef]
- Tanasijevic, L.; Todorovic, M.; Pereira, L.S.; Pizzigalli, C.; Lionello, P. Impacts of climate change on olive crop evapotranspiration and irrigation requirements in the Mediterranean region. Agric. Water Manag. 2014, 144, 54–68. [Google Scholar] [CrossRef]
- Jovanovic, N.; Israel, S. Critical Review of Methods for the Estimation of Actual Evapotranspiration in Hydrological Models. In Evapotranspiration-Remote Sensing and Modeling; IntechOpen Limited: London, UK, 2012. [Google Scholar]
- Zhao, L.; Xia, J.; Xu, C.Y.; Wang, Z.; Sobkowiak, L.; Long, C. Evapotranspiration estimation methods in hydrological models. J. Geogr. Sci. 2013, 23, 359–369. [Google Scholar] [CrossRef]
- Ravazzani, G.; Corbari, C.; Morella, S.; Gianoli, P.; Mancini, M. Modified Hargreaves-Samani equation for the assessment of reference evapotranspiration in Alpine river basins. J. Irrig. Drain. Eng. 2012, 138, 592–599. [Google Scholar] [CrossRef]
- Thompson, J.R.; Green, A.J.; Kingston, D.G. Potential evapotranspiration-related uncertainty in climate change impacts on river flow: An assessment for the Mekong River basin. J. Hydrol. 2014, 510, 259–279. [Google Scholar] [CrossRef] [Green Version]
- Duran-Encalada, J.A.; Paucar-Caceres, A.; Bandala, E.R.; Wright, G.H. The impact of global climate change on water quantity and quality: A system dynamics approach to the US–Mexican transborder region. Eur. J. Oper. Res. 2017, 256, 567–581. [Google Scholar] [CrossRef] [Green Version]
- De Beurs, K.M.; Henebry, G.M.; Owsley, B.C.; Sokolik, I.N. Large scale climate oscillation impacts on temperature, precipitation and land surface phenology in Central Asia. Environ. Res. Lett. 2018, 13, 065018. [Google Scholar] [CrossRef]
- Bo, M.; Mercalli, L.; Pognant, F.; Berro, D.C.; Clerico, M. Urban air pollution, climate change and wildfires: The case study of an extended forest fire episode in northern Italy favoured by drought and warm weather conditions. Energy Rep. 2020, 6, 781–786. [Google Scholar] [CrossRef]
- Gentilucci, M.; Bisci, C.; Burt, P.; Fazzini, M.; Vaccaro, C. Interpolation of Rainfall Through Polynomial Regression in the Marche Region (Central Italy). In Geospatial Technologies for All: Selected Papers of the 21st AGILE Conference on Geographic Information Science; Springer: Berlin/Heidelberg, Germany, 2018; p. 55. [Google Scholar]
- Gentilucci, M.; Barbieri, M.; Burt, P. Climatic Variations in Macerata Province (Central Italy). Water 2018, 10, 1104. [Google Scholar] [CrossRef] [Green Version]
- Dong, Q.; Wang, W.; Shao, Q.; Xing, W.; Ding, Y.; Fu, J. The response of reference evapotranspiration to climate change in Xinjiang, China: Historical changes, driving forces, and future projections. Int. J. Climatol. 2020, 40, 235–254. [Google Scholar] [CrossRef]
- Arguez, A.; Vose, R.S. The definition of the standard WMO climate normal: The key to deriving alternative climate normals. Bull. Am. Meteorol. Soc. 2011, 92, 699–704. [Google Scholar] [CrossRef]
- Valiantzas, J.D. Simplified forms for the standardized FAO-56 Penman–Monteith reference evapotranspiration using limited weather data. J. Hydrol. 2013, 505, 13–23. [Google Scholar] [CrossRef]
- Trajkovic, S.; Kolakovic, S. Comparison of simplified pan-based equations for estimating reference evapotranspiration. J. Irrig. Drain. Eng. 2010, 136, 137–140. [Google Scholar] [CrossRef]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. Lond. Ser. A 1948, 193, 120–145. [Google Scholar]
- Monteith, J.L. Evaporation and Environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather. Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Blaney, H.F.; Criddle, W.D. Determining Water Requirements in Irrigated Areas from Climatological and Irrigation Data; U.S. Dept. Agriculture Soil Conservation Service: Washington, DC, USA, 1950; Volume 96, p. 44.
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Eng. 1982, 108, 225–230. [Google Scholar] [CrossRef]
- Tegos, A.; Malamos, N.; Koutsoyiannis, D. A parsimonious regional parametric evapotranspiration model based on a simplification of the Penman-Monteith formula. J. Hydrol. 2015, 524, 708–717. [Google Scholar] [CrossRef]
- Tegos, A.; Malamos, N.; Efstratiadis, A.; Tsoukalas, I.; Karanasios, A.; Koutsoyiannis, D. Parametric modelling of potential evapotranspiration: A global survey. Water 2017, 9, 795. [Google Scholar] [CrossRef] [Green Version]
- Xu, C.Y.; Singh, V.P. Cross comparison of empirical equations for calculating potential evapotranspiration with data from Switzerland. Water Resour. Manag. 2002, 16, 197–219. [Google Scholar] [CrossRef]
- Shahidian, S.; Serralheiro, R.; Serrano, J.; Teixeira, J.; Haie, N.; Santos, F. Hargreaves and Other Reduced-Set Methods for Calculating Evapotranspiration. In Evapotranspiration–Remote Sensing and Modeling; IntechOpen Limited: London, UK, 2012; pp. 59–80. [Google Scholar]
- Tabari, H.; Talaee, P.H. Local calibration of the Hargreaves and Priestley-Taylor equations for estimating reference evapotranspiration in arid and cold climates of Iran based on the Penman-Monteith model. J. Hydrol. Eng. 2011, 16, 837–845. [Google Scholar] [CrossRef]
- Vanderlinden, K.; Giraldez, J.V.; Van Meirvenne, M. Assessing reference evapotranspiration by the Hargreaves method in southern Spain. J. Irrig. Drain. Eng. 2004, 130, 184–191. [Google Scholar] [CrossRef]
- Fooladmand, H.R.; Haghighat, M. Spatial and temporal calibration of Hargreaves equation for calculating monthly ETo based on Penman-Monteith method. Irrig. Drain. J. Int. Comm. Irrig. Drain. 2007, 56, 439–449. [Google Scholar] [CrossRef]
- Mendicino, G.; Senatore, A. Regionalization of the Hargreaves coefficient for the assessment of distributed reference evapotranspiration in Southern Italy. J. Irrig. Drain. Eng. 2013, 139, 349–362. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, R.; Han, C.; Qing, W. Measurement and estimation of the summertime daily evapotranspiration on alpine meadow in the Qilian Mountains, northwest China. Environ. Earth Sci. 2013, 68, 2253–2261. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; Burt, P.; D’Aprile, F. Preliminary data validation and reconstruction of temperature and precipitation in Central Italy. Geosciences 2018, 8, 202. [Google Scholar] [CrossRef] [Green Version]
- WMO. Guide to Meteorological Instruments and Methods of Observation, 7th ed.; World Meteorological Organization: Geneva, Switzerland, 2008. [Google Scholar]
- Gentilucci, M.; Materazzi, M.; Pambianchi, G.; Burt, P.; Guerriero, G. Temperature variations in Central Italy (Marche region) and effects on wine grape production. Theor. Appl. Climatol. 2020, 140, 303–312. [Google Scholar] [CrossRef]
- Gentilucci, M.; Barbieri, M.; D’Aprile, F.; Zardi, D. Analysis of extreme precipitation indices in the Marche region (central Italy), combined with the assessment of energy implications and hydrogeological risk. Energy Rep. 2020, 6, 804–810. [Google Scholar] [CrossRef]
- Meek, D.W.; Hatfield, J.L. Data quality checking for single station meteorological databases. Agric. For. Meteorol. 1994, 69, 85–109. [Google Scholar] [CrossRef]
- Estévez, J.; Gavilán, P.; Giráldez, J.V. Guidelines on validation procedures for meteorological data from automatic weather stations. J. Hydrol. 2011, 402, 144–154. [Google Scholar] [CrossRef] [Green Version]
- Force, I.A. La Radiazione Solare Globale e la Durata del Soleggiamento in Italia dal 1991 al 2010; Areonautica Militare, Reparto di Sperimentazione di Meteorologica Areonautica: Rome, Italy, 2012; Volume 1, p. 53. [Google Scholar]
- Grykałowska, A.; Kowal, A.; Szmyrka-Grzebyk, A. The basics of calibration procedure and estimation of uncertainty budget for meteorological temperature sensors. Meteorol. App. 2015, 22, 867–872. [Google Scholar] [CrossRef]
- Aguilar, E.; Auer, I.; Brunet, M.; Peterson, T.C.; Wieringa, J. Guidance on Metadata and Homogenization; WMO (World Meteorological Organization): Geneva, Switzerland, 2003. [Google Scholar]
- Zahumenský, I. Guidelines on Quality Control Procedures for Data from Automatic Weather Stations; World Meteorological Organization: Geneva, Switzerland, 2004. [Google Scholar]
- Feng, S.; Hu, Q.; Qian, W. Quality control of daily meteorological data in China, 1951–2000: A new dataset. Int. J. Climatol. A J. R. Meteorol. Soc. 2004, 24, 853–870. [Google Scholar] [CrossRef]
- Kang, H.M.; Yusof, F. Homogeneity tests on daily rainfall series. Int. J. Contemp. Math. Sci. 2012, 7, 9–22. [Google Scholar]
- Dhorde, A.G.; Zarenistanak, M. Three-way approach to test data homogeneity: An analysis of temperature and precipitation series over southwestern Islamic Republic of Iran. J. Indian Geophys. Union’s 2013, 17, 233–242. [Google Scholar]
- Pettitt, A.N. A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Bartier, P.M.; Keller, C.P. Multivariate interpolation to incorporate thematic surface data using inverse distance weighting (IDW). Comput. Geosci. 1996, 22, 795–799. [Google Scholar] [CrossRef]
- Zotarelli, L.; Dukes, M.D.; Romero, C.C.; Migliaccio, K.W.; Morgan, K.T. Step by step calculation of the Penman-Monteith Evapotranspiration (FAO-56 Method). Inst. Food Agric. Sciences. Univ. Fla. 2010, AE459, 1–10. [Google Scholar]
- Smith, M.; Allen, R.; Monteith, J.L.; Perrier, A.; Segeren, A. FAO Penman-Monteith Formula. In Expert Consultation on Revision of FAO Methodologies for Crop Water Requirements; FAO: Rome, Italy, 1990; p. 23. [Google Scholar]
- Allen, R.G. Assessing Integrity of Weather Data for Reference Evapotranspiration Estimation. J. Irrig. Drain. Eng. 1996, 122, 97–106. [Google Scholar] [CrossRef]
- Tetens, O. Uber einige meteorologische Begriffe. Z. Geophys. 1930, 6, 297–309. [Google Scholar]
- McEvoy, A.; Markvart, T.; Castañer, L.; Markvart, T.; Castaner, L. Practical Handbook of Photovoltaics: Fundamentals and Applications; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Anadranistakis, M.; Liakatas, A.; Alexandris, S.; Aggelides, S.; Kerkides, P.; Rizos, S.; Poulovassilis, A. Soil heat flux in the penman-monteith evapotranspiration equation. Acta Hortic. 1997, 449, 69–74. [Google Scholar] [CrossRef]
- Hargreaves, G.H. Simplified Coefficients for Estimating Monthly Solar Radiation in North America and Europe; Deptartment of Biological and Irrigation Engineering, Utah State University: Logan, UT, USA, 1994. [Google Scholar]
- Adamala, S.; Reddy, Y.K. Evaluation of Different Solar Radiation Estimation Methods for Indian Locations. In Water Resources and Environmental Engineering, 2nd ed.; Springer: Singapore, 2019; pp. 47–56. [Google Scholar]
- Annandale, J.; Jovanovic, N.; Benade, N.; Allen, R. Software for missing data error analysis of Penman-Monteith reference evapotranspiration. Irrig Sci. 2002, 21, 57–67. [Google Scholar]
- Allen, R.G.; Walter, I.A.; Elliott, R.; Howell, T.; Itenfisu, D.; Jensen, M. The ASCE Standardized Reference Evapotranspiration Equation; Prepared by Task Committee on Standardization of Reference Evapotranspiration; ASCE Environmental and Water Resources Institute: Reston, VA, USA, 2005. [Google Scholar]
- Jensen, M.E.; Burman, R.D.; Allen, R.G. Evapotranspiration and Irrigation Water Requirements. In ASCE Manuals and Reports of Engineering Practice; ASCE: New York, NK, USA, 1990. [Google Scholar]
- Allen, R.G.; Jensen, M.E.; Wright, J.L.; Burman, R.D. Operational estimates of evapotranspiration. Agron. J. 1989, 81, 650–662. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and surface temperature. Q. J. R. Meteorol. Soc. 1981, 107, 1–27. [Google Scholar] [CrossRef]
- Brutsaert, W. The roughness length for water vapor, sensible heat and other scalars. J. Atm. Sci. 1975, 32, 2028–2031. [Google Scholar] [CrossRef] [Green Version]
- Hargreaves, G.H. Defining and using reference evapotranspiration. J. Irrig. Drain. Eng. 1994, 120, 1132–1139. [Google Scholar] [CrossRef]
- Gentilucci, M.; Materazzi, M.; Pambianchi, G.; Burt, P.; Guerriero, G. Assessment of variations in the temperature-rainfall trend in the province of Macerata (Central Italy), comparing the last three climatological standard normals (1961–1990; 1971–2000; 1981–2010) for biosustainability studies. Environ. Process. 2019, 6, 391–412. [Google Scholar] [CrossRef]
- Pellicone, G.; Caloiero, T.; Modica, G.; Guagliardi, I. Application of several spatial interpolation techniques to monthly rainfall data in the Calabria region (southern Italy). Int. J. Climatol. 2018, 38, 3651–3666. [Google Scholar] [CrossRef]
- De Amorim Borges, P.; Franke, J.; da Anunciação, Y.M.T.; Weiss, H.; Bernhofer, C. Comparison of spatial interpolation methods for the estimation of precipitation distribution in Distrito Federal, Brazil. Theor. Appl. Climatol. 2016, 123, 335–348. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A Review of Spatial Interpolation Methods for Environmental Scientists; Geoscience Australia, Record: Canberra, Australia, 2008; Volume 23, p. 137. [Google Scholar]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Benli, B.; Bruggeman, A.; Oweis, T.; Üstün, H. Performance of Penman-Monteith FAO56 in a semiarid highland environment. J. Irrig. Drain. Eng. 2010, 136, 757–765. [Google Scholar] [CrossRef]
- Gavilán, P.; Lorite, I.J.; Tornero, S.; Berengena, J. Regional calibration of Hargreaves equation for estimating reference ET in a semiarid environment. Agric. Water Manag. 2006, 81, 257–281. [Google Scholar] [CrossRef]
- Berti, A.; Tardivo, G.; Chiaudani, A.; Rech, F.; Borin, M. Assessing reference evapotranspiration by the Hargreaves method in north-eastern Italy. Agric. Water Manag. 2014, 140, 20–25. [Google Scholar] [CrossRef]
- Trajkovic, S. Hargreaves versus Penman-Monteith under humid conditions. J. Irrig. Drain. Eng. 2007, 133, 38–42. [Google Scholar] [CrossRef]
- Alexandris, S.; Stricevic, R.; Petkovic, S. Comparative analysis of reference evapotranspiration from the surface of rainfed grass in central Serbia, calculated by six empirical methods against the Penman-Monteith formula. Eur. Water 2008, 21, 17–28. [Google Scholar]
- Dorji, U.; Olesen, J.E.; Seidenkrantz, M.S. Water balance in the complex mountainous terrain of Bhutan and linkages to land use. J. Hydrol. Reg. Stud. 2016, 7, 55–68. [Google Scholar] [CrossRef] [Green Version]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Hodam, S.; Sarkar, S.; Marak, A.G.; Bandyopadhyay, A.; Bhadra, A. Spatial interpolation of reference evapotranspiration in India: Comparison of IDW and Kriging Methods. J. Inst. Eng. (India) Ser. A 2017, 98, 511–524. [Google Scholar] [CrossRef]
- Manesh, S.S.; Ahani, H.; Rezaeian-Zadeh, M. ANN-based mapping of monthly reference crop evapotranspiration by using altitude, latitude and longitude data in Fars province, Iran. Environ. Dev. Sustain. 2014, 16, 103–122. [Google Scholar] [CrossRef]


| Code | Weather Station | Elevation (m.a.s.l.) |
|---|---|---|
| W1 | Ancona | 91 |
| W2 | Camerino | 581 |
| W3 | Colle di Montecarotto | 350 |
| W4 | Macerata | 303 |
| W5 | Monte Bove | 1917 |
| W6 | Monte Prata | 1813 |
| W7 | Pintura di Bolognola | 1352 |
| W8 | Porto Sant’Elpidio | 9 |
| W9 | San Benedetto del Tronto | 6 |
| W10 | Tolentino | 228 |
| W11 | Urbino | 471 |
| W12 | Villa Fastiggi | 22 |
| Check | Weather Stations | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C. Par. | % | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 | W9 | W10 | W11 | W12 |
| TMax | G. | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| TMax | T. | 0.1 | 0.0 | 0.1 | 0.1 | 0.0 | 0.2 | 0.1 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 |
| TMax | S. | 0.5 | 1.9 | 0.6 | 0.4 | 1.8 | 0.4 | 0.6 | 1.0 | 0.5 | 0.8 | 1.1 | 1.1 |
| TMax | R. | 7.0 | 5.7 | 3.4 | 3.2 | 10.9 | 9.8 | 10.0 | 9.8 | 9.3 | 3.7 | 9.9 | 9.9 |
| Tmean | G. | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Tmean | T. | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Tmean | S. | 1.8 | 1.8 | 1.1 | 0.4 | 1.8 | 0.6 | 0.4 | 1.0 | 1.0 | 0.8 | 0.4 | 1.0 |
| Tmean | R. | 7.0 | 5.7 | 3.4 | 3.2 | 10.9 | 9.8 | 10.8 | 9.8 | 9.3 | 3.7 | 3.3 | 9.9 |
| Tmin | G. | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Tmin | T. | 0.2 | 0.1 | 0.0 | 0.1 | 0.0 | 0.2 | 0.1 | 0.0 | 0.0 | 0.0 | 0.2 | 0.0 |
| Tmin | S. | 0.5 | 1.9 | 0.6 | 0.4 | 1.8 | 0.4 | 0.6 | 1.0 | 0.5 | 0.8 | 0.4 | 1.1 |
| Tmin | R. | 7.0 | 5.7 | 3.4 | 3.2 | 10.9 | 9.8 | 10.0 | 9.8 | 9.3 | 3.7 | 3.3 | 9.9 |
| RH | G. | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.1 | 0.0 | 0.0 |
| RH | T. | 0.0 | 0.2 | 0.0 | 0.0 | 1.1 | 0.4 | 0.8 | 1.4 | 0.0 | 0.0 | 0.0 | 0.0 |
| RH | S. | 0.8 | 0.7 | 0.4 | 0.7 | 1.1 | 3.4 | 1.4 | 1.1 | 0.5 | 2.0 | 0.8 | 1.2 |
| RH | R. | 1.3 | 1.6 | 1.5 | 2.0 | 5.7 | 6.2 | 7.3 | 5.2 | 5.2 | 3.1 | 1.3 | 3.2 |
| Rs | G. | 1.5 | 0.6 | 0.9 | 1.7 | 9.6 | 0.1 | 0.5 | 1.7 | 0.2 | 0.1 | 0.2 | 1.1 |
| Rs | T. | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Rs | S. | 1.1 | 1.6 | 1.3 | 1.8 | 2.5 | 1.2 | 1.9 | 7.4 | 1.8 | 1.2 | 1.0 | 1.4 |
| Rs | R. | 3.7 | 3.5 | 3.4 | 15.2 | 15.1 | 3.7 | 2.8 | 12.8 | 7.7 | 2.5 | 1.9 | 5.2 |
| Ws | G. | 0.4 | 0.2 | 0.0 | 4.2 | 3.4 | 2.9 | 2.2 | 0.1 | 0.0 | 2.9 | 0.2 | 0.0 |
| Ws | T. | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Ws | S. | 0.9 | 0.7 | 0.7 | 1.1 | 2.0 | 1.9 | 1.4 | 0.5 | 0.7 | 1.4 | 0.9 | 0.5 |
| Ws | R. | 1.9 | 2.1 | 1.8 | 4.1 | 8.8 | 9.2 | 7.2 | 3.5 | 5.7 | 5.9 | 1.5 | 3.3 |
| Daily Average | Weather Stations | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MJ/m2 | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 | W9 | W10 | W11 | W12 |
| Rsmeasured SARAH | 14.8 | 14.1 | 14.3 | 14.6 | 12.4 | 13.2 | 12.6 | 15.0 | 15.2 | 15.4 | 14.2 | 14.6 |
| Rsmeasured W. Station | 14.5 | 14.1 | 14.1 | 14.1 | 15.2 | 15.8 | 14.7 | 15.3 | 15.3 | 14.1 | 15.1 | 12.9 |
| ET0 | P. | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 | W9 | W10 | W11 | W12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PM | Jan | 23.9 | 21.4 | 24.8 | 25.5 | 8.5 | 8.9 | 18.8 | 20.8 | 20.2 | 25.1 | 21.8 | 18.5 |
| PM | Feb | 31.0 | 26.8 | 32.0 | 32.5 | 13.4 | 13.6 | 21.7 | 28.9 | 29.4 | 31.2 | 28.4 | 26.8 |
| PM | Mar | 60.0 | 53.4 | 62.6 | 62.6 | 29.4 | 30.5 | 39.9 | 57.4 | 55.8 | 60.6 | 57.4 | 58.2 |
| PM | Apr | 84.5 | 75.2 | 84.5 | 84.0 | 50.0 | 53.5 | 59.9 | 81.1 | 79.2 | 81.1 | 79.8 | 81.4 |
| PM | May | 113.4 | 95.6 | 107.3 | 106.9 | 68.4 | 72.1 | 73.9 | 107.6 | 108.3 | 105.9 | 102.7 | 110.8 |
| PM | Jun | 149.3 | 131.2 | 150.2 | 147.5 | 96.8 | 99.5 | 107.9 | 140.9 | 140.7 | 148.1 | 142.3 | 149.0 |
| PM | Jul | 166.1 | 149.7 | 172.6 | 171.6 | 106.2 | 110.3 | 126.2 | 159.5 | 158.9 | 173.5 | 159.7 | 164.1 |
| PM | Aug | 145.9 | 130.7 | 153.9 | 155.2 | 92.0 | 95.2 | 113.5 | 140.9 | 141.1 | 153.9 | 139.3 | 141.2 |
| PM | Sep | 90.2 | 75.8 | 88.1 | 91.7 | 53.9 | 55.2 | 66.4 | 86.6 | 87.0 | 88.7 | 81.1 | 83.0 |
| PM | Oct | 50.5 | 41.5 | 46.9 | 48.8 | 27.5 | 28.7 | 39.0 | 46.3 | 47.1 | 47.1 | 43.0 | 42.8 |
| PM | Nov | 29.4 | 24.1 | 26.5 | 29.0 | 11.0 | 12.0 | 20.3 | 23.5 | 23.8 | 26.5 | 24.3 | 21.9 |
| PM | Dec | 22.5 | 20.3 | 22.1 | 25.7 | 6.3 | 6.8 | 18.7 | 17.6 | 17.6 | 24.1 | 19.5 | 16.9 |
| PM | Ann | 967 | 846 | 971 | 981 | 563 | 586 | 706 | 911 | 909 | 966 | 899 | 915 |
| ET0 | P. | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 | W9 | W10 | W11 | W12 |
| HS | Jan | 21.1 | 19.6 | 21.0 | 24.1 | 12.8 | 13.2 | 15.9 | 24.1 | 25.4 | 23.3 | 18.6 | 23.2 |
| HS | Feb | 28.6 | 26.7 | 28.4 | 33.4 | 16.5 | 17.7 | 20.7 | 32.1 | 33.5 | 32.0 | 24.6 | 32.2 |
| HS | Mar | 54.0 | 52.3 | 56.1 | 64.3 | 30.5 | 31.9 | 37.2 | 60.0 | 61.4 | 63.4 | 48.8 | 63.9 |
| HS | Apr | 77.0 | 81.1 | 85.4 | 95.8 | 46.4 | 50.0 | 56.8 | 86.6 | 86.2 | 96.2 | 75.9 | 94.1 |
| HS | May | 103.6 | 108.3 | 116.6 | 127.8 | 65.1 | 67.7 | 76.5 | 116.6 | 114.7 | 128.4 | 103.0 | 125.6 |
| HS | Jun | 124.6 | 137.8 | 146.3 | 156.7 | 83.4 | 85.8 | 97.9 | 141.6 | 139.2 | 162.5 | 129.0 | 154.7 |
| HS | Jul | 132.2 | 151.6 | 158.7 | 168.9 | 96.6 | 98.3 | 109.5 | 152.6 | 150.6 | 179.8 | 139.8 | 162.8 |
| HS | Aug | 115.8 | 136.7 | 139.4 | 153.2 | 87.7 | 89.0 | 97.6 | 135.8 | 134.6 | 157.6 | 122.6 | 143.2 |
| HS | Sep | 78.9 | 84.8 | 87.9 | 98.3 | 53.1 | 54.6 | 60.2 | 91.7 | 91.4 | 98.9 | 76.2 | 93.5 |
| HS | Oct | 47.8 | 50.6 | 50.8 | 58.0 | 33.4 | 33.9 | 37.8 | 55.5 | 56.2 | 57.7 | 44.2 | 56.3 |
| HS | Nov | 27.1 | 26.4 | 27.0 | 31.0 | 17.6 | 18.3 | 20.9 | 32.0 | 33.1 | 30.5 | 23.4 | 30.7 |
| HS | Dec | 19.9 | 19.6 | 20.5 | 23.9 | 13.3 | 13.3 | 15.8 | 23.7 | 24.9 | 22.7 | 18.1 | 22.2 |
| HS | Ann | 830 | 895 | 938 | 1035 | 556 | 574 | 647 | 952 | 951 | 1053 | 824 | 1003 |
| W. Station | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 | W9 | W10 | W11 | W12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
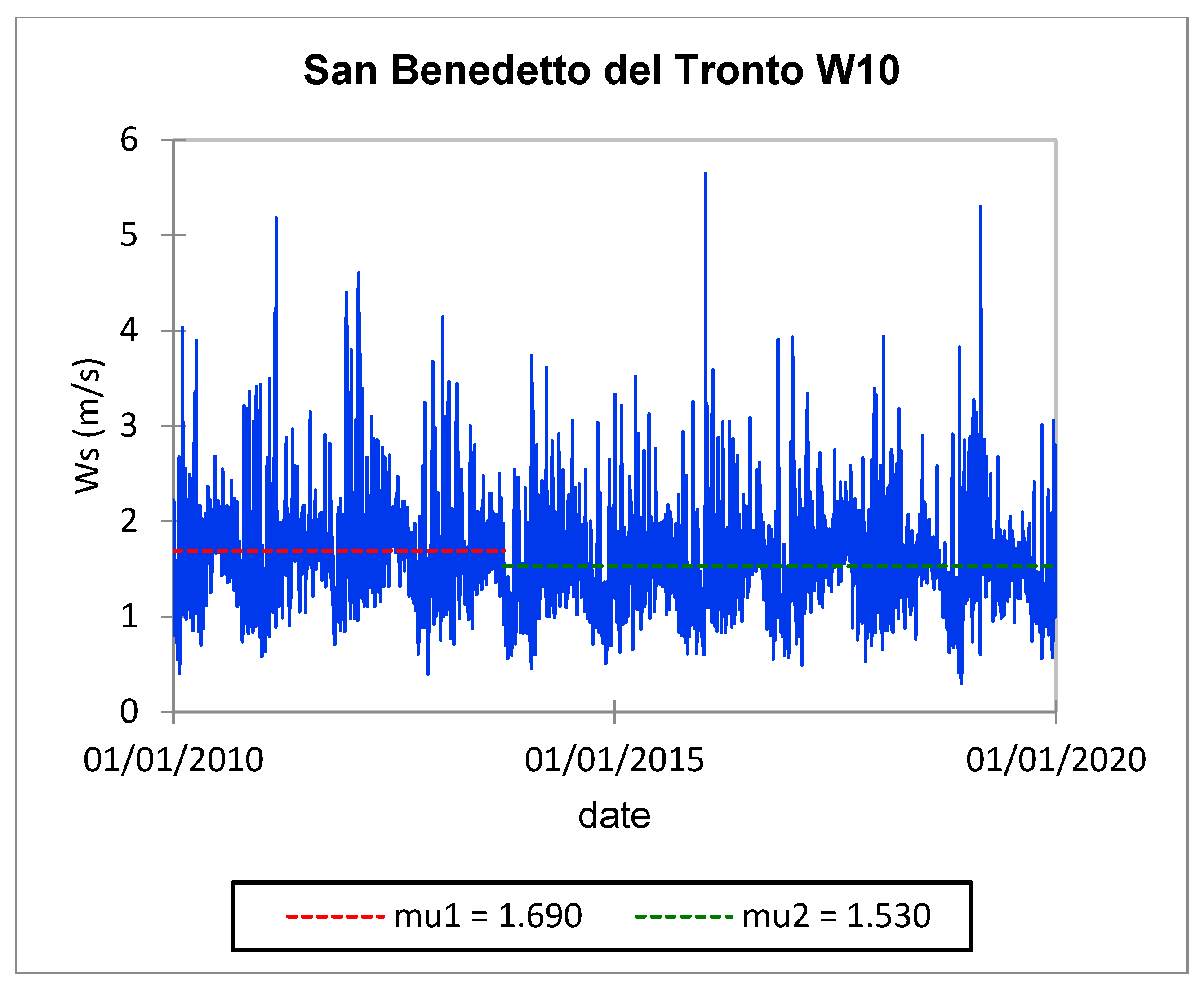
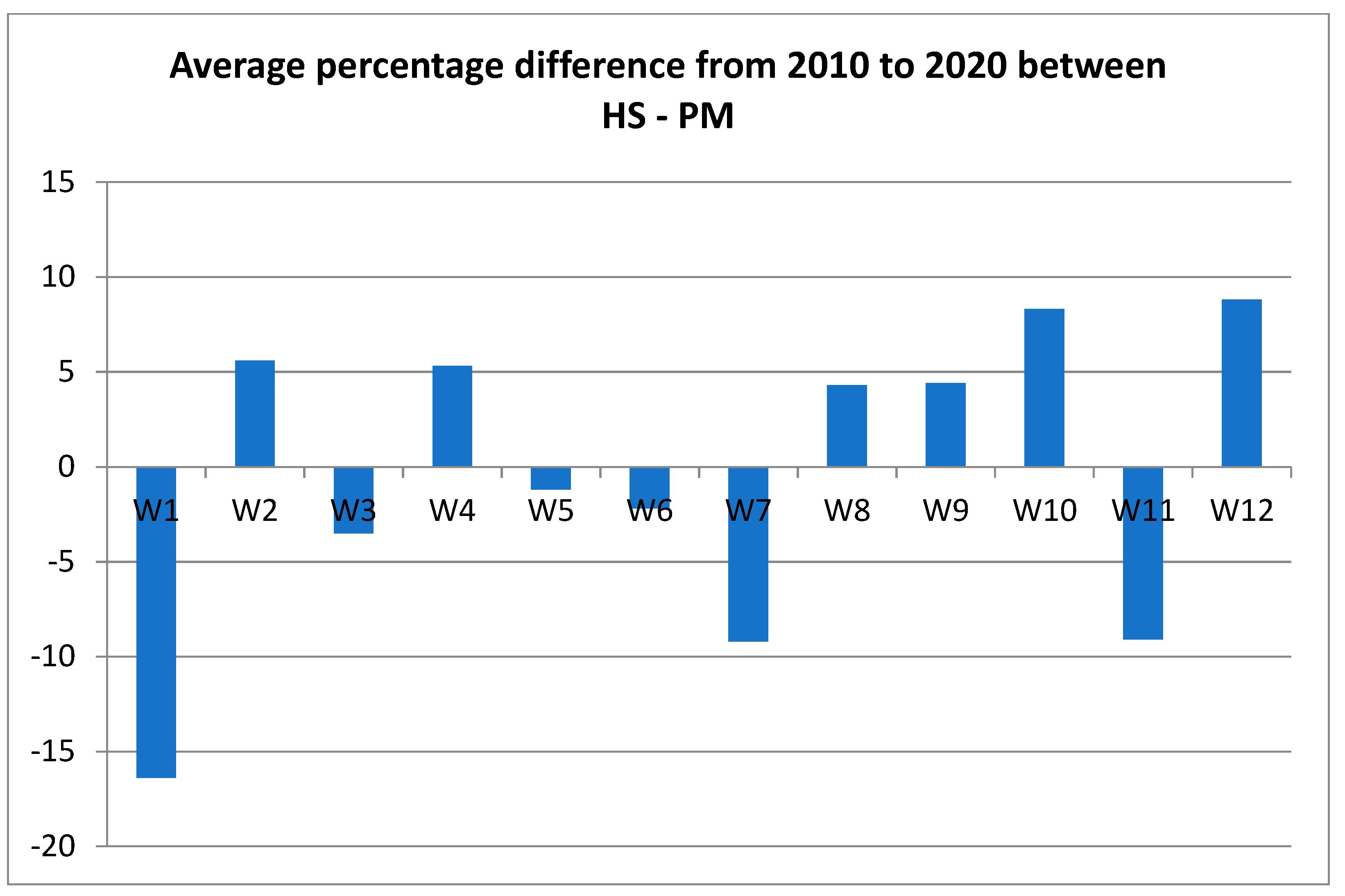
| dif. 2010–2020 | −16.4 | 5.6 | −3.5 | 5.3 | −1.2 | −2.2 | −9.2 | 4.3 | 4.4 | 8.3 | −9.1 | 8.8 |
| 95% conf. int. | ±5.0 | ±3.0 | ±4.7 | ±4.5 | ±2.9 | ±1.8 | ±2.4 | ±2.4 | ±2.6 | ±3.7 | ±3.1 | ±2.3 |
| W.S. | W1 | W2 | W3 | W4 | W5 | W6 | W7 | W8 | W9 | W10 | W11 | W12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jan HC | 2.6 | 2.5 | 2.7 | 2.4 | 1.6 | 1.6 | 2.7 | 2.0 | 1.8 | 2.5 | 2.7 | 1.8 |
| Feb HC | 2.5 | 2.3 | 2.6 | 2.2 | 1.9 | 1.8 | 2.4 | 2.1 | 2.0 | 2.2 | 2.7 | 1.9 |
| Mar HC | 2.6 | 2.3 | 2.6 | 2.2 | 2.2 | 2.2 | 2.5 | 2.2 | 2.1 | 2.2 | 2.7 | 2.1 |
| Apr HC | 2.5 | 2.1 | 2.3 | 2.0 | 2.5 | 2.5 | 2.4 | 2.2 | 2.1 | 1.9 | 2.4 | 2.0 |
| May HC | 2.5 | 2.0 | 2.1 | 1.9 | 2.4 | 2.4 | 2.2 | 2.1 | 2.2 | 1.9 | 2.3 | 2.0 |
| Jun HC | 2.8 | 2.2 | 2.4 | 2.2 | 2.7 | 2.7 | 2.5 | 2.3 | 2.3 | 2.1 | 2.5 | 2.2 |
| Jul HC | 2.9 | 2.3 | 2.5 | 2.3 | 2.5 | 2.6 | 2.6 | 2.4 | 2.4 | 2.2 | 2.6 | 2.3 |
| Aug HC | 2.9 | 2.2 | 2.5 | 2.3 | 2.4 | 2.5 | 2.7 | 2.4 | 2.4 | 2.2 | 2.6 | 2.3 |
| Sep HC | 2.6 | 2.1 | 2.3 | 2.1 | 2.3 | 2.3 | 2.5 | 2.2 | 2.2 | 2.1 | 2.5 | 2.0 |
| Oct HC | 2.5 | 1.9 | 2.2 | 2.0 | 2.0 | 2.0 | 2.3 | 2.0 | 2.0 | 1.9 | 2.3 | 1.8 |
| Nov HC | 2.5 | 2.2 | 2.4 | 2.2 | 1.6 | 1.6 | 2.2 | 1.7 | 1.7 | 2.1 | 2.5 | 1.7 |
| Dec HC | 2.7 | 2.3 | 2.4 | 2.4 | 1.3 | 1.3 | 2.6 | 1.8 | 1.7 | 2.4 | 2.5 | 1.8 |
| Ann HC | 2.7 | 2.1 | 2.4 | 2.2 | 2.3 | 2.3 | 2.5 | 2.2 | 2.2 | 2.1 | 2.5 | 2.1 |
| RMSE | MSE | RMSSE | ASE | RMSE | MSE | RMSSE | ASE | ||
|---|---|---|---|---|---|---|---|---|---|
| OK Jan | 0.00042 | −0.02058 | 0.99948 | 0.00048 | OK Feb | 0.00029 | −0.01014 | 1.00919 | 0.00027 |
| OCK Jan | 0.00042 | 0.05025 | 0.97203 | 0.00045 | OCK Feb | 0.00030 | 0.01955 | 1.04040 | 0.00028 |
| EBK Jan | 0.00043 | 0.01265 | 0.91740 | 0.00047 | EBK Feb | 0.00031 | 0.00523 | 0.94670 | 0.00031 |
| OK Mar | 0.00022 | −0.01469 | 0.99964 | 0.00021 | OK Apr | 0.00023 | −0.00270 | 1.01601 | 0.00022 |
| OCK Mar | 0.00024 | 0.01448 | 1.18229 | 0.00019 | OCK Apr | 0.00019 | 0.00270 | 0.87131 | 0.00019 |
| EBK Mar | 0.00023 | 0.02283 | 0.99274 | 0.00022 | EBK Apr | 0.00022 | −0.00105 | 0.93277 | 0.00021 |
| OK May | 0.00018 | −0.03791 | 0.99523 | 0.00016 | OK Jun | 0.00023 | −0.00484 | 1.00051 | 0.00023 |
| OCK May | 0.00018 | −0.00693 | 0.90759 | 0.00018 | OCK Jun | 0.00019 | 0.02802 | 0.82823 | 0.00020 |
| EBK May | 0.00021 | −0.01225 | 0.95158 | 0.00019 | EBK Jun | 0.00023 | 0.00661 | 0.91972 | 0.00021 |
| OK Jul | 0.00020 | −0.01011 | 1.00730 | 0.00019 | OK Aug | 0.00022 | −0.02360 | 0.99735 | 0.00022 |
| OCK Jul | 0.00020 | −0.04213 | 1.15612 | 0.00017 | OCK Aug | 0.00022 | −0.04539 | 0.97564 | 0.00023 |
| EBK Jul | 0.00021 | 0.02720 | 1.01468 | 0.00020 | EBK Aug | 0.00022 | 0.02864 | 1.01629 | 0.00022 |
| OK Sep | 0.00021 | 0.00201 | 1.06929 | 0.00019 | OK Oct | 0.00025 | −0.03778 | 1.00047 | 0.00024 |
| OCK Sep | 0.00021 | −0.00863 | 1.06453 | 0.00019 | OCK Oct | 0.00023 | 0.00923 | 1.10969 | 0.00020 |
| EBK Sep | 0.00021 | 0.06140 | 1.02250 | 0.00020 | EBK Oct | 0.00023 | 0.06093 | 0.99900 | 0.00022 |
| OK Nov | 0.00034 | −0.00022 | 0.98974 | 0.00033 | OK Dec | 0.00041 | −0.00885 | 0.99847 | 0.00046 |
| OCK Nov | 0.00033 | 0.03827 | 0.96585 | 0.00033 | OCK Dec | 0.00045 | 0.05236 | 0.91954 | 0.00051 |
| EBK Nov | 0.00035 | −0.01738 | 0.97694 | 0.00034 | EBK Dec | 0.00047 | 0.01078 | 0.91282 | 0.00052 |
| OK Year | 0.00021 | 0.00349 | 1.07832 | 0.00019 | |||||
| OCK Year | 0.00022 | 0.00506 | 1.10586 | 0.00019 | |||||
| EBK Year | 0.00021 | −0.03607 | 1.11018 | 0.00021 |
| RMSE | MSE | RMSSE | ASE | RMSE | MSE | RMSSE | ASE | ||
|---|---|---|---|---|---|---|---|---|---|
| SK Jan | 3.61 | −0.03116 | 0.689 | 5.57 | SK Feb | 4.54 | −0.03681 | 0.902 | 5.30 |
| SCK Jan | 3.91 | −0.00706 | 1.008 | 3.88 | SCK Feb | 4.79 | −0.00116 | 0.993 | 4.82 |
| EBK Jan | 3.82 | −0.01709 | 0.992 | 3.89 | EBK Feb | 4.75 | −0.03228 | 0.987 | 4.86 |
| SK Mar | 8.49 | −0.02914 | 0.839 | 10.63 | SK Apr | 11.35 | −0.02982 | 0.854 | 13.83 |
| SCK Mar | 9.06 | −0.00116 | 0.999 | 9.07 | SCK Apr | 11.85 | −0.00483 | 0.985 | 12.02 |
| EBK Mar | 8.94 | −0.03335 | 0.980 | 9.24 | EBK Apr | 11.80 | −0.03532 | 0.978 | 12.20 |
| SK May | 14.62 | −0.0.1844 | 0.837 | 17.74 | SK Jun | 19.79 | −0.03059 | 0.866 | 23.58 |
| SCK May | 15.17 | −0.01990 | 0.992 | 15.27 | SCK Jun | 20.69 | −0.00257 | 0.99494 | 20.77 |
| EBK May | 14.96 | −0.04320 | 0.984 | 15.35 | EBK Jun | 20.47 | −0.03529 | 0.97856 | 21.11 |
| SK Jul | 22.11 | −0.03417 | 0.849 | 27.02 | SK Aug | 19.65 | −0.03368 | 0.871 | 24.15 |
| SCK Jul | 23.40 | −0.00517 | 0.994 | 23.51 | SCK Aug | 20.49 | −0.00556 | 0.991 | 20.67 |
| EBK Jul | 22.98 | −0.03168 | 0.990 | 23.44 | EBK Aug | 20.15 | −0.03273 | 0.986 | 20.65 |
| SK Sep | 11.64 | −0.03121 | 0.862 | 14.46 | SK Oct | 6.98 | −0.06199 | 0.929 | 7.73 |
| SCK Sep | 11.69 | −0.04715 | 1.003 | 11.70 | SCK Oct | 6.87 | −0.03277 | 1.000 | 6.83 |
| EBK Sep | 11.99 | −0.03929 | 0.992 | 12.22 | EBK Oct | 7.12 | −0.04362 | 0.987 | 7.28 |
| SK Nov | 3.95 | −0.04198 | 0.912 | 4.87 | SK Dec | 3.32 | −0.05343 | 0.884 | 4.05 |
| SCK Nov | 3.93 | −0.00271 | 0.998 | 4.02 | SCK Dec | 3.20 | −0.03497 | 0.998 | 3.23 |
| EBK Nov | 4.11 | −0.03503 | 0.987 | 4.23 | EBK Dec | 3.33 | −0.01604 | 0.984 | 3.43 |
| SK Year | 127.47 | −0.03266 | 0.858 | 155.53 | |||||
| SCK Year | 130.30 | −0.04667 | 1.000 | 130.00 | |||||
| EBK Year | 132.41 | −0.03607 | 0.984 | 136.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gentilucci, M.; Bufalini, M.; Materazzi, M.; Barbieri, M.; Aringoli, D.; Farabollini, P.; Pambianchi, G. Calculation of Potential Evapotranspiration and Calibration of the Hargreaves Equation Using Geostatistical Methods over the Last 10 Years in Central Italy. Geosciences 2021, 11, 348. https://doi.org/10.3390/geosciences11080348
Gentilucci M, Bufalini M, Materazzi M, Barbieri M, Aringoli D, Farabollini P, Pambianchi G. Calculation of Potential Evapotranspiration and Calibration of the Hargreaves Equation Using Geostatistical Methods over the Last 10 Years in Central Italy. Geosciences. 2021; 11(8):348. https://doi.org/10.3390/geosciences11080348
Chicago/Turabian StyleGentilucci, Matteo, Margherita Bufalini, Marco Materazzi, Maurizio Barbieri, Domenico Aringoli, Piero Farabollini, and Gilberto Pambianchi. 2021. "Calculation of Potential Evapotranspiration and Calibration of the Hargreaves Equation Using Geostatistical Methods over the Last 10 Years in Central Italy" Geosciences 11, no. 8: 348. https://doi.org/10.3390/geosciences11080348
APA StyleGentilucci, M., Bufalini, M., Materazzi, M., Barbieri, M., Aringoli, D., Farabollini, P., & Pambianchi, G. (2021). Calculation of Potential Evapotranspiration and Calibration of the Hargreaves Equation Using Geostatistical Methods over the Last 10 Years in Central Italy. Geosciences, 11(8), 348. https://doi.org/10.3390/geosciences11080348










