Abstract
Paleomagnetic investigations from sediments in Central and Southern Italy found directional changes of the order of 10 per year during the last geomagnetic field reversal (which took place about 780,000 years ago). These values are orders of magnitudes larger than what is expected from the estimated millennial timescales for geomagnetic field reversals. It is yet unclear whether these extreme changes define the timescale of global dipolar change or whether they indicate a rapid, but spatially localised feature that is not indicative of global variations. Here, we address this issue by calculating the minimum amount of kinetic energy that flows at the top of the core required to instantaneously reproduce these two scenarios. We found that optimised flow structures compatible with the global-scale interpretation of directional change require about one order of magnitude more energy than those that reproduce local change. In particular, we found that the most recently reported directional variations from the Sulmona Basin, in Central Italy, can be reproduced by a core-surface flow with rms values comparable to, or significantly lower than, present-day estimates of about 8 to 22 km/y. Conversely, interpreting the observations as global changes requires rms flow values in excess of 77 km/y, with pointwise maximal velocities of 127 km/y, which we deem improbable. We therefore concluded that the extreme variations reported for the Sulmona Basin were likely caused by a local, transient feature during a longer transition.
1. Introduction
Direct observations of geomagnetic field intensity have been recorded in permanent observatories since the 19th Century [1,2], and directional measurements (i.e., inclination and declination) annotated in maritime logbooks can extend the wealth of direct geomagnetic observations as far back as the 16th Century [3]. Paleomagnetic evidence suggests that a planetary magnetic field generated by internal dynamo processes has existed for the past 3.5–4 billion years [4,5,6,7]. It is clear that the majority of the geomagnetic history of our planet is solely accessible via indirect observations, such as paleointensities and paleodirections from sedimentary or igneous sequences [8,9]. It is therefore far from trivial to establish whether the observed temporal and geographical characteristics of the present geomagnetic field are in line with past behaviour or whether they are somewhat anomalous.
Evidence for paleomagnetic variations that far exceed the average rate of change of currently observed geomagnetic quantities are mounting as new paleomagnetic records are being discovered and analysed. See Figure 1 for a (not complete) compilation of rapid directional variations reported in the literature. A well-known example of such extreme behaviour is the Sheep Creek (California) lava flow records, dated to be 15.58 million years old, from which directional paleomagnetic variations of the order of up to 1 per week [10] have been reported during geomagnetic polarity reversals. These values are astonishing when we consider that the rate of change of the geomagnetic pole latitude during the last 10,000 years, as measured by the CALS10k.2 field model [11], has been at most per year. A number of independent studies [12,13,14,15,16,17,17] have also reported more recent directional paleomagnetic variations of the order of 10 degrees per year, primarily during geomagnetic reversals and excursions (see Figure 1).
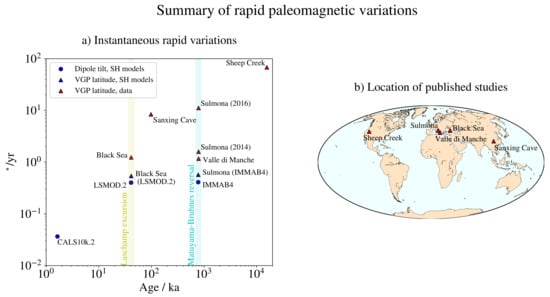
Figure 1.
(a) Summary of rapid paleomagnetic variations from selected, published datasets (red symbols) and geomagnetic, spherical harmonics (SH) models (blue symbols). Circles and triangles indicate, respectively, maximum variations of dipole tilt and VGP latitude (see Section 2 for definitions), in degrees per year, over the timespan covered by the corresponding datasets or field models. Their location on the horizontal axis indicates the epoch at which the maximal variation was obtained (or reported). The sampling locations for the paleomagnetic datasets are reported in (b) and noted in both panels, and more information is available in relevant publications: Black Sea [18,19,20], Sanxing Cave [17], Sulmona Basin [13,14], Valle di Manche [16] and Sheep Creek [10]. The geomagnetic field models IMMAB4 [21], LSMOD.2 [22] and CALS10k.2 [11] have been sampled every 100 y for this calculation.
Analysis of lacustrine sedimentary records from the Sulmona Basin (SUL location), in Central Italy, suggest a subcentennial duration for the Matuyama-Brunhes (M-B) pole reversal [13,14], which took place at an epoch of about 780 ka. Specifically, Reference [13] reported inclination and Virtual Geomagnetic Pole (VGP) latitudinal changes of from which the M-B reversal is estimated to occur in a fraction of a century. Strictly speaking, the lack of measurement of a transitional field indicated that the reversal occurred during an interval equal to or less than the temporal resolution given by the 2 cm thickness of the analysed samples. These considerations led the authors to refine the sampling to 0.3 cm in a subsequent study [14]. Again, no transitional field was recorded, leading the authors to conclude that the M-B reversal occurred over a temporal span of about y, requiring inclination and VGP latitudinal changes of . Whether the temporal resolution of the SUL stratigraphic record is suitable for paleomagnetic studies is debated [23,24]. However, independent reports of similarly rapid paleomagnetic directional variations exist [10,12,15,16,17], compelling us to seek corroborative evidence for the existence of such extreme variations in the Earth’s past. In particular, on-land marine stratigraphic studies in Southern Italy [16] corroborate the observation that the M-B reversal, as observed in the Mediterranean region, had a duration of the order of less than a century. Note that these studies are based on the measurement of locally defined quantities: the geomagnetic inclination and the VGP latitude (which requires knowledge of both inclination and declination). A geomagnetic polarity reversal can unambiguously be defined via global quantities, such as the geomagnetic dipole latitude, whose change in sign defines a global reversal. Although the dipole latitude and the VGP latitude are commensurable quantities, the latter is of a local nature and, depending on location, does not necessarily reflect the global behaviour of the planetary geomagnetic field.
In contrast with the above-mentioned studies, the IMMAB4 geomagnetic field model encompassing the M-B reversal [21] suggests mean VGP latitudinal changes at SUL of about during a 10 millennia-long transitional period and peak values of about (see Table A1 and Figure 1). The comparison of the temporal changes at the Black Sea location between the LSMOD.2 field model (a state-of-the-art model of the Laschamp excursion [22]) and sediment records [18,19,20] is similar to the comparison between the IMMAB4 model and the SUL14 and SUL16 measurements, suggesting a common limitation of the techniques used in geomagnetic field models. Spherical harmonics-based field models suffer from a sparsity and paucity of input observations and make use of spatiotemporal smoothing, which limits their resolution to the largest spatial scales of the geomagnetic field. The IMMAB4 and LSMOD.2 field models have a maximum spherical harmonic degree of and , respectively, in contrast with state-of-the art models of the modern field [25], which are able to capture the spatial variability of the field of internal origin up to . Nevertheless, geomagnetic field models contain a fully consistent description of all geomagnetic quantities (intensity, inclination and declination) globally and continuously in time. Furthermore, it was reported that [26], when sampled every 10 y (as opposed to 100 y, as done in Figure 1), directional rates of change exceeding , though rare, have been found in the LSMOD.2 model, primarily at low latitudes and during epochs of low dipole field intensity, in agreement with numerical studies. In [26], it was argued that rapid variations are caused by the migration of reversed flux patches on the CMB. This justifies the observation of rapid events preferentially at times of low dipole intensity and at low latitudes, where the dipolar field is weaker, since these are the configurations for which more reverse flux patches are observed. This explanation was also corroborated by the present study, since we show that as the nondipolar content of the CMB field is increased, higher rates of change of magnetic inclination, VGP latitude and dipole tilt are instantaneously possible (see Section 4.2 and Section 5 below).
From the calculations reported in Figure 1 and from the results of [26] discussed above, it appears that paleomagnetic field models are capable of reproducing faster variations as the sampling rate is reduced. We investigated the issue and found results similar to [26]. With a sampling rate of 50 y (equal to the temporal spline knot-point spacing of the LSMOD.2 model), we found maximal VGP latitudinal changes at the Black Sea location of the order of , which is about double the value reported in Figure 1. This suggests that faster directional changes can be obtained from the LSMOD.2 model (at least in this case) by increasing the sampling rate of its coefficients. Given the temporal regularisation employed in the creation of the model, it is unclear whether subcentennial variability can be meaningfully captured by the LSMOD.2 model, and we therefore decided to adopt a sampling rate of 100 y in the present study.
Another avenue for investigating rapid variations and, in particular, the dynamics within the core that drive them are numerical simulations of the equations governing the evolution of the geodynamo. This approach offers insights into the link between observed paleomagnetic variations and, for example, the thermal history of the core [27] and the effect of small-scale geomagnetic features, not captured by paleomagnetic observations or field models. Geodynamo simulations are limited by their inability to simulate the Earth’s outer core at planetary parameter values [28,29]. This limitation, which calls for caution when interpreting the result of numerical studies, is even more severe in studies targeting the long-term dynamics involving polarity reversals and geomagnetic excursions, for which multiple geomagnetic diffusion times (of the order of no less than years for the Earth) need to be simulated in order to obtain satisfactory statistical convergence. Nevertheless, upon the careful choice of the input parameters, geodynamo simulations are found to be able to reproduce at least some features of the paleomagnetic observations [30,31]. In particular, most numerical findings [32,33,34] suggest a duration of millennia of polarity reversals, in agreement with paleomagnetic observations and paleomagnetic field models (see for example [21,35,36,37,38,39] and the references therein). Furthermore, recent geodynamo simulations [26] have been able to reproduce VGP latitudinal changes of up to ∼1, compatible with the results from [13], and total directional changes of the order of ∼10. These extreme changes appear to be preferentially recorded at low latitudes and are caused by the movement of reversed flux patches at the core surface. Geodynamo simulations are also capable of core-surface resolution that cannot be captured by observations and geomagnetic field models. Therefore, numerical results can be used to test for the effect of geomagnetic field structures that are not resolved by field models, for both the geological past and the present. For example, the results presented in [26] suggested that geomagnetic features on spatial scales of the order of a few degrees in longitude and latitude, not captured by paleomagnetic observations, are crucial for triggering localised, rapid directional variations. However, as mentioned above, temporal variation calculated using first differences from the LSMOD.2 model sampled every 10 y have similar magnitudes, suggesting that state-of-the-art field models can capture the geomagnetic field features relevant to the generation of rapid directional changes.
A consequence of the lack of high-resolution models of the geomagnetic field during the M-B reversal is that the core-surface velocity field is also largely unknown, barring us from a dynamical and global description of the geomagnetic temporal variations at the surface of the Earth. A derivation of the velocity field is challenging even with today’s high-quality observations, due to the intrinsic nonuniqueness of obtaining core-surface flows from geomagnetic field observations [40]. Satellite-era estimates of the root-mean-squared (rms) velocity at the surface of the core range from 8 to 22 km/y [41,42,43], depending on the epoch, dataset, and methodology, and it has been estimated that undetectable, small-scale flows could contribute to an increase up to a value of 50 km/y [43]. On top of observational limitations, estimating the core-surface flows during the M-B transition is further complicated by a lack of knowledge concerning energy balances in the geodynamo during polarity reversals. For example, some studies suggest that the kinetic energy increases [44,45], while others [46,47] do not show such systematic variations.
An alternative approach to the study of extreme paleomagnetic events was presented in [48], where the authors aimed at reproducing extreme intensity spikes reported for epochs around 1000 BCE in the Middle East [49,50,51,52,53]. The approach of [48] consisted of calculating optimised fluid flows at the top of the core that maximise the rate of change of magnetic intensity at selected archaeological sites. In the context of rapid paleomagnetic variations, for which the global geomagnetic field and the core-surface flows are poorly constrained, the methodology permits a derivation of the maximum rate of change of intensity for a given surface energy budget and for a given configuration of the radial geomagnetic field (which we term the “background field”); equivalently, the method also provides a lower bound to the kinetic energy that is required for flows at the surface of the core to drive a given, observed variation. It was found that optimised flows of rms magnitudes consistent with present-day core flow inversions [43,54] were able to reproduce variations of up to T/y, inconsistent with the earlier estimates of 4–5 T/y [49,50], but in agreement with the revised values of 0.75–1.5 T/y [52].
In the present paper, we expand the methodology presented in [48] and apply it to the study of rapid paleomagnetic directional changes. Our aim was to estimate the configuration and kinetic energy of the core-surface flows that are required by the geomagnetic directional variations reported in [13,14] (SUL14 and SUL16) with focus on both local (inclination and VGP latitude) and global (dipole latitude) geomagnetic quantities. We derived optimised solutions for core-surface flows that can be used to estimate the minimal kinetic energy required to reproduce the SUL observations, both via localised and global flow configurations. In considering local quantities, we favoured the use of inclination, rather than the VGP latitude. The VGP latitude is a function of not only the inclination, but also of the declination and of the site location, and a nontrivial assumption of the geomagnetic field being a geocentric dipole is required in order to efficiently interpret the VGP latitude. Although this assumption has proven useful and robust over long temporal scales (see for example [55], Chapters 2, 14 and 16, and the references therein), its use for the study of rapid variations on short timescales is not, strictly speaking, justified. On the other hand, the interpretation of inclination variations do not require additional assumptions for our purposes. The temporal evolution of the VGP location is commonly calculated and reported in paleomagnetic studies focussing on reversals. We therefore considered the temporal changes of VGP latitude together with the changes in inclination and dipole latitude, for the sake of completeness and comparison with previous work.
The paper is structured as follows: In Section 2, we briefly summarise the optimisation algorithm used to derive core-surface flows that drive the maximal instantaneous changes in dipole tilt, geomagnetic inclination and VGP latitude for a given flow kinetic energy. To build the physical understanding of the algorithm and to highlight the difference in flows that optimise the rate of change of global and local quantities, pedagogical examples are presented in Section 3. Section 4 is devoted to the application of the optimisation algorithm to background magnetic fields provided by the output of a numerical geodynamo simulation in which directional variations of magnitude comparable to SUL16 have been observed [26]. We furthermore examine the sensitivity of the optimal solution to the resolution of the background magnetic field. In Section 5, we apply the optimisation algorithm to rapid directional variations during the M-B reversal, with particular focus on the SUL location: optimal variations are compared with the results from SUL14 and SUL16 in order to estimate the kinetic energy of core-surface flows required to drive the measured variations. A discussion of the results and conclusions are presented in Section 6 and Section 7, respectively.
2. Methodology
The optimisation algorithm described here is analogous to that presented in [48] and has the objective of finding the minimal rms core-surface flow speed required to reproduce the rate of change of a generic geomagnetic quantity . In [48], the quantity of interest was solely the magnetic field intensity at the Earth’s surface , where is the geomagnetic field. Here, we generalise that approach to consider arbitrary functions of and, in general, of the Gauss coefficients (see below). We then specialise the algorithm for the calculation of optimal rates of changes of dipole tilt, inclination and VGP latitude.
Temporal changes in geomagnetic quantities (often referred to as secular variation (SV)) are driven by horizontal fluid flows at the top of the core, which we refer to as the core-mantle boundary (CMB) and that we approximate as a spherical surface with radius km [56]. Note that here, the flow is evaluated not exactly at the CMB, where all components of the velocity field u vanish, but at the top of the free-stream, where only the radial component of the flow vanishes and above which the horizontal components drops to zero across the boundary layer. The thickness of this layer is proportional to , where is the Ekman number, the ratio of viscous dissipation over rotational forces (see [57] and the references therein). Given that in the core, where the notation signifies “order of magnitude”, the distinction between the top of the free-stream and the CMB is negligible for our purposes. All variables, unless otherwise stated, are represented in a spherical coordinate system with the origin at the centre of the Earth and with coordinates where r is the distance from the centre of the Earth, is the colatitude, measured from the direction determined by the Earth’s axis of rotation, and is the longitude, measured in the equatorial plane as the angular distance (positive Eastward) from the Greenwich meridian.
The radial induction equation evaluated at the CMB [58], in its diffusionless form, can be written as:
where is the radial component of B and is the horizontal part of the spatial gradient operator. At a location outside the core, the geomagnetic field is commonly described as an expansion in its Gauss coefficients :
where km is the radius of the Earth, are Schmidt semi-normalised associated Legendre polynomials of degree l and order m and is the highest degree of the expansion. In a more compact notation, useful to simplify the following discussion, the expansion (2) can be written as:
where are the Gauss coefficients and , with and real-valued Schmidt semi-normalised spherical harmonics. Similarly, we express the CMB flow as an expansion over a set of modes :
where k is a shorthand notation for the indexes , with , , the coefficients, measured in km/y of the expansion and the k-th element of a divergence-free basis set consisting of both toroidal and poloidal modes, respectively:
Expansion (4) can then be more explicitly written as:
where and are the real-valued toroidal flow coefficients and and are the real-valued poloidal flow coefficients.
Given a geomagnetic quantity , which is a function of the Gauss components , we seek the minimum rms speed of the CMB flows required to reproduce a given rate of change value of , given a CMB background magnetic field . An easier way of formulating this is to calculate the flows at the CMB, with a given value of , that optimise , which can then be rescaled by the linearity of Equation (1) to achieve the observed value of . Following the same notation as in [48], the rate of change of can be generally expressed (by manipulating Equation (1)) as:
with the vector being a function of the CMB background geomagnetic field , through the coefficients and of the basis set . The exact shape of depends on the functional dependence of on and . Each component represents the contribution to from the flow mode , given the CMB background field . We note that this is a well-defined optimisation problem. For a fixed structure of the flow, Equations (1) and (8) relate and defining an rms flow energy.
In the analysis outlined above, the rms flow speed is:
where is the surface element in spherical coordinates and the integral is evaluated on the surface of the CMB and is a diagonal matrix with elements . The procedure to calculate the coefficients that optimise is formally equivalent to the one reported in [48] and rests on finding a solution to the following maximisation problem:
which allows us to maximise (8) subject to the constraint (expressed via the Lagrange multiplier ) that the rms velocity of the optimal flow be equal to . The solution to (10) gives us the coefficients to the optimal flow :
where:
is found by scaling the coefficients , so that:
Notice that this implies that , and by Equation (8), are both directly proportional to . However, the form of the optimal flows and of the SV they drive are not affected by .
In summary, via the optimisation algorithm described above, we found the coefficients of the CMB horizontal flows that drive the fastest possible instantaneous variations of a given geomagnetic quantity . The algorithm requires one input (the Gauss coefficients of the background magnetic field ) and one parameter (the required rms speed of the horizontal CMB flows ).
The optimisation algorithm permits us to enforce specific flow geometries by, for example, setting some of the elements of q to zero or by imposing specific relations between them. In the remainder of this study, we considered the following flow geometries:
- Unrestricted: no restriction is imposed on the coefficients , and both toroidal and poloidal components are present;
- Poloidal: obtained by setting the toroidal flows to zero, i.e., . A distinguishing feature of purely poloidal flows is the presence of regions of flow downwelling and upwelling, which have been considered as a proxy for enhanced magnetic diffusion [59] and have been connected to the formation of reverse flux patches at the CMB [60], both potentially important features in the interpretation of rapid geomagnetic field variations;
- Toroidal: obtained by setting the poloidal flow to zero, i.e., . A purely toroidal flow allows no upwelling/downwelling since . The physical motivation for a purely toroidal flow derives from the widespread agreement among core flow inversion studies that the toroidal kinetic energy dominates the poloidal kinetic energy at the CMB (see for example [61]). This observation has been considered to confirm the presence of a stratified layer at the top of the outer core [62]. Note however that various studies (e.g., [63,64,65]) suggested that a small poloidal component is necessary to explain the observed SV;
- Columnar: obtained by constraining the flows at the CMB to be the surface expression of columnar flows in the interior of the core and obtained by setting to zero the poloidal coefficients for which is odd and the toroidal coefficients for which is even [66,67]. This representation, encoding equatorial symmetry, is motivated by the evidence for a quasigeostrophic force balance within the outer core [68,69]. The significance of the columnar flows’ approximation to the present study lies in its expected validity over interannual to decadal timescales [68,70]. The columnar flows’ approximation can therefore be considered appropriate for subcentennial field variations, such us the ones presented in SUL14, SUL16, and [16].
The optimisation procedure was implemented numerically by a code written in Fortran 90 that makes use of fftw3 libraries and the Gauss–Legendre quadrature needed by the, respectively, Fourier and Legendre transforms needed to calculate the elements of the vector G. The code is freely available through a GitHub repository (https://github.com/smaffei/OptimalFlow.git).
We note that the elements of the vector G, in Equation (8), can be interpreted as a discrete representation of a Green’s function relating the coefficients of each core flow component to temporal changes of at the Earth’s surface. This differs from the Green functions theory conventionally applied to geomagnetism [71,72], in which changes of are related to the radial magnetic field at the CMB, , and its temporal variations, . The methodology presented here introduces an additional dynamical aspect to the traditional Green function theory, since we relate the radial SV, , to the coefficients of the flows producing it (see Appendix A).
Geomagnetic Directional Quantities
We focussed on the rate of change of geomagnetic dipole tilt , magnetic inclination I and VGP latitude . While is a global quantity, I and are local quantities. A crucial point of the present study is to investigate how rapidly local, as opposed to global, quantities can change in time.
The geomagnetic dipole tilt is defined as:
and represents the colatitude of the geomagnetic pole (the geographical location where the axis of the geomagnetic dipole intercepts the surface of the Earth). Its rate of change is:
The rate of change of the dipole tilt can be used to investigate a global geomagnetic reversal, independent of the observer’s location at the surface of the Earth: a global polarity transition can be defined through the position of the dipole axis with respect to the geographic equator.
The magnetic inclination, or dip angle, is the angle between the Earth’s magnetic field lines and the local horizontal direction at a specific location on the surface of the Earth and is defined as:
where is the local vertical magnetic field component (downward positive) and is the local horizontal magnetic intensity, with and , respectively, the local northward and eastward magnetic field components. The temporal rate of change of the magnetic inclination is then:
where is the magnetic field intensity. The magnetic inclination is a quantity measured in paleomagnetic studies and is influenced by the local details of the background magnetic field.
For completeness, we also considered instantaneous variations of the VGP latitude , calculated from inclination, declination, D, and the coordinates of the observation site [73]:
where:
is the great circle distance between the observation site and the VGP. The rate of change of is:
where:
The quantity is, in a limited way, comparable to in the sense that for a geocentric axial dipole (GAD) field. In reality, since the geomagnetic field contains nondipolar components, the GAD approximation does not hold exactly, and departures between the VGP latitude and the dipole latitude are to be expected. Here, we neglect the VGP longitudinal variations, since a primary purpose of the study was to link the core-surface kinetic energy with the short reversal times found in SUL14 and SUL16. However, the exclusion of the VGP longitude might prevent us from finding the fastest possible directional changes. Similarly, flows that optimise the temporal changes in inclination do not necessarily result in the optimal directional variations, since the declination is not being concurrently optimised.
Rates of change of dipole tilt, inclination and VGP latitude are expressed in terms of spherical harmonic expansions and can be optimised by substituting with, respectively, , I and in Equations (8) and (10) and computing the relevant mathematical form of the elements of G in Equations (11) and (12). Given a background magnetic field, , at the CMB and the rms flow speed value, , this allows us to find the numerical values of the optimal flow coefficients . The optimal variation can then be obtained from Equation (8). Note that, by the relationships (11) and (12), all optimal rates of change are linear functions of the rms velocity . Furthermore, note that the geomagnetic inclination, I, and the VGP latitude, , are inherently local quantities that are observed at the surface of the Earth, while the dipole tilt, , is purely a function of the Gauss coefficients themselves.
3. Pedagogical Examples
In order to validate the numerical code and gain some fundamental understanding of the process presented in Section 2, here we report on the results from the calculation of flows that optimise the rate of change of the dipole tilt and the magnetic inclination I for background magnetic fields (the that, together with the choice of , defines the elements of G in Equation (8)) restricted to dipolar geometries.
3.1. Global vs. Local Quantities
In Figure 2, we show the results of the optimisation algorithm, where in Equation (8) is , and for the unrestricted flow configuration, where is the inclination evaluated at Leeds (U.K.), chosen arbitrarily as the home affiliation of the authors. See Equations (14)–(17) for the definitions of , I and of their temporal variations. For the solution optimising , the background field is solely described by the axial dipole coefficient nT (the value in 2019 from the CHAOS-6-x9 geomagnetic model [25]); for the case, the background is given by a dominant nT component and nT, to numerically remove an ambiguity issue that is illustrated in Appendix B.3. The flow that optimises is clearly global in nature, with no preferred geographical region where flows horizontally converge or diverge. To better quantify the global nature of these flows, we calculated their energy spectra as the total energy contained in each degree l:
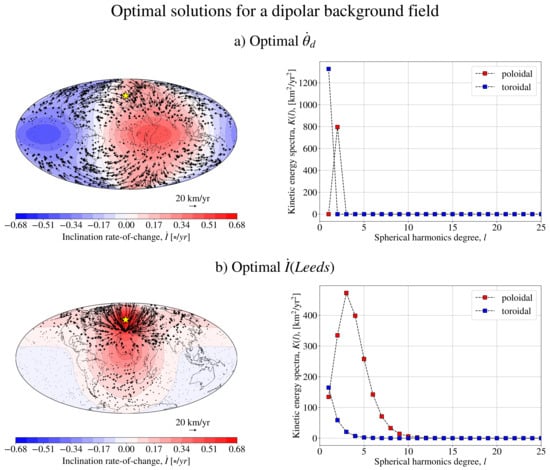
Figure 2.
Flows that optimise the rate of change of (a) and I at Leeds (b) with a background magnetic field given by a dipole. All solutions were calculated for km/y and a background dipole intensity given by 29,410.65 nT. A small ( nT) horizontal component was added for the calculation of . The global plots on the left show the optimal flow and resulting global maps of . The plots on the right show energy spectra for the toroidal and poloidal flow contributions for the same choices of and . In all cases, .
With this definition:
Flow energy spectra are illustrated in the right column of Figure 2. The flow that optimises (Panel a) has only the poloidal and the toroidal modes (as confirmed by the analytical solution (A32)). Conversely, the flow that optimises (Panel b) is distinctively of a local nature, focussed on the geographical vicinity of the optimisation location’s projection on the CMB and characterised by a more continuous spectra that only for converges towards zero.
3.2. Influence of Flow Geometry
In Figure 3 and Figure 4, we show the effect of different flow geometries on the solution that optimises at Leeds. The background field is an axial dipole with = −29,410.65 nT. Inspection of Figure 3 reveals that, since it is the most general, the unrestricted flow is capable of the fastest rate of change for the same value of . Since the poloidal flow components dominate the toroidal contribution (see Figure 2b), the purely poloidal flow drives a rate of change that is not significantly lower than the unrestricted flow solution. As the allowed geometry becomes more restrictive, the flows cannot organise in the most efficient way, and the optimal decreases. The toroidal flows are incapable of upwelling/ downwelling, which are efficient structures for driving localised changes, and they produce a pattern of that is significantly (with respect to the value at the optimisation location) distributed across the globe. In the vicinity of the optimisation location, the optimal columnar flows are morphologically similar to the unrestricted solution, but they are forced to distribute energy in the Southern Hemisphere as well, producing a second region of rapid , which is equal in magnitude, but opposite in sign to (equatorially antisymmetric). Note that this is a consequence of the background field being equatorially antisymmetric: in general, an equatorially symmetric flow does not produce an equatorially antisymmetric inclination rate of change.
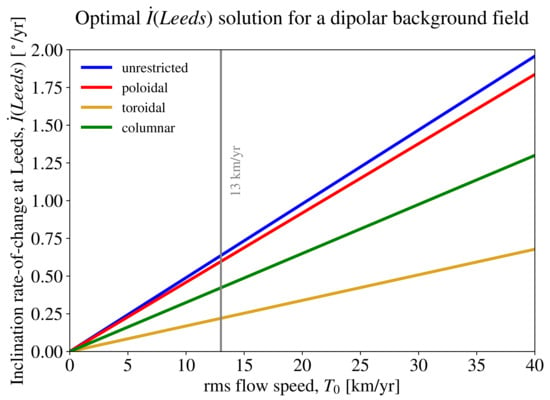
Figure 3.
Rate of change of inclination at Leeds, , for optimal flow calculations with different geometries. The coloured, thick lines were obtained from optimal flow calculations with background fields given by an axial dipole described by 29,410.65 nT, for flows with the indicated geometry and for . The thin, vertical grey line marks the value km/y.
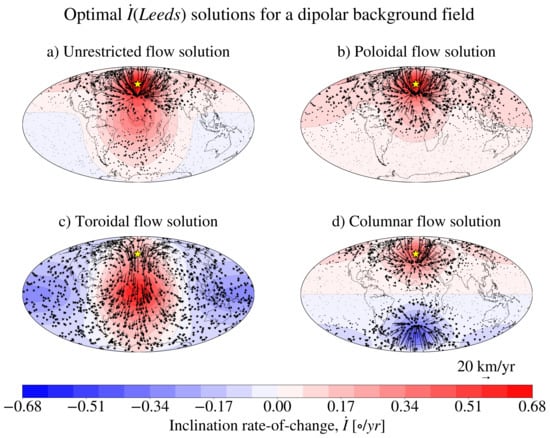
Figure 4.
Optimal flows and global for the solutions optimising at Leeds for km/y and the same axial dipole background magnetic field as for the results reported in Figure 3. Shown are the solutions for unrestricted (a), poloidal (b), toroidal (c) and columnar (d) flow restrictions.
4. Comparison with Geodynamo Results
4.1. Extreme Directional Changes
As previously mentioned, the IMMAB4 model (which is be used as the background for the optimal solutions presented in Section 5) has a resolution of . On the other hand, the time-dependent component of the magnetic field of core origin can be detected up to degree at the Earth’s surface [74]. Smaller scales likely play an important role at the CMB, but their effect on observable scales can presently only be inferred through statistical algorithms [75,76,77,78]. Previous applications of the optimisation algorithm [48] showed that optimal intensity variations do not converge to a stable value even for background magnetic fields with small scales extrapolated up to , independent of the flow geometry.
In this section and the next (Section 4.2), we explore the effect of under-resolved magnetic field scales by applying the optimisation algorithm to a background magnetic field provided by a numerical geodynamo simulation. State-of-the-art numerical simulations are capable of resolving up to [26,69,79,80], well beyond the resolution of both IMMAB4 and modern-day field models, and offer the possibility of studying the effect of small-scale physically generated geomagnetic features, without the need for extrapolation. This exercise also has the purpose of comparing the optimal flows obtained from our calculation with fluid flows that cause extreme events at the modelled Earth’s surface, a task that is not possible for the true Earth’s core. We selected the (where is the magnetic Reynolds number, the ratio of magnetic field diffusion and advection timescales) simulation from [26] as a test case, since it reproduced localised, instantaneous directional changes of y, consistent with the SUL16 values.
For computational convenience, the optimal calculation was restricted to and , still well beyond the resolution used in Section 5 below, with a value of km/y that reproduces the simulation’s value at the optimisation location. The results of the optimal calculation, for unrestricted flow geometry, are shown in Figure 5b. The rate of change of inclination at Earth’s surface (top of Figure 5b) is concentrated around the optimisation location, with much smaller changes at other locations, in analogy with the simulation output. Note that, as shown in Figure 2b and Figure 4 and in agreement with [48], the maximal value of is not reached at the optimisation location: in this case, the maximal value of /y is found to the East of the yellow star.
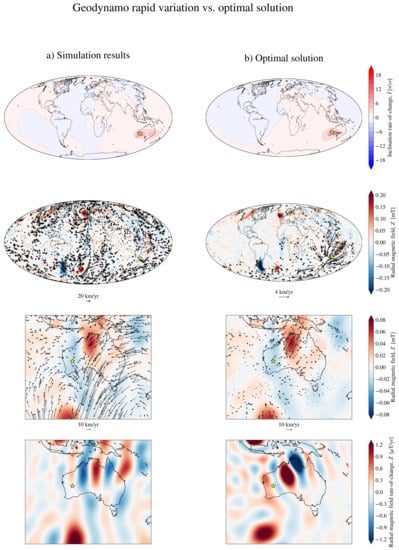
Figure 5.
Numerical (a) and optimal (b) calculations from the geodynamo model from [26]. In all panels, the yellow star marks the location for which is optimised, which is the same location in which extreme directional changes were observed in [26]. Top row: inclination rate of change from the model output and optimal inclination rate of change, both evaluated at the surface of the Earth. Second row: map of the CMB radial magnetic field, (a choice made for ease of comparison with the figures in [26]), at the chosen epoch superimposed with (a) the horizontal flows at the horizontal flow boundary layer (see the main text, Section 4.1) and (b) the optimal flow. Third row: the same as the second row, but zoomed-in on the geographical location around the yellow star. Bottom row: secular variation (SV) from the numerical integration (a) and for the optimal solution (b), in the vicinity of the optimisation location.
We optimised the rate of change of inclination for the same instantaneous magnetic field configuration and location for which maximal directional variations were observed in [26] (see their Figure 1b,e). By calculating the rate of change of inclination at the Earth’s surface via first differences, a maximal dimensional value of /y was obtained from the simulation’s results at a single point (in the location indicated by the yellow star in Figure 5) and instant, with a region of strongly positive variations surrounding it (see the top row of Figure 5a). Note that for the model, we chose here the thermal boundary conditions at the CMB to be geographically homogeneous, and the longitudinal location of the maximal value is not physically significant. The location of velocity and magnetic field features in Figure 5a with respect to the continents is purely for reference.
The second and third rows of Figure 5 illustrate the flows from the simulation (a) and from the optimal calculations (b). Note that the mechanical boundary conditions used in the original simulations are of the no-slip kind: all components of the velocity field vanish at the CMB. The relevant quantity to compare the optimal surface flows is the horizontal flows at the bottom of the velocity boundary layer (see [81] and the references therein). In particular, the horizontal flows illustrated in Figure 5a refer to a depth of 32.9 km below the CMB, where the rms horizontal velocity (calculated over spherical surfaces of different radii) reaches a maximum value before decaying monotonically to zero as the boundary is approached. Note that this depth is consistent with the estimate of the boundary layer thickness based on the Ekman number used in this simulation. At this depth, the dimensional rms value of the horizontal flow is 14.1 km/y, and the radial flows are an order of magnitude weaker. Inspection of the velocity field closer to the CMB confirmed that the morphological features change only marginally with radius, so that we can confidently consider the chosen horizontal flows to be responsible for the SV observed at the boundary of the simulation. The flows from the simulation do not show any localisation in the region around the yellow star, but, locally, they are in agreement with the westward motion of the strong outward field to the east of the yellow star, in agreement with the behaviour observed in [26]. On the other hand, the optimal flows are highly localised around the optimisation location, though the presence of strong, small-scale patches of radial field generates strong flows even at large distances from the optimisation location (see for example the blue patch and strong flows localised below South America). The kinetic energy in the two cases is also different, with the simulated flow rms intensity exceeding by one order of magnitude the required by the optimal flows to reproduce the same value at the optimisation location. The differences in flow morphology and speed magnitude can be explained by noting that the directional variations identified in the run might not be the fastest allowed by the numerical simulation. In this case, a longer simulation run might reveal free-stream flow configurations that are closer to optimal and that might drive considerably faster local directional changes. Alternatively, it is possible that the optimal flow configuration is not realisable due to dynamical constraints that are taken into account in the geodynamo model (for example, via the choice of boundary conditions), but not in the optimisation algorithm. Regardless, there is no guarantee that the directional variations reported in [26] are the fastest attainable by the numerical model.
Locally, the differences in CMB flow morphology and intensity between the simulation output and the optimal calculation are reduced, in particular in correspondence with the patch of positive Z to the northeast of the projection of the optimisation location (see the third row of Figure 5). As a consequence of these similarities, the locally produced SV in the simulation and by optimal flows presents significant analogies. The bottom row of Figure 5 shows the radial SV as obtained via first differences from the simulation results (a) and from the optimal flows (b) via Equation (1). In both cases, the radial SV has a banded structure in the region below the yellow star, although the quantitative details differ. Furthermore, in agreement with the simulation results, the optimal flows produce the directional variations observed at the optimisation location by advecting a patch of strong outward field (the red patch below central Australia) westward.
The results of this section suggest that, when reproducing local extreme directional changes, the optimal flows and resulting SV can be in agreement with the local geomagnetic structure. However, nonlocal features generally will not be reproduced by the optimisation algorithm. We found the required by the optimal solution to be a lower limit for the true rms velocity below the CMB. Optimal calculations performed with different flow geometries (not shown) produce, for the same value of , similar results for (top row of Figure 5b) and the radial SV (bottom row of Figure 5b), with differences in the flow configuration and magnitude of at the Earth’s surface, which are akin to those shown in Figure 4, which suggests that the reproduction of extreme directional variations does not provide enough information to deduce the geometry of the flow causing it.
4.2. Influence of Truncation
We now quantify the effect of the velocity and background magnetic field resolution on the optimal solution. We performed two sets of calculations: in the first, we kept the geomagnetic field resolution fixed at (the maximum resolution adopted in the previous section) and varied the allowed optimal flow resolution, up to ; in the second, we kept fixed and varied the resolution of the background magnetic field from to . We remind the reader that far exceeds the resolution of state-of-the-art paleomagnetic field models. As illustrated in Figure 6, this calculation was performed for both unrestricted and columnar flow geometries, giving, respectively, the upper and lower bound for the optimal calculations for the same value of (as in Figure 3). Figure 6a shows that the choice of guarantees converged results for the chosen background magnetic field, in line with the observation from [48] that is enough to achieve convergence, for a fixed value of . Figure 6b suggests that convergence in is harder to achieve: though the optimal appears to be converging to a stationary value for , values calculated at or at the resolution of other paleo- and archeo-magnetic models (for example, for the LSMOD field models [22,82]) are significantly smaller than the value. Furthermore, the sensitivity to the background field resolution is generally nonmonotonic, as indicated by the local maxima at and . The same calculation, performed with background fields given by various geomagnetic field models with different resolutions (not shown), suggests that the location of these local maxima is sensitive to the instantaneous magnetic field configuration and that their location in Figure 6b should be regarded as coincidental. The same exercise, replicated for optimal calculations and with background fields from different models and simulations, results in behaviours qualitatively similar to Figure 6.
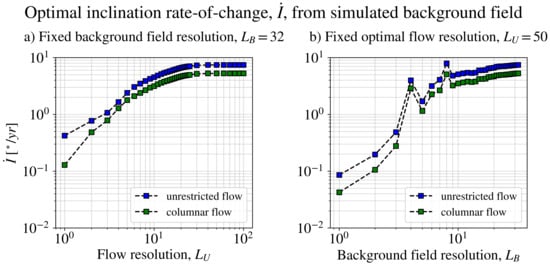
Figure 6.
Convergence study for the optimal calculation of the inclination rate of change with the geodynamo simulation from [26]. The panels show the optimal inclination variation at the location marked by the yellow star in Figure 5, varying the spatial resolution of the fluid flows (a) and the spatial resolution of the background magnetic field (b). In all cases, the rms flow speed is fixed at km/y, the same value used for the results presented in Figure 5, for and .
We can conclude that the optimal calculations based on the IMMAB4 model and presented in the following Section 5 likely underestimate the “true” optimal solution. In turn, this means that the required by the optimal solution to reproduce a given observation is an overestimate of the value required by a fully converged optimal solution. However, our numerical experiments also suggest that for , the optimal solutions are all within the same order of magnitude, so that, considering all other uncertainties regarding the background magnetic field configuration, dating and CMB kinetic energy involved in the optimal calculations, the solutions presented in Section 5 below still provide a valid order of magnitude estimate of the fully converged optima.
5. Paleomagnetic Calculations
We now calculate optimal, instantaneous solutions across the M-B transition, with the IMMAB4 model as the background. We first calculated optimal flows that instantaneously optimise the rate of change of the dipole tilt, , the geomagnetic inclination, , and the VPG latitude, , at the SUL location (42.1512 N, 13.8229 E) during the whole temporal interval covered by the IMMAB4 model (from 794.0 ka to 764.1 ka), sampled every 100 years. For this calculation, we set km/y (for illustrative purposes and in line with [48]), (the full resolution of the IMMAB4 model) and (which guarantees converged results; see Section 4.2). The results, for unrestricted flow configurations, are shown in Figure 7 and Figure 8. The solutions for different flow configurations are shown in Appendix C. Figure 7 shows that the optimal solutions produce the fastest changes during epochs of weak dipole intensity, when the global field is in a multipolar configuration. Specifically, the fastest dipole tilt change is obtained at 774.1 ka for unrestricted, toroidal and columnar flow configurations, while for the poloidal flow, the maximum is obtained at 774.5 ka; the maximum rate of change of inclination at SUL is obtained at 774.4 ka independently of the flow geometry; the optimal VGP latitude rate of change is maximised at 777 ka, for all flow geometries (see Figure A2 and Table A1). To clarify, the optimal solutions represented by the coloured curves in Figure 7 are not estimates of the indicated quantities from the IMMAB4 model. Notice that the maximal value of is higher than the maximal value of (8.57/y and 1.87/y, respectively, and indicated by the arrows in Figure 7). This illustrates how local flows are capable of driving faster changes than global ones, for the same value of .
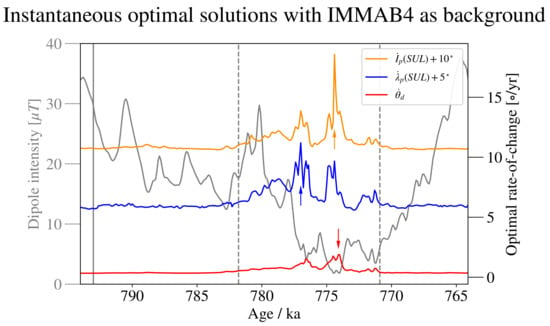
Figure 7.
Time series of instantaneous optimal , and as calculated with the IMMAB4 field model as the background and for km/y. For the ease of inspection, the coloured curves were offset by the indicated amount, and the epochs of maximum optimal variations are indicated by arrows. The grey curve indicates the intensity of the dipole field as predicted by the IMMAB4 model. The vertical dashed lines represent the boundaries of the reversal period according to [21], and the vertical continuous line indicates the epoch to which the plots on the left column of Figure 8 refer.
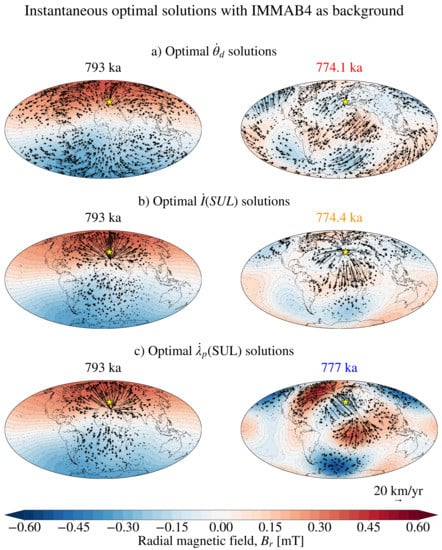
Figure 8.
Optimal flows and background magnetic field that maximise the instantaneous (a), (SUL) (b) and (c) at the indicated epochs for km/y. These flows produce instantaneous realisations of the optimal solutions shown in Figure 7. The yellow star in the right column indicates the SUL location. The left panels refers to the epoch indicated by a continuous vertical line in Figure 7, for which the background field is dominantly dipolar. The right panels show the solutions calculated at the epochs for which the optimised quantities reach their respective maximal values; the indicated epoch is colour coded in the same way as the arrows in Figure 7 to aid the comparison.
Figure 8 shows the flows that optimise (a) , (b) and (c) at 793 ka (indicated by the vertical continuous line in Figure 7 and referring to an arbitrary dipole-dominated epoch) and at epochs of maximum optimal variation for each case (marked by the arrows in Figure 7). As expected, the flows displayed on the left panels of Figure 8 show the same qualitative characteristics as those in Section 3.2, namely the global circulation visible in the flows optimising and the localised nature of the flows optimising . Note that Figure 2b shows that the flow optimising is dominated by a downwelling, whereas the corresponding flow in Figure 8b is dominated by an upwelling, caused by the opposite polarity of the axial dipole field (the epoch 793 ka is still in the Matuyama polarity). The flows in the right panels of Figure 8, calculated for a multipolar background field, display more spatial complexity than the pedagogical examples of Section 3.2.
In line with what was discussed in Section 2 and Section 3, the optimal values shown in Figure 7 are linear in . This is illustrated in Figure 9, where we show the optimal rates of change for , and as a function of the rms velocity , as well as produced by the flow optimising , calculated at the epochs for which the optimal solution is maximal (see Figure 7 and Figure A2). The optimal solutions are compared to the values from SUL14 and SUL16 and to the highest, instantaneous rates of change predicted by the IMMAB4 model, also indicated in Figure 9 (see Table A1 for numerical values). Note that in Panel (d) of Figure 9, the optimal are compared to the SUL14 and SUL16 values of . The intersection of the coloured, continuous lines with the horizontal dashed lines provides the value required by optimal flows to reproduce the paleomagnetic observations SUL14 and SUL16. Figure 9 compares the locally observed SUL14 and SUL16 rapid changes with the variations produced by local and global optimal flows.
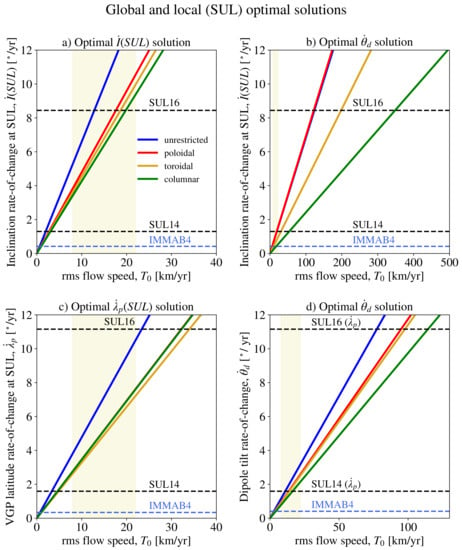
Figure 9.
Maximum optimal values of (a), calculated from the flow producing the maximum optimal (b), and maximum optimal values of (c) and (d), for flow restrictions indicated in the legend. In (b), the red and blue lines are partially superimposed, and in (c), the red and green lines are visually superimposed. The dashed, black lines labelled “SUL14” and “SUL16” report values from, respectively, [13,14] during the M-B transition. The black horizontal lines indicated by “SUL14()” and “SUL16()” in (d) are the same as in (c). The light blue, dashed line labelled “IMMAB4” indicates the maximum rates of change from the IMMAB4 model. The shaded area indicates estimates of CMB flow speed rms values between 1840 and the present day (see [43] and the references therein). Note that the horizontal scale is not the same for all panels.
Since the flows represented in Figure 9 are optimal, we can interpret the values required to reproduce SUL14 and SUL16 as a lower bound for the rms flow intensity on the CMB during the M-B reversal (not accounting for the resolution-dependent corrections indicated in Section 4.2). Panel (a) suggests, for example, that if the SUL16 observation of is generated by localised flows, then values at least as large as the present day are required. For this scenario, pointwise maximal velocities of 54 km/y are observed in the unrestricted flow configuration that reproduces the SUL16 observations. Panel (c) shows similar results, with values required to reproduce SUL16 values of that are about double the values required by . In this case, the unrestricted flow configuration that reproduces SUL16 observations requires pointwise maximal velocities of 125 km/y. Panels (b) and (d) suggest that if the SUL16 observation is associated with flows that optimise , considerably higher (possibly by an order of magnitude) values of are needed: the SUL16 observed value requires an rms intensity of at least 77 km/y, with pointwise maximal velocities of 127 km/y for the unrestricted configuration. The SUL16 value requires, for flows driving a global directional change, rms values of no less than 120 km/y, with pointwise maxima of 241 km/y achieved in the unrestricted configuration; the SUL14 observations, however, could be produced by flows with kinetic energies in line with present-day values.
Figure 9 suggests that flows driving a global polarity reversal are unlikely to be solely responsible for rapid changes of the kind reported in SUL16. However, flows that optimise local variations can reproduce SUL16 observations with values of that are in line with present-day estimates. On the other hand, the (locally observed) SUL14 values can be reproduced by flows driving global directional changes with values of analogous to present-day estimates. Though these flows are optimised, they suggest that SUL14-like local variations can be driven concurrently with a polarity reversal, with CMB flows having kinetic energy that are in line with the energy budget considerations derived from geodynamo simulations of polarity reversals [44,45].
We now focus on the global inclination changes driven by flows that optimise . Figure 10 shows maps of the inclination rate of change driven by flows of different geometries that optimise with the values of required to reproduce the SUL16 values (see Figure 9a). Figure 10 shows that the SV driven by optimal flows with different geometries is morphologically similar. Most prominently, in all cases, the highest values of inclination variation are produced to the northwest of the SUL location (the yellow star). A wider area of high is furthermore located in the European region, which appears to corroborate the findings of anomalously high directional paleomagnetic changes in the Italian peninsula during the M-B reversal [13,14,16]. Other qualitative features that can be reproduced by one or more flow configurations are a sharp dipolar feature located to the south of the Gulf of California (in particular, in the unrestricted and poloidal flows solutions), an extensive region of negative values over Antarctica, mostly positive values of over the entire Eurasian continent, an elongated region of positive values over South America and the South Atlantic ocean (see the unrestricted and poloidal flows solutions) and a patch of positive values over southern African (see the toroidal and columnar flow solutions).
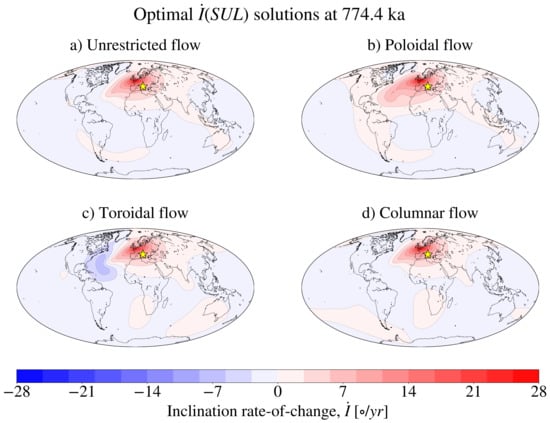
Figure 10.
Rate of change of inclination, driven by flows (the geometry of which is indicated in the figure) that optimise at 774.4 ka for a value of that is required to reproduce the SUL16 value of /y at the SUL location (marked by the yellow star).
Figure 11 shows the inclination rate of change calculated via first differences between the epochs 774.4 ka and 774.5 ka from the IMMAB4 model. The most prominent feature of the field predicted by the IMMAB4 model is the positive maxima localised in the North Atlantic Ocean, to the west of the Iberian peninsula, accompanied by positive values of on the majority of the Eurasian continent. Apart from the magnitude of these variations, the IMMAB4 prediction is morphologically similar to the result from optimal flow calculations (see Figure 10). Other qualitative features predicted by the IMMAB4 model are present in the optimal solution, depending on the flow geometry, namely a sharp dipolar feature located to the south of the Gulf of California (particularly visible in the unrestricted and poloidal flows solutions), an extensive region of negative values over Antarctica, an elongated region of positive values over South America and the South Atlantic ocean (see the unrestricted and poloidal flows solutions) and a patch of positive values over the southern African region (see the toroidal and columnar flow solutions). These similarities suggest that the CMB flows during the M-B reversals (and in particular at the 774.5 ka epoch, according to the IMMAB4 model) could have been morphologically close to an optimal configuration. It is however difficult to assess which flow restriction produced inclination changes that are closest to the IMMAB4 model, since all configurations give rise to a strong patch of positive over northwestern Europe, the main feature of both the optimal solution and the IMMAB4 model at this epoch.
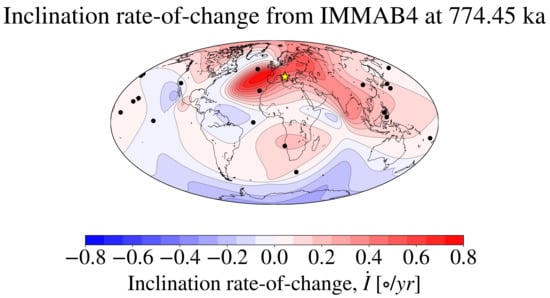
Figure 11.
Inclination rate of change calculated via first differences from the realisations of the IMMAB4 at 774.4 and 774.5 ka. The black dots indicate the location of the paleomagnetic measurements used to constrain the IMMAB4 model (see Leonhardt and Fabian [21] for more details). The yellow star marks the SUL location, to facilitate the comparison with Figure 10.
The presence, in the IMMAB4 model, of an extended area of positive inclination change in Europe appears to corroborate the findings of anomalously high directional paleomagnetic changes in the Italian peninsula during the M-B reversal [13,14,16]. The origin of this anomaly in the model is attributable to a localised flip in inclination (i.e., a local reversal) between 774.5 ka and 774.3 ka. The timing of this sharp inclination transition is very close to that of the most rapid, optimal variation of inclination at SUL (see Figure 7). Note, however, that the magnitude of the inclination change at SUL from the IMMAB4 model (see Figure 11) is about an order of magnitude lower than the SUL observations (see Table A1). This is due to the fact that the IMMAB4 model is not required to reproduce the levels of variation reported by SUL14 and SUL16. It is also important to note that the North Atlantic maxima in the IMMAB4 model shown in Figure 11 is not well constrained by the observations employed to construct the field model (shown by the black dots in Figure 11). Geographically, the paleomagnetic records closest to the European region that are present in the dataset used to create the IMMAB4 model are located in the North Atlantic region [83,84,85]. The duration of the M-B reversal as recorded from these samples was analysed in [21,86], and all predict a duration time greater than ∼4000 years, in line with the observations of [86,87]. Further analysis is therefore required to ascertain which particular records contain the information of the European rapid inclination event shown in Figure 11 and the effect of the inclusion of the Italian data in the modelling process.
6. Discussion
We estimated the magnitude of the core-surface flows during the last polarity reversal. Well established methods of core flow inversion [54] are not applicable in this context due to the lack of spatiotemporal data coverage and resolution in the pre-observatory era. The optimal flow calculations presented in this paper allow a lower bound to be placed on the rms flow speeds required by the SUL14 and SUL16 observations. How the kinetic energy at the CMB during the M-B reversal compares to today’s estimates is an open question; however, geodynamo simulations suggest that during times of low magnetic energy (such as during reversals), the kinetic energy in the core either increases (see for example Figure 5 from [44]) or does not statistically change [46,47]. On the other hand, multiple studies (see [9] and the references therein) suggest that present-day magnetic field intensity is higher than or approximately equal to its maximum value over the past two billion years. Taken together, the evidence suggests that the current rms flow speed value at the CMB represents a low to average value over the same timespan. Therefore, present-day values (which range from 8 to 22 km/y [43]) can be taken as a representative to low estimate for the actual values during the M-B reversal.
The optimal calculations performed in an attempt to reproduce extreme variations found in geodynamo simulations (performed in Section 4.2) warrant some caution in the interpretation of the results presented in Section 5 and in the conclusions we can draw from them. We showed that the inclusion of the CMB magnetic structure up to order results in lower values of , possibly by an order of magnitude, required to reproduce the same rapid directional changes. If we combine this consideration with the results reported in Figure 9, high values of and optimal flow configurations may not be required to locally reproduce neither SUL14 nor SUL16 observations. On the other hand, to reproduce SUL16 values with flows that cause a global directional change, even considering an order of magnitude correction due to resolution, optimised flows require values that are at least similar to present-day estimates. Although there is not enough evidence to rule out a scenario in which the observed SUL16 variations are caused by flows that drive an optimised global change, we deem it improbable, since the CMB flows are unlikely to be in a configuration that optimises . Only the enhanced resolution of the large-scale field during the M-B transition will resolve this issue.
Inspection of Figure 10 shows that, were the flows required to reproduce SUL16 observations close to optimal, they would drive global inclination changes that are morphologically similar, regardless of the flow geometry. Further analysis and future paleomagnetic data collection should focus on the global distribution of during the M-B reversal, with particular attention to the identification of possible high regional values in the European region. Potential sites include the Za Hájovnou cave, in the Czech Republic [88,89], and the Gran Dolina archeological site, in Spain [90,91,92]. However additional work is required to consider the dating uncertainties of the available paleomagnetic measurements for these locations in relation to SUL14 and SUL16, for example within the context of an updated version of the IMMAB4 field model. Confirming the existence of this and other features displayed in Figure 10 via paleomagnetic observations would suggest that the CMB flows were close to an optimal configuration during the M-B reversal, and at least instantaneously, the lower bounds on that can be derived from Figure 9 would be closer to actual values in the past.
In the present study, we made use of the IMMAB4 model as a spatiotemporal representation of the M-B geomagnetic field reversal. Although, to our knowledge, this is currently the most recent field model that predicts the evolution of nondipolar geomagnetic coefficients up to during the reversal, it has been pointed out [93] that the model might not be a reliable representation of the M-B reversal due to the paucity and uneven distribution of the paleomagnetic records used in its generation. In particular, the paleomagnetic records are distributed unevenly in longitude, and the large majority of them were collected in the Northern Hemisphere. It will be desirable, in the future, to produce an updated version of this model, including the latest paleomagnetic record for the M-B reversal (including those from the Italian peninsula discussed in the present paper [14,16]) and that uses different modelling techniques and temporal uncertainty treatments [22,94]. Though it is unlikely that the resolution beyond degree will improve, this would lead to a better representation of the background magnetic field considered here and better estimates of the optimal flows and corresponding temporal variations at the surface of the Earth.
7. Conclusions
In summary, we derived estimates for the minimal rms flow speed at the surface of the core that are in agreement with extremely rapid directional changes recorded in the Italian peninsula during the last geomagnetic field reversal.
In particular, we showed that instantaneous directional variations reported in paleomagnetic measurement studies from depositional sequences in the Sulmona Basin [13,14] can be reproduced by localised fluid flows with rms magnitudes that are either consistent with present-day estimates (between 8 and 22 km/y [43]) or significantly lower. These results suggest that it is at least physically possible that the values reported in both [13] and [14] could be indicative of secular variation produced by localised fluid flows on top of the Earth’s outer core, similar to the flows in Figure 8b,c. We also showed that flows driving global directional change (similar to the ones depicted in Figure 8a) with an rms magnitude consistent with present-day estimates can account for the SUL14 observations reported in [13], but not for the revised SUL16 values [14], for which optimised flows with rms values in excess of 77 km/y are required, which is much higher than present-day estimates. Finally, we could not exclude that the observations of [13] can be reproduced by flows capable of global directional change with kinetic energy values available during the M-B reversal. However, given that the subcentennial reversal times that can be derived from these observations are not corroborated by the majority of independent studies (see for example [21,37,38,39] and the references therein), this scenario seems at odds with our current understanding of geomagnetic field reversals’ phenomenology. Taken together, these considerations suggest that it is unlikely that global directional changes are responsible for the rapid directional changes observed in the Sulmona Basin. Rapid variations reported in both [13,14] are therefore likely to be a purely local phenomenon, driven by localised CMB flows that possibly produced rapid variations over the whole European continent.
Author Contributions
Conceptualization, S.M., P.W.L., J.E.M. and S.G.; methodology, S.M., P.W.L., J.E.M. and S.G.; software, S.M., P.W.L., S.G. and C.J.D.; validation, S.M. and S.G.; formal analysis, S.M., J.E.M., S.G. and C.J.D.; investigation, S.M. and S.G.; resources, S.M., P.W.L., J.E.M., S.G. and C.J.D.; data curation, S.M., J.E.M., S.G. and C.J.D.; writing—original draft preparation, S.M.; writing—review and editing, S.M., P.W.L., J.E.M., S.G. and C.J.D.; visualization, S.M.; supervision, S.M. and P.W.L.; project administration, S.M., P.W.L. and J.E.M.; funding acquisition, P.W.L. and J.E.M. All authors read and agreed to the published version of the manuscript.
Funding
This research was funded by NERC Grant Number NE/P016758/1 (S.M., P.W.L and J.E.M.) and NERC Independent Research Fellowship Grant Number NE/V009052/1 (C.J.D.). S.G. acknowledges funding from the Natural Environment Research Council SPHERES Doctoral Training Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are contained within the article and can be reproduced by means of the code freely available at https://github.com/smaffei/OptimalFlow.git. Paleomagnetic data and geomagnetic field coefficients used to support the present study are available in the articles and datasets referenced in the present paper.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; nor in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CMB | core-mantle boundary |
| M-B | Matuyama-Brunhes |
| SUL | Sulmona |
| SV | secular variation |
Appendix A. Comparison with the Green Functions Formalism
It is worth remarking that the optimisation procedure described in Section 2 is intimately related to a Green’s function analysis of the geomagnetic field, in which the sensitivity of the components of the geomagnetic field on Earth’s surface can be written in terms of the integral of the radial field on the CMB weighted by an averaging kernel [71,72]:
where is the magnetic field at the Earth’s surface, is the radial magnetic field at the CMB, and are the position vectors, respectively, at the Earth’s surface and on the CMB and indicates that the kernels relate each component of with . Since the kernels are not a function of time, a relation formally equivalent to (A1) relates the temporal changes at the Earth’s surface with with , so that it is possible to express temporal changes of any geomagnetic quantity at the Earth’s surface as follows:
Specialisation of Equation (A2) to the cases of can, for example, be obtained by the application of the definition (17), following a procedure similar to that outlined in [72], which shows that is in general a function of the magnetic field at the CMB.
Optimal changes of at the Earth’s surface are driven by changes to the CMB defined by the geometry of the kernel . In analogy with the methodology outlined in Section 2, this can be formalised by seeking maximal values of subject to a given value for the squared integral of on the CMB; we then seek to maximise the following cost function:
where is a Lagrange multiplier. Note that the cost function J is analogous to the cost function maximised in Equation (10). Taking the functional derivative of J with respect to shows that the maximum value occurs when:
which defines the optimal radial SV , proportional to the kernel :
which is analogous to Equation (11) and where the value of is set by the constraint that the integrated squared value of be equal to .
As the kernels are the Green’s functions relating the radial SV, , to temporal variations of , the components of in Equation (8) relate the coefficient of the flow component to . Comparing Equations (A2) with (8) and making use of Equations (1) and (4) allows relating the components of with :
where:
is the radial SV produced by the flow component acting on the magnetic field. The analysis we described in this paper is therefore a generalisation of the Green’s function approach because of an additional dynamical step, obtained by relating changes of the field on the Earth’s surface not only to the SV on the CMB, but to the flow that drives it. This is made explicit by the relation (A6). The SV driven by our optimal flows will differ however from the geomagnetic Green’s function kernels not only because we adopted a constraint in terms of flow energy rather than integrated SV, but also because flow-created SV is only a subset of all possible SV structures on the CMB.
Appendix B. Analytical Calculation of Simple Optimal Solutions
Here, we present analytical solutions for optimal , and with an axial dipolar background field. These solutions have been used to analytically validate some of the results presented in Section 3.
Appendix B.1. Optimisation of
For an initial geomagnetic field described by an axial dipole, where the only Gauss coefficients different from zero is , then:
where a is the radius of the Earth. We now optimise the rate of change (growth or decay rate) of itself. Diffusion-free evolution equations for the coefficients can be obtained by multiplying Equation (1) by , integrating over the CMB area and making use of the orthogonality of :
where and are Kronecker delta functions and is the L-norm of . By setting , Equation (8) then becomes:
where and c is the radius of the outer core, not to be confused with the lower score symbol in , which signifies cosine. Following the selection rules of [95], the only flow for which has a nonzero contribution to the integral in Equation (A10) is the poloidal flow:
Thus, the optimal flow is composed of only this one mode:
The requirement (13) sets the value of the coefficient to be:
a result confirmed by numerical calculations. The optimal rate of change of for this solution is:
With nT, the value in 2019 from the CHAOS-6-x9 geomagnetic model [25] and km y, this flow drives an optimal rate of change of nT y (note that ). For the positive choice of sign, the flow and resulting change in inclination rate of change is shown in Figure A1a.
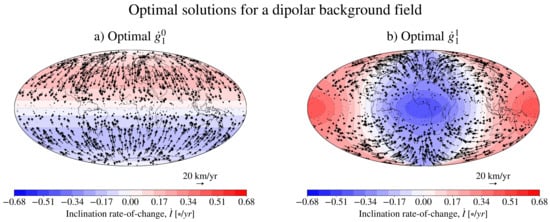
Figure A1.
Flows that optimise the rate of change of (a) and (b) with a background magnetic field given by an axial dipole with nT and km/y. The arrows indicate the direction and intensity of the flow, and the colour scale indicates the resulting rate of change in inclination.
Appendix B.2. Optimisation of
It is useful to repeat the calculation of Appendix B.1 with the goal of optimising instead of . Together with a similar derivation for the optimal , the following results were used to derive the flow (A32) that optimises the rate of change of (see below). The procedure to optimise is similar to that illustrated in Appendix B.1, with instead, the definition that now and Equation (8) becomes:
In this case, two flow modes have a nonzero contribution to :
and the optimal flow is:
where the coefficients and are determined by the optimisation process. The only nonzero elements of G are therefore the ones related to these coefficients:
The Lagrangian multiplier , according to Equation (12), is:
Appendix B.3. Optimisation of
The derivation of an analytical solution for optimal is complicated by the fact that the right-hand side of Equation (15) is singular for . We can see this by rewriting Equation (15) as:
The axial dipole case can be obtained in the limit of . The solution is however undetermined unless the direction of the limit (i.e., assuming positive or negative and ) is specified. If we consider the present field, for example, and , where is the sign function, and the problem is well posed. To obtain well-defined solutions, we then set , with , so that the background field is still close to an axial dipole, but the singularity in Equation (15) is now removed. We then seek a solution that optimises in the same fashion as Equation (A14). Formula (A26) becomes:
Neglecting terms of order , we follow the procedure outlined above and use the selection rules to identify the flow modes that can drive a temporal change of and , which are:
The optimal flow is then:
The determination of the coefficients follows a similar procedure as the one highlighted in Appendix B.2 and gives:
as confirmed by numerical calculations. The optimal rate of change of dipole tilt is:
Notice that being defined by the relative magnitude of the dipole components, the final result does not depend on the value of . With km y, y. The numerical calculation performed with nT reveals excellent agreement with the analytical calculations.
Appendix C. Maximal Variations for Different Flow Geometries
Figure A2a shows time series of the instantaneous optimal rate of change of dipole tilt, , inclination at SUL and VGP latitude at SUL, and these are analogous to the results shown in Figure 7, though illustrating solutions for all the flow geometries considered in this study (unrestricted, poloidal, toroidal and columnar). These solutions were calculated with km/y and using the IMMAB4 model [21] as the background. Illustrated in Figure A2 also are the optimal flows and background magnetic field at the epochs marked by the continuous, vertical line in the top row plots. These epochs indicate the maxima of the unrestricted flow solutions. Different flow geometries can drive a maximal change at different temporal epochs. In the present study, this only happens for the poloidal flow solution for , and the flows and the background field are only marginally different than those reported in Figure A2.
Numerical values for the maximal rates of change from the time series illustrated in Figure A2a are reported in Table A1, together with the SUL14 and SUL16 results and IMMAB4 estimates, for comparison. The SUL14 and SUL16 values have been calculated via first differences across the polarity reversal identified in [13,14], which takes place between two contiguous data points. For the IMMAB4-related values, we calculated both averaged values across the M-B transition (“IMMAB4, M-B avg”) and instantaneous maximum values, using first difference between 100 y-spaced values (“IMMAB4, M-B max”), over the whole model timespan. The “IMMAB4, M-B avg” values were calculated via first differences across the M-B reversal, the beginning and end of which was visually identified in the time series of , and , with the last point of stable polarity in the Matuyama chron and the first point of stable polarity in the Brunhes chron. The optimal values reported in Table A1, appropriately scaled for different values, were used to calculate the results reported in Figure 9.
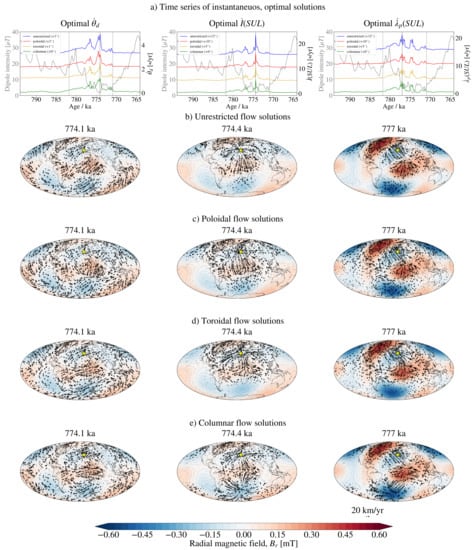
Figure A2.
Instantaneous optimal solutions calculated with the IMMAB4 field model as the background and for = 13 km/y. (a) Time series of the instantaneous optimal rate of change of dipole tilt, inclination at Sulmona and VGP latitude. The coloured curves (indicating solutions for different flow geometries) are offset by the value indicated in the figure for the ease of inspection. The grey curves indicate the intensity of the dipole field as predicted by the IMMAB4 model, for comparison, and the vertical dashed lines represent the boundaries of the reversal period. The vertical continuous lines indicate the instant for which the maximal variation is produced by the unrestricted flow solution (as reported in Figure 7). These epochs are, respectively, 774.1 ka (left panels), 774.4 ka (middle panels) and 777.0 ka (right panels). Maps of the radial background field and optimal flows are shown for these epochs and for unrestricted (b), poloidal (c), toroidal (d) and columnar (e) flows.

Table A1.
Numerical values of , and for optimal flow calculations (indicated by the different flow geometries) with km/y, from the measurements at Sulmona (SUL14 and SUL16) and from the IMMAB4 geomagnetic field model. The optimal values reported here are the maxima from the time series illustrated in Figure A2a. Values indicated with “IMMAB4, M-B avg” values were obtained by calculating differences between points at the beginning and at the end the M-B transition. Values indicated with “IMMAB4, max” refer to the maximum rates of change calculated via first differences. See the main text (Section 1 and Section 5) for details.
Table A1.
Numerical values of , and for optimal flow calculations (indicated by the different flow geometries) with km/y, from the measurements at Sulmona (SUL14 and SUL16) and from the IMMAB4 geomagnetic field model. The optimal values reported here are the maxima from the time series illustrated in Figure A2a. Values indicated with “IMMAB4, M-B avg” values were obtained by calculating differences between points at the beginning and at the end the M-B transition. Values indicated with “IMMAB4, max” refer to the maximum rates of change calculated via first differences. See the main text (Section 1 and Section 5) for details.
| Flow Geometry/Model | |||
|---|---|---|---|
| Unrestricted | 1.87 | 8.57 | 6.21 |
| Poloidal | 1.53 | 6.23 | 4.51 |
| Toroidal | 1.40 | 5.88 | 4.27 |
| Columnar | 1.27 | 5.54 | 4.50 |
| SUL14 | - | 1.30 | 1.65 |
| SUL16 | - | 8.44 | 11.16 |
| IMMAB4, M-B avg | 0.074 | 0.039 | 0.054 |
| IMMAB4, max | 0.41 | 0.43 | 0.57 |
References
- Gauss, C.F. Allgemeine theorie des erdmagnetismus. In Werke; Springer: Berlin/Heidelberg, Germany, 1877; pp. 119–193. [Google Scholar]
- Gubbins, D.; Jones, A.L.; Finlay, C.C. Fall in Earth’s magnetic field is erratic. Science 2006, 312, 900–902. [Google Scholar] [CrossRef] [PubMed]
- Jackson, A.; Jonkers, A.R.; Walker, M.R. Four centuries of geomagnetic secular variation from historical records. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Eng. Sci. 2000, 358, 957–990. [Google Scholar] [CrossRef]
- Usui, Y.; Tarduno, J.A.; Watkeys, M.; Hofmann, A.; Cottrell, R.D. Evidence for a 3.45-billion-year-old magnetic remanence: Hints of an ancient geodynamo from conglomerates of South Africa. Geochem. Geophys. Geosyst. 2009, 10, Q09Z07. [Google Scholar] [CrossRef]
- Tarduno, J.A.; Cottrell, R.D.; Watkeys, M.K.; Hofmann, A.; Doubrovine, P.V.; Mamajek, E.E.; Liu, D.; Sibeck, D.G.; Neukirch, L.P.; Usui, Y. Geodynamo, solar wind, and magnetopause 3.4 to 3.45 billion years ago. Science 2010, 327, 1238–1240. [Google Scholar] [CrossRef]
- Tang, F.; Taylor, R.J.; Einsle, J.F.; Borlina, C.S.; Fu, R.R.; Weiss, B.P.; Williams, H.M.; Williams, W.; Nagy, L.; Midgley, P.A.; et al. Secondary magnetite in ancient zircon precludes analysis of a Hadean geodynamo. Proc. Natl. Acad. Sci. USA 2019, 116, 407–412. [Google Scholar] [CrossRef] [PubMed]
- Tarduno, J.A.; Cottrell, R.D.; Bono, R.K.; Oda, H.; Davis, W.J.; Fayek, M.; van’t Erve, O.; Nimmo, F.; Huang, W.; Thern, E.R.; et al. Paleomagnetism indicates that primary magnetite in zircon records a strong Hadean geodynamo. Proc. Natl. Acad. Sci. USA 2020, 117, 2309–2318. [Google Scholar] [CrossRef] [PubMed]
- Johnson, C.; McFadden, P. 5.11.—Time-Averaged Field and Paleosecular Variation. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Oxford, UK, 2015; pp. 385–417. [Google Scholar] [CrossRef]
- Tauxe, L.; Yamazaki, T. 5.13—Paleointensities. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Oxford, UK, 2015; pp. 461–509. [Google Scholar] [CrossRef]
- Bogue, S.W.; Glen, J.M. Very rapid geomagnetic field change recorded by the partial remagnetization of a lava flow. Geophys. Res. Lett. 2010, 37, L21308. [Google Scholar] [CrossRef]
- Constable, C.; Korte, M.; Panovska, S. Persistent high paleosecular variation activity in southern hemisphere for at least 10,000 years. Earth Planet. Sci. Lett. 2016, 453, 78–86. [Google Scholar] [CrossRef]
- Okada, M.; Niitsuma, N. Detailed paleomagnetic records during the Brunhes-Matuyama geomagnetic reversal, and a direct determination of depth lag for magnetization in marine sediments. Phys. Earth Planet. Inter. 1989, 56, 133–150. [Google Scholar] [CrossRef]
- Sagnotti, L.; Scardia, G.; Giaccio, B.; Liddicoat, J.C.; Nomade, S.; Renne, P.R.; Sprain, C.J. Extremely rapid directional change during Matuyama-Brunhes geomagnetic polarity reversal. Geophys. J. Int. 2014, 199, 1110–1124. [Google Scholar] [CrossRef]
- Sagnotti, L.; Giaccio, B.; Liddicoat, J.C.; Nomade, S.; Renne, P.R.; Scardia, G.; Sprain, C.J. How fast was the Matuyama-Brunhes geomagnetic reversal? A new subcentennial record from the Sulmona Basin, Central Italy. Geophys. J. Int. 2016, 204, 798–812. [Google Scholar] [CrossRef]
- Okada, M.; Suganuma, Y.; Haneda, Y.; Kazaoka, O. Paleomagnetic direction and paleointensity variations during the Matuyama-Brunhes polarity transition from a marine succession in the Chiba composite section of the Boso Peninsula, central Japan. Earth Planets Space 2017, 69, 45. [Google Scholar] [CrossRef]
- Macrì, P.; Capraro, L.; Ferretti, P.; Scarponi, D. A high-resolution record of the Matuyama-Brunhes transition from the Mediterranean region: The Valle di Manche section (Calabria, Southern Italy). Phys. Earth Planet. Inter. 2018, 278, 1–15. [Google Scholar] [CrossRef]
- Chou, Y.M.; Jiang, X.; Liu, Q.; Hu, H.M.; Wu, C.C.; Liu, J.; Jiang, Z.; Lee, T.Q.; Wang, C.C.; Song, Y.F.; et al. Multidecadally resolved polarity oscillations during a geomagnetic excursion. Proc. Natl. Acad. Sci. USA 2018, 115, 8913–8918. [Google Scholar] [CrossRef] [PubMed]
- Nowaczyk, N.; Arz, H.; Frank, U.; Kind, J.; Plessen, B. Dynamics of the Laschamp geomagnetic excursion from Black Sea sediments. Earth Planet. Sci. Lett. 2012, 351, 54–69. [Google Scholar] [CrossRef]
- Nowaczyk, N.; Frank, U.; Kind, J.; Arz, H. A high-resolution paleointensity stack of the past 14 to 68 ka from Black Sea sediments. Earth Planet. Sci. Lett. 2013, 384, 1–16. [Google Scholar] [CrossRef]
- Liu, J.; Nowaczyk, N.R.; Panovska, S.; Korte, M.; Arz, H.W. The Norwegian-Greenland Sea, the Laschamps, and the Mono Lake Excursions Recorded in a Black Sea Sedimentary Sequence Spanning From 68.9 to 14.5 ka. JGR Solid Earth 2020, 125, e2019JB019225. [Google Scholar] [CrossRef]
- Leonhardt, R.; Fabian, K. Paleomagnetic reconstruction of the global geomagnetic field evolution during the Matuyama/Brunhes transition: Iterative Bayesian inversion and independent verification. Earth Planet. Sci. Lett. 2007, 253, 172–195. [Google Scholar] [CrossRef]
- Korte, M.; Brown, M.C.; Panovska, S.; Wardinski, I. Robust characteristics of the laschamp and mono lake geomagnetic excursions: Results from global field models. Front. Earth Sci. 2019, 7, 86. [Google Scholar] [CrossRef]
- Evans, M.; Muxworthy, A. A re-appraisal of the proposed rapid Matuyama-Brunhes geomagnetic reversal in the Sulmona Basin, Italy. Geophys. J. Int. 2018, 213, 1744–1750. [Google Scholar] [CrossRef]
- Sagnotti, L.; Giaccio, B.; Liddicoat, J.C.; Caricchi, C.; Nomade, S.; Renne, P.R. On the reliability of the Matuyama-Brunhes record in the Sulmona Basin—Comment to ‘A reappraisal of the proposed rapid Matuyama-Brunhes geomagnetic reversal in the Sulmona Basin, Italy’ by Evans and Muxworthy (2018). Geophys. J. Int. 2019, 216, 296–301. [Google Scholar] [CrossRef]
- Finlay, C.C.; Olsen, N.; Kotsiaros, S.; Gillet, N.; Tøffner-Clausen, L. Recent geomagnetic secular variation from Swarm and ground observatories as estimated in the CHAOS-6 geomagnetic field model. Earth Planets Space 2016, 68, 112. [Google Scholar] [CrossRef]
- Davies, C.J.; Constable, C.G. Rapid geomagnetic changes inferred from Earth observations and numerical simulations. Nat. Commun. 2020, 11, 3371. [Google Scholar] [CrossRef] [PubMed]
- Aubert, J.; Labrosse, S.; Poitou, C. Modelling the palaeo-evolution of the geodynamo. Geophys. J. Int. 2009, 179, 1414–1428. [Google Scholar] [CrossRef]
- Glatzmaier, G.A. Geodynamo simulations—How realistic are they? Annu. Rev. Earth Planet. Sci. 2002, 30, 237–257. [Google Scholar] [CrossRef]
- Christensen, U.; Wicht, J. 8.10—Numerical Dynamo Simulations. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Oxford, UK, 2015; pp. 245–277. [Google Scholar] [CrossRef]
- Sprain, C.J.; Biggin, A.J.; Davies, C.J.; Bono, R.K.; Meduri, D.G. An assessment of long duration geodynamo simulations using new paleomagnetic modeling criteria (QPM). Earth Planet. Sci. Lett. 2019, 526, 115758. [Google Scholar] [CrossRef]
- Meduri, D.G.; Biggin, A.J.; Davies, C.J.; Bono, R.K.; Sprain, C.J.; Wicht, J. Numerical Dynamo Simulations Reproduce Paleomagnetic Field Behavior. Geophys. Res. Lett. 2021, 48, e2020GL090544. [Google Scholar] [CrossRef]
- Glatzmaier, G.A.; Coe, R.S.; Hongre, L.; Roberts, P.H. The role of the Earth’s mantle in controlling the frequency of geomagnetic reversals. Nature 1999, 401, 885–890. [Google Scholar] [CrossRef]
- Kutzner, C.; Christensen, U.R. Simulated geomagnetic reversals and preferred virtual geomagnetic pole paths. Geophys. J. Int. 2004, 157, 1105–1118. [Google Scholar] [CrossRef]
- Olson, P.L.; Glatzmaier, G.A.; Coe, R.S. Complex polarity reversals in a geodynamo model. Earth Planet. Sci. Lett. 2011, 304, 168–179. [Google Scholar] [CrossRef]
- Shao, J.C.; Fuller, M.; Tanimoto, T.; Dunn, J.R.; Stone, D.B. Spherical harmonic analyses of paleomagnetic data: The time-averaged geomagnetic field for the past 5 Myr and the Brunhes-Matuyama reversal. J. Geophys. Res. Solid Earth 1999, 104, 5015–5030. [Google Scholar] [CrossRef]
- Ingham, M.; Turner, G. Behaviour of the geomagnetic field during the Matuyama-Brunhes polarity transition. Phys. Earth Planet. Inter. 2008, 168, 163–178. [Google Scholar] [CrossRef]
- Valet, J.P.; Fournier, A. Deciphering records of geomagnetic reversals. Rev. Geophys. 2016, 54, 410–446. [Google Scholar] [CrossRef]
- Singer, B.S.; Jicha, B.R.; Mochizuki, N.; Coe, R.S. Synchronizing volcanic, sedimentary, and ice core records of Earth’s last magnetic polarity reversal. Sci. Adv. 2019, 5, eaaw4621. [Google Scholar] [CrossRef] [PubMed]
- Just, J.; Sagnotti, L.; Nowaczyk, N.R.; Francke, A.; Wagner, B. Recordings of Fast Paleomagnetic Reversals in a 1.2 Ma Greigite-Rich Sediment Archive From Lake Ohrid, Balkans. J. Geophys. Res. Solid Earth 2019, 124, 12445–12464. [Google Scholar] [CrossRef]
- Backus, G.; Bullard, E.C. Kinematics of geomagnetic secular variation in a perfectly conducting core. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1968, 263, 239–266. [Google Scholar] [CrossRef]
- Jackson, A. Time-dependency of tangentially geostrophic core surface motions. Phys. Earth Planet. Inter. 1997, 103, 293–311. [Google Scholar] [CrossRef]
- Amit, H.; Olson, P. Time-average and time-dependent parts of core flow. Phys. Earth Planet. Inter. 2006, 155, 120–139. [Google Scholar] [CrossRef]
- Finlay, C.C.; Amit, H. On flow magnitude and field-flow alignment at Earth’s core surface. Geophys. J. Int. 2011, 186, 175–192. [Google Scholar] [CrossRef]
- Driscoll, P.; Olson, P. Effects of buoyancy and rotation on the polarity reversal frequency of gravitationally driven numerical dynamos. Geophys. J. Int. 2009, 178, 1337–1350. [Google Scholar] [CrossRef]
- Olson, P.; Driscoll, P.; Amit, H. Dipole collapse and reversal precursors in a numerical dynamo. Phys. Earth Planet. Inter. 2009, 173, 121–140. [Google Scholar] [CrossRef]
- Wicht, J.; Olson, P. A detailed study of the polarity reversal mechanism in a numerical dynamo model. Geochem. Geophys. Geosystems 2004, 5. [Google Scholar] [CrossRef]
- Olson, P. Gravitational dynamos and the low-frequency geomagnetic secular variation. Proc. Natl. Acad. Sci. USA 2007, 104, 20159–20166. [Google Scholar] [CrossRef] [PubMed]
- Livermore, P.W.; Fournier, A.; Gallet, Y. Core-flow constraints on extreme archeomagnetic intensity changes. Earth Planet. Sci. Lett. 2014, 387, 145–156. [Google Scholar] [CrossRef]
- Ben-Yosef, E.; Tauxe, L.; Levy, T.E.; Shaar, R.; Ron, H.; Najjar, M. Geomagnetic intensity spike recorded in high resolution slag deposit in Southern Jordan. Earth Planet. Sci. Lett. 2009, 287, 529–539. [Google Scholar] [CrossRef]
- Shaar, R.; Ben-Yosef, E.; Ron, H.; Tauxe, L.; Agnon, A.; Kessel, R. Geomagnetic field intensity: How high can it get? How fast can it change? Constraints from Iron Age copper slag. Earth Planet. Sci. Lett. 2011, 301, 297–306. [Google Scholar] [CrossRef]
- Shaar, R.; Tauxe, L.; Ron, H.; Ebert, Y.; Zuckerman, S.; Finkelstein, I.; Agnon, A. Large geomagnetic field anomalies revealed in Bronze to Iron Age archeomagnetic data from Tel Megiddo and Tel Hazor, Israel. Earth Planet. Sci. Lett. 2016, 442, 173–185. [Google Scholar] [CrossRef]
- Ben-Yosef, E.; Millman, M.; Shaar, R.; Tauxe, L.; Lipschits, O. Six centuries of geomagnetic intensity variations recorded by royal Judean stamped jar handles. Proc. Natl. Acad. Sci. USA 2017, 114, 2160–2165. [Google Scholar] [CrossRef] [PubMed]
- Livermore, P.W.; Gallet, Y.; Fournier, A. Archeomagnetic intensity variations during the era of geomagnetic spikes in the Levant. Phys. Earth Planet. Inter. 2021, 312, 106657. [Google Scholar] [CrossRef]
- Holme, R. 8.04—Large-Scale Flow in the Core. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Oxford, UK, 2015; pp. 91–113. [Google Scholar] [CrossRef]
- Tauxe, L.; Banerjee, S.; Butler, R.; Van der Voo, R. Essentials of Paleomagnetism, 5th ed.; University of California Press: Oakland, CA, USA, 2018. [Google Scholar]
- Engdahl, E.R.; Johnson, L.E. Differential PcP Travel Times and the Radius of the Core. Geophys. J. Int. 1974, 39, 435–456. [Google Scholar] [CrossRef]
- Tilgner, A. 8.07—Rotational Dynamics of the Core. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Oxford, UK, 2015; pp. 183–212. [Google Scholar] [CrossRef]
- Roberts, P.; Scott, S. On analysis of the secular variation. J. Geomagn. Geoelectr. 1965, 17, 137–151. [Google Scholar] [CrossRef]
- Amit, H.; Christensen, U.R. Accounting for magnetic diffusion in core flow inversions from geomagnetic secular variation. Geophys. J. Int. 2008, 175, 913–924. [Google Scholar] [CrossRef]
- Terra-Nova, F.; Amit, H.; Hartmann, G.A.; Trindade, R.I. Using archaeomagnetic field models to constrain the physics of the core: Robustness and preferred locations of reversed flux patches. Geophys. J. Int. 2016, 206, 1890–1913. [Google Scholar] [CrossRef]
- Baerenzung, J.; Holschneider, M.; Lesur, V. The flow at the Earth’s core-mantle boundary under weak prior constraints. J. Geophys. Res. Solid Earth 2016, 121, 1343–1364. [Google Scholar] [CrossRef]
- Whaler, K. Does the whole of the Earth’s core convect? Nature 1980, 287, 528–530. [Google Scholar] [CrossRef]
- Whaler, K. Geomagnetic evidence for fluid upwelling at the core-mantle boundary. Geophys. J. Int. 1986, 86, 563–588. [Google Scholar] [CrossRef]
- Amit, H. Can downwelling at the top of the Earth’s core be detected in the geomagnetic secular variation? Phys. Earth Planet. Inter. 2014, 229, 110–121. [Google Scholar] [CrossRef]
- Lesur, V.; Whaler, K.; Wardinski, I. Are geomagnetic data consistent with stably stratified flow at the core-mantle boundary? Geophys. J. Int. 2015, 201, 929–946. [Google Scholar] [CrossRef]
- Pais, M.; Jault, D. Quasi-geostrophic flows responsible for the secular variation of the Earth’s magnetic field. Geophys. J. Int. 2008, 173, 421–443. [Google Scholar] [CrossRef]
- Amit, H.; Pais, M.A. Differences between tangential geostrophy and columnar flow. Geophys. J. Int. 2013, 194, 145–157. [Google Scholar] [CrossRef]
- Gillet, N.; Schaeffer, N.; Jault, D. Rationale and geophysical evidence for quasi-geostrophic rapid dynamics within the Earth’s outer core. Phys. Earth Planet. Inter. 2011, 187, 380–390. [Google Scholar] [CrossRef]
- Aubert, J.; Gastine, T.; Fournier, A. Spherical convective dynamos in the rapidly rotating asymptotic regime. J. Fluid Mech. 2017, 813, 558–593. [Google Scholar] [CrossRef]
- Jault, D. Axial invariance of rapidly varying diffusionless motions in the Earth’s core interior. Phys. Earth Planet. Inter. 2008, 166, 67–76. [Google Scholar] [CrossRef]
- Gubbins, D.; Roberts, N. Use of the frozen flux approximation in the interpretation of archaeomagnetic and palaeomagnetic data. Geophys. J. Int. 1983, 73, 675–687. [Google Scholar] [CrossRef]
- Johnson, C.L.; Constable, C.G. The time-averaged geomagnetic field: Global and regional biases for 0–5 Ma. Geophys. J. Int. 1997, 131, 643–666. [Google Scholar] [CrossRef]
- Gubbins, D.; Herrero-Bervera, E. Encyclopedia of Geomagnetism and Paleomagnetism; Springer Science & Business Media: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Finlay, C.C.; Kloss, C.; Olsen, N.; Hammer, M.D.; Tøffner-Clausen, L.; Grayver, A.; Kuvshinov, A. The CHAOS-7 geomagnetic field model and observed changes in the South Atlantic Anomaly. Earth Planets Space 2020, 72, 1–31. [Google Scholar] [CrossRef]
- Gillet, N.; Pais, M.; Jault, D. Ensemble inversion of time-dependent core flow models. Geochem. Geophys. Geosyst. 2009, 10, Q06004. [Google Scholar] [CrossRef]
- Baerenzung, J.; Holschneider, M.; Lesur, V. Bayesian inversion for the filtered flow at the Earth’s core-mantle boundary. J. Geophys. Res. Solid Earth 2014, 119, 2695–2720. [Google Scholar] [CrossRef]
- Gillet, N.; Barrois, O.; Finlay, C.C. Stochastic forecasting of the geomagnetic field from the COV-OBS. x1 geomagnetic field model, and candidate models for IGRF-12. Earth Planets Space 2015, 67, 71. [Google Scholar] [CrossRef]
- Barrois, O.; Gillet, N.; Aubert, J. Contributions to the geomagnetic secular variation from a reanalysis of core surface dynamics. Geophys. J. Int. 2017, 211, 50–68. [Google Scholar] [CrossRef]
- Schaeffer, N.; Jault, D.; Nataf, H.C.; Fournier, A. Turbulent geodynamo simulations: A leap towards Earth’s core. Geophys. J. Int. 2017, 211, 1–29. [Google Scholar] [CrossRef]
- Sheyko, A.; Finlay, C.; Favre, J.; Jackson, A. Scale separated low viscosity dynamos and dissipation within the Earth’s core. Sci. Rep. 2018, 8, 1–7. [Google Scholar] [CrossRef]
- Jackson, A.; Finlay, C. 5.05—Geomagnetic Secular Variation and Its Applications to the Core. In Treatise on Geophysics, 2nd ed.; Schubert, G., Ed.; Elsevier: Oxford, UK, 2015; pp. 137–184. [Google Scholar] [CrossRef]
- Brown, M.; Korte, M.; Holme, R.; Wardinski, I.; Gunnarson, S. Earth’s magnetic field is probably not reversing. Proc. Natl. Acad. Sci. USA 2018, 115, 5111–5116. [Google Scholar] [CrossRef]
- Clement, B.M.; Kent, D.V. Geomagnetic Polarity Transition Records from Five Hydraulic Piston Core Sites in the North Atlantic; Initial Reports of the Deep Sea Drilling Project 94; Columbia University Academic Commons: New York, NY, USA, 1987. [Google Scholar]
- McElhinny, M.W.; Lock, J. IAGA paleomagnetic databases with Access. Surv. Geophys. 1996, 17, 575–591. [Google Scholar] [CrossRef]
- Channell, J.; Lehman, B. The last two geomagnetic polarity reversals recorded in high-deposition-rate sediment drifts. Nature 1997, 389, 712–715. [Google Scholar] [CrossRef]
- Clement, B.M. Dependence of the duration of geomagnetic polarity reversals on site latitude. Nature 2004, 428, 637–640. [Google Scholar] [CrossRef] [PubMed]
- Clement, B.M.; Kent, D.V. Latitudinal dependency of geomagnetic polarity transition durations. Nature 1984, 310, 488–491. [Google Scholar] [CrossRef][Green Version]
- Kadlec, J.; Chadima, M.; Pruner, P.; Schnabl, P. Paleomagnetické datování sedimentů v jeskyni “Za Hájovnou” v Javoříčku-předběžné vỳsledky. Přírodovědné Studie Muzea Prostějovska 2005, 8, 75–82. [Google Scholar]
- Kadlec, J.; Čížková, K.; Šlechta, S. New updated results of paleomagnetic dating of cave deposits exposed in the “Za Hájovnou” Cave, Javoříčko Karst. Acta Musei Natl. Pragae Ser. B Hist. Nat. 2014, 70, 27–34. [Google Scholar] [CrossRef][Green Version]
- Pares, J.; Perez-Gonzalez, A. Paleomagnetic age for hominid fossils at Atapuerca archaeological site, Spain. Science 1995, 269, 830–832. [Google Scholar] [CrossRef]
- Moreno, D.; Falgueres, C.; Pérez-González, A.; Voinchet, P.; Ghaleb, B.; Despriée, J.; Bahain, J.J.; Sala, R.; Carbonell, E.; de Castro, J.M.B.; et al. New radiometric dates on the lowest stratigraphical section (TD1 to TD6) of Gran Dolina site (Atapuerca, Spain). Quat. Geochronol. 2015, 30, 535–540. [Google Scholar] [CrossRef]
- Parés, J.M.; Álvarez, C.; Sier, M.; Moreno, D.; Duval, M.; Woodhead, J.; Ortega, A.; Campaña, I.; Rosell, J.; de Castro, J.B.; et al. Chronology of the cave interior sediments at Gran Dolina archaeological site, Atapuerca (Spain). Quat. Sci. Rev. 2018, 186, 1–16. [Google Scholar] [CrossRef]
- Panovska, S.; Korte, M.; Constable, C.G. One Hundred Thousand Years of Geomagnetic Field Evolution. Rev. Geophys. 2019, 57, 1289–1337. [Google Scholar] [CrossRef]
- Panovska, S.; Constable, C.G.; Brown, M.C. Global and Regional Assessments of Paleosecular Variation Activity Over the Past 100 ka. Geochem. Geophys. Geosyst. 2018, 19, 1559–1580. [Google Scholar] [CrossRef]
- Bullard, E.C.; Gellman, H. Homogeneous dynamos and terrestrial magnetism. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Sci. 1954, 247, 213–278. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).