Abstract
In 2014, the Varnes classification system for landslides was updated. Complex landslides can still be a problem to classify as the classification does not include the flow type in the hydrodynamical sense. Three examples of Icelandic landslides are presented and later used as case studies in order to demonstrate the methods suggested to analyze the flow. The methods are based on the different physical properties of the flow types of the slides. Three different flow types are presented, named type (i), (ii), and (iii). Types (i) and (ii) do not include turbulent flows and their flow paths are sometimes independent of the velocity. Type (iii) include high velocity flows; they are treated with the translator wave theory, where a new type of a slope factor is used. It allows the slide to stop when the slope has flattened out to the value that corresponds to the stable slope property of the flowing material. The type studies are for a fast slide of this type, also a large slip circle slide that turns into a fast-flowing slide farther down the path and finally a large slide running so fast that it can run for a kilometer on flat land where it stops with a steep front.
1. Introduction
The subject of this paper is hazardous landslides, their physics, and the possibility of modeling them as a part of a disaster prevention procedure. This task begins when a site has been identified as susceptible using a procedure that can involve advanced remote sensing technology [1] and the production of landslide susceptibility maps [2,3] (Figure 6; Table 5). Models can be involved in this work, e.g., GIS based models [4]. Statistical models may apply [3] (p. 6.), [5], or hybrid machine learning approach (an extension of the traditional Artificial Neural Network) [6]. However, when the susceptibility analysis is finished, the appropriate disaster prevention procedures must be devised. This can be everything from just estimating the areal location of the debris after the landslide event to designing and building of retaining dikes or dams. Here, the concern is mainly new methods to estimate the area location using a model. Disaster prevention procedures to be undertaken thereafter depend very much on the local regulations of the civil protection system. They will only be mentioned here as examples.
Sites where a landslide can occur are well known all over the world [7], and scientists are discovering new ones almost every day. In disaster prevention, it is necessary for obvious reasons to define a danger area. It is here that modeling comes in and it must be based on solid geological and geophysical evidence incorporated in a mathematical model.
Such models may be useful in other ways. The model presented here may be used in susceptibility studies though it is not designed for that purpose.
Landslides can cause environmental disasters. They are a natural phenomenon that are responsible for countless human lives and there is no remedy against their occurrence. The way to counteract the danger is preparedness, to assess the hazard, operate a warning system, and keep people out of the way of the danger.
Landslides have different properties that may be described as falls, topples, slides, spreads, or simply flows. These properties are used in landslide classification together with various other classification factors such as material, movement and velocity, where distinction is made between different settings in geology, morphology, topography, and climate.
The classification systems and their relation to physics and modeling are discussed in the next section. To mention new developments, statistics may be used to assess the danger [8], and sometimes they bring about scaling laws known from fractal theory [9]. Yet, statistical methods have not found their way into classification.
Modeling can be applied to any class and types of landslides, also subaqueous landslides [10], which may have enormous consequences in a very large area. Unfortunately, the physics and modeling of landslides can be very different even within the same landslide class. To take an example, a topple may or may not end up as debris or mud slide and there are many similar problems.
A vast literature is devoted to the prediction of landslides. Prediction can be quite successful in defining the danger and mitigation possibilities. However, the timing of the event can usually not be predicted. Landslides come quite suddenly as a result of an instability process [11]. Small cracks may be discovered; they keep widening for a long time, and it becomes quite evident that a landslide will occur at some time, but there is no way to tell for certain when it will happen. Another example is an earthquake that triggers a subaqueous landslide that again causes a disastrous tsunami [12,13].
The scope of this paper is the modeling of landslide physics, as a tool in hazard assessment, mitigation, and protection. It is quite clear that many other factors, outside this scope, may be of equal importance, e.g., economical resources just to name one of these factors.
Section 2 is devoted to the discussion of landslide classification and description of slide events to be analyzed later. Section 3, Section 4 and Section 5 discuss the physics and modeling possibilities. It is concluded that common types of landslides can be included in an analytical model that both quickly can assist in the assessment work and tell researchers what kind of field data is needed. This is demonstrated in three case studies in Section 6.
2. Landslides, Types and Classification
According to [14] a landslide is defined as “a movement of mass of rock, earth, or debris down a slope”. Numerous classifications of landslides have been presented, but the classification published by Varnes in 1978 has for many authors been used as the basis for landslide classification. The Varnes classification is based on five types of movement: fall, topple, slide, spread, and flow and three types of material involved in the movement, rock, debris, and earth [15]. During recent years, his classification has been updated and revised by several authors e.g., [16,17,18,19,20]. In 2014, an update of the Varnes classification was published and several aspects were revised, e.g., modification of the definition of landslide forming material and modifications of the classification system. The revised classification includes 32 different landslides types. Complex landslides are, however, not included as a separate category type, but they suggest the possibility of using composite type, by combining two or more type names [20].
The landslides examples that are presented in Section 6 are of two main types, translational and rotational slides. In case study A, a 1000 m long debris slide is described which occurred on 29 June 1995 in the Sölvadalur valley in North Iceland (Figure 1). The slide is categorized as debris slide as the main part of the slide material is clay rich fine-grained derris, originated from the old rockslide, the Arnbjargarhólar rockslide. They can be related to clay rich volcanogenic sedimentary horizons in the bedrock. The slide started at the elevation 580 m above sea level (m a. s. l.).

Figure 1.
A photo of the Sölvadalur debris slide on 29 June 1995 (location map is on Figure 4). The slide was initiated at 580 m a.s.l. and fell into the Þormóðsstaðará canyon at an elevation of 340 m. The width of the slide at the rim of the canyon is about 4–500 m. Note the farm Þormóðsstaðir to the lower right corner of the photo (Photo by Björn Gíslason, 1995).
In case study B, a large rock avalanche is described which occurred in the caldera rim of the Askja central volcano on 21 July 2014, in the northeastern part of the central highlands in Iceland (Figure 2). The primary movement of the slide was rotation on a concave sliding plane.

Figure 2.
The rockslide in Askja on 7 July 2014 (location map is on Figure 6). The slide was initiated at 1400 m a.s.l. and fell into the Öskjuvatn Lake at 1056 m height. The width of the slide at the main scarp is about 8–900 m and the runout length to the lake is around 1100 m (Photo by Þorsteinn Sæmundsson, 2014).
In case study C a 2300 m long landslide which occurred on 7 July 2018 in the Hítardalur valley in West Iceland is described (Figure 3). As in case study A, the primary movement was a translational slide with non-circular movement on a near planar slip surface, but the slide material involved in the slide was both solid bedrock and loose sediments from the uppermost part of the mountain.

Figure 3.
The Hítardalur landslide on the 7 July 2018 (location map is on Figure 8). The slide was initiated from the uppermost part of the mountain at 640 m a.s.l. The slide was about 2.3 km long and stopped at around 180 m a.s.l. (Photo by Sumarliði Ásgeirsson, 2018).
3. Physical Laws of Landslide Motion
3.1. Slope Stability, Rupture Lines and Zones
Soil ruptures in slopes, as well as the liquefaction of soil layers and wave formation in hydrodynamics, are all instability problems that can be triggered by an external force like an earthquake. The unpredictability of this instability problem can be a reason for the use of statistics on landslides. A lot of research effort is devoted to the problem of landslide triggering [21,22], sometimes with stochastic input routines [23], and others with models describing the aftermath. Hazard assessment is often the research objective [11], or modeling of the flow of the slide itself [24,25], sometimes with the assistance of remote sensing data [26].
The onset of a landslide is an external force causing internal stresses in excess of the material strength of the formation that destabilizes a certain mass of soil or rock, that then becomes a landslide. The stabilizing force is the shear stress and normally the bulk of the destabilizing external force is simply the gravity, but any other external load is a possibility. The stabilizing force is complicated to analyze; here, we consider three particular types. Depending on the typical material property of the soil on the verge of sliding, the shear stress may: (i) depend entirely on friction (granular materials), (ii) be constant (consolidated clays), (iii) depend on the velocity (fluid flow), or a mixture of all three.
A comprehensive description of the physics of soils are originally due to Terzaghi [27]. The motion will take place in statically and kinematically possible rupture zones, consisting of a system of rupture lines. The following rule between the friction force τ and the normal stress σ in the rupture lines, well known from geotechnics, is the basic rule for type (i)
τcr = σ tan ϕ
The basic rule for type (ii) is
where c’ is cohesion of the soil. When c’ = 0, Equation (2) really includes type (i). In very fine clays we may have ϕ ≈ 0, which is the clear-cut type 2. Such type (ii) flows are most common where clay deposits are subjected to sudden pressure from foundations of buildings without given time to consolidate. However, it occurs in nature too, case study B is an example.
τcr = c’ + σ tan ϕ
Type (iii) is the type of a landslide flowing with velocity V.
τ − τcr = a V + b V2
The main physical difference between type (iii) and the other two, is that Equation (3) puts bounds on the velocity, which (i) and (ii) do not. Type (i) and (ii) only define a rupture plane, where τ ≥ τcr. When the slide starts flowing, type (iii) can take over as V increases.
In fluid mechanical terms, type (iii) is actually in two parts when a = 0 we the turbulent flow, when b = 0 we have laminar flow. It must be noted that a = 0 does not mean that the laminar shear stress τlam = 0, it depends on the cross-stream velocity gradient according to Newtons law of viscosity. The full physical description of the shear stress is Equation (3) with V as a running average of the flow velocity over a time sufficiently long to eliminate random velocity fluctuations. The mathematical complexity of the full Equation (3) makes modelers chose either flow type most of the time, laminar (typical for types (i) and (ii)) or turbulent (typical for type (iii)).
As an example, one may take the Voellemy rheology parameters model. In it the shear stress was originally modeled as Equation (3) without the τcr term, but it was later been added in extended versions by including a limiting cohesion as in Equation (2). Then, there are three resistance parameters to be estimated, not one as is done here in the three type studies in Section 6. The Voellemy model is rather popular, nevertheless, and the Voellemy parameters can also be used in a simpler model, of which [28] is an example.
Equations (1)–(3) are valid along the flow lines, and the main physical problem is to find the rupture lines that develop into flow lines as the movement progresses. In a landslide flowing down a slope subjected to gravitational forces only, the flow lines will be more or less parallel to the solid base the slide is flowing on. They will run over, or past, minor irregularities in the bottom configuration and still be (i), (ii) or (iii).
Equations (1)–(3) involve material constants and there in-situ values are only known to a certain degree of approximation. The rupture lines are also a big problem in landslides just starting to move. The triggering problem is to predict when the internal strength of the soils is exceeded, and it starts to move. Besides the static load that can be predicted, there are all kinds of strange stress variations from tremors or regular geophysical events, e.g., earth tides come twice a day and bring very small stress changes to the earth. They may very well cause some movement for a short while, and then stop when the tide is gone. Like their ocean counterparts, earth tides have spring tide twice in the lunar month as an extra complication [29].
An example of a developing rupture is a column of rock on its way to topple [7] (Section 1, Figure 5; Figure 6). It has developed a crack near the top and this crack becomes the rupture line between the toppling rock and the formation that remains in place. The development of such cracks will follow the weakness zones in the rock formation, they cannot be predicted by any formula. The crack will enlarge by time, in most cases at an irregular pace.
All this makes the prediction of the onset of motion in a landslide an almost impossible task, even when all physical material properties are well known. However, the importance of such predictions in disaster prevention is undisputed.
3.2. The Physical Laws of Landslide Motion and Associated Equations
3.2.1. Types (i) and (ii)
Considering type (i), when the rupture lines and zones are developed the slide starts moving, so the slide will start accelerating as soon as τ > σtanϕ. The in-situ value of the friction angle ϕ in the undisturbed formation is usually a little higher than it becomes once disturbed by some movement. Flowing under gravitational forces alone, the slide flows downhill as long as the ground slope θ is greater than ϕ, but when θ becomes smaller the flow stops.
In type (ii) the slide will also start accelerating as soon as τ > c’ + stan ϕ, but configuration of rupture lines and zones can be very different, and a slope little greater than ϕ may not be enough to maintain motion.
If the soil is fine grained (fine silt or clay) the cohesion c’ may be the greater part of the total shear strength (flow resistance), but it may depend heavily upon the porosity (or the void ratio if that measure is preferred) of the soil. This is the classical problem of slope stability, if the porosity increases because of increased internal water pressure the soil may get soaked, the shear strength of the soil drops, and a slide starts. The porosity may thus become the physical property that gets a landslide flowing in wet soils. Such slides have a tendency to start during heavy rainstorms, the higher water content reduces the c’ somewhat and increases the density of the soil. However, it is the ground slope θ that determines if the landslide flows or not.
During onset of the flow, c’ can be a significant part of the total shear strength but can be reduced by the deformation at the start of flow. In such slides we can end up with a shear strength of the soil that can be approximated with a dynamical friction angle ϕ’ and a zero cohesion (c = 0). Supposing as before a slide flowing more or less on a solid base the basic flow equation for types (i) and (ii) is Equation (7), as in [30]:
In Equation (4), we suppose σ = ρg(y − y’)cosθ. Here ρ is density, y the total depth of the flow, but y’ is the distance from the solid base bottom. The message of this equation is that the slide keeps flowing while ϕ’ < θ as before. This mirrors the well-known fact that sand keeps flowing as long as its surface slopes more than the friction angle.
So, going onwards from Equation (4) we must know the topography. For creeping flows (fluid momentum can be disregarded) this is enough when we know the total flowing volume in the landslide. The slide will settle in a sloping cone and fill up the depressions in the landscape it covers. Equation (4) may occasionally be usable even though Equation (3) does not hold for all values of y’.
3.2.2. Type (iii)
To get on with fast flowing landslides (i.e., when fluid momentum cannot be disregarded), a relation between the velocity and the excess shear stress τ − τcr is needed. Supposing Newtonian fluid in a landslide flowing with a free surface, we have the continuity equation and the Saint Venant equations Equations (1) and (2) in [30]. This equation system is better known in river hydraulics and flood studies but works very well in landslide analysis [31]. However, non-linearities and instabilities in the equation system are a problem for general analysis of landslide motion, especially when toppling and falling is involved.
The simplest type is uniform flow on a sloping bottom, in this case Equation (4) may be integrated to give:
τo − τocr = ρgsinθ(1−tanϕ’/tanθ)Rh, Rh = Ah/Ph
Ah and Ph are the area and the perimeter of the flow. The index 0 in τ refers to the bottom value and Rh is the hydraulic radius. We can use Equation (3) and find the velocity directly when a and b are known. However, it takes a long flow channel to accelerate the velocity in a fast-flowing landslide all the way up to the uniform flow value. When velocities are lower than the uniform value, the Rh keeps changing, and we need a flow model to go on. See Section 5.
4. Subaqueous Slides and Tsunamis
Subaqueous slides typically occur in continental slopes and boundary plate fracture zones and they sometimes generate tsunamis that attack very large regions. Such slides can be treated as stratified flow with the slide itself as the layer flowing on the bottom. The debris in the slide will obviously absorb a lot of water that acts as lubrication allowing the slide to obtain larger velocity than it would have done on dry land. In this case, it is more likely that the subaqueous slide will be of type (iii), consequently Equation (3) must be used in the modeling.
All the same laws as for flows on land are still valid, but the buoyancy forces have to be respected. For free surface flows this means that we must use reduced gravity, g’, [32].
g’ = Δg; Δ = (ρ − ρw)/ρ
The subscript w refers to the water. When this is respected, we can use all the same formulas and modeling methods to treat subaqueous slides as for slides on dry land.
Subaqueous slides are known for cutting cables and pipelines, and several are listed in [33]. As can be expected, subaqueous slides are frequent on the continental slopes. It is especially the continental slopes off the coast of Norway that have been studied [34]. There are no large events that have recently been reported, but there have been very big ones in geological history, [10,34,35,36].
Recent events include the Indian ocean disaster in 2004, [37] and the Tohoku earthquake and tsunami in 2011, an enormous disaster in Japan, [12,38]. The location of this disaster is the western rim of the Pacific Ocean. There is tsunami hazard on the eastern rim too, [39]. Both these sides are convergent plate boundaries, and the possibility of large earthquakes is relatively higher than what it is on a diverging plate boundary. But there are exceptions from this rule. There are known fracture zones in the middle of the oceans where large earthquakes are generated. There are also examples of subaqueous slides followed by large tsunamis in inland lakes [40]. See case study B, Section 6.2.
Large earthquakes will normally start a landslide. Subaqueous landslides can flow longer and farther than landslides on dry land and be orders of magnitude bigger [10]. The cause of this is quite difficult to describe, but in a subaqueous slide the water will have the same effect as lubrication oil in an engine. The water content of the slide will increase the longer it flows, so we may expect that the flow of subaqueous landslides can be even closer to water flow, than the flow of a landslide on dry land, and thus flow farther out.
The tsunamis created by subaqueous landslides are an integral part of the landslide process. The tsunami gets its wave energy from the slide. The run of the slide must be modeled, both the track and the velocity in order to estimate the initial wave height and wave energy of the tsunami.
The tsunamis in the Indian Ocean and off the coast of Japan mentioned above were responsible for taking thousands of lives in one disaster event. Thus, big tsunamis are triggered by an earthquake. Earthquakes are well researched and the possibility of designing coastal defenses that can protect vulnerable locations against a tsunami triggered by an earthquake of given magnitude are good. However, if the earthquake triggers a landslide, its energy may be added to the initial wave and the tsunami can become too big for the coastal defense works designed for the earthquake tsunami alone, [12].
5. Constructions of Landslide Models
5.1. Integral Models
The purpose of landslide models is to find the flow path, where the flow stops and the velocity if that is important. Integral models show the movement of soil layers as a whole. The results of this work, numerical or analytical, depend on the boundary conditions: These conditions are an integral part of the model, while many of the basic physical laws can do without them.
The boundary conditions must be taken from topographical maps, or a digital map software that may be a Geographical Information System (GIS).
5.1.1. Type (i)
The slide demands that the ground slope θ > ϕ, but such a slope is in theory unstable from the start, except in soils that possess natural cohesion. Something has to start up the slide, external load, that causes failure of the initial state, independent of the condition θ > ϕ, and keeps the slide going after the onset of the flow. In nature this may be granular flows, debris flows or rockslides. This happens mostly in steep mountain slopes or cliffs.
When a flow once started stops again, it must have a surface where the steepest surface gradient is stable, i.e., θ = ϕ. In a granular material with θ = ϕ, the surface is a circular cone where the part having the top pointing down is the source volume. The part with the top up contains the settling place of the slide, where the same volume comes to rest. To start such a slide in nature, the external load of the winter snow, filled with spring rain may be enough.
In a GIS model, the top up cone is defined first and its volume found, then the top-down cone using the volume of the upper one. Flow models can be made from this of course, the landscape topography can then be used to estimate the velocities and find the time history of the process.
In many cases water is a part of the flow and the result will have a character of an alluvial process rather than a landslide. Nevertheless, the alluvium has a tendency to settle in a cone, but most of the alluvial cones have ground slopes θ < ϕ, where ϕ represents the stable slope of the material in the cone. Alluvial cones may be mistaken for landslides, but alluvial processes are very different from landslides.
There is a rare exception to this sliding controlled by local stability. It is rockslides where the rocks roll down a steep slope and gain such rotational energy that they continue rolling when they have reached level ground (https://coloradogeologicalsurvey.org/hazards/rockfall/ (accessed on 23 February 2021)).
5.1.2. Type (ii)
When it is the shear strength c’ that dominates the resistance rather than the friction ϕ, the slide moves, for kinematic reasons, along a linear or a circular path. Such a rupture is typical for cohesive fine-grained soils like clays and volcanic tephra, the slide moves inside a slip circle (Section 6.2). Taking the simple example of flow down an inclined plane as before, a slide of thickness h can flow while:
c’ < ρghsinθ
We start with the simplest boundary conditions, the landslide flowing in an inclining rectangular wide channel. In sensitive clays (quick clays) the angel θ can be very small but the slide may still be very dangerous [12]. Laminar flow models may be the most suitable. Velocities in laminar flows are usually small and the flow will stop when sinθ < c’/ρgh. However complex flow paths can break up the soil and destroy c’.
In more complex terrain we may be left with the cone problem in Type (i) with sinθ = c’/ρgh, h being the local depth of the slide at rest and c’ cohesive resistance still active in the slide.
5.2. Pseudostationary Flow and Slope Stability
In more complex terrains than the rectangular channel, the flow model is basically the same as long as there is laminar flow. As a basic flow model for the velocity vector Û for small slopes we have Equations (2) and (3). Furthermore Û will be proportional to the gradient ∇·z, z being the geographical elevation level, z = f(x,y) and ∇·z its gradient vector. The vector s is the runout distance vector in any time t, steadily increasing with the time increament dt. The flow lines will be found from:
a Û = ∇·z/|∇·z|(|∇·z| − c’/ρgh), ds = Ûdt
As long as we are only interested in the runout of the slide, [41], but not the actual flow velocity, the value of the coefficient of proportionality, a, is not critical, Equation (8) can be used in a finite element model that calculates the runout distance s, a slide with the right c’ value will stop in the right place. The real problem may be the deformation of the slide itself and the changes in z caused by the slide, [41]. Sometimes the sliding layers are much longer than their thickness, this can call for more sophisticated techniques [42].
The flow does not have to be in piecewise straight lines; another kinematically possible rupture failure is the slip circle. In that case the sliding mass will be a part of a wheel rotating around the center of the slip circle. It is also possible to define the straight line as a circle with very large radius, but sometimes not very practical. Figure 2 is of such an event and the volume involved was 10–20 million cubic meters. It is very difficult to assess the hazard of such slides due to the varying properties of the volcanic rock. This slide is the subject of case study B.
Slip circle slides will not flow a very long way. Typical sites are steep banks caused by river erosion of the soil, [43]. The stability criteria are:
MDS = Wsyms > ∫A√(z2 + y2)c’dA = MSS
Ws is the total soil weight inside the rupture circle, or in three dimensions, inside a wheel cutting the surface and rotating around the horizontal x-axis. The center of the wheel is in {y,z} = {0,0} and the center of gravity of the soil mass is in {xms,yms,zms}, the gravity vector parallel to the z-axis. A is the rupture surface, and {x,y,z} a point on it. Care has to be taken that the rupture is not kinematically possible, in the geotechnical sense, except the rupture wheel is symmetric around the center {xms,yms,zms}.
The left side of Equation (9) is the destabilizing moment MDS, and the right side is the stabilizing moment MSS, which represents all stabilizing moments around {0,0,0}. Note that the slide is only a part of a wheel, so the circular movement will diminish yms in Equation (9), so sooner or later we will have MDS < MSS and the motion stops, if the slide has not flown out of the slip circle segment into a steeper slope and taken on a different character (Section 6.2 case study B)
Most dangerous slip circle is where (MDS − MSS) is at maximum. In the attempt to assess the danger, any MDS − MSS > 0 must be considered dangerous. In complex terrain this has to be done numerically and it is very tedious work to locate the position and radius of the most dangerous rupture wheel. As we can see, the outcome is completely dependent on the correct estimations of the cohesion c’. It can be very variable, especially when geological settings are as complex as in Figure 2 and the rupture can depart from the circular form by creating local failure zones with regional plastic deformation of the respective soils. Ruptures in clays can also behave that way [44].
There are numerous ways and means shown in many textbooks on soil mechanics, to do the mathematics involved in finding the moments in Equation (9).
5.3. Translatory Wave Theory Used on Landslide Flow
In hydrodynamics, the stationary model is usually applied for channel flow. However, there are certain difficulties in using this model on landslides flowing over dry land, just as water floods so often do. To use this model, the slide has to be flowing, i.e., a regular slide that do actually flow with a velocity high enough, so convective acceleration plays its part.
The Saint-Venant Equation system has two possible solutions. The stationary flow, and the translatory wave. Equations (1)–(5) in [30], show the translatory wave model, they lead to a flow profiled in [30] (Figure 1), this flow may look like a wall of fluid flowing over dry land.
The translatory model involves analyses that are complicated in nature but lead to a simple system when fully derived. It can be very useful in studies one has to do, to define the area the slide covers, extent of its boundaries, and limits to the values of the various parameters involved. To start with a simple wave model, can save a lot of effort in trial and error. Simple models can even produce result that are good enough to define hazard areas with sufficient accuracy. They are also valuable as a prelude to studies in a complicated numerical model,
High velocity slides will usually be type (iii), and they can start as type (i) or (ii) slides but end up as type (iii) as is shown in Section 6 case study B. This is because the initial flow deformation can mix the debris into a heterogeneous mass that flows as translatory wave behaving as Equation (5) in [30]. In that state, the cohesion the undisturbed soil had originally, is practically gone and we are left with a ϕ’ that can have a lower value than the slide will have when it has settled in its final resting place. The ϕ’ can be difficult to estimate so it is suggested to use the more convenient slope factor [29], instead:
Sf = sinθ(1 − tanϕ’⁄tanθ) = sinθ(1 − |∇z|/tanθ); ∇z: gradient slope of the slide at rest
The first part of Equation (10) is the definition, the last part the expression one must use to estimate the slope factor from a slide that has stopped in a terrain sloping with the angle θ. The formula for the profile of the slide is repeated here from [29] with the symbols unchanged for convenience.
In Equation (11), c is the no longer cohesion, but the wave velocity of the translatory wave in m/s, when the length is in meters and the time in seconds.
V2 = C2gSfy; c2 = C2gSfy0
It is important to estimate how far a slide runs from its source. When the slope is long and steep enough it is only the volume that limits the runout length. The total volume, VS, must be estimated from topographical maps [45], easy enough after the slide, but may be very difficult for suspectable sites where there have been no slides yet. For a translatory wave of length LVS from the point where the depth is yVS to the beginning of the wave where y = 0,
VS = ∫0LVSydx ≅ yVSLVS
As the front of the translatory wave is very steep, Equation (12) is an expression that is usually accurate enough for the value of the integral. Otherwise, integrating Equation (11) is not a problem when the depth y is well known. The point [x = LVS; y = yVS] must be chosen where the depth of the slide is at its maximum, so this point moves with the slide, actually a little bit faster than the wave velocity c. VS and LVS will be diminished, but a tail will be formed behind the point [x = LVS; y = yVS] containing the volume reduction. What happens in this tail is not very interesting, it is the wave in front that decides for how long the wave can flow, but if the flow path is long enough the tail will, so to speak, eat up the translatory wave. This may be the destiny of small slides.
Bigger slides will flow until they stop with the steep frontal wall of the translatory wave undisturbed, but the slope reduction in the track will eventually stop the wave. If we let index 1 denote the upstream side of a slope change and index 2 the downstream side, the flow must be unchanged, or c1y1 = c2y2 across the slope change. This together with Equation (11) defines y2 > y1 when Sf2 < Sf1, or in words, the depth of the slide increases with diminishing slope. Using Equation (11) to find the variation of y this way is not really a problem, the numerical calculations can be performed in standard programs, e.g., the popular EXCEL. The result will be the height and position of the wave front. An exception from this can occur if the slide has obtained supercritical speed before the slope change (Section 6.3, case study C). In this case, a numerical model containing the full St. Venants equation system, including terms representing both local and convective acceleration may be the only way to model the slide satisfactorily. The same procedure is used in flood studies as discussed in Section 5.3. An example is in [24], a simpler model with Voellemy rheology parameters is demonstrated there.
In a study of landslides this investigation provides data for C, Sf and ϕ’, [Table 1, case study A], such data is valuable in defining the danger area in hazard assessment of potential landslide sites.
6. Case Studies of Hazards, Probability and Mitigation
6.1. Case Study A. Landslide in the Sölvadalur Valley, North Iceland
6.1.1. The Event
On 29 June 1995, a debris slide occurred in the Þormóðsstaðir valley just upstream of its junction with the Sölvadalur valley. This is in the southern part of the region of the much bigger Eyjafjörður valley, in central North Iceland (Figure 1). This slide was among the largest that occurred in Iceland during the 20th century [46,47,48].
The Sölvadalur valley is a tributary valley, located on the eastern side in the innermost part of the Eyjafjörður valley system. It is a deep and narrow, north-south oriented valley and separated from the Eyjafjörður main valley by the 700–900 m high Mt. Hólafjall. The western side of valley is covered by relatively thick post-glacial soil. The eastern valley side is steeper and reaches up to 900–1000 m at the Mt. Skjónafell. The Sölvadalur is drained by the river Núpá which flows in a canyon in the bottom of the valley (Figure 4, upper left corner).
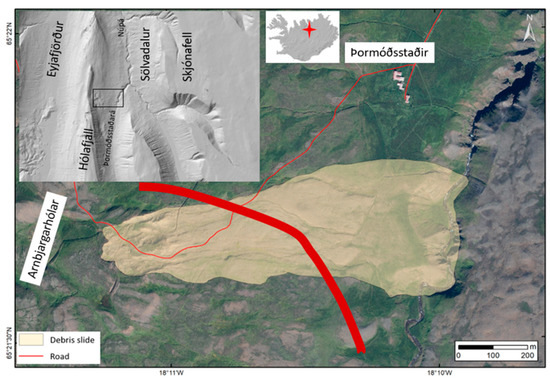
Figure 4.
Overview map of the Sölvadalur landslide. Location in the valley in north Iceland in upper left corner. Location in Iceland shown. The landslide falls close to the farm Þormóðsstaðir, the inserted blue line shows the hypothethical position of a retaining protection wall that would have deflected the slide (aerial photo from Loftmyndir 2018, National Land Survey, Iceland DEM).
The bedrock in the Eyjafjörður area belongs to the Tertiary basaltic series [49,50,51]. The bedrock consists mostly of 2–30 m thick jointed basaltic lava flows, separated by lithified sedimentary horizons of variable origin [52,53]. The bedrock in the Sölvadalur area is though strongly influenced by an ancient central volcano which is located around the Torfufellsdalur valley, southwest from the area. Thick sedimentary layers and rhyolite have been observed in the Mt. Hólafjall, which can be traced to this old central volcano, [54]. They have their effect on the resistance of the soil.
The debris-slide occurred at the end of an intensive snow-melting period, after a relative cold and snowy winter. As the first snow of the winter 1994–1995 was accumulated on unfrozen ground and thus insulated it, the meltwater in the spring of 1995 percolated into the ground and destabilized an old rock-slide debris (see Section 6.1.2). This situation led to an unusually high ground-water level, which eventually brought about a great number of debris-flows and flooding of rivers in Iceland in late spring and early summer 1995 [46,47].
6.1.2. The Slide
The debris slide was initiated as a part of a 6000 to 9000 years old Arnbjargarhólar (Figure 4) rockslide fell down the mountainside, just north of the farm Þormóðsstaðir in the innermost part of the Sölvadalur valley (Figure 4) [55]. Up to 2 m thick soil covers the rockslide material. The lowermost 50 cm of the soil profile are composed of massive humus material, but on top of it a tephra horizon can be seen.
The uppermost part of the debris-slide is located at about 580 m a.s.l. Its head scarp is about 150 m wide, 300 m long and 4–5 m high. The slide is 900 to 1000 m long and about 400 to 500 m wide at the lower end on the western rim of the canyon at 340 m height. The total fall height is about 240 m. The debris mass entered the 40 m deep and up to 180 m wide canyon of the Þormóðsstaðará river. Parts of the slide crossed the canyon up to the opposite rim, (Figure 1 and Figure 4), but the rest dammed up the riverbed, for a short period of time. The river was dammed, and the flood level were traceable at least 300 m upstream in the canyon. The scar of the slide cover about 250,000 m2 of the mountain side and the total volume is estimated between 600,000 and 800,000 m3. It is estimated that the debris mass travelled at around 40–45 km/hour down the slope [46,47].
6.1.3. Evaluation
This is a debris-slide, with a 900 m long and a 4–5 high m head scarp. A slide channel from 580 m a.s.l. where the ground slope is tgθ = 0.3 down to 340 m.
Table 1 and Figure 5 are prepared using Equation (11). It shows the slide in the position just before it starts flowing in the river canyon. Note, that the thickness of the slide, y, is 10 times exaggerated so Figure 5 is really showing the ground level z (yellow line) and 10y on top of that (red line) in order to the profile of the wave becomes clearly visible.

Table 1.
The Sölvadalur slide data computed using Equation (11) with the tabulated data.
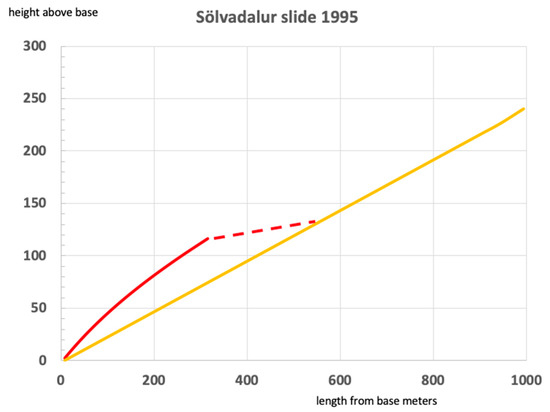
Figure 5.
The slide profile, survey of 1995.
From 400 m. a. s. l down to 300 there is a about 50% slope reduction. A slope reduction down to 0.2 would change the y0 from 5 to 6.6 m and the wave velocity, c, from 12.9 to 9.8 m/s.
This slide was obviously a grave risk for the Þormóðsstaðir farm, a 5 m high translatory wave running at 12.9 m/s would have been a total disaster for the farm, humans and animals alike. To speculate in the hazard assessment, subsequent mitigation possibilities and construction of protection works is therefore interesting. Had the slide danger been anticipated before the event, a protective earth dam could have retained the flow; this kind of mitigation is in use in Iceland [48]. In Figure 4, there is a red line indicating such a mitigating measure. Its length would have been enough to shield off the farm, but to prevent the slide to enter the river canyon a much longer dam is needed. The height of the dam would have to be a staggering 15 m from ground to crest, if the wave were to hit the dam straight on with its 12.9 m/s speed. By cutting the slide route under 45°, the height can be reduced to 10 m or less, but still an enormous undertaking. Such is the force of the translatory wave. However, the economic viability of such an undertaking is beyond the scope of this article.
6.2. Case Study B: The Rockslide in the Askja Caldera in East Iceland
6.2.1. The Event
A large rockslide fell on 21 July 2014 in the Askja Caldera in the northeastern highlands of Iceland (Figure 2 and Figure 6). This is a central volcano of international fame and a popular tourist site. This rockslide is one of the largest rockslides that have occurred in Iceland since the settlement of the island more than 1100 years ago. The slide was initiated in the Suðurbotnar area in the southeastern rim of the caldera and fell into the Öskjuvatn Lake. The lake is about 12 km2, 2.5 to 3.5 km in diameter and up to 220 m deep (Figure 6). No one witnessed the rockslide but members of a rescue team, located about 15 km from the site saw a strange looking cloud or a plume rising from the lake at around 23:27. This cloud was most likely a steam column rising from a high temperature thermal area within the rockslide scar. Earth tremors were observed in nearby seismic stations giving the exact time of the slide at 23:24. Indications of movements prior to the slide obtained from photographs show that slow movement of the slide mass had already begun few years before the slide. It is likely that thick snow cover and rapid melting the days before the slide may have initiated the slide. As the rockslide entered the lake a 20–30 m high tsunami was inundated the shore with vertical runup to 60–80 m [40,56,57,58].
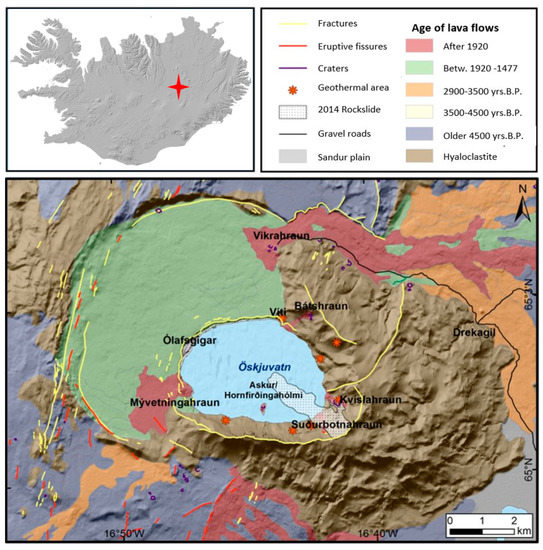
Figure 6.
Overview map of the Askja area in the central highlands of Iceland (Modified after [59]).
6.2.2. The Slide
The scar of the rockslide is about 8–900 m wide at around 1400 m. a.s.l., about 350 m above the lake surface, at 1056 m. a.s.l. The fall height is around 350 m and the runout length about 1100 m above the lake level. Part of the rockslide on the other hand entered the lake and the width of the debris at the lake shore is around 600 m. On basis of bathymetric data of the lake the debris flowed about 1900 m into the lake basins down to about 200 m depth, giving the total runout of 3000 m and a total fall height of about 550 m. The movement of the slide is a rotational one in a slip circle (Figure 7, left). The calculated volume is above the lake surface. If the sliding plane below the lake surface is taken into account, the volume of the slide would be higher. Based on the DEM on Figure 7, right, obtained before and after the rockslide a total volume could be as high as 20 million m3. About 10 million are located above the shoreline so up to 10 million m3 may be in the lake. This data and further information are in [40,56,57,58].
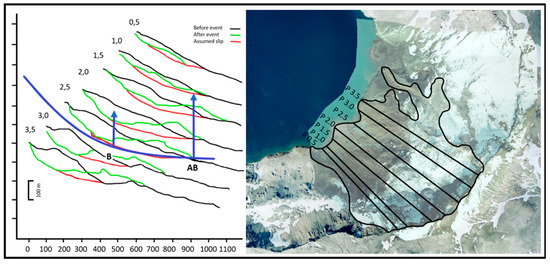
Figure 7.
Longitudinal sections from the DEMs of the rockslide area from before (black curves) and after (green curves) the slide, above the water lake. The interpreted slip circle surface is marked by the reddish curves, modified from [59].
6.2.3. Evaluation
Figure 7 shows profiles 0.5–3.5. Equation (9) and associated text is used to estimate the slip. The slip circle (blue) has a radius of 1100 m. The AB marks the z-axis, y = 0. B marks the vertical through the center of gravity of the undisturbed soil, it is found to be at y = −450 m. The slip circle is 790 m long and the mass is 40,000 m2, its density is assumed 2600 kg/m3. All this results in the moment equation: c’ × 790 × 1100 = 9.8 × 2600 × 40,000 leading to c’ = 1.2 kN/m2 as average shear resistance.
In discussing mitigation and protection works there is little to be said. The c’ =1.2 kN/m2 is rather low for 100 m thick deposits, so more slides of this kind can be expected, and this is a popular tourist site. Slope failures are normally mitigated by driving piles through the potential slip surface to increase the shear resistance. In 100 m thick deposits this is hardly an option. The only possible mitigation seems to be careful risk assessment and keeping the tourists out of the most dangerous areas. The details of such an operation are outside our scope.
6.3. The Landslide in Mt. Fagraskógarfjall in the Hítardalur Valley, West Iceland
6.3.1. The Event
On 7 July 2018, a large landslide occurred in the eastern slope of the Mt. Fagraskógarfjall in the Hítardalur valley, in West Iceland (Figure 3 and Figure 8). The slide is one of the largest landslides that has occurred in Iceland during the last centuries. The landslide was detected by a seismograph at 05:17, but according to eyewitness a smaller landslide was detected in the area around 23:30 on 6 July [59].
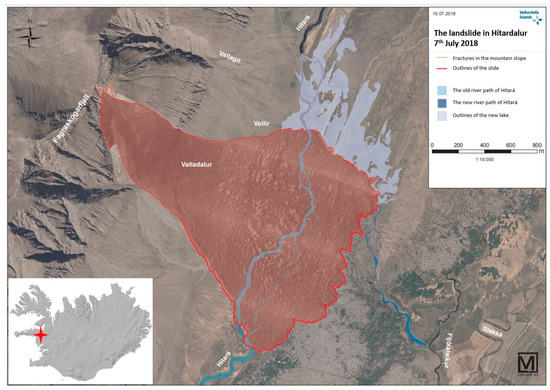
Figure 8.
The Hítardalur landslide on the 7 July 2018 (modified from vedur.is, 2018).
The Hítardalur valley is about 20 km long and up to 5 km wide, orientated in SSW-NNE direction, with relatively steep mountain sides. The slide was originated from the eastern side of the Mt. Fagraskógarfjall which is located in the outermost part on the western valley side, (Figure 8 and Figure 9). The bedrock in the area is composed of tertiary basaltic lava that is considered to be 10 million years old. Thick sedimentary layers of various origin can also be found within the stratigraphic sequence. Quaternary volcanic formations, from the last glaciation and Holocene, e.g., hyaloclastic formations and lavas, occur within in the vicinity of the slide. Faults and fractures are prominent within the region, and can be divided into three groups, NE-SW, N-S and NW-SE [60].
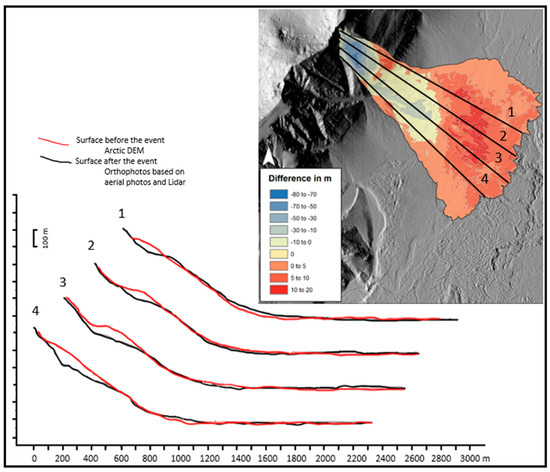
Figure 9.
Longitudinal sections from DEMs of the Hítardalur landslide, modified from [60].
As the slide flowed down to the valley floor and dammed up the Hítará and formed a new lake. As Hítará is a salmon fishing river, this had economic consequences. Later, the river flowed towards the east through a new channel to the river Tálmi, which further downstream merges into the Hítará river.
The width of the debris tongue is approximately 1.5 km and the total runout length about 2.3 km, giving a runout angle of 12–13° (Figure 8). The maximum thickness of the debris tongue, above the valley bottom, is about 30 m, but the average thickness is around 7 m [59].
The volume calculations were made by comparing DEMs prior to the event and then after it (Figure 9). Based on this comparison approximately 7 million m3 of the mountain slope was released from the source area. As the landslide mass fell down the slope, it ploughed through older sediments at the foot of the mountain and on the valley bottom. Due to this erosion, it is difficult to calculate the volume of the slide, but it might be in the range of 10–20 million m3 [59].
6.3.2. The Slide
The Hítardalur landslide, (Figure 3), is of the same kind as in Sölvadalur (Section 6.1), but much larger, about 10,900,000 m3. The uppermost part of the landslide is located at around 640 m a.s.l. and the debris tong is located at 180 m a.s.l. giving a total fall height of about 460 m. The slide flowed down a 28° slope, about 900 m wide in the lower part, from a 400 m wide head scarp about 400 m above the valley floor. There the valley floor is almost level ground and the landslide fans out under 80° for a 400 m more. The difference from Sölvadalur is this fan out and subsequent flow on level or almost level ground. From this point the landslide flows in a 1300 m wide channel for 1000 m on the level ground to a total runout length of 2.3 km. It covers roughly 2 km2, making the mean thickness 5.5 m, but the maximum thickness is 20–30 m (Figure 8).
The fan-out from 400 m width to 1300 m would give rise to an average reduction in flow depth by 3.2. This indicates an average slide thickness about 16 m just below the head scarp, indicating a y0 value of 20 m. Using the Sölvadalur values to estimate the wave velocity, we get c = 26 m/s. This gives us a velocity head (kinetic energy measured in meters) of 34 m at the beginning of the fan out. This gives an energy slope of 2.4%, or approximately 10 times that of a flowing river, which explains how the landslide can cover 1.4 km on almost level ground. This high velocity is at the limit of what the simplified translatory wave theory can handle, as the fluid acceleration and changes in momentum are not included. An in-depth analysis of this slides requires numerical analysis with the full St. Venant’s equation system.
7. Discussion
We have several examples of the use of the translatory wave theory using the special flow factor Equation (10). This raises the question of when it cannot be used. The answer is that this method becomes unreliable when there is interaction between the slide and the ambient fluid, e.g., snow avalanches taking a lot of air, and subaqueous flows taking in a lot of ambient water. In [61] there is a fine treatment of that kind of flows. This theory cannot be used for them. An example of a database where it can be difficult what theory to use for the flow is [62]. This fine work contains the morphology of 322 slides, there is information on area, volume, length and thickness of the slides but the slope profiles, are missing. However, it is quite clear from the paper that many of the slides are behaving in the exact same manner as the Hítardalur landslide; see Figure 3, Figure 8 and Figure 9.
In general, it is very important to gather information on the flow profiles when a landslide is to be modeled. This may not seem so important when the landslide event for slides that happened long time ago, but information on the elevation profiles of the flow path can bring about the geotechnical resistance parameters used to do the calculations shown in Table 1. And these may again provide information on similar parameters in another place where a landslide is suspected to happen and scientists would like to predict the consequences, [12,13,30]. Advanced technologies to obtain such data are described in [63].
8. Conclusions
Landslide types are classified according to their geological and geomorphological properties in a classification system that has been under development for a long time. However, the flow type depends upon the physical properties of the flowing material and Newtons law of motion. The flows can therefore be very different within the same landslide class.
A landslide starts when the shear stress exceeds the shear resistance and a rupture line is formed. Movement starts as a creeping motion where the velocity does not influence the development of the rupture line. Later the flow may develop the character of laminar flow, and the velocity can still be without any influences on the development of the flow. Later the velocity can increase to very high values, turning the slide into a sledgehammer that annihilates everything in its way.
For this, three flow types are defined. The first two, type (i) and type (ii) include the creeping and laminar motion where the velocity does influence the development of the flow only a little. The high velocity slides are included in type (iii). Further research, especially on the influence of increasing velocity on the slide, may bring about an update of the Varne classification system.
The modeling of type (i) and type (ii) slides can be done with a velocity relation that affects the flow very little, so the final position of the slide front depends mainly on how well the shear resistance is modeled and how well the model itself represents the landscape. Many fine slide models of this kind do exist in the literature. For type (iii) slides of higher velocity, the translatory wave theory is used, it combines the equation of motion with the non-stationary solution of St. Venants equation that produces a wave that can flow over dry land with a rather steep front. The flow is stationary in the phase (x-ct) but not in time and is in this respect different from the most popular flow models.
This method can model landslides of a velocity high enough to run over flat land for a considerable runout length. A new slope factor is defined. It defines a velocity according to the shear stress in excess of the shear resistance but not the absolute value of the shear stress as in Newtonian fluids. The translatory flow theory coupled with the new slope factor can make modeling of fast running landslides easier and more reliable.
There are three case studies, A, B, and C. In case study A, a slide threatens a farmstead, it is shown in Table 1 how field data, together with the translatory wave model, can be used to define the maximum height of the slide wall and, slope factor and the Chezy coefficient. Such data can then be used for risk assessment in potential danger areas where slides of similar properties may happen. Case study B demonstrates how a type ii) slide (a slip circle movement) can develop into a high velocity slide farther down the slope. Case study C is similar to case study A but demonstrates a slide of so high velocity that it keeps running for a long time on flat ground. For such slides it is recommended that a numerical model utilizing the full St. Venants equations is used to confirm the results of the translatory wave model.
Author Contributions
The contributions of all authors are the same. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors like to thank Ásta Rut Hjartardóttir, at the University of Iceland for valuable assistance with the figure configuration and Jón Kristinn Helgason, MS at the Icelandic Met Office for providing unpublished data and figures. The authors are grateful to the reviewers for their constructive comments on the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Casagli, N.; Frodella, W.; Morelli, S.; Tofani, V.; Ciampalini, A.; Intrieri, E.; Lu, P. Spaceborne, UAV and ground-based remote sensing techniques for landslide mapping, monitoring and early warning. Geoenviron. Disasters 2017, 4, 9. [Google Scholar]
- Arabameri, A.; Karimi-Sangchini, E.; Pal, S.C.; Saha, A.; Chowdhuri, I.; Lee, S.; Bui, D.T. Novel Credal Decision Tree-Based Ensemble Approaches for Predicting the Landslide Susceptibility. Remote. Sens. 2020, 12, 3389. [Google Scholar] [CrossRef]
- Chowdhuri, I.; Pal, S.C.; Arabameri, A.; Ngo, P.T.T.; Chakrabortty, R.; Malik, S.; Das, B.; Roy, P. Ensemble approach to develop landslide susceptibility map in landslide dominated Sikkim Himalayan region, India. Environ. Earth Sci. 2020, 79, 1–28. [Google Scholar] [CrossRef]
- Pal, S.C.; Das, B.; Malik, S. Potential Landslide Vulnerability Zonation Using Integrated Analytic Hierarchy Process and GIS Technique of Upper Rangit Catchment Area, West Sikkim, India. J. Indian Soc. Remote. Sens. 2019, 47, 1643–1655. [Google Scholar] [CrossRef]
- Pal, S.C.; Chowdhuri, I. GIS-based spatial prediction of landslide susceptibility using frequency ratio model of Lachung River basin, North Sikkim, India. SN Appl. Sci. 2019, 1, 416. [Google Scholar] [CrossRef]
- Pham, B.T.; Prakash, I.; Bui, D.T. Spatial prediction of landslides using a hybrid machine learning approach based on Random Subspace and Classification and Regression Trees. Geomorphol. 2018, 303, 256–270. [Google Scholar] [CrossRef]
- Highland, L.M.; Bobrowsky, P. The Landslide Handbook—A Guide to Understanding Landslides, United States Geological Survey, Landslide Program and National Landslide Information Center, Mail Stop 966, Box 25046; Denver Fed-eral Center: Denver, CO, USA, 2008. Available online: https://pubs.usgs.gov/circ/1325/ (accessed on 23 February 2021).
- Komac, M. A landslide susceptibility model using the Analytical Hierarchy Process method and multivariate statistics in perialpine Slovenia. Geomorphology 2006, 74, 17–28. [Google Scholar] [CrossRef]
- Guzzetti, F.; Malamud, B.D.; Turcotte, D.L.; Reichenbach, P. Power-law correlations of landslide areas in central Italy. Earth Planet. Sci. Lett. 2002, 195, 169–183. [Google Scholar] [CrossRef]
- Masson, D.G.; Harbitz, C.B.; Wynn, R.B.; Pedersen, G.; Løvholt, F. Subaqueous landslides: Processes, triggers and hazard prediction. Philosophical Transactions of the Royal Society A: Mathematical. Phys. Eng. Sci. 2006, 364, 2009–2039. [Google Scholar]
- Sæmundsson, Þ.; Morino, C.; Helgason, J.K.; Conway, S.J.; Pétursson, H.G. The triggering factors of the Móafellshyrna debris slide in northern Iceland: Intense precipitation, earthquake activity and thawing of mountain permafrost. Sci. Total. Environ. 2018, 621, 1163–1175. [Google Scholar] [CrossRef]
- Elíasson, J. Initial Wave Height and Total Energy of Landslide-Generated Tsunamis from Translatory Wave Theory. In Proceedings of the Geotechnics and Earthquake Geotechnics towards Global Sustainability; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 159–174. [Google Scholar]
- Eliasson, J. Earthquake-Generated Landslides and Tsunamis. In Earthquakes—Impact, Community Vulnerability and Resilience; IntechOpen: London, UK, 2019. [Google Scholar]
- Cruden, D.M. A simple definition of a landslide. Bull. Int. Assoc. Eng. Geol. 1991, 43, 27–29. [Google Scholar] [CrossRef]
- Varnes, D.J. Slope Movement Types and Processes. Transportation Research Board Special Report: 11–33. In Special Report 176: Landslides: Analysis and Control; Transportation Research Board: Washington, DC, USA, 1978. [Google Scholar]
- Cruden, D.M.; Varnes, D. Landslide types and processes. In Landslides Investigation and Mitigation; Transportation Research Board: Washington, DC, USA, 1996; pp. 36–75. [Google Scholar]
- Hungr, O.; Evans, S.G.; Bovis, M.J.; Hutchinson, J.N. A review of the classification of landslides of the flow type. Environ. Eng. Geosci. 2001, 7, 221–238. [Google Scholar] [CrossRef]
- Hutchinson, J.H. Morphological and Geotechnical Parameters of Landslides in Relation to Geology and Hydrogeology. In Proceedings of the 4th International Symposium on Landslides; Balkema: Rotterdam, The Netherlands, 1988; pp. 3–35. [Google Scholar]
- Julian, M.; Anthony, E.J. Landslides and climatic variables with specific reference to the Maritime Alps of southeast-ern France. In Temporal Occurrence and Forecasting of Landslides in the European Community, Programme EPOCH; Casale, R., Fantechi, R., Flageolle, J.C., Eds.; European Commission: Brussels, Belgium, 1994; pp. 697–721. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Casadei, M.; Dietrich, W.E.; Miller, N.L. Testing a model for predicting the timing and location of shallow land-slide initiation in soil-mantled landscapes. Earth Surface Process. Landf. 2003, 28, 925–950. [Google Scholar] [CrossRef]
- Crozier, M.J. Prediction of rainfall-triggered landslides: A test of the antecedent water status model. Earth Surface Process. Landf. 1999, 24, 825–833. [Google Scholar] [CrossRef]
- Tsai, T.-L.; Yang, J.-C. Modeling of rainfall-triggered shallow landslide. Environ. Earth Sci. 2006, 50, 525–534. [Google Scholar] [CrossRef]
- Hergarten, S.; Neugebauer, H.J. Self-organized criticality in a landslide model. Geophys. Res. Lett. 1998, 25, 801–804. [Google Scholar] [CrossRef]
- Hussin, H.Y.; Luna, B.Q.; Van Westen, C.J.; Christen, M.; Malet, J.P.; Van Asch, T.W. Parameterization of a nu-merical 2-D debris flow model with entrainment: A case study of the Faucon catchment, Southern French Alps. Nat. Hazards Earth Syst. Sci. 2012, 12, 3075–3090. [Google Scholar] [CrossRef]
- Farahmand, A.M.; Aghakouchak, A.A. A satellite-based global landslide model. Nat. Hazards Earth Syst. Sci. 2013, 13, 1259–1267. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; Wiley: New York, NY, USA, 1943. [Google Scholar]
- Salvatici, T.; Di Roberto, A.; Di Traglia, F.; Bisson, M.; Morelli, S.; Fidolini, F.; Bertagnini, A.; Pompilio, M.; Hungr, O.; Casagli, N. From hot rocks to glowing avalanches: Numerical modelling of gravity-induced pyroclastic density currents and hazard maps at the Stromboli volcano (Italy). Geomorphology 2016, 273, 93–106. [Google Scholar] [CrossRef]
- Sottili, G.; Martino, S.; Palladino, D.M.; Paciello, A.; Bozzano, F. Effects of tidal stresses on volcanic activity at Mount Etna, Italy. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Elíasson, J.; Sæmundsson, Þ. The Translatory Wave Model for Landslides. In Landslides—Investigation and Monitoring; IntechOpen: London, UK, 2020. [Google Scholar]
- Eliasson, J.; Kjaran, S.P.; Holm, S.L.; Gudmundsson, M.T.; Larsen, G. Large hazardous floods as translatory waves. Environ. Model. Softw. 2007, 22, 1392–1399. [Google Scholar] [CrossRef]
- Pedersen, F.B. Environmental Hydraulics: Stratified Flows: Stratified Flows; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Bryant, E. Tsunami: The Underrated Hazard, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Lovholt, F.; Harbitz, C.B.; Haugen, K.B. A parametric study of tsunamis generated by subaqueous slides in the Ormen Lange/Storegga area off western Norway. Mar. Pet. Geol. 2005, 22, 219–231. [Google Scholar] [CrossRef]
- Bondevik, S.; Mangerud, J.; Dawson, S.; Dawson, A.; Lohne, Ø. Record-breaking height for 8000-year-old tsunami in the North Atlantic. Eos 2003, 84, 289–293. [Google Scholar] [CrossRef]
- Grauert, M.; Bjorck, S.; Bondevik, S. Storegga tsunami deposits in a coastal lake on Suduroy, the Faroe Islands. Boreas 2001, 30, 263–271. [Google Scholar] [CrossRef]
- Yeh, H.; Chadha, R.K.; Francis, M.; Katada, T.; Latha, G.; Peterson, C.; Raghuraman, G.; Singh, J.P. Tsunami Runup Survey along the Southeast Indian Coast. Earthq. Spectra 2006, 22, 173–186. [Google Scholar] [CrossRef]
- Mori, N.; Takahashi, T.; Yasuda, T.; Yanagisawa, H. Survey of 2011 Tohoku earthquake tsunami inundation and run-up. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Grilli, S.T.; Taylor, O.D.S.; Baxter, C.D.P.; Maretzki, S. A probabilistic approach for determining subaqueous land-slide tsunami hazard along the upper east coast of the United States. Mar. Geol. 2009, 264, 74–97. [Google Scholar] [CrossRef]
- Gylfadóttir, S.S.; Kim, J.; Helgason, J.K.; Brynjólfsson, S.; Höskuldsson, Á.; Jóhannesson, T.; Harbitz, C.B.; Løvholt, F. The 2014 Lake Askja rockslide-induced tsunami: Optimization of numerical tsunami model using observed data. J. Geophys. Res. Oceans 2017, 122, 4110–4122. [Google Scholar] [CrossRef]
- L’Heureux, J.-S.; Locat, A.; Leroueil, S.; Demers, D.; Locat, J. (Eds.) Landslides in Sensitive Clays—From Geosciences to Risk Management. In Advances in Natural and Technological Hazards Research; Springer: Berlin/Heidelberg, Germany, 2014; Volume 36. [Google Scholar]
- McDougall, S.; Hungr, O. A model for the analysis of rapid landslide motion across three-dimensional terrain. Can. Geotech. J. 2004, 41, 1084–1097. [Google Scholar] [CrossRef]
- Quinn, P.; Diederichs, M.; Rowe, R.; Hutchinson, D. A new model for large landslides in sensitive clay using a fracture mechanics approach. Can. Geotech. J. 2011, 48, 1151–1162. [Google Scholar] [CrossRef]
- Locat, A.; Locat, P.; Demers, D.; Leroueil, S.; Robitaille, D.; Lefebvre, G. The Saint-Jude landslide of 10 May 2010, Quebec, Canada: Investigation and characterization of the landslide and its failure mechanism. Can. Geotech. J. 2017, 54, 1357–1374. [Google Scholar] [CrossRef]
- Amirahmadi, A.; Pourhashemi, S.; Karami, M.; Akbari, E. Modeling of landslide volume estimation. Open Geosci. 2016, 8, 360–370. [Google Scholar] [CrossRef][Green Version]
- Pétursson, H.G. Potential danger of landslides in Sölvadalur, Report to the Icelandic Civil Defense Authorities; Icelandic Government: Akureyri, Iceland, 1997. (In Icelandic) [Google Scholar]
- Sæmundsson, Þ.; Pétursson, H.G. The Sölvadalur debris-slide. In Proceedings of the Nordic Geological Winter Meeting, Aarhus, Denmark, 13–16 January 1998. [Google Scholar]
- Pétursson, H.G.; Sæmundsson, Þ. The 1995 Sölvadalur debris slide in Central North Iceland. In Proceedings of the First Science Meeting of the European Science Foundation ESF—Network SEDIFLUX, Sauðárkrókur, Iceland, 18–21 June 2004; Beylich, A.A., Sæmundsson, Þ., Decaulne, A., Sandberg, O., Eds.; European Science Foundation (ESF): Strasbourg, France, 2004. [Google Scholar]
- Moorbath, S.; Sigurdsson, H.; Goodwin, R. K-Ar ages of oldest exposed rocks in Iceland. Earth Planet. Sci. Lett. 1968, 26, 197–205. [Google Scholar] [CrossRef]
- McDougall, I.; Kristjansson, L.; Sæmundsson, K. Magnetostratigraphy and geochronology of NW-Iceland. J. Geophys. Res. 1984, 89, 7029–7060. [Google Scholar] [CrossRef]
- Watkins, N.D.; Walker, G.P.L. Magnetostratigraphy of eastern Iceland. Am. J. Sci. 1977, 277, 513–584. [Google Scholar] [CrossRef]
- Sæmundsson, K.; Kristjánsson, L.; McDougal, I.; Warkins, N.D. K-Ar dating, geological and paleomagnetic study of a 5-km lava succession in Northern Iceland. J. Geophys. Res. 1980, 85, 3628–3646. [Google Scholar] [CrossRef]
- Sæmundsson, K. Outline of the geology of Iceland. Jökull 1979, 29, 7–28. [Google Scholar]
- Jóhannesson, H. Yfirlit um jarðfræði Tröllaskaga (Miðskaga); Overview of the Geology of Tröllaskagi; Árbók Ferðafélags Íslands: Reykjavík, Iceland, 1991; pp. 39–56. (In Icelandic) [Google Scholar]
- Pétursson, H.G.; Larsen, G. An early Holocene basaltic tephra bed in North Iceland, a possible equivalent to the Saksunar-vatn Ash Bed. In Proceedings of the 20th Nordic Geological Winter Meeting, Reykjavík, Iceland, 7–10 January 1992; p. 133. [Google Scholar]
- Sæmundsson, Þ.; Helgason, J.K.; Brynjólfsson, S.; Höskuldsson, Á.; Hjartardóttir, Á.R.; Sigmundsson, F. The rockslide in the Askja caldera on 21 July 2014. In Proceedings of the European Geosciences Union, General Assembly 2015, Vienna, Austria, 12–17 April 2015. [Google Scholar]
- Sæmundsson, Þ.; Helgason, J.K.; Brynjólfsson, S.; Höskuldsson, Á.; Hjartardóttir, Á.R.; Sigmundsson, F. What did trigger the rockslide in the Askja caldera on 21 July 2014. In Proceedings of the 32nd Nordic Geological Winter Meeting 2016, Helsinki, Finland, 13–15 January 2015. [Google Scholar]
- Helgason, J.K.; Gylfadóttir, S.S.; Brynjólfsson, S.; Grímsdóttir, H.; Höskuldsson, Á.; Sæmundsson, Þ.; Hjartardóttir, Á.R.; Sigmundsson, F.; Jóhannesson, T. Berghlaupið í Öskju 21. júlí 2014. Náttúrufræðingurinn 2019, 89, 5–21, (The rockslide in Askja, in Icelandic). [Google Scholar]
- Helgason, J.K.; Sæmundsson, Þ.; Drouin, V.; Jóhannesson, T.; Grímsdóttir, H.; Jónsson, M.H.; Gylfadóttir, S.S. The Hítardalur landslide in West Iceland in July 2018. In Proceedings of the 21st EGU General Assembly, Vienna, Austria, 7–12 April 2019. [Google Scholar]
- Ragnarsdóttir, K.V. Jarðlagaskipan Fagraskógarfjalls og Vatnshlíðar í Hítardal (e. Geology of Mt. Fagraskógarfjall and Mt. Vatnshlíðarfjall in Hítardalur Valley, in Icelandic). Bachelor Dissertation, University of Iceland, Reykjavík, Iceland, 1979. [Google Scholar]
- Mulder, T.; Alexander, J. The physical character of subaqueous sedimentary density flows and their deposits. Sedimentology 2001, 48, 269–299. [Google Scholar] [CrossRef]
- Moscardelli, L.; Wood, L. Morphometry of mass-transport deposits as a predictive tool. GSA Bull. 2015, 128, B31221. [Google Scholar] [CrossRef]
- Lee, H.J. Undersea landslides: Extent and significance in the Pacific Ocean, an update. Nat. Hazards Earth Syst. Sci. 2005, 5, 877–892. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).