1. Introduction
Cumbre Vieja volcano (CCV) is located in La Palma (Canary Islands, Spain, see
Figure 1). After one week of seismic activity in the area, it erupted on 29 September 2021 at 15:15 h local time. On 25 September, the west side of the main ash cone collapsed and new mouths were open. The lava flow reached the ocean on 29 September and started to create new land offshore (this land is locally denoted as
fajana). This newly formed land reached the island slope on October 10th, and authorities worried about the possibility of a submarine landslide down the slope, which would create some
swell (this was the word used in Spanish TV news). While this work is being written, the eruption continues alternating periods with higher and lower activity; new mouths are open, and new lava flows are arriving to the sea.
CVV has drawn a strong interest among the scientific community since the first published alarming work [
1], in which the tsunami generated by a potential landslide from the western side of CCV was simulated. This work was strongly criticized (for instance, in [
2]) because of the extremely large and non-justified landslide volume considered in the simulation and the linear wave model used. More recent works have considered volumes ranging from 20 to 80 km
(see for instance [
3]), which may be compared with the 500 km
used in [
1].
However, although the tsunamis generated by a landslide in the western side of CCV involving more or less exaggerated volumes have been simulated [
1,
3,
4,
5,
6,
7], this is not the case for a submarine landslide down the island slope. It would be caused by the accumulation of lava in the island shelf, which could eventually lead to the instability of this shelf and then produce a submarine slide of material down the island slope.
The purpose of the present paper consists of simulating the tsunami generated by such potential slide. A nonlinear hydrodynamic model is used. Since the volume involved in the slide is not known, several simulations were carried out to evaluate the consequences of varying involved volumes. The model used is described in
Section 2; the results are presented and discussed in
Section 3.
2. Materials and Methods
The 2D depth-averaged nonlinear barotropic hydrodynamic equations, which describe the propagation of surface shallow water gravity waves, are used in the present modeling work (see, for instance, [
8]). They are:
where
u and
v are the depth averaged water velocities along the
x and
y axis,
h is the depth of water below the mean sea level,
is the displacement of the water surface above the mean sea level measured upwards,
is the total water depth,
is the Coriolis parameter (
, where
is the Earth rotational angular velocity and
is latitude),
g is acceleration due to gravity,
is a mean value of water density and
A is the horizontal eddy viscosity.
and
are friction stresses, which have been written in terms of a quadratic law:
where
k is the bed friction coefficient. Essentially, these equations express mass and momentum conservation. Parameter values were set to
and
m
/s [
9,
10], which are standard values.
This type of model represents a good compromise between accuracy and computational cost [
11] and has been widely used to simulate tsunamis generated by earthquakes (see, for instance, [
12,
13,
14], among many others), case in which the extension of the tsunami source is much larger than water depth. This is not the case for landslides since, now, the spatial extent of the source is usually not much larger than water depth. Three-dimensional models are then applied to obtain a detailed description of the flow field [
15]. Depth-integrated models can still be applied but cannot give such a detailed flow description in the generation area [
11].
All the equations are solved using explicit finite difference schemes [
8] with second-order accuracy. In particular, the MSOU (Monotonic Second-Order Upstream) is used for the advective nonlinear terms in the momentum equations. The time step is fixed as 1 s to ensure stability.
Boundary conditions have to be specified. There is no water flow towards a dry grid cell. A flood/dry algorithm is required since, when the tsunami reaches the coast, new wet or dry grid cells may be generated due to run-up or rundown. The numerical scheme described in [
16] was adopted. Wet grid cells are defined as those with a total water depth
H larger than a threshold value
typically set as a few centimeters. Dry cells are defined as cells where
. Flooding and drying is implemented in the code via the calculation of the water velocity normal to the interface between wet and dry cells. The calculation is performed when the pressure gradient force is directed towards the dry cell. Otherwise, velocity is set to zero at this point. In the case of a non-zero velocity, the water level in the dry cell will increase, and the cell turns into a wet one once the water depth is larger than
. In the present study,
m has been fixed following [
16] and our previous studies [
9,
10]. Nevertheless, runup calculations are not presented in this paper.
This methodology was successfully used in the past to simulate tsunami propagation in the Atlantic Ocean [
9], Mediterranean Sea [
10], Red Sea [
17] and Caspian Sea [
18].
Still waters (zero water elevations and velocities over all the domain) are used as initial conditions in all the domain. The methodology of Tinti [
19] and Cecioni and Bellotti [
11] was adopted to simulate a submarine landslide. Essentially, the motion of the sea bottom is provided as a known input to the hydrodynamic equations. The following term is added to the right hand side of the continuity Equation (Equation (
1)):
where
denotes the instantaneous sea surface elevation caused by the transit of the underwater landslide. This term is the link between the landslide model and the tsunami propagation model. The relation between
and the local thickness of the slide
at the sea bottom is calculated by the means of a transfer function according to:
with
where
H is the local water depth, and
is the length of the slide. If the transfer function is not used, then
, which is a good approximation only if the slide length is much larger than the water depth. Using the transfer function
attributes different potential to landslides of different
and moving at different ocean depths. As a consequence, a shallow water slide will have a higher capacity of exciting waves (
, and thus,
) than if it moves in the deep ocean (
, and thus,
).
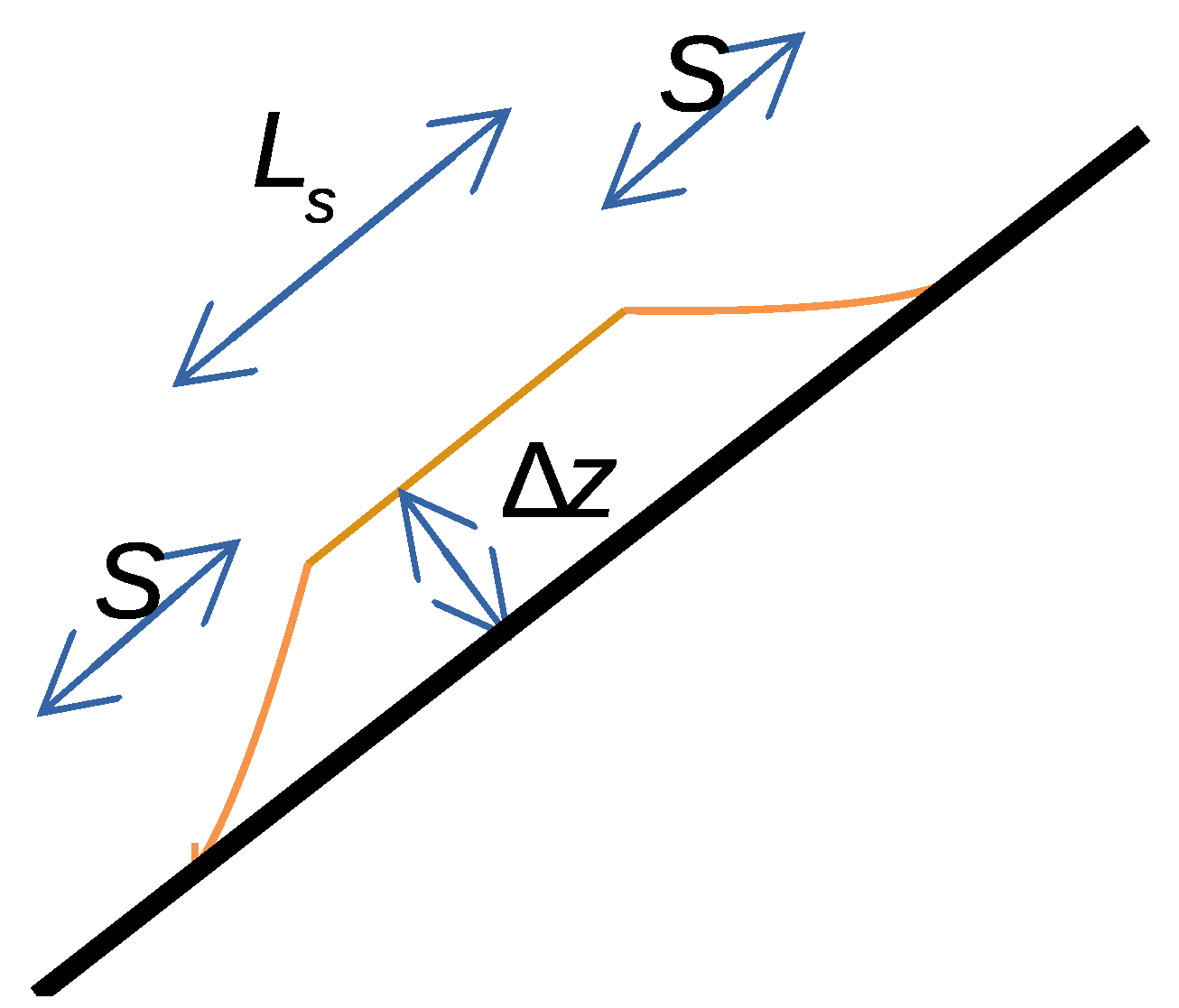
The shape of the slide is represented by a box form of length
, width
B and maximum thickness
. To avoid sharp gradients in
, the edges of the box form are smoothed along both sides over a distance equal to
B from the central line and over a smoothing distance
S by an exponential function in the front and rear end. The full details may be seen in [
20]. The volume of the slide would then be given by the following Equation [
20]:
where the factor 0.9 arises due to the smoothing. A side view of the slide is shown in
Figure 2.
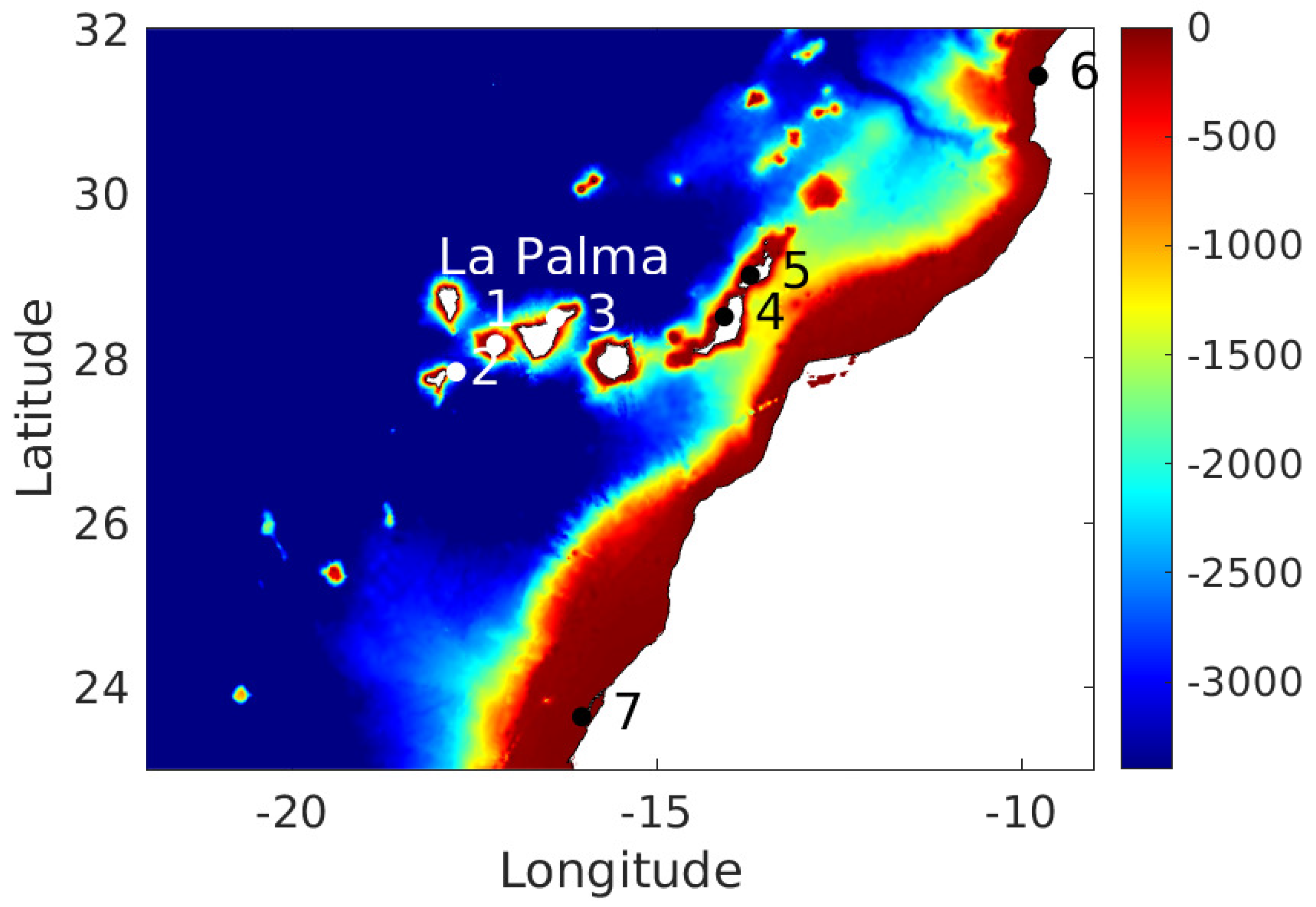
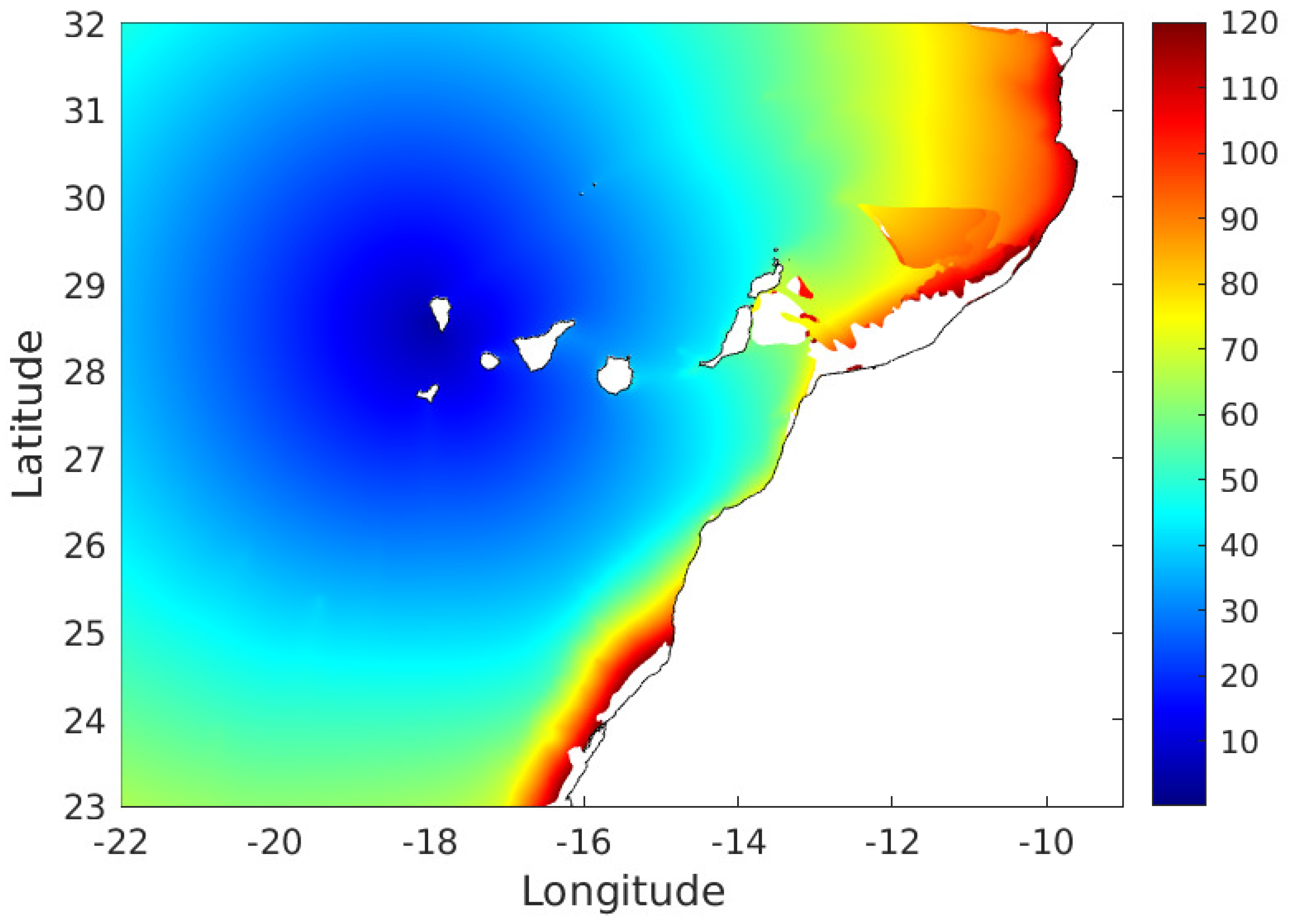
The model domain extends from 23° to 32° N and from 22° to 9° W, with a spatial resolution of 30 s of arc both in longitude and latitude. Topography was obtained from General Bathymetric Chart of the Oceans ((GEBCO)
https://www.gebco.net, accessed on 13 October 2021) database. This is the highest resolution open bathymetric data available online and is presented in
Figure 1, where the location of points where wave heights are extracted are also indicated. The model code was developed and written by the author in
fortran. The running time is about 1 h for a 3 h long simulation on a desktop PC working with Ubuntu 18.04 operating system.
3. Results
As mentioned in the Introduction, a submarine landslide along the island slope is a possibility not discarded by experts and local authorities. It would be caused by the accumulation of lava in the island shelf, which could eventually lead to the instability of this shelf and then produce a submarine slide of material down the island slope.
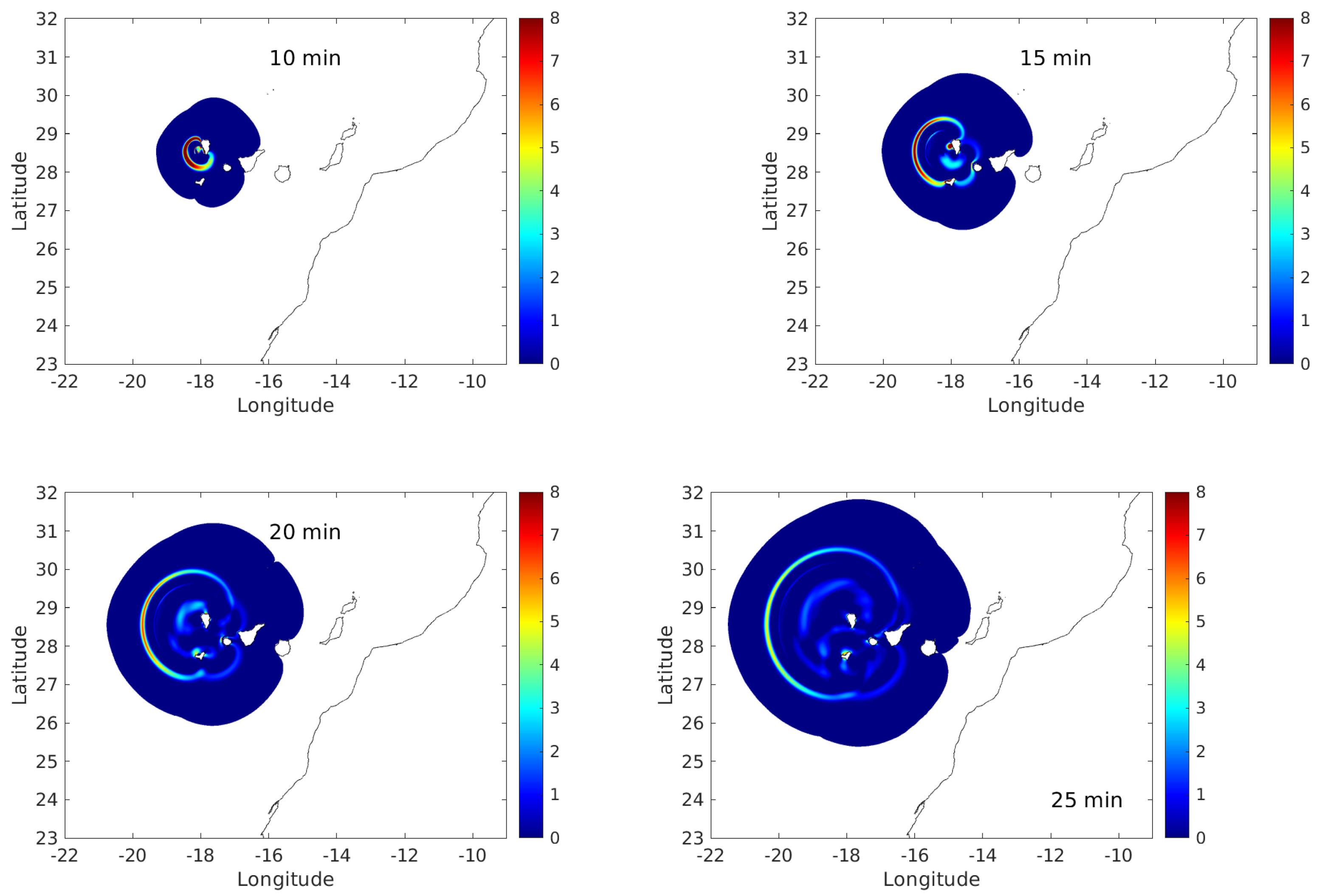
As an example, snapshots of sea surface elevations at several times after a slide are presented in
Figure 3. The volume of this landslide was 4.5 km
, significantly smaller than values used in previous works [
1,
3,
4,
5,
6,
7], but it still seems over-sized due to the narrow shelf of the island and the fact that the lava flow front is of the order of 1 km. Propagation of the tsunami in
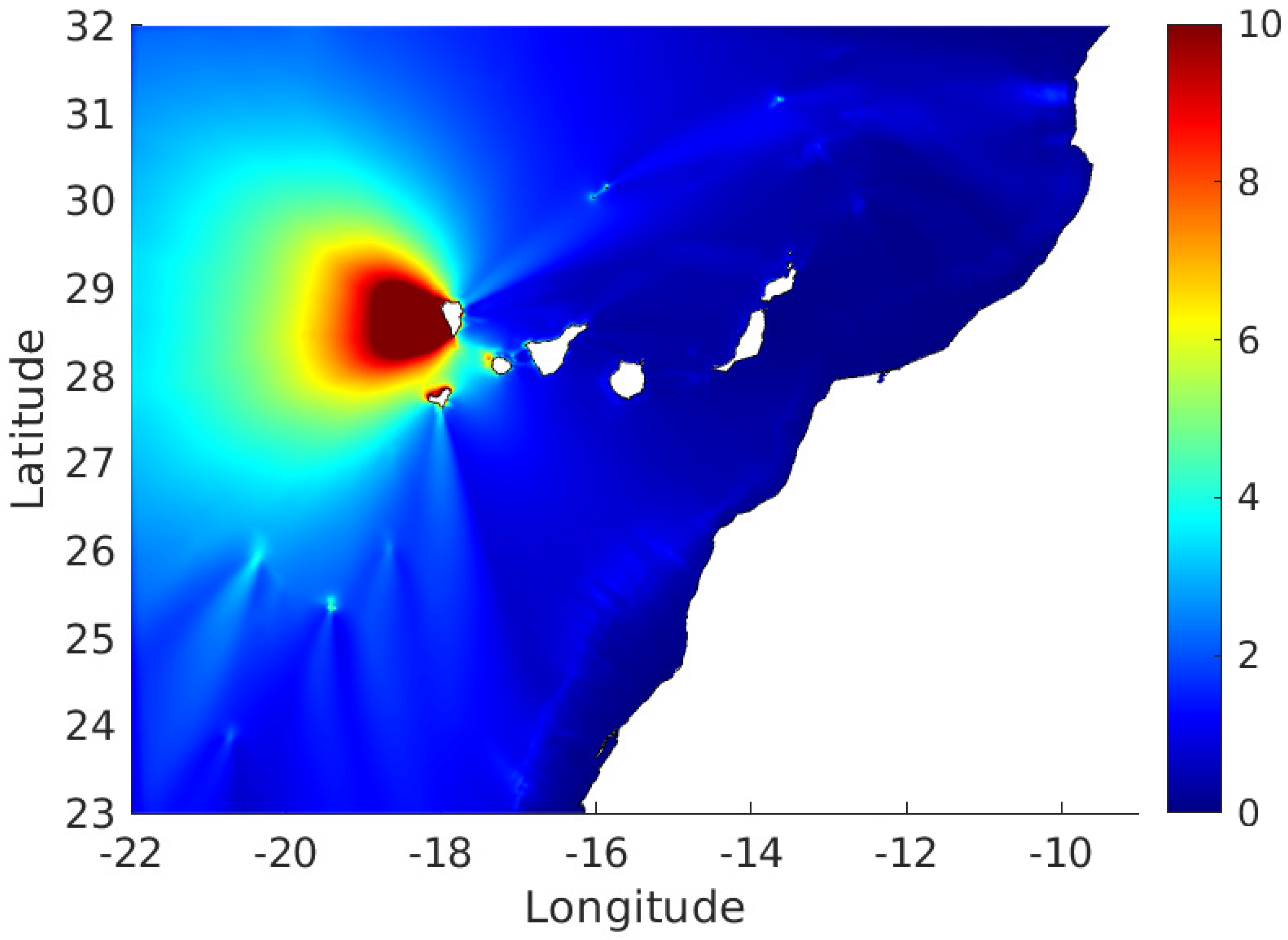
Figure 3 shows essentially the same features, as can be seen in the previous work cited above (although with smaller waves, obviously). Wave amplitudes are presented in
Figure 4. The tsunami is mainly directed to the west due to the fact that the own island acts as a barrier that prevents propagation to the east. The wave amplitude decreases with distance to the source since the energy has to be distributed over a longer front. Thus, amplitude has decreased to about 4 m at −22° longitude. This tsunami would not have significant effects in far coastlines. Nevertheless, high waves are arriving to the close islands of Gomera and, mainly, El Hierro (see
Figure 4). Actually, this may be clearly seen in
Figure 5: the first wave arriving to El Hierro is about 13 m high; in the case of Gomera, its height is about 9 m. Much smaller waves arrive elsewhere.
Figure 6 shows the arrival time of the tsunami (defined as the arrival time of a 1 cm amplitude signal). While the close islands are reached in a few minutes, two hours are required by the tsunami to reach the African coastline. Some regions of Africa coast and the east of Lanzarote and Fuerteventura islands are even not reached by signals larger than 1 cm since such regions are sheltered by, mainly, Fuerteventura.
As commented above, this slide appears to be over-sized; thus, the results in
Figure 4 and
Figure 5 should be interpreted as upper bounds of the generated tsunamis. Using a width of the lava front equal to 1 km (close to reality as said before), a length of 1 km, a smoothing distance of 2 km and a maximum thickness of 50 m, the volume of the slide results 0.13 km
(Equation (
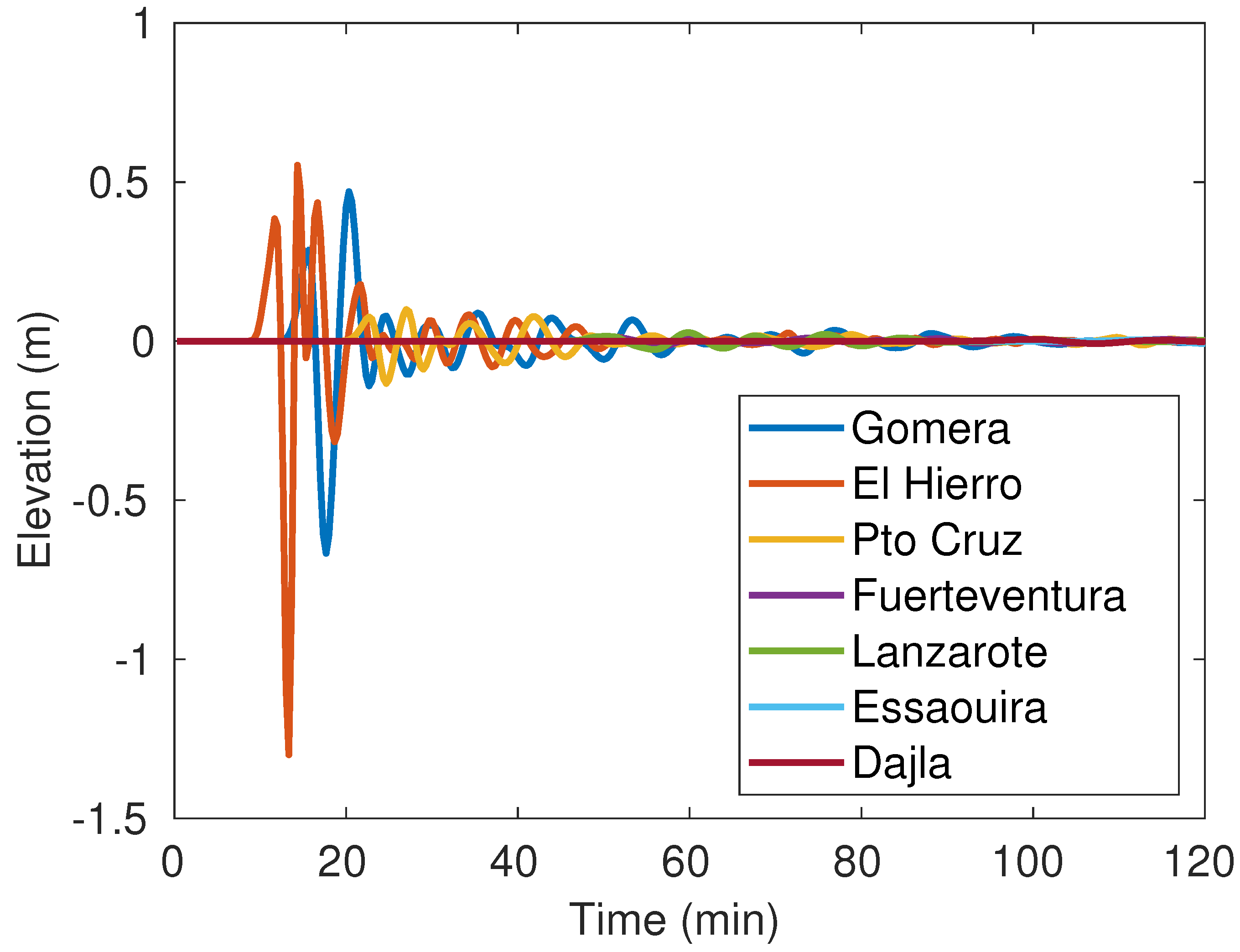
8)). In this case, the time series of surface elevations may be seen in
Figure 7: the maximum wave height is about 0.5 m in Gomera and El Hierro islands, which does not pose any risk to the population. Maximum wave heights that are presented in
Figure 8. It may be seen that the generated tsunami is essentially restricted to the generation region, being not significant far from this region.
It may be concluded that the tsunami generated by a submarine landslide involving a realistic (not over-sized) volume could affect the near islands of Gomera and El Hierro (mainly their north shores), but it would not propagate significantly far away from the Canary Islands (it would not even pose a threat to the African shoreline). Of course, the case would be the same with respect to Europe and American coasts. It should be noted that these landslide tsunamis are different to those originated by submarine earthquakes since the sizes of the tsunami sources are very different. In the present case, the source size is a few kilometers, while in the case of an earthquake in a fault, the tsunami source extends over a hundred of kilometers. Thus, these tsunamis propagate more efficiently away from the source. In addition, the tsunami energy per unit length of the wave front decreases with distance to the source, r, as since energy is distributed over circumferences of larger radii. Even if shoaling leads to an increase in wave height, the small waves computed in the model domain do not indicate that shoaling would lead to significant wave heights in distant coasts (Europe, Africa and America).