1. Introduction
Considering Wilson’s paper (1921) [
1] as an anchor point, we can celebrate the 100th anniversary of the conception of the global electric circuit (GEC). There are plenty of comprehensive reviews of the GEC as a system connecting the atmosphere and ionosphere through electromagnetic coupling and of the history of this concept’s development (Roble and Tzur, 1986; Bering III et al., 1998; Williams, 2009; Williams and Mareev, 2014) [
2,
3,
4,
5]. Until recently, the main problem facing study of the GEC had been finding a realistic balance of currents within the GEC by including—with the exception of thunderstorm discharges—convection clouds and, especially, mesoscale convective systems (Williams and Mareev, 2014) [
5] as a source of positive charge. The most recent publications demonstrate the trend of searching the different sources of the GEC’s variability, such as natural ground radioactivity and solar activity (Slyunyaev et al., 2015) [
6], seasonal variability (Ilin et al., 2019] [
7], and spatial variability, considering the ocean’s and land’s contributions to the GEC (Slyunyaev et al., 2019; Ilin et al., 2020) [
8,
9].
It seems that, in this series of publications, too much attention is paid to the formal parametrization of the GEC’s characteristics, rather than to the physical reasons for the observed variability (Ilin et al., 2020) [
9]. At the same time, a clear indication has appeared that seismic activity contributes essentially to the GEC’s variability (Pulinets, 2009; Pulinets and Davidenko, 2014; Pulinets and Davidenko, 2018) [
10,
11,
12]. According to the morphologies of the observed effects, the main factor in the GEC’s modification is changing boundary layer conductivities (both increases and decreases), leading to the formation of large-scale irregularities in the ionosphere (Morozov and Kupovykh, 2017) [
13]. It should be noted that the impact of conductivity variations on the ionospheric potential (IP) was also considered theoretically in Slyunyaev et al. (2014) [
14]. Especially interesting would be results describing the variations of the IP outside thunderstorm clouds over seismically active regions in fair-weather conditions.
From s solitary case of a seismically active region’s impact on the IP we can make the logical transition to a global seismicity impact on GEC variability. Beginning at magnitude 1.5, we perceive nearly 2740 seismic shocks daily, distributed globally. Has this global distribution of seismic activity any relation with the daily global variability of the electric field? We made such a comparison and came to the striking conclusion that global seismic activity has unitary variation as well, and even more striking—its correlation coefficient with the Carnegie curve is R ≈ 0.86 (Pulinets and Khachikyan, 2020) [
15].
This paper, then, is an attempt to understand the physical reasons for such a relationship—at least, qualitatively.
2. Lightning Activity and Earthquakes
Beginning with Wilson (1921) [
1], it has been generally accepted that the atmospheric electric field is generated by the thunderstorm activity of the planet. Thunderstorm models of atmospheric electricity (e.g., Hays and Roble, 1979) [
16] use thunderclouds as the main source for the generation of potential differences between the ground and ionosphere, which supports observations of a positively charged electric current flowing from the ionosphere to the negatively charged ground in fair-weather regions. The diurnal distribution of global thunderstorm activity is considered a main reason for the form of the unitary variations in the atmospheric electric field, called the Carnegie curve (Liu et al., 2010) [
17]. Regardless of some doubt having arisen over the contribution of lightning to the GEC’s electric field (Mareev et al., 2008; Davydenko et al., 2009) [
18,
19], we will begin with the traditional view of such contribution in the formation of the GEC.
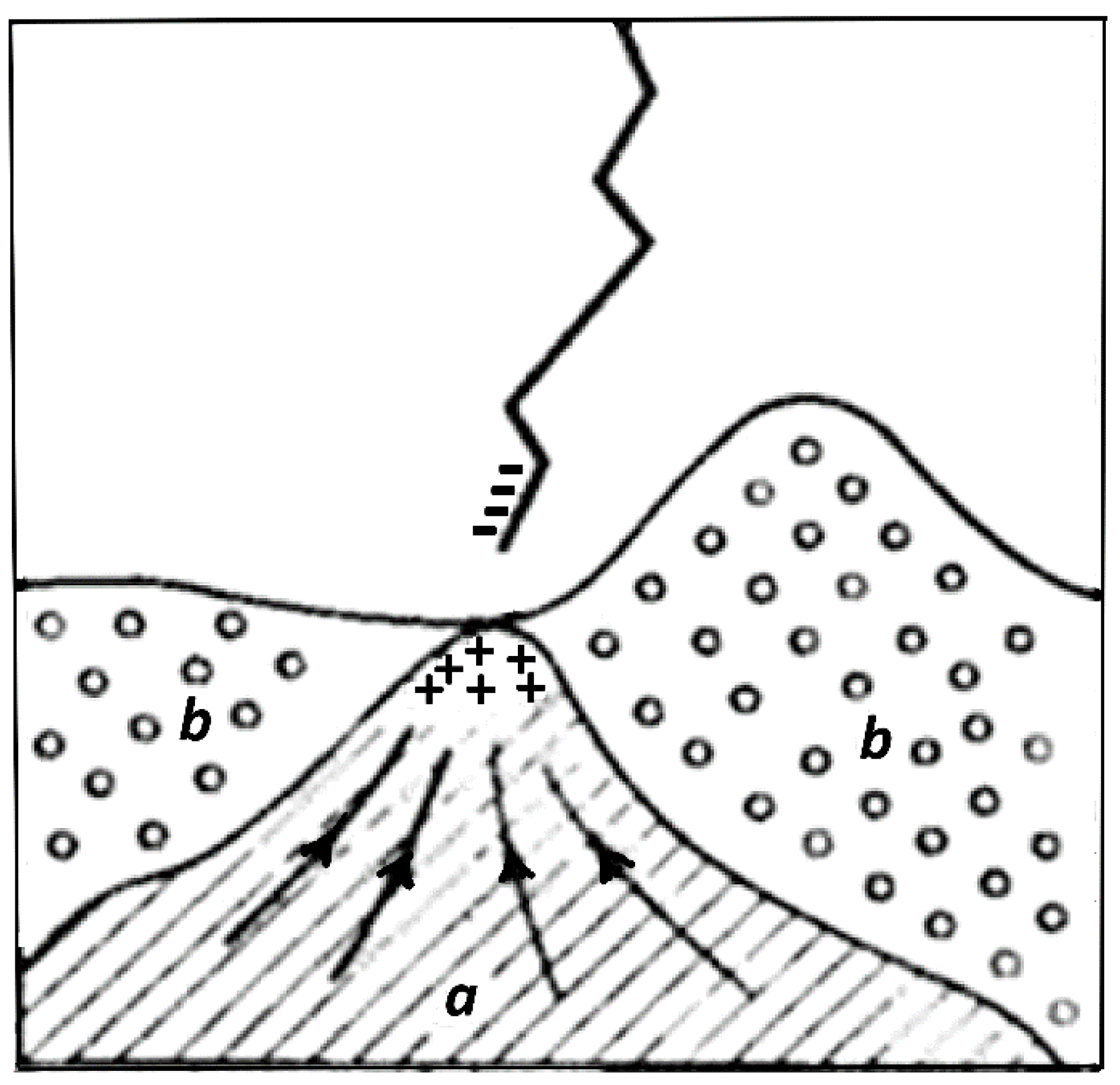
Before considering the global spatial distribution of lightning, let us ask whether there is any selectivity in the locations to which discharge will be directed. The lightning formation process shows that the specific location of lightning’s discharge is determined at the leader stage. If there is a high-rise ground structure (for example, a television tower or a power-line support) directly under a thundercloud, then the emerging leader will move towards the ground along the shortest path, that is, towards the leader, which extends upward from the ground structure. Most often, lightning strikes those power facilities that are effectively grounded and conduct electricity well. When of the same height, discharged lightning strikes the object with better grounding and greater electrical conductivity. With power facilities of different heights and different resistivities of their adjacent soil, it is possible for lightning to strike the lower object, located on ground with better conductivity (
Figure 1).
As a rule, areas of soil and ground-based artificial structures with high conductivity are most often affected.
Let us consider, now, the situation when, instead of soil, we have the increased conductivity of the low layers of atmosphere under the action of natural sources of radioactivity (mainly
222Rn). It is shown in (Golubenko et al., 2020) [
20] that
222Rn makes an essential contribution to near-ground air conductivity. This paper considers normal conditions, ignoring increased radon exhalation in seismically active areas of the globe. For example, according to Chandrashekara et al. (2006) [
21] radon concentration in the air of India’s Mysore City is of order 20 Bq/m
3. At the same time, according to Kobeissi et al. (2015) [
22], in the vicinity of active faults, radon concentration may reach 2000 kBq/m
3—five orders of magnitude greater. This means that we may expect a high rate of lightning strikes within zones of earthquake preparation during the final stage of the seismic cycle.
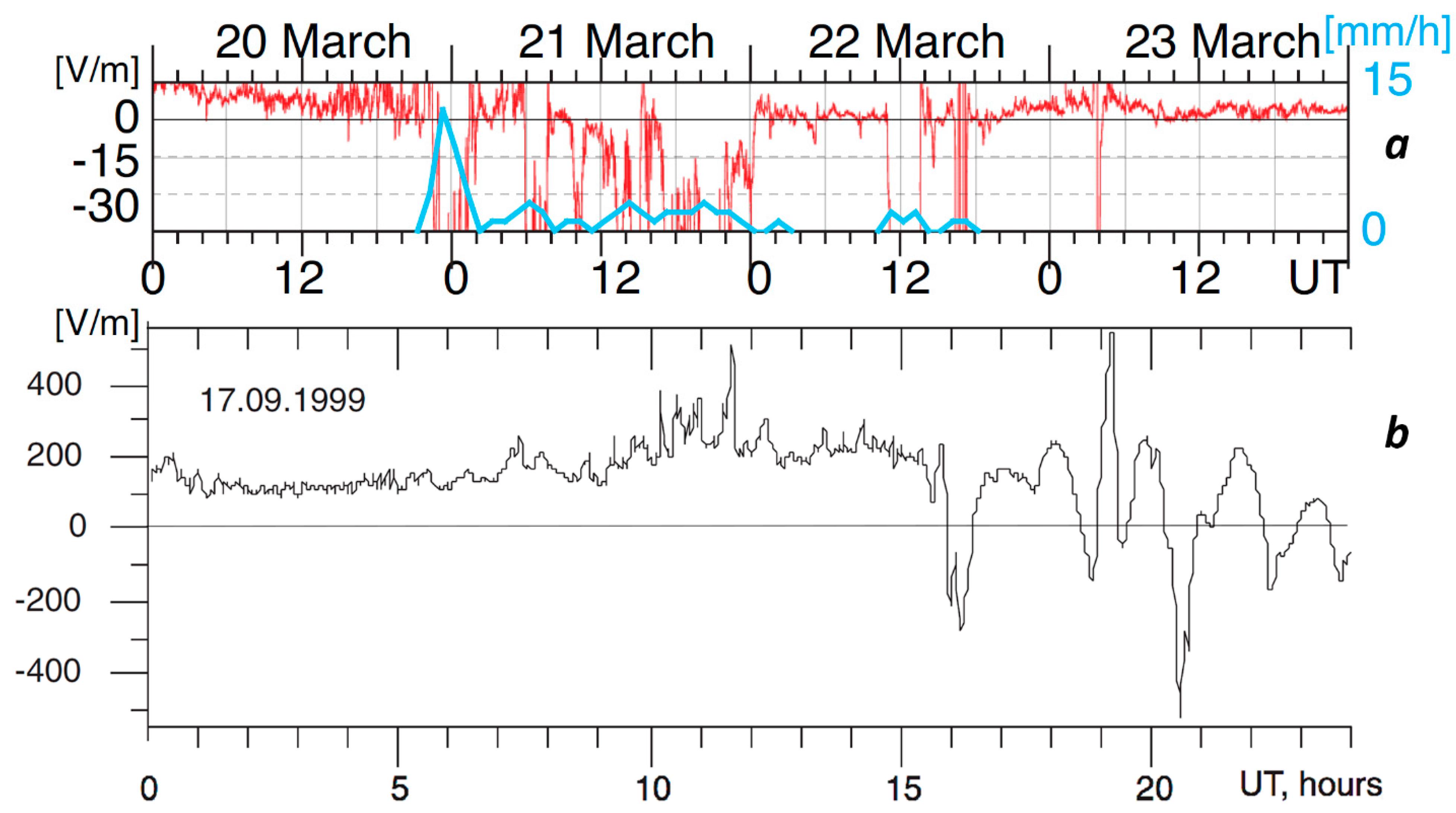
The process of ionization could be compared with the hydrogen explosion at Fukushima NPP, when radioactive
131I,
134Cs and
137Cs were released into the atmosphere, leading to air ionization. As a result, the atmospheric electric field, as measured at the distance 137 km from Fukushima, dropped by more than an order of magnitude (Yamauchi et al., 2012) [
23]. Moreover, during the whole day of 22 March 2011 the atmospheric electric field registered at the Kakioka geophysical observatory had reversed direction in comparison with its fair-weather direction and reached values greater than −60 V/m. This is equivalent to the appearance of a positive charge at the ground surface (
Figure 2a).
This effect is similar to the atmospheric field reversal observed before earthquakes (Vershinin et al., 1999; Mikhailov et al., 2004) [
24,
25]. In
Figure 2b one can see such a reversal, registered one day before the M6 earthquake at Kamchatka (Mikhailov et al., 2004) [
24]; but, in this case, a one-order-stronger electric field (−500 V/m) was observed than that at Fukushima.
Field reversal leads to an increase of the potential difference between the negatively charged lower edge of a thunderstorm cloud and the ground surface, which increases the effect of ionization and the probability of electric discharge to the ionized area.
Experimental results (Liu et al., 2015) [
26] show that lightning activities tend to appear around a forthcoming epicenter and are significantly enhanced a few—especially 17–19—days before M ≥ 6.0 shallow (depth D ≤ 20 km)-land earthquakes. Moreover, the size of the area around the epicenter with a statistical significance for enhanced lightning activity is proportional to the earthquake’s magnitude.
Concluding this section, we can claim that lightning activity increases within the zones of shallow earthquake preparation (in Taiwan, 17–19 days before its strong M ≥ 6.0 seismic event). The probable physical reason for this phenomena is increased radon activity during an earthquake’s preparation phase, which leads to an increase in the electric conductivity of the air within the earthquake preparation zone and to an EF reversal effect, increasing the potential difference between the bottom edge of the thunderstorm cloud and ground surface facilitation of the initiation of the counter discharge leader from the ground surface.
3. Spatial Distribution of Lightning
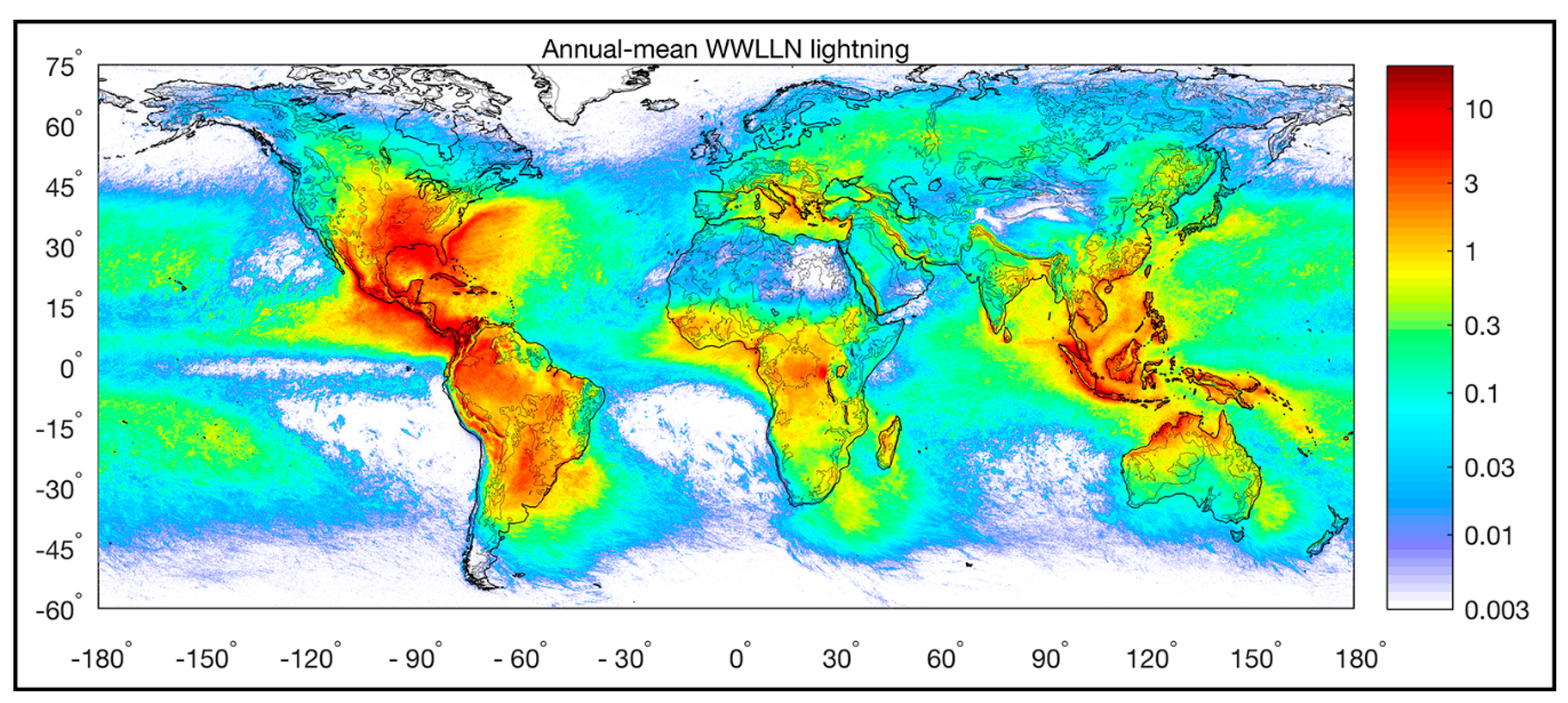
Looking at the global distribution of lightning-strike density (
Figure 3), one immediately can mark the main feature of this distribution: lightning is distributed primarily over continents (Aich et al., 2018) [
27]. The difference looks even more striking when observing the integral of the intensity of thunderstorm activity (
Figure 4) obtained from multi-year observations by the Optical Transient Detector (OTD) (Christian et al., 2003) [
28]. It is interesting that there is no common understanding of the difference in lightning activity between the land and ocean. There are a variety of explanations; the higher concentrations of aerosols serving as condensation nuclei over continents (Christian et al., 2003) [
28], higher convection over continents (Williams and Mareev, 2014) [
5], even including negative gravitational anomalies (Ershova 2015) [
29].
We would like to propose one more explanation for the possibility of seismic activity’s impact on the distribution of lightning discharge. As radon activity is much more intensive over continents, seismically active regions may provide an essential contribution to lightning activity due to the ionization of the air provoked by radon within the zones of earthquake preparation. Taking into account that nearly 2749 earthquakes of M ≥ 1.5 are registered daily, that increased radon exhalation lasts from several days to several months prior to an earthquake and that radon’s half-decay period is 3.8 days, we can claim that the atmosphere is continually impacted by increased emission within seismically active zones. Now we can consider the distribution presented in
Figure 3 from other point of view: we see a linear distribution of increased lightning activity along the entire western shore of the North American continent, including along seismically active California and Mexico. In addition, the whole Maritime continent is one of the most seismically active regions on our planet.
If we will consider aerosols as centers of nucleation for the formation of thunderstorm clouds, we also should consider the ion induced nucleation (IIN) effect (Laakso et al., 2002) [
30], which is the second step in a chain of processes after air ionization provided by radon activity. Our model explains the formation of the aerosol-size particles (1–3 μm) which could be transported to the upper layers of the atmosphere and serve as condensation nuclei for cloud formation (Pulinets et al., 2015) [
31].
Concluding this section, we can add IIN and aerosol formation to the effects of ionization and EF reversal, All these phenomena prevail over continents because of the higher levels of radon over land than over oceans.
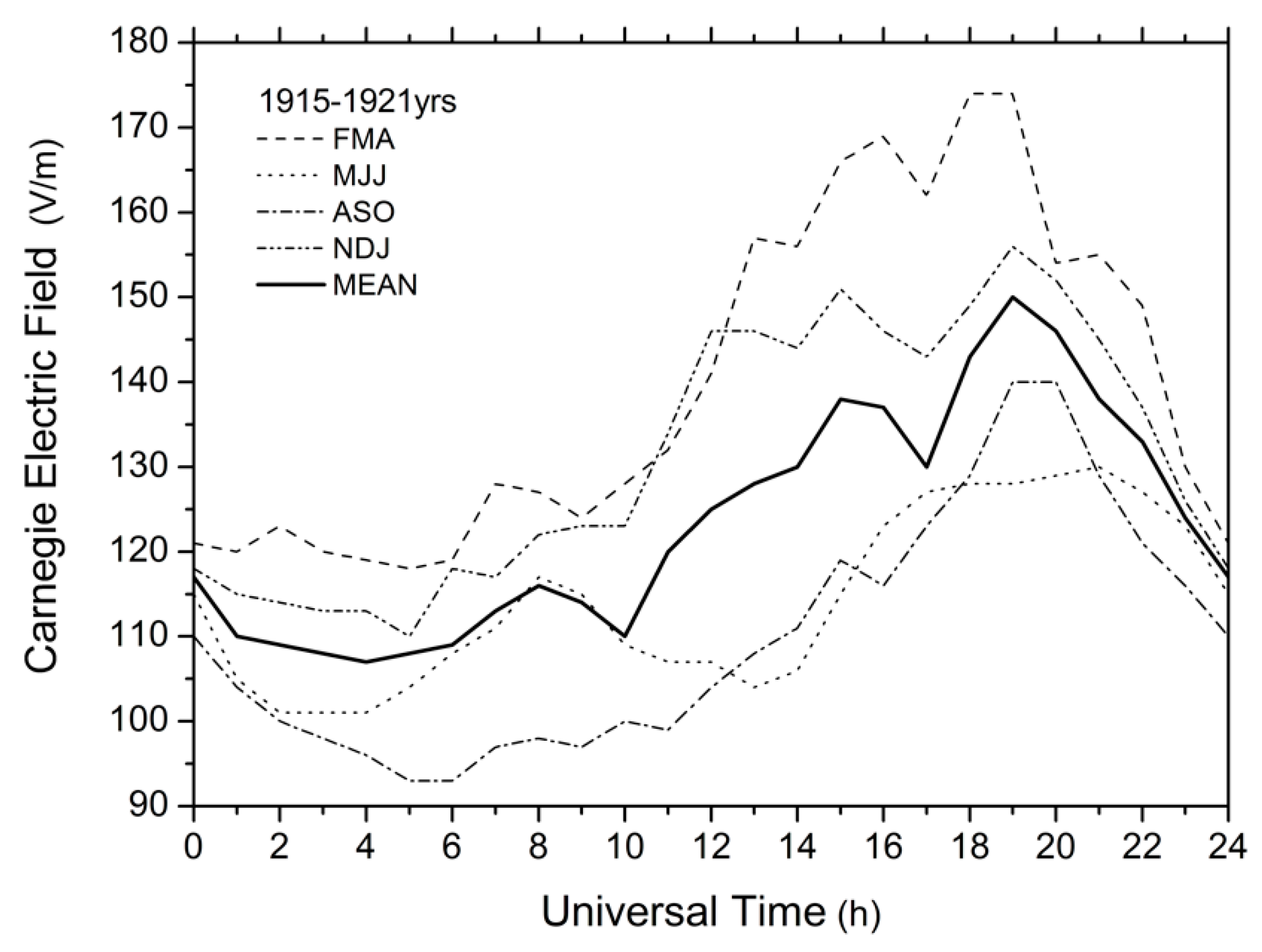
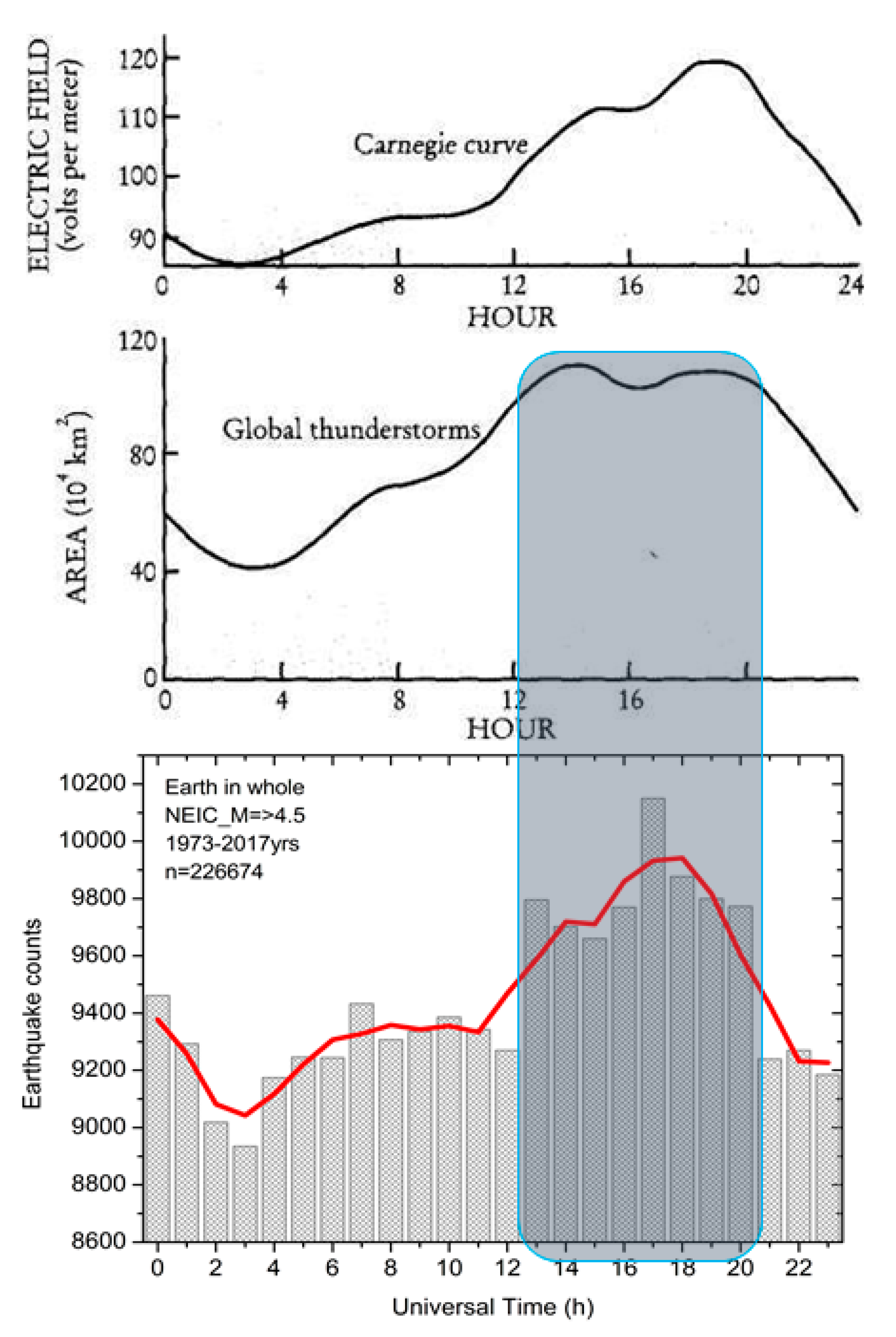
4. Carnegie Curve and Earthquakes
We have discussed, above, the effect of the GEC in regions of stormy weather, where the EF is generated. Yet, the main characteristic of GEC—unitary variation—presents a global dependence of the fair-weather electric field on universal time, called the Carnegie curve (Whipple, 1929; Harrison, 2013) [
32,
33], which demonstrates a steady increase in field strength in fair-weather regions at ~19:00 UT (
Figure 5). It was obtained, first, from measurements of the fair-weather electric field over the oceans, from 1915–1921, onboard the ship
Carnegie and systematized by Mauchly (1926) [
34]. These data are currently available at the following website (
https://malagabay.files.wordpress.com/2014/06/carnegie-iv-v-vi-table.jpg?w=640). The thin curves in
Figure 4 represent the UT variations of the fair-weather electric field separately for four seasons: February–April, FMA; May–July, MJJ; August–October, ASO; and November–January, NDJ. The thick line shows the UT-variation averaged over the entire measurement period of 1915–1921.
Our early works (Pulinets et al., 1998; 2000) [
35,
36] demonstrated that seismoionospheric coupling includes, as the main coupling elements, the Earth’s crust, atmospheric electric field, and ionosphere, which, in turn, are the main structural elements of the Global Electric Circuit. So, it was quite natural to check for relevant phenomena in the global distribution of seismic activity, in terms of universal time (Pulinets and Khachikyan, 2020) [
15]. The results were fascinating, and they became the motivation for the present work.
In this study, we used data on earthquakes with a magnitude of M ≥ 4.5 recorded globally during 1973–2017 (226,674 events) according to the Global Seismological Catalog (NEIC) of the U.S. National Geological Survey (available at
https://earthquake.usgs.gov/earthquakes/search). The selection of the M4.5 lower threshold was determined by our theoretical estimation of the ionospheric sensitivity to seismogenic electric fields’ penetration into the ionosphere (Pulinets et al., 2000) [
36], which depends on the size of the earthquake preparation zone (Dobrovolsky et al., 1979) [
37]. Our calculations show that the minimal size (radius) of the area should be 200 km. Given R = 200 km and using the Dobrovolsky formula, R = 10
0.43M gives us the magnitude 5.35. On the other hand, our experimental results demonstrate that sometime the ionosphere “feels” an earthquake’s preparation from magnitudes slightly larger than 4. So, as a compromise between theory and practice, the value 4.5 was selected to provide for the effectiveness of earthquake preparation effects in the ionosphere.
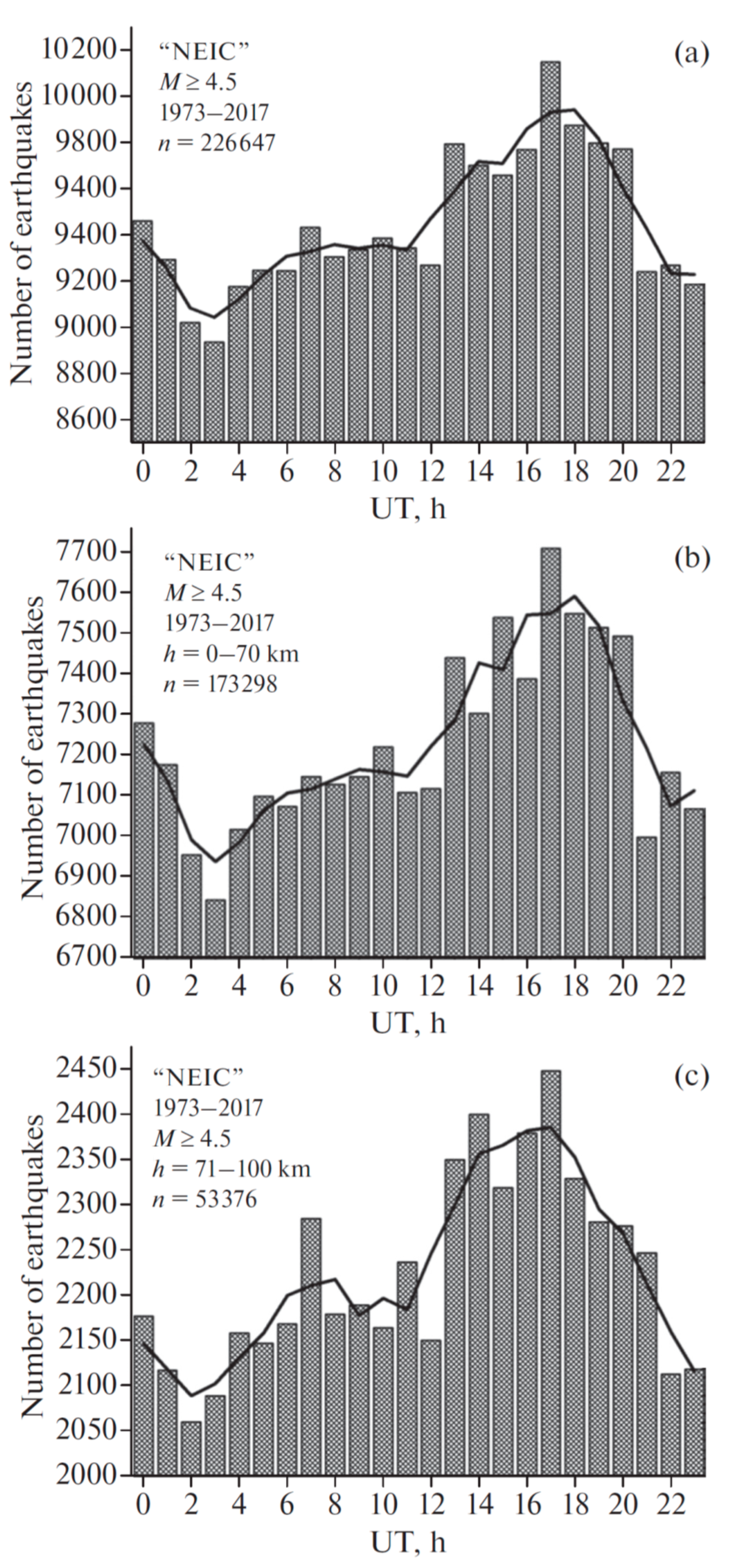
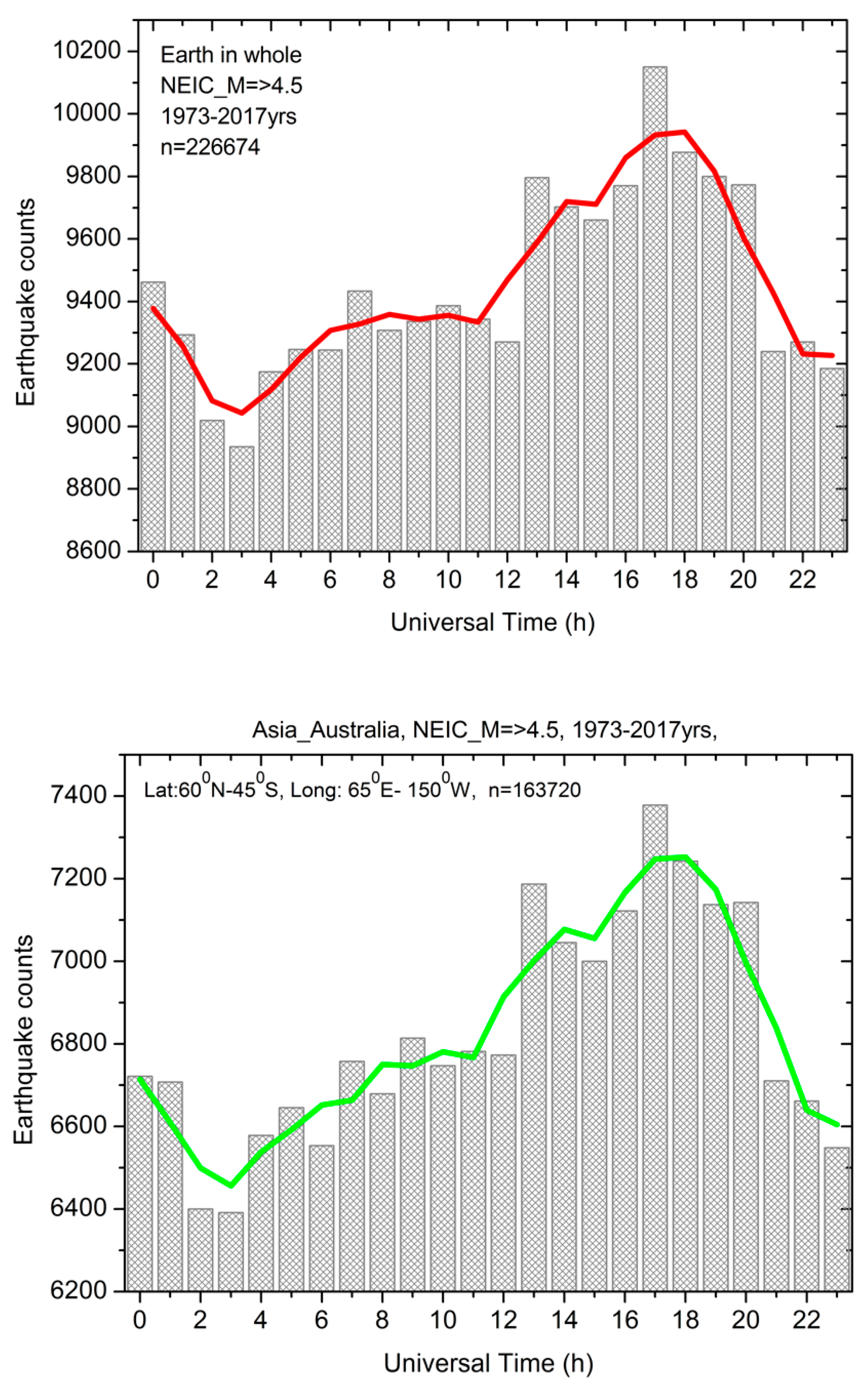
Figure 6 demonstrates the UT variation in the number of globally registered earthquakes (
Figure 6a, histogram and averaged distribution) and, separately, the UT distribution of shallow and moderate-depth earthquakes with a hypocenter depth up to 70 km (
Figure 6b) and of deep focus earthquakes with a hypocenter depth of 71 km or more (
Figure 6c).
The high similarity of curves, which have almost identical character, supports the non-randomness of the detected unitary variation in the seismic regime of the Earth. A visual comparison of
Figure 4 and
Figure 5 indicates that the character of UT variation in the seismic regime has a rather close correspondence with the character of UT variation in the atmospheric gradient of the electric field. For both parameters, the maximum values fall within the time interval ~13:00–20:00 UT, and the minimum values are ~03:00–04:00 UT. For the Carnegie curve, the peak value of the electric field gradient is observed at about ~19:00–20:00 UT (
Figure 4), and the peak value in the number of earthquakes, both for crustal and deep-focus events, is observed at ~17:00–18:00 UT (
Figure 6), i.e., 2 h earlier. For the Carnegie curve (
Figure 4), the potential gradient difference between the minimum value, at 04:00 UT, and the peak value, at 19:00 UT, is ~38%; this ratio is lower in the seismic data. According to the unsmoothed data in
Figure 6 (bars), the difference between the maximum and minimum number of all earthquakes (
Figure 6a) is ~13.6%; for crustal earthquakes this difference is ~12.6% (
Figure 6b) but reaches ~19% for deep-focus earthquakes (
Figure 6c). This result indicates that the amplitude of the unitary variation in the seismic regime of the Earth increases with an increase in hypocenter depth.
In this regard we can claim that this distribution is a kind of global natural phenomena that should be seriously considered, including a search for its physical substantiation.
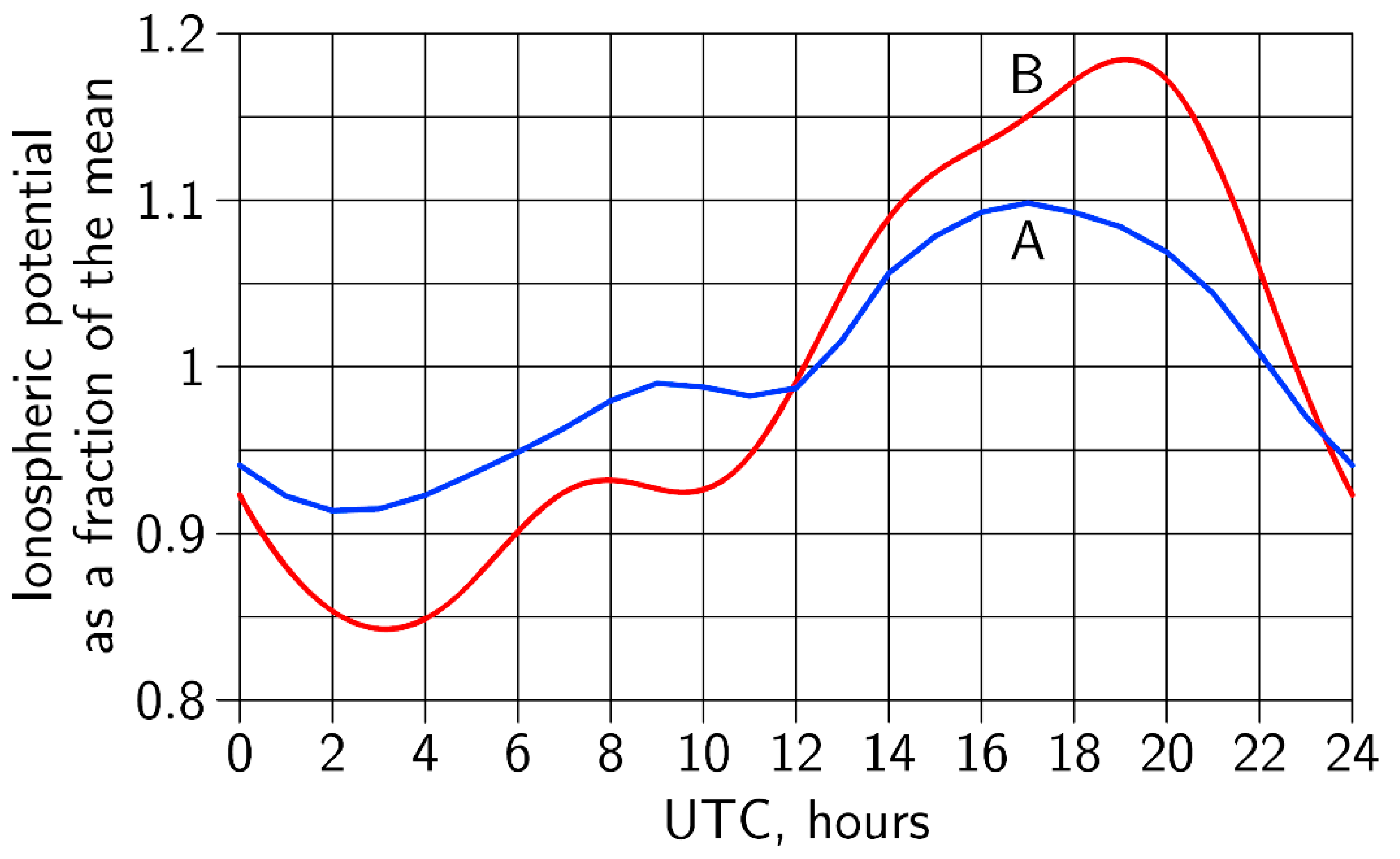
We were surprised by the 2-h difference in the peak time of the curves, which forced us to look for some reasonable explanation—it appeared rather quickly. In one of the latest publications by Slyunyaev et al. (2019) [
8], they modeled the difference in UT distribution for the ionospheric potential between land and ocean. It is demonstrated in their paper that the contribution from land is shifted to an earlier time, by exactly two hours (as in our distributions for seismic activity) and its amplitude variations lower to 19%, as we have shown for deep earthquakes (
Figure 7).
The results of a more recent paper from Ilin et al. (2020) [
9] left us even more confident in the relevance of seismic activity and ionospheric potential variation. In the first paragraph of text, from the Conclusions of the cited paper, is written “the IP variation whose shape is nearly identical to that of the classical Carnegie curve with a correlation coefficient of 0.97, albeit with a smaller peak-to-peak amplitude (18% against 34% of the mean) and maxima and minima shifted by 1–2 h”; we can replace “IP” with “seismic activity” and get almost exactly our results with minor corrections: a peak-to-peak amplitude 19% instead of 18%, and a correlation coefficient 0.86 instead of 0.97.
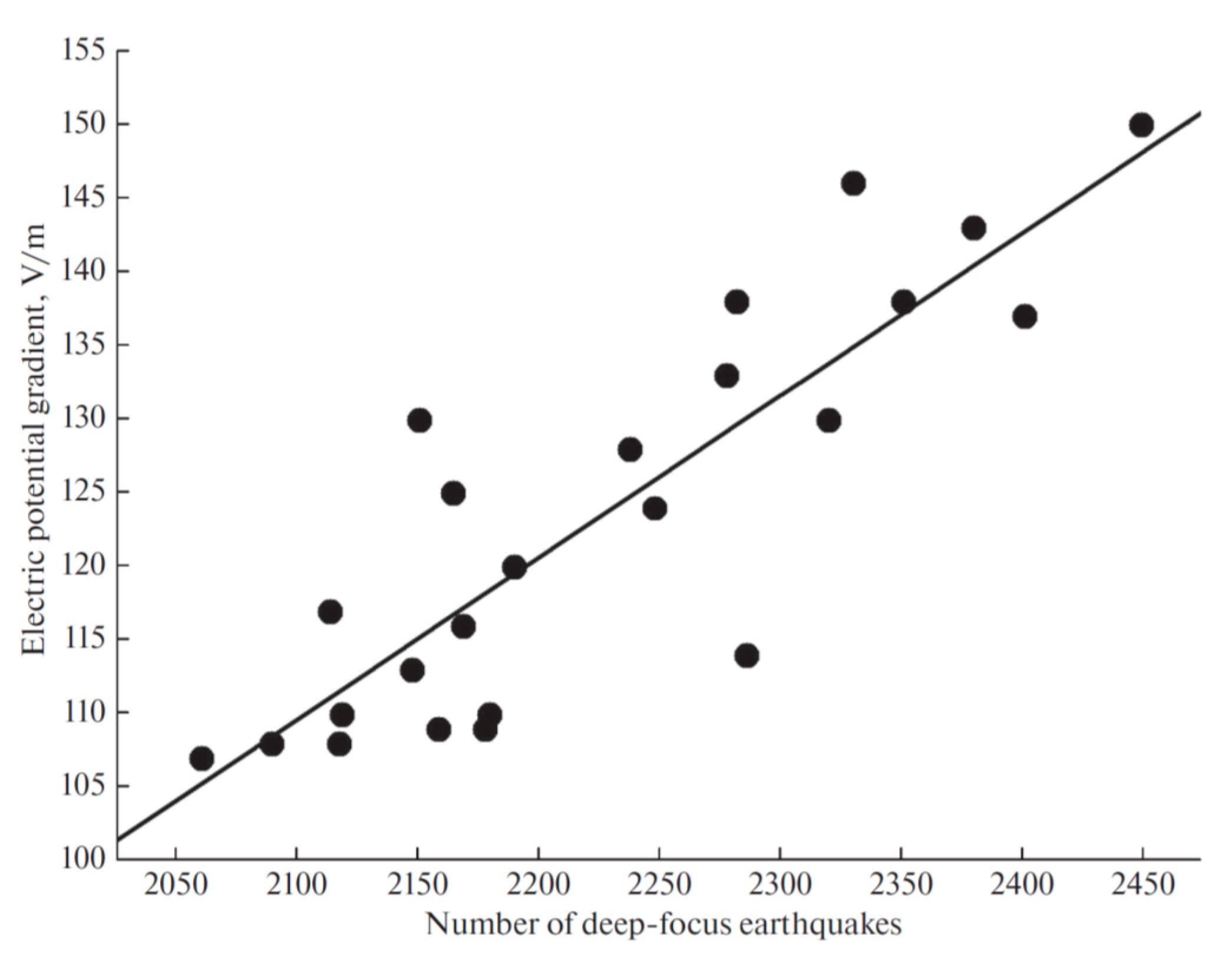
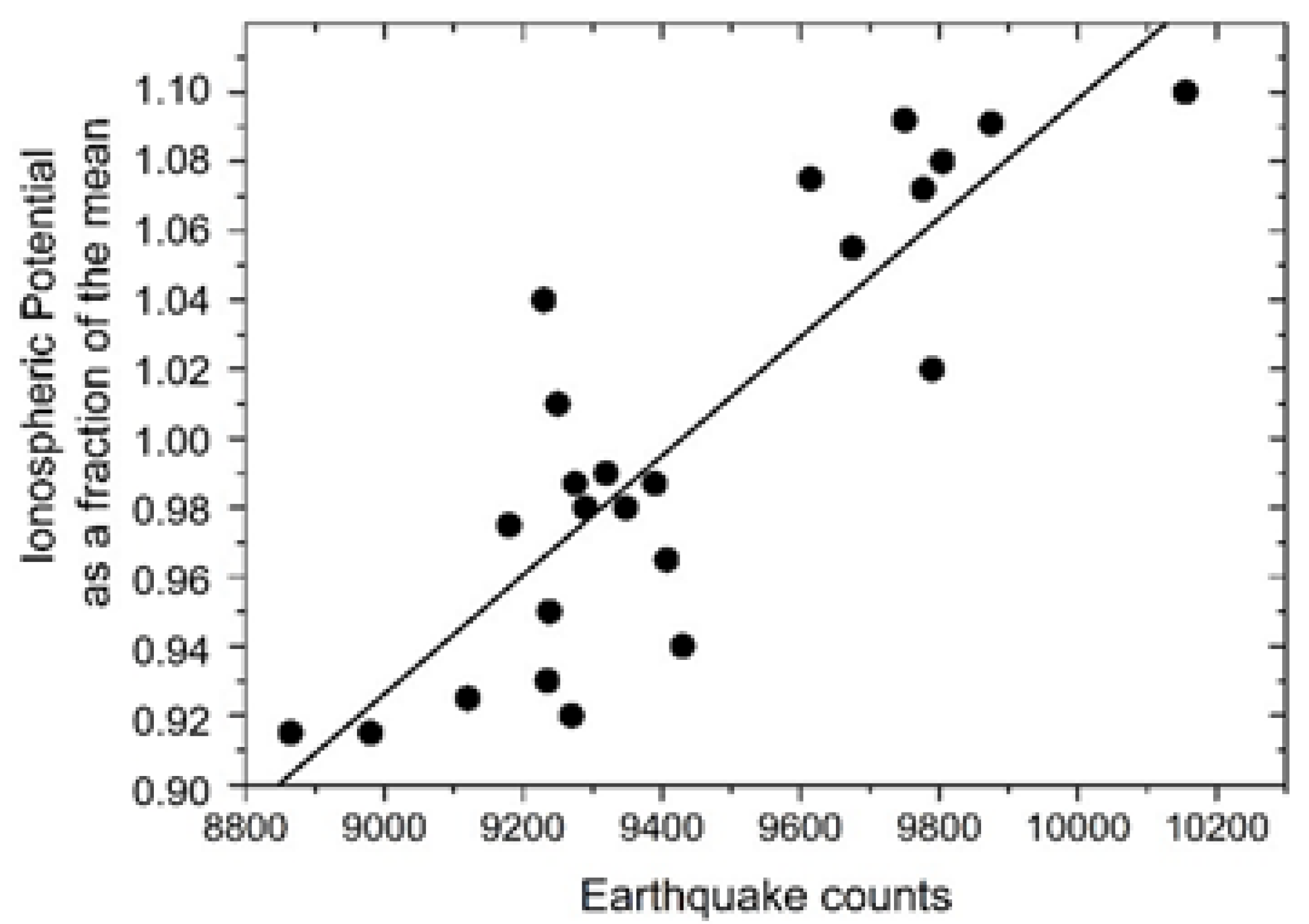
We calculated the cross-correlation coefficient between the Carnegie curve (line B in
Figure 7) and the UT curve for deep earthquakes, presented in the
Figure 6c and taking into account the 2-h shift). The solid line in
Figure 8 represents the linear regression between the ionospheric potential and the number of deep-focus earthquakes, with a correlation coefficient of
R = 0.86 and a standard deviation of
SD = 7.0, at a probability of
p = 95%.
The conducted the same procedure, but without a time shift, to calculate the cross-correlation coefficient between the IP (line A in the
Figure 7) and earthquake frequency. This result is presented in the
Figure 9.
It is interesting to note that a large number of earthquakes are accompanied by larger values of the IP, or vice versa: at large values of the IP, a large number of earthquakes are observed.
Now we arrive at the main question of the paper: how we can interpret this similarity in unitary variations of the ionospheric potential and global distribution of earthquakes? What does this unitary variation mean at all, considered from a geodetic point of view, if we suppose that the curve reflects the value of some parameter at 00 LT (16–18 h UT corresponds to 00 LT at longitudes 120–150 E)?
5. Seismoionospheric Coupling Contribution to the GEC’s Dynamics
If we accept the possibility of a seismic activity contribution to the ionospheric potential through seismoionospheric coupling, let us consider in greater detail how this may happen. In general, the ionosphere is controlled by solar activity, and the morphology of ionospheric behavior is well known and modeled, both theoretically (Namgaladze et al., 1988) [
38] and empirically (Bilitza et al., 2017) [
39]. In all cases, when we observe irregular ionospheric variability we look for the source of such impact. To not become immersed in the different kinds of ionospheric variability, we will directly consider seismicity-induced effects in the ionosphere, and, especially, pre-earthquake effects (Ouzounov et al., 2018) [
40]. Among the recent publications, we found one that could be key in the present discussion (Pulinets and Davidenko, 2018) [
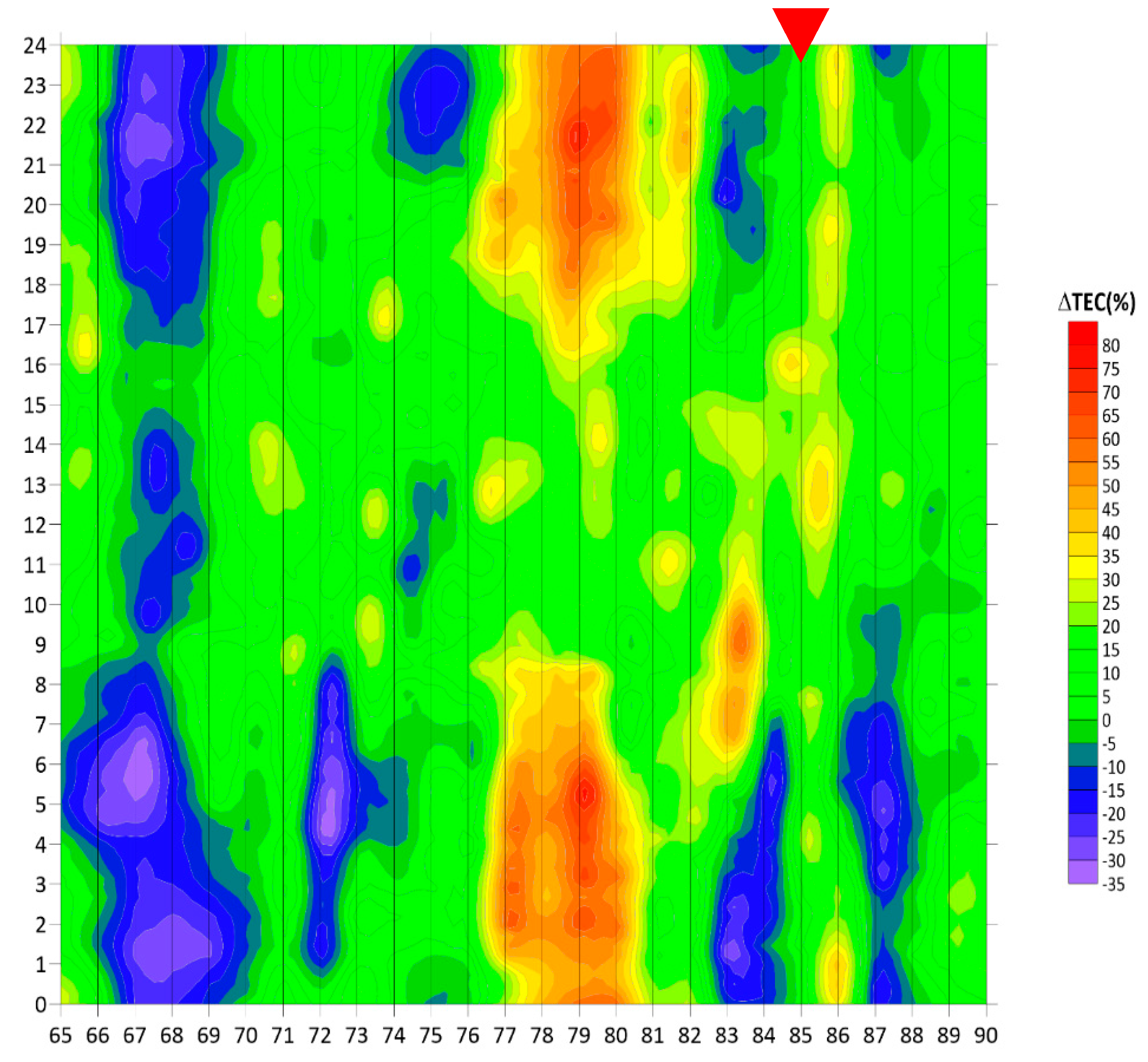
12]. In the majority of earthquake cases, we observe the nighttime positive TEC variation, which appears a few days (from 1 to 10) before the seismic shock. Its remarkable feature is that such ionospheric disturbances appear after sunset and last throughout the night, until sunrise. In
Figure 10 such ionospheric variation is shown for the case of the M7.5 earthquake on 25 March 2020 in the Kuril Islands area; some explanation is necessary. We present the percentage deviation of the TEC (expressed in color tones) in two temporal scales simultaneously: on the vertical scale, we have the local time (every vertical bar is a whole day, from 00:00 to 24:00 UT). The horizontal scale presents the numerically ordered day of the year (i.e., 25 March is 85 DOY). In such presentation, the ionospheric precursor is reminiscent of a red stalactite–stalagmite formation (Pulinets et al., 2015) [
31].
The question arises: is there any relationship of the positive variation in the ionosphere with the ionospheric potential? According to the lithosphere–atmosphere–ionosphere coupling (LAIC) model, the IIN initiated by the ionization produced by radon emanation leads to the formation of large clusters of ions with extremely low mobility, the sharp decrease of which contributes to air-column conductivity. We obtained an effect similar to the effect of dust storms, when, over the area of the dust storm, positive ionospheric anomalies also appear (Pulinets and Davidenko, 2014) [
11]. The effect of air-column conductivity on the local modification of ionospheric potential was estimated by Morozov (2011) [
41]. He calculated that, under concentrations of aerosol particles of 5 × 10
10 m
−3 in the boundary layer of the atmosphere, the ionospheric potential will increase, from 300 kV to 330 kV. In our conditions, according to Pulinets and Davidenko (2018) [
12], the maximum concentration of large-scale clustered ions reached during the nighttime, when the upper boundary of the planetary boundary layer (PBL) has an altitude near 200–300 m and all particles created by ionization are pinned to the Earth’s surface, is what creates the conditions of high aerosol concentration and low air conductivity.
We can now state that the positive variation of the TEC should be accompanied by the positive deviation of the ionosphere potential. So, near-ground processes described by our model (Pulinets et al., 2015) [
31] pumping energy into the ionosphere through the global electric circuit, and simultaneously contribute to the IP.
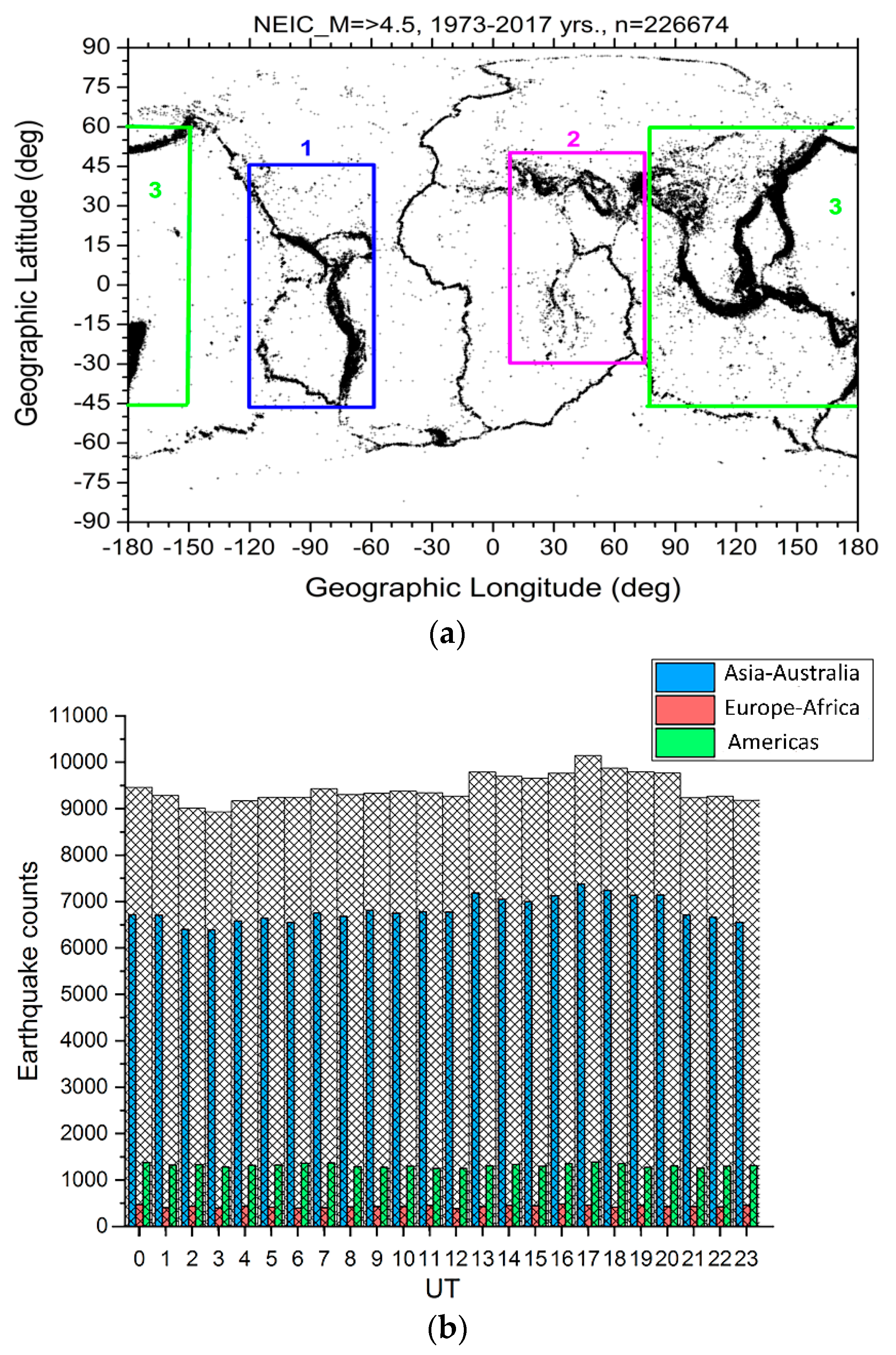
Taking this idea as a possible explanation of the observed UT dependence, we should establish two things: the contributions of the different longitudinal regions of the planet to its overall seismic activity, and revealing which longitudinal areas of the globe in local night correspond to the maxima of the IP distributions. Let us conditionally separate the areas of global seismic activity along three longitudinal zones (top panel of
Figure 11), and divide all 226674 cases from our sample into subsets of earthquakes registered within these zones (
Figure 11b)
One can see that the overwhelming majority of earthquakes takes place in the Asia–Australia longitudinal sector, and they represent the largest contribution to global seismic activity. We doubt if one will find the essential difference between the UT distribution of global earthquakes and earthquakes in the Asia–Australia sector only for the period 1973–2017, as presented in the
Figure 12, but absent the number of earthquakes in each set.
We can draw the conclusion that the Asian–Australian longitudinal sector makes the largest contribution to the world’s earthquakes UT distribution maximum. Taking into account that the main contribution to the IP is pre-earthquake anomalies occurring at nighttime, we need to examine which longitudinal sector corresponds to the interval of ionospheric potential’s UT distribution maximum; and, we obtained the expected answer—the Asian–Australian longitudinal sector. So, the most seismoactive region on the globe shows the largest contribution to the variation in IP coinciding in time with that UT interval for which the IP maximum is observed.
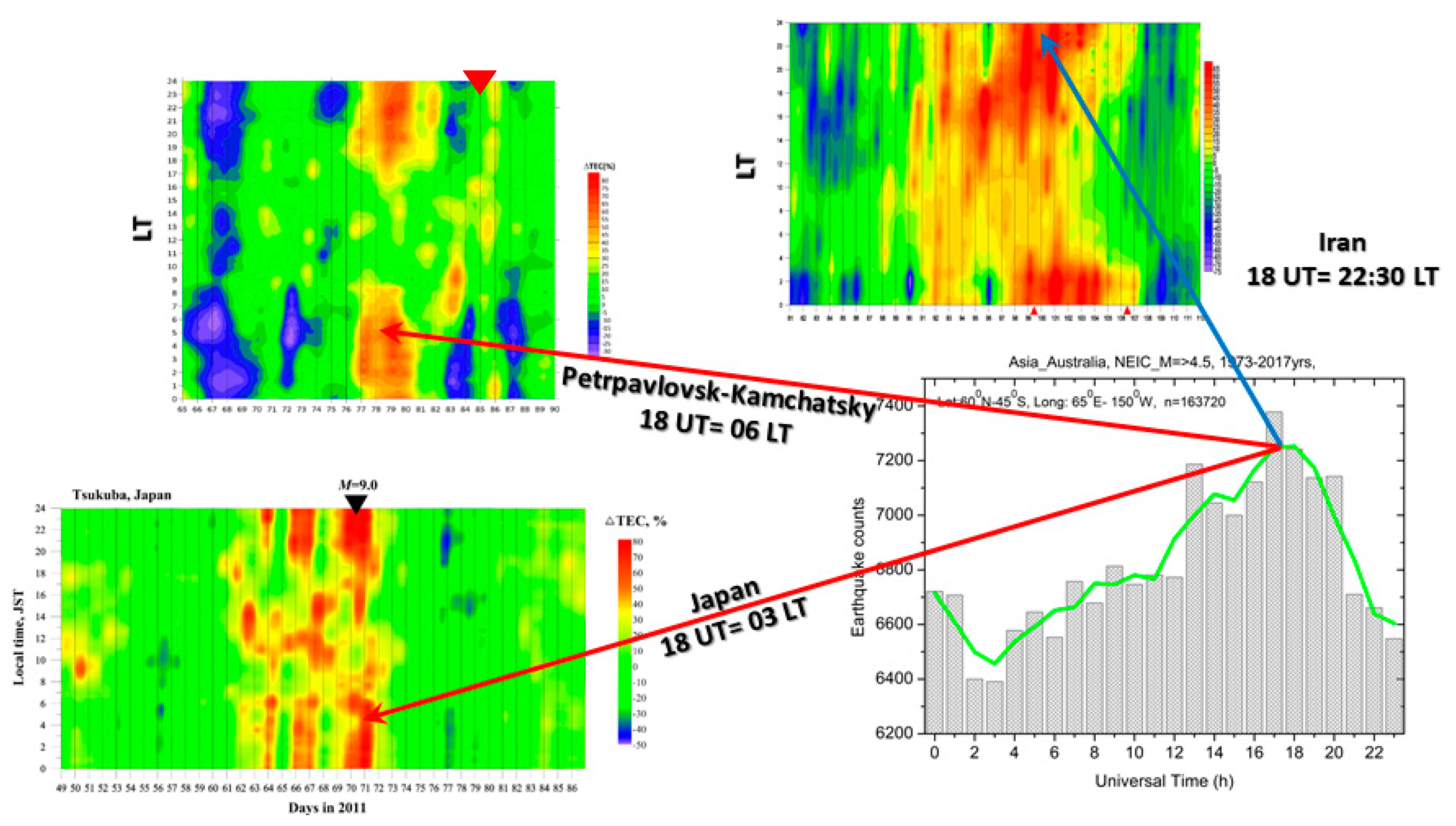
This conclusion is illustrated by
Figure 13. We present three precursory periods for the major earthquakes in the different zones of the Asian–Australian longitudinal sector to examine which local times, in these sectors, correspond to 18:00 UT: they were the M6.3 Bushehr earthquake of 9 April 2013, the M9 Tohoku earthquake, in Japan, on 11 March 2011, and the M7.5 earthquake that struck east of the Kuril Islands on 25 March 2020.
We can see from the
Figure 13 that 18:00 UT corresponds to 22:30 LT in Iran, 03:00 LT in Japan, and 06:00 LT (before sunrise) in the Kuril Islands.
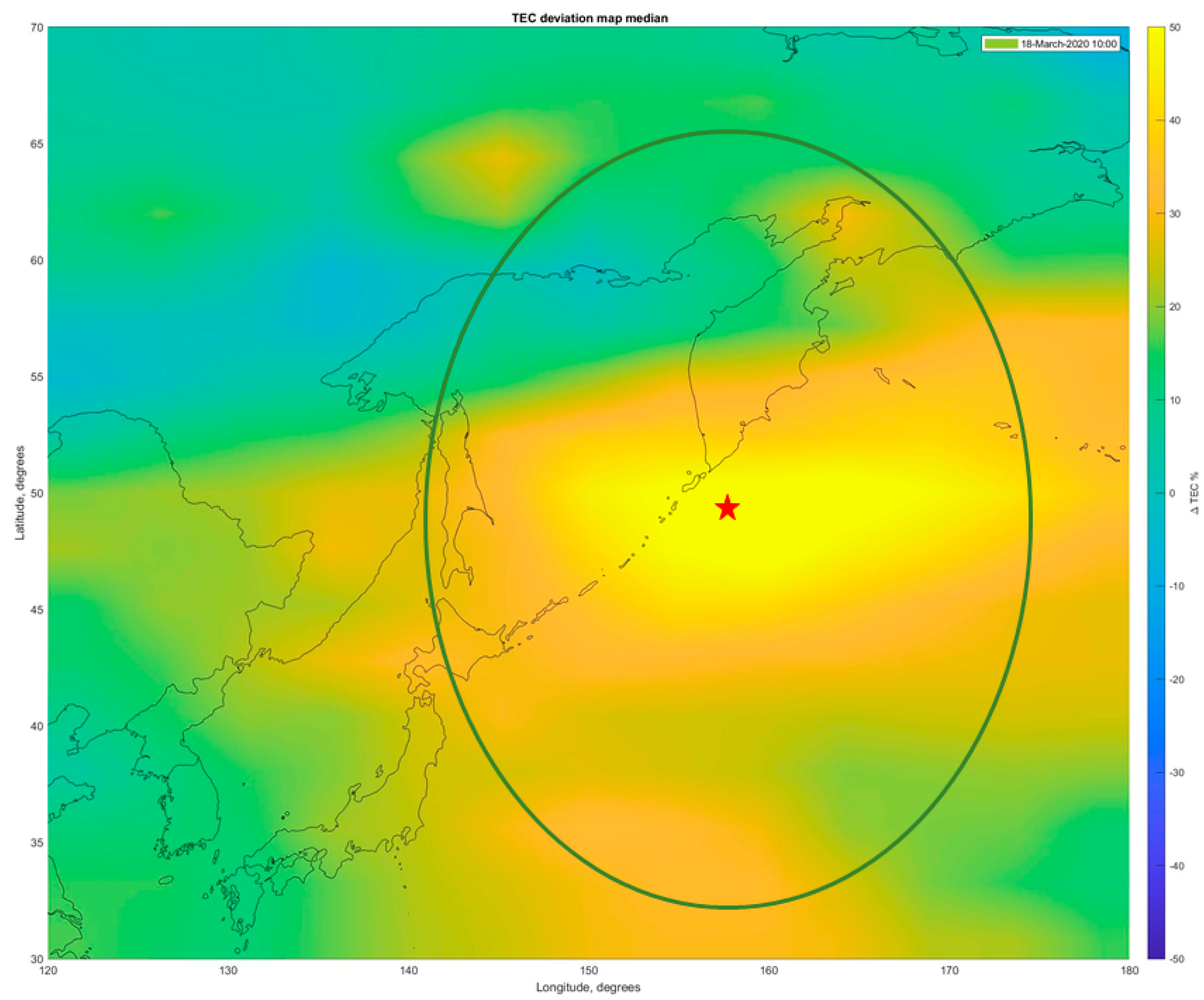
We should also mention that positive irregularities, forming within the ionosphere, scale with magnitude in size, according to Dobrovolsky et al. (1979) [
37] as R(km) = 10
0.43M. In the case of the M7.5 earthquake, R ≈ 1700 km. A differential map for the Kuril Islands’ earthquake of 25 March 2020 is shown in
Figure 14. Taking 1700 km as the radius of the anomalous zone in the ionosphere, we obtain the area of nearly nine million square kilometers. Such a huge area will certainly modulate the ionospheric potential’s distribution.
6. Conclusions
From the discussion above we can conclude that the global seismic activity is providing an essential contribution to the global electric current. This is expressed by the existence of a unitary variation in the global seismic activity having high correlation with the Carnegie curve and IP UT distribution. This contribution is observed in both domains of atmospheric electricity: in the effects of EF generation in thunderstorm activity areas, and in the effects of the ionospheric potential’s modulation in fair-weather areas:
Contribution to lightning activity: (a) near-ground air ionization by increased radon activity in seismically active areas facilitates lightning discharges; (b) a sharp decrease or even direction reversal of the atmospheric electric field increases the potential difference between a thunderstorm’s bottom cloud edge and the ground surface; (c) the generation of aerosols due to IIN effects, which serve as condensation nuclei for the formation of thunderstorm clouds.
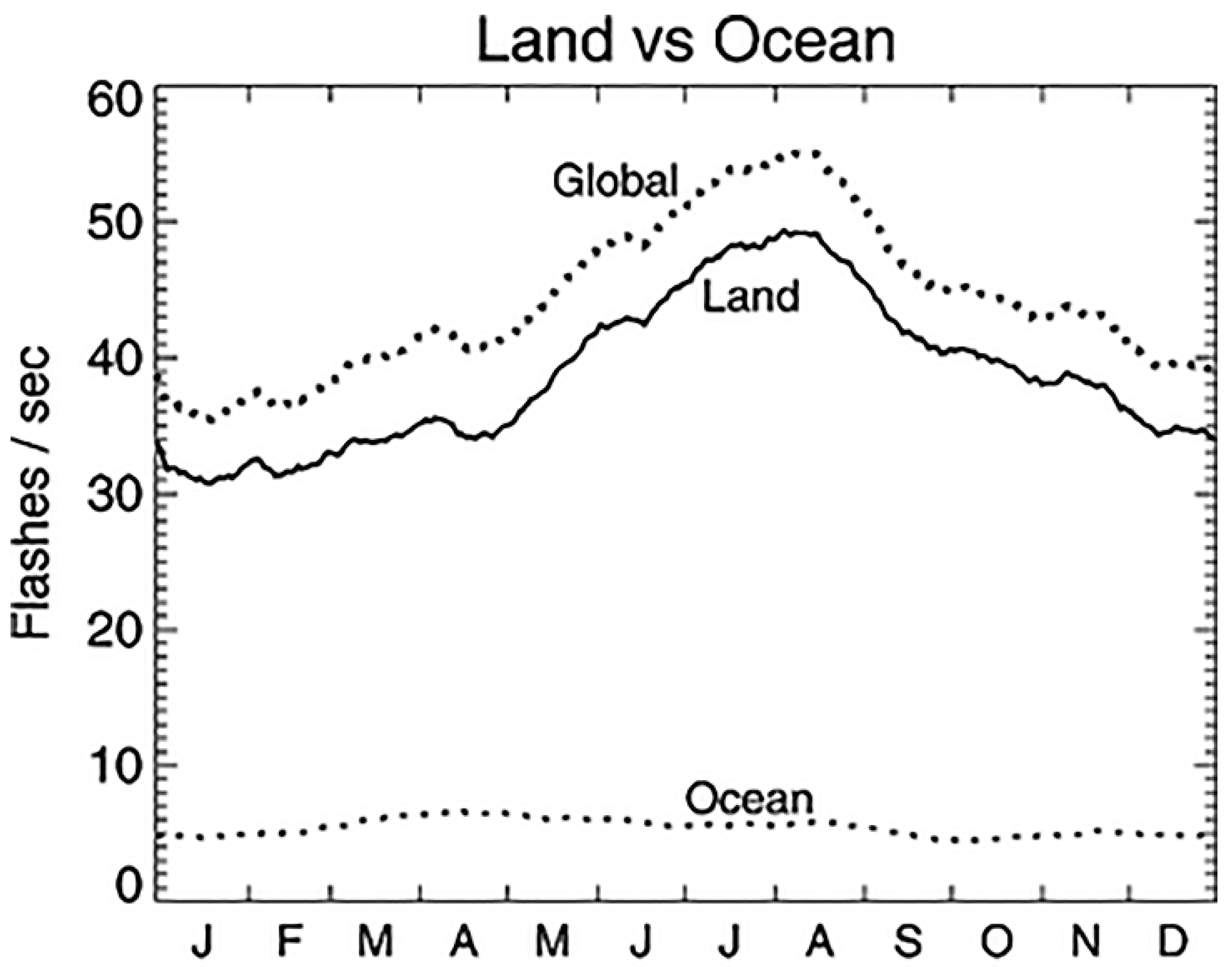
One more argument for the relevance of the seismic activity UT distribution to thunderstorm activity is the similarity of this distribution with continental lightning activity [Whipple and Scrase, 1936; Siingh et al., 2015] [
42,
43] (
Figure 15), where the flat distribution within the interval 12:00–20:00UT can be observed and which can also clearly be distinguished in the UT distributions of seismic activity.
Ionospheric potential modulation: Large-scale increases in the electron concentration in the ionosphere above areas of earthquake preparation lead to increases in the ionospheric potential.
The universal time distribution of the global seismic activity, with consideration of local nighttime intervals as the period in which ionospheric precursors are generated corresponds with the longitudinal distribution of the intensity of seismic activity. The primary maximum in the unitary distribution corresponds to the Asia–Australia longitudinal sector, the most seismically active area on the globe.
Due to the problem’s complexity we consider this publication as a first open-discussion paper, with which we hope to attract the attention of scientists to this intriguing problem of geospheres’ interactions.