Thermodynamic and Kinetic Modelling of Scales Formation at the Soultz-sous-Forêts Geothermal Power Plant
Abstract
:1. Introduction
1.1. Geothermal Energy in the Upper Rhine Graben
1.2. SsF Geothermal Power Plant
1.3. Geochemical Characterization of the Scale during Operation
2. Methods
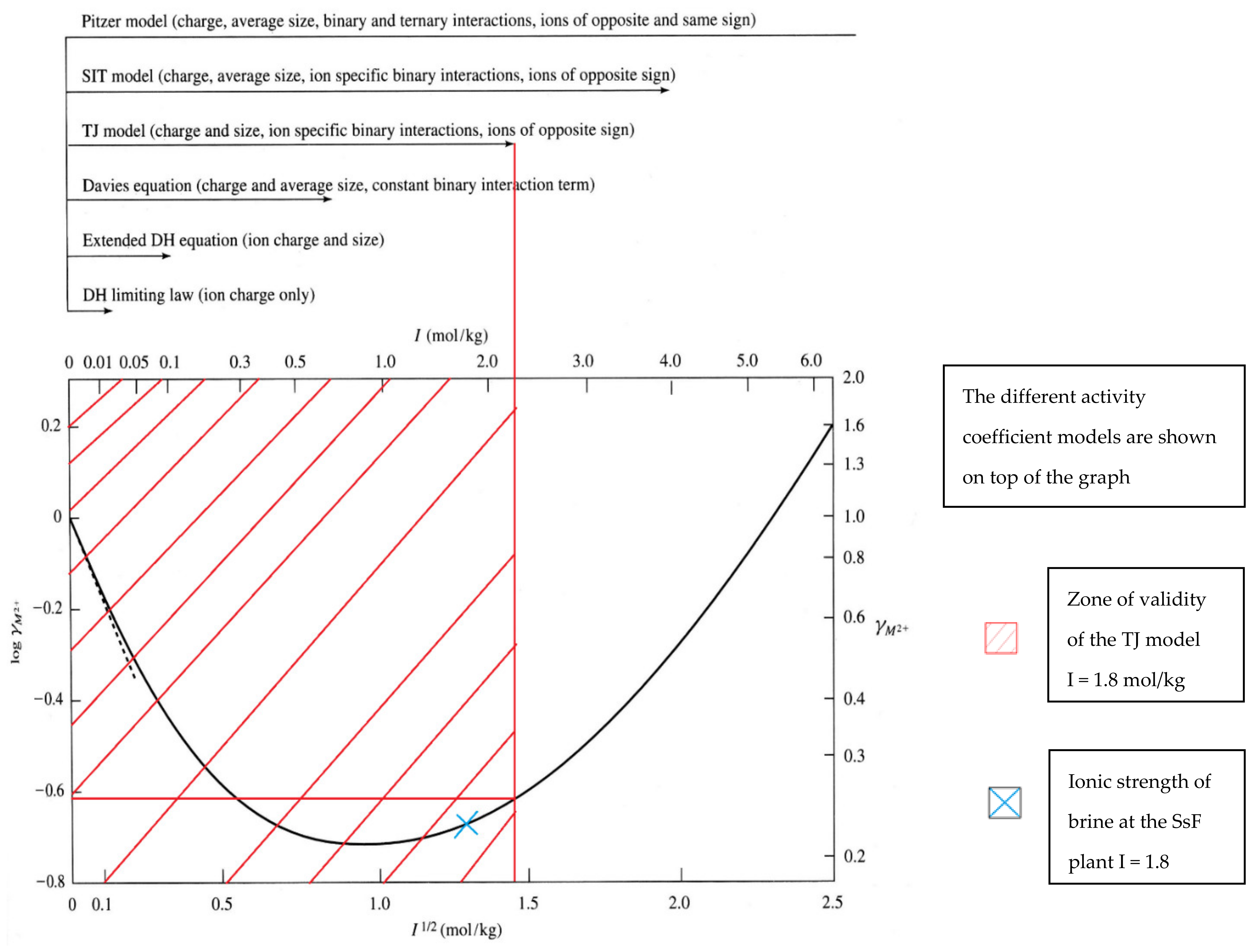
2.1. Verification: Elements
2.2. Verification: Minerals
2.3. Verification: B-Dot Model Database
2.4. Verification: Gas
2.5. Scale Modelling
3. Results
3.1. Thermodynamic Modelling
3.2. Kinetic Modelling
4. Discussion
4.1. Introduction
4.2. Thermodynamic Modelling Analysis
4.3. Kinetic Modelling Analysis
4.4. New Perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Pressure (bar) | 20 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Temperature (°C) | 40 | 50 | 60 | 65 | 90 | 120 | 150 | 175 | 200 | |
| SiO2 | Amorphous_silica | 0.45 | 0.38 | 0.32 | 0.29 | 0.16 | 0.03 | −0.08 | −0.16 | −0.24 |
| CaSO4 | Anhydrite | −0.98 | −0.88 | −0.78 | −0.73 | −0.53 | −0.32 | −0.1 | 0.08 | 0.25 |
| Cu1.75S | Anilite | 2.61 | 1.97 | 1.31 | 0.97 | −0.55 | −1.95 | −3.05 | −3.86 | −4.65 |
| FeAsS | Arsenopyrite | −0.52 | −0.28 | −0.04 | 0.06 | 0.3 | 0.13 | −0.24 | −0.58 | −0.9 |
| BaSO4 | Barite | 1.24 | 1.11 | 0.99 | 0.93 | 0.67 | 0.4 | 0.21 | 0.1 | 0.01 |
| FeSb2S4 | Berthierite | 1.33 | 1.25 | 1.17 | 1.13 | 0.92 | 0.63 | −0.02 | −1.48 | −3.15 |
| Cu5FeS4 | Bornite (alpha) | 17.03 | 15.3 | 13.5 | 12.59 | 8.22 | 3.83 | 0.17 | −2.56 | −5.19 |
| SiO2 | Chalcedony | 1.16 | 1.05 | 0.96 | 0.91 | 0.72 | 0.52 | 0.34 | 0.21 | 0.1 |
| Cu2S | Chalcocite (alpha) | 2.75 | 2.01 | 1.24 | 0.85 | −0.89 | −2.45 | −3.66 | −4.53 | −5.38 |
| CuFeS2 | Chalcopyrite (alpha) | 6.21 | 6.07 | 5.91 | 5.8 | 5.12 | 4.08 | 3.01 | 2.17 | 1.36 |
| SiO2 | Coesite (alpha) | 0.64 | 0.55 | 0.47 | 0.43 | 0.26 | 0.09 | −0.05 | −0.16 | −0.26 |
| CuS | Covellite | 1.42 | 1.07 | 0.71 | 0.53 | −0.36 | −1.28 | −2.09 | −2.7 | −3.28 |
| SiO2 | Cristobalite (alpha) | 0.89 | 0.8 | 0.72 | 0.68 | 0.52 | 0.35 | 0.21 | 0.1 | 0 |
| SiO2 | Cristobalite (beta) | 0.83 | 0.74 | 0.66 | 0.62 | 0.47 | 0.31 | 0.17 | 0.07 | −0.02 |
| Cu1.934S | Djurleite | 2.76 | 2.05 | 1.3 | 0.93 | −0.76 | −2.29 | −3.47 | −4.34 | −5.18 |
| Fe10S11 | Fe10S11 | −19.75 | −15.47 | −11.34 | −9.49 | −2.77 | 0.56 | 1.65 | 1.98 | 2.14 |
| Fe11S12 | Fe11S12 | −21.56 | −16.83 | −12.28 | −10.23 | −2.81 | 0.92 | 2.19 | 2.61 | 2.84 |
| Fe7.016S8 | Fe7.016S8 | −11.61 | −8.67 | −5.83 | −4.55 | 0.01 | 2.12 | 2.67 | 2.74 | 2.72 |
| Fe9S10 | Fe9S10 | −16.97 | −13.14 | −9.45 | −7.79 | −1.8 | 1.11 | 2 | 2.23 | 2.31 |
| PbS | Galena | 2.57 | 2.54 | 2.51 | 2.49 | 2.18 | 1.6 | 1 | 0.53 | 0.05 |
| FeS2 | Marcassite | 4.15 | 4.39 | 4.63 | 4.72 | 4.87 | 4.42 | 3.73 | 3.13 | 2.56 |
| As2S3 | Orpiment | 0.92 | 0.97 | 1.04 | 1.04 | 0.58 | −0.82 | −2.6 | −4.1 | −5.52 |
| FeS2 | Pyrite | 4.84 | 5.06 | 5.28 | 5.36 | 5.45 | 4.96 | 4.23 | 3.6 | 3 |
| SiO2 | Quartz (alpha) | 1.43 | 1.31 | 1.21 | 1.16 | 0.95 | 0.73 | 0.54 | 0.4 | 0.28 |
| SiO2 | Quartz (beta) | 1.21 | 1.11 | 1.02 | 0.97 | 0.78 | 0.59 | 0.42 | 0.29 | 0.18 |
| Na2(Fe3Fe2)Si8O22(OH)2 | Riebeckite | −7.54 | −6.95 | −6.34 | −6.05 | −4.66 | −3.17 | −1.68 | −0.44 | 0.8 |
| Sb2S3 | Stibnite | 3.25 | 2.76 | 2.29 | 2.08 | 1.25 | 0.7 | 0.02 | −1.4 | −3.01 |
Appendix B
References
- Glaas, C. Mineralogical and Structural Controls on Permeability of Deep Naturally Fracturated Crystalline Reservoirs. Ph.D. Thesis, Univerité de Strasbourg, Strasbourg, France, 2021. [Google Scholar]
- Genter, A.; Evans, K.; Cuenot, N.; Fritsch, D.; Sanjuan, B. Contribution of the exploration of deep crystalline fractured reservoir of Soultz to the knowledge of enhanced geothermal systems (EGS). Comptes Rendus Geosci. 2010, 342, 502–516. [Google Scholar] [CrossRef]
- Vidal, J.; Genter, A. Overview of naturally permeable fractured reservoirs in the Upper Rhine Graben: Insights from geothermal wells. Geothermics 2018, 74, 57–73. [Google Scholar] [CrossRef]
- Schill, E.; Genter, A.; Cuenot, N.; Kohl, T. Hydraulic performance history at the Soultz EGS reservoirs from stimulation and long-term circulation tests. Geothermics 2017, 70, 110–124. [Google Scholar] [CrossRef]
- Baujard, C.; Genter, A.; Cuenot, N.; Mouchot, J.; Maurer, V.; Hehn, R.; Ravier, G.; Seibel, O.; Vidal, J. Experience Learnt from a Successful Soft Stimulation and Operational Feedback after 2 Years of Geothermal Power and Heat Production in Rittershoffen and Soultz-sous-Forêts Plants (Alsace, France). GRC Trans. 2018, 42. [Google Scholar] [CrossRef]
- Mouchot, J.; Ravier, G.; Seibel, O.; Pratiwi, A. Deep Geothermal Plants Operation in Upper Rhine Graben: Lessons Learned. In Proceedings of the European Geothermal Congress, The Hague, The Netherlands, 11–14 June 2019. [Google Scholar]
- Bosia, C.; Mouchot, J.; Ravier, G.; Seibt, A.; Jähnichen, S.; Degering, D.; Scheiber, J.; Dalmais, E.; Baujard, C.; Genter, A. Evolution of Brine Geochemical Composition during Operation of EGS Geothermal Plants (Alsace, France). In Proceedings of the 46th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 15–17 February 2021. [Google Scholar]
- Scheiber, J.; Nitschke, F.; Seibt, A.; Genter, A. Geochemical and Mineralogical Monitoring of the Geothermal Power Plant in Soultz-sous-Forêts (France). In Proceedings of the 37th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 30 January–1 February 2012. [Google Scholar]
- Sanjuan, B. Soultz EGS Pilot Plant Exploitation—Phase III: Scientific Program about On-Site Operations of Geochemical Monitoring and Tracing (2010–2013), First Yearly Progress Report BRGM/RP-59902-FR. 2011; Volume 16, p. 92.
- Nitschke, F. Geochemische Charakterisierung des Geothermalen Fluids und der Damit Verbundenen Scalings in der Geothermieanlage Soultz sous Forêts. Master’s Thesis, Institut für Mineralogie und Geochemie (IMG) at Karlsruher Institut of Technology (KIT), Singapore, 2012; p. 126. [Google Scholar]
- Haas-Nüesch, R.; Heberling, F.; Schild, D.; Rothe, J.; Dardenne, K.; Jähnichen, S.; Eiche, E.; Marquardt, C.; Metz, V.; Schäfer, T. Mineralogical characterization of scalings formed in geothermal sites in the Upper Rhine Graben before and after the application of sulfate inhibitors. Geothermics 2018, 71, 264–273. [Google Scholar] [CrossRef]
- Mouchot, J.; Cuenot, N.; Bosia, C.; Genter, A.; Seibel, O.; Ravier, G.; Scheiber, J. First year of operation from EGS geothermal plants in Alsace, France: Scaling issues. In Proceedings of the 43rd Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 12–14 February 2018. [Google Scholar]
- Seibel, O.; Mouchot, J.; Ravier, G.; Ledésert, B.; Sengelen, X.; Hebert, R.; Ragnarsdótti, K.R.; Ólafsson, D.I.; Haraldsdóttir, H.Ó. Optimised valorisation of the geothermal resources for EGS plants in the Upper Rhine Graben. In Proceedings of the World Geothermal Congress 2020+1, Reykjavik, Iceland, 24–27 October 2021. [Google Scholar]
- Ledésert, B.A.; Hébert, R.L.; Mouchot, J.; Bosia, C.; Ravier, G.; Seibel, O.; Dalmais, E.; Ledésert, M.; Trullenque, G.; Sengelen, X.; et al. Scaling in a Geothermal Heat Exchanger at Soultz-sous-Forêts (Upper Rhine Graben, France): A XRD and SEM-EDS Characterization of Sulfide Precipitates. Geosciences 2021, 11, 271. [Google Scholar] [CrossRef]
- Gifaut, E.; Grivé, M.; Blanc, P.; Vieillard, P.; Colàs, E.; Gailhanou, H.; Gaboreau, S.; Marty, N.; Madé, B.; Duro, L. Andra thermodynamic database for performance assessment: Thermochimie. Appl. Geochem. 2014, 49, 225–236. [Google Scholar] [CrossRef]
- Moog, H.C.; Bok, F.; Marquardt, C.M.; Brendler, V. Disposal of nuclear waste in host rock formations featuring high-saline solutions—Implementation of a thermodynamic reference database (THEREDA). Appl. Geochem. 2015, 55, 72–84. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Appelo, C.A.J. Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations: U.S. Geological Survey Techniques and Methods 2013, Book 6, Chapter A43, p. 497. Available online: http://pubs.usgs.gov/tm/06/a43/ (accessed on 12 April 2021).
- Blanc, P.; Lassin, A.; Piantone, P.; Azaroual, M.; Jacquemet, N.; Fabbri, A.; Gaucher, E.C. Thermoddem: A geochemical database focused on low temperature water/rock interactions and waste materials. Appl. Geochem. 2012, 27, 2107–2116. [Google Scholar] [CrossRef]
- Delany, J.M.; Lundeen, S.R. The LLNL Thermochemical Data Base–Revised Data and File Format for the EQ3/6 Package; Lawrence Livermore National Lab.: Livermore, CA, USA, 1991.
- Langmuir, D. Aqueous Environmental Geochemistry; Prentice Hall: Hoboken, NJ, USA, 1997. [Google Scholar]
- Alsemgeest, J.; Auqué, L.F.; Gimeno, M.J. Verification and comparison of two thermodynamic databases through conversion to PHREEQC and multicomponent geothermometrical calculations. Geothermics 2021, 91, 102036. [Google Scholar] [CrossRef]
- Hettkamp, T.; Baumgaertner, J.; Paredes, R.; Ravier, G.; Seibel, O. Industrial Experiences with Downhole Geothermal Line-Shaft Production Pumps in Hostile Environment in the Upper Rhine Valley. In Proceedings of the World Geothermal Congress 2020+1, Reykjavik, Iceland, 24–27 October 2021. [Google Scholar]
- Zhang, Y.; Hu, B.; Teng, Y.; Tu, K.; Zhu, C. A library of BASIC scripts of reaction rates for geochemical modeling using PHREEQC. Comput. Geosci. 2019, 133, 104316. Available online: https://github.com/HydrogeoIU/PHREEQC-Kinetic-Library/blob/master/PHREEQC%20script.txt (accessed on 14 June 2021). [CrossRef]
- Biver, M.; Shotyk, W. Stibnite (Sb2S3) oxidative dissolution kinetics from pH 1 to 11. Geochim. Cosmochim. Acta 2012, 79, 127–139. [Google Scholar] [CrossRef]
- Poonoosamya, J.; Curti, E.; Kosakowski, G.; Grolimund, D.; Van Loon, L.R.; Mäder, U. Barite precipitation following celestite dissolution in a porous medium: A SEM/BSE and μ-XRD/XRF study. Geochim. Cosmochim. Acta 2016, 182, 131–144. [Google Scholar] [CrossRef]
- Lichti, K.A.; Brown, K.L. Prediction and Monitoring of Scaling and Corrosion in pH Adjusted Geothermal Brine Solutions. In Proceedings of the NACE International Corrosion Conference & Expo 2013, Orlando, FL, USA, 17–21 March 2013. [Google Scholar]
- Lichti, K.A.; Ko, M.; Kennedy, J. Heavy Metal Galvanic Corrosion of Carbon Steel in Geothermal Brines. In Proceedings of the NACE International Corrosion Conference & Expo 2016, Vancouver, BC, Canada, 6–10 March 2016. [Google Scholar]





| GPK-2 (Production Well) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Composition of brine | Na | Ca | K | Cl | Mg | Sr | Li | SiO2 | SO4 | Br | Mn | NH4 |
| (mg/L) | 26,400 | 7020 | 3360 | 55,940 | 123 | 422 | 160 | 179 | 108 | 240 | 17 | 23.2 |
| Composition of brine | As | Ba | Cs | Rb | B | Fe | Zn | F | I | Cu | Pb | Cd |
| (mg/L) | 10 | 26 | 14 | 23 | 38 | 26.3 | 2.8 | 1.3 | 1.6 | 0.001 | 0.11 | 0.01 |
| Composition of brine | Sb | Al | U | Ni | HCO3 | COT | ||||||
| (mg/L) | 0.06 | 0.05 | 0.001 | 0.0011 | 197 | 0.9 |
| GPK-2 (Production Well) | ||
|---|---|---|
| Gas dissolved in brine | %vol | Partial pressure (atm) |
| CO2 | 0.882 | 0.882 |
| N2 | 0.0908 | 0.0908 |
| CH4 | 0.0239 | 0.0239 |
| Temperature | S | Pb | Sr | Ba | Sb | As | Fe | Si | Cu | Exchanger |
|---|---|---|---|---|---|---|---|---|---|---|
| 150 | 2.9% | 2.0% | 2.9% | 0.94% | 0.11% | 0.53% | 1.7% | 3.8% | 0.40% | ORC Inlet Evaporator |
| 120 | 11.8% | 26.5% | 0.65% | 1.9% | 3.3% | 6.6% | 7.5% | 8.0% | 16.6% | ORC Inlet Preheater 2 |
| 90 | 11.2% | 36.1% | 0.86% | 3.6% | 3.1% | 5.2% | 8.0% | 16.9% | 5.1% | ORC Inlet Preheater 1 |
| 65 | 13.1% | 46.3% | 0.51% | 2.2% | 6.3% | 7.3% | 4.6% | 8.4% | 4.5% | ORC Outlet Preheater 1 |
| 60 | 13.1% | 74.6% | 0.01% | 0.00% | 6.4% | 3.2% | 0.07% | 1.4% | 0.40% | Test HEX |
| 50 | 14.4% | 66.5% | 0.01% | 0.01% | 11.4% | 4.3% | 0.55% | 1.0% | 0.43% | Test HEX |
| 40 | 16.7% | 64.2% | 0.01% | 0.01% | 10.9% | 4.5% | 0.48% | 1.6% | 0.36% | Test HEX |
| Databases | Nomenclature |
|---|---|
| Phreeqc | D1 |
| Pitzer | D2 |
| ColdChem | D3 |
| Core10 | D4 |
| Frezchem | D5 |
| Iso | D6 |
| LLNL | D7 |
| MINTEQ | D8 |
| Minteq v4 | D9 |
| Pitzer_Old | D10 |
| sit | D11 |
| T_H | D12 |
| WATEQ4F | D13 |
| Thermoddem_06_2017 | D14 |
| PHREEQC_ThermoddemV1.10_15Dec2020 | D15 |
| ThermoChimie_PHREEQC_eDH_v9b0 | D16 |
| THEREDA_2020_PHRQ | D17 |
| CEMDATA18.1-16-01-2019-phaseVol | D18 |
| ThermoChimie_PhreeqC_SIT_oxygen_v10a | D19 |
| D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 | D11 | D12 | D13 | D14 | D15 | D16 | D17 | D18 | D19 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x |
| Pb | x | x | x | x | x | x | x | x | x | x | x | ||||||||
| Sr | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | ||||
| Ba | x | x | x | x | x | x | x | x | x | x | x | x | x | ||||||
| Sb | x | x | x | x | x | x | x | x | |||||||||||
| As | x | x | x | x | x | x | x | x | x | x | |||||||||
| Fe | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||
| Si | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||
| Cu | x | x | x | x | x | x | x | x | x | x | x | x | |||||||
| Al | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | ||||
| B | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||||
| Be | x | x | x | x | x | ||||||||||||||
| Br | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||||
| Ca | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |
| Cd | x | x | x | x | x | x | x | x | x | x | x | ||||||||
| Ce | x | x | x | ||||||||||||||||
| Cl | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |
| Co | x | x | x | x | x | x | x | x | |||||||||||
| Cs | x | x | x | x | x | x | x | x | x | ||||||||||
| Dy | x | x | x | ||||||||||||||||
| Er | x | x | x | ||||||||||||||||
| Eu | x | x | x | x | x | x | x | ||||||||||||
| F | x | x | x | x | x | x | x | x | x | x | x | x | |||||||
| Gd | x | x | x | x | |||||||||||||||
| Ge | x | x | |||||||||||||||||
| Hg | x | x | x | x | x | x | x | ||||||||||||
| Ho | x | x | x | x | x | x | |||||||||||||
| I | x | x | x | x | x | x | x | x | x | x | |||||||||
| In | x | x | x | ||||||||||||||||
| K | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x |
| La | x | x | x | ||||||||||||||||
| Li | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||||
| Lu | x | x | x | ||||||||||||||||
| Mg | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x |
| Mn | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||||
| Mo | x | x | x | x | x | x | x | x | |||||||||||
| Na | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x |
| Nd | x | x | x | x | |||||||||||||||
| Ni | x | x | x | x | x | x | x | x | x | x | |||||||||
| P | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||||
| Pd | x | x | x | x | x | x | |||||||||||||
| Pr | x | x | x | ||||||||||||||||
| Rb | x | x | x | x | x | x | x | x | x | ||||||||||
| Re | x | x | x | ||||||||||||||||
| Rh | x | x | |||||||||||||||||
| Sc | x | x | x | x | |||||||||||||||
| Sm | x | x | x | x | x | x | x | ||||||||||||
| Tb | x | x | x | ||||||||||||||||
| Tm | x | x | x | ||||||||||||||||
| W | x | x | x | x | |||||||||||||||
| Y | x | x | x | ||||||||||||||||
| Yb | x | x | x | ||||||||||||||||
| Zn | x | x | x | x | x | x | x | x | x | x | x | x | x | ||||||
| HCO3 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x * | x | x | x | |
| NH4 | x | x | x | x | x | x | x | x | x | x | x | x | |||||||
| SO3 | x | x | x | x | x | x * | x * | x | x | x | x | x | |||||||
| SO4 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x |
| Total | 23 | 17 | 7 | 26 | 8 | 14 | 55 | 32 | 33 | 14 | 38 | 29 | 30 | 57 | 57 | 38 | 14 | 14 | 37 |
| Databases | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Known Minerals | D1 | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | D10 | D11 | D12 | D13 | D14 | D15 | D16 | D17 | D18 | D19 | |
| Galena | PbS | x | x | x | x | x | x | x | x | x | x | |||||||||
| Quartz | SiO2 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||
| Calcite | CaCO3 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | ||
| Anhydrite | CaSO4 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | ||
| Gypsum | CaSO4:2H20 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |
| Barite | BaSO4 | x | x | x | x | x | x | x | x | x | x | x | x | |||||||
| Halite | NaCl | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |
| Goethite | FeOOH | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||||
| Celestite | SrSO4 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||||
| Arsenopyrite | FeAsS | x | x | x | ||||||||||||||||
| Stibnite | Sb2S3 | x | x | x | x | x | x | x | x | |||||||||||
| Possible Other Minerals | ||||||||||||||||||||
| Hematite | Fe2O3 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | |||||
| Strontianite | SrCO3 | x | x | x | x | x | x | x | x | x | x | x | x | |||||||
| Svanbergite | SrAl3(PO4)(SO4)(OH)6 | x | x | |||||||||||||||||
| Sr3(AsO4)2 | Sr3(AsO4)2 | x | x | x | x | x | x | |||||||||||||
| SrS | SrS | x | x | x | x | x | x | |||||||||||||
| Anglesite | PbSO4 | x | x | x | x | x | x | x | x | x | x | x | ||||||||
| Cerussite | PbCO3 | x | x | x | x | x | x | x | x | x | x | x | ||||||||
| Alamosite | PbSiO3 | x | x | x | x | x | x | x | x | x | ||||||||||
| Beudantite | PbFe3(AsO4)2(OH)5:H2O | x | x | |||||||||||||||||
| Corkite | PbFe3(PO4)(OH)6SO4 | x | x | x | ||||||||||||||||
| Cotunnite | PbCl2 | x | x | x | x | x | x | x | x | x | x | |||||||||
| Duftite | PbCuAsO4(OH) | x | x | |||||||||||||||||
| Hinsdalite | PbAl3(PO4)(SO4)(OH)6 | x | x | x | x | x | x | x | ||||||||||||
| Hydrocerussite | Pb3(CO3)2(OH)2 | x | x | x | x | x | x | x | x | x | ||||||||||
| Jarosite(Pb) | Pb0.5Fe3(SO4)2(OH)6 | x | x | |||||||||||||||||
| Lanarkite | Pb2SO5 | x | x | x | x | x | x | x | x | x | x | |||||||||
| Mimetite | Pb5(AsO4)3Cl | x | x | |||||||||||||||||
| Pb3(AsO4)2 | Pb3(AsO4)2 | x | x | x | x | x | x | x | ||||||||||||
| Pb3SO6 | Pb3SO6 | x | x | x | x | x | ||||||||||||||
| Pb4(OH)6SO4 | Pb4(OH)6SO4 | x | x | x | x | |||||||||||||||
| Pb4SO7 | Pb4SO7 | x | x | x | x | x | ||||||||||||||
| PbSO4(NH3)2 | PbSO4(NH3)2 | x | ||||||||||||||||||
| PbSO4(NH3)4 | PbSO4(NH3)4 | x | ||||||||||||||||||
| Pb(Thiocyanate)2 | Pb(SCN)2 | x | ||||||||||||||||||
| Philipsbornite | PbAl3(AsO4)2(OH)5:H2O | x | x | |||||||||||||||||
| Tsumebite | Pb2Cu(PO4)(SO4)OH | x | x | x | ||||||||||||||||
| Realgar | AsS | x | x | x | x | x | x | x | x | x | x | |||||||||
| Orpiment | As2S3 | x | x | x | x | x | x | x | x | x | x | |||||||||
| Bornite | Cu5FeS4 | x | x | x | x | |||||||||||||||
| Chalcocite | Cu2S | x | x | x | x | x | x | x | x | |||||||||||
| Berthierite | FeSb2S4 | x | x | |||||||||||||||||
| Total | 12 | 7 | 3 | 9 | 4 | 7 | 33 | 25 | 25 | 6 | 21 | 25 | 25 | 35 | 35 | 23 | 2 | 8 | 23 | |
| Molar Mass | GPK-2 | GPK-3 | GPK-2 | GPK-3 | GPK-2 | GPK-3 | |
|---|---|---|---|---|---|---|---|
| M (mg/mol) | mg/L | mol/L | Ionic Strength, I (mol/L or mol/kg) | ||||
| Na | 23,000 | 26,400 | 26,700 | 1.148 | 1.161 | 0.574 | 0.580 |
| Cl | 35,500 | 57,490 | 57,490 | 1.619 | 1.619 | 0.810 | 0.810 |
| K | 39,100 | 3350 | 3350 | 0.086 | 0.086 | 0.043 | 0.043 |
| Ca | 40,100 | 7020 | 7030 | 0.175 | 0.175 | 0.350 | 0.351 |
| Sr | 87,620 | 422 | 434 | 0.005 | 0.005 | 0.010 | 0.010 |
| Br | 79,904 | 240 | 234 | 0.003 | 0.003 | 0.002 | 0.001 |
| Li | 6940 | 160 | 163 | 0.023 | 0.023 | 0.012 | 0.012 |
| SiO2 | 40,100 | 179 | 180 | 0.004 | 0.004 | ||
| Total | 95,261 | 95,581 | 3.063 | 3.077 | 1.799 | 1.807 | |
| Temperature (°C) | Pitzer | LLNL | Thermoddem |
|---|---|---|---|
| 80 | 14 atm | 10 atm | 10 atm |
| 150 | 18 atm | 15 atm | 16 atm |
| Pressure (bar) | 20 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Temperature (°C) | 40 | 50 | 60 | 65 | 90 | 120 | 150 | 175 | 200 | |
| Known Minerals | ||||||||||
| SiO2 | Amorphous_silica | x | x | x | x | x | x | |||
| CaSO4 | Anhydrite | x | x | |||||||
| Sb2S3 | Stibnite | x | x | x | x | x | x | x | ||
| FeAsS | Arsenopyrite | x | x | x | ||||||
| BaSO4 | Barite | x | x | x | x | x | x | x | x | x |
| CuFeS2 | Chalcopyrite (alpha) | x | x | x | x | x | x | x | x | x |
| PbS | Galena | x | x | x | x | x | x | x | x | x |
| SiO2 | Quartz (alpha) | x | x | x | x | x | x | x | x | x |
| SiO2 | Quartz (beta) | x | x | x | x | x | x | x | x | x |
| Possible Other Minerals | ||||||||||
| Cu1.75S | Anilite | x | x | x | x | |||||
| FeSb2S4 | Berthierite | x | x | x | x | x | x | |||
| Cu5FeS4 | Bornite (alpha) | x | x | x | x | x | x | x | ||
| SiO2 | Chalcedony | x | x | x | x | x | x | x | x | x |
| Cu2S | Chalcocite (alpha) | x | x | x | x | |||||
| SiO2 | Coesite (alpha) | x | x | x | x | x | x | |||
| CuS | Covellite | x | x | x | x | |||||
| SiO2 | Cristobalite (alpha) | x | x | x | x | x | x | x | x | x |
| SiO2 | Cristobalite (beta) | x | x | x | x | x | x | x | x | |
| Cu1.934S | Djurleite | x | x | x | x | |||||
| Fe10S11 | Fe10S11 | x | x | x | x | |||||
| Fe11S12 | Fe11S12 | x | x | x | x | |||||
| Fe7.016S8 | Fe7.016S8 | x | x | x | x | x | ||||
| Fe9S10 | Fe9S10 | x | x | x | x | |||||
| FeS2 | Marcassite | x | x | x | x | x | x | x | x | x |
| As2S3 | Orpiment | x | x | x | x | x | ||||
| FeS2 | Pyrite | x | x | x | x | x | x | x | x | x |
| Na2(Fe3Fe2)Si8O22(OH)2 | Riebeckite | x | ||||||||
| Known Minerals | |||
| Minerals precipitated according to saturation index | Minerals considered for thermodynamic modelling | ||
| SiO2 | Amorphous silica | CuFeS2 | Chalcopyrite (alpha) |
| CaSO4 | Anhydrite | PbS | Galena |
| BaSO4 | Barite | Sb2S3 | Stibnite |
| CuFeS2 | Chalcopyrite (alpha) | ||
| PbS | Galena | ||
| SiO2 | Quartz (alpha) | ||
| SiO2 | Quartz (beta) | ||
| Sb2S3 | Stibnite | ||
| Possible Other Minerals | |||
| Minerals precipitated according to saturation index | Minerals considered for thermodynamic modelling | ||
| Cu1.75S | Anilite | Cu1.75S | Anilite |
| FeSb2S4 | Berthierite | FeSb2S4 | Berthierite |
| Cu5FeS4 | Bornite (alpha) | Cu5FeS4 | Bornite (alpha) |
| SiO2 | Coesite (alpha) | CuS | Covellite |
| CuS | Covellite | FeS2 | Marcasite |
| SiO2 | Cristobalite (beta) | As2S3 | Orpiment |
| FeS2 | Marcasite | FeS2 | Pyrite |
| As2S3 | Orpiment | ||
| FeS2 | Pyrite | ||
| Temperature (°C) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| M (g/mol) | 40 | 50 | 60 | 65 | 90 | 120 | 150 | 175 | 200 | |
| As | 74.922 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| Ba | 137.33 | 2.3% | 2.1% | 4.4% | 4.8% | 5.1% | 5.5% | 4.9% | 0.00% | 0.00% |
| Ca | 40.08 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 5.0% | 9.7% |
| Cu | 63.546 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| Fe | 55.847 | 0.60% | 0.52% | 0.45% | 0.65% | 1.3% | 1.4% | 1.4% | 1.2% | 1.1% |
| O | 15.999 | 51.6% | 51.7% | 50.8% | 50.4% | 49.5% | 49.3% | 49.5% | 50.8% | 49.9% |
| Pb | 207.2 | 0.01% | 0.01% | 0.02% | 0.00% | 0.02% | 0.00% | 0.01% | 0.00% | 0.01% |
| S | 32.066 | 1.2% | 1.1% | 1.5% | 1.9% | 2.7% | 2.9% | 2.7% | 5.4% | 9.0% |
| Sb | 121.75 | 0.01% | 0.01% | 0.02% | 0.01% | 0.02% | 0.02% | 0.01% | 0.00% | 0.00% |
| Si | 28.086 | 44.3% | 44.5% | 42.8% | 42.3% | 41.3% | 41.0% | 41.4% | 37.6% | 30.3% |
| Temperature (°C) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| M (g/mol) | 40 | 50 | 60 | 65 | 90 | 120 | 150 | 175 | 200 | |
| As | 74.922 | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| Cu | 63.546 | 0.04% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% | 0.00% |
| Fe | 55.847 | 45.6% | 45.6% | 44.8% | 45.9% | 45.8% | 46.2% | 46.2% | 46.5% | 46.4% |
| Pb | 207.2 | 0.72% | 0.50% | 1.5% | 0.25% | 0.52% | 0.07% | 0.43% | 0.04% | 0.30% |
| S | 32.066 | 52.8% | 52.9% | 52.3% | 53.1% | 53.0% | 53.2% | 53.2% | 53.4% | 53.3% |
| Sb | 121.75 | 0.77% | 1.0% | 1.5% | 0.76% | 0.67% | 0.48% | 0.17% | 0.00% | 0.00% |
| Temperature | Pb | Fe | As | Sb | S | Si | O | Majority |
|---|---|---|---|---|---|---|---|---|
| 65 | 8.88% | 40.77% | 0.14% | 1.13% | 48.73% | 0.16% | 0.18% | S |
| 90 | 2.14% | 45.11% | 0.01% | 0.04% | 52.16% | 0.24% | 0.28% | S |
| 120 | 0.95% | 44.67% | 0.00% | 0.01% | 51.45% | 1.4% | 1.6% | S |
| 150 | 0.60% | 35.72% | 0.00% | 0.00% | 41.12% | 10.5% | 12.0% | S |
| 175 | 0.22% | 15.66% | 0.00% | 0.00% | 18.01% | 30.9% | 35.2% | O |
| 200 | 0.01% | 3.80% | 0.00% | 0.00% | 4.36% | 42.9% | 48.9% | O |
| Temperature | Pb | Fe | As | Sb | S | Majority |
|---|---|---|---|---|---|---|
| 65 | 8.9% | 40.9% | 0.14% | 1.1% | 48.9% | S |
| 90 | 2.2% | 45.4% | 0.01% | 0.04% | 52.4% | S |
| 120 | 0.98% | 46.0% | 0.00% | 0.01% | 53.0% | S |
| 150 | 0.78% | 46.1% | 0.00% | 0.00% | 53.1% | S |
| 175 | 0.64% | 46.2% | 0.00% | 0.00% | 53.2% | S |
| 200 | 0.11% | 46.5% | 0.00% | 0.00% | 53.4% | S |
| Temperature | 65 | 90 | 120 | 150 | |
|---|---|---|---|---|---|
| Pb | SsF plant analyses | 59.7% | 56.8% | 39.9% | 27.3% |
| Thermodynamic model 1 | 0.00% | 0.02% | 0.00% | 0.01% | |
| Thermodynamic model 2 | 0.25% | 0.52% | 0.07% | 0.43% | |
| Kinetic Model 1 | 8.9% | 2.1% | 0.95% | 0.60% | |
| Kinetic Model 2 | 8.9% | 2.2% | 0.98% | 0.78% | |
| Fe | SsF plant analyses | 5.9% | 12.6% | 12.1% | 23.3% |
| Thermodynamic model 1 | 0.65% | 1.34% | 1.37% | 1.36% | |
| Thermodynamic model 2 | 45.9% | 45.8% | 46.2% | 46.2% | |
| Kinetic Model 1 | 40.8% | 45.1% | 44.7% | 35.7% | |
| Kinetic Model 2 | 40.9% | 45.4% | 46.0% | 46.1% | |
| As | SsF plant analyses | 9% | 8% | 13% | 7% |
| Thermodynamic model 1 | 0% | 0% | 0% | 0% | |
| Thermodynamic model 2 | 0.00% | 0.00% | 0.00% | 0.00% | |
| Kinetic Model 1 | 0.14% | 0.01% | 0.00% | 0.00% | |
| Kinetic Model 2 | 0.14% | 0.01% | 0.00% | 0.00% | |
| Sb | SsF plant analyses | 8% | 5% | 3% | 2% |
| Thermodynamic model 1 | 0.01% | 0.02% | 0.02% | 0.01% | |
| Thermodynamic model 2 | 0.76% | 0.67% | 0.48% | 0.17% | |
| Kinetic Model 1 | 1.13% | 0.04% | 0.01% | 0.00% | |
| Kinetic Model 2 | 1.1% | 0.04% | 0.01% | 0.00% | |
| S | SsF plant analyses | 17% | 18% | 32% | 41% |
| Thermodynamic model 1 | 1.9% | 2.7% | 2.9% | 2.7% | |
| Thermodynamic model 2 | 53.1% | 53.0% | 53.2% | 53.2% | |
| Kinetic Model 1 | 48.73% | 52.2% | 51.5% | 41.1% | |
| Kinetic Model 2 | 48.9% | 52.4% | 53.0% | 53.1% |
| Initial Model | Modified Model | |
|---|---|---|
| Arsenopyrite | n = 1.68 | n = 0.8 |
| Orpiment | n2 = −1.26 | n2 = −1.48 |
| Stibnite | n = 0.5 | n = 0.475 |
| Pyrite | n1 = −0.5 | n1 = −0.25 |
| n3 = 0.5 | n3 = 0.55 |
| Temperature | Pb | Fe | As | Sb | S | Cu | Majority |
|---|---|---|---|---|---|---|---|
| 65 | 52.2% | 5.0% | 9.0% | 8.5% | 22.5% | 2.8% | Lead |
| 90 | 45.6% | 16.0% | 9.2% | 1.2% | 25.2% | 2.8% | Lead |
| 120 | 34.9% | 23.5% | 7.0% | 0.42% | 29.6% | 4.6% | Lead |
| 150 | 40.1% | 22.7% | 0.00% | 0.01% | 32.3% | 4.9% | Lead |
| 175 | 41.7% | 23.0% | 0.00% | 0.00% | 32.8% | 2.5% | Lead |
| 200 | 14.4% | 38.0% | 0.00% | 0.00% | 45.8% | 1.8% | Sulfur |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kunan, P.; Ravier, G.; Dalmais, E.; Ducousso, M.; Cezac, P. Thermodynamic and Kinetic Modelling of Scales Formation at the Soultz-sous-Forêts Geothermal Power Plant. Geosciences 2021, 11, 483. https://doi.org/10.3390/geosciences11120483
Kunan P, Ravier G, Dalmais E, Ducousso M, Cezac P. Thermodynamic and Kinetic Modelling of Scales Formation at the Soultz-sous-Forêts Geothermal Power Plant. Geosciences. 2021; 11(12):483. https://doi.org/10.3390/geosciences11120483
Chicago/Turabian StyleKunan, Pierce, Guillaume Ravier, Eléonore Dalmais, Marion Ducousso, and Pierre Cezac. 2021. "Thermodynamic and Kinetic Modelling of Scales Formation at the Soultz-sous-Forêts Geothermal Power Plant" Geosciences 11, no. 12: 483. https://doi.org/10.3390/geosciences11120483
APA StyleKunan, P., Ravier, G., Dalmais, E., Ducousso, M., & Cezac, P. (2021). Thermodynamic and Kinetic Modelling of Scales Formation at the Soultz-sous-Forêts Geothermal Power Plant. Geosciences, 11(12), 483. https://doi.org/10.3390/geosciences11120483







