Metamodel-Based Slope Reliability Analysis—Case of Spatially Variable Soils Considering a Rotated Anisotropy
Abstract
:1. Introduction
2. Random Field Generation
2.1. Spatial Correlation
2.2. K–L Expansion
2.3. Cross-Correlated Log-Normal Random Fields
3. Methodology
3.1. Deterministic Methods
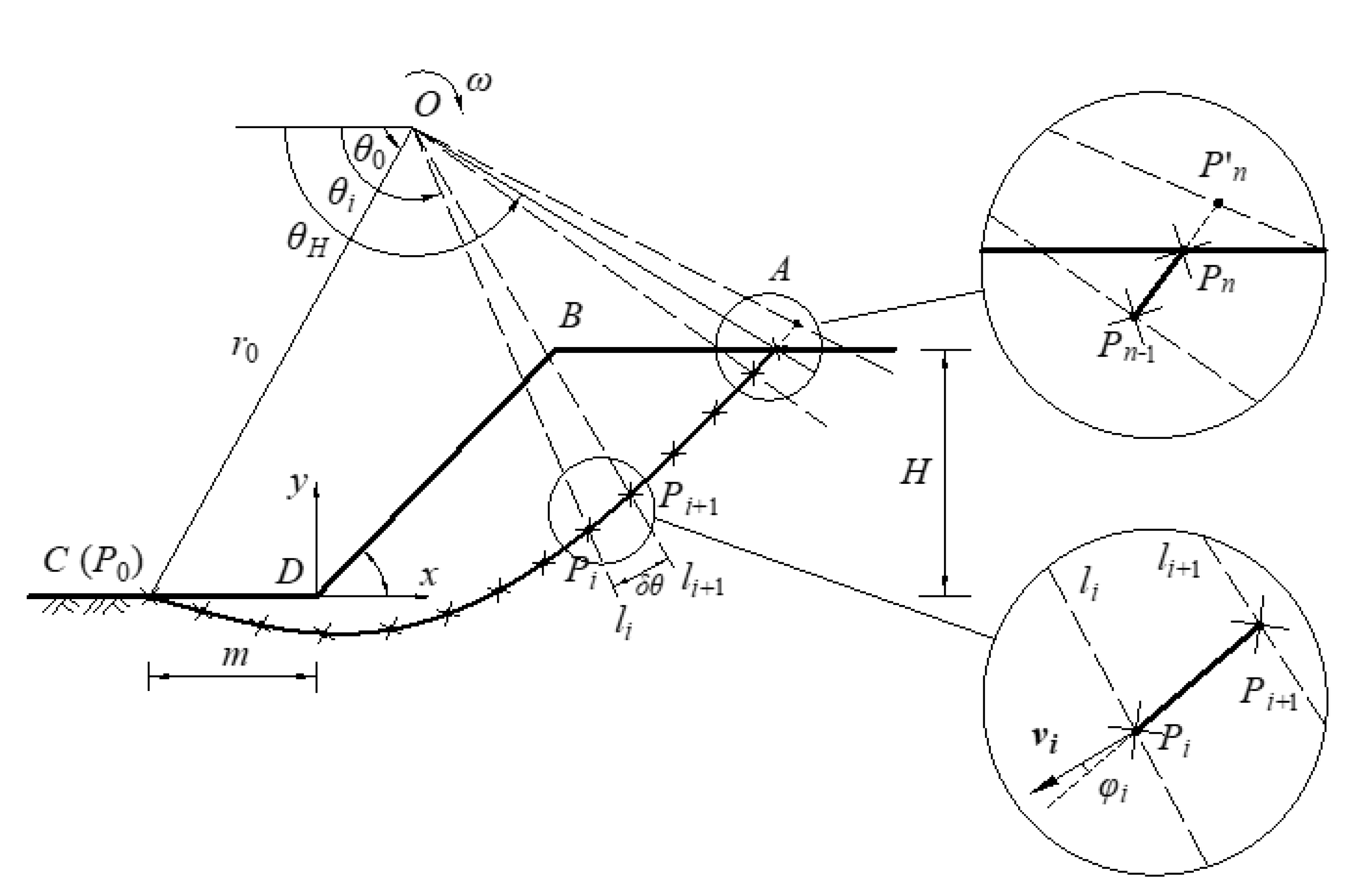
3.1.1. Analytical Model: DKA
3.1.2. Numerical Model: FELA
3.2. Probabilistic Methods
3.2.1. Sparse Polynomial Chaos Expansion
3.2.2. Global Sensitivity Analysis
3.2.3. Combination of SPCE and GSA
4. Proposed Procedure and Studied Slope
4.1. Procedure of the Current Study
4.2. Reference Case and Conducted Results
5. Validation and Efficiency Investigation of the Proposed Procedure
5.1. Comparison with a Previous Study
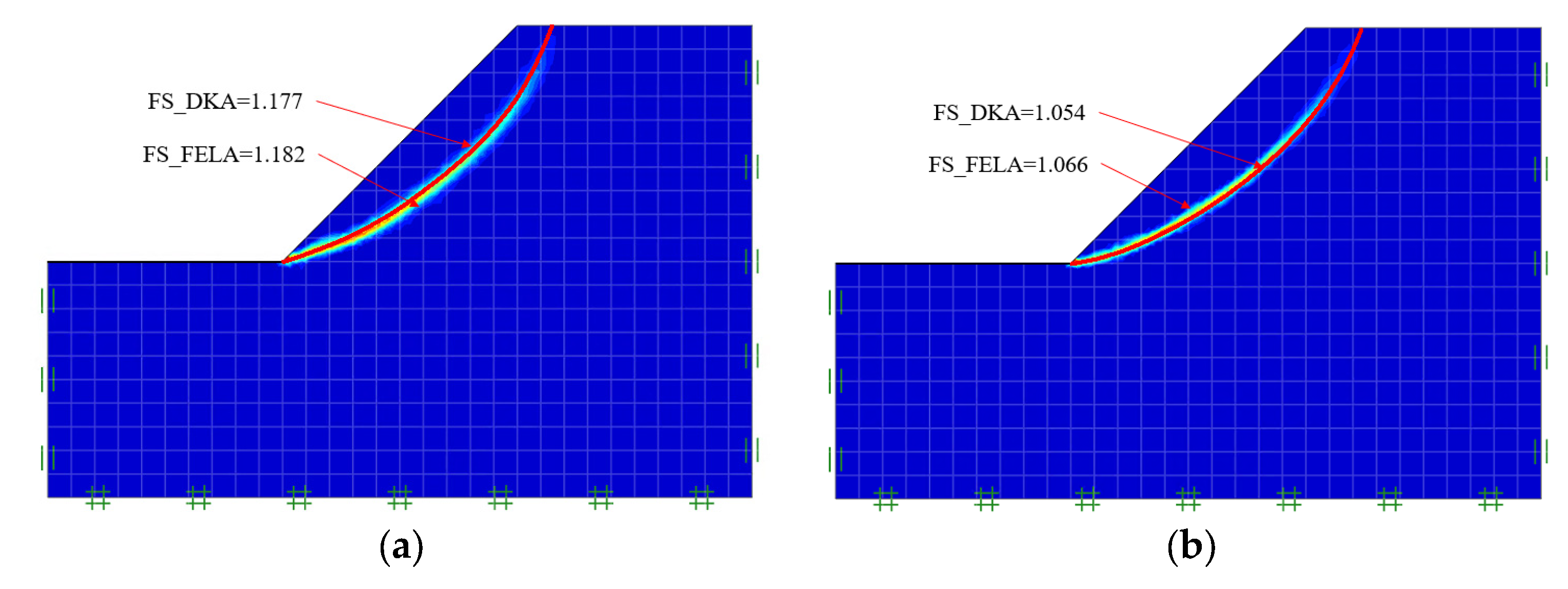
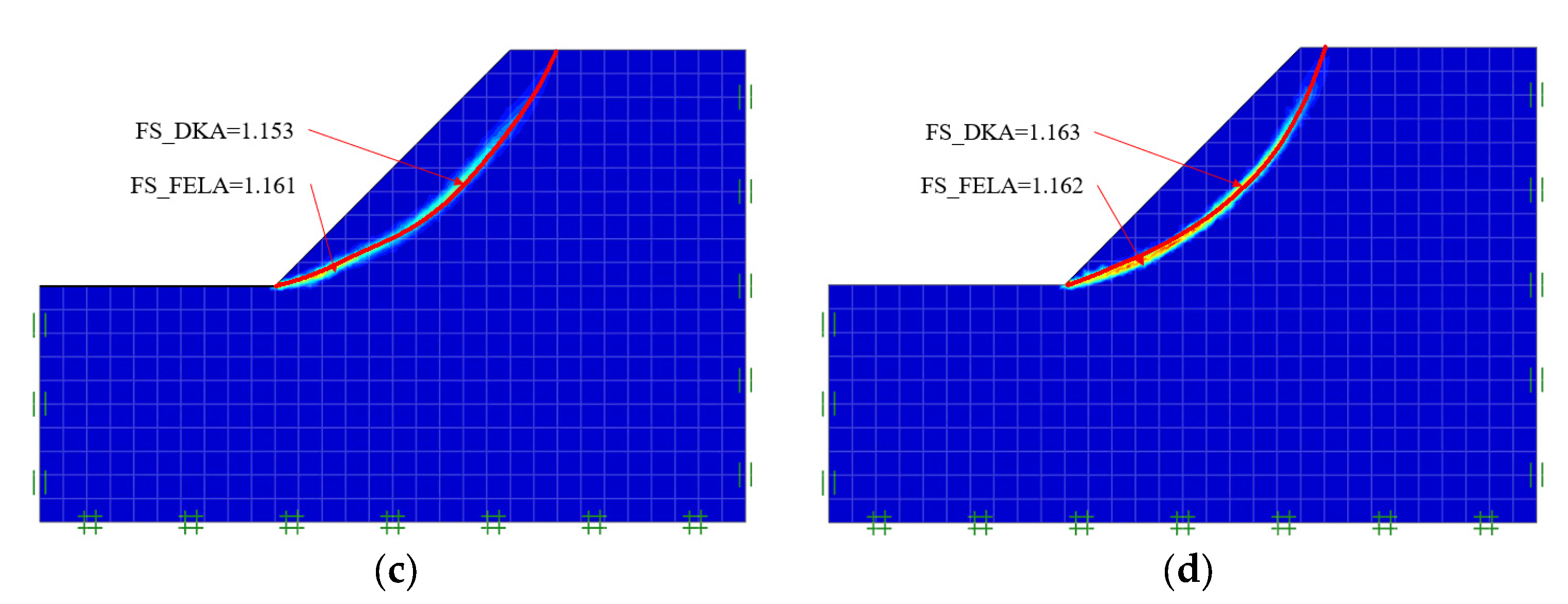
5.2. DKA Accuracy Considering Spatially Varying Soils and Rotated Anisotropy
5.3. Comparison of SPCE/GSA and Direct MCS
6. Effects of Rotated Anisotropy Considering Different Influential Factors
6.1. Effect of the Rotation Angle
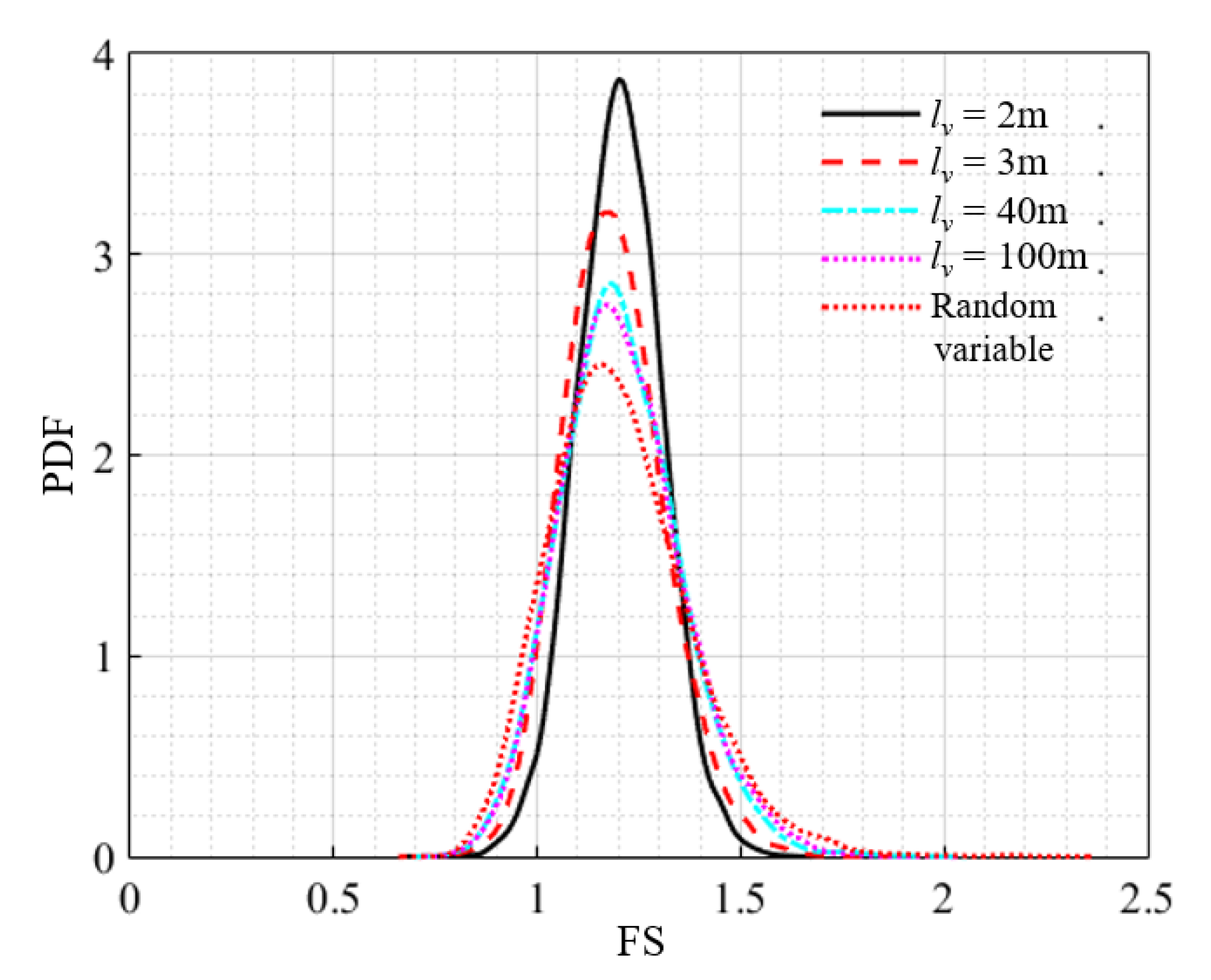
6.2. Effect of the Autocorrelation Length
6.3. Effect of the Cross-Correlation
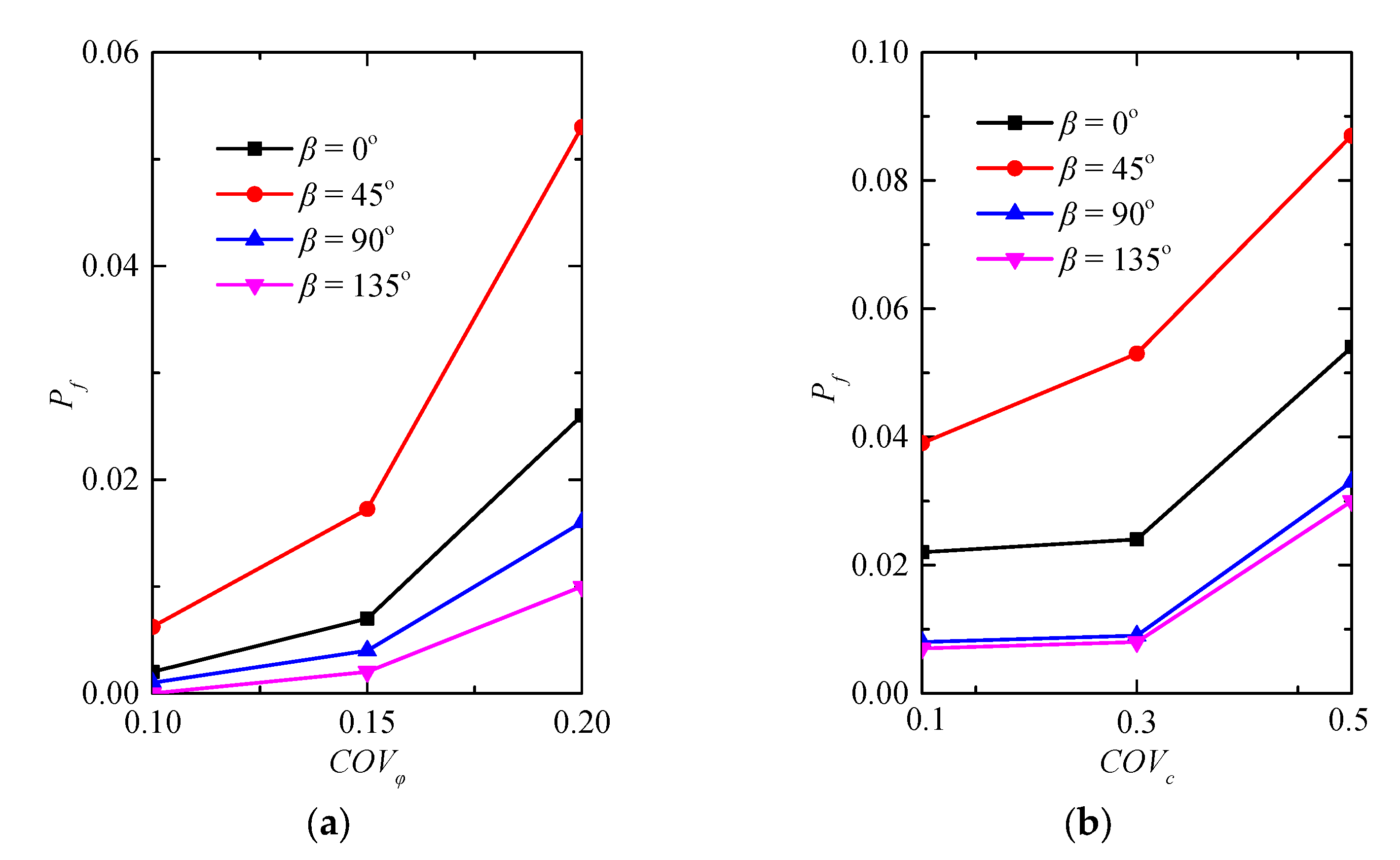
6.4. Effect of the Coefficient of Variation
7. Conclusions
- (1)
- The proposed procedure DSG–MG provides a good insight for the probabilistic stability analyses of slopes by the fact that the analytical method DKA can capture accurately the spatially varied parameters within the random field generation and can give rational results efficiently compared to the FELA ones (5 s and 60 s, respectively, for one deterministic calculation with the two methods); the metamodel constructed using SPCE/GSA can reduce the problem dimension and also the number of deterministic simulations by comparing with the direct MCS; several interesting results (the failure probability, probability density function, statistical moments of the model response, and sensitivity index of each variable) can also be obtained effectively.
- (2)
- The rotation of the anisotropic soil fabric pattern has a significant effect on slope stability. The failure probability is increased drastically when the rotation angle approaches the slope inclination. Using the traditional horizontal random field will then overestimate greatly the slope reliability, particularly for the cases with larger values of autocorrelation length, cross-correlation, and coefficient of variation. Conversely, the slope is safer when the rotated stratification is perpendicular to the slope inclination.
- (3)
- The failure probability is increased with the increase of autocorrelation lengths, coefficient of variation, and cross-correlation coefficient, and the effects of these parameters are more significant when the soil stratification rotation angle is close to the slope inclination, which should be determined with caution.
- (4)
- The rotation of soil stratification and autocorrelation length have almost no influence on the sensitivity index of the cohesion and friction angle, and the influence of the friction angle on the model response variance is higher than the cohesion angle. Conversely, the cross-correlation coefficient and coefficient of variation influence significantly the sensitivity indices, and the Sobol index of cohesion is increased with the cross-correlation coefficient r and coefficient of variation of cohesion COVc increase. The friction angle case presents an opposite trend.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FS | safety factor |
| GSA | Global Sensitivity Analysis |
| H | slope height (Figure 2) |
| lh, lv | autocorrelation distances in the horizontal and vertical directions |
| m | horizontal distance of CD (Figure 2) |
| Pf | failure probability |
| r0 | distance from point O to point C (Figure 2) |
| r | cross-correlation coefficient |
| SPCE | Sparse Polynomial Chaos Expansion |
| vi | velocity vector at point Pi (Figure 2) |
| ω | angular velocity (Figure 2) |
| φi | friction angle at point Pi (Figure 2) |
| δθ | angle between OPi and OPi + 1 (Figure 2) |
| θ0 | angle between the x axis direction and line OC (Figure 2) |
| θi | angle between the x axis direction and line OPi (Figure 2) |
| θH | angle between the x axis direction and line OPn (Figure 2) |
| β | rotation angle of anisotropy stratification |
| μ | mean value |
| μln | mean value of the log-normal random field |
| σ | standard deviation |
| σln | standard deviation of the log-normal random field |
| ρ | autocorrelation function |
References
- Ji, J.; Liao, H.J.; Low, B.K. Modeling 2-D spatial variation in slope reliability analysis using interpolated autocorrelations. Comput. Geotech. 2012, 40, 135–146. [Google Scholar] [CrossRef]
- Jiang, S.H.; Li, D.Q.; Zhang, L.M.; Zhou, C.B. Slope reliability analysis considering spatially variable shear strength parameters using a non-intrusive stochastic finite element method. Eng. Geol. 2014, 168, 120–128. [Google Scholar] [CrossRef]
- Li, X.Y.; Zhang, L.M.; Gao, L.; Zhu, H. Simplified slope reliability analysis considering spatial soil variability. Eng. Geol. 2017, 216, 90–97. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Huang, J. Probabilistic slope stability analysis using RFEM with non-stationary random fields. In Proceedings of the Geotechnical Safety and Risk V, Rotterdam, The Netherlands, 13–16 October 2015; pp. 1–7. [Google Scholar]
- Ji, J.; Chan, C.L. Long embankment failure accounting for longitudinal spatial variation—A probabilistic study. Comput. Geotech. 2014, 61, 50–56. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, L.M.; Xiao, T. Evaluating stability of anisotropically deposited soil slopes. Can. Geotech. J. 2019, 56, 753–760. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G. Influence of anisotropy and rotation on probabilistic slope stability analysis by RFEM. In Proceedings of the 62nd Canadian Geotechnical Conference, Halifax, NS, Canada, 20–24 September 2009; pp. 542–546. [Google Scholar]
- Huang, L.; Cheng, Y.M.; Leung, Y.F.; Li, L. Influence of rotated anisotropy on slope reliability evaluation using conditional random field. Comput. Geotech. 2019, 115, 103133. [Google Scholar] [CrossRef]
- Leshchinsky, B.; Ambauen, S. Limit Equilibrium and Limit Analysis: Comparison of Benchmark Slope Stability Problems. J. Geotech. Geoenviron. Eng. 2015, 141, 04015043. [Google Scholar] [CrossRef]
- Hou, C.; Zhang, T.; Sun, Z.; Dias, D.; Shang, M. Seismic Analysis of Nonhomogeneous Slopes with Cracks Using a Discretization Kinematic Approach. Int. J. Geomech. 2019, 19, 1–14. [Google Scholar] [CrossRef]
- Mollon, G.; Dias, D.; Soubra, A. Two new limit analysis mechanisms for the computation of the collapse pressures of circular tunnels driven by a pressurized shield. In Proceedings of the 2nd International Conference on Computational Methods in Tunnelling, Bochum, Germany, 9–11 September 2009; pp. 849–856. [Google Scholar]
- Du, D.; Zhuang, Y.; Sun, Q.; Yang, X.; Dias, D. Bearing capacity evaluation for shallow foundations on unsaturated soils using discretization technique. Comput. Geotech. 2021, 137, 104309. [Google Scholar] [CrossRef]
- Budetta, P. Some remarks on the use of deterministic and probabilistic approaches in the evaluation of rock slope stability. Geosciences 2020, 10, 163. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, C.; Gao, Y.; Kodikara, J. Effect of 2D spatial variability on slope reliability: A simplified FORM analysis. Geosci. Front. 2018, 9, 1631–1638. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. UQLab: A framework for Uncertainty Quantification in MATLAB. In Proceedings of the 2nd International Conference on Vulnerability, Risk Analysis and Management (ICVRAM2014), Liverpool, UK, 13–16 July 2014; pp. 2554–2563. [Google Scholar]
- Zhou, S.; Guo, X.; Zhang, Q.; Dias, D.; Pan, Q. Influence of a weak layer on the tunnel face stability—Reliability and sensitivity analysis. Comput. Geotech. 2020, 122, 103507. [Google Scholar] [CrossRef]
- Schöbi, R.; Sudret, B.; Marelli, S. Rare Event Estimation Using Polynomial-Chaos Kriging. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2017, 3, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Pan, Q.; Dias, D. Probabilistic evaluation of tunnel face stability in spatially random soils using sparse polynomial chaos expansion with global sensitivity analysis. Acta Geotech. 2017, 12, 1415–1429. [Google Scholar] [CrossRef]
- Guo, X.; Dias, D.; Carvajal, C.; Peyras, L.; Breul, P. A comparative study of different reliability methods for high dimensional stochastic problems related to earth dam stability analyses. Eng. Struct. 2019, 188, 591–602. [Google Scholar] [CrossRef]
- Kordjazi, A.; Pooya Nejad, F.; Jaksa, M.B. Prediction of ultimate axial load-carrying capacity of piles using a support vector machine based on CPT data. Comput. Geotech. 2014, 55, 91–102. [Google Scholar] [CrossRef]
- Pan, Q.; Dias, D. An efficient reliability method combining adaptive Support Vector Machine and Monte Carlo Simulation. Struct. Saf. 2017, 67, 85–95. [Google Scholar] [CrossRef]
- Guo, X.; Dias, D.; Pan, Q. Probabilistic stability analysis of an embankment dam considering soil spatial variability. Comput. Geotech. 2019, 113, 103093. [Google Scholar] [CrossRef]
- Cho, S.E. Probabilistic assessment of slope stability that considers the spatial variability of soil properties. J. Geotech. Geoenviron. Eng. 2010, 136, 975–984. [Google Scholar] [CrossRef]
- Liao, W.; Ji, J. Time-dependent reliability analysis of rainfall-induced shallow landslides considering spatial variability of soil permeability. Comput. Geotech. 2021, 129, 103903. [Google Scholar] [CrossRef]
- Krabbenhoft, K.; Lyamin, A.; Krabbenhoft, J. OptumG2: Theory; Optum Computational Engineering: København, Denmark, 2016. [Google Scholar]
- Sun, Z.; Li, J.; Pan, Q.; Dias, D.; Li, S.; Hou, C. Discrete kinematic mechanism for nonhomogeneous slopes and its application. Int. J. Geomech. 2018, 18, 04018171. [Google Scholar] [CrossRef]
- Zhang, T.; Baroth, J.; Dias, D. Probabilistic basal heave stability analyses of supported circular shafts in non-homogeneous clayey soils. Comput. Geotech. 2021, 140, 104457. [Google Scholar] [CrossRef]
- Pan, Q.; Qu, X.; Liu, L.; Dias, D. A sequential sparse polynomial chaos expansion using Bayesian regression for geotechnical reliability estimations. Int. J. Numer. Anal. Methods Geomech. 2020, 44, 874–889. [Google Scholar] [CrossRef]
- Zhang, T.; Guo, X.; Dias, D.; Sun, Z. Dynamic probabilistic analysis of non-homogeneous slopes based on a simplified deterministic model. Soil Dyn. Earthq. Eng. 2021, 142, 106563. [Google Scholar] [CrossRef]
- Sudret, B. Global sensitivity analysis using polynomial chaos expansions. Reliab. Eng. Syst. Saf. 2008, 93, 964–979. [Google Scholar] [CrossRef]
- Guo, X.; Dias, D. A Practical Framework for Probabilistic Analysis of Embankment Dams. In Dam Engineering Recent Advances in Design and Analysis; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Li, D.Q.; Zheng, D.; Cao, Z.J.; Tang, X.S.; Phoon, K.K. Response surface methods for slope reliability analysis: Review and comparison. Eng. Geol. 2016, 203, 3–14. [Google Scholar] [CrossRef]
- Wang, Y.; Akeju, O.V. Quantifying the cross-correlation between effective cohesion and friction angle of soil from limited site-specific data. Soils Found. 2016, 56, 1055–1070. [Google Scholar] [CrossRef]
- Wu, X.Z. Modelling dependence structures of soil shear strength data with bivariate copulas and applications to geotechnical reliability analysis. Soils Found. 2015, 55, 1243–1258. [Google Scholar] [CrossRef] [Green Version]
- Di Matteo, L.; Valigi, D.; Ricco, R. Laboratory shear strength parameters of cohesive soils: Variability and potential effects on slope stability. Bull. Eng. Geol. Environ. 2013, 72, 101–106. [Google Scholar] [CrossRef]















| Parameters | Notation | Statistics of Parameters | ||||
|---|---|---|---|---|---|---|
| Distribution | Mean | COV | Cross-Correlation Coefficient | Autocorrelation Length (m) | ||
| Cohesion | c (kPa) | Lognormal | 10 | 0.3 | R = −0.7–0.5 | lh: 10–40 lv: 1–3 |
| Friction angle | φ (°) | Lognormal | 30 | 0.2 | lh: 10–40 lv: 1–3 | |
| Unit weight | γ (kN/m3) | - | 20 | - | - | - |
| Deterministic Results | Probabilistic Results | ||
|---|---|---|---|
| FS | Pf | Number of Evaluations | |
| Cho [21] | 1.204 | 0.0138 | 50000 |
| DSG–MG | 1.201 | 0.0136 | 4200 |
| FSG–MG | 1.202 | 0.0130 | 4200 |
| Pf | Mean | Std | Number of Evaluations | |
|---|---|---|---|---|
| MCS | 0.056 | 1.192 | 0.130 | 10,000 |
| DSG–MG | 0.053 | 1.190 | 0.124 | 4000 |
| β (°) | Pf | Mean | Std | SC | Sφ |
|---|---|---|---|---|---|
| 0 | 0.028 | 1.201 | 0.106 | 0.034 | 0.966 |
| 45 | 0.053 | 1.190 | 0.124 | 0.020 | 0.980 |
| 90 | 0.013 | 1.210 | 0.095 | 0.028 | 0.972 |
| 135 | 0.011 | 1.208 | 0.089 | 0.022 | 0.978 |
| lv(m) | Pf | Mean | Std | Sc | Sφ |
|---|---|---|---|---|---|
| 2 | 0.026 | 1.204 | 0.104 | 0.017 | 0.983 |
| 3 | 0.053 | 1.190 | 0.124 | 0.020 | 0.980 |
| 40 | 0.073 | 1.204 | 0.146 | 0.030 | 0.970 |
| 100 | 0.077 | 1.208 | 0.149 | 0.031 | 0.969 |
| Random variables | 0.103 | 1.204 | 0.171 | 0.037 | 0.963 |
| r | Pf | Mean | Std | SC | Sφ |
|---|---|---|---|---|---|
| −0.7 | 0.023 | 1.208 | 0.094 | 0.014 | 0.986 |
| −0.5 | 0.053 | 1.190 | 0.124 | 0.020 | 0.980 |
| −0.25 | 0.085 | 1.204 | 0.142 | 0.137 | 0.863 |
| 0 | 0.111 | 1.201 | 0.157 | 0.255 | 0.745 |
| 0.25 | 0.143 | 1.204 | 0.178 | 0.449 | 0.551 |
| 0.5 | 0.162 | 1.199 | 0.193 | 0.629 | 0.371 |
| COV | Pf | Mean | Std | SC | Sφ |
|---|---|---|---|---|---|
| COVc = 0.3 | |||||
| COVφ = 0.1 | 0.006 | 1.204 | 0.079 | 0.417 | 0.583 |
| 0.15 | 0.017 | 1.206 | 0.098 | 0.136 | 0.864 |
| 0.2 | 0.053 | 1.190 | 0.124 | 0.020 | 0.980 |
| COVφ = 0.2 | |||||
| COVc = 0.1 | 0.039 | 1.216 | 0.120 | 0.011 | 0.989 |
| 0.3 | 0.053 | 1.190 | 0.124 | 0.020 | 0.980 |
| 0.5 | 0.087 | 1.196 | 0.134 | 0.225 | 0.775 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Guo, X.; Baroth, J.; Dias, D. Metamodel-Based Slope Reliability Analysis—Case of Spatially Variable Soils Considering a Rotated Anisotropy. Geosciences 2021, 11, 465. https://doi.org/10.3390/geosciences11110465
Zhang T, Guo X, Baroth J, Dias D. Metamodel-Based Slope Reliability Analysis—Case of Spatially Variable Soils Considering a Rotated Anisotropy. Geosciences. 2021; 11(11):465. https://doi.org/10.3390/geosciences11110465
Chicago/Turabian StyleZhang, Tingting, Xiangfeng Guo, Julien Baroth, and Daniel Dias. 2021. "Metamodel-Based Slope Reliability Analysis—Case of Spatially Variable Soils Considering a Rotated Anisotropy" Geosciences 11, no. 11: 465. https://doi.org/10.3390/geosciences11110465
APA StyleZhang, T., Guo, X., Baroth, J., & Dias, D. (2021). Metamodel-Based Slope Reliability Analysis—Case of Spatially Variable Soils Considering a Rotated Anisotropy. Geosciences, 11(11), 465. https://doi.org/10.3390/geosciences11110465








