Morphotectonic Evolution of an Alluvial Fan: Results of a Joint Analog and Numerical Modeling Approach

Abstract

Surface topography results from complex couplings and feedbacks between tectonics and surface processes. We combine analog and numerical modeling, sharing similar geometry and boundary conditions, to assess the topographic evolution of an alluvial fan crossed by an active thrust fault. This joint approach allows the calibration of critical parameters constraining the river deposition–incision laws, such as the settling velocity of suspended sediments, the bed-rock erodibility, or the slope exponent. Comparing analog and numerical models reveals a slope-dependent threshold process, where a critical slope of ca. 0.081 controls the temporal evolution of the drainage network. We only evidence minor topographic differences between stable and stick-slip fault behavior localized along the fault scarp. Although this topographic signature may increase with the slip rate and the return period of slip events, it remains slight compared to the cumulated displacement along the fault scarp. Our results demonstrate that the study of morphology cannot be used alone to study the slip mode of active faults but can be a valuable tool complementing stratigraphic and geodetic observations. In contrast, we underline the significant signature of the distance between the fault and the sediment source, which controls the degree of channels incision and the density of the drainage network.

1. Introduction

Geomorphological approaches consider the well-established principle that landscape morphology is controlled by the interactions between tectonics, sedimentation, and erosion [1,2,3]. During the last decades, many field methods have been developed to characterize these interactions by documenting surface processes such as soil transport, river incision, or basin-wide denudation [4]. Local landforms, such as fault scarps, offset alluvial fans, or deformed river terraces are associated with well-known geomorphic processes. Thanks to cosmogenic isotopes, processes such as incision or denudation are quantified [1]. They are commonly used to estimate a mean fault slip rate or an average incision rate (e.g., [5,6,7,8]). However, most erosion parameters remain poorly constrained by field observations due to their multivariate and interrelated dependencies on climate, lithology, and vegetation cover (e.g., [9,10]). At the same time, analog and numerical models have been built to explore erosion laws and the associated parameters (e.g., [11,12,13,14,15,16,17]). They underline the complexity of geomorphic processes, including non-linearity, thresholds, feedbacks, and equifinality.

Comparing modeling results with natural landscapes is challenging. A few previous studies combined analog and numerical approaches for studying the surface and tectonic processes at the crustal scale (e.g., [18]). This method is currently used to estimate erosion and sedimentation processes according to the granular composition [19] and the erosion influence on tectonics in a context of crustal shortening [20]. Following this approach, we investigated the evolution of a geomorphologic marker by comparing analog and numerical models.

In this paper, we study the morphotectonic evolution of an alluvial fan crossed by an active reverse fault. We focus on a short time scale of 100 ka to explore poorly studied mechanisms, such as the topographic signature of the fault slip mode. We choose an alluvial fan because this geomorphological object has a high deposition rate and forms rapidly, which corresponds to the study’s time scale. Moreover, it is simple to characterize in terms of its dynamics and geometry. The context of thrust fault allows characterizing several markers, such as the fault scarp and syntectonic deposits. Together, these markers in the morphology are used to study the morphological signature of the fault slip behavior. Last, this setting associated with an alluvial fan crossed by a thrust fault is frequently observed in the field. Here, we assume active tectonic with rapid surface processes, which can be compared to those observed along the Tian Shan’s or the Himalayas’ front.

After defining the experimental setup and the numerical methods, we describe the general assumptions of the approach. Next, we present our results, devoted to focusing on (1) the repeatability of the laboratory experiments; (2) the calibration of the numerical simulation setup from the analog results; and (3) the analysis of the general features of the modeled morphotectonic evolutions.

We paid specific attention to the fault slip mode associated with stick-slip or stable behavior. This parameter is critical for improving seismic hazard assessment. The most commonly used approaches focus on seismic coupling calculation derived from geodetic measurements (e.g., [21]). Weak coupled areas are associated with stable sliding areas of low-stress accumulation and, therefore, potentially less prone to trigger major earthquakes. However, the main limitation of this approach is the short time coverage of observations, which only document a few decades. Another method is the paleoseismology approach conducted by performing trenches and outcrops analyses (e.g., [8,22,23]). The observations then come from stratigraphy, lithology, grain size, and dating. This method provides critical information on the seismic potential by completing the regional seismicity catalogs with the inferred paleo-earthquakes. However, although these paleoseismology studies are critical to collecting missing data necessary to assess the seismic hazard, they remain often limited by the local character of measurements and their time-consuming implementation. Here, we propose a complementary approach to assess the fault slip mode from the analysis of topography.

Finally, based on numerical simulations, we discuss the influence of other parameters, such as the fault slip rate, the return period of slip events, and the fault location relative to the upstream outlet, on the morphological signature of the fault slip behavior.

2. Methods

We developed a joint approach coupling analog and numerical models to address the impact of surface and tectonic processes on topography. Although these models have their specificities associated with their implementation, particular attention was paid to sharing an identical geometry, initial and boundary conditions, and similar external and internal forcings.

2.1. Analog Modeling

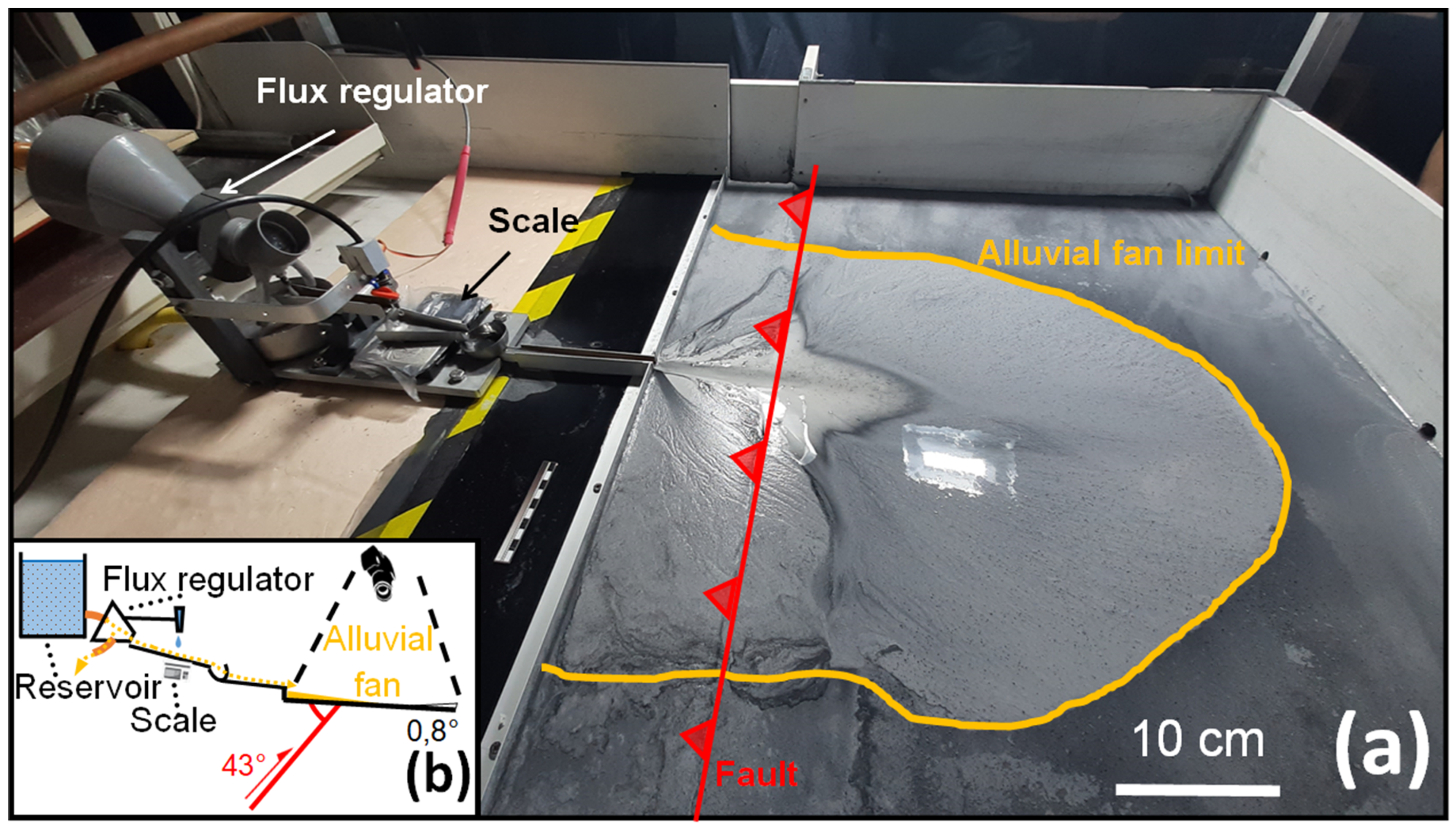
2.1.1. Experimental Setup

Graveleau et al. (2008, 2011) [12,13] initially developed the experimental device to perform morphodynamic experiments at the scale of an active foreland. Here, we adapted this device to investigate the morphologic evolution of a simpler model with a single alluvial fan fed by a single upstream outlet (Figure 1). The model comprised three main parts from upstream to downstream:

• A reservoir, equipped with rotating blades, containing a mix of granular material and water.
• A transfer zone used to reduce and control the flow.
• A sediment deposit area where the fan grows.

A hand control sluice gate allowed the mix of sediments and water to get out of the reservoir into a 1 × 1 × 10 cm aluminum channel. Before the depositional area, the flow went through a mass control device used to monitor the flow transfer rate during the experiments (Figure S1). Next, the transfer zone enabled a slow water flow of 4 drops/s to avoid deposits that could restrain the sediment flow. Finally, the flow reached a 60 × 60 cm deposit area, tilted 0.8° downstream (Figure 2).

A reverse fault crossed the deposit area perpendicular to the stream direction with a dip of 43° upstream (Figure 2b). In our experiments, the fault trace was located 10 cm from the upstream outlet. The hanging wall compartment could be lifted by incremental displacements using a step-by-step computerized motor. This system could reproduce a stable or stick-slip fault behavior depending on the set size and duration of the rigid increments.

We performed five sets of experiments, each simulating a stable and a stick-slip fault behavior and sharing an average fault slip rate of 1 cm/h and a sedimentation rate of ca. 1 cm/h. This sedimentation rate was measured at the top of the alluvial fan formed during the phase with no tectonics. Stick-slip models were characterized by fault slip increments of 500 microns every 180 s (

Table 1. Scaling parameters between experimental and numerical reference models.

Parameter	Experimental Model	Numerical Model
Length	1 mm	10 m
Time	1 s	10 yr
$L$	60 cm	6 km
$T_{fan}$	1.5 h	54 ka
$T_{tecto}$	1 h	36 ka
$v_{ref.}$	1 cm.h−1	2.8 mm.yr−1
$T_{ref.}$	180 s	1.8 ka
$q$	$1.4\times {10}^{-4}$ L.s−1	$140\times {10}^3$ m3.yr−1
$q_s$	$1.4\times {10}^{-5}$ L.s−1	$14\times {10}^3$ m3.yr−1
$S_c$	0.3	0.3

), whereas stable fault slip behavior was simulated with fault increments of 6.2 microns every 2.23 s.

2.1.2. Material Properties

The analog material composition was derived from the water-saturated mixture developed initially by Graveleau and Dominguez (2008) [12], refined by Graveleau et al. (2011) [13] and Strak et al. (2011) [17]. Its solid part comprised several granular materials with micrometric grain sizes such as plastic powder (PVC), silica powder, and micro-beads. The main interests of such a mixture are to reproduce natural deposit sorting processes thanks to contrasted densities and wide grain-size distribution, inducing differential transport distances for each material component. Indeed, it was shown that this type of material is suitable to reproduce realistic geomorphological objects such as river channels, drainage networks, and alluvial fans, sharing strong similarities with their natural equivalents in size, shape, and evolution [10,14,24].

The mixture used in our experiments was composed of 90 % water and 10% granular material, including 30% silica, 51% PVC, 6% anthracite, 10% glass micro-beads, and 3% pumice stone (see Supplementary Materials S2 for physical properties). Compared to the previous material, the main differences were an increase in the percentage of PVC, a decrease in micro-beads, and the addition of pumice powder. Such modifications were made to decrease the density of the material favoring a sediment transport consistent with a single kilometric alluvial fan.

2.1.3. Scaling

Since the pioneer paper of Hubbert (1937) [25], many studies have focused on analog models scaling (e.g., [19,20,26,27,28]). Here, the scaling of our experiments was done by taking into account dynamic, geometric, and kinematic similarity criteria between model parameters and field observations.

Dynamic Scaling

The scaling of morphotectonic models is complex to achieve. Different processes act at different time scales, leading to a wide variance from few mm.yr⁻¹ for tectonic slip rate and incision–deposition rate to few m/s for flow circulation. Moreover, water has a dual role in transport and erosion processes.

In our experiments, the tectonic deformation was concentrated along the fault scarp. Assuming that this deformation can be neglected, the dynamic similarity criterion is constrained by the hydraulic forces balance only [29,30]. This hypothesis can be tested by calculating the dimensionless Reynolds ($Re$) and Froude ($Fr$) numbers [30,31]:

$$Re=\frac{u\times l}{\nu } \mathrm{and} Fr=\frac{u}{\sqrt{g\times l}}$$

(1)

where $u$ is the flow velocity, $l$ is a characteristic length as the flow thickness, $\nu$ is the fluid’s kinematic viscosity, and $g$ is the gravity acceleration.

While some portions of natural rivers are characterized by turbulent flows with a high Reynolds number [29], in analog experiments, the water flow is laminar with a low Reynolds number [13,16]. This discrepancy is mainly related to the use of water in analog experiments. Therefore, the analog models and nature share the same fluid’s kinematic viscosity, $\mathsf{\nu }$, and a similar flow velocity. The Reynolds numbers are then essentially controlled by $l$ (see Equation (1)), which significantly differs from models to nature.

In our experiments, the flow velocity was estimated to be a few mm.s⁻¹–cm.s⁻¹, and the flow thickness to 0.1–1 mm. These values lead to a Froude number of $Fr=0.02-0.6$, consistent with $Fr=0.01-1$ obtained from natural rivers [32]. This good agreement indicates that the flow-inertia-to-gravity ratio is well respected in our experiment. Thus, although rigorous dynamic scaling is difficult and elusive to achieve, the conservation of the Froude number implies that the same force equilibrium controls the dynamic of both the analog models and nature.

Geometric Scaling

The spatial scaling factor $L^{*}$, defining the ratio between a characteristic length in the analog model and nature, is imposed by the size of the apparatus ($L=$ 60 cm, Table 1) and the studied natural object dimensions (5–10 km). We obtained $L^{*}$ in the range of 6–12 × 10⁻⁵, i.e., 1 cm in the analog model upscaled to between 80 m and 170 m in nature. In this paper, to facilitate extrapolating model results to nature, we considered that 1 cm upscales to 100 m (Table 1).

Kinematic Scaling

To evaluate the time scaling, we assumed that accelerations of the simulated geomorphic processes are small enough to be neglected. The time ratio $T^{*}$ is then obtained by comparing average long-term velocities between the model and nature using the following relationship:

$$T^{*}=\frac{ L^{*}}{V^{*}}$$

(2)

where $V^{*}$ is the model-to-nature velocity ratio. Here, $V^{*}$ is defined from the average sedimentation rate. In our experiments, this rate is ca. 1–10 mm/h, whereas field observations range between 1 and 10 mm.yr⁻¹ [33], leading to a $V^{*}$ of ca. 10³–10⁵. These values and the previously calculated $L^{*}$ give a time ratio $T^{*}$ of 6 × 10⁻¹⁰–12 × 10⁻⁸. Thus, 1 s in the model upscales to 0.3–50 years in nature. In this paper, we considered that 1 s upscales to 10 years (Table 1).

The time and velocity scaling factors were then used to constrain the fault slip rate in our models. As we intend to simulate a natural fault slip rate of 1–5 mm.yr⁻¹, we set the device for an analog fault slip rate of 1 cm.h⁻¹ , equivalent to 2.8 mm.yr⁻¹, in our reference model (Table 1).

2.1.4. Model Monitoring and Data Processing

Two camera acquisition systems monitored the model:

• a CCD Panasonic Gx80 camera located above the deposit area took one frame every 30 s. This acquisition gave a collection of 270 high-resolution pictures (4600 × 3500 px) for each experiment. These pictures were used to make a time-lapse video and analyze the fan building phase qualitatively (see movies in Supplementary Materials S3).
• The final morphology was quantified by photogrammetry from 9 high-resolution pictures taken with a Sony Alpha7R2 camera (42 Mpx). After processing the data with Micmac [34] and CloudCompare software [35], we obtained a georeferenced digital elevation model (DEM) composed of about 10 million points with an average spatial resolution of 0.16 mm and an accuracy of 0.6 mm. The DEMs were analyzed using the library Matplotlib in Python.

2.2. Numerical Modeling

We also investigated evolution models numerically using the Landlab2.0 modeling toolkit [11,15]. To account for both surface processes and tectonics, we considered the following governing equation of mass conservation for a land surface elevation $z\left(x,y,t\right)$

$$\frac{\partial z}{\partial t}={\left(\frac{\partial z}{\partial t}\right)}_{hill}+{\left(\frac{\partial z}{\partial t}\right)}_{fluv}+v_z$$

(3)

where $\partial z/\partial t$ is the variation in elevation with time and $v_z$ is the tectonic uplift rate.

Hillslope processes modeling uses the TransportLengthHillslopeDiffuser component of Landlab, derived from the formulation proposed by Carretier et al. (2016) [36]:

$${\left(\frac{\partial z}{\partial t}\right)}_{hill}=q_s\times \frac{1-{\left(\frac{S}{S_c}\right)}^2}{dx}-{\kappa }_{hill} S$$

(4)

where ${\kappa }_{hill}$ is an erodibility coefficient, $S=\frac{\partial z}{\partial x}$ is the local slope, $q_s$ is the sediment flux, $S_c$ is a critical slope, and $dx$ is the model node spacing. This law requires to know a priori two parameters: $S_c$ and ${\kappa }_{hill}$. A critical slope $S_c$ of 0.3 is set for all the numerical models to be consistent with the internal friction coefficient $\phi =20°\pm 10°$ of analog material (see Supplementary Materials S2). Estimating ${\kappa }_{hill}$ is less evident because this parameter exhibits a wide variance due to its dependency on climate, rock type, and vegetation. Soil transport efficiency is often described by a soil transport coefficient $D={\kappa }_{hill}\times dx$, which is a diffusivity-like coefficient. In their recent compilation, Richardson et al. (2019) [10] propose a parameter $D$ ranging between ${10}^{-5}$ and ${10}^{-1}$ m²/yr. Here, we assumed a model node spacing $dx$ of 50 m. This value leads to a range for ${\kappa }_{hill}$ between $2\times {10}^{-7}$ and $2\times {10}^{-3}$ m.yr⁻¹.

Fluvial erosion and deposition were calculated from the Davy and Lague (2009) [37] formulation. A mass balance approach, taking into account transport of both topographic material and river sediment content, was coupled with an explicit representation of the sediment transport distance. We used the Erosion.Deposition component of Landlab [38]

$${\left(\frac{\partial z}{\partial t}\right)}_{fluv}=v_s\times \frac{q_s}{q}-\omega$$

(5)

where $v_s$ is the net settling velocity, and $q$ is the water surface flux. In their approach, Davy and Lague (2009) [37] defined a parameter $\xi =\frac{q}{d^{*}\times v_s}$, which represents the average travel distance of sediment grains from their erosion to their deposition. The parameter $d^{*}$ is the ratio between the mean sediment concentration in the stream and at the bed interface. They demonstrated that detachment-limited and transport-limited models can be encompassed using $\xi \to +\infty$ (i.e., small $v_s$) and $\xi \ll 1$ (i.e., large $v_s$), respectively. This study considered $v_s$ between ${10}^{-2}$ and ${10}^2$ m.yr¹, a range in agreement with the $\xi -q$ relationships tested by Davy and Lague (2009) [37].

The erosion $\omega$ was calculated from the classical power-law type equation

$$\omega ={\kappa }_{river} q^m{S}^n$$

(6)

$m$ and $n$ are two dimensionless exponents, which depend on catchment hydrology and the nature of the dominant erosional process [39,40]. The values of these two parameters are still debated. Based on the compilation presented by Harel et al. (2016) [9], we assumed a concavity index $m/n=0.5$ and a slope exponent $n$ ranging between $0$ and $4$. The erodibility of the river bedrock ${\kappa }_{river}$ is far less constrained. This coefficient mostly depends on climate, lithology, vegetation cover, and the values of the exponents $m$ and $n$. In the following, we considered the range ${10}^{–5}-{10}^0$ according to Stock and Montgomery (1999) [41] and Harel et al. (2016) [9].

An uplift rate $v_z$ was imposed on the hanging wall’s grid nodes to simulate surface tectonic displacements due to a reverse fault slip (Figure 2). In contrast to the experimental device, the elevation change due to horizontal tectonic advection was not considered. This assumption is equivalent to considering in the numerical models; a vertical fault with a slip equals the vertical component of the analog model fault slip.

2.3. Common Modeling Assumptions

Our approach relies on the comparison between the analog and numerical modeling results. The parameter values used in the numerical models come from studies of natural morphological landscapes (see Section 2.1.4). In this paper, the spatial and temporal scales used in the numerical models are therefore identical to those associated with natural processes. Hence, the scaling coefficients presented above define the geometry, the initial and boundary conditions, and the time scale of the numerical models.

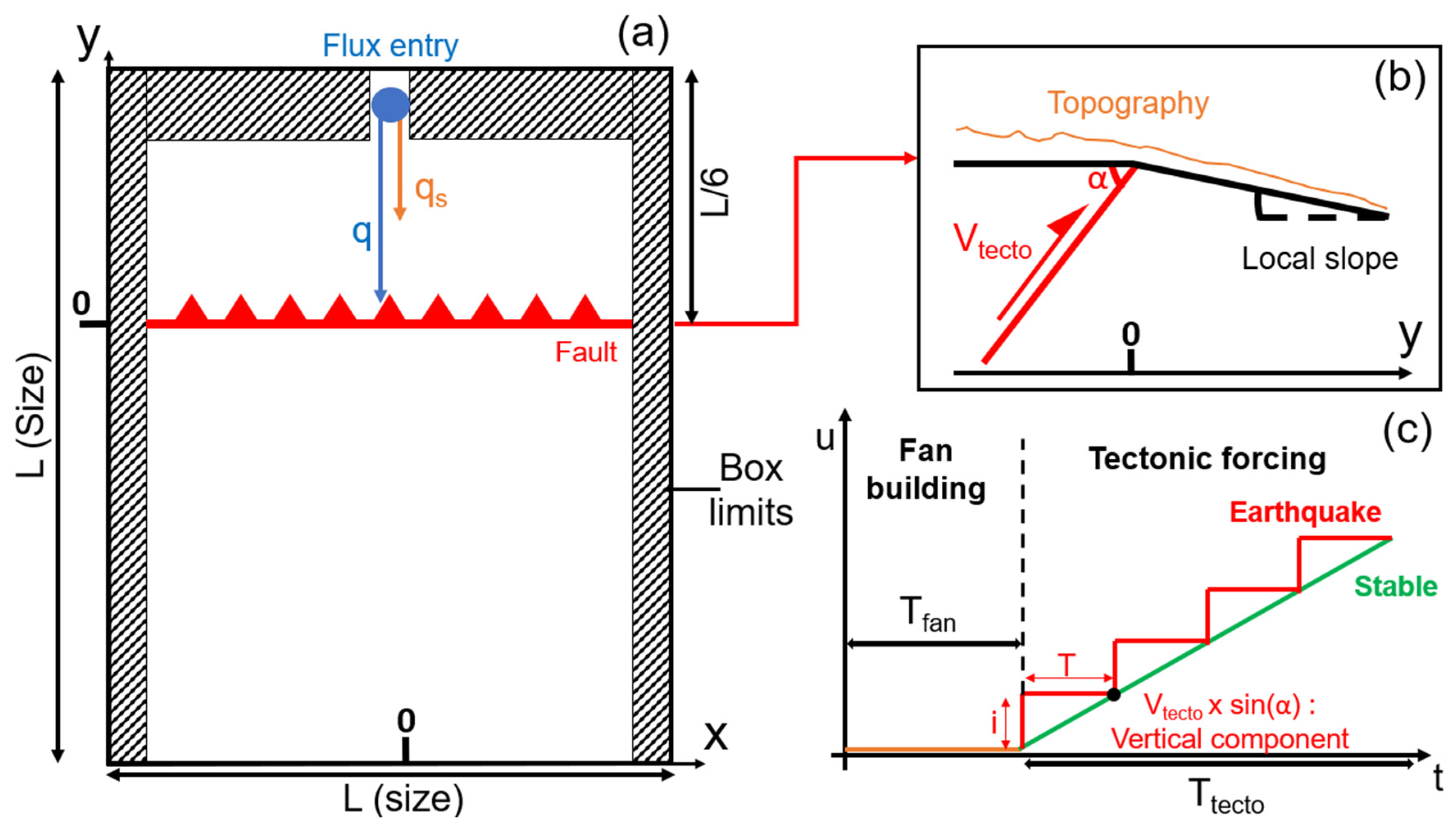
2.3.1. Geometry

For the experimental approach, we considered a square model with a side length $L$ of 60 cm. Its initial topography consisted of an inclined plane of 0.8° leading to a change in elevation of 8.5 mm when y varies from 0 to $L$ (Figure 1 and Figure 2). A reverse fault crossed the model at y = 0 (Figure 2).

The numerical model experiments were performed on a regular square lattice with a similar geometry. Using the scaling factor given in Table 1, we considered a 6000 × 6000 m model with a node spacing of 50 m. This discretization led to a mesh size of 120 × 120, which was a good compromise between computation time and model resolution of the calculated surface.

2.3.2. Initial and Boundary Conditions

Initially, the models did not undergo any external or internal forcing. Top ($y=L/6)$, left ($x=-L/2)$, and right ($x=L/2$) boundaries were closed, i.e., no water or sediment output flux was permitted. An outflow of water and sediment was only allowed through the bottom face ($y=-5L/6$). We simulated the formation and evolution of an alluvial fan by adding a flow of water and sediment coming from the top-center of the model (Figure 2).

In the analog approach, a constant water flux of $1.4\times {10}^{-4}$ L.s⁻¹ with a sediment concentration of 10% was brought from the reservoir described in Section 2.1.1. The water flux was upscaled to $140\times {10}^3$ m³.yr⁻¹ in the numerical approach and imposed from the Landlab variable runoff_rate, assigned to the grid field water_unit_flux_in. The functionality to add an external input sediment flux is not implemented in the current Landlab version. The ErosionDeposition component of Landlab was then modified to provide an external sediment flux of $14\times {10}^3$ m³.yr⁻¹ as a source term to the node with coordinates $\left(x=0, y=L/6\right)$.

Concerning tectonic forcing, the uplift pattern was controlled by a slip rate $v$ along a $\alpha =43°$ dipping thrust fault (Figure 2b) with no flexural response associated with surface loading. In the reference analog model, $v_{ref}$ equaled 1 cm.h⁻¹, leading to $v_{ref}$ = 2.8 mm.yr⁻¹ in numerical models (Table 1). Two fault slip mode end-members were tested (Figure 2c). First, we assumed a stable fault behavior with a constant uplift rate $v_z=v\times sin\left(\alpha \right)$ imposed at all time steps. Next, we assumed a fault stick-slip behavior for which the cumulated slip over a return period $T$ was released during a single time step. The associated coseismic vertical displacement $u_z$ was then defined as the product $v_z\times T$. In the reference analog model, we assumed a return period $T_{ref}=180 \mathrm{s}$, leading to $T_{ref}=1800 \mathrm{yr}$ for the numerical reference model.

2.3.3. Time Scenario

Laboratory experiments evolved through two main stages. The first stage lasted 1.5 h and was dedicated to fan building without tectonics (Figure 2c). Sediments then accumulated on the table so that a sufficient thickness (nearly 10 mm) avoided a too early complete incision of the fan when, in a second phase, the fault was set active during the so-called “tectonic forcing” stage, which lasted 1 h (Figure 2c).

To be consistent with the analog modeling scaling procedure, the total duration of numerical simulations was set to 90 ka with a time step of 10 yr. These simulations were also divided into two stages: (1) a sedimentation stage of 54 ka without tectonics, where the transport and deposition of sediments contributed to forming an alluvial fan, (2) a stage of 36 ka where all surface and tectonic processes acted together.

3. Results

In this section, we first tested the analog experiments’ repeatability. Next, we calibrated the numerical erosion law parameters. Finally, we explored the effect of tectonics and surface processes on alluvial fan morphological evolution.

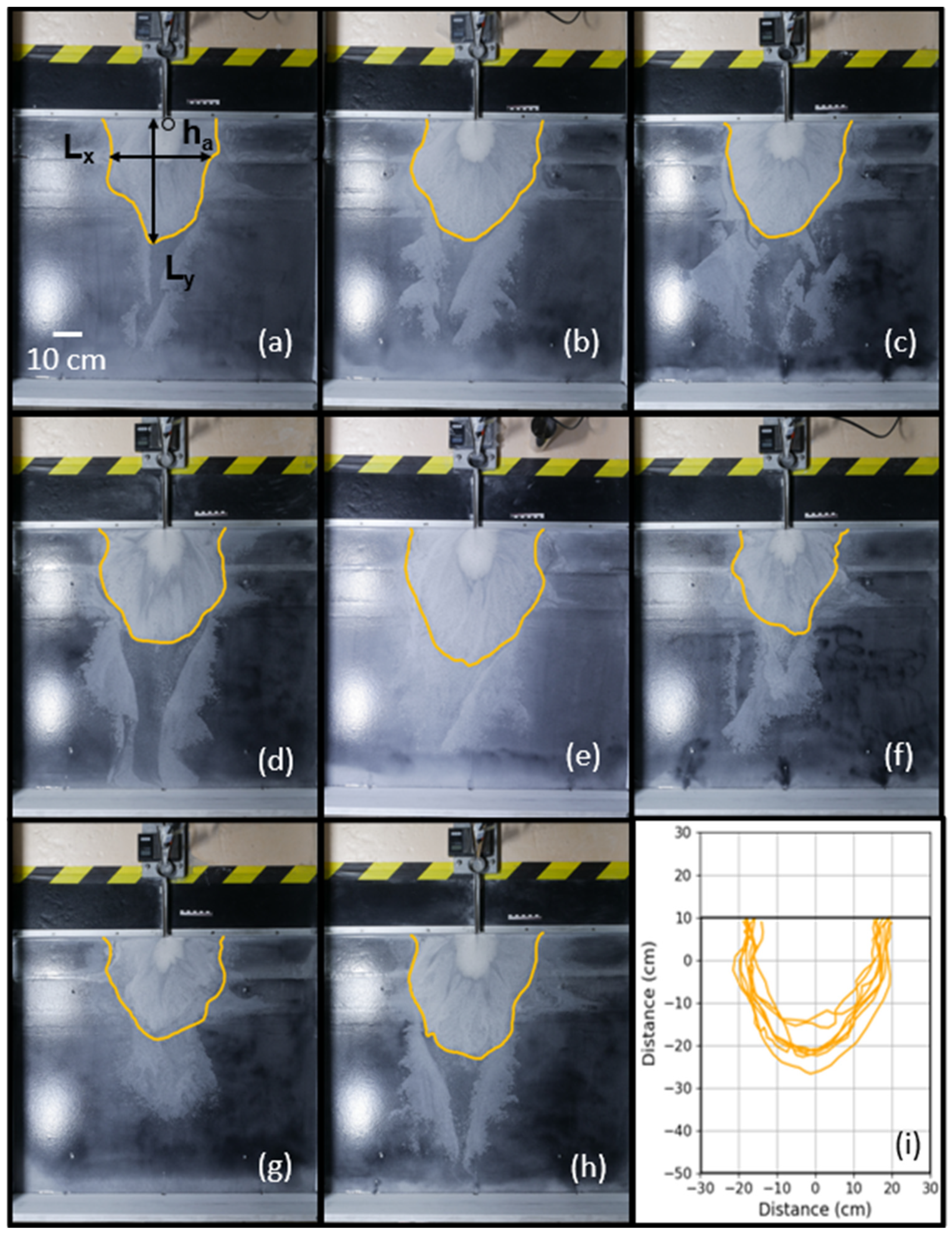
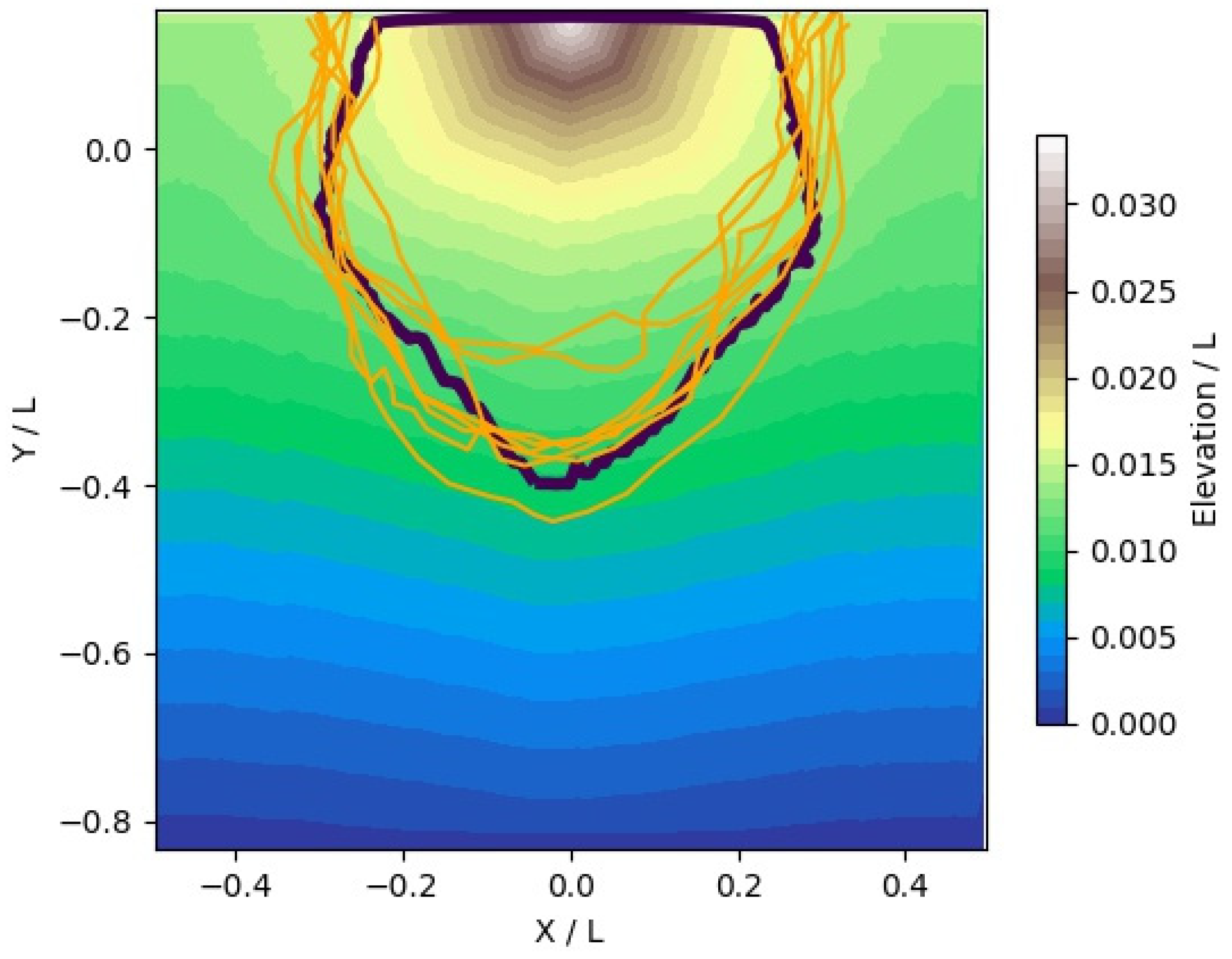
3.1. Repeatability of Analog Experiments

Using the same operators, equipment, and boundary conditions, eight experiments were performed to test the robustness of the analog results. This repeatability test was performed using the conditions presented in Section 2.3. for the first modeling stage, i.e., without tectonic forcing.

Regardless of the experiment, an alluvial fan formed within the first ten minutes and then grew due to the avulsion phenomenon (e.g., [42]). After one hour, the resulting fans had an identical form with a quasi-radial pattern elongated in the y-direction (Figure 3).

Taking advantage of the specific color of deposits, we detected the fan boundaries from the top-view pictures taken after one hour (Figure 3). We then assessed the fan length in the x-direction, $L_x$, and in the y-direction, $L_y$. We also used the fan DEM obtained from Micmac processing to calculate the elevation of the fan apex $h_a$.

Based on the experiment dataset, we estimated the mean value and the standard deviation of these three geometric parameters. Our results demonstrate a good repeatability with $L_x=30.7 \pm 3.7$ cm, $L_y=36.7 \pm 2.2$ cm, $h_a=18.5 \pm 2$ mm. These values were used in the following section to calibrate the erosion law parameters of the numerical models.

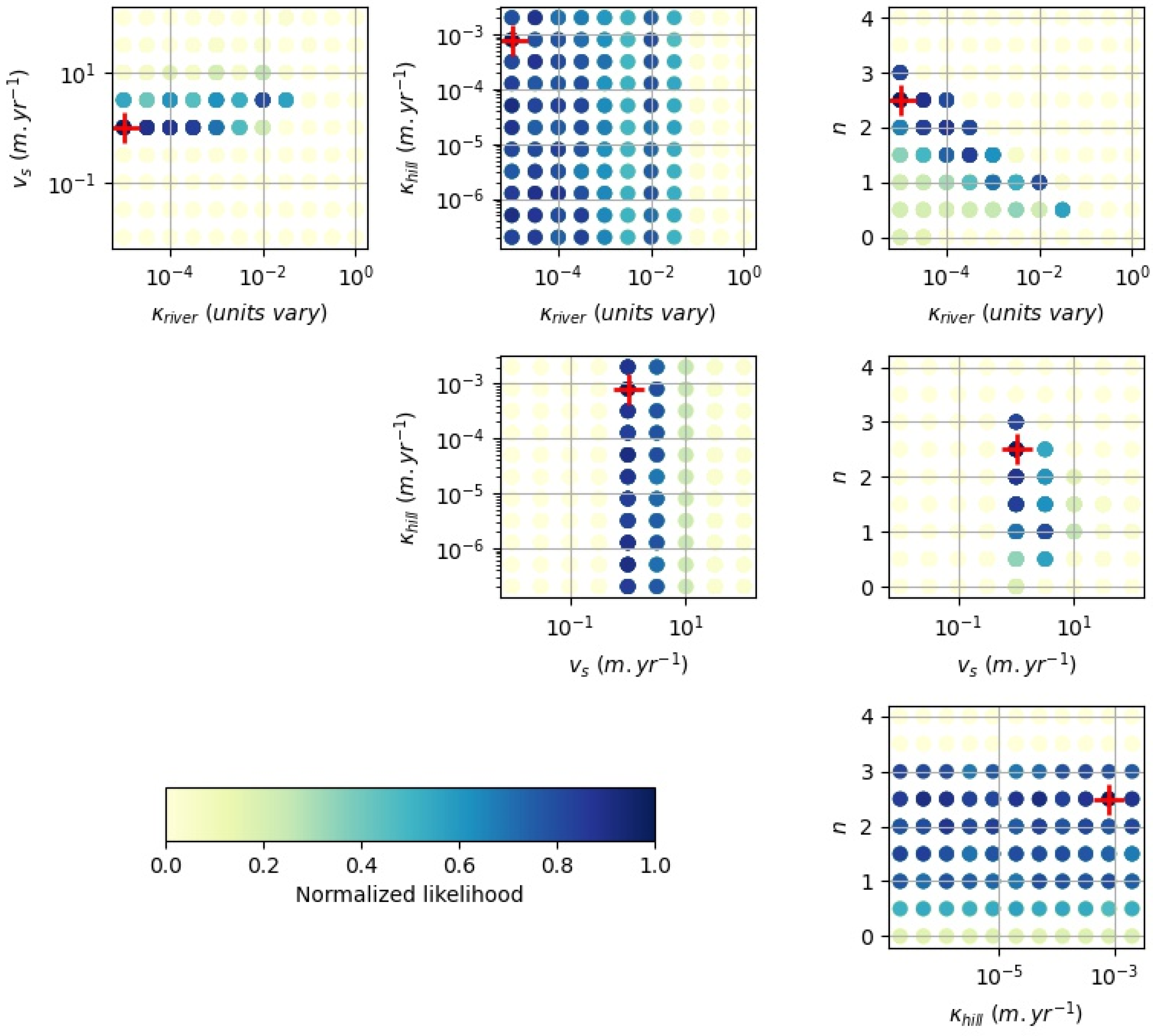
3.2. Calibration of Numerical Erosion Law Parameters from the Alluvial Fan Building Phase

The erosion law parameters depend on climate, lithology, or vegetation cover, and some of them are interdependent, such as ${\kappa }_{hill}$, $m$, and $n$. Therefore, assessing these parameters from natural landscapes results in a wide variance, limiting the use of erosion laws and thus the relevance of numerical models.

We calibrated these parameters by performing a numerical inversion, which compared the geometry of alluvial fans obtained from analog and numerical modeling. We imposed consistent geometry, initial, and boundary conditions for both modeling approaches, verifying the estimated scaling factors. This comparison was performed based on a systematic exploration of the erosion law parameters ${\kappa }_{hill}$, $v_s$, $n$, and ${\kappa }_{river}$ in the ranges of values presented in Section 2.2, resulting in a collection of nearly 10,000 numerical models. We compared the calculated normalized $L_x/L$, $L_y/L$, and $h_a/L$ with those obtained from analog models for each of them. $L_x$ and $L_y$ were obtained (1) by calculating the difference between the final topography and the initial elevation associated with a 0.8° inclined plane and (2) by assuming that the fan boundary is defined by a threshold elevation of 2 mm. One can note that $L=60$ cm for analog models and $L=6$ km for numerical models.

We defined the cost function as the weighted root mean squared error,

$$cost=\sqrt{\frac{1}{3}{\displaystyle \sum }_{i=1}^3\left[{\left(\frac{ob{s}_i-cal{c}_i}{\sigma ob{s}_i}\right)}^2\right]}$$

(7)

The two vectors $obs$ and $\sigma obs$ included $L_x/L$, $L_y/L$, $h_a/L$, and their standard deviation from analog modeling. The vector $calc$ is associated with the same parameters calculated from numerical modeling.

The best model inferred from our inversion was associated with the minimum cost function. It was obtained for ${\kappa }_{river}={10}^{-5}$, $v_s=1 \mathrm{m}.\mathrm{y}{\mathrm{r}}^{-1}$, ${\kappa }_{hill}={8.10}^{-4} \mathrm{m}.\mathrm{y}{\mathrm{r}}^{-1}$, and $n=2.5$ (Figure 4). The quasi-radial pattern elongated in the y-direction observed in the analog model can thus be explained by a low river bedrock erodibility and an equal contribution of incision and sediment transport. The horizontal geometry of the best-fitting simulated fan was characterized by normalized lengths $L_x/L$ of 0.57 and $L_y/L$ of 0.57, consistent with $L_x/L=0.51 \pm 0.06$, $L_y/L=0.61 \pm 0.04$ obtained from analog models. Finally, the numerical and analog approaches gave a very similar topography apex with $h_a/L=0.32$ and $h_a/L=0.31 \pm 0.03$, respectively. Next, we defined the likelihood function as

$$likelihood=exp\left(-cost\right)$$

(8)

The likelihood distribution was normalized with the likelihood of the best-fitting model presented above. Hence, the calculated normalized likelihood ranged between 0 (low agreement between analog and numerical results) and 1 (best agreement).

According to Figure 5, we showed that the erosion parameters did not control the likelihood distribution in the same way. Not surprisingly, the likelihood distribution did not depend on the assumed ${\kappa }_{hill}$ values. Indeed, alluvial fan building was associated with slopes <5°, which prevent hillslope processes. Our calibration approach was thus not relevant to constrain ${\kappa }_{hill}$.

In contrast, fluvial erosion and deposition significantly influenced fan formation by controlling channel avulsion and migration to a new path radiating from the apex fan. Our result suggests a net settling velocity $v_s$ of ca. 1 m.yr⁻¹ (Figure 5). This value was associated with an intermediate case between detachment-limited and transport-limited models [13]. The more likely models also suggested a slope exponent $n$ between 0.5 and 3 and a river bedrock erodibility between ${10}^{-5}$ and ${10}^{-2}$. In more detail, the obtained likelihood distribution showed a semi-logarithmic relationship between $n$ and ${\kappa }_{river}$: a low ${\kappa }_{river}$ is associated with a high $n$, and vice versa (Figure 5). This relationship can be explained by the power incision law itself (Equation (6)), for which a decrease in the exponent $n$ can compensate for a logarithmic increase in ${\kappa }_{hill}$.

Together, these first results demonstrate the robustness of both approaches and allow to put forward their complementarity to study the physical processes controlling landscape evolution. In the following section, we will use this joint approach to study the morphotectonic evolution of an alluvial fan.

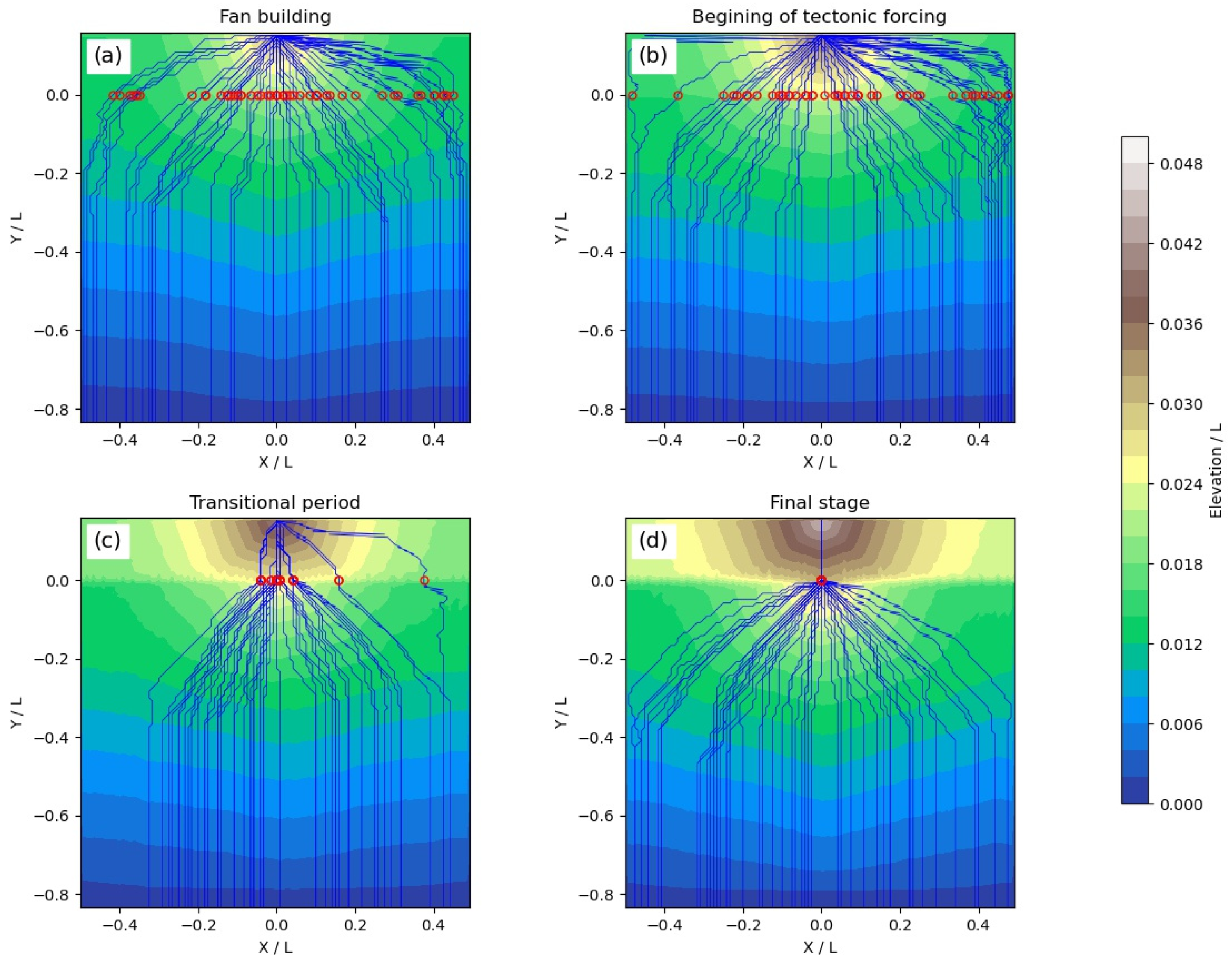
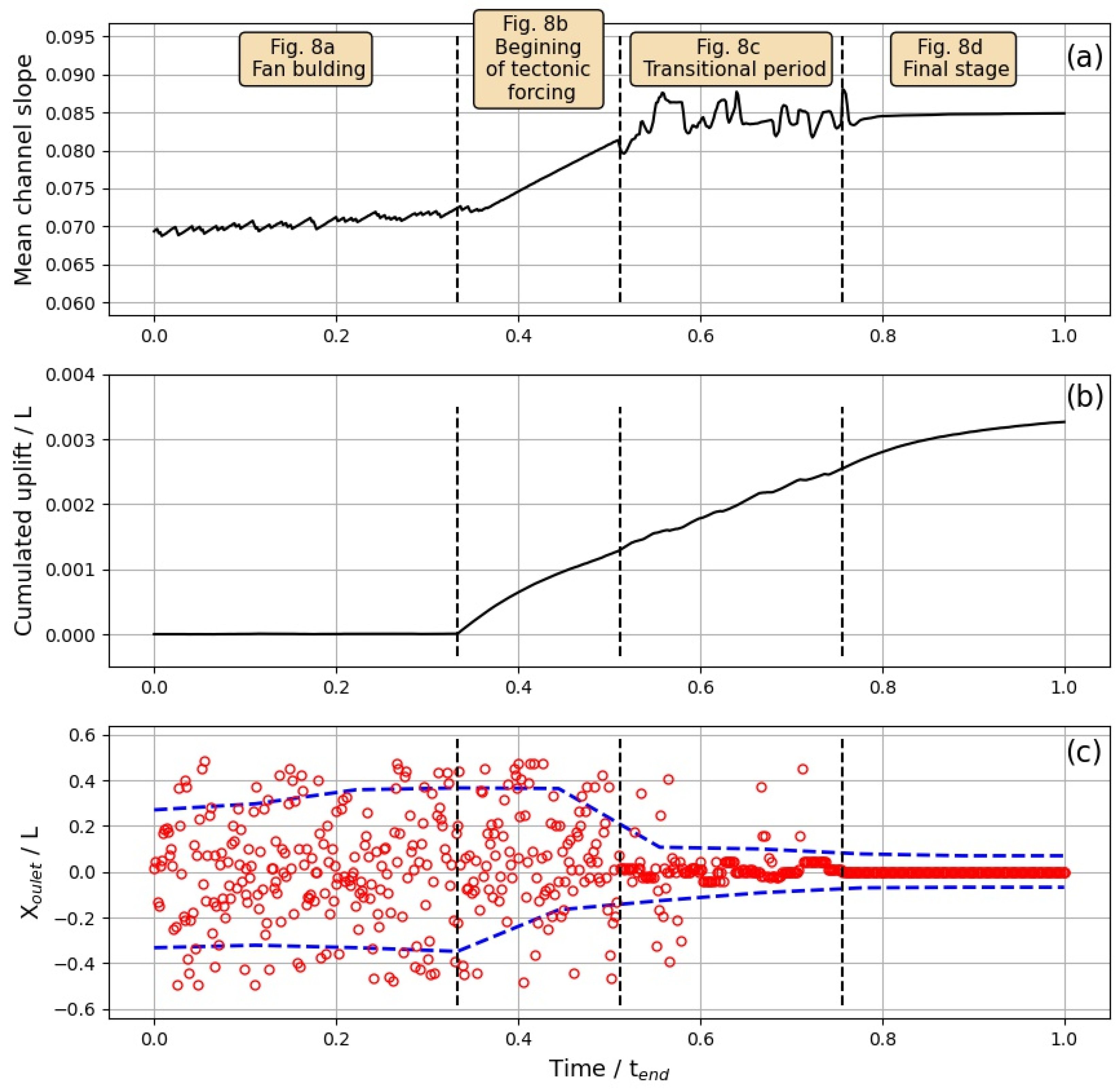
3.3. Morpho-Tectonic Evolution

In the previous section, we modeled an alluvial fan formation only due to water and sediment flux external input. Here, we studied the morphological evolution of a fan affected by additional tectonic forcing, all other conditions remaining unchanged. We assumed a stable fault with a constant uplift rate of 0.7 cm.h⁻¹ and 1.9 mm.yr⁻¹ for analog and numerical models, respectively. This new boundary condition was applied for 1 h for experimental models, leading to an equivalent duration of 36 ka for the numerical models.

The morphology obtained with the analog models exhibited a more complex pattern compared to the surface without tectonic forcing (Figure 6). Two major landforms can be observed from the hanging wall topography: (1) an inherited alluvial fan associated with the fan building stage and (2) a central valley. This valley was narrow at the point source of sediments and widened until it crossed the fault (Figure 6b). On both sides of this central channel, one can mention very narrow abandoned channels suggesting a temporal evolution of the channel network. These abandoned channels represent the direction variations of the sedimentary flux at the outlet. The footwall was marked by a neo-formed fan, highlighted by its semicircular shape and visible drains (Figure 6a). The location of this new fan at the outlet of the central valley underlines the complex tectonic-erosion interactions between the two fault blocks. While the sediments deposited on the footwall were carried in the hanging wall central valley, the footwall fan elevation controlled the incision rate in this valley and its sediment transport capacity.

The numerical simulations were performed using the 200 best-fitting models obtained in the previous calibration section, i.e., those having a normalized likelihood exceeding ca. 0.5. The numerical models most in line with the results of the analog approach suggested a river bedrock erodibility of ${10}^{-4}$, a settling velocity of 1 m.yr⁻¹, and a slope exponent of 2. Hillslope erodibility remained the least constrained parameter. A range between $5\times {10}^{-7}$ m.yr⁻¹ and $2\times {10}^{-3}$ m.yr¹ gave almost identical results. These best-fitting models exhibited a normalized elevation whose deviation from the surface of analog models did not exceed 0.002 (Figure 7). For both approaches, the normalized topographies were thus quite similar with (1) an elevation of up to 0.04, (2) a lateral extension of the inherited fan on the hanging wall of 0.8, and (3) a neo-formed fan on the footwall. The main difference was the absence of a wide central valley. Indeed, in numerical models, the width of this valley was limited to the mesh size used in the numerical models. However, we can see other narrow abandoned valleys on the hanging wall, suggesting a non-static river network with lateral movements of central channels during the simulation (Figure 7b).

To test this hypothesis, we analyzed the temporal evolution of the modeled landscapes in more detail. We identified four distinct stages from the numerical modeling results (Figure 8). During the fan building stage, one can observe a radial network of channels diverging from the apex fan and spreading laterally over the entire model’s width (Figure 8a). At the onset of tectonic forcing, the surface deformation associated with cumulated fault slip is small compared to the geometry inherited from the fan formation. The geometry of the drainage network, therefore, remains unchanged (Figure 8b). Then, during a transition period, the water and sediment flow becomes channeled. A wide central valley forms, where the drains can move laterally (Figure 8c). Finally, when the cumulative displacement on the fault becomes large enough, the central valley deepens, and the channel remains localized along a single drain in the hanging wall (Figure 8d). We observed a similar scenario for analog modeling. A central channel forms by incising the hanging wall alluvial fan after nearly 30 min of tectonic forcing. The drainage network becomes more channeled, forming a valley of ca. 5 cm width at the end of the experiment.

To further compare the two modeling approaches, we estimated the temporal evolution of the zone where the channels and the fault intersect (Figure 6b and Figure 8 and Supplementary Materials S3). Thanks to the drainage network, the width of this zone was defined as the largest distance between the channels. While during the fan building period, a width $L$ was obtained, at the end of the experiment, the width corresponded to the lateral extension of the central valley. Our results demonstrate that the mean channel slope was the key parameter in this temporal evolution. During the fan building period, the channel slope increased gently in response to sediment deposition (Figure 9). This low slope allowed the drains to move laterally along the entire model. The application of tectonic forcing generated a rapid slope increase and a continuous uplift rate. As long as the critical slope of ca. 0.081 was not reached, there was no channelization. Beyond this threshold, one can observe the channelization of the central valley with a pseudo-stable state of the mean channel slope. This slope reached a stable value of 0.85 before the end of the simulations, highlighting an equilibrium state.

Our results confirm the relevance of our joint approach to explaining the obtained topography and the temporal evolution of the drainage network associated with constant tectonic forcing.

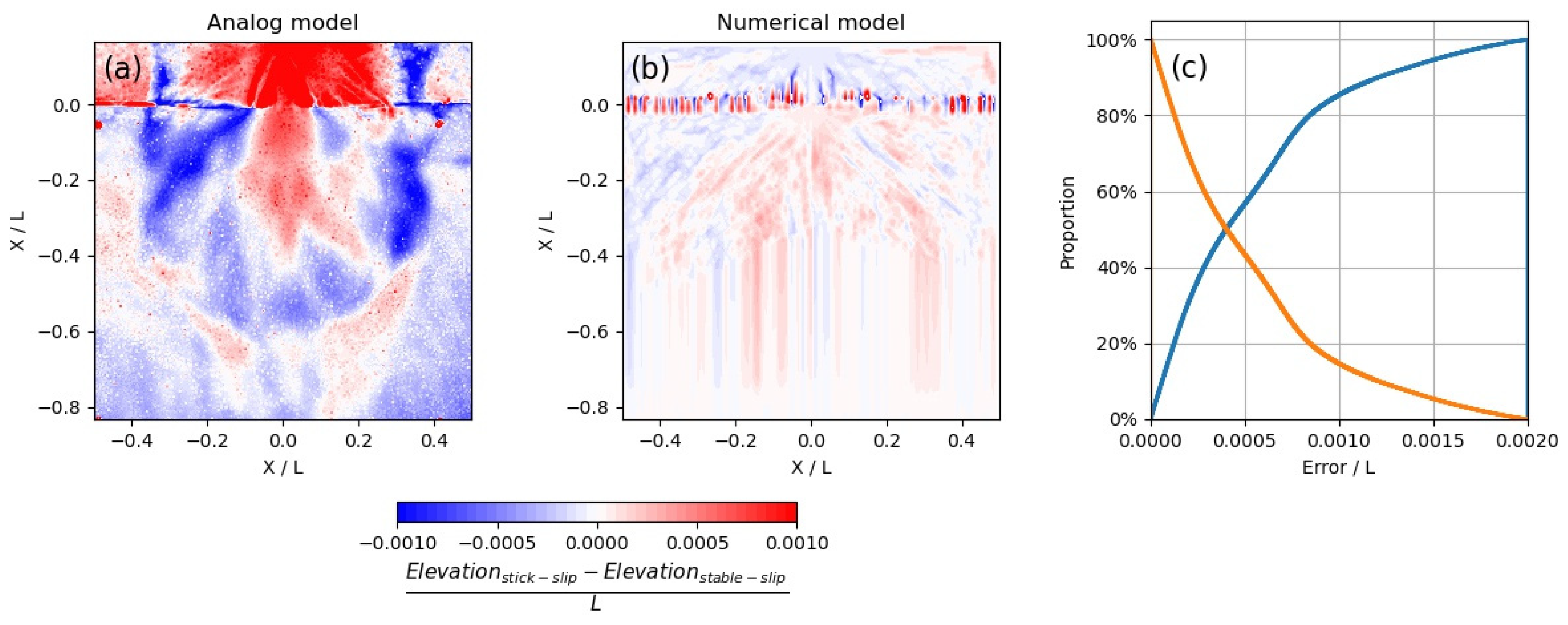
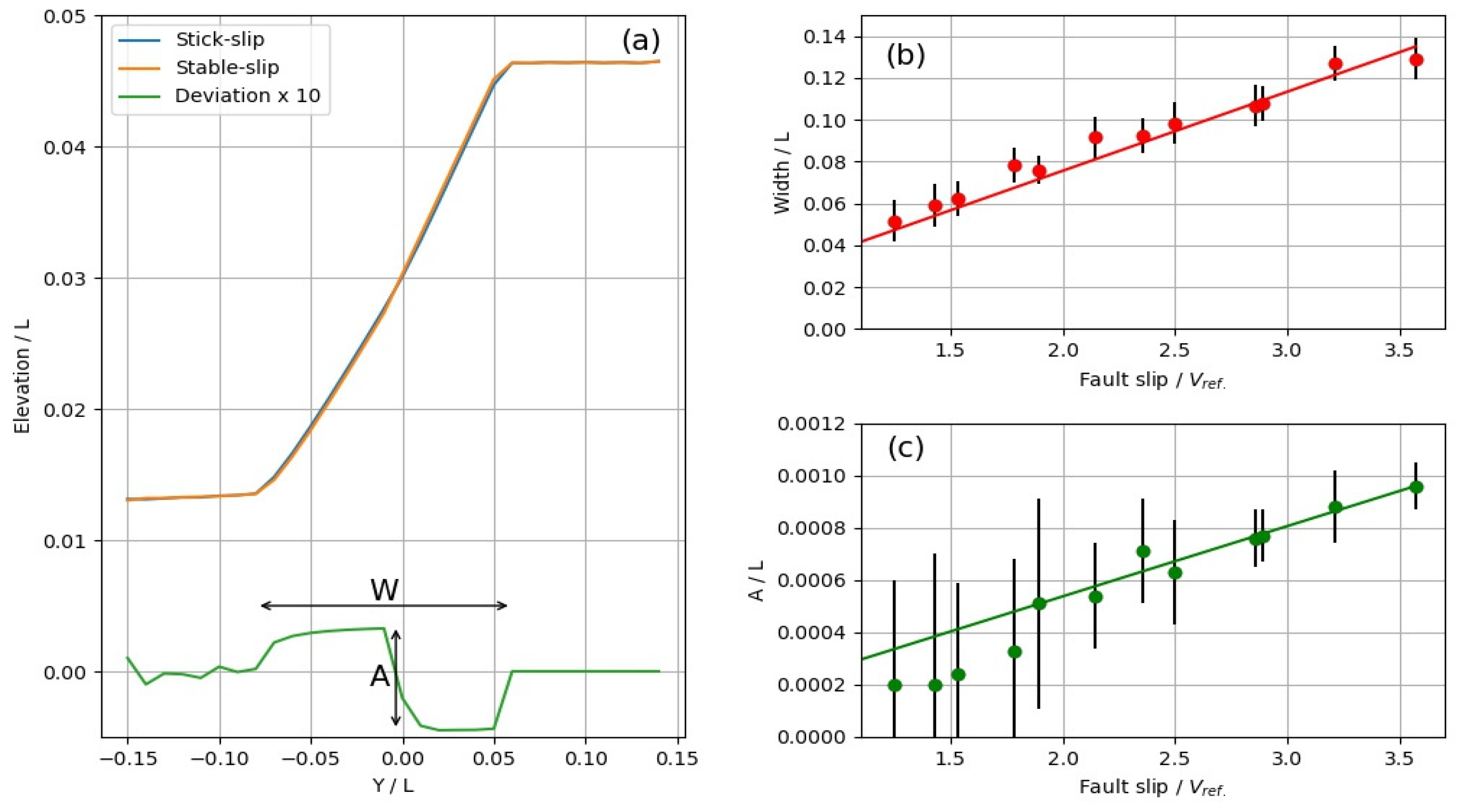
3.4. Stable versus Stick-slip Behaviors

Over the last decade, many studies pointed out the diversity of slip modes along active faults, including stable slip [24], slow slip events [43], and earthquakes [44]. Distinguishing these different slip modes is of primary importance to improve the seismic hazard assessment. Here, we compared the previous results assuming a stable sliding with the topography obtained for a stick-slip fault. The cumulated fault slip remained the same, and we considered a return period $T_{ref}$ of 180 s and 1800 yr for the analog and numerical modeling, respectively (Table 1).

Our results suggest a specific morphological signature associated with the assumed fault slip mode (Figure 10). However, this signature is tenuous and depends on the modeling approach. To analyze these results, we defined the normalized differences in elevation as

$$\mathsf{\Delta }z=\frac{Elevatio{n}_{stick-slip}-Elevatio{n}_{Stable-slip}}{L}$$

(9)

The absolute value of $\mathsf{\Delta }z$ reached up to ${10}^{-3}$ in analog models. This value is larger than that obtained in the numerical simulation. While $\mathsf{\Delta }z$ was positive in analog models, $\mathsf{\Delta }z$ was negative in numerical simulations in the hanging wall. Analog models showed a more complex pattern in the footwall with $\mathsf{\Delta }z>0$ at the center of the neoformed fan and $\mathsf{\Delta }z<0$ at its boundaries (Figure 10a). One can also notice that the highest values of numerical $\mathsf{\Delta }z$ were located near the fault scarp (Figure 10b).

One explanation of these differences in $\mathsf{\Delta }z$ between both approaches comes from the repeatability of analog models (Figure 10c). Based on the comparison of four laboratory experiments, our repeatability test highlights that nearly 40% of the analog model has a normalized error of more than $5\times {10}^{-4}$, which is of the same magnitude as the elevation difference $\mathsf{\Delta }z$. This error shows the limitations of analog modeling, in which both the water and sedimentary input flux needs to be better controlled. The analog results are therefore not robust enough to be conclusive. In the following section, we discuss in more detail the morphological signature of the fault slip mode using only the numerical approach.

To sum up, in this results section, we showed the interest of a joint approach combining analog and numerical models to study the morpho-tectonic evolution of an alluvial fan. The consistency of results obtained during the fan building and tectonic stages makes our results more robust. Analog models are advantageous to calibrate erosion law parameters used in numerical simulations. The numerical approach can overcome some of the analog model limitations, such as the control of sediment input. Our results suggest that the tested analog models correspond to an intermediate case between detachment-limited and transport-limited models, with a low river bed-rock erodibility compensated by a high slope exponent. The mean channel slope appears as a critical parameter controlling the temporal evolution of our modeling. The obtained fault slip mode signature is tenuous and seems challenging to observe in the field.

4. Discussion

The tectonic forcing depends on several parameters, such as the slip rate $v$, the slip return period $T$, the fault dip angle $\alpha$, and the fault location $y_{fault}$. As previously mentioned, the elevation change due to horizontal tectonic advection is not considered in the numerical simulations. Changing $\alpha$ is thus equivalent to changing $v$. Here, we only studied the role played by $v$, $T$, and $y_{fault}$ on the morphotectonic evolution of the alluvial fan. Therefore, we changed these tectonic parameters one by one and compared the results to the reference model used until now (Table 1).

4.1. Effect of Slip Rate on Surface Morphology

For the reference model, we used a homogeneous slip rate $v_{ref}=2.8$ mm.yr⁻¹ along the fault. This value is relatively low compared to field observations in active fault zones (e.g., Marechal et al., 2016). Three slip rates were tested: one is the reference model $v=v_{ref}$ (Table 1), and the other two are associated with a faster slip rate $v=1.5\times v_{ref}$ and $v=3\times v_{ref}$.

Due to tectonic-erosion feedback, whatever the slip mode, the channel incision was more intense when the slip rate increased (Figure 11). In contrast with the reference model, the obtained topography exhibited a well-marked central valley, even for a slight slip rate increase. This topography is in better agreement with the analog model, which showed a valley in the hanging wall widening from its source to its outlet at the fault zone (Figure 6). This result underlines the too low fault slip rate used in the numerical reference model. It should be remembered that only the order of magnitude of the scaling factor is assessed in Section 2.1.3. The coefficient of 1.5 required to explain a large central valley does not question the previously obtained results.

Regardless of the slip rate, finding a difference between a stable or unstable slip pattern is not straightforward. The elevation deviation was calculated from Equation (8). For the three models, we obtained a rather similar pattern for $\mathsf{\Delta }z$. The main difference was in the two zones of the fault scarps with high $\left|\mathsf{\Delta }z\right|$, suggesting a more localized deformation with stable sliding (Figure 11). These two zones were parallel to the fault and had a width and an amplitude dependent on the fault slip rate. Ten additional models with slip rates ranging from $1.2\times v_{ref}$ to $3.6\times v_{ref}$ were tested to confirm this finding. Our result suggests linear relationships between the slip rate, the zone width, and the deviation amplitude: the higher the fault slip velocity, the higher the width, and the higher the amplitude (Figure 12).

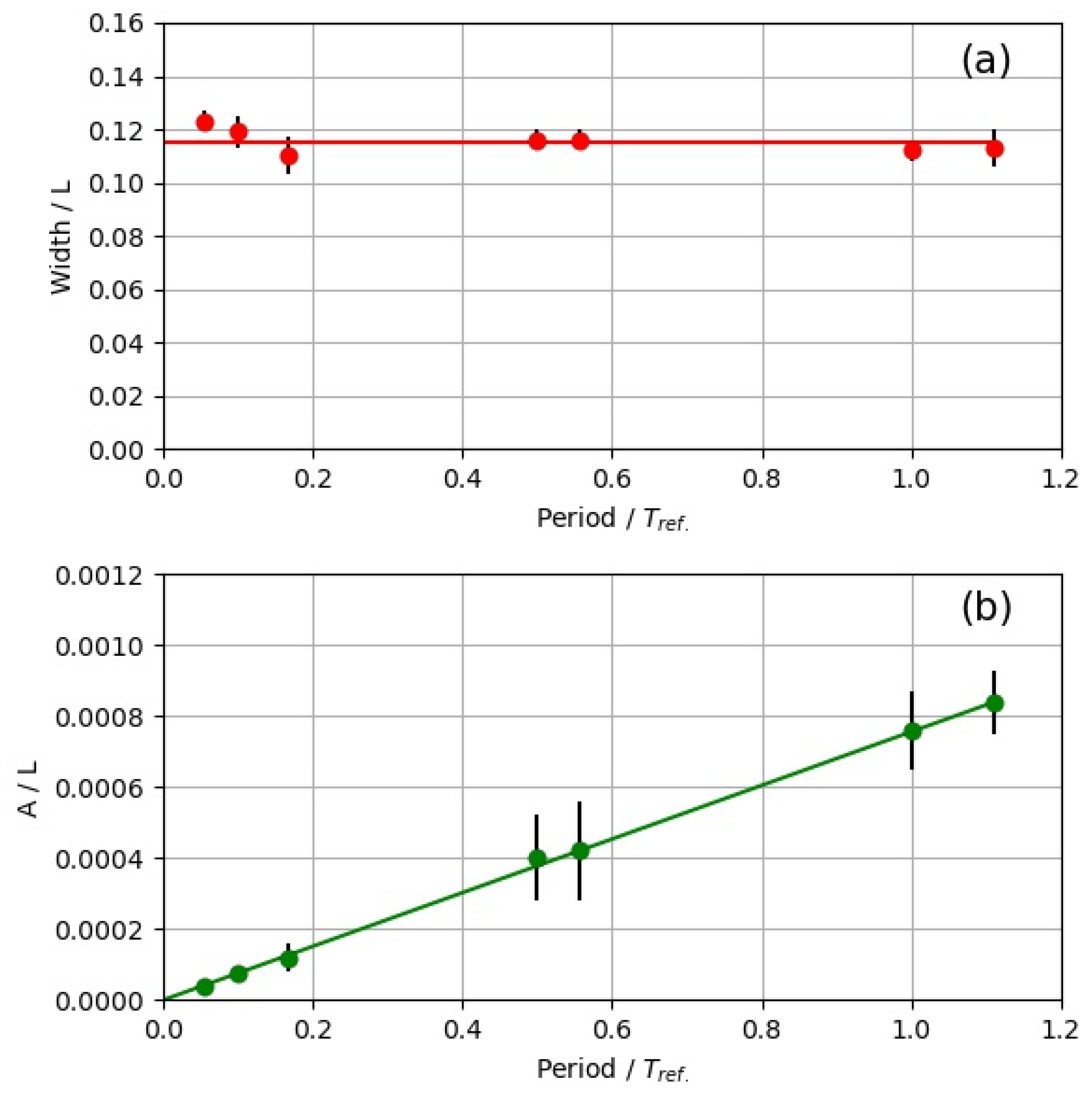
4.2. Return Period

The reference return period $T_{ref}$ is equal to 1800 years (Table 1). Except in particular regions with a very low shortening rate (e.g., [43]), the return period of strong earthquakes (M > 7) is generally a few hundred years (e.g., [23,45]). Here, we ran seven models with return periods between $0.05\times T_{ref}$ and $1.1\times T_{ref}$. A limitation of numerical modeling is that long return periods are associated with a large displacement on nodes in a single time step, leading to numerical instabilities. All these models had the same cumulative slip and were associated with a slip rate of $3\times v_{ref}$.

The return period did not influence the main topographic features of the models. Following the approach described in the previous paragraph, the width of the fault scarp’s zones of high $\left|\mathsf{\Delta }z\right|$ remained constant with a variation of the return period (Figure 13a). Unsurprisingly, the return period influenced the amplitude of the area with higher differences in $\left|\mathsf{\Delta }z\right|$. The stick-slip fault behavior tended towards a stable sliding when the return period became shorter. Our results suggest a linear relationship between the return period and the deviation amplitude: the longer the return period, the higher the amplitude (Figure 13b).

4.3. Distance between Fault and Sediment Source

The accommodation space of deformation along major thrust faults is often complex at the surface. Strain can be distributed along several branches in a fault zone extending for several kilometers [27,46,47,48,49,50]. In the reference model, the distance $d=d_{ref}$ between the sediment source and the fault is equal to 1000 m (Figure 2). Three other distances were tested: $d_{ref}/2$, $d_{ref}\times 2$, and $d_{ref}\times 3$. For all numerical models, we assumed a fault slip rate of $3\times v_{ref}$.

Our simulations underline the significant impact of $d$ on morphology. For large distances, the radial geometry of the drainage network promoted incision of the scarp along its entire length (Figure 14a). This geometry led to a homogeneous drainage density. No secondary alluvial fan was then formed on the foothill. As this distance decreased, the flow of water and sediment became more channeled, forming (1) a central valley that drains most of the flow and (2) a secondary alluvial fan on the foothill (Figure 14b,c). Finally, all water flow and sediment transport occurred in a central valley for the shortest distances (Figure 14c,d). Note that the distance did not control the width of the central valley.

Together, our results demonstrate that $d$ is a key parameter in the morpho-tectonic evolution of an alluvial fan. The closer the fault is to the sediment source, the higher the drainage density in the center of the hanging wall and the higher the surface of the neo-formed alluvial fan.

5. Conclusions

This paper investigated the role of surface processes and tectonics on the evolution of the alluvial fan morphology. We used a joint approach based on analog and numerical models sharing identical geometry and boundary conditions. We demonstrated the excellent repeatability of the analog models by showing that the main geometrical characteristics of the modeled fans can be reproduced with a deviation of ca. 10%. Based on a numerical inversion, we use these experimental results to calibrate erosion law parameters. While our approach is not relevant to assess hillslope erodibility, we found a relationship between bedrock river erodibility and the slope exponent of the incision power law. To our knowledge, this type of combined approach is rarely developed. Our results illustrate its efficiency in better quantifying surface processes that would otherwise remain poorly constrained.

The analog and the numerical results indicated a good consistency on both the final topography and the temporal evolution of the alluvial fan morphology. We obtained similar results concerning the genesis of specific landforms such as (1) an alluvial fan formed during the first modeling stage with no tectonics, (2) a wide central valley in the hanging wall, and (3) a neo-formed alluvial fan in the footwall. A detailed analysis of the model evolution reveals a threshold process controlling the temporal changes in the drainage network geometry. As long as the critical slope of ca. 0.081 was not reached, there was no channelization. Beyond this threshold, the channelization of the central valley took place.

The morphologic signature of fault slip mode is tenuous. We only spotted a minor deviation along the fault scarp. Although this deviation may increase with the fault slip rate and the return time of slip events, it remained low compared to fault scarp cumulated displacement. In nature, such a deviation is challenging to identify. High-resolution topographic data cannot be used alone but appears valuable to complement stratigraphic and geodetic approaches to study the slip mode of active faults.

This study assumed a constant external forcing associated with no time variation in the input water and sediment flux. However, such a constant regime may be seldomly found in nature, and the relative impact of extreme events in shaping landscape remains an open question [51,52]. The role of climate variations must be better considered in future works, including extreme processes such as heavy rainfalls or flash floods, and variations at regional base levels.