Abstract
Seismic sequences are a powerful tool to locally infer geometrical and mechanical properties of faults and fault systems. In this study, we provided detailed location and characterization of events of the 3–7 July 2020 Irpinia sequence (southern Italy) that occurred at the northern tip of the main segment that ruptured during the 1980 Irpinia earthquake. Using an autocorrelation technique, we detected more than 340 events within the sequence, with local magnitude ranging between −0.5 and 3.0. We thus provided double difference locations, source parameter estimation, and focal mechanisms determination for the largest quality events. We found that the sequence ruptured an asperity with a size of about 800 m, along a fault structure having a strike compatible with the one of the main segments of the 1980 Irpinia earthquake, and a dip of 50–55° at depth of 10.5–12 km and 60–65° at shallower depths (7.5–9 km). Low stress drop release (average of 0.64 MPa) indicates a fluid-driven initiation mechanism of the sequence. We also evaluated the performance of the earthquake early warning systems running in real-time during the sequence, retrieving a minimum size for the blind zone in the area of about 15 km.
1. Introduction
Seismic sequences are a useful tool to shed light on fault mechanics and geometry, on the chemical and physical processes occurring on faults and ultimately to illuminate the preparatory phase of large earthquakes. For the goal, diverse dense multi-disciplinary observation infrastructures were created around faults that can potentially host large destructive earthquakes, to understand how those faults slip, what is the seismic and aseismic balance during strain release, and what is the role of fluids in earthquake production.
The study of microseismicity can provide mechanical constraints on the faults, through accurate earthquake location and source parameter computation. Earthquake location can benefit from measurements of P and S wave arrival times and back-azimuth estimation. In dense networks, absolute locations of microearthquakes can reach a sub-kilometric accuracy, using global-search techniques in 3D velocity media tailored for the area [1,2]. When using relative location techniques, such as double differences [3], the accuracy can be pushed down to a decametric scale [4], when relative arrival time determination is performed through cross-correlation [5]. With this resolution, earthquake location can delineate the geometry of faults [3,6] and following event space and time evolution, it is possible to infer the role of the fluids in seismicity migration [7,8].
Source parameters are usually inferred through the fit of a specific rupture model with a simplified description of the observations, such as the displacement amplitude spectrum [9]. Rupture evolution is synthesized in few macroscopic parameters, such as the seismic moment, the source size, and the average stress drop. Large epistemic uncertainties in source parameter estimation come from the medium description, which is usually assumed as homogeneous [10]. This problem can be mitigated either using smaller magnitude earthquakes as empirical Green’s functions [11] or computing a non-parametric, data-driven attenuation function [12]. Source parameters provide insights on the stress released during earthquakes and on the earthquake size, enabling the understanding of the role of fluids in earthquake production [13] and the recognition of possible forcing aseismic mechanisms in sequence generation [14].
Characterization of the seismic activity during sequences can constrain fault geometry and mechanics in the vicinity of the swarm location. This information can be crossed with tomographic models in velocity and attenuation, to get a picture of fluid-filled domains and infer the role of the pore pressure in the stress distribution and release at depth [15].
While in most cases seismic sequences end into background seismicity, sometimes acceleration of the cumulative seismic moment release during sequences can yield a large magnitude event, especially for interplate events [16]. Capability to recognize foreshocks before the occurrence of a large event is fundamental for risk monitoring and reduction. There is a large debate in the seismological community on precursory seismicity before a large event and contrasting results have been obtained in indicating the occurrence of foreshock sequences as a persistent feature of moderate to large events (see for California [17,18]). Nevertheless, when a sequence clearly evolves to a large event, foreshocks emerge only when high-resolution seismic catalogs are available, with a magnitude of completeness much smaller than the one presently available for standard monitoring networks. Thus, advanced techniques for event detection are required to improve the catalog, such as the template matching [19] or autocorrelation algorithms [20].
In this study, we have applied some of these advanced techniques to analyze a seismic sequence that occurred in the area of the 1980, M 6.9, Irpinia earthquake. Since 2005, in this region, INFO (Irpinia Near Fault Observatory) operates ISNet—the Irpinia Seismic Network—with the goal of monitoring the seismicity evolution and its relationship with the underlying fault system [21]. ISNet is a dense, high-dynamic range seismic network of 31 stations, covering an area of about 100 × 70 km2 along the Campania-Lucania Apennine chain, surrounding the fault system that generated the 1980 Irpinia earthquake [22]. The seismic stations are deployed within two imaginary concentric ellipses, with the major axis parallel to the Apennine chain. The mean distance between stations in the outer ellipse is about 20 km, while the distance between the two ellipses is about 10 km. The average inter-station distance within the inner ellipse is less than 10 km. All stations are equipped with a strong-motion accelerometer and a weak motion sensor, the latter being a short-period, a broadband velocimeter or an accelerometer with lower full-scale. Stations of ISNet provide real-time data with controlled delay at the ISNet control center, enabling the network to be the backbone infrastructure for earthquake early warning systems [23] and for near real-time computation of regional ground-shaking maps.
We used ISNet data to investigate the mechanical properties of the Rocca San Felice seismic sequence, that started on 3 July 2020 and lasted for 4 days. In this study, we reviewed the seismotectonic setting of the area, then we applied advanced techniques for event detection and characterization, to enlarge the automatic catalog and to provide accurate locations, based on double-difference techniques. We thus computed source parameters and focal mechanisms to infer the stress release and its main directions, the size of the events, and to discriminate the rupture plane. Finally, we analyze the ground motion and the performances of earthquake early warning systems, as real-time risk reduction tools.
2. Seismotectonic Setting
2.1. Structural Setting of Southern Apennines
The structure of the Southern Apennines is associated with the Meso-Cenozoic tectonic processes that involved the African and European plates and, in accordance with different tectonic phases of rifting, drifting, and shortening, deformed the Corsica-Sardinia and Adriatic-Apulian forelands [24,25]. The backbone of the mountain belt is characterized by E-NE verging duplexes geometries and out-of-sequence thrusting due to orogenic contraction that was active since upper Eocene-Oligocene Miocene up to late Pliocene [26]. Meso-Cenozoic successions of Adriatic-Apulian-African passive margin, deposited as carbonate platforms with interposed pelagic basins, were involved in folding and thrusting according to imbricated structural units detached from their crystalline basement, as documented by seismic profiles obtained since 1980s during hydrocarbon exploration [27]. Migrating eastward over the Apulian foreland, these sheets were tectonically overthrusted by internal units, deposited originally above the oceanic crust of Tethys. Considering the lithostratigraphic relationships, from top to bottom, units are grouped in: (1) post-orogenic intramontane basin units of marine, terrestrial, and volcanic origin, deposited during Plio-Pleistocene or Holocene in the Adriatic-Bradanic foredeep; (2) syntectonic top-thrust basin successions formed during the progressive shortening toward east; (3) orogenic wedge tectonic units involved in the NE-verging overthrusting from upper, internal domains (Tethyan oceanic crust or Adriatic-Apulian continental crust) to the lower, external domains (Apennine carbonate platforms with inter-basins pelagic units); (4) Apulian carbonates, buried, deformed, and overthrusted in the inner belt and undeformed in the outcropping foreland [25,28]. During the Quaternary, the Southern Apennine thrust belt was dissected by NW-SE oriented normal faults that accommodated an extensional tectonic phase, according to a stress field with the axis of maximum extension coaxial to the axis of maximum compression of Apennines belt (SW-NE trend [24,29,30]). In fact, contractional and extensional deformations took place simultaneously in different sectors of the Apennines with both E-migrating fronts at a similar rate of ~4 cm/year.
2.2. Seismogenic Normal Faults
In the Southern Apennines, normal faulting corresponds to a significant deformation process in terms of regional size of structures, morphotectonics, active displacement, and seismogenesis. Normal faults with NW-SE striking regulate the active tectonics in the thrust belt, accommodating an extension of 3–5 mm/year as evidenced by surface geology, borehole breakout, and available fault plane solutions of earthquakes [31,32]. Earthquakes up to X-XI MCS intensity struck the Southern Apennine chain, indicating that this sector is one of the highest seismic hazard areas of the Mediterranean region, with segmented, seismogenic structures capable of generating up to M 7 earthquakes [33,34] (Figure 1). These earthquakes occur principally in the axial sector of the Apennine chain with recurrence periods ≥1000 years and depths down to 10–15 km in the upper crust, in a 30–50 km wide belt that follows the orographic divide [35]. As proposed in different models [36,37,38], normal faults that dissect Apennines show an evolutionary trend from young, high-angle planar faults, seated in the upper crust and characterized by small extensional strains, to mature, listric faults reaching the crystalline basal detachment with high amount of extensional strain. A consequence of progressive E-migration of the extensional front is that normal faults show a different aging and degree of evolution from mature faults of the inner sector of the Apennine chain (to W, toward the Tyrrenian margin) to young faults superimposed on the accretionary wedge along its axial sector (to E, gradually decreasing toward the foreland). Large seismic events are believed to be associated to younger normal faults connected to the extensional front and, in the eastern sector, to fluids reaching an over-pressure condition at shallow depths due to the low permeability of the crust that inhibits their circulation [34].
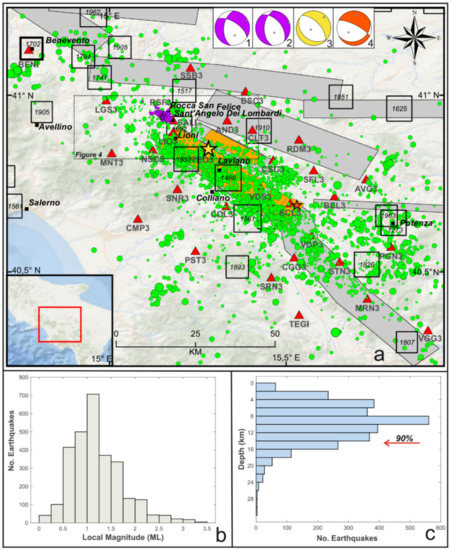
Figure 1.
(a) Epicentral map of the earthquakes (green circles) recorded by Irpinia Seismic Network (ISNet, red triangles) from 2008 to 2020 (http://isnet-bulletin.fisica.unina.it/cgi-bin/isnet-events/isnet.cgi). The analyzed seismic sequence is highlighted with violet circles. The yellow and orange stars refer to the epicentral location of the 1980, M 6.9, and of the 1996, M 4.9 earthquakes. Historical seismicity is shown with black squares (I0 ≥ 6–7 MCS). Seismogenic sources related to the Irpinia fault system are indicated by orange rectangles; potential sources for earthquakes larger than M 5.5 in surrounding areas are indicated in grey (Database of Individual Seismogenic Sources, DISS, Version 3.2.1). Focal mechanism solutions for four instrumental earthquakes are reported (1) Ml 3.0, 3 July 2020, 16:14, Rocca San Felice sequence, from this study; (2) Ml 3.0, 3 July 2020, 16:19, Rocca San Felice sequence, from this study; (3) 1980, M 6.9, Irpinia earthquake [40]; (4) 1996, M 4.9 earthquake [57]. The area plotted in Figure 4 is identified by a dashed rectangle. (b) Histograms of magnitude and (c) depth for the microseismicity inside ISNet. The red arrow points to the depth above which 90% of earthquakes occur.
2.3. 1980 Irpinia Earthquake
The 1980, M 6.9, Irpinia earthquake was the most destructive, instrumental earthquake of the Southern Apennines that occurred along NW-SE trending normal faults. This event is characterized by a complex rupture process involving multiple fault segments according to (at least) three different nucleation episodes delayed each other of 20 s. Several models, characterized by different geometries and locations of activated fault segments, have been proposed to explain its complex rupture [39,40,41,42]. Retrieved seismic moment ranges between 2.4 × 1019 Nm and 3.0 × 1019 Nm, the fault dip activated by the mainshock ranges between 53° and 63° while the strike ranges between 305° and 33° [43]. Location of the event epicenter and surface projection of the three main fault segments are shown in Figure 1.
Kinematic models [41] have proposed the nucleation of the mainshock (0 s) along 30-km-long, NE-dipping, Mount Marzano and Picentini fault segments, with the first subevent activated at 18 s toward a SW, low angle, NE-dipping fault of 20 km length and a second subevent nucleated at 39 s in the Ofanto basin area, along a SW-dipping, antithetic fault. The mainshock initially ruptured at the north tip of the Mount Marzano segment and propagated bilaterally along two NW-SE striking faults. Toward south, it completed the rupture of the Marzano segment and toward north it progressed along the Mount Picentini segment.
The 1980 Irpinia faulting model has been also constrained on the evidence of coseismic surface ruptures [42], and shows that the event activated three main fault segments, along a 38-km-long, NE-dipping scarp with an average N128° direction and one main antithetic blind fault, SW-dipping, that was not capable to reach the surface due to its smaller size, leaving a ground deformation anomaly at NE of mainshock, near the Ofanto river. The NE-dipping fault rupture corresponds to three main strands separated by gaps and anomalies in the continuity of surface faulting identified as: (1) the Cervialto scarp (Mount Picentini, strike of 125°); (2) the Mount Marzano-Valva scarp (strike of 135°) connected southward with the Mount Carpineta scarp (strike ranging between 110° and 135°), and (3) the San Gregorio Magno scarp and related scarplets in and close to the Pantano basin (strike of 120–130°). The Mount Cervialto and Mount Marzano–Mount Carpineta segments have been correlated to the 0 s event (mainshock), the Pantano of San Gregorio Magno segment has been correlated to the 20 s subevent; and the antithetic Ofanto fault segment has been associated with the 40 s subevent. The three segments are represented on the geological map of Figure 2.
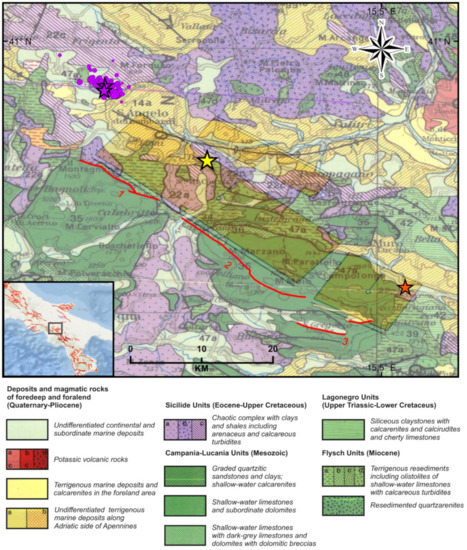
Figure 2.
Geological and structural map of the Irpinia region. Here, surface traces (red lines) and sources (orange boxes, Database of Individual Seismogenic Sources, DISS, Version 3.2.1) of faults activated during the 23 November 1980, M 6.9, Irpinia earthquake (yellow star) are shown. Key: 1 = Cervialto fault segment; 2 = Marzano-Carpineta fault segment; 3 = San Gregorio fault segment. The seismic sequence is highlighted with violet circles and stars; the orange star refers to the epicentral location of the 3 April 1996, Ml 4.9 earthquake.
Finally, relocated aftershocks and 3D velocity models have provided new constraints about the 1980 Irpinia source model [44,45]: (1) the main rupture started at 10 km depth, on a 60° dipping plane, in a high velocity region, associated with stiff Apulian carbonates and propagated upward along the softer Meso-Cenozoic succession; (2) most of the aftershocks are spread in a volume delimited by the NE-dipping, Marzano-Cervialto normal fault segment and the SW-dipping, antithetic normal fault, associated to the 40 s event; (3) seismicity depth is confined in the first 12 km of the upper crust and mainly concentrated beneath the Marzano-Valva fault segment; (4) largest magnitude aftershocks clustered between the fault segments activated at 0 s and 20 s, near their tips; (5) the Marzano segment is bounded by two clusters of seismicity likely separated by a lithological discontinuity, acting as a seismic barrier, where the stress of the main ruptures was concentrated (the northern Sele Valley and the southern tip of the Carpineta fault segment). In particular, the Marzano-Cervialto normal fault segments have been interpreted as two asperities separated by a low-strength zone, referred to as the Sele barrier [41,42]. New tomographic studies [34] confirm that the mainshock nucleated in basement, below the Apulian carbonates, and propagated in the high Vp/high-Vp/Vs region associated with fractured, water-saturated carbonates of the Apulian platform domain, in agreement with well-data (S. Gregorio Magno 1, [25]) and magnetotelluric surveys [46].
2.4. Recent Seismicity of the Irpinia Region
After the 1980 event, no large earthquakes have struck the area. In 1996, a seismic sequence with a mainshock of M 4.9 took place inside the epicentral area of the 1980 earthquake. Present-day low-magnitude seismicity (Ml <3.5) occurs mainly in the first 15 km of the crust showing fault plane solutions with normal and normal-strike slip kinematics, indicating a dominant SW–NE extensional regime in agreement with the inversion of fault-slip data of the Irpinia region [32,47,48,49]. The background low magnitude seismicity appears to be spread into a large volume, and the related stress field is closely linked with the major fault segments activated during the 1980 Irpinia earthquake. In addition, microseismicity seems to be controlled by high pore pressure of water-saturated Apulian carbonates within a fault-bounded crustal volume [15,50]. Location of microseismicity epicentres is shown in Figure 1.
Several studies pointed out a strong relationship between seismicity and high-fluid pressure evidenced by the same location of crustal seismicity and CO2 degassing areas along the Apennines [38,51]. In the Irpinia area, underneath Mount Forcuso, tomographic images reveal a low-Vp/Vs dome-shaped body, 20 km long and 15 km wide, located between 6 km and 11 km depth [34]. This spot is interpreted as a pressurized CO2-rich rock volume, filled below the Apulian platform carbonates by fluid-rich mantle melts intruded into the crust. This anomaly correlates with high heat flow values (100–215 mW/m2) observed along the Mount Forcuso antiform and with geochemical data. This area is characterized by a huge amount of nonvolcanic CO2-rich gas emission [52,53], the main expression of which occurs in the Mefite d’Ansanto degassing site, where deep, mantle-related fluids are released through the active faults, as indicated by geochemical data.
Deep CO2-rich fluids may play a key role in the seismogenesis in the Southern Apennines [15,34,38]. Fluids migrating upward along lithospheric faults can be stored in reservoirs under the Apulian carbonates, sealed by Triassic anhydrites, reaching overpressure conditions that can periodically trigger large normal faulting earthquakes. The influence of high-pressure CO2 in the nucleation of large earthquakes has been also observed in the Central Apennine sector, for the 1997 Colfiorito and the 2009 L’Aquila events [54,55]. The same mechanism has been invoked for the nucleation of the 1980 Irpinia earthquake, being the initiation patch located in the basement, under the Apulian carbonate, at the top of a pressurized CO2 reservoir (low-Vp/Vs anomaly, [34]).
3. Data
The data used for the sequence analysis have been provided by ISNet. The available stations are shown in Figure 1, together with the epicenters of the seismicity covering the period 2008–2020. We used automatic event detections performed by the software Earthworm [56] to identify the seismic sequence. Specifically, when more than three events occur within 10 km and a couple of hours in time, an indicator light is turned on at the network control center and few days of continuous data before and after the declaration of the sequence are extracted for automatic and visual inspection, followed by machine and human controlled procedures to eventually extract additional events. For this sequence, the automatic system identified 43 events, starting from a Ml 1.9 event, declared on 3 July 2020, at 09:31 and ending with a Ml 1.2 event, that occurred on 6 July 2020, at 16:55. The two largest events in the sequence (Ml 3.0) occurred on 3 July 2020, at 16:14 and 16:19. All these events have been manually inspected, providing revised phase pickings (372 P arrival times and 208 S arrival times), locations, and local magnitude estimations.
During the manual revision of data, the near real-time software INERTIA [22] also provided moment magnitude estimations and ground motion maps. This information is made promptly available at the ISNet bulletin webpage (http://isnet.unina.it/). Continuous waveforms, event data and related information (picking, location, magnitude) were also used as starting point for further analysis as detailed in the rest of this paper. In Figure 3, we show an example of waveforms for a Ml 2.8 event of the sequence, that occurred on 5 July 2020, at 15:18. In the section, stations are ordered for increasing distance from the event epicenter. We can recognize the complexity of the waveforms as the distance increases and the diverse duration and frequency content at some stations, owing to site effects and instrumental filters.
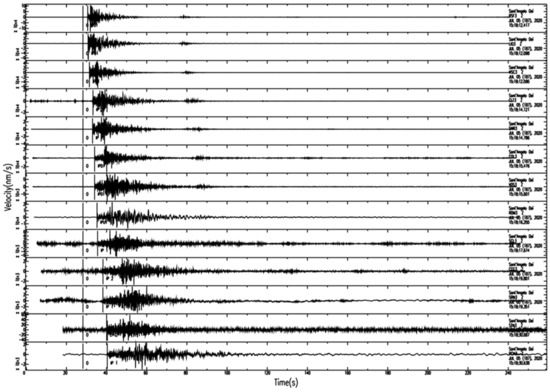
Figure 3.
Example of seismic data, represented for the Ml 2.8 event that occurred on 5 July 2020, at 15:18. In the section, stations are ordered from the top to the bottom for increasing epicentral distance. In the coda of the main event, we can recognize smaller magnitude aftershocks.
4. Refined Seismic Catalog
We scanned the continuous helicorder for 4 days starting from 3 July to improve the detection of microearthquakes during the sequence. We used the autocorrelation algorithm FAST (Fingerprint and Similarity Thresholding) [20,58] with the twofold aim of including in the catalog events featuring low signal-to-noise ratio and diminishing the magnitude of completeness for the sequence.
FAST is based on a locality-sensitive hashing algorithm [59] and performs a computationally efficient similarity search, scanning the signal spectrograms, computed in broad frequency bands, with the aim of detecting similar earthquake waveforms. In contrast with template matching, FAST does not require any template for the detection. This feature enables the technique for the detection of microevents during short and spatially constrained sequences.
Since our goal is the search for very-low magnitude events, we applied the technique to the velocimetric records at the five stations closest to the sequence centroid (RSF3, LIO3, NSC3, AND3, MNT3, Figure 4a), limiting our analysis to the vertical component. The distance of the stations from the centroid ranges from 3 to 17 km. We computed the spectrograms, filtering the records between 1 and 20 Hz and separating the continuous waveforms in moving windows having 6.0 s length with a 0.2 s lag. The squared modulus of the Fourier transform of each time window represents a column in the spectrogram, from which we extracted overlapping fingerprints having 32 samples with a lag of 5 samples. To declare a sequence of consecutive and correlated fingerprints as a candidate event, we fixed uncorrelated permitted gaps at a single station to 3 s, this time being roughly related to the maximum difference between S and P arrival times. Detection was declared if uncorrelated gaps at couples of stations had length below 3 s, mimicking maximum P wave arrival time differences across the selected stations. A sensitivity test was performed to determine the best set of the other parameters (number of hash tables, number of hash functions, number of votes, minimum detection threshold; see [58]) minimizing the false negative events. An event was finally declared when detected at least at 2 stations.
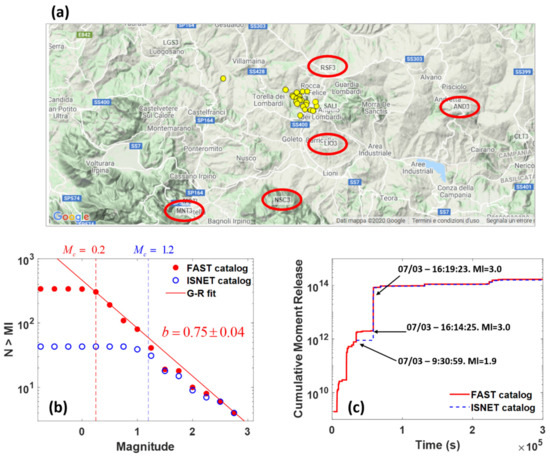
Figure 4.
(a) Selected stations for the FAST (Fingerprint And Similarity Thresholding) analysis: the dots represent the events automatically detected by ISNet. (b) Gutenberg–Richter (GR) analysis for the automatic (blue circles) and FAST (red filled dots) catalogs. For this latter case, the GR is also reported with the b-value estimation. The dashed lines mark the magnitude of completeness for the two catalogs. (c) Cumulative moment release according to the two catalogs. The black arrows indicate the first event automatically detected by ISNet (Ml 1.9) and the two main events of the sequence (Ml 3.0).
Scanning the continuous waveforms with FAST, we retrieved 342 events; the new catalog also includes all the 43 events automatically detected by the ISNet procedures. From a visual inspection of the traces, we retrieved only one false positive detection due to a teleseismic event.
For the computation of the magnitude, we imposed that all the events are co-located with the sequence centroid (40.94° N–15.15° E); the local magnitude was then estimated through the ratio of the maximum amplitudes with the events detected and located by the ISNet procedures.
We investigated the magnitude-frequency distribution for the refined catalog, comparing it with the ISNet automatic catalog (Figure 4b). We estimated a magnitude of completeness of Ml 0.2, nearly one unit smaller than that retrieved for the whole seismic network (Ml 1.1, [60]).
We also reported the b-value estimate from the refined catalog as b = 0.75 ± 0.04. When performing this computation on the automatic detections, we retrieved b = 0.70 ± 0.11, which is compatible with the FAST estimate, but shows larger uncertainty. Nevertheless, it is worth to note that some events having magnitude larger than 1.2 have been missed by the automatic procedures, since some of these events fall in the coda of the previous ones. The cumulative seismic moment release (Figure 4c) is not significantly different for the two catalogs yielding an equivalent total magnitude of 3.5. However, we can recognize a foreshock sequence of 23 events preceding the two largest magnitude events in the sequence, that started about 9 h before the first automatic detection (Ml 1.9, 3 July 2020, 09:31).
5. Accurate Earthquake Location
The absolute locations of the sequence events have been obtained using the NLLoc software [1]—http://www.alomax.net/nlloc—that implements a non-linear, global-search probabilistic location in 3D velocity models.
For double-difference (DD) locations, we applied NLDiffLoc [48], a location tool included in the NLLoc software, that allows to perform DD locations by inverting the differential times through a probabilistic, non-linear approach. We also used the tool Loc2ddct, which allows to calculate differential times; initial absolute location of events and corresponding differential travel-times were used as inputs for DD locations. The DD algorithm performs an optimized exploration of the model parameters space using the annealing Metropolis algorithm [1] seeking a solution that maximizes the likelihood function. The latter is based on the misfit between measured and calculated differential phase arrival times. During the exploration, the algorithm computes the posterior probability density function (PDF), which represents the complete solution of the earthquake location problem. The significance and uncertainty of the solution, i.e., the maximum likelihood point, cannot be assessed independently of the complete PDF. Indeed, Gaussian or normal estimators, such as the expectation value and covariance matrix, can be obtained from samples of this function. These estimators can describe location uncertainty in the case of a (non-) linear PDF with a single maximum and an ellipsoidal form [1]. In addition, the software can handle 3D velocity models, with arbitrary complexity and parameterization, required in the case of crustal volumes with strong lateral variations and irregular topography [61].
We analyzed 903 traces at 21 stations from the 43 best recorded events. Within the manual picking, a weight factor inversely proportional to the uncertainty on arrival time picking has been assigned. In this way, we obtained an average of 14 P and S arrival times for each event, ranging from a minimum of 5 phases to a maximum of 31 phases. We processed the first arrival times with NLLoc using the 3D P- and S-wave velocity models optimized for the Irpinia area through an iterative, linearized, tomographic approach in which the P and S arrival times are jointly inverted for earthquake location and velocity determination [62].
For the DD locations, we performed a selection on the events based on the absolute location quality (i.e., at least 8 phases and an azimuthal gap <230°), keeping only 36 events for the analysis. The absolute arrival times of the selected events are combined to obtain about 4000 P and S differential times used as inputs for the DD location. Since the sequence is clustered, we did not impose a maximum distance between event couples.
The absolute locations show events distributed along the NW-SE direction, with an extension of the pattern of about 4–5 km. The depth of the events ranges from 5 to 15 km. The horizontal and depth errors are within 750 m for most of the events. The rms of the resulting absolute locations is within 0.2 s for almost all the events.
From the absolute location, we achieved the final DD locations (Figure 5). After relative location, the events appear more clustered with an extension of the pattern covering a size of 2–3 km and a clear alignment in the NW-SE direction (Figure 5a). The event depth ranges between 7.5 and 12.5 km (Figure 5b). In a section view, these events are distributed according to a direction inclined of about 45–55° with respect to the horizontal plane, with a NE immersion (Figure 5c,d). Horizontal and vertical location errors are within one hundred meters (Figure 5e–g) and the rms is within 0.06 s for most of the events. Since the location errors are estimated analyzing the likelihood function in the vicinity of the best solution, the resulting errors could be underestimated in the case of multiple maxima in the PDF. However, in our case, a DD location rms of 0.06 s indicates that the hypocenters are located within a sphere of about 300 m radius, if considering a P-wave velocity of 5.5 km/s at 8–10 km of depth [62]. Since the rms also accounts for the uncertainty on the origin time, the effective uncertainty on spatial coordinates could be smaller, coherently with estimates from the posterior PDF.
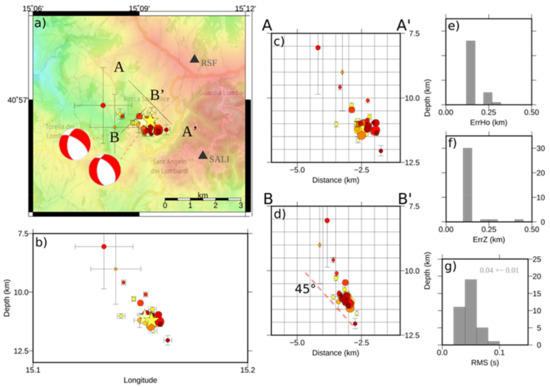
Figure 5.
Double-difference (DD) locations. (a) DD location of 36 events of the sequence located with NLDiffLoc in a 3D velocity model. The color of the event hypocenters is associated with time of occurrence (from yellow to red) and the size to their magnitude. The stars represent the two Ml 3.0 events. For these events, we also reported the focal mechanism. (b) East–west vertical section of the events. (c,d) Cross-section projection of events along the profiles AA′ and BB′, respectively, indicated in the map of panel (a). (e) Histogram of horizontal location errors. (f) Histogram of vertical location errors. (g) Histogram of DD location rms. We reported the mean and the standard deviation of the rms distribution.
6. Source Parameters
We chose the Brune source model [63] to infer source parameters (seismic moment, earthquake size, stress drop, and radiated energy released during the seismic event), which corresponds to an instantaneous pulse applied to the fault. We applied the SPAR (Source PARameters estimator) technique [64], which inverts the observed displacement spectra relying on a probabilistic framework based on the conjunction of states of information between data and model spaces. The inversion strategy allows to jointly retrieve source parameters along with their uncertainties and to investigate the between-parameter correlations. In this approach, theoretical Green’s functions are evaluated in a simplified model accounting for both geometrical spreading and anelastic attenuation. We assumed a constant, frequency independent quality factor, which corresponds to the median value Q = 226 retrieved for the area [65]. For the Irpinia region, it has been demonstrated that a frequency independent quality factor is a model preferable to a frequency dependent quality factor following a power law [65]. Beyond the uncertainty estimation, the shape of the posterior PDF is also used to evaluate the quality of the retrieved estimations and eventually to discard unconstrained solutions. This technique has been efficiently tested and validated on the main events (M > 4.0) of the 2016–2017 central Italy sequence [64].
In Figure 6a, the displacement amplitude spectra have been plotted for the Ml 3.0 event occurred on 3 July 2020, at 16:14. The several curves refer to the diverse stations at which the parameters are constrained during the inversion. For this event, we estimated an average moment magnitude of Mw = 2.91 ± 0.02, a corner frequency of fc = 5.0 ± 0.2 Hz, and a spectral fall-off γ = 2.42 ± 0.04. Source parameters have been estimated for 36 events in the sequence, the same events for which we got accurate double-difference locations. In Figure 6b, we represent the retrieved corner frequencies as a function of the moment magnitude (red points). Despite the large scattering in the data, we recognize that larger magnitude events (Mw > 2.0) show larger stress drops (between 1 and 10 MPa). At smaller moment magnitudes (1.0 < Mw < 2.0), the stress drop is on average smaller, with most of the events having a stress drop between 0.1 and 1 MPa. However, about one-third of the events in this magnitude range shows a stress drop larger than 1 MPa, excluding a saturation of the corner frequency at small magnitude. In Figure 6b, we also represent the corner frequencies as a function of the moment magnitude retrieved for ~720 events occurred in the Irpinia, with magnitude between 1.0 and 3.5 (black points) [65]. We found that our results are very consistent with the findings of [65]. Assuming self-similarity, we retrieved an average stress drop of 0.64 MPa. It is worth to note that estimations of corner frequency for the smallest magnitude events (M < 1.5) may be biased due to limited bandwidth when inverting the spectra. For events with Ml > 1.5, we also retrieve consistent estimates of the moment magnitude as compared to the local magnitude.
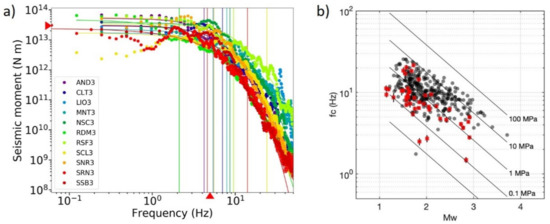
Figure 6.
(a) Displacement spectra for the main event (Ml 3.0, 3 July 2020, 16:14) of the sequence; for this event, we estimated an average moment magnitude of Mw = 2.91 ± 0.02, a corner frequency of fc = 5.0 ± 0.2 Hz, and a spectral fall-off of γ = 2.42 ± 0.04. The intra-event variability on the seismic moment and corner frequency ranges over one order of magnitude. The red arrows point to the mean values of the parameters. (b) Plot of the corner frequency as a function of the moment magnitude (this study—red points; seismicity of the Irpinia region from [65]—black points). Straight lines individuate the curves along which the stress drop is constant.
From the computation of the corner frequencies, we also retrieved the source radius for each of the analyzed events. In Figure 7a, we show the source radius as a function of the moment magnitude: we found that the radius ranges in the interval 150–400 m for the largest magnitude events in the sequence and between 30 and 60 m for an Mw 1.5 event. Looking at the double difference locations, we see that the spatial extension of the events in the sequence is of the same order of magnitude (hundreds of meters) as the size of the largest magnitude events, indicating that the regions fractured by the different events are contiguous and stress transfer is likely to be the main mechanism for event production.
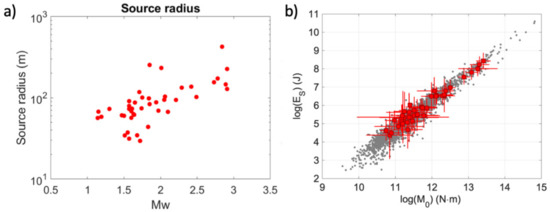
Figure 7.
(a) Source radius as a function of the moment magnitude for the events in the sequence. The source radius ranges from about 50 m for a Mw 1.5 event to about 250 m for a Mw 3.0 event. (b) Scaling of the radiated energy as a function of the seismic moment. The red points correspond to events of this sequence, the gray points represent background events recorded by ISNet.
We finally estimated the radiated seismic energy, relying on a time domain estimator [21], which is grounded on the computation of the squared velocity in the time domain integrated over the S-wave time window [66], after its correction for attenuation along the path. The attenuation model has been determined considering ~2300 local earthquakes recorded by INFO over the last ten years [21].
The velocity integral is computed considering band-pass filtered signals between 0.5 and 40 Hz, and a time window starting 0.1 s before the S-wave onset and ending at different percentages of the cumulated energy as a function of the source to site distance R: (i) 90% when R < 25 km; (ii) 80% when 25 km < R < 50 km; (iii) 70% when R > 50 km. In addition, we imposed a minimum time window length of 5 s and a maximum time window length of 20 s. The radiated energy is finally obtained by averaging the estimates over several recording stations (minimum of 3 stations; the sum of signal to noise ratio for the three components ≥200). In Figure 7b, we represent the radiated energy as a function of the seismic moment. The energy-to-moment scaling observed for the sequence (red squares) is in good agreement with values estimated for the Irpinia seismicity (gray points). The radiated energy trend with seismic moment is also consistent with an average stress drop in the sequence smaller than the value assumed by Kanamori as global average (from 2 to 6 MPa) while the steeper slope suggests a possible deviation from self-similar behavior.
7. Focal Mechanism Solutions
We computed 21 fault plane solutions from the inversion of P-wave polarities for earthquakes with local magnitude ranging between 1.2 and 3.0. Focal mechanism solutions are calculated from the inversion of P-wave polarities using FPFIT code [67] for all the events showing at least 5 P-wave polarities. The two main Ml 3.0 events show a similar normal-fault kinematics with a minor strike-slip component. The nodal planes have NW-SE trending and a dip of about 50–60°. The remaining solutions show a common normal faulting style with a minor and variable strike-slip component.
We classified the fault plane solutions according to the plunge of P- and T-axes to derive the tectonic regime in which the seismic sequence originated. As shown in Figure 8, most of the solutions (~66%) belong to a pure normal fault regime while few solutions (~34%) belong to a normal strike-slip regime. In agreement with this classification, P-plunges range between 45° and 85° and T-plunges range between 0° and 85°. Moreover, T-axis orientations show an azimuth ranging between 25° and 97°, in accordance with the regional stress tensor calculated for the Irpinia region [47].
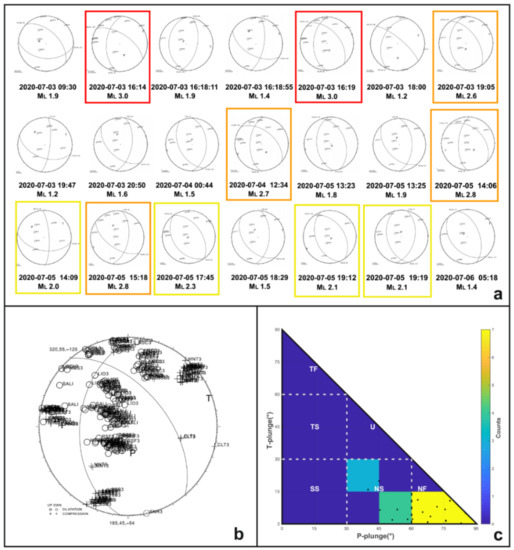
Figure 8.
(a) Fault plane solutions computed for 21 earthquakes of the sequence. Earthquakes with Ml 3.0, 2.5 ≤ Ml < 3.0, and 2.0 ≤ Ml < 2.5 are highlighted in red, orange, and yellow, respectively. (b) Composite focal mechanism solution obtained from the inversion of P-wave polarities for the two main events. (c) Fault plane solution classification according to the plunge of P- and T-axes with specific tectonic regimes (Legend: NF, normal fault; NS, normal-oblique; SS, strike-slip; TF, thrust fault; TS, thrust oblique; U, unknown). The number of earthquakes (color bar) is counted in bins of 15° × 15°.
We calculated the composite focal mechanism using the data of the two main earthquakes (Ml 3.0), as shown in Figure 8. The normal fault kinematics of the solution with NE-SW trending nodal planes (320, 55, −120; 185, 45, −54) is compatible with the fault plane solutions calculated for single earthquakes and well fits all the available polarity data. Despite the uncertainty of the solutions due to the small number of available data and the small size of the events, a good agreement across the solutions is reached. A large group of seismic stations show the same type of P-wave polarity highlighting a similar rupture kinematics and fault plane geometry during the evolution of the seismic sequence. In the lower panel of Figure 8, all the available polarities data are plotted on the composite focal mechanism solution obtained from the inversion of P-wave polarities for the two Ml 3.0 earthquakes of the sequence. Polarities from six stations (LIO3, MNT3, RDM3, SALI, SSB3, VDS3) are the same during the whole sequence, and 4 stations (AND3, CLT3, COL3, RSF3) show a dominant polarity. Only two stations (NSC3 and SNR3) display a large variability, not always consistent with composite fault plane solutions. The results are summarized in Table 1. Discrepancies and variability can be explained with the station location on the focal sphere, close to nodal planes: if uncertainties associated with location and focal mechanism are considered, a little rotation of the rupture plane can justify the polarity variation.

Table 1.
235 P-wave polarity data available for the whole seismic sequence. Data are organized by seismic stations.
Focal mechanism solutions of the main earthquakes show the activation of a NW-SE striking fault structure with 50–60° dip, in agreement with seismogenic sources of the Irpinia region. Despite the low magnitude of the analyzed earthquakes, fault plane solutions reveal a normal fault tectonic regime, consistent with the regional stress field. Considering the spatial distribution of the hypocenters, the NE-dipping nodal plane can be assumed as the preferential one along which the seismic sequence originated, showing the same orientation of the adjacent seismogenic fault segment activated during the 1980 Irpinia earthquake.
8. Ground Motion
The ground motion characteristics were investigated through the main properties of peak values both in terms of acceleration and velocity. A first rough estimation of the frequency content associated with ground motion records can be obtained evaluating the ratio of peak ground acceleration (PGA) to peak ground velocity (PGV) [68,69]. We reported an average ratio value of 4.1 ± 1.6 g/ms−1 which allows to classify the records in the class of high acceleration—low velocity. Such a high ratio suggests that the records are mainly characterized by a short duration, high predominant frequencies, and narrow-band spectra [70].
We also compared the peak values to the ground motion prediction equation (GMPE) inferred for the Irpinia region [71]. The comparison for the Ml 3.0 event of the sequence (3 July 2020, 16:19) is shown in Figure 9a. We observed a good agreement between predictions and observations; these latter are almost all included within one standard deviation in the predictions of the GMPEs.
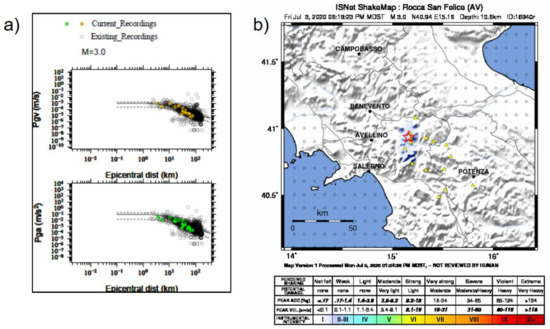
Figure 9.
(a) Comparison between observed peak ground values and the GMPEs (Ground Motion Prediction Equations) [71] for the Ml 3.0, 3 July 2020, 16:19 earthquake. Lines identify the mean GMPE, and the mean plus/minus one standard deviation. Open circles represent peak observations. (b) Shakemap® computed for instrumental intensity, for the same event. The red star corresponds to the event epicenter.
We also present, in Figure 9b, the Shakemap® [72] for the same event, in terms of instrumental intensity, automatically generated at ISNet. The intensity distribution is slightly elongated toward the south direction, with respect to the earthquake epicenter. The maximum instrumental intensity has been estimated to be III, which is consistent with reports provided by the INGV.
9. Early Warning Analysis
During the sequence, two earthquake early warning (EEW) systems, PRESTo and SAVE, were operating at INFO. PRESTo [23] is an open-source software platform for regional (network-based) EEW which integrates algorithms for real-time data collection, event detection, rapid earthquake location, magnitude estimation, and real-time ground motion prediction in the area of interest.
For the current setting at the INFO, the alert in PRESTo is released if at least five stations have detected the event, independently of the estimated event magnitude or shaking intensity in the area.
SAVE is an on-site, P-wave-based EEW approach [73] which has been conceived to operate either with a single station (i.e., a single sensor located at the target site) or with a set of co-located seismic nodes within a small area around the target to protect. SAVE processes the vertical component of both accelerometers and (broadband) velocimeters, and predicts the expected ground shaking at the recording site issuing a local alert level, together with a qualitative assessment of the earthquake magnitude and source-to-site distance, based on measurements on the early portion of the P-wave.
Unfortunately, during the early days of the sequence, some stations of the network suffered from a temporary failure of the communication system. This resulted in tremendous delays of data transmission and in the partial loss of a few recorded data, which prevented EEW systems from correct operation. For this reason, we could not evaluate the performance of the systems for the whole sequence, but each system automatically detected a smaller number of events, depending on the availability of real-time recorded data.
PRESTo detected a total of 21 events of the sequence, but only 10 of these events (with local magnitude between 1.4 and 2.8) did not suffer for real-time data communication problems and had real-time EEW estimates. The list of the detected events is available in Table 2. For each detected event, the table shows the comparison between the local (Ml) magnitude (as computed by INFO) and the estimated magnitude by PRESTo at the first alert. The difference between the first PRESTo estimate and the local magnitude is also reported in the table (ΔM). From the analysis of the PRESTo outputs, we found that the first magnitude estimate is available on average 3.9 s after the first P wave detection at the network and at the same time, the average difference between the estimated magnitude and the bulletin one is 0.1 unit.

Table 2.
List of events detected by PRESTo. The event is identified by its ID, as shown in the ISNet bulletin (http://isnet-bulletin.fisica.unina.it/cgi-bin/isnet-events/isnet.cgi), the local magnitude, the first estimate from PRESTo and the difference between the two magnitudes.
Figure 10a shows the results of PRESTo during the Ml 2.7, event, that occurred on 4 July 2020 at 12:34, while Figure 10b shows the evolution of real-time estimates of magnitude, location, and number of data providing information to the system. As it can be seen from the plot, the first estimates of location and magnitude are available at about 5 s from the origin time, using 5 stations. After 2 s, the estimates of location (epicenter and depth) and magnitude converge and stabilize to the real values. We computed the available lead-time at the main cities of the Campania region, as the difference between the theoretical arrival time of the S-wave and the time of the first alert release. The lead-times are reported in Table 3. The lead-time ranges from 5.8 s at the city of Avellino (~25 km from the event epicenter) to 17.5 s at Naples (~70 km away from the epicenter).
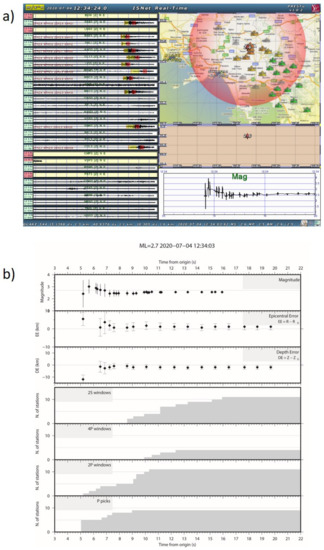
Figure 10.
Performance of PRESTo during the Ml 2.7 event that occurred on 4 July 2020 at 12:34. (a) Screenshot of PRESTo during the event. (b) Real-time estimates of magnitude and location, and the number of available data as a function of time. From top to bottom, the figure shows: magnitude, epicentral error, depth error, number of stations with available 2 s of S wave (2S), 4 s of P wave (4P), 2 s of P wave (2P), and number of available P-wave picks.

Table 3.
Theoretical lead-time. The table shows the epicentral distance and the theoretical lead-time for the main cities of the Campania region.
Finally, for this event, we theoretically estimated the radius of the blind zone (i.e., the area where the S-wave arrives before the alert release) which turned out to be around 15 km from the epicenter.
As for SAVE, at the time of the sequence, the system was running at 3 stations of the network: RSF3, COL3, and AVG3. The station RSF3, which is the closest to the sequence, detected 24 events, COL3 detected 11 events, while no events were detected at the farthest station AVG3.
Figure 11a shows a screenshot of the same Ml 2.7 event analyzed by PRESTo at RSF3. For this event, using 3 s of P-wave, the on-site EEW system estimated a local intensity of III, and no warning was declared at that station. For all the detected events, the magnitude and distance estimates were not available, due to the low signal-to-noise ratio that prevented from the use of the average period of the P-wave as a proxy for the earthquake magnitude. Instead, for all the events, SAVE predicted the expected ground motion intensity at each site. Figure 11b,c shows the cumulative performance in terms of lead-time and predicted vs. observed intensity for RFS3 (Panel b) and COL3 (Panel c).
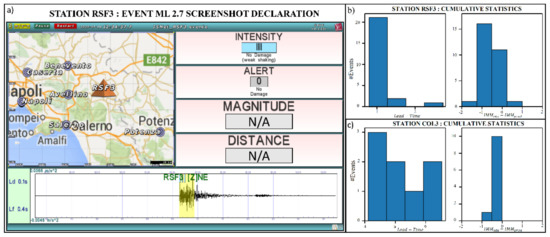
Figure 11.
Performance of SAVE. (a) Screenshot of SAVE during the Ml 2.7 event that occurred on 4 July 2020, at 12:34, recorded at RSF3. (b) Performance of SAVE at RSF3 and (c) COL3. Performances are shown in terms of lead-time (left side) and difference between predicted and observed intensities.
Intensity estimates differ from the real ones of 0 or 1 unit. For the detected events, the available lead-time at the considered stations ranges between 1 to 6 s.
Finally, at the time of the sequence, the ISNet EWapp [74] was under testing by a limited number of users. The smartphones were distributed over the area, but the number was too small to perform a reliable statistical analysis. However, we can report here that the ISNet EWapp received the alerts provided by PRESTo and correctly predicted the expected intensity at each site. For all the events, the predicted intensity never exceeded the threshold of intensity IV at the location of the smartphones.
10. Discussion and Conclusions
In this study, we have analyzed a seismic sequence, detecting more than 340 events with magnitude in the range −0.5 < Ml < 3. The sequence occurred at the northern tip of the main segment of the 1980, M 6.9, Irpinia earthquake, at the boundary of the Monte Cervialto portion of the fault. Double difference locations and focal mechanisms agree in recognizing that the sequence ruptured an asperity along NE-dipping plane, with a dip angle ranging between 50° and 60°. Despite large uncertainties in the smallest magnitude event locations, the hypocenter distribution delineates a structure dipping at 50–55° at depths of 10 to 12 km and becoming steeper at shallower depths (between 7.5 and 9 km), with a dip angle of 60–65°, eventually being a portion of a listric fault. Strike and dip directions are consistent with the ones of the first fault segment that ruptured during the 1980 earthquake [42], indicating that this asperity is just ahead of the northern endpoint of the 1980 event, on the continuation of that segment. Most of the events within the sequence occurred at depths between 10.5 and 11.5 km, indicating that most of the slip was released at a depth comparable with that of the 1980 hypocenter [40]; according to tomographic models of the area [15,34], most of the events either developed in the basement or at its top with few events rupturing the upper Apulian carbonates. This is a common feature of the sequences that occurred in this region [4].
The size of the asperity, inferred from earthquake location is of the order of 800–900 m, corresponding to an approximate source radius of 400–450 m (Figure 5). On the other hand, the cumulative seismic moment results in an equivalent seismic event with moment magnitude of 3.5. If we estimate the source radius for this latter event, using the average stress drop retrieved from the analysis of source parameters, we get a value fully consistent with the extension inferred from earthquake location. When representing on the fault plane the seismic events within their own size, most of the events look contiguous, indicating that the sequence ruptured a single patch along the fault plane. Looking at the inter-event distance (median value of 370 m and standard deviation of 340 m), as compared to the size of main events, we argue that the dominant triggering mechanism within the sequence is the dynamic and static stress transfer, that allows the nucleation of individual events in the sequence.
From the stress drop analysis, we also recognize a strong heterogeneity in the stress release. Despite the large uncertainty in the evaluation of the stress drop, we reported a dual behavior for the earthquakes in the sequence: largest magnitude events featured a stress drop of 1–10 MPa, while stress drop of most of the small magnitude events ranges in the interval 0.1–1 MPa. Those values are fully consistent with the estimates retrieved for the seismicity of the whole region [65]. The largest stress drop values in the sequence are comparable with the stress drop estimated for the 1980 earthquake [75], while smaller values of stress drop in the area are ascribed to high pore-pressure that locally decreases the normal stress [65]. This variability has been observed also in the computation of the apparent stress over a much larger time interval and at the scale of the whole network [21].
It is worth to note that the retrieved stress drop is based on the estimation of the corner frequency and seismic moment from the inversion of the observed displacement spectra, fixing the path correction due to anelastic attenuation to the value found in [65]. To check the robustness of the stress drop estimates, we performed synthetic tests changing the value of the quality factor. Specifically, we have investigated the hypothesis that small events have the same stress drop as the largest magnitude events in the sequence, but their stress drop appears smaller because of an incorrect correction for path effects. Retrieving a stress drop one order of magnitude smaller than the input value at a source-receiver travel time of 5 s, requires an average quality factor as low as 130. This average value is very unlikely in the quality factor distribution represented in [65], when five or more estimates of the source parameters are available. Alternatively, an apparent stress drop at small magnitudes could be due to a complex, frequency dependent quality factor. This hypothesis cannot be rejected a-priori and requires further modeling and testing with respect to the analysis performed in [65], which is beyond the scope of this study.
The sequence started with a series of cracklings with M < 1 events and small stress drops, possibly indicating a fluid induced sequence initiation promoted by low normal stress and local fault lubrication. After the occurrence of many of those small magnitude events, the stress accumulated in the main asperity has reached the yield strength, releasing a large amount of stress in the two mainshocks of the sequence. In the later stage of the sequence, we reported again small stress drop events, some of which also occurred at few kilometers away from the sequence centroid, in the Apulian carbonates layer; these events could be related to local fluid diffusion, activating small pre-existent fractures prone to rupture.
Since the sequence occurred close to the main segment that ruptured during the 1980 earthquake, we may question why this sequence did not nucleate a large earthquake similar to the 0 s event of the Irpinia earthquake. This may be related to the fact that the sequence does not occur on the prolongation of the Monte Cervialto segment, but on a subparallel fault, or the Monte Cervialto fault has a stepover, with a geometrical discontinuity that prevented the jump on the main segment activated during the 1980 earthquake. Additionally, it is possible that the endpoint of the Monte Cervialto fault is a mechanical barrier, with large yield strength not overcome after stress release during the sequence. Investigating the geometrical details of these faults at such a small scale requires the development of new tools that will allow location and characterization of those events of small magnitude (M < 0.5) buried in the noise, and here detected with autocorrelation techniques.
Despite missing some information at the decametric scale, detection of events with Ml < 1, featuring low signal to noise ratio, is very useful in characterizing the time evolution of the sequence and in identifying potential foreshock activity. This sequence has indeed started 16 h before the main events, with initial seismic activity mainly characterized by small cracklings with Ml < 0.5. Thus, only such high-resolution catalogs, extracted with automatic autocorrelation techniques, enable to catch the foreshock initial phase of the sequence, as also pointed out by other studies [17]. It is worth to note that we performed an offline analysis of the events, with autocorrelation techniques running after the occurrence of the main events of the sequence. The near real-time analysis looking at the continuous data before the occurrence of the mainshocks merits further investigation, which is beyond the scope of this study. Within the improved catalog, we also reported a b value of b = 0.70, which is significantly different from the one related to the background seismicity of the area (b = 0.93, [60]). This decrease in the b-value can be related to an increase of the differential stress [76], associated with fluid pressure.
Since the sequence occurred in a sector where the network density is higher and the EEW systems worked at least for a part of the sequence, analysis of the system performance can highlight advantages and limits of actual systems. Specifically, we can individuate a sort of “minimum size” of the blind zone for the regional system, which has been estimated to be 15 km. This size represents the actual limit of regional EEW systems, within which no actions can be activated at the occurrence of an earthquake. This poses also a lower limit in magnitude (Ml < 6), below which EEW is not a viable risk reduction tool, because the blind zone almost superimposes with the area damaged by the earthquake. Onsite systems can provide a still positive, albeit very small lead-time for targets within the blind zone of the regional system, as also shown for the 2016–2017 central Italy sequence [77]. A contraction of the blind zone can be also obtained by estimating the earthquake size on an expanding P-wave time window, using for instance, the shape of the logarithm of the peak displacement in the time domain (LPDT curves [78]). When applied to this sequence, the average discrepancy between the predicted moment magnitude and the value provided by SPAR is 0.36, which is slightly larger than the average uncertainty on the magnitude estimate. This technique also provides a first rough estimate of the stress drop of the event, modeling the LPDT curve with a displacement function characterized by symmetric triangular function. For the sequence, the predicted average stress drop is 0.9 MPa, which is close to the estimate retrieved from spectral analysis.
Author Contributions
Conceptualization, G.F.; data curation, L.E., F.C. and R.R.; formal analysis, G.F., G.M.A., A.C., S.C., G.D.L., L.E., A.E., M.P. and A.S.; methodology, G.F.; software, L.E., M.P. and F.C.; supervision, A.Z.; validation, S.G., A.G.I., S.N., G.R. and S.T.; writing—original draft, G.F. and G.M.A.; writing—review & editing, A.C., S.C., G.D.L., A.E., M.P., A.S., S.G., A.G.I., S.N., G.R. and A.Z. All authors have read and agreed to the published version of the manuscript.
Funding
Data: data products and service provision of this research are funded by MUR, Ministero Università e Ricerca, through the project EPOS-Italia, and by DPC, Dipartimento di Protezione Civile, through a collaboration agreement with the University of Naples Federico II. Part of the research has been founded by the national project PRIN FLUIDS, grant number 20174 × 3P29.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: http://isnet-bulletin.fisica.unina.it/cgi-bin/isnet-events/isnet.cgi.
Acknowledgments
We are grateful to three anonymous reviewers who contributed to improve the manuscript. The geological map of Figure 2 has been redrawn from the map of [79].
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Lomax, A.; Virieux, J.; Volant, P.; Berge-Thierry, C. Probabilistic Earthquake Location in 3D and Layered Models. In Advances in Seismic Event Location; Modern Approaches in Geophysics, Volume 18; Thurber, C.H., Rabinowitz, N., Eds.; Springer: Dordrecht, The Netherlands, 2000. [Google Scholar] [CrossRef]
- Satriano, C.; Lomax, A.; Zollo, A. Real-Time Evolutionary Earthquake Location for Seismic Early Warning. Bull. Seism. Soc. Am. 2008, 98, 1482–1494. [Google Scholar] [CrossRef]
- Waldhauser, F.; Ellsworth, W.L. A double-difference earthquake location algorithm: Method and application to the northern Hayward Fault, California. Bull. Seismol. Soc. Am. 2000, 90, 1353–1368. [Google Scholar] [CrossRef]
- Stabile, T.A.; Satriano, C.; Orefice, A.; Festa, G.; Zollo, A. Anatomy of a microearthquake sequence on an active normal fault. Sci. Rep. 2012, 2, 410. [Google Scholar] [CrossRef] [PubMed]
- Rowe, C.A.; Thurber, C.H.; White, R.A. Dome growth behavior at Soufriere Hills Volcano, Montserrat, revealed by relocation of volcanic event swarms, 1995–1996. J. Volcanol. Geotherm. Res. 2004, 134, 199–221. [Google Scholar] [CrossRef]
- Valoroso, L.; Chiaraluce, L.; Piccinini, D.; Di Stefano, R.; Schaff, D.; Waldhauser, F. Radiography of a normal fault system by 64,000 high-precision earthquake locations: The 2009 L’Aquila (central Italy) case study. J. Geophys. Res. Solid Earth 2013, 118, 1156–1176. [Google Scholar] [CrossRef]
- Chen, X.; Shearer, P.M.; Abercrombie, R.E. Spatial migration of earthquakes within seismic clusters in Southern California: Evidence for fluid diffusion. J. Geophys. Res. Space Phys. 2012, 117. [Google Scholar] [CrossRef]
- Miller, S.A. Aftershocks are fluid-driven and decay rates controlled by permeability dynamics. Nat. Commun. 2020, 11, 5787. [Google Scholar] [CrossRef]
- Abercrombie, R.E. Earthquake source scaling relationships from− 1 to 5 ML using seismograms recorded at 2.5-km depth. J. Geophys. Res. 1995, 100, 24015–24036. [Google Scholar] [CrossRef]
- Prieto, G.A.; Shearer, P.M.; Vernon, F.L.; Kilb, D. Earthquake source scaling and self-similarity estimation from stacking P and S spectra. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Abercrombie, R.E.; Rice, J.R. Can observations of earthquake scaling constrain slip weakening? Geophys. J. Int. 2005, 162, 406–424. [Google Scholar] [CrossRef]
- Oth, A.; Parolai, S.; Bindi, D.; Wenzel, F. Source Spectra and Site Response from S Waves of Intermediate-Depth Vrancea, Romania, Earthquakes. Bull. Seism. Soc. Am. 2009, 99, 235–254. [Google Scholar] [CrossRef]
- Miller, S.A. Properties of large ruptures and the dynamical influence of fluids on earthquakes and faulting. J. Geophys. Res. Solid Earth 2002, 107, ESE-3. [Google Scholar] [CrossRef]
- Dublanchet, P.; Godano, M.; Bernard, P. Inferring fault mechanical conditions from the source parameters of a complex microseismic multiplet in the Corinth rift, Greece. J. Geophys. Res. Solid Earth 2015, 120, 7655–7682. [Google Scholar] [CrossRef]
- Amoroso, O.; Russo, G.; De Landro, G.; Zollo, A.; Garambois, S.; Mazzoli, S.; Parente, M.; Virieux, J. From velocity and attenuation tomography to rock physical modeling: Inferences on fluid-driven earthquake processes at the Irpinia fault system in southern Italy. Geophys. Res. Lett. 2017, 44, 6752–6760. [Google Scholar] [CrossRef]
- Bouchon, M.; Durand, V.; Marsan, D.; Karabulut, H.; Schmittbuhl, J. The long precursory phase of most large interplate earthquakes. Nat. Geosci. 2013, 6, 299–302. [Google Scholar] [CrossRef]
- Trugman, D.T.; Ross, Z.E. Pervasive Foreshock Activity Across Southern California. Geophys. Res. Lett. 2019, 46, 8772–8781. [Google Scholar] [CrossRef]
- Ende, M.P.A.V.D.; Ampuero, J.-P. On the Statistical Significance of Foreshock Sequences in Southern California. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- Gibbons, S.J.; Ringdal, F. The detection of low magnitude seismic events using array-based waveform correlation. Geophys. J. Int. 2006, 165, 149–166. [Google Scholar] [CrossRef]
- Yoon, C.E.; O’Reilly, O.; Bergen, K.J.; Beroza, G.C. Earthquake detection through computationally efficient similarity search. Sci. Adv. 2015, 1, e1501057. [Google Scholar] [CrossRef]
- Picozzi, M.; Bindi, D.; Zollo, A.; Festa, G.; Spallarossa, D. Detecting long-lasting transients of earthquake activity on a fault system by monitoring apparent stress, ground motion and clustering. Sci. Rep. 2019, 9, 16268. [Google Scholar] [CrossRef]
- Iannaccone, G.; Zollo, A.; Elia, L.; Convertito, V.; Satriano, C.; Martino, C.; Festa, G.; Lancieri, M.; Bobbio, A.; Stabile, T.A.; et al. A prototype system for earthquake early-warning and alert management in southern Italy. Bull. Earthq. Eng. 2010, 8, 1105–1129. [Google Scholar] [CrossRef]
- Satriano, C.; Elia, L.; Martino, C.; Lancieri, M.; Zollo, A.; Iannaccone, G. PRESTo, the earthquake early warning system for Southern Italy: Concepts, capabilities and future perspectives. Soil Dyn. Earthq. Eng. 2011, 31, 137–153. [Google Scholar] [CrossRef]
- Doglioni, C. Geological remarks on the relationships between extension and convergent geodynamic settings. Tectonophysics 1995, 252, 253–267. [Google Scholar] [CrossRef]
- Patacca, E.; Scandone, P. Geology of the southern Apennines. Boll. Soc. Geol. It. 2007, 7, 75–119. [Google Scholar]
- Cavazza, W.; Roure, F.M.; Spakman, W.; Stampfli, G.M.; Ziegler, P.A. The TRANSMED Atlas. The Mediterranean Region from Crust to Mantle: The Mediterranean Region from Crust to Mantle: Geological and Geophysical Framework of the Mediterranean and the Surrounding Areas; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Casero, P.; Roure, F.; Vially, R. Tectonic framework and petroleum potential of the southern Apennines. Gener. Accumul. Prod. Eur. Hydrocarb. 1991, 1, 381–387. [Google Scholar]
- Bally, A.; Burbi, L.; Cooper, C.; Ghelardoni, R. Balanced cross sections and seismic reflection profiles across the central Apennines. Memorie della Societa Geologica Italiana 1986, 35, 275–310. [Google Scholar]
- Patacca, E.; Sartori, R.; Scandone, P. Tyrrhenian basin and Apenninic arcs: Kinematic relations since late Tortonian times. Memorie della Societa Geologica Italiana 1990, 45, 425–451. [Google Scholar]
- Frepoli, A.; Amato, A. Contemporaneous extension and compression in the Northern Apennines from earthquake fault-plane solutions. Geophys. J. Int. 1997, 129, 368–388. [Google Scholar] [CrossRef]
- D’Agostino, N.; Avallone, A.; Cheloni, D.; D’Anastasio, E.; Mantenuto, S.; Selvaggi, G. Active tectonics of the Adriatic region from GPS and earthquake slip vectors. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Ascione, A.; Mazzoli, S.; Petrosino, P.; Valente, E. A decoupled kinematic model for active normal faults: Insights from the 1980, MS = 6.9 Irpinia earthquake, southern Italy. GSA Bull. 2013, 125, 1239–1259. [Google Scholar] [CrossRef]
- Chiarabba, C.; Jovane, L.; Distefano, R. A new view of Italian seismicity using 20 years of instrumental recordings. Tectonophysics 2005, 395, 251–268. [Google Scholar] [CrossRef]
- Improta, L.; De Gori, P.; Chiarabba, C. New insights into crustal structure, Cenozoic magmatism, CO2degassing, and seismogenesis in the southern Apennines and Irpinia region from local earthquake tomography. J. Geophys. Res. Solid Earth 2014, 119, 8283–8311. [Google Scholar] [CrossRef]
- Pantosti, D.; Schwartz, D.P.; Valensise, G. Paleoseismology along the 1980 surface rupture of the Irpinia Fault: Implications for earthquake recurrence in the southern Apennines, Italy. J. Geophys. Res. Solid Earth 1993, 98, 6561–6577. [Google Scholar] [CrossRef]
- Buck, W.R. flexural rotation of normal faults. Tectonics 1988, 7, 959–973. [Google Scholar] [CrossRef]
- King, G.; Ellis, M. The origin of large local uplift in extensional regions. Nature 1990, 348, 689–693. [Google Scholar] [CrossRef]
- Ghisetti, F.; Vezzani, L. Normal faulting, transcrustal permeability and seismogenesis in the Apennines (Italy). Tectonophysics 2002, 348, 155–168. [Google Scholar] [CrossRef]
- Westaway, R.; Jackson, J. Surface faulting in the southern Italian Campania-Basilicata earthquake of 23 November 1980. Nat. Cell Biol. 1984, 312, 436–438. [Google Scholar] [CrossRef]
- Westaway, R.; Jackson, J. The earthquake of 1980 November 23 in Campania--Basilicata (southern Italy). Geophys. J. Int. 1987, 90, 375–443. [Google Scholar] [CrossRef]
- Bernard, P.; Zollo, A. The Irpinia (Italy) 1980 earthquake: Detailed analysis of a complex normal faulting. J. Geophys. Res. Solid Earth 1989, 94, 1631–1647. [Google Scholar] [CrossRef]
- Pantosti, D.; Valensise, G. Faulting mechanism and complexity of the November 23, 1980, Campania-Lucania Earthquake, inferred from surface observations. J. Geophys. Res. Solid Earth 1990, 95, 15319–15341. [Google Scholar] [CrossRef]
- Amoruso, A.; Crescentini, L.; Scarpa, R. Faulting geometry for the complex 1980 Campania-Lucania earthquake from levelling data. Geophys. J. Int. 2005, 162, 156–168. [Google Scholar] [CrossRef]
- Amato, A.; Chiarabba, C.; Malagnini, L.; Selvaggi, G. Three-dimensional P-velocity structure in the region of the MS = 6.9 Irpinia, Italy, normal faulting earthquake. Phys. Earth Planet. Inter. 1992, 75, 111–119. [Google Scholar] [CrossRef]
- Amato, A.; Selvaggi, G. Aftershock location and P-velocity structure in the epicentral region, of the 1980 Irpinia earthquake. Annali di Geophysica 1993, 36, 237–243. [Google Scholar]
- Patella, D.; Petrillo, Z.; Siniscalchi, A.; Improta, L.; Di Fiore, B. Magnetotelluric profiling along the CROP-04 section in the Southern Apennines. In CROP PROJECT: Deep Seismic Exploration of the CENTRAL Mediterranean and Italy; Finetti, I.R., Ed.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 263–280. [Google Scholar]
- De Matteis, R.; Matrullo, E.; Rivera, L.; Stabile, T.A.; Pasquale, G.; Zollo, A. Fault Delineation and Regional Stress Direction from the Analysis of Background Microseismicity in the southern Apennines, Italy. Bull. Seism. Soc. Am. 2012, 102, 1899–1907. [Google Scholar] [CrossRef]
- De Landro, G.; Amoroso, O.; Stabile, T.A.; Matrullo, E.; Lomax, A.; Zollo, A. High-precision differential earthquake location in 3-D models: Evidence for a rheological barrier controlling the microseismicity at the Irpinia fault zone in southern Apennines. Geophys. J. Int. 2015, 203, 1821–1831. [Google Scholar] [CrossRef]
- Adinolfi, G.M.; Cesca, S.; Picozzi, M.; Heimann, S.; Zollo, A. Detection of weak seismic sequences based on arrival time coherence and empiric network detectability: An application at a near fault observatory. Geophys. J. Int. 2019, 218, 2054–2065. [Google Scholar] [CrossRef]
- Vassallo, M.; Festa, G.; Bobbio, A.; Serra, M. Low shear velocity in a normal fault system imaged by ambient noise cross correlation: The case of the Irpinia fault zone, Southern Italy. J. Geophys. Res. Solid Earth 2016, 121, 4290–4305. [Google Scholar] [CrossRef]
- Chiarabba, C.; Chiodini, G. Continental delamination and mantle dynamics drive topography, extension and fluid discharge in the Apennines. Geology 2013, 41, 715–718. [Google Scholar] [CrossRef]
- Italiano, F.; Martelli, M.; Martinelli, G.; Nuccio, P.M. Geochemical evidence of melt intrusions along lithospheric faults of the Southern Apennines, Italy: Geodynamic and seismogenic implications. J. Geophys. Res. Solid Earth 2000, 105, 13569–13578. [Google Scholar] [CrossRef]
- Chiodini, G.; Granieri, D.; Avino, R.; Caliro, S.; Costa, A.; Minopoli, C.; Vilardo, G. Non-volcanic CO2Earth degassing: Case of Mefite d’Ansanto (southern Apennines), Italy. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Miller, S.A.; Collettini, C.; Chiaraluce, L.; Cocco, M.; Barchi, M.; Kaus, B.J.P. Aftershocks driven by a high-pressure CO2 source at depth. Nature 2004, 427, 724–727. [Google Scholar] [CrossRef] [PubMed]
- Lucente, F.P.; De Gori, P.; Margheriti, L.; Piccinini, D.; Di Bona, M.; Chiarabba, C.; Agostinetti, N.P. Temporal variation of seismic velocity and anisotropy before the 2009 MW6.3 L’Aquila earthquake, Italy. Geology 2010, 38, 1015–1018. [Google Scholar] [CrossRef]
- Johnson, C.E.; Bittenbinder, A.; Bogaert, B.; Dietz, L.; Kohler, W. Earthworm: A flexible approach to seismic network processing. Iris Newsl. 1995, 14, 1–4. [Google Scholar]
- Cocco, M.; Chiarabba, C.; Di Bona, M.; Selvaggi, G.; Margheriti, L.; Frepoli, A.; Lucente, F.P.; Basili, A.; Jongmans, D.; Campillo, M. The April 1996 Irpinia seismic sequence: Evidence for fault interaction. J. Seism. 1999, 3, 105–117. [Google Scholar] [CrossRef]
- Bergen, K.J.; Beroza, G.C. Detecting earthquakes over a seismic network using single-station similarity measures. Geophys. J. Int. 2018, 213, 1984–1998. [Google Scholar] [CrossRef]
- Andoni, A.; Indyk, P. Near-Optimal Hashing Algorithms for Approximate Nearest Neighbor in High Dimensions. In Proceedings of the 47th Annual IEEE Symposium on Foundations of Computer Science (FOCS’06), Berkeley, CA, USA, 21–24 October 2006; pp. 459–468. [Google Scholar]
- Vassallo, M.; Festa, G.; Bobbio, A. Seismic Ambient Noise Analysis in Southern Italy. Bull. Seism. Soc. Am. 2012, 102, 574–586. [Google Scholar] [CrossRef]
- Michelini, A.; Lomax, A. The effect of velocity structure errors on double-difference earthquake location. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Amoroso, O.; Ascione, A.; Mazzoli, S.; Virieux, J.; Zollo, A. Seismic imaging of a fluid storage in the actively extending Apennine mountain belt, southern Italy. Geophys. Res. Lett. 2014, 41, 3802–3809. [Google Scholar] [CrossRef]
- Brune, J.N. Tectonic stress and the spectra of seismic shear waves from earthquakes. J. Geophys. Res. 1970, 75, 4997–5009. [Google Scholar] [CrossRef]
- Supino, M.; Festa, G.; Zollo, A. A probabilistic method for the estimation of earthquake source parameters from spectral inversion: Application to the 2016–2017 Central Italy seismic sequence. Geophys. J. Int. 2019, 218, 988–1007. [Google Scholar] [CrossRef]
- Zollo, A.; Orefice, A.; Convertito, V. Source parameter scaling and radiation efficiency of microearthquakes along the Irpinia fault zone in southern Apennines, Italy. J. Geophys. Res. Solid Earth 2014, 119, 3256–3275. [Google Scholar] [CrossRef]
- Festa, G.; Zollo, A.; Lancieri, M. Earthquake magnitude estimation from early radiated energy. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Reasenberg, P.; Oppenheimer, D. FPFIT, FPPLOT and FPPAGE: Fortran Computer Programs for Calculating and Displaying Earthquake Fault-Plane Solutions; Open File Report 85–739; US Geological Survey: Menlo Park, CA, USA, 1985; pp. 85–739.
- Zhu, T.J.; Heidebrecht, A.C.; Tso, W.K. Effect of peak ground acceleration to velocity ratio on ductility demand of inelastic systems. Earthq. Eng. Struct. Dyn. 1988, 16, 63–79. [Google Scholar] [CrossRef]
- Ameri, G.; Emolo, A.; Pacor, F.; Gallovič, F. Ground-motion simulations for the 1980 M 6.9 Irpinia earthquake (Southern Italy) and scenario events. Bull. Seismol. Soc. Am. 2011, 101, 1136–1151. [Google Scholar] [CrossRef]
- Kwon, O.S.; Elnashai, A. The effect of material and ground motion uncertainty on the seismic vulnerability curves of RC structure. Eng. Struct. 2006, 28, 289–303. [Google Scholar] [CrossRef]
- Emolo, A.; Convertito, V.; Cantore, L. Ground-motion predictive equations for low-magnitude earthquakes in the Campania–Lucania area, Southern Italy. J. Geophys. Eng. 2011, 8, 46–60. [Google Scholar] [CrossRef]
- Wald, D.J.; Quitoriano, V.; Heaton, T.H.; Kanamori, H.; Scrivner, C.W.; Worden, C.B. TriNet “ShakeMaps”: Rapid Generation of Peak Ground Motion and Intensity Maps for Earthquakes in Southern California. Earthq. Spectra 1999, 15, 537–555. [Google Scholar] [CrossRef]
- Caruso, A.; Colombelli, S.; Elia, L.; Picozzi, M.; Zollo, A. An on-site alert level early warning system for Italy. J. Geophys. Res. Solid Earth 2017, 122, 2106–2118. [Google Scholar] [CrossRef]
- Colombelli, S.; Carotenuto, F.; Elia, L.; Zollo, A. Design and implementation of a mobile device app for network-based earthquake early warning systems (EEWSs): Application to the PRESTo EEWS in southern Italy. Nat. Hazards Earth Syst. Sci. 2020, 20. [Google Scholar] [CrossRef]
- Deschamps, A.; King, G.C.P. The Campania-Lucania (southern Italy) earthquake of 23 November 1980. Earth Planet. Sci. Lett. 1983, 62, 296–304. [Google Scholar] [CrossRef]
- Scholz, C.H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar]
- Festa, G.; Picozzi, M.; Caruso, A.; Colombelli, S.; Cattaneo, M.; Chiaraluce, L.; Elia, L.; Martino, C.; Marzorati, S.; Supino, M.; et al. Performance of Earthquake Early Warning Systems during the 2016–2017 Mw 5–6.5 Central Italy Sequence. Seism. Res. Lett. 2018, 89, 1–12. [Google Scholar] [CrossRef]
- Nazeri, S.; Colombelli, S.; Zollo, A. Fast and accurate determination of earthquake moment, rupture length and stress release for the 2016–2017 Central Italy seismic sequence. Geophys. J. Int. 2019, 217, 1425–1432. [Google Scholar] [CrossRef]
- Bigi, G.; Coli, M.; Cosentino, D.; Parotto, M.; Praturlon, A.; Sartori, R.; Scandone, P.; Turco, E. Structural Model of Italy scale 1:500.000, sheet 4. In C.N.R., Progetto Finalizzato Geodinamica; SELCA: Firenze, Italy, 1992. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).