Stress–Dilatancy Relationship of Erksak Sand under Drained Triaxial Compression
Abstract
1. Introduction
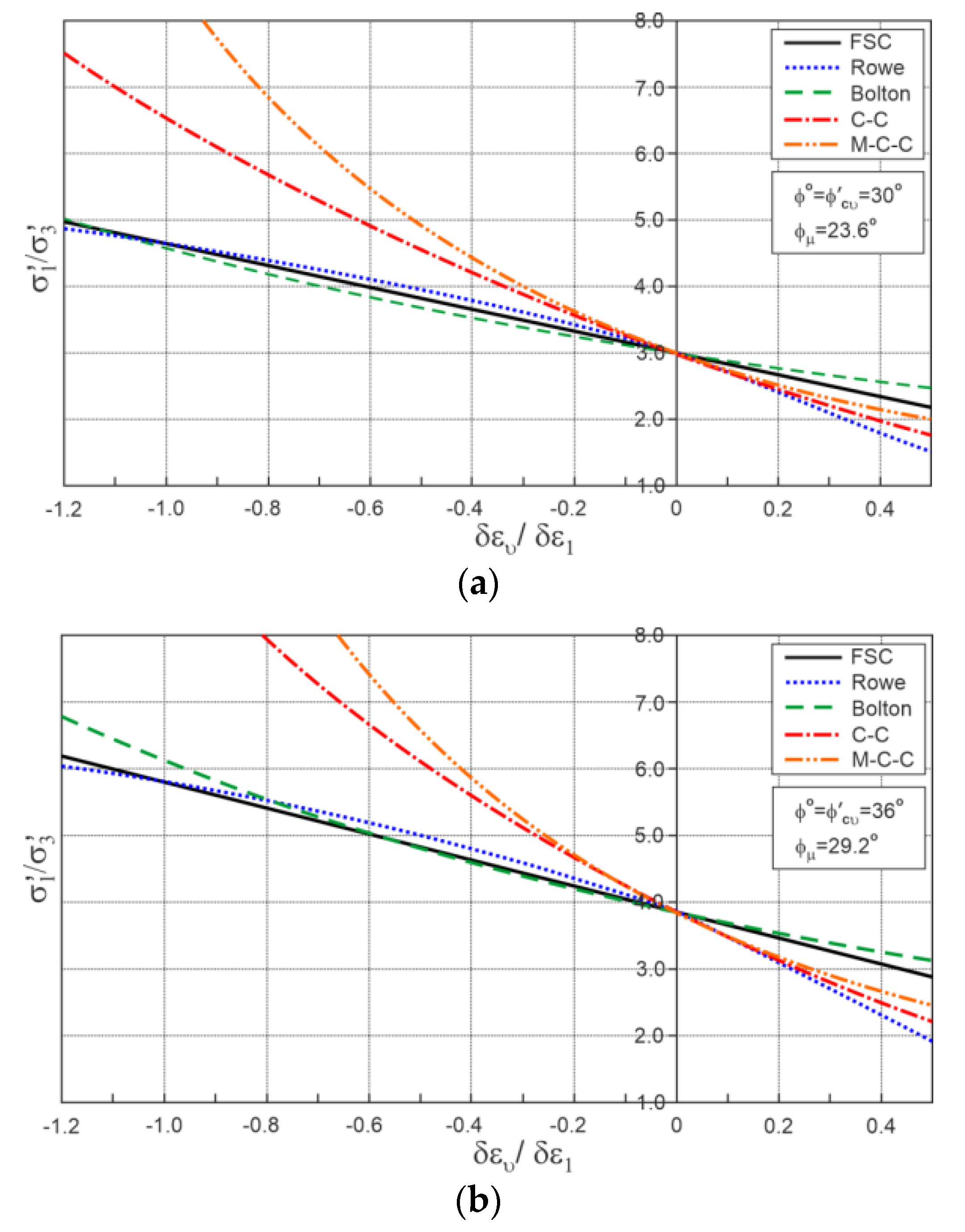
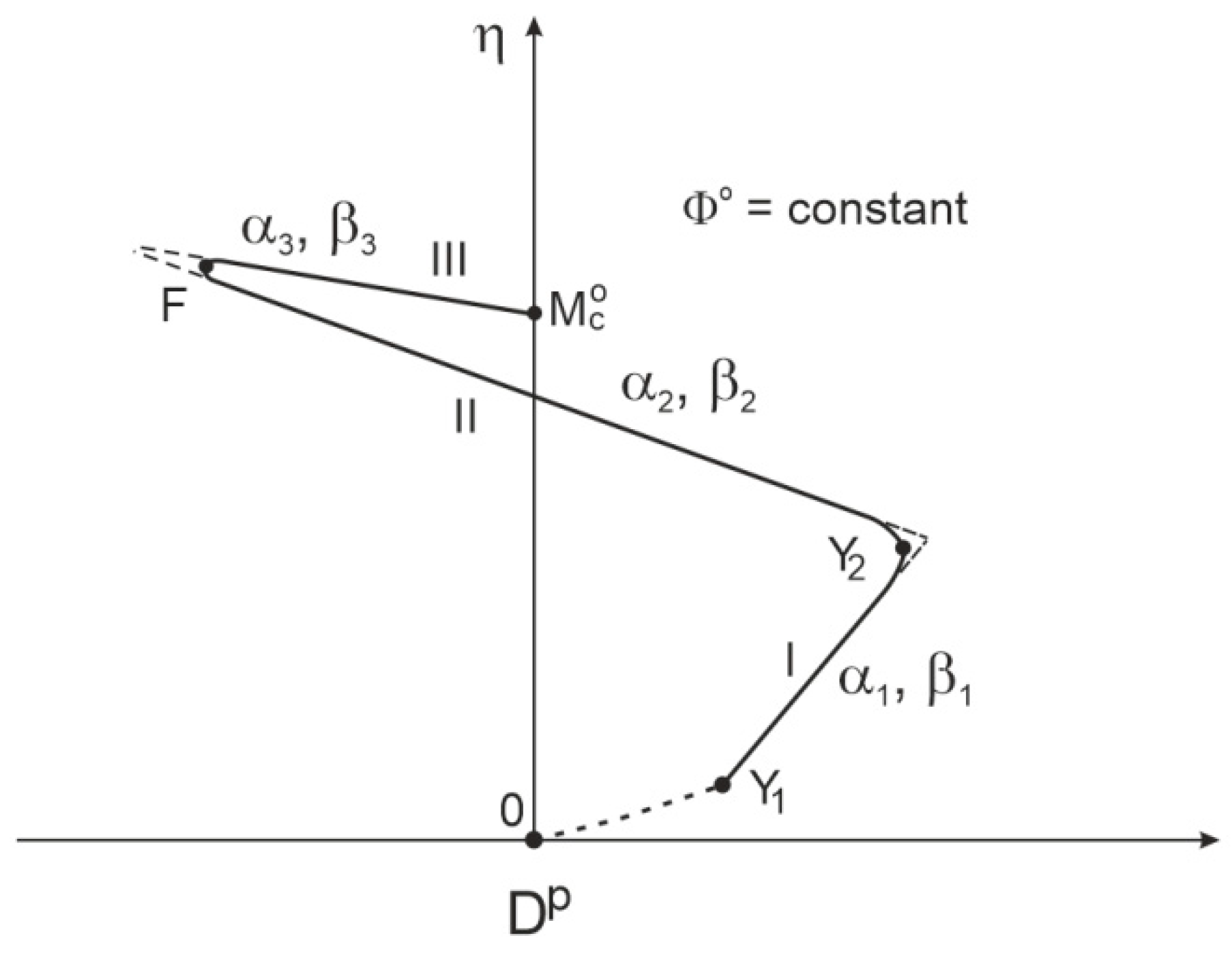
2. Stress–Dilatancy Relationship for Sand
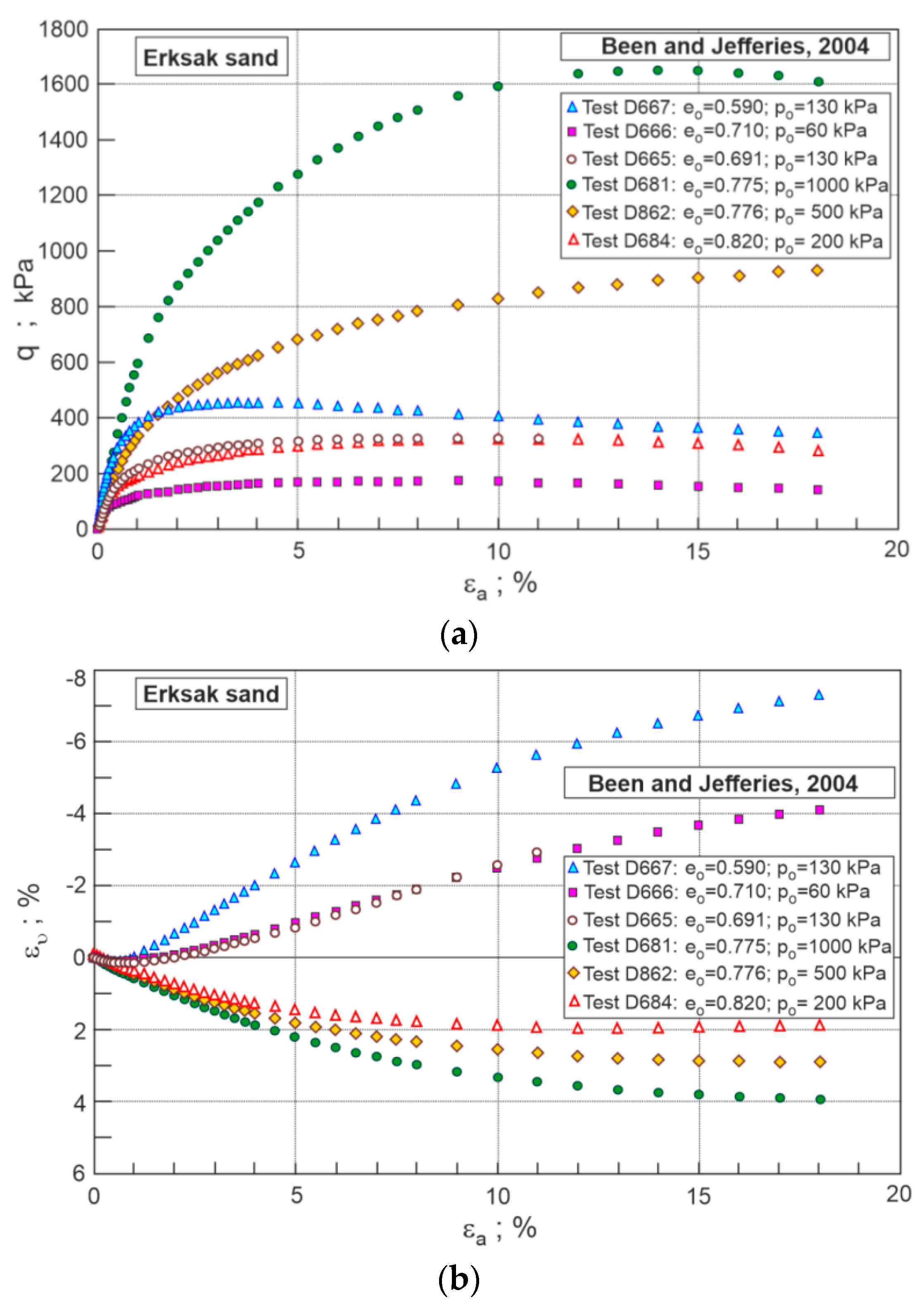
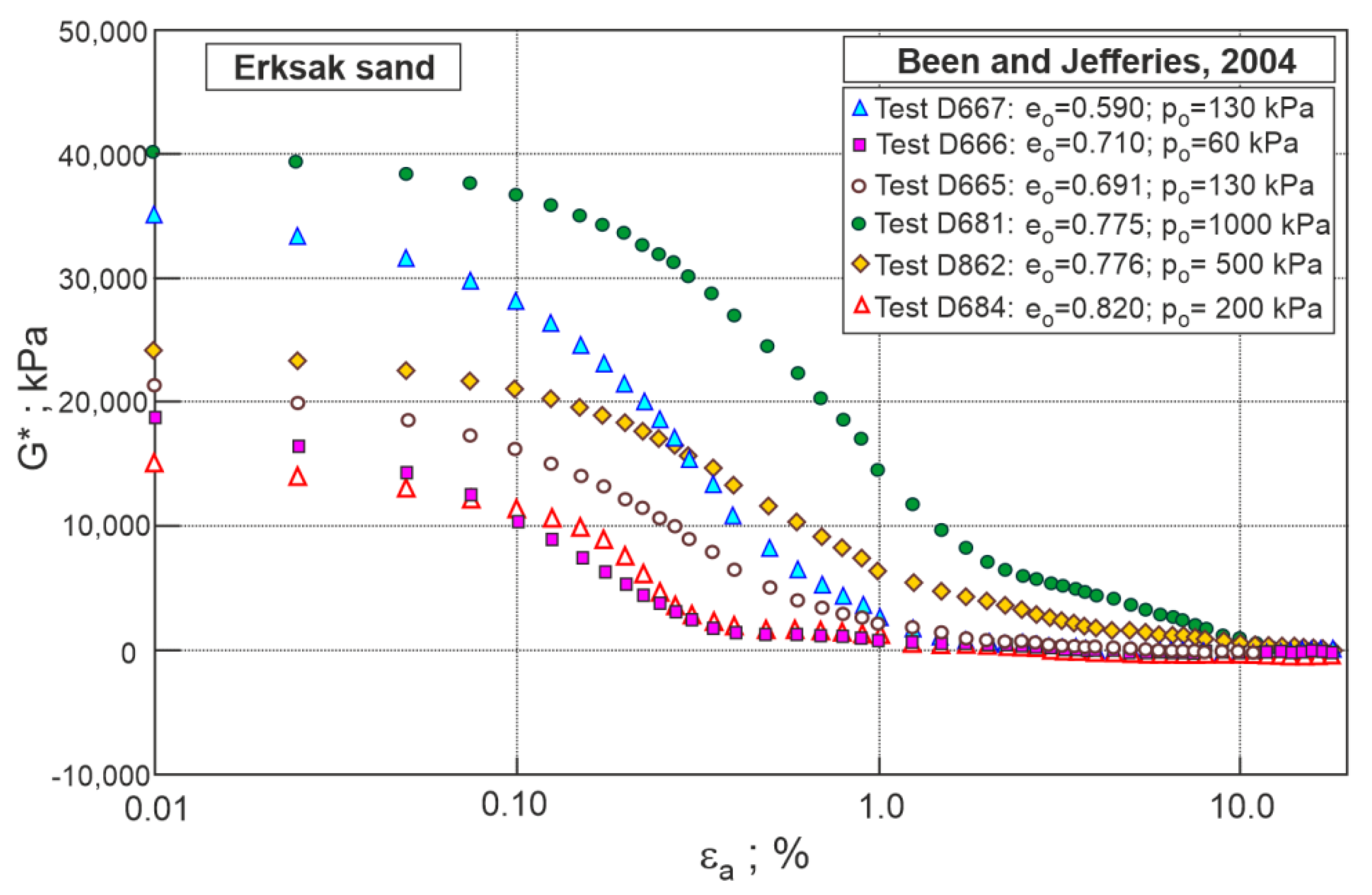
3. Stress–Dilatancy of Erksak Sand
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Taylor, D.W. Fundamentals of Soil Mechanics; John Willey and Sons: New York, NY, USA, 1948. [Google Scholar]
- Roscoe, K.H.; Schofield, A.N.; Wroth, C.P. On the Yielding of Soil. Gèotechnique 1958, 8, 22–53. [Google Scholar] [CrossRef]
- Roscoe, K.H.; Schofield, A.N.; Thurairajah, A. Yielding of Clays in States Wetter Than Critical. Gèotechnique 1963, 13, 211–240. [Google Scholar] [CrossRef]
- Schofield, A.N.; Wroth, C.P. Critical State Soil Mechanics; McGraw-Hill: London, UK, 1968. [Google Scholar]
- Roscoe, K.H.; Burland, J.B. On the Generalized Stress-Strain Behavior of ‘Wet’ Clay, Engineering Plasticity; Heyman, J., Leckie, F., Eds.; Cambridge University Press: Cambridge, UK, 1968; pp. 535–609. [Google Scholar]
- Jefferies, M.G. Nor-Sand: A simple critical state model for sand. Gèotechnique 1993, 43, 91–103. [Google Scholar] [CrossRef]
- Rowe, P.W. The stress–dilatancy relation for static equilibrium of an assembly of particles in contact. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1962, 269, 500–527. [Google Scholar]
- Rowe, P.W. Theoretical meaning and observed values of deformation parameters for soil. In Proceedings of the Stress-Strain Behaviour of Soils, Roscoe Memorial Symposium, Cambridge, UK, 29–31 March 1971; Parry, R.H.G., Ed.; The Whitefriars Press Ltd.: London, UK, 1972; pp. 143–194. [Google Scholar]
- Szypcio, Z. Stress–Dilatancy for soils. Part, I. The frictional state theory. Stud. Geotech. Mech. 2016, 38, 51–57. [Google Scholar] [CrossRef]
- Szypcio, Z. Stress–dilatancy for soils. Part II. Experimental validation for triaxial tests. Stud. Geotech. Mech. 2016, 38, 59–65. [Google Scholar] [CrossRef]
- Bolton, M.D. The strength and dilatancy of sands. Gèotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef]
- Szypcio, Z. Relation between the Friction Angle of Sand at Triaxial Compression and Triaxial Extension and Plane Strain Conditions. Geosciences 2020, 10, 29. [Google Scholar] [CrossRef]
- Szypcio, Z. The influence of particle breakage on stress-dilatancy relationship for granular soils. In Proceedings of the 7th International Symposium on Deformation Characteristics of Geomaterials (IS-Glasgow 2019), Glasgow, UK, 26–28 June 2019; Volume 92, pp. 1–5. [Google Scholar] [CrossRef]
- Szypcio, Z. Stress–dilatancy of gravel for triaxial compression tests. Ann. Wars. Univ. Life Sci. SGGW Land Reclam. 2018, 50, 119–128. [Google Scholar] [CrossRef]
- Dołżyk-Szypcio, K. Stress–dilatancy relationship for railway ballast. Stud. Geotech. Mech. 2018, 40, 79–85. [Google Scholar] [CrossRef]
- Dołżyk-Szypcio, K. Stress–strain behavior of Toyoura sand in undrained triaxial compression. In Proceedings of the 7th International Symposium on Deformation Characteristics of Geomaterials (IS-Glasgow 2019), Glasgow, UK, 26–28 June 2019; Volume 92, pp. 1–4. [Google Scholar] [CrossRef]
- Rahimi, M. Review of Proposed Stress-dilatancy Relationships and Plastic Potential Functions for Uncemented and Cemented Sands. J. Geol. Res. 2019, 2, 19–34. [Google Scholar] [CrossRef]
- De Bono, J.P.; McDowell, G.R. Micromechanics of drained and undrained shearing of compacted and overconsolidated crushable sand. Gèotechnique 2016, 68, 575–589. [Google Scholar] [CrossRef]
- Yin, Z.; Chang, G.S. Stress—Dilatancy behavior for sand under loading and unloading conditions. Int. J. Numer. Anal. Meth. Geomech. 2013, 37, 855–870. [Google Scholar] [CrossRef]
- Sun, Y.; Xiao, Y. Frictional order plasticity model for granular soils subjected to monotonic triaxial compression. Int. J. Solids Struct. 2017, 118–119, 224–232. [Google Scholar] [CrossRef]
- Sun, Y.; Sumelka, W. State dependent frictional plasticity model for the true triaxial behaviour of granular soils. Arch. Mech. 2019, 71, 23–47. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Y.; Ju, W. Cyclic fractional Plastic Model for Granular Soils. Front. Built Environ. 2019, 5, 1–9. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, Y.; Shen, Y. Mathematical aspect of the state-dependent stress-dilatancy of granular soil under triaxial loading. Gèotechnique 2019, 69, 158–165. [Google Scholar] [CrossRef]
- Been, K.; Jefferies, M. Stress-dilatancy in very loose sand. Can. Geotech. J. 2004, 41, 972–989. [Google Scholar] [CrossRef]
- Sasitharan, S. Stress Path Dependency of Dilatancy and Stress-Strain Response of Sand. Master’s Thesis, The University of British Columbia, Vancouver, BC, Canada, 1989. [Google Scholar]
- Vaid, Y.P.; Sasitharan, S. The strength and dilatancy of sand. Can. Geotech. J. 1992, 29, 522–526. [Google Scholar] [CrossRef]
- Ghafghazi, M.; Shuttle, D. Accurate determination of the critical state friction angle from triaxial tests. In Proceedings of the 59th Canadian Geotechnical Conference, Vancouver, BC, Canada, 1–4 October 2006; pp. 278–284. [Google Scholar]
- Been, K.; Jefferies, M.G.; Hachey, J.E. The critical state of sand. Gèotechnique 1991, 41, 365–381. [Google Scholar] [CrossRef]
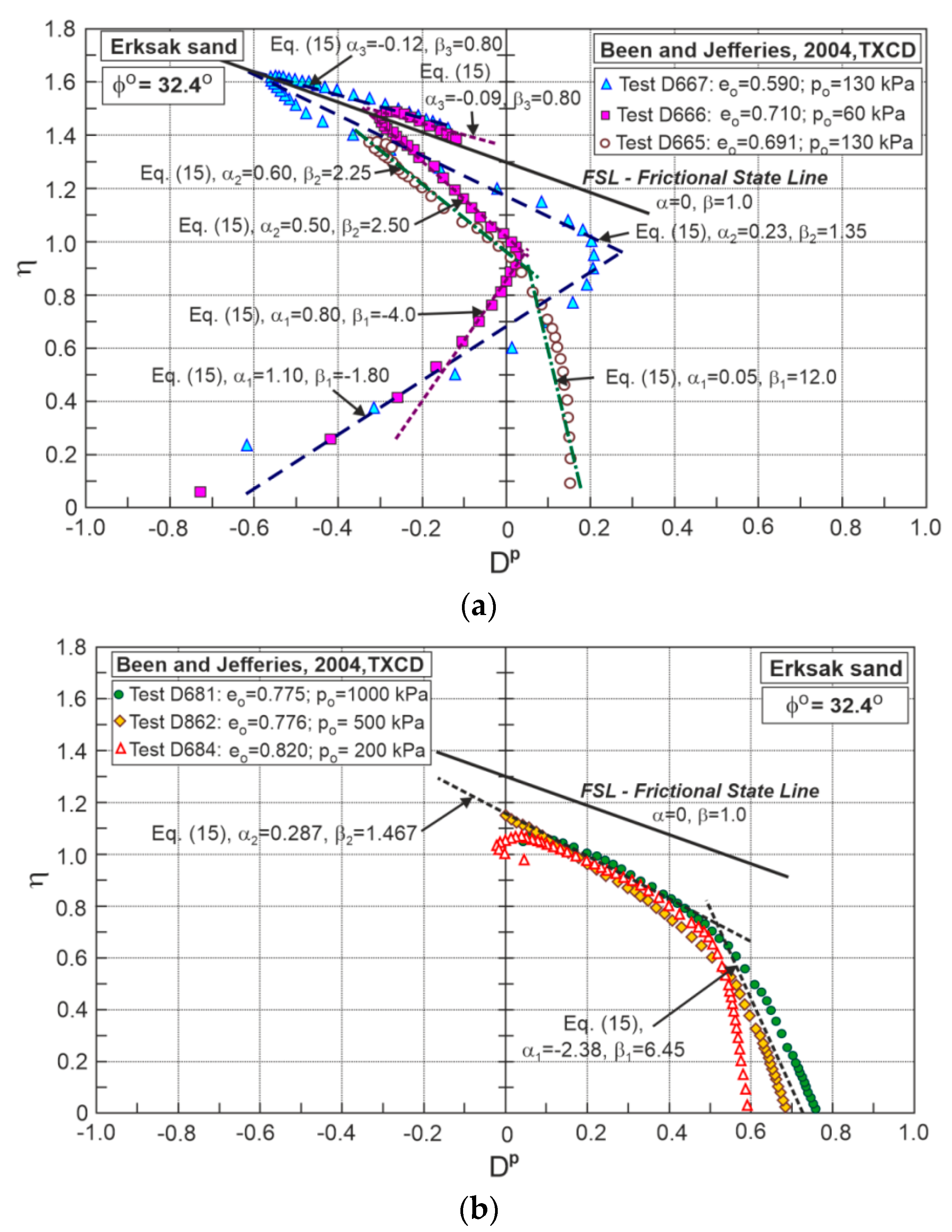
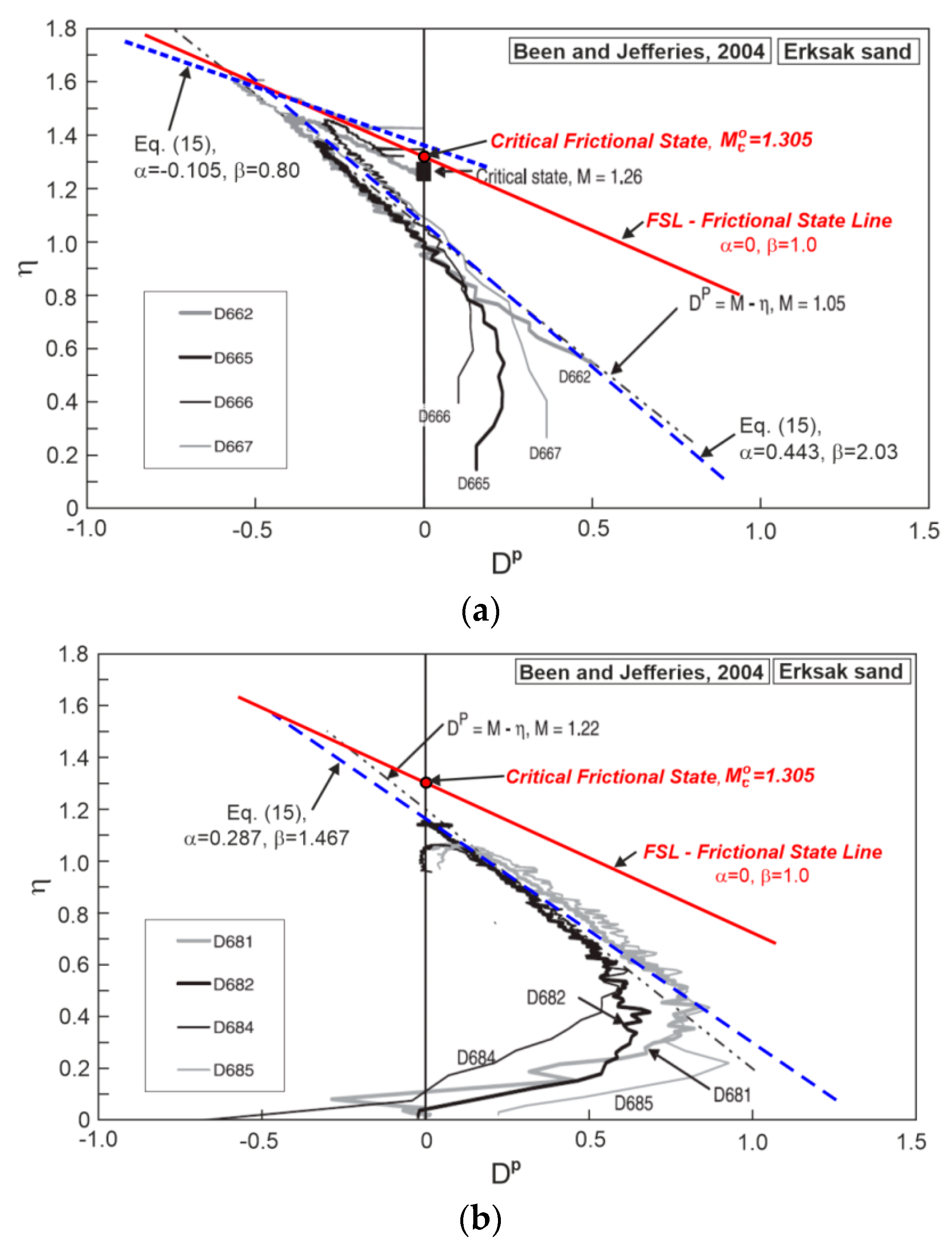

| eo | po | α1 | β1 | α2 | β2 | α3 | β3 |
|---|---|---|---|---|---|---|---|
| - | kPa | - | - | - | - | - | - |
| Dilative behavior | |||||||
| 0.590 | 130 | 1.10 | −1.80 | 0.23 | 1.35 | −0.12 | 0.80 |
| 0.691 | 130 | 0.05 * | 12.00 * | 0.60 | 2.25 | - | - |
| 0.710 | 60 | 0.80 | −4.00 | 0.50 | 2.50 | −0.09 | 0.80 |
| Mean values | 0.95 | −2.90 | 0.443 | 2.03 | −0.105 | 0.80 | |
| Contractive behavior | |||||||
| 0.775 | 1000 | −2.15 | 5.85 | 0.25 | 1.40 | - | - |
| 0.776 | 500 | −2.60 | 7.05 | 0.26 | 1.70 | - | - |
| 0.820 | 200 | −7.20 * | 16.00 * | 0.35 | 1.30 | - | - |
| Mean values | −2.38 | 6.45 | 0.287 | 1.467 | - | - | |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dołżyk-Szypcio, K. Stress–Dilatancy Relationship of Erksak Sand under Drained Triaxial Compression. Geosciences 2020, 10, 353. https://doi.org/10.3390/geosciences10090353
Dołżyk-Szypcio K. Stress–Dilatancy Relationship of Erksak Sand under Drained Triaxial Compression. Geosciences. 2020; 10(9):353. https://doi.org/10.3390/geosciences10090353
Chicago/Turabian StyleDołżyk-Szypcio, Katarzyna. 2020. "Stress–Dilatancy Relationship of Erksak Sand under Drained Triaxial Compression" Geosciences 10, no. 9: 353. https://doi.org/10.3390/geosciences10090353
APA StyleDołżyk-Szypcio, K. (2020). Stress–Dilatancy Relationship of Erksak Sand under Drained Triaxial Compression. Geosciences, 10(9), 353. https://doi.org/10.3390/geosciences10090353





