Prospecting and Evaluation of Underground Massive Ice by Ground-Penetrating Radar
Abstract
1. Introduction
- created and analyzed a model of a single GPR trace for frozen rock mass with massive ice;
- conducted computer and physical simulation of GPR sounding of a frozen rock mass model with the inclusion of massive ice.
2. Method of Experimental Studies
2.1. GPR Method
- amplitude—the magnitude of the maximum pulse (A);
- phase (with what impulse the signal starts, negative or positive);
- traveltime (t);
- center frequency of the Fourier spectrum (fc).
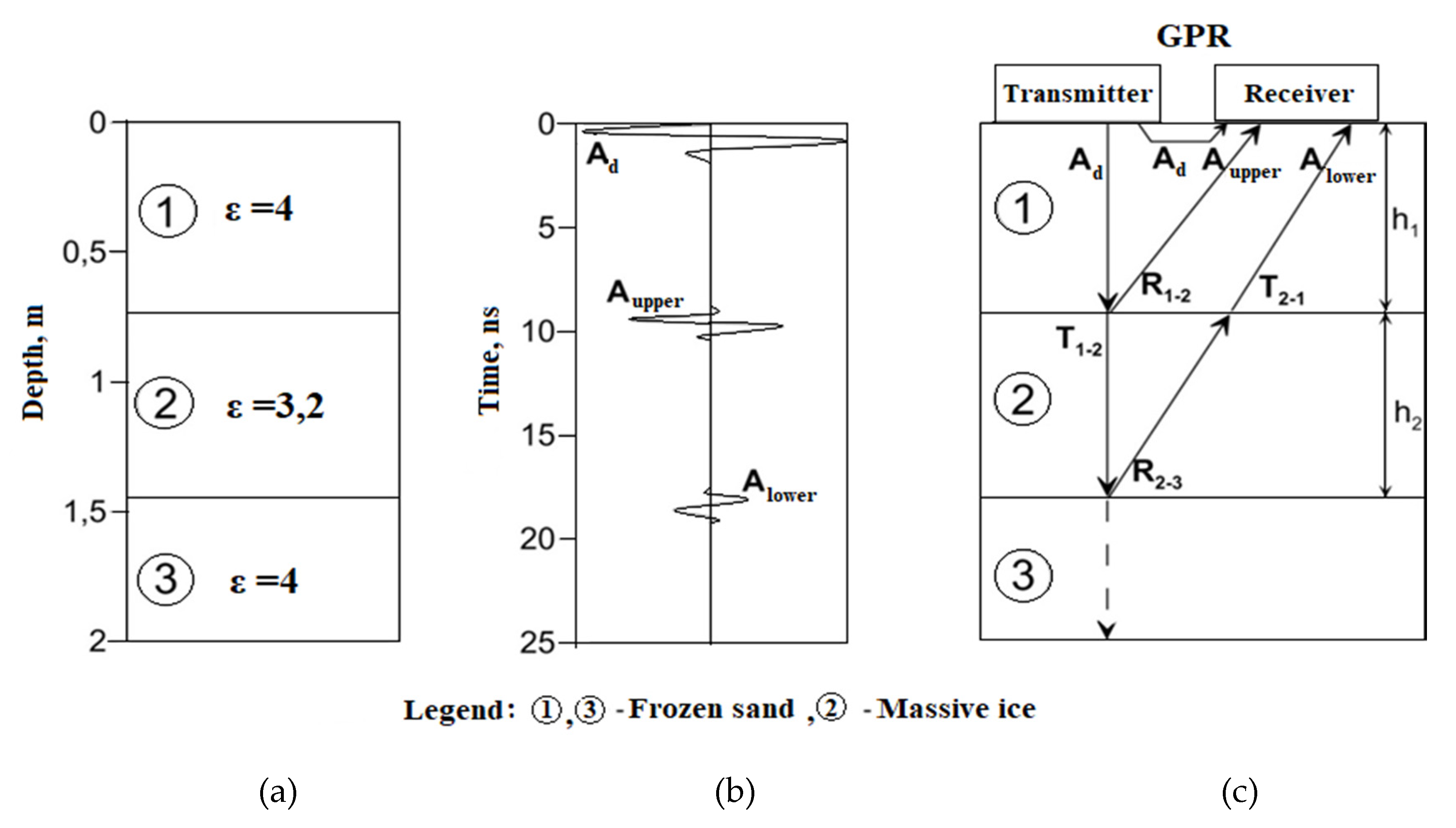
2.2. Theoretical Foundations of Massive Ice Detection by GPR
2.3. Computer Simulation of GPR Measurements
- with one sample of massive ice in a frozen host medium;
- with three samples of massive ice in a frozen host medium.
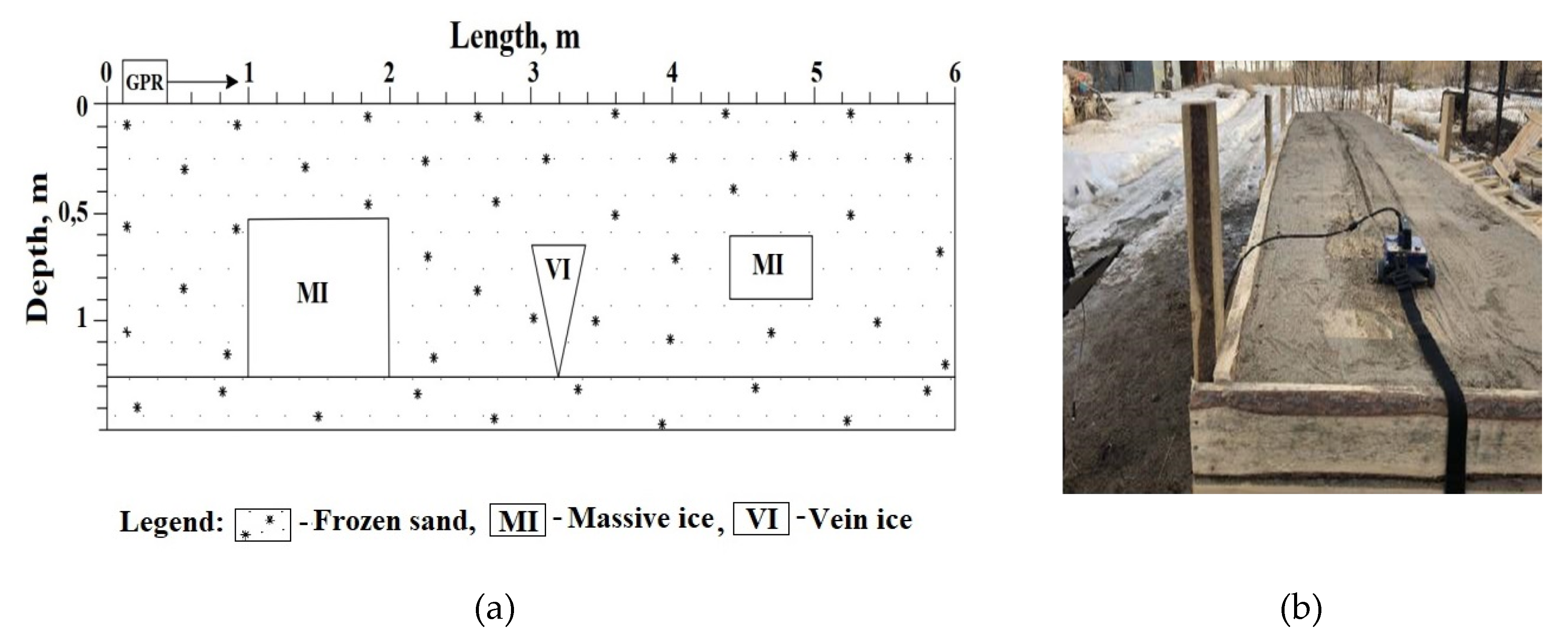
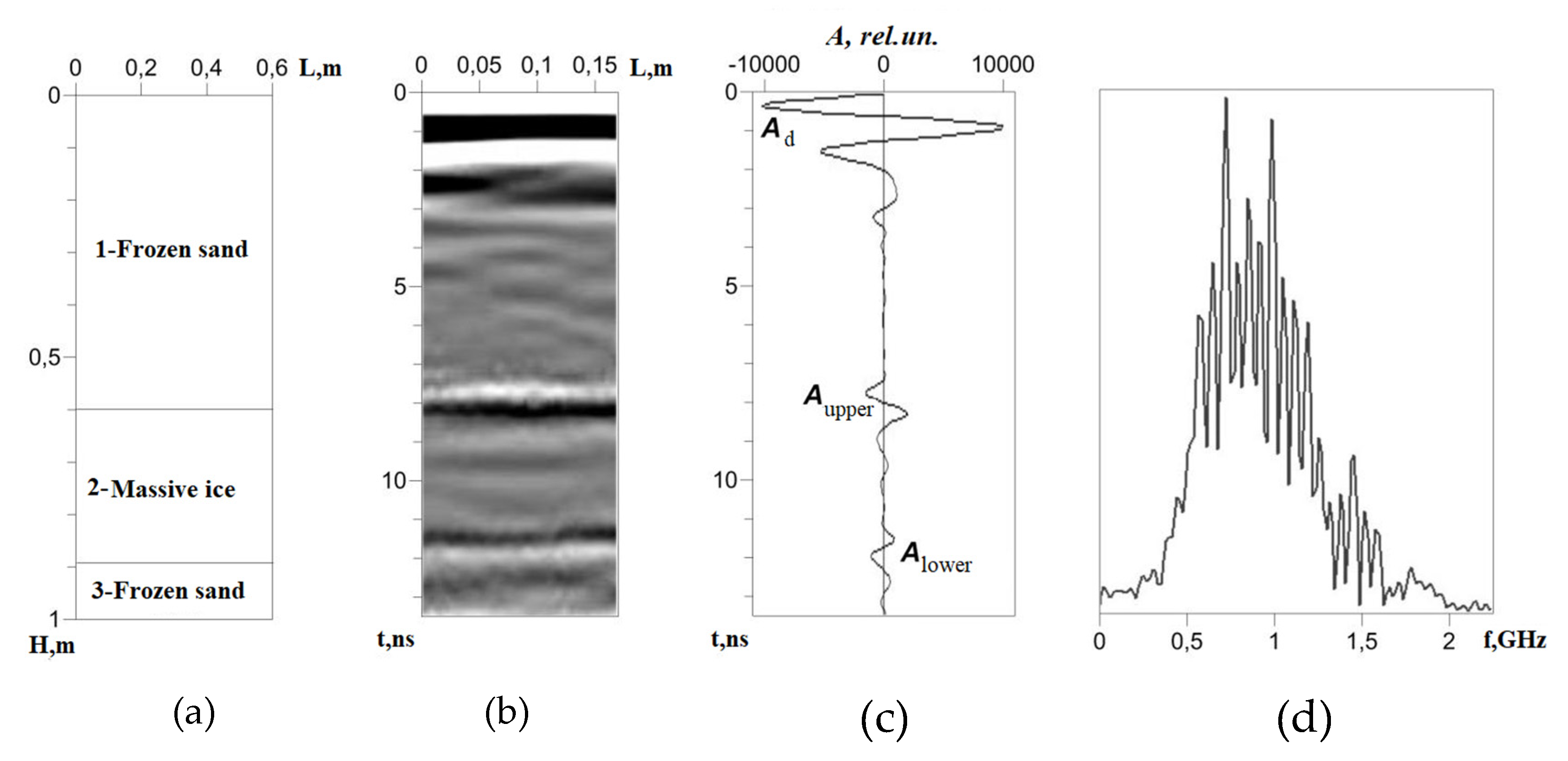
2.4. Physical Simulation of GPR Measurements
3. Results and Discussion
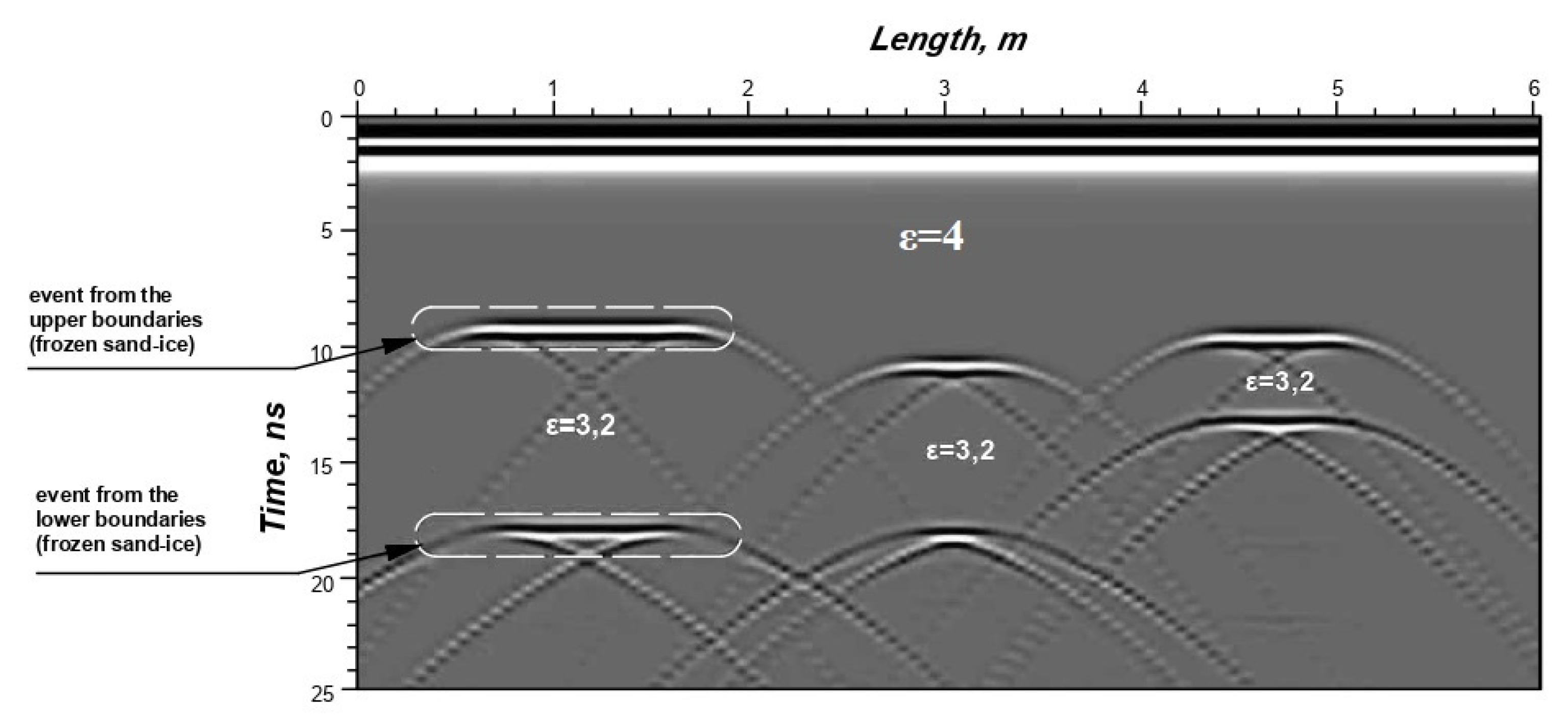
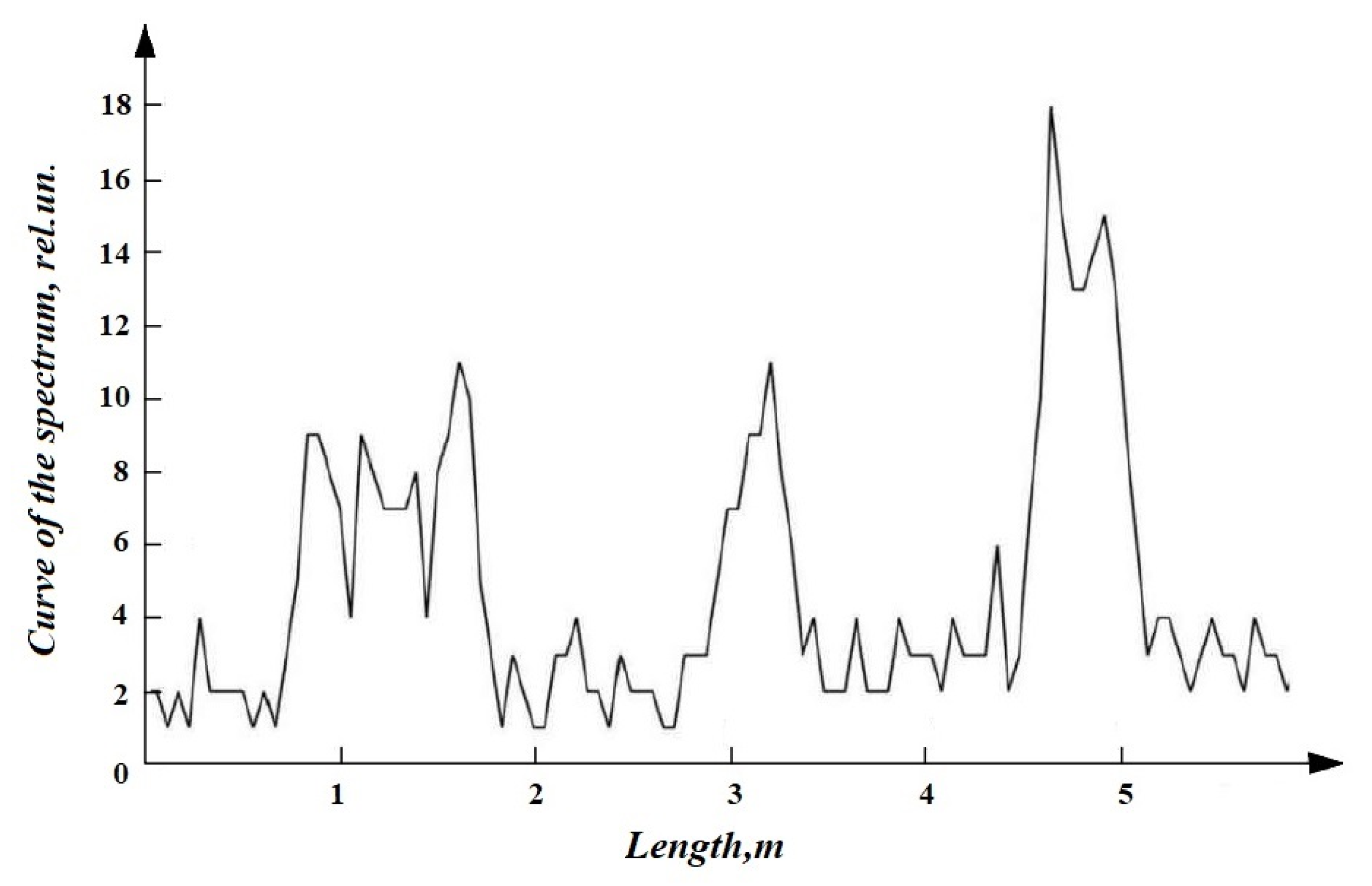
3.1. Computer Simulation
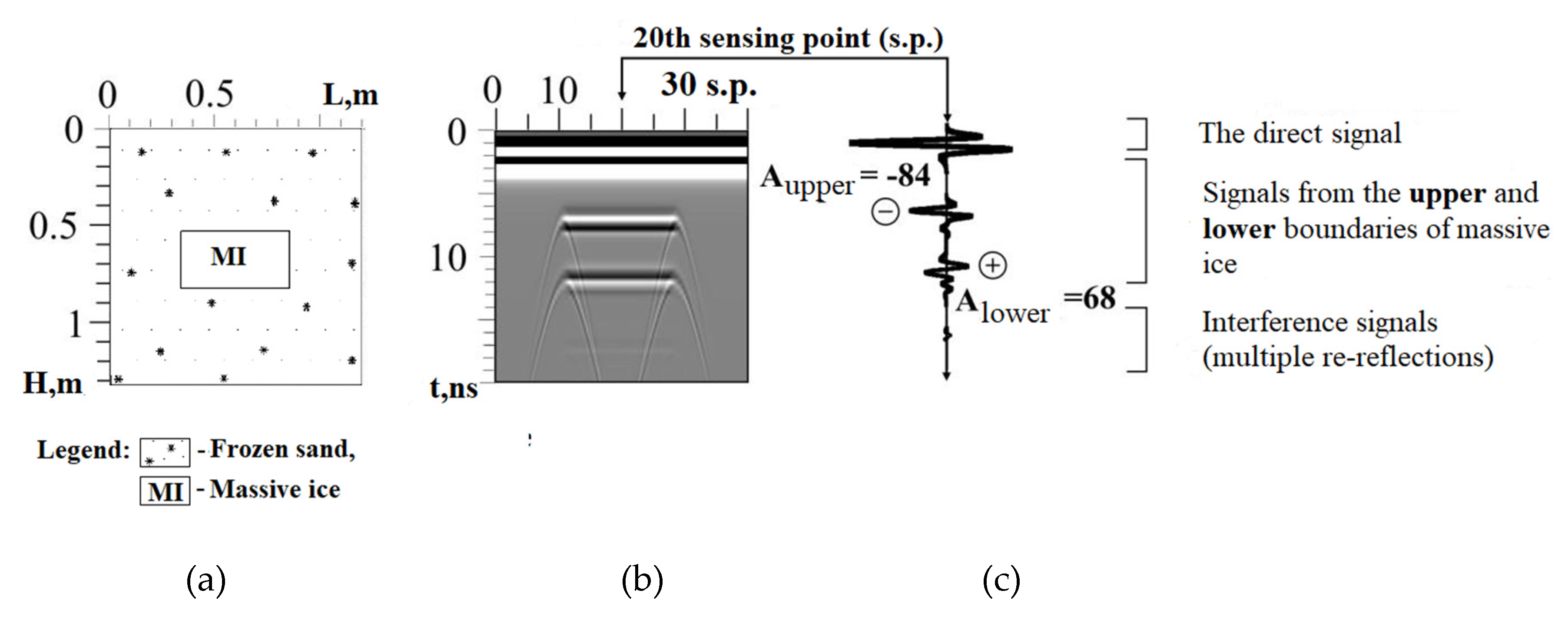
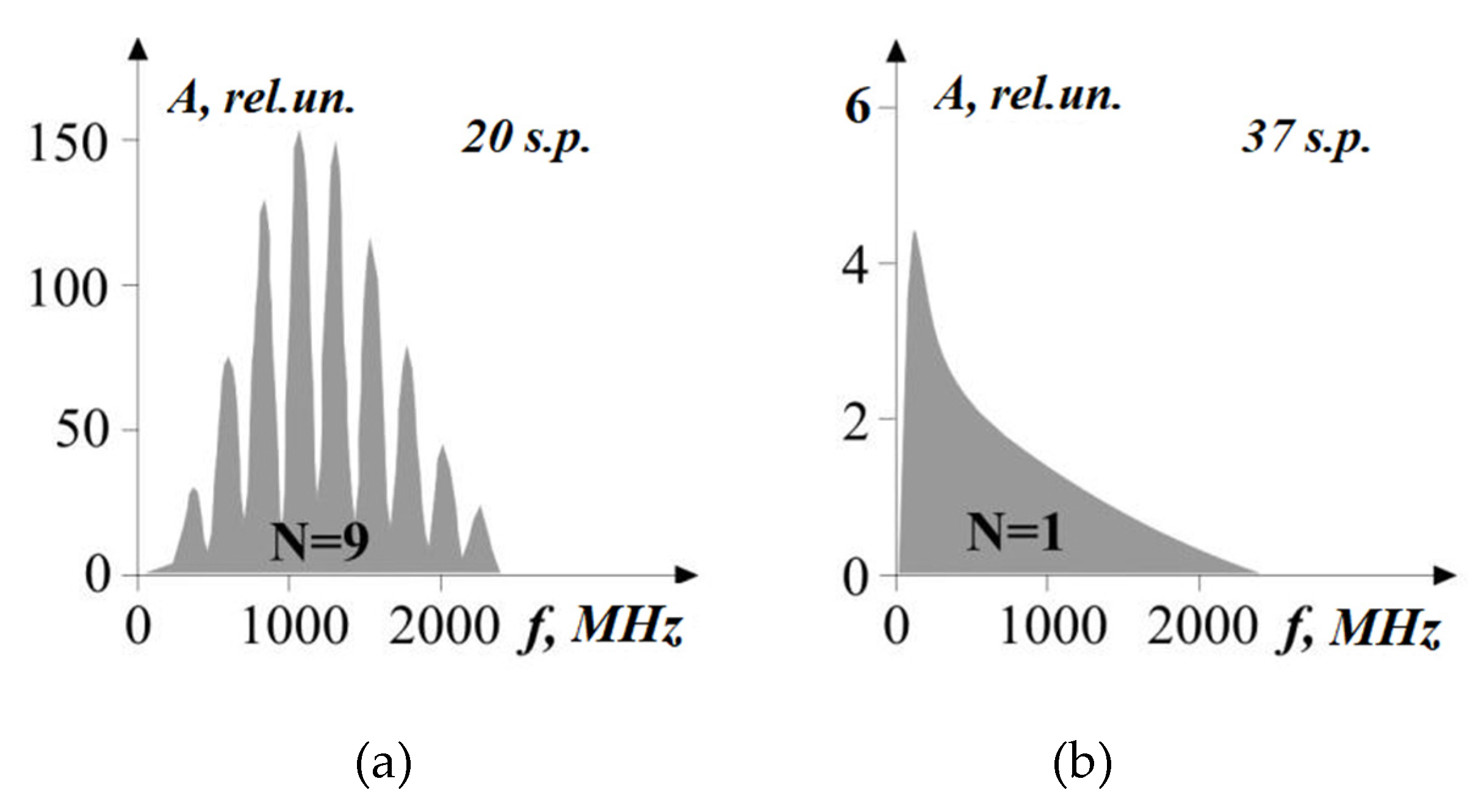
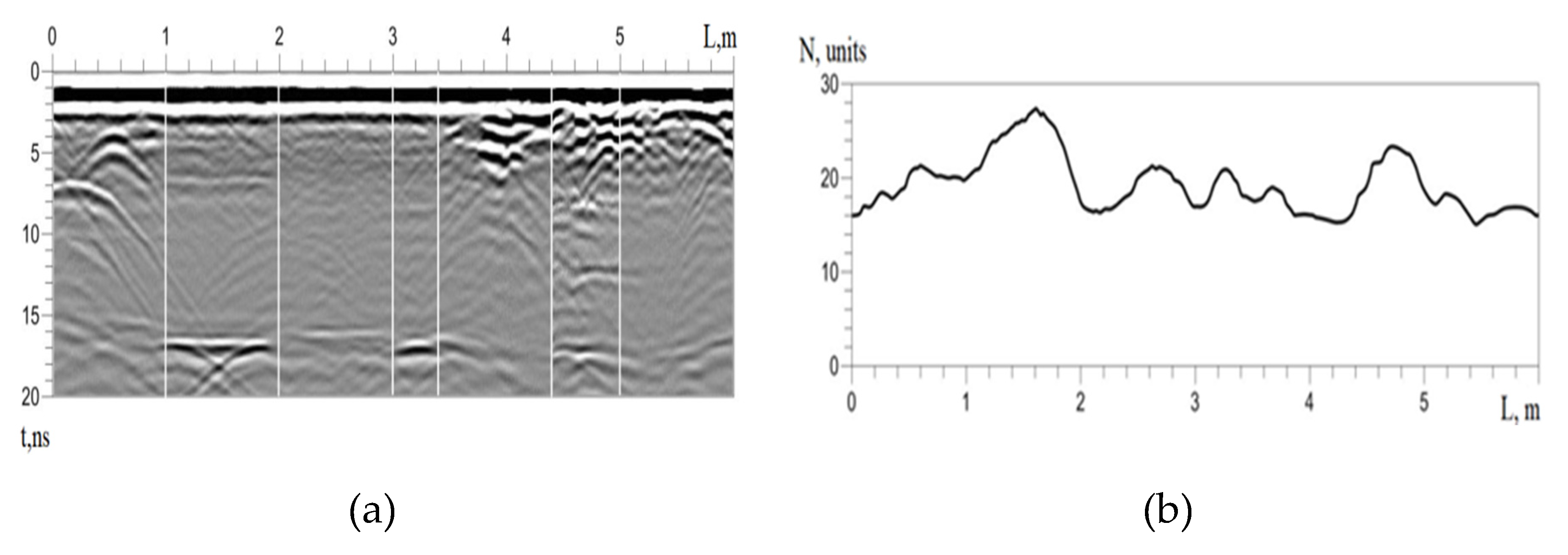
3.2. Physical Simulation
- the presence of two continuous events of the GPR signals located one below the other;
- a change in the phase of the signal from the lower ice boundary, compared with the signal from the upper boundary;
- the Alower/Aupper ratio should be less than 0.95∆t (∆t = tlower − tupper);
- increased “ripple” of the envelope of the Fourier spectrum of GPR trace.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zaikov, K.S.; Kondratov, N.A.; Lipina, S.A.; Bocharova, L.K. Organizational mechanisms for implementing Russia’s Arctic strategy in the 21st century. Arktika Sever 2020, 39, 75–109. [Google Scholar] [CrossRef]
- Karjalainen, O.; Aalto, J.; Luoto, M.; Westermann, S.; Romanovsky, V.E.; Nelson, F.E.; Etzmuller, B.; Hjort, J. Circumpolar permafrost maps and geohazard indices for near-future infrastructure risk assessments. Sci. Data 2019, 6, 190037. [Google Scholar] [CrossRef]
- Vincent, W.F.; Lemay, M.; Allard, M. Arctic permafrost landscapes in transition: Towards an integrated Earth system approach. Arct. Sci. 2017, 3, 39–64. [Google Scholar] [CrossRef]
- Tregubov, O.; Kraev, G.; Maslakov, A. Hazards of activation of cryogenic processes in the Arctic Community: A geopenetrating radar study in Lorino, Chukotka, Russia. Geosciences 2020, 10, 57. [Google Scholar] [CrossRef]
- Instanes, A.; Anisimov, O.; Brigham, L.; Goering, D.; Khrustalev, L.N.; Ladanyi, B.; Larsen, J.O. Infrastructure: Buildings, support systems, and industrial facilities. In Arctic Climate Impact Assessment; Symon, C., Arris, L., Heal, B., Eds.; Cambridge University Press: New York, NY, USA, 2005; Chapter 16; pp. 907–944. [Google Scholar]
- Ford, J.D.; Bell, T.; St-Hilaire-Gravel, D. Vulnerability of community infrastructure to climate change in Nunavut: A case study from Arctic Bay. In Community Adaptation and Vulnerability in Arctic Regions; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2010; pp. 107–130. [Google Scholar] [CrossRef]
- Melvin, A.M.; Larsen, P.; Boehlert, B.; Neumann, J.E.; Chinowsky, P.; Espinet, X.; Martinich, J.; Baumann, M.S.; Rennels, L.; Bothner, A.; et al. Climate damages to Alaska public infrastructure. Proc. Natl. Acad. Sci. USA 2017, 114, E122–E131. [Google Scholar] [CrossRef] [PubMed]
- Shiklomanov, N.; Streletskiy, D. Effect of climate change on Siberian infrastructure. In Regional Environmental Changes in Siberia And Their Global Consequences; Springer Environmental Science and Engineering: Dordrecht, The Netherlands, 2013; pp. 155–170. [Google Scholar] [CrossRef]
- Harris, C.; Arenson, L.U.; Christansen, H.H.; Etzelmuller, B.; Seppälä, M. Permafrost and climate in Europe: Monitoring and modelling thermal, geomorphological and geotechnical responses. Earth Sci. Rev. 2009, 92, 117–171. [Google Scholar] [CrossRef]
- O’Neill, B.; Wolfe, S.; Duchesne, C. New ground ice maps for Canada using a paleogeographic modelling approach. Cryosphere 2019, 13, 753–773. [Google Scholar] [CrossRef]
- Zhang, T.; Barry, R.; Knowles, K.; Heginbottom, J.; Brown, J. Statistics and characteristics of permafrost and ground-ice distribution in the Northern Hemisphere. Polar Geogr. 2008, 31, 47–68. [Google Scholar] [CrossRef]
- Shpolyanskaya, N.A. Massive ground ice as a basis for paleogeographic reconstruction. In Proceedings of the 8th International Conference on Permafrost, Zurich, Switzerland, 21–25 July 2003; Phillips, M., Springman, S.M., Arenson, L.U., Eds.; A.A. Balkema Publishers: Rotterdam, The Netherlands, 2003. [Google Scholar]
- Yoshikawa, K. Notes on open-system pingo ice, Adventdalen, Spitsbergen. Permafr. Periglac. Process. 1993, 4, 327–334. [Google Scholar] [CrossRef]
- Fedorov, A.N.; Vasilyev, N.F.; Torgovkin, Y.I.; Shestakova, A.A.; Varlamov, S.P.; Zheleznyak, M.N.; Shepelev, V.V.; Konstantinov, P.Y.; Kalinicheva, S.S.; Basharin, N.I.; et al. Permafrost-landscape map of the Republic of Sakha (Yakutia) on a scale 1:1,500,000. Geosciences 2018, 8, 465. [Google Scholar] [CrossRef]
- Brown, J.; Ferrians, O.J.; Heginbottom, J.A., Jr.; Melnikov, E.S. Circum-Arctic Map of Permafrost and Ground-Ice Conditions; Circum-Pacific Map Series CP-45; Geological Survey: Washington, DC, USA, 1997. [Google Scholar]
- Tyurin, A.; Isaev, V.; Sergeev, D.; Tumskoi, V.; Volkov, N.; Sokolov, I.; Komarov, O.; Koshurnikov, A.; Gunar, A.; Komarov, I.; et al. Improvement of field methods for engineering geocryological surveying. Mosc. Univ. Geol. Bull. 2019, 74, 70–82. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; King, M.S. The effect of freezing on seismic velocities in unconsolidated permafrost. Geophysics 1986, 51, 1285–1290. [Google Scholar] [CrossRef]
- Dallimore, S.R.; Davis, J.L. Ground probing radar investigations of massive ground ice and near surface geology in continuous permafrost. GSC 1987, 87–1A, 913–918. [Google Scholar] [CrossRef]
- King, M.S.; Zimmerman, R.W.; Corwin, R.F. Seismic and electrical properties of unconsolidated permafrost. Geophys. Prospect 1988, 36, 349–364. [Google Scholar] [CrossRef]
- Draebing, D. Application of refraction seismics in alpine permafrost studies: A review. Earth Sci. Rev. 2016, 155, 136–152. [Google Scholar] [CrossRef]
- Jørgensen, A.; Andreasen, F. Mapping of permafrost surface using ground-penetrating radar at Kangerlussuaq Airport, western Greenland. Cold Reg. Sci. Technol. 2007, 48, 64–72. [Google Scholar] [CrossRef]
- Wollschlager, U.; Gerhards, H.; Yu, Q.; Roth, K. Multi-channel ground-penetrating radar to explore spatial variations in thaw depth and moisture content in the active layer of a permafrost site. Cryosphere 2010, 4, 269–283. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, H.; Li, G. Investigation of the freeze–thaw states of foundation soils in permafrost areas along the China–Russia Crude Oil Pipeline (CRCOP) route using ground-penetrating radar (GPR). Cold Reg. Sci. Technol. 2016, 126, 10–21. [Google Scholar] [CrossRef]
- Wu, T.; Wang, Q.; Zhao, L.; Du, E.; Wang, W.; Batkhishig, O.; Battogtokh, D.; Watanabe, M. Investigating internal structure of permafrost using conventional methods and ground-penetrating radar at Honhor basin, Mongolia. Environ. Earth Sci. 2012, 67, 1869–1876. [Google Scholar] [CrossRef]
- Hauck, C. Frozen ground monitoring using DC resistivity tomography. Geophys. Res. Lett. 2002, 29, 2016. [Google Scholar] [CrossRef]
- Hauck, C. New concepts in geophysical surveying and data interpretation for permafrost terrain. Permafr. Periglac. Process. 2013, 24, 131–137. [Google Scholar] [CrossRef]
- Kneisel, C.; Hauck, C.; Fortier, R.; Morman, B. Advances in geophysical methods for permafrost investigations. Permafr. Periglac. Process. 2008, 19, 157–178. [Google Scholar] [CrossRef]
- Dafflon, B.; Hubbard, S.; Ulrich, C.; Peterson, J.; Wu, Y.; Wainwright, H.; Kneafsey, T. Geophysical estimation of shallow permafrost distribution and properties in an ice-wedge polygon-dominated Arctic tundra region. Geophysics 2016, 81, WA247–WA263. [Google Scholar] [CrossRef]
- Munroe, J.S.; Doolittle, J.A.; Kanevskiy, M.Z.; Hinkel, K.M.; Nelson, F.E.; Jones, B.M.; Shur, Y.; Kimble, J.M. Application of ground-penetrating radar imagery for three-dimensional visualization of near-surface structures in Ice-Rich Permafrost, Barrow, Alaska. Permafr. Periglac. Process. 2007, 18, 309–321. [Google Scholar] [CrossRef]
- Thomson, L.I.; Osinski, G.R.; Pollard, W.H. Application of the Brewster angle to quantify the dielectric properties of ground ice formations. J. Appl. Geophys. 2013, 99, 12–17. [Google Scholar] [CrossRef]
- Watanabe, T.; Matsuoka, N.; Christiansen, H.H. Mudboil and ice-wedge dynamics investigated by electrical resistivity tomography, ground temperatures and surface movements in Svalbard. Geogr. Ann. A 2012, 94, 445–457. [Google Scholar] [CrossRef]
- Hinkel, K.M.; Doolittle, J.A.; Bockheim, J.G.; Nelson, F.E.; Paetzold, R.; Kimble, J.M.; Travis, R. Detection of subsurface permafrost features with ground-penetrating radar, Barrow, Alaska. Permafr. Periglac. Process. 2001, 12, 179–190. [Google Scholar] [CrossRef]
- Watanabe, T.; Matsuoka, N.; Christiansen, H. Ice- and soil-wedge dynamics in the Kapp Linné Area, Svalbard, investigated by two- and three-dimensional GPR and ground thermal and acceleration regimes. Permafr. Periglac. Process. 2013, 24, 39–55. [Google Scholar] [CrossRef]
- De Pascale, G.P.; Pollard, W.H.; Williams, K.K. Geophysical mapping of ground ice using a combination of capacitive coupled resistivity and ground-penetrating radar, Northwest Territories, Canada. J. Geophys. Res. Earth Surf. 2008, 113, F02S90. [Google Scholar] [CrossRef]
- Moorman, B.J.; Robinson, S.D.; Burgess, M.M. Imaging Periglacial Conditions with Ground-penetrating Radar. Permafr. Periglac. Process. 2003, 14, 319–329. [Google Scholar] [CrossRef]
- Angelopoulos, M.C.; Pollard, W.H.; Couture, N.J. The application of CCR and GPR to characterize ground ice conditions at Parsons Lake, Northwest Territories. Cold Reg. Sci. Technol. 2013, 85, 22–33. [Google Scholar] [CrossRef]
- Brandt, O.; Langley, K.; Kohler, J.; Hamran, S. Detection of buried ice and sediment layers in permafrost using multi-frequency Ground Penetrating Radar: A case examination on Svalbard. Remote Sens. Environ. 2007, 111, 212–227. [Google Scholar] [CrossRef]
- Yoshikawa, K.; Leuschen, C.; Ikeda, A.; Harada, K.; Gogineni, P.; Hoekstra, P.; Hinzman, L.; Sawada, Y.; Matsuoka, N. Comparison of geophysical investigations for detection of massive ground ice (pingo ice). J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Shennen, S.; Tronicke, J.; Wetterich, S.; Allrogen, N.; Schwamborn, G.; Schirrmeister, L. 3D ground-penetrating radar imaging of ice complex deposits in northern East Siberia. Geophysics 2016, 81, WA185–WA192. [Google Scholar] [CrossRef]
- Hausmann, H.; Behm, M. Imaging the structure of cave ice by ground-penetrating radar. Cryosphere 2011, 5, 329–340. [Google Scholar] [CrossRef]
- Annan, A.P.; Davis, J.L. Impulse radar soundings in permafrost. Radio Sci. 1976, 11, 383–394. [Google Scholar] [CrossRef]
- Daniels, D. Ground Penetrating Radar, 2nd ed.; The Institution of Electrical Engineers: London, UK, 2004; p. 726. [Google Scholar]
- Finkel’shtejn, M.I.; Mendel’son, V.L.; Kutev, V.A. Radiolokacija Sloistyh Zemnyh Pokrovov; Sov. Radio: Moscow, Russia, 1977; p. 167. [Google Scholar]
- Benedetto, A.; Pajewski, L. Civil Engineering Applications of Ground Penetrating Radar; Springer: Berlin, Germany, 2015; p. 371. [Google Scholar]
- Daniels, D.J. Ground Penetrating Radar; Institution of Engineering and Technology: Stevenage, UK, 2004; p. 761. [Google Scholar]
- Hunter, L.E.; Delaney, A.J.; Lawson, D.E.; Davis, L. Downhole GPR for high-resolution analysis of material properties near Fairbanks, Alaska. Geol. Soc. Spec. Publ. 2003, 211, 275–285. [Google Scholar] [CrossRef]
- Lapazaran, J.J.; Otero, J.; Martin-Espanol, A.; Navarro, F.J. On the errors involved in ice-thickness estimates I: Ground-penetrating radar measurement errors. J. Glaciol. 2016, 62, 1008–1020. [Google Scholar] [CrossRef]
- Harkevich, A.A. Spektry i Analiz; Knizhnyj dom «LIBROKOM»: Moscow, Russia, 2009; p. 240. [Google Scholar]
- Warren, C.; Giannopoulos, A.; Giannakis, I. gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef]
- Lapazaran, J.J.; Otero, J.; Martin-Espanol, A.; Navarro, F.J. On the errors involved in ice-thickness estimates II: Errors in digital elevation models of ice thickness. J. Glaciol. 2016, 62, 1021–1029. [Google Scholar] [CrossRef][Green Version]
- Onana, V.; Koenig, L.; Ruth, J.; Studinger, M.; Harbeck, J. A semiautomated multilayer picking algorithm for ice-sheet radar echograms applied to ground-based near-surface data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 51–69. [Google Scholar] [CrossRef]
- Freeman, G.; Bovik, A.; Holt, J. Automated detection of near surface Martian ice layers in orbital radar data. In Proceedings of the IEEE Southwest Symposium on Image Analysis and Interpretation, Austin, TX, USA, 23–25 May 2010; pp. 117–120. [Google Scholar] [CrossRef]
- Ilisei, A.; Bruzzone, L. A model-based technique for the automatic detection of earth continental ice subsurface targets in radar sounder data. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1911–1915. [Google Scholar] [CrossRef]
- Ilisei, A.; Bruzzone, L. A system for the automatic classification of ice sheet subsurface targets in radar sounder data. IEEE Geosci. Remote Sens. Lett. 2015, 53, 3260–3277. [Google Scholar] [CrossRef]
- Panton, C.; Karlsson, N. Automated mapping of near bed radio-echo layer disruptions in the Greenland Ice Sheet. Earth Planet Sci. Lett. 2015, 432, 323–331. [Google Scholar] [CrossRef]
- Ferro, A.; Bruzzone, L. Automatic extraction and analysis of ice layering in radar sounder data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1622–1634. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sokolov, K.; Fedorova, L.; Fedorov, M. Prospecting and Evaluation of Underground Massive Ice by Ground-Penetrating Radar. Geosciences 2020, 10, 274. https://doi.org/10.3390/geosciences10070274
Sokolov K, Fedorova L, Fedorov M. Prospecting and Evaluation of Underground Massive Ice by Ground-Penetrating Radar. Geosciences. 2020; 10(7):274. https://doi.org/10.3390/geosciences10070274
Chicago/Turabian StyleSokolov, Kirill, Larisa Fedorova, and Maksim Fedorov. 2020. "Prospecting and Evaluation of Underground Massive Ice by Ground-Penetrating Radar" Geosciences 10, no. 7: 274. https://doi.org/10.3390/geosciences10070274
APA StyleSokolov, K., Fedorova, L., & Fedorov, M. (2020). Prospecting and Evaluation of Underground Massive Ice by Ground-Penetrating Radar. Geosciences, 10(7), 274. https://doi.org/10.3390/geosciences10070274






