A Method for Quantitative Interpretation of Stationary Thermal Fields for Layered Media
Abstract
1. Introduction
2. Methods
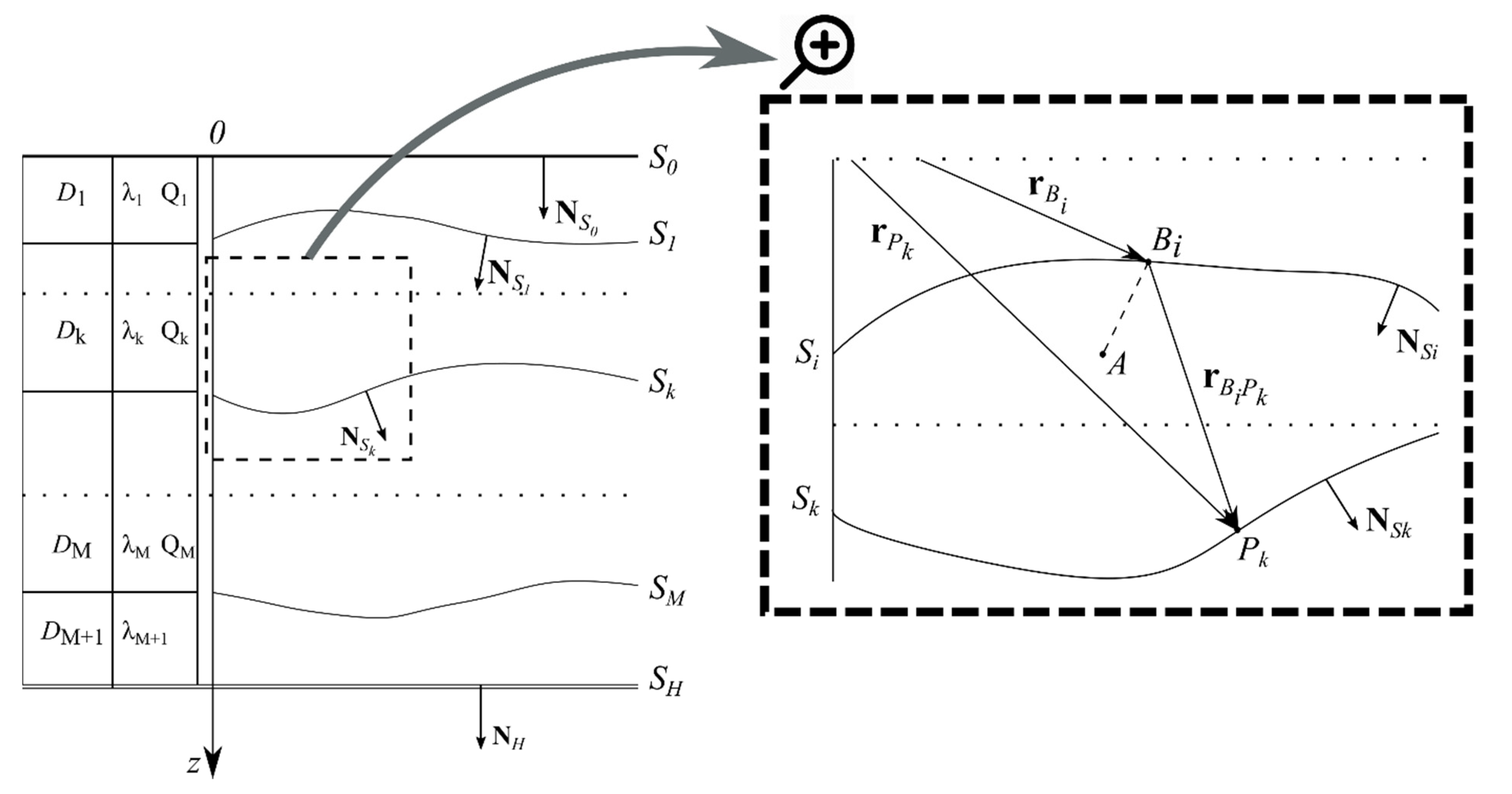
2.1. Generalized Continuous Operator of the Conjugacy Problem
2.2. Integral Transforms and Green’s Formula
2.3. Low Contrast Approximation
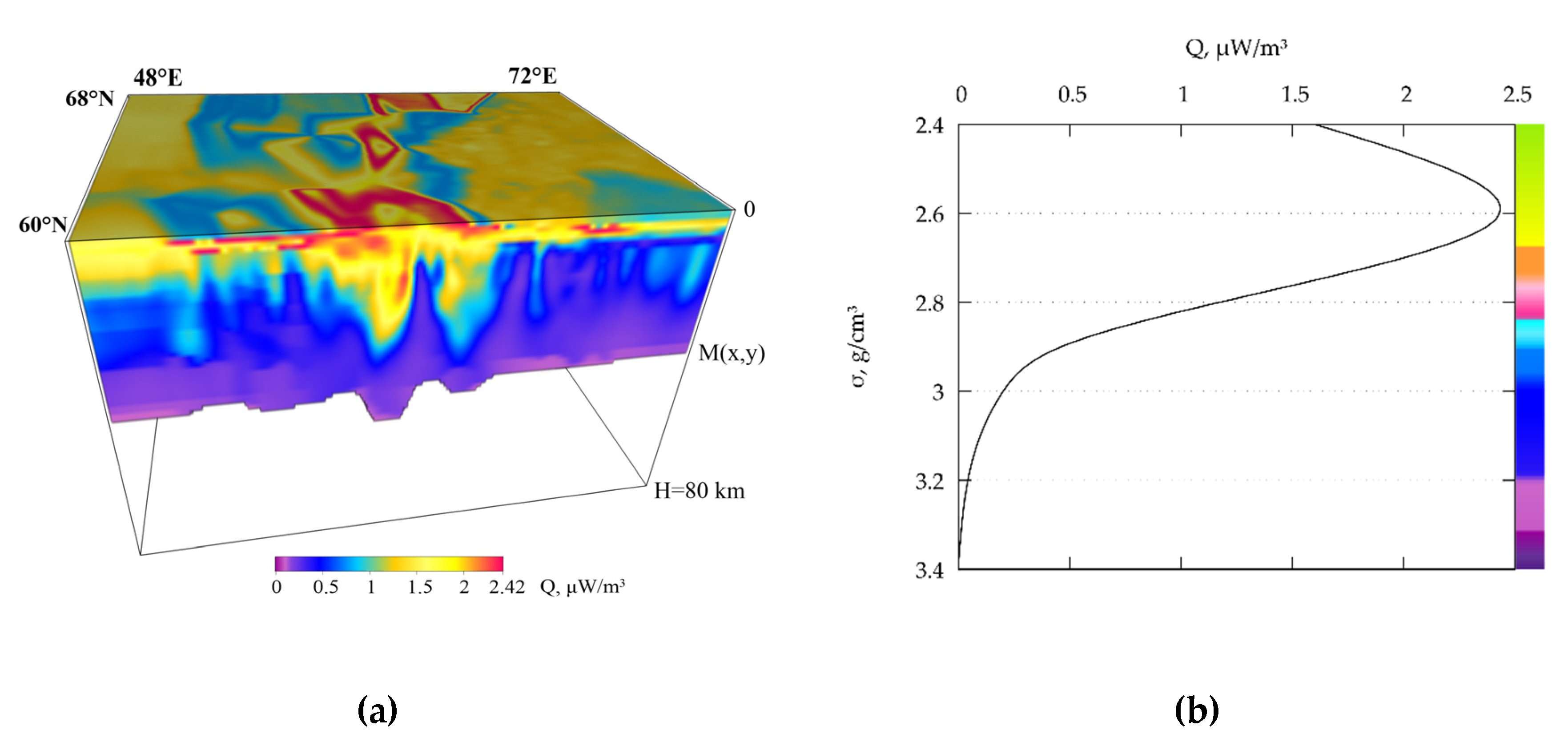
2.4. Mantle Heat Flow
3. Case Study
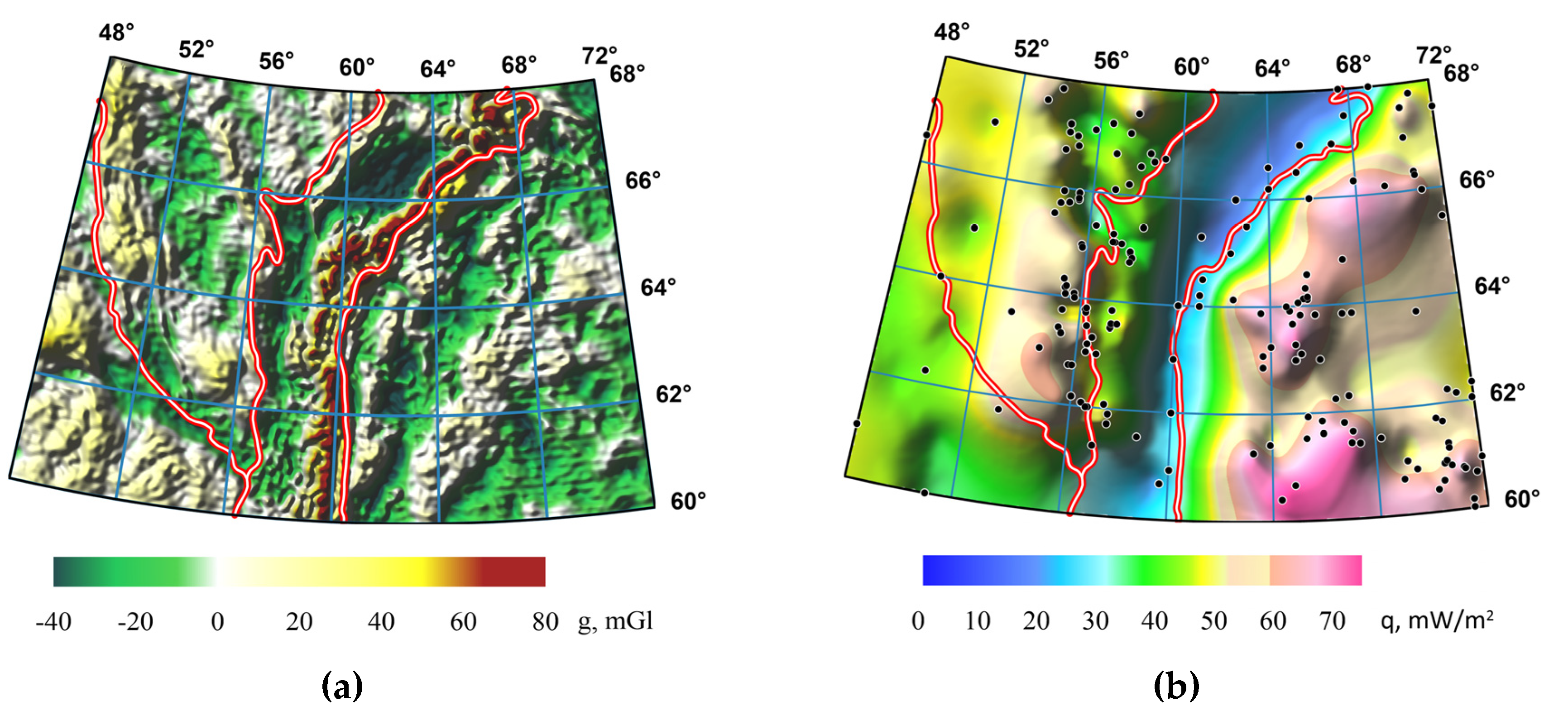
3.1. Initial Data
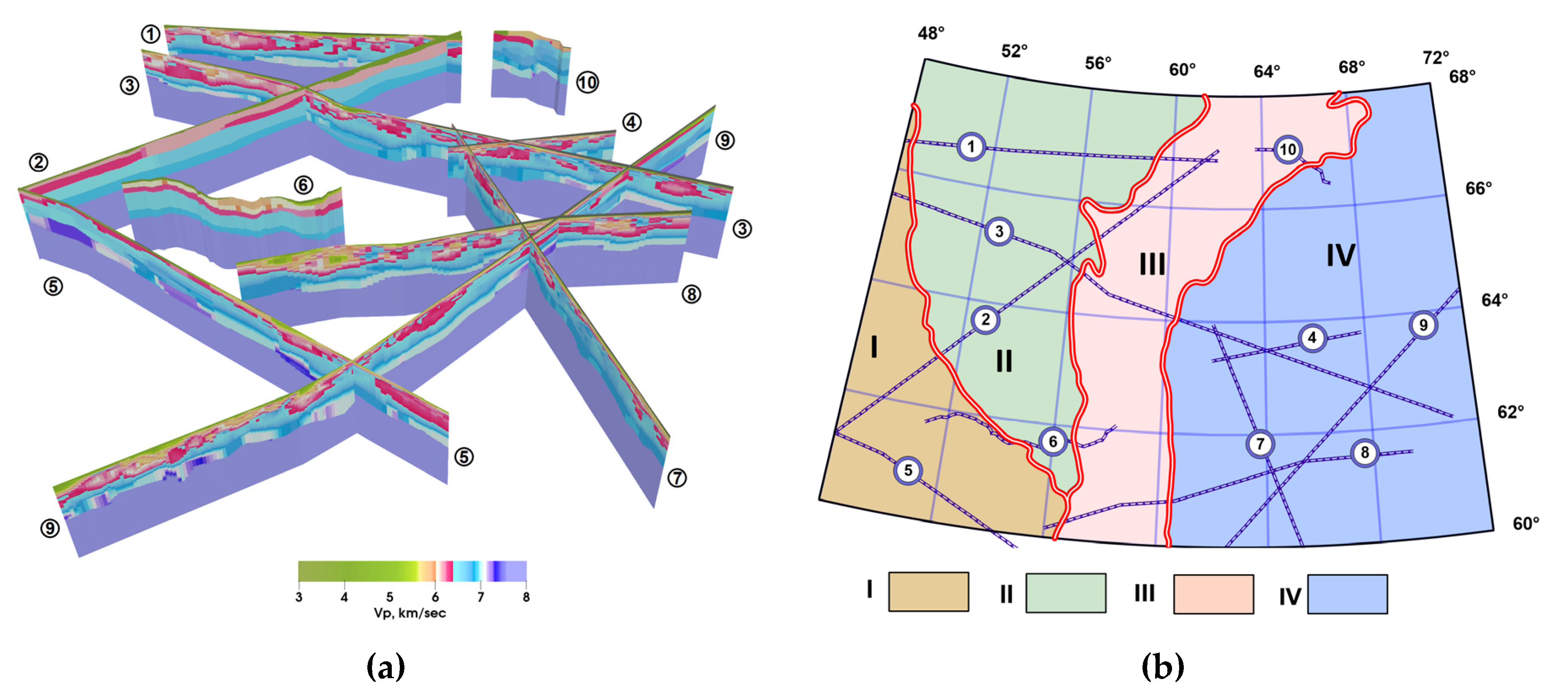
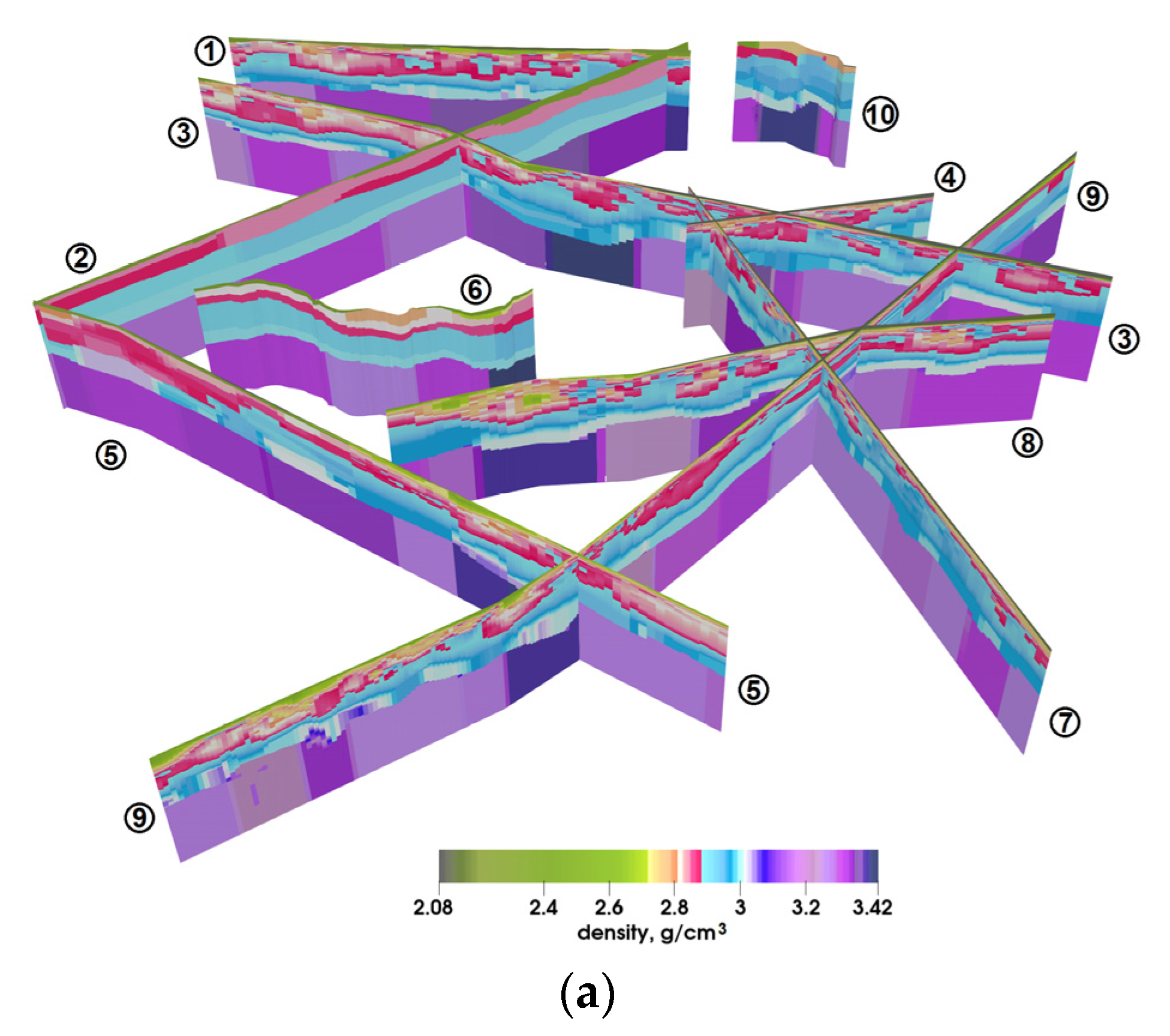
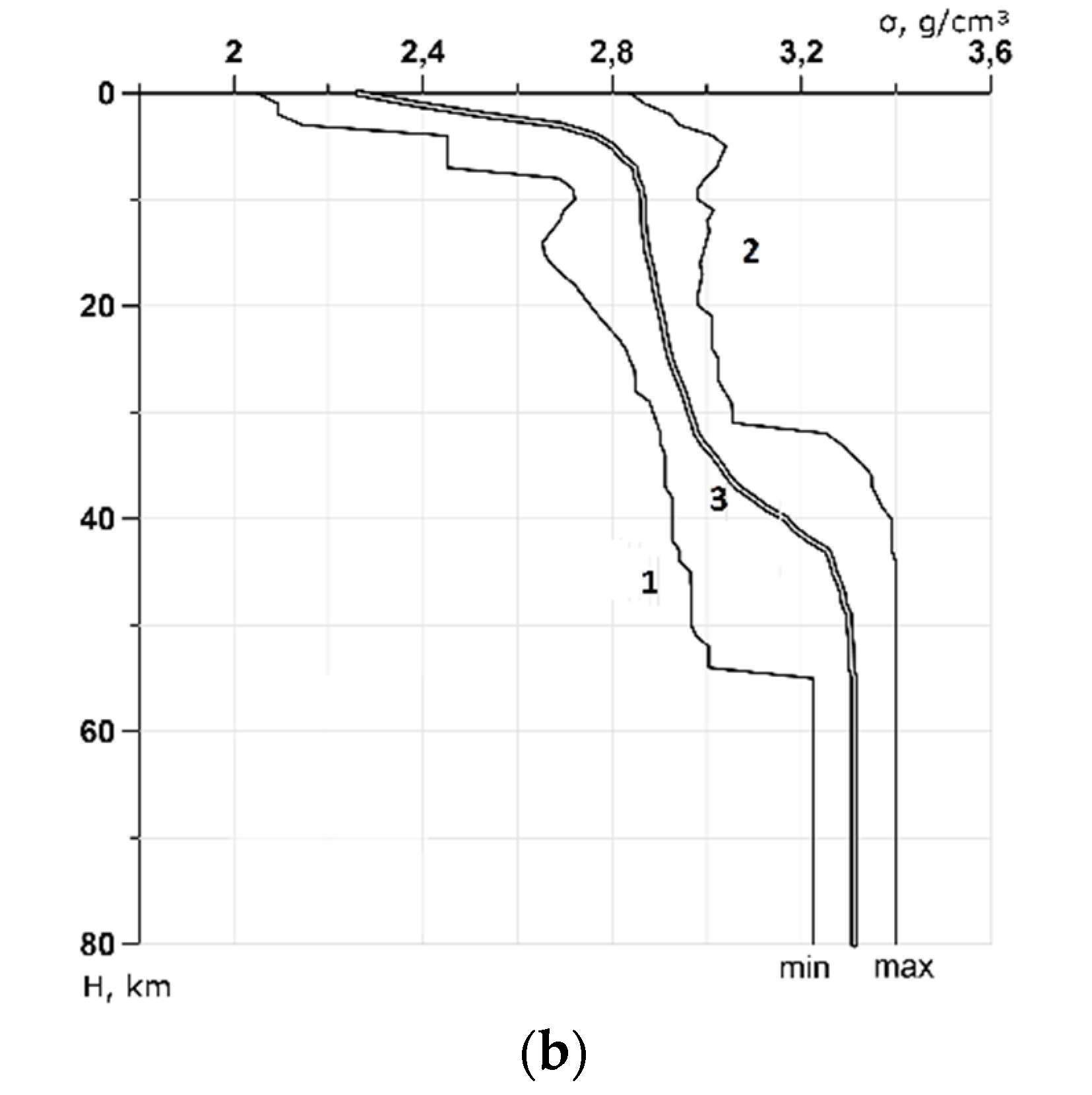
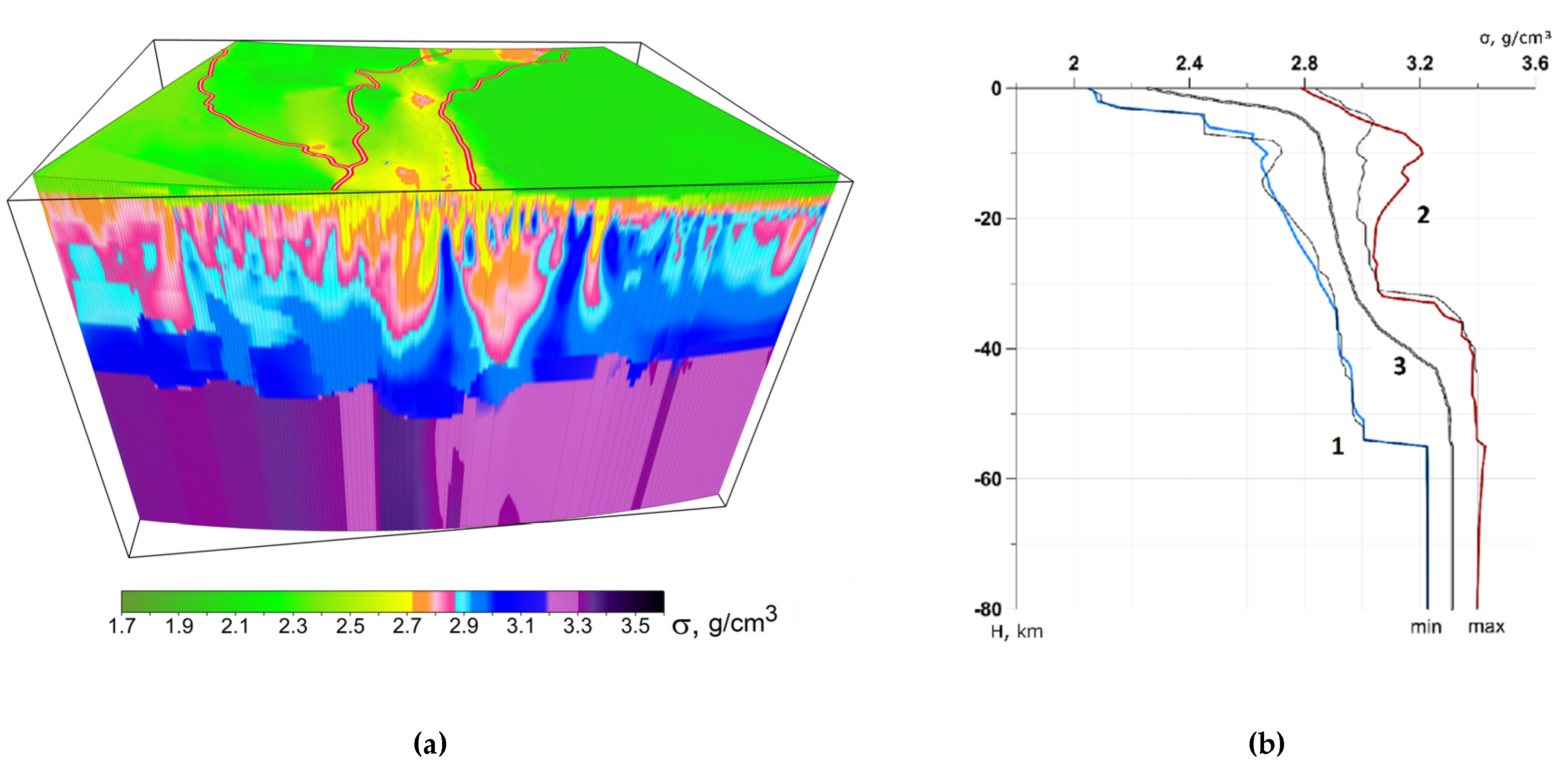
3.2. Initial Density Model
3.3. Refined Density Model
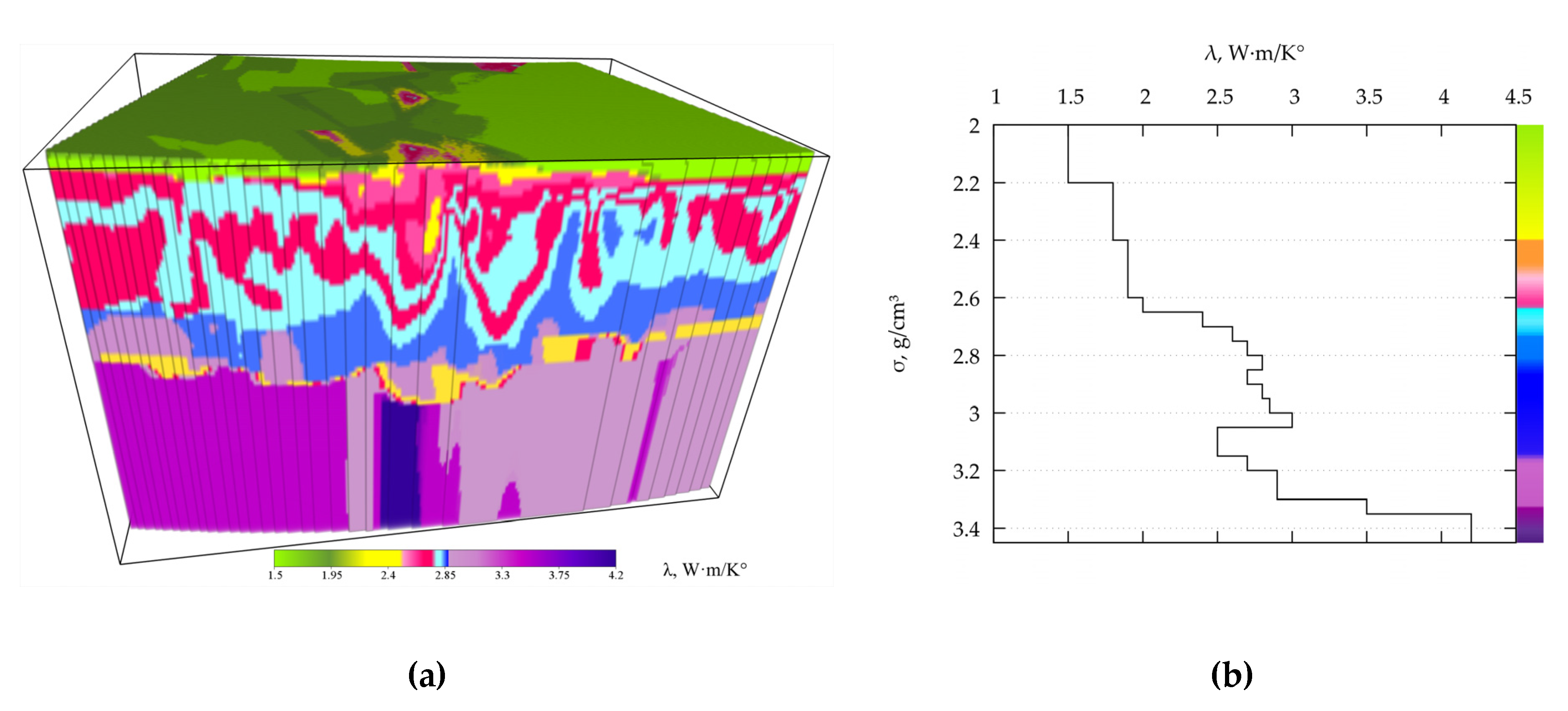
3.4. Grid Approximation of Thermal Physical Parameters of Geothermal Model
3.5. Forward Geothermal Problem
4. Results
Inverse Problem of Analytical Fields Continuation
5. Conclusions
Supplementary Materials
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
Appendix C
| Name | Symbol | Unit | Comment |
|---|---|---|---|
| Calculated temperature | °K | Celsius scale is acceptable too | |
| P-waves velocity | km/s | ||
| Mass density | g/cm3 | ||
| Temperature at earth’s surface level | °C | ||
| Thermal conductivity coefficient | W·m/°K | ||
| Thermal diffusivity coefficient | cm2/s | ||
| Power of thermal sources | Q | μW/m3 | |
| Calculated heat flux at earth’s surface | mW/m2 | ||
| Model layer thickness | H | km | |
| Thermal contact surface | km2 | Element of square | |
| Equation of boundary surface | km | ||
| Implicit form of boundary surface equation | |||
| Unit normal for the contact surface | |||
| Parameter of neighbor surfaces contrast | |||
| Function for the area | |||
| Density of simple layer | °K/km2 | Defined for layer | |
| Delta function | km−1 | ||
| Green’s function for two planes | km−1 | ||
| Green’s function for media with M layers | km−1 |
References
- Crough, S.T.; Thompson, G.A. Thermal model of continental lithosphere. J. Geophys. Res. 1976, 81, 4857–4862. [Google Scholar] [CrossRef]
- Gordienko, V.V.; Pavlenkova, N.I. Combined geothermal-geophysical models of the earth’s crust and upper mantle for the European continent. J. Geodyn. 1985, 4, 75–90. [Google Scholar] [CrossRef]
- Artemieva, I.M. The continental lithosphere: Reconciling thermal, seismic, and petrologic data. Lithos 2009, 109, 23–46. [Google Scholar] [CrossRef]
- Beardsmore, G.; Cull, J. Crustal Heat Flow: A Guide to Measurement and Modelling; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Artemieva, I.M.; Mooney, W.D. Thermal thickness and evolution of Precambrian lithosphere: A global study. J. Geophys. Res. 2001, 106, 16387–16414. [Google Scholar] [CrossRef]
- Sclater, J.G.; Jaupart, C.; Galson, D. The heat flow through oceanic and continental crust and the heat loss of the Earth. Rev. Geophys. Space Phys. 1980, 18, 269–311. [Google Scholar] [CrossRef]
- Khutorskoi, M.D.; Polyak, B.G. Role of radiogenic heat generation in surface heat flow formation. Geotectonics 2016, 50, 179–195. [Google Scholar] [CrossRef]
- Golovanova, I.V. Thermal Field of the Southern Urals; Nauka: Moscow, Russia, 2005. (In Russian) [Google Scholar]
- Kukkonen, I.T.; Golovanova, I.V.; Khachay, Y.V.; Druzhinin, V.S.; Kosarev, A.M.; Schapov, V.A. Low Geothermal heat flow of the Urals fold belt—Implication of low heat production, fluid circulation or palaeoclimate? Tectonophysics 1997, 276, 63–85. [Google Scholar] [CrossRef]
- Pavlenkova, N.I. Rheological properties of the upper mantle of Northern Eurasia and nature of regional boundaries according to the data of long-range seismic profiles. Russ. Geol. Geophys. 2011, 52, 1016–1027. [Google Scholar] [CrossRef]
- Kutas, R.I. Thermal flow and geothermic models of the earth’s crust of the Ukrainian Carpathians. Geofiz. Zhurnal 2014, 36, 3–27. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Ladovskiy, I.V.; Martyshko, P.S.; Byzov, D.D.; Tsidaev, A.G. Conjugacy Problem for Stationary Heat Fields. Dokl. Earth Sci. 2019, 488, 1072–1075. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Samarskii, A.A. Equations of Mathematical Physics; Dover Publications: New York, NY, USA, 1990. [Google Scholar]
- Mises, R.; Frank, P.; Weber, H.; Riemann, B. Die Differential und Integralgleichungen der Mechanik und Physik, 2nd expanded ed.; Mary S. Rosenberg: New York, NY, USA, 1943. [Google Scholar]
- Vladimirov, V.S. Equations of Mathematical Physics, 2nd ed.; Mir Publishers: Moscow, Russia, 1984. [Google Scholar]
- Martyshko, P.S.; Ladovskii, I.V.; Fedorova, N.V.; Byzov, D.D.; Tsidaev, A.G. Theory and Methods of Complex Interpretation of Geophysical Data; UB RAS: Yekaterinburg, Russia, 2016; (In Russian). Available online: http://igfuroran.ru/Math/book.pdf (accessed on 13 December 2019).
- Gel′fand, I.M.; Shilov, G.E. Generalized Functions, Volume 1: Properties and Operations; AMS Chelsea Publishing: Providence, RI, USA, 1959. [Google Scholar]
- Geological-Geophysical Profiles of Russia (Opornie Geologo-Geofizicheskie Pofili Rossii). Available online: https://www.vsegei.ru/ru/info/seismic/ (accessed on 6 December 2019).
- Milanovskiy, E.E. Tektonicheskaya Karta Rossii, Sopredel’nykh Territoriy i Akvatoriy; MGU: Moscow, Russia, 2006. (In Russian) [Google Scholar]
- Bouman, J.; Ebbing, J.; Meekes, S.; Fattah, R.A.; Fuchs, M.; Gradmann, S.; Haagmans, R.; Lieb, V.; Schmidt, M.; Dettmering, D.; et al. GOCE gravity gradient data for lithospheric modeling. Int. J. Appl. Earth Obs. 2015, 35, 16–30. [Google Scholar] [CrossRef]
- Bonvalot, S.; Balmino, G.; Briais, A.; Kuhn, M.; Peyrefitte, A.; Vales, N.; Biancale, R.; Gabalda, G.; Reinquin, F.; Sarrailh, M. World Gravity Map; Commission for the Geological Map of the World, BGI-CGMW-CNES-IRD: Paris, France, 2012. [Google Scholar]
- Bulashevich, Y.P. Informativnost geotermii pri izuchenii zemnoy kory Uralskoy evogeosinklinali. Izv. AN SSSR Fiz. Zemli 1983, 8, 76–83. (In Russian) [Google Scholar]
- Gosnold, W.D.; Panda, B. The Global Heat Flow Database of the International Heat Flow Commission. Available online: https://engineering.und.edu/research/global-heat-flow-database/data.html (accessed on 13 December 2019).
- Artemieva, I.M. Global 1° × 1° thermal model TC1 for the continental lithosphere: Implications for lithosphere secular evolution. Tectonophysics 2006, 416, 245–277. [Google Scholar] [CrossRef]
- Duchkov, A.D.; Zheleznyak, M.N.; Ayunov, D.E.; Veselov, O.V.; Sokolova, L.S.; Kazantsev, S.A.; Gornov, P.Y.; Dobretsov, N.N.; Boldyrev, D.V.; Pchelnikov, A.N.; et al. Geothermal Atlas of Siberia and Far East (2009–2015). Available online: http://maps.nrcgit.ru/geoterm/ (accessed on 6 December 2019).
- Kutas, R. Heat flow, radiogenic heat and crustal thick-ness in south-west USSR. Tectonophysics 1984, 103, 167–174. [Google Scholar] [CrossRef]
- Zui, V.I.; Boborykin, A.M.; Urban, G.I.; Zhuk, M.S. Heat flow and seismicity within western part of the East European platform. Lithosphere (Belarus) 1995, 3, 114–127. [Google Scholar]
- Krüger, L. Konforme Abbildung des Erdellipsoids in die Ebene; Veröffentlichung des Königlich Preuszischen Geodätischen Instituts N. F.: Potsdam, Germany, 1912. [Google Scholar]
- Martyshko, P.S.; Ladovskij, I.V.; Byzov, D.D.; Chernoskutov, A.I. On Solving the Forward Problem of Gravimetry in Curvilinear and Cartesian Coordinates: Krasovskii’s Ellipsoid and Plane Modeling. Izv. Phys. Solid Earth 2018, 54, 565–573. [Google Scholar] [CrossRef]
- Martyshko, P.; Byzov, D.; Ladovskii, I.; Tsidaev, A. 3D density models construction method for layered media. In AIP Conference Proceedings 2164,120010, Proceedings of SGEM2015 Conference 15th International Multidisciplinary Scientific GeoConference SGEM 2015, Albena, Bulgaria, 18–24 June 2015; AIP Publishing: Melville, NY, USA, 2019; Book 2; Volume 1, pp. 2425–2432. [Google Scholar]
- Martyshko, P.S.; Ladovskii, I.V.; Byzov, D.D.; Tsidaev, A.G. Gravity Data Inversion with Method of Local Corrections for Finite Elements Models. Geosciences 2018, 8, 373. [Google Scholar] [CrossRef]
- Martyshko, P.S.; Ladovskiy, I.V.; Byzov, D.D. Solution of the Gravimetric Inverse Problem Using Multidimensional Grids. Dokl. Earth Sci. 2013, 450, 666–671. [Google Scholar] [CrossRef]
- Martyshko, P.; Ladobskii, I.; Byzov, D.; Tsidaev, A. Density Earth’s crust models creation using gravity and seismic data. In AIP Conference Proceedings 2164,120010, Proceedings of SGEM2018 Conference 18th International Multidisciplinary Scientific GeoConference SGEM 2018, Albena, Bulgaria, 2–8 July 2018; AIP Publishing: Melville, NY, USA, 2019; Volume 18, pp. 749–754. [Google Scholar]
- Rybach, L.; Buntebarth, G. Relationship between the petrophysical properties, density, seismic velocity, heat generation and mineralogical constitution. Earth Planet. Sci. Lett. 1982, 57, 367. [Google Scholar] [CrossRef]
- Cermak, V.; Bodri, L.; Rybach, L.; Buttenbarth, G. Relalionship between seismic velocity and heat production: Comparison of two sets of data and test of validity. Earth Planet. Sci. Lett. 1990, 99, 48–57. [Google Scholar] [CrossRef]
- Duchkov, A.D.; Sokolova, L.S. Termicheskaya struktura litosfery Sibirskoy platformy. Russ. Geol. Geophys. 1997, 38, 494–503. [Google Scholar]
- Majorowicz, J.; Wybraniec, S. New terrestrial heat flow map of Europe after regional paleoclimatic correction application. Int. J. Earth Sci. 2011, 100, 881–887. [Google Scholar] [CrossRef]
- Golovanova, I.V.; Sal’manova, R.Y.; Demezhko, D.Y. Climate reconstruction in the Urals from geothermal data. Russ. Geol. Geophys. 2012, 53, 1366–1373. [Google Scholar] [CrossRef]
- Sneddon, I.N. Fourier Transforms; Dover Publications, Inc.: New York, NY, USA, 1995. [Google Scholar]
- Gray, A.; Mathews, G.B. A Treatise on Bessel Functions and Their Applications to Physics; Macmillan and Co., Ltd.: New York, NY, USA, 1952. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ladovskii, I.V.; Martyshko, P.S.; Tsidaev, A.G.; Byzov, D.D. A Method for Quantitative Interpretation of Stationary Thermal Fields for Layered Media. Geosciences 2020, 10, 199. https://doi.org/10.3390/geosciences10050199
Ladovskii IV, Martyshko PS, Tsidaev AG, Byzov DD. A Method for Quantitative Interpretation of Stationary Thermal Fields for Layered Media. Geosciences. 2020; 10(5):199. https://doi.org/10.3390/geosciences10050199
Chicago/Turabian StyleLadovskii, Igor V., Petr S. Martyshko, Alexander G. Tsidaev, and Denis D. Byzov. 2020. "A Method for Quantitative Interpretation of Stationary Thermal Fields for Layered Media" Geosciences 10, no. 5: 199. https://doi.org/10.3390/geosciences10050199
APA StyleLadovskii, I. V., Martyshko, P. S., Tsidaev, A. G., & Byzov, D. D. (2020). A Method for Quantitative Interpretation of Stationary Thermal Fields for Layered Media. Geosciences, 10(5), 199. https://doi.org/10.3390/geosciences10050199





