Bayesian Inference in Snow Avalanche Simulation with r.avaflow
Abstract
1. Introduction
2. Simulation and Postprocessing
3. Avalanche Data
4. Back Calculation
4.1. Mathematical Framework
- The prior probability density encoding the prior knowledge about the model parameters;
- The likelihood function expressing the probability of the observed data when the parameter has a given value .
4.2. Application—Kerngraben Avalanche
5. Forward Calculation and Prediction
5.1. Mathematical Framework
5.2. Forward Calculation—Application to the Kerngraben Avalanche
5.3. Prediction—Application to the Wolfsgruben Avalanche
6. Conditional Runout Probabilities
6.1. Mathematical Framework
6.2. Application to the Kerngraben and Wolfsgruben Avalanche
7. Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- CEN. Eurocode 7: Geotechnical Design—Part 1: General Rules; European Committee for Standardization: Brussels, Belgium, 2004. [Google Scholar]
- Favier, P.; Eckert, N.; Faug, T.; Bertrand, D.; Naaim, M. Avalanche risk evaluation and protective dam optimal design using extreme value statistics. J. Glaciol. 2016, 26, 725–749. [Google Scholar] [CrossRef]
- Ancey, C.; Meunier, M.; Richard, D. Inverse problem in avalanche dynamics models. Water Resour. Res. 2003, 39, 1099. [Google Scholar] [CrossRef]
- Eckert, N.; Parent, E.; Richard, D. Revisiting statistical-topographical methods for avalanche predetermination: Bayesian modelling for runout distance predictive distribution. Cold Reg. Sci. Technol. 2007, 49, 88–107. [Google Scholar] [CrossRef]
- Eckert, N.; Parent, E.; Belanger, L.; Garcia, S. Hierarchical Bayesian modelling for spatial analysis of the number of avalanche occurrences at the scale of the township. Cold Reg. Sci. Technol. 2007, 50, 97–112. [Google Scholar] [CrossRef]
- Eckert, N.; Naaim, M.; Parent, E. Long-term avalanche hazard assessment with a Bayesian depth-averaged propagation model. J. Glaciol. 2010, 56, 563–586. [Google Scholar] [CrossRef]
- Eckert, N.; Parent, E.; Naaim, M.; Richard, D. Bayesian stochastic modelling for avalanche predetermination: From a general system framework to return period computations. Stoch. Environ. Res. Risk Assess. 2008, 22, 185–206. [Google Scholar] [CrossRef]
- Straub, D.; Grêt-Regamey, A. A Bayesian probabilistic framework for avalanche modelling based on observations. Cold Reg. Sci. Technol. 2006, 46, 192–203. [Google Scholar] [CrossRef]
- Mergili, M.; Fischer, J.T.; Krenn, J.; Pudasaini, S.P. r. avaflow v1, an advanced open-source computational framework for the propagation and interaction of two-phase mass flows. Geosci. Model Dev. 2017, 10, 553–569. [Google Scholar] [CrossRef]
- Fischer, J.T. A novel approach to evaluate and compare computational snow avalanche simulation. Nat. Hazards Earth Syst. Sci. 2013, 13, 1655–1667. [Google Scholar] [CrossRef]
- Fischer, J.T.; Kofler, A.; Fellin, W.; Granig, M.; Kleemayr, K. Multivariate parameter optimization for computational snow avalanche simulation. J. Glaciol. 2015, 61, 875–888. [Google Scholar] [CrossRef]
- Lambe, T. Predictions in soil engineering. Géotechnique 1973, 23, 151–202. [Google Scholar] [CrossRef]
- Voellmy, A. Über die Zerstörungskraft von Lawinen. Schweizerische Bauzeitung 1955, 73, 1–25. [Google Scholar]
- Salm, B.; Burkhard, A.; Gubler, H.U. Berechnung von Fliesslawinen: Eine Anleitung fuer Praktiker; mit Beispielen. Mitteilungen Des Eidgenoessischen Instituts Fuer Schnee- Und Lawinenforschung 1990, 47, 1–37. [Google Scholar]
- Buser, O.; Bartelt, P. Production and decay of random kinetic energy in granular snow avalanches. J. Glaciol. 2009, 55, 3–12. [Google Scholar] [CrossRef]
- Rauter, M.; Fischer, J.T.; Fellin, W.; Kofler, A. Snow avalanche friction relation based on extended kinetic theory. Nat. Hazards Earth Syst. Sci. 2016, 16, 2325–2345. [Google Scholar] [CrossRef]
- Schaefer, M. Shear and normal stresses measured on the Weissfluhjoch Snow Chute. Can. Geotech. J. 2015, 52, 1–10. [Google Scholar] [CrossRef]
- Gruber, U.; Bartelt, P. Snow avalanche hazard modelling of large areas using shallow water numerical methods and GIS. Environ. Model. Softw. 2007, 22, 1472–1481. [Google Scholar] [CrossRef]
- Ancey, C.; Meunier, M. Estimating bulk rheological properties of flowing snow avalanches from field data. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Bühler, Y.; Christen, M.; Kowalski, J.; Bartelt, P. Sensitivity of snow avalanche simulations to digital elevation model quality and resolution. Ann. Glaciol. 2011, 52, 72–80. [Google Scholar] [CrossRef]
- Bühler, Y.; von Rickenbach, D.; Stoffel, A.; Margreth, S.; Stoffel, L.; Christen, M. Automated snow avalanche release area delineation—Validation of existing algorithms and proposition of a new object-based approach for large-scale hazard indication mapping. Nat. Hazards Earth Syst. Sci. 2018, 18, 3235–3251. [Google Scholar] [CrossRef]
- Johannesson, T.; Gauer, P.; Issler, P.; Lied, K. The design of avalanche protection dams. In Recent Practical and Theoretical Developments European Commission; Directorate General for Research: Brussels, Belgium, 2009. [Google Scholar]
- Teich, M.; Fischer, J.T.; Feistl, T.; Bebi, P.; Christen, M.; Grêt-Regamey, A. Computational snow avalanche simulation in forested terrain. Nat. Hazards Earth Syst. Sci. 2014, 14, 2233–2248. [Google Scholar] [CrossRef]
- CAA. Observation Guidelines and Recording Standards for Weather Snowpack and Avalanches; Technical Report; Canadian Avalanche Association: Revelstoke, BC, Canada, 2016. [Google Scholar]
- Open Data Österreich. Available online: https://www.data.gv.at/ (accessed on 17 April 2020).
- Maggioni, M.; Gruber, U. The influence of topographic parameters on avalanche release dimension and frequency. Cold Reg. Sci. Technol. 2003, 37, 407–419. [Google Scholar] [CrossRef]
- Bühler, Y.; Kumar, S.; Veitinger, J.; Christen, M.; Stoffel, A. Automated identification of potential snow avalanche release areas based on digital elevation models. Nat. Hazards Earth Syst. Sci. 2013, 13, 1321–1335. [Google Scholar] [CrossRef]
- Veitinger, J.; Purves, R.; Sovilla, B. Potential slab avalanche release area identification from estimated winter terrain: A multi-scale, fuzzy logic approach. Nat. Hazards Earth Syst. Sci. Discuss. 2015, 3, 3569–6614. [Google Scholar] [CrossRef]
- McClung, D.; Gauer, P. Maximum frontal speeds, alpha angles and deposit volumes of flowing snow avalanches. Cold Reg. Sci. Technol. 2018, 153, 78–85. [Google Scholar] [CrossRef]
- Fischer, J.T.; Fromm, R.; Gauer, P.; Sovilla, B. Evaluation of probabilistic snow avalanche simulation ensembles with Doppler radar observations. Cold Reg. Sci. Technol. 2014, 97, 151–158. [Google Scholar] [CrossRef]
- McClung, D.M.; Schaerer, P. The Avalanche Handbook, 3rd ed.; The Mountaineers Books: Seattle, WA, USA, 2006; p. 342. [Google Scholar]
- Gauer, P. Comparison of avalanche front velocity measurements and implications for avalanche models. Cold Reg. Sci. Technol. 2014, 97, 132–150. [Google Scholar] [CrossRef]
- Hastings, W. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Brooks, S.; Gelman, A.; Jones, G.L.; Meng, X.L. Handbook of Markov Chain Monte Carlo; Chapman and Hall/CRC: London, UK, 2011. [Google Scholar]
- Kaipio, J.; Somersalo, E. Statistical and computational inverse problems. In Applied Mathematical Sciences; Springer: Berlin/Heidelberg, Geimany, 2005; Volume 160. [Google Scholar]
- Nummelin, E. General Irreducible Markov Chains and Non-Negative Operators; Cambridge University Press: Cambridge, UK, 2004; Volume 83. [Google Scholar]
- Robert, C.P.; Casella, G. Monte Carlo Statistical Methods, 2nd ed.; Springer Texts in Statistics; Springer: New York, NY, USA, 2004. [Google Scholar]
- Bédard, M.; Rosenthal, J.S. Optimal scaling of Metropolis algorithms: Heading toward general target distributions. Canad. J. Statist. 2008, 36, 483–503. [Google Scholar] [CrossRef]
- Gelman, A.; Roberts, G.U.; Gilks, W.R. Efficient Metropolis jumping rules. In Bayesian Statistics; 5 (Alicante, 1994); Bernardo, J.M., Berger, J.O., Dawid, A.P., Smith, A.F.M., Eds.; Oxford University Press: New York, NY, USA, 1996; pp. 599–607. [Google Scholar]
- Kofler, A.; Fischer, J.; Huber, A.; Fellin, W.; Rauter, M.; Granig, M.; Hainzer, E.; Tollinger, C.; Kleemayr, K. Multivariate parameter optimization for operational application of extended kinetic theory in simulation software. In Proceedings of the International Snow Science Workshop, Breckenridge, CO, USA, 3–7 October 2016. [Google Scholar]
- Sailer, R.; Rammer, L.; Sampl, P. Recalculation of an artificially released avalanche with SAMOS and validation with measurements from a pulsed Doppler radar. Nat. Hazards Earth Syst. Sci. 2002, 2, 211–216. [Google Scholar] [CrossRef]
- Oberndorfer, S.; Granig, M. Modellkalibrierung des Lawinensimulationsprogramms SamosAT; Technical Report; Forsttechnischer Dienst für Wildbach-und Lawinenverbauung, Stabstelle Schnee und Lawinen: Schwaz, Austria, 2007. [Google Scholar]
- Held, L.; Sabanés Bové, D. Applied Statistical Inference; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer Series in Statistics; Springer Science+Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Graham, C.; Talay, D. Stochastic Simulation and Monte Carlo Methods: Mathematical Foundations of Stochastic Simulation, 1st ed.; Stochastic Modelling and Applied Probability 68; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Mergili, M.; Emmer, A.; Juřicová, A.; Cochachin, A.; Fischer, J.T.; Huggel, C.; Pudasaini, S.P. How well can we simulate complex hydro-geomorphic process chains? The 2012 multi-lake outburst flood in the Santa Cruz Valley (Cordillera Blanca, Perú). Earth Surf. Process. Landforms 2018, ESP-16-0360.R3. [Google Scholar] [CrossRef]
- Lavigne, A.; Eckert, N.; Bel, L.; Deschâtres, M.; Parent, E. Modelling the spatio-temporal repartition of right-truncated data: An application to avalanche runout altitudes in Hautes-Savoie. Stoch. Environ. Res. Risk Assess. 2017, 31, 629–644. [Google Scholar] [CrossRef]
- Sampl, P.; Zwinger, T. Avalanche simulation with SAMOS. Ann. Glaciol. 2004, 38, 393–398. [Google Scholar] [CrossRef]
- Christen, M.; Bartelt, P.; Kowalski, J. Back calculation of the In den Arelen avalanche with RAMMS: Interpretation of model results. Ann. Glaciol. 2010, 51, 161–168. [Google Scholar] [CrossRef]
- Valero, C.V.; Wever, N.; Christen, M.; Bartelt, P. Modeling the influence of snow cover temperature and water content on wet-snow avalanche runout. Nat. Hazards Earth Syst. Sci. 2018, 18, 869. [Google Scholar] [CrossRef]
- Sovilla, B.; McElwaine, J.; Köhler, A. The Intermittency Regions of Powder Snow Avalanches. J. Geophys. Res. (Earth Surf.) 2018, 123, 2525–2545. [Google Scholar] [CrossRef]
- Köhler, A.; McElwaine, J.N.; Ash, B.S.A.M.; Brennan, P. The dynamics of surges in the 3 February 2015 avalanches in Vallee de la Sionne. J. Geophys. Res. Earth Surf. 2016, 121, 2192–2210. [Google Scholar] [CrossRef]
- Rauter, M.; Köhler, A. Constraints on Entrainment and Deposition Models in Avalanche Simulations from High-Resolution Radar Data. Geosciences 2019, 10, 9. [Google Scholar] [CrossRef]
- Fellin, W.; Oberguggenberger, M. Robust assessment of shear parameters from direct shear tests. Int. J. Reliab. Saf. 2012, 6, 49–64. [Google Scholar] [CrossRef]
| r [m] | [m] | [ ] | [%] | [%] | [m/s] | [m/s] | |
|---|---|---|---|---|---|---|---|
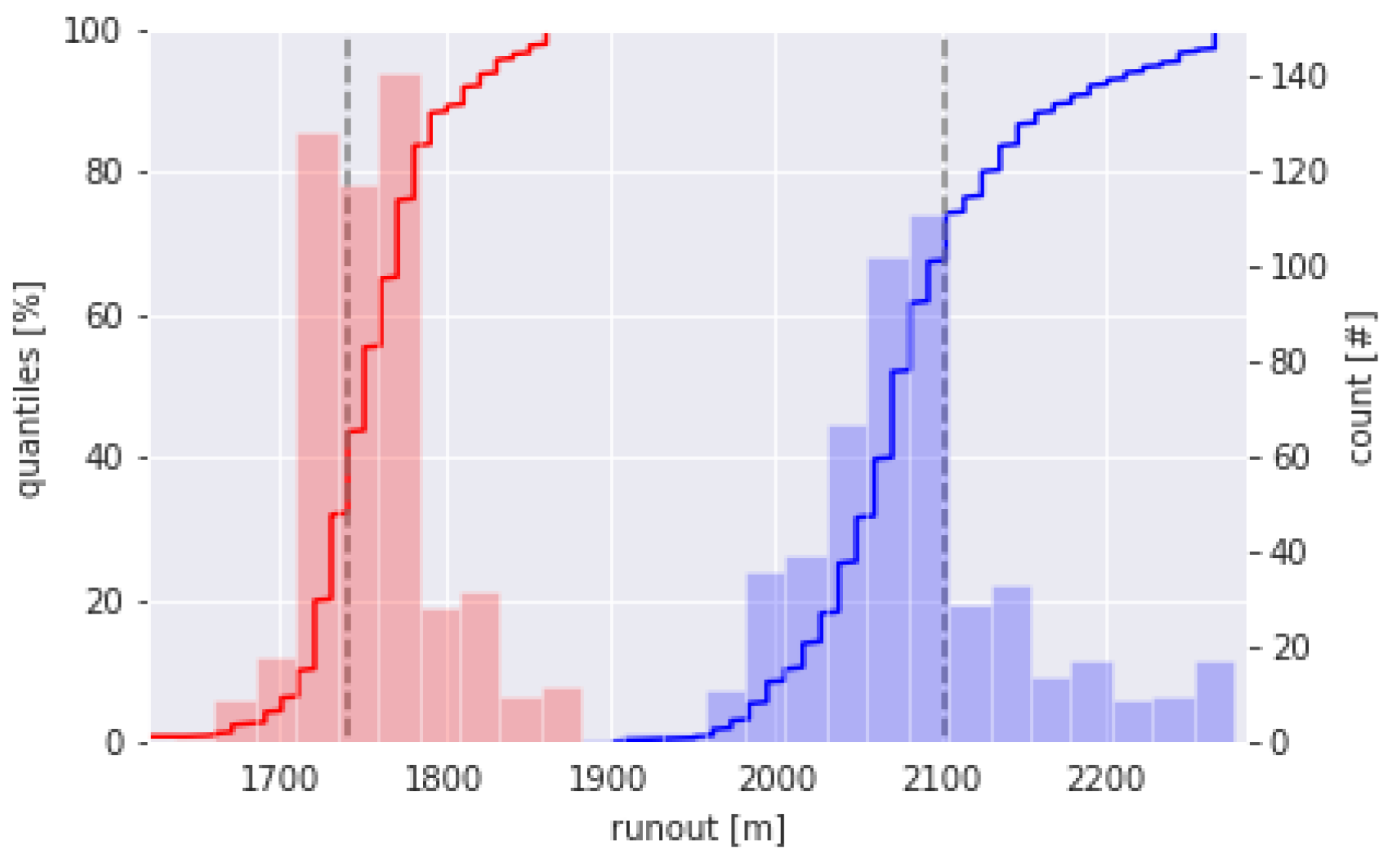
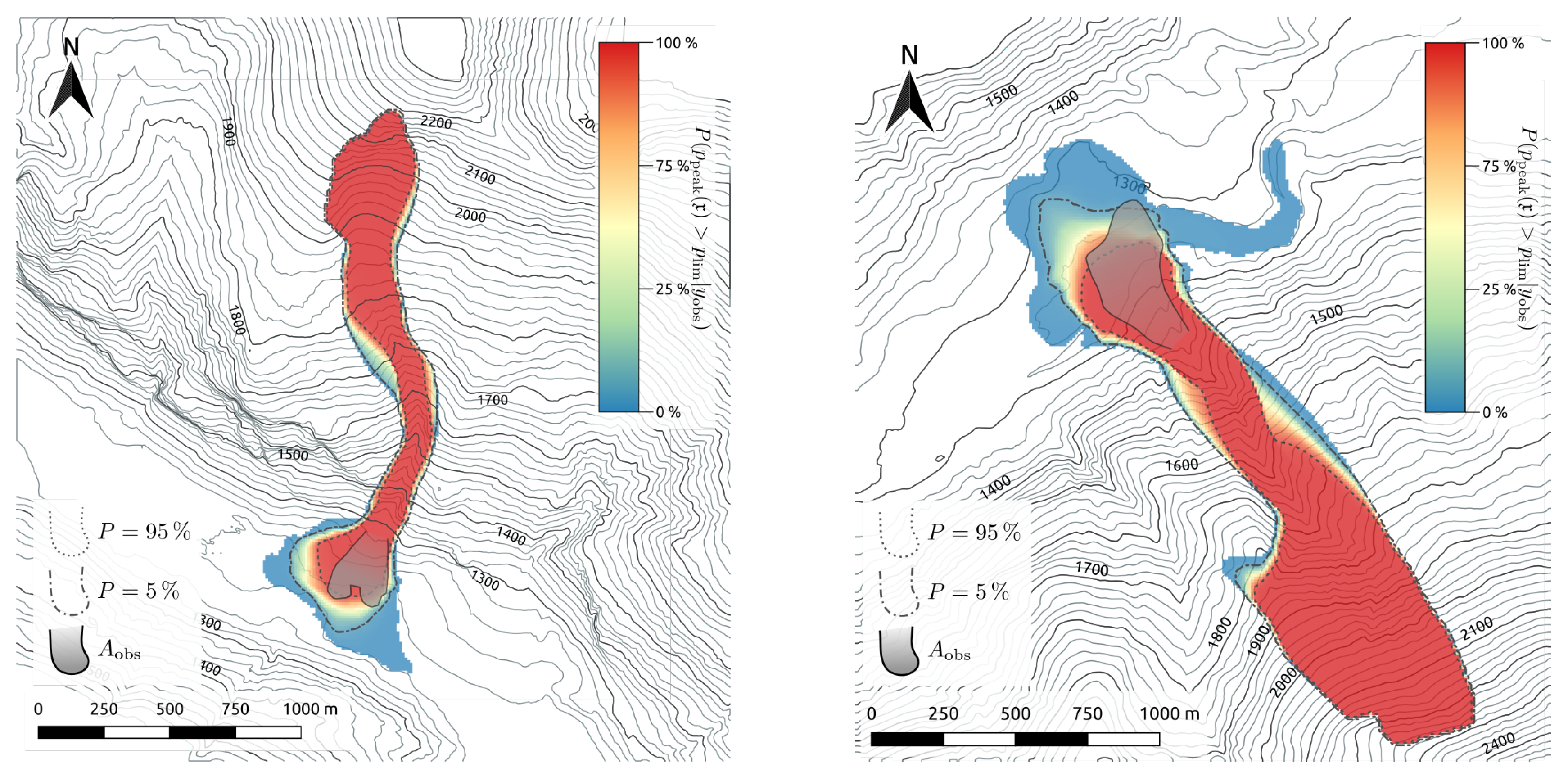
| Kerngraben avalanche | 1741 | 1751 | 241,272 | 0.99 | 0.53 | 55 | 25 |
| Wolfsgruben avalanche | 2103 | 2071 | 550,992 | 0.97 | 0.32 | 58 | 35 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fischer, J.-T.; Kofler, A.; Huber, A.; Fellin, W.; Mergili, M.; Oberguggenberger, M. Bayesian Inference in Snow Avalanche Simulation with r.avaflow. Geosciences 2020, 10, 191. https://doi.org/10.3390/geosciences10050191
Fischer J-T, Kofler A, Huber A, Fellin W, Mergili M, Oberguggenberger M. Bayesian Inference in Snow Avalanche Simulation with r.avaflow. Geosciences. 2020; 10(5):191. https://doi.org/10.3390/geosciences10050191
Chicago/Turabian StyleFischer, Jan-Thomas, Andreas Kofler, Andreas Huber, Wolfgang Fellin, Martin Mergili, and Michael Oberguggenberger. 2020. "Bayesian Inference in Snow Avalanche Simulation with r.avaflow" Geosciences 10, no. 5: 191. https://doi.org/10.3390/geosciences10050191
APA StyleFischer, J.-T., Kofler, A., Huber, A., Fellin, W., Mergili, M., & Oberguggenberger, M. (2020). Bayesian Inference in Snow Avalanche Simulation with r.avaflow. Geosciences, 10(5), 191. https://doi.org/10.3390/geosciences10050191





