Physical Parameters and Contrasts of Wooden Objects in Lacustrine Environment: Ground Penetrating Radar and Geoelectrics
Abstract
1. Introduction
- (i)
- Investigating electric resistivity and dielectric permittivity of modern oak and spruce wood with increasing water moisture contents considering three directions of anisotropy in a long-term experiment. For this purpose, we used small-scale geophysical equipment and compared the results to previous laboratory studies;
- (ii)
- Calculating the physical material contrasts of wood compared to different embedding materials, such as water, clayey subsoil, and sandy subsoil, for ERT and GPR measurements and comparing them to seismic material contrasts based on the work of [11];
- (iii)
- On the basis of the determined contrasts, we performed analytical calculations to investigate the depth penetration and applicability of the ERT and GPR methods for the prospection of wooden objects in water.
2. Materials and Methods
2.1. Preliminary Considerations to Determine Wooden Material Properties
2.2. Experimental Setup
2.3. Determination of the Electric Resistivity
2.4. Determination of the Dielectric Permittivity
2.5. Determination of Relative Material Parameter Contrasts
2.6. Geophysical Detection Swell of Wooden Targets in Lacustrine Environment
3. Results
3.1. Water Absorption, Swelling, and Density Increase of Moisturized Wood during the Experiment
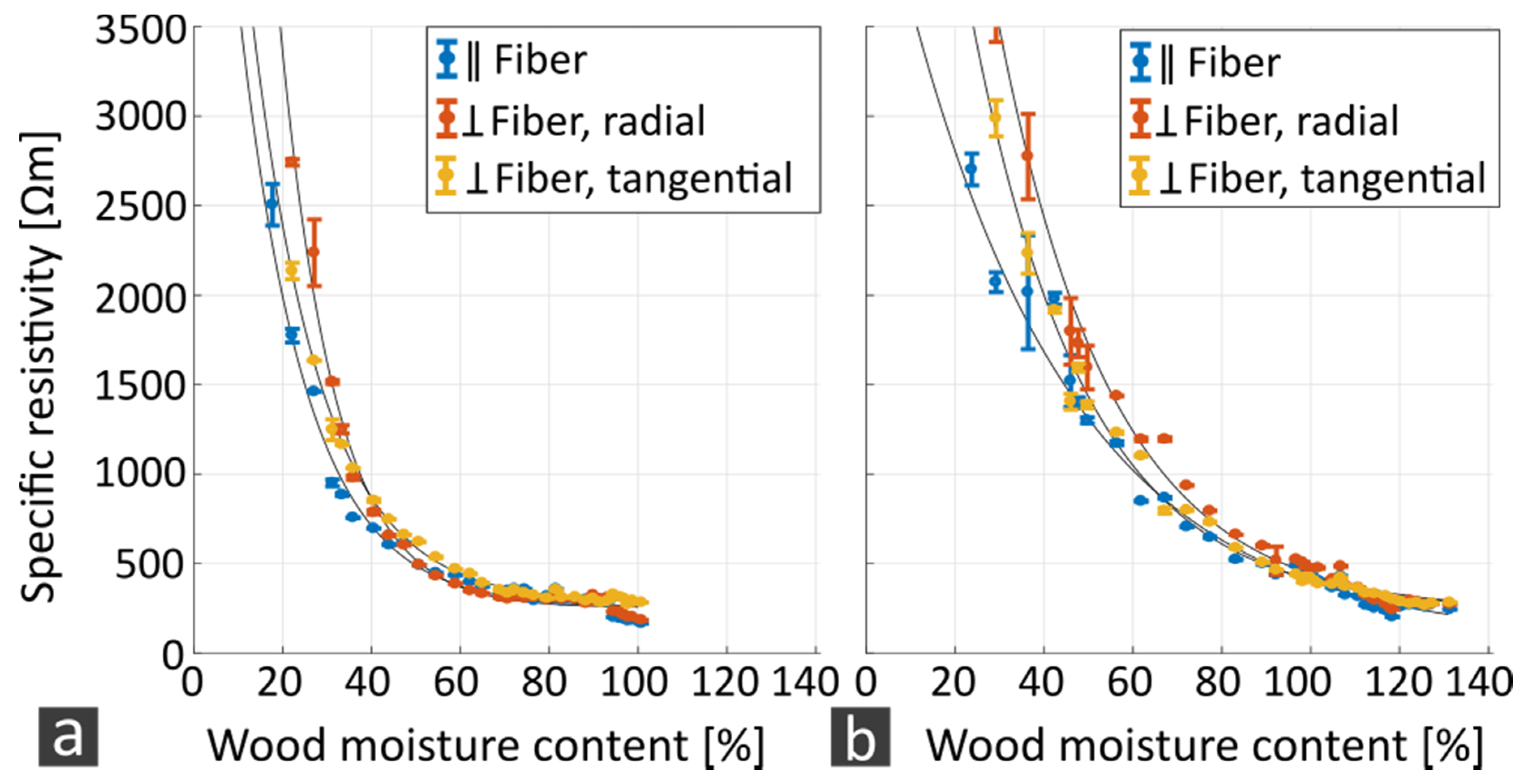
3.2. Electric Resistivity
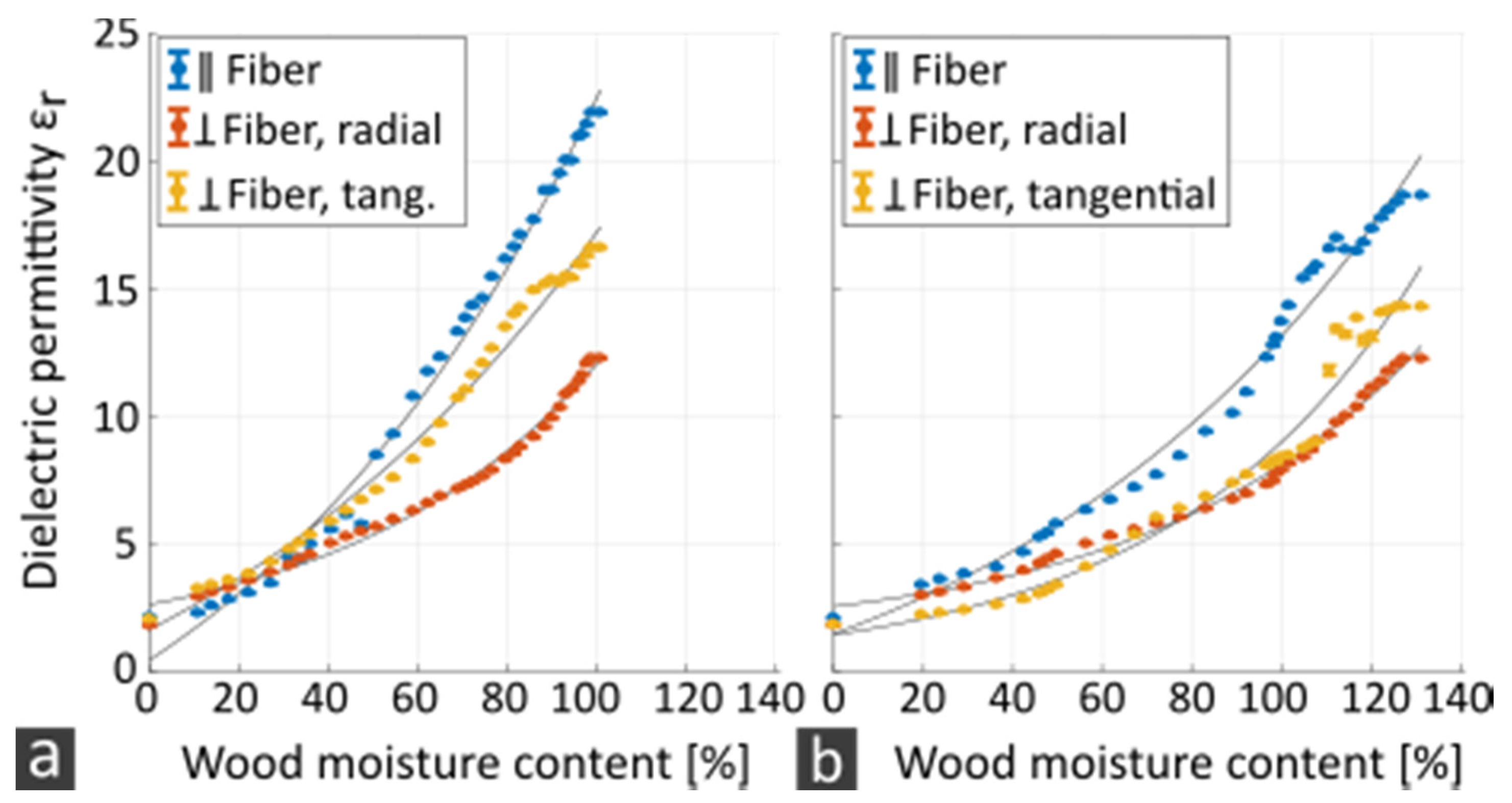
3.3. Dielectric Permittivity
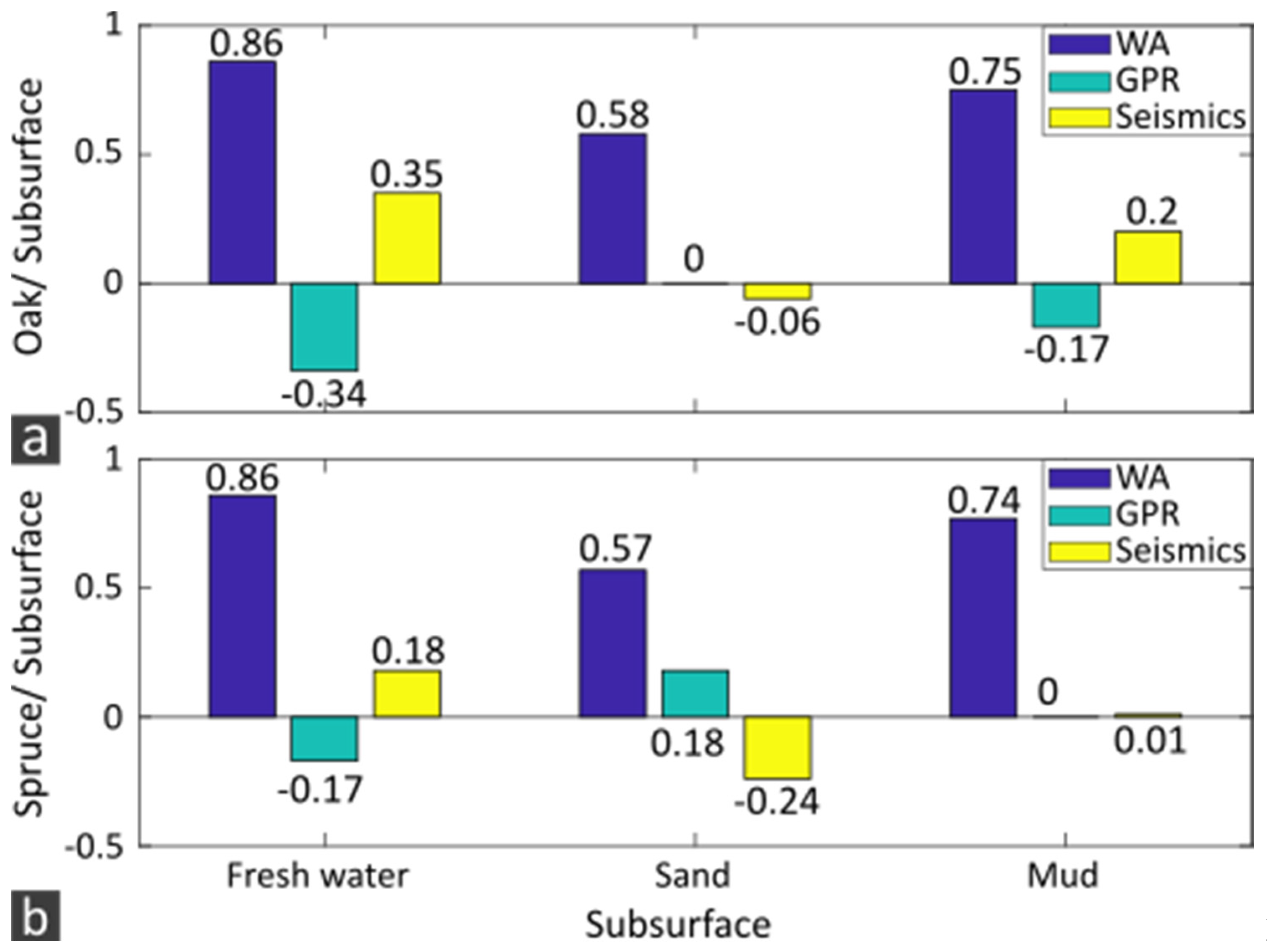
3.4. Relative Material Parameter Contrasts
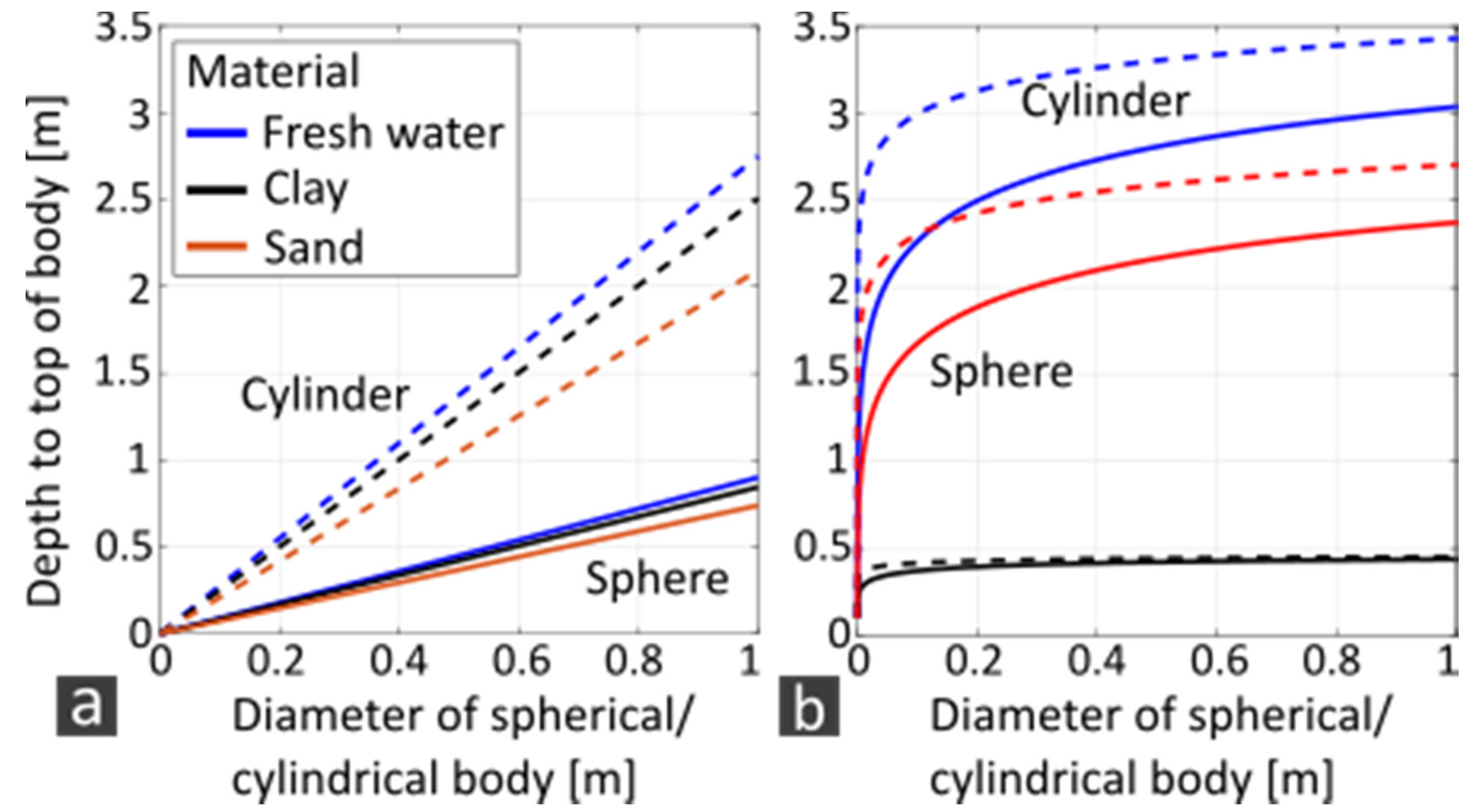
3.5. Geophysical Detection Swell of Wooden Targets in Lacustrine Environment
4. Discussion
4.1. Swelling and Density Increase of Moisturized Wood during the Experiment
4.1.1. Swelling
4.1.2. Density
4.2. Electric Resistivity
4.2.1. Experimental Data
4.2.2. Anisotropy
4.2.3. Wood Species
4.3. Dielectric Permittivity
4.3.1. Experimental Data
4.3.2. Anisotropy
4.3.3. Wood Species
4.4. Relative Material Parameter Contrasts
4.5. Comparison of Measurement Methods
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Müller, C.; Woelz, S.; Ersoy, Y.; Boyce, J.; Jokisch, T.; Wendt, G.; Rabbel, W. Ultra-high-resolution marine 2D–3D seismic investigation of the Liman Tepe/Karantina Island archaeological site (Urla/Turkey). J. Appl. Geophys. 2009, 68, 124–134. [Google Scholar] [CrossRef]
- Woelz, S.; Rabbel, W.; Mueller, C. Shear waves in near surface 3D media–SH–wavefield separation, refraction time migration and tomography. J. Appl. Geophys. 2009, 68, 104–116. [Google Scholar] [CrossRef]
- Fediuk, A.; Wilken, D.; Wunderlich, T.; Rabbel, W.; Seeliger, M.; Laufer, E.; Pirson, F. Marine seismic investigation of the ancient Kane harbour bay, Turkey. Quat. Int. 2018, 511, 43–50. [Google Scholar] [CrossRef]
- Seeliger, M.; Brill, D.; Feuser, S.; Bartz, M.; Erkul, E.; Kelterbaum, D.; Vött, A.; Klein, C.; Pirson, F.; Brückner, H. The purpose and age of underwater walls in the Bay of Elaia of Western Turkey: A multidisciplinary approach. Geoarchaeology 2014, 29, 138–155. [Google Scholar] [CrossRef]
- Wunderlich, T.; Wilken, D.; Erkul, E.; Rabbel, W.; Vött, A.; Fischer, P.; Hadler, H.; Heinzelmann, M. The river harbour of Ostia Antica-stratigraphy, extent and harbour infrastructure from combined geophysical measurements and drillings. Quat. Int. 2018, 473, 55–65. [Google Scholar] [CrossRef]
- Simyrdanis, K.; Papadopoulos, N.; Kim, J.H.; Tsourlos, P.; Moffat, I. Archaeological investigations in the shallow seawater environment with electrical resistivity tomography. Near Surf. Geophys. 2015, 13, 601–611. [Google Scholar] [CrossRef]
- McGrail, S. Ancient Boats in North-West Europe: The Archaeology of Water Transport to AD 1500; Addison-Wesley Longman, Incorporated: London, UK, 1998. [Google Scholar]
- Crumlin-Pedersen, O. Nordic Clinker Construction. In The Philosophy of Shipbuilding. Conceptual Approaches to the Study of Wooden Ships; Hocker, F.M., Ward, C., Eds.; Texas A&M University: College Station, TX, USA, 2004; pp. 37–64. [Google Scholar]
- Diener, A. Holzbau in Mittelalter und Neuzeit; Mitteilungen der Deutschen Gesellschaft für Archäologie des Mittelalters und der Neuzeit: Paderborn, Germany, 2012. [Google Scholar]
- Wilken, D.; Wunderlich, T.; Hollmann, H.; Schwardt, M.; Rabbel, W.; Mohr, C.; Schulte-Kortnack, D.; Nakoinz, O.; Enzmann, J.; Jürgens, F.; et al. Imaging a medieval shipwreck with the new PingPong 3D marine reflection seismic system. Archaeol. Prospect. 2019, 26, 211–223. [Google Scholar] [CrossRef]
- Arnott, S.H.; Dix, J.K.; Best, A.I.; Gregory, D.J. Imaging of buried archaeological materials: The reflection properties of archaeological wood. Mar. Geophys. Res. 2005, 26, 135–144. [Google Scholar] [CrossRef]
- Jol, H.M.; Albrecht, A. Searching for submerged lumber with ground penetrating radar: Rib lake, Wisconsin, USA. In Proceedings of the 10th International Conference on Ground Penetrating Radar, Delft, The Netherlands, 21–24 June 2004. [Google Scholar]
- Kritikakis, G.S.; Papadopoulos, N.; Simyrdanis, K.; Theodoulou, T. Imaging of Shallow Underwater Ancient Ruins with ERT and Seismic Methods. In Proceedings of the 8th Congress of the Balkan Geophysical Society, Chania, Greece, 5–8 October 2015. [Google Scholar]
- Arcone, S.; Finnegan, D.; Boitnott, G. GPR characterization of a lacustrine UXO site. Geophysics 2010, 75, WA221–WA239. [Google Scholar] [CrossRef]
- Ruffell, A. Under-water scene investigation using ground penetrating radar (GPR) in the search for a sunken jet ski, Northern Ireland. Sci. Justice 2006, 46, 221–230. [Google Scholar] [CrossRef]
- Lin, Y.T.; Wu, C.H.; Fratta, D.; Kung, K.J. An integrated acoustic and electromagnetic wave-based technique to estimate subbottom sediment properties in a freshwater environment. Near Surf. Geophys. 2010, 8, 213–221. [Google Scholar] [CrossRef]
- Niemz, P.; Sonderegger, W. Holzphysik: Physik des Holzes und der Holzwerkstoffe, 1st ed.; Carl Hanser Verlag GmbH Co KG: München, Germany, 2017. [Google Scholar]
- Kollmann, F. Principles of Wood Science and Technology; Springer: Berlin/Heidelberg, Germany, 1968. [Google Scholar]
- Skaar, C. Wood-Water Relations; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Stamm, A.J. The Electrical Resistance of Wood as a Measure of Its Moisture Content. Ind. Eng. Chem. 1927, 19, 1021–1025. [Google Scholar] [CrossRef]
- Lin, R.T. A study on the electrical conduction in wood. For. Prod. J. 1965, 15, 506–514. [Google Scholar]
- Kuroda, N.; Tsutsumi, J. Anisotropic behavior of electrical conduction in wood. Mokuzai Gakkaishi 1982, 28, 25–30. [Google Scholar]
- Peyskens, E.; De Pourcq, M.; Stevens, M.; Schalck, J. Dielectric properties of softwood species at microwave frequencies. Wood Sci. Technol. 1984, 18, 267–280. [Google Scholar] [CrossRef]
- Trapp, V.W.; Pungs, L. Einfluß von Temperatur und Feuchte auf das dielektrische Verhalten von Naturholz im großen Frequenzbereich. Holzforsch. Int. J. Biol. Chem. Phys. Technol. Wood 1956, 10, 144–150. [Google Scholar] [CrossRef]
- James, W.L. Dielectric Properties of Wood and Hardboard: Variation with Temperature, Frequency, Moisture Content, and Grain Orientation (245); Department of Agriculture, Forest Service, Forest Products Laboratory: Washington, DC, USA, 1975. [Google Scholar]
- Kröner, K.; Pungs, L. Zur dielektrischen Anisotropie des Naturholzes im großen Frequenzbereich. Holzforsch. Int. J. Biol. Chem. Phys. Technol. Wood 1952, 6, 13–16. [Google Scholar] [CrossRef][Green Version]
- Bartsch, H.J. Taschenbuch Mathematischer Formeln; Fachbuchverlag Leipzig im Carl-Hanser-Verlag: Munich, Germany, 2007. [Google Scholar]
- Telford, W.M.; Geldart, L.P.; Sheriff, R.E.; Keys, D.A. Applied Geophysics; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Rücker, C.; Günther, T.; Wagner, F. pyGIMLi-An Open Source Python Library for Inversion and Modelling in Geophysics. In Proceedings of the 78th EAGE Conference and Exhibition, Vienna, Austria, 30 May–2 June 2016. [Google Scholar]
- Butler, D.K. Near-Surface Geophysics; Society of Exploration Geophysicists: Tulsa, OK, USA, 2005. [Google Scholar]
- Schön, J. Petrophysik: Physikalische Eigenschaften von Gesteinen und Mineralen; Akademie-Verlag: Berlin, Germany, 1983. [Google Scholar]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Annan, P. Ground Penetrating Radar Principles, Procedures and Applications; Sensors and Software: Mississauga, ON, Canada, 2003. [Google Scholar]
- Knödel, K.; Krummel, H.; Lange, G. Handbuch zur Erkundung des Untergrundes von Deponien und Altlasten: Band 3: Geophysik; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Davis, J.L.; Annan, A.P. Ground-penetrating radar for high-resolution mapping of soil and rock stratigraphy. Geophys. Prospect. 1989, 37, 531–551. [Google Scholar] [CrossRef]
- Hilterman, F.J. Amplitudes of seismic waves—A quick look. Geophysics 1975, 40, 745–762. [Google Scholar] [CrossRef]
- Töpfer, K. Die Ortung von Störkörpern mit dem Schlumberger-Meßverfahren. Arch. Meteorol. Geophys. Bioklimatol. Ser. A 1969, 18, 191–220. [Google Scholar] [CrossRef]

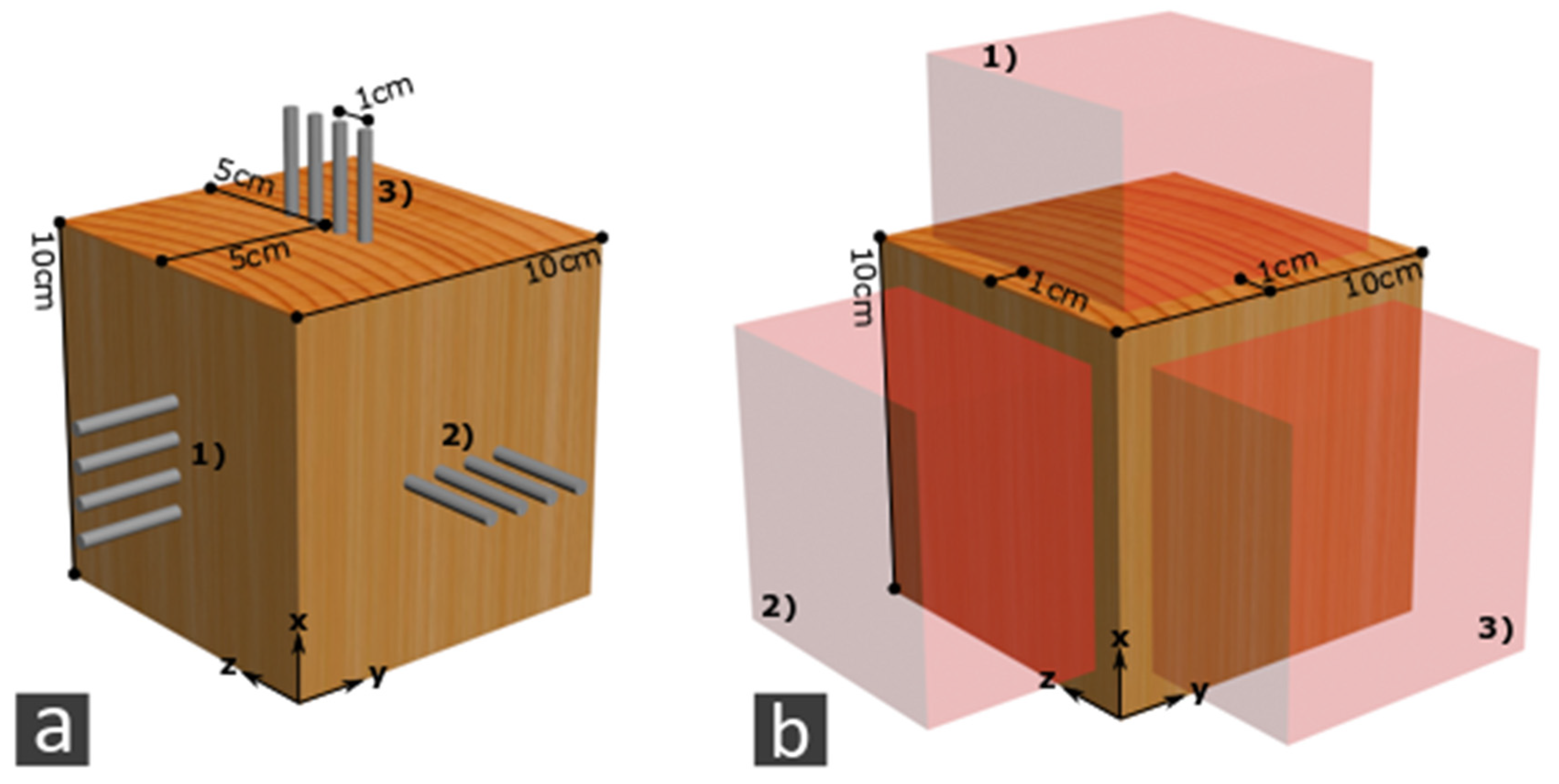
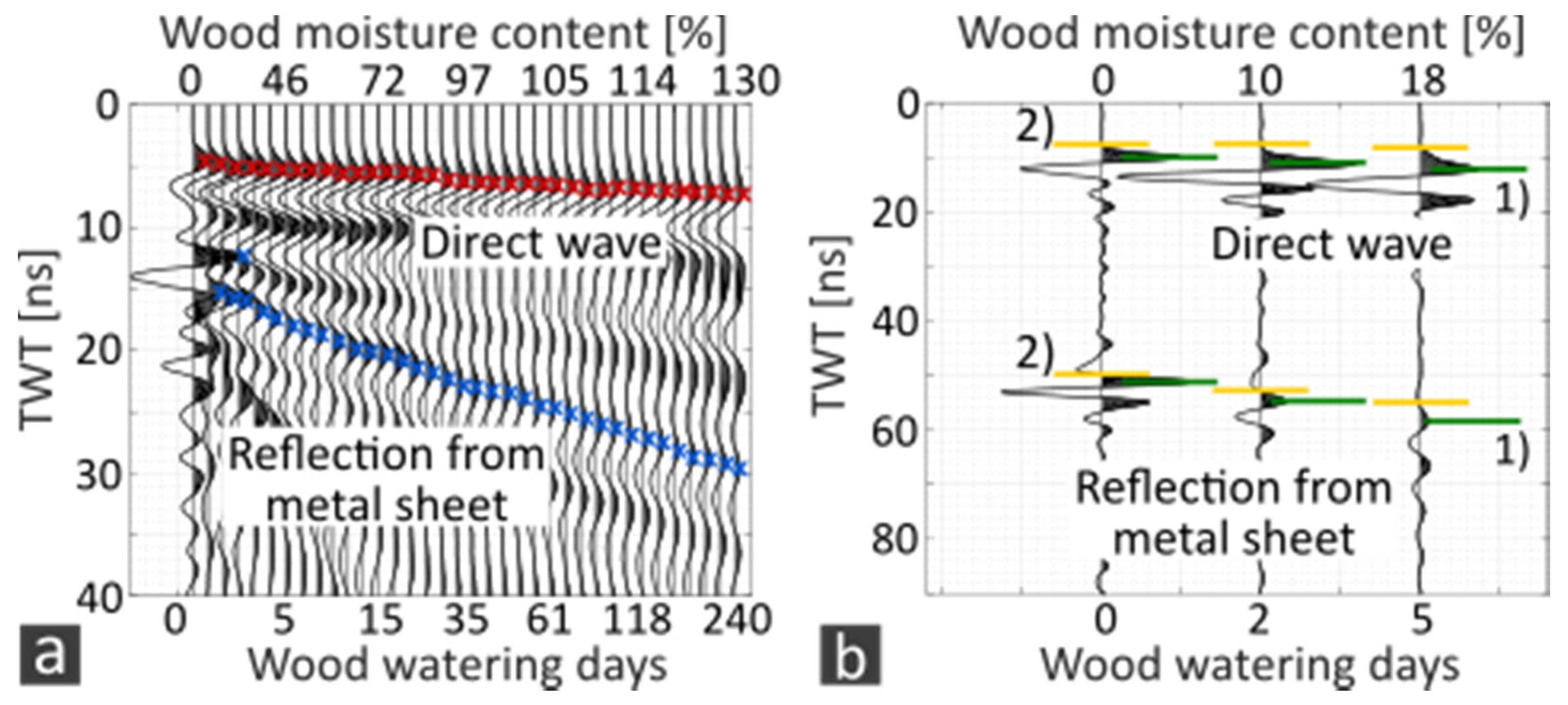
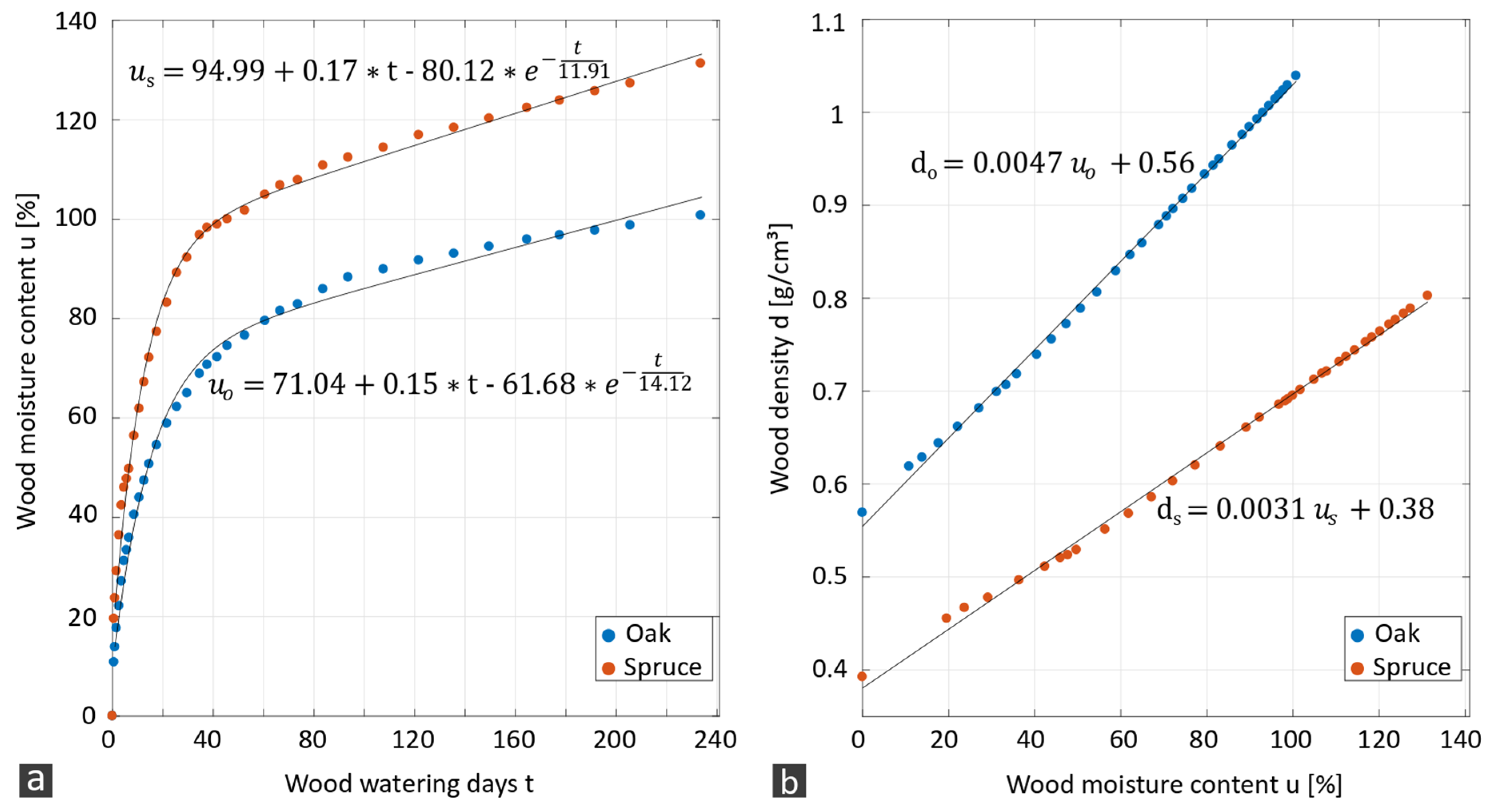
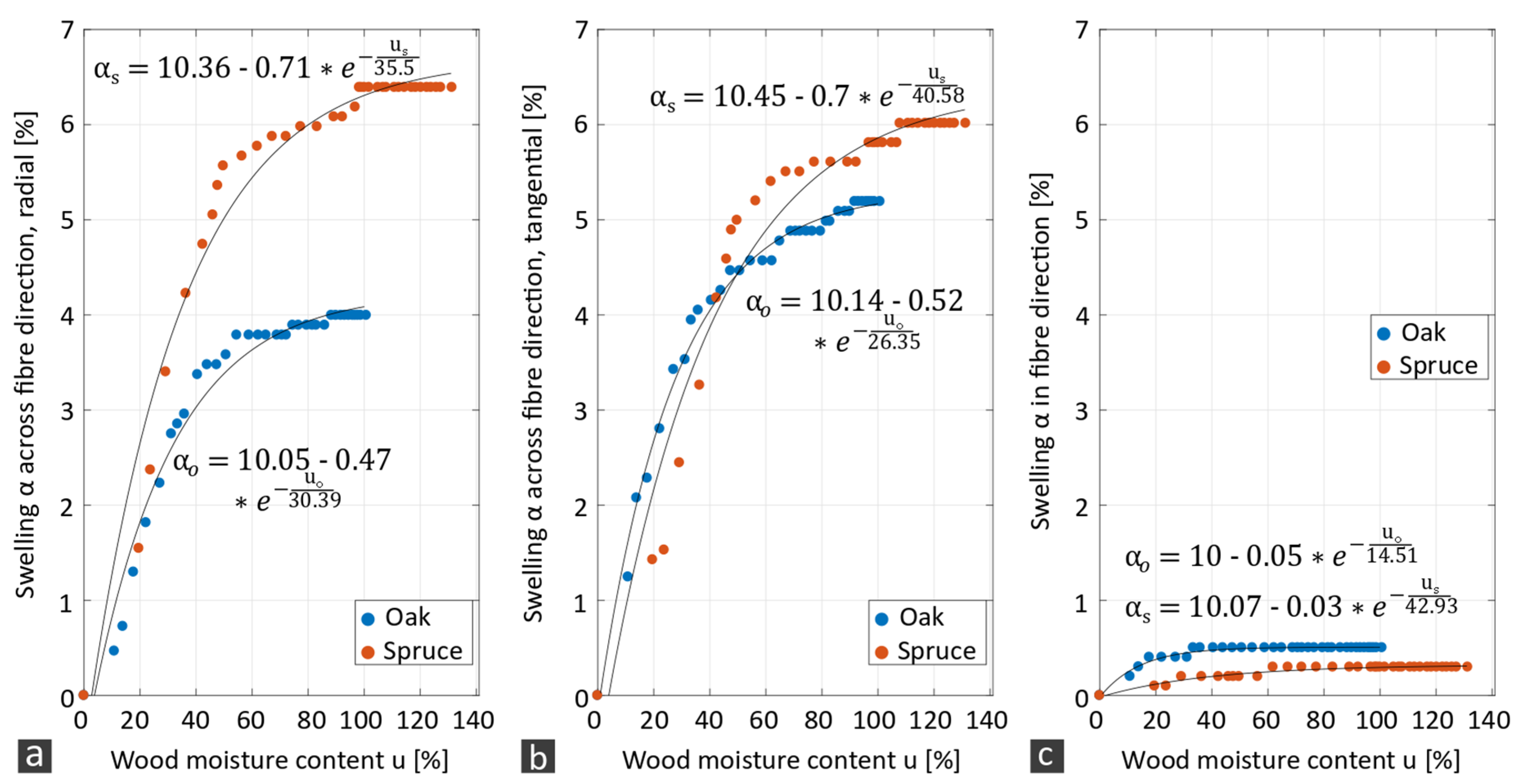
| Embedding Material | Electric Resistivity | Dielectric Permittivity |
|---|---|---|
| Freshwater | 21 Ωm [31] | 81 [31] |
| Saturated sand | 75 Ωm [31,32] | 20 [33] |
| Saturated clay | 40 Ωm [34] | 40 [33] |
| Geoelectric | Freshwater | Saturated Sand | Saturated Clay |
|---|---|---|---|
| Spec. electric resistivity of half space | 21 Ωm | 40 Ωm | 75 Ωm |
| Spec. electric resistivity of wood | 250 Ωm | ||
| GPR | Freshwater | Saturated sand | Saturated clay |
| EM wave velocity of half space | 3.3 cm/ns | 7 cm/ns | 5 cm/ns |
| Attenuation of half space | 0.1 dB/m | 0.17 dB/m | 10 dB/m |
| Reflection coefficient of wood to embedding material | −0.34 | −0.06 | −0.17 |
| Fitted u Curve | Corr. Coeff. | Fitted α Curve | Corr. Coeff. | Fitted Density Curve | Corr. Coeff. | |
|---|---|---|---|---|---|---|
| Oak wood, in Fiber direction | 1 | 0.98 | 1 | |||
| Across Fiber direction, radial to annual rings | . | 0.98 | ||||
| Across Fiber direction, tangential to annual rings | 0.99 | |||||
| Spruce wood, in Fiber direction | 1 | 0.96 | 1 | |||
| across Fiber direction, radial to annual rings | 0.98 | |||||
| across Fiber direction, tangential to annual rings | 0.97 |
| Spruce Wood Kiln-Dry State (0% Moisture Content) | Spruce Wood Moisturized State (130% Moisture Content) | Oak Wood Kiln-Dry State (0% Moisture) | Oak Wood Moisturized State (100% Moisture Content) | |
|---|---|---|---|---|
| Mass [g] | 375.0 | 867.5 | 525.5 | 1055 |
| Density [g/cm³] | 0.39 | 0.80 | 0.57 | 1.04 |
| Volume [cm³] | 955.38 | 1080.79 | 923.21 | 1014.02 |
| Length in fiber [cm] Direction | 10.04 | 10.07 | 9.95 | 10.00 |
| Length across fiber direction, radial [cm] | 9.70 | 10.32 | 9.63 | 10.02 |
| Length across fiber direction, tangent. [cm] | 9.81 | 10.40 | 9.63 | 10.12 |
| Spruce Wood Kiln-Dry State (0% Moisture Content) | Spruce Wood Moisturized State (200% Moisture Content) | Oak Wood Kiln-Dry State (0% Moisture) | Oak Wood Moisturized State (111% Moisture Content) | |
|---|---|---|---|---|
| In Fiber direction | >2500 Ωm | 79 Ωm | >3500 Ωm | 312 Ωm |
| Across Fiber direction, radial to annual rings | >2500 Ωm | 297 Ωm | >3500 Ωm | 272 Ωm |
| Across Fiber direction, tangential to annual rings | >2500 Ωm | 270 Ωm | >3500 Ωm | 286 Ωm |
| ρs: Fitted Curve | Corr. Coeff. | εr: Fitted Curve | Corr. Coeff. | |
|---|---|---|---|---|
| Oak wood, In Fiber direction | 0.99 | 1 | ||
| Across Fiber direction, radial to annual rings | 0.99 | 1 | ||
| Across Fiber direction, tangential to annual rings | 1 | 0.99 | ||
| Spruce wood, In Fiber direction | 0.95 | 0.99 | ||
| Across Fiber direction, radial to annual rings | 0.87 | 1 | ||
| Across Fiber direction, tangential to annual rings | 0.94 | 0.98 |
| Spruce Wood Kiln-Dry State (0% Moisture Content) | Spruce Wood Moisturized State (200% Moisture Content) | Oak Wood Kiln-Dry State (0% Moisture) | Oak Wood Moisturized State (111% Moisture Content) | |
|---|---|---|---|---|
| In Fiber direction | 1.8 | 47 | 2 | 27 |
| Across Fiber direction, radial to annual rings | 1.8 | 37 | 2 | 15 |
| Across Fiber direction, tangential to annual rings | 1.8 | 41 | 2.1 | 20 |
| ERT | GPR | Seismics | |
|---|---|---|---|
| Oak wood compared to fresh water | 0.86 to 0.87 | −0.4 to −0.27 | 0.35 |
| Spruce wood compared to fresh water | 0.87 to 0.58 | −0.19 to −0.14 | 0.18 |
| Oak wood compared to sandy subsoil | 0.56 to 0.61 | −0.07 to 0.07 | −0.06 |
| Spruce wood compared to sandy subsoil | 0.6 to 0.3 | 0.15 to 0.21 | −0.24 |
| Oak wood compared to clayey subsoil | 0.74 to 0.77 | −0.24 to −0.1 | 0.2 |
| Spruce wood compared to clayey subsoil | 0.76 to 0.33 | −0.01 to 0.04 | 0.01 |
| Swelling | Experiment | Literature |
|---|---|---|
| Spruce, in fiber | 0.29% | 0.2%–0.4% |
| Spruce, across fiber, radial | 6.4% | 3.7% |
| Spruce, across fiber, tangential | 6% | 8.5% |
| Oak, in fiber | 0.5% | 0.3%–0.6% |
| Oak, across fiber, Radial | 4% | 4.6% |
| Oak, across fiber, Tangential | 5.1% | 10.9% |
| Measurement Errors | Wood Type | Anisotropy | ||||
|---|---|---|---|---|---|---|
| State | Kiln dry | Wet | Kiln dry | Wet | Kiln dry | Wet |
| Electric Resistivity | <3% | <2% | 30% | 15% | 15% | 5% |
| Dielectric permittivity | <5% | <5% | 3%–19% | 3%–19% | 7% | 32% |
| Wood Moisture Content | Experiment | Literature |
|---|---|---|
| 0% | 1.8 | 1.7 |
| 30% | 3.2 | 3.5 |
| 80% | 6.1 | 7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fediuk, A.; Wilken, D.; Wunderlich, T.; Rabbel, W. Physical Parameters and Contrasts of Wooden Objects in Lacustrine Environment: Ground Penetrating Radar and Geoelectrics. Geosciences 2020, 10, 146. https://doi.org/10.3390/geosciences10040146
Fediuk A, Wilken D, Wunderlich T, Rabbel W. Physical Parameters and Contrasts of Wooden Objects in Lacustrine Environment: Ground Penetrating Radar and Geoelectrics. Geosciences. 2020; 10(4):146. https://doi.org/10.3390/geosciences10040146
Chicago/Turabian StyleFediuk, Annika, Dennis Wilken, Tina Wunderlich, and Wolfgang Rabbel. 2020. "Physical Parameters and Contrasts of Wooden Objects in Lacustrine Environment: Ground Penetrating Radar and Geoelectrics" Geosciences 10, no. 4: 146. https://doi.org/10.3390/geosciences10040146
APA StyleFediuk, A., Wilken, D., Wunderlich, T., & Rabbel, W. (2020). Physical Parameters and Contrasts of Wooden Objects in Lacustrine Environment: Ground Penetrating Radar and Geoelectrics. Geosciences, 10(4), 146. https://doi.org/10.3390/geosciences10040146





