Abstract
In this study, we present a novel approach combining the advantages of tesseroids in representing geophysical structures though their voxel-like discretization features with a spherical harmonic representation of the magnetic field. Modelling of the Earth lithospheric magnetic field is challenging since part of the spectra is hidden by the core field and the forward modeled field of a lithospheric magnetization is always biased by the spectral range used. In our approach, a spherical harmonic representation of the magnetic field of spherical prisms (tesseroids) is used for high-resolution magnetic inversion of lithospheric field models. The use of filtered spherical harmonic models of the magnetic field of each tesseroid ensures that the resulting field matches the spectral range of the input data. For the inversion, we use the projected gradient method. The projected gradient method easily allows us to assign an initial guess (i.e., a-priori assumption) for the inversion and avoids negative values of susceptibilities. The latter is providing more plausible models since induced magnetization is assumed to be dominant over the continents and, for the oceans, a remanence model can be subtracted. We show an application of the technique to a synthetic dataset and a satellite-derived lithospheric field model where the model geometry is based on seismic information. We also demonstrate a proof-of-concept for high-resolution tile-wise inversion for the Bangui anomaly in Africa.
1. Introduction
The Earth’s magnetic field contains a signal from various sources including the core, ionosphere, magnetosphere, and the Earth’s magnetic lithosphere [1]. The lithospheric magnetic field reflects the tectonic setting and geological provinces of the Earth, as shown by the typical stripe anomalies over the oceans reflecting seafloor spreading [2]. Often the lithospheric magnetic anomalies are interpreted from aeromagnetic surveys, where the contribution of the inducing core field is routinely reduced during processing. Aeromagnetic surveys commonly have limitations with respect to long wavelengths due to the survey extension or the methods by which individual surveys are stitched together.
Global models of the lithospheric magnetic field, on the other hand, can provide a global heterogeneous coverage and are usually based on a spherical harmonic representation [3]. For these models, the reliable spectral range is defined by the part not dominated by the main field and within the measuring bandwidth of the data sources. The main field associated with the core dominates the spherical harmonic coefficients up to 15°. Therefore, lithospheric models like LCS-1 [4] only define a reliable lithospheric field spectral content for more than 15°.
LCS-1 provides the coefficients to degree and order 185 based on measurements from the CHAMP and Swarm satellite missions. Reference [5] showed that a combination of the gradient observations with the vector information improves the lithospheric field determination, and the reliable range can be increased to degree n = 154 in comparison to only vector measurements, which can reach degree n = 138 only. However, for previous models like the various generations of MF (e.g., [3]), it is stated that satellite-data provide the full signal to degree and order 85, while some signal loss occurs at higher degrees. LCS-1 is using data from the multi-satellite mission Swarm and shifts this range to 133° and provides even higher coefficients. This improvement is significant since the reliable spectral range of the satellite lithospheric field is currently one of the basic limitations concerning the robustness of interpreting the lithospheric field model in terms of magnetization and magnetic crustal thickness on continental or global scales.
There are experimental data sets derived from Swarm (and older CHAMP) data, which are non-regularized based on the inversion approach from References [6,7]. These already shift resolution up to 200° and should be used for further future analysis.
A number of studies previously presented models of the lithospheric magnetization within the spherical harmonic degree range corresponding to the satellite-derived lithospheric field. First magnetic crustal models were presented by References [8,9], based on seismic crustal thickness estimated and susceptibility estimations from geology. These models took in account only an induced magnetization and were not coinciding with Magsat anomaly maps [10]. The Standard Earth Magnetization Model [11] included both induced and remanent magnetizations, using the 3SMAC model [12] to set different tectonic areas (i.e., magnetic properties) and a remanent magnetization in oceans from Reference [13]. This model was updated several times by adding further crustal models and information about heat-flow [14]. References [15,16] introduced a model where ranges of susceptibilities and magnetizations were assigned for each geological region of the world, according to the geographical information system (GIS). The model was adjusted via iterative inversion to fit satellite-derived (mostly from CHAMP satellite mission) lithospheric field model MF7 [3]. The result was the vertically integrated susceptibility (VIS) model and vertically integrated remanent magnetization (VIM) for the oceanic crust. Later, the remanent model was modified by making plate reconstruction corrections and improving oceanic remanence estimates [17]. However, the VIS model is still considered the reference for any later attempts.
Another limitation in inferring information for the magnetic sources comes from the non-uniqueness of the magnetization solution due to the existence of magnetization structures that do not produce any visible magnetic field, which are known as annihilators [18,19,20]. That means that any inversion requires a priori information or a reference model to result in plausible susceptibilities.
All these inversion and modelling approaches used fitting and/or inversion based on point dipole sources. That allows only a simplified representation of the geometry of the crust, especially when seismic and other types of information are considered. However, modelling of aeromagnetic surveys requires a better representation of the source bodies and, therefore, often Cartesian or Fourier-based approaches are used [21]. A representation with magnetic tesseroids [22] provides a versatile discretization that can be used for modelling both satellite and airborne data. The forward modelling code of Reference [22] allows the calculation of the magnetic field in spherical coordinates using spherical prisms, which are also called tesseroids (magnetic sources).
However, magnetic inversion of satellite-measured data within a particular wavelength window, corresponding to the reliable lithospheric field, is only viable if the signal of the individual sources is also filtered to the same spectral range. Therefore, the calculated field (across the entire spherical surface) of each tesseroid can be converted into a spherical harmonic representation. This enables the inversion for the reliable wavelength range while keeping the geometrically confined and discretized lithospheric magnetization model. This set-up allows a reliable calculation of the magnetic field at any altitude above the Earth’s surface.
In the following, we first outline the inversion method that is designed to have an adequate source discretization and inverts for a specific spherical harmonic range only. The validity of the approach is demonstrated with a synthetic example and next applied to the satellite-model LCS-1 in order to provide a global lithospheric susceptibility model, which, as we demonstrate at the end, can serve as a reference or background model for further studies on local scales.
2. Methodology
2.1. Tesseroid Forward Field
The software package magnetic tesseroids [22] is used for the forward calculation. Magnetic tesseroids calculates the vector magnetic field of a given tesseroid model on a specified grid. The magnetic contributions of all tesseroids in the model are summed up in the resulting data grid of the magnetic field vector components. In case of only induced magnetization, the vector magnetic field of each tesseroid is directly proportional to its magnetic susceptibility [22].
where
, and are the rotation matrices.
is the tesseroid’s gravity tensor in the coordinate system of the computation point and is the magnetizing field in the coordinate system of the tesseroid’s center .
Therefore, the magnetic field vector in each point of the two-dimensional spherical grid can be expressed by the equation below.
where , are the indices of the computational point within this spherical grid with longitudes and latitudes.
2.2. Spherical Harmonic Model
In this study, we utilize the software package SHTools [23] to convert the forward calculated spherical grids () into a spherical harmonic representation. For the inversion, we set calculated grids () to be equidistant with the number of points . To convert the grid into a spherical harmonic model, SHTools utilizes the algorithm of efficient computation of the spherical harmonic expansion of functions defined on a two-dimensional sphere [24]. The relative errors using the method on sampled grids are similar to grids with datapoints at Gauss-Legendre quadrature spacing (see Reference [24] for more details).
2.3. Projected Gradient Inversion
Generally, geophysical inversion is ill-posed. Due to the presence of noise in the observed data and rounding errors in forward calculation, the existence, uniqueness, and stability of the inversion are hard to guarantee. For unique solution, constraints or a specific inversion method must be applied. However, in classical methods like least-squares inversion or Tikhonov regularization, the resulting susceptibilities are not constrained. Hence, the inversion can result in negative susceptibilities, which are unreasonable if occurring for large areas over the continents. In case of a constrained inversion over a small-scale anomaly, a strong misfit between the observed field and forward calculated field of the inversion result would indicate possible remanent magnetization. However, large-scale remanent sources are uncommon for the continental crust and for the scale of our analysis.
Therefore, we adopt the projected gradient method [25], which allows us to exclude negative susceptibility values and to set a priori constraints.
The projected gradient method is a way to solve a constrained optimization problem, or, more specifically, a non-negative least square linear inversion problem. The optimization problem is illustrated in the formula below.
where is the sensitivity matrix, which represents the magnetic field spherical harmonic coefficients of each tesseroid, is the magnetic susceptibility, and represents the spherical harmonic coefficients of the observed magnetic field model.
The cost function is shown below.
where , , and the constrained optimization problem becomes a constrained quadratic programming (QP) problem.
The Gradient Descent type method is a standard way to solve the quadratic optimization problem. To ensure a non-negative solution to the optimization problem, the projection operator is used to force the iteration back to the constraint range. Specifically, the projected gradient method iteratively uses the gradient projection to update the current solution to by the following rule.
where
is the step size and is the search direction which is defined by the equation below.
To find a reasonable step size in each iteration, there are sub-iterations to either increase or decrease the initial guess by until satisfies the sufficient decrease condition.
However, the computational complexity per iteration is relatively large to find a step size satisfying the condition. To reduce the cost of checking this condition, Lin (2007) uses a Taylor expansion of the cost function and simplifies the sufficient decrease condition as shown in the equation below.
We use the Projected Gradient Method with the simplified form of the sufficient decrease condition for our analysis, in the way it is presented here.
3. Data
For both the synthetic and real data application, we use a similar set of data to confine the geometry and parameters space. For the synthetic inversion, a global lithospheric field model is forward calculated from a crustal model with predefined susceptibility. The same geometry is later used for the inversion of a measured lithospheric magnetic field model.
3.1. Model Geometry
For all calculations, we assume the entire crust to be magnetic and set the geometry of the model, which defines the size of the tesseroids. The top of the model is the top of the crystalline basement as provided from the model CRUST 1.0 [26], originally with a 1° × 1° resolution (Figure 1a), but, for the global application, it is resampled to a 2° × 2° resolution. The base of the model is the Moho boundary. The Moho depth model is taken from Reference [27] (Figure 1b). The model is based on a similar catalogue as the Moho depth in CRUST 1.0, but, based on a geostatistical kriging approach, it provides uncertainties, which can be potentially exploited in further modifications. This set-up defines a one-layered crust, which is presented with tesseroids with variable thickness.
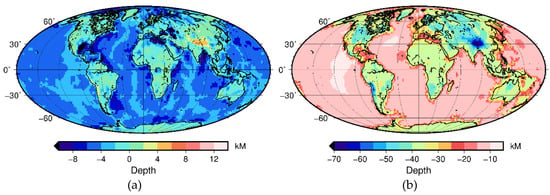
Figure 1.
Upper and lower boundaries of the synthetic model: (a) basement depth taken from CRUST1.0 [26] and (b) Moho depth taken from Reference [27].
3.2. Magnetization Direction and Susceptibility
Induced magnetization in the crust is a response of the mainly ferrimagnetic rock properties to the inducing main field. We use International Geomagnetic Reference Field model, year 2014 [28], to define the direction and strength of the inducing field in the center-point of each tesseroid.
For the initial susceptibility distribution in the model, we use the VIS model [16]. For each tesseroid, the susceptibility is calculated from their model by dividing the VIS model by the height of the tesseroid. The VIS value used is the mid-tesseroid value (Figure 2a).
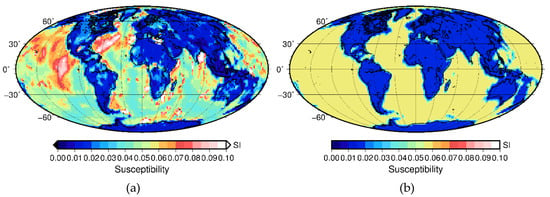
Figure 2.
Susceptibility distribution in synthetic models: (a) susceptibility based on a vertically integrated susceptibility model (Hemant and Maus, 2005). (b) Initial guess with averaged susceptibilities from Hemant VIS-based initial guess . Crustal domain boundaries are taken from the age of the oceanic crust map [2].
To explore the effect of a-priori information (initial guess) on the inversion, we calculate a simplified susceptibility distribution with averaged values for oceanic and continental crust (Figure 2b). We use the map of the age of the oceanic crust [2], separate the oceanic and continental crust, and calculate the mean average susceptibility from the VIS model in Figure 2. This results in an average value for the continental crust of 0.0154 SI and for the oceanic crust of 0.0555 SI.
While we neglect remanence in the synthetic tests, we also consider remanent magnetization as a priori information in the application to real data. For this, we use the remanent magnetization vectors from Reference [17] and calculate the corresponding field using 1-km thin tesseroids to imitate original dipole methods of Reference [17]. The model of Reference [17] relies on many initial assumptions, such as shape of the sources in the oceanic crust, which may not coincide with the actual sources in the real crust. However, it is currently the best available model to subtract the remanent field of the oceans.
3.3. Lithospheric Magnetic Field Models
3.3.1. LCS-1
For the global inversion of real data, we choose the lithospheric magnetic field model LCS-1, which is the spherical harmonic model of the lithospheric field derived from the CHAMP and Swarm satellite observations (Olsen et al., 2017). Figure 3a shows the field for spherical harmonic degrees 16-89 at 400-km height, which represents satellite orbit height. The lower cut-off is in line with the original model, while the higher cut-off is chosen to be in line with our model parametrization.
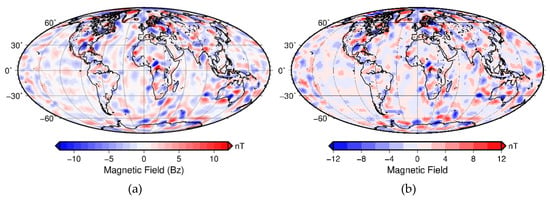
Figure 3.
LCS-1 with and without remanence: (a) LCS-1 with degrees from n = 16 to 89, (b) LCS-1 without modelled remanent field (Figure 3b), within degrees from n = 16 to 89.
We use the remanent magnetization model of Masterton et al. (2013) [19] and calculate the corresponding magnetic field for the spherical harmonic degrees 16–89. For this, we assign the remanent vector model to a spherical shell of 1-m thickness made of tesseroids 0.25° in longitudinal and latitudinal width. From this, we calculate the remanent field (Bz component) at the altitude of 400 km (Figure 4). Truncated spherical harmonic model of the calculated remanent field is shown in Figure 4b and the residual after subtracting this field from LCS-1 in Figure 3b.
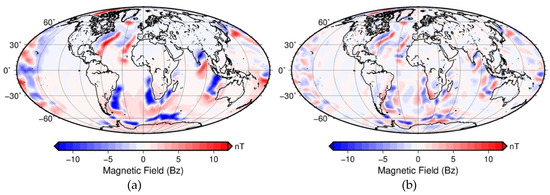
Figure 4.
Spherical harmonic model of the remanent field derived from Reference [19]: (a) all spherical harmonic degrees from n = 1 to 89, (b) truncated model with degrees from n = 16 to 89.
3.3.2. Synthetic Observed Field
For the analysis, we create a synthetic input data set for testing our inverse approach. For this, we use magnetic tesseroids [22] to calculate the magnetic field of a crustal model at the satellite altitude of 400 km. The grid spacing is chosen to be 1°, which approximately corresponds to a spherical harmonic degree of n = 89, due to RAM limitations. The calculated grid is converted into a spherical harmonic model with a maximal degree N = 89 using SHTools [23] (see Figure 5a). To further imitate a satellite-derived lithospheric magnetic field model, we truncate all degrees below and including degree n = 15. The filtered synthetic observed Bz component is shown in Figure 5b.
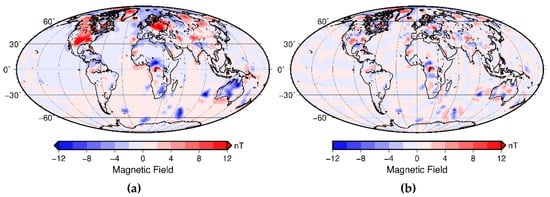
Figure 5.
Spherical harmonic model of the synthetic field: (a) all spherical harmonic degrees from n = 1 to 89, (b) truncated model with degrees from n = 16 to 89.
4. Results
4.1. Synthetic Test
The first test explores how the inversion of a truncated field recovers the initial true model used to create the synthetic field. The loss of the long wavelength part between 1° and 15° implies that the inversion might tend to result in solutions that may not match susceptibility distribution in the true model.
The projected gradient method requires an initial solution that is used as a first guess before iterations start. To explore how the truncation of the field affects the inversion results, we introduce two a priori models: with the susceptibility distribution from the true model (see Figure 2a), and with averaged susceptibility values for oceanic and continental crustal areas (Figure 2b).
4.1.1. A-Priori Model from a True Susceptibility Model
This first test helps identify the error introduced by grid processing and creation of spherical harmonic models of each tesseroid field within the algorithm. For the inversion, using a truncated field with a true model as an initial assumption, we expect that manipulations with grids introduce a rounding error and a complete fit cannot be achieved. After the first iteration, the projected gradient norm reaches its minimum (approx. 75,696 × 10−4) and remains the same for all further iterations.
One can use the iteration value of 75,696 × 10−4 for the linear norm to set up a threshold for future inversions, since this value represents the error introduced by re-gridding and represents the conversion to spherical harmonics.
RMS of the difference between the true model and the inversion result after the first iteration is about 0.0 SI, i.e., the non-zero linear norm value after the initial iteration does not affect the result and the way floating point numbers from the result are stored in the output text files (max 18 digits after the point).
4.1.2. Initial Guess with Averaged Susceptibility for Oceanic and Continental Crust
Next, we explore the effect of the a priori model. Earth lithosphere magnetization is not well known. Hence, the effect of the a priori assumptions might seriously affect the results. For this, we compare the results of the inversion (Figure 6b) with the initial guess (Figure 2b) with the true model (Figure 2a). Figure 7 and Figure 8 indicate that the fit for the field is very good for degrees n > 15 and the RMS of the difference between the observed and calculated field is very low (0.00933 nT) (Figure 6b).
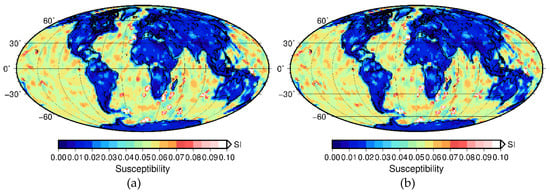
Figure 6.
Synthetic dataset inversion result with the initial guess : (a) with N = 1000, (b) with N = 10,000.
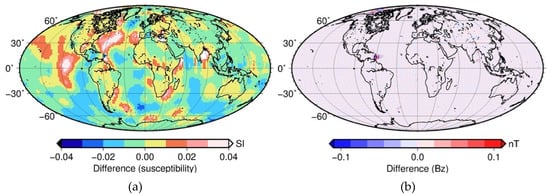
Figure 7.
Different grids for the inversion with the initial guess with averaged values for a continental and oceanic crust (Figure 2b). (a) Difference between the true model (model from Figure 2a, not initial guess from Figure 2b) and the inversion result , where = 10,000 is the number of iterations. (b) Difference between the synthetic truncated observed magnetic field component Bz (from Figure 3b) and truncated forward calculated component Bz of the inversion result .
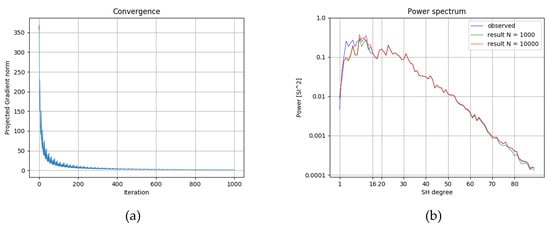
Figure 8.
Inversion convergence (values of ) and spectrums of the synthetic field and the field of the inversion result. (a) Values of projected gradient at each iteration (up until iteration N = 1000). (b) Power spectrum of the synthetic observed field spherical harmonic model (Figure 3a) with all degrees and power spectrum of the forward calculated spherical harmonic model of the inversion result after N = 1000 (green) and N = 10,000 (red) iterations.
However, the long-wavelength part of the spectra is very different. The resulting susceptibility distribution is similar in short-wavelength patterns to the true model (Figure 2a), but has an overall decreased amplitude, especially for spatially large areas (Figure 7a). This can be explained by the differences in the long-wavelength range. The inversion provides only susceptibilities in the limited spectral range. To explain degrees 16–85, the amplitude of long-wavelength anomalies (and, therefore, susceptibility of spatially wide sources) can be lower than in the true model. That is also seen in the spectral representation in Figure 8.
4.2. Inversion of LCS-1
For the inversion with real data, we again choose VIS-based model . The geometry of the model is the same as in the synthetic example and we only replace the synthetic data set with the observed lithospheric magnetic field.
For the inversion, we invert LCS-1 directly after removing the remanent field as an additional a-priori parameter.
The inversion result is shown in Figure 9a, and the comparison of the result’s spectrum against the original LCS-1 is shown in Figure 9b. RMS of the difference between the observed truncated field and forward calculated truncated field of the result is 0.03938 nT.
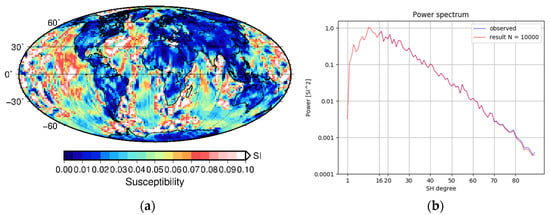
Figure 9.
Inversion result and spectrums: (a) Inversion result with the initial guess after N = 10,000 iterations. (b) Power spectrum of LCS-1 and power spectrum of the forward calculated spherical harmonic model of the inversion result after N = 10,000 iterations.
5. Discussion
5.1. Performance of Inversion
A synthetic inversion case with averaged susceptibilities for oceanic and continental crust as an initial guess () showed that powers of spherical harmonic degrees for N = 1000 iterations are, overall, lower than for N = 10,000 iterations (see Figure 8b).
A minimal value for the linear norm of projected gradient after N = 10,000 iteration is approximately 2157.838 × 10−4 (iteration 9999), which is two magnitudes higher than the threshold estimated in the very first test.
A higher number of iterations appears to increase the number or artifacts in the inversion result (see Figure 6 for example), which can be attributed to the existence of short-wavelength anomalies (with the wavelength close to approximately 1°) in the input that cannot be caused by 2° × 2° tesseroids. Thus, the issue is a regularization problem, which is not discussed here.
5.2. Use of a-Priori Model
Our results confirm that a good a-priori model for long-wavelength anomalies is necessary for accurate results. Currently, the existing dataset that can be used as an initial guess for the inversion of real data is a Hemant VIS-based model .
Since synthetic inversion for the initial guess, which is different from the true model, showed deviation in long-wavelength below degree n = 16, one cannot expect that long-wavelength sources were recovered correctly in the inversion result (Figure 9). A similar conclusion was made in Reference [29].
This is especially evident for the inversion results where the initial model in Reference [16] does neither represent the detailed surface geology nor a realistic susceptibility model due to the absence of such information (e.g., parts of Africa and Antarctica). The inversion does change the initial guess and leads to a further refinement of the sources, but, apparently, the amplitude stays as low as possible to fit the short-wavelength.
The application to the Bangui anomaly (Figure 10 and Figure 11) shows how the inversion changes the initial susceptibility model by adjusting the local values. Clearly, the choice of the a priori information largely influences the inversion results. Therefore, defining the a priori model with uncertainties could lead to further improvement by adding a stochastic element to the inversion. However, such a model does not exist on a global scale.
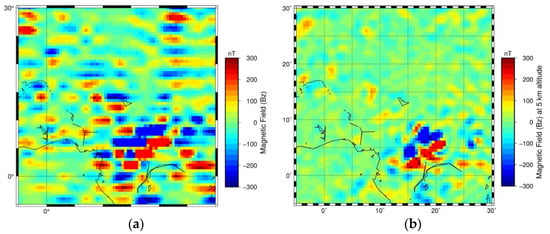
Figure 10.
Magnetic field of the tile inversion result and LCS-1 at the airborne altitude: (a) forward calculated field of the inversion result at a 5-km altitude and (b) LCS-1 calculated at a 5-km altitude.

Figure 11.
Susceptibility models for Bangui area in Africa: (a) Initial guess . (b) Inversion result . (c) Tile inversion result with resolution of 0.5°.
Therefore, an alternative would be to use actual rock susceptibility measurements and their statistical properties. Databases of such a measurement exist for Norway [30], Fennoscandia [31], and Canada [32] and can be used to provide an initial guess of a mean susceptibility and its standard deviation. A refined inversion could be done for those areas to explore the influence by a priori information with more detail.
5.3. Layering of the Model
Another shortcoming of our current models is that the vertical structure of the crust is not well expressed by a single layer. Measurements from outcrops may not adequately represent the entire crust an since the susceptibility of rocks beneath the surface might be different. Therefore, further developments could be adding more information on the crustal structure from seismic information or models like CRUST 1.0. For example, Reference [16] have based their model on a classification of the ratio of magnetization in the upper and lower crust. The lower crust is, in general, assumed to be less magnetic than the upper crust. However, the most prominent satellite lithospheric anomalies can be expected to have a significant contribution from the lower crust or even the upper mantle [33]. Therefore, one of the next steps should be to add the possibility of layering the crust and to modify the inversion for this. While this is already possible with the current set-up, one has to consider depth-weighting or regularization or the use of aeromagnetic data in the inversion.
5.4. Regularization
The other solution to help the inversion resolve long-wavelength sources more realistically is to make a stochastic inversion, which would control lower degree power spectra at each iteration. Such an approach would still require an initial guess for power spectra of lower degrees (such as Reference [34]), derived from the field of an a-priori initial susceptibility guess/model. Control over power spectra would result in the appearance of long-wavelength anomalies in the result, which would correspond to highlighted spherical harmonic degrees.
Such measures would impose implicit regularization on the inversion. Explicit regularization in the inversion, such as a way to guarantee smoothness of the result, may be detrimental to fitting a shorter wavelength. Figure 6 shows that the N = 10,000 solution, which is less smooth than the N = 1000 solution, fits the short-wavelength spectrum better. We do not discuss explicit regularization in the inversion further because we expect to use the tile-wise approach later to refine the result.
5.5. Application to Airborne Data—Proof of Concept
While there are many potential ways to enhance the analysis, the current model can already be used as a reference in modelling regional data. For areas on a regional or local scale, the current model can be used for the surrounding areas to avoid edge effects, but might also serve as a first guess for the model domain.
A tile-wise approach can be applied, when we select a moving window-tile and calculate the field from the areas surrounding this tile using susceptibilities from the global inversion. Then, we can subtract this far-field effect from the observed field and repeat the inversion for this tile with higher resolution.
Usage of tesseroids as sources instead of dipoles allows scalability of the method, and this approach can be used for the inversion of airborne data. In addition, inversion results can be tested against airborne data, which can be helpful to refine inversion results and models in the future.
As a proof of concept, we demonstrate the results of the tile-wise inversion with grid and tesseroid model resolution of 0.5 degrees for the Bangui Anomaly area. We have chosen this area because it features the most prominent anomaly at satellite height. Although remanence was proposed as a primary source for this anomaly (see Reference [35]), that is not necessarily true and depends on the geophysical data used as a constraint. For the demonstration of the concept, the nature of the anomaly is secondary.
We used data without a remanent field from Figure 4b, and removed the forward calculated surrounding field as an input. is used as an initial guess for tile inversion. The forward calculated field of the inversion result at the airborne altitude (5 km) is shown in Figure 10 against the original LCS-1 (up to 179°). One can see that the field on the airborne altitude was recovered through the inversion of the data on the satellite altitude, even though there are artifacts related to discretization (Figure 10b).
Figure 11 shows the process of refinement of the results for Bangui area. Figure 11a demonstrates the initial assumption , while Figure 11b shows the global inversion result with LCS-1 data (from Section 4.2). Lastly, Figure 11c shows the tile inversion for this area with the resulting Figure 11b as an initial assumption.
6. Conclusions
We developed an approach for global high-resolution inversion of satellite magnetic data using spherical harmonic models of tesseroids. Our method utilizes algorithms from the SHTools [23] package to convert forward calculated grids of tesseroids into spherical harmonic models and Projected Gradient [25] to perform the inversion.
Our approach is compared to classical spherical harmonic approaches that are very versatile and easily allows us to couple different geophysical, voxel-based approaches. For example, it can be easily linked to the LitMod3D software [36], which is a popular software for integrated geophysical and petrological modelling of the lithosphere.
Using the developed approach, we investigated caveats of the global magnetic inversion. One major finding was that selection of a-priori information, i.e., susceptibility distribution in the crust, significantly affect the long-wavelength part of the inversion results for a forward calculated magnetic field.
There are two possible ways to ensure more accurate inversion results. The first one is to enforce a particular power for lower degrees via stochastic inversion in order to fit some suggested low-degree power spectra. The other option is to use measured susceptibilities across the globe to set up a more accurate a-priori model. However, the global model presented in this paper can already serve as a background model for more detailed local modelling studies.
Author Contributions
Conceptualization, E.B. and J.E. Methodology, E.B. and D.Y. Software, E.B. Validation, E.B. Formal analysis, E.B. Investigation, E.B. and D.Y. Resources, J.E. Data curation, E.B. Writing—original draft preparation, E.B., D.Y. and J.E. Writing—review and editing, E.B. and J.E. Visualization, E.B. Supervision, J.E. Project administration, J.E. Funding acquisition, J.E. All authors have read and agreed to the published version of the manuscript.
Funding
The German Research Council (DFG) as part of the Special Priority Programme SPP 1788 ‘Dynamic Earth’ and the ESA Support to Science Element 3D Earth funded this study. The Chinese Science Council funded the PhD project of Dilixiati Yixiati.
Acknowledgments
Big thanks to Nils Holzrichter for finding small bugs and beta-testing the code and to Max Moorkamp for discussions. We thank the editor and two anonymous reviewers for their comments, which helped improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Langel, R.; Hinze, W.J. The Magnetic Field of the Earth’s Lithosphere; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Müller, R.D.; Sdrolias, M.; Gaina, C.; Roest, W.R. Age, spreading rates, and spreading asymmetry of the world’s ocean crust. Geochem. Geophys. Geosyst. 2008, 9. [Google Scholar] [CrossRef]
- Maus, S. Magnetic Field Model MF7. 2010. Available online: http://www.geomag.us/models/MF7.html (accessed on 1 March 2020).
- Olsen, N.; Ravat, D.; Finlay, C.C.; Kother, L.K. LCS-1: A high-resolution global model of the lithospheric magnetic field derived from CHAMP and Swarm satellite observations. Geophys. J. Int. 2017, 211, 1461–1477. [Google Scholar] [CrossRef]
- Kotsiaros, S.; Olsen, N. End-to-End simulation study of a full magnetic gradiometry mission. Geophys. J. Int. 2014, 196, 100–110. [Google Scholar] [CrossRef]
- Thébault, E. Global lithospheric magnetic field modelling by successive regional analysis. Earth Planets Space 2006, 58, 485–495. [Google Scholar] [CrossRef]
- Thébault, E.; Vigneron, P.; Maus, S.; Chulliat, A.; Sirol, O.; Hulot, G. Swarm SCARF Dedicated Lithospheric Field Inversion chain. Earth Planets Space 2013, 65, 7. [Google Scholar] [CrossRef]
- Meyer, J.; Hufen, J.-H.; Siebert, M.; Hahn, A. Investigations of the internal geomagnetic field by means of a global model of the earth’s crust. J. Geophys. Z. Geophys. 1983, 52, 71–84. [Google Scholar]
- Hahn, A.; Ahrendt, H.; Meyer, J.; Hufen, J.H. A model of magnetic sources within the Earth’s crust compatible with the field measured by the satellite Magsat. Geologisches Jahrbuch 1984, 75, 125–156. [Google Scholar]
- Langel, R.; Ousley, G.; Berbert, J.; Murphy, J.; Settle, M. The MAGSAT mission. Geophys. Res. Lett. 1982, 9, 243–245. [Google Scholar] [CrossRef]
- Purucker, M.; Langel, R.; Rajaram, M.; Raymond, C. Global magnetization models with a priori information. J. Geophys. Res. Solid Earth 1998, 103, 2563–2584. [Google Scholar] [CrossRef]
- Nataf, H.-C.; Ricard, Y. 3SMAC: An a priori tomographic model of the upper mantle based on geophysical modeling. Phys. Earth Planet. Inter. 1996, 95, 101–122. [Google Scholar] [CrossRef]
- Dyment, J.; Arkani-Hamed, J. Contribution of lithospheric remanent magnetization to satellite magnetic anomalies over the world’s oceans. J. Geophys. Res. Solid Earth 1998, 103, 15423–15441. [Google Scholar] [CrossRef]
- Purucker, M.; Langlais, B.; Olsen, N.; Hulot, G.; Mandea, M. The southern edge of cratonic North America: Evidence from new satellite magnetometer observations. Geophys. Res. Lett. 2002, 29, 56-1–56-4. [Google Scholar] [CrossRef]
- Hemant, K. Modelling and Interpretation of Global Lithospheric Magnetic Anomalies. Ph.D. Thesis, Deutsches GeoForschungsZentrum GFZ, Potsdam, Germany, 2003. [Google Scholar]
- Hemant, K.; Maus, S. Geological modeling of the new CHAMP magnetic anomaly maps using a geographical information system technique. J. Geophys. Res. Solid Earth 2005, 110, B12103. [Google Scholar] [CrossRef]
- Masterton, S.M.; Gubbins, D.; Müller, R.D.; Singh, K.H. Forward modelling of oceanic lithospheric magnetization. Geophys. J. Int. 2013, 192, 951–962. [Google Scholar] [CrossRef]
- Lesur, V.; Jackson, A. Exact solutions for internally induced magnetization in a shell. Geophys. J. Int. 2000, 140, 453–459. [Google Scholar] [CrossRef]
- Lesur, V.; Vervelidou, F. Retrieving lithospheric magnetization distribution from magnetic field models. Geophys. J. Int. 2019, 220, 981–995. [Google Scholar] [CrossRef]
- Maus, S.; Haak, V. Magnetic field annihilators: Invisible magnetization at the magnetic equator. Geophys. J. Int. 2003, 155, 509–513. [Google Scholar] [CrossRef]
- Götze, H.-J.; Lahmeyer, B. Application of three-dimensional interactive modeling in gravity and magnetics. Geophysics 1988, 53, 1096–1108. [Google Scholar] [CrossRef]
- Baykiev, E.; Ebbing, J.; Brönner, M.; Fabian, K. Forward modeling magnetic fields of induced and remanent magnetization in the lithosphere using tesseroids. Comput. Geosci. 2016, 96, 124–135. [Google Scholar] [CrossRef]
- Wieczorek, M.A.; Meschede, M. SHTools: Tools for Working with Spherical Harmonics. Geochem. Geophys. Geosyst. 2018, 19, 2574–2592. [Google Scholar] [CrossRef]
- Driscoll, J.R.; Healy, D.M. Computing Fourier Transforms and Convolutions on the 2-Sphere. Adv. Appl. Math. 1994, 15, 202–250. [Google Scholar] [CrossRef]
- Lin, C. Projected Gradient Methods for Nonnegative Matrix Factorization. Neural Comput. 2007, 19, 2756–2779. [Google Scholar] [CrossRef] [PubMed]
- Laske, G.; Masters, G.; Ma, Z.; Pasyanos, M. Update on CRUST1.0—A 1-Degree Global Model of Earth’s Crust. In Geophysical Research Abstracts; EGU General Assembly: Vienna, Austria, 2013; Volume 15. [Google Scholar]
- Szwillus, W.; Afonso, J.C.; Ebbing, J.; Mooney, W.D. Global Crustal Thickness and Velocity Structure from Geostatistical Analysis of Seismic Data. J. Geophys. Res. Solid Earth 2019, 124, 1626–1652. [Google Scholar] [CrossRef]
- Thébault, E.; Finlay, C.C.; Beggan, C.D.; Alken, P.; Aubert, J.; Barrois, O.; Bertrand, F.; Bondar, T.; Boness, A.; Brocco, L.; et al. International Geomagnetic Reference Field: The 12th generation. Earth Planets Space 2015, 67, 79. [Google Scholar] [CrossRef]
- Vervelidou, F.; Lesur, V. Unveiling Earth’s Hidden Magnetization. Geophys. Res. Lett. 2018, 45, 12283–12292. [Google Scholar] [CrossRef]
- Olesen, O.; Brönner, M.; Ebbing, J.; Gellein, J.; Gernigon, L.; Koziel, J.; Lauritsen, T.; Myklebust, R.; Pascal, C.; Sand, M.; et al. New aeromagnetic and gravity compilations from Norway and adjacent areas: Methods and applications. In Geological Society, London, Petroleum Geology Conference Series; Geological Society of London: London, UK, 2010; Volume 7, pp. 559–586. [Google Scholar]
- Korhonen, J.V.; Aaro, S.; All, T.; Nevanlinna, H.; Skilbrei, J.R.; Säävuori, H.; Vaher, R.; Zhdanova, L.; Koistinen, T. Magnetic Anomaly Map of the Fennoscandian Shield 1: 2 000 000; Geological Surveys of Finland, Norway and Sweden and Ministry of Natural Resources of Russian Federation: 2002. Available online: https://www.researchgate.net/publication/228566513_Preliminary_magnetic_and_gravity_anomaly_maps_of_the_Fennoscandian_shield_1_10_000_000 (accessed on 1 March 2020).
- Enkin, R.J.; Hamilton, T.S.; Morris, W.A. The Henkel Petrophysical Plot: Mineralogy and Lithology from Physical Properties. Geochem. Geophys. Geosyst. 2020, 21, e2019GC008818. [Google Scholar] [CrossRef]
- Idoko, C.M.; Conder, J.A.; Ferré, E.C.; Filiberto, J. The potential contribution to long wavelength magnetic anomalies from the lithospheric mantle. Phys. Earth Planet. Inter. 2019, 292, 21–28. [Google Scholar] [CrossRef]
- Thébault, E.; Vervelidou, F. A statistical spatial power spectrum of the Earth’s lithospheric magnetic field. Geophys. J. Int. 2015, 201, 605–620. [Google Scholar] [CrossRef]
- Ravat, D.; Wang, B.; Wildermuth, E.; Taylor, P.T. Gradients in the interpretation of satellite-altitude magnetic data: An example from central Africa. J. Geodyn. 2002, 33, 131–142. [Google Scholar] [CrossRef]
- Fullea, J.; Afonso, J.C.; Connolly, J.A.D.; Fernàndez, M.; García-Castellanos, D.; Zeyen, H. LitMod3D: An interactive 3-D software to model the thermal, compositional, density, seismological, and rheological structure of the lithosphere and sublithospheric upper mantle. Geochem. Geophys. Geosyst. 2009, 10. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).