Implementation and Use of a Mechanical Cone Penetration Test Database for Liquefaction Hazard Assessment of the Coastal Area of the Tuscany Region
Abstract
1. Introduction
- structures resting on a liquefied soil could suffer relevant differential settlements, tilting, or overturning;
- buried structures are subject to hydraulic heave;
- in free-field conditions, pore water pressure increase and ejecta of sand could damage lifeline systems and several infrastructures;
- instabilities of both natural and artificial slopes can be triggered.
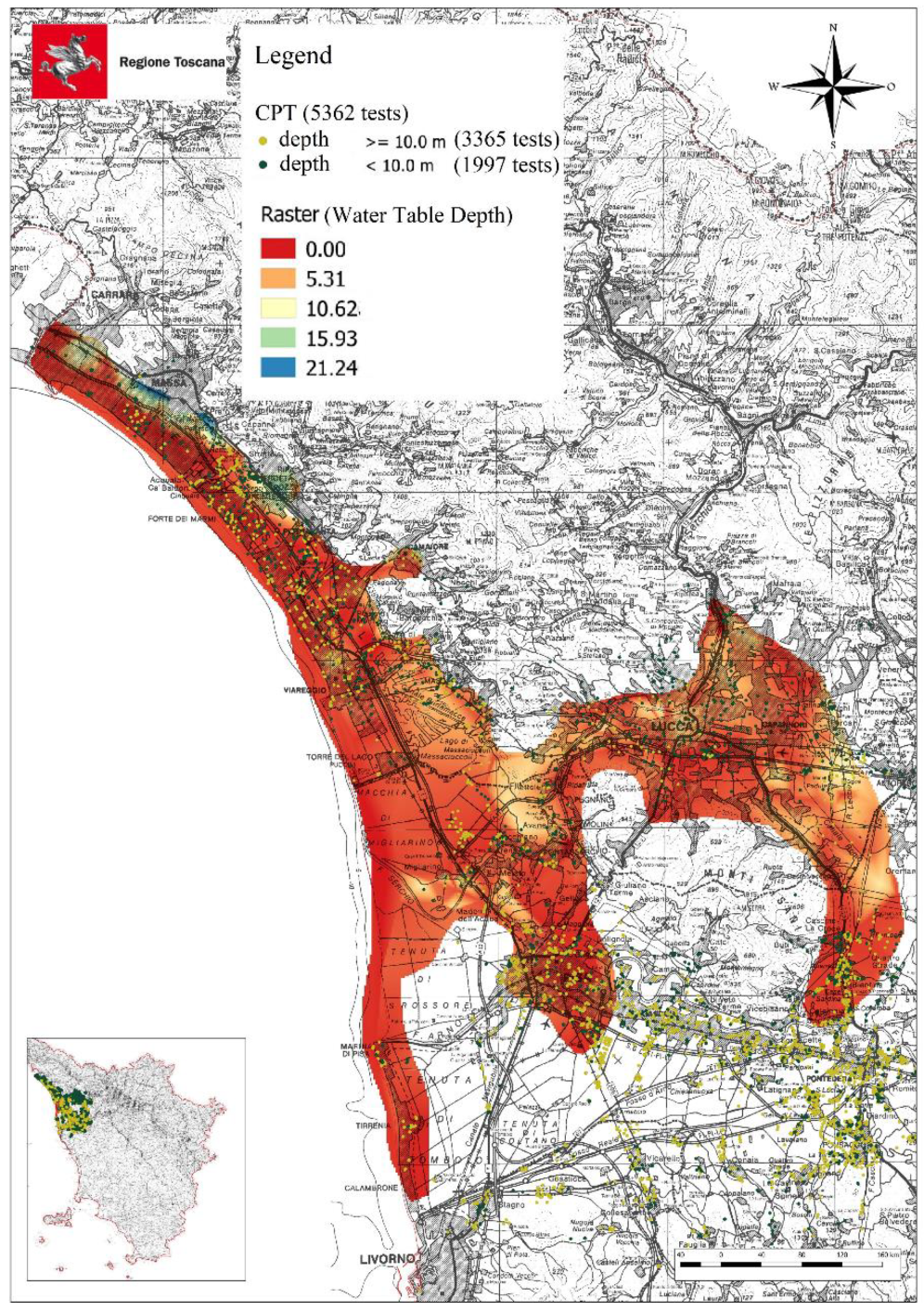
2. Implementation of the CPT Database of the Tuscany Region
- CPT test database from the Tuscany region (managed by the consortium LaMMA), and available on [45];
- CPT test database available from the seismic microzonation studies of the municipalities of the Tuscany region;
- CPT test database from the provinces of the Tuscany region.
3. Main Geological Features and Historical Liquefaction of the Study Area
4. CPT-Based Assessment of Liquefaction Hazard
4.1. Definition of the Seismic Demand
4.2. Considered Liquefaction Evaluation Procedures (LEPs)
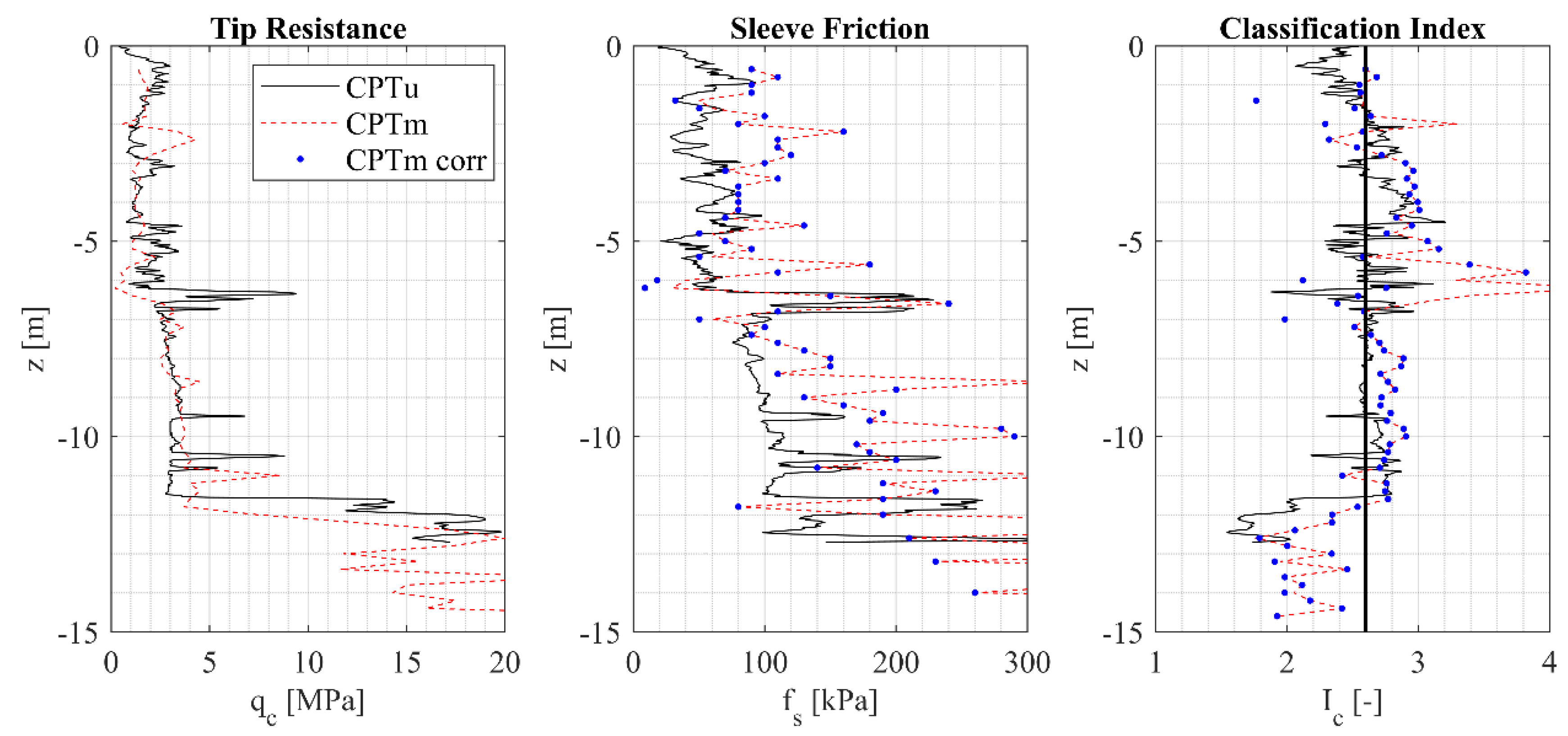
4.3. CPTm Correction Procedure
- the first correlation is between fs measured with CPTm and that obtained from CPTu;
- the second correlation is between the correction factor (ΔIC) and the cone tip resistance (qc), which is applied in the case of silt mixtures that are non-correctly identified by the SBTn classification system.
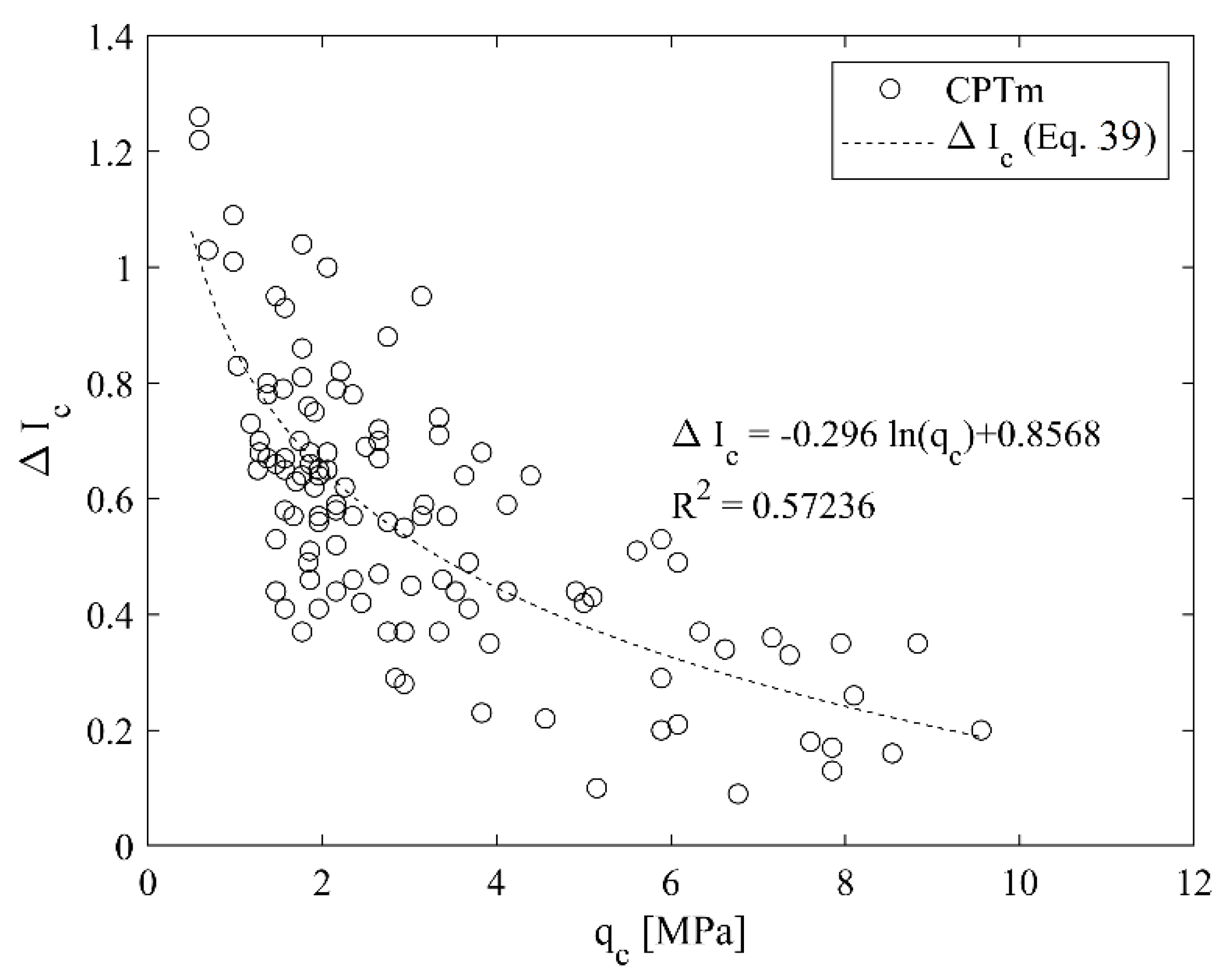
4.3.1. Sleeve Friction (fs) Correction
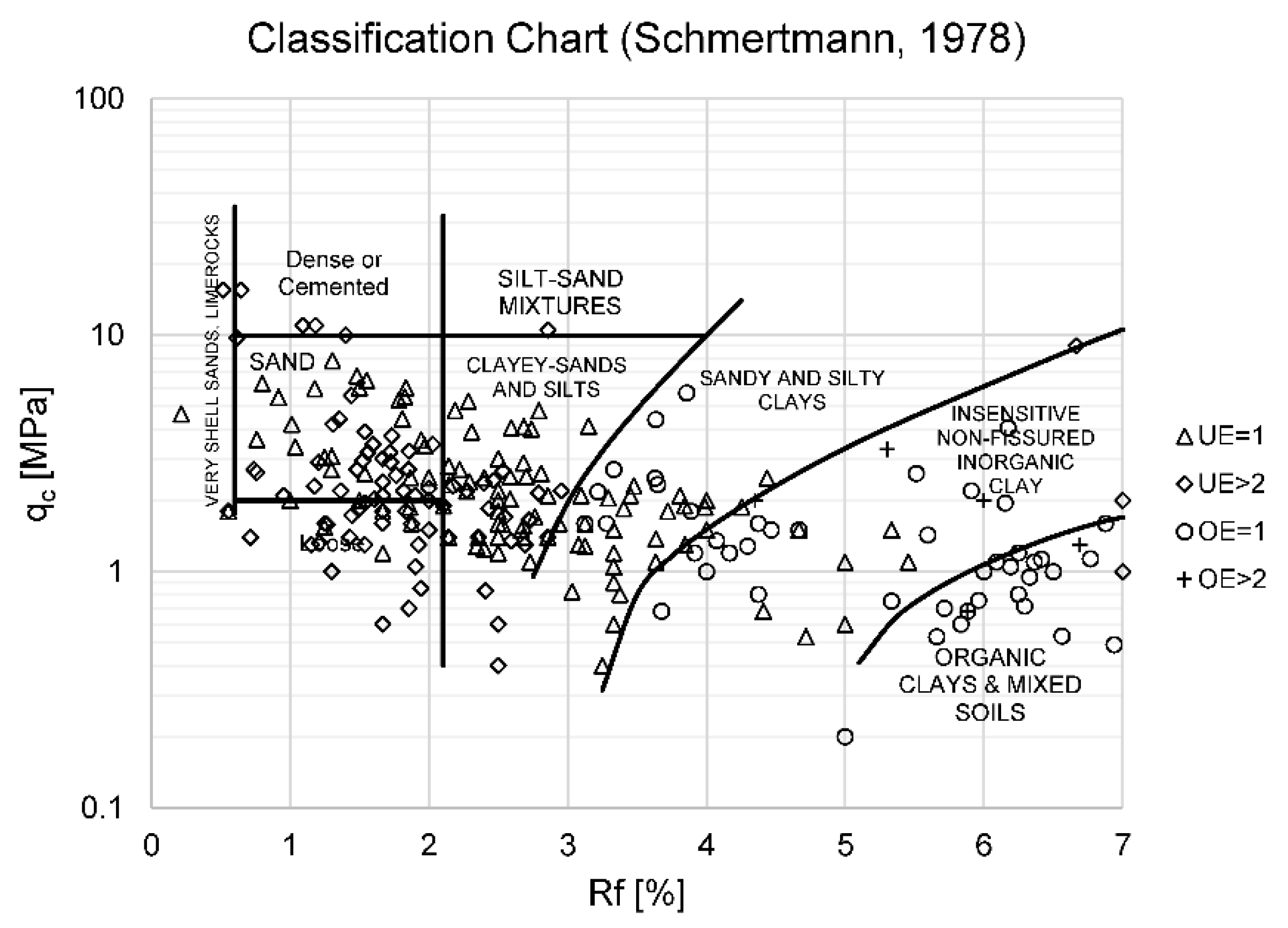
4.3.2. Soil Classification Index IC Correction
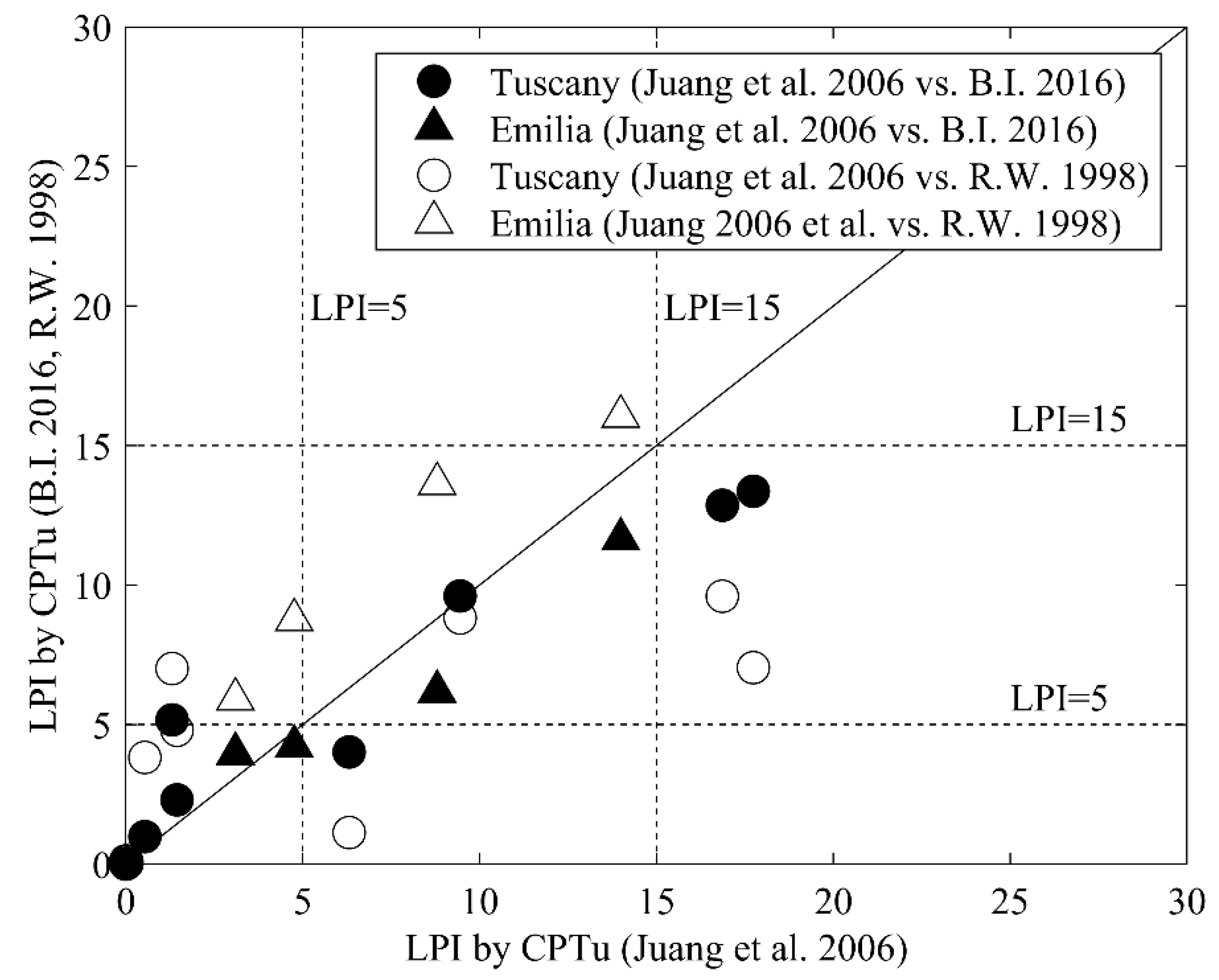
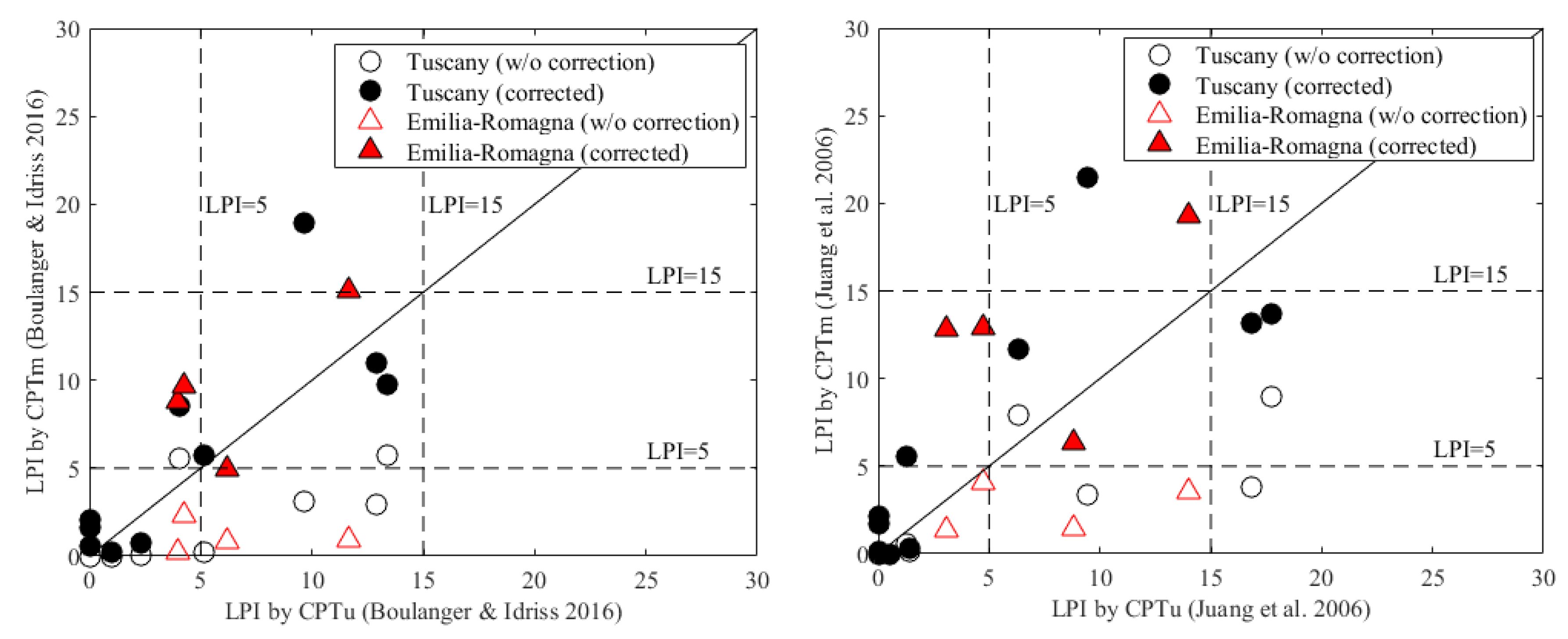
5. Liquefaction Hazard Assessment: CPTu vs. CPTm
6. Liquefaction Hazard Assessment for the Study Area
- (1)
- for the Versilia macro-area (Table 7, Figure 15), where most of the available tests were carried out down to depths of 5–8 m (31%) and 8–10 m (24%), the three LEPs without applying the fs and Ic corrections agree to recognize a zero or low severity for most of the tests. After applying the corrections described in Section 4.3 to the Robertson and Wride [16] method, the high severity and very high severity classes increase from 11.9% and 2.0% to about 45.5% and 20.8%, respectively (considering only those tests with depths equal to or higher than 15 m). When the corrections are applied to the Boulanger and Idriss [24] and Juang et al. [19] approaches, the increase in the high and very high severity classes is less dramatic, especially for the very high severity class (LPI > 15);
- (2)
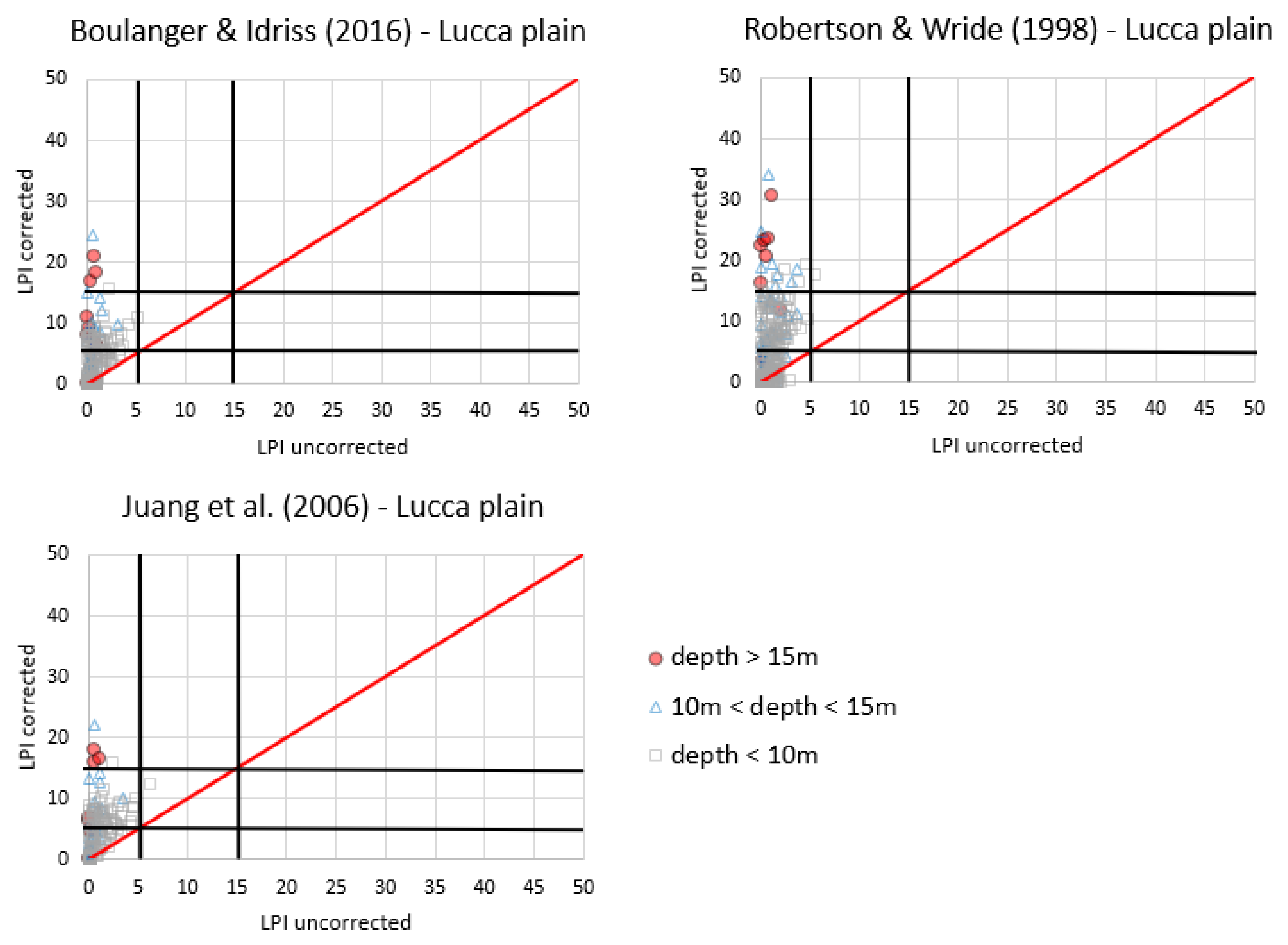
- for the macro-area of the Lucca plain (Table 8, Figure 16), where 40% and 24% of the available tests were carried out down to depths of 5–8 m and 8–10 m, respectively, the three LEPs without applying the fs and Ic corrections agree to classify all the tests in the zero or low severity classes. Very different results are obtained after applying the corrections. In fact, only 30.5% of the tests remain in the low, 42.4% fall in the high, and 23.7% in the very high severity class by using the LEP by Robertson and Wride [16] (considering only those tests with depths equal to or higher than 10 m). After applying the corrections to the Boulanger and Idriss [24] and Juang et al. [19] approaches, especially the very high severity class increases in a negligible way;
- (3)
- for the macro-area of the Pisa plain (Table 9, Figure 17), where 49%, 17%, and 6% of the available tests were carried out down to depths of 8–10 m, 10–15 m, and greater than 20 m, respectively, the three LEPs without applying the fs and Ic corrections agree to classify most of the tests in the zero or low liquefaction severity classes. After applying the corrections, the three LEPs exhibit the same trend that was observed for the other two macro-areas, even though with different percentages.
- the study area could be split into two main classes: urbanized areas that have existed for many centuries and areas that were only urbanized after the Second World War. More specifically, the near-sea plains were uninhabited until the end of the Second World War. Indeed, these areas have only been urbanized since the 1960s. The database was developed mainly to help in evaluating the liquefaction risk in recently urbanized areas;
- on the other hand, there is no historical evidence of relevant liquefaction phenomena in the historically inhabited areas. Therefore, for those areas, a low to moderate liquefaction risk is expected;
- a similar or not very different picture is expected for recently urbanized areas in the case of the same geological features (Holocene, alluvial deposits mainly consisting of sand and silt mixtures);
- it has been shown that the Robertson and Wride [16] approach gives higher values of the LPI. On the other hand, the applied corrections have the only aim of obtaining the same predictions from both CPTm and CPTu. The results obtained with this approach could have been affected by the assumptions we made regarding some factors (i.e., rd, MSF and Kσ);
7. Conclusions
- when the corrections are applied to CPTm, the three considered LEPs predict the same severity class inferred from CPTu;
- in any case, the Robertson and Wride [16] approach leads to a conservative estimate of LPI, whereas the Boulanger and Idriss [24] and Juang et al. [19] approaches lead to less conservative LPI estimates. Nevertheless, the estimates obtained by using the Boulanger and Idriss [24] and Juang et al. [19] methods are closer to those obtained from CPTu tests, at least for the CPTm-CPTu pairs compared herein.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kramer, S. Geotechnical Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Caputo, R.; Papathanassiou, G. Brief communication “Ground failure and liquefaction phenomena triggered by the 20 May 2012 Emilia-Romagna (Northern Italy) earthquake: Case study of Sant’Agostino-San Carlo-Mirabello zone”. Nat. Hazards Earth Syst. Sci. 2012, 12, 3177. [Google Scholar] [CrossRef]
- Papathanassiou, G.; Caputo, R.; Rapti-Caputo, D. Liquefaction phenomena along the paleo-Reno River caused by the May 20, 2012, Emilia (northern Italy) earthquake. Ann. Geophys. 2012, 55. [Google Scholar] [CrossRef]
- Emergeo Working Group. Liquefaction phenomena associated with the Emilia earthquake sequence of May-June 2012 (Northern Italy). Nat. Hazards Earth Syst. Sci. 2013, 13, 935–947. [Google Scholar] [CrossRef]
- Lo Presti, D.C.F.; Sassu, M.; Luzi, L.; Pacor, F.; Castaldini, D.; Tosatti, G.; Meisina, C.; Zizioli, D.; Zucca, F.; Rossi, G.; et al. A report on the 2012 seismic sequence in Emilia (Northern Italy). In Proceedings of the Seventh International Conference on case Histories in Geotechnical Engineering, Chicago, IL, USA, 29 April–4 May 2013. [Google Scholar]
- Vannucchi, G.; Crespellani, T.; Facciorusso, J.; Ghinelli, A.; Madiai, C.; Puliti, A.; Renzi, S. Soil liquefaction phenomena observed in recent seismic events in Emilia-Romagna Region, Italy. Int. J. Earthq. Eng. 2012, 2, 20–29. [Google Scholar]
- Lombardi, D.; Bhattacharya, S. Liquefaction of soil in the Emilia-Romagna region after the 2012 Northern Italy earthquake sequence. Nat. Hazards 2014, 73, 1749–1770. [Google Scholar] [CrossRef]
- Papathanassiou, G.; Mantovani, A.; Tarabusi, G.; Rapti, D.; Caputo, R. Assessment of liquefaction potential for two liquefaction prone areas considering the May 20, 2012 Emilia (Italy) earthquake. Eng. Geol. 2015, 189, 1–16. [Google Scholar] [CrossRef]
- Cubrinovski, M.; Bradley, B.; Wotherspoon, L.; Green, R.; Bray, J.; Wood, C.; Taylor, M. Geotechnical aspects of the 22 February 2011 Christchurch earthquake. Bull. N. Z. Soc. Earthq. Eng. 2011, 44, 205–226. [Google Scholar] [CrossRef]
- Bray, J.D.; Zupan, J.D.; Cubrinovski, M.; Taylor, M. CPT-based liquefaction assessments in Christchurch, New Zealand. In Proceedings of the Papers of the 3rd International Symposium on Cone Penetration Testing, Las Vegas, NV, USA, 12–14 May 2014. [Google Scholar]
- Maurer, B.W.; Green, R.A.; Cubrinovski, M.; Bradley, B.A. Evaluation of the liquefaction potential index for assessing liquefaction hazard in Christchurch, New Zealand. J. Geotech. Geoenviron. Eng. 2014, 140, 04014032. [Google Scholar] [CrossRef]
- Maurer, B.W.; Green, R.A.; Cubrinovski, M.; Bradley, B.A. Assessment of CPT-based methods for liquefaction evaluation in a liquefaction potential index framework. Géotechnique 2015, 65, 328–336. [Google Scholar] [CrossRef]
- Khoshnevisan, S.; Juang, H.; Zhou, Y.G.; Gong, W. Probabilistic assessment of liquefaction-induced lateral spreads using CPT—Focusing on the 2010–2011 Canterbury earthquake sequence. Eng. Geol. 2015, 192, 113–128. [Google Scholar] [CrossRef]
- Cetin, K.O.; Seed, R.B.; Der Kiureghian, A.; Tokimatsu, K.; Harder Jr, L.F.; Kayen, R.E.; Moss, R.E. Standard penetration test-based probabilistic and deterministic assessment of seismic soil liquefaction potential. J. Geotech. Geoenviron. Eng. 2004, 130, 1314–1340. [Google Scholar] [CrossRef]
- Seed, H.B.; Idriss, I.M. Simplified Procedure for Evaluating Soil Liquefaction Potential. J. Soil Mech. Found. Div. ASCE 1971, 97, 1249–1273. [Google Scholar]
- Robertson, P.K.; Wride, C.E. Evaluating Cyclic Liquefaction Potential Using the Cone Penetration Test. Can. Geotech. J. 1998, 35, 442–459. [Google Scholar] [CrossRef]
- Youd, T.L. Liquefaction resistance of soils: Summary report from the 1996 NCEER and 1998 NCEER/NSF workshops on evaluation of liquefaction resistance of soils. J. Geotech. Geoenviron. Eng. 2001, 127, 817–833. [Google Scholar] [CrossRef]
- Juang, C.H.; Yuan, H.; Lee, D.H.; Lin, P.S. Simplified cone penetration test-based method for evaluating liquefaction resistance of soils. J. Geotech. Geoenviron. Eng. 2003, 129, 66–80. [Google Scholar] [CrossRef]
- Juang, C.H.; Fang, S.Y.; Khor, E.H. First-order reliability method for probabilistic liquefaction triggering analysis using CPT. J. Geotech. Geoenviron. Eng. 2006, 132, 337–350. [Google Scholar] [CrossRef]
- Moss, R.E.; Seed, R.B.; Kayen, R.E.; Stewart, J.P.; Der Kiureghian, A.; Cetin, K.O. CPT-based probabilistic and deterministic assessment of in situ seismic soil liquefaction potential. J. Geotech. Geoenviron. Eng. 2006, 132, 1032–1051. [Google Scholar] [CrossRef]
- Idriss, I.M.; Boulanger, R.W. Semi-empirical procedures for evaluating liquefaction potential during earthquakes. J. Soil Dyn. Earthq. Eng. 2006, 26, 115–130. [Google Scholar] [CrossRef]
- Idriss, I.M.; Boulanger, R.W. Soil Liquefaction during Earthquakes; Earthquake Engineering Research Institute: Oakland, CA, USA, 2008. [Google Scholar]
- Boulanger, R.W.; Idriss, I.M. CPT and SPT Based Liquefaction Triggering Procedures; Report No. UCD/CGM-14/01; Center for Geotechnical Modeling, Department of Civil and Environmental Engineering, University of California: Davis, CA, USA, 2014; p. 134. [Google Scholar]
- Boulanger, R.W.; Idriss, I.M. CPT-based liquefaction triggering procedure. J. Geotech. Geoenviron. Eng. 2016, 142, 04015065. [Google Scholar] [CrossRef]
- Robertson, P.K.; Campanella, R.G. Liquefaction potential of sands using the cone penetration test. J. Geotech. Div. ASCE 1985, 22, 277–286. [Google Scholar]
- Yuan, H.; Yang, S.H.; Andrus, R.D.; Juang, C.H. Liquefaction-induced ground failure: A study of the Chi-Chi earthquake cases. Eng. Geol. 2004, 71, 141–155. [Google Scholar] [CrossRef]
- Kayabali, K. Soil liquefaction evaluation using shear wave velocity. Eng. Geol. 1996, 44, 121–127. [Google Scholar] [CrossRef]
- Andrus, R.D.; Stokoe, K.H. Liquefaction Resistance of Soils from Shear-Wave Velocity. J. Geotech. Geoenviron. Eng. 2000, 126, 1015–1025. [Google Scholar] [CrossRef]
- Vaid, Y.P.; Hughes, J.M.; Byrne, P.M. Dilation Angle and Liquefaction Potential. J. Geotech. Eng. Div. 1981, 107, 1003–1008. [Google Scholar]
- Robertson, P.K.; Campanella, R.G. Estimating liquefaction potential of sands using the flat plate dilatometer. Geotech. Test. J. 1986, 9, 38–40. [Google Scholar]
- Tsai, P.H.; Lee, D.H.; Kung, G.T.C.; Juang, C.H. Simplified DMT-based methods for evaluating liquefaction resistance of soils. Eng. Geol. 2009, 103, 13–22. [Google Scholar] [CrossRef]
- Iwasaki, T.; Tokida, K.; Tatsuko, F.; Yasuda, S. A practical method for assessing soil liquefaction potential based on case studies at various sites in Japan. In Proceedings of the 2nd International Conference on Microzonation for Safer Construction-Research and Application, San Francisco, CA, USA, 26 November–1 December 1978; Volume 2, pp. 885–896. [Google Scholar]
- Tonkin and Taylor. Liquefaction Vulnerability Study; Tonkin e Taylor Ltd.: Auckland, New Zealand, 2013. [Google Scholar]
- Sonmez, H. Modification of the liquefaction potential index and liquefaction susceptibility mapping for a liquefaction-prone area (Inegol, Turkey). Environ. Geol. 2003, 44, 862–871. [Google Scholar] [CrossRef]
- Mayne, P.W. Synthesis 368: Cone Penetration Testing. NCHRP; Transportation Research Board, National Academy Press: Washington, DC, USA, 2007. [Google Scholar]
- Boulanger, R.W.; DeJong, J.T. Inverse filtering procedure to correct cone penetration data for thin-layer and transition effects. In Proceedings of the Cone Penetration Testing 2018, Delft, The Netherlands, 21–22 June 2018; pp. 25–44. [Google Scholar]
- Robertson, P.K.; Campanella, R.G.; Gillespie, D.; Greig, J. Use of piezometer cone data. In Use of in Situ Tests in Geotechnical Engineering; ASCE: Reston, VA, USA, 1986; pp. 1263–1280. [Google Scholar]
- Robertson, P.K. Soil Classification Using the Cone Penetration Test. Can. Geotech. J. 1990, 27, 151–158. [Google Scholar] [CrossRef]
- Robertson, P.K. Interpretation of cone penetration tests—A unified approach. Can. Geotech. J. 2009, 46, 1337–1355. [Google Scholar] [CrossRef]
- Lo Presti, D.; Meisina, C.; Squeglia, N. Use of cone penetration tests for soil profiling. Ital. Geotech. J. 2009, 2, 9–33. [Google Scholar]
- Meisina, C.; Persichillo, M.G.; Francesconi, M.; Creatini, M.; Lo Presti, D.C. Differences between mechanical and electrical cone penetration test in the liquefaction hazard assessment and soil profile reconstruction. In Proceedings of the ICCE International Conference of Civil Engineering, Tirana, Albania, 12–14 October 2017; pp. 95–105. [Google Scholar]
- Meisina, C.; Stacul, S.; Lo Presti, D. Empirical correlations to improve the use of mechanical CPT in the liquefaction potential evaluation and soil profile reconstruction. In Proceedings of the 4th International Symposium on Cone Penetration Testing, CPT’18, Delft, The Netherlands, 21–22 June 2018; p. 435. [Google Scholar]
- Lo Presti, D.; Giusti, I.; Cosanti, B.; Squeglia, N.; Pagani, E. Interpretation of CPTu in “unusual” soils. Riv. Ital. Geotec. 2016, 4, 25–44. [Google Scholar]
- Regione Emilia Romagna (Italy). La Banca Dati Geognostica. 2011. Available online: http://ambiente.regione.emilia-romagna.it/geologia/cartografia/webgis-banchedati/banca-dati-geognostica (accessed on 3 February 2020).
- Regione Toscana. Geoscopio: Geological Database. 2019. Available online: http://www502.regione.toscana.it/geoscopio/geologia.html (accessed on 3 February 2020).
- NTC. Norme Tecniche per le Costruzioni 2018. Aggiornamento delle ‘Norme tecniche per le costruzioni’. Gazzetta Ufficiale Serie Generale n.42 del 20-02-2018—Suppl. Ordinario n. 8. Italian Building Code (in Italian). 2018. Available online: https://www.gazzettaufficiale.it/eli/id/2018/2/20/18A00716/sg (accessed on 3 February 2020).
- Galli, P.; Meloni, F. Liquefazione Storica. Un catalogo nazionale. Quat. Ital. J. Quat. Sci. 1993, 6, 271–292. [Google Scholar]
- Groholski, D.R.; Hashash, Y.M.; Kim, B.; Musgrove, M.; Harmon, J.; Stewart, J.P. Simplified model for small-strain nonlinearity and strength in 1D seismic site response analysis. J. Geotech. Geoenviron. Eng. 2016, 142, 04016042. [Google Scholar] [CrossRef]
- Angina, A.; Steri, A.; Stacul, S.; Lo Presti, D. Free-Field Seismic Response Analysis: The Piazza dei Miracoli in Pisa Case Study. Int. J. Geotech. Earthq. Eng. 2018, 9, 1–21. [Google Scholar] [CrossRef]
- Fiorentino, G.; Nuti, C.; Squeglia, N.; Lavorato, D.; Stacul, S. One-dimensional nonlinear seismic response analysis using strength-controlled constitutive models: The case of the leaning tower of Pisa’s subsoil. Geosciences 2018, 8, 228. [Google Scholar] [CrossRef]
- Liao, S.S.C.; Whitman, R.V. Catalogue of Liquefaction and Non-Liquefaction Occurrences during Earthquakes; Res. Rep. Dept. of Civ. Engrg.; Massachusetts Institute of Technology: Cambridge, MA, USA, 1986. [Google Scholar]
- Spallarossa, D.; Barani, S. Disaggregazione della pericolosità sismica in termini di MR-ε. Progetto DPC-INGV S1 Deliv. D14 2007. [Google Scholar]
- Pagani Geotechnical Equipment. 2017. Available online: http://www.pagani-geotechnical.com (accessed on 3 February 2020).
- Viggiani, C.; Pepe, M. Il Sottosuolo della Torre. In La Torre Restituita; Gli Studi e gli Interventi che Hanno Consentito la Stabilizzazione Della Torre di Pisa; Poligrafico dello Stato: Rome, Italy, 2005. [Google Scholar]
- Squeglia, N.; Stacul, S.; Abed, A.A.; Benz, T.; Leoni, M. m-PISE: A novel numerical procedure for pile installation and soil extraction. Application to the case of Leaning Tower of Pisa. Comput. Geotech. 2018, 102, 206–215. [Google Scholar] [CrossRef]
- Schmertmann, J.H. Guidelines for Cone Penetration Test. In Performance and Design; U.S. Department of Transportation: Washington, DC, USA, 1978. [Google Scholar]
- Lo Presti, D.; Stacul, S.; Meisina, C.; Bordoni, M.; Bittelli, M. Preliminary Validation of a Novel Method for the Assessment of Effective Stress State in Partially Saturated Soils by Cone Penetration Tests. Geosciences 2018, 8, 30. [Google Scholar] [CrossRef]









| Municipality | n CPTm | n CPTu | 0 < z ≤ 5 m | 5 < z ≤ 8 m | 8 < z ≤ 10 m | 10 < z ≤ 15 m | 15 < z ≤ 20 m | >20 m |
|---|---|---|---|---|---|---|---|---|
| Camaiore | 103 | 13 | 2 | 31 | 63 | 19 | 0 | 1 |
| Carrara | 18 | - | 2 | 12 | 2 | 0 | 2 | 0 |
| Forte dei Marmi | 91 | - | 3 | 27 | 53 | 8 | 0 | 0 |
| Massa | 77 | - | 19 | 30 | 20 | 7 | 1 | 0 |
| Massarosa | 93 | - | 2 | 31 | 30 | 25 | 3 | 2 |
| Montignoso | 79 | - | 9 | 14 | 9 | 26 | 21 | 0 |
| Pietrasanta | 188 | - | 21 | 70 | 49 | 25 | 21 | 2 |
| Serravezza | 33 | - | 5 | 7 | 13 | 8 | 0 | 0 |
| Viareggio | 87 | - | 7 | 24 | 28 | 20 | 8 | 0 |
| TOTAL | 769 | 13 | 70 | 246 | 267 | 138 | 56 | 5 |
| Municipality | n CPTm | n CPTu | 0 < z ≤ 5 m | 5 < z ≤ 8 m | 8 < z ≤ 10 m | 10 < z ≤ 15 m | 15 < z ≤ 20 m | >20 m |
|---|---|---|---|---|---|---|---|---|
| Bientina | 347 | - | 5 | 85 | 170 | 58 | 15 | 14 |
| Buti | 88 | - | 24 | 17 | 30 | 15 | 0 | 2 |
| Calci | 22 | - | 15 | 5 | 2 | 0 | 0 | 0 |
| Calcinaia | 206 | - | 1 | 21 | 148 | 23 | 13 | 0 |
| Cascina | 510 | - | 7 | 79 | 299 | 69 | 22 | 34 |
| Collesalvetti | 223 | - | 5 | 30 | 84 | 43 | 29 | 32 |
| Crespina | 53 | - | 3 | 7 | 25 | 13 | 4 | 1 |
| Fauglia | 50 | - | 4 | 7 | 24 | 8 | 6 | 1 |
| Lari | 129 | - | 8 | 18 | 68 | 13 | 21 | 1 |
| Livorno | 17 | - | 0 | 0 | 8 | 5 | 1 | 3 |
| Pisa | 488 | - | 14 | 64 | 168 | 133 | 60 | 49 |
| Ponsacco | 338 | - | 7 | 57 | 198 | 47 | 26 | 3 |
| Pontedera | 534 | 3 | 8 | 83 | 301 | 88 | 25 | 32 |
| San Giuliano Terme | 156 | - | 15 | 19 | 73 | 32 | 3 | 14 |
| Vicopisano | 93 | - | 8 | 21 | 47 | 14 | 3 | 0 |
| Vecchiano | 199 | - | 32 | 48 | 46 | 31 | 22 | 20 |
| TOTAL | 3453 | 3 | 156 | 561 | 1691 | 592 | 250 | 206 |
| Municipality | n CPTm | n CPTu | 0 < z ≤ 5 m | 5 < z ≤ 8 m | 8 < z ≤ 10 m | 10 < z ≤ 15 m | 15 < z ≤ 20 m | >20 m |
|---|---|---|---|---|---|---|---|---|
| Altopascio | 53 | - | 9 | 26 | 9 | 8 | 1 | 0 |
| Capannori | 100 | - | 22 | 34 | 28 | 9 | 7 | 0 |
| Lucca | 80 | - | 25 | 40 | 14 | 1 | 0 | 0 |
| Porcari | 45 | - | 2 | 11 | 17 | 15 | 0 | 0 |
| TOTAL | 278 | 0 | 58 | 111 | 68 | 33 | 8 | 0 |
| Florence | Massa Carrara | ||
| Municipality | as (g) | Municipality | as (g) |
| Vicchio | 0.320 | Carrara | 0.206 |
| Montignoso | 0.212 | ||
| Massa | 0.200 | ||
| Livorno | Pisa | ||
| Municipality | as (g) | Municipality | as (g) |
| Livorno | 0.182 | Bientina | 0.175 |
| Collesalvetti | 0.208 | Buti | 0.180 |
| Lucca | Calci | 0.179 | |
| Municipality | as (g) | Calcinaia | 0.180 |
| Altopascio | 0.191 | Cascina | 0.180 |
| Camaiore | 0.188 | Crespina | 0.210 |
| Capannori | 0.200 | Fauglia | 0.209 |
| Forte dei Marmi | 0.192 | Lari | 0.210 |
| Lucca | 0.196 | Pisa | 0.177 |
| Massarosa | 0.189 | Ponsacco | 0.203 |
| Pietrasanta | 0.196 | Pontedera | 0.190 |
| Porcari | 0.195 | San Giuliano Terme | 0.182 |
| Viareggio | 0.182 | Vicopisano | 0.178 |
| Serravezza | 0.210 | Vecchiano | 0.181 |
| Schmertmann [56] | IC (PM) | SBTn [38] | IC (SBTn) | SBTn Class Description |
|---|---|---|---|---|
| Organic clay and mixed soils | - | 2 | IC > 3.60 | Organic soils, peats |
| Insensitive non-fissured inorganic clays | 3.275 | 3 | 2.95 < IC < 3.60 | Clays: clay to silty clay |
| Sandy and silty clays | 2.775 | 4 | 2.60 < IC < 2.95 | Silt mixtures: silty sand to sandy silt |
| Clayey sands and silts | 2.325 | 5 | 2.05 < IC < 2.60 | Sand mixtures: silty sand to sandy silt |
| Silt–sand mixtures | 2.325 | 5 | 2.05 < IC < 2.60 | Sand mixtures: silty sand to sandy silt |
| Sands | 1.68 - | 6 7 | 1.31 < IC < 2.05 IC < 1.31 | Sands: clean sand to silty sand Gravely sands to sands |
| Dense or cemented sands | - | 8 | - | Very stiff sand to clayey sand |
| Very shell sands, lime rocks | - | 8 | - | Very stiff sand to clayey sand |
| CPTu | CPTm | Distance (m) | GWT (m) | Region | Municipality | as (g) | Magnitude |
|---|---|---|---|---|---|---|---|
| 28000599_CPT_6688 | 28000599_CPT_6666 | 38.70 | 3.12 | Tuscany | Pontedera | 0.19 | 5.5 |
| 28000599_CPT_6690 | 28000599_CPT_6669 | 29.82 | 2.62 | Tuscany | Pontedera | 0.19 | 5.5 |
| 28000599_CPT_6689 | 28000599_CPT_9995 | 18.77 | 3.43 | Tuscany | Pontedera | 0.19 | 5.5 |
| CPTU1 | 00405 | 159.58 | 2.00 | Tuscany | Camaiore | 0.188 | 5.5 |
| CPTU4 | 00634 | 99.18 | 1.80 | Tuscany | Camaiore | 0.188 | 5.5 |
| CPTU7 | 00224 | 147.80 | 1.95 | Tuscany | Camaiore | 0.188 | 5.5 |
| CPTe11 | CPT1 | 2.00 | 2.0 | Tuscany | Vicchio | 0.32 | 6.37 |
| CPTe12 | CPT3 | 2.00 | 2.0 | Tuscany | Vicchio | 0.32 | 6.37 |
| CPTe13 | CPT6 | 2.00 | 2.0 | Tuscany | Vicchio | 0.32 | 6.37 |
| CPTe15 | CPT9bis | 10.00 | 2.0 | Tuscany | Vicchio | 0.32 | 6.37 |
| CPTu (203010U502) | CPT (203010C121) | 13.00 | 1.20 | Emilia-Romagna | Sant’Agostino | 0.21 | 5.9 |
| CPTu (185130U508) | CPT (185130C142) | 36.00 | 3.80 | Emilia-Romagna | Sant’Agostino | 0.21 | 5.9 |
| CPTu (185130U512) | CPT (185130C137) | 36.00 | 4.50 | Emilia-Romagna | Sant’Agostino | 0.21 | 5.9 |
| CPTu (185130U514) | CPT (185130C135) | 24.00 | 4.55 | Emilia-Romagna | Sant’Agostino | 0.21 | 5.9 |
| LPI | Boulanger and Idriss [24] | Boulanger and Idriss [24] Corrected | Robertson and Wride [16] | Robertson and Wride [16] Corrected | Juang et al. [19] | Juang et al. [19] Corrected |
|---|---|---|---|---|---|---|
| LPI = 0 | 21 (20.8%) | 6 (5.9%) | 16 (15.8%) | 2 (2.0%) | 24 (23.8%) | 13 (12.9%) |
| 0 < LPI ≤ 5 | 67 (66.3%) | 49 (48.5%) | 71 (70.3%) | 32 (31.7%) | 59 (58.4%) | 29 (28.7%) |
| 5 < LPI ≤ 15 | 13 (12.9%) | 35 (34.7%) | 12 (11.9%) | 46 (45.5%) | 17 (16.8%) | 46 (45.5%) |
| LPI > 15 | 0 (0.0%) | 11 (10.9%) | 2 (2.0%) | 21 (20.8%) | 1 (1.0%) | 13 (12.9%) |
| LPI | Boulanger and Idriss [24] | Boulanger and Idriss [24] Corrected | Robertson and Wride [16] | Robertson and Wride [16] Corrected | Juang et al. [19] | Juang et al. [19] Corrected |
|---|---|---|---|---|---|---|
| LPI = 0 | 13 (22.0%) | 3 (5.1%) | 6 (10.2%) | 2 (3.4%) | 14 (23.7%) | 4 (6.8%) |
| 0 < LPI ≤ 5 | 46 (78.0%) | 37 (62.7%) | 53 (89.8%) | 18 (30.5%) | 45 (76.3%) | 40 (67.8%) |
| 5 < LPI ≤ 15 | 0 (0%) | 15 (25.4%) | 0 (0%) | 25 (42.4%) | 0 (0%) | 11 (18.6%) |
| LPI > 15 | 0 (0%) | 4 (6.8%) | 0 (0%) | 14 (23.7%) | 0 (0%) | 4 (6.8%) |
| LPI | Boulanger and Idriss [24] | Boulanger and Idriss [24] Corrected | Robertson and Wride [16] | Robertson and Wride [16] Corrected | Juang et al. [19] | Juang et al. [19] Corrected |
|---|---|---|---|---|---|---|
| LPI = 0 | 178 (27.5%) | 9 (1.4%) | 145 (22.4%) | 10 (1.5%) | 160 (24.7%) | 8 (1.2%) |
| 0 < LPI ≤ 5 | 454 (70.1%) | 171 (26.4%) | 484 (74.7%) | 157 (24.2%) | 471 (72.7%) | 204 (31.5%) |
| 5 < LPI ≤ 15 | 12 (1.9%) | 275 (42.4%) | 11 (1.7%) | 242 (37.3%) | 12 (1.9%) | 260 (40.1%) |
| LPI > 15 | 4 (0.6%) | 193 (29.8%) | 8 (1.2%) | 239 (36.9%) | 5 (0.8%) | 176 (27.2%) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stacul, S.; Magalotti, A.; Baglione, M.; Meisina, C.; Lo Presti, D. Implementation and Use of a Mechanical Cone Penetration Test Database for Liquefaction Hazard Assessment of the Coastal Area of the Tuscany Region. Geosciences 2020, 10, 128. https://doi.org/10.3390/geosciences10040128
Stacul S, Magalotti A, Baglione M, Meisina C, Lo Presti D. Implementation and Use of a Mechanical Cone Penetration Test Database for Liquefaction Hazard Assessment of the Coastal Area of the Tuscany Region. Geosciences. 2020; 10(4):128. https://doi.org/10.3390/geosciences10040128
Chicago/Turabian StyleStacul, Stefano, Aurora Magalotti, Massimo Baglione, Claudia Meisina, and Diego Lo Presti. 2020. "Implementation and Use of a Mechanical Cone Penetration Test Database for Liquefaction Hazard Assessment of the Coastal Area of the Tuscany Region" Geosciences 10, no. 4: 128. https://doi.org/10.3390/geosciences10040128
APA StyleStacul, S., Magalotti, A., Baglione, M., Meisina, C., & Lo Presti, D. (2020). Implementation and Use of a Mechanical Cone Penetration Test Database for Liquefaction Hazard Assessment of the Coastal Area of the Tuscany Region. Geosciences, 10(4), 128. https://doi.org/10.3390/geosciences10040128







