Topographic Analysis of Landslide Distribution Using AW3D30 Data
Abstract
:1. Introduction
2. Study Area
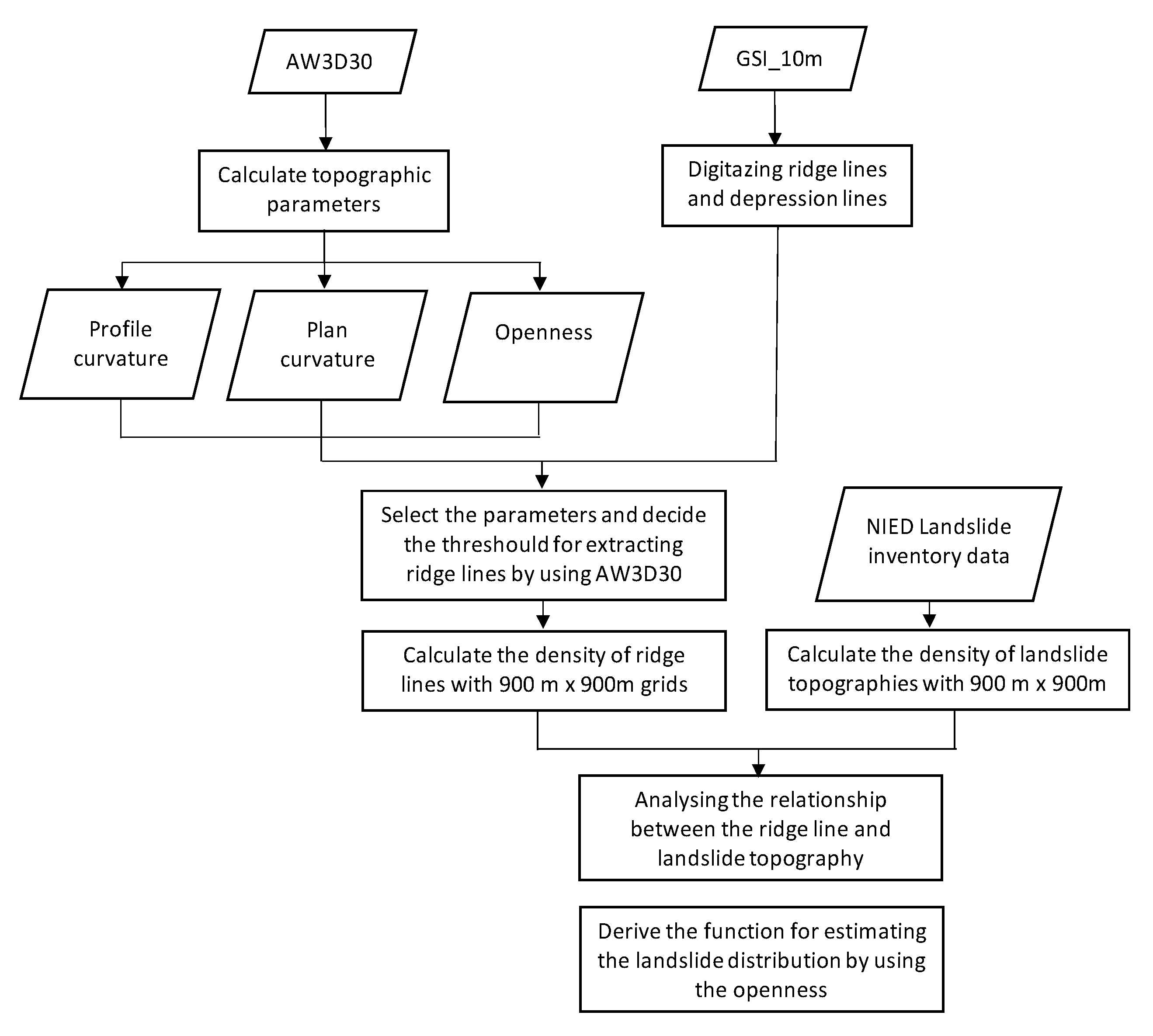
3. DEM and Landslide Datasets
4. Ridgeline Extraction
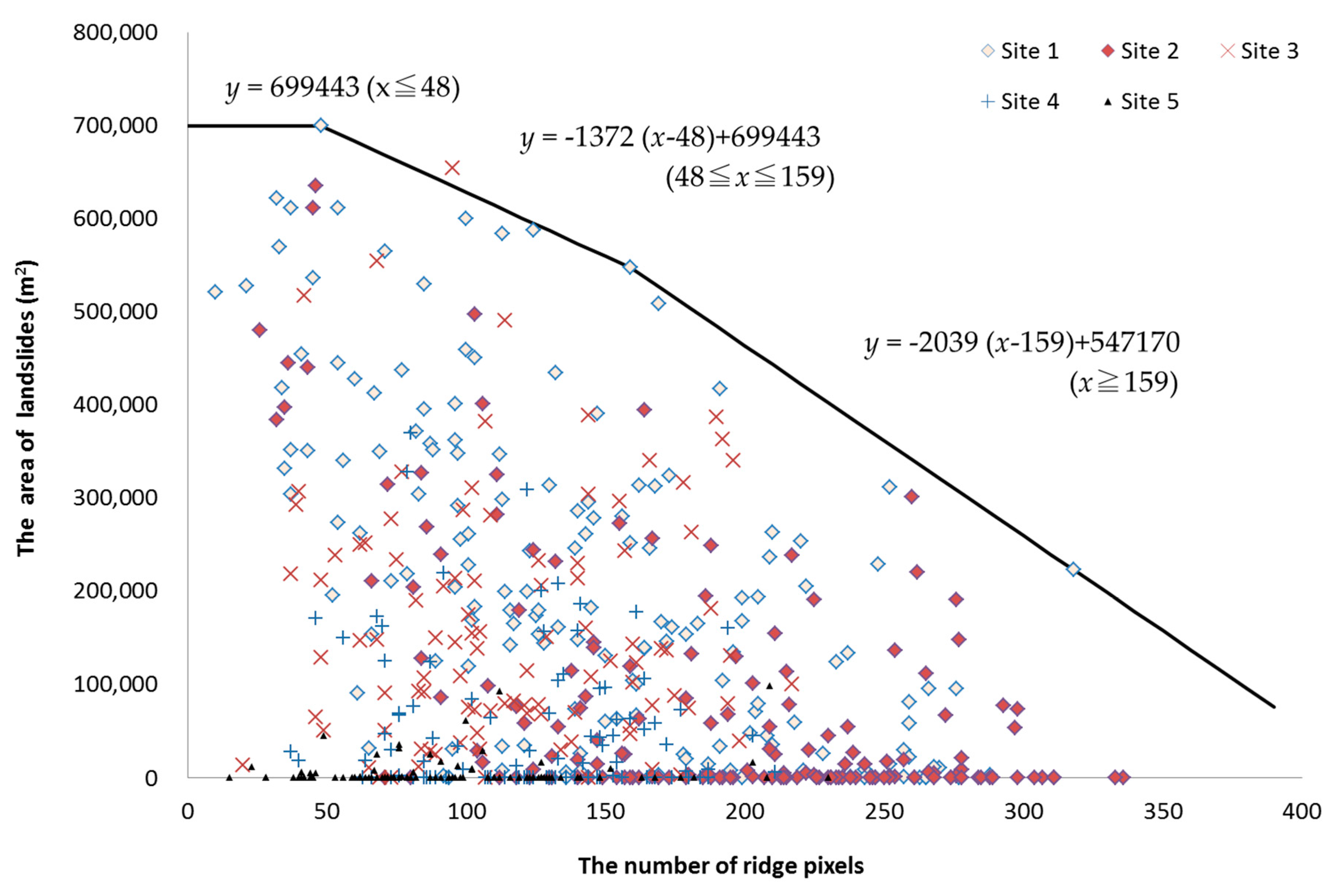
5. Landslide Distributions Relative to Ridgelines
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, Q.; Fan, X.; Huang, R.; Westen, C. Landslide dams triggered by the Wenchuan Earthquake, Sichuan Province, southwest China. Bull. Eng. Geol. Environ. 2009, 68, 373–386. [Google Scholar] [CrossRef]
- Lacroix, P. Landslides triggered by the Gorkha earthquake in the Langtang valley, volumes and initiation processes. Earth Planets Space 2016, 68, 46. [Google Scholar] [CrossRef] [Green Version]
- Dai, F.C.; Lee, F.C.; Ngai, Y.Y. Landslide risk assessment and management: An overview. Eng. Geol. 2002, 64, 65–87. [Google Scholar] [CrossRef]
- Kirschbaum, D.B.; Stanley, T.; Simmons, J. A dynamic landslide hazard assessment system for Central America and Hispaniola. Nat. Hazards Earth Syst. Sci. 2015, 15, 2257–2272. [Google Scholar] [CrossRef] [Green Version]
- Froude, M.J.; Petley, D.V. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.; Zhan, W.; Dong, X.; Westen, C.; Xu, Q.; Dai, L.; Yang, Q.; Huang, R.; Havenith, H. Analyzing successive landslide dam formation by different triggering mechanisms: The case of the Tangjiawan landslide, Sichuan, China. Eng. Geol. 2018, 243, 128–144. [Google Scholar] [CrossRef]
- Chang, K.; Chan, Y.; Chen, R.; Hsieh, Y. Geomorphological evolution of landslides near an active normal fault in northern Taiwan, as revealed by lidar and unmanned aircraft system data. Nat. Hazards Earth Syst. Sci. 2018, 18, 709–727. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Ma, C.; Wang, Z. Prediction of landslide position of loose rock mass at mountain tunnel exit. Adv. Civ. Eng. 2019, 2019, 1–9. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K. Landslide inventory maps: New tools for an old problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef] [Green Version]
- Varnes, D. Slope Movement Types and Processes. In Landslides: Analysis and Control; Schuster, R., Krizek, R., Eds.; National Research Council; Transportation Research Board; Special Report 176; National Academy of Science: Washington, DC, USA, 1978; pp. 11–33. [Google Scholar]
- International Association for Engineering Geology and the Environment (IAEG) Commission. Suggested nomenclature for landslides. Bull. Int. Assoc. Eng. Geol. 1990, 41, 13–16. [Google Scholar] [CrossRef]
- Tarolli, P.; Tarboton, D. A new method for determination of most likely landslide initiation points and the evaluation of digital terrain model scale in terrain stability mapping. Hydrol. Earth Sys. Sci. 2006, 10, 663–677. [Google Scholar] [CrossRef] [Green Version]
- Booth, A.; Roering, J.; Perron, J. Automated landslide mapping using spectral analysis and high-resolution topographic data: Puget Sound lowlands, Washington, and Portland Hills, Oregon. Geomorphology 2009, 109, 132–147. [Google Scholar] [CrossRef]
- Hölbling, D.; Betts, H.; Spiekermann, R.; Phillips, C. Identifying Spatio-Temporal Landslide Hotspots on North Island, New Zealand, by Analyzing Historical and Recent Aerial Photography. Geosciences 2016, 6, 48. [Google Scholar] [CrossRef] [Green Version]
- Pawluszek, K. Landslide features identification and morphology investigation using high-resolution DEM derivatives. Nat. Hazards 2019, 96, 311–330. [Google Scholar] [CrossRef] [Green Version]
- Keefer, D. The Loma Prieta, California, Earthquake of October 17, 1989—Landslides; USGS Professional Paper 1551–C; US Government Printing Office: Washington, DC, USA, 1998.
- AIST. GeomapNavi, Geological Map Display System of Geological Survey of Japan; AIST: Warrendale, PA, USA, 2014. [Google Scholar]
- Hasegawa, S.; Tamura, E.; Kanbara, D. Georisks along active faults of Median Tectonic Line in Shikoku, Southwest Japan. In Proceedings of the 10th Asian Regional Conference of IAEG, Kyoto, Japan, 26–29 September 2015; pp. 1–8. [Google Scholar]
- Alganci, U.; Besol, B.; Sertel, E. Accuracy assessment of different digital surface models. ISPRS Int. J. Geo-Inf. 2018, 7, 114. [Google Scholar] [CrossRef] [Green Version]
- Tadono, T.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Precise Global DEM Generation by ALOS PRISM. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 4, 71–76. [Google Scholar] [CrossRef] [Green Version]
- Tadono, T.; Nagai, H.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Initial Validation of the 30 m-mesh Global Digital Surface Model Generated by ALOS PRISM. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS 2016, 157–162. [Google Scholar] [CrossRef]
- National Research Institute for Earth Science and Disaster Prevention. Digital Archive for Landslide Distribution Maps. Available online: http://dil-opac.bosai.go.jp/publication/nied_tech_note/landslidemap/gis.html (accessed on 10 February 2020).
- Dou, J.; Bui, D.; Yunus, A.; Jia, K.; Song, X.; Revhaug, I.; Xia, H.; Zhu, Z. Optimization of causative factors for landslide susceptibility evaluation using remote sensing and GIS data in parts of Niigata, Japan. PLoS ONE 2015, 10, e0133262. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, J.; Evans, I.; Brinkmann, J. Comparison of polynomial models for land surface curvature calculation. Int. J. Geogr. Inf. Sci. 2003, 17, 797–814. [Google Scholar] [CrossRef]
- Shary, P.; Sharaya, L.; Mitusov, A. Fundamental quantitative methods of land surface analysis. Geoderma 2002, 107, 1–32. [Google Scholar] [CrossRef]
- Bergonse, R.; Reis, E. Controlling factors of the size and location of large gully systems: A regression-based exploration using reconstructed pre-erosion topography. Catena 2016, 147, 621–631. [Google Scholar] [CrossRef]
- Conoscenti, C.; Angileri, S.; Cappadonia, C.; Rotigliano, E.; Agnesi, V.; Märker, M. Gully erosion susceptibility assessment by means of GIS-based logistic regression: A case of Sicily (Italy). Geomorphology 2014, 204, 399–411. [Google Scholar] [CrossRef] [Green Version]
- Dewitte, O.; Daoudi, M.; Bosco, C.; Eeckhaut, M. Predicting the susceptibility to gully initiation in data-poor regions. Geomorphology 2015, 228, 101–115. [Google Scholar] [CrossRef]
- Gutiérrez, Á.; Schnabel, S.; Felicísimo, Á. Modelling the occurrence of gullies in rangelands of southwest Spain. Earth Surf. Proc. Landf. 2009, 34, 1894–1902. [Google Scholar] [CrossRef]
- Nonomura, A.; Hasegawa, S.; Matsumoto, H.; Takahashi, M.; Masumoto, M.; Fujisawa, K. Curvature derived from LiDAR digital elevation models as simple indicators of debris-flow susceptibility. J. Mt. Sci. 2015, 16, 95–107. [Google Scholar] [CrossRef]
- Yokoyama, R.; Shirasawa, M.; Pike, R. Visualizing topography by openness: A new application of image processing to Digital Elevation Models. Photogramm. Eng. Remote Sens. 2002, 68, 257–265. [Google Scholar]
- Kaihara, S.; Arakawa, M.; Tetsuga, H.; Sato, T.; Maeda, M.; Nakayama, H.; Furukawa, K. A study on the method of critical line in the each slope using data envelopment analysis. J. Jpn. Soc. Eros. Control Eng. 2015, 16, 95–107. [Google Scholar]
- Charnes, A.; Cooper, W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Cooper, W.; Seiford, L.; Zhu, J. Data envelopment analysis, History, Models, and Interpretations. In Handbook on Data Envelopment Analysis; Springer: Boston, MA, USA, 2011; pp. 1–39. [Google Scholar]
- CRAN. Available online: https://cran.r-project.org/web/packages/rDEA/rDEA.pdf (accessed on 12 June 2016).
- Ministry of Land, Infrastructure, Transport and Tourism, Government of Japan. Shikoku Regional Development Bureau. Available online: https://www.skr.mlit.go.jp/kokai/project_evaluation/h23/2nd/pdf/6.pdf (accessed on 12 October 2011).
- Yanagida, M.; Hasegawa, S. Morphological dating and dissection process of landslide topography. In Landslide, Proceedings of the 7th International Conference and Field Workshop on Landslides, 28 August–15 September 1993, Czech and Slovakia; Novosad, S., Wagner, P., Eds.; A.A. Balkema: Rotterdam, The Netherlands; Brookfield: Toronto, ON, Canada, 1993; pp. 117–122. [Google Scholar]
- NASA. Landsat Science. Available online: https://www.nasa.gov/jpl/landsat-8-reveals-extent-of-quake-disaster-in-nepal-s-langtang-valley (accessed on 12 February 2020).
- Nappo, N.; Peduto, D.; Mavrouli, O.; Westen, C.; Gullà, G. Slow-moving landslides interacting with the road network: Analysis of damage using ancillary data, in situ surveys and multi-source monitoring data. Eng. Geol. 2019, 260, 105244. [Google Scholar] [CrossRef]
- Li, L.; Yao, X.; Yao, J.; Zhou, Z.; Feng, X.; Liu, X. Analysis of deformation characteristics for a reservoir landslide before and after impoundment by multiple D-InSAR observations at Jinshajiang River, China. Nat. Hazards 2019, 98, 719–733. [Google Scholar] [CrossRef]
- Hao, J.; Wu, T.; Wu, X.; Hu, G.; Zou, D.; Zhu, X.; Zhao, L.; Li, R.; Xie, C.; Ni, J.; et al. Investigation of a small landslide in the Qinghai-Tibet Plateau by InSAR and absolute deformation model. Remote Sens. 2019, 11, 2126. [Google Scholar] [CrossRef] [Green Version]
- Van Western, C.J.; Van Asch, T.W.J.; Soeters, R. Landslide hazard and risk zonation—Why is it sill so difficult? Bull. Eng. Geol. Environ. 2006, 65, 167–184. [Google Scholar] [CrossRef]
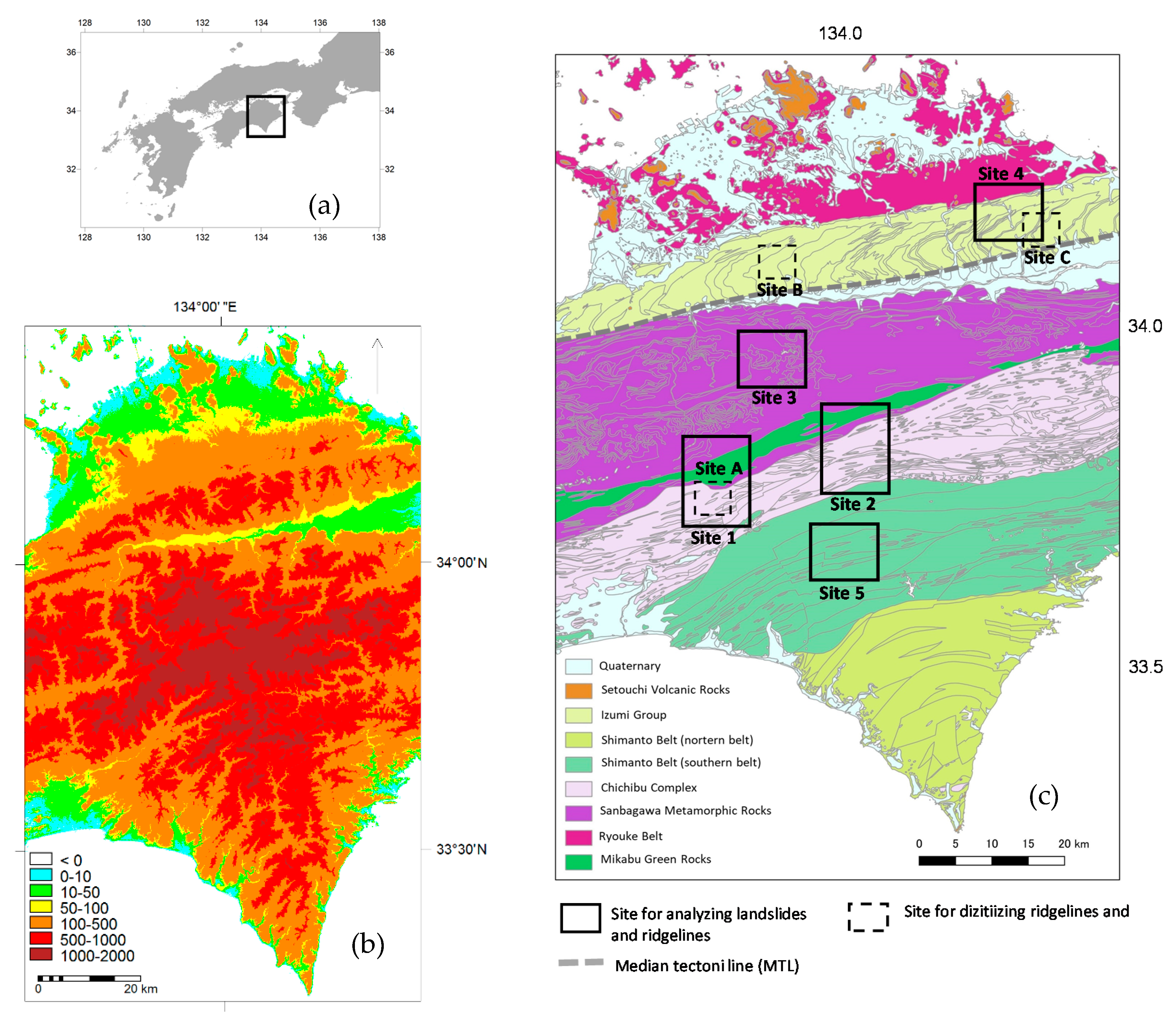

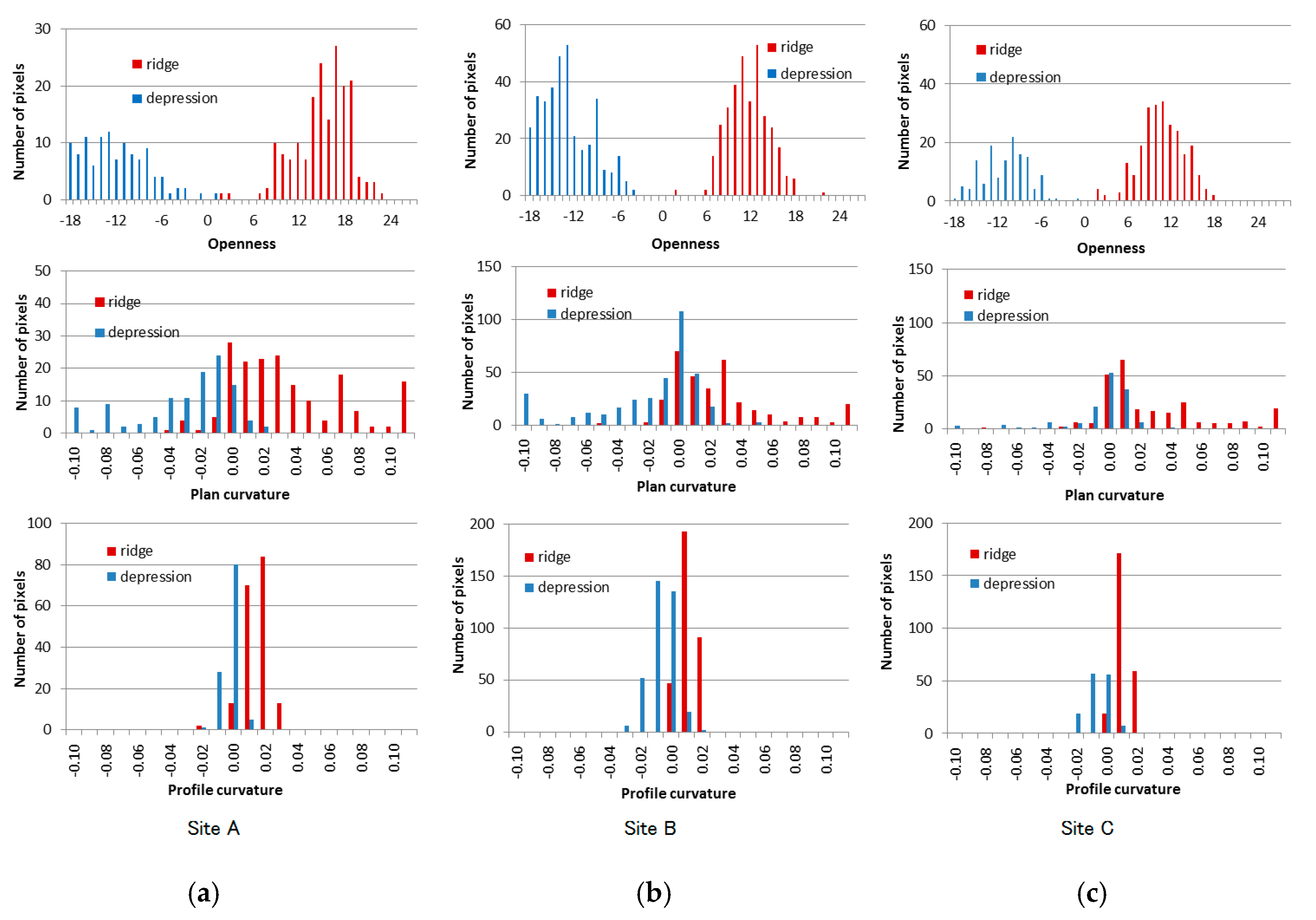
| Site A | Site B | Site C | Average | |
|---|---|---|---|---|
| Average (ave) | 14.7 | 11.2 | 10.4 | - |
| Standard deviation (σ) | 3.6 | 2.8 | 3.1 | - |
| Ave-σ | 11.1 | 8.5 | 7.3 | 9.0 |
| Ave-2σ | 7.5 | 5.7 | 4.2 | 5.8 |
| Site 1 | Site 2 | Site 3 | Site 4 | Site 5 | |
|---|---|---|---|---|---|
| Average (m2) | 209,965 | 81,739 | 52,421 | 162,660 | 5811 |
| Standard deviation (m2) | 176,874 | 132,260 | 77,824 | 131,828 | 16,406 |
| The number of grids | 160 | 160 | 100 | 100 | 100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nonomura, A.; Hasegawa, S.; Kanbara, D.; Tadono, T.; Chiba, T. Topographic Analysis of Landslide Distribution Using AW3D30 Data. Geosciences 2020, 10, 115. https://doi.org/10.3390/geosciences10040115
Nonomura A, Hasegawa S, Kanbara D, Tadono T, Chiba T. Topographic Analysis of Landslide Distribution Using AW3D30 Data. Geosciences. 2020; 10(4):115. https://doi.org/10.3390/geosciences10040115
Chicago/Turabian StyleNonomura, Atsuko, Shuichi Hasegawa, Daisuke Kanbara, Takeo Tadono, and Tatsuro Chiba. 2020. "Topographic Analysis of Landslide Distribution Using AW3D30 Data" Geosciences 10, no. 4: 115. https://doi.org/10.3390/geosciences10040115
APA StyleNonomura, A., Hasegawa, S., Kanbara, D., Tadono, T., & Chiba, T. (2020). Topographic Analysis of Landslide Distribution Using AW3D30 Data. Geosciences, 10(4), 115. https://doi.org/10.3390/geosciences10040115






