Abstract
Detrital monazite geochronology has been used in provenance studies. However, there are complexities in the interpretation of age spectra due to their wide occurrence in both igneous and metamorphic rocks. We use the multinomial logistic regression (MLR) and cross-validation (CV) techniques to establish a geochemical discrimination of monazite source rocks. The elemental abundance-based geochemical discrimination was tested by selecting 16 elements from granitic and metamorphic rocks. The MLR technique revealed that light rare earth elements (REEs), Eu, and some heavy REEs are important discriminators that reflect elemental fractionation during magmatism and/or metamorphism. The best model yielded a discrimination rate of ~97%, and the CV method validated this approach. We applied the discrimination model to detrital monazites from African rivers. The detrital monazites were mostly classified as granitic and of garnet-bearing metamorphic origins; however, their proportion of metamorphic origin was smaller than the proportion that was obtained by using the elemental-ratio-based discrimination proposed by Itano et al. in Chemical Geology (2018). Considering the occurrence of metamorphic rocks in the hinterlands and the different age spectra between monazite and zircon in the same rivers, a ratio-based discrimination would be more reliable. Nevertheless, our study demonstrates the advantages of machine-learning-based approaches for the quantitative discrimination of monazite.
1. Introduction
Detrital minerals have been widely used to investigate sedimentary provenances at a regional scale [1,2], ancient orogenic cycles [3,4], and Hadean geological events [5,6]. This approach has become more common since the development of laser ablation–inductively coupled plasma–mass spectrometry (LA–ICP–MS) techniques in the 1990s. Detrital zircon has been used extensively for detrital mineral studies because it can be U–Pb dated to a high precision and is resistant to physical and chemical weathering [4,7]. More recently, detrital monazite has been used to study orogenic events [8,9,10,11].
Monazite is a light rare earth element (REE) phosphate that can be used as a U–Th–Pb geochronometer as well as an Sm–Nd isotopic tracer for crustal growth [12,13,14]. There is an important difference in the occurrence of igneous monazite and zircon: Monazite is restricted to low-Ca silicic rocks, whereas zircon is abundant in various silicic rock types [15,16,17]. Moreover, the ubiquitous occurrence of monazite in low- to high-grade metamorphic rocks contrasts with the limited occurrence of zircon in high-grade metamorphic rocks [18,19]. Thus, detrital monazite provides information for a wide range of metamorphic conditions, which is complementary to the detrital zircon record [8,9,20]. The distinct occurrences of these two minerals lead to differences in detrital monazite and zircon age spectra [9]. However, the wide occurrence of monazite can lead to ambiguity in interpretations of its age spectra.
Geochemical data can be used to distinguish the source rock type of accessory minerals [21,22]. For example, the abundances of trace elements, including REEs, in zircon can be used as an indicator of the source rock type [21]. Itano et al. (2018) [23] also showed that igneous and metamorphic monazites have distinct trace element signatures and that source rock types can be determined by using elemental ratios such as the Eu anomaly and depletion in heavy REEs. However, geochemical discriminations of monazite origins that use elemental abundances have not been fully explored.
Recent geochemical studies [24,25] have demonstrated that machine learning methods can potentially perform geochemical discriminations and feature selections by using high-dimensional data. The machine learning technique is also quantitative in nature. In this study, we present a machine-learning-based approach for geochemical discrimination by using elemental abundances of monazite from different rock types. We applied the multinomial logistic regression (MLR) technique to geochemical data for monazite from various source rock types. The MLR method is one of several established machine learning techniques, and it is particularly useful in classification problems where the dependent variable is categorical [26]. To assess the method’s prediction accuracy, the cross-validation (CV) technique has also been used to quantitatively investigate MLR’s discrimination performance [26]. We further applied the proposed elemental-abundance-based discrimination model to detrital monazites to demonstrate the utility of geochemical discrimination in identifying the source rock types of detrital monazites. The obtained discrimination results are compared with the previously reported geochronological data [9] and the geochemical discrimination method of Itano et al. (2016, 2018) [9,23], which was based on elemental ratios.
2. Datasets and Methods
We used 336 LA–ICP–MS analyses of monazite to cover a compositional range of diverse rock types as training data: granitic rocks (N = 138) [23,27,28], leucogranites–leucosomes (N = 60) [27,28], and greenschist-facies (N = 2) [29], amphibolite-facies (N = 44) [27,29,30], granulite-facies (N = 84) [27,28,30], and eclogite-facies metamorphic rocks (N = 8) [31]. The detailed lithologies, sampling localities, and chemical compositions are described in the electronic Supplementary Information Table S1. Our method used the following 16 major and trace elements: REE (from La to Lu), Th, and U. The monazite analyses were reclassified into garnet-free metamorphic rocks (greenschist facies and garnet-free amphibolite facies), garnet-bearing metamorphic rocks (garnet-bearing amphibolite, granulite, and eclogite facies), granitic rocks, and leucogranites (leucogranites and leucosomes) to simplify the classification. Though some studies have determined elemental abundances by using an electron probe microanalyzer (EPMA), we used only LA–ICP–MS data because EPMA data are less precise and accurate due to their lower sensitivity and X-ray interferences [31]. One measurement of an individual grain or the average of multiple measurements of a single grain was adopted as a single data point. For monazite grains with chemical zoning from high-grade metamorphic rocks with prograde-retrograde overgrowths, analyses of individual domains were taken to be different data points. Most of these trace element data yielded non-Gaussian distributions and wide variations. The analyzed dataset was normalized with a Box–Cox transformation prior to data analysis [32,33] to improve interpretability and minimize undesirable effects on the machine learning algorithm [25].
Detrital monazites that were separated from river sands were used for the application of the developed geochemical discrimination in this study. We used the geochemical data of 523 U–Pb dated detrital monazite grains from five major African rivers: the Niger, Nile, Congo, Zambezi, and Orange rivers; these data were reported by Itano et al. (2016) [9]. The trace elements, including REEs, Th, and U, were obtained by using LA–ICP–MS. A single data point represented a measurement of an individual grain. The U–Pb age data of these samples defined several age peaks between ~700 and 500 Ma, corresponding to the period of Pan-African orogeny, and between 1200 and 1000 Ma [9]. Moreover, the U–Pb ages of detrital zircons from the same rivers were reported by Iizuka et al. (2013) [34].
Multinomial logistic regression (MLR) analysis was conducted on the labeled data. The logistic regression can model the probabilities for binary classification problems [25,26]. When a response variable was categorical, the relationship between the logarithm of the odds and explanatory variables was modeled as follows:
where p, x, and β are the predicted probability, explanatory variable, and regression coefficient optimized by a maximum likelihood estimation, respectively [35]. This logistic regression approach can be extended to a multiclass classification problem, and the group membership probabilities are given as a log-linear function of x for any classes k, including the baseline category:
where K is the number of classes. New unknown data are classified into group k in which the obtained probability is the largest. In this study, we established a classification model that could discriminate the source rock types of monazite (garnet-free and garnet-bearing metamorphic, granitic, and leucogranite rocks). The maximum number of variables in the present study was 16, and the total number of possible combinations of variables was 65,535 (216 − 1). The MLR analyses were conducted for all 65,535 combinations of elements, and we explored the element combinations that provided the clearest discrimination. This naive approach for variable selection is called the exhaustive search (ES) method [36,37], which has recently been applied to various geochemical problems [38,39,40].
The discrimination rate for unknown samples and the predictive capability of the model for unknown data (i.e., the generalization capability of the discrimination model) were assessed with the CV method, which allowed us to address the problem of overfitting. In the leave-one-out approach that was adopted in this study, the following process was repeated for all combinations of original samples: One data point was left out of the training data and used for the validation of the trained model. This has been demonstrated to be a simple and effective evaluation technique [25,26,38]. The discrimination rate was calculated as the accuracy rate by using the test data with known source rocks. The CV error was calculated as the average of the cross entropy error as follows by using the predicted probabilities (y) for any class (k) and the one-hot vectors of the correct label for all CV iterations to objectively estimate the discrimination capability:
where N is the number of iterations of cross validation.
The Akaike’s information criteria (AIC) statistic is a relative measure of model parsimony [41] that was also calculated for the model selection in addition to the CV error. We selected the prediction model with the best discrimination rate, CV error, and AIC in terms of predictability and interpretability.
The 336 trace element data of monazites from known source rocks were used as training data for the MLR. The discrimination rate, CV error, and AIC were calculated with cross validation by using the training data for a particular element set. This calculation was made for all the 65,535 combinations of the element set. The R source code used for the analyses is provided in the electronic Supplementary Information.
3. Results
Most combinations of trace elements had discrimination rates of 93%–94%, and the combinations with discrimination rates higher than 95% accounted for 3.7% of all combinations (Figure 1).
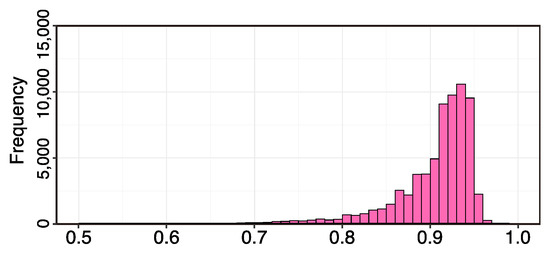
Figure 1.
Histogram of the discrimination rates that were obtained through the exhaustive search approach (65,535 combinations). The highest frequency value was between 0.93–0.94.
The results were first sorted by the discrimination rate and then by the AIC in Figure 2. The highest discrimination rates of ~97% were obtained when 8–10 elements were used, whereas the lowest discrimination rate was obtained when using one element (i.e., La) (Figure 2a,d). Using more elements generally yielded higher discrimination rates, and the discrimination rate decreased and the CV error and AIC increased when the number of used elements was less than six (Figure 2a–c). The discrimination rate that was obtained by using any combination of >10 elements did not exceed the rates of most discriminatory models that used 8–10 elements (Figure 2d,e), which is consistent with the discrimination performance in terms of the AIC (Figure 2c). The classification accuracy of the MLR is presented as a confusion matrix for one of the best-fitting models that used eight elements (La, Ce, Pr, Nd, Sm, Eu, Lu, and Th) (Figure 2g). All samples yielded high classification scores, although leucogranite samples tended to be erroneously classified as garnet-bearing metamorphic samples.
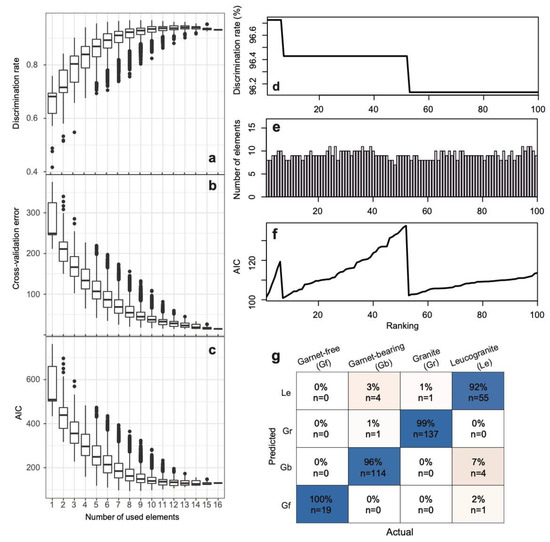
Figure 2.
Multinomial logistic regression analysis results. (a) Discrimination rate, (b) cross-validation error, and (c) Akaike’s information criteria (AIC) versus the number of elements used. (a–c) The upper and lower sides of boxes represent the third and first quartiles, respectively, with the median value shown as the horizontal line. The whiskers (vertical lines) correspond to the 1.5-fold interquartile range from the first and third quartiles. Data points apart from these whiskers are plotted as points. (d–f) The top 100 cases with discrimination rates are shown for when the results were first sorted by the discrimination rate and then by the AIC. (g) Confusion matrix for the models that used eight elements (La, Ce, Pr, Nd, Sm, Eu, Lu, and Th), showing the accuracy of the multinomial logistic regression (MLR). Rows represent instances in a predicted class, and columns represent instances in the actual class for garnet-free and garnet-bearing metamorphic, granite and leucogranite samples. The percentage values in the main diagonal cells indicate the proportion of the data that was correctly classified.
Figure 3 shows the regression coefficients for each category when the garnet-free metamorphic rock was the baseline category. The combinations of elements that yielded high discrimination rates generally included the light REEs, Eu, Th, and some heavy REEs, whereas the middle REEs and U were rarely selected in the top 100 ranks (Figure 3). Conversely, light and middle REEs tended to be excluded in the models with low discrimination rates. These features of the elemental selection were generally observed through all ranks. The regression coefficients for the middle REEs (apart from Eu) were positive, whereas those of heavy REEs were generally negative for the garnet-bearing metamorphic rocks (Figure 3a). In contrast, the regression coefficients for the granitic rocks were characterized by a significant difference between the positive Sm coefficients and the negative coefficients for its adjacent REEs (Figure 3b). The regression coefficients for the leucogranites showed both features and significant contrasts in the coefficients for the light REEs (Figure 3c).
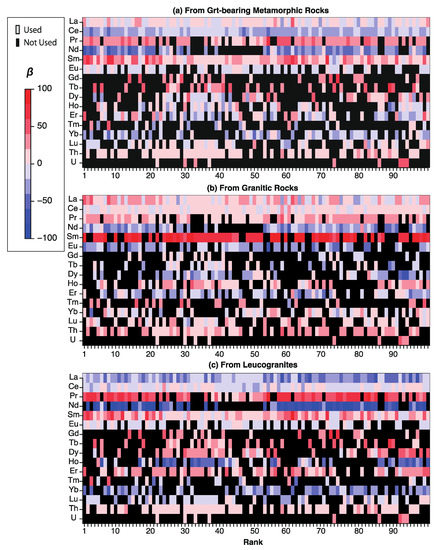
Figure 3.
Combinations of elements that were used or not used, as well as regression coefficients (β) for each element and class. The elements that were not used are shown in black, and the regression coefficients are visualized on a color map where red and blue represent positive and negative correlations, respectively.
4. Discussion
4.1. Discrimination Performance
The discrimination performance improved as an increasing number of elements was used. However, the best discrimination performance was achieved when using 8–10 elements. This can be attributed to overfitting of the training data when using >10 elements, which is a general phenomenon of the ES method. Indeed, using all the elements and data points of the training data resulted in an accuracy rate of 98%, which is higher than the discrimination rate of 93% that was calculated with the CV method that used all elements and 97% for the discriminatory models that used 8–10 elements. This indicates overfitting, which can lead to a failure in predicting the source of an unknown sample. This interpretation is consistent with the local minimum of the AIC when eight elements were used (Figure 2b,c). The results that were obtained by using the exhaustive search approach exemplified the importance of selecting an appropriate set of elements for geochemical discrimination.
Many of the discrimination rates that were obtained by using the CV approach were >90% (Figure 1). Given the preceding discussion, it is likely that the discrimination performance was correctly estimated for the dataset that was considered in this study. This geochemical discrimination can be used to assess the origin of detrital monazite, provided that the monazite shows the same variations in elemental abundances as the dataset that was used for establishing the models.
4.2. Feature Selection: Monazite Geochemistry
The combinations of elements yielding high discrimination rates were not random but instead included particular elements such as light REEs, Eu, Th, and some heavy REEs (Figure 3), thereby indicating that these elements were essential for the discrimination. The improvement of the discrimination rate when using these trace elements in monazite is consistent with the previously-held view that trace element abundances are governed by particular co-existing accessory phases [23,30]. Surprisingly, major elements in monazite were part of the element combinations with the highest discrimination rate. The variations in monazite major element contents might have been controlled by differences in light REE contents in the source rocks.
The differences in regression coefficients could be related to the key formation processes of the source rocks. The regression coefficients for middle REEs showed different behaviors than those of heavy REEs in the garnet-bearing metamorphic rocks (Figure 3a). This can be explained by the strong partitioning of heavy REEs in garnet [42,43]. In fact, monazite co-existing with garnet has been shown to exhibit a significant depletion of heavy REEs relative to middle REEs [12,27,29,30,44].
The contrasting coefficients for Sm and Eu in the granites (Figure 3b) reflect the fractionation of these elements due to monazite crystallization in the granitic magmas. This is consistent with the prominent negative Eu anomalies that are commonly observed in monazite from granitic rocks. Unlike other REEs, Eu can be divalent, resulting in its preferential incorporation into feldspar [43,45,46]. Thus, the fractional crystallization of feldspar during granitic magma differentiation causes Eu fractionation in residual melts and subsequent crystallizing phases. This fractionation results in larger negative Eu anomalies in monazites from granitic rocks as compared to those from metamorphic rocks [9,46,47].
For the leucogranites, contrasting regression coefficients were observed between middle and heavy REEs and between Sm and Eu (Figure 3c); these characteristics were also observed within the garnet-bearing metamorphic rocks and granitic rocks, respectively. This implies that monazite compositions in leucogranites are controlled by both feldspars and heavy REE-rich minerals such as garnet and zircon. In general, leucogranites are characterized by highly fractionated compositions (SiO2 = 70.5–75.5 wt%; higher Al2O3 and lower FeOT and MgO contents than normal granite) and are considered to be generated by the partial melting of sedimentary rocks [48,49]. The extensive differentiation of such peraluminous magmas is likely accompanied by significant fractional crystallization of both feldspars and heavy-REE-rich minerals.
4.3. Application to Detrital Monazite from Major African Rivers
In this section, we now apply the above developed model by using eight elements (i.e., La, Ce, Pr, Nd, Sm, Eu, Lu, and Th abundances) to the previously mentioned source rock discrimination of detrital monazites from five major African rivers. For comparison, we also apply the geochemical discrimination model of Itano et al. (2018), which was based on elemental ratios, to the same dataset. By combining the discrimination results with the geochronological data for the detrital monazite and zircon, we also discuss the validity and limitations of the newly developed geochemical discrimination.
Itano et al., (2018) [23] showed that the Eu anomaly and depletion of heavy REEs relative to middle REEs in monazite vary among different source rock types. Figure 4 shows plots of Nd versus Eu abundances and [Gd/Lu]N and [Eu/Eu*]N of the monazite with known source rock types (the N subscript denotes CI chondrite-normalized values [50] and [Eu/Eu*]N = [Eu]N/([Sm]N[Gd]N)0.5). The plots reveal the following features: (i) Monazites from granitic rocks showed significant negative Eu anomalies; (ii) monazites from garnet-free metamorphic rocks were characterized by slight negative Eu anomalies and heavy REE depletion; (iii) monazites from garnet-bearing metamorphic rocks were characterized by significant heavy REE depletion; and (iv) monazites from leucogranites showed both negative Eu anomalies and heavy REE depletion. Based on this finding, Itano et al. (2018) [23] proposed a discrimination model of monazite source rock types that used [Gd/Lu]N and [Eu/Eu*]N, as described in Table 1.
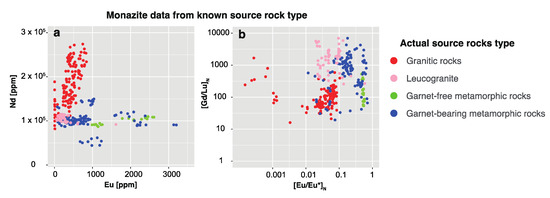
Figure 4.
Variations in chemical compositions of monazites from various rock types plotted with the actual rock type. (a) Plot of Nd versus Eu and (b) plot of [Gd/Lu]N versus [Eu/Eu*]N. Plot of [Gd/Lu]N versus [Eu/Eu*]N shows a clearer clustering than that of Nd versus Eu.

Table 1.
Geochemical criteria for monazite source rock type based on the Eu anomaly and relative depletion of heavy-to-middle rare earth elements.
The predicted source rock types for the African detrital monazites when using the elemental-abundance-based and elemental-ratio-based discriminations are shown as a function of U–Pb age in Figure 5. When the abundance-based discrimination was applied, most of the detrital monazites were classified as having granitic or garner-bearing metamorphic source rocks. The proportion of monazite grains that were classified as having granitic source rocks was approximately 63%. The grains of granitic origins showed a prominent U–Pb age peak at 600–580 Ma, whereas those of metamorphic origin showed peaks at 620–600 and ~500 Ma (Figure 5a). The ratio-based discrimination also indicated the importance of both granitic and metamorphic source rocks and gave the age peaks at 620–600 and ~500 Ma (Figure 5b). This consistency suggests that the monazite age spectrum was successfully deconvoluted into igneous and metamorphic activities by using the elemental-abundance-based discrimination as well as the elemental-ratio-based discrimination.
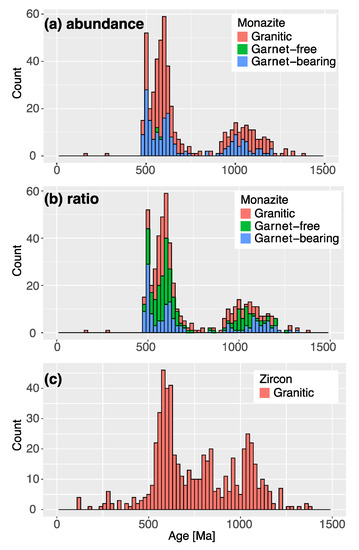
Figure 5.
(a,b) U–Pb age histograms of detrital monazite and (c) zircon from five African rivers (data from Itano et al. 2016). The cumulative relative frequencies were calculated for each river. The source rock type was classified into granitic (red), garnet-free (green), and garnet-bearing metamorphic rocks (blue), with (a) the elemental-ratio-based and (b) elemental-abundance-based discriminations.
Compared to the abundance-based discrimination, however, the ratio-based discrimination classified many grains as having both garnet-free metamorphic origins and garnet-bearing origins. The discrepancy between the results of the two discrimination models is highlighted by plots of the classified source rocks for the detrital monazites as a function of Nd versus Eu abundances (Figure 6a,c) and [Gd/Lu]N versus [Eu/Eu*]N (Figure 6b,d). The detrital monazite grains with restricted Eu anomalies and heavy REE depletions were, by definition, classified as having garnet-free metamorphic rocks in the ratio-based discrimination (Figure 6d); conversely, their source rocks were mainly categorized as garnet-bearing metamorphic rocks in the abundance-based discrimination (Figure 6b). Considering that the drainage basins of these African rivers contained garnet-free metamorphic rocks [9], the paucity of monazite from garnet-free source rock in the abundance-based discrimination model may question the validity of the discrimination between garnet-free and garnet-bearing source rocks. Alternatively, this result might be interpreted as resulting from significantly low modal abundances of monazite grains in the garnet-free metamorphic rocks relative to granitic and garnet-bearing metamorphic rocks in the drainage basins.
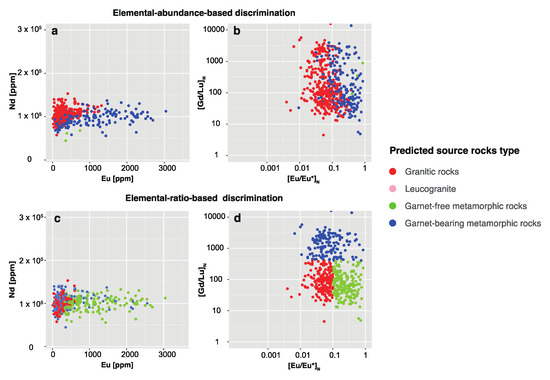
Figure 6.
Comparison of source rock types predicted by (a,b) elemental-abundance-based discrimination and (c,d) elemental-ratio-based discrimination. (a,c) Plot of Nd versus Eu and (b,d) plot of [Gd/Lu]N versus [Eu/Eu*]N.
A comparison between the age spectra for detrital monazite and zircon independently provides insight into the origins of the detrital monazites (Figure 5). The detrital zircons from the same African rivers were analyzed for U–Pb age [34]. Since the analyzed zircon grains had oscillatory or sector zoning in cathodoluminescence images, the zircon age spectrum (Figure 5c) should reflect igneous rather than metamorphic events. A large age peak at 500–480 Ma is defined by the detrital monazite (Figure 5a,b), whereas the detrital zircon does not show a clear peak at this age (Figure 5c). The difference indicates that the monazite age peak at 500–480 Ma reflects metamorphic events. This view is highly compatible with the results of the ratio-based discrimination, which indicated that the 500–480 Ma monazite population was dominated by grains of metamorphic origin (Figure 5b). By contrast, this view is difficult to reconcile with those of the abundance-based discrimination, which indicated nearly equal proportions of the grains of granitic and metamorphic origin (Figure 5a). Accordingly, we consider that the results from the ratio-based approach were more reliable than those that were obtained by the abundance-based approach.
The differences in the two discrimination approaches may have been due to the difference in what the elemental abundances and elemental ratios reflected. The REE abundances in monazite are controlled not only by partitioning between co-existing phases but also by the compositions of the metamorphic protoliths and primary magmas. In general, REEs have similar geochemical properties and only exhibit large fractionations when particular REE-rich phases are involved. As such, REE ratios can vary only slightly, even if there are large variations in the REE abundances for a particular rock type. Therefore, the elemental ratio could be a more direct indicator of a particular elemental fractionation process that characterizes host lithology. Though discrimination that uses the multidimensional data of elemental abundances can exploit both absolute and relative elemental abundances, this approach might be more susceptible to a lack of data coverage of monazite trace-elements.
A further complete dataset for monazites from individual rock types could further improve the elemental-abundance-based model. The monazite geochemical dataset for each rock type depends on relatively few reference samples and grains from specific rock samples. The currently available data may be biased or may not encompass the actual compositional range for a particular rock type. For example, monazite trace element data have been less commonly reported than major element data, because most monazite studies have used electron microprobe techniques for geochemical characterization and chemical Th–U-total Pb isochron method (CHIME) dating [51,52,53,54,55,56,57]. Furthermore, the application of other classification techniques, such as random forest, support vector machine, and sparse multinomial regression, would also be an interesting avenue for future research [25].
5. Conclusions
We applied the multinomial logistic regression and cross-validation techniques to a geochemical discrimination of monazite by using 16 elements. Monazite from granitic, garnet-free, and garnet-bearing metamorphic rocks can be most clearly discriminated with 8–10 elements, including the light REEs, Eu, Lu, and Th, with a discrimination accuracy of ~97%. The contrasting regression coefficients between Eu and other REEs, as well as between middle and heavy REEs, highlight the geochemical importance of feldspar and garnet fractionation during monazite formation. Though the developed geochemical discrimination successfully classified the igneous and metamorphic source rocks of detrital monazites, the proportions of garnet-free and garnet-bearing metamorphic source rocks that were classified by the elemental-abundance-based discrimination were smaller than those classified by the elemental-ratio-based discrimination. The occurrence of a wide range of metamorphic rocks in the hinterlands, combined with the different age spectra between monazite and zircon in the same rivers, suggests that the ratio-based discrimination method is more reliable. A further complete trace element dataset of monazite can bring a more robust elemental-abundance-based discrimination. Our study has shown that the machine-learning-based approach can provide robust insights into the origins of detrital monazites.
Supplementary Materials
The following are available online at https://www.mdpi.com/2076-3263/10/2/63/s1, Table S1: Compiled dataset of monazite geochemical compositions from various types of source rock, Source code: The R source code used for multinomial regression analysis.
Author Contributions
Conceptualization, K.I.; Methodology, K.I., K.U., and T.K.; Software, K.I.; Writing Original Draft Preparation, K.I.; Writing Review and Editing, K.I., K.U., T.I., and T.K. All authors have read and agreed to the published version of the manuscript.
Funding
K.I. was supported by a Grant-in-Aid for JSPS Research Fellows (Grant No. JP19J00913). K.U. was supported by a JSPS KAKENHI Grant (No. JP19K04026). T.I. was supported by a JSPS KAKENHI Grant (No. JP18H01301). T.K. was supported by JST PRESTO (No. JPMJPR1676) and JSPS KAKENHI (No. JP19K04027) Grants.
Acknowledgments
This paper was significantly improved by three anonymous reviewers. We are grateful to Stallard Scientific Editing and Editage (www.editage.com) for their help in English language improvements of the manuscript. We thank the Joint Usage/Research Center programs of the Earthquake Research Institute, University of Tokyo, Japan, 2018-B-01 (Data-driven Geoscience: Application to Dynamics in Mobile Belts) for discussions during this study. I would also like to express my gratitude to J.M. Guotana for his help.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Morton, A.C. Geochemical studies of detrital heavy minerals and their application to provenance research. Geol. Soc. Lond. Spéc. Publ. 1991, 57, 31–45. [Google Scholar] [CrossRef]
- Fedo, C.M.; Sircombe, K.N.; Rainbird, R.H. Detrital zircon analysis of the sedimentary record. Rev. Miner. Geochem. 2003, 53, 277–303. [Google Scholar] [CrossRef]
- Bodet, F.; Schärer, U. Evolution of the SE-Asian continent from U-Pb and Hf isotopes in single grains of zircon and baddeleyite from large rivers. Geochim. et Cosmochim. Acta 2000, 64, 2067–2091. [Google Scholar] [CrossRef]
- Campbell, I.H.; Reiners, P.W.; Allen, C.M.; Nicolescu, S.; Upadhyay, R. He–Pb double dating of detrital zircons from the Ganges and Indus Rivers: Implication for quantifying sediment recycling and provenance studies. Earth Planet. Sci. Lett. 2005, 237, 402–432. [Google Scholar] [CrossRef]
- Cavosie, A.J.; Valley, J.W.; Wilde, S.A. Chapter 2.5 The Oldest Terrestrial Mineral Record: A Review of 4400 to 4000 Ma Detrital Zircons from Jack Hills, Western Australia. Precambrian Ophiolites Relat. Rocks 2007, 15, 91–111. [Google Scholar]
- Wilde, S.A.; Valley, J.W.; Peck, W.H.; Graham, C.M. Evidence from detrital zircons for the existence of continental crust and oceans on the Earth 4.4 Gyr ago. Nature 2001, 409, 175–178. [Google Scholar] [CrossRef]
- Goldstein, S.; O’Nions, R.; Hamilton, P. A Sm-Nd isotopic study of atmospheric dusts and particulates from major river systems. Earth Planet. Sci. Lett. 1984, 70, 221–236. [Google Scholar] [CrossRef]
- Hietpas, J.; Samson, S.; Moecher, D.; Schmitt, A.K. Recovering tectonic events from the sedimentary record: Detrital monazite plays in high fidelity. Geology 2010, 38, 167–170. [Google Scholar] [CrossRef]
- Itano, K.; Iizuka, T.; Chang, Q.; Kimura, J.-I.; Maruyama, S. U–Pb chronology and geochemistry of detrital monazites from major African rivers: Constraints on the timing and nature of the Pan-African Orogeny. Precambrian Res. 2016, 282, 139–156. [Google Scholar] [CrossRef]
- Liu, X.C.; Wu, Y.B.; Fisher, C.M.; Hanchar, J.M.; Beranek, L.; Gao, S.; Wang, H. Tracing crustal evolution by U-Th-Pb, Sm-Nd, and Lu-Hf isotopes in detrital monazite and zircon from modern rivers. Geology 2017, 45, 103–106. [Google Scholar] [CrossRef]
- Gaschnig, R.M. Benefits of a Multiproxy Approach to Detrital Mineral Provenance Analysis: An Example from the Merrimack River, New England, USA. Geochem. Geophys. Geosyst. 2019, 20, 1557–1573. [Google Scholar] [CrossRef]
- Iizuka, T.; McCulloch, M.T.; Komiya, T.; Shibuya, T.; Ohta, K.; Ozawa, H.; Sugimura, E.; Collerson, K.D. Monazite geochronology and geochemistry of meta-sediments in the Narryer Gneiss Complex, Western Australia: constraints on the tectonothermal history and provenance. Contrib. Miner. Pet. 2010, 160, 803–823. [Google Scholar] [CrossRef]
- Iizuka, T.; Nebel, O.; MuCulloch, M.T. Tracing the provenance and recrystallization processes of the Earth’s oldest detritus at Mt. Narryer and Jack Hills, Western Australia: An in situ Sm-Nd isotopic study of monazite. Earth Planet Sci. Lett. 2011, 308, 350–358. [Google Scholar] [CrossRef]
- Goudie, D.J.; Fisher, C.M.; Hanchar, J.M.; Crowley, J.L.; Ayers, J.C. Simultaneous in situ determination of U-Pb and Sm-Nd isotopes in monazite by laser ablation ICP-MS. Geochem. Geophys. Geosyst. 2014, 15, 2575–2600. [Google Scholar] [CrossRef]
- Lee, D.E.; Bastron, H. Fractionation of rare-earth elements in allanite and monazite as related to geology of the Mt. Wheeler mine area, Nevada. Geochim. Cosmochim. Acta 1967, 31, 339–356. [Google Scholar] [CrossRef]
- Watt, G.R.; Harley, S.L. Accessory phase controls on the geochemistry of crustal melts and restites produced during water-undersaturated partial melting. Contrib. Miner. Pet. 1993, 114, 550–566. [Google Scholar] [CrossRef]
- Kelts, A.B.; Ren, M.; Anthony, E.Y. Monazite occurrence, chemistry, and chronology in the granitoid rocks of the Lachlan Fold Belt, Australia: An electron microprobe study. Am. Miner. 2008, 93, 373–383. [Google Scholar] [CrossRef]
- Overstreet, W.C. The Geologic Occurrence of Monazite; US Geological Survey: Reston, VI, USA, 1967. [Google Scholar]
- Williams, M.L.; Jercinovic, M.J.; Hetherington, C.J. Microprobe Monazite Geochronology: Understanding Geologic Processes by Integrating Composition and Chronology. Annu. Rev. Earth Planet. Sci. 2007, 35, 137–175. [Google Scholar] [CrossRef]
- Hietpas, J.; Samson, S.; Moecher, D. A direct comparison of the ages of detrital monazite versus detrital zircon in Appalachian foreland basin sandstones: Searching for the record of Phanerozoic orogenic events. Earth Planet. Sci. Lett. 2011, 310, 488–497. [Google Scholar] [CrossRef]
- Belousova, E.; Griffin, W.; O’Reilly, S.Y.; Fisher, N. Igneous zircon: trace element composition as an indicator of source rock type. Contrib. Miner. Pet. 2002, 143, 602–622. [Google Scholar] [CrossRef]
- Suggate, S.M.; Hall, R. Using detrital garnet compositions to determine provenance: A new compositional database and procedure. Geol. Soc. Lond. Spec. Publ. 2014, 386, 373–393. [Google Scholar] [CrossRef]
- Itano, K.; Iizuka, T.; Hoshino, M. REE-Th-U and Nd isotope systematics of monazites in magnetite- and ilmenite-series granitic rocks of the Japan arc: Implications for its use as a tracer of magma evolution and detrital provenance. Chem. Geol. 2018, 484, 69–80. [Google Scholar] [CrossRef]
- Petrelli, M.; Perugini, D. Solving petrological problems through machine learning: the study case of tectonic discrimination using geochemical and isotopic data. Contrib. Miner. Pet. 2016, 171, 81. [Google Scholar] [CrossRef]
- Ueki, K.; Hino, H.; Kuwatani, T. Geochemical Discrimination and Characteristics of Magmatic Tectonic Settings: A Machine-Learning-Based Approach. Geochem. Geophys. Geosyst. 2018, 19, 1327–1347. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Buick, I.; Clark, C.; Rubatto, D.; Hermann, J.; Pandit, M.; Hand, M. Constraints on the Proterozoic evolution of the Aravalli–Delhi Orogenic belt (NW India) from monazite geochronology and mineral trace element geochemistry. Lithos 2010, 120, 511–528. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, H.; Gao, S.; Hu, Z.; Liu, X.; Gong, H. LA–ICP–MS monazite U–Pb age and trace element constraints on the granulite-facies metamorphism in the Tongbai orogen, central China. J. Asian Earth Sci. 2014, 82, 90–102. [Google Scholar] [CrossRef]
- Mottram, C.M.; Warren, C.J.; Regis, D.; Roberts, N.M.; Harris, N.B.; Argles, T.W.; Parrish, R.R. Developing an inverted Barrovian sequence; insights from monazite petrochronology. Earth Planet. Sci. Lett. 2014, 403, 418–431. [Google Scholar] [CrossRef]
- Rubatto, D.; Hermann, J.; Buick, I.S. Temperature and Bulk Composition Control on the Growth of Monazite and Zircon During Low-pressure Anatexis (Mount Stafford, Central Australia). J. Pet. 2006, 47, 1973–1996. [Google Scholar] [CrossRef]
- Holder, R.M.; Hacker, B.R.; Kylander-Clark, A.R.; Cottle, J.M. Monazite trace-element and isotopic signatures of (ultra)high-pressure metamorphism: Examples from the Western Gneiss Region, Norway. Chem. Geol. 2015, 409, 99–111. [Google Scholar] [CrossRef]
- Box, G.E.P.; Cox, D.R. An Analysis of Transformations. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Guerrero, V.M.; Johnson, R.A. Use of the Box–Cox transformation with binary response models. Biometrika 1982, 69, 309–314. [Google Scholar] [CrossRef]
- Iizuka, T.; Campbell, I.H.; Allen, C.M.; Gill, J.B.; Maruyama, S.; Makoka, F. Evolution of the African continental crust as recorded by U–Pb, Lu–Hf and O isotopes in detrital zircons from modern rivers. Geochim. et Cosmochim. Acta 2013, 107, 96–120. [Google Scholar] [CrossRef]
- Agresti, A.; Kateri, M. Categorical Data Analysis. In International Encyclopedia of Statistical Science; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2011; pp. 206–208. [Google Scholar]
- Nagata, K.; Kitazono, J.; Nakajima, S.; Eifuku, S.; Tamura, R.; Okada, M. An Exhaustive Search and Stability of Sparse Estimation for Feature Selection Problem. IPSJ Online Trans. 2015, 8, 25–32. [Google Scholar] [CrossRef]
- Igarashi, Y.; Nagata, K.; Kuwatani, T.; Omori, T.; Nakanishi-Ohno, Y.; Okada, M. Three levels of data-driven science. J. Physics: Conf. Ser. 2016, 699, 12001. [Google Scholar] [CrossRef]
- Kuwatani, T.; Nagata, K.; Okada, M.; Watanabe, T.; Ogawa, Y.; Komai, T.; Tsuchiya, N. Machine-learning techniques for geochemical discrimination of 2011 Tohoku tsunami deposits. Sci. Rep. 2014, 4, 7077. [Google Scholar] [CrossRef] [PubMed]
- Nakamura, K.; Yasutaka, T.; Kuwatani, T.; Komai, T. Development of a predictive model for lead, cadmium and fluorine soil–water partition coefficients using sparse multiple linear regression analysis. Chemosphere 2017, 186, 501–509. [Google Scholar] [CrossRef]
- Ueki, K.; Kuwatani, T.; Okamoto, A.; Akaho, S.; Iwamori, H. Thermodynamic modeling of hydrous-melt–olivine equilibrium using exhaustive variable selection. Phys. Earth Planet. Inter. 2020, 106430. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schnetzler, C.; A Philpotts, J. Partition coefficients of rare-earth elements between igneous matrix material and rock-forming mineral phenocrysts—II. Geochim. Cosmochim. Acta 1970, 34, 331–340. [Google Scholar] [CrossRef]
- Fujimaki, H.; Tatsumoto, M.; Aoki, K.-I. Partition coefficients of Hf, Zr, and ree between phenocrysts and groundmasses. J. Geophys. Res. Space Phys. 1984, 89, B662. [Google Scholar] [CrossRef]
- Štípská, P.; Hacker, B.R.; Racek, M.; Holder, R.; Kylander-Clark, A.R.C.; Schulmann, K.; Hasalová, P. Monazite dating of prograde and retrograde P-T-d paths in the Barrovian terrane of the Thaya window, Bohemian Massif. J. Petrol. 2015, 56, 1007–1035. [Google Scholar] [CrossRef]
- Bea, F.; Pereira, M.; Stroh, A. Mineral/leucosome trace-element partitioning in a peraluminous migmatite (a laser ablation-ICP-MS study). Chem. Geol. 1994, 117, 291–312. [Google Scholar] [CrossRef]
- Bea, F.; Mitchell, J.N.; Scoates, J.S.; Frost, C.D.; Kolker, A. Residence of REE, Y, Th and U in Granites and Crustal Protoliths; Implications for the Chemistry of Crustal Melts. J. Pet. 1996, 37, 521–552. [Google Scholar] [CrossRef]
- Xie, L.; Wang, R.C.; Wang, D.Z.; Qiu, J.S. A survey of accessory mineral assemblages in peralkaline and more aluminous A-type granites of the southeast coastal area of China. Miner. Mag. 2006, 70, 709–729. [Google Scholar] [CrossRef]
- Guo, S.; Li, S. Petrochemical characteristics of leucogranite and a case study of Bengbu leucogranites. Sci. Bull. 2009, 54, 1923–1930. [Google Scholar] [CrossRef]
- Hopkinson, T.N.; Harris, N.B.; Warren, C.J.; Spencer, C.J.; Roberts, N.M.; Horstwood, M.S.; Parrish, R.R. Eimf The identification and significance of pure sediment-derived granites. Earth Planet. Sci. Lett. 2017, 467, 57–63. [Google Scholar] [CrossRef]
- McDonough, W.; Sun, S.-S. The composition of the Earth. Chem. Geol. 1995, 120, 223–253. [Google Scholar] [CrossRef]
- Cocherie, A.; Legendre, O.; Peucat, J.; Kouamelan, A. Geochronology of polygenetic monazites constrained by in situ electron microprobe Th-U-total lead determination: implications for lead behaviour in monazite. Geochim. Cosmochim. Acta 1998, 62, 2475–2497. [Google Scholar] [CrossRef]
- Jercinovic, M.J.; Williams, M.L. Analytical perils (and progress) in electron microprobe trace element analysis applied to geochronology: Background acquisition, interferences, and beam irradiation effects. Am. Miner. 2005, 90, 526–546. [Google Scholar] [CrossRef]
- Montel, J.-M.; Foret, S.; Veschambre, M.; Nicollet, C.; Provost, A. Electron microprobe dating of monazite. Chem. Geol. 1996, 131, 37–53. [Google Scholar] [CrossRef]
- Pyle, J.M.; Spear, F.S.; Wark, D.A.; Daniel, C.G.; Storm, L.C. Contributions to precision and accuracy of monazite microprobe ages. Am. Miner. 2005, 90, 547–577. [Google Scholar] [CrossRef]
- Suzuki, K.; Adachi, M. Denudation history of the high T/P Ryoke metamorphic belt, southwest Japan: constraints from CHIME monazite ages of gneisses and granitoids. J. Metamorph. Geol. 1998, 16, 23–37. [Google Scholar] [CrossRef]
- Suzuki, K.; Adachi, M. Precambrian provenance and Silurian metamorphism of the Tsubonosawa paragneiss in the South Kitakami terrane, Northeast Japan, revealed by the Th-U-total Pb chemical isochron ages of monazite, zircon and xenotime. Geochem. J. 1991, 25, 357–376. [Google Scholar] [CrossRef]
- Suzuki, K.; Kato, T. CHIME dating of monazite, xenotime, zircon and polycrase: Protocol, pitfalls and chemical criterion of possibly discordant age data. Gondwana Res. 2008, 14, 569–586. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).