Innovative Seismic Microzonation Maps of Urban Areas for the Management of Building Heritage: A Catania Case Study
Abstract
1. Introduction
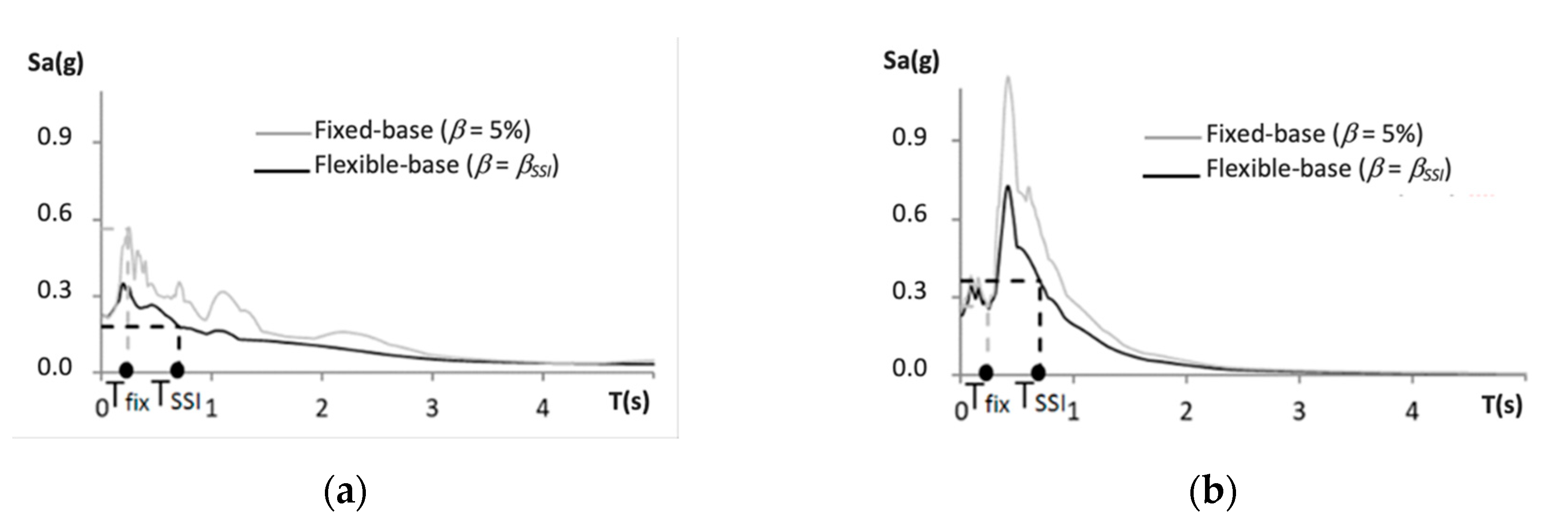
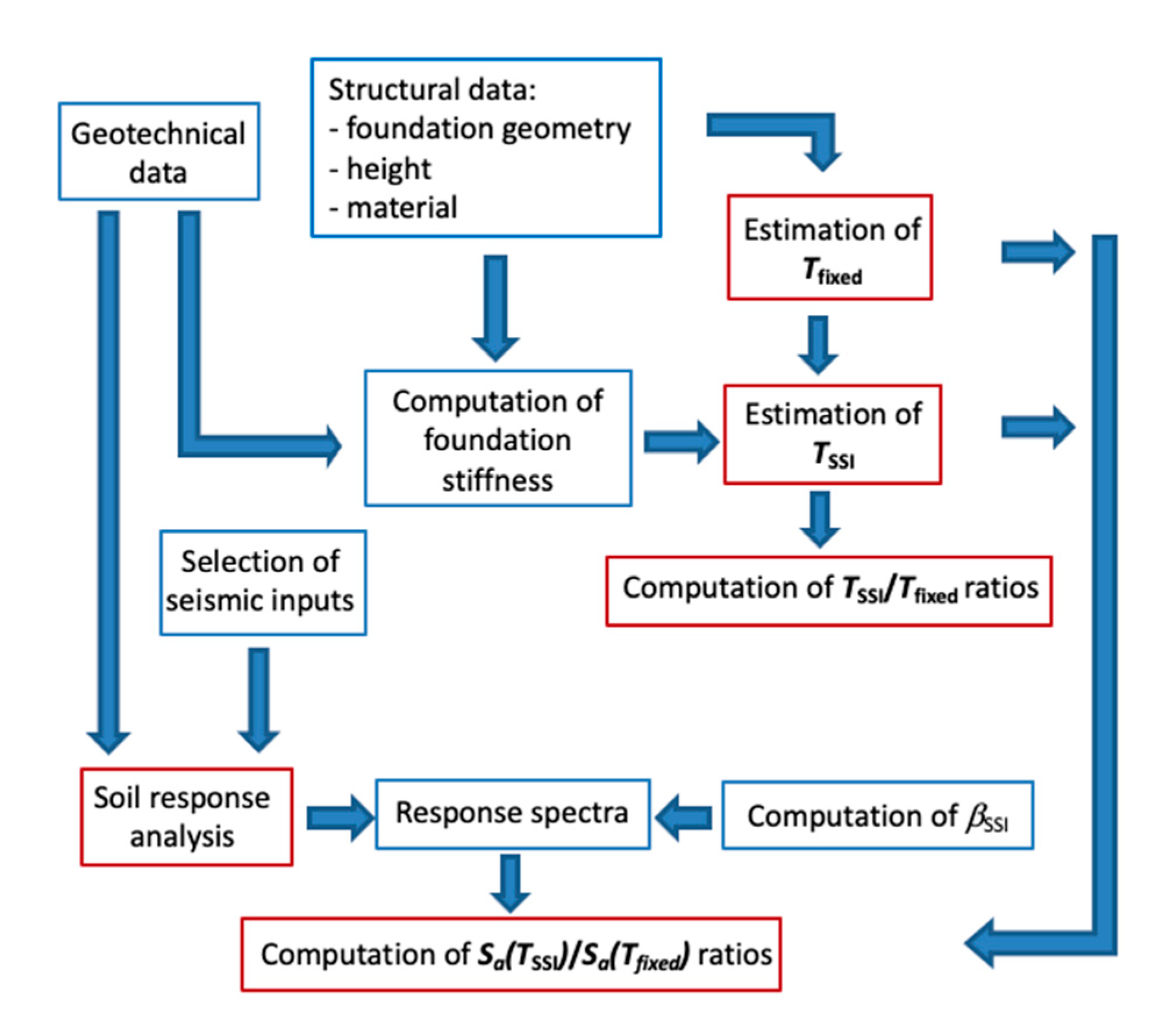
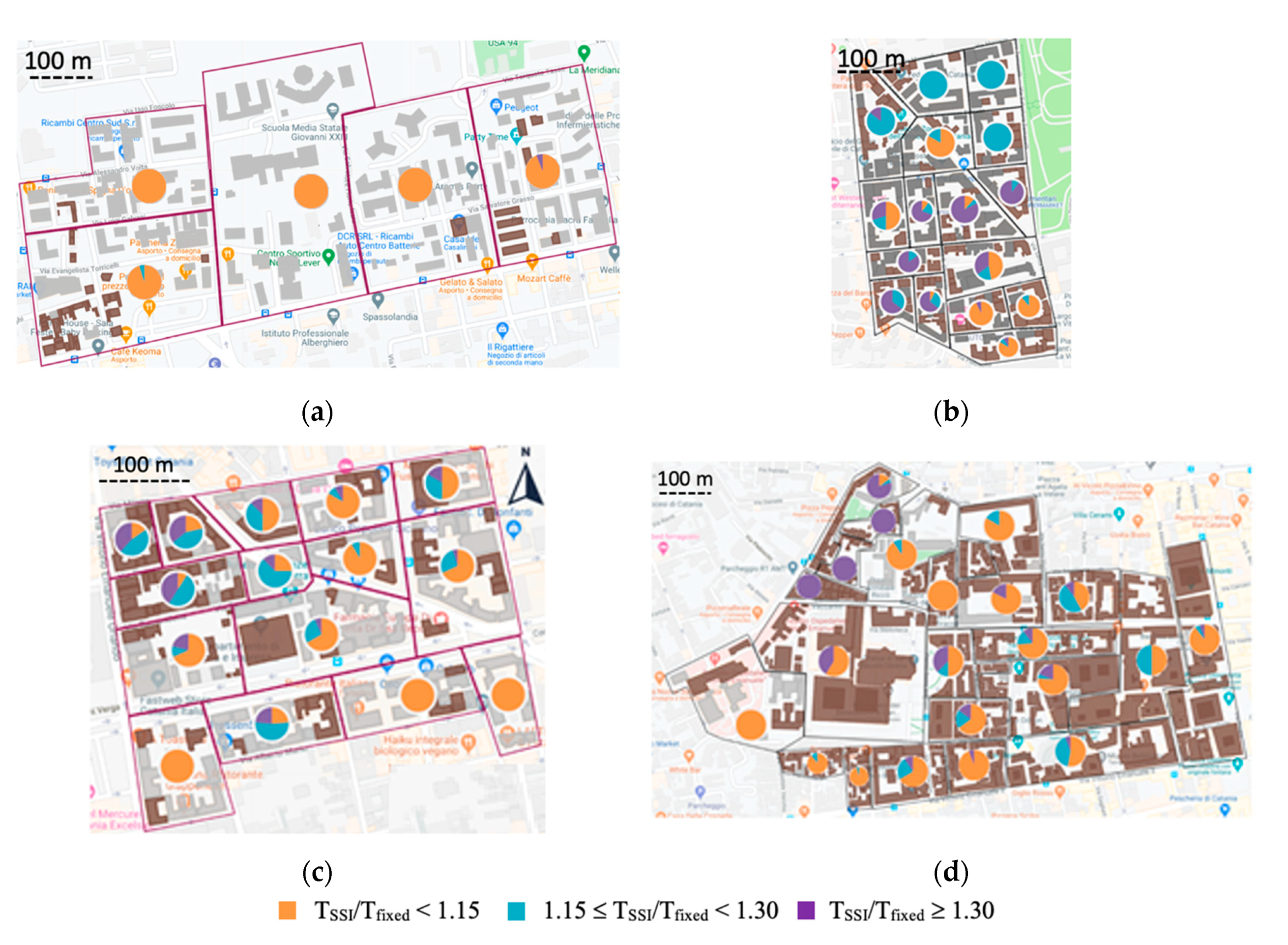
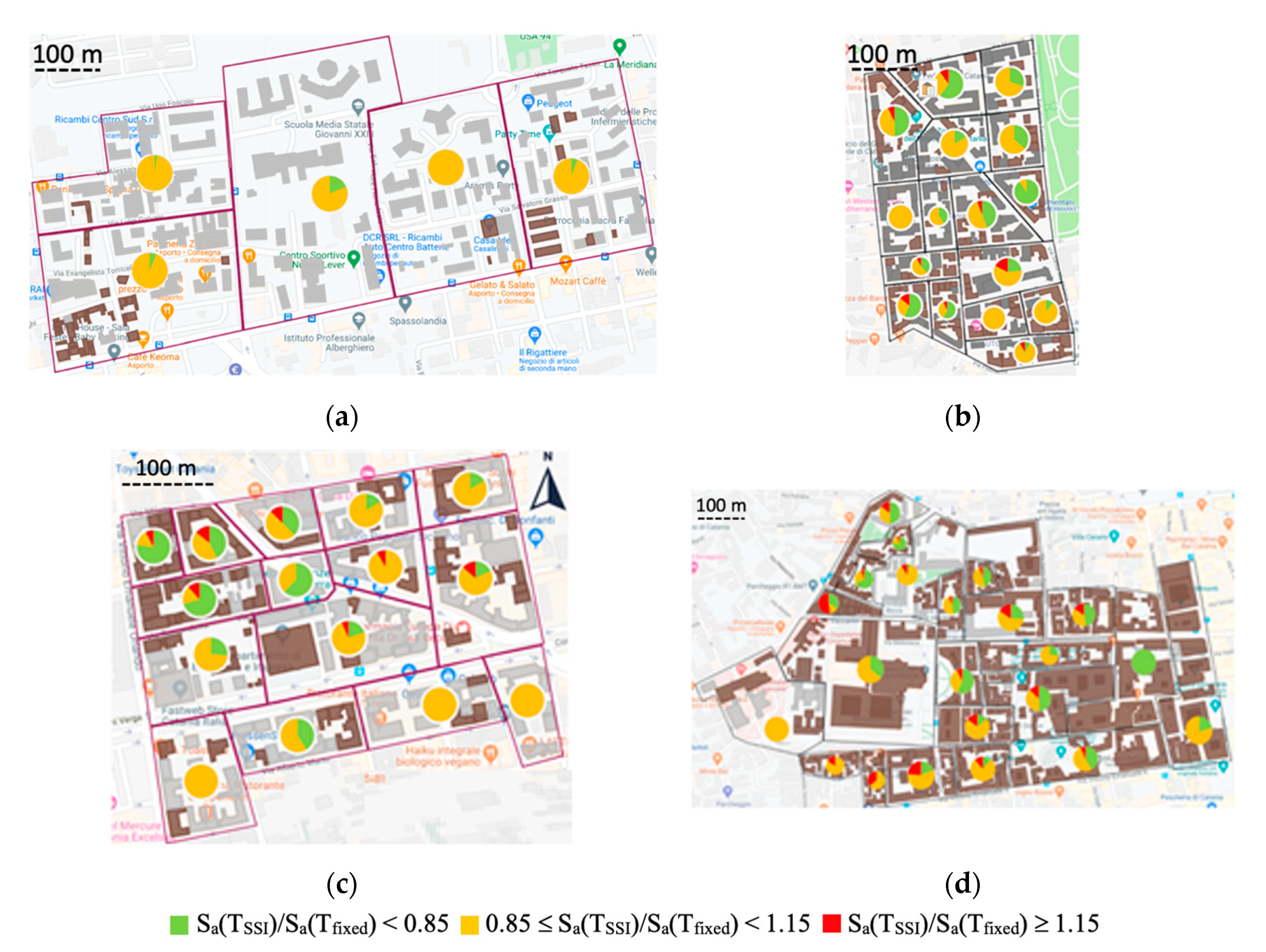
2. Evaluation of SSI Effects for the Estimation of the Design Accelerations
3. The Catania Case History
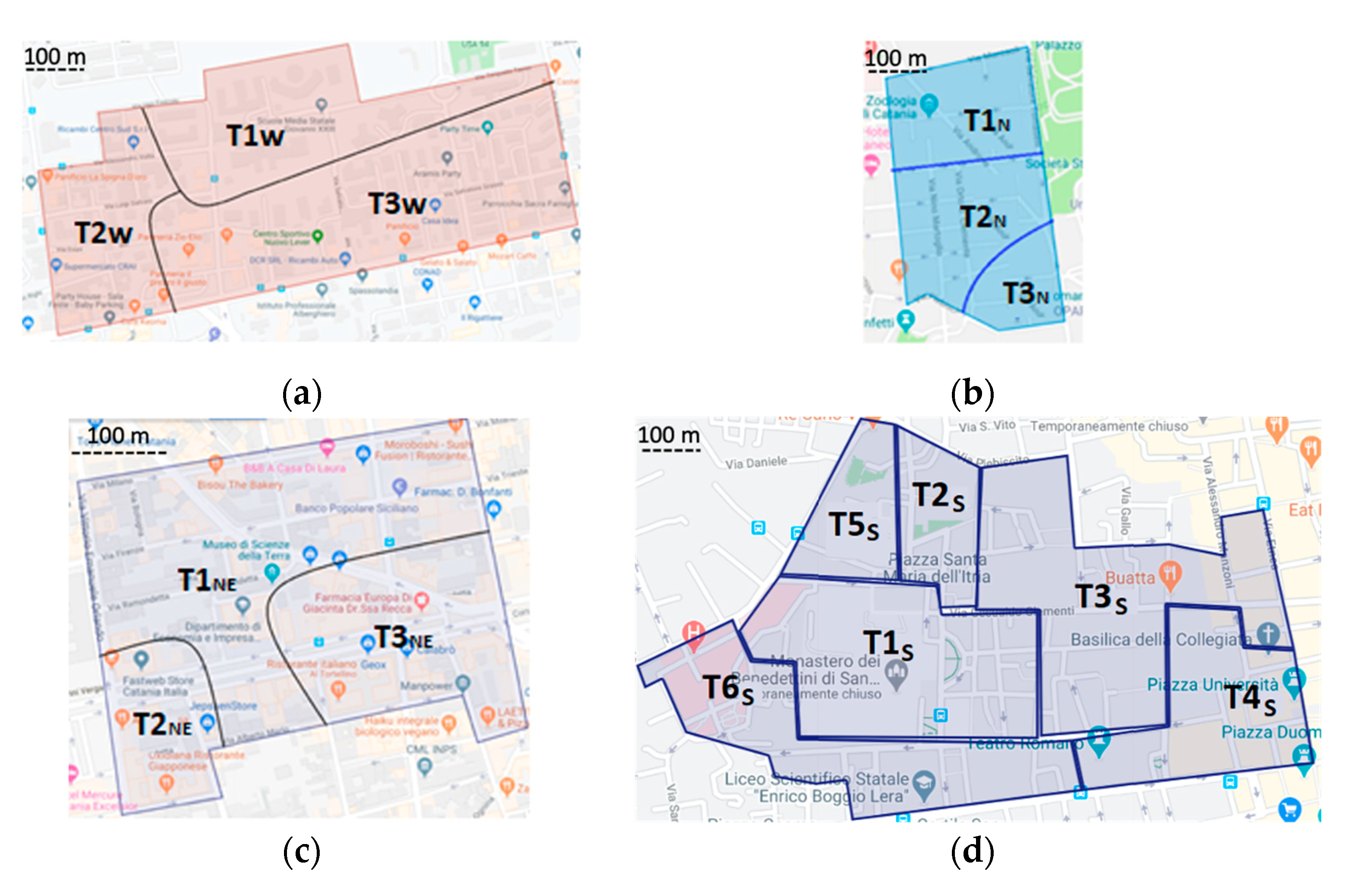
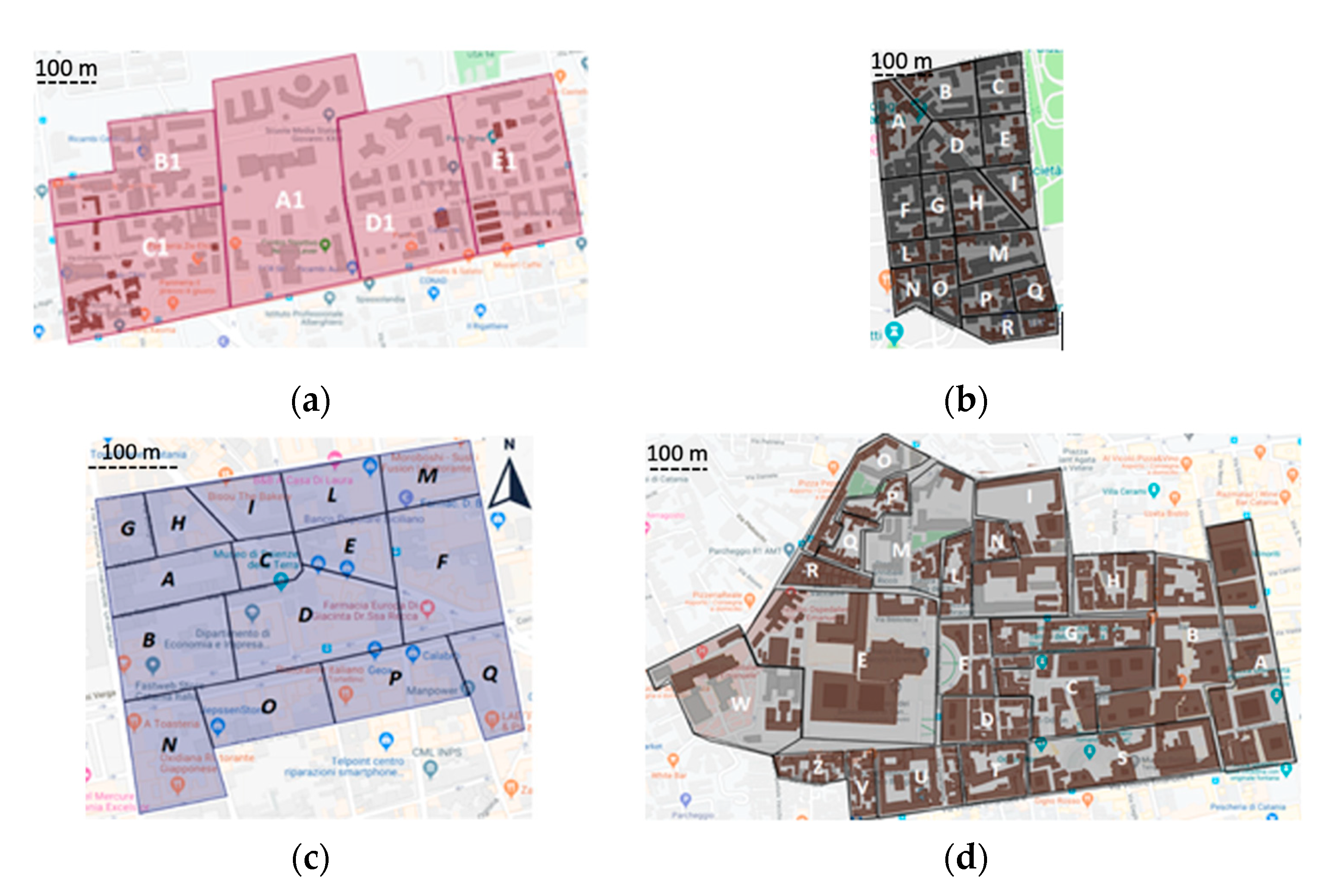
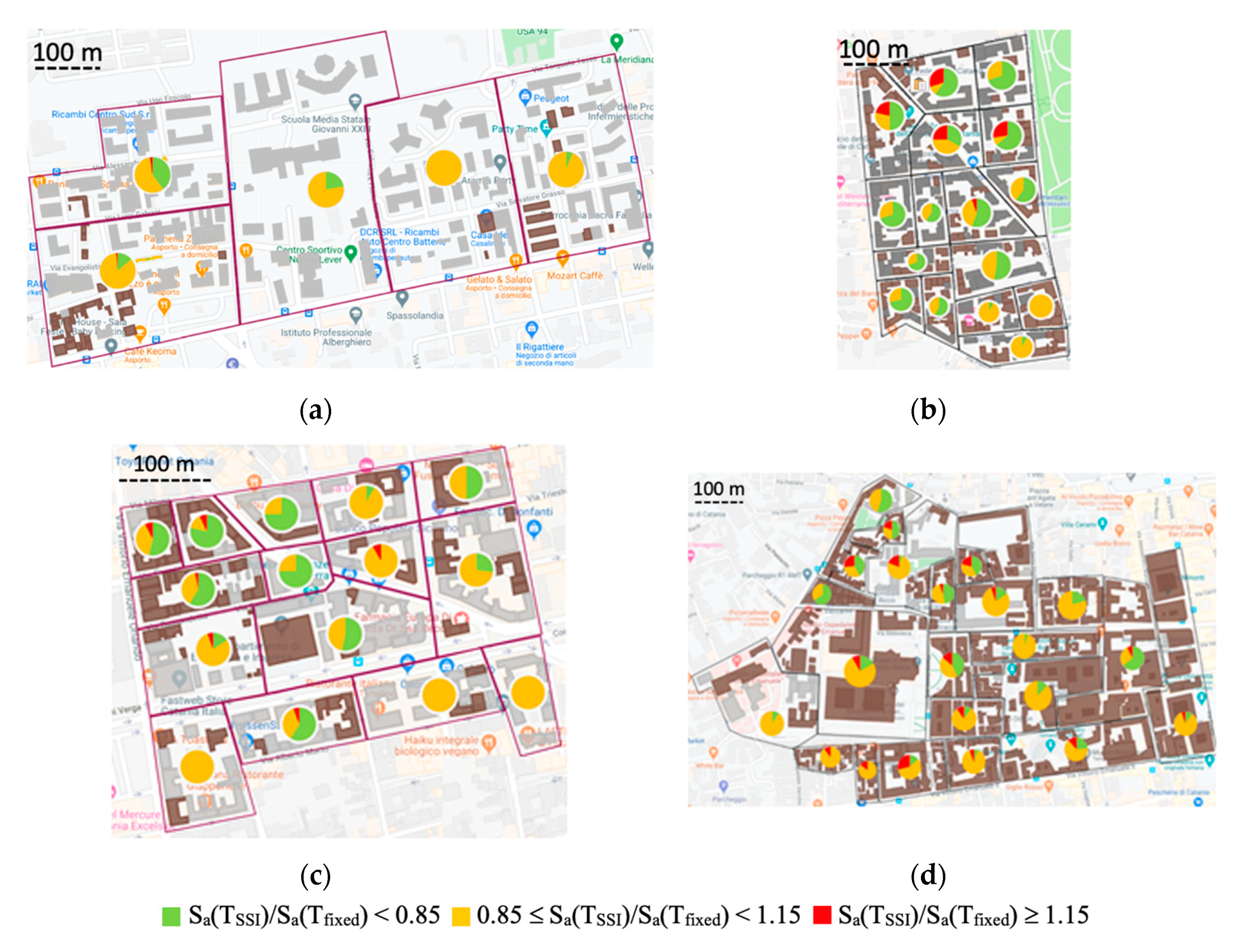
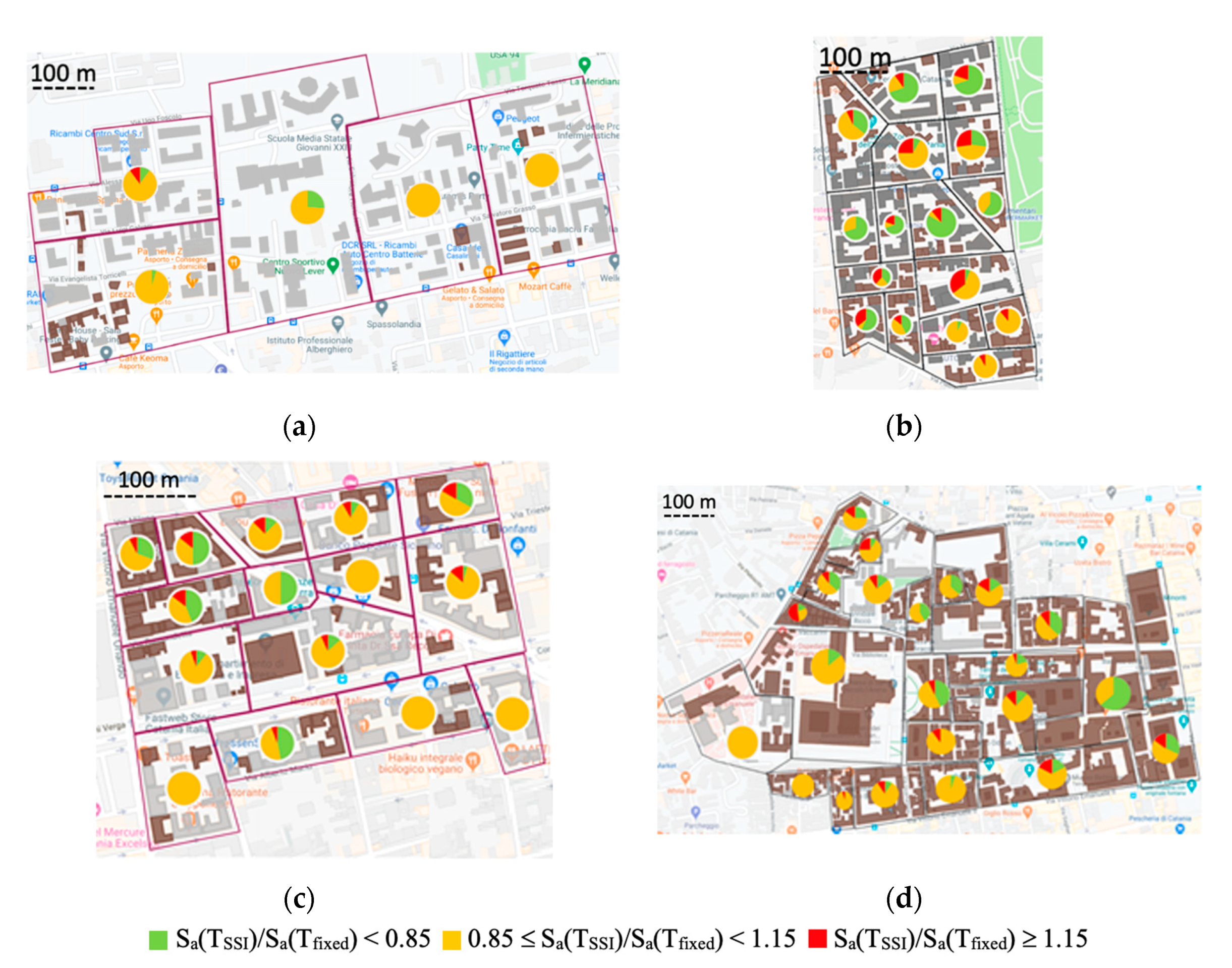
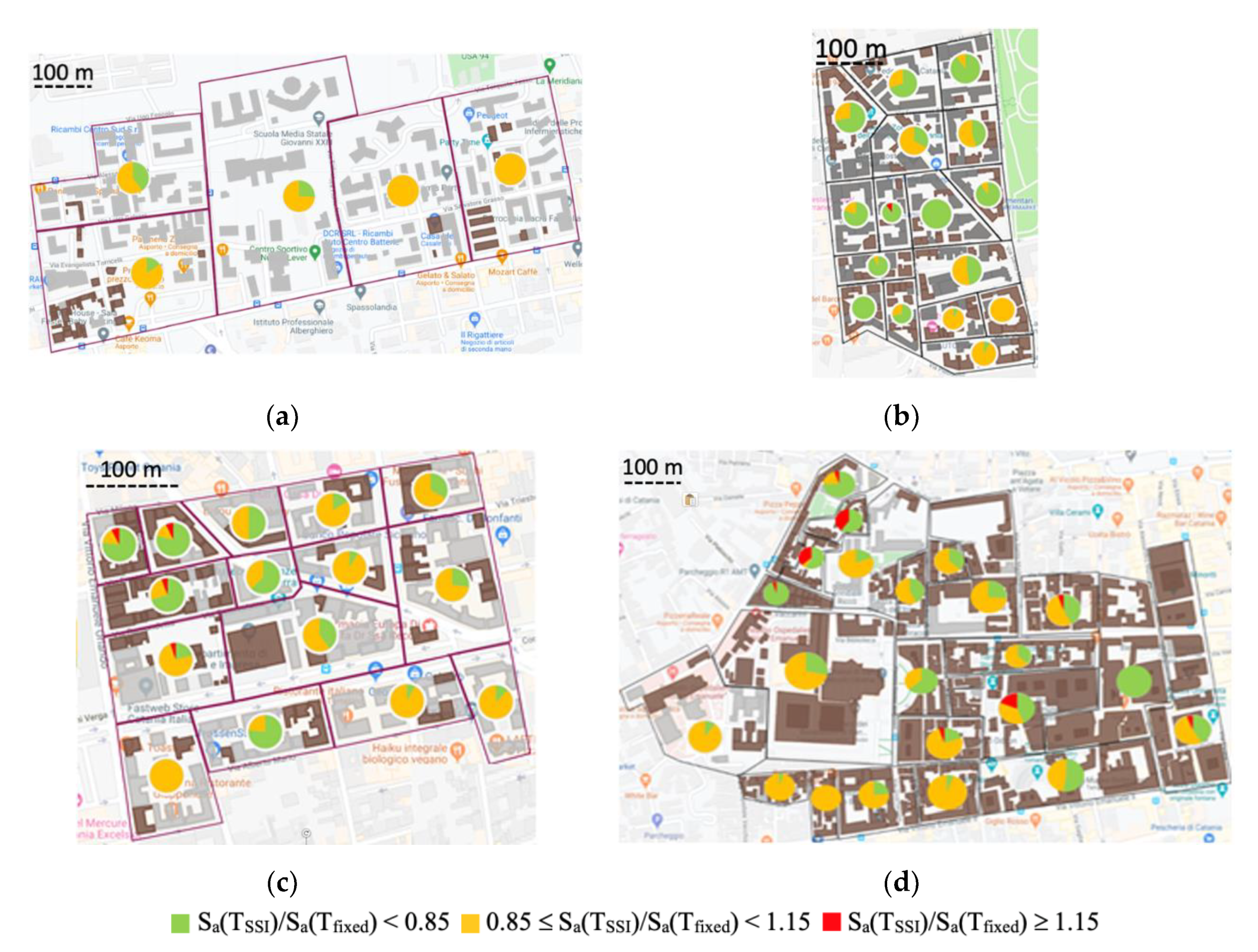
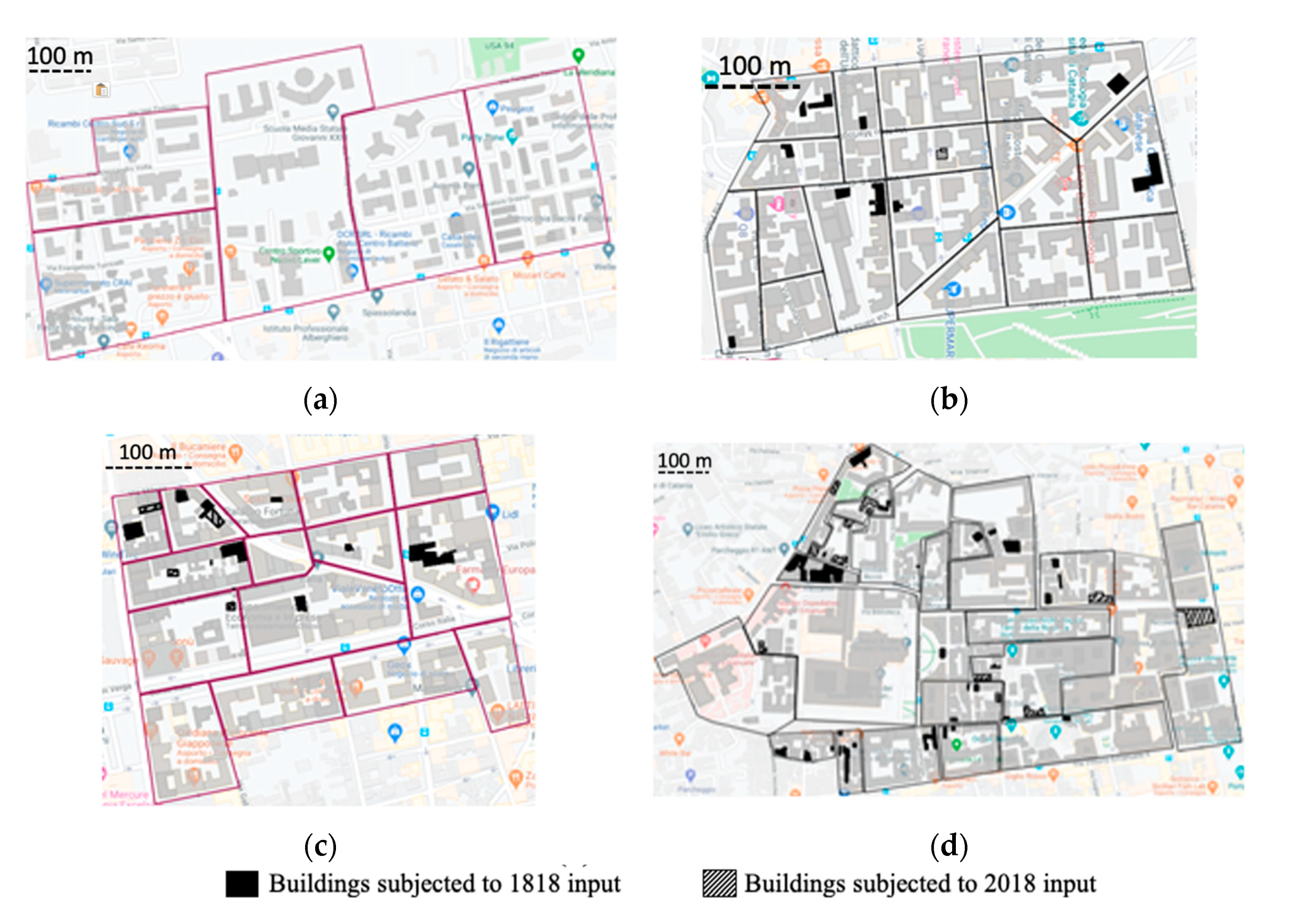
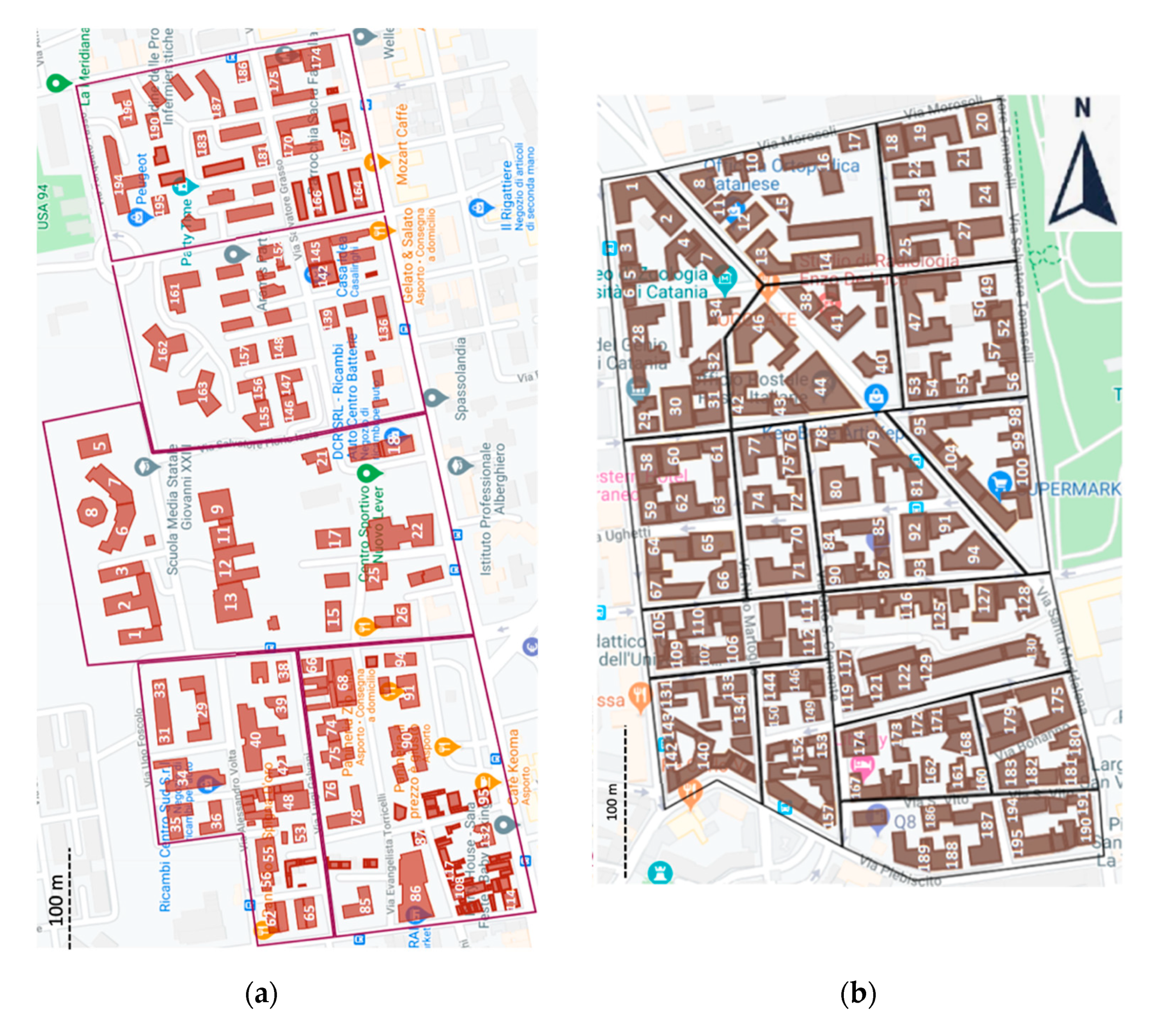
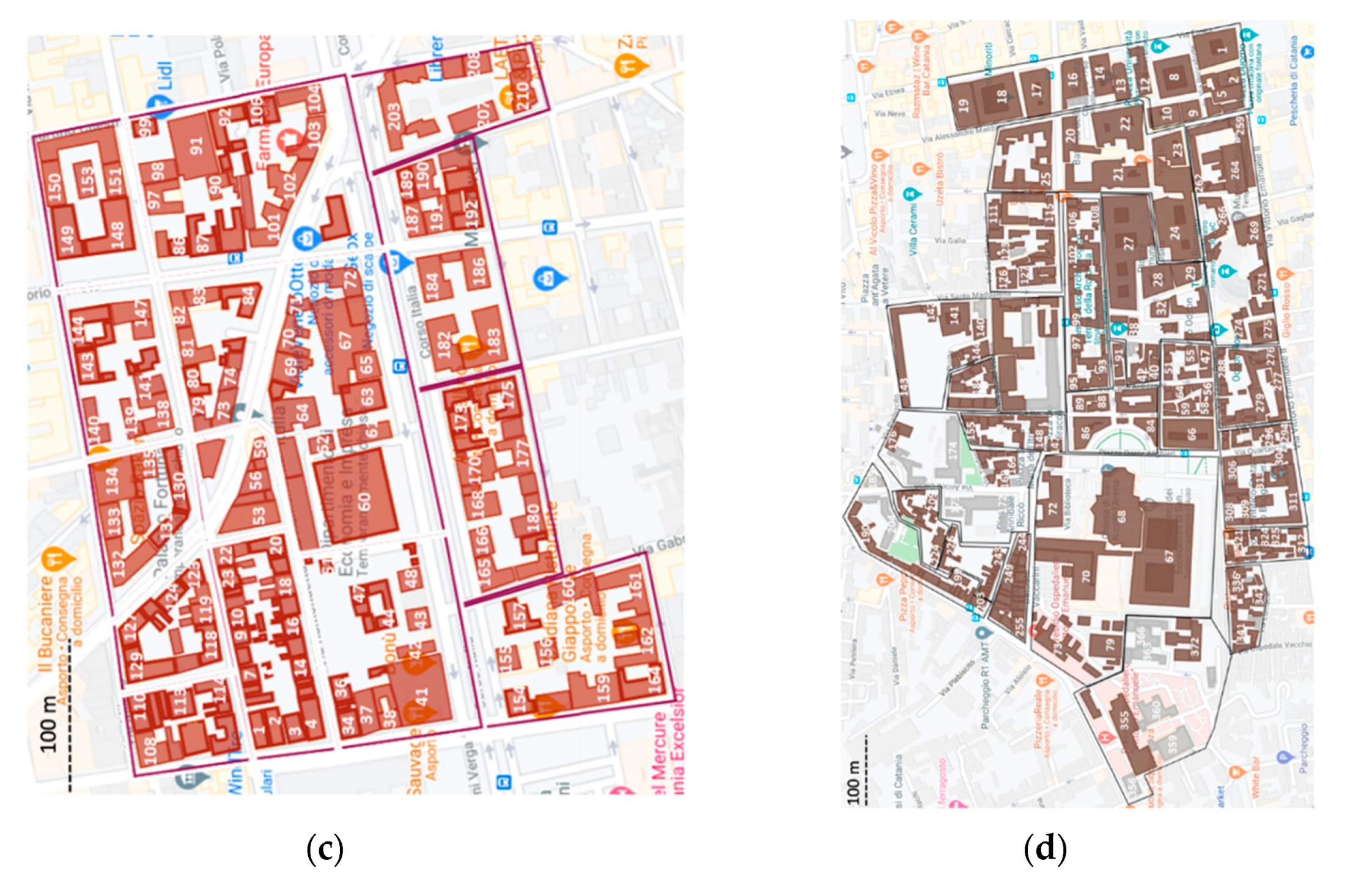
3.1. The Investigated Areas
3.2. The Utilized Inputs
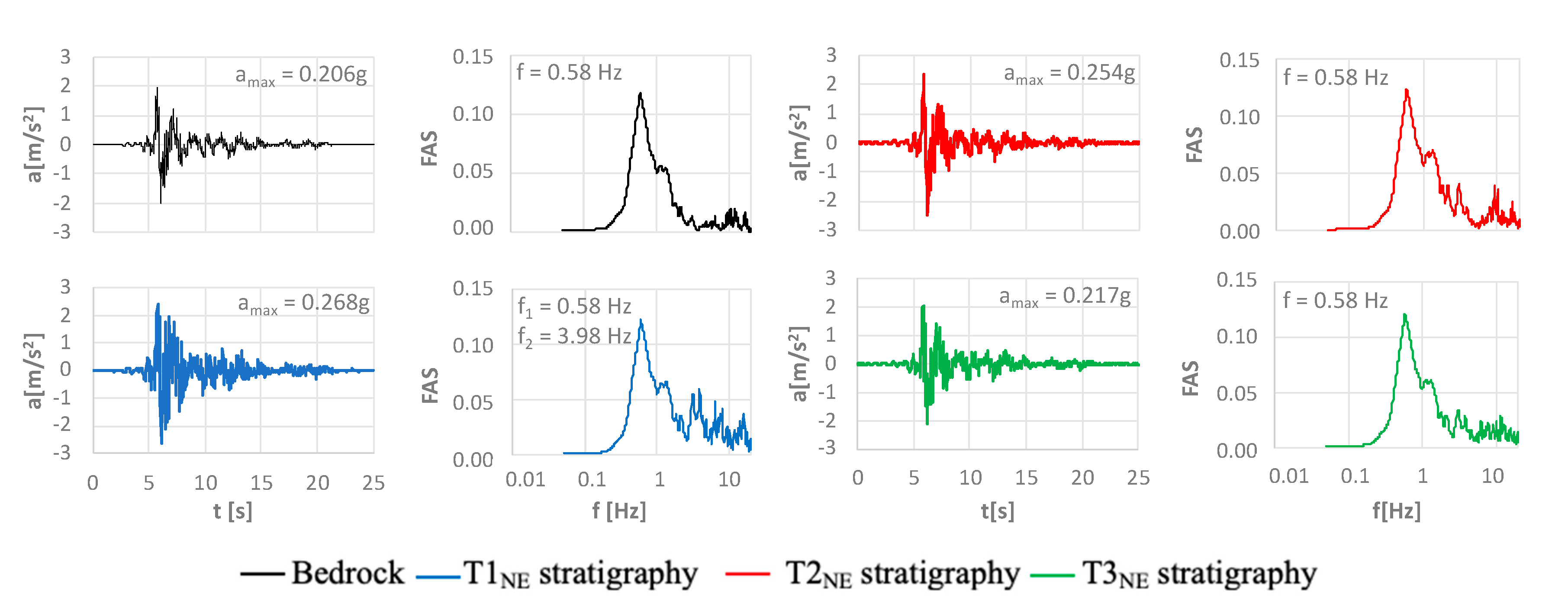
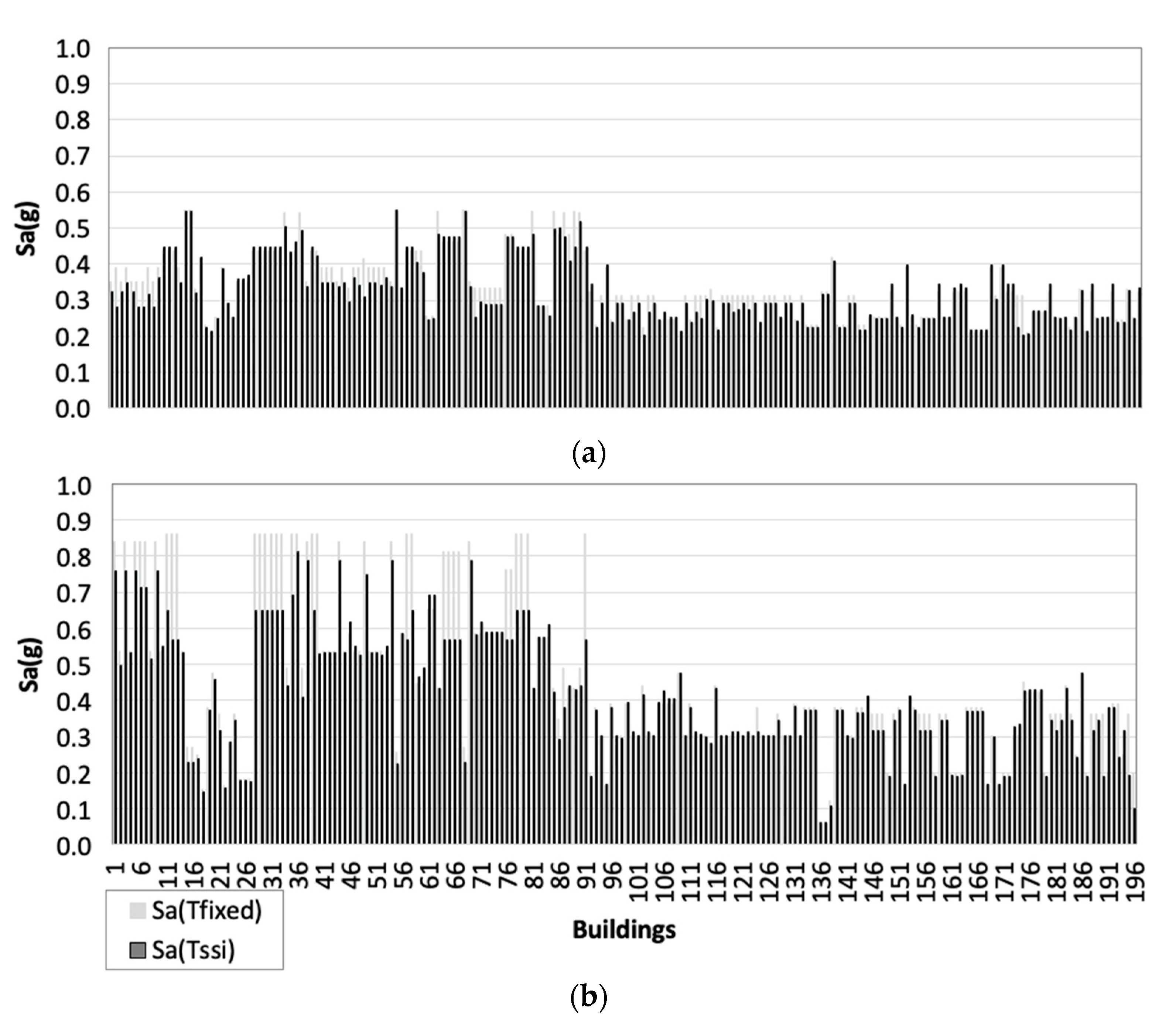
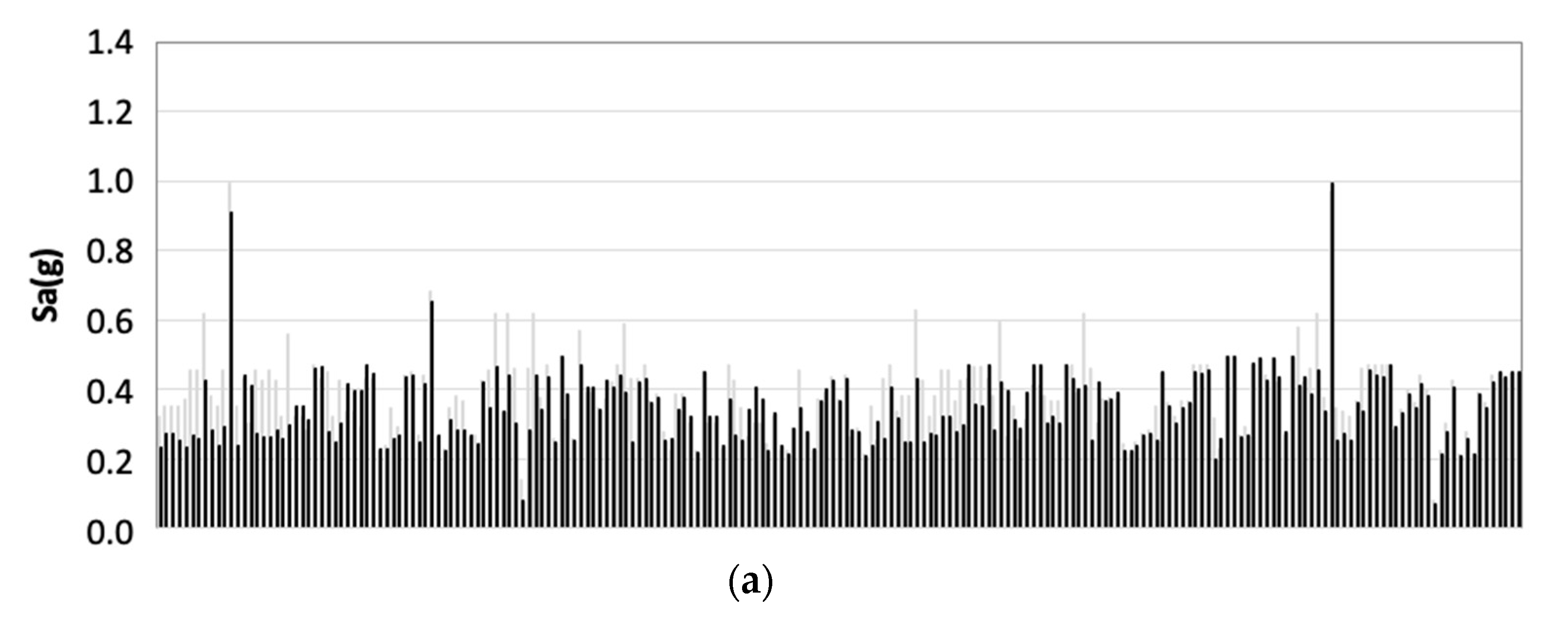
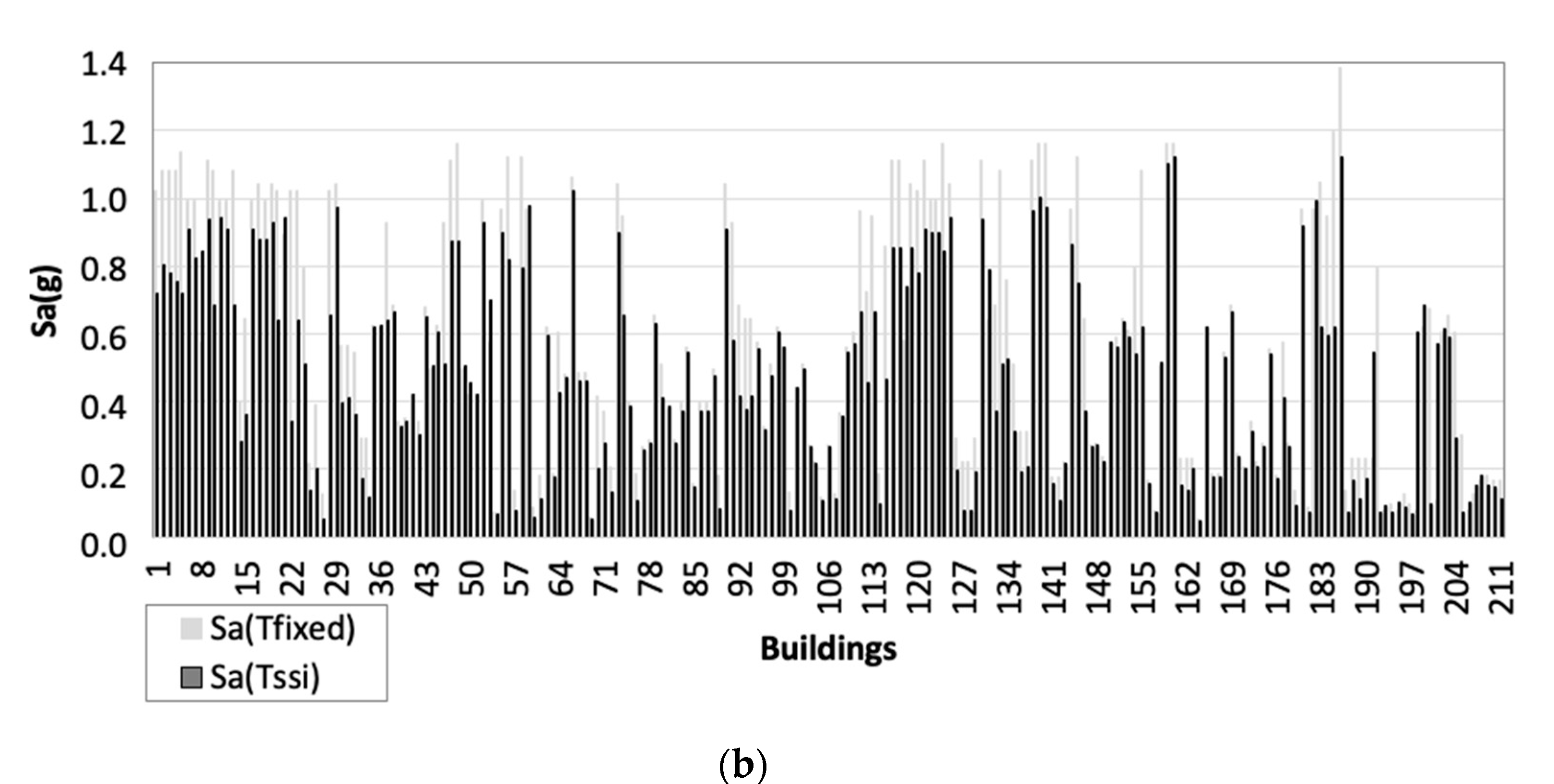
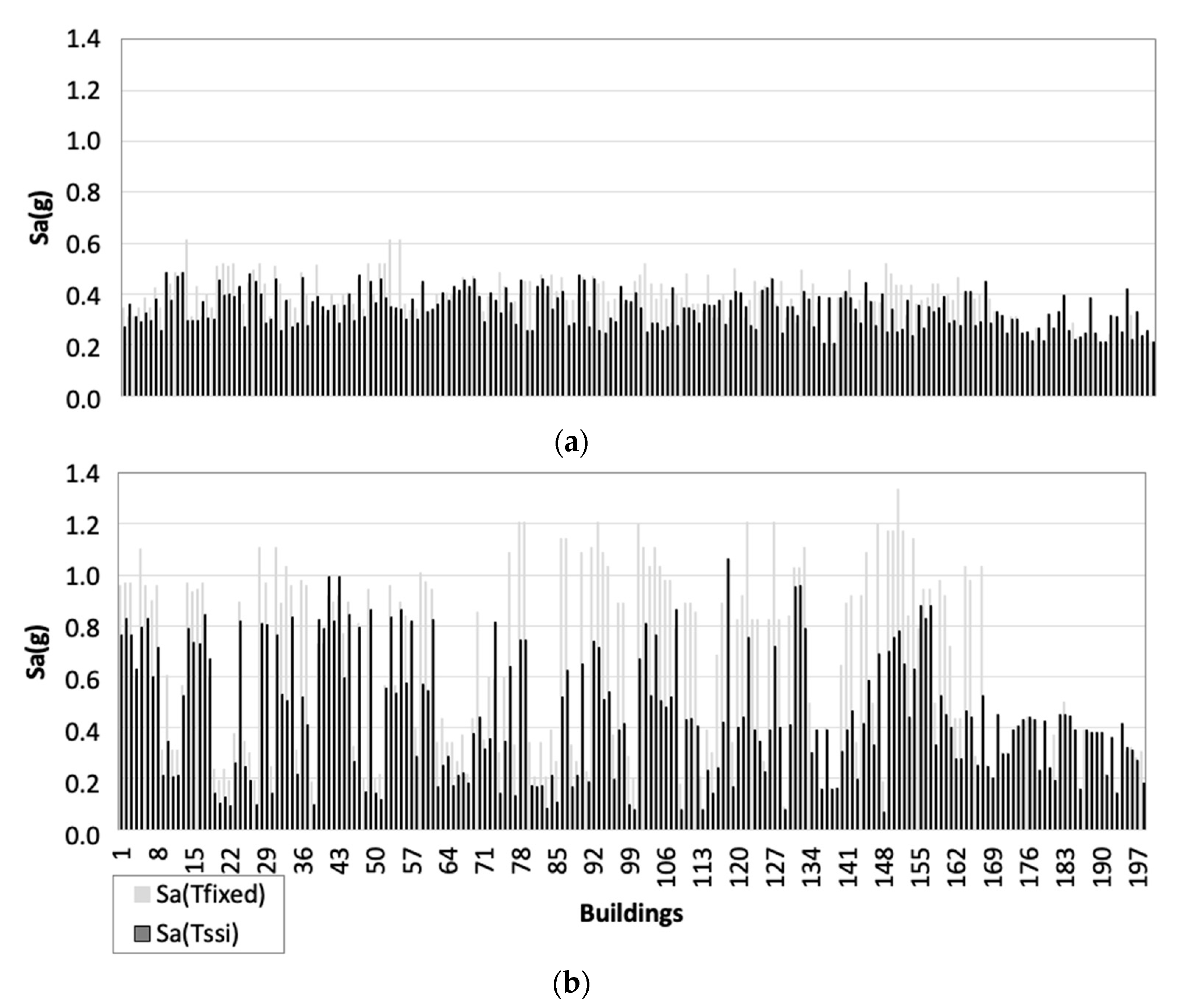
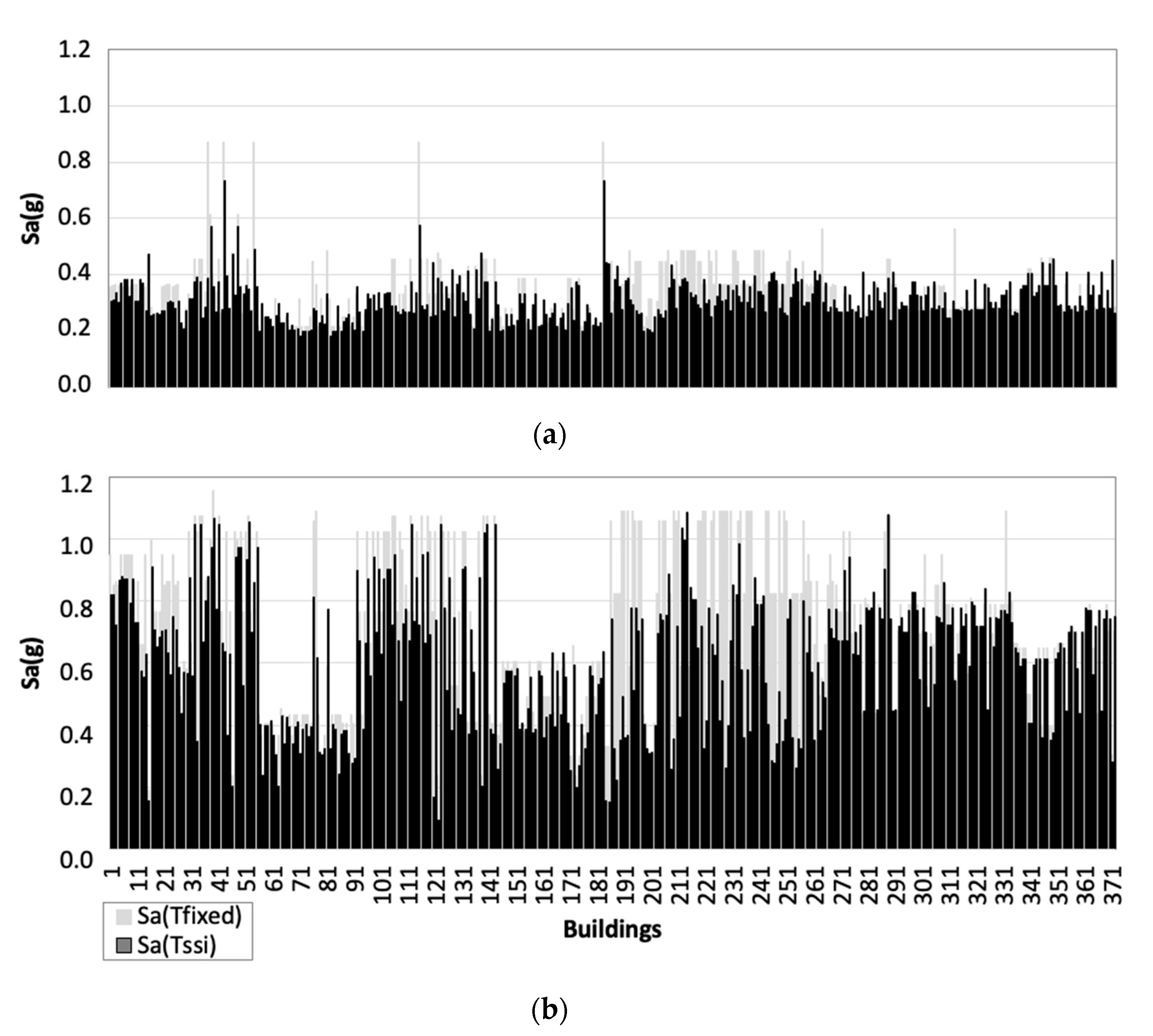
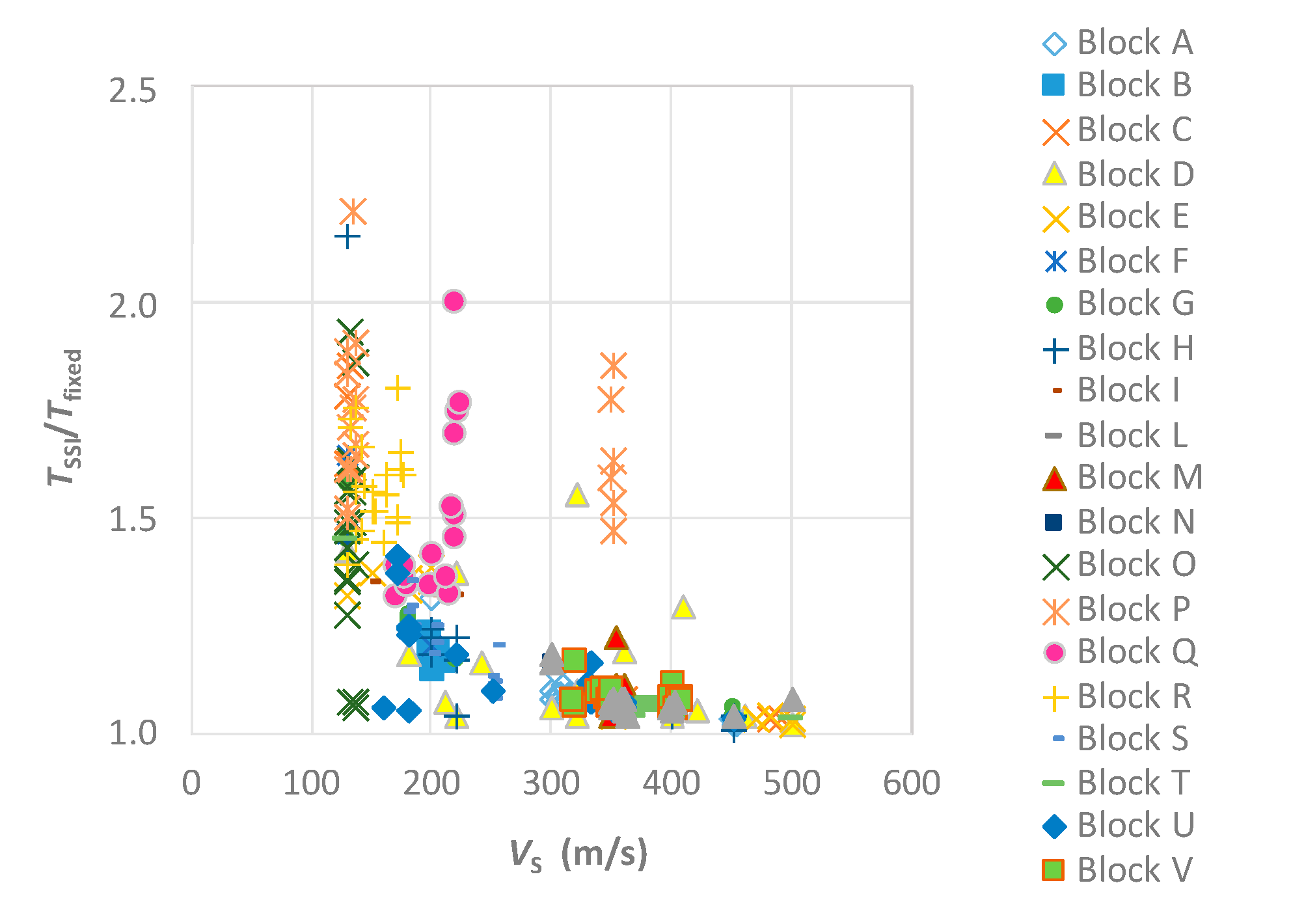
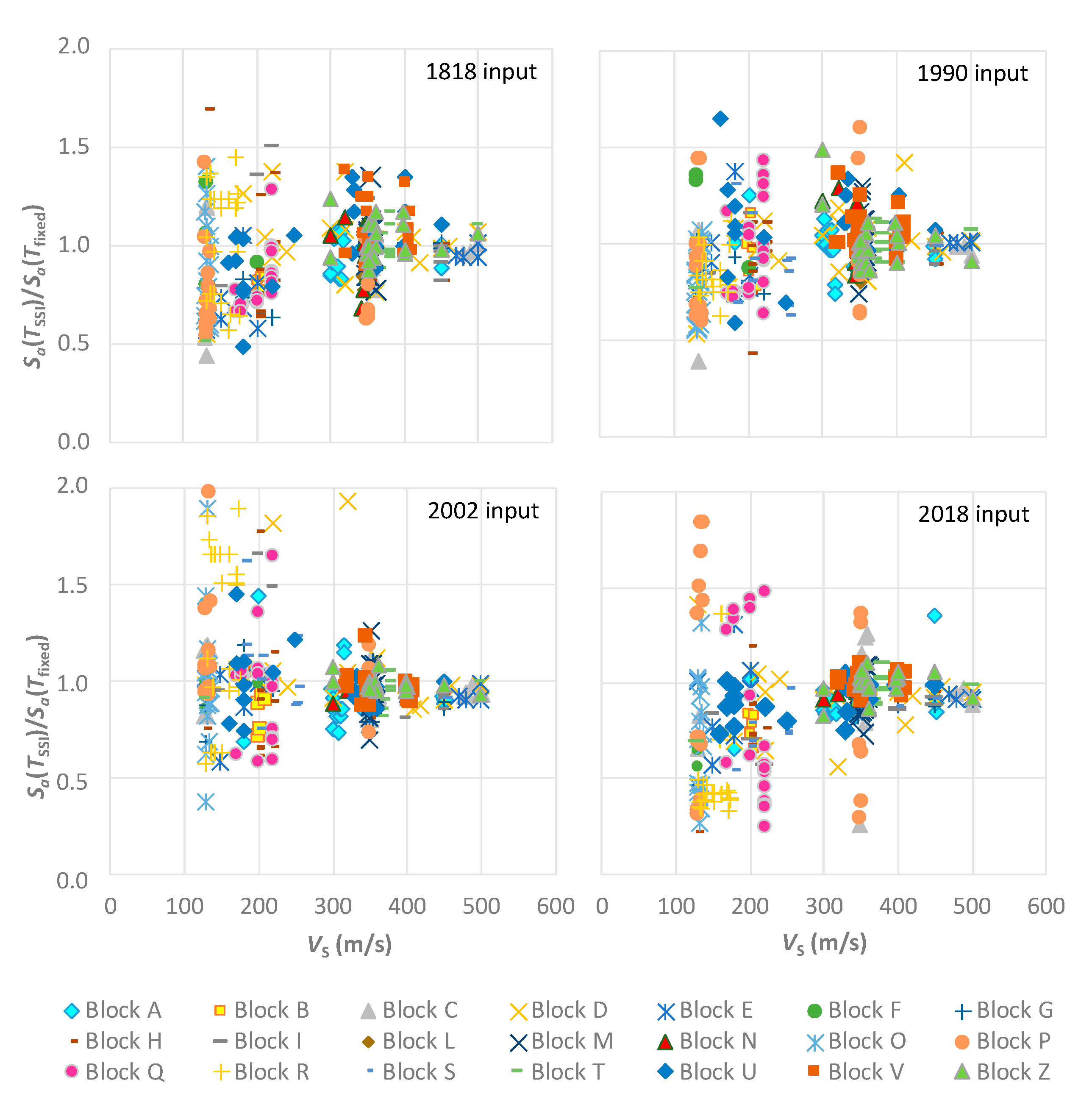
4. The 1-D Site Response Analysis
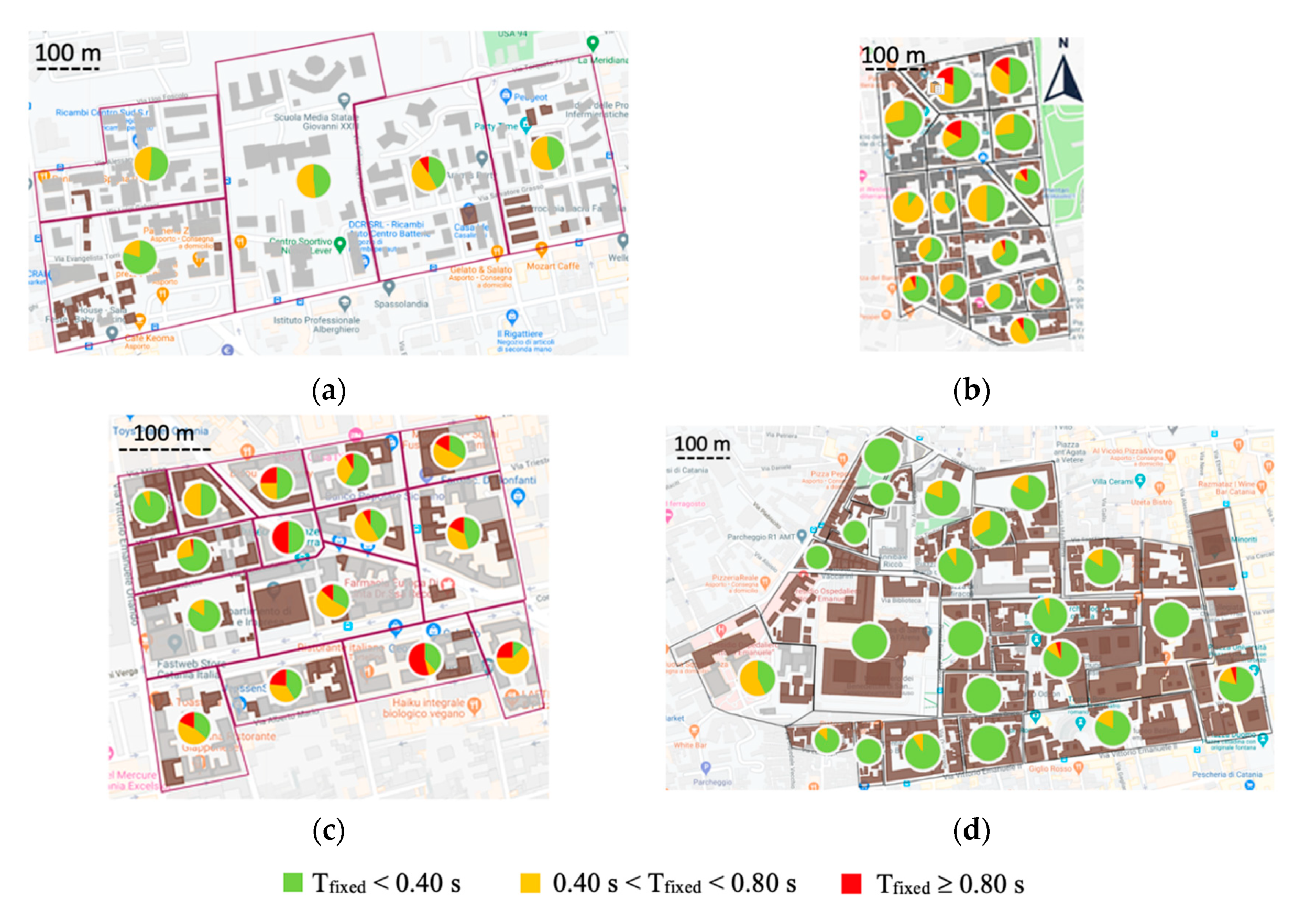
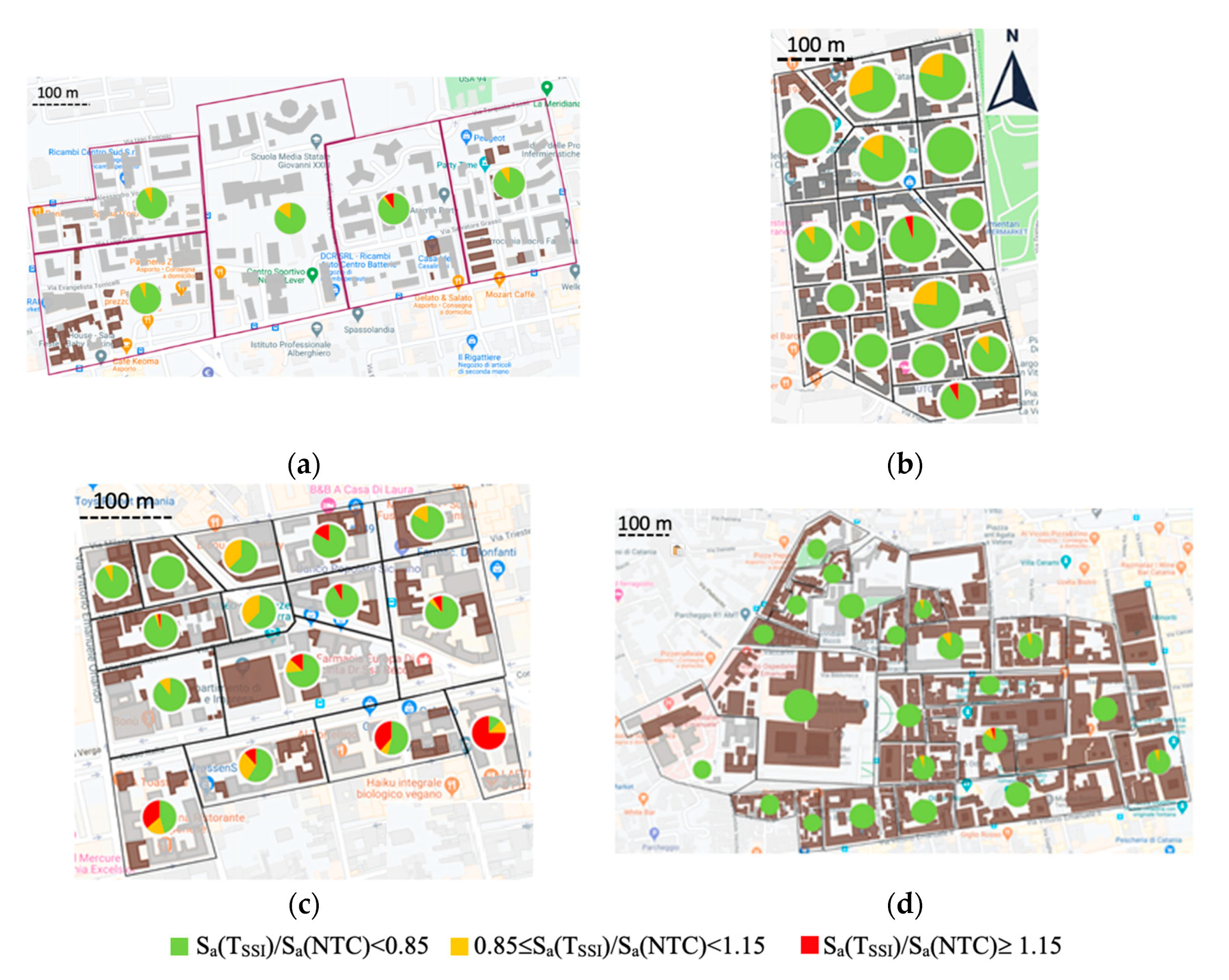
5. New Seismic Microzonation Maps for the Investigated Areas
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Grassi, F.; Massimino, M.R. Evaluation of kinematic bending moments in a pile foundation using the finite element approach. WIT Trans. Built Environ. 2009, 104, 479–488. [Google Scholar]
- Anastasopoulos, I.; Loli, M.; Georgarakos, T.; Drosos, V. Shaking Table Testing of Rocking−Isolated Bridge Pier on Sand. J. Earthq. Eng. 2013, 17, 1–32. [Google Scholar] [CrossRef]
- Gazetas, G. 4th Ishihara lecture: Soil–foundation–structure systems beyond conventional seismic failure thresholds. Soil Dyn. Earthq. Eng. 2015, 68, 23–39. [Google Scholar] [CrossRef]
- De Silva, F.; Pitilakis, D.; Ceroni, F.; Sica, S.; Silvestri, F. Experimental and numerical dynamic identification of a historic masonry bell tower accounting for different types of interaction. Soil Dyn. Earthq. Eng. 2018, 109, 235–250. [Google Scholar] [CrossRef]
- Abate, G.; Grasso, S.; Massimino, M.R. The role of shear wave velocity and non-linearity of soil in the seismic response of a coupled tunnel-soil-above ground building system. Geosciences 2019, 9, 473. [Google Scholar] [CrossRef]
- Arabpanahan, M.; Mirghaderi, S.R.; Hosseini, A.; Ghalandarzadeh, A.; Sharif, A.P. Hysteretic cyclic response of “SDOF-embedded foundation” system rocking on sand: An experimental study. Bull. Earthq. Eng. 2019, 17, 5897–5958. [Google Scholar] [CrossRef]
- Abate, G.; Massimino, M.R. Dynamic soil-structure interaction analysis by experimental and numerical modelling. Riv. Ital. Geotec. 2016, 50, 44–70. [Google Scholar]
- Abate, G.; Massimino, M.R.; Romano, S. Finite Element Analysis of DSSI Effects for a Building of Strategic Importance in Catania (Italy). Procedia Eng. 2016, 158, 374–379. [Google Scholar] [CrossRef][Green Version]
- Massimino, M.R.; Abate, G.; Grasso, S.; Pitilakis, D. Some aspects of DSSI in the dynamic response of fully-coupled soil-structure systems. Riv. Ital. Geotec. 2019, 1, 44–70. [Google Scholar]
- NTC 2018. D.M. 17/01/18—Updating of technical standards for buildings. Off. J. Ital. Repub. 2018, 42. Available online: https://www.gazzettaufficiale.it/eli/gu/2018/02/20/42/so/8/sg/pdf (accessed on 19 November 2020).
- Veletsos, A.S.; Meek, J. Dynamic behaviour of building-foundation systems. Earthq. Eng. Struct. Dyn. 1974, 3, 121–138. [Google Scholar] [CrossRef]
- Building Seismic Safety Council (BSSC). NEHRP Recommended Seismic Provisions for New Buildings and Other Structures; FEMA P-750; Federal Emergency Management Agency: Washington, DC, USA, 2009. [Google Scholar]
- Rovithis, E.; Kirtas, E.; Bliziotis, D.; Maltezos, E.; Pitilakis, D.; Makra, K.; Savvaidis, A.; Karakostas, C.; Lekidis, V. A LiDAR-aided urban-scale assessment of soil-structure interaction effects: The case of Kalochori residential area (N. Greece). Bull. Earthq. Eng. 2017, 15, 4821–4850. [Google Scholar] [CrossRef]
- Gueguen, P.; Brad, P. Site-City Seismic Interaction in Mexico City-Like Environments: An Analytical Study. Bull. Seismol. Soc. Am. 2002, 92, 794–811. [Google Scholar] [CrossRef]
- Knappett, J.A.; Madden, P.; Caucis, K. Seismic structure-soil-structure interaction between pairs of adjacent building structures. Geotechnique 2015, 65, 429–441. [Google Scholar] [CrossRef]
- Isbiliroglu, Y.; Taborda, R.; Bielak, J. Coupled soil-structure interaction effects of building clusters during earthquakes. Earthq. Spectra 2015, 31, 463–500. [Google Scholar] [CrossRef]
- NTC 2008. D.M. 14/01/08—New technical standards for buildings. Off. J. Ital. Repub. 2008, 29. Available online: https://www.camera.it/cartellecomuni/leg15/RapportoAttivitaCommissioni/commissioni/allegati/08/08_all_dm_2008.pdf (accessed on 19 November 2020).
- Veletsos, A.S.; Verbic, B. Vibration of Viscoelastic Foundations. Earthq. Eng. Struct. Dyn. 1973, 2, 87–105. [Google Scholar] [CrossRef]
- U. S. Department of Homeland Security; FEMA. Improvement of Nonlinear Static Seismic Analysis Procedures; FEMA 440; Federal Emergency Management Agency: Washington, DC, USA, 2005. [Google Scholar]
- EC8—Design of Structures for Earthquake Resistance. European Pre-Standard. ENV 1998. Europ. Com. for Stand. Brux. 2003. Available online: https://www.phd.eng.br/wp-content/uploads/2015/02/en.1998.1.2004.pdf (accessed on 19 November 2020).
- Worku, A. Soil-structure-interaction provisions. A potential tool to consider for economical seismic design of buildings? J. S. Afr. Inst. Civ. Eng. 2014, 56, 54–62. [Google Scholar]
- Building Seismic Safety Council (BSSC). National Earthquake Hazard. Reduction Program. (NEHRP): Recommended Provisions (and Commentary) for Seismic Regulations for New Buildings and Other Structures; FEMA 450-1 and 450–2; BSSC: Washington, DC, USA, 2004. [Google Scholar]
- Building Seismic Safety Council (BSSC). National Earthquake Hazard. Reduction Program. (NEHRP): Recommended Provisions for Seismic Regulations for Buildings and Other Structures; FEMA 750; BSSC: Washington, DC, USA, 2010. [Google Scholar]
- Chopra, K.A. Dynamics of Structures, Theory and Ap-plications to Earthquake Engineering; Prentice Hall International: Des Moines, IA, USA, 1995. [Google Scholar]
- Cavallaro, A.; Grasso, S.; Maugeri, M. Volcanic soil characterization and site response analysis in the city of Catania. In Proceedings of the 8th US National Conference on Earthquake Engineering 2006, San Francisco, CA, USA, 18–22 April 2006; Volume 2, pp. 835–844. [Google Scholar]
- Cavallaro, A.; Grasso, S.; Ferraro, A. A Geotechnical Engineering Study for the Safeguard, Restoration and Strengthening of Historical Heritage. Procedia Eng. 2016, 158, 134–139. [Google Scholar] [CrossRef][Green Version]
- Castelli, F.; Grasso, S.; Lentini, V.; Massimino, M.R. In situ measurements for evaluating liquefaction potential under cyclic loading. In Proceedings of the 1st IMEKO TC4 International Workshop on Metrology for Geotechnics, MetroGeotechnics 2016, Benevento, Italy, 17–18 March 2016; pp. 79–84, Code 121564. [Google Scholar]
- Grasso, S.; Massimino, M.R. A GIS for data mining in seismic microzonation studies. Smart Innov. Syst. Technol. 2019, 142, 191–201. [Google Scholar]
- Faccioli, E.; Pessina, V. The Catania Project: Earthquake Damage Scenarios for High Risk Area in the Mediterranean; Faccioli, E., Pessina, V., Eds.; CNR-Gruppo Nazionale per la Difesa dai Terremoti: Roma, Italy, 2000; 225p. [Google Scholar]
- Maugeri, M. Advances in earthquake engineering. In Seismic Prevention of Damage: A Case Study in a Mediterranean City; WIT Press: Southampton, UK, 2005; Volume 14. [Google Scholar]
- Grasso, S.; Maugeri, M. Vulnerability of physical environment of the city of Catania using GIS technique. In Seismic Prevention of Damage: A Case Study in a Mediterranean City; Maugeri, M., Ed.; WIT Press: Southampton, UK, 2005; Chapter IX; pp. 155–175. [Google Scholar]
- Grasso, S.; Laurenzano, G.; Maugeri, M.; Priolo, E. Seismic response in Catania by different methodologies. In Seismic Prevention of Damage: A Case Study in a Mediterranean City; Maugeri, M., Ed.; WIT Press: Southampton, UK, 2005; Chapter IV; pp. 63–79. [Google Scholar]
- Abate, G.; Bosco, M.; Massimino, M.R.; Maugeri, M. Limit state analysis for the Catania fire-station (Italy). In Proceedings of the 8th US National Conference on Earthquake Engineering 2006, San Francisco, CA, USA, 18–22 April 2006; Volume 11, pp. 6532–6541. [Google Scholar]
- Abate, G.; Corsico, S.; Massimino, M.R. FEM Modelling of the Seismic Behaviour of a Tunnel-Soil-Aboveground Building System: A Case History in Catania (Italy). Procedia Eng. 2016, 158, 380–385. [Google Scholar] [CrossRef]
- Caruso, S.; Ferraro, A.; Grasso, S.; Massimino, M.R. Site Response Analysis in eastern Sicily based on direct and indirect Vs measurements. In Proceedings of the 1st IMEKO TC4 International Workshop on Metrology for Geotechnics, MetroGeotechnics, Benevento, Italy, 17–18 March 2016; pp. 115–120. [Google Scholar]
- Castelli, F.; Cavallaro, A.; Ferraro, A.; Grasso, S.; Lentini, V.; Massimino, M.R. Static and dynamic properties of soils in Catania (Italy). Ann. Geophys. 2018, 61, 221. [Google Scholar] [CrossRef]
- Ferraro, A.; Grasso, S.; Massimino, M.R. Site effects evaluation in Catania (Italy) by means of 1-D numerical analysis. Ann. Geophys. 2018, 61, 224. [Google Scholar] [CrossRef]
- Massimino, M.R.; Abate, G.; Corsico, S.; Louarn, R. Comparison between two approaches for non-linear FEM modelling of the seismic behaviour of a coupled soil–structure system. Geotech. Geol. Eng. 2019, 37, 1957–1975. [Google Scholar] [CrossRef]
- Kottke, A.R.; Rathie, E.M.; Wang, X. Technical Manual for Strata; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2013. [Google Scholar]


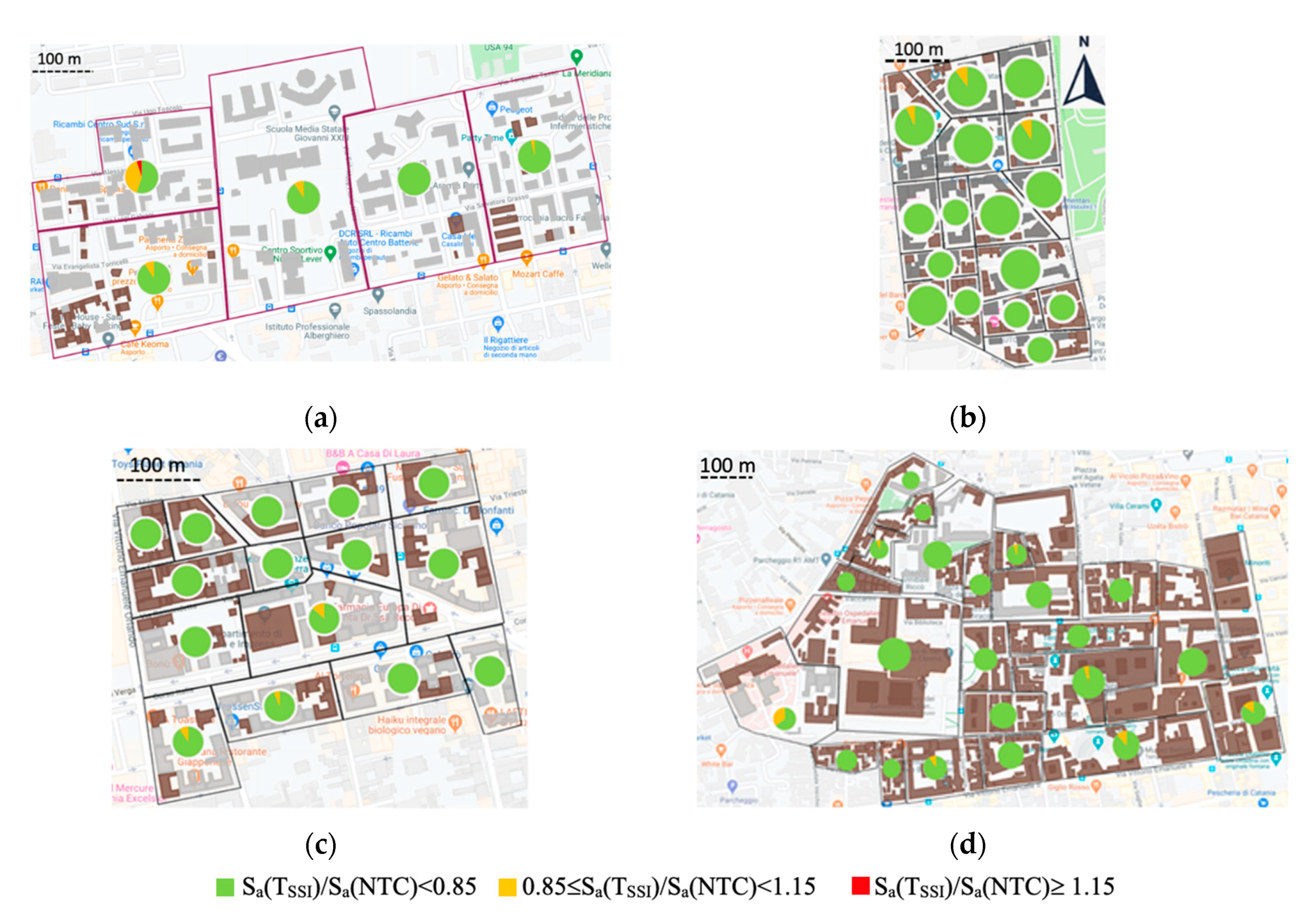
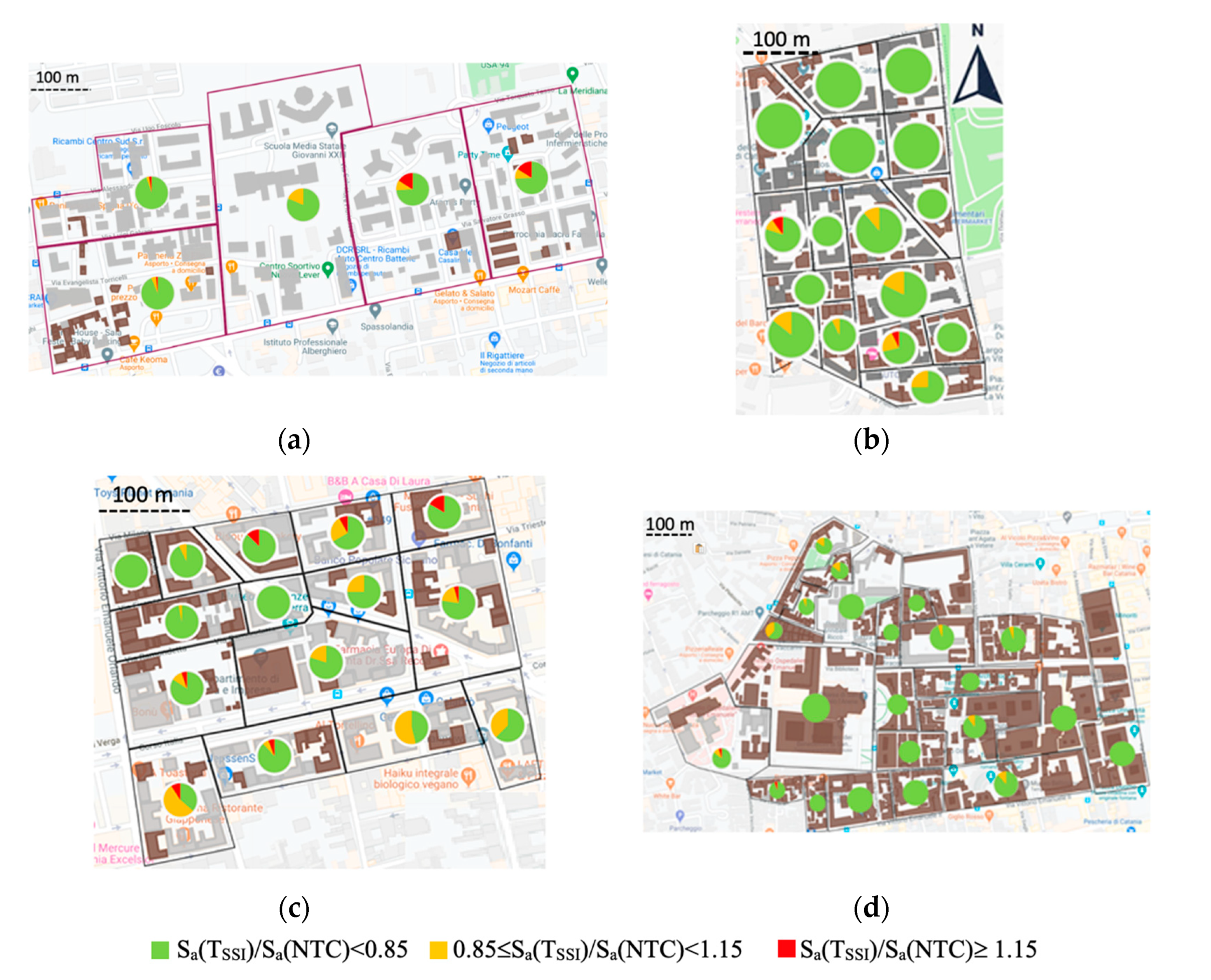

| Lithotype Label | Corresponding Lithotype | γ (kN/m3) | Vs (m/s) |
|---|---|---|---|
| R-Df | Topsoil and fill (R); debris and landslides (Dt) | 17.0–19.0 | 130–220 |
| X | Scoriaceous lavas and volcanoclastic rocks | 18.0–18.5 | 180–300 |
| Alg | Coarse alluvial deposits | 18.0–19.5 | 210–280 |
| Asg | Yellowish or brown clays and sandy silts | 19.3–20.0 | 220–400 |
| Aa | Silty clays and grey-bluish clays | 19.5–20.0 | 450–600 |
| M | Marine deposits | 18.3–18.7 | 210–280 |
| P | Pyroclastic rocks | 16.0–17.0 | 250–500 |
| Cc | Calcarenites and block-calcarenites | 21.0–23.5 | 500–800 |
| E1-E2 | Fractured to slightly fractured lavas | 22.0–24.0 | 350–500 |
| Ai | Clayey interlayers in Cc unit | 21.0–23.5 | 300–650 |
| Alf | Fine alluvial deposits | 18.5–19.5 | 130–210 |
| SG | Yellow or brown quartz sands | 19.8–20.8 | 350–500 |
| Data | M (Richter) | f1 (Hz) | Epicenter |
|---|---|---|---|
| 20.02.1818 | 6.0 | 0.58 | Aci Sant’Antonio |
| 13.12.1990 | 5.7 | 1.59 | Augusta |
| 29.10.2002 | 4.4 | 0.35 | Santa Venerina |
| 26.12.2018 | 4.8 | 2.55 | Etna |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abate, G.; Bramante, S.; Massimino, M.R. Innovative Seismic Microzonation Maps of Urban Areas for the Management of Building Heritage: A Catania Case Study. Geosciences 2020, 10, 480. https://doi.org/10.3390/geosciences10120480
Abate G, Bramante S, Massimino MR. Innovative Seismic Microzonation Maps of Urban Areas for the Management of Building Heritage: A Catania Case Study. Geosciences. 2020; 10(12):480. https://doi.org/10.3390/geosciences10120480
Chicago/Turabian StyleAbate, Glenda, Simone Bramante, and Maria Rossella Massimino. 2020. "Innovative Seismic Microzonation Maps of Urban Areas for the Management of Building Heritage: A Catania Case Study" Geosciences 10, no. 12: 480. https://doi.org/10.3390/geosciences10120480
APA StyleAbate, G., Bramante, S., & Massimino, M. R. (2020). Innovative Seismic Microzonation Maps of Urban Areas for the Management of Building Heritage: A Catania Case Study. Geosciences, 10(12), 480. https://doi.org/10.3390/geosciences10120480






