Gas Permeability of Salt Crusts Formed by Evaporation from Porous Media
Abstract
1. Introduction
2. Materials and Methods
2.1. Evaporation Experiments
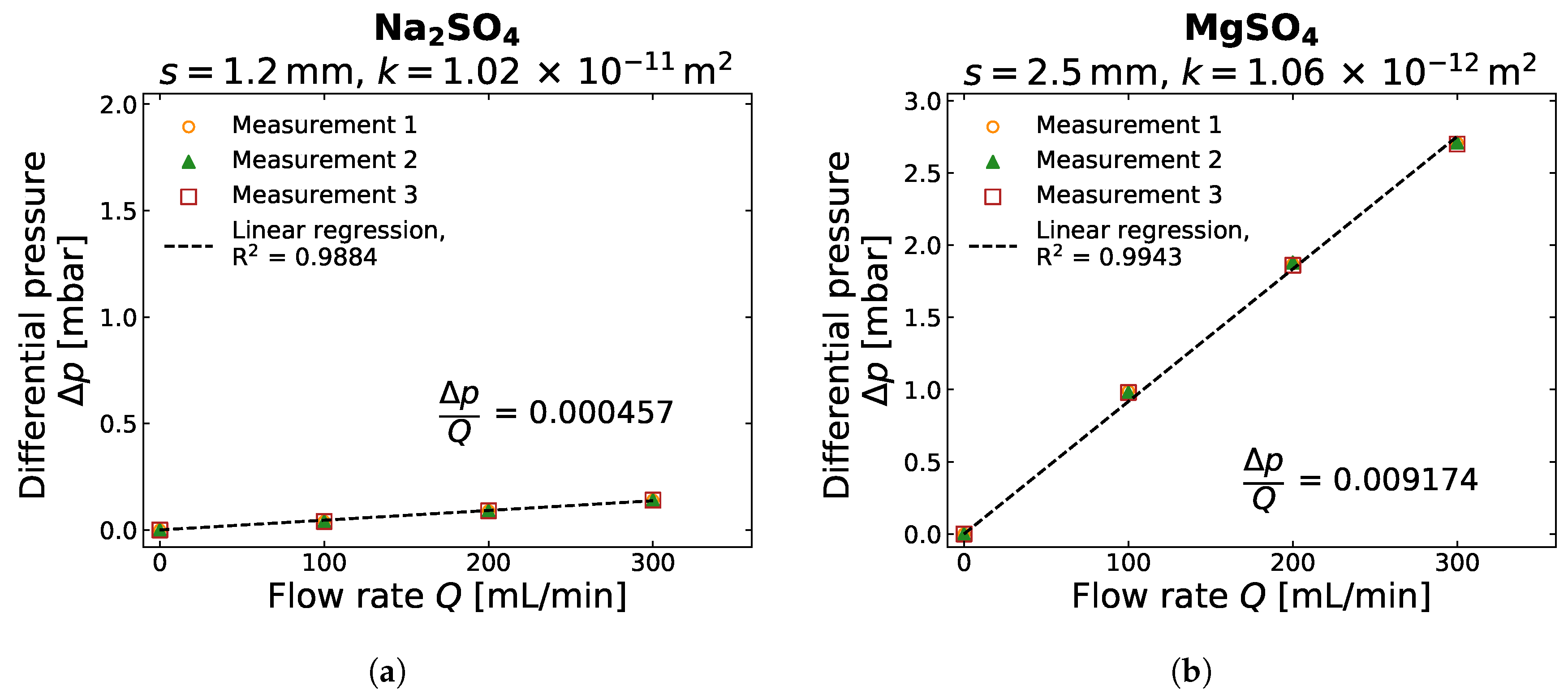
2.2. Gas Permeability Determination
3. Results and Discussion
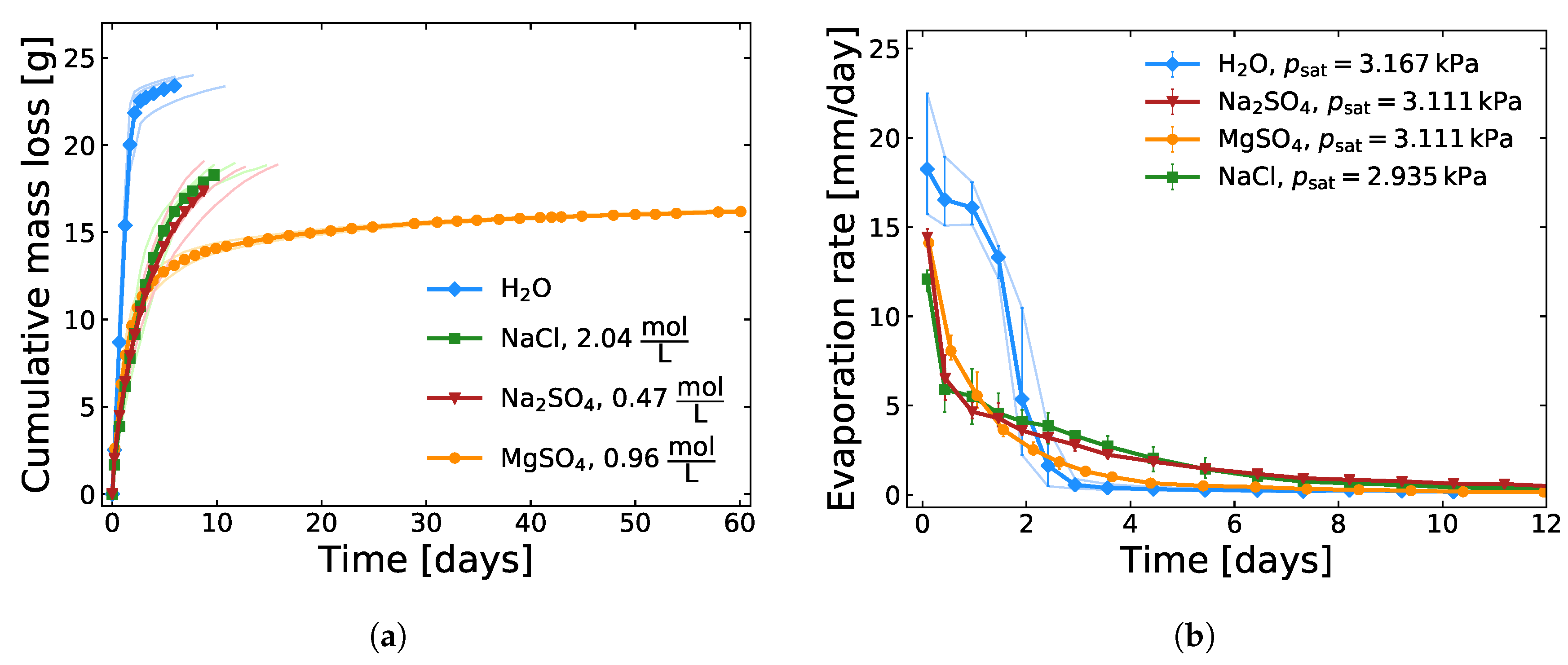
3.1. Evaporation of Saline Solutions
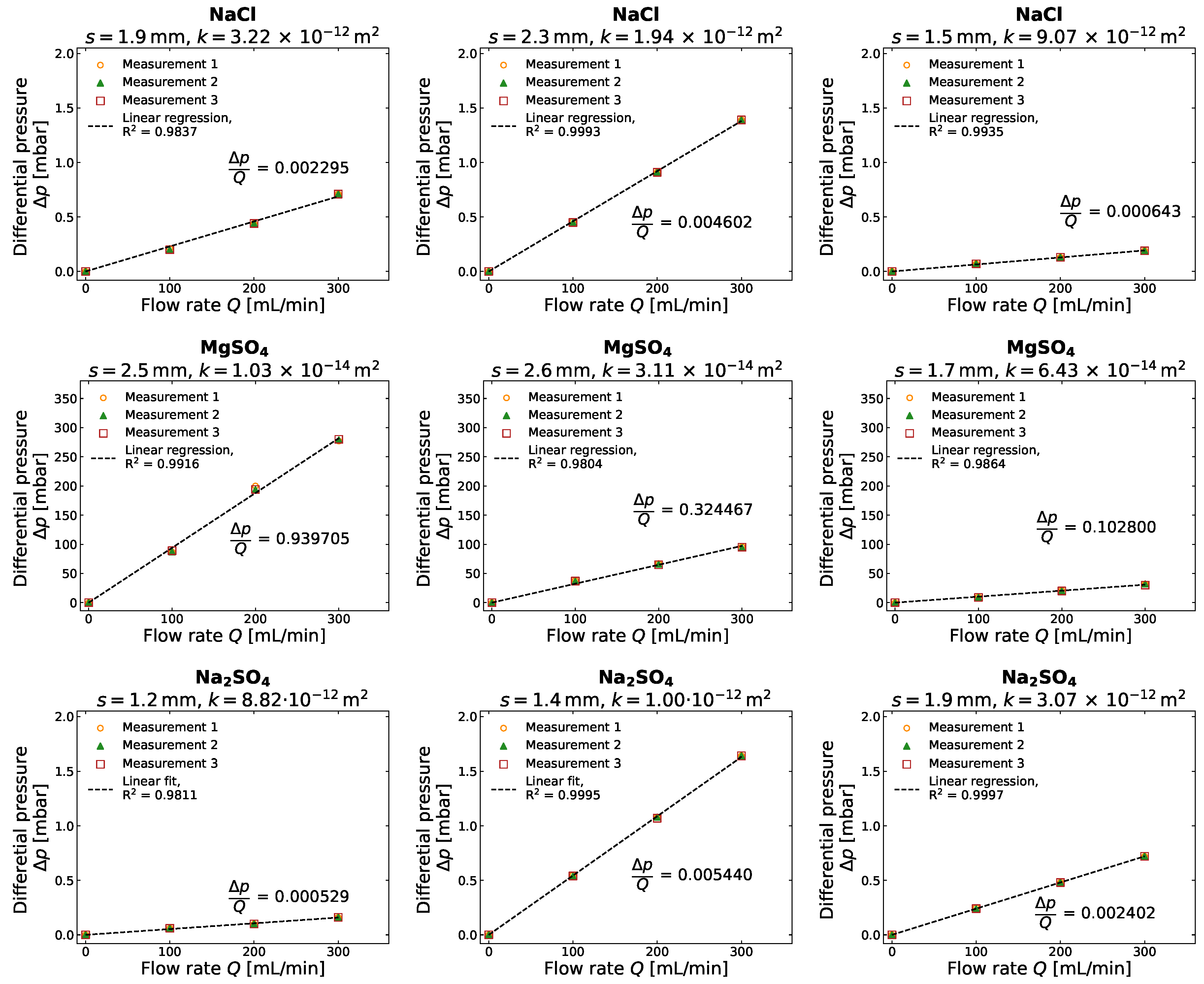
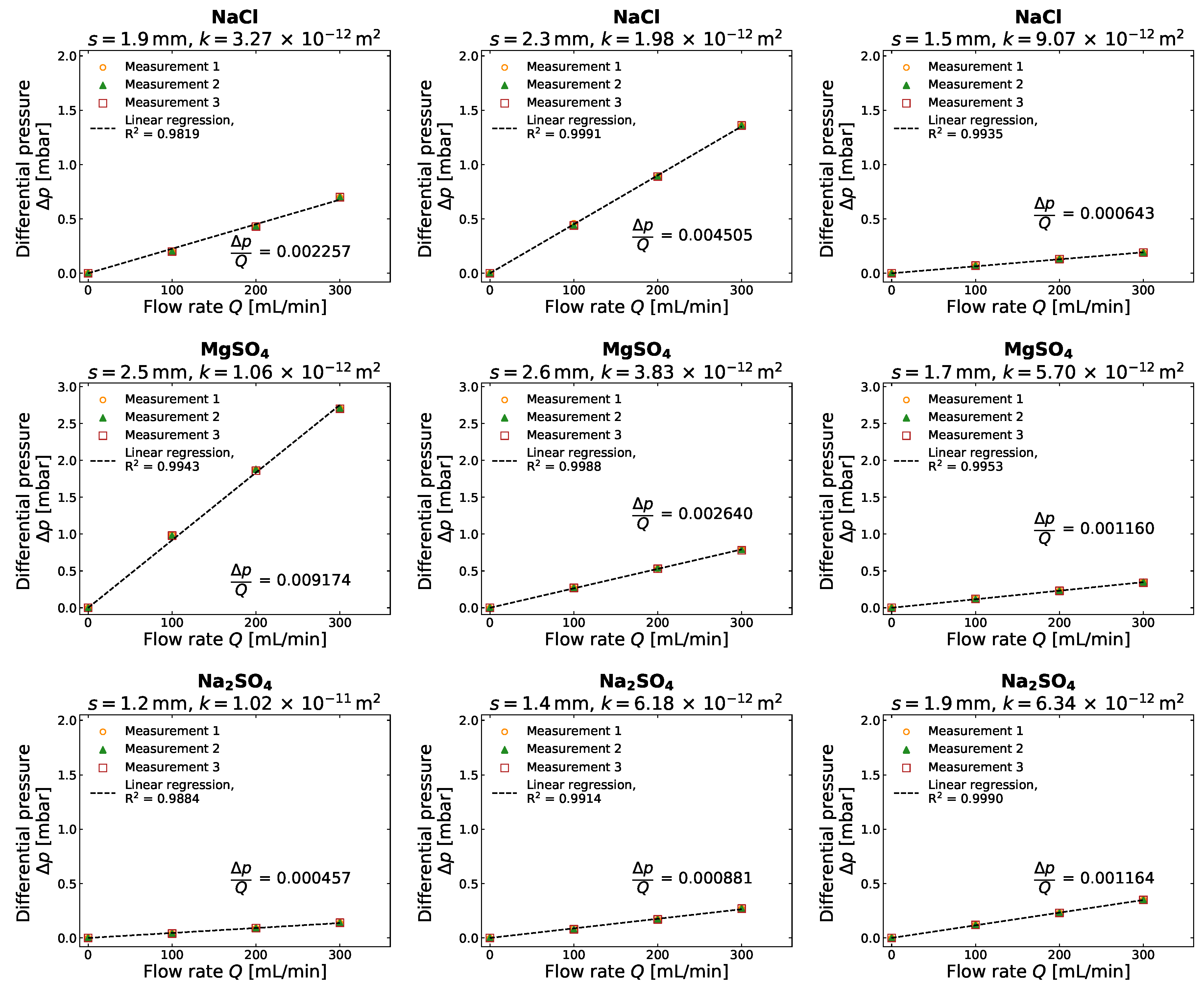
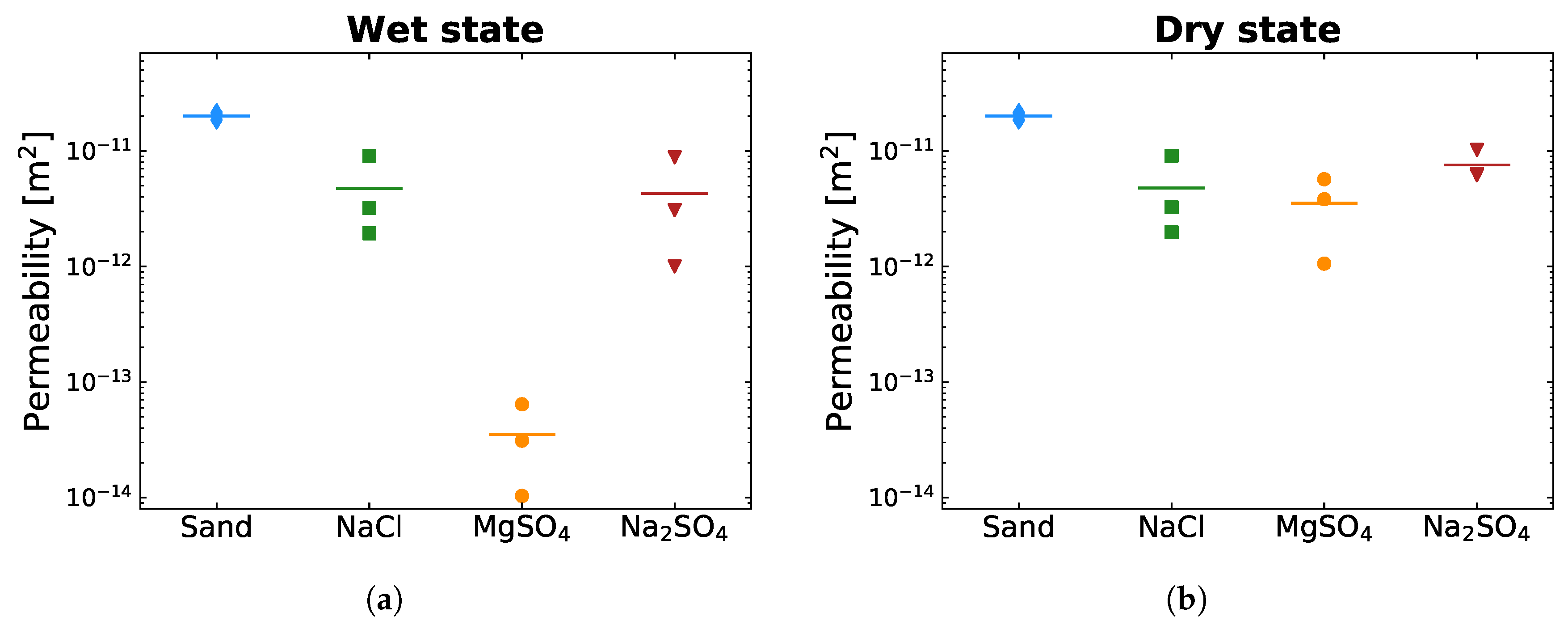
3.2. Gas Permeability of Different Salt Crusts
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Evaluation of Laminar Flow Conditions for the Gas Permeameter Set-Up
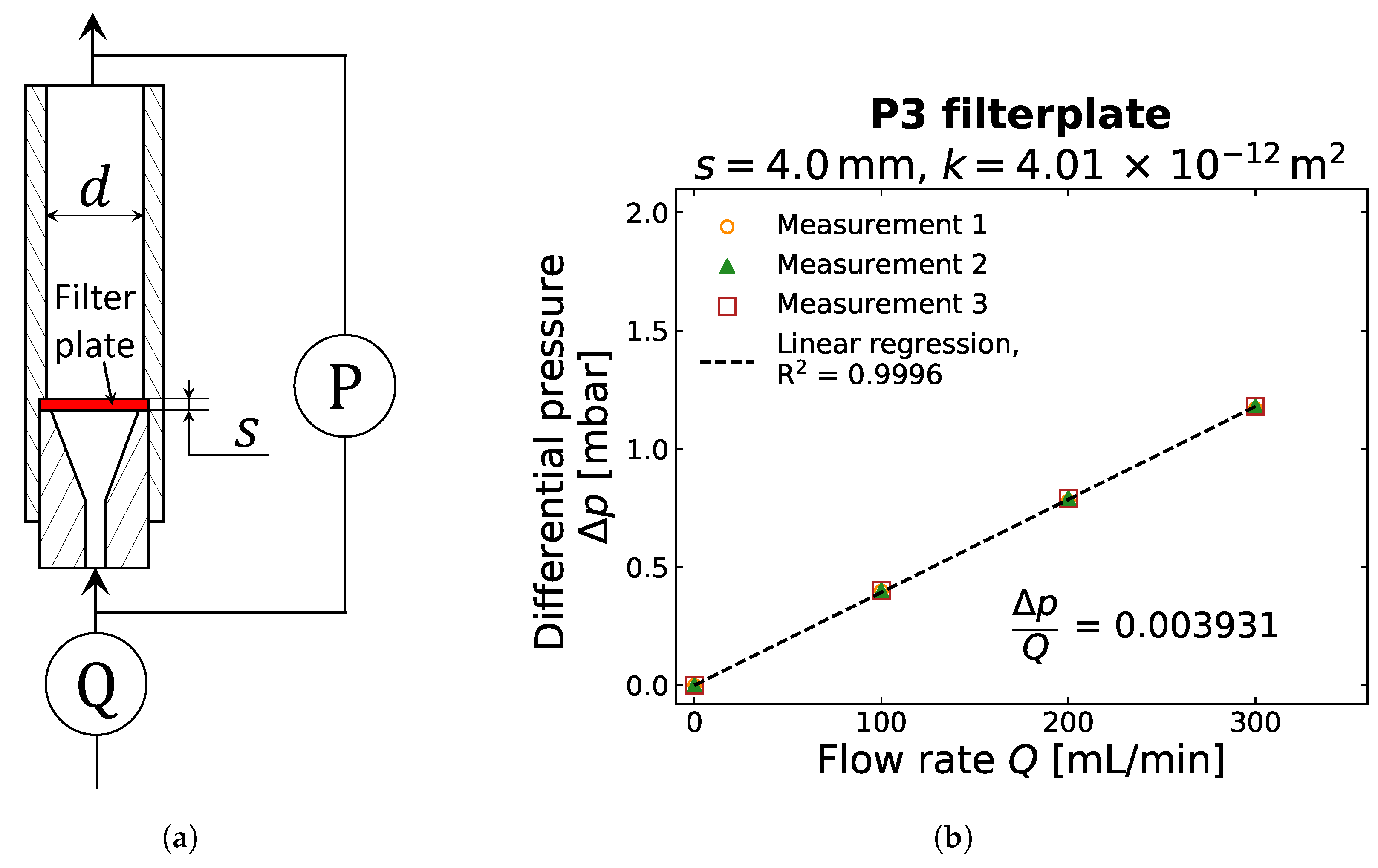
Appendix B. Detailed Results for Gas Compressibility and Gas Permeability Determination
| Crust | Measured | Measured at Position | Mean Crust Thickness s | |||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| [mm] | [mm] | [mm] | [mm] | [mm] | ||
| top | 16.6 | 17.4 | 17.0 | 17.1 | 1.9 | |
| NaCl | bottom | 120.9 | 120.8 | 121.1 | 121.4 | |
| thickness | 2.5 | 1.8 | 1.9 | 1.5 | ||
| top | 17.5 | 17.8 | 18.3 | 17.9 | 2.3 | |
| NaCl | bottom | 119.8 | 119.6 | 119.9 | 119.9 | |
| thickness | 2.7 | 2.6 | 1.8 | 2.2 | ||
| top | 18.5 | 18.4 | 18.6 | 18.5 | 2.5 | |
| MgSO | bottom | 118.8 | 119.0 | 118.9 | 119.2 | |
| thickness | 2.7 | 2.6 | 2.5 | 2.3 | ||
| top | 18.7 | 18.8 | 18.9 | 18.9 | 2.6 | |
| MgSO | bottom | 118.8 | 118.5 | 118.4 | 118.7 | |
| thickness | 2.5 | 2.7 | 2.7 | 2.4 | ||
| top | 18.7 | 18.7 | 18.5 | 18.7 | 1.7 | |
| MgSO | bottom | 119.5 | 119.4 | 119.9 | 119.8 | |
| thickness | 1.8 | 1.9 | 1.6 | 1.5 | ||
| top | 18.4 | 18.4 | 18.6 | 18.3 | 1.2 | |
| NaSO | bottom | 120.2 | 120.5 | 120.3 | 120.4 | |
| thickness | 1.4 | 1.1 | 1.1 | 1.3 | ||
| top | 17.9 | 18.0 | 18.3 | 17.9 | 1.4 | |
| NaSO | bottom | 120.5 | 120.7 | 120.5 | 120.5 | |
| thickness | 1.6 | 1.3 | 1.2 | 1.6 | ||
| top | 17.8 | 17.9 | 17.6 | 18.2 | 1.9 | |
| NaSO | bottom | 120.1 | 120.4 | 120.3 | 120.0 | |
| thickness | 2.1 | 1.7 | 2.1 | 1.8 | ||
References
- Nkonya, E.; Anderson, W. Exploiting provisions of land economic productivity without degrading its natural capital. J. Arid. Environ. 2015, 112, 33–43. [Google Scholar] [CrossRef]
- Pitman, M.G.; Läuchli, A. Global Impact of Salinity and Agricultural Ecosystems. In Salinity: Environment-Plants-Molecules; Läuchli, A., Lüttge, U., Eds.; Springer: Dordrecht, The Netherlands, 2002; pp. 3–20. [Google Scholar] [CrossRef]
- Vereecken, H.; Burauel, P.; Groeneweg, J.; Klumpp, E.; Mittelstaedt, W.; Narres, H.D.; Putz, T.; van der Kruk, J.; Vanderborght, J.; Wendland, F. Research at the Agrosphere Institute: From the Process Scale to the Catchment Scale. Vadose Zone J. 2009, 8, 664–669. [Google Scholar] [CrossRef]
- Chaves, M.M.; Flexas, J.; Pinheiro, C. Photosynthesis under drought and salt stress: Regulation mechanisms from whole plant to cell. Ann. Bot. 2009, 103, 551–560. [Google Scholar] [CrossRef] [PubMed]
- Oster, J.D. Irrigation with Poor Quality Water. Agric. Water Manag. 1994, 25, 271–297. [Google Scholar] [CrossRef]
- Gupta, R.K.; Abrol, I.P.; Finkl, C.W.; Kirkham, M.B.; Arbestain, M.C.; Macías, F.; Chesworth, W.; Germida, J.J.; Loeppert, R.H.; Cook, M.G.; et al. Soil salinity and salinization. In Encyclopedia of Soil Science; Springer: Dordrecht, The Netherlands, 2008; pp. 699–704. [Google Scholar] [CrossRef]
- Jambhekar, V.A.; Helmig, R.; Schroder, N.; Shokri, N. Free-Flow-Porous-Media Coupling for Evaporation-Driven Transport and Precipitation of Salt in Soil. Transp. Porous Media 2015, 110, 251–280. [Google Scholar] [CrossRef]
- Driessen, P.M.; Schoorl, R. Mineralogy and Morphology of Salt Efflorescences on Saline Soils in the Great Konya Basin, Turkey. J. Soil Sci. 1973, 24, 436–442. [Google Scholar] [CrossRef]
- Dowuona, G.; Mermut, A.; Krouse, H. Isotopic composition of salt crusts in Saskatchewan, Canada. Chem. Geol. Isot. Geosci. Sect. 1992, 94, 205–213. [Google Scholar] [CrossRef]
- Smoot, J.P.; Castens-Seidell, B.; Renaut, R.W.; Last, W.M. Sedimentary Features Produced by Efflorescent Salt Crusts, Saline Valley and Death Valley, California. In Sedimentology and Geochemistry of Modern and Ancient Saline Lakes Models; Society for Sedimentary Geology: Tulsa, OK, USA, 1994; Volume 50. [Google Scholar] [CrossRef]
- Liao, R.K.; Yu, H.L.; Lin, H.; Yang, P.L. A quantitative study on three-dimensional pore parameters and physical properties of sodic soils restored by FGD gypsum and leaching water. J. Environ. Manag. 2019, 248, 10. [Google Scholar] [CrossRef]
- Nachshon, U.; Weisbrod, N.; Dragila, M.I.; Grader, A. Combined evaporation and salt precipitation in homogeneous and heterogeneous porous media. Water Resour. Res. 2011, 47, 16. [Google Scholar] [CrossRef]
- Nachshon, U.; Shahraeeni, E.; Or, D.; Dragila, M.; Weisbrod, N. Infrared thermography of evaporative fluxes and dynamics of salt deposition on heterogeneous porous surfaces. Water Resour. Res. 2011, 47, 16. [Google Scholar] [CrossRef]
- Eloukabi, H.; Sghaier, N.; Ben Nasrallah, S.; Prat, M. Experimental study of the effect of sodium chloride on drying of porous media: The crusty-patchy efflorescence transition. Int. J. Heat Mass Transf. 2013, 56, 80–93. [Google Scholar] [CrossRef]
- Flatt, R.J.; Scherer, G.W. Hydration and crystallization pressure of sodium sulfate: A critical review. In Materials Issues in Art and Archaeology Vi; Vandiver, P.B., Goodway, M., Mass, J.L., Eds.; Materials Research Society: Warrendale, PA, USA, 2002; Volume 712, pp. 29–34. [Google Scholar]
- Tsui, N.; Flatt, R.J.; Scherer, G.W. Crystallization damage by sodium sulfate. J. Cult. Herit. 2003, 4, 109–115. [Google Scholar] [CrossRef]
- Espinosa-Marzal, R.M.; Scherer, G.W. Impact of in-pore salt crystallization on transport properties. Environ. Earth Sci. 2013, 69, 2657–2669. [Google Scholar] [CrossRef]
- Scherer, G.W. Theory of Drying. J. Am. Ceram. Soc. 1990, 73, 3–14. [Google Scholar] [CrossRef]
- Or, D.; Lehmann, P.; Shahraeeni, E.; Shokri, N. Advances in Soil Evaporation Physics-A Review. Vadose Zone J. 2013, 12, 16. [Google Scholar] [CrossRef]
- Lehmann, P.; Assouline, S.; Or, D. Characteristic lengths affecting evaporative drying of porous media. Phys. Rev. E 2008, 77, 16. [Google Scholar] [CrossRef] [PubMed]
- Jambhekar, V.A.; Mejri, E.; Schroder, N.; Helmig, R.; Shokri, N. Kinetic Approach to Model Reactive Transport and Mixed Salt Precipitation in a Coupled Free-Flow-Porous-Media System. Transp. Porous Media 2016, 114, 341–369. [Google Scholar] [CrossRef]
- Rad, M.N.; Shokri, N. Nonlinear effects of salt concentrations on evaporation from porous media. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Rad, M.N.; Shokri, N.; Keshmiri, A.; Withers, P.J. Effects of Grain and Pore Size on Salt Precipitation During Evaporation from Porous Media. Transp. Porous Media 2015, 110, 281–294. [Google Scholar] [CrossRef]
- Shokri-Kuehni, S.M.S.; Vetter, T.; Webb, C.; Shokri, N. New insights into saline water evaporation from porous media: Complex interaction between evaporation rates, precipitation, and surface temperature. Geophys. Res. Lett. 2017, 44, 5504–5510. [Google Scholar] [CrossRef]
- Bergstad, M.; Or, D.; Withers, P.J.; Shokri, N. The influence of NaCl concentration on salt precipitation in heterogeneous porous media. Water Resour. Res. 2017, 53, 1702–1712. [Google Scholar] [CrossRef]
- Shokri-Kuehni, S.M.S.; Bergstad, M.; Sahimi, M.; Webb, C.; Shokri, N. Iodine k-edge dual energy imaging reveals the influence of particle size distribution on solute transport in drying porous media. Sci. Rep. 2018, 8, 9. [Google Scholar] [CrossRef] [PubMed]
- Nachshon, U.; Weisbrod, N.; Katzir, R.; Nasser, A. NaCl Crust Architecture and Its Impact on Evaporation: Three-Dimensional Insights. Geophys. Res. Lett. 2018, 45, 6100–6108. [Google Scholar] [CrossRef]
- Weisbrod, N.; Nachshon, U.; Dragila, M.; Grader, A. Micro-CT Analysis to Explore Salt Precipitation Impact on Porous Media Permeability. In Transport and Reactivity of Solutions in Confined Hydrosystems; NATO Science for Peace and Security Series C: Environmental Security; Springer: Dordrecht, The Netherlands, 2014; pp. 231–241. [Google Scholar]
- Nachshon, U.; Weisbrod, N. Beyond the Salt Crust: On Combined Evaporation and Subflorescent Salt Precipitation in Porous Media. Transp. Porous Media 2015, 110, 295–310. [Google Scholar] [CrossRef]
- Jelinkova, V.; Snehota, M.; Pohlmeier, A.; van Dusschoten, D.; Cislerova, M. Effects of entrapped residual air bubbles on tracer transport in heterogeneous soil: Magnetic resonance imaging study. Org. Geochem. 2011, 42, 991–998. [Google Scholar] [CrossRef]
- ROBU Glasfilter-Geräte GmbH, Hattert, Germany. VitraPOR® Sinterfilter. 2019. Available online: www.robuglas.com (accessed on 21 March 2020).
- Westphal, G.; Kristen, G.; Wegener, W.; Ambatiello, P.; Geyer, H.; Epron, B.; Bonal, C.; Steinhauser, G.; Götzfried, F. Sodium Chloride. In Ullmann’s Encyclopedia of Industrial Chemistry; American Cancer Society: Atlanta, GA, USA, 2010; pp. 320–322. [Google Scholar] [CrossRef]
- Clarke, E.C.W. Evaluaiton of the thermodynamic functions for aqueous sodium-chloride from equilibrium and calometric measurements below 154-degrees-C. J. Phys. Chem. Ref. Data 1985, 14, 489–610. [Google Scholar] [CrossRef]
- Merck KGaA. Material Data Safety Sheet—Sodium Chloride, 7.16th ed.; Merck KGaA: Darmstadt, Germany, 2018. [Google Scholar]
- Müller, E. Magnesium—Teil B, Die Verbindungen des Magnesium. In Gmelins Handbuch der Anorganischen Chemie; Pietsch, E., Ed.; Verlag Chemie: Berlin, Germany, 1939; pp. 243–249. [Google Scholar]
- Guendouzi, M.E.; Mounir, A.; Dinane, A. Water activity, osmotic and activity coefficients of aqueous solutions of Li2SO4, Na2SO4, K2SO4, (NH4)2SO4, MgSO4, MnSO4, NiSO4, CuSO4, and ZnSO4 at T = 298.15 K. J. Chem. Thermodyn. 2003, 35, 209–220. [Google Scholar] [CrossRef]
- Th. Geyer GmbH & Co. KG, Renningen, Germany. Technical Data Sheet—Magnesium Sulfate Heptahydrat. 2020. Available online: www.thgeyer.de (accessed on 15 February 2020).
- Plessen, H.V. Sodium Sulfates. In Ullmann’s Encyclopedia of Industrial Chemistry; American Cancer Society: Atlanta, GA, USA, 2000; pp. 383–385. [Google Scholar] [CrossRef]
- Merck KGaA. Material Data Safety Sheet—Sodium Sulfate, 8.2 ed.; Merck KGaA: Darmstadt, Germany, 2019. [Google Scholar]
- Weingärtner, H.; Teermann, I.; Borchers, U.; Balsaa, P.; Lutze, H.V.; Schmidt, T.C.; Franck, E.U.; Wiegand, G.; Dahmen, N.; Schwedt, G.; et al. Water, 1. Properties, Analysis, and Hydrological Cycle. In Ullmann’s Encyclopedia of Industrial Chemistry; American Cancer Society: Atlanta, GA, USA, 2016; pp. 1–40. [Google Scholar] [CrossRef]
- Quartzwerke GmbH. Stoffdaten F32–F36; Quartzwerke: Frechen, Germany, 2009. [Google Scholar]
- Glover, P.W.J.; Walker, E. Grain-size to effective pore-size transformation derived from electrokinetic theory. Geophysics 2009, 74, E17–E29. [Google Scholar] [CrossRef]
- Licsandru, G.; Noiriel, C.; Duru, P.; Geoffroy, S.; Abou Chakra, A.; Prat, M. Dissolution-precipitation-driven upward migration of a salt crust. Phys. Rev. E 2019, 100, 9. [Google Scholar] [CrossRef]
- Balboni, E.; Espinosa-Marzal, R.M.; Doehne, E.; Scherer, G.W. Can drying and re-wetting of magnesium sulfate salts lead to damage of stone? Environ. Earth Sci. 2011, 63, 1463–1473. [Google Scholar] [CrossRef]
- Ball, B.; Schjønning, P. Air Permeability. In Methods in Soil Analysis: Part 4 Physical Methods; Dane, J.H., Topp, C.G., Eds.; SSSA Book Series; Soil Science Society of America: Madison, WI, USA, 2020. [Google Scholar] [CrossRef]
- Green, D.W.; Perry, R.H. Perry’s Chemical Engineers’ Handbook, 8th ed.; The McGraw-Hill Companies: New York, NY, USA, 2008. [Google Scholar]
- An, N.; Tang, C.S.; Xu, S.K.; Gong, X.P.; Shi, B.; Inyang, H.I. Effects of soil characteristics on moisture evaporation. Eng. Geol. 2018, 239, 126–135. [Google Scholar] [CrossRef]
- Nield, J.M.; Neuman, C.M.; O’Brien, P.; Bryant, R.G.; Wiggs, G.F.S. Evaporative sodium salt crust development and its wind tunnel derived transport dynamics under variable climatic conditions. Aeolian Res. 2016, 23, 51–62. [Google Scholar] [CrossRef]
- Rust, A.C.; Cashman, K.V. Permeability of vesicular silicic magma: Inertial and hysteresis effects. Earth Planet. Sci. Lett. 2004, 228, 93–107. [Google Scholar] [CrossRef]
- Takeuchi, S.; Nakashima, S.; Tomiya, A. Permeability measurements of natural and experimental volcanic materials with a simple permeameter: Toward an understanding of magmatic degassing processes. J. Volcanol. Geotherm. Res. 2008, 177, 329–339. [Google Scholar] [CrossRef]
- Chilton, T.H.; Colburn, A.P. Pressure drop in packed tubes. Ind. Eng. Chem. 1931, 23, 913–919. [Google Scholar] [CrossRef]
- Zeng, Z.W.; Grigg, R. A criterion for non-Darcy flow in porous media. Transp. Porous Media 2006, 63, 57–69. [Google Scholar] [CrossRef]
- Schlichting, H.; Gersten, K. Boundary-Layer Theory, 9th ed.; Springer: Berlin/Heidelberg, Germany, 2017; Chapter 1; p. 12. [Google Scholar] [CrossRef]


| Substance | Physical Properties | Solutions Prepared for Evaporation Experiments | Reference | |||
|---|---|---|---|---|---|---|
| Molar mass | Maximum | Initial | Initial density | Initial vapor | ||
| solubility | concentration | pressure | ||||
| [g/mol] | [mol/L] | [mol/L] | [g/cm] | [kPa] at 25 C | ||
| NaCl | 58.44 | 6.13 | 2.04 | 1.079 | 2.935 | [32,33,34] |
| MgSO7HO | 246.48 | 2.88 | 0.96 | 1.107 | 3.111 | [35,36,37] |
| NaSO | 142.04 | 1.41 | 0.47 | 1.058 | 3.111 | [36,38,39] |
| HO | 18.01 | - | - | 0.998 | 3.169 | [40] |
| Particle Size | Mass Fraction [%] |
|---|---|
| >0.335 | 5 |
| 0.250–0.355 | 28 |
| 0.180–0.250 | 49 |
| 0.125–0.180 | 16 |
| 0.090–0.125 | 2 |
| <0.090 | - |
| Solution | Initial Evaporation Rate | Initial Evaporation Rate Mormalized | Vapor Pressure Difference | Vapor Pressure Difference Normalized |
|---|---|---|---|---|
| [mm/day] | [-] | [kPa] | [-] | |
| NaCl | 12.1 | 0.66 | 1.985 | 0.89 |
| MgSO7 | 14.1 | 0.77 | 2.161 | 0.97 |
| NaSO | 14.4 | 0.79 | 2.161 | 0.97 |
| HO | 18.3 | 1 | 2.217 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piotrowski, J.; Huisman, J.A.; Nachshon, U.; Pohlmeier, A.; Vereecken, H. Gas Permeability of Salt Crusts Formed by Evaporation from Porous Media. Geosciences 2020, 10, 423. https://doi.org/10.3390/geosciences10110423
Piotrowski J, Huisman JA, Nachshon U, Pohlmeier A, Vereecken H. Gas Permeability of Salt Crusts Formed by Evaporation from Porous Media. Geosciences. 2020; 10(11):423. https://doi.org/10.3390/geosciences10110423
Chicago/Turabian StylePiotrowski, Joseph, Johan Alexander Huisman, Uri Nachshon, Andreas Pohlmeier, and Harry Vereecken. 2020. "Gas Permeability of Salt Crusts Formed by Evaporation from Porous Media" Geosciences 10, no. 11: 423. https://doi.org/10.3390/geosciences10110423
APA StylePiotrowski, J., Huisman, J. A., Nachshon, U., Pohlmeier, A., & Vereecken, H. (2020). Gas Permeability of Salt Crusts Formed by Evaporation from Porous Media. Geosciences, 10(11), 423. https://doi.org/10.3390/geosciences10110423







