A Generic Shear Wave Velocity Profiling Model for Use in Ground Motion Simulation
Abstract
:1. Introduction
2. Shear-Wave Velocity Modeling
2.1. Compressional Wave Velocity (VP) Profiling Model
2.2. Modeling of VS/VP
0.577(Z/2)0.00652 0.2 < Z ≤ 2.0,
0.577 Z > 2.0.
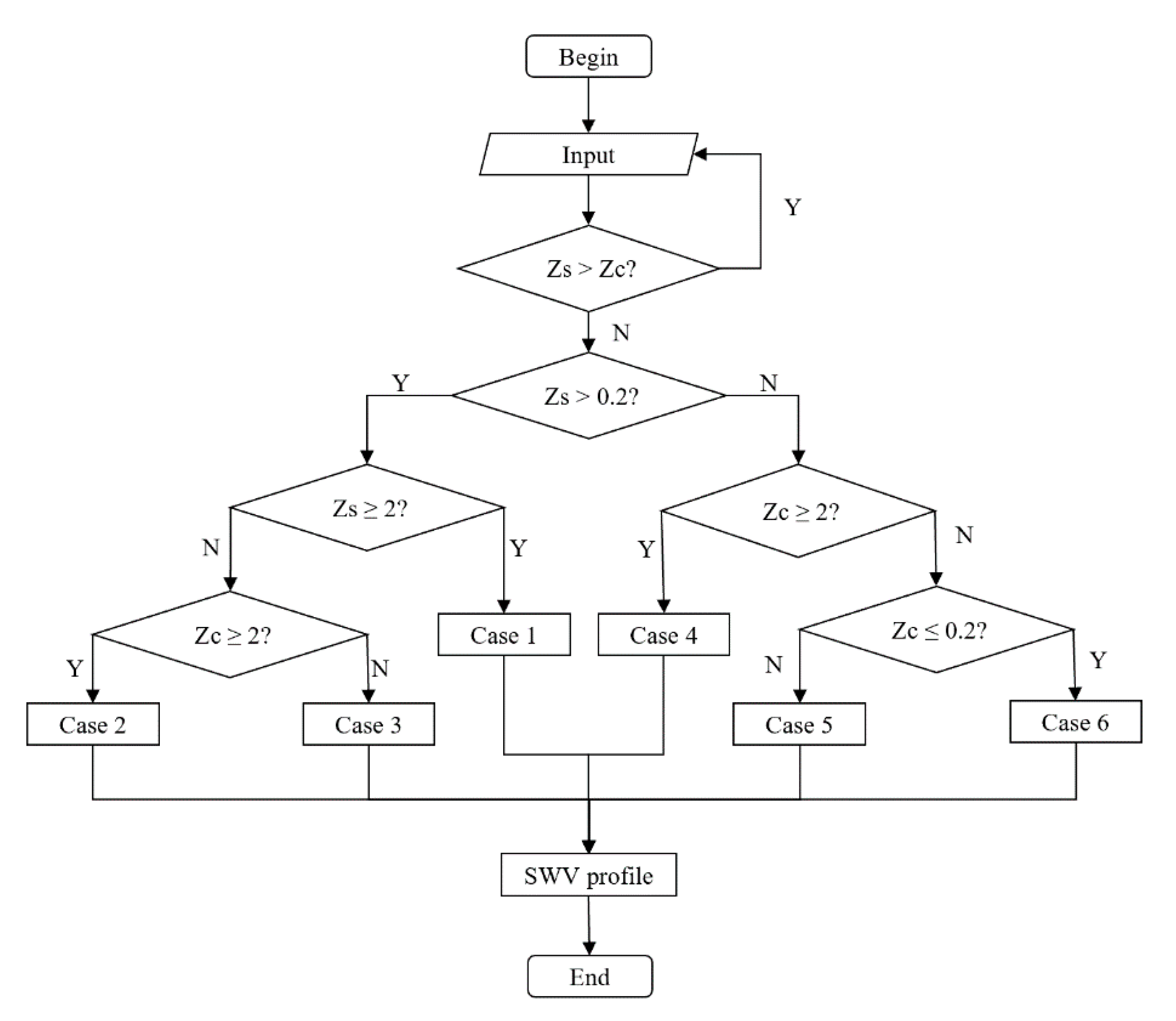
2.3. Shear-Wave Velocity Profile Modeling
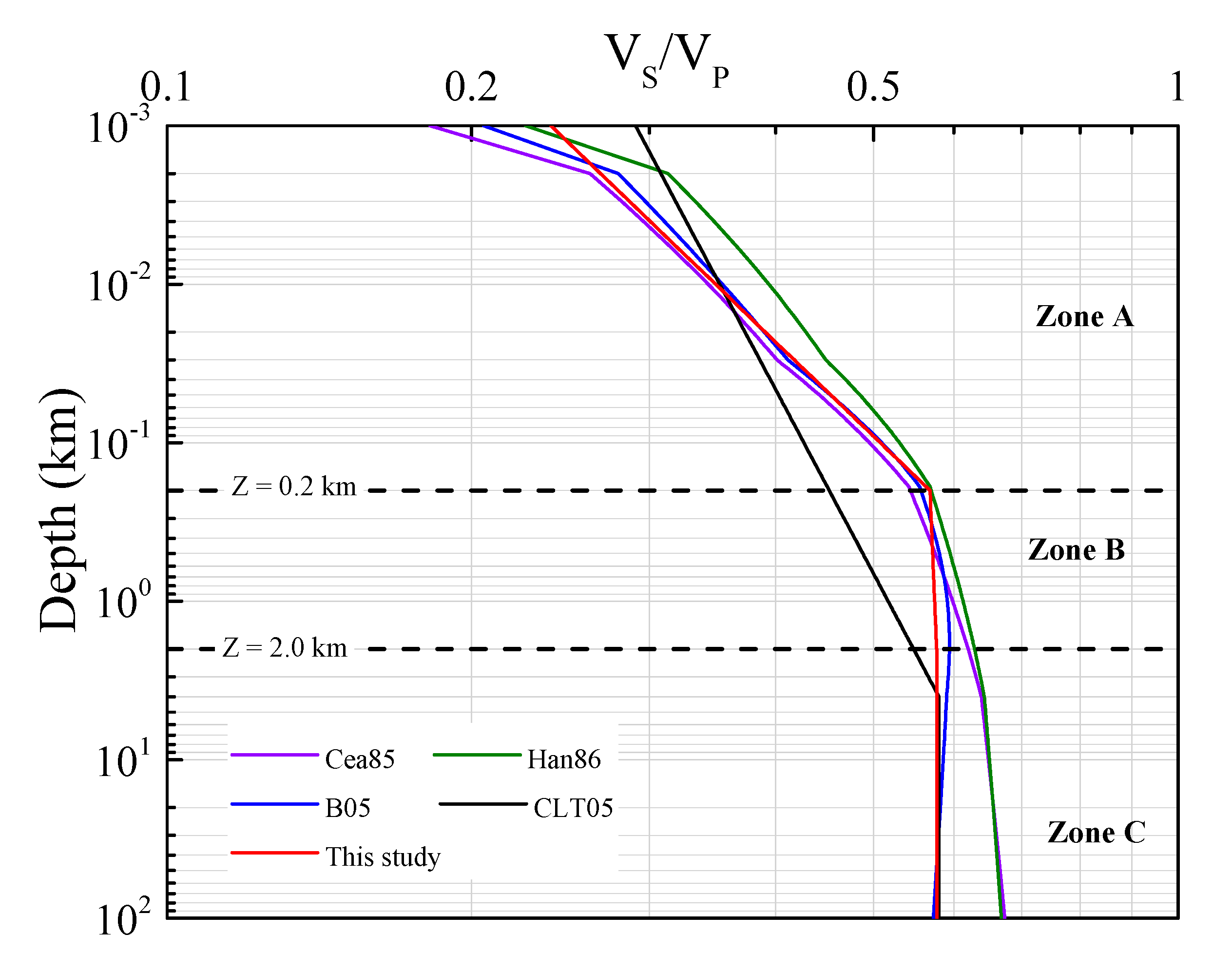
3. Validation of the Proposed VS Profiling Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Data Availability
References
- Boore, D.M. Simulation of Ground Motion Using the Stochastic Method. Pure Appl. Geophys. 2003, 160, 635–676. [Google Scholar] [CrossRef] [Green Version]
- Boore, D.M.; Joyner, W.B. Site Amplifications for Generic Rock Sites. Bull. Seismol. Soc. Am. 1997, 8787, 327–341. [Google Scholar]
- Chandler, A.M.; Lam, N.T.K.; Tsang, H.H. Shear wave velocity modelling in crustal rock for seismic hazard analysis. Soil Dyn. Earthq. Eng. 2005, 25, 167–185. [Google Scholar] [CrossRef]
- Lam, N.T.K.; Wilson, J.; Hutchinson, G. Generation of Synthetic Earthquake Accelerograms Using Seismological Modelling: A Review. J. Earthq. Eng. 2000, 4, 321–354. [Google Scholar] [CrossRef]
- Atkinson, G.M.; Boore, D.M. Earthquake Ground-Motion Prediction Equations for Eastern North America. Bull. Seismol. Soc. Am. 2006, 96, 2181–2205. [Google Scholar] [CrossRef]
- Lam, N.T.K.; Wilson, J.L.; Chandler, A.M.; Hutchinson, G.L. Response spectral relationships for rock sites derived from the component attenuation model. Earthq. Eng. Struct. Dyn. 2000, 29, 1457–1489. [Google Scholar] [CrossRef]
- Abrahamson, N.A.; Kuehn, N.M.; Walling, M.; Landwehr, M. Probabilistic Seismic Hazard Analysis in California Using Nonergodic Ground-Motion Models. Bull. Seismol. Soc. Am. 2019, 109, 1235–1249. [Google Scholar] [CrossRef]
- Ambraseys, N.N.; Douglas, J.; Sarma, S.K.; Smit, P.M. Equations for the estimation of strong ground motions from shallow crustal earthquakes using data from Europe and the Middle East: Horizontal peak ground acceleration and spectral acceleration. Bull. Earthq. Eng. 2005, 3, 1–53. [Google Scholar] [CrossRef] [Green Version]
- Atkinson, G.M.; Boore, D.M. Ground-Motion Relations for Eastern North America. Bull. Seismol. Soc. Am. 1995, 85, 17–30. [Google Scholar]
- Atkinson, G.M. Empirical Attenuation of Ground Motion Spectral Amplitudes in Southeastern Canada and the Northeastern United States. Bull. Seismol. Soc. Am. 2004, 94, 1079–1095. [Google Scholar] [CrossRef]
- Atkinson, G.M. Ground-Motion Prediction Equations for Eastern North America from a Referenced Empirical Approach: Implications for Epistemic Uncertainty. Bull. Seismol. Soc. Am. 2008, 98, 1304–1318. [Google Scholar] [CrossRef]
- Yenier, E.; Atkinson, G.M. Regionally Adjustable Generic Ground-Motion Prediction Equation Based on Equivalent Point-Source Simulations: Application to Central and Eastern North America. Bull. Seismol. Soc. Am. 2015, 105, 1989–2009. [Google Scholar] [CrossRef]
- Allen, T.I. Stochastic ground-motion prediction equations for southeastern australian earthquakes using updated source and attenuation parameters. Geosci. Aust. Rec. 2012, 69, 55. [Google Scholar]
- Somerville, P.; Graves, R.; Collins, N.; Song, S.G.; Ni, S.; Cummins, P. Source and ground motion models for australian earthquakes. In Proceedings of the Annual Conference of the Australian Earthquake Engineering Society (AEES), Newcastle, Australia, 11–13 December 2009. [Google Scholar]
- BSSC. 2000 Edition NEHRP Recommmded Provisions for Seismic Regulations for New Buildings and Other Structures. FEMA 2001, 368–369. [Google Scholar]
- Boore, D.M. Short Note: Determining Generic Velocity and Density Models for Crustal Amplification Calculations, with an Update of the Boore and Joyner (1997) Generic Amplification for Vs(Z) = 760 m/s. Bull. Seismol. Soc. Am. 2016, 106, 316–320. [Google Scholar] [CrossRef]
- Castaños, H.; Lomnitz, C. PSHA: Is it science? Eng. Geol. 2002, 66, 315–317. [Google Scholar] [CrossRef]
- Lam, N.T.K.; Tsang, H.H.; Lumantarna, E.; Wilson, J.L. Minimum loading requirements for areas of low seismicity. Earthq. Struct. 2016, 11, 539–561. [Google Scholar] [CrossRef]
- Tsang, H.H.; Sheikh, M.N.; Lam, N.T.K.; Chandler, A.M.; Lo, S.H. Regional differences in attenuation modelling for Eastern China. J. Asian Earth Sci. 2010, 39, 441–459. [Google Scholar] [CrossRef] [Green Version]
- Brocher, T.M. Empirical relations between elastic wavespeeds and density in the Earth’s crust. Bull. Seismol. Soc. Am. 2005, 95, 2081–2092. [Google Scholar] [CrossRef]
- Brocher, T.M.; Brabb, E.E.; Catchings, R.D.; Fuis, G.S.; Fumal, T.E.; Jachens, R.A. A crustalscale 3-D seismic velocity model for the San Francisco Bay area, California. Eos Trans. AGU 1997, 78, F435–F436. [Google Scholar]
- Fletcher, J.B.; Boatwright, J.; Lindh, A.G. Wave propagation and site response in the Santa Clara Valley. Bull. Seismol. Soc. Am. 2003, 93, 480–500. [Google Scholar] [CrossRef]
- Christensen, N.I. Seismic Velocity Structure and Composition of the Continental Crust: A Global View. J. Geophys. Res. 1995, 100, 9761–9788. [Google Scholar] [CrossRef]
- Downs, H. The Nature of the Lower Continental Crust of Europe: Petrologic and Geochemical Evidence from Xenoliths. Phys. Earth. Planet. Inter. 1993, 79, 195–218. [Google Scholar] [CrossRef]
- Faust, L.Y. Seismic Velocity as a Function of Depth and Geologic Time. Geophysics 1951, 16, 192–206. [Google Scholar] [CrossRef]
- Magistrale, H.; McLaughlin, K.; Day, S. A Geological-based 3D Velocity Model of the Los Angeles Basin Sediments. Bull. Seismol. Soc. Am. 1996, 86, 1161–1166. [Google Scholar]
- Fliedner, M.M.; Klemperer, S.; Christensen, N.I. Three-dimensional Seismic Model of the Sierra Nevada arc California and Its Implications for Crustal and Upper Mantle Composition. J. Geophys. Res. 2000, 105, 10899–10921. [Google Scholar] [CrossRef]
- Lee, R.L.; Bradley, B.A.; Ghisetti, F.C.; Pettinga, J.R.; Hughes, M.W.; Thompson, E.M. A geology-based 3D seismic velocity model of canterbury, New Zealand. In Proceedings of the 2015 New Zealand Society for Earthquake Engineering Annual Conference (NZSEE), Rotorua, New Zealand, 10–12 April 2015. [Google Scholar]
- Zhao, B.; Zhang, Z.; Bai, Z.; Badal, J.; Zhang, Z. Shear Velocity and Vp/Vs Ratio Structure of the Crust beneath the Southern Margin of South China Continent. J. Asian Earth Sci. 2013, 62, 167–179. [Google Scholar] [CrossRef]
- Kwong, J.S.M. Pilot Study on the Use of Suspension PS Logging; Technical Note TN 2/98; GEO. Hong Kong Government: Hong Kong, China, 1998.
- Tam, K.W. Anisotropy in Seismic Wave Velocity in Jointed Rocks in Hong Kong. Master’s Thesis, The University of Hong Kong, Hong Kong, China, 2002. [Google Scholar]
- Malin, P.E.; Gillespie, M.H.; Leary, P.C.; Henyey, T.L. Crustal structure near Palmdale, California, from borehole-determined ray parameters. Bull. Seismol. Soc. Am. 1981, 71, 1783–1804. [Google Scholar]
- Stewart, R.R.; Turpening, R.M.; Toksoz, M.N. Study of a subsurface fracture zone by vertical seismic profiling. Geophys. Res Lett. 1981, 8, 1132–1135. [Google Scholar] [CrossRef]
- Archuleta, R.J. Analysis of near source static and dynamic measurements from the 1979 Imperial Valley earthquake. Bull. Seismol. Soc. Am. 1982, 72, 1927–1956. [Google Scholar]
- Brocher, T.M.; Fuis, G.S.; Lutter, W.J.; Christensen, N.I.; Ratchkovski, N.A. Seismic Velocity Models for the Denali Fault Zone along the Richardson Highway, Alaska. Bull. Seismol. Soc. Am. 2004, 94, 85–106. [Google Scholar] [CrossRef] [Green Version]
- Boore, D.M. P- and S-Velocities from Surface-to-Borehole Logging (Open-File Report). (30–191). 2003. Available online: http://www.daveboore.com/data_online.html (accessed on 5 October 2019).
- Baise, L.G.; Dreger, D.S.; Glaser, S.D. The Effect of Shallow San Francisco Bay Sediments on Waveforms Recorded during the Mw 4.6 Bolinas, California. Bull. Seismol. Soc. Am. 2003, 93, 465–479. [Google Scholar] [CrossRef]
- Wang, Z.; Butler III, D.T.; Woolery, E.W.; Wang, L. Seismic Hazard Assessment for the Tianshui Urban Area, Gansu Province, China. Int. J. Geophys. 2012, 2012, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Ramirez-Guzman, L.; Zeng, Y.; Mooney, W.D. Rupture History of the 2008 Mw 7.9 Wenchuan, China, Earthquake: Evaluation of Separate and Joint Inversions of Geodetic, Teleseismic, and Strong-Motion Data. Bull. Seism. Soc. Am. 2013, 103, 353–370. [Google Scholar]
- Lin, G.; Amelung, F.; Shearer, P.M.; Okubo, P.G. Location and size of the shallow magma reservoir beneath Kilauea caldera, constraints from near-source Vp/Vs ratios. Geophys. Res. Lett. 2015, 42, 8349–8357. [Google Scholar] [CrossRef] [Green Version]
- Bhowmick, S. Role of Vp/Vs and Poisson’s Ratio in the Assessment of Foundation(s) for Important Civil Structure(s). Geotech. Geol. Eng. 2017, 35, 527–534. [Google Scholar] [CrossRef]
- Castagna, J.P.; Batzle, M.L.; Eastwood, R.L. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks. Geophysics 1985, 50, 571–581. [Google Scholar] [CrossRef]
- Han, D.H. Effects of Porosity and Clay Content on Acoustic Properties of Sandstones and Unconsolidated Sediments. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1986. [Google Scholar]
- Roberts, J.; Asten, M.W.; Tsang, H.H.; Venkatesan, S.; Lam, N.T.K. Shear wave velocity profiling in melbourne silurian mudestone using the SPAC method. In Proceedings of the a Conference of the Australian Earthquake Engineering Society (AEES), Mount Grambier, Australia, 5–7 November 2004. [Google Scholar]
- Hoffman, D.; Anderson, N.; Rogers, J.D. St. Louis Metro Area Shear-Wave Velocity Testing; External Grant Award Number: 06HQGR0026; U.S. Geological Survey: Reston, VA, USA, 2008; 24p.
- Chandler, A.M.; Lam, N.T.K.; Tsang, H.H. Near-surface attenuation modelling based on rock shear-wave velocity profile. Soil Dyn. Earthq. Eng. 2006, 26, 1004–1014. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, T.; Suzuki, H. A Study on Technical Methodologies Underpinning Site Selection Process for Geological Disposal, A Study on Site Screening System for Geological Disposal; Nagra Project Report, Microtremor Measurements; Radioactive Waste Management Center (RWMC): Tokyo, Japan, 2001; pp. 1–28. [Google Scholar]
- Campus, P.; Fäh, D. Seismic Monitoring of Explosions: A Method to Extract Information on the Isotropic Component of the Seismic Source. J. Seismol. 1997, 1, 205–218. [Google Scholar] [CrossRef]
- Poggi, V.; Edwards, B.; Fäh, D. Derivation of a Reference Shear-Wave Velocity Model from Empirical Site Amplification. Bull. Seismol. Soc. Am. 2011, 101, 258–274. [Google Scholar] [CrossRef]
- Laske, G.; Ma, Z.; Masters, G.; Pasyanos, M. CRUST 1.0: A New Global Crustal Model at 1 × 1 Degrees. 2013. Available online: https://igppweb.ucsd.edu/~gabi/crust1.html (accessed on 9 December 2019).
- Chen, S. Global Comparisons of Earthquake Source Spectra. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2000. [Google Scholar]
- Lermo, J.; Chavez-Garcia, J. Site Effect Evaluation Using Spectral Ratios with Only One Station. Bull. Seismol. Soc. Am. 1993, 83, 1574–1594. [Google Scholar]
- Langston, C.A. Structure under Mount Rainier, Washington, inferred from teleseismic body waves. J. Geophys. Res. 1979, 84, 4749–4762. [Google Scholar] [CrossRef] [Green Version]
- Atkinson, G.M.; Cassidy, J.F. Integrated Use of Seismograph and Strong-Motion Data to Determine Soil Amplification: Response of the Fraser River Delta to the Duvall and Georgia Strait Earthquakes. Bull. Seismol. Soc. Am. 2000, 90, 1028–1040. [Google Scholar] [CrossRef]
- Abercrombie, R.E. Near-surface Attenuation and Site Effects from Comparison of Surface and Deep Borehole Recordings. Bull. Seismol. Soc. Am. 1997, 87, 731–744. [Google Scholar]
- Joyner, W.B.; Warrick, R.E.; Fumal, T.E. The Effect of Quaternary Alluvium on Strong Ground Motion in the Coyote Lake, California, Earthquake of 1979. Bull. Seismol. Soc. Am. 1981, 71, 1333–1349. [Google Scholar]
- Baker, G.S.; Schmeissner, C.; Steeples, D.W. Seismic reflections from depths of less than two meters. Geophys. Res. Lett. 1999, 26, 279–282. [Google Scholar] [CrossRef] [Green Version]
- Krinitzsky, E.L. How to obtain earthquake ground motions for engineering design. Eng. Geol. 2002, 65, 1–16. [Google Scholar] [CrossRef]
- Hunter, J.A.; Crow, H.L. Shear Wave Velocity Measurement Guidelines for Canadian Seismic Site Characterization in Soil and Rock; Open File 7078; Geological Survey of Canada: Ottawa, ON, Canada, 2012; 227p.
- Kayaball, K.; Akin, M. Seismic hazard map of Turkey using the deterministic approach. Eng. Geol. 2003, 69, 127–137. [Google Scholar] [CrossRef]
- Klüge, J.U.; Mualchin, L.; Panza, G.F. A Scenario-based procedure for seismic hazard analysis. Eng. Geol. 2006, 88, 1–22. [Google Scholar] [CrossRef]
- Krinitzsky, E.L. Deterministic versus probabilistic seismic hazard analysis for critical structures. Eng. Geol. 1995, 40, 1–7. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |

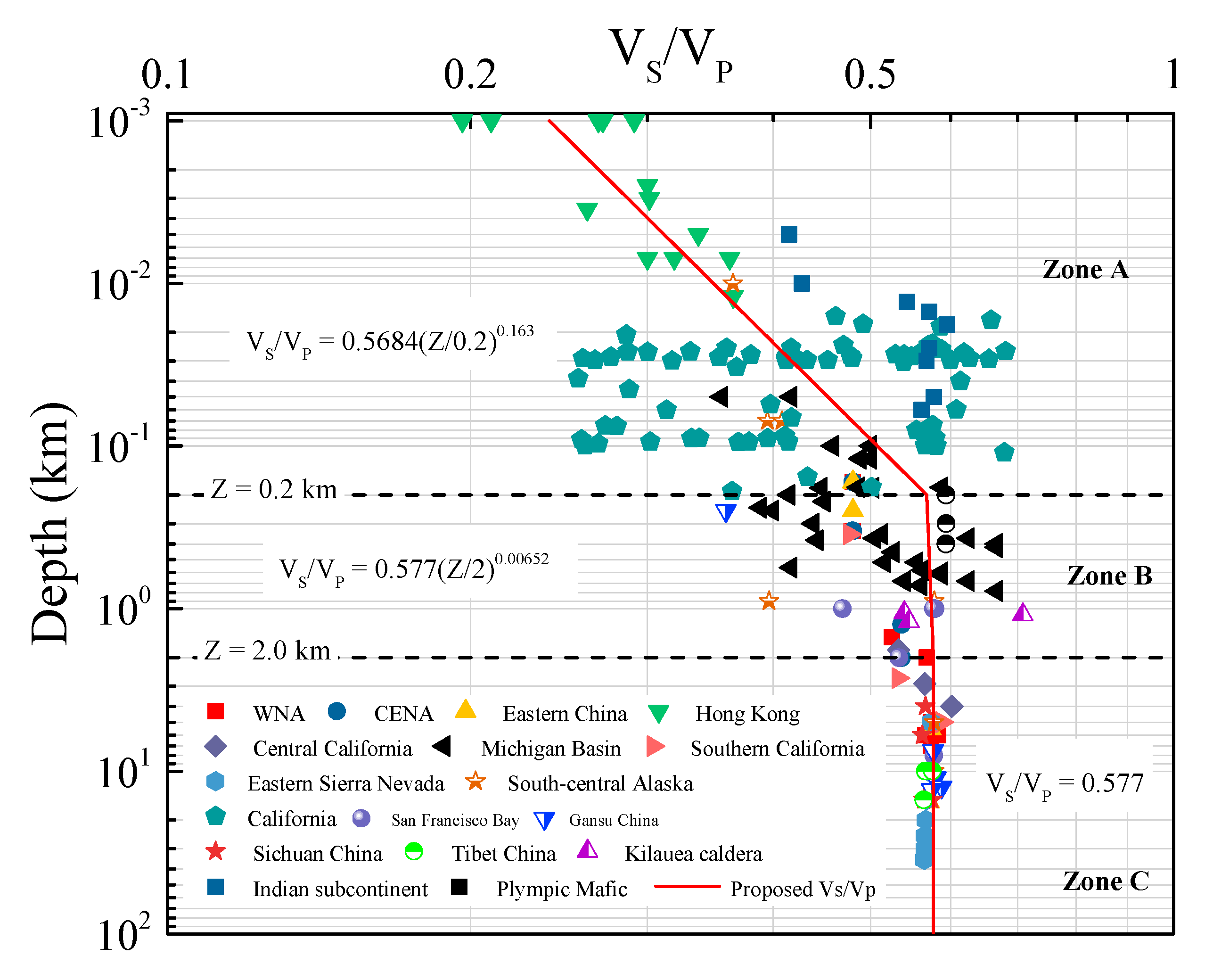

| Region | Data Acquisition Method | No. of Recordings | Citations |
|---|---|---|---|
| WNA | Seismic refraction data | 10 | [3] |
| CENA | Seismic refraction data | 4 | [3] |
| Eastern China | Seismic refraction data | 4 | [3] |
| Hong Kong | Engineering borehole data | 14 | [30,31] |
| Central California | Engineering borehole data | 3 | [32] |
| Michigan Basin | Vertical seismic profiling experiment | 39 | [33] |
| Southern California | Qualitative analysis of near-source data | 3 | [34] |
| Eastern Sierra Nevada | Seismic refraction data | 7 | [27] |
| South-central Alaska | Seismic refraction and reflection survey and laboratory experiment | 7 | [35] |
| California | Engineering borehole data | 69 | [36] |
| San Francisco Bay Area | Seismic refraction data | 5 | [37] |
| Gansu, China | Seismic refraction data | 6 | [38] |
| Sichuan, China | Seismic refraction data | 4 | [39] |
| Tibet, China | Seismic refraction data | 3 | [39] |
| Kilauea caldera | In situ estimate | 3 | [40] |
| Indian subcontinent | Seismic cross-hole tests | 9 | [41] |
| ENA | Engineering borehole data | 3 | [2] |
| Equations | Citations |
|---|---|
| VS = 0.862VP − 1.172 | [42] |
| VS = 0.794VP − 0.787 | [43] |
| VS = 0.7858 − 1.2344VP +0.7949VP2 − 0.1238VP3 + 0.0064VP4 | [20] |
| VS = 0.58 × (Z/4)1/12VP, Z ≤ 4 km VS = 0.58VP, Z > 4 km | [3] |
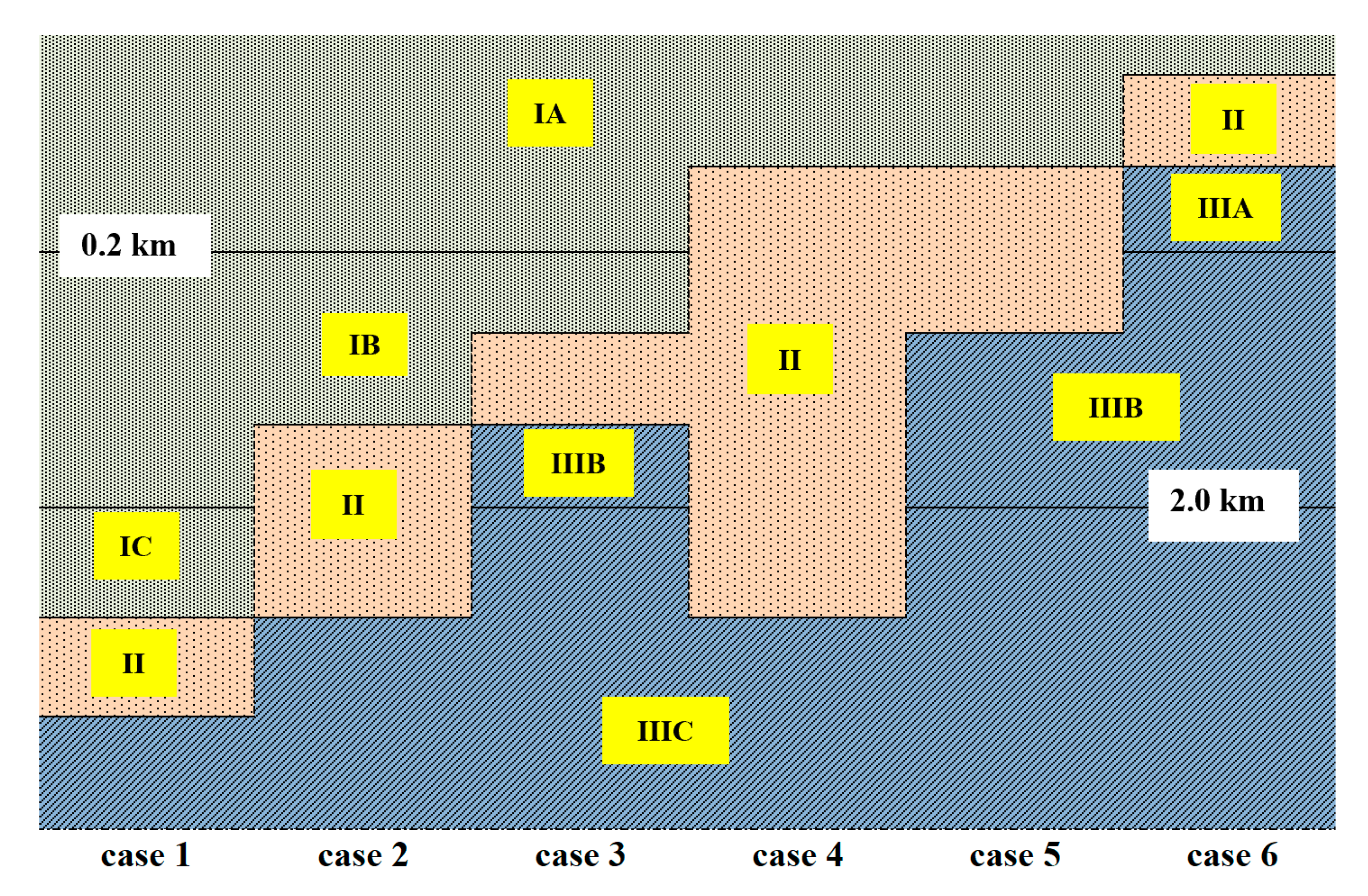
| Case | Depth Range (km) | VS (km/s) | Zone |
|---|---|---|---|
| Case 1 (ZS ≥ 2) | 0 < Z ≤ 0.2 | VS0.03 (Z/0.03)0.3297 | IA |
| 0.2 < Z ≤ 2 | VS0.2 (Z/0.2)0.1732 | IB | |
| 2 < Z ≤ ZS | VS2 (Z/2)0.1667 | IC | |
| ZS < Z ≤ ZC | VSZC (Z/ZC)n | II | |
| ZC < Z | VS8 (Z/8)0.0833 | IIIC | |
| Case 2 (0.2 < ZS < 2 ≤ ZC) | Z ≤ 0.2 | VS0.03 (Z/0.03)0.3297 | IA |
| 0.2 < Z ≤ ZS | VS0.2 (Z/0.2)0.1732 | IB | |
| ZS < Z ≤ ZC | VSZC (Z/ZC)n | II | |
| ZC < Z | VS8 (Z/8)0.0833 | IIIC | |
| Case 3 (0.2 < ZS < ZC ≤ 2) | 0 < Z ≤ 0.2 | VS0.03 (Z/0.03)0.3297 | IA |
| 0.2 < Z ≤ ZS | VS0.2 (Z/0.2)0.1732 | IB | |
| ZS < Z ≤ ZC | VSZC (Z/ZC)n | II | |
| ZC < Z ≤ 2 | VS2 (Z/2)0.0899 | IIIB | |
| 2 < Z | VS8 (Z/8)0.0833 | IIIC | |
| Case 4 (ZS < 0.2 < 2 ≤ ZC) | 0 < Z ≤ ZS | VSZI (Z/ZI)0.3297 | IA |
| ZS < Z ≤ ZC | VSZC (Z/ZC)n | II | |
| ZC < Z | VS8 (Z/8)0.0833 | IIIC | |
| Case 5 (ZS < 0.2 < ZC ≤ 2) | Z ≤ ZS | VSZI (Z/ZI)0.3297 | IA |
| ZS < Z ≤ ZC | VSZC (Z/ZC)n | II | |
| ZC < Z ≤ 2 | VS2 (Z/2)0.0899 | IIIB | |
| 2 < Z | VS8 (Z/8)0.0833 | IIIC | |
| Case 6 (ZC ≤ 0.2) | 0 < Z ≤ ZS | VSZI (Z/ZI)0.3297 | IA |
| ZS < Z ≤ ZC | VSZC (Z/ZC)n | II | |
| ZC < Z ≤ 0.2 | VS0.2 (Z/0.2)0.2463 | IIIA | |
| 0.2 < Z ≤ 2 | VS2 (Z/2)0.0899 | IIIB | |
| 2 < Z | VS8 (Z/8)0.0833 | IIIC |
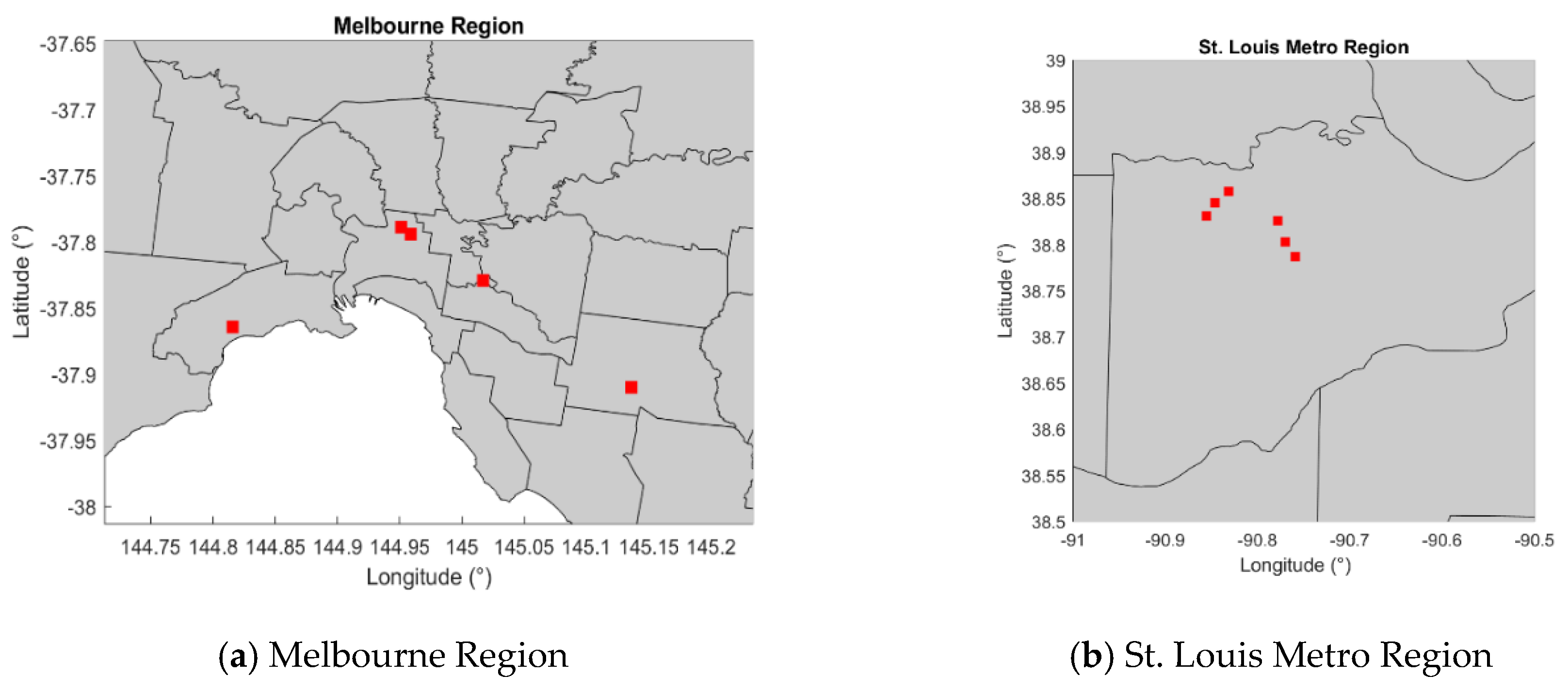
| Region | Location Name | Latitude | Longitude |
|---|---|---|---|
| Melbourne Region | Trinity College | −37.79 | 144.96 |
| Royal Park | −37.79 | 144.95 | |
| Monash Uni | −37.91 | 145.14 | |
| Burnley | −37.83 | 145.02 | |
| Altona | −37.86 | 144.82 | |
| St. Louis Metro Region | Lake St Louis Blvd. interchange | 38.80 | −90.77 |
| US 61 west service road | 38.83 | −90.86 | |
| Parr Road east side | 38.86 | −90.83 | |
| Guthrie Road east side | 38.83 | −90.78 | |
| Lake St. Louis Blvd. west side | 38.79 | −90.76 | |
| Mexico Rd | 38.85 | −90.85 | |
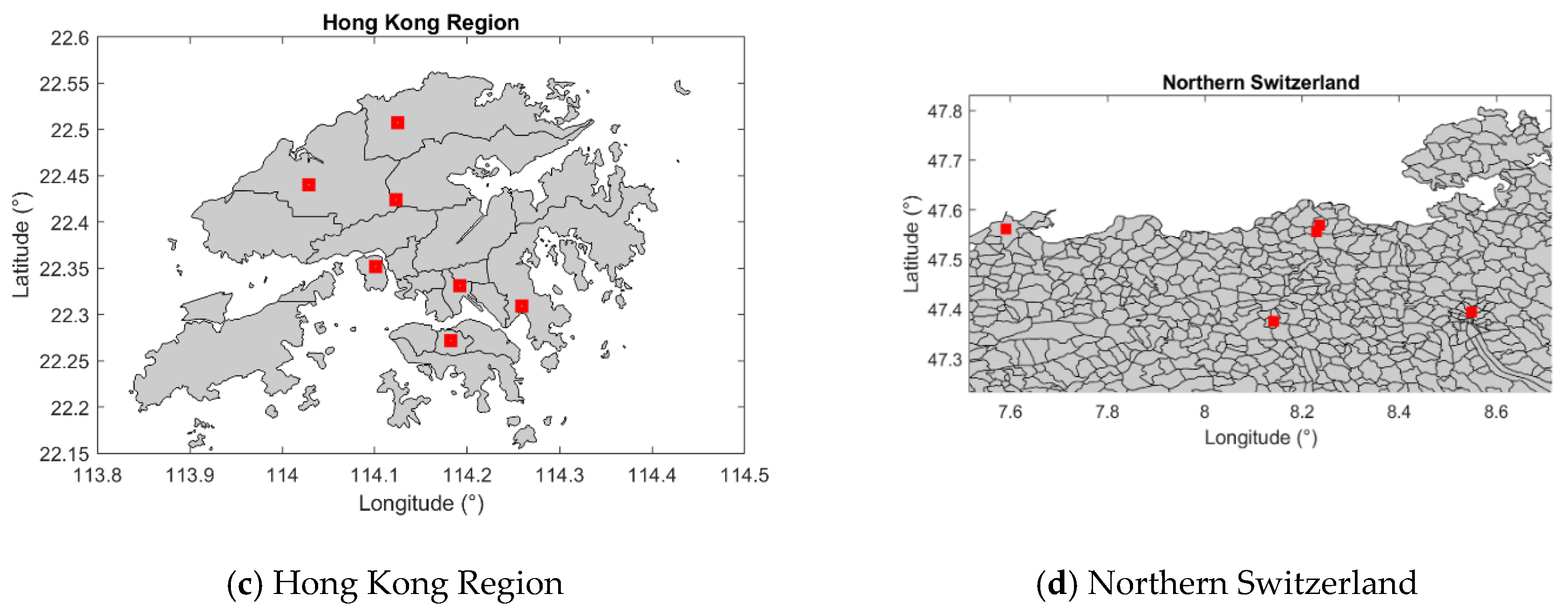
| Hong Kong Region | Yuen Long | 22.44 | 114.03 |
| Tsing Yi | 22.35 | 114.10 | |
| Sheung Shui | 22.51 | 114.13 | |
| Happy Valley | 22.27 | 114.18 | |
| Tseung Kwan O | 22.31 | 114.26 | |
| Kowloon City | 22.33 | 114.19 | |
| New Territories | 22.42 | 114.12 | |
| Northern Switzerland | Boettstein | 47.57 | 8.24 |
| Beznau | 47.56 | 8.23 | |
| Schafisheim | 47.38 | 8.14 | |
| Basel | 47.56 | 7.59 | |
| Zentralschweiz | 47.39 | 8.55 |
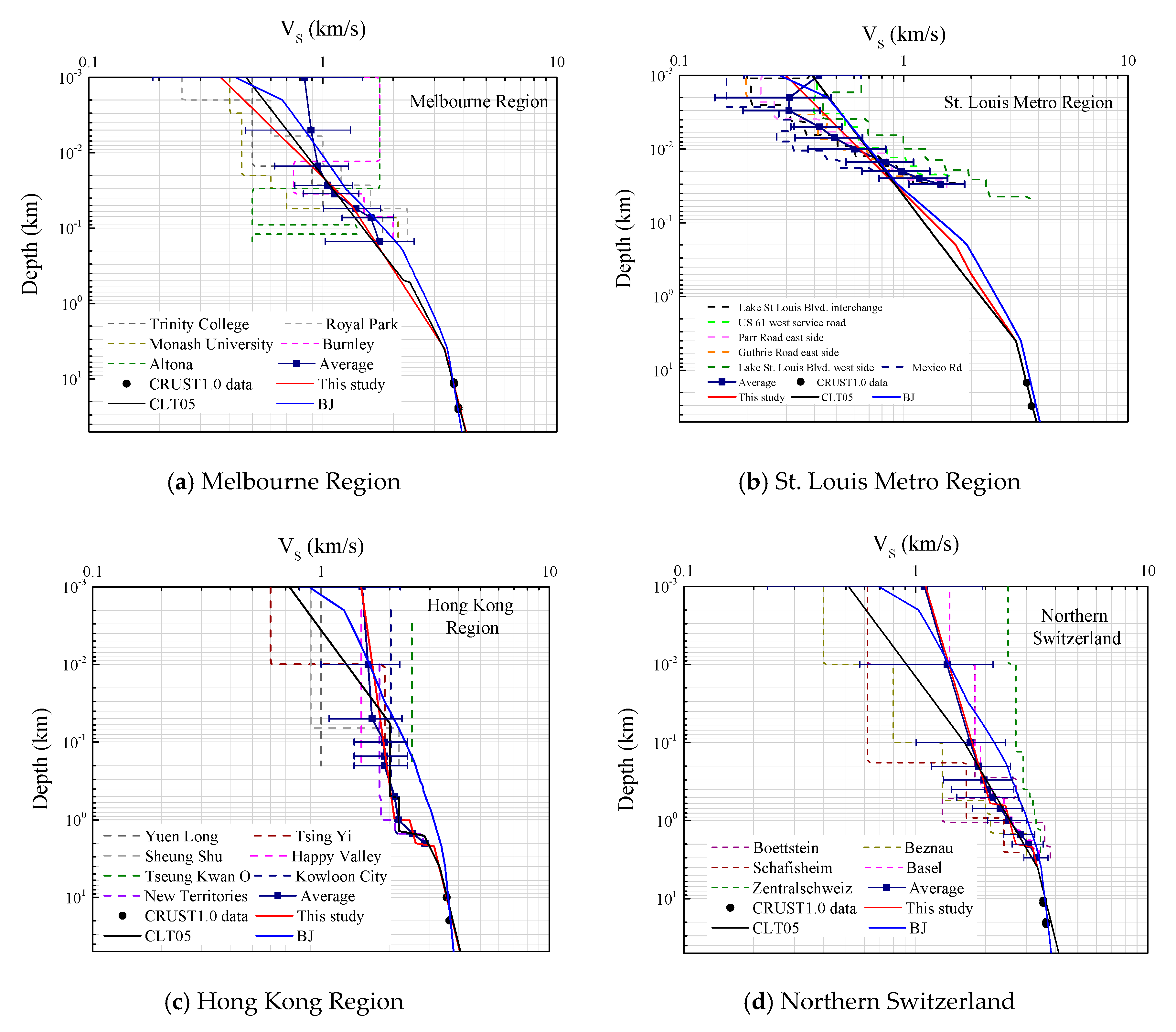
| Region | Melbourne Region | St. Louis Metro Region | Hong Kong Region | Northern Switzerland |
|---|---|---|---|---|
| ZS (km) | 0.05 | 0.5 | 0.001 | 0.001 |
| ZC (km) | 4.0 | 4.0 | 1.0 | 0.62 |
| VSZI (km/s) | 1.1 | 2.0 | 1.50 | 1.10 |
| VS2 (km/s) | / | / | 2.60 | 2.70 |
| VS8 (km/s) | 3.5 | 3.6 | 3.5 | 3.6 |
| n | 0.21 | 0.22 | 0.049 | 0.10 |
| VS30 (km/s) * | 0.96 | 0.69 | 1.61 | 1.37 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Xiang, X.; Sun, J.; Zhang, Y. A Generic Shear Wave Velocity Profiling Model for Use in Ground Motion Simulation. Geosciences 2020, 10, 408. https://doi.org/10.3390/geosciences10100408
Tang Y, Xiang X, Sun J, Zhang Y. A Generic Shear Wave Velocity Profiling Model for Use in Ground Motion Simulation. Geosciences. 2020; 10(10):408. https://doi.org/10.3390/geosciences10100408
Chicago/Turabian StyleTang, Yuxiang, Xinmei Xiang, Jing Sun, and Yongshan Zhang. 2020. "A Generic Shear Wave Velocity Profiling Model for Use in Ground Motion Simulation" Geosciences 10, no. 10: 408. https://doi.org/10.3390/geosciences10100408
APA StyleTang, Y., Xiang, X., Sun, J., & Zhang, Y. (2020). A Generic Shear Wave Velocity Profiling Model for Use in Ground Motion Simulation. Geosciences, 10(10), 408. https://doi.org/10.3390/geosciences10100408




