Development of Machine Learning Models for Estimating Metabolizable Protein Supply from Feed in Lactating Dairy Cows
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
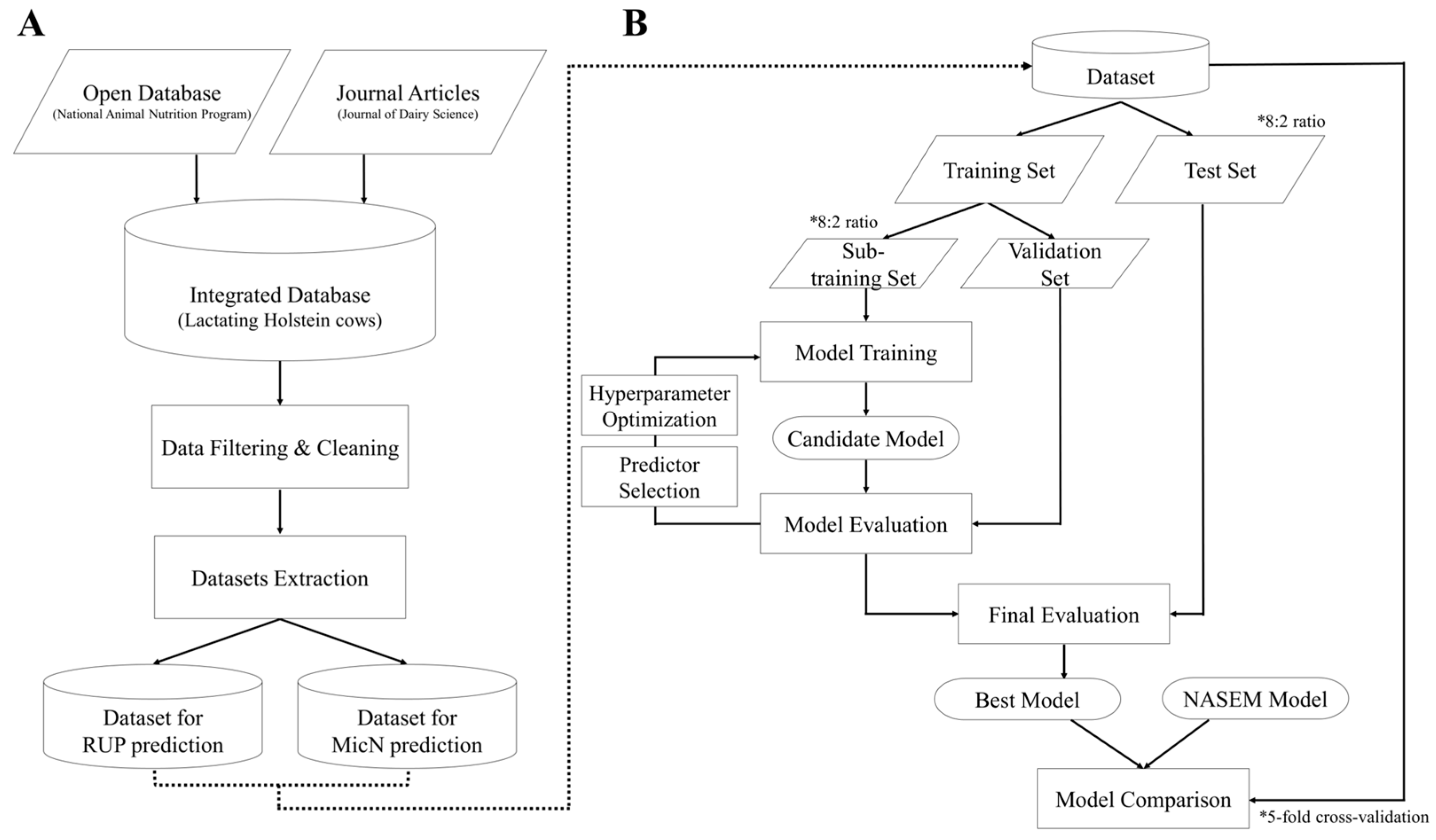
2.1. Database Construction and Dataset Extraction
Dt_CPBInc + Dt_CPCInc], for c = 1 to Nc
(38.7 × ADF/NDF) − (0.121 × ForWet) + (1.51 × DMI) × ((NDF/100) × DMI)]/100
(0.154 × ForWet)) × (St/100) × DMI]/100
2.2. Model Development and Model Evaluation
3. Results
3.1. RUP Prediction
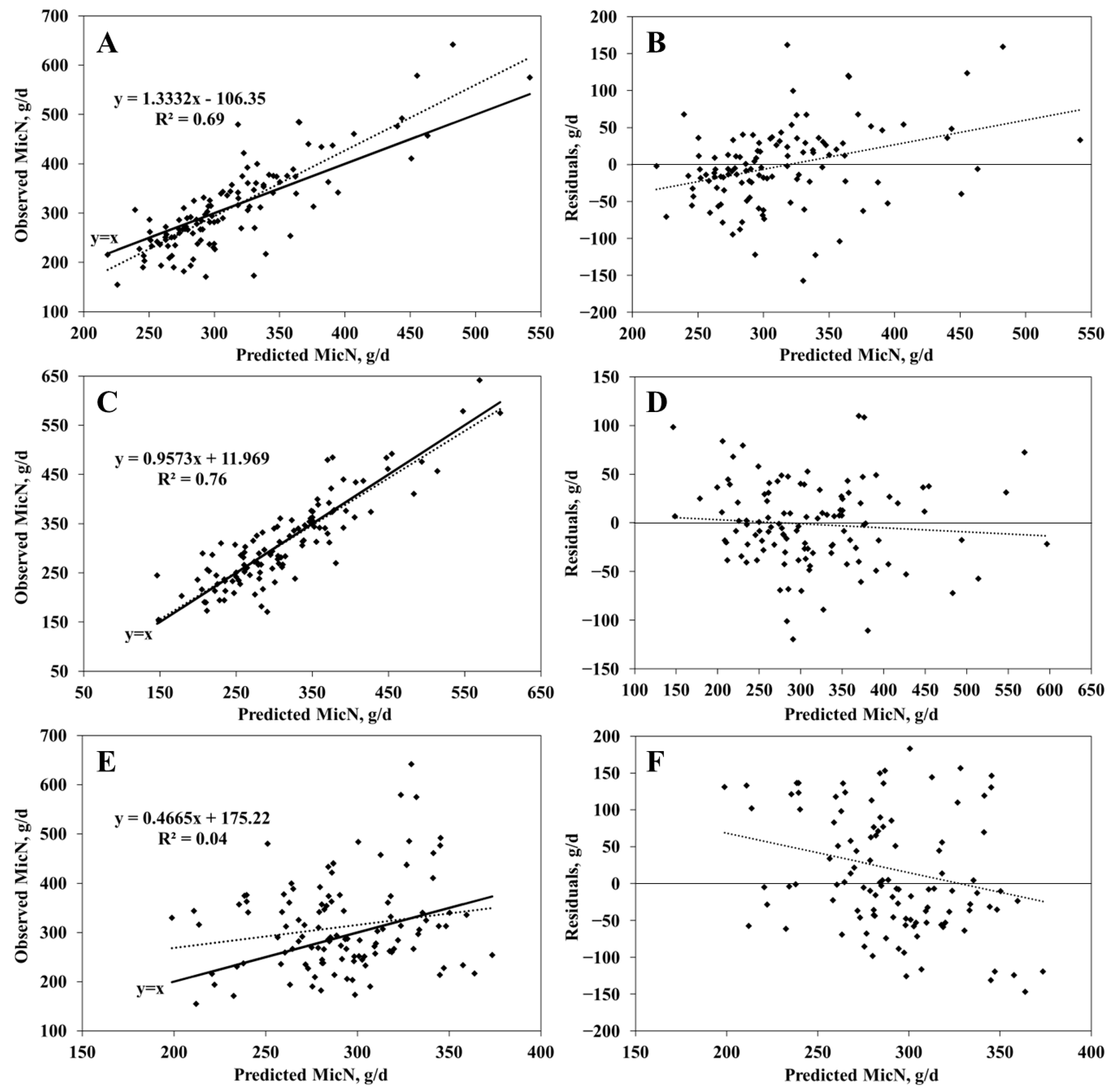
3.2. MicN Prediction
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Colman, D.R.; Beever, D.E.; Jolly, R.W.; Drackley, J.K. Gaining from technology for improved dairy cow nutrition: Economic, environmental, and animal health benefits. Prof. Anim. Sci. 2011, 27, 505–517. [Google Scholar] [CrossRef]
- VandeHaar, M.J.; St-Pierre, N. Major advances in nutrition: Relevance to the sustainability of the dairy industry. J. Dairy Sci. 2006, 89, 1280–1291. [Google Scholar] [CrossRef] [PubMed]
- Clark, J.H.; Davis, C.L. Future improvement of milk production: Potential for nutritional improvement. J. Anim. Sci. 1983, 57, 750–764. [Google Scholar] [CrossRef] [PubMed]
- Huhtanen, P.; Hristov, A.N. A meta-analysis of the effects of dietary protein concentration and degradability on milk protein yield and milk N efficiency in dairy cows. J. Dairy Sci. 2009, 92, 3222–3232. [Google Scholar] [CrossRef]
- NASEM. Nutrient Requirements of Dairy Cattle; National Academy Press: Washington, DC, USA, 2021. [Google Scholar]
- NRC. Nutrient Requirements of Dairy Cattle, 8th rev. ed.; National Academy Press: Washington, DC, USA, 2001. [Google Scholar]
- Hanigan, M.D.; Souza, V.C.; Martineau, R.; Daley, V.L.; Kononoff, P. Predicting ruminally undegraded and microbial protein flows from the rumen. J. Dairy Sci. 2021, 104, 8685–8707. [Google Scholar] [CrossRef]
- White, R.R.; Roman-Garcia, Y.; Firkins, J.L.; Kononoff, P.; VandeHaar, M.J.; Tran, H.; McGill, T.; Garnett, R.; Hanigan, M.D. Evaluation of the National Research Council (2001) dairy model and derivation of new prediction equations. 2. Rumen degradable and undegradable protein. J. Dairy Sci. 2017, 100, 3611–3627. [Google Scholar] [CrossRef]
- Tedeschi, L.O.; Fox, D.G. The Ruminant Nutrition System: Volume I—An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants, 3rd ed.; XanEdu: Ann Arbor, MI, USA, 2020. [Google Scholar]
- Tedeschi, L.O.; Fox, D.G. The Ruminant Nutrition System: Volume II—Tables of Equations and Coding; XanEdu: Ann Arbor, MI, USA, 2020. [Google Scholar]
- Allen, M.S. Do more mechanistic models increase accuracy of prediction of metabolisable protein supply in ruminants? Anim. Prod. Sci. 2019, 59, 1991–1998. [Google Scholar] [CrossRef]
- Rius, A.G.; McGilliard, M.L.; Umberger, C.A.; Hanigan, M.D. Interactions of energy and predicted metabolizable protein in determining nitrogen efficiency in the lactating dairy cow. J. Dairy Sci. 2010, 93, 2034–2043. [Google Scholar] [CrossRef]
- Tedeschi, L.O.; Nagaraja, T.G. Rumen Health Compendium, 2nd ed.; Kendall Hunt: Dubuque, IA, USA, 2025. [Google Scholar]
- Tedeschi, L.O. ASN-ASAS Symposium: Future of Data Analytics in Nutrition: Mathematical modeling in ruminant nutrition: Approaches and paradigms, extant models, and thoughts for upcoming predictive analytics. J. Anim. Sci. 2019, 97, 1921–1944. [Google Scholar] [CrossRef]
- Tedeschi, L.O. ASAS-NANP Symposium: Mathematical modeling in animal nutrition: The progression of data analytics and artificial intelligence in support of sustainable development in animal science. J. Anim. Sci. 2022, 100, skac111. [Google Scholar] [CrossRef]
- Cockburn, M. Review: Application and prospective discussion of machine learning for the management of dairy farms. Animals 2020, 10, 1690. [Google Scholar] [CrossRef] [PubMed]
- Slob, N.; Catal, C.; Kassahun, A. Application of machine learning to improve dairy farm management: A systematic literature review. Prev. Vet. Med. 2021, 187, 105237. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Pan, S.; Wang, J.; Vasilakos, A.V. Machine learning on big data: Opportunities and challenges. Neurocomputing 2017, 237, 350–361. [Google Scholar] [CrossRef]
- Borchers, M.R.; Chang, Y.M.; Proudfoot, K.L.; Wadsworth, B.A.; Stone, A.E.; Bewley, J.M. Machine-learning-based calving prediction from activity, lying, and ruminating behaviors in dairy cattle. J. Dairy Sci. 2017, 100, 5664–5674. [Google Scholar] [CrossRef]
- Pastell, M.E.; Kujala, M. A probabilistic neural network model for lameness detection. J. Dairy Sci. 2007, 90, 2283–2292. [Google Scholar] [CrossRef]
- Post, C.; Rietz, C.; Büscher, W.; Müller, U. Using sensor data to detect lameness and mastitis treatment events in dairy cows: A comparison of classification models. Sensors 2020, 20, 3863. [Google Scholar] [CrossRef]
- Sun, Z.; Samarasinghe, S.; Jago, J. Detection of mastitis and its stage of progression by automatic milking systems using artificial neural networks. J. Dairy Res. 2010, 77, 168–175. [Google Scholar] [CrossRef]
- Taneja, M.; Byabazaire, J.; Jalodia, N.; Davy, A.; Olariu, C.; Malone, P. Machine learning based fog computing assisted data-driven approach for early lameness detection in dairy cattle. Comput. Electron. Agric. 2020, 171, 105286. [Google Scholar] [CrossRef]
- Vázquez-Diosdado, J.A.; Gruhier, J.; Miguel-Pacheco, G.G.; Green, M.; Dottorini, T.; Kaler, J. Accurate prediction of calving in dairy cows by applying feature engineering and machine learning. Prev. Vet. Med. 2023, 219, 106007. [Google Scholar] [CrossRef]
- Lee, M.; Park, S.; Seo, S. Development of a model for prediction of partial mixed ration intake in lactating dairy cows using support vector regression algorithm and sensor data. J. Korea Acad. Ind. Coop. Soc. 2024, 25, 611–622. [Google Scholar] [CrossRef]
- Murphy, M.D.; O’Mahony, M.J.; Shalloo, L.; French, P.; Upton, J. Comparison of modelling techniques for milk-production forecasting. J. Dairy Sci. 2014, 97, 3352–3363. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, Q.T.; Fouchereau, R.; Frénod, E.; Gerard, C.; Sincholle, V. Comparison of forecast models of production of dairy cows combining animal and diet parameters. Comput. Electron. Agric. 2020, 170, 105258. [Google Scholar] [CrossRef]
- Tedeschi, L.O. The prevailing mathematical modeling classifications and paradigms to support the advancement of sustainable animal production. Animal 2023, 17, 100813. [Google Scholar] [CrossRef] [PubMed]
- Jeon, S.; Kang, H.; Park, S.; Seo, S. Evaluation of the equations to predict net energy requirement for lactation in the cattle feeding system: Based on the literature database. Agriculture 2022, 12, 654. [Google Scholar] [CrossRef]
- Burges, C.J.C. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 1995. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tedeschi, L.O. Assessment of the adequacy of mathematical models. Agric. Syst. 2006, 89, 225–247. [Google Scholar] [CrossRef]
- Moraes, L.E.; Kebreab, E.; Firkins, J.L.; White, R.R.; Martineau, R.; Lapierre, H. Predicting milk protein responses and the requirement of metabolizable protein by lactating dairy cows. J. Dairy Sci. 2018, 101, 310–327. [Google Scholar] [CrossRef]
- Bell, A.W.; Burhans, W.S.; Overton, T.R. Protein nutrition in late pregnancy, maternal protein reserves and lactation performance in dairy cows. Proc. Nutr. Soc. 2000, 59, 119–126. [Google Scholar] [CrossRef]
- Roche, J.R.; Bell, A.W.; Overton, T.R.; Loor, J.J. Nutritional management of the transition cow in the 21st century–a paradigm shift in thinking. Anim. Prod. Sci. 2013, 53, 1000–1023. [Google Scholar] [CrossRef]
- de Souza, R.A.; Tempelman, R.J.; Allen, M.S.; VandeHaar, M.J. Updating predictions of dry matter intake of lactating dairy cows. J. Dairy Sci. 2019, 102, 7948–7960. [Google Scholar] [CrossRef] [PubMed]
- Shadpour, S.; Chud, T.C.S.; Hailemariam, D.; Oliveira, H.R.; Plastow, G.; Stothard, P.; Lassen, J.; Baldwin, R.; Miglior, F.; Baes, C.F.; et al. Predicting dry matter intake in Canadian Holstein dairy cattle using milk mid-infrared reflectance spectroscopy and other commonly available predictors via artificial neural networks. J. Dairy Sci. 2022, 105, 8257–8271. [Google Scholar] [CrossRef] [PubMed]
- Soyeurt, H.; Froidmont, E.; Dufrasne, I.; Hailemariam, D.; Wang, Z.; Bertozzi, C.; Colinet, F.G.; Dehareng, F.; Gengler, N. Contribution of milk mid-infrared spectrum to improve the accuracy of test-day body weight predicted from stage, lactation number, month of test and milk yield. Livest. Sci. 2019, 227, 82–89. [Google Scholar] [CrossRef]
- Schadt, I.; Mertens, D.R.; Van Soest, P.J.; Azzaro, G.; Licitra, G. Stage of lactation and corresponding diets affect in situ protein degradation by dairy cows. J. Dairy Sci. 2014, 97, 7995–8007. [Google Scholar] [CrossRef]
- Fox, D.G.; Tedeschi, L.O.; Tylutki, T.P.; Russell, J.B.; Van Amburgh, M.E.; Chase, L.E.; Pell, A.N.; Overton, T.R. The Cornell Net Carbohydrate and Protein System model for evaluating herd nutrition and nutrient excretion. Anim. Feed Sci. Technol. 2004, 112, 29–78. [Google Scholar] [CrossRef]
- Chan, J.Y.L.; Leow, S.M.H.; Bea, K.T.; Cheng, W.K.; Phoong, S.W.; Hong, Z.W.; Chen, Y.-L. Mitigating the multicollinearity problem and its machine learning approach: A review. Mathematics 2022, 10, 1283. [Google Scholar] [CrossRef]
- Garg, A.; Tai, K. Comparison of statistical and machine learning methods in modelling of data with multicollinearity. Int. J. Model. Identif. Control 2013, 18, 295–312. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, H.; Wang, H.; Yan, T. Can machine learning algorithms perform better than multiple linear regression in predicting nitrogen excretion from lactating dairy cows. Sci. Rep. 2022, 12, 12478. [Google Scholar] [CrossRef]
- Davison, C.; Bowen, J.M.; Michie, C.; Rooke, J.A.; Jonsson, N.; Andonovic, I.; Tachtatzis, C.; Gilroy, M.; Duthie, C.A. Predicting feed intake using modelling based on feeding behaviour in finishing beef steers. Animal 2021, 15, 100231. [Google Scholar] [CrossRef]
- Shine, P.; Murphy, M.D.; Upton, J.; Scully, T. Machine-learning algorithms for predicting on-farm direct water and electricity consumption on pasture based dairy farms. Comput. Electron. Agric. 2018, 150, 74–87. [Google Scholar] [CrossRef]
- Goddard, H.; Shamir, L. SVMnet: Non-parametric image classification based on convolutional ensembles of support vector machines for small training sets. IEEE Access 2022, 10, 24029–24038. [Google Scholar] [CrossRef]
- Xu, H.; Kinfu, K.A.; LeVine, W.; Panda, S.; Dey, J.; Ainsworth, M.; Peng, Y.-C.; Kusmanov, M.; Engert, F.; White, C.M. When are deep networks really better than decision forests at small sample sizes, and how? arXiv 2021, arXiv:2108.13637. [Google Scholar] [CrossRef]
- Ali, J.; Khan, R.; Ahmad, N.; Maqsood, I. Random forests and decision trees. Int. J. Comput. Sci. Issues (IJCSI) 2012, 9, 272. [Google Scholar]
- Lechner, M.; Okasa, G. Random Forest estimation of the ordered choice model. Empir. Econ. 2024, 68, 1–106. [Google Scholar] [CrossRef]
- Lee, M.C. Using support vector machine with a hybrid feature selection method to the stock trend prediction. Expert Syst. Appl. 2009, 36, 10896–10904. [Google Scholar] [CrossRef]
- Rossi, F.; Villa, N. Support vector machine for functional data classification. Neurocomputing 2006, 69, 730–742. [Google Scholar] [CrossRef]
- Karaçalı, B.; Ramanath, R.; Snyder, W.E. A comparative analysis of structural risk minimization by support vector machines and nearest neighbor rule. Pattern Recognit. Lett. 2004, 25, 63–71. [Google Scholar] [CrossRef]
- Shawe-Taylor, J.; Bartlett, P.L.; Williamson, R.C.; Anthony, M. Structural risk minimization over data-dependent hierarchies. IEEE Trans. Inf. Theory 1998, 44, 1926–1940. [Google Scholar] [CrossRef]
- Wu, D.; Yang, H.; Chen, X.; He, Y.; Li, X. Application of image texture for the sorting of tea categories using multi-spectral imaging technique and support vector machine. J. Food Eng. 2008, 88, 474–483. [Google Scholar] [CrossRef]

| Variables | n | Mean | Median | Min | Max |
|---|---|---|---|---|---|
| No. of articles | 436 | - | - | - | - |
| No. of treatments | 1779 | - | - | - | - |
| No. of animals per treatment | 1779 | 11.2 | 8.0 | 2.0 | 58.0 |
| Animal information | |||||
| Days in milk (day) | 1397 | 102.3 | 99.0 | 1.0 | 323.0 |
| Parity | 1472 | 1.9 | 2.0 | 1.0 | 2.0 |
| Body weight (kg) | 1481 | 629.6 | 624.0 | 476.0 | 861.9 |
| Dry matter intake (kg/d) | 1779 | 21.7 | 21.7 | 8.8 | 32.0 |
| Milk yield (kg/d) | 1674 | 33.5 | 33.9 | 10.2 | 58.5 |
| Milk composition (%) | |||||
| Lactose | 1125 | 4.7 | 4.8 | 3.7 | 5.7 |
| Fat | 1582 | 3.7 | 3.7 | 2.1 | 5.6 |
| Crude protein | 1584 | 3.1 | 3.1 | 2.6 | 4.1 |
| Dietary chemical composition (%) | |||||
| Dry matter | 1004 | 54.0 | 52.6 | 13.5 | 96.3 |
| Organic matter | 1045 | 92.4 | 92.6 | 46.1 | 98.9 |
| Crude protein | 1665 | 16.6 | 16.6 | 9.3 | 29.6 |
| Neutral detergent fiber (NDF) | 1520 | 32.9 | 32.5 | 17.6 | 60.8 |
| Forage NDF | 874 | 23.5 | 22.8 | 6.6 | 54.3 |
| Acidic detergent fiber (ADF) | 1222 | 20.4 | 20.2 | 8.8 | 61.6 |
| Fat | 743 | 3.9 | 3.7 | 0.3 | 8.9 |
| Ash | 793 | 7.4 | 7.3 | 1.1 | 16.5 |
| Non-starch carbohydrate | 604 | 39.4 | 40.2 | 16.8 | 51.2 |
| Starch | 931 | 24.7 | 25.4 | 0.2 | 47.6 |
| N flows at the duodenum (g/d) | |||||
| Total N | 442 | 541.7 | 534.5 | 200.9 | 1110.0 |
| Microbial N | 577 | 296.0 | 276.8 | 74.0 | 763.0 |
| Non-ammonia N | 550 | 506.8 | 504.7 | 73.0 | 1078.0 |
| Ammonia N | 433 | 20.6 | 17.5 | 1.8 | 121.9 |
| Non-ammonia, non-microbial N | 542 | 214.6 | 215.2 | 33.1 | 576.0 |
| Digestibility (%) | |||||
| Dry matter | 664 | 67.6 | 67.9 | 19.7 | 85.0 |
| Organic matter | 772 | 69.1 | 69.5 | 43.8 | 85.2 |
| Crude protein | 694 | 67.5 | 67.9 | 40.3 | 86.6 |
| NDF | 776 | 49.6 | 48.6 | 19.5 | 84.0 |
| ADF | 408 | 45.3 | 45.1 | 18.0 | 75.3 |
| Fat | 225 | 89.2 | 89.0 | 1.0 | 177.0 |
| Starch | 385 | 94.1 | 95.8 | 13.8 | 99.9 |
| Rumen characteristics | |||||
| pH | 460 | 6.1 | 6.1 | 5.5 | 6.9 |
| Total volatile fatty acid (mM) | 436 | 112.9 | 113.0 | 11.0 | 746.4 |
| Ammonia N (mg/dL) | 438 | 13.0 | 12.3 | 1.4 | 40.6 |
| Variables | n | Mean | Median | Min | Max |
|---|---|---|---|---|---|
| No. of articles | 145 | - | - | - | - |
| No. of treatments | 542 | - | - | - | - |
| No. of animals per treatment | 542 | 6.6 | 4.0 | 2.0 | 40.0 |
| Animal information | |||||
| Days in milk (day) | 376 | 108.8 | 97.0 | 16.0 | 323.0 |
| Parity | 432 | 1.9 | 2.0 | 1.0 | 2.0 |
| Body weight (kg) | 424 | 607.6 | 600.0 | 480.0 | 788.0 |
| Dry matter intake (kg/d) | 542 | 20.1 | 19.9 | 8.8 | 31.8 |
| Milk yield (kg/d) | 448 | 29.2 | 29.3 | 10.2 | 44.7 |
| Dietary chemical composition (% DM) | |||||
| Dry matter (% as-fed) | 314 | 60.5 | 57.5 | 15.7 | 91.5 |
| Organic matter | 351 | 92.2 | 92.5 | 46.1 | 97.7 |
| Crude protein | 495 | 17.2 | 17.3 | 9.6 | 29.6 |
| Neutral detergent fiber | 437 | 32.4 | 32.3 | 17.6 | 50.9 |
| Acidic detergent fiber | 393 | 19.4 | 19.0 | 8.8 | 35.5 |
| Fat | 71 | 4.2 | 4.0 | 1.6 | 6.9 |
| Ash | 99 | 7.1 | 7.1 | 5.1 | 11.7 |
| Non-starch carbohydrate | 34 | 37.1 | 37.4 | 22.0 | 47.9 |
| Starch | 231 | 27.9 | 28.5 | 2.5 | 47.6 |
| N flows at the duodenum (g/d) | |||||
| Total N | 426 | 540.4 | 533.1 | 200.9 | 1110.0 |
| Microbial N | 542 | 296.9 | 276.9 | 74.0 | 763.0 |
| Non-ammonia N | 542 | 512.4 | 505.5 | 173.0 | 1078.0 |
| Ammonia N | 425 | 20.3 | 17.5 | 1.8 | 121.9 |
| Non-ammonia, non-microbial N | 542 | 214.6 | 215.2 | 33.1 | 576.0 |
| Variables | n | Mean | Median | Min | Max |
|---|---|---|---|---|---|
| No. of articles | 153 | - | - | - | - |
| No. of treatments | 577 | - | - | - | - |
| No. of animals per treatment | 577 | 6.5 | 4.0 | 2.0 | 40.0 |
| Animal information | |||||
| Days in milk (day) | 390 | 108.3 | 97.0 | 16.0 | 323.0 |
| Parity | 454 | 1.8 | 2.0 | 1.0 | 2.0 |
| Body weight (kg) | 459 | 608.4 | 600.0 | 480.0 | 788.0 |
| Dry matter intake (kg/d) | 577 | 20.0 | 19.9 | 8.8 | 31.8 |
| Milk yield (kg/d) | 483 | 29.0 | 28.8 | 10.2 | 44.7 |
| Dietary chemical composition (% DM) | |||||
| Dry matter (% as-fed) | 346 | 59.6 | 57.1 | 15.7 | 93.9 |
| Organic matter | 379 | 92.1 | 92.5 | 46.1 | 97.7 |
| Crude protein | 530 | 17.3 | 17.3 | 9.6 | 29.6 |
| Neutral detergent fiber | 464 | 32.4 | 32.3 | 17.6 | 50.9 |
| Acidic detergent fiber | 408 | 19.5 | 19.0 | 8.8 | 35.5 |
| Fat | 90 | 3.9 | 3.9 | 1.6 | 6.9 |
| Ash | 118 | 7.2 | 7.2 | 5.1 | 11.7 |
| Non-starch carbohydrate | 52 | 37.6 | 37.6 | 22.0 | 47.9 |
| Starch | 250 | 27.1 | 27.8 | 2.5 | 47.6 |
| N flows at the duodenum (g/d) | |||||
| Total N | 442 | 541.7 | 534.5 | 200.9 | 1110.0 |
| Microbial N | 577 | 296.0 | 276.8 | 74.0 | 763.0 |
| Non-ammonia N | 550 | 506.8 | 504.7 | 73.0 | 1078.0 |
| Ammonia N | 433 | 20.6 | 17.5 | 1.8 | 121.9 |
| Non-ammonia, non-microbial N | 542 | 214.6 | 215.2 | 33.1 | 576.0 |
| Performance | ||||||
|---|---|---|---|---|---|---|
| % RMSEP 1 | ||||||
| Model | R2 | RMSEP, kg/d | Mean Bias | Slope Bias | Random Bias | CCC |
| RFR | 0.64 | 0.352 | 7.3 | 3.0 | 89.8 | 0.74 |
| SVR | 0.38 | 0.460 | 4.2 | 4.1 | 91.7 | 0.59 |
| Performance | ||||||
|---|---|---|---|---|---|---|
| % RMSEP 1 | ||||||
| Model | R2 | RMSEP, kg/d | Mean Bias | Slope Bias | Random Bias | CCC |
| RFR | 0.60 | 0.326 | 4.7 1 | 5.2 2 | 90.1 | 0.71 |
| SVR | 0.53 | 0.349 | 3.7 | 1.2 | 95.1 | 0.68 |
| NASEM | 0.27 | 0.437 | 2.9 | 3.2 3 | 93.9 | 0.45 |
| Performance | ||||||
|---|---|---|---|---|---|---|
| % RMSEP 1 | ||||||
| Model | R2 | RMSEP, g/d | Mean Bias | Slope Bias | Random Bias | CCC |
| RFR | 0.82 | 49.8 | 1.1 | 4.1 | 94.8 | 0.89 |
| SVR | 0.89 | 38.6 | 0.0 | 4.9 | 95.0 | 0.94 |
| Performance | ||||||
|---|---|---|---|---|---|---|
| % RMSEP 1 | ||||||
| Model | R2 | RMSEP, g/d | Mean Bias | Slope Bias | Random Bias | CCC |
| RFR | 0.69 | 52.0 | 4.9 | 14.1 1 | 81.1 | 0.73 |
| SVR | 0.76 | 42.4 | 1.8 | 5.6 | 92.7 | 0.86 |
| NASEM | 0.04 | 90.7 | 5.5 2 | 6.4 | 88.2 | 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.; Kim, D.H.; Seo, S.; Tedeschi, L.O. Development of Machine Learning Models for Estimating Metabolizable Protein Supply from Feed in Lactating Dairy Cows. Animals 2025, 15, 687. https://doi.org/10.3390/ani15050687
Lee M, Kim DH, Seo S, Tedeschi LO. Development of Machine Learning Models for Estimating Metabolizable Protein Supply from Feed in Lactating Dairy Cows. Animals. 2025; 15(5):687. https://doi.org/10.3390/ani15050687
Chicago/Turabian StyleLee, Mingyung, Dong Hyeon Kim, Seongwon Seo, and Luis O. Tedeschi. 2025. "Development of Machine Learning Models for Estimating Metabolizable Protein Supply from Feed in Lactating Dairy Cows" Animals 15, no. 5: 687. https://doi.org/10.3390/ani15050687
APA StyleLee, M., Kim, D. H., Seo, S., & Tedeschi, L. O. (2025). Development of Machine Learning Models for Estimating Metabolizable Protein Supply from Feed in Lactating Dairy Cows. Animals, 15(5), 687. https://doi.org/10.3390/ani15050687





