Next Article in Journal
Long-Term Heat Stress and Genetic Responses in Growth Traits of Thai Native Synthetic Chicken Lines
Previous Article in Journal
Feeding a Bitter Mix of Gentian and Grape Seed Extracts with Caffeine Reduces Appetite and Body Fat Deposition and Improves Meat Colour in Pigs
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Animals
Volume 15
Issue 14
10.3390/ani15142127
animals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Development of Machine Learning-Based Sub-Models for Predicting Net Protein Requirements in Lactating Dairy Cows

by
Mingyung Lee
1,
Dong Hyeon Kim
2,
Seongwon Seo
3 and
Luis O. Tedeschi
1,*
1
Department of Animal Science, Texas A&M University, College Station, TX 77843-2471, USA
2
Dairy Science Division, National Institute of Animal Science, Rural Development Administration, Cheonan 31000, Republic of Korea
3
Division of Animal and Dairy Sciences, Chungnam National University, Daejeon 34134, Republic of Korea
*
Author to whom correspondence should be addressed.
Animals 2025, 15(14), 2127; https://doi.org/10.3390/ani15142127
Submission received: 13 June 2025 / Revised: 15 July 2025 / Accepted: 16 July 2025 / Published: 18 July 2025
(This article belongs to the Section Animal Nutrition)
Browse Figures
Versions Notes

Simple Summary

Accurately estimating the protein requirements of lactating dairy cows is crucial for enhancing nutrient utilization and promoting sustainable milk production. This study explored the application of machine learning (ML) techniques to predict two components of protein requirement—net protein for maintenance (NPm) and net protein for lactation (NPl)—utilizing a dataset compiled from published experimental studies on lactating Holstein cows. Random forest regression (RFR) and support vector regression (SVR) algorithms were trained to approximate target values calculated using the NASEM (2021) equations. Among the two approaches, the RFR model consistently outperformed SVR in terms of predictive accuracy, explaining over 80 percent of the variation in both NPm and NPl. These findings demonstrate the potential of ML models to serve as surrogate approximators of mechanistic outputs, offering computational efficiency and practical applicability in precision feeding programs. Further research is warranted to validate these models under field conditions and to explore their integration into hybrid modeling frameworks.

Abstract

A reliable estimation of protein requirements in lactating dairy cows is necessary for formulating nutritionally adequate diets, improving feed efficiency, and minimizing nitrogen excretion. This study aimed to develop machine learning-based models to predict net protein requirements for maintenance (NPm) and lactation (NPl) using random forest regression (RFR) and support vector regression (SVR). A total of 1779 observations were assembled from 436 peer-reviewed publications and open-access databases. Predictor variables included farm-ready variables such as milk yield, dry matter intake, days in milk, body weight, and dietary crude protein content. NPm was estimated based on the National Academies of Sciences, Engineering, and Medicine (NASEM, 2021) equations, while NPl was derived from milk true protein yield. The model adequacy was evaluated using 10-fold cross-validation. The RFR model demonstrated higher predictive performance than SVR for both NPm (R2 = 0.82, RMSEP = 22.38 g/d, CCC = 0.89) and NPl (R2 = 0.82, RMSEP = 95.17 g/d, CCC = 0.89), reflecting its capacity to model the rule-based nature of the NASEM equations. These findings suggest that RFR may provide a valuable approach for estimating protein requirements with fewer input variables. Further research should focus on validating these models under field conditions and exploring hybrid modeling frameworks that integrate mechanistic and machine learning approaches.

1. Introduction

Accurately quantifying nutrient requirements is fundamental to the nutritional management of lactating dairy cows, as it directly influences milk production, animal health, economic viability, and the long-term sustainability of dairy operations [1,2,3]. Among these nutrients, protein plays a pivotal role not only as the principal substrate for milk protein synthesis but also as a critical component supporting a range of metabolic and physiological processes in lactating cows [4,5]. Unlike metabolizable protein, which denotes the quantity of absorbable amino acids supplied to the small intestine, net protein requirements (NP) represent the actual protein demands of the animal for maintenance (NPm) and lactation (NPl), adjusted for metabolic losses and the efficiency of utilization [6,7]. Reliable estimates of NP are essential for aligning nutrient supply with physiological demand, given that overestimation can lead to inefficient nitrogen utilization and increased environmental emissions such as ammonia volatilization and nitrate leaching. In contrast, underestimation may compromise milk yield (MY) and animal welfare [8,9].
To address these challenges, NP requirements have traditionally been estimated using mechanistic feeding models, including those proposed by the NRC (2001; [6]), its recent update by the NASEM (2021; [7]), and many nutrition models for ruminant animals based on the Cornell Net Carbohydrate and Protein System framework such as the Ruminant Nutrition System [10,11]. These models employ fixed-form biological equations based on variables such as feed composition, body weight, and milk production. While these equations are grounded in well-established physiological principles, their applicability may be constrained in heterogeneous production environments or under dynamically changing farm conditions [12,13,14].
Recent advances in machine learning (ML) offer a promising alternative to traditional modeling approaches by enabling data-driven characterization of complex and nonlinear biological systems [15,16,17]. ML algorithms, such as random forest and support vector machine algorithms, are particularly effective when applied to high-dimensional datasets and are capable of identifying latent patterns and variable interactions that may be overlooked by conventional models [18,19]. In dairy science, ML has been applied to a variety of predictive tasks, including MY, feed intake, and metabolic disorders [20,21]. However, its application for estimating nutrient requirements, particularly as surrogate models that replicate outputs of mechanistic systems, remains relatively underinvestigated.
The objective of the present study was to develop machine learning-based models for predicting NP requirements for maintenance and lactation in lactating dairy cows. The target values used to train the ML models were not obtained from direct empirical measurements, but were derived from the NASEM (2021) equations because direct measurements of net protein requirements are not readily available. As such, these models are intended to serve as computationally efficient approximators of NASEM predictions, like a meta-modeling approach, rather than replacements for the underlying biological framework. We hypothesized that machine learning models can approximate NASEM (2021)-based predictions of protein requirements using readily available input variables. This study builds upon our previous work, which developed ML models to predict metabolizable protein supply components, namely rumen-undegradable protein (RUP) and duodenal microbial nitrogen (MicN), using the same comprehensive database [22]. While the earlier study addressed the supply side of protein nutrition, this study focuses on the requirement side. These ML-based sub-models are expected to enhance usability, reduce implementation complexity, and support real-time decision-making in precision feeding programs. Furthermore, this work provides a foundation for the development of hybrid intelligent mechanistic models (HIMM; [17,23,24]), which aim to combine mechanistic insight with data-driven flexibility to improve the accuracy and adaptability of dairy nutritional management.

2. Materials and Methods

2.1. Database Construction and Dataset Extraction

The dataset used in this study was identical to that developed and described by Lee et al. [22]. Briefly, it was constructed by integrating two publicly available and peer-reviewed databases, both of which contain observations exclusively from lactating Holstein cows. The final combined dataset included 1779 observations extracted from 436 peer-reviewed publications. The first component was obtained from 319 articles published between 2016 and 2020 in the Animal Nutrition section of the Journal of Dairy Science, which contributed 1326 observations and had been previously compiled by Jeon et al. [25]. The second component was obtained from the National Animal Nutrition Program (https://animalnutrition.org; accessed on 17 October 2023), comprising 453 observations from 117 articles published between 1979 and 2017. The dataset represents a wide range of geographical and production contexts, including studies conducted in North America, Europe, Asia, Africa, and Latin America, and covers various feeding systems such as total mixed ration and pasture-based operations. To ensure the integrity of the dataset, all records were thoroughly screened to eliminate duplication across the two sources. A full description of the database construction process, along with summary statistics, was provided by Lee et al. [22].

2.2. Variable Selection and Calculations

For NPm (g/d), the reference values were calculated as the sum of scurf protein, endogenous urinary protein, and metabolic fecal protein based on equations proposed by NASEM (2021). The NPm (g/d) was estimated as follows:
NPm (g/d) = NPscurf + NPendogenous urinary excretion + NPmetabolic fecal protein
The scurf protein requirement was calculated as follows ([7]):
NPscurf (g/d) = 0.20 × BW0.60 × (TP/CP)
where BW represents body weight in kilograms, TP is true protein, CP is crude protein, and the TP/CP ratio of scurf is 0.85.
The endogenous urinary protein requirement was calculated using the following equation ([7]):
NPendogenous urinary excretion (g/d) = 53 × 6.25 × BW × 0.001
where 53 (mg N/kg BW) is the endogenous urinary nitrogen excretion per kilogram of BW, 6.25 is the standard conversion factor from nitrogen to crude protein, and the TP/CP ratio for endogenous urinary protein is 1.0.
Metabolic fecal protein was estimated as follows ([7]):
NPmetabolic fecal protein (g/d) = [(11.62 + 0.134 × NDF) × DMI] × 0.73
where NDF is the percentage of neutral detergent fiber on a dry matter basis, and DMI is the daily dry matter intake (kg). The TP/CP ratio for metabolic fecal protein is 0.73.
The reference NPl (g/d) value was estimated based on the milk true protein content using the following equation:
NPl (g/d) = MY × Milk CP × 0.951 (1000/100)
where MY is milk yield (kg), Milk CP represents the crude protein concentration in milk (%), and the TP/CP ratio for milk is 0.951. Milk CP values were directly obtained from the datasets and were not calculated from nitrogen; hence, no N-to-CP conversion factor (e.g., 6.34) was applied.
To prevent circular reasoning in model development, variables directly used in the calculation of NPm and NPl values based on the NASEM (2021) equations were excluded from the candidate predictor set. Instead, candidate variables were selected based on biological relevance and availability under typical field conditions. These included animal-related factors such as days in milk (DIM), parity, BW (kg), DMI (kg/d), and MY (kg/d), as well as dietary components expressed as a percentage of dry matter (% DM), including dry matter (DM, % as-fed), organic matter (OM), CP, neutral detergent fiber (NDF), acid detergent fiber (ADF), non-starch carbohydrate (NSC), fat, ash, and starch. Although BW, MY, DMI, and NDF are included in the NASEM equations, each variable was retained as a model input only when not directly used in the calculation of the corresponding target variable. Specifically, BW, DMI, and NDF were excluded from the NPm prediction model, and MY was excluded from the NPl prediction model. Additionally, variables such as milk composition, total tract digestibility, rumen characteristics, and post-digestion outcomes were also excluded as these variables are not always available at the farm level. Separate datasets were constructed for NPm and NPl prediction, each comprising the target variable and its respective candidate explanatory variables. Descriptive statistics for these datasets are provided in Table 1 and Table 2.

2.3. Model Development and Evaluation

Variables with insufficient data were excluded from the dataset before model development for predicting NPm and NPl. The resulting dataset was partitioned into training (80%) and test (20%) sets. The training set was further split into a sub-training set (80%) and a validation set (20%) for the purpose of selecting the optimal combination of input variables and hyperparameters. Model selection was based on performance in the validation set, evaluated using the coefficient of determination (R2), root mean square error of prediction (RMSEP), and concordance correlation coefficient (CCC), with an emphasis on achieving both high precision and accuracy. The optimal model was subsequently retrained using the entire training set and evaluated on the independent test set. A new dataset containing only the input variables selected for the final model was then extracted from the original dataset, and a 10-fold cross-validation was conducted to assess the model’s robustness and generalizability. An overview of the dataset refinement and modeling procedures was presented by Lee et al. [22].
All statistical analyses and modeling procedures were performed using R software (version 4.4.2; [26]). To predict NPm and NPl, both random forest regression (RFR) and support vector regression (SVR) algorithms were applied. SVR, an extension of the support vector machine algorithm, was implemented using a Gaussian radial basis function kernel, which includes two key hyperparameters: gamma and cost [27,28]. These hyperparameters were optimized via grid search within a 10-fold cross-validation framework using the tune function in the e1071 package [29] in R. Random forest algorithm is a widely used ensemble learning method suitable for both classification and regression tasks [18], and is largely employed in the animal science literature [30]. Its hyperparameters, namely the number of trees (ntree) and the number of variables randomly selected at each split (mtry), were fine-tuned through grid search. Modeling was performed using the randomForest package [31] in R. Model adequacy between predicted values and reference values calculated from the NASEM (2021) equations was evaluated using several statistical metrics as described by Tedeschi [32], including the R2, RMSEP, and CCC. The strength of agreement based on CCC was interpreted using the categories proposed by Hinkle et al. [33]: negligible (0.00–0.30), low (0.30–0.50), moderate (0.50–0.70), high (0.70–0.90), and very high (0.90–1.00). Residual analyses were conducted to assess both mean and slope biases. Statistical significance was declared at p < 0.05, and trends were considered for 0.05 ≤ p < 0.10.

3. Results

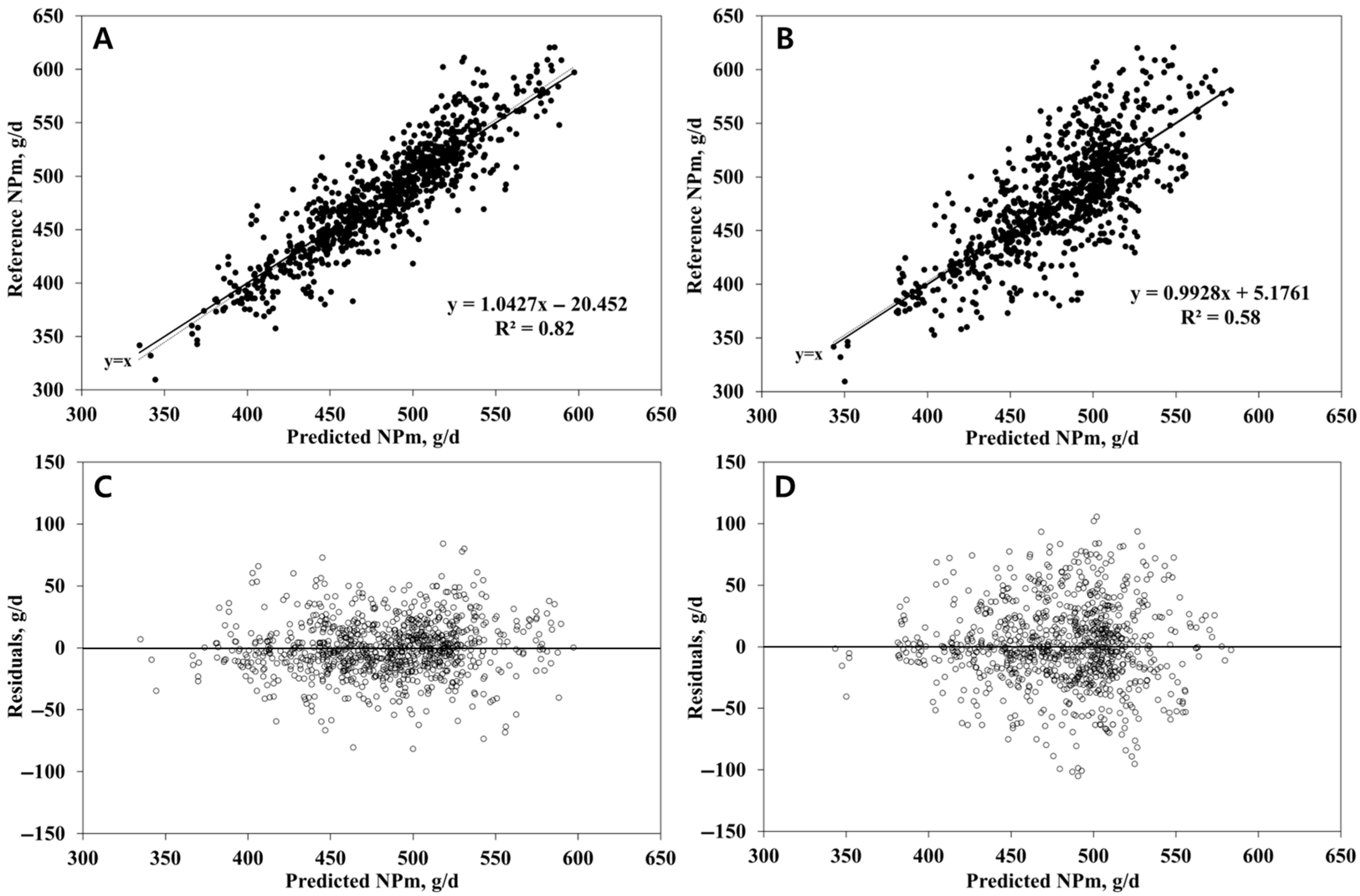
3.1. NPm Prediction

In the dataset constructed for NPm prediction, variables with insufficient observations were excluded to improve model reliability. Specifically, dietary OM, fat, ash, NSC, and starch were removed if the number of observations was fewer than 100 (i.e., <20% of the dataset) or if their co-occurrence with other predictors was insufficient. After filtering, 288 treatment means were retained. Of these, 80% (n = 231) were used for model development, and the remaining 20% (n = 57) were reserved as a hold-out test set. The final input variables, which were MY, DIM, and parity, were selected based on validation performance. The RFR model, tuned with 150 trees and 3 variables per split, outperformed the SVR model (cost = 5, gamma = 1) in predictive ability. As summarized in Table 3, RFR achieved 18% higher R2 than SVR (0.77 vs. 0.65) and reduced prediction error by approximately 6 g/d (RMSEP: 23.35 vs. 29.35 g/d). Agreement with reference values, as reflected by CCC, was also higher for RFR (0.87 vs. 0.80). In both RFR and SVR models, mean and slope biases were statistically non-significant (p > 0.10), while random bias accounted for over 95% of the RMSEP. Model generalizability was evaluated using 10-fold cross-validation on the full dataset (n = 1288) (Table 3). The RFR model maintained its advantage, yielding 41% higher R2 and 11 g/d lower RMSEP compared to SVR (RFR: R2 = 0.82, RMSEP = 22.38 g/d; SVR: R2 = 0.58, RMSEP = 33.34 g/d). CCC values similarly favored RFR (0.89 vs. 0.73). In both RFR and SVR models, random bias accounted for most of the prediction errors, contributing more than 95% of the RMSEP across all validation methods. By contrast, mean and slope bias represented only minor proportions of the error structure. These findings are graphically supported by Figure 1. Variable importance was computed across folds, normalized to sum to one, and averaged. Among the input variables, MY was identified as the most influential predictor for NPm, with a relative importance score of 0.515 ± 0.006, followed by DIM (0.374 ± 0.009) and parity (0.111 ± 0.010).

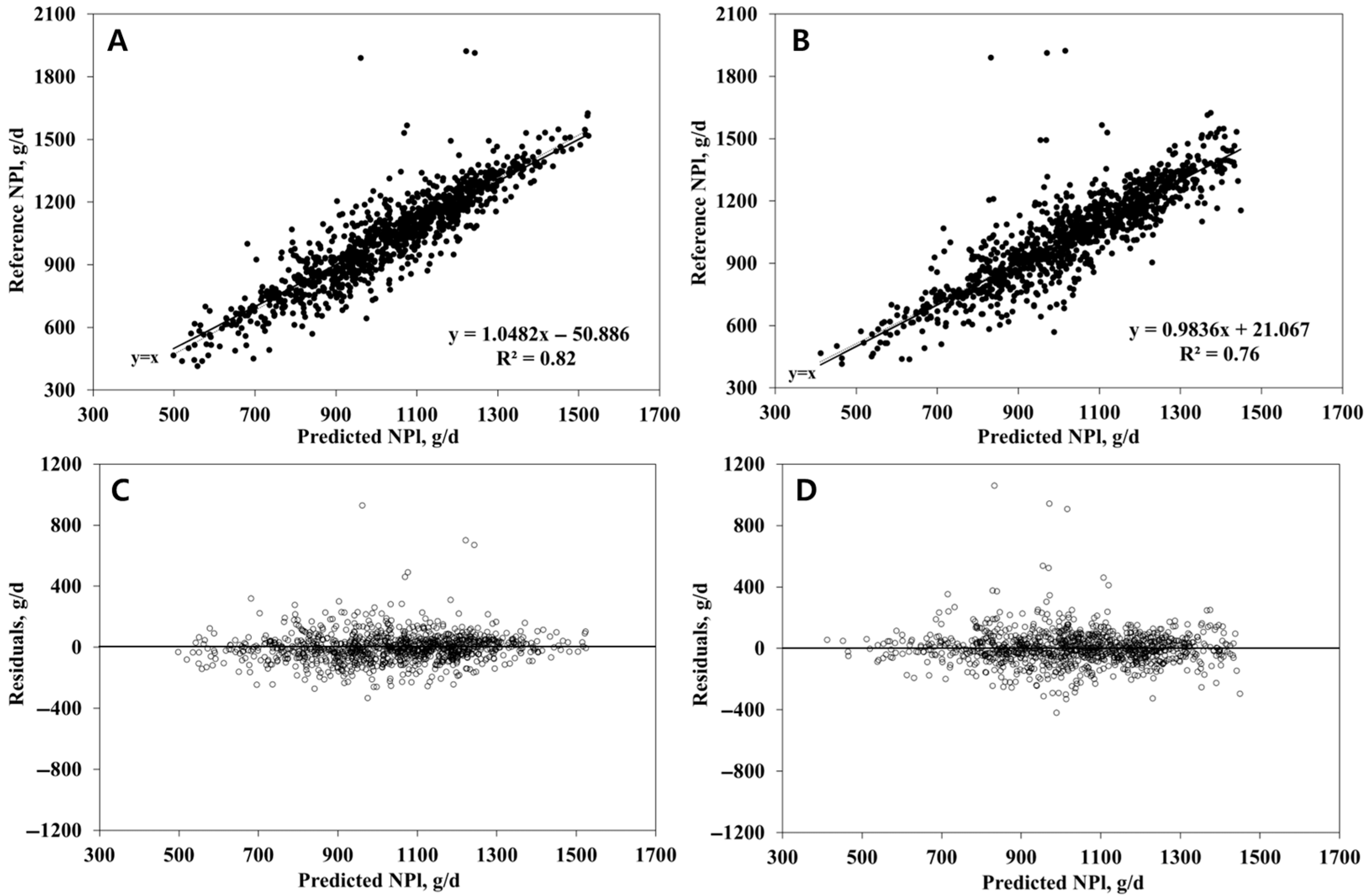
3.2. NPl Prediction

The same exclusion criteria were applied to the NPl dataset. After filtering, 668 treatment means remained, with 80% (n = 534) used for model development and 20% (n = 134) for evaluation. The final selected input variables were DMI, DIM, BW, and dietary CP concentration. The RFR model was set up with ntree = 150 and mtry = 3, and the SVR model used cost = 1 and gamma = 1. As shown in Table 4, both models performed comparably on the test set, with R2 values differing by only 0.01 (0.79 vs. 0.78) and RMSEP values differing by less than 1 g/d (90.45 vs. 91.36 g/d). CCC was identical (0.88), and mean and slope biases were minimal and statistically insignificant (p > 0.10), with random error accounting for over 99% of the total prediction error. In the 10-fold cross-validation (n = 668), RFR achieved higher predictive accuracy, with 8% higher R2 and a 13.9 g/d reduction in RMSEP relative to SVR (RFR: R2 = 0.82, RMSEP = 95.17 g/d; SVR: R2 = 0.76, RMSEP = 109.06 g/d) (Table 4 and Figure 2). CCC was also slightly higher for RFR (0.89 vs. 0.86), and random error contributed more than 98% to the total prediction error in both models. As in the NPl prediction, where variable importance was averaged across folds, DMI emerged as the most dominant predictor (0.526 ± 0.009), followed by DIM (0.236 ± 0.007), BW (0.151 ± 0.004), and CP (0.086 ± 0.004).

4. Discussion

Understanding the NP requirements of lactating dairy cows is a critical component of formulating diets that meet physiological needs while minimizing nitrogen waste [8,34]. Mechanistic models, such as those provided by NASEM (2021), offer structured estimations based on biological principles; however, their practical use can be constrained by computational complexity, rigid input requirements, and limited adaptability to diverse farm conditions. These limitations often arise from fixed equations that do not account for nonlinear interactions among intake, metabolism, and production variables. In response to these challenges, the present study developed machine learning-based sub-models to approximate NASEM-predicted NP requirements using a limited set of biologically meaningful and field-accessible variables. This approach aims to enhance model usability in commercial settings and support more flexible, data-driven decision-making in precision feeding systems.
In the present study, BW was intentionally excluded as an input variable for predicting NPm. Although BW has traditionally been considered the primary determinant in mechanistic models, such as those by NASEM (2021), its removal was aimed at avoiding circular reasoning and exploring the predictive utility of alternative physiological indicators. Variables such as MY, DIM, and parity showed high predictive performance, which may be attributed to their biological relevance as well as potential indirect associations with BW [6,7]. In previous studies, these variables have been used as predictors of body weight [35,36]. However, rather than simply serving as substitutes for body size, these variables may provide more dynamic insights into metabolic activity and stage-specific protein turnover. For instance, MY can reflect the energetic burden of milk synthesis, particularly under negative energy balance during early lactation, when gluconeogenesis and tissue mobilization are intensified. DIM, in turn, serves as a temporal marker of physiological adjustments occurring throughout lactation [37,38].
The observed prominence of MY in the NPm model aligns with these physiological interpretations. Specifically, MY contributed over 50% to variable importance, approximately five times more than parity. This suggests a notable association between productive performance and maintenance protein requirements. Similar relationships have been described in nitrogen balance studies, where MY has been positively associated with both nitrogen output and metabolic protein requirements [8,39]. Furthermore, recent factorial models have emphasized the role of MY in metabolizable protein estimation [40], and data-driven approaches have identified MY as a key predictor of nitrogen excretion in dairy cows [41]. These converging lines of evidence indicate that the predictive prominence of MY in the current model not only reflects statistical structure but also captures fundamental biological processes related to protein maintenance needs.
In contrast, DMI emerged as the most dominant predictor of NPl, followed by DIM, BW, and dietary CP. This pattern is consistent with nutritional mechanisms where nutrient intake and lactation stage directly influence amino acid availability for milk protein synthesis [42,43]. Greater dry matter intake typically increases metabolizable protein supply, thereby enhancing amino acid availability for milk protein synthesis [44]. This physiological linkage supports the strong predictive role of DMI observed in the model. DMI, being a highly dynamic and variable indicator, fluctuates in response to physiological demands, feed availability, and lactation stage [45,46,47]. This makes it a more immediate and informative signal of nutrient supply and metabolic activity, naturally giving it greater influence on protein-output predictions. Similarly, DIM is important in predictive models as it reflects various complex physiological changes across lactation stages [48,49,50]. The combination of DMI and DIM in our model effectively captured both short-term nutritional input and longer-term physiological adaptation. While BW was included, its contribution was relatively modest, likely due to its more static nature compared to dynamic indicators, such as DMI [51,52,53]. Nevertheless, BW provides essential baseline information on the cow’s metabolic scale and protein reserves, offering auxiliary information that enhances prediction robustness. The relatively lower importance of dietary CP may reflect inter-animal variation in nitrogen use efficiency, influenced by factors such as microbial protein synthesis, energy–protein synchronization, and nutrient digestibility [8,54]. Although crude protein is commonly used to estimate nitrogen intake, it does not capture protein digestibility or amino acid composition, which ultimately determine the availability of metabolizable protein for milk synthesis. Nutritional models such as NASEM (2021), which form the basis for our target variables, address these limitations by partitioning dietary protein into degradable and undegradable fractions and explicitly modeling the flows of metabolizable protein and amino acids. However, such detailed inputs are rarely available in routine farm data. In this context, dietary CP was retained in our model as a practical and accessible proxy that enables the machine learning algorithm to capture important aspects of protein nutrition using commonly measured variables. Accordingly, while CP played a less dominant role than DMI or DIM, its inclusion contributed to the comprehensive explanatory power of the model by representing general nitrogen supply. Together, the four selected variables (DMI, DIM, BW, and CP) provided a biologically relevant and complementary set of predictors that supported the robustness and accuracy of the NPl model.
In the present study, the RFR model exhibited predictive accuracy that was consistently comparable to or exceeded that of the SVR model for both NPm and NPl predictions. This outcome presents a notable contrast to our previous findings [22], where the optimal model depended on the specific prediction target. In that study, RFR was superior for estimating RUP, while SVR was significantly more effective for predicting MicN. This divergence between the two studies suggests that the relative performance of these algorithms may be dependent on the intrinsic nature of the target variable. The consistent advantage of the RFR model in the current study could be attributed to the nature of the prediction targets. For this work, the machine learning models were trained to approximate NPm and NPl values that were calculated using the factorial and empirically informed equations of the NASEM (2021) model. The ensemble structure of the RFR algorithm, which partitions data based on conditional rules, appears particularly well-suited for modeling a system defined by a set of fixed equations and interacting components [18,55]. Similar strengths in handling complex interactions have been observed for RFR in other animal science fields [56,57].
Conversely, the better performance of SVR for MicN prediction in our previous study likely reflects a different underlying principle. The synthesis of microbial nitrogen is a fundamental biological process that may follow a smoother and more continuous global function in response to nutrient availability. The SVR algorithm may be better designed to capture such global trends with kernel transformations and global optimization, which can be particularly beneficial for problems involving smoother underlying functions [28,58]. There have been previous studies where SVR has demonstrated good performance in modeling complex systems in the dairy industry. For example, it has been successfully used to predict farm-level electricity consumption [59] and effectively utilized to quantify biological markers such as the somatic cell count in raw milk [60]. This interpretation is further supported by the observation in our previous study that the SVR model for MicN exhibited no significant predictive bias [22], whereas the RFR model did. Taken together, these two studies appear to provide a clear illustration of a model–problem-fit principle. When the task is to approximate a rule-based system, as in the current study, the RFR algorithm seems to be highly effective. When the task is to model a smoother biological process, such as MicN synthesis, the SVR algorithm can be more suitable. These findings are consistent with the broader literature supporting the use of tree-based models in dairy applications. For instance, a systematic review reported that decision tree-based methods were the most frequently applied in dairy production [21]. This suggests that the selection of a machine learning algorithm can be guided by the underlying structure of the problem, enabling the development of robust and flexible tools for applications in dairy nutrition modeling.
The sub-models developed in this study were designed to function as computationally efficient approximators of nutrient requirements as defined by the NASEM (2021) framework rather than to directly predict empirically measured values. This approach offers practical advantages, including compatibility with existing nutrient systems and ease of implementation in precision feeding environments. By using routinely collected variables such as MY, DIM, and DMI, the models operate with low computational demands, making them suitable for real-time dietary decision support. This feature is particularly valuable in diverse production environments where detailed input data required by mechanistic models may be limited. By relying on routinely available variables, the models offer a practical balance between biological relevance and field-level applicability. Moreover, their low computational demands enhance potential integration into real-time monitoring or decision-support tools across various farm settings. More accurate estimates of protein needs may help reduce overfeeding and subsequent nitrogen excretion, thereby contributing to sustainability goals in dairy production. However, important limitations must be acknowledged. Since the models were trained in outputs derived from mechanistic equations, they may inherit any structural biases or simplifications inherent to the NASEM framework. Furthermore, the models have not yet been subjected to external validation, meaning their performance across diverse breeds, management systems, and environmental conditions remains untested. Therefore, the immediate next step is to empirically validate these models using independent, farm-level datasets that include measured nitrogen balance data. While previous research has shown that machine learning models of nitrogen excretion can outperform traditional linear approaches [40], which lends support to the potential of our models, direct validation is essential to confirm their real-world accuracy and robustness.
Ultimately, the development of these models aligns with the broader objective, as discussed in our previous work [22], of advancing toward HIMM. This framework seeks to integrate the biological foundations of mechanistic models with the adaptive, data-driven power of machine learning. The RUP and MicN models from our prior study demonstrate how ML can refine predictions on the supply side of metabolizable protein. Complementarily, the NPm and NPl models from the present study illustrate how ML can create efficient surrogate models for the requirements side. A fully realized HIMM could integrate both types of components, using real-time data to create adaptive, individualized feeding strategies that enhance both productivity and environmental sustainability.

5. Conclusions

In this study, we hypothesized that machine learning models could approximate NASEM (2021)-based predictions of net protein requirements using readily available input variables. The results support this hypothesis: both NPm and NPl models, trained with limited field-accessible data from lactating Holstein dairy cows, achieved high agreement with NASEM-calculated reference values. Specifically, the RFR model explained approximately 80 percent of the variation in both outcomes, with R2 values of 0.82 for NPm and NPl based on 10-fold cross-validation. These findings confirm that ML algorithms, particularly tree-based methods, can serve as effective surrogate approximators of mechanistic nutrient models. Furthermore, the strong performance of models based on dynamic physiological and intake-related variables (e.g., MY and DMI) highlights their practical utility in real-time nutritional decision-making. While these models do not replace mechanistic frameworks, they offer a low-complexity tool compatible with on-farm applications. Future work should validate the models with empirical nitrogen balance data and explore their integration into HIMM to enhance flexibility and adaptability in dairy nutrition management.

Author Contributions

Conceptualization, M.L. and S.S.; methodology, M.L. and L.O.T.; software, M.L.; validation, M.L.; formal analysis, M.L.; investigation, M.L. and D.H.K.; data curation, M.L. and L.O.T.; writing—original draft preparation, M.L.; writing—review and editing, S.S. and D.H.K.; supervision, L.O.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research was partially funded by the National Institute of Animal Science (NIAS), Rural Development Administration (Project No. RS-2022-RD009986; Wanju-gun, Republic of Korea), and the National Animal Nutrition Program (NANP; https://animalnutrition.org/; accessed on 17 October 2023), which is a National Research Support Project (NRSP-9) supported by agInnovation, the State Agricultural Experiment Stations, the Natural Resources Conservation Service, and Hatch Funds provided by the National Institute of Food and Agriculture, U.S. Department of Agriculture, Washington, DC. The NANP also partially provided the feed composition and animal performance datasets used in the analyses of this study. The NANP supports the use and sharing of these datasets and knowledge on feed analysis methods.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors upon request. The NANP dataset is available at https://animalnutrition.org/ (accessed on 17 October 2023).

Conflicts of Interest

The authors declare that they have no conflicts of interest.

References

  1. Capper, J.L.; Cady, R.A.; Bauman, D.E. The environmental impact of dairy production: 1944 compared with 2007. J. Anim. Sci. 2009, 87, 2160–2167. [Google Scholar] [CrossRef] [PubMed]
  2. Eastridge, M.L. Major advances in applied dairy cattle nutrition. J. Dairy Sci. 2006, 89, 1311–1323. [Google Scholar] [CrossRef] [PubMed]
  3. VandeHaar, M.J.; St-Pierre, N. Major advances in nutrition: Relevance to the sustainability of the dairy industry. J. Dairy Sci. 2006, 89, 1280–1291. [Google Scholar] [CrossRef] [PubMed]
  4. Huhtanen, P.; Hristov, A.N. A meta-analysis of the effects of dietary protein concentration and degradability on milk protein yield and milk N efficiency in dairy cows. J. Dairy Sci. 2009, 92, 3222–3232. [Google Scholar] [CrossRef] [PubMed]
  5. Lapierre, H.; Lobley, G.E. Nitrogen recycling in the ruminant: A review. J. Dairy Sci. 2001, 84, E223–E236. [Google Scholar] [CrossRef]
  6. NRC. Nutrient Requirements of Dairy Cattle, 8th ed.; National Academy Press: Washington, DC, USA, 2001. [Google Scholar]
  7. NASEM. Nutrient Requirements of Dairy Cattle; National Academy Press: Washington, DC, USA, 2021. [Google Scholar]
  8. Castillo, A.R.; Kebreab, E.; Beever, D.E.; France, J. A review of efficiency of nitrogen utilisation in lactating dairy cows and its relationship with environmental pollution. J. Anim. Feed Sci. 2000, 9, 1–32. [Google Scholar] [CrossRef]
  9. Kebreab, E.; France, J.; Mills, J.A.N.; Allison, R.; Dijkstra, J. A dynamic model of N metabolism in the lactating dairy cow and an assessment of impact of N excretion on the environment. J. Anim. Sci. 2002, 80, 248–259. [Google Scholar] [CrossRef] [PubMed]
  10. Tedeschi, L.O.; Fox, D.G. The Ruminant Nutrition System: An Applied Model for Predicting Nutrient Requirements and Feed Utilization in Ruminants, 3rd ed.; Kendall Hunt: Dubuque, IA, USA, 2020; Volume 1, Available online: https://he.kendallhunt.com/product/ruminant-nutrition-system-volume-1-hard-cover (accessed on 7 February 2025).
  11. Tedeschi, L.O.; Fox, D.G. The Ruminant Nutrition System: Tables of Equations and Coding, 3rd ed.; Kendall Hunt: Dubuque, IA, USA, 2020; Volume 2, Available online: https://he.kendallhunt.com/product/ruminant-nutrition-system-volume-2-hard-cover (accessed on 7 February 2025).
  12. Allen, M.S. Do more mechanistic models increase accuracy of prediction of metabolisable protein supply in ruminants? Anim. Prod. Sci. 2019, 59, 1991–1998. [Google Scholar] [CrossRef]
  13. Fox, D.G.; Tedeschi, L.O.; Tylutki, T.P.; Russell, J.B.; Van Amburgh, M.E.; Chase, L.E.; Pell, A.N.; Overton, T.R. The Cornell Net Carbohydrate and Protein System model for evaluating herd nutrition and nutrient excretion. Anim. Feed Sci. Technol. 2004, 112, 29–78. [Google Scholar] [CrossRef]
  14. Hanigan, M.D.; Souza, V.C.; Martineau, R.; Daley, V.L.; Kononoff, P. Predicting ruminally undegraded and microbial protein flows from the rumen. J. Dairy Sci. 2021, 104, 8685–8707. [Google Scholar] [CrossRef] [PubMed]
  15. Cockburn, M. Review: Application and prospective discussion of machine learning for the management of dairy farms. Animals 2020, 10, 1690. [Google Scholar] [CrossRef] [PubMed]
  16. De Vries, A.; Bliznyuk, N.; Pinedo, P. Invited Review: Examples and opportunities for artificial intelligence (AI) in dairy farms. Appl. Anim. Sci. 2023, 39, 14–22. [Google Scholar] [CrossRef]
  17. Tedeschi, L.O. ASN-ASAS Symposium: Future of data analytics in nutrition: Mathematical modeling in ruminant nutrition: Approaches and paradigms, extant models, and thoughts for upcoming predictive analytics. J. Anim. Sci. 2019, 97, 1921–1944. [Google Scholar] [CrossRef] [PubMed]
  18. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
  19. Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009; Volume 2. [Google Scholar]
  20. Shine, P.; Murphy, M.D. Over 20 years of machine learning applications on dairy farms: A comprehensive mapping study. Sensors 2022, 22, 52. [Google Scholar] [CrossRef] [PubMed]
  21. Slob, N.; Catal, C.; Kassahun, A. Application of machine learning to improve dairy farm management: A systematic literature review. Prev. Vet. Med. 2021, 187, 105237. [Google Scholar] [CrossRef] [PubMed]
  22. Lee, M.; Kim, D.H.; Seo, S.; Tedeschi, L.O. Development of machine learning models for estimating metabolizable protein supply from feed in lactating dairy cows. Animals 2025, 15, 687. [Google Scholar] [CrossRef] [PubMed]
  23. Tedeschi, L.O. ASAS-NANP Symposium: Mathematical modeling in animal nutrition: The progression of data analytics and artificial intelligence in support of sustainable development in animal science. J. Anim. Sci. 2022, 100, skac111. [Google Scholar] [CrossRef] [PubMed]
  24. Tedeschi, L.O. The prevailing mathematical modeling classifications and paradigms to support the advancement of sustainable animal production. Animal 2023, 17, 100813. [Google Scholar] [CrossRef] [PubMed]
  25. Jeon, S.; Kang, H.; Park, S.; Seo, S. Evaluation of the equations to predict net energy requirement for lactation in the cattle feeding system: Based on the literature database. Agriculture 2022, 12, 654. [Google Scholar] [CrossRef]
  26. RC Team. R: A Language and Environment for Statistical Computing. 2024. Available online: https://www.R-project.org/ (accessed on 14 June 2024).
  27. Burges, C.J.C. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
  28. Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
  29. Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F.; Chang, C.-C.; Lin, C.-C. e1071: Misc Functions of the Department of Statistics, Probability Theory Group, R Package Version 1.7.16; Vienna University of Technology (TU Wien): Vienna, Austria, 2019. [Google Scholar]
  30. Tedeschi, L.O. ASAS-NANP Symposium: Mathematical modeling in animal nutrition: Synthetic database generation for non-normal multivariate distributions: A rank-based method with application to ruminant methane emissions. J. Anim. Sci. 2025, skaf136. [Google Scholar] [CrossRef] [PubMed]
  31. Breiman, L.; Cutler, A.; Liaw, A.; Wiener, M. Randomforest: Breiman and Cutler’s Random Forests for Classification and Regression, R Package Version 4.7.1.2; R Foundation for Statistical Computing: Vienna, Austria, 2002. [Google Scholar]
  32. Tedeschi, L.O. Assessment of the adequacy of mathematical models. Agric. Syst. 2006, 89, 225–247. [Google Scholar] [CrossRef]
  33. Hinkle, D.E.; Wiersma, W.; Jurs, S.G. Applied Statistics for the Behavioral Sciences, 5th ed.; Houghton Mifflin College Division: Boston, MA, USA, 2003; Volume 663. [Google Scholar]
  34. Groff, E.B.; Wu, Z. Milk production and nitrogen excretion of dairy cows fed different amounts of protein and varying proportions of alfalfa and corn silage. J. Dairy Sci. 2005, 88, 3619–3632. [Google Scholar] [CrossRef] [PubMed]
  35. Jeon, E.; Cho, S.; Hwang, S.; Cho, K.; Gondro, C.; Choi, N.-J. Development of prediction model for body weight and energy balance indicators from milk traits in lactating dairy cows based on deep neural networks. J. King Saud Univ.-Sci. 2024, 36, 103008. [Google Scholar] [CrossRef]
  36. Tedde, A.; Grelet, C.; Ho, P.N.; Pryce, J.E.; Hailemariam, D.; Wang, Z.; Plastow, G.; Gengler, N.; Brostaux, Y.; Froidmont, E.; et al. Validation of dairy cow bodyweight prediction using traits easily recorded by dairy herd improvement organizations and its potential improvement using feature selection algorithms. Animals 2021, 11, 1288. [Google Scholar] [CrossRef] [PubMed]
  37. Bjerre-Harpøth, V.; Friggens, N.C.; Thorup, V.M.; Larsen, T.; Damgaard, B.M.; Ingvartsen, K.L.; Moyes, K.M. Metabolic and production profiles of dairy cows in response to decreased nutrient density to increase physiological imbalance at different stages of lactation. J. Dairy Sci. 2012, 95, 2362–2380. [Google Scholar] [CrossRef] [PubMed]
  38. Weber, C.; Hametner, C.; Tuchscherer, A.; Losand, B.; Kanitz, E.; Otten, W.; Sauerwein, H.; Bruckmaier, R.M.; Becker, F.; Kanitz, W.; et al. Hepatic gene expression involved in glucose and lipid metabolism in transition cows: Effects of fat mobilization during early lactation in relation to milk performance and metabolic changes. J. Dairy Sci. 2013, 96, 5670–5681. [Google Scholar] [CrossRef] [PubMed]
  39. Ingvartsen, K.L. Feeding- and management-related diseases in the transition cow: Physiological adaptations around calving and strategies to reduce feeding-related diseases. Anim. Feed Sci. Technol. 2006, 126, 175–213. [Google Scholar] [CrossRef]
  40. Silva, H.M.d.; Oliveira, A.S.d. A new protein requirement system for dairy cows. J. Dairy Sci. 2023, 106, 1757–1772. [Google Scholar] [CrossRef] [PubMed]
  41. Chen, X.; Zheng, H.; Wang, H.; Yan, T. Can machine learning algorithms perform better than multiple linear regression in predicting nitrogen excretion from lactating dairy cows. Sci. Rep. 2022, 12, 12478. [Google Scholar] [CrossRef] [PubMed]
  42. Gross, J.J. Limiting factors for milk production in dairy cows: Perspectives from physiology and nutrition. J. Anim. Sci. 2022, 100, skac044. [Google Scholar] [CrossRef] [PubMed]
  43. Lapierre, H.; Martineau, R.; Hanigan, M.D.; van Lingen, H.J.; Kebreab, E.; Spek, J.W.; Ouellet, D.R. Review: Impact of protein and energy supply on the fate of amino acids from absorption to milk protein in dairy cows. Animal 2020, 14, s87–s102. [Google Scholar] [CrossRef] [PubMed]
  44. Hristov, A.N.; Price, W.J.; Shafii, B. A meta-analysis examining the relationship among dietary factors, dry matter intake, and milk and milk protein yield in dairy cows. J. Dairy Sci. 2004, 87, 2184–2196. [Google Scholar] [CrossRef] [PubMed]
  45. Azizi, O.; Kaufmann, O.; Hasselmann, L. Relationship between feeding behaviour and feed intake of dairy cows depending on their parity and milk yield. Livest. Sci. 2009, 122, 156–161. [Google Scholar] [CrossRef]
  46. Chen, L.; Thorup, V.M.; Kudahl, A.B.; Østergaard, S. Effects of heat stress on feed intake, milk yield, milk composition, and feed efficiency in dairy cows: A meta-analysis. J. Dairy Sci. 2024, 107, 3207–3218. [Google Scholar] [CrossRef] [PubMed]
  47. Rumphorst, T.; Scheu, T.; Koch, C.; Sundrum, A. Inter- and intra-individual variation in the behavior of feed intake on nutrient availability in early lactating dairy cows. Animals 2022, 12, 37. [Google Scholar] [CrossRef] [PubMed]
  48. de Souza, R.A.; Tempelman, R.J.; Allen, M.S.; VandeHaar, M.J. Updating predictions of dry matter intake of lactating dairy cows. J. Dairy Sci. 2019, 102, 7948–7960. [Google Scholar] [CrossRef] [PubMed]
  49. Græsbøll, K.; Kirkeby, C.; Nielsen, S.S.; Halasa, T.; Toft, N.; Christiansen, L.E. Models to estimate lactation curves of milk yield and somatic cell count in dairy cows at the herd level for the use in dimulations and predictive models. Front. Vet. Sci. 2016, 3, 115. [Google Scholar] [CrossRef] [PubMed]
  50. Roseler, D.K.; Fox, D.G.; Chase, L.E.; Pell, A.N.; Stone, W.C. Development and evaluation of equations for prediction of feed intake for lactating Holstein dairy cows. J. Dairy Sci. 1997, 80, 878–893. [Google Scholar] [CrossRef] [PubMed]
  51. Ellis, J.L.; Qiao, F.; Cant, J.P. Prediction of dry matter intake throughout lactation in a dynamic model of dairy cow performance. J. Dairy Sci. 2006, 89, 1558–1570. [Google Scholar] [CrossRef] [PubMed]
  52. Gross, J.J. Dairy cow physiology and production limits. Anim. Front. 2023, 13, 44–50. [Google Scholar] [CrossRef] [PubMed]
  53. Poncheki, J.K.; Canha, M.L.S.; Viechnieski, S.L.; Almeida, R.d. Analysis of daily body weight of dairy cows in early lactation and associations with productive and reproductive performance. Rev. Bras. Zootec. 2015, 44, 187–192. [Google Scholar] [CrossRef]
  54. Roche, J.R.; Bell, A.W.; Overton, T.R.; Loor, J.J. Nutritional management of the transition cow in the 21st century—A paradigm shift in thinking. Anim. Prod. Sci. 2013, 53, 1000–1023. [Google Scholar] [CrossRef]
  55. Grömping, U. Variable importance assessment in regression: Linear regression versus random forest. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
  56. Hamadani, A.; Ganai, N.A.; Mudasir, S.; Shanaz, S.; Alam, S.; Hussain, I. Comparison of artificial intelligence algorithms and their ranking for the prediction of genetic merit in sheep. Sci. Rep. 2022, 12, 18726. [Google Scholar] [CrossRef] [PubMed]
  57. Kozaklı, Ö.; Ceyhan, A.; Noyan, M. Comparison of machine learning algorithms and multiple linear regression for live weight estimation of Akkaraman lambs. Trop. Anim. Health Prod. 2024, 56, 250. [Google Scholar] [CrossRef] [PubMed]
  58. Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
  59. Shine, P.; Scully, T.; Upton, J.; Murphy, M.D. Annual electricity consumption prediction and future expansion analysis on dairy farms using a support vector machine. Appl. Energy 2019, 250, 1110–1119. [Google Scholar] [CrossRef]
  60. Zhu, Z.; Zhu, X.; Guo, W. Quantitatively determining the somatic cell count of raw milk using dielectric spectra and support vector regression. J. Dairy Sci. 2022, 105, 772–781. [Google Scholar] [CrossRef] [PubMed]
Animals 15 02127 g001
Figure 1. Plots of the reference (upper) and residual values (reference minus predicted values, lower) versus the model-predicted net protein requirement for maintenance (g/d), based on predictions (n = 1288) from 10-fold cross-validation. (A,C) are plots of a model developed with a random forest regression algorithm. (B,D) are plots of a model developed with a support vector regression algorithm.
Figure 1. Plots of the reference (upper) and residual values (reference minus predicted values, lower) versus the model-predicted net protein requirement for maintenance (g/d), based on predictions (n = 1288) from 10-fold cross-validation. (A,C) are plots of a model developed with a random forest regression algorithm. (B,D) are plots of a model developed with a support vector regression algorithm.
Animals 15 02127 g001
Animals 15 02127 g002
Figure 2. Plots of the reference (upper) and residual values (reference minus predicted values, lower) versus the model-predicted net protein requirement for lactation (g/d), based on predictions (n = 668) from 10-fold cross-validation. (A,C) are plots of a model developed with a random forest regression algorithm. (B,D) are plots of a model developed with a support vector regression algorithm.
Figure 2. Plots of the reference (upper) and residual values (reference minus predicted values, lower) versus the model-predicted net protein requirement for lactation (g/d), based on predictions (n = 668) from 10-fold cross-validation. (A,C) are plots of a model developed with a random forest regression algorithm. (B,D) are plots of a model developed with a support vector regression algorithm.
Animals 15 02127 g002
Table 1. Descriptive statistics of the dataset for net protein requirement for maintenance modeling.
Table 1. Descriptive statistics of the dataset for net protein requirement for maintenance modeling.
VariablesnMeanMedianMinMax
No. of articles323
No. of treatments1288
No. of animals per study15,17647.04.0384.045.15
No. of animals per treatment15,17611.82.052.09.10
Animal information
      Days in milk (day)1093105.51.0323.059.50
      Parity10841.81.02.00.28
      Body weight (kg)1288635.1476.0861.958.56
      Dry matter intake (kg/d)128822.411.332.03.70
      Milk yield (kg/d)125134.310.258.58.17
Dietary chemical composition (% DM)
      Dry matter (% as-fed)76753.913.596.312.17
      Organic matter78792.346.198.92.73
      Crude protein128016.69.329.61.96
      Neutral detergent fiber128832.817.660.85.03
      Acidic detergent fiber95120.48.839.73.78
      Fat6523.90.38.91.22
      Ash6917.41.116.51.61
      Non-starch carbohydrate52739.416.851.25.52
      Starch76524.50.247.66.64
Net protein requirements for maintenance (g/d)1288480.3309.7621.152.24
Table 2. Descriptive statistics of the dataset for net protein requirement for lactation modeling.
Table 2. Descriptive statistics of the dataset for net protein requirement for lactation modeling.
VariablesnMeanMedianMinMax
No. of articles332
No. of treatments1584
No. of animals per study18,93148.44.0777.056.72
No. of animals per treatment18,93112.02.058.09.72
Animal information
      Days in milk (day)1304100.41.0323.061.15
      Parity13411.91.02.00.28
      Body weight (kg)1352630.3476.0861.959.35
      Dry matter intake (kg/d)158422.110.832.03.73
      Milk yield (kg/d)158433.910.258.58.07
Dietary chemical composition (% DM)
      Dry matter (% as-fed)93253.313.596.311.62
      Organic matter90992.446.198.92.63
      Crude protein151016.59.329.61.95
      Neutral detergent fiber139232.921.060.84.81
      Acidic detergent fiber110320.410.361.63.71
      Fat7243.90.38.91.20
      Ash7567.31.116.51.56
      Non-starch carbohydrate59039.516.851.25.30
      Starch87224.80.247.66.68
Net protein requirements for lactation (g/d)15841014.9357.91923.7234.26
Table 3. Performance of net protein requirement for maintenance (g/d) prediction models developed using random forest regression and support vector regression algorithms, evaluated by test set prediction and 10-fold cross-validation.
Table 3. Performance of net protein requirement for maintenance (g/d) prediction models developed using random forest regression and support vector regression algorithms, evaluated by test set prediction and 10-fold cross-validation.
RFRSVR
ModelHold-Out 110-Fold CV 2Hold-Out10-Fold CV
R20.770.820.650.58
RMSEP, g/d23.3522.3829.3533.34
Mean bias (% RMSEP) 30.33.40.12.4
Slope bias (% RMSEP) 30.31.52.80.1
Random bias (% RMSEP)99.495.197.197.5
CCC0.870.890.800.73
RFR, random forest regression; SVR, support vector regression; NASEM, NRC dairy (2021); RMSEP, root mean square error of prediction; CCC, concordance correlation coefficient. 1 Hold-out evaluation: performance on an independent 20% test set (n = 57). 2 10-fold cross-validation: cross-validation results on the full dataset (n = 1288) using final selected variables. 3 There were no statistically significant mean and slope biases (p > 0.10).
Table 4. Performance of net protein requirement for lactation (g/d) prediction models developed using random forest regression and support vector regression algorithms, evaluated by test set prediction and 10-fold cross-validation.
Table 4. Performance of net protein requirement for lactation (g/d) prediction models developed using random forest regression and support vector regression algorithms, evaluated by test set prediction and 10-fold cross-validation.
RFRSVR
ModelHold-Out 110-Fold CV 2Hold-Out10-Fold CV
R20.790.820.780.76
RMSEP, g/d90.4595.1791.36109.06
Mean Bias (% RMSEP) 30.00.40.30.8
Slope Bias (% RMSEP) 30.11.20.11.0
Random Bias (% RMSEP)99.998.499.698.2
CCC0.880.890.880.86
RFR, random forest regression; SVR, support vector regression; NASEM, NRC dairy (2021); RMSEP, root mean square error of prediction; CCC, concordance correlation coefficient. 1 Hold-out evaluation: performance on an independent 20% test set (n = 57). 2 10-fold cross-validation: cross-validation results on the full dataset (n = 668) using final selected variables. 3 There were no statistically significant mean and slope biases (p > 0.10).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Lee, M.; Kim, D.H.; Seo, S.; Tedeschi, L.O. Development of Machine Learning-Based Sub-Models for Predicting Net Protein Requirements in Lactating Dairy Cows. Animals 2025, 15, 2127. https://doi.org/10.3390/ani15142127

AMA Style

Lee M, Kim DH, Seo S, Tedeschi LO. Development of Machine Learning-Based Sub-Models for Predicting Net Protein Requirements in Lactating Dairy Cows. Animals. 2025; 15(14):2127. https://doi.org/10.3390/ani15142127

Chicago/Turabian Style

Lee, Mingyung, Dong Hyeon Kim, Seongwon Seo, and Luis O. Tedeschi. 2025. "Development of Machine Learning-Based Sub-Models for Predicting Net Protein Requirements in Lactating Dairy Cows" Animals 15, no. 14: 2127. https://doi.org/10.3390/ani15142127

APA Style

Lee, M., Kim, D. H., Seo, S., & Tedeschi, L. O. (2025). Development of Machine Learning-Based Sub-Models for Predicting Net Protein Requirements in Lactating Dairy Cows. Animals, 15(14), 2127. https://doi.org/10.3390/ani15142127

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop