A Scoping Review of Mathematical Models Used to Investigate the Role of Dogs in Chagas Disease Transmission
Abstract
Simple Summary
Abstract
1. Introduction
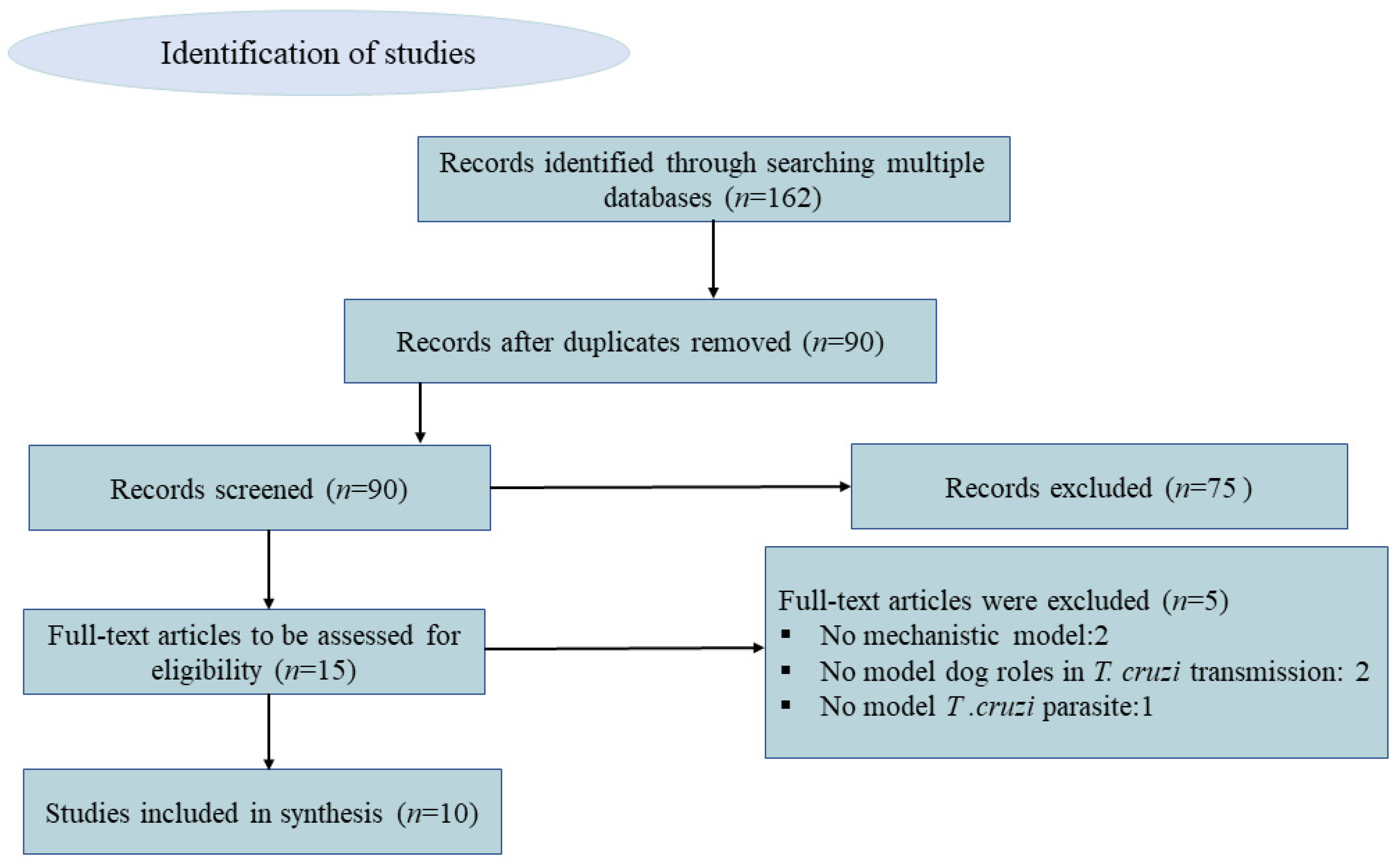
2. Methods
Literature Search
3. Results
3.1. Purpose of the Modeling Articles
3.2. Mathematical Models
3.3. Transmission Routes of Trypanosoma cruzi
3.4. Model Parameterization
3.5. Reproductive Numbers
3.6. Key Outcomes of the Modeling Studies
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gürtler, R.E.; Cardinal, M.V. Dogs and Their Role in the Eco-Epidemiology of Chagas Disease. In Dog Parasites Endangering Human Health; Parasitology Research Monographs; Springer International Publishing: Cham, Switzerland, 2020; pp. 73–106. [Google Scholar] [CrossRef]
- Kribs-Zaleta, C. Estimating Contact Process Saturation in Sylvatic Transmission of Trypanosoma cruzi in the United States. PLoS Negl. Trop. Dis. 2010, 4, e656. [Google Scholar] [CrossRef] [PubMed]
- Klotz, J.H.; Dorn, P.L.; Logan, J.L.; Stevens, L.; Pinnas, J.L.; Schmidt, J.O.; Klotz, S.A. “Kissing Bugs”: Potential Disease Vectors and Cause of Anaphylaxis. Clin. Infect. Dis. 2010, 50, 1629–1634. [Google Scholar] [CrossRef]
- Jansen, A.M.; Xavier, S.C.C.; Roque, A.L.R. Ecological aspects of Trypanosoma cruzi. In American Trypanosomiasis Chagas Disease; Elsevier: Amsterdam, The Netherlands, 2017; pp. 243–264. [Google Scholar] [CrossRef]
- Assembly 72 World Health. World Chagas Disease Day: Report by the Director-General. 1 Jan 2019. Available online: https://apps.who.int/iris/handle/10665/328955 (accessed on 28 October 2022).
- Bennett, C. Chagas Disease Surveillance Activities—Seven States, 2017. MMWR Morb. Mortal. Wkly. Rep. 2018, 67, 738–741. [Google Scholar] [CrossRef] [PubMed]
- Gurtler, R.E.; Cohen, J.E.; Cecere, M.C.; Chuit, R. Shifting Host Choices of the Vector of Chagas Disease, Triatoma Infestans, in Relation to the Availability of Host in Houses in North-West Argentina. J. Appl. Ecol. 1997, 34, 699. [Google Scholar] [CrossRef]
- Macpherson, C.N.L. Dog zoonoses and human health: A global perspective—Mini Review. CABI Rev. 2013, 2013, 1–2. [Google Scholar] [CrossRef]
- Gürtler, R.E.; del Pilar Fernández, M.; Cardinal, M.V. Eco-Epidemiology of Vector-Borne Transmission of Trypanosoma cruzi in Domestic Habitats. In Triatominae—The Biology of Chagas Disease Vectors; Springer International Publishing: Cham, Switzerland, 2021; pp. 447–489. [Google Scholar] [CrossRef]
- Gürtler, R.E.; Cardinal, M.V. Reservoir host competence and the role of domestic and commensal hosts in the transmission of Trypanosoma cruzi. Acta Trop. 2015, 151, 32–50. [Google Scholar] [CrossRef]
- Gürtler, R.E.; Cecere, M.C.; Vázquez-Prokopec, G.M.; Ceballos, L.A.; Gurevitz, J.M.; Fernández, M.d.P.; Kitron, U.; Cohen, J.E. Domestic Animal Hosts Strongly Influence Human-Feeding Rates of the Chagas Disease Vector Triatoma infestans in Argentina. PLoS Negl. Trop. Dis. 2014, 8, e2894. [Google Scholar] [CrossRef]
- Curtis-Robles, R.; Meyers, A.C.; Auckland, L.D.; Zecca, I.B.; Skiles, R.; Hamer, S.A. Parasitic interactions among Trypanosoma cruzi, triatomine vectors, domestic animals, and wildlife in Big Bend National Park along the Texas-Mexico border. Acta Trop. 2018, 188, 225–233. [Google Scholar] [CrossRef]
- Kjos, S.A.; Marcet, P.L.; Yabsley, M.J.; Kitron, U.; Snowden, K.F.; Logan, K.S.; Barnes, J.C.; Dotson, E.M. Identification of Bloodmeal Sources and Trypanosoma cruzi Infection in Triatomine Bugs (Hemiptera: Reduviidae) from Residential Settings in Texas, the United States. J. Med. Entomol. 2013, 50, 1126–1139. [Google Scholar] [CrossRef]
- Ibáñez-Cervantes, G.; Martínez-Ibarra, A.; Nogueda-Torres, B.; López-Orduña, E.; Alonso, A.L.; Perea, C.; Maldonado, T.; Hernández, J.M.; León-Avila, G. Identification by Q-PCR of Trypanosoma cruzi lineage and determination of blood meal sources in triatomine gut samples in México. Parasitol. Int. 2013, 62, 36–43. [Google Scholar] [CrossRef]
- Villalobos, G.; de la Torre, P.; Laclette, J.P.; Espinoza, B.; Martínez-Hernández, F. Entomological Indices, Feeding Sources, and Molecular Identification of Triatoma phyllosoma (Hemiptera: Reduviidae) One of the Main Vectors of Chagas Disease in the Istmo de Tehuantepec, Oaxaca, Mexico. Am. J. Trop. Med. Hyg. 2011, 85, 490–497. [Google Scholar] [CrossRef]
- Zárate, L.G.; Zárate, R.J.; Tempelis, C.H.; Goldsmith, R.S. The Biology and Behavior of Triatoma Barberi (Hemiptera: Reduviidae) in Mexico: I. Blood meal sources and infection with Trypanosoma cruzi. J. Med. Entomol. 1980, 17, 103–116. [Google Scholar] [CrossRef]
- Grassly, N.C.; Fraser, C. Mathematical models of infectious disease transmission. Nat. Rev. Microbiol. 2008, 6, 477–487. [Google Scholar] [CrossRef] [PubMed]
- Koff, R.S. Infectious diseases of humans: Dynamics and control. By, R.M. Anderson and R.M. May, 757 pp. Oxford: Oxford University Press, 1991. $95.00. Hepatology 1992, 15, 169. [Google Scholar] [CrossRef]
- Glasser, J. Mathematical Modeling and Public Policy: Responding to Health Crises. Emerg. Infect. Dis. 2004, 10, 2050–2051. [Google Scholar] [CrossRef] [PubMed]
- Ross, S. Report on the Prevention of Malaria in Mauritiusrit; Waterlow & Sons Limited: London, UK, 1908. [Google Scholar]
- Ross, S. The Prevention of Malaria; Dutton: New York, NY, USA, 1911. [Google Scholar]
- Smith, D.L.; Battle, K.E.; Hay, S.I.; Barker, C.M.; Scott, T.W.; McKenzie, F.E. Ross, Macdonald, and a Theory for the Dynamics and Control of Mosquito-Transmitted Pathogens. PLoS Pathog. 2012, 8, e1002588. [Google Scholar] [CrossRef]
- Heesterbeek, H.; Anderson, R.M.; Andreasen, V.; Bansal, S.; De Angelis, D.; Dye, C.; Eames, K.T.D.; Edmunds, W.J.; Frost, S.D.W.; Funk, S.; et al. Modeling infectious disease dynamics in the complex landscape of global health. Science 2015, 347, aaa4339. [Google Scholar] [CrossRef]
- Reiner, R.C.; Perkins, T.A.; Barker, C.M.; Niu, T.; Chaves, L.F.; Ellis, A.M.; George, D.B.; Le Menach, A.; Pulliam, J.R.C.; Bisanzio, D.; et al. A systematic review of mathematical models of mosquito-borne pathogen transmission: 1970–2010. J. R. Soc. Interface 2013, 10, 20120921. [Google Scholar] [CrossRef]
- Cruz-Pacheco, G.; Esteva, L.; Vargas, C. Control measures for Chagas disease. Math. Biosci. 2012, 237, 49–60. [Google Scholar] [CrossRef]
- Cohen, J.E.; Gürtler, R.E. Modeling Household Transmission of American Trypanosomiasis. Science 2001, 293, 694–698. [Google Scholar] [CrossRef]
- Flores-Ferrer, A.; Waleckx, E.; Rascalou, G.; Dumonteil, E.; Gourbière, S. Trypanosoma cruzi transmission dynamics in a synanthropic and domesticated host community. PLoS Negl. Trop. Dis. 2019, 13, e0007902. [Google Scholar] [CrossRef] [PubMed]
- Spagnuolo, A.M.; Shillor, M.; Stryker, G.A. A model for Chagas disease with controlled spraying. J. Biol. Dyn. 2011, 5, 299–317. [Google Scholar] [CrossRef]
- Spagnuolo, A.M.; Shillor, M.; Kingsland, L.; Thatcher, A.; Toeniskoetter, M.; Wood, B. A logistic delay differential equation model for Chagas disease with interrupted spraying schedules. J. Biol. Dyn. 2012, 6, 377–394. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.Y.; Bartsch, S.M.; Skrip, L.; Hertenstein, D.L.; Avelis, C.M.; Mbah, M.N.; Tilchin, C.; Dumonteil, E.O.; Galvani, A. Are the London Declaration’s 2020 goals sufficient to control Chagas disease? Modeling scenarios for the Yucatan Peninsula. PLoS Negl. Trop. Dis. 2018, 12, e0006337. [Google Scholar] [CrossRef]
- Fabrizio, M.C.; Schweigmann, N.J.; Bartoloni, N.J. Modelling inter-human transmission dynamics of Chagas disease: Analysis and application. Parasitology 2014, 141, 837–848. [Google Scholar] [CrossRef]
- Fabrizio, M.C.; Schweigmann, N.J.; Bartoloni, N.J. Analysis of the transmission of Trypanosoma cruzi infection through hosts and vectors. Parasitology 2016, 143, 1168–1178. [Google Scholar] [CrossRef]
- Coffield, D.J., Jr.; Spagnuolo, A.M.; Shillor, M.; Mema, E.; Pell, B.; Pruzinsky, A.; Zetye, A. A Model for Chagas Disease with Oral and Congenital Transmission. PLoS ONE 2013, 8, e67267. [Google Scholar] [CrossRef]
- Bartsch, S.M.; Peterson, J.K.; Hertenstein, D.L.; Skrip, L.; Ndeffo-Mbah, M.; Galvani, A.P.; Dobson, A.P.; Lee, B.Y. Comparison and validation of two computational models of Chagas disease: A thirty year perspective from Venezuela. Epidemics 2017, 18, 81–91. [Google Scholar] [CrossRef]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Ndeffo-Mbah, M.L.; Vigliotti, V.S.; Skrip, L.A.; Dolan, K.; Galvani, A.P. Dynamic Models of Infectious Disease Transmission in Prisons and the General Population. Epidemiol. Rev. 2018, 40, 40–57. [Google Scholar] [CrossRef]
- Hunter, E.; Mac Namee, B.; Kelleher, J.D. A Comparison of Agent-Based Models and Equation Based Models for Infectious Disease Epidemiology. In Proceedings of the 26th AIAI Irish Conference on Artificial Intelligence and Cognitive Science, Dublin, Ireland, 6–7 December 2018. [Google Scholar] [CrossRef]
- Smith, N.R.; Trauer, J.M.; Gambhir, M.; Richards, J.S.; Maude, R.; Keith, J.; Flegg, J. Agent-based models of malaria transmission: A systematic review. Malar. J. 2018, 17, 299. [Google Scholar] [CrossRef] [PubMed]
- Heffernan, J.M.; Smith, R.J.; Wahl, L.M. Perspectives on the basic reproductive ratio. J. R. Soc. Interface 2005, 2, 281–293. [Google Scholar] [CrossRef] [PubMed]
- Roberts, M.G.; Heesterbeek, J.A.P. A new method for estimating the effort required to control an infectious disease. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2003, 270, 1359–1364. [Google Scholar] [CrossRef] [PubMed]
- Heesterbeek, J.A.P.; Roberts, M.G. The type-reproduction number T in models for infectious disease control. Math. Biosci. 2007, 206, 3–10. [Google Scholar] [CrossRef] [PubMed]
| Transmission Routes | Population Involved | Settings | Author |
|---|---|---|---|
| Vectorial | Triatomines, humans & dogs | Domestic & Peridomestic | Cohen & Gurtler [26], Flores-Ferre et al. [27], Spagnuolo et al. [28,29], Lee et al. [30] |
| Domestic | Cruz-Pacheco et al. [25], Coffield Jr et al. [33], Fabrizio et al. [31,32], Bartsch et al. [34] | ||
| Congenital | Humans and dogs | Domestic & Peridomestic | Lee et al. [30] |
| Humans only | Domestic | Cruz-Pacheco et al. [25], Coffield Jr et al. [33], Fabrizio et al. [31,32] | |
| Transfusion | Humans only | Domestic & Peridomestic | Lee et al. [30] |
| Domestic | Fabrizio et al. [31,32] | ||
| Oral consumption | Dogs only | Domestic | Coffield Jr et al. [33] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiatsonu, E.; Busselman, R.E.; Ndeffo-Mbah, M.L. A Scoping Review of Mathematical Models Used to Investigate the Role of Dogs in Chagas Disease Transmission. Animals 2023, 13, 555. https://doi.org/10.3390/ani13040555
Fiatsonu E, Busselman RE, Ndeffo-Mbah ML. A Scoping Review of Mathematical Models Used to Investigate the Role of Dogs in Chagas Disease Transmission. Animals. 2023; 13(4):555. https://doi.org/10.3390/ani13040555
Chicago/Turabian StyleFiatsonu, Edem, Rachel E. Busselman, and Martial L. Ndeffo-Mbah. 2023. "A Scoping Review of Mathematical Models Used to Investigate the Role of Dogs in Chagas Disease Transmission" Animals 13, no. 4: 555. https://doi.org/10.3390/ani13040555
APA StyleFiatsonu, E., Busselman, R. E., & Ndeffo-Mbah, M. L. (2023). A Scoping Review of Mathematical Models Used to Investigate the Role of Dogs in Chagas Disease Transmission. Animals, 13(4), 555. https://doi.org/10.3390/ani13040555






